Redes neurais em trading: Análise de nuvem de pontos (PointNet)

Introdução

As nuvens de pontos são estruturas simples e padronizadas que evitam a heterogeneidade combinatória e a complexidade das malhas. Como não têm uma forma convencional, a maioria dos pesquisadores geralmente transforma esses conjuntos de dados em grades voxel 3D convencionais ou conjuntos de imagens antes de passá-los para a arquitetura da rede profunda. No entanto, essa conversão torna os dados resultantes excessivamente volumosos e pode introduzir artefatos de quantização, que muitas vezes ocultam as invariâncias naturais dos dados.

Por esse motivo, alguns pesquisadores recorreram a outra representação de dados para geometria 3D, utilizando apenas a nuvem de pontos. Modelos que operam com essa representação dos dados brutos devem considerar que a nuvem de pontos é um conjunto de pontos e é invariante a permutações de seus elementos. Isso exige uma certa simetrização nos cálculos do modelo.

Uma das soluções para esse problema é descrita no artigo "PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation". O modelo apresentado, chamado PointNet, é uma solução arquitetônica unificada que aceita diretamente a nuvem de pontos como entrada e retorna tanto os rótulos de classe para todo o conjunto de dados quanto os rótulos de segmentos (partes) para cada ponto dos dados brutos.

A arquitetura básica do modelo é surpreendentemente simples. Nos estágios iniciais, cada ponto é processado de maneira idêntica e independente. Na configuração padrão, cada ponto é representado apenas por suas três coordenadas (x, y, z). Medidas adicionais podem ser incorporadas ao calcular normais e outros objetos locais ou globais.

O ponto-chave da abordagem do PointNet é o uso de uma única função simétrica, o MaxPooling Essencialmente, a rede aprende um conjunto de funções de otimização que selecionam os objetos mais interessantes ou informativos na nuvem de pontos e codificam o motivo da escolha. Já as camadas totalmente conectadas na saída do modelo agregam esses valores ótimos em um descritor global da forma completa.

Esse formato dos dados brutos permite a aplicação fácil de transformações rígidas ou afins, pois cada ponto é transformado de maneira independente. Por esse motivo, os autores do método adicionam um modelo de transformação espacial dependente dos dados, que tenta canonizá-los antes de serem processados no PointNet, aumentando ainda mais a eficiência da solução.

1. Algoritmo PointNet

Os autores do método PointNet desenvolveram um framework de aprendizado profundo que utiliza diretamente conjuntos não ordenados de pontos como dados brutos. A nuvem de pontos é representada como um conjunto de pontos 3D {Pi|i=1,…,n}, onde cada ponto Pi é um vetor contendo suas coordenadas (x, y, z), além de canais adicionais de características, como cor e outros atributos.

Os dados brutos do modelo consistem em um subconjunto de pontos do espaço euclidiano que possuem três propriedades principais:

• Não ordenados. Diferentemente das matrizes de pixels em imagens, a nuvem de pontos é um conjunto de elementos sem uma ordem definida. Em outras palavras, um modelo que recebe um conjunto de N pontos 3D deve ser invariante a N! permutações na ordem de entrada do conjunto de dados brutos.
• Interação entre os pontos. Os pontos são extraídos de um espaço com métrica de distância. Isso significa que os pontos não são isolados e que pontos vizinhos formam subconjuntos significativos. Portanto, o modelo deve ser capaz de capturar estruturas locais a partir de pontos próximos, bem como as interações combinatórias entre elas.
• Invariância a transformações. Como um objeto geométrico, a representação aprendida do conjunto de pontos deve ser invariante a certas transformações. Por exemplo, a rotação e a translação simultâneas dos pontos não devem alterar nem a categoria global da nuvem de pontos nem sua segmentação.

A arquitetura do PointNet foi construída de modo que os modelos de classificação e segmentação de dados compartilhem grande parte de suas estruturas. Ela é composta por três módulos principais:

• uma camada de pooling máximo como uma função simétrica para agregar informações de todos os pontos,
• uma estrutura para combinação de dados locais e globais,
• duas redes de alinhamento conjuntas, que alinham tanto os pontos brutos quanto os objetos pontuais.

Para tornar o modelo invariante à permutação dos dados brutos, existem três estratégias:

1. ordenar os dados brutos em uma sequência canônica;
2. usar os dados brutos como uma sequência para treinar uma RNN, garantindo que o conjunto de treinamento inclua todas as possíveis permutações;
3. utilizar uma função simétrica simples para agregar informações de cada ponto. Quando uma função simétrica recebe n vetores como entrada e gera um novo vetor invariante à ordem de entrada.

A ordenação dos dados brutos pode parecer uma solução simples. No entanto, no espaço multidimensional, não existe uma ordenação estável diante de pequenas perturbações nos pontos, em sentido geral. Portanto, a ordenação não resolve completamente o problema da disposição dos dados. Além disso, o modelo tem dificuldade em aprender uma correspondência consistente entre os dados brutos e os resultados esperados. Nos experimentos realizados pelos autores do método, foi observado que a aplicação de uma MLP diretamente a um conjunto ordenado de pontos apresentou um desempenho ruim, ainda que ligeiramente melhor do que o processamento direto de dados brutos não ordenados.

Embora as RNNs apresentem uma boa resistência à ordem dos dados brutos em sequências curtas (de algumas dezenas de elementos), elas são difíceis de escalar para conjuntos com milhares de elementos. No artigo original, os autores também demonstraram empiricamente que um modelo baseado em RNN não supera o algoritmo proposto pelo PointNet.

A ideia central do PointNet consiste em aproximar uma função geral definida sobre um conjunto de pontos, aplicando uma função simétrica aos elementos transformados desse conjunto.

O módulo básico proposto empiricamente pelos autores do método é extremamente simples: inicialmente, a função h é aproximadamente estimada utilizando uma MLP, enquanto g é obtida por uma composição de uma função de variável única e a função de pooling máximo. A eficácia dessa abordagem foi confirmada por meio de experimentos. A partir da coleta de funções h, é possível aprender uma série de funções f para capturar diferentes propriedades do conjunto de dados brutos.

Apesar da simplicidade do módulo principal, ele possui características interessantes e pode alcançar alto desempenho em diversas aplicações.

Na saída do módulo chave proposto, forma-se um vetor [f1,…,fK], que representa a assinatura global do conjunto de dados brutos. A partir disso, é possível treinar facilmente um classificador SVM ou MLP utilizando a forma dos atributos globais para realizar a classificação. No entanto, a segmentação ponto a ponto exige a combinação de informações locais e globais. Esse objetivo pode ser alcançado de maneira simples, porém altamente eficaz.

Após calcular o vetor de atributos globais da nuvem de pontos, os autores do PointNet propõem devolvê-lo a cada objeto pontual, concatenando o objeto global a cada um deles. Em seguida, são extraídas novas características dos pontos com base nos objetos pontuais combinados (dessa vez, cada característica leva em conta tanto as informações locais quanto as globais).

Com essa modificação, o PointNet consegue prever a quantidade de pontos por unidade, considerando tanto a geometria local quanto a semântica global. Por exemplo, é possível prever com precisão as normais de cada ponto, confirmando que o modelo é capaz de sintetizar informações da vizinhança local do ponto. Os resultados experimentais apresentados pelos autores do método demonstram que o modelo proposto pode alcançar o estado da arte na segmentação de partes de formas e na segmentação de cenas.

A rotulagem semântica da nuvem de pontos deve ser invariante caso a nuvem sofra determinadas transformações geométricas, como transformações rígidas. Portanto, os autores do método esperam que a representação aprendida para o conjunto de pontos permaneça invariante a essas transformações.

Uma solução natural para isso é alinhar todo o conjunto de dados brutos a um espaço canônico antes da extração de características. O formato de entrada das nuvens de pontos permite alcançar esse objetivo de maneira simples. Basta prever a matriz de transformação afim por meio de uma minirrede (T-net) e aplicá-la diretamente às coordenadas dos pontos brutos. A própria minirrede se assemelha à rede principal e é composta por módulos básicos de extração de características independentes por ponto, pooling máximo e camadas totalmente conectadas.

ssa ideia pode ser estendida ao alinhamento do espaço de características. É possível inserir outra rede de alinhamento nos objetos pontuais e prever uma matriz de transformação de características para alinhar os objetos provenientes de diferentes nuvens de pontos brutas. No entanto, a matriz de transformação no espaço de características tem uma dimensão muito maior do que a matriz de transformação espacial, o que aumenta significativamente a complexidade da otimização. Por esse motivo, os autores do método adicionam um termo de regularização ao erro na fase de treinamento do SoftMax. Para isso, restringem a matriz de transformação de características para que ela se aproxime de uma matriz ortogonal:

onde A é a matriz de alinhamento de características prevista pela minirrede.

Uma transformação ortogonal não resulta na perda de informações na entrada, tornando-se, assim, desejável. Ao adicionar o termo de regularização, os autores do PointNet descobriram que a otimização se torna mais estável e o modelo atinge um melhor desempenho.

Abaixo, é apresentada a visualização do método PointNet elaborada pelos autores.

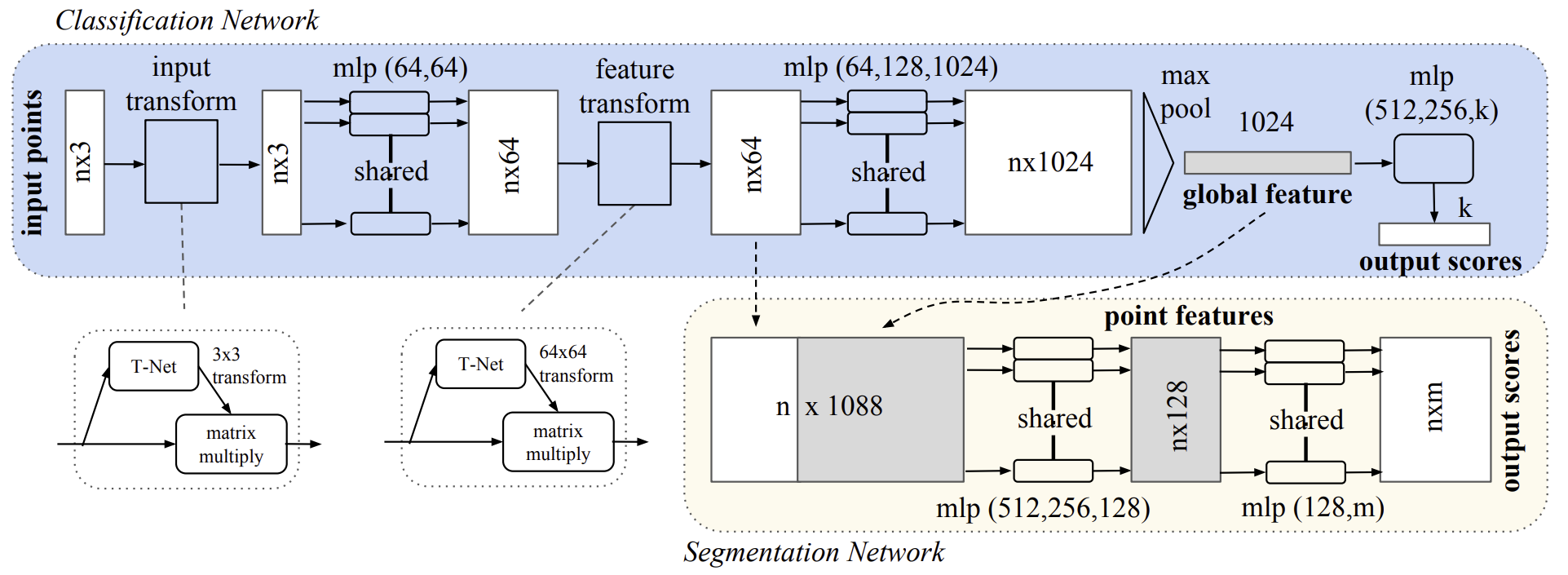
2. Implementação em MQL5

Na seção anterior, exploramos a descrição teórica das abordagens propostas pelos autores do método PointNet. Agora, chegou o momento de passar para a parte prática do artigo, na qual implementaremos nossa própria visão dessas abordagens utilizando MQL5.

2.1 Criação da classe PointNet

Para implementar os algoritmos do PointNet no código, criaremos uma nova classe chamada CNeuronPointNetOCL, que herdará a funcionalidade base da camada totalmente conectada CNeuronBaseOCL. A estrutura dessa nova classe está apresentada abaixo.

class CNeuronPointNetOCL   :  public CNeuronBaseOCL
  {
protected:
   CNeuronPointNetOCL   *cTNet1;
   CNeuronBaseOCL       *cTurned1;
   CNeuronConvOCL       cPreNet[2];
   CNeuronBatchNormOCL  cPreNetNorm[2];
   CNeuronPointNetOCL   *cTNet2;
   CNeuronBaseOCL       *cTurned2;
   CNeuronConvOCL       cFeatureNet[3];
   CNeuronBatchNormOCL  cFeatureNetNorm[3];
   CNeuronTransposeOCL  cTranspose;
   CNeuronProofOCL      cMaxPool;
   CNeuronBaseOCL       cFinalMLP[2];
   //---
   virtual bool         OrthoganalLoss(CNeuronBaseOCL *NeuronOCL, bool add = false);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override ;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronPointNetOCL(void) {};
                    ~CNeuronPointNetOCL(void);
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint output, bool use_tnets,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronPointNetOCL; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Já é comum observar uma grande quantidade de objetos aninhados na estrutura da classe. No entanto, neste caso, há alguns detalhes específicos. Primeiro, além dos objetos estáticos, podemos notar a presença de alguns objetos dinâmicos. No destrutor da classe, precisaremos removê-los da memória do dispositivo.

CNeuronPointNetOCL::~CNeuronPointNetOCL(void)
  {
   if(!!cTNet1)
      delete cTNet1;
   if(!!cTNet2)
      delete cTNet2;
   if(!!cTurned1)
      delete cTurned1;
   if(!!cTurned2)
      delete cTurned2;
  }

Ainda assim, não criamos esses objetos no construtor da classe, permitindo que ele permaneça vazio.

Outro ponto importante é que dois dos objetos dinâmicos aninhados são instâncias da própria classe CNeuronPointNetOCL que estamos criando. É como uma "matrioska dentro de uma matrioska".

Ambos esses detalhes estão diretamente relacionados ao método proposto pelos autores para o alinhamento dos dados brutos e das características a um espaço canônico. Explicaremos isso com mais detalhes durante a implementação dos métodos da classe.

A inicialização de uma nova instância do objeto da classe ocorre, como de costume, no método Init. Nos parâmetros desse método, recebemos as principais constantes que definem a arquitetura do objeto a ser criado.

Vale destacar que, neste caso, foi tomada a decisão de construir um algoritmo para a classificação de nuvens de pontos. A ideia geral é criar um Codificador de estado do ambiente, utilizando as abordagens do PointNet, que retorna uma distribuição probabilística associando o estado atual do ambiente a uma determinada categoria. A política do Ator, por sua vez, será voltada para mapear um determinado tipo de estado do ambiente a um conjunto específico de parâmetros de negociação, buscando a máxima rentabilidade possível dentro do estado analisado. A partir disso, derivam-se os principais parâmetros da arquitetura da classe:

• window — tamanho da janela de parâmetros de um único ponto dentro da nuvem analisada;
• units_count — número de pontos na nuvem;
• output — tamanho do tensor de resultados;
• use_tnets — necessidade de criar modelos para projeção dos dados brutos e das características no espaço canônico.

Aqui, é importante notar que o parâmetro output indica o tamanho total do buffer de resultados. Ele não deve ser confundido com o parâmetro de janela de resultados usado anteriormente. Isso porque, neste caso, esperamos que a saída represente um descritor do estado analisado do ambiente. O tamanho do tensor de resultados pode ser logicamente associado ao número de tipos possíveis de classificação dos estados do ambiente. 

bool CNeuronPointNetOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                              uint window, uint units_count, uint output, bool use_tnets,
                              ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, output, optimization_type, batch))
      return false;

No corpo do método, como de costume, primeiro chamamos o método homônimo da classe pai, onde já foram implementados os controles mínimos necessários para validar os parâmetros recebidos e inicializar os objetos herdados. Durante esse processo, verificamos o resultado da execução das operações do método chamado.

Em seguida, inicializamos os objetos aninhados. O primeiro passo é verificar se é necessário criar modelos internos para a projeção dos dados brutos e das características no espaço canônico.

//--- Init T-Nets
   if(use_tnets)
     {
      if(!cTNet1)
        {
         cTNet1 = new CNeuronPointNetOCL();
         if(!cTNet1)
            return false;
        }
      if(!cTNet1.Init(0, 0, OpenCL, window, units_count, window * window, false, optimization, iBatch))
         return false;

Se a criação dos modelos de projeção for necessária, verificamos a validade do ponteiro para o objeto do modelo e, se necessário, criamos uma nova instância da classe CNeuronPointNetOCL. Depois disso, inicializamos a classe.

É importante destacar que o tamanho dos dados brutos do objeto gerador da matriz de projeção corresponde ao tamanho dos dados brutos recebidos pela classe principal a partir do programa externo. No entanto, o tamanho do buffer de resultados equivale ao quadrado da janela de dados brutos. Isso ocorre porque a saída desse modelo deve ser uma matriz quadrada para projetar os dados brutos no espaço canônico. Além disso, definimos false para o parâmetro que indica a necessidade de criar matrizes de projeção dos dados brutos e das características. Isso impede a criação recursiva descontrolada de objetos, evitando uma estrutura de transformação dentro de outra estrutura de transformação, o que não faria sentido. 

Nesse ponto, também verificamos o ponteiro para o objeto de gravação dos dados corrigidos e, se necessário, criamos uma nova instância desse objeto.

      if(!cTurned1)
        {
         cTurned1 = new CNeuronBaseOCL();
         if(!cTurned1)
            return false;
        }
      if(!cTurned1.Init(0, 1, OpenCL, window * units_count, optimization, iBatch))
         return false;

Em seguida, inicializamos essa camada interna. Seu tamanho corresponde ao tensor dos dados brutos.

Realizamos operações semelhantes para o modelo de projeção das características. A única diferença está nas dimensões das camadas internas.

      if(!cTNet2)
        {
         cTNet2 = new CNeuronPointNetOCL();
         if(!cTNet2)
            return false;
        }
      if(!cTNet2.Init(0, 2, OpenCL, 64, units_count, 64 * 64, false, optimization, iBatch))
         return false;
      if(!cTurned2)
        {
         cTurned2 = new CNeuronBaseOCL();
         if(!cTurned2)
            return false;
        }
      if(!cTurned2.Init(0, 3, OpenCL, 64 * units_count, optimization, iBatch))
         return false;
     }

Prosseguimos então para a formação da MLP de extração primária das características dos pontos. Como nesta etapa os autores do PointNet propõem a extração independente das características de cada ponto, substituímos as camadas totalmente conectadas por camadas convolucionais, com um tamanho de passo equivalente ao tamanho da janela dos dados analisados. Em nosso caso, isso corresponde ao tamanho do vetor de descrição de um único ponto.

//--- Init PreNet
   if(!cPreNet[0].Init(0, 0, OpenCL, window, window, 64, units_count, optimization, iBatch))
      return false;
   cPreNet[0].SetActivationFunction(None);
   if(!cPreNetNorm[0].Init(0, 1, OpenCL, 64 * units_count, iBatch, optimization))
      return false;
   cPreNetNorm[0].SetActivationFunction(LReLU);
   if(!cPreNet[1].Init(0, 2, OpenCL, 64, 64, 64, units_count, optimization, iBatch))
      return false;
   cPreNet[1].SetActivationFunction(None);
   if(!cPreNetNorm[1].Init(0, 3, OpenCL, 64 * units_count, iBatch, optimization))
      return false;
   cPreNetNorm[1].SetActivationFunction(None);

Entre as camadas convolucionais, inserimos camadas de normalização em lote e aplicamos a função de ativação sobre elas. Neste caso, utilizamos duas camadas de cada tipo, com a dimensionalidade proposta pelos autores do método.

De maneira semelhante, adicionamos um perceptron de três camadas para a extração de características de nível mais alto.

//--- Init Feature Net
   if(!cFeatureNet[0].Init(0, 4, OpenCL, 64, 64, 64, units_count, optimization, iBatch))
      return false;
   cFeatureNet[0].SetActivationFunction(None);
   if(!cFeatureNetNorm[0].Init(0, 5, OpenCL, 64 * units_count, iBatch, optimization))
      return false;
   cFeatureNet[0].SetActivationFunction(LReLU);
   if(!cFeatureNet[1].Init(0, 6, OpenCL, 64, 64, 128, units_count, optimization, iBatch))
      return false;
   cFeatureNet[1].SetActivationFunction(None);
   if(!cFeatureNetNorm[1].Init(0, 7, OpenCL, 128 * units_count, iBatch, optimization))
      return false;
   cFeatureNetNorm[1].SetActivationFunction(LReLU);
   if(!cFeatureNet[2].Init(0, 8, OpenCL, 128, 128, 512, units_count, optimization, iBatch))
      return false;
   cFeatureNet[2].SetActivationFunction(None);
   if(!cFeatureNetNorm[2].Init(0, 9, OpenCL, 512 * units_count, iBatch, optimization))
      return false;
   cFeatureNetNorm[2].SetActivationFunction(None);

Essencialmente, a arquitetura dos dois últimos blocos é a mesma. A única diferença está no número e no tamanho das camadas. Logicamente, seria possível unificá-los em um único bloco. No entanto, optamos por mantê-los separados para permitir a inserção, entre eles, de um bloco de transformação das características no espaço canônico.

Na próxima etapa, após a extração das características dos pontos, o algoritmo PointNet aplica a função MaxPooling, que seleciona o valor máximo de cada elemento do vetor de características dos pontos em toda a nuvem analisada. Dessa forma, pressupõe-se que a nuvem de pontos seja representada por um vetor de características que contém os valores máximos correspondentes de todas as características extraídas das diferentes regiões analisadas.

Já dispomos da classe CNeuronProofOCL, que executa uma funcionalidade semelhante, mas em uma dimensão diferente. Portanto, primeiramente, transpomos a matriz das características dos pontos extraídas.

   if(!cTranspose.Init(0, 10, OpenCL, units_count, 512, optimization, iBatch))
      return false;

Em seguida, formamos o vetor dos valores máximos.

   if(!cMaxPool.Init(512, 11, OpenCL, units_count, units_count, 512, optimization, iBatch))
      return false;

O descritor gerado para a nuvem de pontos analisada é então processado por uma MLP de três camadas. No entanto, decidimos aplicar uma pequena otimização: em vez de definir três camadas totalmente conectadas, utilizamos apenas duas camadas internas. Como terceira camada, aproveitamos diretamente o próprio objeto criado, pois ele já herda todas as funcionalidades necessárias da classe pai.

//--- Init Final MLP
   if(!cFinalMLP[0].Init(256, 12, OpenCL, 512, optimization, iBatch))
      return false;
   cFinalMLP[0].SetActivationFunction(LReLU);
   if(!cFinalMLP[1].Init(output, 13, OpenCL, 256, optimization, iBatch))
      return false;
   cFinalMLP[1].SetActivationFunction(LReLU);

No final da execução do método de inicialização do objeto da classe, definimos explicitamente a função de ativação e retornamos um resultado lógico indicando a conclusão bem-sucedida das operações para o programa chamador.

   SetActivationFunction(None);
//---
   return true;
  }

Com a implementação do método de inicialização concluída, passamos para a construção dos algoritmos de propagação para frente do PointNet, dentro do método feedForward. Como de costume, esse método recebe como parâmetro um ponteiro para o objeto dos dados brutos.

bool CNeuronPointNetOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- PreNet
   if(!cTNet1)
     {
      if(!cPreNet[0].FeedForward(NeuronOCL))
         return false;
     }

No corpo do método, há uma bifurcação no algoritmo, que depende da necessidade de projeção dos dados brutos para o espaço canônico. Ao inicializar o objeto, salvamos internamente uma variável de controle que indica se a projeção dos dados é necessária. No entanto, para verificar essa necessidade durante a execução, basta checar a validade dos ponteiros dos objetos correspondentes. Afinal, os modelos de projeção só são criados quando necessário. Por padrão, eles não são criados.

Assim, se não houver um ponteiro válido para o objeto do modelo de projeção dos dados brutos, apenas passamos diretamente o ponteiro dos dados recebidos para o método de propagação para frente da primeira camada convolucional do bloco de extração preliminar de características.

Se, por outro lado, a projeção dos dados para o espaço canônico for necessária, os dados recebidos são enviados para o método de propagação para frente do modelo responsável pela geração da matriz de transformação dos dados.

   else
     {
      if(!cTurned1)
         return false;
      if(!cTNet1.FeedForward(NeuronOCL))
         return false;

Na saída do modelo de projeção, obtemos uma matriz quadrada de transformação dos dados. Com base no tamanho do tensor de resultados, podemos determinar a dimensão da janela de dados.

      int window = (int)MathSqrt(cTNet1.Neurons());

Em seguida, utilizamos a operação de multiplicação matricial para obter a projeção da nuvem de pontos bruta no espaço canônico.

      if(IsStopped() ||
         !MatMul(NeuronOCL.getOutput(), cTNet1.getOutput(), cTurned1.getOutput(), NeuronOCL.Neurons() / window,
                                                                                                window, window))
         return false;

Essa projeção das coordenadas dos pontos transformados é então enviada como entrada para a primeira camada do bloco de extração primária de características.

      if(!cPreNet[0].FeedForward(cTurned1.AsObject()))
         return false;
     }

Neste ponto, independentemente da necessidade de projeção dos dados brutos no espaço canônico, já realizamos a propagação para frente da primeira camada do bloco de extração primária de características. A partir disso, seguimos chamando sequencialmente os métodos de propagação para frente de todas as camadas desse bloco.

   if(!cPreNetNorm[0].FeedForward(cPreNet[0].AsObject()))
      return false;
   if(!cPreNet[1].FeedForward(cPreNetNorm[0].AsObject()))
      return false;
   if(!cPreNetNorm[1].FeedForward(cPreNet[1].AsObject()))
      return false;

Em seguida, precisamos determinar se as características extraídas dos pontos também devem ser projetadas no espaço canônico. O algoritmo utilizado aqui segue a mesma lógica da projeção das coordenadas dos pontos.

//--- Feature Net
   if(!cTNet2)
     {
      if(!cFeatureNet[0].FeedForward(cPreNetNorm[1].AsObject()))
         return false;
     }
   else
     {
      if(!cTurned2)
         return false;
      if(!cTNet2.FeedForward(cPreNetNorm[1].AsObject()))
         return false;
      int window = (int)MathSqrt(cTNet2.Neurons());
      if(IsStopped() ||
         !MatMul(cPreNetNorm[1].getOutput(), cTNet2.getOutput(), cTurned2.getOutput(),
                                     cPreNetNorm[1].Neurons() / window, window, window))
         return false;
      if(!cFeatureNet[0].FeedForward(cTurned2.AsObject()))
         return false;
     }

Após essa etapa, finalizamos as operações de extração das características dos pontos na nuvem analisada.

   if(!cFeatureNetNorm[0].FeedForward(cFeatureNet[0].AsObject()))
      return false;
   uint total = cFeatureNet.Size();
   for(uint i = 1; i < total; i++)
     {
      if(!cFeatureNet[i].FeedForward(cFeatureNetNorm[i - 1].AsObject()))
         return false;
      if(!cFeatureNetNorm[i].FeedForward(cFeatureNet[i].AsObject()))
         return false;
     }

Na fase seguinte, transpomos o tensor de características extraído e formamos o vetor descritor da nuvem analisada.

   if(!cTranspose.FeedForward(cFeatureNetNorm[total - 1].AsObject()))
      return false;
   if(!cMaxPool.FeedForward(cTranspose.AsObject()))
      return false;

Conforme o algoritmo de classificação do PointNet, esse descritor então passa por processamento dentro da MLP, onde realizamos a propagação para frente através de duas camadas totalmente conectadas internas.

   if(!cFinalMLP[0].FeedForward(cMaxPool.AsObject()))
      return false;
   if(!cFinalMLP[1].FeedForward(cFinalMLP[0].AsObject()))
      return false;

Em seguida, chamamos o método equivalente da classe pai, passando um ponteiro para a camada interna.

   if(!CNeuronBaseOCL::feedForward(cFinalMLP[1].AsObject()))
      return false;
//---
   return true;
  }

Lembrando que, neste caso, a classe pai é uma camada totalmente conectada. Portanto, ao chamar o método de propagação para frente da classe pai, executamos a propagação da camada totalmente conectada, mas, desta vez, utilizando objetos herdados da classe pai, e não de uma camada aninhada.

Após a conclusão bem-sucedida de todas as operações do método de propagação para frente, retornamos um valor lógico indicando que as operações foram realizadas corretamente para o programa chamador.

Com isso, finalizamos a implementação do método de propagação para frente e passamos para a construção dos métodos de propagação reversa, que são divididos em dois blocos: a distribuição do gradiente do erro e o ajuste dos parâmetros treináveis do modelo.

Já mencionamos diversas vezes que a distribuição do gradiente do erro segue exatamente a mesma sequência do algoritmo de propagação para frente, porém no sentido inverso. No entanto, neste caso, há um detalhe importante Para as matrizes de projeção dos dados, os autores do PointNet introduziram uma regularização que força a matriz de projeção a se aproximar o máximo possível de uma matriz ortogonal. Essas operações de regularização não afetam a propagação para frente, pois são utilizadas apenas durante a otimização dos parâmetros. Além disso, para executá-las, será necessário trabalhar adicionalmente no lado da implementação OpenCL.

Para começar, vamos analisar a fórmula de regularização proposta.

É evidente que os autores do método exploram a propriedade segundo a qual, ao multiplicar uma matriz ortogonal por sua transposta, o resultado é a matriz identidade.

Se analisarmos melhor, veremos que multiplicar uma matriz pela sua transposta significa que cada elemento da matriz resultante corresponde ao produto escalar entre duas linhas da matriz original. Para que uma matriz seja ortogonal, o produto escalar de uma linha por ela mesma deve resultar em 1, enquanto o produto escalar entre diferentes linhas deve ser 0.

No entanto, é importante lembrar que estamos tratando da regularização no contexto da propagação reversa. Isso significa que não basta calcular o erro, é necessário também determinar o gradiente do erro para cada elemento.

Para implementá-lo no OpenCL, criaremos um kernel chamado OrthogonalLoss. Esse kernel recebe como parâmetros ponteiros para dois buffers de dados: um contendo a matriz original e outro reservado para armazenar os gradientes do erro. Adicionaremos também um flag que definirá se os gradientes serão sobrescritos ou acumulados nos valores já armazenados.

__kernel void OrthoganalLoss(__global const float *data,
                             __global float *grad,
                             const int add
                            )
  {
   const size_t r = get_global_id(0);
   const size_t c = get_local_id(1);
   const size_t cols = get_local_size(1);

Não especificamos explicitamente as dimensões das matrizes, mas isso não é um problema. Planejamos executar o kernel em um espaço de tarefas bidimensional, cujas dimensões serão baseadas no número de linhas e colunas da matriz.

No corpo do kernel, identificamos imediatamente o fluxo atual em ambos os eixos do espaço de tarefas.

Vale lembrar que estamos lidando com uma matriz quadrada. Portanto, para determinar o tamanho total da matriz, basta conhecer a quantidade de fluxos em apenas um dos eixos.

Para distribuir as operações de multiplicação vetorial entre vários fluxos, criamos grupos de trabalho locais ao longo das linhas da matriz original. Para o compartilhamento de dados entre os fluxos, utilizamos um array na memória local do contexto OpenCL.

   __local float Temp[LOCAL_ARRAY_SIZE];
   uint ls = min((uint)cols, (uint)LOCAL_ARRAY_SIZE);

Em seguida, determinamos as constantes de deslocamento para acessar os elementos corretos dentro do buffer de dados original.

   const int shift1 = r * cols + c;
   const int shift2 = c * cols + r;

Depois disso, carregamos os valores dos elementos correspondentes a partir do buffer de dados.

   float value1 = data[shift1];
   float value2 = (shift1==shift2 ? value1 : data[shift2]);

Aqui, adotamos uma estratégia para minimizar o número de acessos à memória global, eliminando leituras redundantes dos elementos diagonais da matriz.

Também verificamos a validade dos valores carregados, substituindo quaisquer valores inválidos por zero.

   if(isinf(value1) || isnan(value1))
      value1 = 0;
   if(isinf(value2) || isnan(value2))
      value2 = 0;

Em seguida, multiplicamos os elementos para garantir a validade dos resultados.

   float v2 = value1 * value2;
   if(isinf(v2) || isnan(v2))
      v2 = 0;

Na etapa seguinte, criamos um laço de soma paralela, no qual os valores multiplicados são acumulados em elementos individuais do array local, garantindo a sincronização dos fluxos dentro do grupo de trabalho.

   for(int i = 0; i < cols; i += ls)
     {
      //---
      if(i <= c && (i + ls) > c)
         Temp[c - i] = (i == 0 ? 0 : Temp[c - i]) + v2;
      barrier(CLK_LOCAL_MEM_FENCE);
     }

Em seguida, criamos um laço de soma para agregar os valores acumulados nos elementos do array local.

   uint count = min(ls, (uint)cols);
   do
     {
      count = (count + 1) / 2;
      if(c < ls)
         Temp[c] += (c < count && (c + count) < cols ? Temp[c + count] : 0);
      if(c + count < ls)
         Temp[c + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Durante essa operação, damos atenção especial à sincronização dos fluxos dentro do grupo de trabalho.

Como resultado dessas operações, o primeiro elemento do array local conterá o produto escalar das duas linhas analisadas da matriz. A partir desse valor, podemos então calcular o erro.

   const float sum = Temp[0];
   float loss = -pow((float)(r == c) - sum, 2.0f);

No entanto, essa é apenas uma parte do processo. O próximo passo é determinar o gradiente do erro para cada elemento da matriz original. Inicialmente, calculamos o gradiente do erro no nível da multiplicação vetorial.

   float g = (2 * (sum - (float)(r == c))) * loss;

Depois, propagamos o gradiente do erro para o primeiro elemento do produto dos valores do fluxo atual.

   g = value2 * g;

Também verificamos obrigatoriamente a validade do gradiente calculado.

   if(isinf(g) || isnan(g))
      g = 0;

Após essa verificação, armazenamos o gradiente no buffer global de gradientes de erro.

   if(add == 1)
      grad[shift1] += g;
   else
      grad[shift1] = g;
  }

Aqui, também verificamos o flag que define se o valor do gradiente de erro deve ser sobrescrito ou acumulado, executando a operação correspondente.

Vale destacar que, dentro do kernel, calculamos o gradiente do erro apenas para um dos elementos do produto. O gradiente do erro para o segundo elemento do produto será calculado em um fluxo separado, no qual a linha e a coluna da matriz são invertidas.

A execução desse kernel é colocada na fila de execução dentro do método CNeuronPointNetOCL::OrthogonalLoss. O algoritmo desse método segue exatamente os princípios básicos de enfileiramento de kernels OpenCL, que já foram discutidos diversas vezes em artigos anteriores. Recomendo que você analise o código completo desse método, que está disponível no material anexado.

Agora, vamos explorar o algoritmo do método de distribuição do gradiente do erro, chamado calcInputGradients. Nos parâmetros desse método, como de costume, recebemos um ponteiro para o objeto da camada anterior, que, neste caso, recebe o gradiente do erro no nível dos dados brutos.

bool CNeuronPointNetOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

No início do corpo do método, verificamos imediatamente a validade do ponteiro recebido, pois, caso contrário, não faz sentido continuar a execução das operações.

Depois, propagamos o gradiente do erro através do perceptron que interpreta o descritor da nuvem de pontos.

   if(!CNeuronBaseOCL::calcInputGradients(cFinalMLP[1].AsObject()))
      return false;
   if(!cFinalMLP[0].calcHiddenGradients(cFinalMLP[1].AsObject()))
      return false;

Através da camada de MaxPooling, seguido de uma transposição, propagamos o gradiente do erro para as características dos pontos correspondentes.

   if(!cMaxPool.calcHiddenGradients(cFinalMLP[0].AsObject()))
      return false;
   if(!cTranspose.calcHiddenGradients(cMaxPool.AsObject()))
      return false;

Por fim, propagamos o gradiente do erro através das camadas de extração de características dos pontos, seguindo, naturalmente, a ordem inversa da propagação para frente.

   uint total = cFeatureNet.Size();
   for(uint i = total - 1; i > 0; i--)
     {
      if(!cFeatureNet[i].calcHiddenGradients(cFeatureNetNorm[i].AsObject()))
         return false;
      if(!cFeatureNetNorm[i - 1].calcHiddenGradients(cFeatureNet[i].AsObject()))
         return false;
     }
   if(!cFeatureNet[0].calcHiddenGradients(cFeatureNetNorm[0].AsObject()))
      return false;

Até aqui, tudo segue um fluxo relativamente padrão. No entanto, agora chegamos ao nível de projeção das características dos pontos no espaço canônico. Se essa projeção não for necessária, apenas passamos o gradiente do erro diretamente para o bloco de extração primária de características.

   if(!cTNet2)
     {
      if(!cPreNetNorm[1].calcHiddenGradients(cFeatureNet[0].AsObject()))
         return false;
     }

No segundo caso, o algoritmo se torna mais complexo. Primeiro, propagamos o gradiente do erro até o nível da projeção dos dados.

   else
     {
      if(!cTurned2)
         return false;
      if(!cTurned2.calcHiddenGradients(cFeatureNet[0].AsObject()))
         return false;

Em seguida, distribuímos o gradiente do erro entre as características dos pontos e a matriz de projeção. Aqui, se olharmos alguns passos à frente, perceberemos que o gradiente do erro das características dos pontos também será propagado através do modelo gerador da matriz de projeção. Portanto, para evitar a sobrescrita de informações necessárias mais adiante, nesta etapa não passamos o gradiente do erro para a última camada do bloco de extração preliminar de características, mas sim para a penúltima camada.

Vale lembrar que a última camada desse bloco é a de normalização em lote, enquanto a penúltima é uma camada convolucional de extração independente das características individuais dos pontos. Ambas as camadas possuem buffers de gradientes de erro com o mesmo tamanho, o que permite substituir os buffers sem o risco de ultrapassar seus limites.

      int window = (int)MathSqrt(cTNet2.Neurons());
      if(IsStopped() ||
         !MatMulGrad(cPreNetNorm[1].getOutput(), cPreNet[1].getGradient(), cTNet2.getOutput(), 
                     cTNet2.getGradient(), cTurned2.getGradient(), cPreNetNorm[1].Neurons() / window,
                                                                                       window, window))
         return false;

Depois de dividir o gradiente do erro em dois fluxos de dados, adicionamos o gradiente do erro da regularização no nível da matriz de projeção.

      if(!OrthoganalLoss(cTNet2.AsObject(), true))
         return false;

A seguir, propagamos o gradiente do erro através do bloco responsável pela formação da matriz de projeção.

      if(!cPreNetNorm[1].calcHiddenGradients((CObject*)cTNet2))
         return false;

E então, somamos os gradientes de erro provenientes dos dois fluxos de informação.

      if(!SumAndNormilize(cPreNetNorm[1].getGradient(), cPreNet[1].getGradient(), cPreNetNorm[1].getGradient(),
                                                                                         1, false, 0, 0, 0, 1))
         return false;
     }

A partir deste ponto, podemos tranquilamente propagar o gradiente do erro através do bloco de extração primária de características, até atingir o nível da projeção dos dados brutos.

   if(!cPreNet[1].calcHiddenGradients(cPreNetNorm[1].AsObject()))
      return false;
   if(!cPreNetNorm[0].calcHiddenGradients(cPreNet[1].AsObject()))
      return false;
   if(!cPreNet[0].calcHiddenGradients(cPreNetNorm[0].AsObject()))
      return false;

Aqui, aplicamos um algoritmo idêntico ao usado para distribuir o gradiente do erro na projeção das características. O caso mais simples ocorre quando não há matriz de projeção dos dados: nesse cenário, apenas repassamos o gradiente do erro para o buffer da camada anterior.

   if(!cTNet1)
     {
      if(!NeuronOCL.calcHiddenGradients(cPreNet[0].AsObject()))
         return false;
     }

Porém, se a projeção dos dados for necessária, primeiro propagamos o gradiente do erro até o nível da projeção.

      if(!cTurned1)
         return false;
      if(!cTurned1.calcHiddenGradients(cPreNet[0].AsObject()))
         return false;

Em seguida, distribuímos o gradiente do erro em dois fluxos, de acordo com sua influência no resultado final.

      int window = (int)MathSqrt(cTNet1.Neurons());
      if(IsStopped() ||
         !MatMulGrad(NeuronOCL.getOutput(), NeuronOCL.getGradient(), cTNet1.getOutput(), cTNet1.getGradient(),
                     cTurned1.getGradient(), NeuronOCL.Neurons() / window, window, window))
         return false;

Depois, adicionamos ao gradiente do erro resultante o valor da regularização.

      if(!OrthoganalLoss(cTNet1, true))
         return false;

Aqui, enfrentamos um problema de sobrescrita do gradiente do erro. Neste ponto, não temos buffers disponíveis para armazenar os dados temporários. Ao distribuir o gradiente do erro em dois fluxos, já gravamos os valores no buffer da camada anterior. Agora, ao propagar o gradiente do erro através do bloco gerador da matriz de projeção dos dados brutos, essas operações sobrescreveriam os valores do gradiente do erro, resultando na perda dos dados armazenados anteriormente. Para evitar essa perda, precisamos copiar os valores para um buffer apropriado. Mas onde podemos encontrá-lo? Durante a inicialização da classe, não criamos buffers dedicados ao armazenamento de dados intermediários. Neste momento, percebemos que podemos utilizar o buffer da camada de gravação da projeção dos dados. Esse buffer tem o mesmo tamanho do tensor dos dados brutos. Além disso, o gradiente do erro armazenado nesse buffer já foi distribuído entre os dois fluxos e não será mais utilizado nas próximas operações.

Ao mesmo tempo, a igualdade dos tamanhos dos buffers sugere a possibilidade de transferência direta dos dados. Mas e se, em vez de copiar os dados diretamente, apenas substituirmos os ponteiros dos buffers de dados? Afinal, a operação de substituição de ponteiro é muito mais eficiente do que copiar completamente os dados do buffer e não depende do seu tamanho.

      CBufferFloat *temp = NeuronOCL.getGradient();
      NeuronOCL.SetGradient(cTurned1.getGradient(), false);
      cTurned1.SetGradient(temp, false);

Após essa troca dos ponteiros dos buffers de dados, podemos tranquilamente propagar o gradiente do erro da matriz de projeção dos dados até a camada anterior.

      if(!NeuronOCL.calcHiddenGradients(cTNet1.AsObject()))
         return false;
      if(!SumAndNormilize(NeuronOCL.getGradient(), cTurned1.getGradient(), NeuronOCL.getGradient(),
                                                                            1, false, 0, 0, 0, 1))
         return false; 
     }
//---
   return true;
  }

Por fim, no encerramento das operações do método, somamos o gradiente do erro dos dois fluxos de informação e retornamos um valor lógico indicando que as operações foram realizadas corretamente para o programa chamador.

A atualização dos parâmetros treináveis do modelo é realizada no método updateInputWeights. O algoritmo desse método é bastante simples: chamamos sequencialmente os métodos homônimos dos objetos internos que contêm os parâmetros treináveis. Além disso, não podemos esquecer de chamar o método equivalente da classe pai, pois utilizamos sua funcionalidade como a terceira camada da MLP responsável pela avaliação do descritor da nuvem de pontos. Nesta seção do artigo, não entraremos em detalhes sobre a implementação do código desse método. Recomendo que você o estude por conta própria nos arquivos anexados a este material.

Com isso, finalizamos a análise dos algoritmos utilizados na implementação dos métodos da classe CNeuronPointNetOCL. Nos arquivos anexados ao artigo, você encontrará o código completo dessa classe e de todos os seus métodos.

2.2 Arquitetura dos modelos

Após a implementação das abordagens propostas pelos autores do PointNet utilizando MQL5, passamos agora para a integração desse novo objeto à arquitetura dos nossos modelos. Conforme mencionado anteriormente, a classe CNeuronPointNetOCL foi incorporada à arquitetura do Codificador do Estado do Ambiente, definida no método CreateEncoderDescriptions.

Vale destacar que praticamente todo o algoritmo foi implementado dentro de um único bloco. Isso nos permite construir um modelo de arquitetura de alto nível bastante conciso e compacto. É importante enfatizar o termo "arquitetura de alto nível", pois, sob o nome aparentemente simples do bloco CNeuronPointNetOCL, esconde-se uma arquitetura de rede neural altamente complexa e multinível.

Na entrada do modelo, como de costume, alimentamos os dados brutos, que são então normalizados e padronizados pela camada de normalização em lote.

bool CreateEncoderDescriptions(CArrayObj *&encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Depois disso, os dados são imediatamente enviados para o nosso novo bloco PointNet.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPointNetOCL;
   descr.window = BarDescr;                        // Variables
   descr.count = HistoryBars;                      // Units
   descr.window_out = LatentCount;                 // Output Dimension
   descr.step = int(true);                         // Use input and feature transformation
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Aqui, é importante destacar que não especificamos nenhuma função de ativação na saída do bloco CNeuronPointNetOCL. Essa escolha foi feita intencionalmente para permitir que o usuário expanda a arquitetura do bloco de identificação da nuvem de pontos. No entanto, para este experimento, apenas adicionaremos uma camada SoftMax para converter os resultados obtidos em valores probabilísticos.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = LatentCount;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Com isso, a arquitetura do nosso novo modelo de Codificador do estado do ambiente está finalizada.

Também simplificamos a arquitetura dos modelos Ator e Crítico. Substituímos o bloco de atenção cruzada multi-head por uma camada de concatenação de dados simples. Recomendo, no entanto, que você analise essas modificações menores diretamente nos arquivos anexados.

É importante também comentar sobre os programas de treinamento das redes. As mudanças na arquitetura dos modelos não alteraram a estrutura dos dados de entrada e saída, o que nos permite continuar utilizando os programas já desenvolvidos para interagir com o ambiente e os dados coletados anteriormente para treinamento offline. Porém, o conjunto de dados coletado anteriormente não contém rótulos de classe para os estados selecionados do ambiente. Criá-los manualmente exigiria um esforço adicional significativo. Para evitar esse trabalho extra, decidimos seguir um caminho diferente: treinar o Codificador do estado do ambiente simultaneamente com a política do Ator. Portanto, removemos o Expert Advisor de treinamento separado do Codificador do estado do ambiente ("StudyEncoder.mq5"). Em vez disso, realizamos pequenas alterações no programa de treinamento do Ator e do Crítico ("Study.mq5"), de modo que o Codificador do estado do ambiente possa ser treinado em conjunto. Você pode conferir essas alterações nos arquivos anexados.

Lembrando que, nos anexos, você encontrará o código completo da classe apresentada neste artigo, bem como todos os seus métodos e os algoritmos das demais aplicações utilizadas no desenvolvimento deste trabalho. Agora, avançamos para a etapa final do nosso estudo: o teste e a avaliação dos resultados obtidos.

3. Testes

Nesta pesquisa, exploramos um novo método de processamento de dados brutos na forma de nuvens de pontos, utilizando o PointNet, e implementamos nossa própria abordagem para os conceitos propostos pelos autores do método, utilizando MQL5. Agora, chegou o momento de avaliar a eficácia dessas abordagens para a resolução dos nossos problemas. Para isso, treinaremos os modelos apresentados neste artigo utilizando dados históricos reais do par EUR/USD. Dentro do nosso experimento, a fase de treinamento será realizada com os dados históricos de 2023 como conjunto de treinamento. Já a fase de teste será realizada com os dados de janeiro de 2024. Em ambos os casos, utilizaremos o timeframe H1 e os parâmetros padrão para todos os indicadores analisados.

De modo geral, utilizamos os parâmetros de treinamento e teste das redes sem alterá-los em vários artigos. Portanto, o treinamento inicial é realizado com os conjuntos de dados previamente coletados.

Ao mesmo tempo, o treinamento do Codificador do Estado do Ambiente ocorre em paralelo ao treinamento da política do Ator. Como já sabemos, o treinamento do Ator é iterativo, com atualizações periódicas do conjunto de dados de treinamento. Essa abordagem permite manter a relevância dos dados de treinamento e garantir que eles estejam alinhados com a faixa de ações da política atual do Ator. Como resultado, conseguimos ajustar a política treinada com mais precisão.

Após algumas iterações de treinamento das redes, conseguimos obter uma política do Ator capaz de gerar lucro tanto no conjunto de treinamento quanto no conjunto de teste. Os resultados dos testes estão apresentados abaixo.

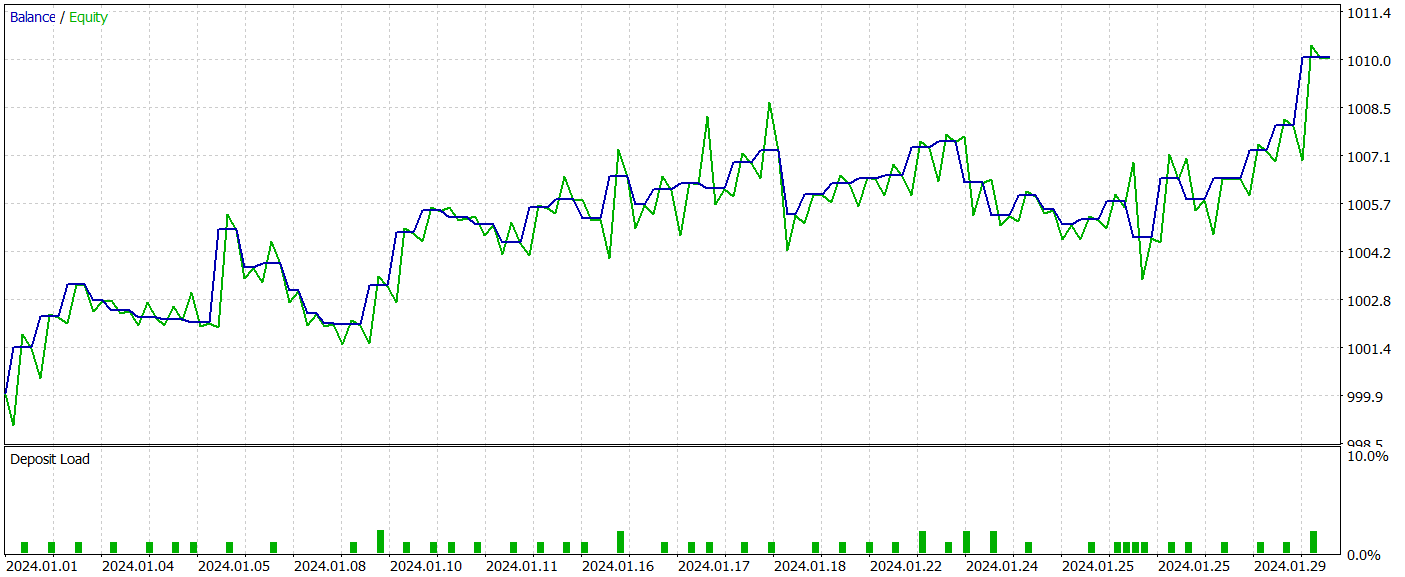
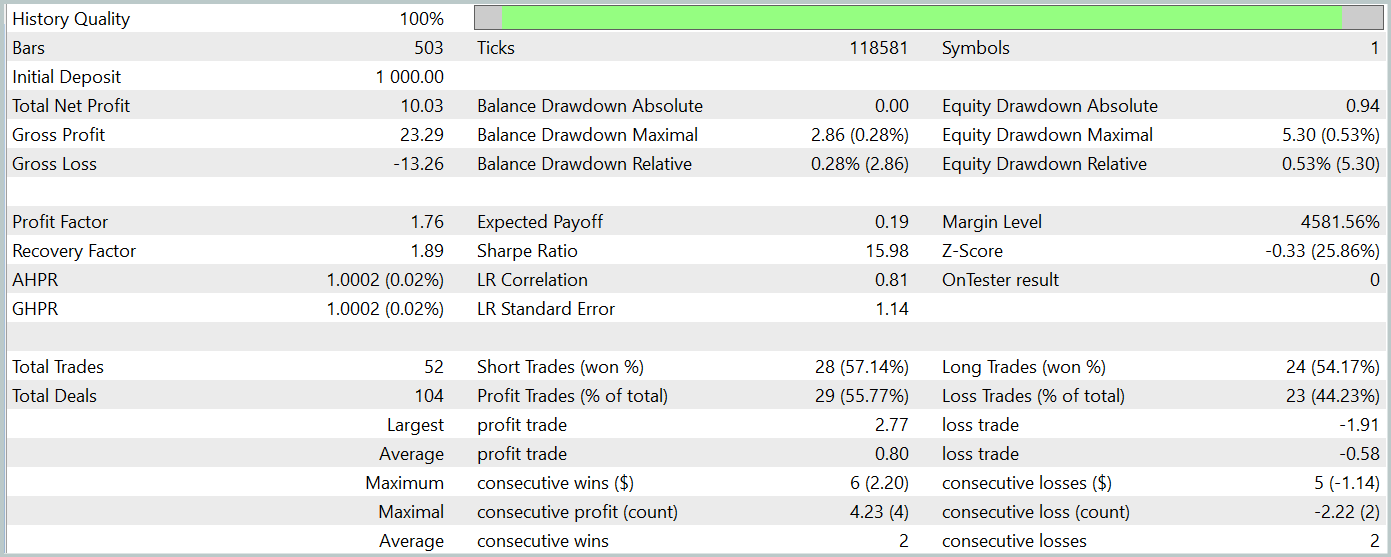
Durante o período de teste, o modelo realizou 52 operações de trading, das quais 55,77% foram fechadas com lucro. Vale destacar que houve paridade entre posições longas e curtas (24 operações de compra contra 28 de venda). Além disso, tanto o lucro máximo quanto o lucro médio por operação superaram os valores correspondentes das operações perdedoras, resultando em um profit factor de 1,76. O gráfico de saldo apresenta uma tendência clara de crescimento. No entanto, devido ao curto período de teste e ao número relativamente pequeno de operações realizadas, ainda não podemos afirmar com certeza a estabilidade da política treinada no longo prazo.

De modo geral, as abordagens implementadas apresentam um grande potencial, mas ainda exigem testes adicionais.

Considerações finais

Neste artigo, exploramos o método PointNet, uma solução arquitetônica unificada que processa diretamente nuvens de pontos como dados brutos. A aplicação do PointNet no trading possibilita a análise eficiente de dados complexos e multidimensionais, como padrões de preço, sem a necessidade de convertê-los para outros formatos. Isso abre novas possibilidades para previsões de tendências de mercado mais precisas e para a melhoria dos algoritmos de tomada de decisão, o que pode aumentar significativamente a eficiência das estratégias de negociação nos mercados financeiros.

Na parte prática deste artigo, implementamos nossa própria versão das abordagens propostas utilizando MQL5, treinamos os modelos com dados históricos reais e realizamos testes do Expert Advisor utilizando a política treinada no testador de estratégias do MetaTrader 5. Os resultados dos testes foram promissores, indicando o potencial das técnicas aplicadas. No entanto, é essencial lembrar que todas as implementações apresentadas neste artigo são experimentais e foram desenvolvidas apenas para demonstrar as possibilidades das abordagens propostas. Antes de utilizar esses programas em mercados financeiros reais, é necessária uma fase adicional de aprimoramento, que inclui treinamento adicional e testes rigorosos das redes. implementadas.

Referências

PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation

Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA para coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para coleta de exemplos pelo método Real-ORL
3	Study.mq5	Expert Advisor	EA para treinamento de Modelos
4	Test.mq5	Expert Advisor	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criar uma rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL