Redes neuronales en el trading: Transformador jerárquico de doble torre (Hidformer)

Introducción

Los modelos de redes neuronales capaces de considerar la estructura temporal de los datos y detectar patrones ocultos se han hecho especialmente populares en la previsión financiera. Sin embargo, los enfoques tradicionales basados en redes neuronales presentan limitaciones por su elevada complejidad computacional y la insuficiente interpretabilidad de los resultados. En este sentido, en los últimos años, las arquitecturas basadas en mecanismos de atención que ofrecen análisis más precisos de series temporales y datos financieros han atraído la atención de los investigadores.

Los modelos más populares son los basados en la arquitectura Transformer y sus modificaciones. En el artículo "Hidformer: Transformer-Style Neural Network in Stock Price Forecasting" se presenta una de estas modificaciones, denominada Hidformer. Este modelo está diseñado específicamente para el análisis de series temporales y se centra en mejorar la precisión de las previsiones usando mecanismos de atención optimizados, una detección eficaz de las dependencias a largo plazo y la adaptación a las particularidades de los datos financieros. La principal ventaja del Hidformer es su capacidad para considerar dependencias temporales complejas, lo cual resulta especialmente importante para analizar el mercado bursátil, donde los precios de los activos dependen de multitud de factores.

Los autores del framework propusieron mejorar el procesamiento de las dependencias temporales, reduciendo la complejidad computacional del modelo y mejorando la precisión de la predicción. Esto convierte a Hidformer en una herramienta prometedora para el análisis financiero y la previsión.

El algoritmo de Hidformer

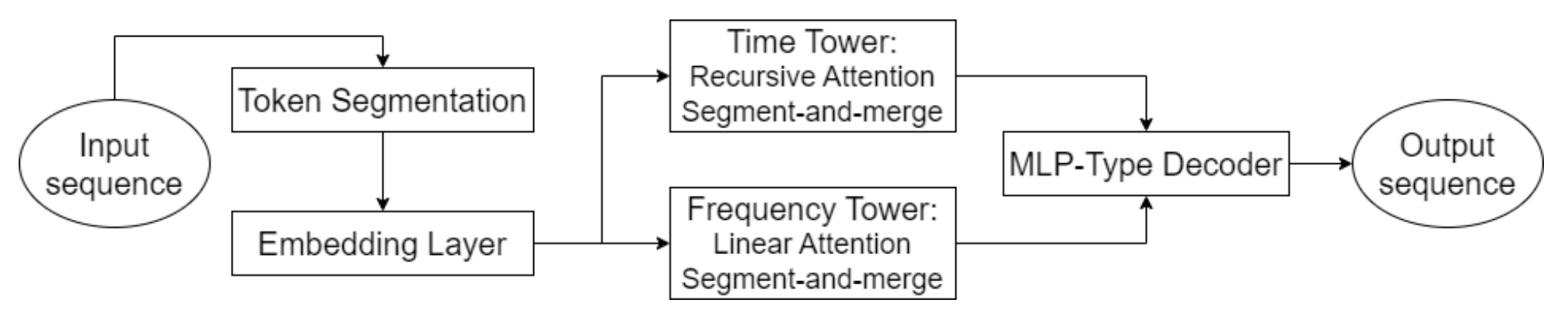
Una de las características clave del Hidformer es el procesamiento paralelo de datos por dos codificadores. El primero analiza las características temporales identificando las tendencias y patrones en una línea temporal, mientras que el segundo opera en el dominio de la frecuencia, lo cual permite identificar dependencias más profundas y eliminar el ruido del mercado. Este planteamiento nos permite poner de relieve patrones ocultos en los datos, lo cual resulta fundamental a la hora de prever los precios en el mercado bursátil, donde las señales pueden quedar enmascaradas por el ruido del mercado. Los datos de origen se dividen en subsecuencias que luego se combinan en cada paso de procesamiento para mejorar la detección de patrones significativos.

Esta técnica resulta especialmente útil para analizar activos volátiles como las acciones tecnológicas o las criptomonedas, ya que ayuda a separar las tendencias fundamentales de las fluctuaciones a corto plazo. En lugar de la atención multicabeza estándar utilizada en la arquitectura Transformer, los autores del Hidformer propusieron utilizar un mecanismo de atención recursiva en el codificador temporal y un mecanismo de atención lineal para buscar dependencias en el espectro de frecuencias. Esto redujo el consumo de recursos informáticos y mejoró la estabilidad de las previsiones, lo cual hace que el modelo sea eficaz al procesar grandes cantidades de datos de mercado.

El descodificador del modelo se basa en un perceptrón multicapa, que permite predecir toda la secuencia de precios en un solo paso. Como resultado, se excluyen los errores que podrían acumularse en la previsión paso a paso. Esta arquitectura es especialmente útil para las previsiones financieras, ya que reduce la probabilidad de acumular imprecisiones en la previsión a largo plazo.

A continuación le mostramos la visualización del framework Hidformer realizada por el autor.

Implementación con MQL5

Tras una breve introducción a los aspectos teóricos del framework Hidformer, pasamos a la implementación de nuestra propia visión de los enfoques propuestos usando MQL5. E iniciaremos nuestro trabajo aplicando algoritmos de atención modificados.

En primer lugar, veamos el algoritmo de la atención recursiva propuesta. Originalmente, el algoritmo de atención recursiva se propuso para tareas de diálogo visual, pues encuentra el contexto correcto de la pregunta actual en la historia disponible del diálogo anterior. Obviamente, el procesamiento recursivo de datos, a cambio del cálculo paralelo de la atención multicabeza, dificultará nuestra tarea. Por otro lado, el enfoque recursivo nos permite evitar procesar toda la historia deteniéndonos en el mensaje más cercano encontrado con el contexto adecuado.

Estas reflexiones nos llevan a construir un algoritmo de atención multiescala. Antes ya hemos analizado varios algoritmos para captar características locales y globales cambiando la ventana de atención. Pero entonces usamos diferentes niveles de atención en objetos separados. Ahora propongo modificar ligeramente el algoritmo de atención multicabeza que construimos, dando a cada cabeza su propia ventana de contexto. Además, le propongo definir la ventana de contexto no en torno al elemento analizado, sino desde el principio de la secuencia. Recordemos que almacenamos los datos más recientes al principio de la secuencia. Este enfoque nos permitirá valorar la historia analizada en el contexto de la situación actual del mercado.

Atención a la modificación en el lado OpenCL

En primer lugar, aplicaremos los cambios anteriormente descritos en el lado del programa OpenCL. Para ello crearemos un nuevo kernel MultiScaleRelativeAttentionOut. La mayor parte de su código la transferiremos del kernel donante MHRelativeAttentionOut. La lista de parámetros del kernel se ha mantenido sin cambios.

__kernel void MultiScaleRelativeAttentionOut(__global const float * q,        ///<[in] Matrix of Querys
                                             __global const float * k,        ///<[in] Matrix of Keys
                                             __global const float * v,        ///<[in] Matrix of Values
                                             __global const float * bk,       ///<[in] Matrix of Positional Bias Keys
                                             __global const float * bv,       ///<[in] Matrix of Positional Bias Values
                                             __global const float * gc,       ///<[in] Global content bias vector
                                             __global const float * gp,       ///<[in] Global positional bias vector
                                             __global float * score,          ///<[out] Matrix of Scores
                                             __global float * out,            ///<[out] Matrix of attention
                                             const int dimension              ///< Dimension of Key
                                            )
  {
//--- init
   const uint q_id = get_global_id(0);
   const uint k_id = get_local_id(1);
   const uint h = get_global_id(2);
   const uint qunits = get_global_size(0);
   const uint kunits = get_local_size(1);
   const uint heads = get_global_size(2);
   const int shift_q = dimension * (q_id * heads + h);
   const int shift_kv = dimension * (heads * k_id + h);
   const int shift_gc = dimension * h;
   const int shift_s = kunits * (q_id *  heads + h) + k_id;
   const int shift_pb = q_id * kunits + k_id;
   const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE);
   const uint window = fmax((kunits + h) / (h + 1), fmin(3, kunits));
   float koef = sqrt((float)dimension);

En el cuerpo del método, primero hacemos el trabajo preparatorio. Aquí definimos todas las constantes necesarias, incluida la ventana contextual.

Debemos señalar que no creamos un búfer aparte para transmitir los tamaños de contexto individuales de cada cabeza de atención. En su lugar, simplemente dividimos la longitud de la secuencia analizada por el identificador de la cabeza de atención incrementado en "1", ya que los identificadores empiezan por "0". Así, la primera cabeza de atención analiza toda la secuencia y, a continuación, se realiza una reducción múltiple del contexto a analizar.

A continuación debemos determinar los coeficientes de influencia. Y aquí, cada flujo de operaciones calcula un coeficiente para el elemento correspondiente. Sin embargo, las operaciones solo se realizan dentro de la ventana contextual. Los demás elementos obtienen automáticamente un factor de influencia cero.

   __local float temp[LOCAL_ARRAY_SIZE];
//--- score
   float sc = 0;
   if(k_id < window)
     {
      for(int d = 0; d < dimension; d++)
        {
         float val_q = q[shift_q + d];
         float val_k = k[shift_kv + d];
         float val_bk = bk[shift_kv + d];
         sc += val_q * val_k + val_q * val_bk + val_k * val_bk + gc[shift_q + d] * val_k + 
                                                                 gp[shift_q + d] * val_bk;
        }
      sc = sc / koef;
     }

Para aumentar la estabilidad de la determinación de los coeficientes, implementaremos sus desplazamientos en la zona de validez de los valores. Para ello, buscaremos el valor máximo entre los coeficientes calculados, excluyendo los valores fuera de la ventana contextual.

//--- max value
   for(int cur_k = 0; cur_k < kunits; cur_k += ls)
     {
      if(k_id < window)
         if(k_id >= cur_k && k_id < (cur_k + ls))
           {
            int shift_local = k_id % ls;
            temp[shift_local] = (cur_k == 0 ? sc : fmax(temp[shift_local], sc));
           }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   uint count = min(ls, kunits);
//---
   do
     {
      count = (count + 1) / 2;
      if(k_id < (window + 1) / 2)
         if(k_id < ls)
            temp[k_id] = (k_id < count && (k_id + count) < kunits ? fmax(temp[k_id + count],
                                                                  temp[k_id]) : temp[k_id]);
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Y solo entonces determinaremos el valor exponencial del coeficiente menos el valor máximo.

   if(k_id < window)
      sc = IsNaNOrInf(exp(fmax(sc - temp[0], -120)), 0);
   barrier(CLK_LOCAL_MEM_FENCE);

Sin embargo, debemos prestar especial atención a la ejecución de operaciones dentro de la ventana contextual. Al llevar el valor máximo a "0", hacemos que el exponente máximo resulte igual a "1". Al mismo tiempo, todos los demás coeficientes reciben valores entre 0 y 1. Este enfoque aumenta la estabilidad de la función SoftMax. Pero recordemos que a los coeficientes situados fuera de la ventana contextual se les asignaron valores nulos de forma automática. Calcularlos exponencialmente les daría el coeficiente de influencia máximo, lo cual es muy poco deseable. Por eso debemos dejarlos con "0".

A continuación, sumamos los valores de los coeficientes resultantes en el grupo de trabajo.

//--- sum of exp
   for(int cur_k = 0; cur_k < kunits; cur_k += ls)
     {
      if(k_id >= cur_k && k_id < (cur_k + ls))
        {
         int shift_local = k_id % ls;
         temp[shift_local] = (cur_k == 0 ? 0 : temp[shift_local]) + sc;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   count = min(ls, (uint)kunits);
   do
     {
      count = (count + 1) / 2;
      if(k_id < count && k_id < (window + 1) / 2)
         temp[k_id] += ((k_id + count) < kunits ? temp[k_id + count] : 0);
      if(k_id + count < ls)
         temp[k_id + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Y normalizamos cada coeficiente dividiéndolo por la suma resultante.

//--- score
   float sum = IsNaNOrInf(temp[0], 1);
   if(sum <= 1.2e-7f)
      sum = 1;
   sc /= sum;
   score[shift_s] = sc;
   barrier(CLK_LOCAL_MEM_FENCE);

Los valores normalizados se almacenan en el búfer de datos correspondiente.

Ahora, tras obtener los coeficientes de influencia normalizados de los distintos elementos de la secuencia, podemos definir el valor ajustado del elemento actual. Para ello, organizamos un ciclo en cuyo cuerpo multiplicamos Value por los coeficientes de influencia correspondientes y sumamos los valores obtenidos.

//--- out
   int shift_local = k_id % ls;
   for(int d = 0; d < dimension; d++)
     {
      float val_v = v[shift_kv + d];
      float val_bv = bv[shift_kv + d];
      float val = IsNaNOrInf(sc * (val_v + val_bv), 0);
      //--- sum of value
      for(int cur_v = 0; cur_v < kunits; cur_v += ls)
        {
         if(k_id >= cur_v && k_id < (cur_v + ls))
            temp[shift_local] = (cur_v == 0 ? 0 : temp[shift_local]) + val;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      //---
      count = min(ls, (uint)kunits);
      do
        {
         count = (count + 1) / 2;
         if(k_id < count && (k_id + count) < kunits)
            temp[k_id] += temp[k_id + count];
         if(k_id + count < ls)
            temp[k_id + count] = 0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      //---
      if(k_id == 0)
         out[shift_q + d] = IsNaNOrInf(temp[0], 0);
      barrier(CLK_LOCAL_MEM_FENCE);
     }
  }

Los resultados de las operaciones se guardarán en el búfer de datos correspondiente.

El uso de los coeficientes de influencia cero guardados nos permite utilizar las herramientas existentes para realizar algoritmos de pasada inversa. Por lo tanto, completaremos el trabajo en el lado del programa OpenCL. Puede ver su código completo en el archivo adjunto.

Creación de objetos de atención multiescala

A continuación, debemos crear objetos de atención multiescala al margen del programa principal. Y aquí decidimos usar al máximo la funcionalidad de la herencia de objetos. Y simplemente creamos objetos Self-Attention y Cross-Attention basados en los métodos similares existentes, sobreescribiendo solo el método de llamada al kernel creado anteriormente. A continuación le mostramos la estructura de los nuevos objetos.

class CNeuronMultiScaleRelativeSelfAttention   :  public CNeuronRelativeSelfAttention
  {
protected:
   //---
   virtual bool      AttentionOut(void);

public:
                     CNeuronMultiScaleRelativeSelfAttention(void) {};
                    ~CNeuronMultiScaleRelativeSelfAttention(void) {};
   //---
   virtual int       Type(void) override   const   {  return defNeuronMultiScaleRelativeSelfAttention; }
  };

class CNeuronMultiScaleRelativeCrossAttention   :  public CNeuronRelativeCrossAttention
  {
protected:
   virtual bool      AttentionOut(void);

public:
                     CNeuronMultiScaleRelativeCrossAttention(void) {};
                    ~CNeuronMultiScaleRelativeCrossAttention(void) {};
   //---
   virtual int       Type(void) override   const   {  return defNeuronMultiScaleRelativeCrossAttention; }
  };

Para llamar el kernel, usamos el algoritmo clásico para ponerlo en la cola de ejecución. Ya hemos analizado métodos parecidos muchas veces, así que no le resultará difícil familiarizarse con él. El código completo de los métodos anteriores figura en el archivo adjunto.

El objeto de la atención recursiva

Los objetos de atención multiescala implementados anteriormente nos permiten analizar datos con distintas ventanas de contexto, pero no se trata de la atención recursiva propuesta por los autores del framework Hidformer. Solo hemos hecho el trabajo preparatorio.

La siguiente etapa de nuestro trabajo consiste en construir un objeto de atención recursiva que nos permita analizar los datos actuales en el contexto de la historia observada previamente. Para ello, aprovecharemos algunos avances en el campo de la construcción de módulos de memoria. En concreto, mantendremos un contexto de estados observados en una profundidad histórica determinada, que se usará para estimar el estado actual. Implementamos dicho algoritmo dentro del método CNeuronRecursiveAttention, cuya estructura presentamos a continuación.

class CNeuronRecursiveAttention  :  public CNeuronMultiScaleRelativeCrossAttention
  {
protected:
   CNeuronMultiScaleRelativeSelfAttention cSelfAttention;
   CNeuronTransposeOCL  cTransposeSA;
   CNeuronConvOCL       cConvolution;
   CNeuronEmbeddingOCL  cHistory;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
   override  { return false; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput,
                                        CBufferFloat *SecondGradient,
                                        ENUM_ACTIVATION SecondActivation = None)
   override  { return false; }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
   override  { return false; }

public:
                     CNeuronRecursiveAttention(void) {};
                    ~CNeuronRecursiveAttention(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint history_size,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronRecursiveAttention; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual bool      Clear(void) override;
  };

Como clase padre, en este caso, usaremos el objeto de atención cruzada multiescala implementado anteriormente.

En el cuerpo del método vemos el conjunto habitual de métodos virtuales redefinidos y una serie de objetos internos, cuyo propósito conoceremos durante la construcción de los algoritmos de pasada directa e inversa.

Todos los objetos internos se declaran estáticos, lo cual nos permite dejar vacíos el constructor y el destructor de la clase, mientras que la inicialización de todos los objetos heredados y declarados se realiza en el método Init.

bool CNeuronRecursiveAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                        uint window, uint window_key, uint units_count,
                                                         uint heads, uint history_size,
                                       ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronMultiScaleRelativeCrossAttention::Init(numOutputs, myIndex, open_cl, window,
                                               window_key, units_count, heads, window_key,
                                                  history_size, optimization_type, batch))
      return false;

En los parámetros del método obtenemos una serie de constantes que nos permiten interpretar sin ambigüedades la arquitectura del objeto creado. Y aquí debemos señalar que, a pesar de heredar de la clase de atención cruzada, nuestro objeto trabaja con un único flujo de datos de origen. El segundo flujo de información necesario para el correcto funcionamiento de los métodos de la clase padre se construye dentro de nuestro objeto. Y el tamaño de la secuencia analizada del segundo flujo de información se establece como la profundidad de la historia del contexto almacenado history_size.

En el cuerpo del método, como viene siendo tradición, llamamos al método homónimo de la clase padre, transmitiéndole el conjunto de parámetros necesarios. Recordemos que el método de la clase padre ya implementa los puntos de control necesarios y la inicialización de todos los objetos heredados, incluidas las interfaces básicas.

A continuación inicializamos los objetos internos recién declarados. Y el primero de nuestra lista es el objeto Self-Attention multiescala.

   int index = 0;
   if(!cSelfAttention.Init(0, index, OpenCL, iWindow, iWindowKey, iUnits, iHeads, 
                                                           optimization, iBatch))
      return false;

El uso de este objeto permite determinar los elementos de los datos de entrada que tienen la máxima influencia en el estado actual del instrumento financiero analizado.

A continuación, debemos añadir el contexto del estado actual del entorno a la memoria de nuestra unidad de atención recursiva. Al hacerlo, queremos preservar el contexto de las secuencias unitarias individuales. Por ello, primero transponemos los datos de origen.

   index++;
   if(!cTransposeSA.Init(0, index, OpenCL, iUnits, iWindow, optimization, iBatch))
      return false;

A continuación, extraemos el contexto de las secuencias unitarias usando la capa convolucional.

   index++;
   if(!cConvolution.Init(0, index, OpenCL, iUnits, iUnits, iWindowKey, 1, iWindow,
                                                            optimization, iBatch))
      return false;

Nótese que en los parámetros de la capa de convolución indicamos un elemento de la secuencia analizada, y transmitimos el número de secuencias unitarias al parámetro del número de variables independientes. Este enfoque nos permite realizar análisis totalmente independientes de secuencias unitarias, ya que usamos un conjunto individual de parámetros entrenados para extraer el contexto de cada una. Esto nos permite realizar un análisis más profundo de la secuencia multimodal original.

A continuación, utilizamos la capa de generación de incorporaciones para capturar el contexto del estado del entorno analizado y añadirlo a la pila de memoria de la secuencia histórica.

   index++;
   uint windows[] = { iWindowKey * iWindow };
   if(!cHistory.Init(0, index, OpenCL, iUnitsKV, iWindowKey, windows))
      return false;
//---
   return true;
  }

Una vez que todas las operaciones se han ejecutado correctamente, retornamos el resultado lógico de su trabajo al programa que realiza la llamada y finalizamos el método.

Nuestro siguiente paso consiste en implementar el método feedForward, cuyo algoritmo parece bastante lineal.

bool CNeuronRecursiveAttention::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cSelfAttention.FeedForward(NeuronOCL))
      return false;

En los parámetros del método, obtenemos el puntero al objeto de datos de origen que contiene las series temporales multimodales. El puntero resultante se transmite inmediatamente al módulo Self-Attention para analizar las dependencias en la descripción actual del estado del entorno. Luego transponemos los resultados de los análisis para facilitar su tratamiento posterior.

   if(!cTransposeSA.FeedForward(cSelfAttention.AsObject()))
      return false;

Y extraemos el contexto de las secuencias unitarias usando la capa de convolución.

   if(!cConvolution.FeedForward(cTransposeSA.AsObject()))
      return false;

Después pasamos los datos preparados al objeto de generación de incorporación, donde se extrae el contexto del estado analizado y se añade a la pila de memoria.

   if(!cHistory.FeedForward(cConvolution.AsObject()))
      return false;

Ahora nos queda enriquecer los resultados del análisis anterior en el bloque Self-Attention con el contexto de la secuencia histórica observada anteriormente. Para ello, usaremos el método homónimo de la clase padre, transmitiéndole la información necesaria.

   return CNeuronMultiScaleRelativeCrossAttention::feedForward(cSelfAttention.AsObject(),
                                                                   cHistory.getOutput());
  }

Aquí cabe señalar que usaremos el objeto de atención multiescala que creamos antes para analizar el estado actual en el contexto de los estados observados anteriormente. Este enfoque nos permite asignar más peso a los datos de la historia inmediata, reduciendo su importancia a lo largo del tiempo. No obstante, también tenemos la opción de recuperar puntos clave de las "profundidades de la memoria".

Cuando el método finalice, retornaremos el resultado lógico de las operaciones al programa que realiza la llamada.

Debido a la aparente simplicidad del método de pasada directa, resulta fácil pasar por alto el doble uso de los resultados del objeto de Self-Attention multiescala. Sin embargo, esta circunstancia impone una sobrecarga en el algoritmo de pasada inversa que implementamos en el método calcInputGradients.

bool CNeuronRecursiveAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

En los parámetros del método de pasada inversa, obtenemos el puntero al mismo objeto de datos de origen, solo que ahora tenemos que pasarle el gradiente de error correspondiente a su efecto sobre el resultado del modelo.

En el cuerpo del método comprobamos directamente la relevancia del puntero obtenido, porque de lo contrario no podemos transmitir los datos a un objeto inexistente, y las operaciones posteriores carecerán de sentido. Por ello, continuaremos trabajando con el método solo si pasamos con éxito este punto de control.

Como ya sabe, los flujos de información de las pasadas directa e inversa se corresponden por completo, solo que tienen un carácter opuesto. Ya hemos completado el método de pasada directa llamando al método homónimo de la clase padre. Como consecuencia, las operaciones de pasada inversa se iniciarán llamando al método heredado. Este distribuirá el gradiente de error obtenido previamente entre los dos flujos de información según su influencia en el resultado final.

   if(!CNeuronMultiScaleRelativeCrossAttention::calcInputGradients(cSelfAttention.AsObject(),
                                                                        cHistory.getOutput(),
                                                                      cHistory.getGradient(),
                                                     (ENUM_ACTIVATION)cHistory.Activation()))
      return false;

Primero asignamos el gradiente de error del flujo de información auxiliar que se corresponde con la memoria de nuestro objeto. Aquí reducimos el error a la capa convolucional de extracción del contexto de secuencias unitarias.

   if(!cConvolution.calcHiddenGradients(cHistory.AsObject()))
      return false;

Y hasta la capa de transposición de resultados del bloque Self-Attention.

   if(!cTransposeSA.calcHiddenGradients(cConvolution.AsObject()))
      return false;

Ahora debemos pasar el gradiente de error a la capa de Self-Attention multiescala. Pero previamente hemos transmitido el gradiente de error del flujo de información principal que necesitamos preservar. Para ello, utilizamos la sustitución de punteros en los búferes de datos. En primer lugar, pasamos al objeto el puntero al búfer libre, guardando previamente el búfer existente.

   CBufferFloat *temp = cSelfAttention.getGradient();
   if(!cSelfAttention.SetGradient(cTransposeSA.getPrevOutput(), false) ||
      !cSelfAttention.calcHiddenGradients(cTransposeSA.AsObject()) ||
      !SumAndNormilize(temp, cSelfAttention.getGradient(), temp, iWindow, false, 0, 0, 0, 1) ||
      !cSelfAttention.SetGradient(temp, false))
      return false;

Y luego bajamos el gradiente de error y sumamos los valores de los dos flujos de información. Después, devolvemos al estado inicial los punteros a los búferes de datos.

Ahora lo único que debemos hacer es pasar el gradiente de error a la capa de datos de origen.

   if(!NeuronOCL.calcHiddenGradients(cSelfAttention.AsObject()))
      return false;
//---
   return true;
  }

Y al final del método, retornamos el resultado lógico de las operaciones al programa que realiza la llamada.

Puede leer el código completo de este objeto y todos sus métodos por sí mismo en el archivo adjunto.

El objeto de atención lineal

Además del objeto de atención recursiva implementado, los autores del framework propusieron usar la atención lineal en la torre de análisis del espectro de frecuencias.

La atención lineal ("Linear Attention") es una forma de optimizar el mecanismo de atención tradicional en los transformadores. A diferencia de la Self-Attention clásica, que utiliza operaciones matriciales completamente conectadas con complejidad cuadrática, la atención lineal reduce la complejidad computacional, lo cual la hace eficaz para procesar secuencias largas.

En la atención lineal se introduce una descomposición de las funciones φ(Q) y φ(K) que nos permite representar la atención como:

Ventajas de la atención lineal

1. Complejidad lineal: coste computacional reducido, lo cual permite procesar secuencias largas.
2. Menor consumo de memoria: no es necesario almacenar la matriz completa de coeficientes de dependencia Score, lo cual reduce la cantidad de memoria necesaria.
3. Eficacia en tareas en línea: la atención lineal resulta adecuada para el procesamiento de datos en flujo porque las actualizaciones son incrementales.
4. Flexibilidad en la elección de las funciones del kernel: el uso de diferentes funciones φ(x) puede adaptar la atención a las particularidades del problema.

La implementación del algoritmo de atención lineal se representa en el objeto CNeuronLinerAttention, cuya estructura mostramos a continuación.

class CNeuronLinerAttention   :  public CNeuronBaseOCL
  {
protected:
   uint                 iWindow;
   uint                 iWindowKey;
   uint                 iUnits;
   uint                 iVariables;
   //---
   CNeuronConvOCL       cQuery;
   CNeuronConvOCL       cKey;
   CNeuronTransposeVRCOCL  cKeyT;
   CNeuronBaseOCL       cKeyValue;
   CNeuronBaseOCL       cAttentionOut;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronLinerAttention(void) {};
                    ~CNeuronLinerAttention(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key,
                          uint units_count, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronLinerAttention; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Aquí vemos un conjunto básico de métodos redefinidos y algunos objetos internos que juegan un papel clave en el algoritmo que estamos construyendo. Nos familiarizaremos con su funcionalidad con más detalle durante la implementación de los métodos de la nueva clase.

Todos los métodos declarados se crean estáticamente, lo cual nos permite dejar el constructor y el destructor de la clase vacíos, mientras que la inicialización de todos los objetos heredados y declarados se realiza en Init. En los parámetros de este método obtenemos una serie de parámetros que nos permiten definir de forma inequívoca la arquitectura del objeto creado.

bool CNeuronLinerAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                 uint window, uint window_key, uint units_count,
                                 uint variables, ENUM_OPTIMIZATION optimization_type,
                                 uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables,
                                                                 optimization_type, batch))
      return false;

En el cuerpo del método, llamamos inmediatamente al método homónimo de la clase padre. En este caso, se trata de una capa totalmente conectada.

A continuación, guardamos los parámetros clave de la arquitectura en variables internas. E inicializamos los objetos internos.

   iWindow = window;
   iWindowKey = fmax(window_key, 1);
   iUnits = units_count;
   iVariables = variables;

Aquí inicializamos primero las capas convolucionales de generación de las entidades Query y Key. Al generar las consultas, usamos una función de activación sigmoidal que indicará la proporción de influencia de otros elementos sobre el objeto.

   int index = 0;
   if(!cQuery.Init(0, index, OpenCL, iWindow, iWindow, iWindowKey, iUnits, iVariables,
                                                                optimization, iBatch))
      return false;
   cQuery.SetActivationFunction(SIGMOID);
   index++;
   if(!cKey.Init(0, index, OpenCL, iWindow, iWindow, iWindowKey, iUnits, iVariables, 
                                                                optimization, iBatch))
      return false;
   cKey.SetActivationFunction(TANH);

Y para las claves, usamos como función de activación la tangente hiperbólica, lo cual nos permitirá determinar la influencia directa e inversa del elemento correspondiente.

Aquí es también donde inicializamos el objeto Key de transposición de la matriz.

   index++;
   if(!cKeyT.Init(0, index, OpenCL, iVariables, iUnits, iWindowKey, optimization, iBatch))
      return false;
   cKeyT.SetActivationFunction(TANH);

Y un objeto para registrar el producto de las matrices Key y Value.

   index++;
   if(!cKeyValue.Init(0, index, OpenCL, iWindow * iWindowKey, optimization, iBatch))
      return false;
   cKeyValue.SetActivationFunction(None);

Tenga en cuenta que no estamos usando la capa de generación de entidades Value. En su lugar, tenemos previsto utilizar directamente los datos de origen.

Los resultados de la atención se guardan en un objeto interno especialmente creado,

   index++;
   if(!cAttentionOut.Init(0, index, OpenCL, Neurons(), optimization, iBatch))
      return false;
   cAttentionOut.SetActivationFunction(None);

mientras que para crear los enlaces residuales utilizamos las interfaces de la clase padre. Por consiguiente, utilizaremos la sustitución de punteros por el búfer de gradiente de error, lo cual eliminará operaciones innecesarias de copiado de datos.

   if(!SetGradient(cAttentionOut.getGradient(), true))
      return false;
//---
   return true;
  }

Y antes de terminar, retornaremos el resultado lógico de las operaciones al programa que realiza la llamada.

Una vez finalizado el trabajo de inicialización de objetos, pasamos a construir el algoritmo de pasada directa dentro del método feedForward.

bool CNeuronLinerAttention::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cQuery.FeedForward(NeuronOCL))
      return false;
   if(!cKey.FeedForward(NeuronOCL) ||
      !cKeyT.FeedForward(cKey.AsObject()))
      return false;

En los parámetros del método obtenemos el puntero al objeto de secuencia de datos fuente multidimensional, que utilizamos inmediatamente para formar las entidades Query y Key.

A continuación, determinamos el efecto de cada objeto en la secuencia analizada, multiplicando la matriz Key transpuesta por los datos de origen.

   if(!MatMul(cKeyT.getOutput(), NeuronOCL.getOutput(), cKeyValue.getOutput(),
                                     iWindowKey, iUnits, iWindow, iVariables))
      return false;

Para obtener resultados de atención lineal, multiplicamos el tensor Query por el resultado de la operación anterior.

   if(!MatMul(cQuery.getOutput(), cKeyValue.getOutput(), cAttentionOut.getOutput(),
                                          iUnits, iWindowKey, iWindow, iVariables))
      return false;

Ahora solo nos queda añadir los enlaces residuales y normalizar los resultados de la operación.

   if(!SumAndNormilize(NeuronOCL.getOutput(), cAttentionOut.getOutput(), Output,
                                                     iWindow, true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

Después devolvemos el resultado lógico de las operaciones al programa que realiza la llamada y finalizamos el método.

A continuación debemos organizar la distribución de los gradientes de error entre todos los objetos internos y los datos de entrada según su influencia en la salida del modelo. Como es habitual, realizamos estas operaciones en el método calcInputGradients, en cuyos parámetros obtenemos el puntero al objeto de datos de origen. Solo que esta vez se usará para registrar los resultados del trabajo.

bool CNeuronLinerAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

En el cuerpo del método comprobamos directamente la relevancia del puntero obtenido. Ya hemos hablado antes de la importancia de superar este punto de control.

Luego sustituimos los punteros al búfer de datos, y el gradiente de error obtenido de la capa neuronal descendente se incluye automáticamente en el objeto interior de los resultados de la atención lineal. Y luego lo distribuimos por los flujos de información.

   if(!MatMulGrad(cQuery.getOutput(), cQuery.getGradient(),
                  cKeyValue.getOutput(), cKeyValue.getGradient(),
                  cAttentionOut.getGradient(),
                  iUnits, iWindowKey, iWindow, iVariables))
      return false;
   if(!MatMulGrad(cKeyT.getOutput(), cKeyT.getGradient(),
                  NeuronOCL.getOutput(), cAttentionOut.getPrevOutput(),
                  cKeyValue.getGradient(),
                  iWindowKey, iUnits, iWindow, iVariables))
      return false;

Nótese aquí que debemos transmitir el gradiente de error por 4 flujos de información a la capa de datos de origen:

• la entidad Query;
• la entidad Key;
• el producto Key*Value;
• los enlaces residuales.

En la última operación, almacenamos el gradiente de error del producto Key*Value en un búfer libre, mientras que el gradiente de los enlaces residuales se transfiere completamente desde el nivel de resultados del objeto actual. También debemos decir que estos gradientes no están corregidos para la derivada de la función de activación del objeto de datos de origen. Sin embargo, cuando el gradiente de error se distribuye por las capas convolucionales de generación de entidades, se corrige por la derivada de la función de activación. Con el fin de obtener datos comparables para todos los flujos de información, sumamos los valores disponibles y ajustamos la derivada de la función de activación del objeto de datos de origen. Luego guardamos los resultados en un búfer de datos libre.

   if(!SumAndNormilize(Gradient, cAttentionOut.getPrevOutput(), cAttentionOut.getPrevOutput(),
                       iWindow, false, 0, 0, 0, 1))
      return false;
//---
   if(NeuronOCL.Activation() != None)
      if(!DeActivation(NeuronOCL.getOutput(), cAttentionOut.getPrevOutput(),
                       cAttentionOut.getPrevOutput(), NeuronOCL.Activation()))
         return false;

Asimismo, corregimos los gradientes de error en los otros flujos de información usando las derivadas de las funciones de activación correspondientes.

   if(cKeyT.Activation() != None)
      if(!DeActivation(cKeyT.getOutput(), cKeyT.getGradient(),
                       cKeyT.getGradient(), cKeyT.Activation()))
         return false;
   if(cQuery.Activation() != None)
      if(!DeActivation(cQuery.getOutput(), cQuery.getGradient(),
                       cQuery.getGradient(), cQuery.Activation()))
         return false;

Luego distribuimos el gradiente de error según el flujo de información de la entidad Key y lo sumamos con los datos acumulados previamente.

   if(!cKey.calcHiddenGradients(cKeyT.AsObject()) ||
      !NeuronOCL.calcHiddenGradients(cKey.AsObject()) ||
      !SumAndNormilize(NeuronOCL.getGradient(), cAttentionOut.getPrevOutput(),
                       cAttentionOut.getPrevOutput(), iWindow, false, 0, 0, 0, 1))
      return false;

Del mismo modo, pasamos el error a lo largo del flujo de información de la entidad Query, tras lo cual transmitimos el gradiente de error total al objeto de datos de origen.

   if(!NeuronOCL.calcHiddenGradients(cQuery.AsObject()) ||
      !SumAndNormilize(NeuronOCL.getGradient(), cAttentionOut.getPrevOutput(),
                       NeuronOCL.getGradient(), iWindow, false, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

Al final de las operaciones de los métodos, retornamos el resultado lógico de su ejecución al programa que realiza la llamada.

Con esto concluirá nuestra revisión de algoritmos para construir los métodos lineales de objetos de atención. Puede ver el código completo de esta clase y todos sus métodos en el archivo adjunto.

Hemos hecho un buen trabajo, pero, de momento, hemos alcanzado el final del artículo. Finalizaremos lo iniciado en el próximo artículo, donde lo llevaremos a su conclusión lógica.

Conclusión

Hoy nos hemos familiarizado con el framework Hidformer, que ha demostrado su eficacia en la predicción de series temporales, incluidos los datos financieros. Este dispone de un codificador de doble torre con análisis separado de los datos de origen en forma de secuencia temporal y sus características de frecuencia. Esto dota al Hidformer de una gran flexibilidad y adaptabilidad a las diferentes condiciones del mercado.

En la parte práctica del artículo, hemos implementado algunos componentes propuestos por los autores del framework Hidformer. Pero nuestro trabajo aún no ha terminado; lo continuaremos en un futuro próximo.

Enlaces

• Hidformer: Transformer-Style Neural Network in Stock Price Forecasting
• Hidformer: Hierarchical dual-tower transformer using multi-scale mergence for long-term time series forecasting
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema y la arquitectura del modelo
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código del programa OpenCL