Redes neuronales en el trading: Modelo Universal de Generación de Trayectorias (UniTraj)

Introducción

El análisis del comportamiento multiagente tiene gran importancia en diversos ámbitos, como las finanzas, la conducción autónoma y los sistemas de videovigilancia. Para comprender las acciones de los agentes, resulta necesario abordar una serie de tareas clave, como el seguimiento y la identificación de objetos, la modelización de trayectorias y el reconocimiento de acciones. El modelado de trayectorias desempeña un papel importante en el proceso de análisis de los movimientos de los agentes. A pesar de las dificultades vinculadas con la dinámica del entorno y las sutiles interacciones entre agentes, recientemente se han logrado avances significativos en esta tarea. Los principales avances se centran en tres áreas clave: predicción de trayectorias, recuperación de datos perdidos y modelización espaciotemporal.

No obstante, la mayoría de los enfoques están especializados en tareas específicas, y son difíciles de generalizar a otras tareas. La resolución de algunos problemas requiere el uso de dependencias espaciotemporales tanto directas como inversas que no suelen considerarse en los modelos orientados a la previsión. Otros algoritmos han resuelto el problema del cálculo condicional de las trayectorias de varios agentes, pero pasando por alto a menudo las futuras trayectorias de los agentes, lo cual limita su utilidad práctica a la hora de comprender por completo los movimientos donde la predicción de trayectorias futuras resulta crucial para planificar fases posteriores en lugar de limitarse a reconstruir trayectorias históricas.

En el artículo "Deciphering Movement: Unified Trajectory Generation Model for Multi-Agent" se presenta el modelo universal Unified TrajectoryGeneration (UniTraj), que integra diversas tareas de trayectoria en un marco común. En concreto, los autores del método combinan distintos tipos de datos de entrada en una única forma unificada: una trayectoria aleatoria incompleta con una máscara que indica la visibilidad de cada agente en cada paso temporal. El modelo procesa de manera uniforma los datos de origen de cada tarea como trayectorias enmascaradas para crear trayectorias completas a partir de las incompletas.

Para modelar las dependencias espaciotemporales en distintas representaciones de la trayectoria, los autores del método proponen el módulo Ghost Spatial Masking (GSM) integrado en un codificador basado en el Transformer. Usando las capacidades de los recientes modelos de espacio de estados (SSM) populares, especialmente el modelo Mamba, los autores adaptan y mejoran el método en un codificador temporal Mamba bidireccional para la generación a largo plazo de trayectorias multiagente. Además, proponen el sencillo pero eficaz módulo Bidirectional Temporal Scaled (BTS), que escanea exhaustivamente las trayectorias manteniendo la integridad de las relaciones temporales en la secuencia. Los resultados experimentales presentados en el artículo del autor confirman el rendimiento estable y excepcional del método propuesto.

1. Algoritmo UniTraj

Para procesar diferentes condiciones iniciales dentro de un marco único, los autores del método proponen un modelo de trayectoria generativo y unificado que procesa cualquier entrada arbitraria como una secuencia de trayectoria enmascarada. Las regiones visibles de la trayectoria se usan como restricciones o entradas, mientras que las regiones faltantes son objetivos para resolver el problema generativo. Y así se forma la siguiente definición del problema:

Necesitamos definir una trayectoria completa X[N, T, D], donde N es el número de agentes, T representa la longitud de la trayectoria y D supone la dimensionalidad de los estados de los agentes. Denotaremos los estados del agente i en el tiempo t como xi,t[D]. Además, usaremos una matriz binaria de enmascaramiento M[N, T]. La variable mi,t tendrá el valor 1 si se conoce la ubicación del agente i en el momento t, y 0 en caso contrario. Así, la trayectoria quedará dividida por la máscara en dos segmentos: la región visible, definida como Xv=X⊙M, y la ausencia de región, definida como Xm=X⊙(1−M). El objetivo de la tarea consistirá en generar una trayectoria completa Y'={X'v,X'm}, donde X'v será la trayectoria reconstruida y X'm será la nueva trayectoria generada. Por coherencia, los autores del método se refieren a la trayectoria original como la verdad fundamental Y=X={Xv, Xm}.

De manera más formal, el objetivo consistirá en entrenar un modelo generativo f(⋅) con parámetros θ que produzca la trayectoria completa Y'.

El enfoque general para estimar los parámetros del modelo θ implica la descomposición multiplicadora de la distribución conjunta de la trayectoria y la maximización de la verosimilitud logarítmica.

Consideraremos el uso del agente i en el paso de tiempo t con la posición xi,t. Primero calcularemos la velocidad relativa 𝒗i,t restando las coordenadas de los pasos temporales adyacentes. Para los lugares faltantes, rellenaremos los valores con 0, multiplicando elemento por elemento por la máscara. Además, definiremos un vector de una categoría 𝒄i,t para representar las categorías de los agentes. Esta categorización resulta crucial en los juegos deportivos, en los que los jugadores pueden utilizar determinadas estrategias ofensivas o defensivas. Las características del agente se proyectarán sobre un vector de características de alta dimensionalidad 𝒇i,xt. Los vectores de características iniciales se calcularán del modo siguiente:

donde φx(⋅) es una función proyectiva con pesos 𝐖x, ⊙ representa la multiplicación elemento a elemento y ⊕ indica la concatenación.

Los autores del método introducen φx(⋅) utilizando MLP. Este enfoque permite incorporar información sobre localización, velocidad, visibilidad y categoría para extraer entidades espaciales y analizarlas posteriormente.

A diferencia de otras tareas de modelización secuencial, para nosotros será crucial considerar las interacciones sociales densas. La investigación existente sobre las interacciones humanas usa predominantemente mecanismos de atención como la atención cruzada y la atención gráfica para captar esta dinámica. Sin embargo, como UniTraj resuelve un único problema con datos de entrada arbitrariamente incompletos, resulta importante que el modelo propuesto explore los patrones de ausencia espaciales y temporales. Los autores del método proponen un nuevo y eficaz módulo Ghost Spatial Masking (GSM) para abstraer y generalizar las estructuras espaciales de los datos que faltan. Este módulo puede integrarse perfectamente en el Transformer sin complicar la estructura del modelo.

El Transformer se propuso originalmente para modelar dependencias temporales de datos secuenciales, y los autores de UniTraj aplican un diseño de Self-Attention multicabeza en la dimensión espacial. En cada paso temporal, se considera la incorporación de cada uno de los N agentes y se transmite como datos de entrada al codificador del Transformer. Este enfoque está diseñado para extraer características espaciales invariantes del orden de los agentes, dada cualquier posible disposición del orden de los agentes que pueda darse en la práctica. Por ello, en este caso, será preferible sustituir la codificación de posición sinusoidal por una codificación totalmente entrenable.

Como resultado, el codificador del Transformer producirá objetos espaciales Fs,xt para todos los agentes en cada paso temporal t. A continuación, estos objetos se concatenarán a lo largo de la dimensión temporal para obtener características espaciales a lo largo de toda la trayectoria.

Dada la capacidad del modelo Mamba para captar dependencias temporales a largo plazo, los autores de UniTraj lo han adaptado para integrarlo en la infraestructura propuesta. Sin embargo, adaptar el modelo Mamba para generar una trayectoria única supone todo un reto, debido principalmente a la falta de una arquitectura específicamente adaptada a las trayectorias del modelo. La modelización eficaz de las trayectorias requerirá una captura cuidadosa de las características espaciotemporales, lo cual se ve complicado por el carácter incompleto de las trayectorias.

Para mejorar la eficacia de la extracción temporal de objetos preservando las relaciones faltantes, se introducirá una Mamba temporal bidireccional. Esta adaptación incorporará varios bloques Mamba residuales emparejados con el innovador módulo Bidirectional Temporal Scaled (BTS).

Inicialmente, se procesará la máscara M de toda la trayectoria. La desplegaremos a lo largo de la dimensión temporal para producir M', lo cual facilitará el entrenamiento del modelo para las relaciones temporales ausentes utilizando tanto la máscara original como la invertida en el módulo BTS. Este proceso generará una matriz de escalado S y su correspondiente versión inversa S'. En concreto, para el agente i en el paso temporal t, si,t se calculará del siguiente modo:

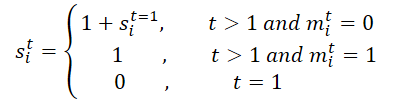
A continuación, proyectaremos la matriz de escalado S y su versión invertida S' en la matriz de características del siguiente modo:

donde φs(⋅) serán funciones proyectivas con pesos 𝐖s.

Los autores del método implementan φs(⋅) utilizando MLP y la función de activación ReLU. La matriz de escalado propuesta está diseñada para calcular la distancia entre la última observación y el paso temporal actual, lo cual ayuda a cuantificar el impacto de las lagunas temporales, especialmente cuando se trata de patrones perdidos complejos. La idea es que la influencia de una variable que ha estado ausente durante cierto tiempo disminuye con el tiempo. Y usando una función exponencial negativa y ReLU podremos garantizar que el impacto decaerá de forma monótona en un rango razonable entre 0 y 1.

El proceso de codificación descrito anteriormente está diseñado para determinar los parámetros de la distribución gaussiana para la posterior aproximada. En concreto, la media μq y la desviación típica σq de la distribución gaussiana posterior se calculan del siguiente modo:

Muestreamos las variables latentes 𝒁 a partir de una distribución gaussiana a priori 𝒩(0, I).

Para mejorar la capacidad del modelo de generar trayectorias plausibles, combinaremos esta función Fz,x con la variable latente 𝒁 antes de suministrarla al descodificador. A continuación se calculará el proceso de generación de trayectorias:

donde φdec será la función decodificadora implementada mediante MLP.

Dada una trayectoria incompleta arbitraria, el modelo UniTraj generará una trayectoria completa. Durante el entrenamiento, se calculará el error de reconstrucción de las regiones visibles y el error de reconstrucción de los datos enmascarados.

A continuación, le mostramos la versión de autor del método UniTraj.

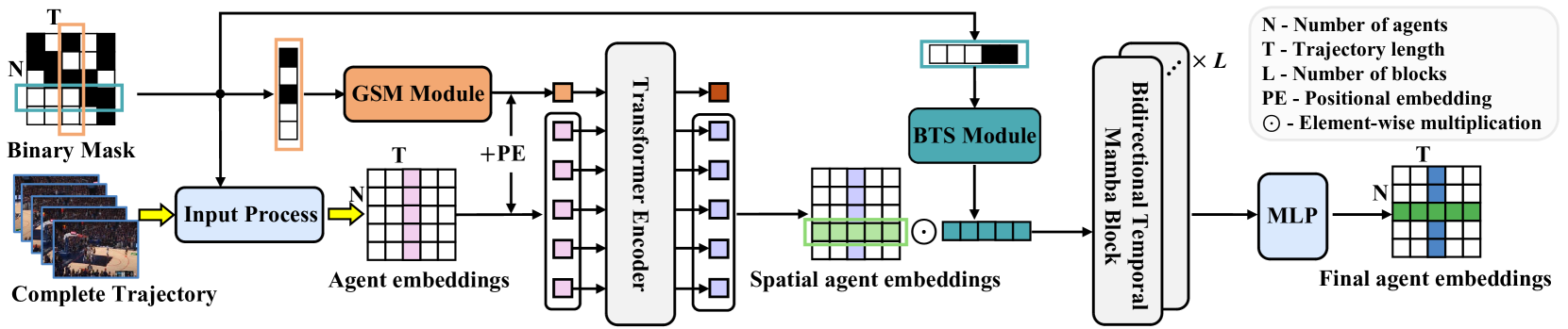
2. Implementación usando los recursos MQL5

Tras considerar la descripción teórica del método UniTraj propuesto, vamos a pasar, como es habitual, a la parte práctica de nuestro artículo, donde implementaremos nuestra visión de los enfoques propuestos utilizando herramientas MQL5. Y aquí debemos señalar inmediatamente que el algoritmo propuesto diferirá constructivamente de los métodos que hemos analizado.

Lo primero será, por supuesto, el proceso de enmascaramiento. Al transmitir los datos iniciales al modelo, los autores del método nos sugieren preparar una máscara adicional que determine qué datos ve el modelo y qué datos debe generar. Esto nos añadirá un poco más de trabajo. Y en este caso, aumentará el tiempo de decisión, lo cual no resulta deseable. Por ello, querríamos organizar la generación de máscaras dentro del modelo.

El segundo punto consistirá en transferir la trayectoria completa al modelo. Y aunque podemos obtenerla durante las pruebas, no podremos hacerlo durante la explotación. Obviamente, el modelo permite enmascarar los datos faltantes con su posterior recuperación. Pero en cualquier caso necesitaremos transferir un tensor de mayor volumen al modelo, lo cual conllevará un mayor consumo de memoria y una carga extra en la transferencia de volumen adicional. Y esto también afectará al tiempo de toma de decisiones.

Claro que podemos limitarnos a transmitir únicamente datos históricos durante el entrenamiento y la explotación, pero entonces se perderá gran parte de la funcionalidad del método propuesto.

Así que hemos decidido dividir el volumen de transferencia de datos en 2 partes: datos históricos y trayectoria futura. Esta última se suministrará solo durante el entrenamiento del modelo para extraer las dependencias espaciotemporales. En el modo de explotación del modelo, el tensor de valores futuros no se transmitirá y el modelo funcionará en modo de predicción de datos.

Y, obviamente, en este artículo hemos tenido que hacer algunas adiciones en la parte OpenCL del programa.

2.1 Complementando el programa OpenCL

En la primera fase de nuestro artículo, prepararemos nuevos kernels en el lado OpenCL del programa. En primer lugar, crearemos un kernel de preparación de datos UniTrajPrepare. En el cuerpo de un kernel dado, concatenaremos los datos históricos y la información conocida sobre el movimiento posterior, considerando el enmascaramiento.

En los parámetros del kernel obtendremos los punteros a 5 búferes de datos: 4 de datos de origen y 1 de resultados. Y también las dimensiones de la profundidad de la historia analizada y el horizonte de planificación.

__kernel void UniTrajPrepare(__global const float *history,
                             __global const float *h_mask,
                             __global const float *future,
                             __global const float *f_mask,
                             __global float *output,
                             const int h_total,
                             const int f_total
                            )
  {
   const size_t i = get_global_id(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

Planificaremos la ejecución del kernel en un espacio de tareas bidimensional. La primera dimensión tendrá el tamaño del mayor de los 2 periodos de tiempo (profundidad de la historia y horizonte de planificación). La segunda dimensión indicará el número de parámetros que deben analizarse.

En el cuerpo del kernel, primero identificaremos un flujo en un espacio de tareas determinado. Y determinaremos el desplazamiento en los búferes de datos.

   const int shift_in = i * variables + v;
   const int shift_out = 3 * shift_in;
   const int shift_f_out = 3 * (h_total * variables + v);

A continuación, trabajaremos con los datos históricos. En primer lugar, determinaremos la velocidad de cambio del parámetro con respecto a la máscara. Y luego guardaremos en el búfer de resultados el valor del parámetro considerando la máscara, la velocidad calculada anteriormente y la propia máscara.

//--- history
   if(i < h_total)
     {
      float mask = h_mask[shift_in];
      float h = history[shift_in];
      float v = (i < (h_total - 1) && mask != 0 ? (history[shift_in + variables] - h) * mask : 0);
      if(isnan(v) || isinf(v))
         v = h = mask = 0;
      output[shift_out] = h * mask;
      output[shift_out + 1] = v;
      output[shift_out + 2] = mask;
     }

También calcularemos parámetros similares para valores futuros.

//--- future
   if(i < f_total)
     {
      float mask = f_mask[shift_in];
      float f = future[shift_in];
      float v = (i < (f_total - 1) && mask != 0 ? (future[shift_in + variables] - f) * mask : 0);
      if(isnan(v) || isinf(v))
         v = f = mask = 0;
      output[shift_f_out + shift_out] = f * mask;
      output[shift_f_out + shift_out + 1] = v;
      output[shift_f_out + shift_out + 2] = mask;
     }
  }

A continuación, guardaremos el kernel de la pasada inversa de las operaciones UniTrajPrepareGrad anteriores.

__kernel void UniTrajPrepareGrad(__global float *history_gr,
                                 __global float *future_gr,
                                 __global const float *output,
                                 __global const float *output_gr,
                                 const int h_total,
                                 const int f_total
                                )
  {
   const size_t i = get_global_id(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

Tenga en cuenta que no especificaremos punteros a los búferes de datos de origen y la máscara en los parámetros del método de pasada inversa. En su lugar, utilizaremos el búfer de resultados del kernel de pasada directa UniTrajPrepare donde se almacenan los datos especificados. Además, no transmitiremos el gradiente de error al nivel de la máscara, ya que no tiene sentido.

El espacio de tareas del kernel de pasada inversa será idéntico al comentado anteriormente para el kernel de pasada directa.

En el cuerpo del kernel, identificaremos el flujo actual en el espacio de tareas y determinaremos el desplazamiento en los búferes de datos.

   const int shift_in = i * variables + v;
   const int shift_out = 3 * shift_in;
   const int shift_f_out = 3 * (h_total * variables + v);

De forma similar al kernel de pasada directa, organizaremos el trabajo en 2 etapas. Primero distribuiremos el gradiente de error al nivel de los datos históricos.

//--- history
   if(i < h_total)
     {
      float mask = output[shift_out + 2];
      float grad = 0;
      if(mask > 0)
        {
         grad = output_gr[shift_out] * mask;
         grad -= (i < (h_total - 1) && mask != 0 ? (output_gr[shift_out + 1]) * mask : 0);
         grad += (i > 0 ? output[shift_out + 1 - 3 * variables] * output[shift_out + 2 - 3 * variables] : 0);
         if(isnan(grad) || isinf(grad))
            grad = 0;
         //---
        }
      history_gr[shift_in] = grad;
     }

Y luego transmitiremos el gradiente de error a los valores predichos conocidos.

//--- future
   if(i < f_total)
     {
      float mask = output[shift_f_out + shift_out + 2];
      float grad = 0;
      if(mask > 0)
        {
         grad = output_gr[shift_f_out + shift_out] * mask;
         grad -= (i < (h_total - 1) && mask != 0 ? (output_gr[shift_f_out + shift_out + 1]) * mask : 0);
         grad += (i > 0 ? output[shift_f_out + shift_out + 1 - 3 * variables] * 
                          output[shift_f_out + shift_out + 2 - 3 * variables] : 0);
         if(isnan(grad) || isinf(grad))
            grad = 0;
         //---
        }
      future_gr[shift_in] = grad;
     }
  }

Otro algoritmo que tendremos que implementar en la parte OpenCL es la creación de la matriz de escalado. En el kernel UniTrajBTS, calcularemos las matrices de escalado directa e inversa.

Aquí, también utilizaremos los resultados de la pasada directa del kernel de preparación de datos como datos de entrada. A partir de sus datos, calcularemos el desplazamiento desde el último valor desenmascarado en las direcciones directa y inversa, que guardaremos en los búferes de datos correspondientes. 

__kernel void UniTrajBTS(__global const float * concat_inp,
                         __global float * d_forw,
                         __global float * d_bakw,
                         const int total
                        )
  {
   const size_t i = get_global_id(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

Utilizaremos un espacio de tareas bidimensional. Pero en la primera dimensión solo tendremos 2 flujos, que se corresponderán con el cálculo de la matriz de escalado directa e inversa. Y en la segunda dimensión, como antes, especificaremos el número de variables a analizar.

Tras identificar el flujo en el espacio de tareas, dividiremos el algoritmo del kernel en función del valor de la primera dimensión.

   if(i == 0)
     {
      const int step = variables * 3;
      const int start = v * 3 + 2;
      float last = 0;
      d_forw[v] = 0;
      for(int p = 1; p < total; p++)
        {
         float m = concat_inp[start + p * step];
         d_forw[p * variables + v] = last = 1 + (1 - m) * last;
        }
     }

Al calcular la matriz de escalado directa, determinaremos el desplazamiento hasta la máscara del primer elemento de la variable analizada y el paso al siguiente elemento. Después se organizará un ciclo de iteración consecutiva de máscaras del elemento analizado con el cálculo de coeficientes de escalado según la fórmula dada.

Para la matriz de escalado inversa, el algoritmo será idéntico. Determinaremos solo el desplazamiento hasta el último elemento y nos desplazaremos en orden inverso.

   else
     {
      const int step = -(variables * 3);
      const int start = (total - 1) * variables + v * 3 + 2;
      float last = 0;
      d_bakw[(total - 1) + v] = 0;
      for(int p = 1; p < total; p++)
        {
         float m = concat_inp[start + p * step];
         d_bakw[(total - 1 - p) * variables + v] = last = 1 + (1 - m) * last;
        }
     }
  }

Nótese que el algoritmo presentado solo funcionará con máscaras cuya distribución del gradiente de error no sea significativa. Por esta razón, no crearemos un kernel de pasada inversa de este algoritmo. Y con esto completaremos el trabajo en el lado OpenCL del programa. Podrá ver su código completo en el archivo adjunto.

2.2 Aplicación del algoritmo UniTraj

Tras realizar el trabajo preparatorio en el lado OpenCL del programa, procederemos a implementar los enfoques propuestos en el lado del programa principal. Aquí organizaremos el algoritmo UniTraj dentro de la clase CNeuronUniTraj, cuya estructura se muestra a continuación.

class CNeuronUniTraj    :  public CNeuronBaseOCL
  {
protected:
   uint              iVariables;
   float             fDropout;
   //---
   CBufferFloat      cHistoryMask;
   CBufferFloat      cFutureMask;
   CNeuronBaseOCL    cData;
   CNeuronLearnabledPE cPE;
   CNeuronMVMHAttentionMLKV   cEncoder;
   CNeuronBaseOCL    cDForw;
   CNeuronBaseOCL    cDBakw;
   CNeuronConvOCL    cProjDForw;
   CNeuronConvOCL    cProjDBakw;
   CNeuronBaseOCL    cDataDForw;
   CNeuronBaseOCL    cDataDBakw;
   CNeuronBaseOCL    cConcatDataDForwBakw;
   CNeuronMambaBlockOCL cSSM[4];
   CNeuronConvOCL    cStat;
   CNeuronTransposeOCL cTranspStat;
   CVAE              cVAE;
   CNeuronTransposeOCL cTranspVAE;
   CNeuronConvOCL    cDecoder[2];
   CNeuronTransposeOCL cTranspResult;
   //---
   virtual bool      Prepare(const CBufferFloat* history, const CBufferFloat* future);
   virtual bool      PrepareGrad(CBufferFloat* history_gr, CBufferFloat* future_gr);
   virtual bool      BTS(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override { return feedForward(NeuronOCL, NULL); }
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override 
                                       { return calcInputGradients(NeuronOCL, NULL, NULL, None); }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override 
                                       { return updateInputWeights(NeuronOCL, NULL); }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                                                   CBufferFloat *SecondGradient, 
                                                            ENUM_ACTIVATION SecondActivation = None) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *second) override;
   //---

public:
                     CNeuronUniTraj(void) {};
                    ~CNeuronUniTraj(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint heads, uint units_count, 
                          uint forecast, float dropout, ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronUniTrajOCL; }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Como podemos ver, la estructura de la clase declara un gran número de objetos internos cuya funcionalidad conoceremos durante la implementación de los métodos. En este caso, todos los objetos se declararán estáticamente. Esto nos permitirá dejar el constructor y el destructor de la clase vacíos, y dejar la gestión de la memoria al sistema.

La inicialización de todos los objetos internos se realizará en el método Init, en cuyos parámetros obtendremos las constantes principales que nos permitirán identificar unívocamente la arquitectura del objeto.

bool CNeuronUniTraj::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint heads, uint units_count, 
                          uint forecast, float dropout, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * (units_count + forecast), 
                                                                   optimization_type, batch))
      return false;

En el cuerpo del método, como siempre, llamaremos primero al método homónimo de la clase padre, que ya implementará el control mínimo necesario sobre la inicialización de los objetos heredados.

Una vez ejecutadas con éxito las operaciones de la clase padre, guardaremos las constantes obtenidas del programa externo, entre las que se encuentran el número de variables analizadas en los datos de origen y la proporción de elementos enmascarados durante el entrenamiento.

   iVariables = window;
   fDropout = MathMax(MathMin(dropout, 1), 0);

Y luego procederemos a inicializar los objetos declarados. Aquí crearemos principalmente los búferes de enmascaramiento para los datos históricos y previstos.

   if(!cHistoryMask.BufferInit(iVariables * units_count, 1) ||
      !cHistoryMask.BufferCreate(OpenCL))
      return false;
   if(!cFutureMask.BufferInit(iVariables * forecast, 1) ||
      !cFutureMask.BufferCreate(OpenCL))
      return false;

A continuación, inicializaremos la capa interna de datos de origen concatenados.

   if(!cData.Init(0, 0, OpenCL, 3 * iVariables * (units_count + forecast), optimization, iBatch))
      return false;

Y crearemos una capa de tamaño similar de codificación entrenable de posiciones.

   if(!cPE.Init(0, 1, OpenCL, cData.Neurons(), optimization, iBatch))
      return false;

Y luego vendrá el codificador del Transformer para extraer las dependencias espacio-temporales.

   if(!cEncoder.Init(0, 2, OpenCL, 3, window_key, heads, (heads + 1) / 2, iVariables, 1, 1, 
                                                  (units_count + forecast), optimization, iBatch))
      return false;

Aquí cabe señalar que los autores del método han realizado una serie de experimentos y han llegado a la conclusión de que el rendimiento óptimo del método se consigue usando 1 bloque de codificador del Transformer y 4 bloques Mamba. Por lo tanto, en este caso utilizaremos solo 1 capa de Encoder.

Y observe que el tamaño de la ventana de datos de origen es "3", lo cual se corresponde con 3 parámetros de 1 indicador en cada paso temporal (valor, velocidad y máscara). En este caso, fijaremos el número de elementos de la secuencia al nivel del número de variables analizadas, mientras que el número de canales independientes será igual a la profundidad total de la historia y la previsión analizadas. De este modo, organizaremos la evaluación de las dependencias entre los indicadores analizados en 1 paso temporal.

A continuación, pasaremos al bloque BTS y crearemos los objetos de matriz de escalado directa e inversa.

   if(!cDForw.Init(0, 3, OpenCL, iVariables * (units_count + forecast), optimization, iBatch))
      return false;;
   if(!cDBakw.Init(0, 4, OpenCL, iVariables * (units_count + forecast), optimization, iBatch))
      return false;

Y luego añadiremos capas de convolución de la proyección de estas matrices.

   if(!cProjDForw.Init(0, 5, OpenCL, 1, 1, 3, iVariables, (units_count + forecast), optimization, iBatch))
      return false;
   cProjDForw.SetActivationFunction(SIGMOID);
   if(!cProjDBakw.Init(0, 6, OpenCL, 1, 1, 3, iVariables, (units_count + forecast), optimization, iBatch))
      return false;
   cProjDBakw.SetActivationFunction(SIGMOID);

Las proyecciones resultantes se multiplicarán elemento a elemento por los resultados del Codificador y los resultados de las operaciones se escribirán en los siguientes objetos.

   if(!cDataDForw.Init(0, 7, OpenCL, cData.Neurons(), optimization, iBatch))
      return false;
   if(!cDataDBakw.Init(0, 8, OpenCL, cData.Neurons(), optimization, iBatch))
      return false;

A continuación, concatenaremos los datos obtenidos en un único tensor.

   if(!cConcatDataDForwBakw.Init(0, 9, OpenCL, 2 * cData.Neurons(), optimization, iBatch))
      return false;

Que transmitiremos a la unidad SSM. Como ya hemos mencionado, en este bloque inicializaremos 4 capas Mamba consecutivas.

   for(uint i = 0; i < cSSM.Size(); i++)
     {
      if(!cSSM[i].Init(0, 10 + i, OpenCL, 6 * iVariables, 12 * iVariables, 
                                 (units_count + forecast), optimization, iBatch))
         return false;
     }

En este caso, los autores del método proponen usar enlaces residuales respecto a la capa Mamba. Iremos un poco más lejos y usaremos la clase CNeuronMambaBlockOCLque creamos al trabajar con la clase TrajLLM.

Proyectaremos los resultados obtenidos en medidas estadísticas de la distribución objetivo.

   uint id = 10 + cSSM.Size();
   if(!cStat.Init(0, id, OpenCL, 6, 6, 12, iVariables * (units_count + forecast), optimization, iBatch))
      return false;

Pero antes de muestrear y reparametrizar los valores, tendremos que cambiar ligeramente el orden de los datos. Para ello, usaremos la capa de transposición.

   id++;
   if(!cTranspStat.Init(0, id, OpenCL, iVariables * (units_count + forecast), 12, optimization, iBatch))
      return false;
   id++;
   if(!cVAE.Init(0, id, OpenCL, cTranspStat.Neurons() / 2, optimization, iBatch))
      return false;

Luego traduciremos los valores muestreados a la dimensionalidad de los canales de información independientes.

   id++;
   if(!cTranspVAE.Init(0, id, OpenCL, cVAE.Neurons() / iVariables, iVariables, optimization, iBatch))
      return false;

Y pasaremos los datos por el descodificador, a cuya salida obtendremos la secuencia objetivo generada.

   id++;
   uint w = cTranspVAE.Neurons() / iVariables;
   if(!cDecoder[0].Init(0, id, OpenCL, w, w, 2 * (units_count + forecast), iVariables, optimization, iBatch))
      return false;
   cDecoder[0].SetActivationFunction(LReLU);
   id++;
   if(!cDecoder[1].Init(0, id, OpenCL, 2 * (units_count + forecast), 2 * (units_count + forecast), 
                                                 (units_count + forecast), iVariables, optimization, iBatch))
      return false;
   cDecoder[1].SetActivationFunction(TANH);

Y ahora solo nos quedará llevar el resultado obtenido a la dimensionalidad de los datos de origen.

   id++;
   if(!cTranspResult.Init(0, id, OpenCL, iVariables, (units_count + forecast), optimization, iBatch))
      return false;

Para eliminar operaciones innecesarias de copiado de datos, realizaremos un intercambio de punteros en los búferes de datos.

   if(!SetOutput(cTranspResult.getOutput(), true) ||
      !SetGradient(cTranspResult.getGradient(), true))
      return false;
   SetActivationFunction((ENUM_ACTIVATION)cDecoder[1].Activation());
//---
   return true;
  }

No se olvide de controlar el proceso de ejecución de las operaciones en cada etapa; en la finalización del método retornaremos el valor lógico de la operación del método al programa que realiza la llamada.

Una vez inicializada la instancia de la clase, procederemos a implementar los métodos de pasada directa. Primero haremos un pequeño trabajo preparatorio para organizar la cola de los kernels creados anteriormente.  Aquí utilizaremos algoritmos ya probados, que podrá leer usted mismo en el archivo adjunto. Y dentro del ámbito de este artículo le propongo considerar el método feedForward de nivel superior, donde describiremos el algoritmo completo a "grandes trazos".

bool CNeuronUniTraj::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   if(!NeuronOCL)
      return false;

En los parámetros del método obtendremos los punteros a los 2 objetos que contienen valores históricos y previstos. En el cuerpo del método, comprobaremos inmediatamente la pertinencia del puntero a los datos históricos. Como recordará, según nuestra lógica, siempre hay datos históricos. Y puede que no haya valores predictivos.

A continuación, organizaremos el proceso de generación del tensor de enmascaramiento aleatorio de datos históricos.

//--- Create History Mask
   int total = cHistoryMask.Total();
   if(!cHistoryMask.BufferInit(total, 1))
      return false;
   if(bTrain)
     {
      for(int i = 0; i < int(total * fDropout); i++)
         cHistoryMask.Update(RND(total), 0);
     }
   if(!cHistoryMask.BufferWrite())
      return false;

Tenga en cuenta que el enmascaramiento solo se realizará durante el proceso entrenamiento. En el modo de explotación, utilizaremos toda la información disponible.

Después organizaremos un proceso similar para los valores previstos. Pero aquí hay un matiz a considerar. Si hay valores predichos, generaremos un tensor de enmascaramiento aleatorio. Pero en el caso de que no haya información sobre el próximo movimiento, llenaremos el tensor de enmascaramiento completo con valores cero.

//--- Create Future Mask
   total = cFutureMask.Total();
   if(!cFutureMask.BufferInit(total, (!SecondInput ? 0 : 1)))
      return false;
   if(bTrain && !!SecondInput)
     {
      for(int i = 0; i < int(total * fDropout); i++)
         cFutureMask.Update(RND(total), 0);
     }
   if(!cFutureMask.BufferWrite())
      return false;

Tras generar los tensores de enmascaramiento, podremos realizar el paso de preparación y concatenación de datos.

//--- Prepare Data
   if(!Prepare(NeuronOCL.getOutput(), SecondInput))
      return false;

A continuación, añadiremos la codificación de la posición y la transmitiremos al codificador del Transformer.

//--- Encoder
   if(!cPE.FeedForward(cData.AsObject()))
      return false;
   if(!cEncoder.FeedForward(cPE.AsObject()))
      return false;

Luego, según el algoritmo UniTraj, se utilizará el bloque BTS. Y crearemos las matrices de escalado directa e inversa.

//--- BTS
   if(!BTS())
      return false;

Después haremos sus proyecciones.

   if(!cProjDForw.FeedForward(cDForw.AsObject()))
      return false;
   if(!cProjDBakw.FeedForward(cDBakw.AsObject()))
      return false;

Multiplicado por los resultados del Codificador.

   if(!ElementMult(cEncoder.getOutput(), cProjDForw.getOutput(), cDataDForw.getOutput()))
      return false;
   if(!ElementMult(cEncoder.getOutput(), cProjDBakw.getOutput(), cDataDBakw.getOutput()))
      return false;

Y combinaremos los valores obtenidos en un único tensor.

   if(!Concat(cDataDForw.getOutput(), cDataDBakw.getOutput(), cConcatDataDForwBakw.getOutput(),
              3, 3, cData.Neurons() / 3))
      return false;

Acto seguido, analizaremos los datos en un modelo de espacio de estados.

//--- SSM
   if(!cSSM[0].FeedForward(cConcatDataDForwBakw.AsObject()))
      return false;
   for(uint i = 1; i < cSSM.Size(); i++)
      if(!cSSM[i].FeedForward(cSSM[i - 1].AsObject()))
         return false;

A continuación, obtendremos una proyección de las medidas estadísticas de la distribución objetivo.

//--- VAE
   if(!cStat.FeedForward(cSSM[cSSM.Size() - 1].AsObject()))
      return false;

Y los valores muestrales de una distribución dada.

   if(!cTranspStat.FeedForward(cStat.AsObject()))
      return false;
   if(!cVAE.FeedForward(cTranspStat.AsObject()))
      return false;

El descodificador generará la secuencia de destino.

//--- Decoder
   if(!cTranspVAE.FeedForward(cVAE.AsObject()))
      return false;
   if(!cDecoder[0].FeedForward(cTranspVAE.AsObject()))
      return false;
   if(!cDecoder[1].FeedForward(cDecoder[0].AsObject()))
      return false;
   if(!cTranspResult.FeedForward(cDecoder[1].AsObject()))
      return false;
//---
   return true;
  }

Que llevaremos a la dimensionalidad de los datos de origen. 

Como recordará, en el método de inicialización del objeto hemos intercambiado los punteros a los búferes de datos, por lo que en esta fase no será necesario copiar los valores recibidos de los objetos internos a los búferes heredados de nuestra clase. Y para completar el método de pasada directa, solo necesitaremos transmitir el resultado lógico del método al programa que realiza la llamada.

Ya hemos construido el algoritmo de pasada directa. Y el siguiente paso, normalmente, consistirá en organizar los procesos de pasada inversa. Son totalmente compatibles con la pasada directa, pero el flujo de información se dará en sentido contrario. No obstante, aún nos queda trabajo por delante, y el formato de los artículos tiene sus propias dimensiones. Así que dejaré los métodos de pasada inversa para que el lector los explore por su cuenta. Le recuerdo que en el archivo adjunto encontrará el código completo de esta clase y todos sus métodos.

2.3 Arquitectura del modelo

Tras hacer realidad nuestra visión de los algoritmos del método UniTraj, procederemos a implementarlos en nuestros modelos. Al igual que otros métodos de análisis de trayectorias de datos históricos, usaremos el algoritmo propuesto en el marco del modelo de codificador del estado del entorno. Recordemos que la arquitectura del modelo especificado se especifica en el método CreateEncoderDescriptions.

bool CreateEncoderDescriptions(CArrayObj *&encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

Desde el programa externo, el método recibirá el puntero al objeto de array dinámico en el que escribiremos la arquitectura del modelo a crear. En el cuerpo del método comprobaremos inmediatamente la relevancia del puntero recibido y, si es necesario, crearemos un nuevo objeto. Después pasaremos a la descripción de la solución arquitectónica.

La primera capa que utilizaremos es la completamente conectada, donde escribiremos los datos de origen.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Aquí registramos la información del movimiento histórico de los precios y los valores de los indicadores analizados para una determinada profundidad de la historia. Los datos del terminal los obtendremos "tal cual", sin ningún procesamiento previo. Obviamente, esos datos serían muy poco comparables. Por ello, les daremos un aspecto comparable utilizando una capa de normalización de datos por lotes.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Luego transmitiremos inmediatamente los datos normalizados a nuestro nuevo bloque UniTraj. Al mismo tiempo, fijaremos el factor de enmascaramiento en el 50% de los datos recibidos. 

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronUniTrajOCL;
   descr.window = BarDescr;                          //window
   descr.window_out = EmbeddingSize;                 //Inside Dimension
   descr.count = HistoryBars;                        //Units
   descr.layers = NForecast;                         //Forecast
   descr.step=4;                                     //Heads
   descr.probability=0.5f;                           //DropOut
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

A la salida del bloque, obtendremos una trayectoria objetivo libre que contendrá tanto los datos históricos reconstruidos como los valores previstos para un horizonte de planificación determinado. A los datos resultantes se añadirán las medidas estadísticas de los datos de origen, extraídas al normalizar los datos.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = BarDescr * (NForecast+HistoryBars);
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y coincidirán con los valores previstos en el dominio de la frecuencia.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = BarDescr;
   descr.count =  NForecast+HistoryBars;
   descr.step = int(true);
   descr.probability = 0.7f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Debido a la compleja arquitectura de nuestro nuevo bloque CNeuronUniTraj, dispondremos de una descripción bastante breve y concisa del modelo creado, que no reducirá en absoluto sus capacidades.

Debemos decir que aumentar el tamaño del tensor de los resultados del modelo del codificador del entorno ha requerido correcciones puntuales tanto en el modelo del Actor como en el del Crítico. Pero estos cambios son tan poco sustanciales que podrá comprobarlos usted mismo en el archivo adjunto. Los ajustes del programa de entrenamiento del modelo del Codificador, en cambio, serán más significativos.

2.4 Programa de entrenamiento del modelo

Los cambios introducidos en la arquitectura del modelo del codificador del entorno junto con los enfoques de entrenamiento propuestos por los autores del método UniTraj han dado lugar a la necesidad de ajustar el asesor de entrenamiento de este modelo "...\Experts\UniTraj\StudyEncoder.mq5".

Lo primero que hemos hecho ha sido ajustar el bloque de control del modelo en cuanto a la comprobación del tamaño de la capa de resultados. Se trata de una edición puntual en el método de inicialización del asesor experto.

   Encoder.getResults(Result);
   if(Result.Total() != (NForecast+HistoryBars) * BarDescr)
     {
      PrintFormat("The scope of the Encoder does not match the forecast state count (%d <> %d)",
                                             (NForecast+HistoryBars) * BarDescr, Result.Total());
      return INIT_FAILED;
     }

Pero como podrá adivinar, el trabajo principal nos esperará en el método de entrenamiento del modelo Train.

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);

Como antes, en el cuerpo del método, primero generaremos un vector de probabilidades de selección de trayectorias durante el entrenamiento basado en los rendimientos obtenidos. El objetivo de esta operación consiste en utilizar trayectorias rentables más a menudo, lo que le permitirá entrenar una estrategia más rentable.

A continuación, declararemos las variables necesarias.

   vector<float> result, target, state;
   bool Stop = false;
   const int Batch = 1000;
   int b = 0;
//---
   uint ticks = GetTickCount();

Y organizaremos un sistema de ciclos de entrenamiento de modelos.

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter += b)
     {
      int tr = SampleTrajectory(probability);
      int start = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 5 - NForecast));
      if(start <= 0)
         continue;

Recordemos que el bloque Mamba es recurrente por naturaleza, lo cual podrá a prueba su proceso de aprendizaje. En primer lugar, muestrearemos una trayectoria de la memoria de reproducción de experiencias y seleccionaremos el estado de inicio del entrenamiento en ella. A continuación, organizaremos un ciclo anidado de iteración secuencial de estados en la trayectoria seleccionada.

      for(b = 0; (b < Batch && (iter + b) < Iterations); b++)
        {
         int i = start + b;
         if(i >= MathMin(Buffer[tr].Total, Buffer_Size) - NForecast)
            break;

Primero cargaremos los datos históricos de los parámetros analizados desde el búfer de reproducción de experiencias.

         state.Assign(Buffer[tr].States[i].state);
         if(MathAbs(state).Sum() == 0)
            break;
         bState.AssignArray(state);

Y cargaremos inmediatamente los valores posteriores verdaderos.

         //--- Collect target data
         if(!Result.AssignArray(Buffer[tr].States[i + NForecast].state))
            continue;
         if(!Result.Resize(BarDescr * NForecast))
            continue;

Luego dividiremos aleatoriamente el proceso de entrenamiento en 2 flujos con una probabilidad del 50%.

         //--- State Encoder
         if((MathRand() / 32767.0) < 0.5)
           {
            if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               Stop = true;
               break;
              }
           }

En el primer caso, como antes, suministraremos a la entrada del modelo solo datos históricos y realizaremos una pasada directa. Y en el segundo caso, también daremos al modelo los verdaderos valores posteriores del próximo movimiento de precios. Así, suministraremos a la entrada del modelo toda la información real sobre los estados históricos y posteriores del sistema.

         else
           {
            if(Result.GetIndex()>=0)
              Result.BufferWrite();
            if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, Result))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               Stop = true;
               break;
              }
           }

Recordemos que nuestro algoritmo implica un enmascaramiento aleatorio del 50% de los datos adquiridos durante el entrenamiento. Por lo tanto, en este modo, el modelo aprenderá a recuperar los datos enmascarados.

En la salida del modelo obtendremos la trayectoria completa como un único tensor, por lo que combinaremos los 2 búferes de datos de origen en un único tensor y lo utilizaremos para la pasada inversa el modelo, durante la cual ajustaremos los parámetros entrenados del modelo para minimizar la recuperación global de datos y el error de predicción.

         //--- Collect target data
         if(!bState.AddArray(Result))
            continue;
         if(!Encoder.backProp((CBufferFloat*)GetPointer(bState), (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Ahora solo tendremos que informar al usuario del progreso del entrenamiento y pasar a la siguiente iteración del sistema de ciclos.

         //---
         if(GetTickCount() - ticks > 500)
           {
            double percent = double(iter + b) * 100.0 / (Iterations);
            string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", 
                                          percent, Encoder.getRecentAverageError());
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

Y después de completar con éxito todas las iteraciones de los ciclos de entrenamiento del modelo, borraremos el campo de comentarios del gráfico del instrumento. Luego enviaremos los resultados del entrenamiento al registro del terminal e inicializaremos el proceso de finalización del modelo.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder", Encoder.getRecentAverageError());
   ExpertRemove();
//---
  }

No tenemos previsto suministrar los valores previstos a la entrada del modelo durante la ejecución del mismo. Por lo tanto, el programa de entrenamiento de la política del Actor se ha mantenido sin cambios. El código completo de todos los programas y clases usados en la elaboración de este artículo figura en el anexo.

3. Simulación

Más arriba hemos asimilado la descripción teórica de un nuevo método de trabajo con secuencias temporales multimodales UniTraj. También hemos implementado nuestra visión de los enfoques propuestos usando MQL5. Ahora pasaremos a la fase final de nuestro trabajo, en la que evaluaremos la eficacia de los enfoques propuestos para resolver nuestros problemas.

A pesar de los cambios introducidos en la arquitectura del modelo y en el programa de entrenamiento del modelo de codificador del estado del entorno, la estructura de la muestra de entrenamiento utilizada no ha cambiado. Y esto nos permitirá empezar a entrenar el modelo utilizando muestras de entrenamiento recogidas previamente.

Permítanme recordarles que para el entrenamiento del modelo utilizaremos los datos históricos reales de EURUSD, con el marco temporal H1 para todo el año 2023. Los parámetros de todos los indicadores analizados se han usado por defecto.

En la primera pasada, hemos entrenado el modelo del codificador del estado del entorno. Ya hemos dicho muchas veces que no necesitamos actualizar la muestra de entrenamiento durante la entrenamiento del Codificador del estado. Así que entrenaremos el modelo hasta obtener los resultados deseados. Debemos decir que el modelo resultante no se caracteriza por su ligereza. Y su entrenamiento requiere tiempo. No obstante, el proceso de entrenamiento ha ido bastante bien. Y después de entrenarlo, hemos obtenido una proyección visualmente buena del movimiento previsto de los precios.

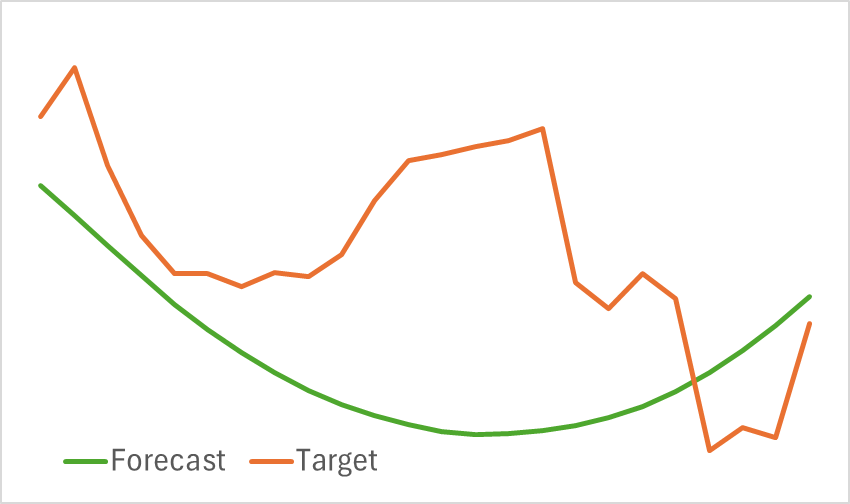
Al mismo tiempo, debemos decir que la línea de movimiento de las previsiones está muy suavizada. Lo mismo podemos decir de la trayectoria reconstruida. A primera vista, hay una eliminación significativa del ruido de los datos de origen. En la próxima fase de entrenamiento del modelo averiguaremos hasta qué punto resulta útil para aprender una política rentable del Actor.

La segunda fase de nuestras pruebas consistirá en un proceso iterativo de entrenamiento de los modelos del Actor y Crítico. En esta fase buscaremos una política del Actor que sea rentable, y que se base en el análisis del movimiento de precios previsto obtenido del Codificador del entorno. En este caso, el codificador retornará tanto el movimiento de precios históricos previsto como el movimiento de precios reconstruido.

Para probar el rendimiento de los modelos entrenados, utilizaremos los datos históricos de enero de 2024 con todos los demás parámetros intactos.

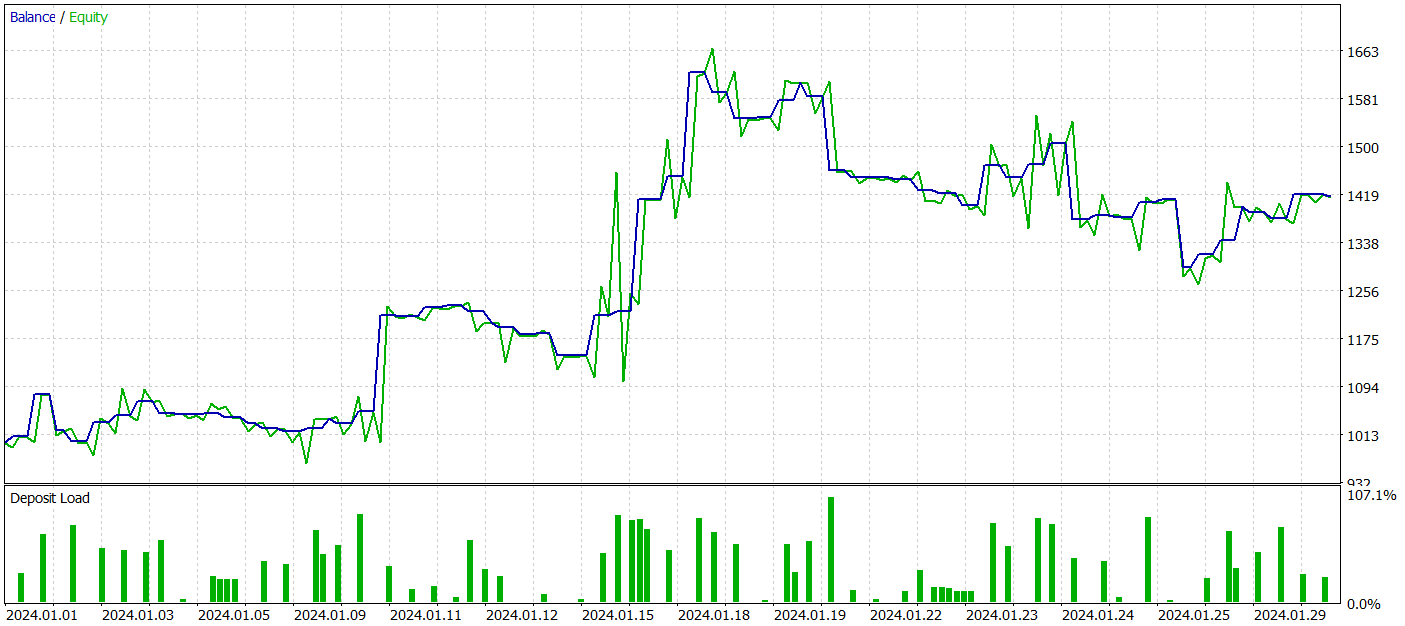
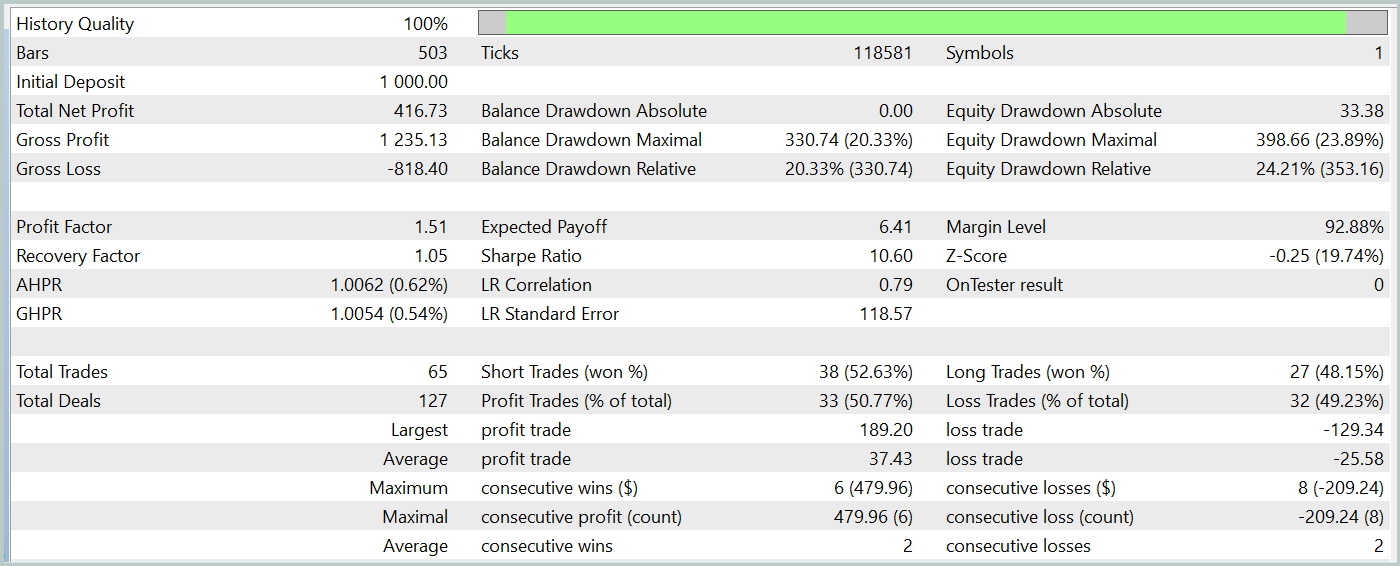
Durante el periodo de prueba, nuestro modelo del Actor entrenado ha sido capaz de generar más de un 40% de beneficios con una reducción máxima del capital de poco más del 24%. Hemos realizado un total de 65 transacciones y aproximadamente la mitad de ellas (33 transacciones) se han cerrado con beneficios. Y gracias a que las la transacciones rentables máxima y media superan significativamente los indicadores perdedores similares, el factor de beneficio se ha fijado en un nivel de 1,51. Obviamente, el periodo de prueba de 1 mes y 65 transacciones realizadas no nos permite hablar de ingresos estables en el futuro. Pero, en general, el resultado obtenido es superior al obtenido por el método Traj-LLM.

Conclusión

El método UniTraj analizado en este artículo muestra potencial como herramienta versátil para procesar trayectorias de agentes en una amplia variedad de escenarios. Este enfoque resuelve el problema clave de la adaptación del modelo a múltiples tareas, lo que mejora el rendimiento respecto a los métodos tradicionales. El procesamiento unificado de los datos de origen enmascarados convierte a UniTraj en una solución flexible y eficaz.

En la parte práctica del artículo, hemos implementado los enfoques propuestos usando herramientas MQL5. Asimismo, los hemos implementado en el modelo de Codificador del estado del entorno. También hemos entrenado y probado los modelos entrenados con datos históricos reales. Los resultados obtenidos sirven perfectamente para evaluar la eficacia de los enfoques propuestos, lo cual nos permite utilizarlos en la construcción de estrategias comerciales reales.

Enlaces

Deciphering Movement: Unified Trajectory Generation Model for Multi-Agent

Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	StudyEncoder.mq5	Asesor	Asesor de entrenamiento del Codificador
5	Test.mq5	Asesor	Asesor para la prueba de modelos
6	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
7	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
8	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL