Ökonometrischer Ansatz zur Ermittlung von Marktmustern: Autokorrelation, Heatmaps und Streudiagramme
Ein kurzer Überblick über das bisherige Material und die Voraussetzungen für das Erstellen eines neuen Modells
Im ersten Artikel stellten wir das Konzept des Marktgedächtnisses vor, das als langfristige Abhängigkeit von Preiserhöhungen irgendeiner Größenordnung bestimmt wird. Ferner betrachteten wir das Konzept der "Saisonmuster", die auf den Märkten existieren. Bisher existierten diese beiden Konzepte getrennt voneinander. Der Zweck des Artikels besteht darin zu zeigen, dass das "Marktgedächtnis" saisonaler Natur ist, was sich durch eine maximierte Korrelation von Zuwächsen beliebiger Ordnung für nahe gelegene Zeitintervalle und durch eine minimierte Korrelation für entfernte Zeitintervalle ausdrückt.
Lassen Sie uns die folgende Hypothese aufstellen:
Die Korrelation von Preiszuwächsen hängt vom Vorhandensein von saisonalen Mustern sowie von der Häufung von nahegelegenen Zuwächsen ab.
Versuchen wir, sie in einem freien intuitiven und leicht mathematischen Stil zu bestätigen oder zu widerlegen.
Der klassische ökonometrische Ansatz zur Identifizierung von Mustern in Preiszuwächsen ist die Autokorrelation.
Nach dem klassischen Ansatz wird die Abwesenheit von Mustern in Preisschritten durch das Fehlen einer seriellen Korrelation bestimmt. Wenn es keine Autokorrelation gibt, wird sich die Serie von Zuwächsen als zufällig erweisen, und die weitere Suche nach Mustern vergeblich sein.
Sehen wir uns ein Beispiel für die visuelle Analyse von EURUSD-Zuwächsen mit Hilfe der Autokorrelationsfunktion an. Alle Beispiele werden mit IPython durchgeführt.
def standard_autocorrelation(symbol, lag):
rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time')
rates = rates.diff(lag).dropna()
from pandas.plotting import autocorrelation_plot
plt.figure(figsize=(10, 5))
autocorrelation_plot(rates)
standard_autocorrelation('EURUSD', 50)
Diese Funktion konvertiert H1-Schlusskurse in relevante Differenzen mit dem angegebenen Zeitraum (es wird die Verzögerung 50 verwendet) und zeigt das Autokorrelationsdiagramm an.
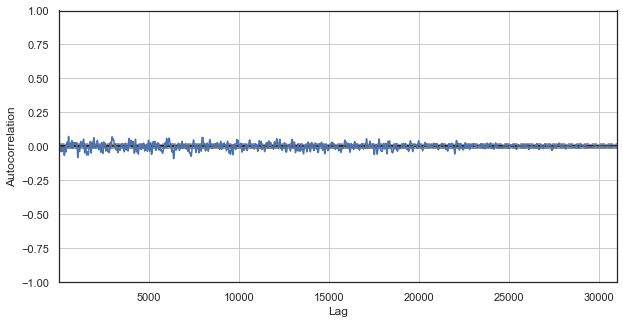
Abb. 1. Klassisches Korrelogramm der Preiszuwächse
Das Autokorrelationsdiagramm zeigt keine Muster in den Preiszuwächsen. Die Korrelationen zwischen benachbarten Zuwächsen schwanken um Null, was auf die Zufälligkeit der Zeitreihe hinweist. Wir könnten unsere ökonometrische Analyse genau hier beenden, indem wir zu dem Schluss kommen, dass der Markt zufällig ist. Ich schlage jedoch vor, die Autokorrelationsfunktion aus einem anderen Blickwinkel zu betrachten: im Zusammenhang mit den saisonalen Mustern.
Ich nahm an, dass die Korrelation von Preiserhöhungen durch das Vorhandensein saisonaler Muster erzeugt werden könnte. Lassen Sie uns daher aus dem Beispiel alle Stunden außer einer bestimmten ausschließen. Wir werden also eine neue Zeitreihe erstellen, die ihre eigenen spezifischen Eigenschaften haben wird. Erstellen Sie eine Autokorrelationsfunktion für diese Reihe:
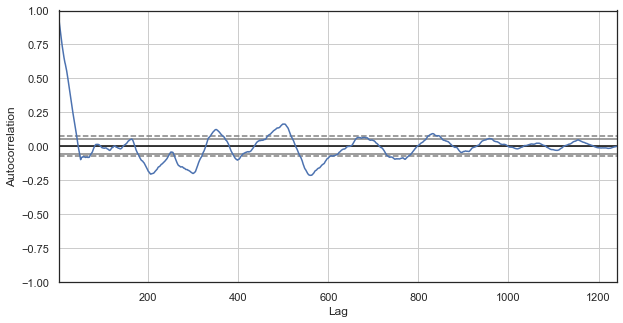
Abb. 2. Ein Korrelogramm der Preiserhöhungen mit ausgeschlossenen Stunden (wobei nur noch die 1. Stunde für jeden Tag übrig bleibt)
Das Korrelogramm sieht für die neue Serie besser aus. Es besteht eine starke Abhängigkeit der aktuellen Zuwächse von den vorherigen. Die Abhängigkeit nimmt ab, wenn das Zeitdelta zwischen den Zuwächsen zunimmt. Das bedeutet, dass der Zuwachs der 1. Stunde des aktuellen Tages stark mit dem 1. Stundenzuwachs des Vortages korreliert, und so weiter. Diese sehr wichtige Information deutet auf die Existenz von jahreszeitlichen Mustern hin, d.h. Zuwächse haben ein Gedächtnis.
Der nutzerdefinierte Ansatz zur Identifizierung von Mustern in Preiszuwächsen ist die saisonale Autokorrelation.
Wir haben festgestellt, dass es eine Korrelation zwischen dem Zuwachs der 1. Stunde des aktuellen Tages und der Erhöhung der vorhergehenden 1. Stunden gibt, die jedoch abnimmt, wenn der Abstand zwischen den Tagen zunimmt. Nun wollen wir sehen, ob es eine Korrelation zwischen den benachbarten Stunden gibt. Zu diesem Zweck modifizieren wir den Code:
def seasonal_autocorrelation(symbol, lag, hour1, hour2):
rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time')
rates = rates.drop(rates.index[~rates.index.hour.isin([hour1, hour2])]).diff(lag).dropna()
from pandas.plotting import autocorrelation_plot
plt.figure(figsize=(10, 5))
autocorrelation_plot(rates)
seasonal_autocorrelation('EURUSD', 50, 1, 2)
Löschen wir hier alle Stunden außer der ersten und der zweiten, berechnen dann die Differenzen für die neue Serie und bauen die Autokorrelationsfunktion auf:
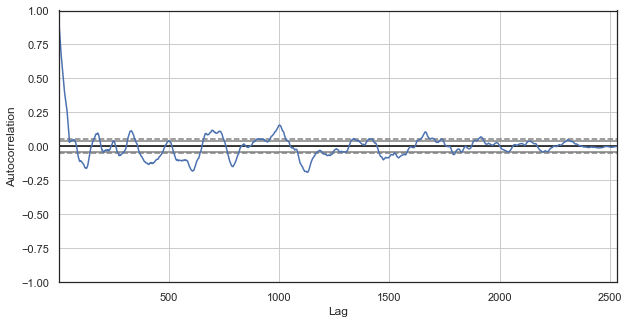
Abb. 3. Ein Korrelogramm der Preiszuwächse mit ausgeschlossenen Stunden (wobei nur die 1. und 2. Stunde für jeden Tag übrig bleibt)
Offensichtlich gibt es auch eine hohe Korrelation für die Serie der nächsten Stunden, was auf ihre Korrelation und gegenseitige Beeinflussung hinweist. Können wir für alle Stundenpaare, nicht nur für die ausgewählten, einen zuverlässigen relativen Wert erhalten? Verwenden wir dazu die unten beschriebenen Methoden.
Heatmap der saisonalen Korrelationen für alle Stunden
Lassen Sie uns den Markt weiter erforschen und versuchen, die ursprüngliche Hypothese zu bestätigen. Betrachten wir das Gesamtbild. Die untenstehende Funktion entfernt nacheinander Stunden aus der Zeitreihe, so dass nur eine Stunde übrig bleibt. Sie bildet die Preisdifferenz für diese Reihe und bestimmt die Korrelation mit der für andere Stunden gebildeten Reihe:
#calculate correlation heatmap between all hours def correlation_heatmap(symbol, lag, corrthresh): out = pd.DataFrame() rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume']) rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') for i in range(24): ratesH = None ratesH = rates.drop(rates.index[~rates.index.hour.isin([i])]).diff(lag).dropna() out[str(i)] = ratesH['close'].reset_index(drop=True) plt.figure(figsize=(10, 10)) corr = out.corr() # Generate a mask for the upper triangle mask = np.zeros_like(corr, dtype=np.bool) mask[np.triu_indices_from(mask)] = True sns.heatmap(corr[corr >= corrthresh], mask=mask) return out out = correlation_heatmap(symbol='EURUSD', lag=25, corrthresh=0.9)
Die Funktion akzeptiert die Folge der Zuwächse (Zeitverzögerung) sowie die Korrelationsschwelle, um Stunden mit geringer Korrelation fallen zu lassen. Hier ist das Ergebnis:

Abb. 4. Heatmap der Korrelationen zwischen den Zuwächsen für verschiedene Stunden für den Zeitraum 2015-2020.
Es ist klar, dass die folgenden Cluster die maximale Korrelation aufweisen: 0-5 und 10-14 Stunden. Im vorigen Artikel haben wir ein Handelssystem erstellt, das auf dem ersten Cluster basiert, der auf eine andere Art und Weise (mit Hilfe von Boxplot) entdeckt wurde. Jetzt sind die Muster auch auf der Heatmap sichtbar. Betrachten wir nun den zweiten interessanten Cluster und analysieren ihn. Hier ist die zusammenfassende Statistik für den Cluster:
out[['10','11','12','13','14']].describe()
| 10 | 11 | 12 | 13 | ||
|---|---|---|---|---|---|
| count | 1265.000000 | 1265.000000 | 1265.000000 | 1265.000000 | 1265.000000 |
| mean | -0.001016 | -0.001015 | -0.001005 | -0.000992 | -0.000999 |
| std | 0.024613 | 0.024640 | 0.024578 | 0.024578 | 0.024511 |
| min | -0.082850 | -0.084550 | -0.086880 | -0.087510 | -0.087350 |
| 25% | -0.014970 | -0.015160 | -0.014660 | -0.014850 | -0.014820 |
| 50% | -0.000900 | -0.000860 | -0.001210 | -0.001350 | -0.001280 |
| 75% | 0.013460 | 0.013690 | 0.013760 | 0.014030 | 0.013690 |
| max | 0.082550 | 0.082920 | 0.085830 | 0.089030 | 0.086260 |
Die Parameter für alle Cluster-Stunden liegen recht nahe beieinander, jedoch ist ihr Durchschnittswert für die analysierte Stichprobe negativ (etwa 100 fünfstellige Punkte). Eine Verschiebung der durchschnittlichen Zuwächse deutet darauf hin, dass der Markt in diesen Stunden eher schrumpft als wächst. Es ist auch erwähnenswert, dass eine Zunahme der Verzögerung der Zuwächse zu einer größeren Korrelation zwischen den Stunden aufgrund des Auftretens einer Trendkomponente führt, während eine Abnahme der Verzögerung zu niedrigeren Werten führt. Die relative Anordnung von Clustern ist jedoch fast unverändert.
So korrelieren beispielsweise bei einer einzelnen Verzögerung die Zuwächse der Stunden 12, 13 und 14 immer noch stark:
plt.figure(figsize=(10,5)) plt.plot(out[['12','13','14']]) plt.legend(out[['12','13','14']]) plt.show()
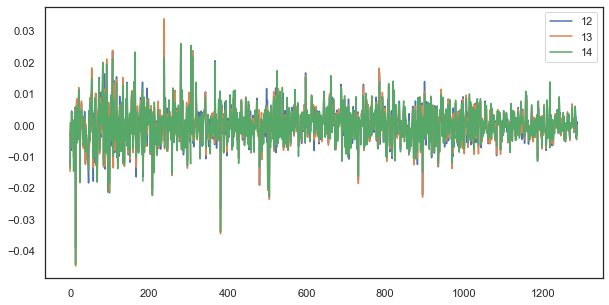
Abb. 5. Visuelle Ähnlichkeit zwischen der Serie von Zuwächsen mit einer einzigen Verzögerung, die aus verschiedenen Stunden besteht
Formel der Regelmäßigkeit: einfach, aber gut
Erinnern Sie sich an die Hypothese:
Die Korrelation von Preiszuwächsen hängt vom Vorhandensein von saisonalen Mustern sowie von der Häufung von nahegelegenen Zuwächsen ab.
Wir haben im Autokorrelationsdiagramm und auf der Heatmap gesehen, dass es eine Abhängigkeit der Stundenzuwächse sowohl von vergangenen Werten als auch von nahegelegenen Stundenzuwächsen gibt. Das erste Phänomen ergibt sich aus dem Wiederauftreten von Ereignissen zu bestimmten Stunden des Tages. Das zweite Phänomen hängt mit der Häufung der Volatilität in bestimmten Zeiträumen zusammen. Diese beiden Phänomene sollten getrennt betrachtet und möglichst kombiniert werden. In diesem Artikel werden wir eine zusätzliche Studie über die Abhängigkeit bestimmter Stundenzuwächse (wobei alle anderen Stunden aus der Zeitreihe entfernt werden) von ihren vorherigen Werten durchführen. Der interessanteste Teil der Untersuchung wird im nächsten Artikel durchgeführt.
# calculate joinplot between real and predicted returns def hourly_signals_statistics(symbol, lag, hour, hour2, rfilter): rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume']) rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') # price differences for every hour series H = rates.drop(rates.index[~rates.index.hour.isin([hour])]).reset_index(drop=True).diff(lag).dropna() H2 = rates.drop(rates.index[~rates.index.hour.isin([hour2])]).reset_index(drop=True).diff(lag).dropna() # current returns for both hours HF = H[1:].reset_index(drop=True); HL = H2[1:].reset_index(drop=True) # previous returns for both hours HF2 = H[:-1].reset_index(drop=True); HL2 = H2[:-1].reset_index(drop=True) # Basic equation: ret[-1] = ret[0] - (ret[lag] - ret[lag-1]) # or Close[-1] = (Close[0]-Close[lag]) - ((Close[lag]-Close[lag*2]) - (Close[lag-1]-Close[lag*2-1])) predicted = HF-(HF2-HL2) real = HL # correlation joinplot between two series outcorr = pd.DataFrame() outcorr['Hour ' + str(hour)] = H['close'] outcorr['Hour ' + str(hour2)] = H2['close'] # real VS predicted prices out = pd.DataFrame() out['real'] = real['close'] out['predicted'] = predicted['close'] out = out.loc[((out['predicted'] >= rfilter) | (out['predicted'] <=- rfilter))] # plptting results from scipy import stats sns.jointplot(x='Hour ' + str(hour), y='Hour ' + str(hour2), data=outcorr, kind="reg", height=7, ratio=6).annotate(stats.pearsonr) sns.jointplot(x='real', y='predicted', data=out, kind="reg", height=7, ratio=6).annotate(stats.pearsonr) hourly_signals_statistics('EURUSD', lag=25, hour=13, hour2=14, rfilter=0.00)
Hier ist eine Erklärung dessen, was in der obigen Auflistung getan wird. Es gibt zwei Reihen, die durch das Entfernen unnötiger Stunden gebildet werden und auf deren Grundlage die Preiszuwächse (ihre Differenz) berechnet werden. Die Stunden für die Serien werden in den Parametern "hour" und "hour2" festgelegt. Dann erhalten wir Sequenzen mit einer Verzögerung von 1 für jede Stunde, d.h. die Serie HF ist HL um einen Wert voraus — dies ermöglicht die Berechnung des tatsächlichen und des vorhergesagten Zuwachses sowie der Differenz zwischen ihnen. Zuerst konstruieren wir ein Streudiagramm für die Zuwächse der 1. und 2. Stunde:
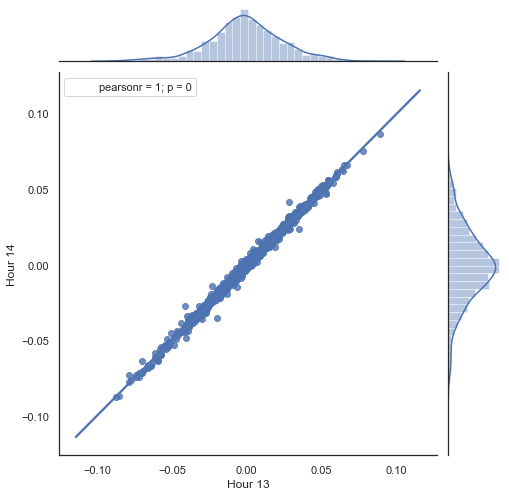
Abb. 5. Streudiagramm für die Zuwächse der Stunde 13 und 14 für den Zeitraum 2015-2020.
Wie erwartet, sind die Zuwächse hoch korreliert. Versuchen wir nun die nächsten Zuwächse auf der Grundlage der vorherigen vorherzusagen. Dazu gibt es hier eine einfache Formel, die den nächsten Wert vorhersagen kann:
Basisgleichung: ret[-1] = ret[0] - (ret[lag] - ret[lag-1])
oder Close[-1] = (Close[0]-Close[lag]) - ((Close[lag]-Close[lag*2]) - (Close[lag-1]-Close[lag*2-1]))
Hier ist die Erklärung der resultierenden Formel. Um den zukünftigen Zuwachs vorherzusagen, gehen wir vom Nullbalken aus. Wir prognostizieren den Wert des nächsten Zuwachses ret[-1]. Dazu subtrahieren wir dazu die Differenz des vorherigen Zuwachses (mit einer "Verzögerung") und des nächsten (Verzögerung-1) vom aktuellen Zuwachs. Wenn die Korrelation der Zuwächse zwischen zwei benachbarten Stunden stark ist, kann erwartet werden, dass der vorhergesagte Zuwachs durch diese Gleichung beschrieben wird. Im Folgenden wird die Gleichung für die Schlusskurse erklärt. Die Zukunftsprognose basiert also auf drei Steigerungen. Der zweite Codeteil sagt zukünftige Zuwächse voraus und vergleicht sie mit den tatsächlichen Zuwächsen. Hier ist ein Diagramm:
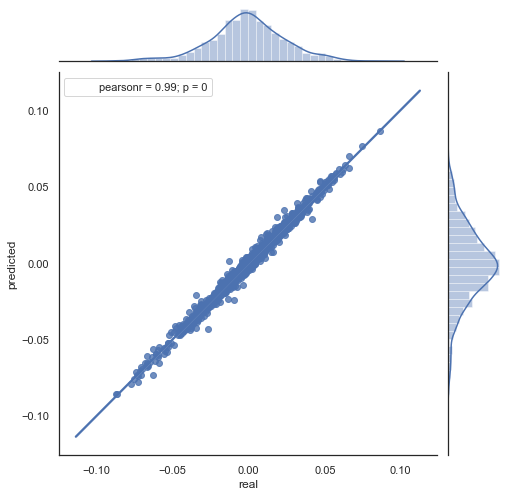
Abb. 6. Streudiagramm für tatsächliche und vorhergesagte Zuwächse für den Zeitraum 2015-2020.
Wie Sie sehen, sind die Diagramme in den Abbildungen 5 und 6 ähnlich. Das bedeutet, dass die Methode zur Bestimmung der Muster über die Korrelation adäquat ist. Gleichzeitig sind die Werte über das Diagramm verstreut; sie liegen nicht auf der gleichen Linie. Dies sind Prognosefehler, die sich negativ auf die Vorhersage auswirken. Sie sollten separat behandelt werden (was den Rahmen dieses Artikels sprengt). Eine Prognose um Null ist nicht wirklich interessant: Wenn die Prognose für den nächsten Preiszuwachs gleich der aktuellen ist, können Sie keinen Gewinn daraus erzielen. Die Prognosen können mit dem Parameter rfilter gefiltert werden.
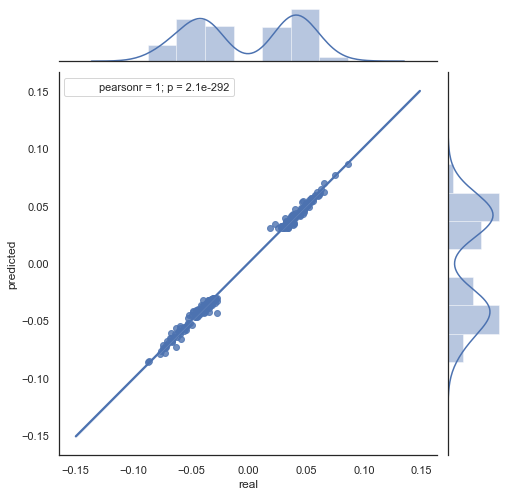
Abb. 7. Streudiagramm für tatsächliche und vorhergesagte Zuwächse mit rfilter = 0,03 für den Zeitraum 2015-2020.
Beachten Sie, dass die Heatmap mit Daten von 2015 bis zum aktuellen Datum erstellt wurde. Verschieben wir den Starttag zurück auf das Jahr 2000:
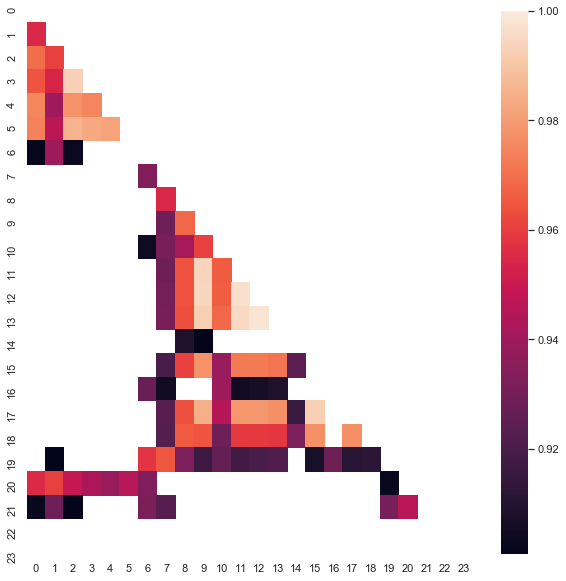
Abb. 8. Die Heatmap der Korrelationen zwischen den Zuwächsen für verschiedene Stunden für den Zeitraum von 2000 bis 2020.
| 10 | 11 | 12 | 13 | ||
|---|---|---|---|---|---|
| count | 5151.000000 | 5151.000000 | 5151.000000 | 5151.000000 | 5151.000000 |
| mean | 0.000470 | 0.000470 | 0.000472 | 0.000472 | 0.000478 |
| std | 0.037784 | 0.037774 | 0.037732 | 0.037693 | 0.037699 |
| min | -0.221500 | -0.227600 | -0.222600 | -0.221100 | -0.216100 |
| 25% | -0.020500 | -0.020705 | -0.020800 | -0.020655 | -0.020600 |
| 50% | 0.000100 | 0.000100 | 0.000150 | 0.000100 | 0.000250 |
| 75% | 0.023500 | 0.023215 | 0.023500 | 0.023570 | 0.023420 |
| max | 0.213700 | 0.212200 | 0.210700 | 0.212600 | 0.208800 |
Wie Sie sehen können, ist die Heatmap etwas dünner, während die Abhängigkeit zwischen den Stunden 13 und 14 abgenommen hat. Gleichzeitig ist der durchschnittliche Wert der Zuwächse positiv, was dem Kauf eine höhere Priorität einräumt. Eine Verschiebung des Durchschnittswertes wird es nicht erlauben, in beiden Zeitintervallen effektiv zu handeln, so dass Sie sich entscheiden müssen.
Betrachten wir die sich ergebende Streuungsgrafik für diesen Zeitraum (hier gebe ich nur die aktuelle \Prognosegrafik wieder):

Abb. 9. Streudiagramm für tatsächliche und prognostizierte Zuwächse mit rfilter = 0,03, für den Zeitraum 2000 - 2020.
Die Streuung der Werte hat zugenommen, was für einen so langen Zeitraum ein negativer Faktor ist.
Auf diese Weise haben wir eine Formel und eine ungefähre Vorstellung von der Verteilung der tatsächlichen und vorausgesagten Zuwächse für bestimmte Stunden erhalten. Zur besseren Übersichtlichkeit können die Abhängigkeiten in 3D visualisiert werden.
# calculate joinplot between real an predicted returns def hourly_signals_statistics3D(symbol, lag, hour, hour2, rfilter): rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume']) rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') rates = pd.DataFrame(rates['close'].diff(lag)).dropna() out = pd.DataFrame(); for i in range(hour, hour2): H = None; H2 = None; HF = None; HL = None; HF2 = None; HL2 = None; predicted = None; real = None; H = rates.drop(rates.index[~rates.index.hour.isin([hour])]).reset_index(drop=True) H2 = rates.drop(rates.index[~rates.index.hour.isin([i+1])]).reset_index(drop=True) HF = H[1:].reset_index(drop=True); HL = H2[1:].reset_index(drop=True); # current hours HF2 = H[:-1].reset_index(drop=True); HL2 = H2[:-1].reset_index(drop=True) # last day hours predicted = HF-(HF2-HL2) real = HL out3D = pd.DataFrame() out3D['real'] = real['close'] out3D['predicted'] = predicted['close'] out3D['predictedABS'] = predicted['close'].abs() out3D['hour'] = i out3D = out3D.loc[((out3D['predicted'] >= rfilter) | (out3D['predicted'] <=- rfilter))] out = out.append(out3D) import plotly.express as px fig = px.scatter_3d(out, x='hour', y='predicted', z='real', size='predictedABS', color='hour', height=1000, width=1000) fig.show() hourly_signals_statistics3D('EURUSD', lag=24, hour=10, hour2=23, rfilter=0.000)
Diese Funktion verwendet die bereits bekannte Formel zur Berechnung der vorausgesagten und der tatsächlichen Werte. Jedes einzelne Streudiagramm zeigt die tatsächliche/prognostizierte Abhängigkeit für jede Stunde, wenn das Signal aus der zehnten Stunde des Vortages stammt. Als Beispiel werden die Stunden von 10.00 bis 23.00 Uhr verwendet. Die Korrelation zwischen den nächsten Stunden ist maximal. Mit zunehmendem Abstand nimmt die Korrelation ab (Streudiagramme werden eher wie Kreise). Beginnend mit Stunde 16 haben weitere Stunden eine geringe Abhängigkeit von der Stunde 10 des Vortages. Mit Dateien aus dem Anhang können Sie das 3D-Objekt drehen und Fragmente auswählen, um detailliertere Informationen zu erhalten.
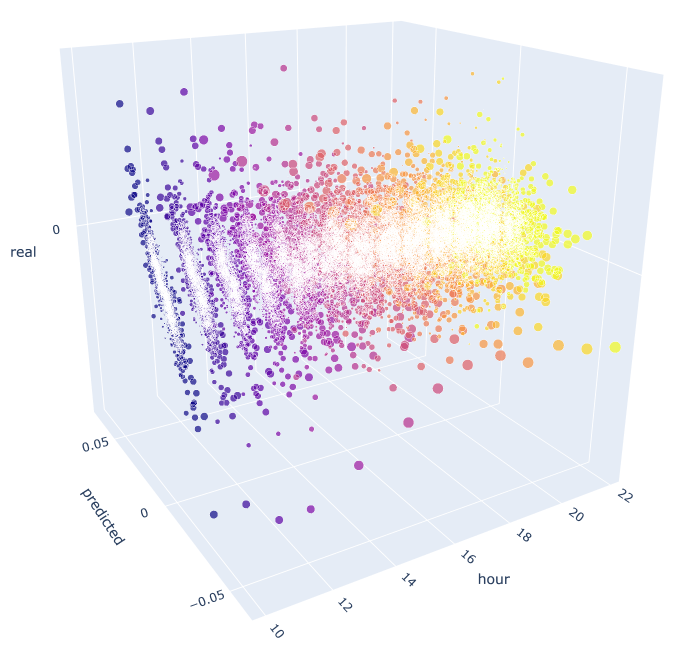
Abb. 10. 3D-Streudiagramm für tatsächliche und vorhergesagte Zuwächse von 2015 bis 2020.
Jetzt ist es an der Zeit, einen Expert Advisor zu erstellen, um zu sehen, ob er funktioniert.
Beispiel für einen Expert Advisor, der mit den identifizierten saisonalen Mustern handelt
Ähnlich wie bei einem Beispiel aus dem vorherigen Artikel wird der Roboter ein saisonales Muster handeln, das nur auf der statistischen Beziehung zwischen dem aktuellen Zuwachs und dem vorherigen für eine bestimmte Stunde basiert. Der Unterschied besteht darin, dass andere Stunden gehandelt werden und ein auf der vorgeschlagenen Formel basierendes Prinzip verwendet wird.
Betrachten wir ein Beispiel für die Verwendung der resultierenden Formel für den Handel, basierend auf der statistischen Studie:
input int OpenThreshold = 30; //Open threshold input int OpenThreshold1 = 30; //Open threshold 1 input int OpenThreshold2 = 30; //Open threshold 2 input int OpenThreshold3 = 30; //Open threshold 3 input int OpenThreshold4 = 30; //Open threshold 4 input int Lag = 10; input int stoploss = 150; //Stop loss input int OrderMagic = 666; //Orders magic input double MaximumRisk=0.01; //Maximum risk input double CustomLot=0; //Custom lot
Das folgende Intervall mit Mustern wurde so festgelegt: {10, 11, 12, 13, 14}. Auf dieser Grundlage kann der Parameter "Open threshold" für jede Stunde individuell eingestellt werden. Diese Parameter sind ähnlich wie "rfilter" in Abb. 9. Die Variable 'Lag' enthält den Verzögerungswert für die Zuwächse (erinnern Sie sich, wir haben die Verzögerung von 25 standardmäßig analysiert, d.h. fast einen Tag für den H1-Zeitrahmen). Die Verzögerungen könnten für jede Stunde separat eingestellt werden, aber der Einfachheit halber wird hier derselbe Wert für alle Stunden verwendet. Auch der Stop-Loss ist für alle Positionen gleich. Alle diese Parameter können optimiert werden.
Die Handelslogik ist wie folgt:
void OnTick() { //--- if(!isNewBar()) return; CopyClose(NULL, 0, 0, Lag*2+1, prArr); ArraySetAsSeries(prArr, true); const double pr = (prArr[1] - prArr[Lag]) - ((prArr[Lag] - prArr[Lag*2]) - (prArr[Lag-1] - prArr[Lag*2-1])); TimeToStruct(TimeCurrent(), hours); if(hours.hour >=10 && hours.hour <=14) { //if(countOrders(0)==0) // if(pr >= signal && CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_BUY)) // OrderSend(Symbol(),OP_BUY,LotsOptimized(), Ask,0,Bid-stoploss*_Point,NormalizeDouble(Ask + signal, _Digits),NULL,OrderMagic,INT_MIN); if(CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_SELL)) { if(pr <= -signal && hours.hour==10) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal, _Digits),NULL,OrderMagic); if(pr <= -signal1 && hours.hour==11) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal1, _Digits),NULL,OrderMagic); if(pr <= -signal2 && hours.hour==12) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal2, _Digits),NULL,OrderMagic); if(pr <= -signal3 && hours.hour==13) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal3, _Digits),NULL,OrderMagic); if(pr <= -signal4 && hours.hour==14) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal4, _Digits),NULL,OrderMagic); } } }
Die Konstante 'pr' wird nach der oben angegebenen Formel berechnet. Diese Formel prognostiziert den Preisanstieg des nächsten Balkens. Anschließend wird die Bedingung für jede Stunde geprüft. Wenn der Zuwachs den Mindestschwellenwert für die jeweilige Stunde erreicht, wird ein Verkaufsgeschäft eröffnet. Wir haben bereits herausgefunden, dass die Verschiebung der durchschnittlichen Zuwächse in die negative Zone Käufe im Intervall von 2015 bis 2020 unwirksam macht, Sie können dies selbst überprüfen.
Starten wir die genetische Optimierung mit den in Abb. 11 angegebenen Parametern und sehen wir uns das Ergebnis an:
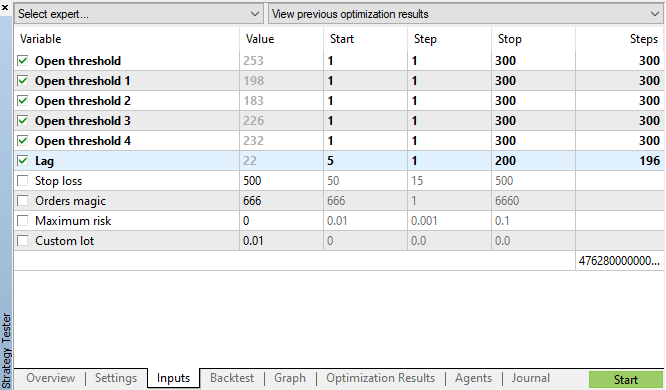
Abb. 11. Die Tabelle der Parameter für die genetische Optimierung
Schauen wir uns das Optimierungsdiagramm an. Im optimierten Intervall liegen die effizientesten Lag-Werte zwischen 17-30 Stunden, was unserer Annahme über die Abhängigkeit der Zuwächse einer bestimmten Stunde des aktuellen Tages von der gleichen Stunde des Vortags sehr nahe kommt:
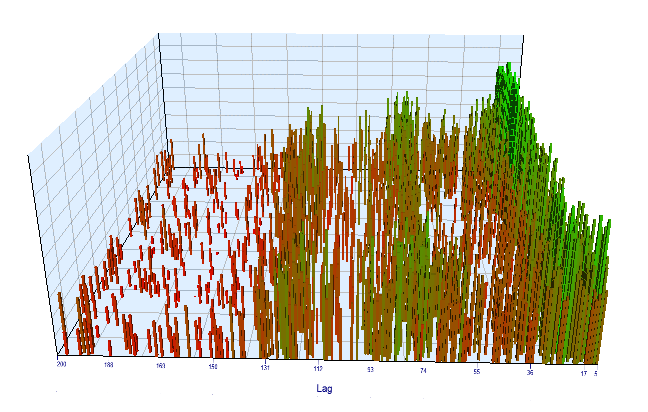
Abb. 12. Beziehung der Variable 'Lag' zur Variable 'Order threshold' im optimierten Intervall
Das Vorwärtsdiagramm sieht ähnlich aus:
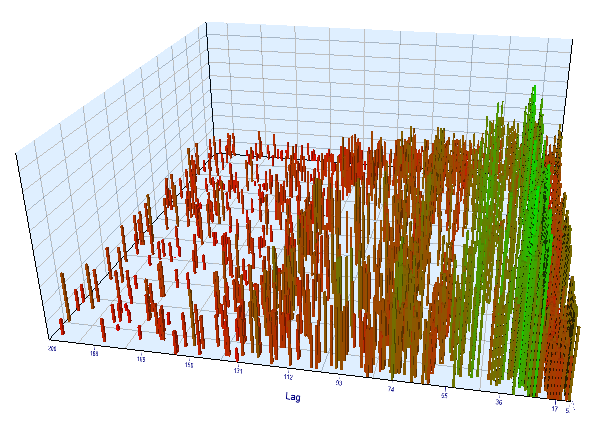
Abb. 13. Beziehung der Variable 'Lag' zur Variable 'Order threshold' im Vorwärtsintervall
Hier sind die besten Ergebnisse aus den Backtest- und Vorwärtsoptimierungstabellen:
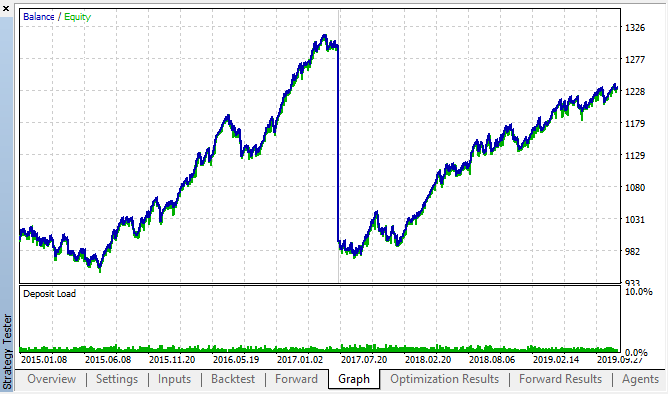
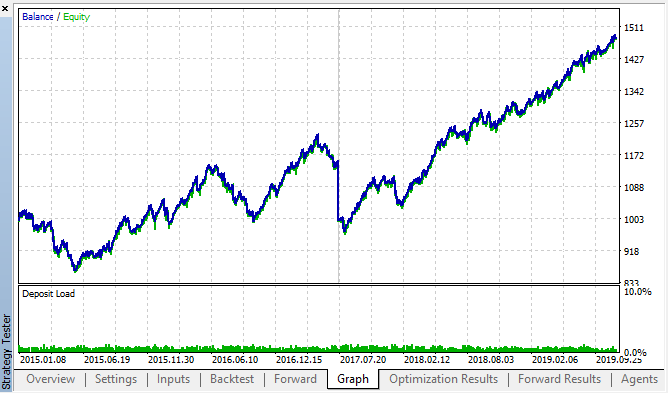
Abb. 14, 15. Die Diagramme für Backtest und Vorwärtsoptimierung.
Vergessen wir nicht, dass das Muster über das gesamte Intervall 2015-2020 fortbesteht. Wir können davon ausgehen, dass der ökonometrische Ansatz perfekt funktioniert hat. Es gibt Abhängigkeiten zwischen den gleichen Stundenschritten für die nächsten Wochentage, mit einer gewissen Clusterbildung (die Abhängigkeit kann nicht mit der gleichen Stunde, sondern mit einer nahen Stunde sein). Im nächsten Artikel werden wir analysieren, wie das zweite Muster verwendet werden kann.
Überprüfung der Zuwächse auf einem anderen Zeitrahmen
Machen wir eine zusätzliche Überprüfung des Zeitrahmens von M15. Angenommen, wir suchen nach der gleichen Korrelation zwischen der aktuellen Stunde und der gleichen Stunde des Vortages. In diesem Fall muss die effektive Verzögerung um das Vierfache größer sein und etwa 24*4 = 96 betragen, da jede Stunde vier M15-Perioden enthält. Ich habe den Expert Advisor mit den gleichen Einstellungen und mit dem M15-Zeitrahmen optimiert.
In dem optimierten Intervall ist die resultierende effektive Verzögerung <60, was seltsam ist. Wahrscheinlich hat der Optimierer ein anderes Muster gefunden, oder der EA war überoptimiert.
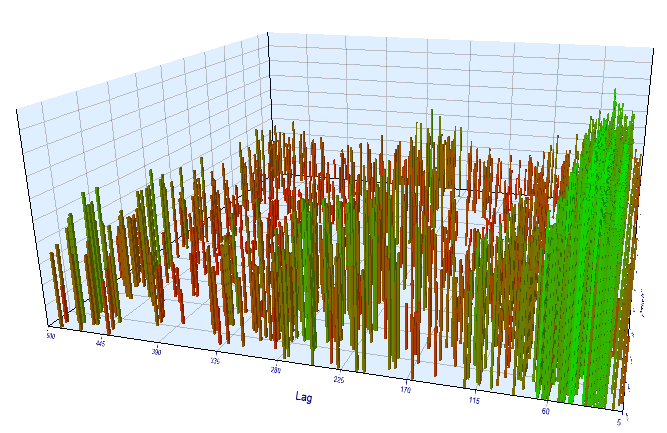
Abb. 16. Beziehung der Variable 'Lag' zur Variable 'Order threshold' im optimierten Intervall
Was die Vorwärtstestergebnisse betrifft, so ist die effektive Verzögerung normal und entspricht 100, was das Muster bestätigt.
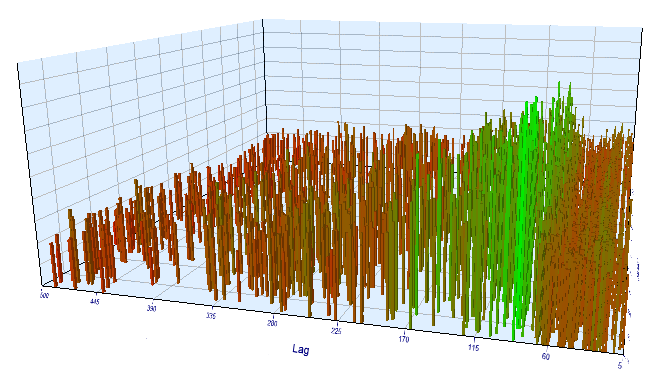
Abb. 17. Beziehung der Variable 'Lag' zur Variable 'Order threshold' im Vorwärtsintervall
Sehen wir uns die besten Backtest- und Forward-Ergebnisse an:
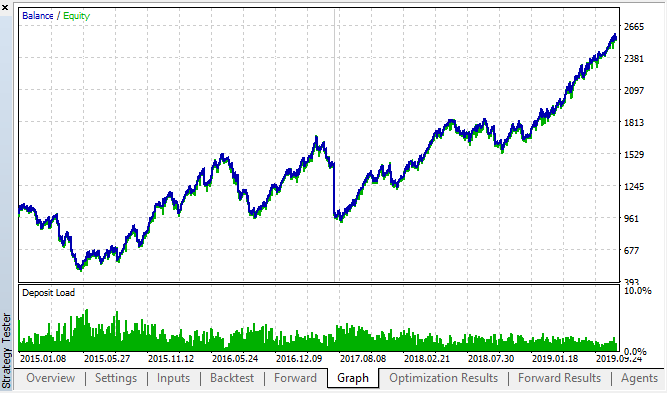
Abb. 18. Backtest und Vorwärts; der beste Vorwärtsdurchlauf
Die sich daraus ergebende Kurve ähnelt der Kurve des H1-Diagramms, wobei die Anzahl der Geschäfte deutlich zunimmt. Wahrscheinlich kann die Strategie für niedrigere Zeitrahmen optimiert werden.
Schlussfolgerung
In diesem Artikel stellen wir die folgende Hypothese auf:
Die Korrelation von Preiszuwächsen hängt vom Vorhandensein von saisonalen Mustern sowie von der Häufung von nahegelegenen Zuwächsen ab.
Der erste Teil wurde vollständig bestätigt: Es besteht eine Korrelation zwischen den Stundenabständen der verschiedenen Wochen. Die zweite Aussage wurde implizit bestätigt: Die Korrelation hat eine Clusterbildung, was bedeutet, dass die aktuellen Stundenzuwächse auch von den Zuwächsen benachbarter Stunden abhängen.
Bitte beachten Sie, dass der vorgeschlagene Expert Advisor keineswegs die einzig mögliche Variante für den Handel mit den gefundenen Korrelationen ist. Die vorgeschlagene Logik spiegelt die Ansicht des Autors über Korrelationen wider, während die EA-Optimierung nur durchgeführt wurde, um die durch statistische Forschung gefundenen Muster zusätzlich zu bestätigen.
Da der zweite Teil unserer Studie zusätzliche substanzielle Forschung erfordert, werden wir im nächsten Artikel ein einfaches maschinelles Lernmodell verwenden, um den zweiten Teil der Hypothese vollständig zu bestätigen oder zu widerlegen.
Der Anhang enthält ein gebrauchsfertiges Rahmenwerk im Jupyter-Notebook-Format, das Sie zur Untersuchung anderer Finanzinstrumente verwenden können. Die Ergebnisse können mit dem beigefügten Test-AA weiter getestet werden.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/5451
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Die Handelssignale mehrerer Währungen überwachen (Teil 1): Entwicklung der Anwendungsstruktur
Die Handelssignale mehrerer Währungen überwachen (Teil 1): Entwicklung der Anwendungsstruktur
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Vielen Dank, dass Sie so wertvolle Informationen weitergeben.
Wenn man diese Artikel liest, bekommt man Lust zu experimentieren.
Vielen Dank für Ihr Feedback.
Ich empfehle Ihnen, den Artikel im Original zu lesen, wenn Sie gelesen werden wollen. Machen Sie sich keine Sorgen wegen der Sprache, das Übersetzungsprogramm wird seine Arbeit tun.
https://www.mql5.com/ru/forum/330111
Ich danke Ihnen.
Guten Tag, bitte erklären Sie mir, wie die Wärmekarte aufgebaut ist:
Wir nehmen die Inkremente von der Stunde eines Tages zur Stunde eines anderen Tages auf diese Weise:
Wenn die Funktion dann mit einem Lag-Wert von 25 aufgerufen wird, erhalten wir in RateH die Differenz nicht von benachbarten Tagen, sondern von 25 Tagen zwischen den Tagen, weil wir vorher alle Stunden, die nicht mit i zusammenfallen, rausgeworfen haben, und eine Reihe der Form 2020-01-01 00:00:00|90, 2020-01-02 00:00:00:00|87, 2020-01-03 00:00:00:00|88, und wenn wir dann lag 25 darauf anwenden und die Differenz zählen, und dann na rauswerfen - erhalten wir eine Reihe 2020-01-25 00:00:00|1, 2020-01-26 00:00:00|3, 2020-01-27 00:00:00|-2 - und so für jede Stunde. Was für eine Art von Heatmap haben wir am Ende erstellt?
Vielleicht bin ich irgendwo verwirrt, bitte helfen Sie mir, die Sache zu entwirren.
Oi
Bitte fragen Sie, ob Sie wissen, dass der Cointegração
Gostaria de perguntar se você sabe se esse indicador existe no mql5, ou quem criou a base for ele.
an
Cássio