Statistische Verteilungen in MQL5 - Das Beste aus R und noch schneller
Das umfasst die Cauchy-, Weibull-, Normal-, Log-Normal-, logistische, exponentielle, gleichmäßige und die Gamma-Verteilung, das zentrale und nicht-zentrale Beta, die Chi-Quadrat und F-Verteilung von Fisher, die Studentsche T-Verteilung, so wie die diskrete und negative Binomialverteilung und die geometrische, hypergeometrische und Poisson-Verteilung. Darüber hinaus gibt es die Funktionen zur Berechnung der theoretischen Momente von Verteilungen, um den Grad der Übereinstimmung mit einer realen Verteilung einzuschätzen.
Die Standardbibliothek für MQL5 wurde um mehrere mathematische Funktionen für R erweitert, und die Rechengeschwindigkeit um das 3- bis 7-fache erhöht im Vergleich zur ursprünglichen Version für R. Zugleich wurden Fehler in bestimmten Funktionen in R entdeckt.
Inhalt
- Funktionen zur Berechnung der statistischen Eigenschaften von Array-Elementen
- Funktionen für die Arbeit mit statistischen Verteilungen
2.1. Normalverteilung
- 2.1.1. MathProbabilityDensityNormal()
- 2.1.2. MathCumulativeDistributionNormal()
- 2.1.3. MathQuantileNormal()
- 2.1.4. MathRandomNormal()
- 2.1.5. MathMomentsNormal()
2.2. Log-Normalverteilung
- 2.2.1. MathProbabilityDensityLognormal()
- 2.2.2. MathCumulativeDistributionLognormal()
- 2.2.3. MathQuantileLognormal()
- 2.2.4. MathRandomLognormal()
- 2.2.5. MathMomentsLognormal()
2.3. Betaverteilung
- 2.3.1. MathProbabilityDensityBeta()
- 2.3.2. MathCumulativeDistributionBeta()
- 2.3.3. MathQuantileBeta()
- 2.3.4. MathRandomBeta()
- 2.3.5. MathMomentsBeta()
2.4. Nichtzentrale Betaverteilung
- 2.4.1. MathProbabilityDensityNoncentralBeta()
- 2.4.2. MathCumulativeDistributionNoncentralBeta()
- 2.4.3. MathQuantileNoncentralBeta()
- 2.4.4. MathRandomNoncentralBeta()
- 2.4.5. MathMomentsNoncentralBeta()
2.5. Gamma-Verteilung
- 2.5.1. MathProbabilityDensityGamma()
- 2.5.2. MathCumulativeDistributionGamma()
- 2.5.3. MathQuantileGamma()
- 2.5.4. MathRandomGamma()
- 2.5.5. MathMomentsGamma()
2.6. Chi-Quadrat Verteilung
- 2.6.1. MathProbabilityDensityChiSquare()
- 2.6.2. MathCumulativeDistributionChiSquare()
- 2.6.3. MathQuantileChiSquare()
- 2.6.4. MathRandomChiSquare()
- 2.6.5. MathMomentsChiSquare()
2.7. Nichtzentrale Chi-QuadraT-Verteilung
- 2.7.1. MathProbabilityDensityNoncentralChiSquare()
- 2.7.2. MathCumulativeDistributionNoncentralChiSquare()
- 2.7.3. MathQuantileNoncentralChiSquare()
- 2.7.4. MathRandomNoncentralChiSquare()
- 2.7.5. MathMomentsNoncentralChiSquare()
2.8. Exponentielle Verteilung- 2.8.1. MathProbabilityDensityExponential()
- 2.8.2. MathCumulativeDistributionExponential()
- 2.8.3. MathQuantileExponential()
- 2.8.4. MathRandomExponential()
- 2.8.5. MathMomentsExponential()
2.9. F-Verteilung- 2.9.1. MathProbabilityDensityF()
- 2.9.2. MathCumulativeDistributionF()
- 2.9.3. MathQuantileF()
- 2.9.4. MathRandomF()
- 2.9.5. MathMomentsF()
2.10. Nichtzentrale F-Verteilung
- 2.10.1. MathProbabilityDensityNoncentralF()
- 2.10.2. MathCumulativeDistributionNoncentralF()
- 2.10.3. MathQuantileNoncentralF()
- 2.10.4. MathRandomNoncentralF()
- 2.10.5. MathMomentsNoncentralF()
2.11. T-Verteilung
- 2.11.1. MathProbabilityDensityT()
- 2.11.2. MathCumulativeDistributionT()
- 2.11.3. MathQuantileT()
- 2.11.4. MathRandomT()
- 2.11.5. MathMomentsT()
2.12 Nichtzentrale T-Verteilung
- 2.12.1. MathProbabilityDensityNoncentralT()
- 2.12.2. MathCumulativeDistributionNoncentralT()
- 2.12.3. MathQuantileNoncentralT()
- 2.12.4. MathRandomNoncentralT()
- 2.12.5. MathMomentsNoncentralT()
2.13. Logistische Verteilung
- 2.13.1. MathProbabilityDensityLogistic()
- 2.13.2. MathCumulativeDistributionLogistic()
- 2.13.3. MathQuantileLogistic()
- 2.13.4. MathRandomLogistic()
- 2.13.5. MathMomentsLogistic()
2.14. Cauchy-Verteilung
- 2.14.1. MathProbabilityDensityCauchy()
- 2.14.2. MathCumulativeDistributionCauchy()
- 2.14.3. MathQuantileCauchy()
- 2.14.4. MathRandomCauchy()
- 2.14.5. MathMomentsCauchy()
2.15. Gleichverteilung
- 2.15.1. MathProbabilityDensityUniform()
- 2.15.2. MathCumulativeDistributionUniform()
- 2.15.3. MathQuantileUniform()
- 2.15.4. MathRandomUniform()
- 2.15.5. MathMomentsUniform()
2.16. Weibull-Verteilung
- 2.16.1. MathProbabilityDensityWeibull()
- 2.16.2. MathCumulativeDistributionWeibull()
- 2.16.3. MathQuantileWeibull()
- 2.16.4. MathRandomWeibull()
- 2.16.5. MathMomentsWeibull()
2.17. Binomial-Verteilung
- 2.17.1. MathProbabilityDensityBinomial()
- 2.17.2. MathCumulativeDistributionBinomial()
- 2.17.3. MathQuantileBinomial()
- 2.17.4. MathRandomBinomial()
- 2.17.5. MathMomentsBinomial()
2.18. Negative Binomial-Verteilung
- 2.18.1. MathProbabilityDensityNegativeBinomial()
- 2.18.2. MathCumulativeDistributionNegativeBinomial()
- 2.18.3. MathQuantileNegativeBinomial()
- 2.18.4. MathRandomNegativeBinomial()
- 2.18.5. MathMomentsNegativeBinomial()
2.19. Geometrische Verteilung
- 2.19.1. MathProbabilityDensityGeometric()
- 2.19.2. MathCumulativeDistributionGeometric()
- 2.19.3. MathQuantileGeometric()
- 2.19.4. MathRandomGeometric()
- 2.19.5. MathMomentsGeometric()
2.20. Hypergeometrische Verteilung
- 2.20.1. MathProbabilityDensityHypergeometric()
- 2.20.2. MathCumulativeDistributionHypergeometric()
- 2.20.3. MathQuantileHypergeometric()
- 2.20.4. MathRandomHypergeometric()
- 2.20.5. MathMomentsHypergeometric()
2.21. Poisson-Verteilung
- 2.21.1. MathProbabilityDensityPoisson()
- 2.21.2. MathCumulativeDistributionPoisson()
- 2.21.3. MathQuantilePoisson()
- 2.21.4. MathRandomPoisson()
- 2.21.5. MathMomentsPoisson()
- Tabelle korrespondierender, statistischer Funktionen in R
- Ein Beispiel für die Verwendung der Funktionen
- Vergleich der Berechnungsgeschwindigkeiten
- Erkannte Berechnungsfehler in R
- Referenzen
Einführung
Die Sprache R ist eines der besten Instrumente für eine statistische Bearbeitung und Analyse von Daten.
Dank der Verfügbarkeit und Unterstützung vieler statistischer Verteilungen wird sie vielfach für die Bearbeitung und Analyse von Daten verwendet. Die Verwendung der Wahrscheinlichkeitstheorie und der mathematischen Statistik ermöglicht einen frischen Blick auf die Daten des Finanzmarktes und bietet neue Möglichkeiten der Erstellung von Handelsstrategien. Durch diese statistische Bibliothek werden alle ihre Möglichkeiten in MQL5 verfügbar.
Die statistische Bibliothek enthält Funktionen zur Berechnung statistischer Eigenschaften von Daten, so wie Funktionen für statistischen Verteilungen.
Dieser Artikel betrachtet die wichtigsten Funktionen der Bibliothek und bietet ein Beispiel für den praktischen Einsatz.
1. Funktionen zur Berechnung der statistischen Eigenschaften von Array-Elementen
Diese Gruppe von Funktionen berechnet die Standardmerkmale (Mittelwert, Varianz, schiefe, Kurtosis, Median, Effektivwert und Standardabweichungen) der Elemente eines Arrays
1.1. MathMean
Die Funktion berechnet den Mittelwert (erstes Moment) der Elemente eines Arrays. Im Fehlerfall retourniert sie NaN (keine Zahl). Analog zu mean() in R.
double MathMean( const double &array[] // [in] Array mit Daten );
1.2. MathVariance
Die Funktion berechnet die Varianz (zweites Moment) der Elemente eines Arrays. Im Fehlerfall retourniert sie NaN. Analog zu var() in R.
double MathVariance( const double &array[] // [in] Array mit Daten );
1.3. MathSkewness
Die Funktion berechnet die Schiefe (drittes Moment) der Elemente eines Arrays. Im Fehlerfall retourniert sie NaN. Analog zu skewness() in R (Bibliothek e1071).
double MathSkewness( const double &array[] // [in] Array mit Daten );
1.4. MathKurtosis
Die Funktion berechnet die Kurtosis (viertes Moment) der Elemente eines Arrays. Im Fehlerfall retourniert sie NaN. Analog zu kurtosis() in R (Bibliothek e1071).
double MathKurtosis( const double &array[] // [in] Array mit Daten );
1.5. MathMoments
Die Funktion berechnet die ersten 4 Momente (Mittelwert, Varianz, Schiefe, Kurtosis) der Elemente eines Arrays. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMoments( const double &array[], // [in] Array mit Daten double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) const int start=0, // [in] Anfangsindex der Berechnung const int count=WHOLE_ARRAY // [in] Anzahl der Elemente für die Berechnung );
1.6. MathMedian
Die Funktion berechnet den Medianwert der Elemente eines Arrays. Im Fehlerfall retourniert sie NaN. Analog zu median() in R.
double MathMedian( double &array[] // [in] Array with data );
1.7. MathStandardDeviation
Die Funktion berechnet die Standardabweichung der Elemente eines Arrays. Im Fehlerfall retourniert sie NaN. Analog zu sd() in R.
double MathStandardDeviation( const double &array[] // [in] Array mit Daten );
1.8. MathAverageDeviation
Die Funktion berechnet die durchschnittliche Abweichung der Elemente eines Arrays. Im Fehlerfall retourniert sie NaN. Analog zu aad() in R.
double MathAverageDeviation( const double &array[], // [in] Array mit Daten );
Alle Funktionen, die die Kurtosis berechnen, verwenden die Exzesswölbung relativ zur Normalverteilung (Exzesswölbung=Kurtosis-3), d. h. die Exzesswölbung einer Normalverteilung beträgt Null.
Sie ist positiv, wenn die Spitze der Verteilung um den Erwartungswert steil ist, und negativ bei einer flachen Wölbung.
2. Statistische Verteilungen
Die statistische Bibliothek von MQL5 enthält 5 Funktionen für statistische Verteilungen:
- Berechnung der Dichte der Wahrscheinlichkeit (die Funktionen MathProbabilityDensityX());
- Berechnung der Wahrscheinlichkeiten (die Funktionen MathCumulativeDistributionX());
Die Wahrscheinlichkeitsfunktion ist gleich der Wahrscheinlichkeit einer Zufallsvariablen im Bereich von (-inf; x]). - Berechnung der Verteilung der Quantile (die Funktionen MathQuantileX());
Das Quantil x einer Verteilung korrespondiert mit einer Zufallsvariablen, die in den Bereich (-inf, x] mit einer durch ihre Parameter gegebenen Verteilung mit der angegebenen Wahrscheinlichkeit fällt. - Erzeugung von Zufallszahlen mit einer gegebenen Verteilung (die Funktionen MathRandomX());
- Berechnung der theoretischen Momente der Verteilungen (die Funktionen MathMomentsX());
2.1. Normalverteilung
2.1.1. MathProbabilityDensityNormal
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion einer Normalverteilung mit den Parametern mu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.double MathProbabilityDensityNormal( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] Der Parameter mean (Erwartungswert) der Verteilung const double sigma, // [in] Der Parameter sigma (Standardabweichung) der Verteilung const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion einer Normalverteilung mit den Parametern mu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityNormal( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] Der Parameter mean (Erwartungswert) der Verteilung const double sigma, // [in] Der Parameter sigma (Standardabweichung) der Verteilung int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet die Werte der Wahrscheinlichkeitsdichtefunktion einer Normalverteilung mit den Parametern mu und sigma für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu dnorm() in R.
bool MathProbabilityDensityNormal( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] Der Parameter mean (Erwartungswert) der Verteilung const double sigma, // [in] Der Parameter sigma (Standardabweichung) der Verteilung const bool log_mode, // [in] Parameter zur Berechnung des Logarithmus des Wertes, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte berechnet double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet die Werte der Wahrscheinlichkeitsdichtefunktion einer Normalverteilung mit den Parametern mu und sigma für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false.
bool MathProbabilityDensityNormal( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] Der Parameter mean (Erwartungswert) der Verteilung const double sigma, // [in] Der Parameter sigma (Standardabweichung) der Verteilung double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.1.2. MathCumulativeDistributionNormal
Die Funktion berechnet den Wert der Normalverteilung mit den Parametern mu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionNormal( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] Erwartungswert const double sigma, // [in] Standardabweichung const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter zur Berechnung des Logarithmus des Wertes, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Normalverteilung mit den Parametern mu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionNormal( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] Erwartungswert const double sigma, // [in] Standardabweichung int &error_code // [out] Variable für den Fehlercode );Die Funktion berechnet den Wert der Normalverteilung mit den Parametern mu und sigma für den Array mit Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'. Analog zu pnorm() in R.
bool MathCumulativeDistributionNormal( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] Erwartungswert const double sigma, // [in] Standardabweichung const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter zur Berechnung des Logarithmus des Wertes, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der Normalverteilung mit den Parametern mu und sigma für den Array mit Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathCumulativeDistributionNormal( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] Erwartungswert const double sigma, // [in] Standardabweichung double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.1.3. MathQuantileNormal
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Normalverteilung mit den Parametern mu und sigma. Im Fehlerfall retourniert sie NaN.
double MathQuantileNormal( const double probability, // [in] Wahrscheinlichkeitswert der Zufallsvariablen const double mu, // [in] Erwartungswert const double sigma, // [in] Standardabweichung const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Normalverteilung mit den Parametern mu und sigma. Im Fehlerfall retourniert sie NaN.
double MathQuantileNormal( const double probability, // [in] Wahrscheinlichkeitswert der Zufallsvariablen const double mu, // [in] Erwartungswert const double sigma, // [in] Standardabweichung int &error_code // [out] Variable für den Fehlercode );Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Normalverteilung mit den Parametern mu und sigma. Im Fehlerfall retourniert sie false. Analog zu qnorm() in R.
bool MathQuantileNormal( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double mu, // [in] Erwartungswert const double sigma, // [in] Standardabweichung const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Normalverteilung mit den Parametern mu und sigma. Im Fehlerfall retourniert sie 'false'.
bool MathQuantileNormal( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double mu, // [in] Erwartungswert const double sigma, // [in] Standardabweichung double &result[] // [out] Array mit den Werten der Quantile );
2.1.4. MathRandomNormal
Die Funktion erzeugt eine normalverteilte Pseudozufallszahl mit den Parametern mu und Sigma. Im Fehlerfall retourniert sie NaN.
double MathRandomNormal( const double mu, // [in] Erwartungswert const double sigma, // [in] Standardabweichung int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt normalverteilte Pseudozufallszahlen gemäß den Parametern mu und Sigma. Im Fehlerfall retourniert sie false. Analog zu rnorm() in R.
bool MathRandomNormal( const double mu, // [in] Erwartungswert const double sigma, // [in] Standardabweichung const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.1.5. MathMomentsNormal
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der Normalverteilung. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsNormal( const double mu, // [in] Erwartungswert const double sigma, // [in] Standardabweichung double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.2. Log-Normalverteilung
2.2.1. MathProbabilityDensityLognormal
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion einer Log-Normalverteilung mit den Parametern mu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityLognormal( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] Logarithmus des Erwartungswertes (log mean) const double sigma, // [in] Logarithmus der Standardabweichung (log standard deviation) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion einer Log-Normalverteilung mit den Parametern mu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityLognormal( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] Logarithmus des Erwartungswertes (log mean) const double sigma, // [in] Logarithmus der Standardabweichung (log standard deviation) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet die Werte der Wahrscheinlichkeitsdichtefunktion einer Log-Normalverteilung mit den Parametern mu und sigma für einen Array der Zufallsvariable x[]. Im Fehlerfall retourniert sie NaN. Analog zu dlnorm() in R.
bool MathProbabilityDensityLognormal( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] Logarithmus des Erwartungswertes (log mean) const double sigma, // [in] Logarithmus der Standardabweichung (log standard deviation) const bool log_mode, // [in] Parameter zur Berechnung des Logarithmus des Wertes, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte berechnet double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet die Werte der Wahrscheinlichkeitsdichtefunktion einer Log-Normalverteilung mit den Parametern mu und sigma für einen Array der Zufallsvariable x[]. Im Fehlerfall retourniert sie false.
bool MathProbabilityDensityLognormal( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] Logarithmus des Erwartungswertes (log mean) const double sigma, // [in] Logarithmus der Standardabweichung (log standard deviation) double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.2.2. MathCumulativeDistributionLognormal
Die Funktion berechnet den Wert der Log-Normalverteilung mit den Parametern mu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionLognormal( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] Logarithmus des Erwartungswertes (log mean) const double sigma, // [in] Logarithmus der Standardabweichung (log standard deviation) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Log-Normalverteilung mit den Parametern mu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionLognormal( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] Logarithmus des Erwartungswertes (log mean) const double sigma, // [in] Logarithmus der Standardabweichung (log standard deviation) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Log-Normalverteilung mit den Parametern mu und sigma für einen Array der Zufallsvariable x[]. Im Fehlerfall retourniert sie false. Analog zu plnorm() in R.
bool MathCumulativeDistributionLognormal( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] Logarithmus des Erwartungswertes (log mean) const double sigma, // [in] Logarithmus der Standardabweichung (log standard deviation) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der Log-Normalverteilung mit den Parametern mu und sigma für einen Array der Zufallsvariable x[]. Im Fehlerfall retourniert sie 'false'.
bool MathCumulativeDistributionLognormal( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] Logarithmus des Erwartungswertes (log mean) const double sigma, // [in] Logarithmus der Standardabweichung (log standard deviation) double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.2.3. MathQuantileLognormal
Die Funktion berechnet den Wert der Umkehrfunktion der Log-Normalverteilung mit den Parametern mu und sigma für die angegebenen Wahrscheinlichkeit. Im Fehlerfall retourniert sie NaN.
double MathQuantileLognormal( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double mu, // [in] Logarithmus des Erwartungswertes (log mean) const double sigma, // [in] Logarithmus der Standardabweichung (log standard deviation) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Umkehrfunktion der Log-Normalverteilung mit den Parametern mu und sigma für die angegebenen Wahrscheinlichkeit. Im Fehlerfall retourniert sie NaN.
double MathQuantileLognormal( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double mu, // [in] Logarithmus des Erwartungswertes (log mean) const double sigma, // [in] Logarithmus der Standardabweichung (log standard deviation) int &error_code // [out] Variable für den Fehlercode );
Für die angegebenen Array 'probability[]' mit Wahrscheinlichkeitswerten berechnet die Funktion die Umkehrfunktion der Normalverteilung mit den Parametern mu und sigma. Im Fehlerfall retourniert sie false. Analog zu qlnorm() in R.
bool MathQuantileLognormal( const double &probability[], // [in] Array mit den Wahrscheinlichkeitswerten der Zufallsvariablen const double mu, // [in] Logarithmus des Erwartungswert (log mean) const double sigma, // [in] Logarithmus der Standardabweichung (log standard deviation) const bool tail, // [in] Parameter, wenn false, wird mit einer '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die angegebenen Array 'probability[]' mit Wahrscheinlichkeitswerten berechnet die Funktion die Umkehrfunktion der Normalverteilung mit den Parametern mu und sigma. Im Fehlerfall retourniert sie false.
bool MathQuantileLognormal( const double &probability[], // [in] Array mit den Wahrscheinlichkeitswerten der Zufallsvariablen const double mu, // [in] Logarithmus des Erwartungswertes (log mean) const double sigma, // [in] Logarithmus der Standardabweichung (log standard deviation) double &result[] // [out] Array mit den Werten der Quantile );
2.2.4. MathRandomLognormal
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der Log-Normalverteilung mit den Parametern mu und sigma. Im Fehlerfall retourniert sie NaN.
double MathRandomLognormal( const double mu, // [in] Logarithmus des Erwartungswertes (log mean) const double sigma, // [in] Logarithmus der Standardabweichung (log standard deviation) int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt Pseudozufallszahlen auf Basis der Log-Normalverteilung mit den Parametern mu und sigma. Im Fehlerfall retourniert sie 'false'. Analog zu rlnorm() in R.
bool MathRandomLognormal( const double mu, // [in] Logarithmus des Erwartungswertes (log mean) const double sigma, // [in] Logarithmus der Standardabweichung (log standard deviation) const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.2.5. MathMomentsLognormal
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der Log-Normalverteilung. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsLognormal( const double mu, // [in] Logarithmus des Erwartungswertes (log mean) const double sigma, // [in] Logarithmus der Standardabweichung (log standard deviation) double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.3. Betaverteilung
2.3.1. MathProbabilityDensityBeta
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Betaverteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityBeta( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Betaverteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityBeta( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Betaverteilung mit den Parametern a und b für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu dbeta() in R.
bool MathProbabilityDensityBeta( const double &x[], // [in] Wert der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const bool log_mode, // [in] Parameter zur Berechnung des Logarithmus des Wertes, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte berechnet double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Betaverteilung mit den Parametern a und b für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathProbabilityDensityBeta( const double &x[], // [in] Wert der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.3.2. MathCumulativeDistributionlBeta
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Betaverteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionBeta( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Betaverteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionBeta( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Betaverteilung mit den Parametern a und b für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu pbeta() in R.
bool MathCumulativeDistributionBeta( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Betaverteilung mit den Parametern a und b für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathCumulativeDistributionBeta( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.3.3. MathQuantileBeta
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Betaverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie NaN.
double MathQuantileBeta( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Betaverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie NaN.
double MathQuantileBeta( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) int &error_code // [out] Variable für den Fehlercode );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Betaverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie false. Analog zu qbeta() in R.
bool MathQuantileBeta( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Betaverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie false.
bool MathQuantileBeta( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) double &result[] // [out] Array mit den Werten der Quantile );
2.3.4. MathRandomBeta
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der Betaverteilung mit den Parametern mu und Sigma. Im Fehlerfall retourniert sie NaN.
double MathRandomBeta( const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt Pseudozufallszahlen auf Basis der Betaverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie false. Analog zu rbeta() in R.
bool MathRandomBeta( const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.3.5. MathMomentsBeta
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der Betaverteilung. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsBeta( const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.4. Nichtzentrale Betaverteilung
2.4.1. MathProbabilityDensityNoncentralBeta
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der nichtzentralen Betaverteilung mit den Parametern a, b und lambda für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.double MathProbabilityDensityNoncentralBeta( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const double lambda, // [in] Parameter der Nichtzentralität const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der nichtzentralen Betaverteilung mit den Parametern a, b und lambda für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityNoncentralBeta( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const double lambda, // [in] Parameter der Nichtzentralität int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der nichtzentralen Betaverteilung mit den Parametern a, b und lambda für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu dbeta() in R.
bool MathProbabilityDensityNoncentralBeta( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const double lambda, // [in] Parameter der Nichtzentralität const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der nichtzentralen Betaverteilung mit den Parametern a, b und lambda für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathProbabilityDensityNoncentralBeta( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const double lambda, // [in] Parameter der Nichtzentralität double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.4.2. MathCumulativeDistributionNoncentralBeta
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der nichtzentralen Betaverteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionNoncentralBeta( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const double lambda, // [in] Parameter der Nichtzentralität const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der nichtzentralen Betaverteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionNoncentralBeta( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const double lambda, // [in] Parameter der Nichtzentralität int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Betaverteilung mit den Parametern a und b für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'. Analog zu pbeta() in R.
bool MathCumulativeDistributionNoncentralBeta( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const double lambda, // [in] Parameter der Nichtzentralität const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Betaverteilung mit den Parametern a und b für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false.
bool MathCumulativeDistributionNoncentralBeta( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const double lambda, // [in] Parameter der Nichtzentralität double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.4.3. MathQuantileNoncentralBeta
Die Funktion berechnet den Wert der Umkehrfunktion der Wahrscheinlichkeitsverteilung der nichtzentralen Betaverteilung mit den Parametern a, b und lambda für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathQuantileNoncentralBeta( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const double lambda, // [in] Parameter der Nichtzentralität const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Umkehrfunktion der Wahrscheinlichkeitsverteilung der nichtzentralen Betaverteilung mit den Parametern a, b und lambda für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathQuantileNoncentralBeta( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const double lambda, // [in] Variable für den Fehlercode int &error_code // [out] Variable für den Fehlercode );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der nichtzentralen Betaverteilung mit den Parametern a, b und lambda. Im Fehlerfall retourniert sie false. Analog zu qbeta() in R.
bool MathQuantileNoncentralBeta( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const double lambda, // [in] Variable für den Fehlercode const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der nichtzentralen Betaverteilung mit den Parametern a, b und lambda. Im Fehlerfall retourniert sie false.
bool MathQuantileNoncentralBeta( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const double lambda, // [in] Noncentrality parameter double &result[] // [out] Array mit den Werten der Quantile );
2.4.4. MathRandomNoncentralBeta
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der nichtzentralen Betaverteilung mit den Parametern a, b und lambda. Im Fehlerfall retourniert sie NaN.
double MathRandomNoncentralBeta( const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const double lambda, // [in] Parameter der Nichtzentralität int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt Pseudozufallszahlen auf Basis der nichtzentralen Betaverteilung mit den Parametern a, b und lambda. Im Fehlerfall retourniert sie false. Analog zu rbeta() in R.
bool MathRandomNoncentralBeta( const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const double lambda, // [in] Parameter der Nichtzentralität const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.4.5. MathMomentsNoncentralBeta
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der nichtzentralen Betaverteilung mit den Parametern a, b und lambda. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
double MathMomentsNoncentralBeta( const double a, // [in] Der erste Parameter der Betaverteilung (shape1) const double b, // [in] Der zweite Parameter der Betaverteilung (shape2) const double lambda, // [in] Parameter der Nichtzentralität double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.5. Gamma-Verteilung
2.5.1. MathProbabilityDensityGamma
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Gammaverteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.double MathProbabilityDensityGamma( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Der erste Parameter der Verteilung (shape) const double b, // [in] Der zweite Parameter der Verteilung (scale) const bool log_mode, // [in] Parameter zur Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Gammaverteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityGamma( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Der erste Parameter der Verteilung (shape) const double b, // [in] Der zweite Parameter der Verteilung (scale) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Gammaverteilung mit den Parametern a und b für den Array der Zufallsvariable x[]. Im Fehlerfall retourniert sie false. Analog zu dgamma() in R.
bool MathProbabilityDensityGamma( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Der erste Parameter der Verteilung (shape) const double b, // [in] Der zweite Parameter der Verteilung (scale) const bool log_mode, // [in] Parameter zur Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte berechnet double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Gammaverteilung mit den Parametern a und b für den Array der Zufallsvariable x[]. Im Fehlerfall retourniert sie false.
bool MathProbabilityDensityGamma( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Der erste Parameter der Verteilung (shape) const double b, // [in] Der zweite Parameter der Verteilung (scale) double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.5.2. MathCumulativeDistributionGamma
Die Funktion berechnet den Wert der Gammaverteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionGamma( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Der erste Parameter der Verteilung (shape) const double b, // [in] Der zweite Parameter der Verteilung (scale) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Gammaverteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionGamma( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Der erste Parameter der Verteilung (shape) const double b, // [in] Der zweite Parameter der Verteilung (scale) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Gammaverteilung mit den Parametern a und b für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu pgamma() in R.
bool MathCumulativeDistributionGamma( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Der erste Parameter der Verteilung (shape) const double b, // [in] Der zweite Parameter der Verteilung (scale) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der Gammaverteilung mit den Parametern a und b für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false.
bool MathCumulativeDistributionGamma( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Der erste Parameter der Verteilung (shape) const double b, // [in] Der zweite Parameter der Verteilung (scale) double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.5.3. MathQuantileGamma
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Betaverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie NaN.
double MathQuantileGamma( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double a, // [in] Der erste Parameter der Verteilung (shape) const double b, // [in] Der zweite Parameter der Verteilung (scale) const bool tail, // [in] Parameter, wenn false, wird für eine 1.0-Wahrschenlichkeit gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Betaverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie NaN.
double MathQuantileGamma( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double a, // [in] Der erste Parameter der Verteilung (shape) const double b, // [in] Der zweite Parameter der Verteilung (scale) int &error_code // [out] Variable für den Fehlercode );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Gammaverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie false. Analog zu qgamma() in R.
bool MathQuantileGamma( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double a, // [in] Der erste Parameter der Verteilung (shape) const double b, // [in] Der zweite Parameter der Verteilung (scale) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Gammaverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie false.
bool MathQuantileGamma( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double a, // [in] Der erste Parameter der Verteilung (shape) const double b, // [in] Der zweite Parameter der Verteilung (scale) double &result[] // [out] Array mit den Werten der Quantile );
2.5.4. MathRandomGamma
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der Gammaverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie NaN.
double MathRandomGamma( const double a, // [in] Der erste Parameter der Verteilung (shape) const double b, // [in] Der zweite Parameter der Verteilung (scale) int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt eine Pseudozufallszahlen auf Basis der Gammaverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie false. Analog zu rgamma() in R.
bool MathRandomGamma( const double a, // [in] Der erste Parameter der Verteilung (shape) const double b, // [in] Der zweite Parameter der Verteilung (scale) const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.5.5. MathMomentsGamma
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der Gammaverteilung mit den Parametern a und b. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsGamma( const double a, // [in] Der erste Parameter der Verteilung (shape) const double b, // [in] Der zweite Parameter der Verteilung (scale) double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.6. Chi-Quadrat Verteilung
2.6.1. MathProbabilityDensityChiSquare
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Chi-QuadraT-Verteilung mit dem Parameter nu für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityChiSquare( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Chi-QuadraT-Verteilung mit dem Parameter nu für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityChiSquare( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Chi-QuadraT-Verteilung mit dem Parameter nu für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu dchisq() in R.
bool MathProbabilityDensityChiSquare( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Chi-QuadraT-Verteilung mit dem Parameter nu für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathProbabilityDensityChiSquare( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.6.2. MathCumulativeDistributionChiSquare
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Chi-QuadraT-Verteilung mit dem Parameter nu für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionChiSquare( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter zur Berechnung des Logarithmus des Wertes, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Chi-QuadraT-Verteilung mit dem Parameter nu für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionChiSquare( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Chi-QuadraT-Verteilung mit dem Parameter nu für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu pchisq() in R.
bool MathCumulativeDistributionChiSquare( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Chi-QuadraT-Verteilung mit dem Parameter nu für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathCumulativeDistributionChiSquare( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.6.3. MathQuantileChiSquare
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Chi-QuadraT-Verteilung. Im Fehlerfall retourniert sie NaN.
double MathQuantileChiSquare( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool tail, // [in] Parameter, wenn false, wird für eine 1.0-Wahrschenlichkeit gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Chi-QuadraT-Verteilung. Im Fehlerfall retourniert sie NaN.
double MathQuantileChiSquare( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) int &error_code // [out] Variable für den Fehlercode );
Für den angegebene Array von Wahrscheinlichkeiten 'probability[]' berechnet die Funktion den Wert der Umkehrfunktion der Chi-QuadraT-Verteilung. Im Fehlerfall retourniert sie false. Analog zu qchisq() in R.
bool MathQuantileChiSquare( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für den angegebene Array von Wahrscheinlichkeiten 'probability[]' berechnet die Funktion den Wert der Umkehrfunktion der Chi-QuadraT-Verteilung. Im Fehlerfall retourniert sie false.
bool MathQuantileChiSquare( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) double &result[] // [out] Array mit den Werten der Quantile );
2.6.4. MathRandomChiSquare
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der Chi-QuadraT-Verteilung mit dem Parameter nu. Im Fehlerfall retourniert sie NaN.
double MathRandomChiSquare( const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt Pseudozufallszahlen auf Basis der Chi-QuadraT-Verteilung mit dem Parameter nu. Im Fehlerfall retourniert sie false. Analog zu rchisq() in R.
bool MathRandomChiSquare( const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.6.5. MathMomentsChiSquare
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der Chi-QuadraT-Verteilung mit dem Parameter nu. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsChiSquare( const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.7. Nichtzentrale Chi-QuadraT-Verteilung
2.7.1. MathProbabilityDensityNoncentralChiSquare
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der nichtzentralen Chi-QuadraT-Verteilung mit den Parametern nu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityNoncentralChiSquare( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der nichtzentralen Chi-QuadraT-Verteilung mit den Parametern nu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityNoncentralChiSquare( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der nichtzentralen Chi-QuadraT-Verteilung mit dem Parameter nu für einen Array der Zufallsvariable x[]. Im Fehlerfall retourniert sie false. Analog zu dchisq() in R.
bool MathProbabilityDensityNoncentralChiSquare( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der nichtzentralen Chi-QuadraT-Verteilung mit dem Parameter nu für einen Array der Zufallsvariable x[]. Im Fehlerfall retourniert sie false.
bool MathProbabilityDensityNoncentralChiSquare( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.7.2. MathCumulativeDistributionNoncentralChiSquare
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der nichtzentralen Chi-QuadraT-Verteilung mit den Parametern nu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionNoncentralChiSquare( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der nichtzentralen Chi-QuadraT-Verteilung mit den Parametern nu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionNoncentralChiSquare( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der nichtzentralen Chi-QuadraT-Verteilung mit den Parametern nu und sigma für einen Array der Zufallsvariable x[]. Im Fehlerfall retourniert sie 'false'. Analog zu pchisq() in R.
bool MathCumulativeDistributionNoncentralChiSquare( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der nichtzentralen Chi-QuadraT-Verteilung mit den Parametern nu und sigma für einen Array der Zufallsvariable x[]. Im Fehlerfall retourniert sie 'false'.
bool MathCumulativeDistributionNoncentralChiSquare( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.7.3. MathQuantileNoncentralChiSquare
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der nichtzentralen Chi-QuadraT-Verteilung mit den Parametern nu und sigma. Im Fehlerfall retourniert sie NaN.
double MathQuantileNoncentralChiSquare( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der nichtzentralen Chi-QuadraT-Verteilung mit den Parametern nu und sigma. Im Fehlerfall retourniert sie NaN.
double MathQuantileNoncentralChiSquare( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität int &error_code // [out] Variable für den Fehlercode );
Für den angegebenen Array 'probability[]' mit Wahrscheinlichkeitswerten berechnet die Funktion den Wert der Umkehrfunktion der nichtzentralen Chi-QuadraT-Verteilung mit den Parametern nu und sigma. Im Fehlerfall retourniert sie false. Analog zu qchisq() in R.
bool MathQuantileNoncentralChiSquare( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für den angegebenen Array 'probability[]' mit Wahrscheinlichkeitswerten berechnet die Funktion den Wert der Umkehrfunktion der nichtzentralen Chi-QuadraT-Verteilung mit den Parametern nu und sigma. Im Fehlerfall retourniert sie false.
bool MathQuantileNoncentralChiSquare( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität double &result[] // [out] Array mit den Werten der Quantile );
2.7.4. MathRandomNoncentralChiSquare
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der nichtzentralen Chi-QuadraT-Verteilung mit den Parametern nu und sigma. Im Fehlerfall retourniert sie NaN.
double MathRandomNoncentralChiSquare( const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt Pseudozufallszahlen auf Basis der nichtzentralen Chi-QuadraT-Verteilung mit den Parametern nu und sigma. Im Fehlerfall retourniert sie false. Analog zu rchisq() in R.
bool MathRandomNoncentralChiSquare( const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.7.5. MathMomentsNoncentralChiSquare
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der nichtzentralen Chi-QuadraT-Verteilung mit dem Parameter nu und sigma. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsNoncentralChiSquare( const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.8. Exponentielle Verteilung
2.8.1. MathProbabilityDensityExponential
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion einer exponentiellen Verteilung mit dem Parameter mu für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityExponential( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] Parameter der Verteilung (Erwartungswert) const bool log_mode, // [in] Parameter zur Logarithmusberechnung, if log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion einer exponentiellen Verteilung mit dem Parameter mu für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityExponential( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] Parameter der Verteilung (Erwartungswert) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet die Werte der Wahrscheinlichkeitsdichtefunktion einer exponentiellen Normalverteilung mit dem Parameter mu für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu dexp() in R.
bool MathProbabilityDensityExponential( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] Parameter der Verteilung (Erwartungswert) const bool log_mode, // [in] Parameter zur Berechnung des Logarithmus des Wertes, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte berechnet double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet die Werte der Wahrscheinlichkeitsdichtefunktion einer exponentiellen Normalverteilung mit dem Parameter mu für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false.
bool MathProbabilityDensityExponential( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] Parameter der Verteilung (Erwartungswert) double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.8.2. MathCumulativeDistributionExponential
Die Funktion berechnet den Wert der Exponentialverteilung mit dem Parameter mu für die Zufallsvariable x. Im Fehlerfall retourniert sie 'false'. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionExponential( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] Parameter der Verteilung (Erwartungswert) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Exponentialverteilung mit dem Parameter mu für die Zufallsvariable x. Im Fehlerfall retourniert sie 'false'. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionExponential( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] Parameter der Verteilung (Erwartungswert) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Exponentialverteilung mit dem Parameter mu für die Zufallsvariable x. Im Fehlerfall retourniert sie 'false'. Im Fehlerfall retourniert sie false. Analog zu pexp() in R.
bool MathCumulativeDistributionExponential( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] Parameter der Verteilung (Erwartungswert) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der Exponentialverteilung mit dem Parameter mu für die Zufallsvariable x. Im Fehlerfall retourniert sie 'false'. Im Fehlerfall retourniert sie 'false'.
bool MathCumulativeDistributionExponential( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] Parameter der Verteilung (Erwartungswert) double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.8.3. MathQuantileExponential
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Exponentialverteilung mit dem Parameter mu. Im Fehlerfall retourniert sie NaN.
double MathQuantileExponential( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double mu, // [in] Parameter der Verteilung (Erwartungswert) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Exponentialverteilung mit dem Parameter mu. Im Fehlerfall retourniert sie NaN.
double MathQuantileExponential( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double mu, // [in] Parameter der Verteilung (Erwartungswert) int &error_code // [out] Variable für den Fehlercode );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Exponentialverteilung mit den Parametern mu. Im Fehlerfall retourniert sie false. Analog zu qexp() in R.
bool MathQuantileExponential( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double mu, // [in] Parameter der Verteilung (Erwartungswert) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Exponentialverteilung mit den Parametern mu. Im Fehlerfall retourniert sie 'false'.
bool MathQuantileExponential( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double mu, // [in] Parameter der Verteilung (Erwartungswert) double &result[] // [out] Array mit den Werten der Quantile );
2.8.4. MathRandomExponential
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der Exponentialverteilung mit dem Parameter mu. Im Fehlerfall retourniert sie NaN.
double MathRandomExponential( const double mu, // [in] Parameter der Verteilung (Erwartungswert) int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt Pseudozufallszahlen auf Basis der Exponentialverteilung mit dem Parameter mu. Im Fehlerfall retourniert sie false. Analog zu rexp() in R.
bool MathRandomExponential( const double mu, // [in] Parameter der Verteilung (Erwartungswert) const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.8.5. MathMomentsExponential
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der Exponentialverteilung mit dem Parameter mu. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsExponential( const double mu, // [in] Parameter der Verteilung (Erwartungswert) double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.9. F-Verteilung
2.9.1. MathProbabilityDensityF
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der F-Verteilung von Fisher mit den Parametern nu1 und nu2 für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityF( const double x, // [in] Wert der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der F-Verteilung von Fisher mit den Parametern nu1 und nu2 für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityF( const double x, // [in] Wert der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der F-Verteilung von Fisher mit den Parametern nu1 und nu2 für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu df() in R.
bool MathProbabilityDensityF( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der F-Verteilung von Fisher mit den Parametern nu1 und nu2 für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false.
bool MathProbabilityDensityF( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.9.2. MathCumulativeDistributionF
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der F-Verteilung von Fisher mit den Parametern nu1 und nu2 für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionF( const double x, // [in] Wert der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der F-Verteilung von Fisher mit den Parametern nu1 und nu2 für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionF( const double x, // [in] Wert der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade)) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der F-Verteilung von Fisher mit den Parametern nu1 und nu2 für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu pf() in R.
bool MathCumulativeDistributionF( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der F-Verteilung von Fisher mit den Parametern nu1 und nu2 für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false.
bool MathCumulativeDistributionF( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.9.3. MathQuantileF
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der F-Verteilung von Fisher mit den Parametern nu1 und nu2. . Im Fehlerfall retourniert sie NaN.
double MathQuantileF( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool tail, // [in] Parameter, wenn false, wird für eine 1.0-Wahrschenlichkeit gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der F-Verteilung von Fisher mit den Parametern nu1 und nu2. . Im Fehlerfall retourniert sie NaN.
double MathQuantileF( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der F-Verteilung von Fisher mit den Parametern nu1 und nu2. . Im Fehlerfall retourniert sie false. Analog zu qf() in R.
bool MathQuantileF( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool tail, // [in] Parameter, wenn false, wird für eine 1.0-Wahrschenlichkeit gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der F-Verteilung von Fisher mit den Parametern nu1 und nu2. . Im Fehlerfall retourniert sie false.
bool MathQuantileF( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) double &result[] // [out] Array mit den Werten der Quantile );
2.9.4. MathRandomF
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der F-Verteilung von Fisher mit den Parametern nu1 und nu2. Im Fehlerfall retourniert sie NaN.
double MathRandomF( const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt Pseudozufallszahlen auf Basis der F-Verteilung von Fisher mit den Parametern nu1 und nu2. Im Fehlerfall retourniert sie false. Analog zu rf() in R.
bool MathRandomF( const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.9.5. MathMomentsF
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der F-Verteilung von Fisher mit den Parametern nu1 und nu2. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsF( const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.10. Nichtzentrale F-Verteilung
2.10.1. MathProbabilityDensityNoncentralF
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der nichtzentralen F-Verteilung von Fisher mit den Parametern nu1, nu2 und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityNoncentralF( const double x, // [in] Wert der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der nichtzentralen F-Verteilung von Fisher mit den Parametern nu1, nu2 und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityNoncentralF( const double x, // [in] Wert der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der nichtzentralen F-Verteilung von Fisher mit den Parametern nu1, nu2 und sigma für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu df() in R.
double MathProbabilityDensityNoncentralF( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der nichtzentralen F-Verteilung von Fisher mit den Parametern nu1, nu2 und sigma für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
double MathProbabilityDensityNoncentralF( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.10.2. MathCumulativeDistributionlNoncentralF
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der nichtzentralen F-Verteilung von Fisher mit den Parametern nu1, nu2 und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionNoncentralF( const double x, // [in] Wert der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der nichtzentralen F-Verteilung von Fisher mit den Parametern nu1, nu2 und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionNoncentralF( const double x, // [in] Wert der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der nichtzentralen F-Verteilung von Fisher mit den Parametern nu1, nu2 und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie false. Analog zu pf() in R.
bool MathCumulativeDistributionNoncentralF( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der nichtzentralen F-Verteilung von Fisher mit den Parametern nu1, nu2 und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
bool MathCumulativeDistributionNoncentralF( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.10.3. MathQuantileNoncentralF
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der nichtzentralen F-Verteilung von Fisher mit den Parametern nu1, nu2 und sigma. Im Fehlerfall retourniert sie NaN.
double MathQuantileNoncentralF( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der nichtzentralen F-Verteilung von Fisher mit den Parametern nu1, nu2 und sigma. Im Fehlerfall retourniert sie NaN.
double MathQuantileNoncentralF( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der nichtzentralen F-Verteilung von Fisher mit den Parametern nu1, nu2 und sigma. Im Fehlerfall retourniert sie false. Analog zu qf() in R.
bool MathQuantileNoncentralF( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der nichtzentralen F-Verteilung von Fisher mit den Parametern nu1, nu2 und sigma. Im Fehlerfall retourniert sie false.
bool MathQuantileNoncentralF( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität double &result[] // [out] Array mit den Werten der Quantile );
2.10.4. MathRandomNoncentralF
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der nichtzentralen F-Verteilung von Fisher mit den Parametern nu1, nu2 und sigma. Im Fehlerfall retourniert sie NaN.
double MathRandomNoncentralF( const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt Pseudozufallszahlen auf Basis der nichtzentralen F-Verteilung von Fisher mit den Parametern nu1, nu2 und sigma. Im Fehlerfall retourniert sie false. Analog zu rf() in R.
bool MathRandomNoncentralF( const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität double &result[] // [out] Array mit den Werten der Quantile );
2.10.5. MathMomentsNoncentralF
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der nichtzentralen F-Verteilung von Fisher mit den Parametern nu1, nu2 und sigma. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsNoncentralF( const double nu1, // [in] Der erste Parameter der Verteilung (Anzahl der Freiheitsgrade) const double nu2, // [in] Der zweite Parameter der Verteilung (Anzahl der Freiheitsgrade) const double sigma, // [in] Parameter der Nichtzentralität double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.11. T-Verteilung
2.11.1. MathProbabilityDensityT
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Studentschen T-Verteilung mit dem Parameter nu für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityT( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool log_mode, // [in] Parameter zur Logarithmusberechnung, if log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Studentschen T-Verteilung mit dem Parameter nu für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityT( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Studentschen T-Verteilung mit dem Parameter nu für den Array der Zufallsvariable x[]. Im Fehlerfall retourniert sie false. Analog zu dt() in R.
bool MathProbabilityDensityT( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool log_mode, // [in] Parameter zur Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte berechnet double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Studentschen T-Verteilung mit dem Parameter nu für den Array der Zufallsvariable x[]. Im Fehlerfall retourniert sie 'false'.
bool MathProbabilityDensityT( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) double &result[] // [out] Array der Werte der Funktion der Wahrscheinlichkeitsdichte );
2.11.2. MathCumulativeDistributionT
Die Funktion berechnet den Wert der Studentschen T-Verteilung mit dem Parameter nu für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionT( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Studentschen T-Verteilung mit dem Parameter nu für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionT( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Studentschen T-Verteilung mit dem Parameter nu für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu pt() in R.
bool MathCumulativeDistributionT( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der Studentschen T-Verteilung mit dem Parameter nu für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false.
bool MathCumulativeDistributionT( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.11.3. MathQuantileT
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Studentschen T-Verteilung mit dem Parameter nu. Im Fehlerfall retourniert sie NaN.
double MathQuantileT( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Studentschen T-Verteilung mit dem Parameter nu. Im Fehlerfall retourniert sie NaN.
double MathQuantileT( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) int &error_code // [out] Variable für den Fehlercode );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Studentschen T-Verteilung mit dem Parameter nu. Im Fehlerfall retourniert sie false. Analog zu qt() in R.
bool MathQuantileT( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Studentschen T-Verteilung mit dem Parameter nu. Im Fehlerfall retourniert sie 'false'.
bool MathQuantileT( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) double &result[] // [out] Array mit den Werten der Quantile );
2.11.4. MathRandomT
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der Studentschen T-Verteilung mit dem Parameter nu. Im Fehlerfall retourniert sie NaN.
double MathRandomT( const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt Pseudozufallszahlen auf Basis der Studentschen T-Verteilung mit dem Parameter nu. Im Fehlerfall retourniert sie 'false'. Analog zu rt() in R.
bool MathRandomT( const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.11.5. MathMomentsT
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der Studentschen T-Verteilung mit dem Parameter nu. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
double MathMomentsT( const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.12. Nichtzentrale T-Verteilung
2.12.1. MathProbabilityDensityNoncentralT
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion dernichtzentralen Studentschen T-Verteilung mit dem Parameter nu für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityNoncentralT( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double delta, // [in] Parameter der Nichtzentralität const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion dernichtzentralen Studentschen T-Verteilung mit dem Parameter nu für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityNoncentralT( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double delta, // [in] Parameter der Nichtzentralität int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der nichtzentralen Studentsche T-Verteilung mit dem Parameter nu für den Array der Zufallsvariable x[]. Im Fehlerfall retourniert sie false. Analog zu dt() in R.
bool MathProbabilityDensityNoncentralT( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double delta, // [in] Parameter der Nichtzentralität const bool log_mode, // [in] Parameter zur Berechnung des Logarithmus des Wertes, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte berechnet double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der nichtzentralen Studentsche T-Verteilung mit dem Parameter nu für den Array der Zufallsvariable x[]. Im Fehlerfall retourniert sie false.
bool MathProbabilityDensityNoncentralT( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double delta, // [in] Parameter der Nichtzentralität double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.12.2. MathCumulativeDistributionlNoncentralT
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der nichtzentralen Studentschen T-Verteilung mit den Parametern nu und delta für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionNoncentralT( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double delta, // [in] Parameter der Nichtzentralität const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der nichtzentralen Studentschen T-Verteilung mit den Parametern nu und delta für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionNoncentralT( const double x, // [in] Wert der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double delta, // [in] Parameter der Nichtzentralität int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der nichtzentralen Studentsche T-Verteilung mit den Parametern nu und delta für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu pt() in R.
bool MathCumulativeDistributionNoncentralT( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double delta, // [in] Parameter der Nichtzentralität const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der nichtzentralen Studentsche T-Verteilung mit den Parametern nu und delta für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathCumulativeDistributionNoncentralT( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double delta, // [in] Parameter der Nichtzentralität double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.12.3. MathQuantileNoncentralT
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der nichtzentralen Studentschen T-Verteilung mit den Parametern nu und delta. Im Fehlerfall retourniert sie NaN.
double MathQuantileNoncentralT( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double delta, // [in] Parameter der Nichtzentralität const bool tail, // [in] Parameter, wenn false, wird für eine 1.0-Wahrschenlichkeit gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der nichtzentralen Studentschen T-Verteilung mit den Parametern nu und delta. Im Fehlerfall retourniert sie NaN.
double MathQuantileNoncentralT( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double delta, // [in] Parameter der Nichtzentralität int &error_code // [out] Variable für den Fehlercode );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der nichtzentralen Studentsche T-Verteilung mit dem Parameter nu. Im Fehlerfall retourniert sie false. Analog zu qt() in R.
bool MathQuantileNoncentralT( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double delta, // [in] Parameter der Nichtzentralität const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der nichtzentralen Studentsche T-Verteilung mit dem Parameter nu. Im Fehlerfall retourniert sie 'false'.
bool MathQuantileNoncentralT( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double delta, // [in] Parameter der Nichtzentralität double &result[] // [out] Array mit den Werten der Quantile );
2.12.4. MathRandomNoncentralT
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der nichtzentralen Studentsche T-Verteilung mit den Parametern nu und delta. Im Fehlerfall retourniert sie NaN.
double MathRandomNoncentralT( const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double delta, // [in] Parameter der Nichtzentralität int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt Pseudozufallszahlen auf Basis der nichtzentralen Studentsche T-Verteilung mit den Parametern nu und delta. Im Fehlerfall retourniert sie false. Analog zu rt() in R.
bool MathRandomNoncentralT( const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double delta, // [in] Parameter der Nichtzentralität const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.12.5. MathMomentsNoncentralT
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der nichtzentralen Studentsche T-Verteilung mit dem Parameter nu und delta. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
double MathMomentsNoncentralT( const double nu, // [in] Parameter der Verteilung (Anzahl der Freiheitsgrade) const double delta, // [in] Parameter der Nichtzentralität double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.13. Logistische Verteilung
2.13.1. MathProbabilityDensityLogistic
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der logistischen Verteilung mit den Parametern mu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityLogistic( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] mean Parameter der Verteilung const double sigma, // [in] scale Parameter der Verteilung const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der logistischen Verteilung mit den Parametern mu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityLogistic( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] mean Parameter der Verteilung const double sigma, // [in] scale Parameter der Verteilung int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet die Werte der Wahrscheinlichkeitsdichtefunktion einer logistischen Verteilung mit den Parametern mu und sigma für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'. Analog zu dlogis() in R.
bool MathProbabilityDensityLogistic( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] mean Parameter der Verteilung const double sigma, // [in] scale Parameter der Verteilung const bool log_mode, // [in] Parameter zur Berechnung des Logarithmus des Wertes, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte berechnet double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet die Werte der Wahrscheinlichkeitsdichtefunktion einer logistischen Verteilung mit den Parametern mu und sigma für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathProbabilityDensityLogistic( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] mean Parameter der Verteilung const double sigma, // [in] scale Parameter der Verteilung double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.13.2. MathCumulativeDistributionlLogistic
Die Funktion berechnet den Wert der logistischen Verteilung mit den Parametern mu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionLogistic( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] mean Parameter der Verteilung const double sigma, // [in] scale Parameter der Verteilung const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der logistischen Verteilung mit den Parametern mu und sigma für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionLogistic( const double x, // [in] Wert der Zufallsvariablen const double mu, // [in] mean Parameter der Verteilung const double sigma, // [in] scale Parameter der Verteilung int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der logistischen Verteilung mit den Parametern mu und sigma für den Array mit Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu plogis() in R.
bool MathCumulativeDistributionLogistic( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] mean Parameter der Verteilung const double sigma, // [in] scale Parameter der Verteilung const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der logistischen Verteilung mit den Parametern mu und sigma für den Array mit Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu plogis() in R.
bool MathCumulativeDistributionLogistic( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double mu, // [in] mean Parameter der Verteilung const double sigma, // [in] scale Parameter der Verteilung double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.13.3. MathQuantileLogistic
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der logistischen Verteilung mit den Parametern mu und sigma. Im Fehlerfall retourniert sie NaN.
double MathQuantileLogistic( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double mu, // [in] mean Parameter der Verteilung const double sigma, // [in] scale Parameter der Verteilung const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der logistischen Verteilung mit den Parametern mu und sigma. Im Fehlerfall retourniert sie NaN.
double MathQuantileLogistic( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double mu, // [in] mean Parameter der Verteilung const double sigma, // [in] scale Parameter der Verteilung int &error_code // [out] Variable für den Fehlercode );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der logistischen Verteilung mit den Parametern mu und sigma. Im Fehlerfall retourniert sie false. Analog zu qlogis() in R.
bool MathQuantileLogistic( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double mu, // [in] mean Parameter der Verteilung const double sigma, // [in] scale Parameter der Verteilung const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der logistischen Verteilung mit den Parametern mu und sigma. Im Fehlerfall retourniert sie 'false'.
bool MathQuantileLogistic( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double mu, // [in] mean Parameter der Verteilung const double sigma, // [in] scale Parameter der Verteilung double &result[] // [out] Array mit den Werten der Quantile );
2.13.4. MathRandomLogistic
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der logistischen Verteilung mit den Parametern mu und sigma. Im Fehlerfall retourniert sie NaN.
double MathRandomLogistic( const double mu, // [in] mean Parameter der Verteilung const double sigma, // [in] scale Parameter der Verteilung int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt Pseudozufallszahlen auf Basis der logistischen Verteilung mit den Parametern mu und sigma. Im Fehlerfall retourniert sie false. Analog zu rlogis() in R.
bool MathRandomLogistic( const double mu, // [in] mean Parameter der Verteilung const double sigma, // [in] scale Parameter der Verteilung const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.13.5. MathMomentsLogistic
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der logistischen Verteilung mit dem Parameter mu und sigma. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsLogistic( const double mu, // [in] mean Parameter der Verteilung const double sigma, // [in] scale Parameter der Verteilung double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.14. Cauchy-Verteilung
2.14.1. MathProbabilityDensityCauchy
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Cauchy-Verteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityCauchy( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] mean Parameter der Verteilung const double b, // [in] scale Parameter der Verteilung const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Cauchy-Verteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityCauchy( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] mean Parameter der Verteilung const double b, // [in] scale Parameter der Verteilung int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Cauchy-Verteilung mit den Parametern a und b für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'. Analog zu dcauchy() in R.
bool MathProbabilityDensityCauchy( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] mean Parameter der Verteilung const double b, // [in] scale Parameter der Verteilung const bool log_mode, // [in] Parameter zur Berechnung des Logarithmus des Wertes, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte berechnet double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Cauchy-Verteilung mit den Parametern a und b für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathProbabilityDensityCauchy( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] mean Parameter der Verteilung const double b, // [in] scale Parameter der Verteilung double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.14.2. MathCumulativeDistributionCauchy
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Cauchy-Verteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionCauchy( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] mean Parameter der Verteilung const double b, // [in] scale Parameter der Verteilung const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Cauchy-Verteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionCauchy( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] mean Parameter der Verteilung const double b, // [in] scale Parameter der Verteilung int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Cauchy-Verteilung mit den Parametern a und b für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'. Analog zu pcauchy() in R.
bool MathCumulativeDistributionCauchy( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] mean Parameter der Verteilung const double b, // [in] scale Parameter der Verteilung const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Cauchy-Verteilung mit den Parametern a und b für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathCumulativeDistributionCauchy( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] mean Parameter der Verteilung const double b, // [in] scale Parameter der Verteilung double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.14.3. MathQuantileCauchy
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Cauchy-Verteilung mit den Parametern a und b. Im Fehlerfall retourniert sie NaN.
double MathQuantileCauchy( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double a, // [in] mean Parameter der Verteilung const double b, // [in] scale Parameter der Verteilung const bool tail, // [in] Parameter, wenn false, wird für eine 1.0-Wahrschenlichkeit gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Cauchy-Verteilung mit den Parametern a und b. Im Fehlerfall retourniert sie NaN.
double MathQuantileCauchy( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double a, // [in] mean Parameter der Verteilung const double b, // [in] scale Parameter der Verteilung int &error_code // [out] Variable für den Fehlercode );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Cauchy-Verteilung mit den Parametern a und b. Im Fehlerfall retourniert sie false. Analog zu qcauchy() in R.
bool MathQuantileCauchy( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double a, // [in] mean Parameter der Verteilung const double b, // [in] scale Parameter der Verteilung const bool tail, // [in] Parameter, wenn false, wird für eine 1.0-Wahrschenlichkeit gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Cauchy-Verteilung mit den Parametern a und b. Im Fehlerfall retourniert sie 'false'.
bool MathQuantileCauchy( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double a, // [in] mean Parameter der Verteilung const double b, // [in] scale Parameter der Verteilung double &result[] // [out] Array mit den Werten der Quantile );
2.14.4. MathRandomCauchy
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der Cauchy-Verteilung mit den Parametern a und b. Im Fehlerfall retourniert sie NaN.
double MathRandomCauchy( const double a, // [in] mean Parameter der Verteilung const double b, // [in] scale Parameter der Verteilung int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt Pseudozufallszahlen auf Basis der Cauchy-Verteilung mit den Parametern a und b. Im Fehlerfall retourniert sie false. Analog zu rcauchy() in R.
double MathRandomCauchy( const double a, // [in] mean Parameter der Verteilung const double b, // [in] scale Parameter der Verteilung const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.14.5. MathMomentsCauchy
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der Cauchy-Verteilung. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsCauchy( const double a, // [in] mean Parameter der Verteilung const double b, // [in] scale Parameter der Verteilung double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.15. Gleichverteilung
2.15.1. MathProbabilityDensityUniform
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Gleichverteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityUniform( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Parameter a der Verteilung (Untergrenze) const double b, // [in] Parameter b der Verteilung (Obergrenze) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Gleichverteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityUniform( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Parameter a der Verteilung (Untergrenze) const double b, // [in] Parameter b der Verteilung (Obergrenze) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Gleichverteilung mit den Parametern a und b für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu dunif() in R.
Sbool MathProbabilityDensityUniform( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Parameter a der Verteilung (Untergrenze) const double b, // [in] Parameter b der Verteilung (Obergrenze) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Gleichverteilung mit den Parametern a und b für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false.
Sbool MathProbabilityDensityUniform( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Parameter a der Verteilung (Untergrenze) const double b, // [in] Parameter b der Verteilung (Obergrenze) double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.15.2. MathCumulativeDistributionUniform
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Gleichverteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.double MathCumulativeDistributionUniform( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Parameter a der Verteilung (Untergrenze) const double b, // [in] Parameter b der Verteilung (Obergrenze) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Gleichverteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionUniform( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Parameter a der Verteilung (Untergrenze) const double b, // [in] Parameter b der Verteilung (Obergrenze) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Gleichverteilung mit den Parametern a und b für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu punif() in R.
bool MathCumulativeDistributionUniform( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Parameter a der Verteilung (Untergrenze) const double b, // [in] Parameter b der Verteilung (Obergrenze) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Gleichverteilung mit den Parametern a und b für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false.
bool MathCumulativeDistributionUniform( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Parameter a der Verteilung (Untergrenze) const double b, // [in] Parameter b der Verteilung (Obergrenze) double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.15.3. MathQuantileUniform
Für die spezifische Wahrscheinlichkeit berechnet die Funktion den Wert der Umkehrfunktion der Gleichverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie NaN.
double MathQuantileUniform( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double a, // [in] Parameter a der Verteilung (Untergrenze) const double b, // [in] Parameter b der Verteilung (Obergrenze) const bool tail, // [in] Parameter, wenn false, wird für eine 1.0-Wahrschenlichkeit gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet int &error_code // [out] Variable für den Fehlercode );
Für die spezifische Wahrscheinlichkeit berechnet die Funktion den Wert der Umkehrfunktion der Gleichverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie NaN.
double MathQuantileUniform( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double a, // [in] Parameter a der Verteilung (Untergrenze) const double b, // [in] Parameter b der Verteilung (Obergrenze) int &error_code // [out] Variable für den Fehlercode );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Gleichverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie 'false'. Analog zu qunif() in R.
bool MathQuantileUniform( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double a, // [in] Parameter a der Verteilung (Untergrenze) const double b, // [in] Parameter b der Verteilung (Obergrenze) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Gleichverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie false.
bool MathQuantileUniform( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double a, // [in] Parameter a der Verteilung (Untergrenze) const double b, // [in] Parameter b der Verteilung (Obergrenze) double &result[] // [out] Array mit den Werten der Quantile );
2.15.4. MathRandomUniform
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der Gleichverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie NaN . Im Fehlerfall retourniert sie NaN.
double MathRandomUniform( const double a, // [in] Parameter a der Verteilung (Untergrenze) const double b, // [in] Parameter b der Verteilung (Obergrenze) int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der Gleichverteilung mit den Parametern a und b. Im Fehlerfall retourniert sie false. Analog zu runif() in R.
bool MathRandomUniform( const double a, // [in] Parameter a der Verteilung (Untergrenze) const double b, // [in] Parameter b der Verteilung (Obergrenze) const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.15.5. MathMomentsUniform
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der Gleichverteilung. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsUniform( const double a, // [in] arameter a der Verteilung (Untergrenze) const double b, // [in] Parameter b der Verteilung (Obergrenze) double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.16. Weibull-Verteilung
2.16.1. MathProbabilityDensityWeibull
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Weibull-Verteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityWeibull( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Parameter der Verteilung (shape) const double b, // [in] Parameter der Verteilung (scale) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Weibull-Verteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityWeibull( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Parameter der Verteilung (shape) const double b, // [in] Parameter der Verteilung (scale) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Weibull-Verteilung mit den Parametern a und b für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu dweibull() in R.
bool MathProbabilityDensityWeibull( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Parameter der Verteilung (shape) const double b, // [in] Parameter der Verteilung (scale) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Weibull-Verteilung mit den Parametern a und b für einen Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false.
bool MathProbabilityDensityWeibull( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Parameter der Verteilung (shape) const double b, // [in] Parameter der Verteilung (scale) double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.16.2. MathCumulativeDistributionWeibull
Die Funktion berechnet den Wert der Weibull-Verteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.double MathCumulativeDistributionWeibull( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Parameter der Verteilung (shape) const double b, // [in] Parameter der Verteilung (scale) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Weibull-Verteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionWeibull( const double x, // [in] Wert der Zufallsvariablen const double a, // [in] Parameter der Verteilung (shape) const double b, // [in] Parameter der Verteilung (scale) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Weibull-Verteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie false. Analog zu pweibull() in R.
bool MathCumulativeDistributionWeibull( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Parameter der Verteilung (shape) const double b, // [in] Parameter der Verteilung (scale) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Weibull-Verteilung mit den Parametern a und b für die Zufallsvariable x. Im Fehlerfall retourniert sie false.
bool MathCumulativeDistributionWeibull( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double a, // [in] Parameter der Verteilung (shape) const double b, // [in] Parameter der Verteilung (scale) double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.16.3. MathQuantileWeibull
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Weibull-Verteilung mit den Parametern a und b. Im Fehlerfall retourniert sie NaN.
double MathQuantileWeibull( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double a, // [in] Parameter der Verteilung (shape) const double b, // [in] Parameter der Verteilung (scale) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion den Wert der Umkehrfunktion der Weibull-Verteilung mit den Parametern a und b. Im Fehlerfall retourniert sie NaN.
double MathQuantileWeibull( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double a, // [in] Parameter der Verteilung (shape) const double b, // [in] Parameter der Verteilung (scale) int &error_code // [out] Variable für den Fehlercode );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Weibull-Verteilung mit den Parametern a und b. Im Fehlerfall retourniert sie false. Analog zu qweibull() in R.
bool MathQuantileWeibull( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double a, // [in] Parameter der Verteilung (shape) const double b, // [in] Parameter der Verteilung (scale) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Weibull-Verteilung mit den Parametern a und b. Im Fehlerfall retourniert sie false.
bool MathQuantileWeibull( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double a, // [in] Parameter der Verteilung (shape) const double b, // [in] Parameter der Verteilung (scale) double &result[] // [out] Array mit den Werten der Quantile );
2.16.4. MathRandomWeibull
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der Weibull-Verteilung mit den Parametern a und b. Im Fehlerfall retourniert sie NaN.
double MathRandomWeibull( const double a, // [in] Parameter der Verteilung (shape) const double b, // [in] Parameter der Verteilung (scale) int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt Pseudozufallszahlen auf Basis der Weibull-Verteilung mit den Parametern a und b. Im Fehlerfall retourniert sie false. Analog zu rweibull() in R.
bool MathRandomWeibull( const double a, // [in] Parameter der Verteilung (shape) const double b, // [in] Parameter der Verteilung (scale) const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.16.5. MathMomentsWeibull
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der Weibull-Verteilung. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsWeibull( const double a, // [in] Parameter der Verteilung (shape) const double b, // [in] Parameter der Verteilung (scale) double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.17. Binomial-Verteilung
2.17.1. MathProbabilityDensityBinomial
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Binomialverteilung mit den Parametern n und p für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityBinomial( const double x, // [in] Wert der Zufallsvariablen (integer) const double n, // [in] Parameter der Verteilung (Anzahl der Tests) const double p, // [in] Parameter der Verteilung (Erfolgswahrscheinlichkeit für jeden Test) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Binomialverteilung mit den Parametern n und p für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityBinomial( const double x, // [in] Wert der Zufallsvariablen (integer) const double n, // [in] Parameter der Verteilung (Anzahl der Tests) const double p, // [in] Parameter der Verteilung (Erfolgswahrscheinlichkeit für jeden Test) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Binomialverteilung mit den Parametern n und p für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu dbinom() in R.
bool MathProbabilityDensityBinomial( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double n, // [in] Parameter der Verteilung (Anzahl der Tests) const double p, // [in] Parameter der Verteilung (Erfolgswahrscheinlichkeit für jeden Test) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Binomialverteilung mit den Parametern n und p für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false.
bool MathProbabilityDensityBinomial( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double n, // [in] Parameter der Verteilung (Anzahl der Tests) const double p, // [in] Parameter der Verteilung (Erfolgswahrscheinlichkeit für jeden Test) double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.17.2. MathCumulativeDistributionBinomial
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Binomialverteilung mit den Parametern n und p für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionBinomial( const double x, // [in] Wert der Zufallsvariablen (integer) const double n, // [in] Parameter der Verteilung (Anzahl der Tests) const double p, // [in] Parameter der Verteilung (Erfolgswahrscheinlichkeit für jeden Test) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Binomialverteilung mit den Parametern n und p für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionBinomial( const double x, // [in] Wert der Zufallsvariablen (integer) const double n, // [in] Parameter der Verteilung (Anzahl der Tests) const double p, // [in] Parameter der Verteilung (Erfolgswahrscheinlichkeit für jeden Test) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Binomialverteilung mit den Parametern n und p für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu pbinom() in R.
bool MathCumulativeDistributionBinomial( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double n, // [in] Parameter der Verteilung (Anzahl der Tests) const double p, // [in] Parameter der Verteilung (Erfolgswahrscheinlichkeit für jeden Test) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der Binomialverteilung mit den Parametern n und p für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathCumulativeDistributionBinomial( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double n, // [in] Parameter der Verteilung (Anzahl der Tests) const double p, // [in] Parameter der Verteilung (Erfolgswahrscheinlichkeit für jeden Test) double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.17.3. MathQuantileBinomial
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion die Umkehrfunktion der Binomialverteilung mit den Parametern n und p. Im Fehlerfall retourniert sie NaN.
double MathQuantileBinomial( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double n, // [in] Parameter der Verteilung (Anzahl der Tests) const double p, // [in] Parameter der Verteilung (Erfolgswahrscheinlichkeit für jeden Test) const bool tail, // [in] Parameter, wenn false, wird für eine 1.0-Wahrschenlichkeit gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion die Umkehrfunktion der Binomialverteilung mit den Parametern n und p. Im Fehlerfall retourniert sie NaN.
double MathQuantileBinomial( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double n, // [in] Parameter der Verteilung (Anzahl der Tests) const double p, // [in] Parameter der Verteilung (Erfolgswahrscheinlichkeit für jeden Test) int &error_code // [out] Variable für den Fehlercode );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Binomialverteilung mit den Parametern n und p. Im Fehlerfall retourniert sie false. Analog zu qbinom() in R.
bool MathQuantileBinomial( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double n, // [in] Parameter der Verteilung (Anzahl der Tests) const double p, // [in] Parameter der Verteilung (Erfolgswahrscheinlichkeit für jeden Test) const bool tail, // [in] Parameter, wenn false, wird für eine 1.0-Wahrschenlichkeit gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der Binomialverteilung mit den Parametern n und p. Im Fehlerfall retourniert sie 'false'.
bool MathQuantileBinomial( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double n, // [in] Parameter der Verteilung (Anzahl der Tests) const double p, // [in] Parameter der Verteilung (Erfolgswahrscheinlichkeit für jeden Test) double &result[] // [out] Array mit den Werten der Quantile );
2.17.4. MathRandomBinomial
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der Binomialverteilung mit den Parametern n und p. Im Fehlerfall retourniert sie NaN . Im Fehlerfall retourniert sie NaN.
double MathRandomBinomial( const double n, // [in] Parameter der Verteilung (Anzahl der Tests) const double p, // [in] Parameter der Verteilung (Erfolgswahrscheinlichkeit für jeden Test) int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der Binomialverteilung mit den Parametern n und p. Im Fehlerfall retourniert sie false. Analog zu rbinom() in R.
bool MathRandomBinomial( const double n, // [in] Parameter der Verteilung (Anzahl der Tests) const double p, // [in] Parameter der Verteilung (Erfolgswahrscheinlichkeit für jeden Test) const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.17.5. MathMomentsBinomial
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der Binomialverteilung mit den Parametern n und p. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsBinomial( const double n, // [in] Anzahl der Tests const double p, // [in] Wahrscheinlichkeit eines Erfolges in jedem Test double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.18. Negative Binomial-Verteilung
2.18.1. MathProbabilityDensityNegativeBinomial
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der negativen Binomialverteilung mit den Parametern r und p für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityNegativeBinomial( const double x, // [in] Wert der Zufallsvariablen (integer) const double r, // [in] Anzahl der Tests double p, // [in] Wahrscheinlichkeit eines Erfolges const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der negativen Binomialverteilung mit den Parametern r und p für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityNegativeBinomial( const double x, // [in] Wert der Zufallsvariablen (integer) const double r, // [in] Anzahl der Tests double p, // [in] Wahrscheinlichkeit eines Erfolges int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der negativen Binomialverteilung mit den Parametern r und p für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu dnbinom() in R.
bool MathProbabilityDensityNegativeBinomial( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double r, // [in] Anzahl der Tests double p, // [in] Wahrscheinlichkeit eines Erfolges const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der negativen Binomialverteilung mit den Parametern r und p für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathProbabilityDensityNegativeBinomial( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double r, // [in] Anzahl der Tests double p, // [in] Wahrscheinlichkeit eines Erfolges double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.18.2. MathCumulativeDistributionNegativeBinomial
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der negativen Binomialverteilung mit den Parametern r und p für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionNegativeBinomial( const double x, // [in] Wert der Zufallsvariablen (integer) const double r, // [in] Anzahl der Tests double p, // [in] Wahrscheinlichkeit eines Erfolges const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der negativen Binomialverteilung mit den Parametern r und p für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionNegativeBinomial( const double x, // [in] Wert der Zufallsvariablen (integer) const double r, // [in] Anzahl der Tests double p, // [in] Wahrscheinlichkeit eines Erfolges int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der negativen Binomialverteilung mit den Parametern r und p für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu pnbinom() in R.
bool MathCumulativeDistributionNegativeBinomial( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double r, // [in] Anzahl der Tests double p, // [in] Wahrscheinlichkeit eines Erfolges const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der negativen Binomialverteilung mit den Parametern r und p für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathCumulativeDistributionNegativeBinomial( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double r, // [in] Anzahl der Tests double p, // [in] Wahrscheinlichkeit eines Erfolges double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.18.3. MathQuantileNegativeBinomial
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion die Umkehrfunktion der negativen Binomialverteilung mit den Parametern r und p. Im Fehlerfall retourniert sie NaN.
double MathQuantileNegativeBinomial( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double r, // [in] Anzahl erfolgreicher Tests double p, // [in] Erfolgswahrscheinlichkeit const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion die Umkehrfunktion der negativen Binomialverteilung mit den Parametern r und p. Im Fehlerfall retourniert sie NaN.
double MathQuantileNegativeBinomial( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double r, // [in] Anzahl erfolgreicher Tests double p, // [in] Erfolgswahrscheinlichkeit int &error_code // [out] Variable für den Fehlercode );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der negativen Binomialverteilung mit den Parametern n und p. Im Fehlerfall retourniert sie false. Analog zu qnbinom() in R.
bool MathQuantileNegativeBinomial( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double r, // [in] Anzahl erfolgreicher Tests double p, // [in] Erfolgswahrscheinlichkeit const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der negativen Binomialverteilung mit den Parametern n und p. Im Fehlerfall retourniert sie 'false'.
bool MathQuantileNegativeBinomial( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double r, // [in] Anzahl erfolgreicher Tests double p, // [in] Erfolgswahrscheinlichkeit double &result[] // [out] Array mit den Werten der Quantile );
2.18.4. MathRandomNegativeBinomial
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der negativen Binomialverteilung mit den Parametern r und p. Im Fehlerfall retourniert sie NaN . Im Fehlerfall retourniert sie NaN.
double MathRandomNegativeBinomial( const double r, // [in] Anzahl der Tests double p, // [in] Erfolgswahrscheinlichkeit int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der negativen Binomialverteilung mit den Parametern r und p. Im Fehlerfall retourniert sie false. Analog zu rnbinom() in R.
bool MathRandomNegativeBinomial( const double r, // [in] Anzahl der Tests double p, // [in] Erfolgswahrscheinlichkeit const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.18.5. MathMomentsNegativeBinomial
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der negativen Binomialverteilung mit den Parametern r und p. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsNegativeBinomial( const double r, // [in] Anzahl der Tests double p, // [in] Erfolgswahrscheinlichkeit double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.19. Geometrische Verteilung
2.19.1. MathProbabilityDensityGeometric
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der geometrische Verteilung mit dem Parameter p für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityGeometric( const double x, // [in] Wert der Zufallsvariablen const double p, // [in] Parameter der Verteilung (Wahrscheinlichkeit des Auftretens in einem Test) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der geometrische Verteilung mit dem Parameter p für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityGeometric( const double x, // [in] Wert der Zufallsvariablen const double p, // [in] Parameter der Verteilung (Wahrscheinlichkeit des Auftretens in einem Test) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der geometrische Verteilung mit dem Parameter p für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu dgeom() in R.
bool MathProbabilityDensityGeometric( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double p, // [in] Parameter der Verteilung (Wahrscheinlichkeit des Auftretens in einem Test) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der geometrische Verteilung mit dem Parameter p für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathProbabilityDensityGeometric( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double p, // [in] Parameter der Verteilung (Wahrscheinlichkeit des Auftretens in einem Test) double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.19.2. MathCumulativeDistributionGeometric
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der geometrische Verteilung mit dem Parameter p für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionGeometric( const double x, // [in] Wert der Zufallsvariablen const double p, // [in] Parameter der Verteilung (Wahrscheinlichkeit des Auftretens in einem Test) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' berechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der geometrische Verteilung mit dem Parameter p für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionGeometric( const double x, // [in] Wert der Zufallsvariablen const double p, // [in] Parameter der Verteilung (Wahrscheinlichkeit des Auftretens in einem Test) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der geometrische Verteilung mit dem Parameter p für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu pgeom() in R.
bool MathCumulativeDistributionGeometric( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double p, // [in] Parameter der Verteilung (Wahrscheinlichkeit des Auftretens in einem Test) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' berechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsverteilung der geometrische Verteilung mit dem Parameter p für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false.
bool MathCumulativeDistributionGeometric( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double p, // [in] Parameter der Verteilung (Wahrscheinlichkeit des Auftretens in einem Test) double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.19.3. MathQuantileGeometric
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion die Umkehrfunktion der geometrische Verteilung mit dem Parameter p. Im Fehlerfall retourniert sie NaN.
double MathQuantileGeometric( const double probability, // [in] Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double p, // [in] Parameter der Verteilung (Wahrscheinlichkeit des Auftretens in einem Test) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion die Umkehrfunktion der geometrische Verteilung mit dem Parameter p. Im Fehlerfall retourniert sie NaN.
double MathQuantileGeometric( const double probability, // [in] Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double p, // [in] Parameter der Verteilung (Wahrscheinlichkeit des Auftretens in einem Test) int &error_code // [out] Variable für den Fehlercode );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der geometrischen Verteilung mit dem Parameter p. Im Fehlerfall retourniert sie false. Analog zu qgeom() in R.
bool MathQuantileGeometric( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double p, // [in] Parameter der Verteilung (Wahrscheinlichkeit des Auftretens in einem Test) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte berechnet die Funktion die Umkehrfunktion der geometrischen Verteilung mit dem Parameter p. Im Fehlerfall retourniert sie false.
bool MathQuantileGeometric( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double p, // [in] Parameter der Verteilung (Wahrscheinlichkeit des Auftretens in einem Test) double &result[] // [out] Array mit den Werten der Quantile );
2.19.4. MathRandomGeometric
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der geometrischen Verteilung mit dem Parameter p. Im Fehlerfall retourniert sie NaN.
double MathRandomGeometric( const double p, // [in] Parameter der Verteilung (Wahrscheinlichkeit des Auftretens in einem Test) int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt Pseudozufallszahlen auf Basis der geometrischen Verteilung mit dem Parameter p. Im Fehlerfall retourniert sie false. Analog zu rgeom() in R.
bool MathRandomGeometric( const double p, // [in] Parameter der Verteilung (Wahrscheinlichkeit des Auftretens in einem Test) const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.19.5. MathMomentsGeometric
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der geometrischen Verteilung mit dem Parameter p. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsGeometric( const double p, // [in] Parameter der Verteilung (Wahrscheinlichkeit des Auftretens in einem Test) double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.20. Hypergeometrische Verteilung
2.20.1. MathProbabilityDensityHypergeometric
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der hypergeometrischen Verteilung mit den Parametern m, k und n für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityHypergeometric( const double x, // [in] Wert der Zufallsvariablen (integer) const double m, // [in] Gesamtzahl der Objekte (integer) const double k, // [in] NAnzahl der Objekte mit den gewünschten Eigenschaften (integer) const double n, // [in] Anzahl der gezogenen Objekte(integer) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der hypergeometrischen Verteilung mit den Parametern m, k und n für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityHypergeometric( const double x, // [in] Wert der Zufallsvariablen (integer) const double m, // [in] Gesamtzahl der Objekte (integer) const double k, // [in] NAnzahl der Objekte mit den gewünschten Eigenschaften (integer) const double n, // [in] Anzahl der gezogenen Objekte(integer) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der hypergeometrischen Verteilung mit den Parametern m, k und n für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu dhyper() in R.
bool MathProbabilityDensityHypergeometric( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double m, // [in] Gesamtzahl der Objekte (integer) const double k, // [in] NAnzahl der Objekte mit den gewünschten Eigenschaften (integer) const double n, // [in] Anzahl der gezogenen Objekte(integer) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der hypergeometrischen Verteilung mit den Parametern m, k und n für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathProbabilityDensityHypergeometric( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double m, // [in] Gesamtzahl der Objekte (integer) const double k, // [in] NAnzahl der Objekte mit den gewünschten Eigenschaften (integer) const double n, // [in] Anzahl der gezogenen Objekte(integer) double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.20.2. MathCumulativeDistributionHypergeometric
Die Funktion berechnet den Wert der Wahrscheinlichkeitsfunktion der hypergeometrischen Verteilung mit den Parametern m, k und n für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionHypergeometric( const double x, // [in] Gesamtzahl der Objekte (integer) const double m, // [in] Gesamtzahl der Objekte (integer) const double k, // [in] Anzahl der Objekte mit den gewünschten Eigenschaften (integer) const double n, // [in] Anzahl der gezogenen Objekte(integer) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' berechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsfunktion der hypergeometrischen Verteilung mit den Parametern m, k und n für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionHypergeometric( const double x, // [in] Gesamtzahl der Objekte (integer) const double m, // [in] Gesamtzahl der Objekte (integer) const double k, // [in] Anzahl der Objekte mit den gewünschten Eigenschaften (integer) const double n, // [in] Anzahl der gezogenen Objekte(integer) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsfunktion der hypergeometrischen Verteilung mit den Parametern m, k und n für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'. Analog zu phyper() in R.
bool MathCumulativeDistributionHypergeometric( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double m, // [in] Gesamtzahl der Objekte (integer) const double k, // [in] Anzahl der Objekte mit den gewünschten Eigenschaften (integer) const double n, // [in] Anzahl der gezogenen Objekte(integer) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' berechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet double &result[] // [out] Array mit den Werten der Verteilungsfunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsfunktion der hypergeometrischen Verteilung mit den Parametern m, k und n für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathCumulativeDistributionHypergeometric( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double m, // [in] Gesamtzahl der Objekte (integer) const double k, // [in] Anzahl der Objekte mit den gewünschten Eigenschaften (integer) const double n, // [in] Anzahl der gezogenen Objekte(integer) double &result[] // [out] Array mit den Werten der Verteilungsfunktion );
2.20.3. MathQuantileHypergeometric
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion die Umkehrfunktion der hypergeometrischen Verteilung berechnet mit den Parametern m, k und n. Im Fehlerfall retourniert sie NaN.
double MathQuantileHypergeometric( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double m, // [in] Gesamtzahl der Objekte Total (integer) const double k, // [in] Anzahl der Objekte mit den gewünschten Eigenschaften (integer) const double n, // [in] Anzahl der gezogenen Objekte (integer) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' berechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion die Umkehrfunktion der hypergeometrischen Verteilung berechnet mit den Parametern m, k und n. Im Fehlerfall retourniert sie NaN.
double MathQuantileHypergeometric( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double m, // [in] Gesamtzahl der Objekte (integer) const double k, // [in] Anzahl der Objekte mit den gewünschten Eigenschaften (integer) const double n, // [in] Anzahl der gezogenen Objekte (integer) int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' wird die Umkehrfunktion der hypergeometrischen Verteilung berechnet mit den Parametern m, k und n. Im Fehlerfall retourniert sie 'false'. Im Fehlerfall retourniert sie 'false'. Analog zu qhyper() in R.
bool MathQuantileHypergeometric( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double m, // [in] Gesamtzahl der Objekte (integer) const double k, // [in] Anzahl der Objekte mit den gewünschten Eigenschaften (integer) const double n, // [in] Anzahl der gezogenen Objekte (integer) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' berechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die angegebene Wahrscheinlichkeit 'probability' wird die Umkehrfunktion der hypergeometrischen Verteilung berechnet mit den Parametern m, k und n. Im Fehlerfall retourniert sie 'false'. Im Fehlerfall retourniert sie 'false'.
bool MathQuantileHypergeometric( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double m, // [in] Gesamtzahl der Objekte (integer) const double k, // [in] Anzahl der Objekte mit den gewünschten Eigenschaften (integer) const double n, // [in] Anzahl der gezogenen Objekte (integer) double &result[] // [out] Array mit den Werten der Quantile );
2.20.4. MathRandomHypergeometric
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der hypergeometrischen Verteilung mit den Parametern m, n und k. Im Fehlerfall retourniert sie NaN . Im Fehlerfall retourniert sie NaN.
double MathRandomHypergeometric( const double m, // [in] Gesamtzahl der Objekte (integer) const double k, // [in] Anzahl der Objekte mit den gewünschten Eigenschaften (integer) const double n, // [in] Anzahl der gezogenen Objekte(integer) int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der hypergeometrischen Verteilung mit den Parametern m, n und k. Im Fehlerfall retourniert sie false. Analog zu rhyper() in R.
bool MathRandomHypergeometric( const double m, // [in] Gesamtzahl der Objekte (integer) const double k, // [in] Anzahl der Objekte mit den gewünschten Eigenschaften (integer) const double n, // [in] Anzahl der gezogenen Objekte(integer) const int data_count, // [in] Anzahl der benötigten Daten double &result[] // [out] Array mit den Werten der Pseudozufallszahlen );
2.20.5. MathMomentsHypergeometric
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der hypergeometrischen Verteilung mit den Parametern m, n und k. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsHypergeometric( const double m, // [in] Gesamtzahl der Objekte (integer) const double k, // [in] Anzahl der Objekte mit den gewünschten Eigenschaften (integer) const double n, // [in] Anzahl der gezogenen Objekte(integer) double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
2.21. Poisson-Verteilung
2.21.1. MathProbabilityDensityPoisson
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Poisson-Verteilung mit dem Parameter lambda für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityPoisson( const double x, // [in] Wert der Zufallsvariablen const double lambda, // [in] Parameter der Verteilung (mean) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Poisson-Verteilung mit dem Parameter lambda für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathProbabilityDensityPoisson( const double x, // [in] Wert der Zufallsvariablen const double lambda, // [in] Parameter der Verteilung (mean) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Poisson-Verteilung mit dem Parameter lambda für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu dpois() in R.
bool MathProbabilityDensityPoisson( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double lambda, // [in] Parameter der Verteilung (mean) const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeitsdichte zurückgegeben double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
Die Funktion berechnet den Wert der Wahrscheinlichkeitsdichtefunktion der Poisson-Verteilung mit dem Parameter lambda für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie 'false'.
bool MathProbabilityDensityPoisson( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double lambda, // [in] Parameter der Verteilung (mean) double &result[] // [out] Array der Werte der Wahrscheinlichkeitsdichtefunktion );
2.21.2. MathCumulativeDistributionPoisson
Die Funktion berechnet den Wert der Poisson-Verteilung mit den Parametern lambda für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionPoisson( const double x, // [in] Wert der Zufallsvariablen const double lambda, // [in] Parameter der Verteilung (mean) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Poisson-Verteilung mit den Parametern lambda für die Zufallsvariable x. Im Fehlerfall retourniert sie NaN.
double MathCumulativeDistributionPoisson( const double x, // [in] Wert der Zufallsvariablen const double lambda, // [in] Parameter der Verteilung (mean) int &error_code // [out] Variable für den Fehlercode );
Die Funktion berechnet den Wert der Poisson-Verteilung mit den Parametern lambda für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false. Analog zu ppois() in R.
bool MathCumulativeDistributionPoisson( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double lambda, // [in] Parameter der Verteilung (mean) const bool tail, // [in] Parameter, wenn true, wird die Wahrscheinlichkeit einer Zufallsvariablen, die nicht größer als x ist, berechnet const bool log_mode, // [in] Parameter der Logarithmusberechnung, wenn log_mode=true, wird der natürliche Logarithmus der Wahrscheinlichkeit berechnet double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
Die Funktion berechnet den Wert der Poisson-Verteilung mit den Parametern lambda für den Array der Zufallsvariablen x[]. Im Fehlerfall retourniert sie false.
bool MathCumulativeDistributionPoisson( const double &x[], // [in] Array mit den Werten der Zufallsvariablen const double lambda, // [in] Parameter der Verteilung (mean) double &result[] // [out] Array mit den Werten der Wahrscheinlichkeitsfunktion );
2.21.3. MathQuantilePoisson
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion die Umkehrfunktion der Poisson-Verteilung mit dem Parameter lambda. Im Fehlerfall retourniert sie NaN.
double MathQuantilePoisson( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double lambda, // [in] Parameter der Verteilung (mean) const bool tail, // [in] Parameter, wenn false, wird für eine '1.0-probability' gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird mit einer 'Exp(probability)' gerechnet int &error_code // [out] Variable für den Fehlercode );
Für die angegebene Wahrscheinlichkeit 'probability' berechnet die Funktion die Umkehrfunktion der Poisson-Verteilung mit dem Parameter lambda. Im Fehlerfall retourniert sie NaN.
double MathQuantilePoisson( const double probability, // [in] Der Wert der Wahrscheinlichkeit des Auftretens einer Zufallsvariablen const double lambda, // [in] Parameter der Verteilung (mean) int &error_code // [out] Variable für den Fehlercode );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte wird die Umkehrfunktion der Poisson-Verteilung berechnet mit dem Parameter lambda. Im Fehlerfall retourniert sie false. Analog zu qpois() in R.
double MathQuantilePoisson( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double lambda, // [in] Parameter der Verteilung (mean) const bool tail, // [in] Parameter, wenn false, wird für eine 1.0-Wahrschenlichkeit gerechnet const bool log_mode, // [in] Parameter, wenn log_mode=true, wird für eine 'Exp(probability)' berechnet double &result[] // [out] Array mit den Werten der Quantile );
Für die im Array 'probability[]' angegebenen Wahrscheinlichkeitswerte wird die Umkehrfunktion der Poisson-Verteilung berechnet mit dem Parameter lambda. Im Fehlerfall retourniert sie 'false'.
double MathQuantilePoisson( const double &probability[],// [in] Array mit den Wahrscheinlichkeitswerten einer Zufallsvariablen const double lambda, // [in] Parameter der Verteilung (mean) double &result[] // [out] Array mit den Werten der Quantile );
2.21.4. MathRandomPoisson
Die Funktion erzeugt eine Pseudozufallszahl auf Basis der Poisson-Verteilung mit dem Parameter lambda. Im Fehlerfall retourniert sie NaN.
double MathRandomPoisson( const double lambda, // [in] Parameter der Verteilung (mean) int &error_code // [out] Variable für den Fehlercode );
Die Funktion erzeugt Pseudozufallszahlen auf Basis der Poisson-Verteilung mit dem Parameter lambda. Im Fehlerfall retourniert sie false. Analog zu rpois() in R.
double MathRandomPoisson( const double lambda, // [in] Parameter der Verteilung (mean) int &error_code // [out] Variable für den Fehlercode );
2.21.5. MathMomentsPoisson
Die Funktion berechnet die theoretischen, numerischen Werte der ersten 4 Momente der Poisson-Verteilung mit dem Parameter lambda. Gibt nach erfolgreicher Berechnung 'true' zurück, andernfalls 'false'.
bool MathMomentsPoisson( const double lambda, // [in] Parameter der Verteilung (mean) double &mean, // [out] Variable des Mittelwerts (1. Moment) double &variance, // [out] Variable der Varianz (2. Moment) double &skewness, // [out] Variable der Schiefe (3. Moment) double &kurtosis, // [out] Variable der Kurtosis (4. Moment) int &error_code // [out] Variable für den Fehlercode );
3. Tabelle korrespondierender, statistischer Funktionen in R
Der Einfachheit halber zeigt die Tabelle 1-2 die Funktionen der statistischen Bibliothek und die entsprechenden Funktionen der Sprache R.
| Nr. | Berechneter Wert | Die Funktion in MQL5 | Die Funktion in R |
|---|---|---|---|
| 1 | Mittelwert | MathMean | mean |
| 2 | Varianz | MathVariance | var |
| 3 | Schiefe | MathSkewness | skewness |
| 4 | Kurtosis | MathKurtosis | kurtosis |
| 5 | Median | MathMedian | median |
| 6 | Standardabweichung | MathStandardDeviation | sd |
| 7 | Durchschnittliche Abweichung | MathAverageDeviation | aad |
Tabelle 1. Funktionen zur Berechnung der statistischen Eigenschaften der Daten eines Arrays
| Nr. | Verteilung | Dichtefunktion | Die Funktion in MQL5 | Die Funktion in R |
|---|---|---|---|---|
| 1 | Normal | 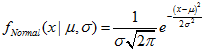 | MathProbabilityDensityNormal MathCumulativeDistributionNormal MathQuantileNormal MathRandomNormal | dnorm pnorm qnorm rnorm |
| 2 | Beta | | MathProbabilityDensityBeta MathCumulativeDistributionBeta MathQuantileBeta MathRandomBeta | dbeta pbeta qbeta rbeta |
| 3 | Binomial | | MathProbabilityDensityBinomial MathCumulativeDistributionBinomial MathQuantileBinomial MathRandomBinomial | dbinom pbinom qbinom rbinom |
| 4 | Cauchy | 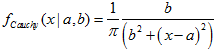 | MathProbabilityDensityCauchy MathCumulativeDistributionCauchy MathQuantileCauchy MathRandomCauchy | dcauchy pcauchy qcauchy rcauchy |
| 5 | Chi-Quadrat | 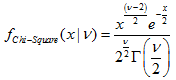 | MathProbabilityDensityChiSquare MathCumulativeDistributionChiSquare MathQuantileChiSquare MathRandomChiSquare | dchisq pchisq qchisq rchisq |
| 6 | Exponential | | MathProbabilityDensityExponential MathCumulativeDistributionExponential MathQuantileExponential MathRandomExponential | dexp pexp qexp rexp |
| 7 | F-Verteilung | 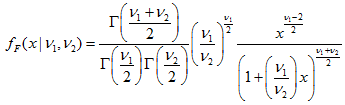 | MathProbabilityDensityF MathCumulativeDistributionF MathQuantileF MathRandomF | df pf qf rf |
| 8 | Gamma | | MathProbabilityDensityGamma MathCumulativeDistributionGamma MathQuantileGamma MathRandomGamma | dgamma pgamma qgamma rgamma |
| 9 | Geometrisch | | MathProbabilityDensityGeometric MathCumulativeDistributionGeometric MathQuantileGeometric MathRandomGeometric | dgeom pgeom qgeom rgeom |
| 10 | Hypergeometrisch | 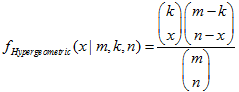 | MathProbabilityDensityHypergeometric MathCumulativeDistributionHypergeometric MathQuantileHypergeometric MathRandomHypergeometric | dhyper phyper qhyper rhyper |
| 11 | Logistisch | 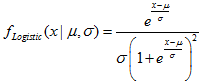 | MathProbabilityDensityLogistic MathCumulativeDistributionLogistic MathQuantileLogistic MathRandomLogistic | dlogis plogis qlogis rlogis |
| 12 | Log-Normal | | MathProbabilityDensityLognormal MathCumulativeDistributionLognormal MathQuantileLognormal MathRandomLognormal | dlnorm plnorm qlnorm rlnorm |
| 13 | Negative Binomial | | MathProbabilityDensityNegativeBinomial MathCumulativeDistributionNegativeBinomial MathQuantileNegativeBinomial MathRandomNegativeBinomial | dnbinom pnbinom qnbinom rnbinom |
| 14 | Nichtzentrale Beta | 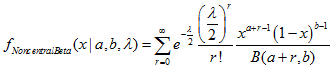 | MathProbabilityDensityNoncentralBeta MathCumulativeDistributionNoncentralBeta MathQuantileNoncentralBeta MathRandomNoncentralBeta | dbeta pbeta qbeta rbeta |
| 15 | Nichtzentrale Chi-Quadrat | 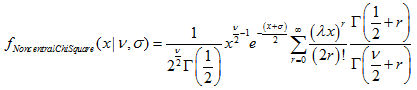 | MathProbabilityDensityNoncentralChiSquare MathCumulativeDistributionNoncentralChiSquare MathQuantileNoncentralChiSquare MathRandomNoncentralChiSquare | dchisq pchisq qchisq rchisq |
| 16 | Nichtzentrale F-Verteilung | 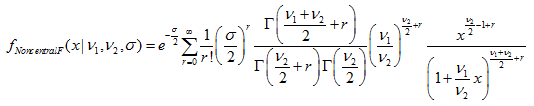 | MathProbabilityDensityNoncentralF() MathCumulativeDistributionNoncentralF() MathQuantileNoncentralF() MathRandomNoncentralF() | df pf qf rf |
| 17 | Nichtzentrale T-Verteilung | 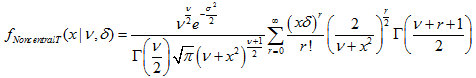 | MathProbabilityDensityNoncentralT MathCumulativeDistributionNoncentralT MathQuantileNoncentralT MathRandomNoncentralT | dt pt qt rt |
| 18 | Poisson | | MathProbabilityDensityPoisson MathCumulativeDistributionPoisson MathQuantilePoisson MathRandomPoisson | dpois ppois qpois rpois |
| 19 | T-Verteilung | 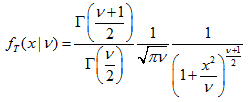 | MathProbabilityDensityT MathCumulativeDistributionT MathQuantileT MathRandomT | dt pt qt rt |
| 20 | Gleichverteilung | | MathProbabilityDensityUniform MathCumulativeDistributionUniform MathQuantileUniform MathRandomUniform | dunif punif qunif runif |
| 21 | Weibull | 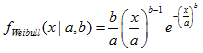 | MathProbabilityDensityWeibull MathCumulativeDistributionWeibull MathQuantileWeibull MathRandomWeibull | dweibull pweibull qweibull rweibull |
Tabelle 2. Die Funktionen für die Arbeit mit statistischen Verteilungen
Die MQL5 statistische Bibliothek beinhaltet auch Funktionen zur Berechnung mathematischer Funktionen auf Array. Diese Funktionen sind unten in der Tabelle 3 aufgelistet.
| Beschreibung | MQL5 | R |
|---|---|---|
| Erzeugt eine Sequenz von Werten | bool MathSequence(const double from,const double to,const double step,double &result[]) bool MathSequenceByCount(const double from,const double to,const int count,double &result[]) bool MathSequence(const int from,const int to,const int step,int &result[]) bool MathSequenceByCount(const int from,const int to,const int count,int &result[]) | seq() |
| Erzeugt eine sich wiederholende Sequenz | bool MathReplicate(const double &array[],const int count,double &result[]) bool MathReplicate(const int &array[],const int count,int &result[]) | rep() |
| Erzeugt ein Array mit umgekehrter Reihenfolge von Elementen | bool MathReverse(const double &array[],double &result[]) bool MathReverse(const int &array[],int &result[]) | rev(x) |
| Vergleicht Arrays und gibt true zurück, wenn alle Elemente miteinander übereinstimmen | bool MathIdentical(const double &array1[],const double &array2[]) bool MathIdentical(const int &array1[],const int &array2[]) | identical() |
| Erzeugt ein Array mit nur eindeutigen Werten | bool MathUnique(const double &array[],double &result[]) bool MathUnique(const int &array[],int &result[]) | unique() |
| Erzeugt ein Integer-Array mit einer Permutation entsprechend der Reihenfolge der Elemente eines Arrays nach der Sortierung | bool MathOrder(const double &array[],int &result[]) bool MathOrder(const int &array[],int &result[]) | order() |
| Nimmt eine Stichprobe aus den Elementen eines Arrays vor. Das Argument replace=true erlaubt es, eine zufällige Stichprobe von Elementen mit Zurückführung zur ursprünglichen Sequenz vorzunehmen. Das Array probabilities[] definiert die Wahrscheinlichkeiten für die Stichprobe von Elementen. | bool MathSample(const double &array[],const int count,double &result[]) bool MathSample(const double &array[],const int count,const bool replace,double &result[]) bool MathSample(const double &array[],double &probabilities[],const int count,double &result[]) bool MathSample(const double &array[],double &probabilities[],const int count,const bool replace,double &result[]) bool MathSample(const int &array[],const int count,int &result[]) bool MathSample(const int &array[],const int count,const bool replace,int &result[]) bool MathSample(const int &array[],double &probabilities[],const int count,int &result[]) bool MathSample(const int &array[],double &probabilities[],const int count,const bool replace,int &result[]) | sample() |
| Gibt die Summe der Elemente eines Arrays zurück | double MathSum(const double &array[]) | sum() |
| Gibt das Produkt der Elemente eines Arrays zurück | double MathProduct(const double &array[]) | prod() |
| Erzeugt ein Array mit kumulativen Summen | bool MathCumulativeSum(const double &array[],double &result[]) bool MathCumulativeSum(double &array[]) | cumsum() |
| Erzeugt ein Array mit kumulativen Produkten | bool MathCumulativeProduct(const double &array[],double &result[]) bool MathCumulativeProduct(double &array[]) | cumprod() |
| Erzeugt ein Array mit kumulativen Minima | bool MathCumulativeMin(const double &array[],double &result[]) bool MathCumulativeMin(double &array[]) | cummin() |
| Erzeugt ein Array mit kumulativen Maxima | bool MathCumulativeMax(const double &array[],double &result[]) bool MathCumulativeMax(double &array[]) | cummax() |
| Erzeugt ein Array mit den Differenzen von Elementen y[i]=x[i+lag]-x[i] | bool MathDifference(const double &array[],const int lag,double &result[]) bool MathDifference(const double &array[],const int lag,const int differences,double &result[]) bool MathDifference(const int &array[],const int lag,int &result[]) bool MathDifference(const int &array[],const int lag,const int differences,int &result[]) | diff() |
| Gibt den minimalen Wert der Elemente eines Arrays zurück | double MathMin(const double &array[]) | min() |
| Gibt den maximalen Wert der Elemente des Arrays zurück | double MathMax(const double &array[]) | max() |
| Berechnet Maxima und Minima der Elemente eines Arrays | bool MathRange(const double &array[],double &min,double &max) | range() |
| Berechnet den Mittelwert der Elemente eines Arrays | double MathMean(const double &array[]) | mean() |
| Berechnet die Standardabweichung der Elemente eines Arrays | double MathStandardDeviation(const double &array[]) | sd() |
| Berechnet den Median der Elemente eines Arrays | double MathMedian(double &array[]) | median() |
| Berechnet die Ränge der Elemente eines Arrays. | bool MathRank(const int &array[],double &rank[]) bool MathRank(const double &array[],double &rank[]) | rank() |
| Berechnet die Korrelationskoeffizienten nach Pearson, Spearman und Kendall | bool MathCorrelationPearson(const double &array1[],const double &array2[],double &r) bool MathCorrelationPearson(const int &array1[],const int &array2[],double &r) bool MathCorrelationSpearman(const double &array1[],const double &array2[],double &r) bool MathCorrelationSpearman(const int &array1[],const int &array2[],double &r) bool MathCorrelationKendall(const double &array1[],const double &array2[],double &tau) bool MathCorrelationKendall(const int &array1[],const int &array2[],double &tau) | corr() |
| Berechnet Stichprobenquantile entsprechend den angegebenen Wahrscheinlichkeiten | bool MathQuantile(const double &array[],const double &probs[],double &quantile[]) | qunatile() |
| Berechnet Tukey's five number summary (minimum, lower-hinge, median, upper-hinge, maximum) für die Elemente eines Arrays | bool MathTukeySummary(const double &array[],const bool removeNAN,double &minimum,double &lower_hinge,double &median,double &upper_hinge,double &maximum) | fivenum() |
| Berechnet die Logarithmen der Elemente eines Arrays (natürliche und zu einer angegebenen Basis) | bool MathLog(const double &array[],double &result[]) bool MathLog(const double &array[],const double base,double &result[]) bool MathLog(double &array[]) bool MathLog(double &array[],const double base) | log() |
| Berechnet die Logarithmen der Elemente eines Array zur Basis 2 | bool MathLog2(const double &array[],double &result[]) bool MathLog2(double &array[]) | log2() |
| Berechnet die Logarithmen der Elemente eines Array zur Basis 10 | bool MathLog10(const double &array[],double &result[]) bool MathLog10(double &array[]) | log10() |
| Berechnet den Wert der Funktion log(1+x) für die Elemente eines Arrays | bool MathLog1p(const double &array[], double &result[]) bool MathLog1p(double &array[]) | log1p() |
| Berechnet den Wert der Funktion exp(x) für die Elemente eines Arrays | bool MathExp(const double &array[], double &result[]) bool MathExp(double &array[]) | exp() |
| Berechnet den Wert der Funktion exp(x)-1 für die Elemente eines Arrays | bool MathExpm1(const double &array[], double &result[]) bool MathExpm1(double &array[]) | expm1() |
| Berechnet den Wert der Funktion sin(x) für die Elemente eines Arrays | bool MathSin(const double &array[], double &result[]) bool MathSin(double &array[]) | sin() |
| Berechnet den Wert der Funktion cos(x) für die Elemente eines Arrays | bool MathCos(const double &array[], double &result[]) bool MathCos(double &array[]) | cos() |
| Berechnet den Wert der Funktion tan(x) für die Elemente eines Arrays | bool MathTan(const double &array[], double &result[]) bool MathTan(double &array[]) | tan() |
| Berechnet den Wert der Funktion arcsin(x) für die Elemente eines Arrays | bool MathArcsin(const double &array[], double &result[]) bool MathArcsin(double &array[]) | arcsin() |
| Berechnet den Wert der Funktion arccos(x) für die Elemente eines Arrays | bool MathArccos(const double &array[], double &result[]) bool MathArccos(double &array[]) | arccos() |
| Berechnet den Wert der Funktion arctan(x) für die Elemente eines Arrays | bool MathArctan(const double &array[], double &result[]) bool MathArctan(double &array[]) | arctan() |
| Berechnet den Wert der Funktion arctan(y/x) für die Elemente eines Arrays | bool MathArctan2(const double &array1[], const double &array2[], double &result[]) | arctan2() |
| Berechnet den Wert der Funktion sin(pi*x) für die Elemente eines Arrays | bool MathSinPi(const double &array[], double &result[]) bool MathSinPi(double &array[]) | sinpi() |
| Berechnet den Wert der Funktion cos(pi*x) für die Elemente eines Arrays | bool MathCosPi(const double &array[], double &result[]) bool MathCosPi(const double &array[]) | cospi() |
| Berechnet den Wert der Funktion tan(pi*x) für die Elemente eines Arrays | bool MathTanPi(const double &array[], double &result[]) bool MathTanPi(double &array[]) | tanpi() |
| Berechnet die absoluten Werte der Elemente eines Arrays | bool MathAbs(const double &array[], double &result[]) bool MathAbs(double &array[]) | abs() |
| Berechnet die Quadratwurzeln der Elemente eines Arrays | bool MathSqrt(const double &array[], double &result[]) bool MathSqrt(double &array[]) | sqrt() |
| Gibt die nächst größte ganze Zahl für die Elemente eines Arrays zurück | bool MathCeil(const double &array[], double &result[]) bool MathCeil(double &array[]) | ceil() |
| Gibt die nächst kleinste ganze Zahl für die Elemente eines Arrays zurück | bool MathFloor(const double &array[], double &result[]) bool MathFloor(double &array[]) | floor() |
| Berechnet den ganzzahligen Teil der Elemente eines Arrays | bool MathTrunc(const double &array[], const int digits, double &result[]) bool MathTrunc(double &array[]) | trunc() |
| Berechnet den abgerundeten Teil der Elemente eines Arrays | bool MathRound(const double &array[], const int digits, double &result[]) bool MathRound(double &array[],int digits) | round() |
| Berechnet für die Elemente eines Arrays den Wert, der auf die in der Matisse angegebene Stellenzahl abgerundet wird | bool MathSignif(const double &array[], const int digits, double &result[]) bool MathSignif(double &array[], const int digits) | signinf() |
| Berechnet den Wert der Funktion sinh(x) für die Elemente eines Arrays | bool MathSinh(const double &array[],double &result[]) bool MathSinh(double &array[]) | sinh() |
| Berechnet den Wert der Funktion cosh(x) für die Elemente eines Arrays | bool MathCosh(const double &array[],double &result[]) bool MathCosh(double &array[]) | cosh() |
| Berechnet den Wert der Funktion tanh(x) für die Elemente eines Arrays | bool MathTanh(const double &array[],double &result[]) bool MathTanh(double &array[]) | tanh() |
| Berechnet den Wert der Funktion arcsinh(x) für die Elemente eines Arrays | bool MathArcsinh(const double &array[],double &result[]) bool MathArcsinh(double &array[]) | asinh() |
| Berechnet den Wert der Funktion arccosh(x) für die Elemente eines Arrays | bool MathArccosh(const double &array[],double &result[]) bool MathArccosh(double &array[]) | acosh() |
| Berechnet den Wert der Funktion arctanh(x) für die Elemente eines Arrays | bool MathArctanh(const double &array[],double &result[]) bool MathArctanh(double &array[]) | atanh() |
| Berechnet das Ergebnis der binären Operation NOT für die Elemente eines Arrays | bool MathBitwiseNot(const int &array[],int &result[]) bool MathBitwiseNot(int &array[]) | bitwNot() |
| Berechnet das Ergebnis der binären Operation AND für die Elemente eines Arrays | bool MathBitwiseAnd(const int &array1[],const int &array2[],int &result[]) | bitwAnd() |
| Berechnet das Ergebnis der binären Operation OR für die Elemente eines Arrays | bool MathBitwiseOr(const int &array1[],const int &array2[],int &result[]) | bitwOr() |
| Berechnet das Ergebnis der binären Operation XOR für die Elemente eines Arrays | bool MathBitwiseXor(const int &array1[],const int &array2[],int &result[]) | bitwXor() |
| Berechnet das Ergebnis der binären Operation SHL für die Elemente eines Arrays | bool MathBitwiseShiftL(const int &array[],const int n,int &result[]) bool MathBitwiseShiftL(int &array[],const int n) | bitwShiftL() |
| Berechnet das Ergebnis der binären Operation SHR für die Elemente eines Arrays | bool MathBitwiseShiftR(const int &array[],const int n,int &result[]) bool MathBitwiseShiftR(int &array[],const int n) | bitwShiftR() |
Tabelle 3. Mathematische Funktionen zur Berechnung von Werten in Arrays
4. Ein Beispiel für die Verwendung der Funktionen
Betrachten wir die praktische Anwendung von statistischen Funktionen am Beispiel der Normalverteilung.
Angenommen, es sollen die folgenden Probleme gelöst werden:
- Berechnen Sie die Wahrscheinlichkeit einer Zufallsvariablen im Intervall [mu-sigma,mu+sigma], die mit den Werten mu und sigma normalverteilt ist.
- Finden Sie den Wertebereich der normalverteilten Zufallsvariablen x mit den Parametern mu und sigma, die symmetrisch zu mu sind, welches ein Konfidenzintervall von 95% bedeutet.
- Generieren Sie 1000000 Zufallszahlen auf Basis der Normalverteilung mit den Parametern mu und sigma, berechnen Sie ein Histogramm und die ersten 4 Momente und vergleichen Sie mit den theoretischen Werten.
Ein Beispiel für die Lösung im NormalExample Skript:
//+------------------------------------------------------------------+ //| NormalExample.mq5 | //| Copyright 2016, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" //--- lade die Funktionen für das Rechnen mit der Normalverteilung #include <Math\Stat\Normal.mqh> //+------------------------------------------------------------------+ //| CalculateHistogram | //+------------------------------------------------------------------+ void CalculateHistogram(double &data[],const int ncells=200,const string filename="normal.csv") { if(ArraySize(data)<=0) return; int n=ArraySize(data); //--- finde Minimum und Maximum im Array 'data' double minv,maxv,range; minv=data[0]; maxv=data[0]; for(int i=1; i<n; i++) { minv=MathMin(minv,data[i]); maxv=MathMax(maxv,data[i]); } //--- berechne den Bereich 'range' range=maxv-minv; // Print("Min=",minv," Max=",maxv," range=",range," size=",n); if(range==0) return; //--- Arrays für die Erstellung des Histogramms double x[]; double y[]; //--- setze die Werte des Histogramms ArrayResize(x,ncells); ArrayResize(y,ncells); for(int i=0; i<ncells; i++) { x[i]=minv+i*range/(ncells-1); y[i]=0; } //--- berechne das Histogramm for(int i=0; i<n; i++) { double v=(maxv-data[i])/range; int ind=int((v*(ncells-1))); y[ind]++; } //--- Prüfung des Dateinamens if(filename=="") return; //--- öffne die Datei zum Lesen ResetLastError(); int filehandle=FileOpen(filename,FILE_WRITE|FILE_TXT|FILE_ANSI); //--- Daten in die Datei schreiben if(filehandle!=INVALID_HANDLE) { for(int i=0; i<ncells; i++) { string str=StringFormat("%6.20f;%6.20f",x[i],y[i]); FileWrite(filehandle,str); } FileClose(filehandle); PrintFormat("Histogram saved to file %s",filename); } else PrintFormat("Error calling FileOpen, error code=%d",GetLastError()); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- 1. Berechne die Wahrscheinlichkeit einer normalverteilten Zufallsvariablen, //--- mit den Parametern mu und sigma innerhalb des Intervalls [mu-sigma,mu+sigma] //--- Zuweisung der Parameterwerte double mu=5.0; double sigma=1.0; //--- Zuweisung des Intervalls double x1=mu-sigma; double x2=mu+sigma; //--- Variable für die Wahrscheinlichkeitsrechnung double cdf1,cdf2,probability; //--- Variable für den Fehlercode int error_code1,error_code2; //--- Berechnung der Werte der Verteilungsfunktion cdf1=MathCumulativeDistributionNormal(x1,mu,sigma,error_code1); cdf2=MathCumulativeDistributionNormal(x2,mu,sigma,error_code2); //--- Prüfung auf Fehler if(error_code1==ERR_OK && error_code2==ERR_OK) { //--- Berechnung der Wahrscheinlichkeit probability=cdf2-cdf1; //--- Ausgabe des Ergebnisses PrintFormat("x1=%5.8f, x2=%5.8f, Probability=%5.8f",x1,x2,probability); } //--- 2. Finden Sie den Wertebereich der normalverteilten Zufallsvariablen x mit den Parametern mu und sigma, //--- die symmetrisch zu mu sind, welches ein Konfidenzintervall von 95% bedeutet. //--- Setzen des Wertes des Konfidenzintervalls probability=0.95; //--- Setzen der Wahrscheinlichkeiten an den Intervallgrenzen double p1=(1.0-probability)*0.5; double p2=probability+(1.0-probability)*0.5; //--- Berechnen der Intervallgrenzen x1=MathQuantileNormal(p1,mu,sigma,error_code1); x2=MathQuantileNormal(p2,mu,sigma,error_code2); //--- Prüfung auf Fehler if(error_code1==ERR_OK && error_code2==ERR_OK) { //--- Ausgabe des Ergebnisses PrintFormat("x1=%5.8f, x2=%5.8f",x1,x2); } //--- 3. Generieren Sie 1000000 Zufallszahlen auf Basis der Normalverteilung mit den Parametern mu und sigma, //--- berechnen Sie mit den ermittelten Werten ein Histogramm und die ersten 4 Momente und vergleichen sie Sie mit den theoretischen Werten //--- Setzen der Anzahl der Werte und Vorbereiten des Arrays int data_count=1000000; double data[]; ArrayResize(data,data_count); //--- Zufallszahlen generieren und im Array sichern for(int i=0; i<data_count; i++) { data[i]=MathRandomNormal(mu,sigma,error_code1); } //--- Setzen des Index des ersten Wertes und den Anzahl der Daten für die Berechnung int start=0; int count=data_count; //--- Berechnen der ersten 4 Momente der generierten Werte double mean=MathMean(data,start,count); double variance=MathVariance(data,start,count); double skewness=MathSkewness(data,start,count); double kurtosis=MathKurtosis(data,start,count); //--- Variablen für die theoretischen Momente double normal_mean=0; double normal_variance=0; double normal_skewness=0; double normal_kurtosis=0; //--- Anzeige der Werte der berechneten Momente PrintFormat(" mean=%.10f, variance=%.10f skewness=%.10f kurtosis=%.10f",mean,variance,skewness,kurtosis); //--- Berechnen der theoretischen Werte der Momente und Vergleich mit den erhaltenen Werten if(MathMomentsNormal(mu,sigma,normal_mean,normal_variance,normal_skewness,normal_kurtosis,error_code1)) { PrintFormat("Normal mean=%.10f, Normal variance=%.10f Normal skewness=%.10f Normal kurtosis=%.10f",normal_mean,normal_variance,normal_skewness,normal_kurtosis); PrintFormat("delta mean=%.4f, delta variance=%.4f delta skewness=%.4f delta kurtosis=%.4f",mean-normal_mean,variance-normal_variance,skewness-normal_skewness,kurtosis-normal_kurtosis); } //--- Berechne das Histogramm der Verteilung und sichere es in der Datei normal.csv int ncells=50; CalculateHistogram(data,ncells,"normal.csv"); }
Die Ergebnisse des Skriptes::
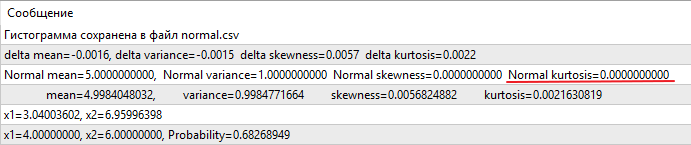
Abb. 1. Ergebnisse des Skriptes TestNormal.mq5
Beachten Sie, für alle Berechnungen wurde der Wert des Parameters 'kurtosis' auf "excess kurtosis=kurtosis-3" gesetzt und ist daher für eine Normalverteilung gleich Null.
Das berechnete Histogramm ist in der Datei normal.csv gesichert (Abb.2)
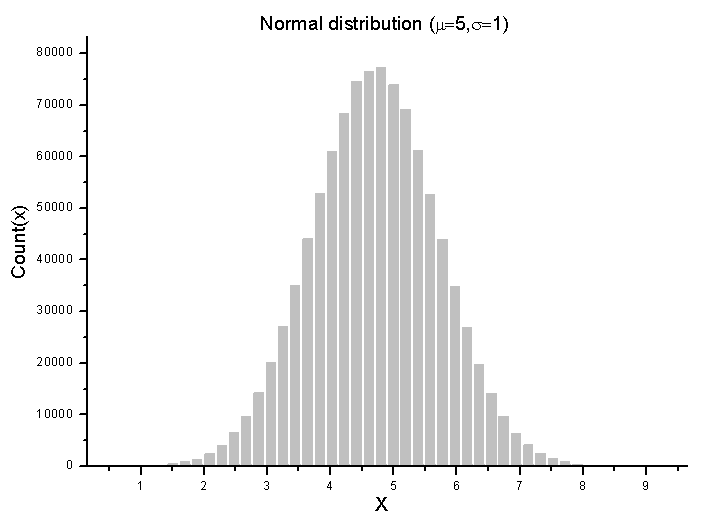
Abb. 2. Histogramm der Verteilung der Zufallszahlen, die auf Basis der Normalverteilung mit den Parametern mu=5 und sigma=1 erstellt wurde
5. Vergleich der Berechnungsgeschwindigkeiten
Um die Rechengeschwindigkeiten der statistischen Funktionen zu vergleichen, gibt es das Skripte für die Berechnung der Rechenzeit von Wahrscheinlichkeitsdichtefunktion ('probability density functions': pdf), kumulative Verteilungsfunktionen ('cumulative distribution functions': cdf), Quantilberechnungen und die Erzeugung der Pseudozufallszahlen.
Die Berechnung wurde durchgeführt mit einem Array von 51 Werten. Für kontinuierliche Funktionen wird im Bereich von 0 bis 1, für diskrete Funktionen zwischen 0 und 50 gerechnet. Die Zeitberechnungen der statistischen Funktionen von R wird unter Verwendung der Bibliothek microbenchmark durchgeführt. Die Rechenzeit der MQL5 Funktionen wurde mittels GetMicrosecondCount() gemessen. Das Skript TestStatBenchmark.mq5 findet sich im Verzeichnis terminal_data_folder\MQL5\Scripts\UnitTests\Stat. Das Skript für R und die Ergebnisse der Zeitmessungen sind im Anhang.
Die Berechnungen wurden durchgeführt auf einem Intel Core i7-4790, CPU 3.6 Ghz, 16 GB RAM, Windows 10 x64.
Die Ergebnisse der Zeitmessungen (in Mikrosekunden, µs) zeigt Tabelle 3.
| Nr. | Verteilung | MQL5 Zeit zur Berechnung der PDF (µs) | R Zeit zur Berechnung der PDF (µs) | PDF R/MQL5 | MQL5 Zeit zur Berechnung the CDF (µs) | R Zeit zur Berechnung the CDF (µs) | CDF R/MQL5 | MQL5 Zeit zur Berechnung der Quantile (µs) | R Zeit zur Berechnung der Quantile (µs) | Quantile R/MQL5 | MQL5 Zeit zur Erzeugung von Zufallszahlen (µs) | R Zeit zur Erzeugung von Zufallszahlen (µs) | Zufall R/MQL5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Binomial | 4.39 | 11.663 | 2.657 | 13.65 | 25.316 | 1.855 | 50.18 | 66.845 | 1.332 | 318.73 | 1816.463 | 5.699 |
| 2 | Beta | 1.74 | 17.352 | 9.972 | 4.76 | 15.076 | 3.167 | 48.72 | 129.992 | 2.668 | 688.81 | 1723.45 | 2.502 |
| 3 | Gamma | 1.31 | 8.251 | 6.347 | 8.09 | 14.792 | 1.828 | 50.83 | 64.286 | 1.265 | 142.84 | 1281.707 | 8.973 |
| 4 | Cauchy | 0.45 | 1.423 | 3.162 | 1.33 | 15.078 | 11.34 | 1.37 | 2.845 | 2.077 | 224.19 | 588.517 | 2.625 |
| 5 | Exponential | 0.85 | 3.13 | 3.682 | 0.77 | 2.845 | 3.695 | 0.53 | 2.276 | 4.294 | 143.18 | 389.406 | 2.72 |
| 6 | Gleichverteilung | 0.42 | 2.561 | 6.098 | 0.45 | 1.423 | 3.162 | 0.18 | 2.846 | 15.81 | 40.3 | 247.467 | 6.141 |
| 7 | Geometrisch | 2.3 | 5.121 | 2.227 | 2.12 | 4.552 | 2.147 | 0.81 | 5.407 | 6.675 | 278 | 1078.045 | 3.879 |
| 8 | Hypergeometrisch | 1.85 | 11.095 | 5.997 | 0.9 | 8.819 | 9.799 | 0.75 | 9.957 | 13.28 | 302.55 | 880.356 | 2.91 |
| 9 | Logistisch | 1.27 | 4.267 | 3.36 | 1.11 | 4.267 | 3.844 | 0.71 | 3.13 | 4.408 | 178.65 | 626.632 | 3.508 |
| 10 | Weibull | 2.99 | 5.69 | 1.903 | 2.74 | 4.268 | 1.558 | 2.64 | 6.828 | 2.586 | 536.37 | 1558.472 | 2.906 |
| 11 | Poisson | 2.91 | 5.974 | 2.053 | 6.26 | 8.534 | 1.363 | 3.43 | 13.085 | 3.815 | 153.59 | 303.219 | 1.974 |
| 12 | F | 3.86 | 10.241 | 2.653 | 9.94 | 22.472 | 2.261 | 65.47 | 135.396 | 2.068 | 1249.22 | 1801.955 | 1.442 |
| 13 | Chi-Quadrat | 2.47 | 5.974 | 2.419 | 7.71 | 13.37 | 1.734 | 44.11 | 61.725 | 1.399 | 210.24 | 1235.059 | 5.875 |
| 14 | Nichtzentrale Chi-Quadrat | 8.05 | 14.223 | 1.767 | 45.61 | 209.068 | 4.584 | 220.66 | 10342.96 | 46.873 | 744.45 | 1997.653 | 2.683 |
| 15 | Nichtzentrale F | 19.1 | 28.446 | 1.489 | 14.67 | 46.935 | 3.199 | 212.21 | 2561.991 | 12.073 | 1848.9 | 2912.141 | 1.575 |
| 16 | Nichtzentrale Beta | 16.3 | 26.739 | 1.64 | 10.48 | 43.237 | 4.126 | 153.66 | 2290.915 | 14.909 | 2686.82 | 2839.893 | 1.057 |
| 17 | Negative Binomial | 6.13 | 11.094 | 1.81 | 12.21 | 19.627 | 1.607 | 14.05 | 60.019 | 4.272 | 1130.39 | 1936.498 | 1.713 |
| 18 | Normal | 1.15 | 4.267 | 3.71 | 0.81 | 3.983 | 4.917 | 0.7 | 2.277 | 3.253 | 293.7 | 696.321 | 2.371 |
| 19 | Lognormal | 1.99 | 5.406 | 2.717 | 3.19 | 8.819 | 2.765 | 3.18 | 6.259 | 1.968 | 479.75 | 1269.761 | 2.647 |
| 20 | T | 2.32 | 11.663 | 5.027 | 8.01 | 19.059 | 2.379 | 50.23 | 58.596 | 1.167 | 951.58 | 1425.92 | 1.498 |
| 21 | Nichtzentrale T | 38.47 | 86.757 | 2.255 | 27.75 | 39.823 | 1.435 | 1339.51 | 1930.524 | 1.441 | 1550.27 | 1699.84 | 1.096 |
| <PDF R/MQL5> | 3.474 | <CDF R/MQL5> | 3.465 | <Quantile R/MQL5> | 7.03 | <Random R/MQL5> | 3.13 |
Tabelle 4. Rechenzeiten der statistischen Funktionen in R und MQL5 (in Mikrosekunden)
Die Minimalwerte wurden von R genommen, die Mittelwerte (pdf_mean, cdf_mean, quantile_mean, random_mean) hingegen von MQL5.
Table 3 zeigt, dass selbst unter solchen Bedingungen die Funktionen der statistischen Bibliothek von MQL5 um ein Vielfaches schneller sind als die aus R. Im Durchschnitt rechnet MQL5 3 bis 7 mal schneller als R, obwohl R direkt in C++ geschrieben wurde.
Tatsächlich zeigt sich, dass der MQL5 Compiler viel schneller ist als direkte Umsetzungen der R-Funktionen in C++, und das zeigt die hohe Qualität unserer Entwickler. Übersetzungen von R nach MQL5 erzeugen eine deutliche Geschwindigkeitsverbesserung und es gibt keine Notwendigkeit DLLs Dritter zu verwenden.
6. Erkannte Berechnungsfehler in R
Während des Testens mit R wurden Fehler bei der Berechnung der Quantile der nichtzentralen T-Verteilung entdeckt.
Zum Beispiel:
> n <- 10 > k <- seq(0,1,by=1/n) > nt_pdf<-dt(k, 10,8, log = FALSE) > nt_cdf<-pt(k, 10,8, log = FALSE) > nt_quantile<-qt(nt_cdf, 10,8, log = FALSE) > nt_pdf [1] 4.927733e-15 1.130226e-14 2.641608e-14 6.281015e-14 1.516342e-13 3.708688e-13 9.166299e-13 [8] 2.283319e-12 5.716198e-12 1.433893e-11 3.593699e-11 > nt_cdf [1] 6.220961e-16 1.388760e-15 3.166372e-15 7.362630e-15 1.742915e-14 4.191776e-14 1.021850e-13 [8] 2.518433e-13 6.257956e-13 1.563360e-12 3.914610e-12 > k [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 > nt_quantile [1] -Inf -1.340781e+154 -1.340781e+154 -1.340781e+154 -1.340781e+154 -1.340781e+154 [7] -1.340781e+154 7.000000e-01 8.000000e-01 9.000000e-01 1.000000e+00
Zur Berechnung der Studentschen t-Verteilung verwendet R den AS 243 Algorithmus, vorgeschlagen von Lenth [6]. Ihr Vorteil ist eine schnelle rekursive Berechnung einer unendlichen Reihe von Mitgliedern mit einer inkompletten Betafunktion. Aber im Artikel [7] wird gezeigt, dass durch einen Fehler in der Genauigkeitsabschätzung während der Summierung der Mitglieder der Reihen dieser Algorithmus zu einem Fehler führt (Tabelle 2 im Artikel [7]), besonders für große Werte des delta-Parameters für die Nichtzentralität. Die Autoren von [7] schlugen eine korrigierte Version des Algorithmus zur rekursiven Berechnung der Wahrscheinlichkeit der nichtzentralen T-Verteilung vor.
Die statistische Bibliothek von MQL5 verwendet diesen korrigierten Algorithmus, der im Artikel [7] vorgeschlagen wurde und der korrekte Ergebnisse liefert.
Es sollte erwähnt werden, dass in der Sprache R die Wahrscheinlichkeitsdichte für die Verteilungen von Gamma, Chi-Quadrat und Nichtzentrale Chi-Quadrat im Punkt x=0 unendlich ist:
> dgamma(0,0.5,1) [1] Inf > dchisq(0,df=0.5,ncp=1) [1] Inf > dchisq(0,df=0.5,ncp=0) [1] Inf
In R werden daher Limitwerte für die Wahrscheinlichkeitsdichte im Punkt x=0 definiert. Trotz des Unendlich im Punkt x=0 gibt es beim Integrieren keine Abweichung und das Integral der Dichte ist endlich.
Die Wahrscheinlichkeiten (zum Beispiel für x=0.1) stimmen mit den Werten von Wolfram Alpha (Gamma, ChiSquare, NoncentralChiSquare) überein.
> pgamma(0.1,0.5,1) [1] 0.3452792 > pchisq(0.1,df=0.5,ncp=0) [1] 0.5165553 > pchisq(0.1,df=0.5,ncp=1) [1] 0.3194965
Wolfram Alpha (Mathematica) und Matlab verwenden unterschiedliche Definitionen der Dichte im Punkt x=0:
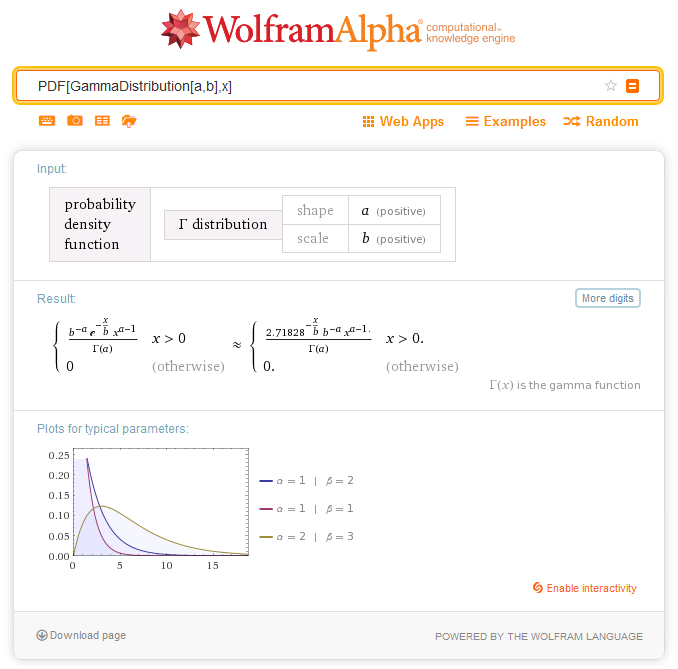
Abb. 3. Definition der Wahrscheinlichkeitsdichte der Gammaverteilung in Wolfram Alpha
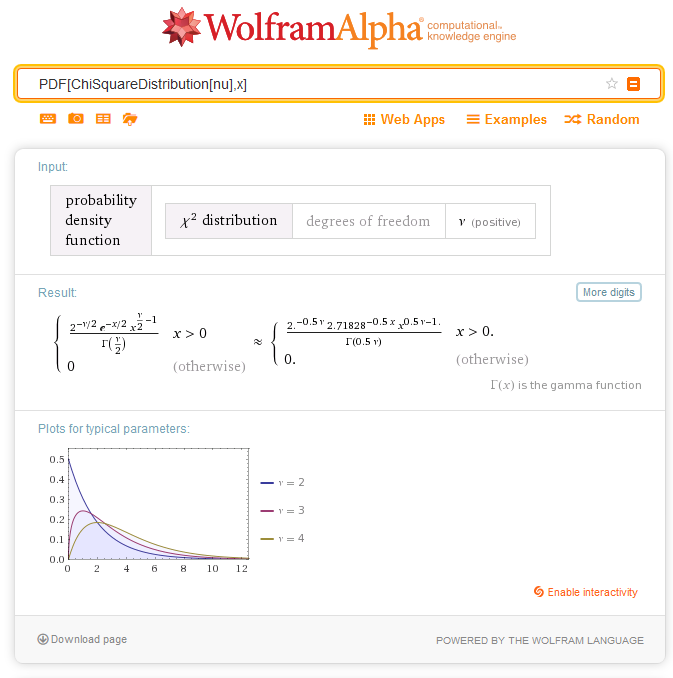
Abb. 4. Definition der Wahrscheinlichkeitsdichte der Chi-Quadrat-Verteilung in Wolfram Alpha
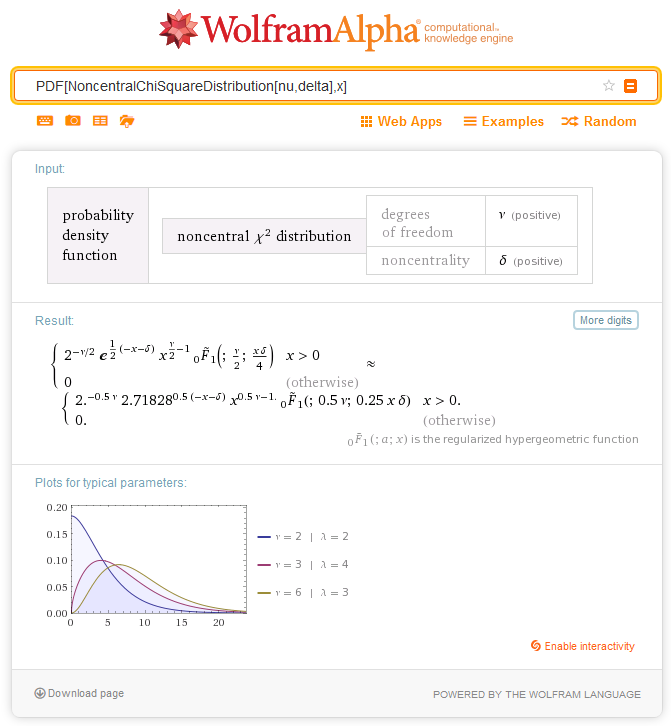
Abb. 5. Definition der Wahrscheinlichkeitsdichte der nichtzentralen Chi-Quadrat-Verteilung in Wolfram Alpha
In der Statistik-Bibliothek von MQL5 wird die Dichte dieser Verteilungen im Punkt x=0 als Null definiert.
Um die Genauigkeit der Berechnungen zu garantieren und Dritten Qualitätstests zu ermöglichen, sind mehrere Skripte für derartige Tests in der Standardausgabe inkludiert. Sie befinden sich im Verzeichnis /Scripts/UnitTests/Stat.
Schlussfolgerung
Der Artikel beschäftigt sich mit den wichtigsten Funktionen der statistischen Bibliothek von MQL5.
Sie erlauben die Berechnung statistischer Werte von Daten und das Arbeiten mit den grundlegenden statistischen Verteilungen in der Sprache R. Des Weiteren enthält die Bibliothek Funktionen zur Berechnung der theoretischen Momente von Verteilungen, um den Grad der Übereinstimmung mit einer realen Verteilung einzuschätzen.
Wegen der hohen Effizienz des neuen 64-bit Compilers von MQL5 werden auch komplexe mathematische Berechnungen um ein Vielfaches schneller ausgeführt als in R, und das erleichtert den Prozess der Entwicklungsarbeit.
Referenzen
- The R Project for Statistical Computing.
- N. Balakrishnan, N. L. Johnson, S. Kotz "Continuous Univariate Distributions: Volume 1." Wiley-Interscience, 1994.
- N. Balakrishnan, N. L. Johnson, S. Kotz "Continuous Univariate Distributions: Volume 2." Wiley-Interscience, 2000.
- N. L. Johnson, S. Kotz, A. W. Kemp "Univariate Discrete Distributions", Wiley-Interscience, 2005.
- Forbes C., Evans M., Hastings N., Peacock B., "Statistical Distributions", 4th Edition, John Wiley and Sons, 2011.
- Lenth, R.V., "Cumulative distribution function of the noncentral t distribution", Appled Statistics, vol. 38 (1989), 185–189.
- D. Benton, K. Krishnamoorthy, "Computing discrete mixtures of continuous distributions: noncentral chisquare, noncentral t and the distribution of the square of the sample multiple correlation coefficient", Computational Statistics & Data Analysis, 43, (2003), 249-267
Anhang. Ergebnisse der Messungen der Rechenzeiten der statistischen Funktionen
Das Skript zur Evaluierung der Rechenzeiten der statistischen Funktionen in R mit dessen Ergebnissen sind zusammen mit den Ergebnisses des Skriptes TestStatBenchmark.mq5 im Anhang beigefügt.
Script in R:
n <- 50
k <- seq(0,n,by=1)
binomial_pdf <- microbenchmark(pdf<-dbinom(k, 50, 0.6, log = FALSE))
binomial_cdf <- microbenchmark(cdf<-pbinom(k, 50, 0.6, log = FALSE))
binomial_quantile <- microbenchmark(quantile<-qbinom(cdf, 50, 0.6, log = FALSE))
binomial_random <- microbenchmark(random<-rbinom(10000, 50, 0.6))
print(binomial_pdf)
print(binomial_cdf)
print(binomial_quantile)
print(binomial_random)
n <- 50
k <- seq(0,1,by=1/n)
beta_pdf <- microbenchmark(pdf<-dbeta(k, 2, 4, log = FALSE))
beta_cdf <- microbenchmark(cdf<-pbeta(k, 2, 4, log = FALSE))
beta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2, 4, log = FALSE))
beta_random <- microbenchmark(random<-rbeta(10000, 2, 4,))
print(beta_pdf)
print(beta_cdf)
print(beta_quantile)
print(beta_random)
n <- 50
k <- seq(0,1,by=1/n)
gamma_pdf <- microbenchmark(pdf<-dgamma(k, 1,1, log = FALSE))
gamma_cdf <- microbenchmark(cdf<-pgamma(k, 1,1, log = FALSE))
gamma_quantile <- microbenchmark(quantile<-qgamma(cdf, 1, 1, log = FALSE))
gamma_random <- microbenchmark(random<-rgamma(10000, 1,1))
print(gamma_pdf)
print(gamma_cdf)
print(gamma_quantile)
print(gamma_random)
n <- 50
k <- seq(0,1,by=1/n)
cauchy_pdf <- microbenchmark(pdf<-dcauchy(k, 2,1, log = FALSE))
cauchy_cdf <- microbenchmark(cdf<-pgamma(k, 2,1, log = FALSE))
cauchy_quantile <- microbenchmark(quantile<-qcauchy(cdf, 2, 1, log = FALSE))
cauchy_random <- microbenchmark(random<-rcauchy(10000, 2, 1))
print(cauchy_pdf)
print(cauchy_cdf)
print(cauchy_quantile)
print(cauchy_random)
n <- 50
k <- seq(0,1,by=1/n)
exponential_pdf <- microbenchmark(pdf<-dexp(k, 2, log = FALSE))
exponential_cdf <- microbenchmark(cdf<-pexp(k, 2, log = FALSE))
exponential_quantile <- microbenchmark(quantile<-qexp(cdf, 2, log = FALSE))
exponential_random <- microbenchmark(random<-rexp(10000, 2))
print(exponential_pdf)
print(exponential_cdf)
print(exponential_quantile)
print(exponential_random)
n <- 50
k <- seq(0,1,by=1/n)
uniform_pdf <- microbenchmark(pdf<-dunif(k, 0, 10, log = FALSE))
uniform_cdf <- microbenchmark(cdf<-punif(k, 0, 10, log = FALSE))
uniform_quantile <- microbenchmark(quantile<-qunif(cdf, 0, 10, log = FALSE))
uniform_random <- microbenchmark(random<-runif(10000, 0, 10))
print(uniform_pdf)
print(uniform_cdf)
print(uniform_quantile)
print(uniform_random)
n <- 50
k <- seq(0,n,by=1)
geometric_pdf <- microbenchmark(pdf<-dgeom(k, 0.3, log = FALSE))
geometric_cdf <- microbenchmark(cdf<-pgeom(k, 0.3, log = FALSE))
geometric_quantile <- microbenchmark(quantile<-qgeom(cdf, 0.3, log = FALSE))
geometric_random <- microbenchmark(random<-rgeom(10000, 0.3))
print(geometric_pdf)
print(geometric_cdf)
print(geometric_quantile)
print(geometric_random)
n <- 50
k <- seq(0,n,by=1)
hypergeometric_pdf <- microbenchmark(pdf<-dhyper(k, 12,38,11, log = FALSE))
hypergeometric_cdf <- microbenchmark(cdf<-phyper(k, 12,38,11, log = FALSE))
hypergeometric_quantile <- microbenchmark(quantile<-qhyper(cdf, 12,38,11, log = FALSE))
hypergeometric_random <- microbenchmark(random<-rhyper(10000, 12,38,11))
print(hypergeometric_pdf)
print(hypergeometric_cdf)
print(hypergeometric_quantile)
print(hypergeometric_random)
n <- 50
k <- seq(0,1,by=1/n)
logistic_pdf <- microbenchmark(pdf<-dlogis(k, 1,2, log = FALSE))
logistic_cdf <- microbenchmark(cdf<-plogis(k, 1,2, log = FALSE))
logistic_quantile <- microbenchmark(quantile<-qlogis(cdf, 1,2, log = FALSE))
logistic_random <- microbenchmark(random<-rlogis(10000, 1,2))
print(logistic_pdf)
print(logistic_cdf)
print(logistic_quantile)
print(logistic_random)
n <- 50
k <- seq(0,1,by=1/n)
weibull_pdf <- microbenchmark(pdf<-dweibull(k, 5,1, log = FALSE))
weibull_cdf <- microbenchmark(cdf<-pweibull(k, 5,1, log = FALSE))
weibull_quantile <- microbenchmark(quantile<-qweibull(cdf, 5,1, log = FALSE))
weibull_random <- microbenchmark(random<-rweibull(10000, 5,1))
print(weibull_pdf)
print(weibull_cdf)
print(weibull_quantile)
print(weibull_random)
n <- 50
k <- seq(0,n,by=1)
poisson_pdf <- microbenchmark(pdf<-dpois(k, 1, log = FALSE))
poisson_cdf <- microbenchmark(cdf<-ppois(k, 1, log = FALSE))
poisson_quantile <- microbenchmark(quantile<-qpois(cdf, 1, log = FALSE))
poisson_random <- microbenchmark(random<-rpois(10000, 1))
print(poisson_pdf)
print(poisson_cdf)
print(poisson_quantile)
print(poisson_random)
n <- 50
k <- seq(0,1,by=1/n)
f_pdf <- microbenchmark(pdf<-df(k, 10,20, log = FALSE))
f_cdf <- microbenchmark(cdf<-pf(k, 10,20, log = FALSE))
f_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,log = FALSE))
f_random <- microbenchmark(random<-rf(10000, 10,20))
print(f_pdf)
print(f_cdf)
print(f_quantile)
print(f_random)
n <- 50
k <- seq(0,1,by=1/n)
chisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,log = FALSE))
chisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2, log = FALSE))
chisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2, log = FALSE))
chisquare_random <- microbenchmark(random<-rchisq(10000, 2))
print(chisquare_pdf)
print(chisquare_cdf)
print(chisquare_quantile)
print(chisquare_random)
n <- 50
k <- seq(0,1,by=1/n)
nchisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,1, log = FALSE))
nchisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2,1,log = FALSE))
nchisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2,1, log = FALSE))
nchisquare_random <- microbenchmark(random<-rchisq(10000, 2,1))
print(nchisquare_pdf)
print(nchisquare_cdf)
print(nchisquare_quantile)
print(nchisquare_random)
n <- 50
k <- seq(0,1,by=1/n)
nf_pdf <- microbenchmark(pdf<-df(k, 10,20,2, log = FALSE))
nf_cdf <- microbenchmark(cdf<-pf(k, 10,20,2, log = FALSE))
nf_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,2, log = FALSE))
nf_random <- microbenchmark(random<-rf(10000, 10,20,2))
print(nf_pdf)
print(nf_cdf)
print(nf_quantile)
print(nf_random)
n <- 50
k <- seq(0,1,by=1/n)
nbeta_pdf <- microbenchmark(pdf<-dbeta(k, 2,4,1, log = FALSE))
nbeta_cdf <- microbenchmark(cdf<-pbeta(k, 2,4,1, log = FALSE))
nbeta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2,4,1, log = FALSE))
nbeta_random <- microbenchmark(random<-rbeta(10000, 2,4,1))
print(nbeta_pdf)
print(nbeta_cdf)
print(nbeta_quantile)
print(nbeta_random)
n <- 50
k <- seq(0,n,by=1)
nbinom_pdf <- microbenchmark(pdf<-dnbinom(k, 2, 0.5, log = FALSE))
nbinom_cdf <- microbenchmark(cdf<-pnbinom(k, 2, 0.5, log = FALSE))
nbinom_quantile <- microbenchmark(quantile<-qnbinom(cdf, 2, 0.5, log = FALSE))
nbinom_random <- microbenchmark(random<-rnbinom(10000, 2, 0.5))
print(nbinom_pdf)
print(nbinom_cdf)
print(nbinom_quantile)
print(nbinom_random)
n <- 50
k <- seq(0,1,by=1/n)
normal_pdf <- microbenchmark(pdf<-dnorm(k, 1, 1, log = FALSE))
normal_cdf <- microbenchmark(cdf<-pnorm(k, 1, 1, log = FALSE))
normal_quantile <- microbenchmark(quantile<-qnorm(cdf, 1,1, log = FALSE))
normal_random <- microbenchmark(random<-rnorm(10000, 1,1))
print(normal_pdf)
print(normal_cdf)
print(normal_quantile)
print(normal_random)
n <- 50
k <- seq(0,1,by=1/n)
lognormal_pdf <- microbenchmark(pdf<-dlnorm(k, 0.5,0.6, log = FALSE))
lognormal_cdf <- microbenchmark(cdf<-plnorm(k, 0.5,0.6, log = FALSE))
lognormal_quantile <- microbenchmark(quantile<-qlnorm(cdf, 0.5,0.6, log = FALSE))
lognormal_random <- microbenchmark(random<-rlnorm(10000, 0.5,0.6))
print(lognormal_pdf)
print(lognormal_cdf)
print(lognormal_quantile)
print(lognormal_random)
n <- 50
k <- seq(0,1,by=1/n)
t_pdf <- microbenchmark(pdf<-dt(k, 8, log = FALSE))
t_cdf <- microbenchmark(cdf<-pt(k, 8, log = FALSE))
t_quantile <- microbenchmark(quantile<-qt(cdf, 8, log = FALSE))
t_random <- microbenchmark(random<-rt(10000, 8))
print(t_pdf)
print(t_cdf)
print(t_quantile)
print(t_random)
n <- 50
k <- seq(0,1,by=1/n)
nt_pdf <- microbenchmark(pdf<-dt(k, 10,1, log = FALSE))
nt_cdf <- microbenchmark(cdf<-pt(k, 10,1, log = FALSE))
nt_quantile <- microbenchmark(quantile<-qt(cdf, 10,1, log = FALSE))
nt_random <- microbenchmark(random<-rt(10000, 10,1))
print(nt_pdf)
print(nt_cdf)
print(nt_quantile)
print(nt_random)
Das Ergebnis:
R version 3.2.5 (2016-04-14) -- "Very, Very Secure Dishes" Copyright (C) 2016 The R Foundation for Statistical Computing Platform: x86_64-w64-mingw32/x64 (64-bit) R is free software and comes with ABSOLUTELY NO WARRANTY. You are welcome to redistribute it under certain conditions. Type 'license()' or 'licence()' for distribution details. R is a collaborative project with many contributors. Type 'contributors()' for more information and 'citation()' on how to cite R or R packages in publications. Type 'demo()' for some demos, 'help()' for on-line help, or 'help.start()' for an HTML browser interface to help. Type 'q()' to quit R. [Workspace loaded from ~/Test/111/.RData] > library(microbenchmark) > n <- 50 > k <- seq(0,n,by=1) > binomial_pdf <- microbenchmark(pdf<-dbinom(k, 50, 0.6, log = FALSE)) > binomial_cdf <- microbenchmark(cdf<-pbinom(k, 50, 0.6, log = FALSE)) > binomial_quantile <- microbenchmark(quantile<-qbinom(cdf, 50, 0.6, log = FALSE)) > binomial_random <- microbenchmark(random<-rbinom(10000, 50, 0.6)) > print(binomial_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dbinom(k, 50, 0.6, log = FALSE) 11.663 11.948 13.37888 12.233 12.233 47.503 100 > print(binomial_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pbinom(k, 50, 0.6, log = FALSE) 25.316 25.602 29.63195 25.886 35.557 93.868 100 > print(binomial_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qbinom(cdf, 50, 0.6, log = FALSE) 66.845 67.13 72.09098 67.699 73.672 130.276 100 > print(binomial_random) Unit: milliseconds expr min lq mean median uq max neval random <- rbinom(10000, 50, 0.6) 1.816463 1.89056 1.948185 1.929814 1.989262 2.308835 100 > > > n <- 50 > k <- seq(0,1,by=1/n) > beta_pdf <- microbenchmark(pdf<-dbeta(k, 2, 4, log = FALSE)) > beta_cdf <- microbenchmark(cdf<-pbeta(k, 2, 4, log = FALSE)) > beta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2, 4, log = FALSE)) > beta_random <- microbenchmark(random<-rbeta(10000, 2, 4,)) > print(beta_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dbeta(k, 2, 4, log = FALSE) 17.352 17.637 19.99512 17.638 18.206 109.797 100 > print(beta_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pbeta(k, 2, 4, log = FALSE) 15.076 15.361 16.83489 15.646 15.9295 75.379 100 > print(beta_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qbeta(cdf, 2, 4, log = FALSE) 129.992 130.277 140.8325 131.4145 143.93 201.672 100 > print(beta_random) Unit: milliseconds expr min lq mean median uq max neval random <- rbeta(10000, 2, 4, ) 1.72345 1.794132 1.862292 1.836515 1.901226 2.823963 100 > > n <- 50 > k <- seq(0,1,by=1/n) > gamma_pdf <- microbenchmark(pdf<-dgamma(k, 1,1, log = FALSE)) > gamma_cdf <- microbenchmark(cdf<-pgamma(k, 1,1, log = FALSE)) > gamma_quantile <- microbenchmark(quantile<-qgamma(cdf, 1, 1, log = FALSE)) > gamma_random <- microbenchmark(random<-rgamma(10000, 1,1)) > print(gamma_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dgamma(k, 1, 1, log = FALSE) 8.251 8.8195 10.92684 9.104 9.389 122.312 100 > print(gamma_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pgamma(k, 1, 1, log = FALSE) 14.792 15.646 20.43306 20.055 21.334 106.099 100 > print(gamma_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qgamma(cdf, 1, 1, log = FALSE) 64.286 64.854 70.09419 65.139 67.13 162.988 100 > print(gamma_random) Unit: milliseconds expr min lq mean median uq max neval random <- rgamma(10000, 1, 1) 1.281707 1.330347 1.410961 1.362631 1.421226 2.322204 100 > > n <- 50 > k <- seq(0,1,by=1/n) > cauchy_pdf <- microbenchmark(pdf<-dcauchy(k, 2,1, log = FALSE)) > cauchy_cdf <- microbenchmark(cdf<-pgamma(k, 2,1, log = FALSE)) > cauchy_quantile <- microbenchmark(quantile<-qcauchy(cdf, 2, 1, log = FALSE)) > cauchy_random <- microbenchmark(random<-rcauchy(10000, 2, 1)) > print(cauchy_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dcauchy(k, 2, 1, log = FALSE) 1.423 1.708 2.8431 1.709 2.278 67.415 100 > print(cauchy_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pgamma(k, 2, 1, log = FALSE) 15.078 15.646 16.51914 15.93 16.215 33.281 100 > print(cauchy_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qcauchy(cdf, 2, 1, log = FALSE) 2.845 3.13 3.8044 3.131 3.415 56.606 100 > print(cauchy_random) Unit: microseconds expr min lq mean median uq max neval random <- rcauchy(10000, 2, 1) 588.517 615.823 663.8658 637.7255 674.845 1520.356 100 > > n <- 50 > k <- seq(0,1,by=1/n) > exponential_pdf <- microbenchmark(pdf<-dexp(k, 2, log = FALSE)) > exponential_cdf <- microbenchmark(cdf<-pexp(k, 2, log = FALSE)) > exponential_quantile <- microbenchmark(quantile<-qexp(cdf, 2, log = FALSE)) > exponential_random <- microbenchmark(random<-rexp(10000, 2)) > print(exponential_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dexp(k, 2, log = FALSE) 3.13 3.414 4.08887 3.415 3.415 67.699 100 > print(exponential_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pexp(k, 2, log = FALSE) 2.845 3.13 4.38756 3.414 3.5565 58.597 100 > print(exponential_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qexp(cdf, 2, log = FALSE) 2.276 2.561 3.80729 2.5615 2.846 44.659 100 > print(exponential_random) Unit: microseconds expr min lq mean median uq max neval random <- rexp(10000, 2) 389.406 408.8895 440.9583 418.4185 444.8715 1371.875 100 > > > n <- 50 > k <- seq(0,1,by=1/n) > uniform_pdf <- microbenchmark(pdf<-dunif(k, 0, 10, log = FALSE)) > uniform_cdf <- microbenchmark(cdf<-punif(k, 0, 10, log = FALSE)) > uniform_quantile <- microbenchmark(quantile<-qunif(cdf, 0, 10, log = FALSE)) > uniform_random <- microbenchmark(random<-runif(10000, 0, 10)) > print(uniform_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dunif(k, 0, 10, log = FALSE) 2.561 2.846 3.78734 3.13 3.131 66.277 100 > print(uniform_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- punif(k, 0, 10, log = FALSE) 1.423 1.708 2.41635 1.992 1.993 53.477 100 > print(uniform_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qunif(cdf, 0, 10, log = FALSE) 2.846 3.131 5.13561 3.415 3.6995 82.774 100 > print(uniform_random) Unit: microseconds expr min lq mean median uq max neval random <- runif(10000, 0, 10) 247.467 258.7035 317.1567 279.6095 357.2635 1267.769 100 > > > n <- 50 > k <- seq(0,n,by=1) > geometric_pdf <- microbenchmark(pdf<-dgeom(k, 0.3, log = FALSE)) > geometric_cdf <- microbenchmark(cdf<-pgeom(k, 0.3, log = FALSE)) > geometric_quantile <- microbenchmark(quantile<-qgeom(cdf, 0.3, log = FALSE)) > geometric_random <- microbenchmark(random<-rgeom(10000, 0.3)) > print(geometric_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dgeom(k, 0.3, log = FALSE) 5.121 5.122 6.14258 5.406 5.406 60.304 100 > print(geometric_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pgeom(k, 0.3, log = FALSE) 4.552 4.836 5.50548 4.837 5.1215 46.081 100 > print(geometric_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qgeom(cdf, 0.3, log = FALSE) 5.407 5.974 7.12107 5.975 6.259 71.681 100 > print(geometric_random) Unit: milliseconds expr min lq mean median uq max neval random <- rgeom(10000, 0.3) 1.078045 1.127681 1.192608 1.156125 1.199361 1.604267 100 > > n <- 50 > k <- seq(0,n,by=1) > hypergeometric_pdf <- microbenchmark(pdf<-dhyper(k, 12,38,11, log = FALSE)) > hypergeometric_cdf <- microbenchmark(cdf<-phyper(k, 12,38,11, log = FALSE)) > hypergeometric_quantile <- microbenchmark(quantile<-qhyper(cdf, 12,38,11, log = FALSE)) > hypergeometric_random <- microbenchmark(random<-rhyper(10000, 12,38,11)) > print(hypergeometric_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dhyper(k, 12, 38, 11, log = FALSE) 11.095 13.939 17.07667 14.224 14.935 101.548 100 > print(hypergeometric_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- phyper(k, 12, 38, 11, log = FALSE) 8.819 9.387 12.60515 9.672 12.517 62.01 100 > print(hypergeometric_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qhyper(cdf, 12, 38, 11, log = FALSE) 9.957 10.3835 13.00618 10.81 11.948 64.286 100 > print(hypergeometric_random) Unit: microseconds expr min lq mean median uq max neval random <- rhyper(10000, 12, 38, 11) 880.356 938.9515 993.8324 963.9835 996.8365 1375.289 100 > > n <- 50 > k <- seq(0,1,by=1/n) > logistic_pdf <- microbenchmark(pdf<-dlogis(k, 1,2, log = FALSE)) > logistic_cdf <- microbenchmark(cdf<-plogis(k, 1,2, log = FALSE)) > logistic_quantile <- microbenchmark(quantile<-qlogis(cdf, 1,2, log = FALSE)) > logistic_random <- microbenchmark(random<-rlogis(10000, 1,2)) > print(logistic_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dlogis(k, 1, 2, log = FALSE) 4.267 4.552 5.94354 4.553 4.837 53.477 100 > print(logistic_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- plogis(k, 1, 2, log = FALSE) 4.267 4.552 5.96056 4.837 4.837 96.428 100 > print(logistic_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qlogis(cdf, 1, 2, log = FALSE) 3.13 3.415 4.1742 3.415 3.699 56.036 100 > print(logistic_random) Unit: microseconds expr min lq mean median uq max neval random <- rlogis(10000, 1, 2) 626.632 649.956 696.2128 675.2725 715.805 1589.191 100 > > n <- 50 > k <- seq(0,1,by=1/n) > weibull_pdf <- microbenchmark(pdf<-dweibull(k, 5,1, log = FALSE)) > weibull_cdf <- microbenchmark(cdf<-pweibull(k, 5,1, log = FALSE)) > weibull_quantile <- microbenchmark(quantile<-qweibull(cdf, 5,1, log = FALSE)) > weibull_random <- microbenchmark(random<-rweibull(10000, 5,1)) > print(weibull_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dweibull(k, 5, 1, log = FALSE) 5.69 5.974 7.21775 5.975 6.259 85.619 100 > print(weibull_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pweibull(k, 5, 1, log = FALSE) 4.268 4.552 7.83782 4.8365 7.966 90.455 100 > print(weibull_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qweibull(cdf, 5, 1, log = FALSE) 6.828 7.112 7.96587 7.113 7.397 48.641 100 > print(weibull_random) Unit: milliseconds expr min lq mean median uq max neval random <- rweibull(10000, 5, 1) 1.558472 1.59744 1.659753 1.632853 1.679502 2.616603 100 > > n <- 50 > k <- seq(0,n,by=1) > poisson_pdf <- microbenchmark(pdf<-dpois(k, 1, log = FALSE)) > poisson_cdf <- microbenchmark(cdf<-ppois(k, 1, log = FALSE)) > poisson_quantile <- microbenchmark(quantile<-qpois(cdf, 1, log = FALSE)) > poisson_random <- microbenchmark(random<-rpois(10000, 1)) > print(poisson_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dpois(k, 1, log = FALSE) 5.974 6.543 7.30316 6.544 6.828 54.046 100 > print(poisson_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- ppois(k, 1, log = FALSE) 8.534 8.819 10.25846 9.104 9.388 64.286 100 > print(poisson_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qpois(cdf, 1, log = FALSE) 13.085 13.086 14.37438 13.37 13.654 61.157 100 > print(poisson_random) Unit: microseconds expr min lq mean median uq max neval random <- rpois(10000, 1) 303.219 314.8815 327.5787 324.552 341.335 373.477 100 > > n <- 50 > k <- seq(0,1,by=1/n) > f_pdf <- microbenchmark(pdf<-df(k, 10,20, log = FALSE)) > f_cdf <- microbenchmark(cdf<-pf(k, 10,20, log = FALSE)) > f_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,log = FALSE)) > f_random <- microbenchmark(random<-rf(10000, 10,20)) > print(f_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- df(k, 10, 20, log = FALSE) 10.241 10.81 12.43159 10.811 11.095 71.112 100 > print(f_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pf(k, 10, 20, log = FALSE) 22.472 22.757 25.66972 23.041 23.3265 86.189 100 > print(f_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qf(cdf, 10, 20, log = FALSE) 135.396 136.25 166.7057 157.7255 186.171 255.717 100 > print(f_random) Unit: milliseconds expr min lq mean median uq max neval random <- rf(10000, 10, 20) 1.801955 1.889706 1.947645 1.929528 1.98272 2.725546 100 > > n <- 50 > k <- seq(0,1,by=1/n) > chisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,log = FALSE)) > chisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2, log = FALSE)) > chisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2, log = FALSE)) > chisquare_random <- microbenchmark(random<-rchisq(10000, 2)) > print(chisquare_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dchisq(k, 2, log = FALSE) 5.974 6.259 7.06416 6.4015 6.544 52.339 100 > print(chisquare_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pchisq(k, 2, log = FALSE) 13.37 13.655 15.46392 13.655 13.94 99.841 100 > print(chisquare_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qchisq(cdf, 2, log = FALSE) 61.725 62.2945 68.40176 62.7215 72.25 132.553 100 > print(chisquare_random) Unit: milliseconds expr min lq mean median uq max neval random <- rchisq(10000, 2) 1.235059 1.29408 1.38993 1.333903 1.401743 2.205582 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nchisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,1, log = FALSE)) > nchisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2,1,log = FALSE)) > nchisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2,1, log = FALSE)) > nchisquare_random <- microbenchmark(random<-rchisq(10000, 2,1)) > print(nchisquare_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dchisq(k, 2, 1, log = FALSE) 14.223 14.509 17.3866 14.793 15.6455 37.548 100 > print(nchisquare_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pchisq(k, 2, 1, log = FALSE) 209.068 210.49 231.6357 223.1475 240.499 309.193 100 > print(nchisquare_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qchisq(cdf, 2, 1, log = FALSE) 10.34296 10.65955 10.90239 10.83733 11.02563 12.31558 100 > print(nchisquare_random) Unit: milliseconds expr min lq mean median uq max neval random <- rchisq(10000, 2, 1) 1.997653 2.073457 2.187417 2.114845 2.183111 3.134576 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nf_pdf <- microbenchmark(pdf<-df(k, 10,20,2, log = FALSE)) > nf_cdf <- microbenchmark(cdf<-pf(k, 10,20,2, log = FALSE)) > nf_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,2, log = FALSE)) > nf_random <- microbenchmark(random<-rf(10000, 10,20,2)) > print(nf_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- df(k, 10, 20, 2, log = FALSE) 28.446 30.153 34.12338 30.438 31.291 68.836 100 > print(nf_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pf(k, 10, 20, 2, log = FALSE) 46.935 61.8685 64.53899 63.433 65.708 106.953 100 > print(nf_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qf(cdf, 10, 20, 2, log = FALSE) 2.561991 2.640355 2.719223 2.68999 2.744461 3.737598 100 > print(nf_random) Unit: milliseconds expr min lq mean median uq max neval random <- rf(10000, 10, 20, 2) 2.912141 2.989225 3.100073 3.035163 3.110825 4.062433 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nbeta_pdf <- microbenchmark(pdf<-dbeta(k, 2,4,1, log = FALSE)) > nbeta_cdf <- microbenchmark(cdf<-pbeta(k, 2,4,1, log = FALSE)) > nbeta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2,4,1, log = FALSE)) > nbeta_random <- microbenchmark(random<-rbeta(10000, 2,4,1)) > print(nbeta_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dbeta(k, 2, 4, 1, log = FALSE) 26.739 27.308 31.31301 27.592 30.5795 56.891 100 > print(nbeta_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pbeta(k, 2, 4, 1, log = FALSE) 43.237 43.806 55.11814 56.321 57.7435 167.255 100 > print(nbeta_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qbeta(cdf, 2, 4, 1, log = FALSE) 2.290915 2.375111 2.440959 2.431146 2.49927 2.644764 100 > print(nbeta_random) Unit: milliseconds expr min lq mean median uq max neval random <- rbeta(10000, 2, 4, 1) 2.839893 3.002737 3.143906 3.073848 3.150932 4.302789 100 > > n <- 50 > k <- seq(0,n,by=1) > nbinom_pdf <- microbenchmark(pdf<-dnbinom(k, 2, 0.5, log = FALSE)) > nbinom_cdf <- microbenchmark(cdf<-pnbinom(k, 2, 0.5, log = FALSE)) > nbinom_quantile <- microbenchmark(quantile<-qnbinom(cdf, 2, 0.5, log = FALSE)) > nbinom_random <- microbenchmark(random<-rnbinom(10000, 2, 0.5)) > print(nbinom_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dnbinom(k, 2, 0.5, log = FALSE) 11.094 11.379 13.37031 11.664 11.948 78.508 100 > print(nbinom_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pnbinom(k, 2, 0.5, log = FALSE) 19.627 19.913 22.94469 20.197 20.482 130.277 100 > print(nbinom_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qnbinom(cdf, 2, 0.5, log = FALSE) 60.019 60.588 69.73866 61.442 74.099 122.028 100 > print(nbinom_random) Unit: milliseconds expr min lq mean median uq max neval random <- rnbinom(10000, 2, 0.5) 1.936498 2.029226 2.086237 2.072035 2.125084 2.354061 100 > > n <- 50 > k <- seq(0,1,by=1/n) > normal_pdf <- microbenchmark(pdf<-dnorm(k, 1, 1, log = FALSE)) > normal_cdf <- microbenchmark(cdf<-pnorm(k, 1, 1, log = FALSE)) > normal_quantile <- microbenchmark(quantile<-qnorm(cdf, 1,1, log = FALSE)) > normal_random <- microbenchmark(random<-rnorm(10000, 1,1)) > print(normal_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dnorm(k, 1, 1, log = FALSE) 4.267 4.552 5.7927 4.553 4.837 75.663 100 > print(normal_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pnorm(k, 1, 1, log = FALSE) 3.983 4.269 5.94911 4.553 4.979 50.632 100 > print(normal_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qnorm(cdf, 1, 1, log = FALSE) 2.277 2.561 3.42042 2.845 2.846 45.227 100 > print(normal_random) Unit: microseconds expr min lq mean median uq max neval random <- rnorm(10000, 1, 1) 696.321 728.747 779.1994 749.7965 778.3835 1541.12 100 > > n <- 50 > k <- seq(0,1,by=1/n) > lognormal_pdf <- microbenchmark(pdf<-dlnorm(k, 0.5,0.6, log = FALSE)) > lognormal_cdf <- microbenchmark(cdf<-plnorm(k, 0.5,0.6, log = FALSE)) > lognormal_quantile <- microbenchmark(quantile<-qlnorm(cdf, 0.5,0.6, log = FALSE)) > lognormal_random <- microbenchmark(random<-rlnorm(10000, 0.5,0.6)) > print(lognormal_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dlnorm(k, 0.5, 0.6, log = FALSE) 5.406 5.69 6.89638 5.975 6.259 50.917 100 > print(lognormal_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- plnorm(k, 0.5, 0.6, log = FALSE) 8.819 9.387 12.3463 9.3885 12.6595 71.681 100 > print(lognormal_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qlnorm(cdf, 0.5, 0.6, log = FALSE) 6.259 6.544 7.38277 6.544 6.828 58.881 100 > print(lognormal_random) Unit: milliseconds expr min lq mean median uq max neval random <- rlnorm(10000, 0.5, 0.6) 1.269761 1.329209 1.380386 1.362632 1.401743 2.247395 100 > > n <- 50 > k <- seq(0,1,by=1/n) > t_pdf <- microbenchmark(pdf<-dt(k, 8, log = FALSE)) > t_cdf <- microbenchmark(cdf<-pt(k, 8, log = FALSE)) > t_quantile <- microbenchmark(quantile<-qt(cdf, 8, log = FALSE)) > t_random <- microbenchmark(random<-rt(10000, 8)) > print(t_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dt(k, 8, log = FALSE) 11.663 12.233 15.71413 12.517 16.0725 76.517 100 > print(t_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pt(k, 8, log = FALSE) 19.059 20.6235 23.23485 21.05 21.619 127.717 100 > print(t_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qt(cdf, 8, log = FALSE) 58.596 58.882 64.84339 59.166 62.01 151.611 100 > print(t_random) Unit: milliseconds expr min lq mean median uq max neval random <- rt(10000, 8) 1.42592 1.480676 1.553132 1.51424 1.569565 2.44679 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nt_pdf <- microbenchmark(pdf<-dt(k, 10,1, log = FALSE)) > nt_cdf <- microbenchmark(cdf<-pt(k, 10,1, log = FALSE)) > nt_quantile <- microbenchmark(quantile<-qt(cdf, 10,1, log = FALSE)) > nt_random <- microbenchmark(random<-rt(10000, 10,1)) > print(nt_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dt(k, 10, 1, log = FALSE) 86.757 88.037 92.88671 89.317 91.4505 130.276 100 > print(nt_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pt(k, 10, 1, log = FALSE) 39.823 40.2505 44.51695 40.6765 49.352 70.829 100 > print(nt_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qt(cdf, 10, 1, log = FALSE) 1.930524 1.981866 2.038755 2.0224 2.079715 2.594987 100 > print(nt_random) Unit: milliseconds expr min lq mean median uq max neval random <- rt(10000, 10, 1) 1.69984 1.764693 1.867469 1.814044 1.893263 2.856959 100
Ergebnisse des Skriptes TestStatBenchmark.mq5:
PP 0 13:06:15.252 TestStatBenchmark (EURUSD,H1)
KJ 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): pdf_mean=4.39, pdf_median=4.00, pdf_min=3.00, pdf_max=40.00, pdf_stddev=2.21, pdf_avgdev=0.95
MS 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): cdf_mean=13.65, cdf_median=12.00, cdf_min=11.00, cdf_max=54.00, cdf_stddev=4.09, cdf_avgdev=2.37
GF 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): quantile_mean=50.18, quantile_median=45.00, quantile_min=43.00, quantile_max=108.00, quantile_stddev=9.97, quantile_avgdev=7.41
QO 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): random_mean=318.73, random_median=312.00, random_min=284.00, random_max=478.00, random_stddev=28.74, random_avgdev=22.22
LP 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): pdf_mean=1.74, pdf_median=2.00, pdf_min=1.00, pdf_max=18.00, pdf_stddev=1.07, pdf_avgdev=0.53
EI 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): cdf_mean=4.76, cdf_median=4.00, cdf_min=3.00, cdf_max=68.00, cdf_stddev=3.07, cdf_avgdev=1.19
LM 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): quantile_mean=48.72, quantile_median=44.00, quantile_min=43.00, quantile_max=111.00, quantile_stddev=10.21, quantile_avgdev=6.96
QG 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): random_mean=688.81, random_median=680.00, random_min=625.00, random_max=976.00, random_stddev=43.92, random_avgdev=31.81
HE 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): pdf_mean=1.31, pdf_median=1.00, pdf_min=1.00, pdf_max=13.00, pdf_stddev=0.82, pdf_avgdev=0.47
GL 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): cdf_mean=8.09, cdf_median=7.00, cdf_min=7.00, cdf_max=92.00, cdf_stddev=3.67, cdf_avgdev=1.40
CF 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): quantile_mean=50.83, quantile_median=46.00, quantile_min=45.00, quantile_max=106.00, quantile_stddev=9.27, quantile_avgdev=6.72
GR 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): random_mean=142.84, random_median=132.00, random_min=128.00, random_max=260.00, random_stddev=19.73, random_avgdev=15.32
QD 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): pdf_mean=0.45, pdf_median=0.00, pdf_min=0.00, pdf_max=11.00, pdf_stddev=0.85, pdf_avgdev=0.54
QK 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): cdf_mean=1.33, cdf_median=1.00, cdf_min=1.00, cdf_max=12.00, cdf_stddev=0.81, cdf_avgdev=0.48
MR 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): quantile_mean=1.37, quantile_median=1.00, quantile_min=1.00, quantile_max=14.00, quantile_stddev=0.89, quantile_avgdev=0.51
IK 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): random_mean=224.19, random_median=215.00, random_min=200.00, random_max=352.00, random_stddev=26.86, random_avgdev=20.34
PQ 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): pdf_mean=0.85, pdf_median=1.00, pdf_min=0.00, pdf_max=18.00, pdf_stddev=1.40, pdf_avgdev=0.54
GK 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): cdf_mean=0.77, cdf_median=1.00, cdf_min=0.00, cdf_max=16.00, cdf_stddev=0.94, cdf_avgdev=0.47
HE 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): quantile_mean=0.53, quantile_median=0.00, quantile_min=0.00, quantile_max=10.00, quantile_stddev=0.78, quantile_avgdev=0.54
HL 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): random_mean=143.18, random_median=130.00, random_min=128.00, random_max=272.00, random_stddev=21.58, random_avgdev=16.98
LK 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): pdf_mean=0.42, pdf_median=0.00, pdf_min=0.00, pdf_max=12.00, pdf_stddev=0.82, pdf_avgdev=0.52
CE 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): cdf_mean=0.45, cdf_median=0.00, cdf_min=0.00, cdf_max=16.00, cdf_stddev=0.96, cdf_avgdev=0.55
LO 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): quantile_mean=0.18, quantile_median=0.00, quantile_min=0.00, quantile_max=1.00, quantile_stddev=0.38, quantile_avgdev=0.29
GE 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): random_mean=40.30, random_median=36.00, random_min=35.00, random_max=83.00, random_stddev=7.61, random_avgdev=5.41
OP 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): pdf_mean=2.30, pdf_median=2.00, pdf_min=1.00, pdf_max=14.00, pdf_stddev=1.30, pdf_avgdev=0.52
DK 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): cdf_mean=2.12, cdf_median=2.00, cdf_min=1.00, cdf_max=18.00, cdf_stddev=1.69, cdf_avgdev=0.53
NE 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): quantile_mean=0.81, quantile_median=1.00, quantile_min=0.00, quantile_max=10.00, quantile_stddev=0.68, quantile_avgdev=0.39
IL 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): random_mean=278.00, random_median=271.00, random_min=251.00, random_max=429.00, random_stddev=28.23, random_avgdev=21.62
PG 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): pdf_mean=1.85, pdf_median=2.00, pdf_min=1.00, pdf_max=15.00, pdf_stddev=1.07, pdf_avgdev=0.48
CM 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): cdf_mean=0.90, cdf_median=1.00, cdf_min=0.00, cdf_max=17.00, cdf_stddev=0.85, cdf_avgdev=0.32
NP 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): quantile_mean=0.75, quantile_median=1.00, quantile_min=0.00, quantile_max=12.00, quantile_stddev=0.96, quantile_avgdev=0.48
FE 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): random_mean=302.55, random_median=295.00, random_min=272.00, random_max=466.00, random_stddev=30.20, random_avgdev=22.99
ML 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): pdf_mean=1.27, pdf_median=1.00, pdf_min=0.00, pdf_max=91.00, pdf_stddev=3.04, pdf_avgdev=0.56
DR 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): cdf_mean=1.11, cdf_median=1.00, cdf_min=0.00, cdf_max=17.00, cdf_stddev=1.34, cdf_avgdev=0.40
IH 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): quantile_mean=0.71, quantile_median=1.00, quantile_min=0.00, quantile_max=12.00, quantile_stddev=0.79, quantile_avgdev=0.47
GL 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): random_mean=178.65, random_median=164.00, random_min=162.00, random_max=309.00, random_stddev=24.09, random_avgdev=17.94
MJ 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): pdf_mean=2.99, pdf_median=3.00, pdf_min=2.00, pdf_max=17.00, pdf_stddev=1.63, pdf_avgdev=0.57
GD 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): cdf_mean=2.74, cdf_median=3.00, cdf_min=2.00, cdf_max=19.00, cdf_stddev=1.23, cdf_avgdev=0.58
FO 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): quantile_mean=2.64, quantile_median=2.00, quantile_min=2.00, quantile_max=19.00, quantile_stddev=1.64, quantile_avgdev=0.76
DJ 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): random_mean=536.37, random_median=526.00, random_min=483.00, random_max=759.00, random_stddev=46.99, random_avgdev=34.40
HR 0 13:06:18.485 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): pdf_mean=2.91, pdf_median=3.00, pdf_min=2.00, pdf_max=15.00, pdf_stddev=1.40, pdf_avgdev=0.58
IL 0 13:06:18.486 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): cdf_mean=6.26, cdf_median=6.00, cdf_min=5.00, cdf_max=23.00, cdf_stddev=2.38, cdf_avgdev=1.07
HE 0 13:06:18.486 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): quantile_mean=3.43, quantile_median=3.00, quantile_min=2.00, quantile_max=20.00, quantile_stddev=1.48, quantile_avgdev=0.68
DL 0 13:06:18.486 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): random_mean=153.59, random_median=144.00, random_min=138.00, random_max=265.00, random_stddev=18.57, random_avgdev=13.99
IH 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): pdf_mean=3.86, pdf_median=4.00, pdf_min=3.00, pdf_max=21.00, pdf_stddev=1.78, pdf_avgdev=0.76
GS 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): cdf_mean=9.94, cdf_median=9.00, cdf_min=7.00, cdf_max=36.00, cdf_stddev=3.82, cdf_avgdev=2.15
OI 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): quantile_mean=65.47, quantile_median=59.00, quantile_min=57.00, quantile_max=147.00, quantile_stddev=12.99, quantile_avgdev=9.64
DE 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): random_mean=1249.22, random_median=1213.00, random_min=1127.00, random_max=1968.00, random_stddev=117.69, random_avgdev=72.17
EL 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): pdf_mean=2.47, pdf_median=2.00, pdf_min=2.00, pdf_max=13.00, pdf_stddev=1.32, pdf_avgdev=0.65
JK 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): cdf_mean=7.71, cdf_median=7.00, cdf_min=7.00, cdf_max=23.00, cdf_stddev=1.91, cdf_avgdev=0.88
KQ 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): quantile_mean=44.11, quantile_median=41.00, quantile_min=40.00, quantile_max=120.00, quantile_stddev=8.17, quantile_avgdev=5.38
CL 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): random_mean=210.24, random_median=196.00, random_min=190.00, random_max=437.00, random_stddev=29.14, random_avgdev=21.00
HD 0 13:06:21.098 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): pdf_mean=8.05, pdf_median=8.00, pdf_min=7.00, pdf_max=24.00, pdf_stddev=2.41, pdf_avgdev=1.09
MR 0 13:06:21.098 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): cdf_mean=45.61, cdf_median=42.00, cdf_min=41.00, cdf_max=97.00, cdf_stddev=8.25, cdf_avgdev=5.70
FN 0 13:06:21.098 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): quantile_mean=220.66, quantile_median=211.50, quantile_min=196.00, quantile_max=362.00, quantile_stddev=24.71, quantile_avgdev=19.45
LI 0 13:06:21.099 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): random_mean=744.45, random_median=728.00, random_min=672.00, random_max=1082.00, random_stddev=62.42, random_avgdev=43.24
RE 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): pdf_mean=19.10, pdf_median=18.00, pdf_min=16.00, pdf_max=50.00, pdf_stddev=4.67, pdf_avgdev=2.64
FS 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): cdf_mean=14.67, cdf_median=13.00, cdf_min=12.00, cdf_max=39.00, cdf_stddev=3.94, cdf_avgdev=2.44
EN 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): quantile_mean=212.21, quantile_median=203.00, quantile_min=189.00, quantile_max=347.00, quantile_stddev=24.37, quantile_avgdev=19.30
EF 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): random_mean=1848.90, random_median=1819.00, random_min=1704.00, random_max=2556.00, random_stddev=118.75, random_avgdev=78.66
EN 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): pdf_mean=16.30, pdf_median=15.00, pdf_min=14.00, pdf_max=43.00, pdf_stddev=4.32, pdf_avgdev=2.43
EP 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): cdf_mean=10.48, cdf_median=10.00, cdf_min=8.00, cdf_max=32.00, cdf_stddev=3.02, cdf_avgdev=1.72
ME 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): quantile_mean=153.66, quantile_median=141.00, quantile_min=135.00, quantile_max=283.00, quantile_stddev=20.83, quantile_avgdev=16.16
QJ 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): random_mean=2686.82, random_median=2649.00, random_min=2457.00, random_max=3753.00, random_stddev=150.32, random_avgdev=98.23
OO 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): pdf_mean=6.13, pdf_median=6.00, pdf_min=5.00, pdf_max=24.00, pdf_stddev=2.38, pdf_avgdev=1.22
DG 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): cdf_mean=12.21, cdf_median=11.00, cdf_min=11.00, cdf_max=33.00, cdf_stddev=3.07, cdf_avgdev=1.58
LJ 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): quantile_mean=14.05, quantile_median=13.00, quantile_min=12.00, quantile_max=82.00, quantile_stddev=4.81, quantile_avgdev=2.28
EM 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): random_mean=1130.39, random_median=1108.00, random_min=1039.00, random_max=1454.00, random_stddev=69.41, random_avgdev=51.70
GP 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): pdf_mean=1.15, pdf_median=1.00, pdf_min=0.00, pdf_max=19.00, pdf_stddev=1.34, pdf_avgdev=0.45
OI 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): cdf_mean=0.81, cdf_median=1.00, cdf_min=0.00, cdf_max=17.00, cdf_stddev=1.16, cdf_avgdev=0.49
CN 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): quantile_mean=0.70, quantile_median=1.00, quantile_min=0.00, quantile_max=13.00, quantile_stddev=0.82, quantile_avgdev=0.49
EG 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): random_mean=293.70, random_median=281.00, random_min=256.00, random_max=537.00, random_stddev=43.28, random_avgdev=31.62
FD 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): pdf_mean=1.99, pdf_median=2.00, pdf_min=1.00, pdf_max=18.00, pdf_stddev=1.48, pdf_avgdev=0.48
PN 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): cdf_mean=3.19, cdf_median=3.00, cdf_min=2.00, cdf_max=17.00, cdf_stddev=1.61, cdf_avgdev=0.64
DH 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): quantile_mean=3.18, quantile_median=3.00, quantile_min=2.00, quantile_max=19.00, quantile_stddev=1.77, quantile_avgdev=0.64
NR 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): random_mean=479.75, random_median=468.00, random_min=428.00, random_max=754.00, random_stddev=48.26, random_avgdev=34.30
FL 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): pdf_mean=2.32, pdf_median=2.00, pdf_min=1.00, pdf_max=15.00, pdf_stddev=1.29, pdf_avgdev=0.54
QE 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): cdf_mean=8.01, cdf_median=7.00, cdf_min=6.00, cdf_max=39.00, cdf_stddev=3.13, cdf_avgdev=1.73
MM 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): quantile_mean=50.23, quantile_median=45.00, quantile_min=44.00, quantile_max=113.00, quantile_stddev=10.28, quantile_avgdev=7.73
KG 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): random_mean=951.58, random_median=931.00, random_min=859.00, random_max=1439.00, random_stddev=78.14, random_avgdev=49.72
CQ 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): pdf_mean=38.47, pdf_median=35.00, pdf_min=32.00, pdf_max=164.00, pdf_stddev=9.66, pdf_avgdev=6.38
OO 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): cdf_mean=27.75, cdf_median=25.00, cdf_min=24.00, cdf_max=80.00, cdf_stddev=7.02, cdf_avgdev=4.63
PF 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): quantile_mean=1339.51, quantile_median=1306.00, quantile_min=1206.00, quantile_max=2262.00, quantile_stddev=128.18, quantile_avgdev=74.83
OR 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): random_mean=1550.27, random_median=1520.00, random_min=1418.00, random_max=2317.00, random_stddev=112.08, random_avgdev=73.74
LQ 0 13:06:31.979 TestStatBenchmark (EURUSD,H1)
GH 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) 21 of 21 passed
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/2742
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
 Neuronales Netz: Selbstoptimierender Expert Advisor
Neuronales Netz: Selbstoptimierender Expert Advisor
 Schnellauswertung des Signals: Handelsaktivitäten, Diagramme von Belastungsgrad und MFE/MAE-Verteilung
Schnellauswertung des Signals: Handelsaktivitäten, Diagramme von Belastungsgrad und MFE/MAE-Verteilung
 Grafische Interfaces X: Updates für die Easy And Fast Bibliothek (Build 3)
Grafische Interfaces X: Updates für die Easy And Fast Bibliothek (Build 3)
 Arbeiten mit Körben von Währungspaaren am Devisenmarkt
Arbeiten mit Körben von Währungspaaren am Devisenmarkt
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Formel in der Dokumentation:
Ist das Analogon in Wikipedia:
Ich habe mir den Code angesehen.
Die Funktion MathRandomNoncentralBeta() hat Zeilen wie diese:
In der gleichen Wikipedia steht dies:
The noncentral beta distribution (Type I) is the distribution of the ratio
wobei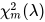 einenichtzentrale Chi-Quadrat-Zufallsvariable mit Freiheitsgraden m und dem Nicht-Zentralitätsparameter 𝜆 ist, und 𝜒 𝑛 2 eine zentrale chi-Quadrat-Zufallsvariable mit Freiheitsgraden n ist, die unabhängig von 𝜒 𝑚 2 ( 𝜆 ) ist.
einenichtzentrale Chi-Quadrat-Zufallsvariable mit Freiheitsgraden m und dem Nicht-Zentralitätsparameter 𝜆 ist, und 𝜒 𝑛 2 eine zentrale chi-Quadrat-Zufallsvariable mit Freiheitsgraden n ist, die unabhängig von 𝜒 𝑚 2 ( 𝜆 ) ist.
Das heißt, es werden zwei Zufallsvariablen genommen, wobei die erste aus einer nicht zentralen chi-Quadrat-Verteilung und die zweite aus einer zentralen stammt. Wahrscheinlich kann der Code dahingehend korrigiert werden:
Die geänderten Graphen im Beispiel werden unten stehen.
Das sind die Ergebnisse.
Auch nicht sehr gut... Im Allgemeinen gehört die Arbeit mit nicht-zentralen Beta-Verteilungen eher zu den nicht-trivialen Aufgaben. Wir haben es geschafft, Boost aus dem offenen Quellcode zu sehen. Und es wird komplizierter sein als das, was wir jetzt in SB haben.
Die gleiche Wikipedia hat es:
Das heißt, es werden zwei Zufallsvariablen genommen, wobei die erste aus einer nicht zentralen Chi-Quadrat-Verteilung und die zweite aus einer zentralen Verteilung stammt. Wahrscheinlich kann der Code dahingehend korrigiert werden:
Die geänderten Graphen im Beispiel werden unten stehen.
Vielen Dank, Sie haben Recht, wir müssen durch diese Formel zu berechnen, aber es war ein weiterer Fehler, der Lambda Nicht-Zentralität Parameter sollte ohne Multiplikator 2 sein.
Test-Skript:
Ergebnis:
Ich habe auch die CFD-Funktion für die nichtzentrale Beta-Verteilung überprüft.
Einige fragwürdige Ergebnisse:
Alternative Quellen verwenden den ASA310-Algorithmus:
Zum Beispiel einige der Ergebnisse in Wolfram Mathematica:
Was der Wahrheit mehr oder weniger ähnlich ist...