群体算法的混合 -顺序结构和并行结构

MetaTrader 5 — 示例 | 22 十月 2024, 11:04

205

Andrey Dik

1.概述

让我们来看看混合优化算法的三种主要选择：

1.将算法搜索策略混合为一个。每种算法都有自己的一套技能和能力。在共同追求成功的过程中，混合它们的逻辑结构提供了各种特性。这是一种风格各异的舞蹈，每一步都是对整体动作的补充和增强。这种方法的一个例子就是前一篇文章中讨论的细菌觅食优化与遗传算法的结合。

2.将迭代分为一种算法的部分工作和另一种算法的最终工作，就像传递接力棒一样，使每种算法的运行保持一致。算法就像运动队，每个运动队都专注于自己的比赛阶段。接力棒在他们之间传递，意味着知识和成果的转移，创造了从一个阶段到下一个阶段的平稳高效过渡，就像一个协调良好的团队的和谐一样，使迭代的总数保持不变。

3.每种算法的并行操作以及随后的独特最佳结果组合，就像集体创作，每种算法都是艺术家，将其独特的能量注入共同的世界画布。在每次迭代中，合并最佳结果。每一次迭代都补充和扩展了对所研究问题的理解，创造了最佳解决方案的共同愿景。

这些算法混合选项为不同方法和策略的创造性组合提供了重要机会，从而在优化方面带来了新的发现和改进。就像在艺术世界中，各种风格和技术激发了独特作品的创作一样，不同算法的和谐组合可以带来最佳结果和对复杂问题的有效探索。

在寻找最优解决方案的世界里，选项空间中的每一步都很重要，重要的是不仅要搜索，而且要有信心地找到，以实现预期的结果。我们在上一篇文章中在种群优化算法领域进行的实验研究揭示了一个重要方面：成功与初始条件的依赖性，在该研究中，我们强制算法放置在全局最小点以达到全局最大点。一些算法很难离开最小点，失去了效率，但其他算法是通用稳定性的光辉例子，对起始位置的依赖性很小。它们中的一些在早期阶段成功地探索了这一空间，而另一些则试图在后期阶段改进成果。每种算法的这些独特功能都可以成功地加以利用，增强其优点，减少其缺点。我们希望将不同的策略结合起来，可以产生更有效的方法，成功地探索空间，并在工作的不同阶段提高成果。重要的是要补充一点，由于标准化，算法的混合变得更加容易。现在，所有的群体算法都被归入一个类，这为创造性组合和全新的可能性打开了大门。

2.使用 GWO 和 COA 做实验

在本实验中，我们将采用两种性能和特征各不相同的算法：GWO 和 COAm。GWO 位于排名表的末尾，而 COAm 则位于中间。让我们试着看看在顺序和并行操作中使用它们的组合能取得什么样的结果。在本文中，我们将不考虑混合搜索策略的逻辑元素，因为这对每种算法组合来说都非常具体，无法在一篇文章的框架内探讨。

灰狼优化器（GWO）是一种基于模拟灰狼群狩猎的元启发式随机算法。
GWO 算法的主要特点：

模拟族群行为。该算法采用狼群的分层结构，每只狼扮演不同的角色（阿尔法、贝塔、德尔塔、欧米茄）。
搜索全局最大值。阿尔法狼、贝塔狼和德尔塔狼被认为是适应能力最强的狼，它们离猎物最近，而其他狼往往离它们更近。GWO 会迅速走向一个潜在的全局极端。
适应性强。随着算法的运行，狼群不断重新排列，从而适应不断变化的环境。

布谷鸟优化算法（COAm）是一种最新的启发式算法，其灵感来源于大自然。它的依据是一些杜鹃物种的寄生性。
COAm 算法的主要特点：

模拟布谷鸟行为。该算法采用布谷鸟的繁殖策略，即布谷鸟在其他鸟类的巢中产卵。
搜索全局最大值。巢中的蛋被理解为优化问题的可能解决方案，而杜鹃蛋则代表新的解决方案。
适应性强。如果杜鹃蛋的质量比亲蛋高，就会被替换掉。否则，亲卵就会留在巢中。

因此，将这些算法混合起来，大概可以利用它们的综合优势更高效地解决优化问题。图 1 显示了 GWO 和 COAm 运行的顺序图。第一阶段完成后，当一些迭代被分配给 GWO 时，一种算法的代理状态会转移到另一种算法。每个代理都会重生为一个新的物种（在本例中，狼变成了杜鹃），个体在种群中的地位得以保持。

GWOCOA

图 1.混合算法，GWO+COA

让我们来看看事件的可能发展过程：

1.开始：
   - 我们从 10,000 次迭代开始，这是有限的资源，因此每次迭代对实现最优解都至关重要。
2.步骤 1（0-5000 次迭代）：
   - 将迭代总数对半分，从 GWO 算法开始。
   - 由于 "狼群 "在搜索空间内迅速扩散，它们很快就会在这一时期中期收敛到一个潜在的全局极值。
3.第 2 步（5000-10000 次迭代）：
   - 在最初的 5000 次迭代之后，我们将狼的位置与杜鹃在这些点上的位置相一致。
   - 布谷鸟搜索与列维飞行接过指挥棒，进一步完善极值。
4.结果：
- 通过将 GWO 算法和带有列维飞行的布谷鸟搜索相结合，我们有望在有限的迭代次数内获得更精确、更稳定的全局极值。

因此，使用这种策略可以在有限的迭代次数内优化全局极值搜索，确保收敛速度和结果精度之间的平衡。

声明 "C_AO_GWO_COAm" 类，它是 "C_AO" 类的继承者。该类的构造函数设置了优化参数的默认值，如 "popSize" 群体大小和 GWO 算法与 COAm 算法之间的 "ratio" 比率。这个类将允许使用两种算法的顺序操作，而处理方法将保持不变，并允许我们使用我们的测试台而不做任何改动。

该类还定义了用于设置参数 (SetParams)、初始化优化 (Init)、移动 (Moving) 和更新 (Revision) 全局解决方案以及向代理插入 (Injection) 坐标值的方法。

该类中的重要变量包括 "ratio"（GWO 和 COAm 之间的比率），以及 C_AO_GWO 和 C_AO_COAm 类对象，分别用于实现灰狼优化算法和布谷鸟优化算法。

该类还有一些变量，用于跟踪每种算法（GWO 和 COAm）的 epoch 数和当前 epoch。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_GWO_COAm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_GWO_COAm () { }
  C_AO_GWO_COAm ()
  {
    ao_name = "GWO_COAm";
    ao_desc = "Grey Wolf Optimizer and Cuckoo Optimization Algorithm M";

    popSize = 50;    //population size
    ratio   = 0.5;   //the ratio of GWO and COAm

    ArrayResize (params, 2);

    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "ratio";   params [1].val = ratio;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    ratio   = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving    ();
  void Revision  ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  double ratio;  //the ratio of GWO and COAm

  private: //-------------------------------------------------------------------
  C_AO_GWO  AO1;
  C_AO_COAm AO2;

  int epochCount;
  int epochNow;

  int epochGWO;
  int epochCOAm;
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_GWO_COAm 类中的 Init 方法用于初始化优化过程。在此设置初始值，创建代理，并为 GWO 和 COAm 算法设置初始化参数。

标准初始化的成功与否可通过 StandardInit 方法进行验证，该方法使用传递的参数设置最小和最大搜索范围。
GWO 和 COAm 算法各自的 epoch 数是根据 "ratio" 和 epoch 总数（epochCount）计算得出的。
GWO 和 COAm 算法的参数通过 SetParams 和 Init 方法进行设置和初始化。
如果初始化成功，该方法返回 "true"。

该方法提供了 GWO 和 COAm 算法的初始设置和初始化，以便在给定参数和约束条件下优化问题。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_GWO_COAm::Init (const double &rangeMinP  [], //minimum search range
                          const double &rangeMaxP  [], //maximum search range
                          const double &rangeStepP [], //step search
                          const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochCount   = epochsP;
  epochNow     = 0;

  epochGWO  = int(epochCount *ratio);
  epochCOAm = epochCount - epochGWO;

  AO1.params [0].val = popSize;
  AO2.params [0].val = popSize;

  AO1.SetParams ();
  AO2.SetParams ();

  AO1.Init (rangeMinP, rangeMaxP, rangeStepP, epochGWO);
  AO2.Init (rangeMinP, rangeMaxP, rangeStepP, epochCOAm);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

在 C_AO_GWO_COAm 类的 Moving 方法代码中，"epochNow" 变量的值会增加 1。"epochNow" 计数器用于确定 GWO 和 COAm 分别运行的阶段。

如果 "epochNow" 小于 "epochGWO"，则调用 AO1 (GWO) 对象的 Moving 方法，然后将 "AO1.a" 代理数组中的元素复制到 "a" 代理数组中。

如果 "epochNow" 等于 "epochGWO"，则在 "AO2"（COAm）对象上调用 Moving 方法，然后将 "AO1.a" 数组中的值插入到 "AO2.a" 数组的相应元素中，也就是说，这就是狼变杜鹃的过程。最后，"AO2.a" 数组中的所有元素都被复制到 "a" 数组中，以便访问执行程序中的 "a" 代理。

这种方法可确保代理在每个优化时间段按照所选的 GWO 和 COAm 算法顺序移动。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Moving ()
{
  epochNow++;

  if (epochNow < epochGWO)
  {
    AO1.Moving ();
    for (int i = 0; i < popSize; i++)
    {
      a [i] = AO1.a [i];
    }
    return;
  }

  AO2.Moving ();

  if (epochNow == epochGWO)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        AO2.Injection (i, c, AO1.a [i].c [c]);
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    a [i] = AO2.a [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

Revision 方法将计算出的代理适应度值传送给算法的相应代理。

根据 "epochNow" 和 "epochGWO" 变量的值，将对 GWO 或 COAm 算法执行以下操作：

将适应度值复制给代理。
执行 Revision 方法。
执行全局解决方案更新。

因此，该方法实现了根据相应算法当前执行阶段，用 GWO 和 COAm 算法的解决方案更新全局解决方案的逻辑。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Revision ()
{
  if (epochNow < epochGWO)
  {
    for (int i = 0; i < popSize; i++) AO1.a [i].f = a [i].f;

    AO1.Revision ();

    if (AO1.fB > fB)
    {
      fB = AO1.fB;
      ArrayCopy (cB, AO1.cB, 0, 0, WHOLE_ARRAY);
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++) AO2.a [i].f = a [i].f;

    AO2.Revision ();

    if (AO2.fB > fB)
    {
      fB = AO2.fB;
      ArrayCopy (cB, AO2.cB, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

混合算法运行的可视化突出了以下现象：GWO 经常陷入局部极值，过早停止快速运动。相比之下，COA 算法会留下各种不同的结果，有时会产生一系列令人印象深刻的终点。

Hilly

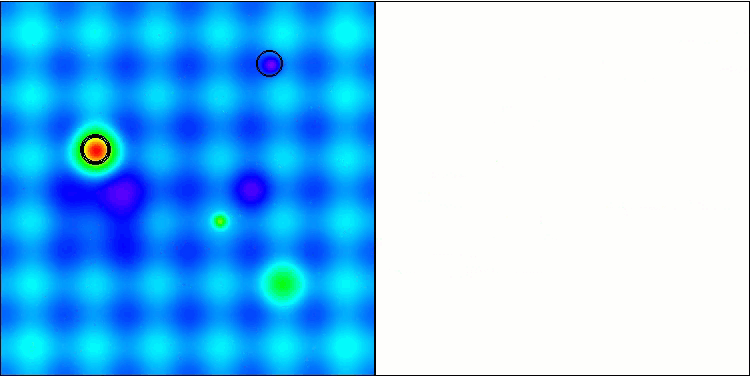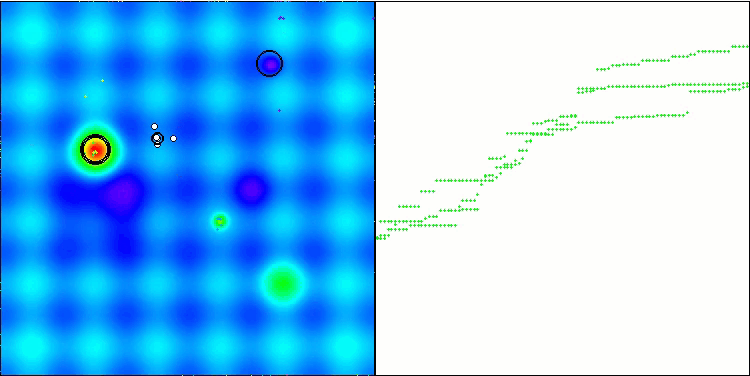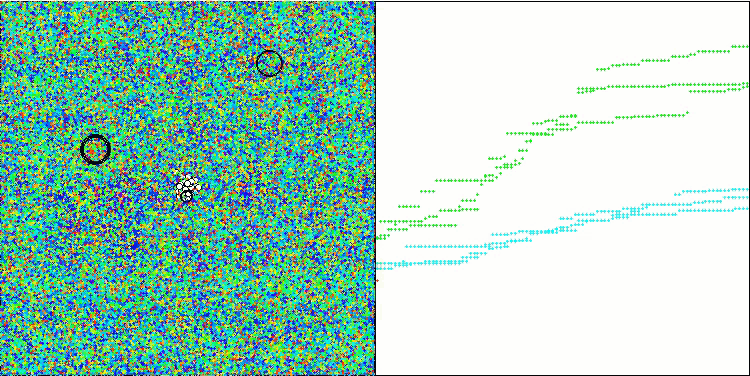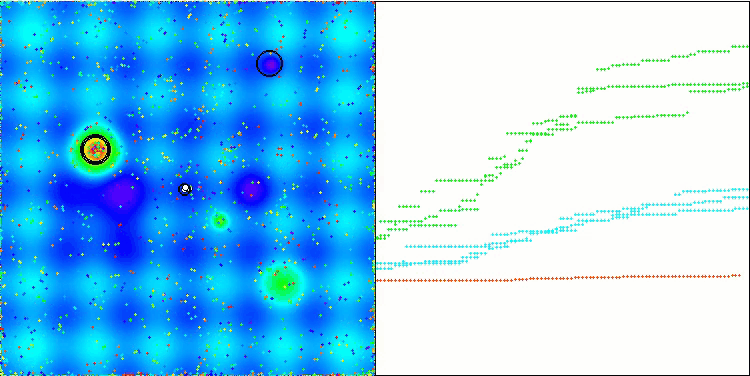
GWO-COAm 上的 Hilly 测试函数

Forest

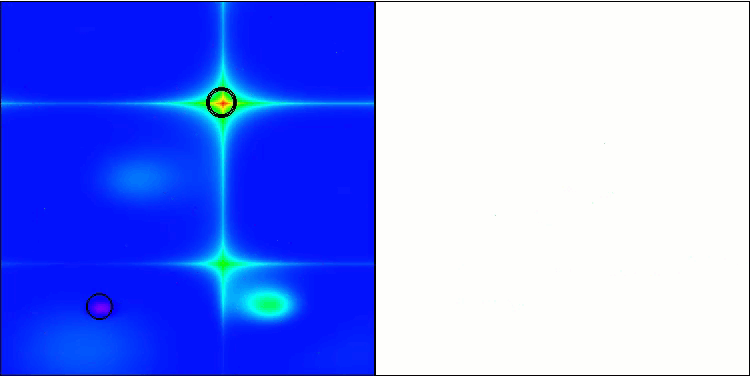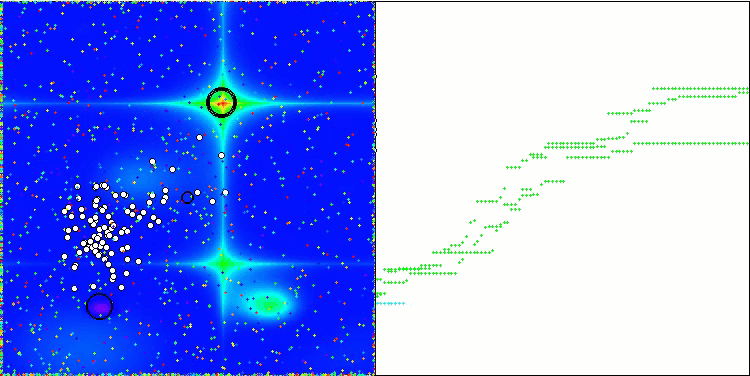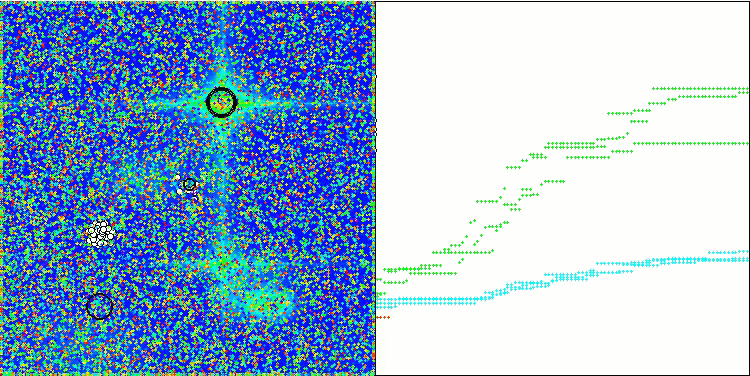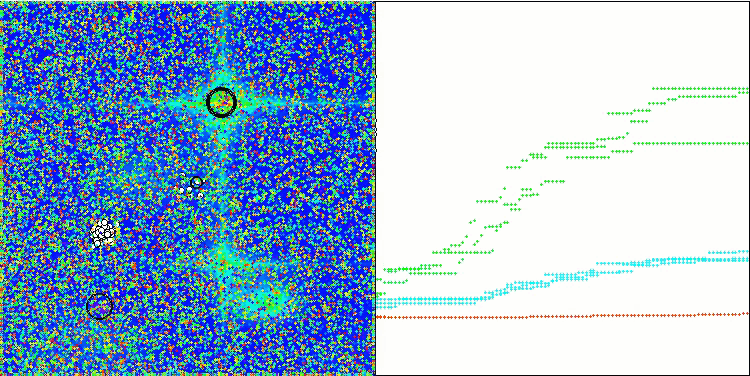
GWO-COAm 上的 Forest 测试函数

Megacity

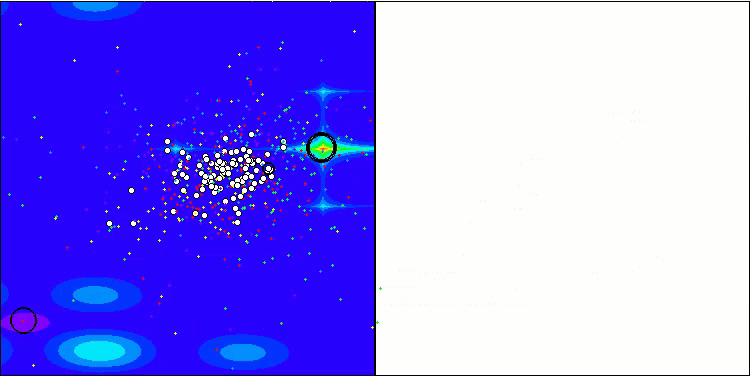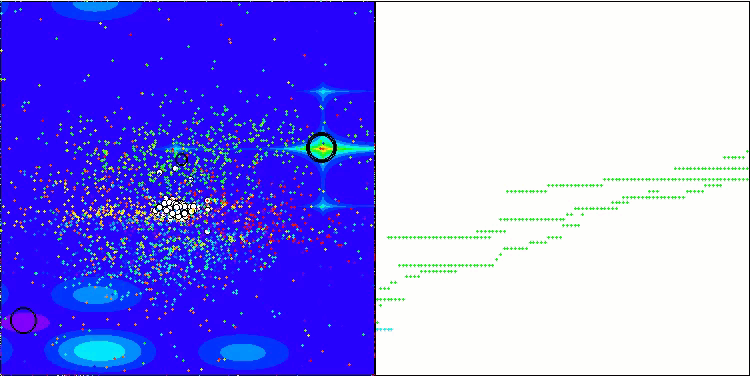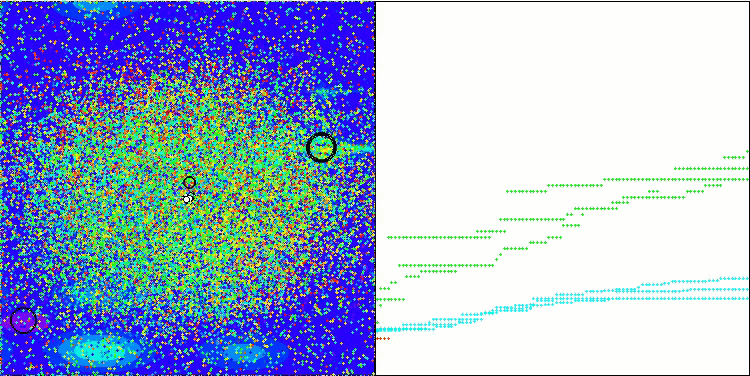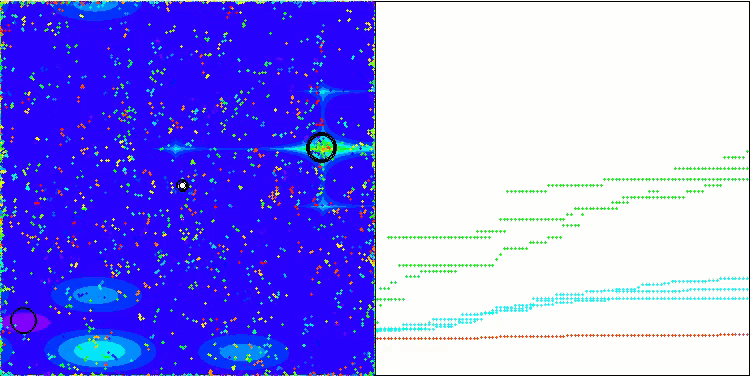
GWO-COAm 上的 Megacity 测试函数

因此，我们进行了一项实验，试图通过依次结合 GWO 和 COAm 算法来创建一种混合算法。然而，这并没有带来预期的结果（提高最佳性能）。GWO 经常陷入局部最大值而停止前进，而 COAm 算法则无法接过接力棒，其特点是最终结果有很大的分散性，这取决于实验运行的次数。

GWO-COAm 试验台结果（顺序结构）：

GWO_COAm|Grey Wolf Optimizer and Cuckoo Optimization Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs:10000; result：0.729041499138184
25 Hilly's；Func runs：10000; result：0.4465971838522985
500 Hilly's；Func runs：10000; result：0.2685674823439256
=============================
5 Forest's; Func runs：10000; result：0.6963174902735325
25 Forest's; Func runs：10000; result：0.347940898514357
500 Forest's; Func runs：10000; result：0.16776831572853218
=============================
5 Megacity's; Func runs:10000; result：0.5492307692307692
25 Megacity's; Func runs:10000; result：0.2464615384615385
500 Megacity's；Func runs：10000; result：0.10724615384615484
=============================
All score:3.55917 (39.55%)

其结果与 COAm 单独运行的结果相当。情况有所改善，但遗憾的是，这种改善微不足道。不过，在单独的独立运行中，COAm 有时会产生类似的结果。

让我们尝试创建一种混合方法，将并行工作与每次迭代交换两个算法的代理的最佳位置结合起来，这两个算法不仅会独立工作，还会为了共同的目标相互交换最佳解决方案。

现在，让我们尝试使用 GWO 和 COAm 算法的并行操作。为此，我们实际上不必改变联合算法的类。我只提供需要进行重大修改的方法的代码。

与顺序结构不同，这里我们同时启动了两种算法的 Moving 方法。之后，将这些算法的代理复制到组合类的代理中，以便进行后续的适应度函数计算。因此，该方法将两个对象 "AO1" 和 "AO2" 的数据合并到当前对象数组 "a" 中。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Moving ()
{
  AO1.Moving ();
  AO2.Moving ();

  int cnt = 0;
  for (int i = 0; i < popSize / 2; i++)
  {
    a [cnt] = AO1.a [i];
    cnt++;
  }

  for (int i = 0; i < popSize / 2; i++)
  {
    a [cnt] = AO2.a [i];
    cnt++;
  }
}
//——————————————————————————————————————————————————————————————————————————————

并行操作结构的 Moving 方法的区别如下：在将适应度值传输给 "AO1" 和 "AO2" 对象代理、执行其 Revision 方法并更新全局解之后，代理成对地从一种算法复制到另一种算法。这意味着两个最佳代理在算法之间交换，这有助于两个算法丰富彼此的最佳特性，提高解决问题的性能。这种方法允许共享每种算法取得的最佳解决方案。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Revision ()
{
  int cnt = 0;

  for (int i = 0; i < popSize / 2; i++)
  {
    AO1.a [i].f = a [cnt].f;
    cnt++;

    if (AO1.a [i].f > fB)
    {
      fB = AO1.a [i].f;
      ArrayCopy (cB, AO1.a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  for (int i = 0; i < popSize / 2; i++)
  {
    AO2.a [i].f = a [cnt].f;
    cnt++;

    if (AO2.a [i].f > fB)
    {
      fB = AO2.a [i].f;
      ArrayCopy (cB, AO2.a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  AO1.Revision ();
  AO2.Revision ();
  
  S_AO_Agent temp [];
  ArrayResize (temp, popSize / 2);
  
  for (int i = 0; i < 2; i++) temp [i] = AO1.a [i]; 

  for (int i = 0; i < 2; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      AO1.Injection (i, coords - 1, AO2.a [i].c [c]);
      AO2.Injection (i, coords - 1, temp  [i].c [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

GWO-COAm 试验台结果（并行结构）：

GWO_COAm|Grey Wolf Optimizer and Cuckoo Optimization Algorithm M|50.0|
=============================
5 Hilly's; Func runs:10000; result：0.6930620289919492
25 Hilly's；Func runs：10000; result：0.4389512737634269
500 Hilly's；Func runs：10000; result：0.26733735583025275
=============================
5 Forest's; Func runs：10000; result：0.6512995888741085
25 Forest's; Func runs：10000; result：0.33119611021722106
500 Forest's; Func runs：10000; result：0.16858175021299981
=============================
5 Megacity's; Func runs:10000; result：0.4615384615384615
25 Megacity's; Func runs:10000; result：0.23015384615384615
500 Megacity's；Func runs：10000; result：0.1059538461538471
=============================
All score:3.34807 (37.20%)

遗憾的是，性能没有提高。

3.使用 ESG 和 SDSm 做实验

在上文讨论的 GWO 和 COAm 杂交选项中，使用了不同 "权重类别" 的算法。合理的做法是，使用功能相近的算法，使它们真正实现互补。因此，我们将使用顺序结构和并行结构再进行两次实验。为此，我们将使用 ESG 和 SDSm 算法。

将这两种算法结合成一种混合算法，可以创造出随机性和社会动力的独特组合。

随机扩散搜索（（SDSm）是一种群体优化算法。

算法的主要特点：

对解决方案进行部分评估。代理对假设（搜索问题的候选解决方案）进行部分评估，从而降低了算法的计算复杂度。
分发有前景的解决方案。代理通过直接的个体交流交换有关假设的信息。高质量的解决方案可以从具有相同假设的代理群中识别出来。
数学理由。SDSm 具有深厚的数学基础，因此更加可靠和可预测。

SDSm 是一种进化优化方法，它将随机搜索和扩散相结合，用于解决高维空间中的优化问题。

社会群体进化（ESG）是一种多群体优化算法。

算法的主要特点：

社会团体 - 该算法的运行对象不是单个粒子，而是通过合作和经验交流联合起来的社会群体。每个小组都有自己的决策中心和一组作为优化代理的粒子。
集体运动 - 社会群体中的粒子在参数空间中相互作用、共同运动。这样，各小组就可以探索参数空间的不同区域，并分享找到的最佳解决方案的信息。
本地和全局经验 - 每个社会群体都会存储其内部最佳解决方案的信息（本地经验）。在所有组别中，还有一个总体得分最高的组别（全局经验）。

ESG 架构简单，收敛性高，计算要求低。

进行顺序操作和并行操作实验的代码与上述代码完全相同，只是我们需要替换这些类的相应对象的声明，而不是 GWO 和 COAm。

ESG-SDSm 测试台结果（顺序结构）：

ESG_SDSm|Evolution_of_Social_Groups and Stochastic Diffusion Search M|200.0|0.5|
=============================
5 Hilly's; Func runs:10000; result：0.9642488921252973
25 Hilly's；Func runs：10000; result：0.7526240638447592
500 Hilly's；Func runs：10000; result：0.2961693434072249
=============================
5 Forest's; Func runs：10000; result：0.9897783503200446
25 Forest's; Func runs：10000; result：0.7608845505131734
500 Forest's; Func runs：10000; result：0.2130287247171918
=============================
5 Megacity's; Func runs:10000; result：0.82
25 Megacity's; Func runs:10000; result：0.5421538461538462
500 Megacity's；Func runs：10000; result：0.11932307692307798
=============================
All score:5.45821 (60.65%)

ESG-SDSm 试验台结果（并行结构）：

ESG_SDSm|Evolution_of_Social_Groups and Stochastic Diffusion Search M|200.0|
=============================
5 Hilly's; Func runs:10000; result：0.9561232188424761
25 Hilly's；Func runs：10000; result：0.7493199026465321
500 Hilly's；Func runs：10000; result：0.3176797705433513
=============================
5 Forest's; Func runs：10000; result：0.9726744619317564
25 Forest's; Func runs：10000; result：0.7494321306074204
500 Forest's; Func runs：10000; result：0.22498291462144127
=============================
5 Megacity's; Func runs:10000; result：0.836923076923077
25 Megacity's; Func runs:10000; result：0.5261538461538462
500 Megacity's；Func runs：10000; result：0.13435384615384738
=============================
All score:5.46764 (60.75%)

结果表明，顺序和并行混合结构的结果非常接近随机算法的通常误差。它们略低于这些算法的单独运算结果。

4.总结

本文所探讨的混合算法是为了覆盖当前排名表中的不同位置，并了解每种算法的不同性能对总体结果的影响。算法的搜索能力大致相等是否重要，以确保对其对最终结果的影响进行平衡分析和公平比较？

在本文中，我们将各种优化算法视为混合算法的组成部分。我们的目标是涵盖在当前排名表中占据不同位置的各种算法，以找出每种算法的不同性能对整体结果的影响。

算法在搜索能力上大致相等是否重要仍然是一个悬而未决的问题。如果主要目标是找到最佳解决方案，这可能并不重要。

在实验中，我们选择了能力差异很大的算法，如 GWO 和 COA。这些算法代表了两种不同的优化方法，将它们结合起来可以为我们提供宝贵的经验。作为比较，我们还选择了性能非常相似的算法，如 ESG 和 SDSm。

以下是当前的算法评级表。它包括我们讨论过的所有算法，并将随着新数据的出现而更新。

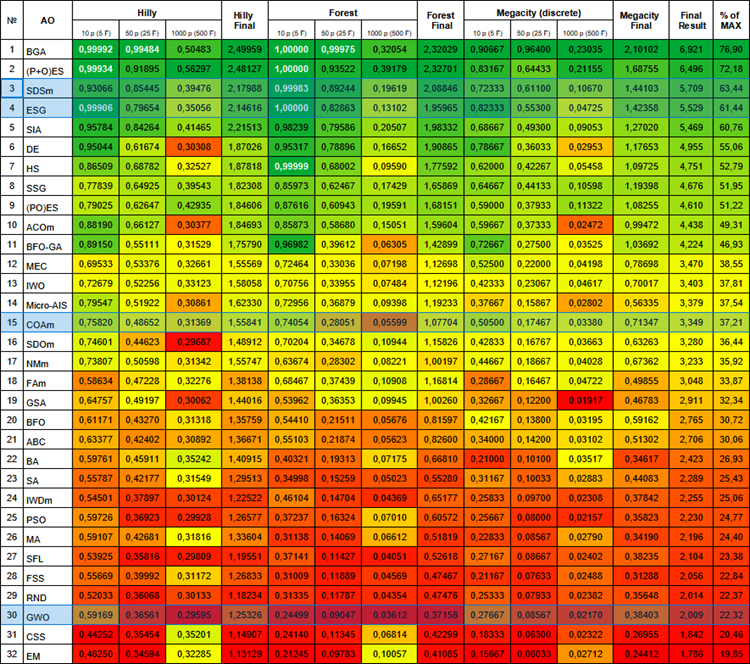
群体算法评级表

当我们试图创建一种混合方法，将 ESG 和 SDSm 算法代理的并行工作和最佳位置交换以及顺序结构结合起来时，我们遇到了一个模糊的现象。在研究过程中，我们发现将这两种方法结合在一起，并没有产生协同效应和增强效果，而是产生了一般的结果。很可能是这些不同策略之间的互动不够有效，妨碍了其核心原则的充分整合。

实验结果表明，在这些条件下，顺序混合结构和并行混合结构都无法获得理想的结果，这凸显了精心选择算法以实现成功组合的重要性。算法最初必须具备某些特质：要么搜索效果好，要么不够精细，反之亦然。只有在这种情况下，混合方法才能提高两种算法的性能。通过融合算法逻辑（根据第一种结构）进行混合的成功经验突显了这种方法的潜力，然而，它需要付出不平凡的努力、仔细的干预和联合融合逻辑的发展来实现最佳结果。

这一观察结果不仅强调了算法的个体特征的重要性，还强调了它们在混合背景下的相互作用的重要性。就像在自然界中，不同物种的组合可以导致独特的适应一样，在优化的世界里，算法的组合需要微调和协调。也许，正是在意想不到的组合和失败的尝试中，我们找到了优化领域新发现和新改进的钥匙。

这一经验凸显了在创建混合优化方法时仔细分析和选择算法的重要性。不仅要考虑每种算法的各自特点，还要考虑它们在特定任务框架内的相互作用，这样才能在寻找最佳解决方案方面取得成功。

尝试、实验、创造和组合。一如既往，所有工具和源代码都附在下面。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/14389

附加的文件 |

下载ZIP

The_world_of_AO_Hybrid.zip (41 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。