Redes neurais em trading: Segmentação de dados com base em expressões de referência

Introdução

3D Referring Expression Segmentation (3D-RES) é uma área crescente no campo multimodal, que vem despertando grande interesse entre os pesquisadores. Essa tarefa tem como objetivo segmentar instâncias-alvo com base em expressões fornecidas em linguagem natural. No entanto, os métodos tradicionais de 3D-RES são limitados a casos com um único alvo, o que restringe significativamente sua aplicação prática. Em cenários reais, as instruções muitas vezes resultam em situações onde o alvo não é encontrado, ou é necessário identificar vários alvos ao mesmo tempo. Essa realidade representa um desafio que os modelos existentes de 3D-RES não conseguem resolver. Para preencher essa lacuna, os autores do trabalho "3D-GRES: Generalized 3D Referring Expression Segmentation" propuseram um novo método Generalized 3D Referring Expression Segmentation (3D-GRES), projetado para interpretar instruções que indicam uma quantidade arbitrária de alvos.

A principal tarefa do 3D-GRES é identificar com precisão vários alvos dentro de um grupo de objetos semelhantes. A chave para resolver esse tipo de problema está na divisão da tarefa, permitindo que várias consultas processem simultaneamente a localização de uma instrução linguística com múltiplos objetos. Cada consulta é responsável por uma instância específica dentro de uma cena com vários objetos. Os autores do 3D-GRES propuseram o módulo Multi-Query Decoupled Interaction Network (MDIN), que facilita a interação entre consultas, superpontos e texto. Para lidar de forma eficaz com um número arbitrário de alvos, foi adicionado um mecanismo que permite que várias consultas se dividam e colaborem na geração de resultados com múltiplos objetos. Cada consulta, por sua vez, é responsável por um alvo em uma instância com múltiplos objetos.

Para garantir uma cobertura uniforme das metas principais no conjunto de pontos pelos queries treináveis, os autores do método apresentaram um novo módulo de queries esparsos (TSQ), baseado no texto das expressões de referência. Além disso, para alcançar simultaneamente a capacidade de distinção entre as queries e manter a coerência semântica geral, foi desenvolvida uma estratégia de otimização com separação de múltiplos objetos (MDO). Essa estratégia divide a máscara com múltiplos objetos em supervisões individuais de objetos únicos, preservando a capacidade de distinção de cada query. A ligação entre a função das queries e as características dos superpontos na cena do conjunto de pontos com a semântica do texto garante a coerência semântica entre vários alvos.

1. Algoritmo 3D-GRES

A tarefa clássica de 3D-RES é focada na criação de uma máscara 3D para um único objeto-alvo dentro de uma cena de conjunto de pontos, guiada por uma expressão de referência. Essa tarefa tradicional possui limitações importantes. Primeiro, ela não se aplica a cenários onde nenhum objeto da cena corresponde à expressão fornecida. Segundo, ela não contempla casos em que múltiplos objetos correspondem aos critérios descritos. Esse descompasso significativo entre as capacidades do modelo e sua aplicabilidade no mundo real limita o uso prático das tecnologias 3D-RES. 

Para superar essas limitações, foi proposto o método Generalized 3D Referring Expression Segmentation (3D-GRES), voltado para a identificação de uma quantidade arbitrária de objetos a partir de descrições textuais. O 3D-GRES analisa a cena 3D do conjunto de pontos P e a expressão textual de referência E. Como resultado, são geradas máscaras 3D correspondentes M, que podem estar vazias, ou conter um ou mais objetos. O método proposto permite encontrar vários objetos com o uso de expressões multiobjetivo e verificar a existência de objetos específicos na cena através de expressões como “nothing”, proporcionando maior flexibilidade e confiabilidade na extração de objetos e interação.

O 3D-GRES inicialmente processa as expressões de referência originais, codificando-as em tokens textuais 𝒯 usando o modelo pré-treinado RoBERTa. Para facilitar o alinhamento multimodal, os objetos codificados são então projetados em um espaço multimodal de dimensionalidade D. A esses tokens obtidos é adicionado um codificador posicional.

Para o conjunto de pontos original com posições P e características F, os Superpoints são extraídos por meio de uma 3D U-Net esparsa, sendo então projetados no espaço multimodal de dimensão D.

A Multi-Query Decoupled Interaction Network (MDIN) utiliza múltiplas queries para processar instâncias separadas em cenas com múltiplos alvos, unificando-as em um resultado final. Para cenas sem objetos-alvo definidos, as previsões são feitas com base nas pontuações de confiança de cada query, sendo os indicadores de alvo definidos como zero quando todas as queries apresentam baixa pontuação.

MDIN é composto por vários módulos idênticos, cada um contendo os módulos de agregação Query-Superpoint (QSA) e de agregação de expressões linguísticas com Query (QLA), que facilitam a interação entre Query, Superpoint e o texto. Ao contrário dos modelos que analisamos anteriormente, que utilizam inicialização aleatória das Query, o MDIN utiliza o módulo de queries esparsos (TSQ), orientado por texto, para gerar Query esparsas, garantindo uma cobertura eficaz da cena. Para dar suporte a múltiplas queries, é implementada a estratégia de otimização com separação de múltiplos objetos (MDO).

A Query pode ser vista como uma âncora na cena do conjunto de pontos. Durante a interação da Query com o Superpoint, elas capturam informações globais da cena do conjunto de pontos. É importante destacar que os superpontos selecionados individualmente atuam como queries no processo de interação, o que proporciona uma agregação local mais forte. Essa orientação local cria condições favoráveis para a separação das queries.

Inicialmente, calcula-se a distribuição de similaridade entre a característica do superponto S e o embedding das queries Qf. Em seguida, as queries agregam os superpontos relacionados com base nas distribuições de similaridade. A cena atualizada, considerando Qs, é então alimentada no módulo QLA para modelar a interação Query-Query e Query-Language. O QLA é composto por um bloco de Self-Attention para as funções das queries Qs e uma atenção cruzada multimodal que modela as dependências entre cada palavra e cada query.

Depois disso, a função das queries considerando as relações Qr, as funções considerando a linguagem Ql e as funções das queries com base na cena Qs são somadas e fundidas com o uso de uma MLP.

Para alcançar uma distribuição esparsa das queries inicializadas dentro da cena do conjunto de pontos, preservando ao máximo as informações geométricas e semânticas, os autores do 3D-GRES aplicam a técnica de amostragem dos pontos mais distantes diretamente nos Superpoints.

Para melhorar a separação das queries e atribuí-las a objetos distintos, os autores do método utilizam os atributos internos das queries geradas pelo TSQ. Cada query se origina de um superponto no conjunto de pontos, o que naturalmente a associa a um objeto específico. As queries voltadas para instâncias-alvo são responsáveis pela segmentação dessas instâncias, enquanto as instâncias não relacionadas são atribuídas à query mais próxima. Esse método emprega restrições visuais preliminares para desvincular as queries e associá-las a objetos distintos.

A visualização desenvolvida pelos autores para o método 3D-GRES é apresentada abaixo.

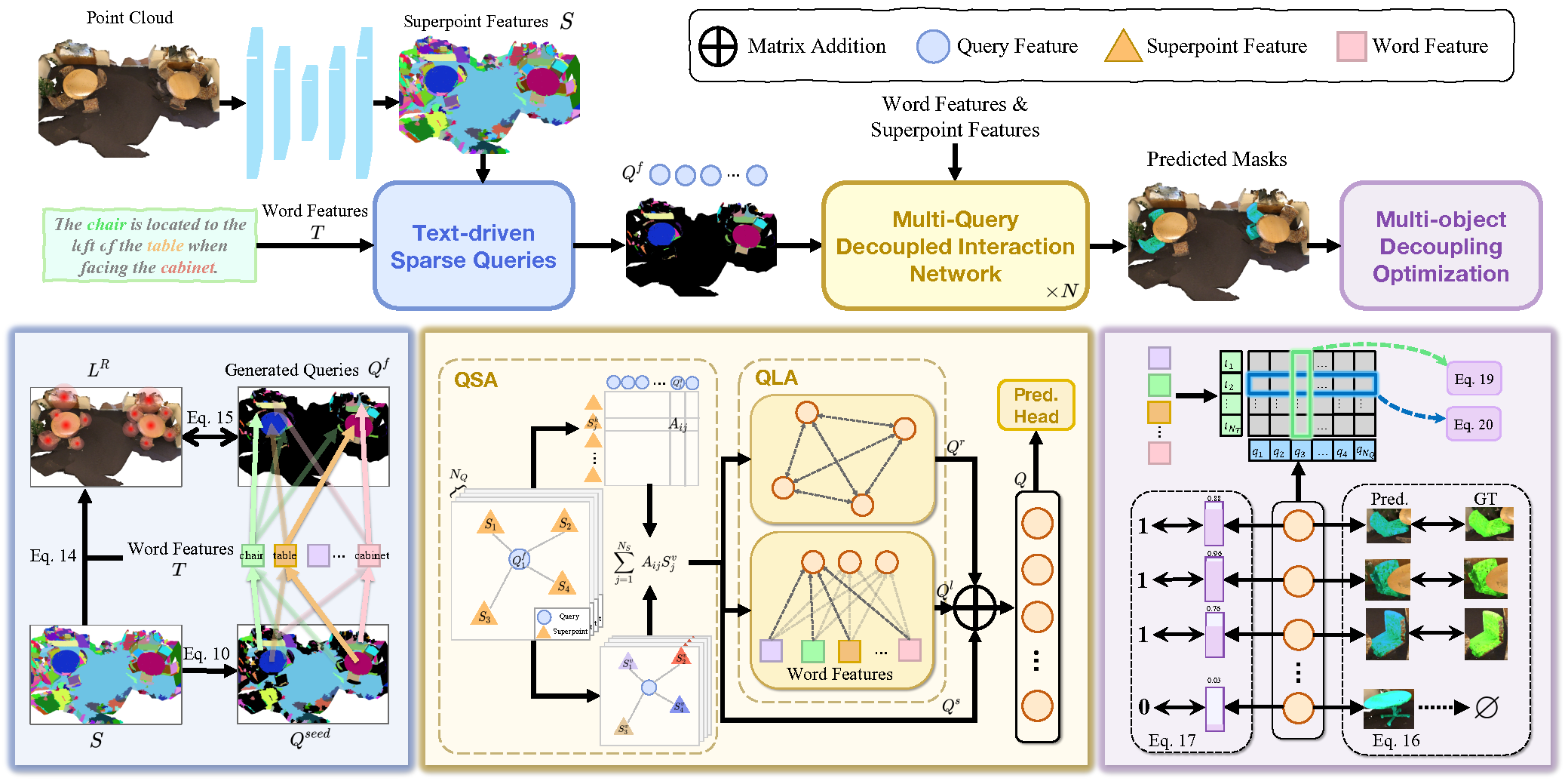
2. Implementação com MQL5

Após explorarmos os aspectos teóricos do método 3D-GRES, passamos agora à parte prática do nosso artigo, onde vamos implementar nossa visão dos conceitos propostos utilizando os recursos do MQL5. E antes de tudo, vamos refletir sobre o que diferencia o algoritmo proposto dos métodos que analisamos anteriormente. E o que eles têm em comum.

Claro, o principal diferencial está na natureza multimodal do método 3D-GRES. Pela primeira vez, nos deparamos com expressões textuais de referência, que têm o objetivo de tornar nossa análise mais direcionada. E sem dúvida, vamos aproveitar essa proposta. Apenas não utilizaremos um modelo de linguagem; em vez disso, para definição da tarefa, alimentaremos o modelo com informações sobre o estado da conta e as posições abertas. Dessa forma, proporemos ao modelo, com base no embedding do estado da conta, que ele procure pontos de entrada ou saída.

Outro ponto que merece atenção. O 3D-GRES, assim como os modelos analisados anteriormente, utiliza um conjunto de queries treináveis. Mas há uma diferença no princípio de sua formação. SPFormer e MAFT utilizavam queries estáticas, que eram otimizadas durante o treinamento e permaneciam inalteradas durante a fase de execução do modelo. Assim, o modelo decorava certos padrões e depois atuava segundo um 'esquema pré-programado'. Já os autores do 3D-GRES propõem formar as queries com base nos dados brutos, tornando-as mais locais e dinâmicas. E para uma cobertura máxima do espaço da cena analisada, são aplicadas diversas heurísticas. Também vamos adotar essa ideia.

Além disso, o método 3D-GRES utiliza codificação posicional de tokens. Isso o aproxima do método MAFT, que foi o ponto de partida na escolha da classe pai para nossa implementação. E começamos nosso trabalho complementando o programa OpenCL.

2.1 Diversificação das queries

Para garantir uma cobertura máxima do espaço da cena com queries treináveis, introduzimos um erro de diversificação, que tem o objetivo de 'repelir' as queries entre si:

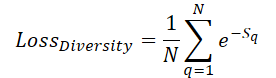
Aqui, Sq indica a distância até a query q. É evidente que, para S=0, o erro é igual a 1. E à medida que a distância média entre as queries aumenta, o erro tende a '0'. Assim, durante o treinamento, o modelo irá distribuir as queries de forma mais uniforme.

No entanto, o que nos interessa não é tanto o valor do erro, mas sim a direção de ajuste dos parâmetros das queries no sentido de afastá-las ao máximo das demais. Por isso, na nossa implementação, calculamos diretamente o gradiente do erro e o somamos ao fluxo principal de distribuição do erro da execução do modelo, com posterior otimização dos parâmetros. O algoritmo descrito será implementado no kernel DiversityLoss.

Nos parâmetros desse kernel, vamos passar ponteiros para 2 buffers globais de dados e 2 variáveis. O primeiro buffer de dados contém as características atuais das queries, e no segundo vamos armazenar o gradiente do erro de diversificação. 

__kernel void DiversityLoss(__global const float *data,
                            __global float *grad,
                            const int activation,
                            const int add
                           )
  {
   const size_t main = get_global_id(0);
   const size_t slave = get_local_id(1);
   const size_t dim = get_local_id(2);
   const size_t total = get_local_size(1);
   const size_t dimension = get_local_size(2);

Nosso kernel irá operar em um espaço de tarefas tridimensional. As duas primeiras dimensões correspondem ao número de queries analisadas, enquanto a terceira define a dimensionalidade do vetor de características de cada query. Para minimizar o acesso à memória global, que é mais lenta, vamos agrupar os fluxos em grupos de trabalho com base nas duas últimas dimensões do espaço de tarefas.

No corpo do kernel, como de costume, primeiro identificamos o fluxo de trabalho dentro do espaço de tarefas em todas as dimensões. Depois, declaramos um array na memória local para troca de dados entre os fluxos individuais do grupo de trabalho.

   __local float Temp[LOCAL_ARRAY_SIZE];

E definimos o deslocamento nos buffers globais de dados até os valores que vamos analisar.

   const int shift_main = main * dimension + dim;
   const int shift_slave = slave * dimension + dim;

Em seguida, carregamos os valores dos buffers globais de dados e calculamos a diferença entre eles.

   const int value_main = data[shift_main];
   const int value_slave = data[shift_slave];
   float delt = value_main - value_slave;

Observe que o espaço de tarefas e os grupos de trabalho foram organizados de forma que cada fluxo leia apenas 2 valores da memória global. A seguir, precisamos calcular a soma das distâncias de todos os fluxos. Para isso, primeiro organizamos um laço que acumula a soma dos valores individuais nos elementos do array local.

   for(int d = 0; d < dimension; d++)
     {
      for(int i = 0; i < total; i += LOCAL_ARRAY_SIZE)
        {
         if(d == dim)
           {
            if(i <= slave && (i + LOCAL_ARRAY_SIZE) > slave)
              {
               int k = i % LOCAL_ARRAY_SIZE;
               float val = pow(delt, 2.0f) / total;
               if(isinf(val) || isnan(val))
                  val = 0;
               Temp[k] = ((d == 0 && i == 0) ? 0 : Temp[k]) + val;
              }
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
     }

E aqui vale destacar que, inicialmente, salvamos a diferença simples entre os dois valores na variável delt. Só antes de somar a distância ao array local é que elevamos essa diferença ao quadrado. Isso acontece porque a derivada da nossa função de perda utiliza diretamente essa diferença. E mantemos esse valor para evitar o recálculo.

Na próxima etapa, vamos reunir a soma de todos os valores do nosso array local.

   const int ls = min((int)total, (int)LOCAL_ARRAY_SIZE);
   int count = ls;
   do
     {
      count = (count + 1) / 2;
      if(slave < count)
        {
         Temp[slave] += ((slave + count) < ls ? Temp[slave + count] : 0);
         if(slave + count < ls)
            Temp[slave + count] = 0;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Somente então calculamos o valor do erro de diversificação da query analisada e o gradiente de erro do elemento correspondente.

   float loss = exp(-Temp[0]);
   float gr = 2 * pow(loss, 2.0f) * delt / total;
   if(isnan(gr) || isinf(gr))
      gr = 0;

Em seguida, vamos iniciar o processo interessante de acumular os gradientes de erro para cada característica da query analisada. O algoritmo de soma dos gradientes de erro é similar ao que descrevemos acima para a soma das distâncias.

   for(int d = 0; d < dimension; d++)
     {
      for(int i = 0; i < total; i += LOCAL_ARRAY_SIZE)
        {
         if(d == dim)
           {
            if(i <= slave && (i + LOCAL_ARRAY_SIZE) > slave)
              {
               int k = i % LOCAL_ARRAY_SIZE;
               Temp[k] = ((d == 0 && i == 0) ? 0 : Temp[k]) + gr;
              }
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      //---
      int count = ls;
      do
        {
         count = (count + 1) / 2;
         if(slave < count && d == dim)
           {
            Temp[slave] += ((slave + count) < ls ? Temp[slave + count] : 0);
            if(slave + count < ls)
               Temp[slave + count] = 0;
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      if(slave == 0 && d == dim)
        {
         if(isnan(Temp[0]) || isinf(Temp[0]))
            Temp[0] = 0;
         if(add > 0)
            grad[shift_main] += Deactivation(Temp[0],value_main,activation);
         else
            grad[shift_main] = Deactivation(Temp[0],value_main,activation);
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
  }

Observe que o algoritmo descrito acima combina as iterações da propagação para frente e da propagação reversa. Isso nos permite utilizá-lo apenas durante o treinamento do modelo e eliminar essas operações durante a execução, o que impacta diretamente no tempo de tomada de decisão.

Com isso, encerramos o trabalho com o programa OpenCL e passamos à construção da nossa classe de implementação dos conceitos do método 3D-GRES.

2.2 Classe do método 3D-GRES

Para implementar os conceitos propostos pelos autores do método 3D-GRES, no lado do programa principal, vamos criar um novo objeto CNeuronGRES. Como mencionado anteriormente, a funcionalidade básica será herdada da classe CNeuronMAFT. A estrutura da nova classe é apresentada abaixo.

class CNeuronGRES :  public CNeuronMAFT
  {
protected:
   CLayer            cReference;
   CLayer            cRefKey;
   CLayer            cRefValue;
   CLayer            cMHRefAttentionOut;
   CLayer            cRefAttentionOut;
   //---
   virtual bool      CreateBuffers(void);
   virtual bool      DiversityLoss(CNeuronBaseOCL *neuron, const int units,
                                   const int dimension, const bool add = false);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                        CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None)
                                        override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;

public:
                     CNeuronGRES(void) {};
                    ~CNeuronGRES(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count, uint heads,
                          uint window_sp, uint units_sp, uint heads_sp,
                          uint ref_size, uint layers, uint layers_to_sp,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronGRES; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Junto com a funcionalidade básica, herdaremos da classe pai uma ampla gama de objetos internos, que atenderão à maior parte de nossas necessidades. A maior parte, mas não todas. Por isso, adicionaremos objetos para trabalhar com expressões de referência. Todos os objetos serão declarados como estáticos, o que nos permite manter o construtor e o destruidor da classe 'vazios'. A inicialização de todos os objetos declarados e herdados será feita no método Init, cujos parâmetros nos fornecem as constantes principais que permitem definir com clareza a arquitetura do objeto a ser criado.

bool CNeuronGRES::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                       uint window, uint window_key, uint units_count, uint heads,
                       uint window_sp, uint units_sp, uint heads_sp,
                       uint ref_size, uint layers, uint layers_to_sp,
                       ENUM_OPTIMIZATION optimization_type, uint batch
                      )
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

Infelizmente, a estrutura da classe que estamos desenvolvendo é bem diferente da estrutura da classe pai, o que nos impede de utilizar integralmente todos os métodos da classe original. Isso também afeta o algoritmo do método de inicialização. Aqui, precisaremos inicializar não apenas os objetos adicionados, mas também os herdados.

No corpo do método de inicialização, primeiro chamamos o método de mesmo nome da camada totalmente conectada da classe base, onde é feita a verificação inicial dos parâmetros recebidos e a ativação das interfaces de troca de dados entre as camadas neurais no funcionamento do modelo.

Em seguida, salvamos os parâmetros recebidos nas variáveis internas da nossa classe.

   iWindow = window;
   iUnits = units_count;
   iHeads = heads;
   iSPUnits = units_sp;
   iSPWindow = window_sp;
   iSPHeads = heads_sp;
   iWindowKey = window_key;
   iLayers = MathMax(layers, 1);
   iLayersSP = MathMax(layers_to_sp, 1);

Nesse ponto, também declaramos algumas variáveis para armazenamento temporário de ponteiros para objetos de diferentes camadas neurais que iremos inicializar dentro do nosso método.

   CNeuronBaseOCL *base = NULL;
   CNeuronTransposeOCL *transp = NULL;
   CNeuronConvOCL *conv = NULL;
   CNeuronLearnabledPE *pe = NULL;

Depois, passamos à criação dos objetos para geração das queries treináveis. Aqui vale lembrar que os autores do método 3D-GRES propuseram o uso de queries dinâmicas com base no conjunto de pontos original. No entanto, o conjunto de pontos analisado pode ser diferente das queries treináveis, tanto no número de elementos quanto no tamanho do vetor de características que descreve cada elemento. Resolvemos esse problema em 2 etapas. Primeiro, transpomos o tensor dos dados originais e, em seguida, usamos uma camada convolucional para alterar a quantidade de elementos na sequência. O uso da camada convolucional nos permite executar essa operação dentro de sequências unitárias independentes.

//--- Init Querys
   cQuery.Clear();
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, 0, OpenCL, iSPUnits, iSPWindow, optimization, iBatch) ||
      !cQuery.Add(transp))
      return false;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 1, OpenCL, iSPUnits, iSPUnits, iUnits, 1, iSPWindow, optimization, iBatch) ||
      !cQuery.Add(conv))
      return false;
   conv.SetActivationFunction(SIGMOID);

Na segunda etapa, realizamos a transposição reversa do tensor e projetamos ele no espaço multimodal.

   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, 2, OpenCL, iSPWindow, iUnits, optimization, iBatch) ||
      !cQuery.Add(transp))
      return false;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 3, OpenCL, iSPWindow, iSPWindow, iWindow, iUnits, 1, optimization, iBatch) ||
      !cQuery.Add(conv))
      return false;
   conv.SetActivationFunction(SIGMOID);

Agora só nos resta adicionar a codificação posicional totalmente treinável.

   pe = new CNeuronLearnabledPE();
   if(!pe ||
      !pe.Init(0, 4, OpenCL, iWindow * iUnits, optimization, iBatch) ||
      !cQuery.Add(pe))
      return false;

De forma semelhante ao algoritmo da classe pai, extraímos para um fluxo de informação separado os dados de codificação posicional das queries.

   base = new CNeuronBaseOCL();
   if(!base ||
      !base.Init(0, 5, OpenCL, pe.Neurons(), optimization, iBatch) ||
      !base.SetOutput(pe.GetPE()) ||
      !cQPosition.Add(base))
      return false;

O algoritmo de geração da arquitetura do modelo Superpoints foi totalmente transferido da classe pai sem alterações.

//--- Init SuperPoints
   int layer_id = 6;
   cSuperPoints.Clear();
   for(int r = 0; r < 4; r++)
     {
      if(iSPUnits % 2 == 0)
        {
         iSPUnits /= 2;
         CResidualConv *residual = new CResidualConv();
         if(!residual ||
            !residual.Init(0, layer_id, OpenCL, 2 * iSPWindow, iSPWindow, iSPUnits, optimization, iBatch) ||
            !cSuperPoints.Add(residual))
            return false;
        }
      else
        {
         iSPUnits--;
         conv = new CNeuronConvOCL();
         if(!conv ||
            !conv.Init(0, layer_id, OpenCL, 2 * iSPWindow, iSPWindow, iSPWindow, iSPUnits, 1, optimization, 
                                                                                                 iBatch) ||
            !cSuperPoints.Add(conv))
            return false;
         conv.SetActivationFunction(SIGMOID);
        }
      layer_id++;
     }
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, layer_id, OpenCL, iSPWindow, iSPWindow, iWindow, iSPUnits, 1, optimization, iBatch) ||
      !cSuperPoints.Add(conv))
      return false;
   conv.SetActivationFunction(SIGMOID);
   layer_id++;
   pe = new CNeuronLearnabledPE();
   if(!pe ||
      !pe.Init(0, layer_id, OpenCL, conv.Neurons(), optimization, iBatch) ||
      !cSuperPoints.Add(pe))
      return false;
   layer_id++;

Para gerar o embedding da expressão de referência, utilizamos uma MLP totalmente conectada, com a adição de uma camada de codificação posicional.

//--- Reference
   cReference.Clear();
   base = new CNeuronBaseOCL();
   if(!base ||
      !base.Init(iWindow * iUnits, layer_id, OpenCL, ref_size, optimization, iBatch) ||
      !cReference.Add(base))
      return false;
   layer_id++;
   base = new CNeuronBaseOCL();
   if(!base ||
      !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch) ||
      !cReference.Add(base))
      return false;
   base.SetActivationFunction(SIGMOID);
   layer_id++;
   pe = new CNeuronLearnabledPE();
   if(!pe ||
      !pe.Init(0, layer_id, OpenCL, base.Neurons(), optimization, iBatch) ||
      !cReference.Add(pe))
      return false;
   layer_id++;

Aqui vale observar que, na saída da MLP, obtemos um tensor com dimensões compatíveis com o tensor das queries treináveis. Isso foi feito para possibilitar a decomposição da expressão de referência em vários componentes semânticos, o que permite realizar uma análise mais abrangente da situação atual do mercado.

Neste ponto, concluímos o trabalho de inicialização dos objetos responsáveis pelo pré-processamento dos dados brutos. Em seguida, criamos um laço para inicializar os objetos das camadas neurais internas. Mas, antes disso, limpamos os arrays das coleções de objetos internos.

//--- Inside layers
   cQKey.Clear();
   cQValue.Clear();
   cSPKey.Clear();
   cSPValue.Clear();
   cSelfAttentionOut.Clear();
   cCrossAttentionOut.Clear();
   cMHCrossAttentionOut.Clear();
   cMHSelfAttentionOut.Clear();
   cMHRefAttentionOut.Clear();
   cRefAttentionOut.Clear();
   cRefKey.Clear();
   cRefValue.Clear();
   cResidual.Clear();
   for(uint l = 0; l < iLayers; l++)
     {
      //--- Cross-Attention
      //--- Query
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1,optimization, iBatch) ||
         !cQuery.Add(conv))
         return false;
      layer_id++;

No corpo do laço, começamos pela inicialização dos objetos de atenção cruzada Query-Superpoint. Aqui criamos o objeto responsável pela geração das entidades Query para o bloco de atenção. Depois, se necessário, adicionamos os objetos para geração das entidades Key e Value.

      if(l % iLayersSP == 0)
        {
         //--- Key
         conv = new CNeuronConvOCL();
         if(!conv ||
            !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iSPUnits, 1, 
                                                                             optimization, iBatch) ||
            !cSPKey.Add(conv))
            return false;
         layer_id++;
         //--- Value
         conv = new CNeuronConvOCL();
         if(!conv ||
            !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iSPUnits, 1, 
                                                                             optimization, iBatch) ||
            !cSPValue.Add(conv))
            return false;
         layer_id++;
        }

Adicionamos uma camada de registro dos resultados da atenção com múltiplas cabeças.

      //--- Multy-Heads Attention Out
      base = new CNeuronBaseOCL();
      if(!base ||
         !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
         !cMHCrossAttentionOut.Add(base))
         return false;
      layer_id++;

E uma camada de normalização dos resultados.

      //--- Cross-Attention Out
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0, layer_id, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 1,
                                                                                 optimization, iBatch) ||
         !cCrossAttentionOut.Add(conv))
         return false;
      layer_id++;

O bloco de atenção cruzada é finalizado com uma camada de conexões residuais.

      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base ||
         !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch) ||
         !cResidual.Add(base))
         return false;
      layer_id++;

Na etapa seguinte, inicializamos o bloco Self-Attention para análise das dependências Query-Query. Nesse bloco, todas as entidades são geradas com base nos resultados do bloco de atenção cruzada anterior.

      //--- Self-Attention
      //--- Query
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) ||
         !cQuery.Add(conv))
         return false;
      layer_id++;
      //--- Key
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) ||
         !cQKey.Add(conv))
         return false;
      layer_id++;
      //--- Value
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) ||
         !cQValue.Add(conv))
         return false;
      layer_id++;

Além disso, para cada camada interna, geramos todas as entidades com o mesmo número de cabeças de atenção.

Adicionamos a camada de registro dos resultados da atenção com múltiplas cabeças.

      //--- Multy-Heads Attention Out
      base = new CNeuronBaseOCL();
      if(!base ||
         !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
         !cMHSelfAttentionOut.Add(base))
         return false;
      layer_id++;

E uma camada de normalização dos resultados.

      //--- Self-Attention Out
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0, layer_id, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 1,
                                                                                  optimization, iBatch) ||
         !cSelfAttentionOut.Add(conv))
         return false;
      layer_id++;

Paralelamente ao bloco Self-Attention, funciona o bloco de atenção cruzada da Query com as expressões semânticas de referência. Aqui, a entidade Query é gerada a partir dos resultados do bloco de atenção cruzada anterior.

      //--- Reference Cross-Attention
      //--- Query
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) ||
         !cQuery.Add(conv))
         return false;
      layer_id++;

O tensor Key-Value é formado a partir dos embeddings semânticos preparados anteriormente.

      //--- Key
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) ||
         !cRefKey.Add(conv))
         return false;
      layer_id++;
      //--- Value
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) ||
         !cRefValue.Add(conv))
         return false;
      layer_id++;

Assim como no bloco Self-Attention, todas as entidades são geradas em cada nova camada com a mesma quantidade de cabeças de atenção.

Depois, adicionamos as camadas de atenção com múltiplas cabeças e de normalização dos resultados.

      //--- Multy-Heads Attention Out
      base = new CNeuronBaseOCL();
      if(!base ||
         !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
         !cMHRefAttentionOut.Add(base))
         return false;
      layer_id++;
      //--- Cross-Attention Out
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindowKey*iHeads, iWindowKey*iHeads, iWindow, iUnits, 1, 
                                                                             optimization, iBatch) ||
         !cRefAttentionOut.Add(conv))
         return false;
      layer_id++;
      if(!conv.SetGradient(((CNeuronBaseOCL*)cSelfAttentionOut[cSelfAttentionOut.Total() - 1]).getGradient(),
                                                                                                        true))
         return false;

E esse bloco é finalizado com uma camada de conexões residuais, que unifica os resultados dos três blocos de atenção.

      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch))
         return false;
      if(!cResidual.Add(base))
         return false;
      layer_id++;

O processamento final das queries enriquecidas é realizado no bloco FeedForward com conexão residual, cuja estrutura é semelhante ao Transformer tradicional.

      //--- Feed Forward
      conv = new CNeuronConvOCL();
      if(!conv || 
         !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, 4*iWindow, iUnits, 1, optimization, iBatch))
         return false;
      conv.SetActivationFunction(LReLU);
      if(!cFeedForward.Add(conv))
         return false;
      layer_id++;
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0, layer_id, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, 1, optimization, iBatch))
         return false;
      if(!cFeedForward.Add(conv))
         return false;
      layer_id++;
      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch))
         return false;
      if(!base.SetGradient(conv.getGradient()))
         return false;
      if(!cResidual.Add(base))
         return false;
      layer_id++;

Além disso, vamos reaproveitar da classe pai o algoritmo de ajuste dos centros dos objetos, que não foi previsto pelos autores do método 3D-GRES.

      //--- Delta position
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch))
         return false;
      conv.SetActivationFunction(SIGMOID);
      if(!cQPosition.Add(conv))
         return false;
      layer_id++;
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, conv.Neurons(), optimization, iBatch))
         return false;
      if(!base.SetGradient(conv.getGradient()))
         return false;
      if(!cQPosition.Add(base))
         return false;
      layer_id++;
     }

E seguimos para a próxima iteração do laço de criação dos objetos da camada interna. Após a conclusão bem-sucedida de todas as iterações do laço, substituiremos os ponteiros dos buffers de dados, o que permitirá reduzir o número de operações de cópia de dados e acelerar o processo de treinamento.

   base = cResidual[iLayers * 3 - 1];
   if(!SetGradient(base.getGradient()))
      return false;
//---
   SetOpenCL(OpenCL);
//---
   return true;
  }

Ao final das operações do método, retornamos o resultado lógico das operações realizadas ao programa chamador.

Vale destacar que, assim como no artigo anterior, extraímos a criação dos buffers auxiliares de dados para um método separado chamado CreateBuffers. Recomendo que você consulte esse método por conta própria. O código completo está disponível no anexo.

Após a inicialização do objeto da nossa nova classe, passamos à construção do algoritmo de propagação para frente, que está implementado no método feedForward. Desta vez, os parâmetros do método incluem dois ponteiros para os objetos dos dados brutos. Um contém o conjunto de pontos analisado, e o outro representa a expressão de referência.

bool CNeuronGRES::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
//--- Superpoints
   CNeuronBaseOCL *superpoints = NeuronOCL;
   int total_sp = cSuperPoints.Total();
   for(int i = 0; i < total_sp; i++)
     {
      if(!cSuperPoints[i] ||
         !((CNeuronBaseOCL*)cSuperPoints[i]).FeedForward(superpoints))
         return false;
      superpoints = cSuperPoints[i];
     }

No corpo do método, organizamos diretamente o laço de propagação para frente da nossa pequena rede de geração de Superpoints. Em seguida, de forma semelhante, geramos as queries.

//--- Query
   CNeuronBaseOCL *query = NeuronOCL;
   for(int i = 0; i < 5; i++)
     {
      if(!cQuery[i] ||
         !((CNeuronBaseOCL*)cQuery[i]).FeedForward(query))
         return false;
      query = cQuery[i];
     }

Já para a criação do tensor de embeddings semânticos da expressão de referência, será necessário um pouco mais de trabalho. Isso porque a expressão de referência é recebida na forma de um buffer de dados. E o método de propagação para frente dos objetos internos exige como entrada uma camada neural. Portanto, usamos a primeira camada do modelo interno de geração de embeddings semânticos da expressão de referência para armazenar os dados brutos, da mesma forma que na rede principal. Só que, neste caso, não copiamos todo o conteúdo do buffer, apenas substituímos os ponteiros para os objetos.

//--- Reference
   CNeuronBaseOCL *reference = cReference[0];
   if(!SecondInput)
      return false;
   if(reference.getOutput() != SecondInput)
      if(!reference.SetOutput(SecondInput, true))
         return false;

Depois disso, organizamos o laço de propagação para frente da rede interna.

   for(int i = 1; i < cReference.Total(); i++)
     {
      if(!cReference[i] ||
         !((CNeuronBaseOCL*)cReference[i]).FeedForward(reference))
         return false;
      reference = cReference[i];
     }

Com isso, encerramos o pré-processamento dos dados brutos e seguimos para o algoritmo principal de decodificação dos dados. Para isso, organizamos um laço de iteração sobre as camadas internas do nosso Decodificador.

   CNeuronBaseOCL *inputs = query, *key = NULL, *value = NULL, *base = NULL, *cross = NULL, *self = NULL;
//--- Inside layers
   for(uint l = 0; l < iLayers; l++)
     {
      //--- Calc Position bias
      cross = cQPosition[l * 2];
      if(!cross ||
         !CalcPositionBias(cross.getOutput(),
                           ((CNeuronLearnabledPE*)superpoints).GetPE(), cPositionBias[l],
                           iUnits, iSPUnits, iWindow))
         return false;

Aqui, primeiro definimos os coeficientes de deslocamento posicional, de forma semelhante ao método MAFT. Essa é uma das modificações que fizemos em relação ao algoritmo original do 3D-GRES. Os autores do método usavam uma MLP para gerar a máscara de atenção.

Em seguida, temos o bloco de atenção cruzada QSA, no qual ocorre a análise das dependências Query-Superpoint. Neste ponto, geramos os tensores das entidades Query, Key e Value. As duas últimas são geradas apenas se necessário.

      //--- Cross-Attention
      query = cQuery[l * 3 + 5];
      if(!query || !query.FeedForward(inputs))
         return false;
      key = cSPKey[l / iLayersSP];
      value = cSPValue[l / iLayersSP];
      if(l % iLayersSP == 0)
        {
         if(!key || !key.FeedForward(superpoints))
            return false;
         if(!value || !value.FeedForward(cSuperPoints[total_sp - 2]))
            return false;
        }

E realizamos a análise das dependências considerando os coeficientes de deslocamento posicional.

      if(!AttentionOut(query, key, value, cScores[l * 3], cMHCrossAttentionOut[l], cPositionBias[l],
                                               iUnits, iHeads, iSPUnits, iSPHeads, iWindowKey, true))
         return false;

Os resultados da atenção com múltiplas cabeças são normalizados após serem escalados e somados com os valores da conexão residual.

      base = cCrossAttentionOut[l];
      if(!base || !base.FeedForward(cMHCrossAttentionOut[l]))
         return false;
      value = cResidual[l * 3];
      if(!value ||
         !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, false, 0, 0, 0, 1)||
         !SumAndNormilize(cross.getOutput(), value.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1))
         return false;
      inputs = value;

O próximo passo é executar o módulo QLA. Aqui, precisamos organizar a propagação para frente de dois blocos de atenção:

• Self-Attention → Query-Query;
• Cross-Attention → Query-Reference.

Primeiro, ativamos o bloco Self-Attention. Nesse ponto, geramos por completo os tensores das entidades Query, Key e Value com base nos dados recebidos do bloco anterior do Decodificador.

      //--- Self-Atention
      query = cQuery[l * 3 + 6];
      if(!query || !query.FeedForward(inputs))
         return false;
      key = cQKey[l];
      if(!key || !key.FeedForward(inputs))
         return false;
      value = cQValue[l];
      if(!value || !value.FeedForward(inputs))
         return false;

Analisamos as dependências utilizando o módulo tradicional de atenção com múltiplas cabeças.

      if(!AttentionOut(query, key, value, cScores[l * 3 + 1], cMHSelfAttentionOut[l], -1, 
                                        iUnits, iHeads, iUnits, iHeads, iWindowKey, false))
         return false;
      self = cSelfAttentionOut[l];
      if(!self || !self.FeedForward(cMHSelfAttentionOut[l]))
         return false;

Depois, escalamos os resultados obtidos.

O bloco de atenção cruzada é construído da mesma maneira. A única diferença é que as entidades Key e Value são geradas a partir dos embeddings semânticos da expressão de referência.

      //--- Reference Cross-Attention
      query = cQuery[l * 3 + 7];
      if(!query || !query.FeedForward(inputs))
         return false;
      key = cRefKey[l];
      if(!key || !key.FeedForward(reference))
         return false;
      value = cRefValue[l];
      if(!value || !value.FeedForward(reference))
         return false;
      if(!AttentionOut(query, key, value, cScores[l * 3 + 2], cMHRefAttentionOut[l], -1, 
                                       iUnits, iHeads, iUnits, iHeads, iWindowKey, false))
         return false;
      cross = cRefAttentionOut[l];
      if(!cross || !cross.FeedForward(cMHRefAttentionOut[l]))
         return false;

Em seguida, somamos os resultados dos três blocos de atenção e normalizamos os dados resultantes.

      value = cResidual[l * 3 + 1];
      if(!value ||
         !SumAndNormilize(cross.getOutput(), self.getOutput(), value.getOutput(), iWindow, false, 0, 0, 0, 1) ||
         !SumAndNormilize(inputs.getOutput(), value.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1))
         return false;
      inputs = value;

Logo após, temos o bloco FeedForward do Transformer tradicional, com conexão residual e normalização dos dados.

      //--- Feed Forward
      base = cFeedForward[l * 2];
      if(!base || !base.FeedForward(inputs))
         return false;
      base = cFeedForward[l * 2 + 1];
      if(!base || !base.FeedForward(cFeedForward[l * 2]))
         return false;
      value = cResidual[l * 3 + 2];
      if(!value ||
         !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1))
         return false;
      inputs = value;

Acredito que você tenha notado que o algoritmo de propagação para frente que construímos é uma espécie de fusão entre os métodos 3D-GRES e MAFT. E só nos resta adicionar o toque final herdado do método MAFT — o ajuste das posições das queries.

      //--- Delta Query position
      base = cQPosition[l * 2 + 1];
      if(!base ||
         !base.FeedForward(inputs))
         return false;
      value = cQPosition[(l + 1) * 2];
      query = cQPosition[l * 2];
      if(!value ||
         !SumAndNormilize(query.getOutput(), base.getOutput(), value.getOutput(), iWindow, false, 0, 0, 0,0.5f))
         return false;
     }

Em seguida, passamos para a próxima camada do Decodificador. Após completar a iteração por todas as camadas internas do Decodificador, somamos os valores enriquecidos das queries com sua codificação posicional. Os resultados são encaminhados para a próxima camada do nosso modelo através das interfaces básicas.

   value = cQPosition[iLayers * 2];
   if(!value ||
      !SumAndNormilize(inputs.getOutput(), value.getOutput(), Output, iWindow, true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

Agora só precisamos retornar ao programa chamador o resultado lógico da execução das operações.

Com isso, encerramos o desenvolvimento dos métodos de propagação para frente e iniciamos a implementação dos algoritmos de propagação reversa. Como de costume, dividiremos todo o processo em 2 etapas:

• Distribuição dos gradientes de erro (calcInputGradients);
• Otimização dos parâmetros do modelo (updateInputWeights).

Na primeira etapa, percorremos o fluxo das operações da propagação para frente, só que em ordem inversa. Na segunda, apenas invocamos os métodos de mesmo nome nas camadas internas que possuem parâmetros treináveis. À primeira vista, tudo parece como de costume, mas há um detalhe relacionado à diversificação das queries. Por isso, vamos analisar com mais atenção o algoritmo do método calcInputGradients, onde ocorre a distribuição do gradiente de erro.

Nos parâmetros do método, recebemos ponteiros para 3 objetos, além de uma constante da função de ativação usada para a segunda fonte de dados brutos.

bool CNeuronGRES::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                     CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!NeuronOCL || !SecondGradient)
      return false;

No corpo do método, verificamos a validade apenas de dois ponteiros. Vale lembrar que, durante a propagação para frente, salvamos o ponteiro da segunda fonte dos dados brutos. Portanto, a ausência de um ponteiro válido entre os parâmetros, neste momento, não é algo crítico para nós. Mas isso não se aplica ao buffer destinado ao armazenamento dos gradientes de erro. Por isso, verificamos sua validade antes de iniciar a execução.

Logo em seguida, declaramos algumas variáveis para o armazenamento temporário de ponteiros para objetos. E com isso, encerramos nossa etapa de preparação.

   CNeuronBaseOCL *residual = GetPointer(this), *query = NULL, *key = NULL, *value = NULL,
                   *key_sp = NULL, *value_sp = NULL, *base = NULL;

Em seguida, organizamos o laço de iteração reversa pelas camadas internas do Decodificador.

//--- Inside layers
   for(int l = (int)iLayers - 1; l >= 0; l--)
     {
      //--- Feed Forward
      base = cFeedForward[l * 2];
      if(!base || !base.calcHiddenGradients(cFeedForward[l * 2 + 1]))
         return false;
      base = cResidual[l * 3 + 1];
      if(!base || !base.calcHiddenGradients(cFeedForward[l * 2]))
         return false;

Aqui, graças à substituição planejada dos ponteiros dos buffers de dados nos objetos internos, evitamos operações desnecessárias de cópia de dados e iniciamos o processo de propagação do gradiente de erro pelo bloco FeedForward.

O gradiente de erro obtido no nível dos dados brutos do bloco FeedForward é somado aos valores correspondentes nos resultados da nossa classe, o que representa o fluxo de dados das conexões residuais desse bloco. O resultado dessas operações é encaminhado ao buffer de resultados do bloco Self-Attention.

      //--- Residual
      value = cSelfAttentionOut[l];
      if(!value ||
         !SumAndNormilize(base.getGradient(), residual.getGradient(), value.getGradient(), iWindow, false,
                                                                                              0, 0, 0, 1))
         return false;
      residual = value;

É importante destacar que, na entrada do bloco FeedForward, fornecemos a soma dos resultados dos três blocos de atenção. E, portanto, precisamos repassar o gradiente de erro recebido de todas essas fontes. Lembrando que, ao somar os dados, o gradiente de erro é repassado integralmente a todos os termos da soma. Os resultados do bloco QSA foram utilizados como fontes também para outros módulos do nosso Decodificador. Por isso, o gradiente de erro desse bloco será coletado posteriormente, seguindo a lógica dos fluxos de conexões residuais. Para evitar cópias desnecessárias de gradientes de erro no bloco de atenção cruzada Query-Reference, planejamos previamente a substituição dos ponteiros durante a inicialização dos objetos. Dessa forma, ao transmitir os dados para o bloco Self-Attention, enviamos simultaneamente os mesmos dados ao bloco de atenção cruzada Query-Reference. Esse pequeno truque permite reduzir o uso de memória e o tempo de treinamento do modelo ao eliminar operações redundantes.

Depois, propagamos o gradiente de erro pelo bloco de atenção cruzada Query-Reference.

      //--- Reference Cross-Attention
      base = cMHRefAttentionOut[l];
      if(!base || !base.calcHiddenGradients(cRefAttentionOut[l], NULL))
         return false;
      query = cQuery[l * 3 + 7];
      key = cRefKey[l];
      value = cRefValue[l];
      if(!AttentionInsideGradients(query, key, value, cScores[l * 3 + 2], base, 
                                    iUnits, iHeads, iUnits, iHeads, iWindowKey))
         return false;

E repassamos o gradiente de erro da entidade Query para o módulo QSA, somando previamente o gradiente de erro obtido do bloco FeedForward (fluxo de conexões residuais).

      base = cResidual[l * 3];
      if(!base || !base.calcHiddenGradients(query, NULL))
         return false;
      value = cCrossAttentionOut[l];
      if(!SumAndNormilize(base.getGradient(), residual.getGradient(),value.getGradient(), iWindow, false,
                                                                                               0, 0, 0, 1))
         return false;
      residual = value;

Da mesma forma, propagamos o gradiente de erro pelo bloco Self-Attention.

      //--- Self-Attention
      base = cMHSelfAttentionOut[l];
      if(!base || !base.calcHiddenGradients(cSelfAttentionOut[l], NULL))
         return false;
      query = cQuery[l * 3 + 6];
      key = cQKey[l];
      value = cQValue[l];
      if(!AttentionInsideGradients(query, key, value, cScores[l * 2 + 1], base, 
                                     iUnits, iHeads, iUnits, iHeads, iWindowKey))
         return false;

Agora, porém, precisamos adicionar ao módulo QSA o gradiente de erro de todas as três entidades. Para isso, transmitimos o gradiente de erro até o nível da camada de conexões residuais e somamos os valores obtidos à soma já acumulada dos gradientes do módulo QSA.

      base = cResidual[l * 3 + 1];
      if(!base.calcHiddenGradients(query, NULL))
         return false;
      if(!SumAndNormilize(base.getGradient(), residual.getGradient(), residual.getGradient(), iWindow, false, 
                                                                                                  0, 0, 0, 1))
         return false;
      if(!base.calcHiddenGradients(key, NULL))
         return false;
      if(!SumAndNormilize(base.getGradient(), residual.getGradient(), residual.getGradient(), iWindow, false, 
                                                                                                  0, 0, 0, 1))
         return false;
      if(!base.calcHiddenGradients(value, NULL))
         return false;
      if(!SumAndNormilize(base.getGradient(), residual.getGradient(), residual.getGradient(), iWindow, false, 
                                                                                                  0, 0, 0, 1))
         return false;

A soma dos valores acumulados do gradiente também será transmitida ao fluxo paralelo de informação do codificador posicional das queries, somando-o aos gradientes do outro fluxo de informação.

      //--- Qeury position
      base = cQPosition[l * 2];
      value = cQPosition[(l + 1) * 2];
      if(!base ||
         !SumAndNormilize(value.getGradient(), residual.getGradient(), base.getGradient(), iWindow, false,
                                                                                               0, 0, 0, 1))
         return false;

Agora só nos resta propagar o gradiente de erro através do módulo QSA. Aqui, utilizamos o mesmo algoritmo de propagação de gradiente pelo bloco de atenção, mas com um ajuste para reunir os gradientes das entidades Key e Value vindos de várias camadas do Decodificador. Primeiro, acumulamos os gradientes de erro em buffers temporários, e os valores finais são armazenados nos buffers dos respectivos objetos.

      //--- Cross-Attention
      base = cMHCrossAttentionOut[l];
      if(!base || !base.calcHiddenGradients(residual, NULL))
         return false;
      query = cQuery[l * 3 + 5];
      if(((l + 1) % iLayersSP) == 0 || (l + 1) == iLayers)
        {
         key_sp = cSPKey[l / iLayersSP];
         value_sp = cSPValue[l / iLayersSP];
         if(!key_sp || !value_sp ||
            !cTempCrossK.Fill(0) || !cTempCrossV.Fill(0))
            return false;
        }
      if(!AttentionInsideGradients(query, key_sp, value_sp, cScores[l * 2], base, 
                                                           iUnits, iHeads, iSPUnits, iSPHeads, iWindowKey))
         return false;
      if(iLayersSP > 1)
        {
         if((l % iLayersSP) == 0)
           {
            if(!SumAndNormilize(key_sp.getGradient(), GetPointer(cTempCrossK), key_sp.getGradient(), 
                                                                           iWindowKey, false, 0, 0, 0, 1))
               return false;
            if(!SumAndNormilize(value_sp.getGradient(), GetPointer(cTempCrossV), value_sp.getGradient(), 
                                                                           iWindowKey, false, 0, 0, 0, 1))
               return false;
           }
         else
           {
            if(!SumAndNormilize(key_sp.getGradient(), GetPointer(cTempCrossK), GetPointer(cTempCrossK), 
                                                                           iWindowKey, false, 0, 0, 0, 1))
               return false;
            if(!SumAndNormilize(value_sp.getGradient(), GetPointer(cTempCrossV), GetPointer(cTempCrossV),
                                                                           iWindowKey, false, 0, 0, 0, 1))
               return false;
           }
        }

O gradiente de erro da entidade Query é transmitido para o nível dos dados brutos, somando-se aos dados do fluxo de conexões residuais. Em seguida, avançamos para a próxima iteração do laço de retropropagação das camadas do Decodificador.

      if(l == 0)
         base = cQuery[4];
      else
         base = cResidual[l * 3 - 1];
      if(!base || !base.calcHiddenGradients(query, NULL))
         return false;
      //--- Residual
      if(!SumAndNormilize(base.getGradient(), residual.getGradient(), base.getGradient(), iWindow, false,
                                                                                              0, 0, 0, 1))
         return false;
      residual = base;
     }

Depois de propagar com sucesso o gradiente de erro por todas as camadas do Decodificador, precisamos levá-lo até o nível dos dados brutos, passando pelas operações do módulo de pré-processamento de dados. Primeiro, propagamos o gradiente de erro das queries treináveis. Para isso, fazemos a propagação através da camada de codificação posicional.

//--- Qeury
   query = cQuery[3];
   if(!query || !query.calcHiddenGradients(cQuery[4]))
      return false;

Neste ponto, realizamos a injeção do gradiente de erro do codificador posicional a partir do respectivo fluxo de informação.

   base = cQPosition[0];
   if(!DeActivation(base.getOutput(), base.getGradient(), base.getGradient(), SIGMOID) ||
      !(((CNeuronLearnabledPE*)cQuery[4]).AddPEGradient(base.getGradient())))
      return false;

Depois, adicionamos o gradiente de erro da diversificação das queries, mas aqui trabalhamos sem qualquer informação de codificação posicional. Essa decisão foi tomada intencionalmente para evitar que o erro de diversificação interfira na codificação posicional.

   if(!DiversityLoss(query, iUnits, iWindow, true))
      return false;

Em seguida, executamos um simples laço de retropropagação pelas camadas da nossa rede de geração de queries, transmitindo o gradiente de erro até o nível dos dados brutos.

   for(int i = 2; i >= 0; i--)
     {
      query = cQuery[i];
      if(!query || !query.calcHiddenGradients(cQuery[i + 1]))
         return false;
     }
   if(!NeuronOCL.calcHiddenGradients(query, NULL))
      return false;

É importante observar que também precisamos transmitir o gradiente de erro da rede interna de geração de Superpoints até o nível dos dados brutos. Para evitar qualquer perda de dados, salvamos o ponteiro do buffer de gradientes do objeto de dados brutos em uma variável local. E substituímos esse ponteiro no objeto de dados brutos pelo buffer correspondente à camada de transposição da rede de geração de queries.

Lembrando que a camada de transposição não possui parâmetros treináveis, portanto, não há risco ao perder os gradientes de erro nesse ponto.

   CBufferFloat *inputs_gr = NeuronOCL.getGradient();
   if(!NeuronOCL.SetGradient(query.getGradient(), false))
      return false;

Na etapa seguinte, vamos distribuir o gradiente de erro através da rede de geração de Superpoints. No entanto, é importante observar que, durante a retropropagação pelas camadas do Decodificador, não transmitimos o gradiente de erro para essa rede. Sendo assim, precisamos primeiro reunir os gradientes de erro das entidades Key e Value. Sabemos que temos pelo menos um tensor de cada entidade. Mas há mais um detalhe: a entidade Key foi gerada a partir dos resultados da última camada da rede Superpoints (incluindo a codificação posicional), enquanto a Value veio da penúltima camada, sem considerar a codificação posicional. E o gradiente de erro deve ser propagado seguindo exatamente esses fluxos de informação.  

Para isso, primeiro calculamos o gradiente de erro da primeira camada da entidade Key e o transmitimos para a última camada da rede interna.

//--- Superpoints
//--- From Key
   int total_sp = cSuperPoints.Total();
   CNeuronBaseOCL *superpoints = cSuperPoints[total_sp - 1];
   if(!superpoints || !superpoints.calcHiddenGradients(cSPKey[0]))
      return false;

Depois, verificamos a quantidade de camadas da entidade Key e, se necessário, substituímos os buffers de dados para evitar a perda do gradiente de erro já acumulado.

   if(cSPKey.Total() > 1)
     {
      CBufferFloat *grad = superpoints.getGradient();
      if(!superpoints.SetGradient(GetPointer(cTempSP), false))
         return false;

Em seguida, organizamos um laço de iteração pelas camadas restantes dessa entidade, calculando o gradiente de erro e somando-o aos valores já acumulados.

      for(int i = 1; i < cSPKey.Total(); i++)
        {
         if(!superpoints.calcHiddenGradients(cSPKey[i]) ||
            !SumAndNormilize(superpoints.getGradient(), grad, grad, iWindow, false, 0, 0, 0, 1))
            return false;
        }

Após a execução bem-sucedida de todas as iterações do laço, retornamos o ponteiro para o buffer com a soma total dos gradientes acumulados.

      if(!superpoints.SetGradient(grad, false))
         return false;
     }

Assim, na última camada da rede Superpoints, conseguimos reunir o gradiente de erro de todas as camadas da entidade Key e agora podemos transmiti-lo para o nível imediatamente inferior dessa rede.

   superpoints = cSuperPoints[total_sp - 2];
   if(!superpoints || !superpoints.calcHiddenGradients(cSuperPoints[total_sp - 1]))
      return false;

Agora precisamos fazer o mesmo para a entidade Value. Usamos o mesmo algoritmo. Mas com a diferença de que o buffer de gradientes de erro já contém dados provenientes da camada seguinte. Por isso, realizamos imediatamente a substituição dos buffers de dados e, em seguida, percorremos o laço para reunir as informações dos fluxos paralelos de dados.

//--- From Value
   CBufferFloat *grad = superpoints.getGradient();
   if(!superpoints.SetGradient(GetPointer(cTempSP), false))
      return false;
   for(int i = 0; i < cSPValue.Total(); i++)
     {
      if(!superpoints.calcHiddenGradients(cSPValue[i]) ||
         !SumAndNormilize(superpoints.getGradient(), grad, grad, iWindow, false, 0, 0, 0, 1))
         return false;
     }
   if(!superpoints.SetGradient(grad, false))
      return false;

Neste ponto, também adicionamos os erros de diversificação, o que permite maximizar a diversidade dos Superpoints..

   if(!DiversityLoss(superpoints, iSPUnits, iSPWindow, true))
      return false;

Na sequência, dentro do laço de retropropagação das camadas da rede Superpoints, levamos o gradiente de erro até o nível dos dados brutos.

   for(int i = total_sp - 3; i >= 0; i--)
     {
      superpoints = cSuperPoints[i];
      if(!superpoints || !superpoints.calcHiddenGradients(cSuperPoints[i + 1]))
         return false;
     }
//--- Inputs
   if(!NeuronOCL.calcHiddenGradients(cSuperPoints[0]))
      return false;

Vale lembrar que parte do gradiente de erro, no nível dos dados brutos, foi armazenada anteriormente durante o processamento do fluxo de informação das queries. Naquele momento, também realizamos a substituição dos buffers de dados. Agora, somamos os gradientes de erro dos dois fluxos de informação. E então, retornamos o ponteiro para o buffer de dados.

   if(!SumAndNormilize(NeuronOCL.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1))
      return false;
   if(!NeuronOCL.SetGradient(inputs_gr, false))
      return false;

Dessa forma, conseguimos reunir o gradiente de erro de dois fluxos de informação para a primeira fonte dos dados brutos. Mas ainda precisamos transmitir o gradiente de erro para o segundo objeto dos dados brutos. Para isso, começamos sincronizando os ponteiros dos buffers de gradiente de erro do segundo objeto de dados com a primeira camada da rede Reference.

   base = cReference[0];
   if(base.getGradient() != SecondGradient)
     {
      if(!base.SetGradient(SecondGradient))
         return false;
      base.SetActivationFunction(SecondActivation);
     }

Depois, na última camada dessa rede, reunimos o gradiente de erro de todos os tensores das entidades Key e Value. O algoritmo é o mesmo que analisamos anteriormente.

   base = cReference[2];
   if(!base ||
      !base.calcHiddenGradients(cRefKey[0]))
      return false;
   inputs_gr = base.getGradient();
   if(!base.SetGradient(GetPointer(cTempQ), false))
      return false;
   if(!base.calcHiddenGradients(cRefValue[0]))
      return false;
   if(!SumAndNormilize(base.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1))
      return false;
   for(uint i = 1; i < iLayers; i++)
     {
      if(!base.calcHiddenGradients(cRefKey[i]))
         return false;
      if(!SumAndNormilize(base.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1))
         return false;
      if(!base.calcHiddenGradients(cRefValue[i]))
         return false;
      if(!SumAndNormilize(base.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1))
         return false;
     }
   if(!base.SetGradient(inputs_gr, false))
      return false;

Propagamos o gradiente de erro pela camada de codificação posicional.

   base = cReference[1];
   if(!base.calcHiddenGradients(cReference[2]))
      return false;

E adicionamos o erro de diversificação dos vetores para garantir o máximo de diversidade entre os componentes semânticos.

   if(!DiversityLoss(base, iUnits, iWindow, true))
      return false;

Em seguida, transmitimos o gradiente de erro até o nível dos dados brutos.

   base = cReference[0];
   if(!base.calcHiddenGradients(cReference[1]))
      return false;
//---
   return true;
  }

Ao final da execução do método, só nos resta retornar ao programa chamador o resultado lógico da execução das operações.

Com isso, encerramos a análise dos algoritmos dos métodos da nossa nova classe. O código completo dessa classe e de todos os seus métodos pode ser consultado no anexo. Lá também você encontrará a descrição da arquitetura dos modelos treináveis e todos os programas utilizados na preparação deste artigo.

A arquitetura dos modelos treináveis foi praticamente toda reaproveitada de trabalhos anteriores. Apenas fizemos uma modificação em uma camada do Codificador da descrição do estado do ambiente.

Além disso, foram feitas correções pontuais nos programas de treinamento dos modelos e de interação com o ambiente, devido à necessidade de fornecer uma segunda fonte de dados ao Codificador do estado do ambiente. Mas essas alterações são localizadas. Como mencionado anteriormente, usamos como expressão de referência o vetor de descrição do estado da conta. A preparação desse vetor já era realizada antes, pois ele era utilizado pelo nosso Ator.

3. Teste

Trabalhamos duro e, com a ajuda do MQL5, construímos uma espécie de fusão entre os métodos propostos pelos autores do 3D-GRES e do MAFT. Agora é hora de avaliar o resultado. Vamos treinar o modelo com a tecnologia proposta usando dados históricos reais e testar a política do Ator já treinado.

Para o treinamento do modelo, utilizamos dados históricos reais do instrumento EURUSD durante todo o ano de 2023 no timeframe H1. Os parâmetros dos indicadores analisados são mantidos com os valores padrão.

Durante o treinamento dos modelos, utilizamos o algoritmo validado em nossos trabalhos anteriores.

O teste da política do Ator treinado foi realizado no testador de estratégias do MetaTrader 5 com dados históricos de janeiro de 2024, mantendo todos os outros parâmetros inalterados. Os resultados do teste são apresentados a seguir.

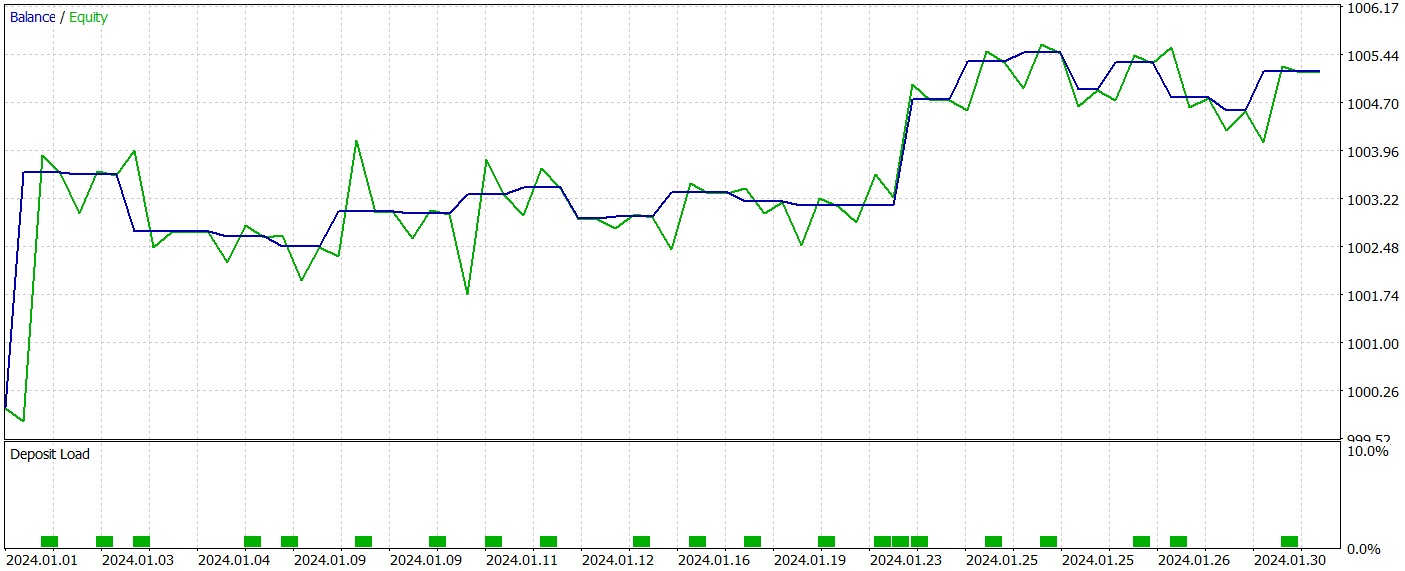
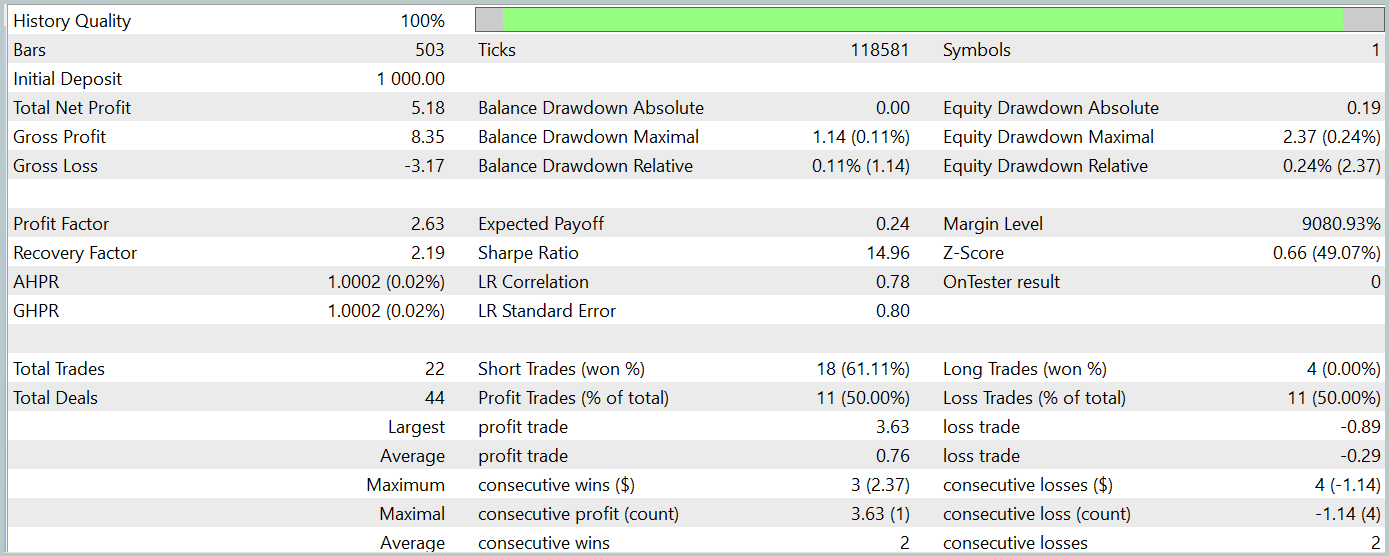
Durante o período de teste, o modelo realizou 22 operações, das quais exatamente metade foi encerrada com lucro. É notável que o lucro médio por operação vencedora foi mais de duas vezes superior à perda média por operação perdedora. E, na melhor operação, a diferença foi de quatro vezes. Isso permitiu que o modelo alcançasse um profit factor de 2,63. No entanto, o número reduzido de operações e o curto período de teste não permitem avaliar a eficácia do modelo em longos períodos. Antes de utilizar o modelo em condições reais, é necessário treiná-lo com um histórico mais amplo de dados e realizar testes mais completos. 

Conclusão

As abordagens propostas pelos autores do método Generalized 3D Referring Expression Segmentation (3D-GRES) podem encontrar aplicação no trading, oferecendo uma análise mais profunda dos dados de mercado. O método proposto pode ser adaptado para segmentação e análise de múltiplos sinais de mercado, permitindo interpretar com maior precisão situações complexas do mercado, melhorando a qualidade das previsões e das decisões de trading.

Na parte prática deste artigo, apresentamos uma das formas de implementar essas abordagens usando os recursos do MQL5 e demonstramos como aplicá-las. Os experimentos realizados mostram o potencial das soluções propostas para uso em casos reais.

Links

• 3D-GRES: Generalized 3D Referring Expression Segmentation
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA para coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para coleta de exemplos com o método Real-ORL
3	Study.mq5	Expert Advisor	EA para treinamento dos Modelos
4	Test.mq5	Expert Advisor	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca com código OpenCL