Chemical reaction optimization (CRO) algorithm (Part I): Process chemistry in optimization

Contents

1. Introduction
2. Implementation of chemical operators
   

1. Introduction

Chemical reaction optimization (CRO) is an exciting and innovative method inspired by the very essence of chemical transformations. Imagine watching a dance of molecules, where every movement and collision play a key role in solving complex problems. This method cleverly weaves together the principles of energy conservation, decomposition and synthesis of molecules, creating a flexible and adaptive approach to optimization.

CRO is a method that loosely couples chemical reactions with optimization, using general principles of molecular interactions that are defined by the first two laws of thermodynamics. The Chemical Reaction Optimization (CRO) algorithm was proposed and published by Lam and Li in 2012.

The first law of thermodynamics (the law of energy conservation) states that energy cannot be created or destroyed. It can be converted from one form to another and passed from one entity to another. In the context of CRO, a chemical reacting system consists of substances and the environment, and each particle has potential and kinetic energy.

The second law of thermodynamics states that the entropy of a system tends to increase, where entropy is a measure of disorder, the system craving more freedom. Potential energy is the energy stored in a molecule relative to its molecular configuration. As the potential energy of the molecules is released and converted into kinetic energy, the system becomes increasingly chaotic. But it is in this chaos that CRO finds its strength, capturing and directing energy flows towards the optimal solution.

For example, when molecules with higher kinetic energy (converted from potential energy) move faster, the system becomes more disordered and its entropy increases. Thus, all reacting systems tend to reach a state of equilibrium, in which potential energy is reduced to a minimum. At CRO, we capture this phenomenon by converting potential energy into kinetic energy and gradually losing the energy of chemical molecules in the environment.

A chemical system undergoing a chemical reaction is unstable and, having excess energy, tries to get rid of it and stabilize. The system consists of molecules, which are the smallest particles of a compound and are classified into different types according to their basic chemical properties.

Chemical reactions form a complex dance where molecules collide, create and break bonds, changing their structures. Each step of this dance is a sequence of subreactions leading to more stable products with minimal energy. Molecules store energy in their chemical bonds, and even small changes in their structure can lead to amazing transformations that result in more stable products. Molecular structure influences the chemical behavior of a compound, and even minor changes in structure can result in significant differences in chemical properties.

Chemical reactions are initiated by collisions of molecules, which can be unimolecular (with external substances) or bimolecular (with other molecules). These collisions can be either efficient or inefficient, depending on such factors as activation energy and steric effects. In this way, the molecules dance, intertwining and separating, creating new shapes and structures.

It is important to note that chemical reactions often result in the formation of more stable products with lower Gibbs energies. This process occurs through sequential and/or parallel steps involving the formation of intermediate compounds and passage through transition states. Understanding these processes is important for finding optimal conditions for chemical reactions and clarifying the mechanisms of transformation of chemical compounds.

Also, chemical synthesis can occur as a result of both effective and ineffective collisions of reactants. The efficiency of collisions depends on such factors as activation energy, steric effects, etc. Intermolecular synthesis, in contrast to intramolecular one, leads to more significant changes in molecular structures.

The CRO algorithm is akin to a virtuoso choreographer that uses the laws of chemistry like musical notes to create incredibly complex and elegant optimization solutions. Now let's take everything point by point - from complex to simple concepts.

2. Implementation of chemical operators

The basic unit in CRO is the "molecule". In a population, each of them has certain characteristics, such as "potential and kinetic energies", "molecular structures", etc. Elementary reactions define interactions between molecules. We can define a class, in which the data fields represent characteristics of the molecule and the methods describe elementary reactions.

One of the main concepts in CRO is energy conservation. This principle ensures that the total energy in the system remains constant throughout the optimization process. Conservation of energy determines the transitions between different states of molecules during reactions, maintaining a balance of energies that influences the search for optimal solutions.

Using manipulable agents (molecules), elementary reactions and the concept of energy conservation, CRO offers a flexible and adaptive method for solving complex optimization problems. The ability to customize operators, dynamically change population size, and integrate different attributes make CRO a promising approach in the field of metaheuristics. Its unique features and flexibility allow researchers to explore new opportunities in optimization.

The CRO algorithm uses the following operators:

1. Intermolecular ineffective collision. This operator models the process, in which two molecules collide but remain intact, and their structures are slightly changed. This allows the algorithm to perform a local search in the vicinity of current solutions.

2. Decomposition. This operator models the process, in which a molecule collides with a wall and breaks apart into two new molecules. This allows the algorithm to explore new areas of the solution space.

3. Intra molecular reaction. This operator models the process, in which a molecule collides with a wall and remains intact, but its structure changes slightly. This allows the algorithm to perform a local search in the vicinity of the current solution.

4. Synthesis. This operator models the process, in which two molecules collide and combine to form a single new molecule. This allows the algorithm to combine good solutions to create potentially better solutions.

Each of these operators plays an important role in the CRO algorithm, allowing it to explore the search space and find optimal solutions. Their collaboration provides a balance between exploration (searching new areas of the search space) and exploitation (improving current best solutions).

Let's consider each individual chemical operator in the algorithm (search for the global minimum):

Algorithm #1: On-wall Ineffective Collision

1. Input data: Mω
molecule2. Generating a new position of the molecule: ω = N(ω)
3. Calculation of potential energy of the new position: PEω = f(ω)
4. Increase collision counter: NumHitω = NumHitω + 1
5. If potential energy of a new position + kinetic energy ≥ potential energy of current position, then:
   6. Generate a random number 'a' in the range [KELossRate, 1]
   7. Kinetic energy update: KEω = (PEω − PEω + KEω) × a
   8. Buffer update: buffer = buffer + (PEω − PEω + KEω) × (1 − a)
   9. Maintaining the current position and energies
   10. If potential energy of a new position < minimum potential energy, then update the minimum values
11. Condition end

Algorithm #2: Decomposition

1. Input data: Mω
molecule2. Creating two new molecules Mω1 and Mω2
3. Obtaining positions for new molecules: ω1 and ω2 from ω
4. Calculating potential energy for new molecules: PEω1 = f(ω1) and PEω2 = f(ω2)
5. If potential energy of the current position + kinetic energy ≥ total potential energy of the new positions, then:
   6. Calculation of energy for decomposition: Edec = PEω + KEω − (PEω1 + PEω2)
   7. Proceed to step 13
8. Otherwise:
   9. Random number generation δ1, δ2 in the range [0, 1]
   10. Calculation of energy for decomposition: Edec = PEω + KEω + δ1δ2 × buffer − (PEω1 + PEω2)
   11. If Edec ≥ 0, then:
       12. Buffer update
       13. Random number generation δ3 in the range [0, 1]
       14. Distribution of kinetic energy between new molecules
       15. Maintaining minimum values for each new molecule
       16. Destruction of the current molecule
   17. Otherwise:
       18. Increase collision counter
       19. Destruction of new molecules
   20. End of condition

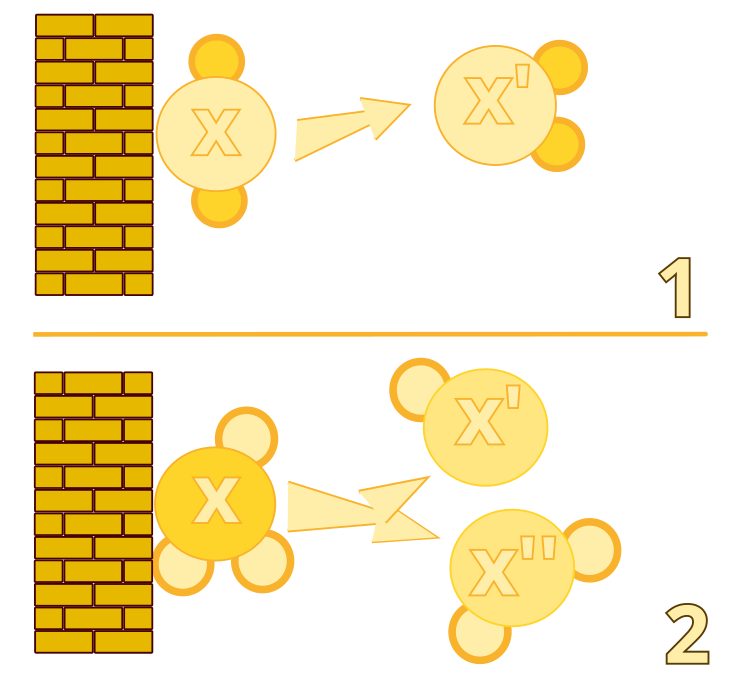
Figure 1. Inefficient wall collision: algorithm #1. Decomposition: algorithm #2

Algorithm #3: Intermolecular Ineffective Collision

1. Input data: Mω1 and Mω2
molecules2. Generating new positions for molecules: ω1 = N(ω1) and ω2 = N(ω2)
3. Calculation of potential energy for new positions: PEω1 = f(ω1) and PEω2 = f(ω2)
4. Increase collision counters: NumHitω1 = NumHitω1 + 1 and NumHitω2 = NumHitω2 + 1
5. Calculation of the energy of intermolecular interaction: Einter = (PEω1 + PEω2 + KEω1 + KEω2) − (PEω1 + PEω2)
6. If Einter ≥ 0, then:
   7. Random number generation δ4 in the range [0, 1]
   8. Distribution of kinetic energy between molecules: KEω1 = Einter × δ4 and KEω2 = Einter × (1 − δ4)
   9. Update molecule positions and energies
   10. If potential energy of a new position is less than the minimum potential energy, then update the minimum values for each molecule
11. End of condition

Algorithm #4: Synthesis

1. Input data: Mω1 and Mω2
molecules2. Creating a new Mω
molecule3. Obtaining a position for a new molecule: ω from ω1 and ω2
4. Calculating potential energy for a new molecule: PEω = f(ω)
5. If the total potential energy and kinetic energy for the new molecule is greater than or equal to the total potential energy and kinetic energy for the original molecules, then:
   6. Distribution of excess kinetic energy to a new molecule: KEω = (PEω1 + PEω2 + KEω1 + KEω2) − PEω
   7. Updating minimum values for new molecule
   8. Destruction of the original molecules
9. Otherwise:
   10. Increase collision counters for source molecules
   11. Destruction of a new molecule
12. End of condition

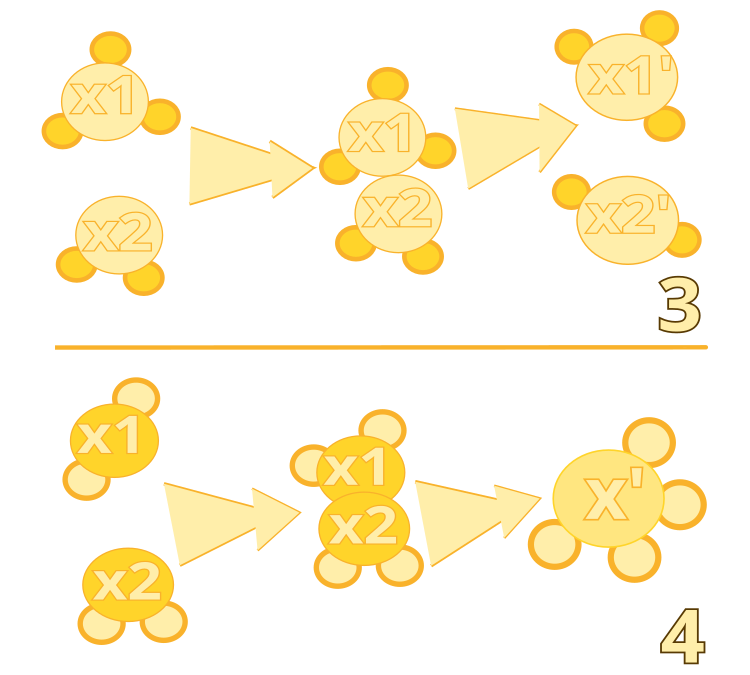
Figure 2. Inefficient intermolecular collision: algorithm #3. Synthesis: algorithm #4

The proposed description of the CRO algorithm reflects the author's vision of this approach. However, it does not take into account some important points that can significantly affect the performance and search capabilities of the algorithm.

The algorithm involves the conservation of energy in a closed space and the transition from one type of energy to another. However, the authors do not disclose the correspondence between the numerical energy indicators and the value of the target (fitness) function. It is obvious that the role of the fitness is defined by the authors as potential energy, and kinetic energy acts as a mechanism for compensating for the decrease in potential energy (the sum of all energies should ideally be a constant).

For example, if the criterion of an optimization problem is the profit factor, then the values of the target function will fluctuate in a small range compared to a problem where the balance is used as a criterion. In this case, we see that the values of the target function will vary depending on the specific optimization criterion, but the authors use constants as an external parameter of the algorithm that cannot be compared with the energies calculated in the algorithm.

Thus, the original CRO algorithm (without modifications) has a significantly limited list of tasks, in which it can be applied, so it is not universal. In this series of articles, we consider only universal algorithms applicable to optimization problems in general, and if any algorithm does not allow this, we usually modify it and bring it to a single general form.

The second point is that the original algorithm provides for the calculation of the fitness function in a disordered manner, in different parts of the logic, which will inevitably lead to problems when used in practical tasks and integrated into projects. We will fix this as well. To do this, we will need to split the chemical operators into two parts: the operators themselves and the so-called "post-operators", the first of which modifies the position of the molecules, and the second performs the necessary actions with the molecules after calculating their fitness.

The third point is that the original algorithm provides for a dynamic population size of molecules. New molecules appear and some of the old ones are destroyed. There are no mechanisms for regulating the population size, and it can vary within very wide limits. Thus, experiments have shown that with certain settings of external parameters, the population can grow from the initial 50 molecules to more than a thousand. We also solved this problem by sequentially filling the population with molecules as a result of executing operators, using a simple counter and storing the index of parent molecules in the parent population. This allows us to keep the population size constant and at the same time eliminate the need to perform the operation of removing molecules - the daughter molecules, when the conditions are met, simply replace the corresponding parent molecules.

These changes made it possible to bring the CRO algorithm to a form suitable for solving optimization problems in general, to make it convenient to integrate the algorithm into projects, and at the same time to preserve the general original concept of chemical reactions. The CRO algorithm is described in detail. If you wish, you can try to implement the accounting of potential and kinetic energies in the algorithm.

Let's move on to the code. Describe the types of reactions in the list so that we can choose the appropriate post-operator after the reactions and the structure of the molecules.

E_ReactionType enumeration:

1. synthesis is a process, in which two molecules combine to form a new one.
2. interMolecularInefColl is an intermolecular ineffective collision, in which molecules collide but do not react with each other.
3. decomposition is a process, in which a complex molecule is broken down into simpler components.
4. inefCollision is an inefficient collision with the wall, which changes the structure of the molecule.

It defines the S_CRO_Agent structure, which represents a model of the molecule in the context of the algorithm. Let's look at what fields the following structure contains:

• structure[] - an array representing the molecule structure.
• NumHit - a counter of the number of "hits" or molecule interactions.
• indMolecule_1 and indMolecule_2 - indices of interacting molecules.
• KE - a variable representing the kinetic energy of a molecule.
• f - fitness function (molecule fitness).
• rType - E_ReactionType type variable, the type of reaction a molecule participates in.

"Init" - structure method that initializes the fields. It takes the coords integer argument applied to resize the structure array using the ArrayResize function. NumHit, indMolecule_1, indMolecule_2, f and KE are initialized using zeros or -DBL_MAX.

This code represents the basic data structure for molecules in CRO algorithm and initializes their fields when a new molecule is created.

enum E_ReactionType
{
  synthesis,
  interMolecularInefColl,
  decomposition,
  inefCollision
};
// Molecule structure
struct S_CRO_Agent
{
    double structure [];
    int    NumHit;
    int    indMolecule_1;
    int    indMolecule_2;
    double KE;
    double f;
    E_ReactionType rType;


    // Initialization method
    void Init (int coords)
    {
      ArrayResize (structure, coords);
      NumHit        = 0;
      indMolecule_1 = 0;
      indMolecule_2 = 0;
      f             = -DBL_MAX;
      KE            = -DBL_MAX;
    }
};

The InefCollision method of the C_AO_CRO class is an inefficient collision that involves the creation of a new molecule by the displacement of one parent molecule. Here is what happens in this method:

1. The method accepts the index of the parent molecule and the link to the molCNT molecule counter. If molCNT exceeds or equal to the popSize population size, the method returns false and completes its work.

2. The method determines the index of a new molecule index1_, which will be created as a result of the collision.

3. The structure of the parent molecule is copied into the structure of the new one.

4. Next, the N function is executed for each coordinate of the new molecule. The function generates new coordinate values in the vicinity of the old ones.

5. New coordinate values are adjusted using the SeInDiSp function, so that they remain in the specified range from rangeMin to rangeMax.

6. Then the indMolecule_1, rType and NumHit field values of the new molecule are set. indMolecule_1 stores the index of the parent molecule, rType is set to inefCollision, while NumHit is reset.

7. At the end of the method, the molCNT molecule counter is increased by 1 and the method returns true.

//——————————————————————————————————————————————————————————————————————————————
// Ineffective collision. Obtaining a new molecule by displacing a parent one.
bool C_AO_CRO::InefCollision (int index, int &molCNT)
{
  if (molCNT >= popSize) return false;

  int index1_ = molCNT;

  ArrayCopy (Mfilial [index1_].structure, Mparent [index].structure);

  for (int c = 0; c < coords; c++)
  {
    N (Mfilial [index1_].structure [c], c);
    Mfilial [index1_].structure [c] = u.SeInDiSp (Mfilial [index1_].structure [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }

  Mfilial [index1_].indMolecule_1 = index;                 // save the parent molecule index
  Mfilial [index1_].rType         = inefCollision;
  Mfilial [index1_].NumHit        = 0;

  molCNT++;
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

The PostInefCollision method in the C_AO_CRO class is meant for handling the results of the ineffective collision of the mol molecule with other molecules in chemical reaction simulation. The method does the following:

1. Declare the ind variable and initialize it using the indMolecule_1 value from the mol object.

2. The conditional expression checks whether the f value of the mol object exceeds the f value of the parent molecule with the ind index.

3. If the condition is true, then the mol structure is copied into the structure of the parent molecule with the ind index.

4. The f value of the parent molecule is updated using the f value from mol.

5. The NumHit counter of the parent molecule is reset to zero.

6. If the mol.f > Mparent [ind].f condition is false, the NumHit counter of the parent molecule is increased by one.

In general, this method updates the structure and fitness function value of the parent molecule based on the results of an inefficient collision. If the new mol structure leads to an improvement in fitness, it replaces the structure of the parent molecule and the NumHit counter is reset. Otherwise, the NumHit counter of the parent molecule is increased.

//——————————————————————————————————————————————————————————————————————————————
// Handling the results of an ineffective collision.
void C_AO_CRO::PostInefCollision (S_CRO_Agent &mol)
{
  int ind = mol.indMolecule_1;

  if (mol.f > Mparent [ind].f)
  {
    ArrayCopy (Mparent [ind].structure, mol.structure);
    Mparent [ind].f = mol.f;
    Mparent [ind].NumHit = 0;
  }
  else
  {
    Mparent [ind].NumHit++;
  }
}
//——————————————————————————————————————————————————————————————————————————————

The Decomposition method of the C_AO_CRO class is a decomposition process that involves the creation of two new molecules by decomposing one parent molecule. Here is what happens in this method:

1. The method accepts the index parent molecule and a link to the molCNT molecule counter. If molCNT exceeds or is equal to popSize - 1, the method returns false and completes its work.

2. The method then determines the indices of two new molecules - index1_ and index2_, which will be created as a result of decomposition.

3. The structure of the parent molecule is copied into the structures of the new ones.

4. Next, the N function is executed for each coordinate of the new molecules. The function generates new coordinate values in the vicinity of the old ones. This is done separately for the first half of the coordinates for index1_ of the first daughter molecule and the second half of the coordinates for index2_ of the second molecule, respectively.

5. New coordinate values are adjusted using the SeInDiSp function, so that they remain in the specified range from rangeMin to rangeMax.

6. Then the indMolecule_1, indMolecule_2, rType and NumHit field values of the new molecule are set. indMolecule_1 and indMolecule_2 save the indices of the parent and sister molecules, respectively, rType is set to decomposition, while NumHit is set to zero.

7. At the end of the method, the molCNT molecule counter is increased by 2, and the method returns true.

//——————————————————————————————————————————————————————————————————————————————
// Decomposition. Obtaining two new molecules by decomposing a parent one.
bool C_AO_CRO::Decomposition (int index,  int &molCNT)
{
  if (molCNT >= popSize - 1) return false;

  // Creating two new molecules M_ω'_1 and M_ω'_2 from M_ω
  int index1_ = molCNT;
  int index2_ = molCNT + 1;

  ArrayCopy (Mfilial [index1_].structure, Mparent [index].structure);
  ArrayCopy (Mfilial [index2_].structure, Mparent [index].structure);

  for (int c = 0; c < coords / 2; c++)
  {
    N (Mfilial [index1_].structure [c], c);
    Mfilial [index1_].structure [c] = u.SeInDiSp  (Mfilial [index1_].structure [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
  for (int c = coords / 2; c < coords; c++)
  {
    N (Mfilial [index2_].structure [c], c);
    Mfilial [index2_].structure [c] = u.SeInDiSp  (Mfilial [index2_].structure [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }

  Mfilial [index1_].indMolecule_1 = index;                 // save the parent molecule index
  Mfilial [index1_].indMolecule_2 = index2_;               // save the index of the second daughter molecule
  Mfilial [index1_].rType         = decomposition;
  Mfilial [index1_].NumHit        = 0;

  Mfilial [index2_].indMolecule_1 = index1_;               // save the index of the first daughter molecule
  Mfilial [index2_].indMolecule_2 = -1;                    // mark the molecule so we do not handle it twice
  Mfilial [index2_].rType         = decomposition;
  Mfilial [index2_].NumHit        = 0;

  molCNT += 2;
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

The PostDecomposition method of the C_AO_CRO class handles the results of the molecule decomposition. The method does the following:

1. The method accepts a reference to the mol molecule obtained as a result of decomposition. If indMolecule_2 of the molecule is equal to "-1" (meaning that the molecule has already been processed), the method completes its work.

2. The ind index of the parent molecule is then extracted together with the indices of the two "daughter" molecules index1_ and index2_.

3. Next, check whether the f fitness function value of the first "daughter" molecule exceeds the f function values of the second "daughter" and parent molecules. If this is the case, then the first "daughter" molecule replaces the parent one. The NumHit value of the replaced molecule is reset and the flag is set.

4. If flag is still false, then a similar check is carried out for the second "daughter" molecule.

5. If after all the checks, flag is still false, the NumHit of the parent molecule is increased by 1.

The PostDecomposition method is responsible for updating the states of the parent molecule after the decomposition in the CRO algorithm.

//——————————————————————————————————————————————————————————————————————————————
// Handling decomposition results.
void C_AO_CRO::PostDecomposition (S_CRO_Agent &mol)
{
  if (mol.indMolecule_2 == -1) return;

  int ind = mol.indMolecule_1;

  int index2_ = mol.indMolecule_2;
  int index1_ = Mfilial [index2_].indMolecule_1;

  bool flag = false;

  if (Mfilial [index1_].f > Mfilial [index2_].f && Mfilial [index1_].f > Mparent [ind].f)
  {
    ArrayCopy (Mparent [ind].structure, Mfilial [index1_].structure);
    Mparent [ind].f = Mfilial [index1_].f;
    Mparent [ind].NumHit = 0;
    flag = true;
  }

  if (!flag)
  {
    if (Mfilial [index2_].f > Mfilial [index1_].f && Mfilial [index2_].f > Mparent [ind].f)
    {
      ArrayCopy (Mparent [ind].structure, Mfilial [index2_].structure);
      Mparent [ind].f = Mfilial [index2_].f;
      Mparent [ind].NumHit = 0;
      flag = true;
    }
  }

  if (!flag)
  {
    Mparent [ind].NumHit++;
  }
}
//——————————————————————————————————————————————————————————————————————————————

The InterMolInefColl method of the C_AO_CRO class is an inefficient collision that involves the creation of two new molecules by changing two parent molecules. Here is what happens in this method:

1. The method accepts indices of the two parent molecules - index1 and index2 and a link to the molCNT molecule counter. If molCNT exceeds or is equal to popSize - 1, the method returns false and completes its work.

2. The method then determines the indices of two new daughter molecules index1_ and index2_, which will be created as a result of the collision.

3. The structures of the parent molecule are copied into the structures of the new ones.

4. Next, the N function is executed for each coordinate of the new molecules. The function generates new coordinate values in the vicinity of the old ones.

5. Then the new coordinate values are adjusted using the SeInDiSp function, so that they remain in the specified range from rangeMin to rangeMax.

6. Then the indMolecule_1, indMolecule_2, rType and NumHit field values of the new molecule are set. indMolecule_1 and indMolecule_2 preserve the indices of the parent molecules, rType is set to interMolecularInefColl, while NumHit is set to zero.

7. At the end of the method, the molCNT molecule counter is increased by 2, and the method returns true.

//——————————————————————————————————————————————————————————————————————————————
// Intermolecular ineffective collision. Obtaining two new molecules by changing two parent ones
bool C_AO_CRO::InterMolInefColl (int index1, int index2, int &molCNT)
{
  if (molCNT >= popSize - 1) return false;

  int index1_ = molCNT;
  int index2_ = molCNT + 1;

  // Obtaining molecules
  ArrayCopy (Mfilial [index1_].structure, Mparent [index1].structure);
  ArrayCopy (Mfilial [index2_].structure, Mparent [index2].structure);

  // Generating new molecules ω'_1 = N(ω1) and ω'_2 = N(ω2) in the vicinity of ω1 and ω2
  for (int c = 0; c < coords; c++)
  {
    N (Mfilial [index1_].structure [c], c);
    N (Mfilial [index2_].structure [c], c);
  }

  for (int c = 0; c < coords; c++)
  {
    Mfilial [index1_].structure [c] = u.SeInDiSp  (Mfilial [index1_].structure [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    Mfilial [index2_].structure [c] = u.SeInDiSp  (Mfilial [index2_].structure [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }

  Mfilial [index1_].indMolecule_1 = index1;                 // save the index of the first parent molecule
  Mfilial [index1_].indMolecule_2 = index2_;                // save the index of the second daughter molecule
  Mfilial [index1_].rType         = interMolecularInefColl;
  Mfilial [index1_].NumHit        = 0;

  Mfilial [index2_].indMolecule_1 = index2;                 // save the index of the second parent molecule
  Mfilial [index2_].indMolecule_2 = -1;                     // mark the molecule so we do not handle it twice
  Mfilial [index2_].rType         = interMolecularInefColl;
  Mfilial [index2_].NumHit        = 0;

  molCNT += 2;
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

The PostInterMolInefColl method of the C_AO_CRO class handles the results of the intermolecular ineffective collisions. The method has the following objectives:

1. The method accepts a reference to the mol molecule obtained as a result of collision. If indMolecule_2 of the molecule is equal to "-1" (meaning that the molecule has already been processed), the method completes its work.

2. The ind1 and ind2 indices of the two parent molecules are then extracted.

3. Next, check if the f sum of the fitness values of a new molecule and its "sister" exceeds the f sum of fitness values of both parent molecules. If this is true, the new molecules replace the parent ones. The NumHit values of the replaced molecules are reset.

4. Otherwise, the NumHit values of the parent molecules are increased by 1.

The PostInterMolInefColl method is responsible for updating the states of parent molecules after the intermolecular inefficient collision in the CRO algorithm.

//——————————————————————————————————————————————————————————————————————————————
// Handling the results of an intermolecular ineffective collision.
void C_AO_CRO::PostInterMolInefColl (S_CRO_Agent &mol)
{
  if (mol.indMolecule_2 == -1) return;

  int ind1 = mol.indMolecule_1;
  int ind2 = Mfilial [mol.indMolecule_2].indMolecule_1;
  
  Mparent [ind1].NumHit++;
  Mparent [ind2].NumHit++;

  if (mol.f + Mfilial [mol.indMolecule_2].f > Mparent [ind1].f + Mparent [ind2].f)
  {
    ArrayCopy (Mparent [ind1].structure, mol.structure);
    Mparent [ind1].f = mol.f;

    ArrayCopy (Mparent [ind2].structure, Mfilial [mol.indMolecule_2].structure);
    Mparent [ind2].f = Mfilial [mol.indMolecule_2].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

The last chemical reaction operator in the algorithm - the Synthesis method of the C_AO_CRO class - is a synthesis process that involves the creation of a new molecule by fusing two parent molecules.

1. The method accepts indices of the two parent molecules - index1 and index2 and a link to the molCNT molecule counter. If molCNT exceeds or is equal to the popSize population size, the method returns false and completes its work.

2. In the loop, for each coordinate of the new molecule, the following is done: if a random number is less than 0.5, the coordinate receives the value of the corresponding coordinate of the first parent molecule Mparent[index1].structure[i]. Otherwise, it receives the value of the corresponding coordinate of the second parent molecule Mparent[index2].structure[i].

3. Then the indMolecule_1, indMolecule_2, rType and NumHit field values of the new molecule are set. indMolecule_1 and indMolecule_2 preserve the indices of the parent molecules, rType is set to synthesis, while NumHit is set to zero.

4. At the end of the method, the molCNT molecule counter is increased, and the method returns true.

//——————————————————————————————————————————————————————————————————————————————
// Synthesis. Obtaining a new molecule by fusing two parent ones
bool C_AO_CRO::Synthesis (int index1, int index2, int &molCNT)
{
  if (molCNT >= popSize) return false;

  // Create a new M_ω' molecule from M_ω1 and M_ω2
  for (int i = 0; i < coords; i++)
  {
    if (u.RNDprobab () < 0.5) Mfilial [molCNT].structure [i] = Mparent [index1].structure [i];
    else                      Mfilial [molCNT].structure [i] = Mparent [index2].structure [i];
  }

  Mfilial [molCNT].indMolecule_1 = index1; // save the index of the first parent molecule
  Mfilial [molCNT].indMolecule_2 = index2; // save the index of the second parent molecule
  Mfilial [molCNT].rType         = synthesis;
  Mfilial [molCNT].NumHit        = 0;

  molCNT++;
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

The PostSynthesis method of the C_AO_CRO class handles the synthesis results. Here is what happens in it:

1. The method accepts a reference to the mol molecule obtained as a result of synthesis. The ind1 and ind2 indices of the two parent molecules are then extracted from it.

2. Next, check if the f fitness value of a new molecule exceeds the f fitness values of both parent molecules. If this is the case, then the new molecule replaces the one of the parent molecules whose f value is less. The NumHit value of the replaced molecule is set to zero.

3. Otherwise, the NumHit values of the parent molecules are increased by 1.

The PostSynthesis method is responsible for updating the states of parent molecules after the synthesis process in the CRO algorithm.

//——————————————————————————————————————————————————————————————————————————————
// Handling synthesis results.
void C_AO_CRO::PostSynthesis (S_CRO_Agent &mol)
{
  int ind1 = mol.indMolecule_1;
  int ind2 = mol.indMolecule_2;

  if (mol.f > Mparent [ind1].f && mol.f > Mparent [ind2].f)
  {
    if (Mparent [ind1].f < Mparent [ind2].f)
    {
      ArrayCopy (Mparent [ind1].structure, mol.structure);
      Mparent [ind1].f = mol.f;
      Mparent [ind1].NumHit = 0;
    }
    else
    {
      ArrayCopy (Mparent [ind2].structure, mol.structure);
      Mparent [ind2].f = mol.f;
      Mparent [ind2].NumHit = 0;
    }
  }
  else
  {
    Mparent [ind1].NumHit++;
    Mparent [ind2].NumHit++;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Finally, let's describe the N method of the C_AO_CRO class used to change the molecule structure in the chemical reaction operators. The method is used to generate a new value for the molecule coordinate within a given range:

1. The method accepts the coord molecule coordinate, which needs to be modified as a reference, and the coordPos coordinate position in the structure.

2. The dist distance is calculated next, which is the difference between the maximum and minimum values of the range, multiplied by the molecPerturb parameter indicating the spread of values in the vicinity of the current coordinate value.

3. The minimum (min) and maximum (max) values of a new coordinate are then defined. These values are equal to the old coordinate value plus or minus the dist distance, but they cannot go beyond the specified range from rangeMin[coordPos] to rangeMax[coordPos].

4. Finally, the new coordinate value is generated using the u.GaussDistribution Gaussian distribution function, which takes the old value of the coordinate, the minimum and maximum values of the standard deviation, equal to 8.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CRO::N (double &coord, int coordPos)
{
  double dist = (rangeMax [coordPos] - rangeMin [coordPos]) * molecPerturb;

  double min = coord - dist; if (min < rangeMin [coordPos]) min = rangeMin [coordPos];
  double max = coord + dist; if (max > rangeMax [coordPos]) max = rangeMax [coordPos];

  coord = u.GaussDistribution (coord, min, max, 8);
}
//——————————————————————————————————————————————————————————————————————————————

We have analyzed all the chemical operators in terms of their functionality and role in the optimization process. This analysis has provided us with deep insight into the mechanisms that define the dynamics of molecules in chemical reaction modeling (CRO).

In the next article, we will build the algorithm and test it on the test functions. We will configure and combine the studied operators into a full-fledged CRO algorithm so that it is ready for use on practical tasks. We will then conduct a series of experiments on a wide range of test functions that will allow us to evaluate the efficiency and robustness of our approach.

Having received the results of the work, we will draw conclusions about the strengths and weaknesses of the algorithm, as well as possible directions for further improvements. This will allow us not only to improve our method, but also to provide useful recommendations for researchers working in the field of optimization and modeling of chemical processes.

Thus, the next article will be a key step in our research as we will move from theory to practice, testing and improving our algorithm to achieve the best results in solving complex optimization problems.