
Neuronale Netze leicht gemacht (Teil 12): Dropout
Inhalt
- Einführung
- 1. Dropout: Eine Methode zur Erhöhung der Konvergenz von neuronalen Netzwerken
- 2. Umsetzung
- 2.1. Erstellen einer neuen Klasse für unser Modell
- 2.2. Vorwärtsdurchlauf
- 2.3. Rückwärtsdurchlauf
- 2.4. Methoden zum Speichern und Laden von Daten
- 2.5. Änderungen in den Basisklassen des neuronalen Netzwerks
- 3. Test
- Schlussfolgerung
- Referenzen
- Die Programme dieses Artikels
Einführung
Seit dem Beginn dieser Artikelserie haben wir bereits große Fortschritte beim Studium verschiedener neuronaler Netzwerkmodelle gemacht. Aber der Lernprozess wurde immer ohne unsere Beteiligung durchgeführt. Gleichzeitig besteht immer der Wunsch, dem neuronalen Netz irgendwie zu helfen, die Trainingsergebnisse zu verbessern, was man auch als Konvergenz des neuronalen Netzes bezeichnen kann. In diesem Artikel werden wir eine solche Methode mit dem Namen Dropout betrachten.
1. Dropout: Eine Methode zur Erhöhung der Konvergenz von neuronalen Netzwerken
Beim Training eines neuronalen Netzwerks wird eine große Anzahl von Merkmalen in jedes Neuron eingespeist, und es ist schwierig, die Auswirkungen jedes einzelnen Merkmals zu bewerten. Infolgedessen werden die Fehler einiger Neuronen durch die korrekten Werte anderer Neuronen geglättet, während diese Fehler am Ausgang des neuronalen Netzwerks akkumuliert werden. Dies führt dazu, dass das Training bei einem bestimmten lokalen Minimum mit einem ziemlich großen Fehler aufhört. Dieser Effekt wird als Co-Adaptation der Merkmalsdetektoren bezeichnet, bei der sich der Einfluss der einzelnen Merkmale an die Umgebung anpasst. Besser wäre der gegenteilige Effekt, wenn die Umgebung in einzelne Merkmale zerlegt wird und es möglich ist, den Einfluss jedes Merkmals separat zu bewerten.
Im Jahr 2012 schlug eine Gruppe von Wissenschaftlern der Universität Toronto vor, einen Teil der Neuronen zufällig aus dem Lernprozess auszuschließen, um das Problem der komplexen Koadaptation zu lösen [12]. Eine Verringerung der Anzahl der Merkmale im Training erhöht die Wichtigkeit jedes Merkmals, und eine ständige Veränderung der quantitativen und qualitativen Zusammensetzung der Merkmale verringert das Risiko ihrer Koadaptation. Diese Methode wird Dropout genannt. Manchmal wird die Anwendung dieser Methode mit Entscheidungsbäumen verglichen: Durch das Auslassen einiger Neuronen erhalten wir bei jeder Trainingsiteration ein neues neuronales Netz mit eigenen Gewichten. Nach den Regeln der Kombinatorik haben solche Netze eine recht hohe Variabilität.
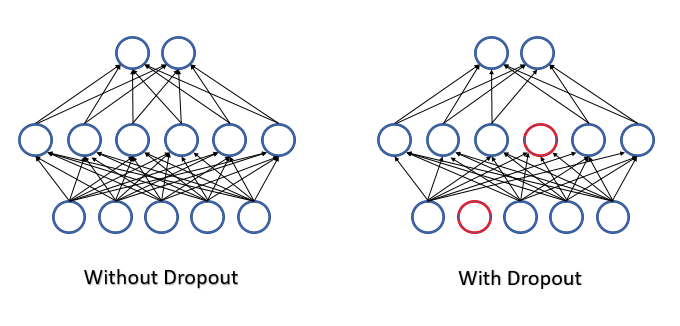
Alle Merkmale und Neuronen werden während des Betriebs des neuronalen Netzes bewertet und so erhalten wir die genaueste und unabhängige Bewertung des aktuellen Zustands der analysierten Umgebung.
Die Autoren erwähnen in ihrem Artikel (12) die Möglichkeit, die Methode zu nutzen, um die Qualität der vortrainierten Modelle zu erhöhen.
Aus der Sicht der Mathematik können wir diesen Prozess so beschreiben, dass jedes einzelne Neuron mit einer bestimmten vorgegebenen Wahrscheinlichkeit p aus dem Prozess herausfällt. Mit anderen Worten, das Neuron wird am Lernprozess des neuronalen Netzes mit der Wahrscheinlichkeit q=1-p teilnehmen.
Die Liste der Neuronen, die ausgeschlossen werden, wird durch einen Pseudo-Zufallszahlengenerator mit Normalverteilung bestimmt. Diese Vorgehensweise erlaubt es, einen möglichst gleichmäßigen Ausschluss von Neuronen zu erreichen. In der Praxis wird ein Vektor mit einer Größe gleich der Eingabesequenz erzeugt. "1" im Vektor wird für das Merkmal verwendet, das im Training verwendet werden soll, und "0" wird für die auszuschließenden Elemente verwendet.
Der Ausschluss der analysierten Merkmale führt jedoch zweifellos zu einer Verringerung des Betrags am Eingang der Neuronenaktivierungsfunktion. Um diesen Effekt zu kompensieren, werden wir den Wert jedes Merkmals mit dem 1/q-Koeffizienten multiplizieren. Dieser Koeffizient wird die Werte erhöhen, da die Wahrscheinlichkeit q immer im Bereich zwischen 0 und 1 liegt.
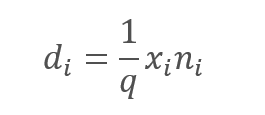 ,
,
wobei:
d — Elemente des Ergebnisvektors Dropout,
q — die Wahrscheinlichkeit der Verwendung des Neurons im Trainingsprozess,
x — die Elemente des Maskierungsvektors,
n — Elemente der Eingangssequenz.
Im Rückwärtsdurchlauf (feed-backward) während des Lernprozesses wird der Fehlergradient mit der Ableitung der obigen Funktion multipliziert. Wie man sieht, ist der Rückwärtsdurchlauf (feed-backward) im Fall von Dropout ähnlich wie der Vorwärtsdurchlauf (feed-forward) unter Verwendung des Maskierungsvektors aus dem Vorwärtsdurchlauf.
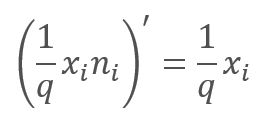
Während des Betriebs des neuronalen Netzes wird der Maskierungsvektor mit "1" gefüllt, so dass die Werte in beide Richtungen reibungslos weitergegeben werden können.
In der Praxis ist der Koeffizient 1/q während des gesamten Trainings konstant, so dass wir diesen Koeffizienten einfach einmal berechnen und anstelle von "1" in den Maskierungstensor schreiben können. So können wir die Operationen der Neuberechnung des Koeffizienten und seiner Multiplikation mit "1" der Maske in jeder Trainingsiteration ausschließen.
2. Umsetzung
Nachdem wir nun die theoretischen Aspekte betrachtet haben, gehen wir dazu über, die Varianten zur Implementierung dieser Methode in unserer Bibliothek zu betrachten. Das Erste, worauf wir stoßen, ist die Implementierung von zwei verschiedenen Algorithmen. Einer davon wird für den Trainingsprozess benötigt und der zweite wird für die Produktion verwendet werden. Dementsprechend müssen wir dem Neuron explizit angeben, nach welchem Algorithmus es im Einzelfall arbeiten soll. Zu diesem Zweck werden wir das Flag bTrain auf der Ebene des Basisneurons einführen. Der Wert des Flags wird auf true für das Training und auf false für Tests gesetzt.
class CNeuronBaseOCL : public CObject { protected: bool bTrain; ///< Training Mode Flag
Die folgenden Hilfsmethoden steuern die Flag-Werte.
virtual void TrainMode(bool flag) { bTrain=flag; }///< Set Training Mode Flag virtual bool TrainMode(void) { return bTrain; }///< Get Training Mode Flag
Das Flag ist bewusst auf der Ebene des Basisneurons implementiert. Dies ermöglicht die Verwendung von Dropout-bezogenem Code in der weiteren Entwicklung.
2.1. Erstellen einer neuen Klasse für unser Modell
Um den Dropout-Algorithmus zu implementieren, erstellen wir die neue Klasse CNeuronDropoutOCL, die wir als separate Schicht in unser Modell einbinden werden. Die neue Klasse erbt direkt von der Basisneuronen-Klasse CNeuronBaseOCL. Wir deklarieren die Variablen im Teil protected:
- OutProbability — die angegebene Wahrscheinlichkeit, dass ein Neuron ausfällt.
- OutNumber — die Anzahl der Neuronen, die ausfallen sollen.
- dInitValue — der Wert zur Initialisierung des Maskierungsvektors; im theoretischen Teil des Artikels wurde dieser Koeffizient als 1/q. angegeben.
Deklarieren wir außerdem zwei Zeiger auf Klassen:
- DropOutMultiplier — ein Dropout-Vektor.
- PrevLayer — ein Zeiger auf das Objekt der vorherigen Schicht; er wird beim Testen und bei der praktischen Anwendung verwendet.
class CNeuronDropoutOCL : public CNeuronBaseOCL { protected: CNeuronBaseOCL *PrevLayer; double OutProbability; double OutNumber; CBufferDouble *DropOutMultiplier; double dInitValue; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); ///<\brief Feed Forward method of calling kernel ::FeedForward().@param NeuronOCL Pointer to previous layer. virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) {return true;} ///< Method for updating weights.@param NeuronOCL Pointer to previous layer. //--- int RND(void) { xor128; return (int)((double)(Neurons()-1)/UINT_MAX*rnd_w); } ///< Generates a random neuron position to turn off public: CNeuronDropoutOCL(void); ~CNeuronDropoutOCL(void); //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons,double out_prob, ENUM_OPTIMIZATION optimization_type); ///< Method of initialization class.@param[in] numOutputs Number of connections to next layer.@param[in] myIndex Index of neuron in layer.@param[in] open_cl Pointer to #COpenCLMy object. #param[in] numNeurons Number of neurons in layer #param[in] out_prob Probability of neurons shutdown @param optimization_type Optimization type (#ENUM_OPTIMIZATION)@return Boolen result of operations. //--- virtual int getOutputIndex(void) { return (bTrain ? Output.GetIndex() : PrevLayer.getOutputIndex()); } ///< Get index of output buffer @return Index virtual int getGradientIndex(void) { return (bTrain ? Gradient.GetIndex() : PrevLayer.getGradientIndex()); } ///< Get index of gradient buffer @return Index //--- virtual int getOutputVal(double &values[]) { return (bTrain ? Output.GetData(values) : PrevLayer.getOutputVal(values)); } ///< Get values of output buffer @param[out] values Array of data @return number of items virtual int getOutputVal(CArrayDouble *values) { return (bTrain ? Output.GetData(values) : PrevLayer.getOutputVal(values)); } ///< Get values of output buffer @param[out] values Array of data @return number of items virtual int getGradient(double &values[]) { return (bTrain ? Gradient.GetData(values) : PrevLayer.getGradient(values)); } ///< Get values of gradient buffer @param[out] values Array of data @return number of items virtual CBufferDouble *getOutput(void) { return (bTrain ? Output : PrevLayer.getOutput()); } ///< Get pointer of output buffer @return Pointer to object virtual CBufferDouble *getGradient(void) { return (bTrain ? Gradient : PrevLayer.getGradient()); } ///< Get pointer of gradient buffer @return Pointer to object //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); ///< Method to transfer gradient to previous layer by calling kernel ::CalcHiddenGradient(). @param NeuronOCL Pointer to next layer. //--- virtual bool Save(int const file_handle);///< Save method @param[in] file_handle handle of file @return logical result of operation virtual bool Load(int const file_handle);///< Load method @param[in] file_handle handle of file @return logical result of operation //--- virtual int Type(void) const { return defNeuronDropoutOCL; }///< Identificator of class.@return Type of class };
Die Liste der Klassenmethoden dürfte Ihnen bekannt sein, da sie alle die Methoden der Elternklasse überschreiben. Die einzige Ausnahme ist die Methode RND, die dazu dient, Pseudozufallszahlen aus der Gleichverteilung zu erzeugen. Der Algorithmus dieser Methode wurde in dem Artikel 13 beschrieben. Um eine größtmögliche Zufälligkeit der Werte in allen Objekten unseres neuronalen Netzes zu gewährleisten, ist der Pseudo-Zufallszahlengenerator als Makro-Substitution mit globalen Variablen implementiert.
#define xor128 rnd_t=(rnd_x^(rnd_x<<11)); \ rnd_x=rnd_y; \ rnd_y=rnd_z; \ rnd_z=rnd_w; \ rnd_w=(rnd_w^(rnd_w>>19))^(rnd_t^(rnd_t>>8)) uint rnd_x=MathRand(), rnd_y=MathRand(), rnd_z=MathRand(), rnd_w=MathRand(), rnd_t=0;
Der vorgeschlagene Algorithmus erzeugt eine Folge von Ganzzahlen im Bereich [0,UINT_MAX=4294967295]. Daher wird bei der Methode zu Erzeugung einer Pseudo-Zufallssequenz nach der Ausführung des Makros der resultierende Wert auf die Größe der Sequenz normiert.
int RND(void) { xor128; return (int)((double)(Neurons()-1)/UINT_MAX*rnd_w); }
Wenn Sie frühere Artikel innerhalb dieser Serie gelesen haben, ist Ihnen vielleicht aufgefallen, dass wir in früheren Versionen Methoden für die Arbeit mit den Datenpuffern der Klasse nicht von anderen Objekten überschrieben haben. Diese Methoden werden verwendet, um Daten zwischen den Schichten des neuronalen Netzes auszutauschen, wenn Neuronen auf die Daten der vorherigen oder nächsten Schicht zugreifen.
Diese Lösung wurde gewählt, um den Betrieb des neuronalen Netzes in der praktischen Anwendung zu optimieren. Vergessen wir nicht, dass die Dropout-Schicht nur für das Training des neuronalen Netzes verwendet wird. Während des Testens und der weiteren Anwendung ist dieser Algorithmus deaktiviert. Durch Überschreiben der Methoden zum Zugriff auf den Datenpuffer haben wir das Überspringen der Dropout-Schicht ermöglicht. Alle überschriebenen Methoden folgen dem gleichen Prinzip. Anstatt die Daten zu kopieren, implementieren wir das Ersetzen der Puffer der Dropout-Schicht mit den Puffern der vorherigen Schicht. So ist die Geschwindigkeit eines neuronalen Netzes mit Dropout-Schicht im weiteren Betrieb vergleichbar mit der Geschwindigkeit eines ähnlichen Netzes ohne Dropout, während wir alle Vorteile des Neuronendropouts in der Trainingsphase erhalten.
virtual int getOutputIndex(void) { return (bTrain ? Output.GetIndex() : PrevLayer.getOutputIndex()); }
Der gesamte Code aller Klassenmethoden befindet sich in der Anlage.
2.2. Vorwärtsdurchlauf
Traditionell implementieren wir einen Vorwärtsdurchlauf in der Methode feedForward. Zu Beginn der Methode prüfen wir die Gültigkeit des empfangenen Zeigers auf die vorherige Schicht des neuronalen Netzes und des Zeigers auf das OpenCL-Objekt. Danach speichern wir die in der vorherigen Schicht verwendete Aktivierungsfunktion und den Zeiger auf das Objekt der vorherigen Schicht. In der Praxis des neuronalen Netzes endet hier der Vorwärtsdurchlauf der Dropout-Schicht. Ein weiterer Versuch, von der nächsten Schicht auf diese Schicht zuzugreifen, aktiviert den oben beschriebenen Mechanismus zum Ersetzen von Datenpuffern.
bool CNeuronDropoutOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- activation=(ENUM_ACTIVATION)NeuronOCL.Activation(); PrevLayer=NeuronOCL; if(!bTrain) return true;
Die nachfolgenden Iterationen sind nur für den Trainingsmodus des neuronalen Netzes relevant. Erzeugen wir zunächst einen Maskierungsvektor, in dem wir die Neuronen definieren, die bei diesem Schritt herausfallen sollen. Wir schreiben die Maske in den DropOutMultiplier-Puffer, prüfen die Verfügbarkeit des zuvor erstellten Objekts und erstellen ggf. ein neues. Initialisieren wir noch den Puffer mit Anfangswerten. Um die Berechnungen zu reduzieren, wollen wir den Puffer mit einem steigenden Faktor 1/q initialisieren.
if(CheckPointer(DropOutMultiplier)==POINTER_INVALID) DropOutMultiplier=new CBufferDouble(); if(!DropOutMultiplier.BufferInit(NeuronOCL.Neurons(),dInitValue)) return false; for(int i=0;i<OutNumber;i++) { uint p=RND(); double val=DropOutMultiplier.At(p); if(val==0 || val==DBL_MAX) { i--; continue; } if(!DropOutMultiplier.Update(RND(),0)) return false; }
Wir organisieren nach der Pufferinitialisierung eine Schleife mit der Anzahl der Wiederholungen, die gleich der Anzahl der auszuscheidenden Neuronen ist. Die zufällig ausgewählten Elemente des Puffers werden durch Nullwerte ersetzt. Um das Risiko zu vermeiden, zweimal "0" in eine Zelle zu schreiben, implementieren wir eine zusätzliche Prüfung innerhalb der Schleife.
Nach der Generierung der Maske legen wir einen Puffer direkt im GPU-Speicher an und übertragen die Daten.
if(!DropOutMultiplier.BufferCreate(OpenCL)) return false;
Nun müssen wir zwei Vektoren elementweise multiplizieren. Das Ergebnis dieser Operation wird die Ausgabe der Dropout-Schicht sein. Die Vektor-Multiplikationsoperation wird auf einer GPU mit OpenCL implementiert. Der effizienteste Weg, die Elemente zu multiplizieren, ist die Verwendung von Vektoroperationen. Ich habe im OpenCL-Kernel Variablen vom Typ double4 verwendet, d. h. ein Vektor mit vier Elementen. Daher wird die Anzahl der gestarteten Threads 4-mal kleiner sein als die Anzahl der Elemente in Vektoren.
uint global_work_offset[1]= {0}; uint global_work_size[1]; int i=Neurons()%4; global_work_size[0]=(Neurons()-i)/4+(i>0 ? 1 : 0);
Als Nächstes geben wir die anfänglichen Datenpuffer und Variablen an und starten die Ausführung des Kernels.
if(!OpenCL.SetArgumentBuffer(def_k_Dropout,def_k_dout_input,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_Dropout,def_k_dout_map,DropOutMultiplier.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_Dropout,def_k_dout_out,Output.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_Dropout,def_k_dout_dimension,Neurons())) return false; ResetLastError(); if(!OpenCL.Execute(def_k_Dropout,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Dropout: %d",GetLastError()); return false; }
Das Ergebnis der im Kernel ausgeführten Operation wird am Ende der Methode erhalten. Hier wird der Maskierungspuffer aus dem GPU-Speicher gelöscht.
if(!Output.BufferRead()) return false; DropOutMultiplier.BufferFree(); //--- return true; }
Wir verlassen nach Abschluss der Operationen die Methode mit true.
Die Beschreibung der Vorwärtsdurchlauf-Methode wäre unvollständig ohne die Betrachtung der Operationen auf der GPU-Seite. Hier ist der Kernel-Code.
__kernel void Dropout (__global double *inputs, ///<[in] Input matrix __global double *map, ///<[in] Dropout map matrix __global double *out, ///<[out] Output matrix int dimension ///< Dimension of matrix )
Der Kernel erhält in Parametern Zeiger auf zwei Eingangstensoren mit den Anfangsdaten und dem Ergebnistensor sowie die Größe der Vektoren.
Wir bestimmen im Kernel-Code die zu multiplizierenden Elemente entsprechend der Thread-Nummer. Danach wird der Code in zwei Zweige aufgeteilt. Der erste Zweig ist der Hauptzweig: Verwendung der Vektoroperationen, um die vier aufeinanderfolgenden Elemente zu multiplizieren und Schreiben der erhaltenen Daten in die entsprechenden Elemente des Ergebnispuffers.
{
const int i=get_global_id(0)*4;
if(i+3<dimension)
{
double4 k=(double4)(inputs[i],inputs[i+1],inputs[i+2],inputs[i+3])*(double4)(map[i],map[i+1],map[i+2],map[i+3]);
out[i]=k.s0;
out[i+1]=k.s1;
out[i+2]=k.s2;
out[i+3]=k.s3;
}
else
for(int k=i;k<min(dimension,i+4);k++)
out[i+k]=(inputs[i+k]*map[i+k]);
}
Der zweite Zweig wird nur aktiviert, wenn die Anzahl der Elemente in den Tensoren kein Vielfaches von 4 ist, und die restlichen Elemente werden in der Schleife multipliziert. Eine solche Schleife wird nicht mehr als 3 Iterationen haben und somit nicht zeitkritisch sein.
Der gesamte Code aller Klassen und Methoden befindet sich in der Anlage.
2.3. Rückwärtsdurchlauf
Der Rückwärtsdurchlauf in allen bisher betrachteten Neuronen wurde in 2 Methoden aufgeteilt:
- calcInputGradients — Propagieren eines Fehlergradienten an die vorherige Schicht.
- updateInputWeights — Aktualisieren der Gewichte der neuronalen Schicht.
Im Fall von Dropout verfügen wir nicht über den Gewichtstensor. Um jedoch die allgemeine Struktur der Objekte beizubehalten, werden wir die Methode updateInputWeights überschreiben - in diesem Fall wird sie jedoch immer true zurückgeben.
virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) {return true;} ///< Method for updating weights.
Kommen wir nun zur Implementierung der Methode calcInputGradients. Diese Methode erhält als Parameter einen Zeiger auf die vorherige Schicht. Zu Beginn der Methode prüfen wir die Gültigkeit des empfangenen Zeigers und eines Zeigers auf das OpenCL-Objekt. Anschließend wird der Algorithmus wie im Vorwärtsdurchlauf auf den Trainings- und den Operationsprozess aufgeteilt. Im Test- oder Betriebsmodus verlassen wir hier die Methode, da aufgrund des Datenpufferaustauschs die nächste neuronale Schicht den Gradienten direkt in den Puffer der vorherigen Schicht geschrieben hat, wodurch unnötige Iterationen in der Dropout-Schicht vermieden werden.
bool CNeuronDropoutOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- if(!bTrain) return true;
Im Trainingsmodus wird der Gradient auf eine andere Weise propagiert. Der folgende Algorithmus ist nur für das Training des neuronalen Netzes relevant. Wie bei der Vorwärtsdurchlauf-Methode wird die Gültigkeit des Zeigers auf den Maskierungspuffer DropOutMultiplier überprüft. Im Gegensatz zum Vorwärtsdurchlauf führt ein Validierungsfehler jedoch nicht zum Anlegen eines neuen Puffers - in diesem Fall verlassen wir die Methode mit false. Das liegt daran, dass der Rückwärtsdurchlauf die vom Vorwärtsdurchlauf erzeugte Maske verwendet. Diese Vorgehensweise gewährleistet die Vergleichbarkeit der Daten und die korrekte Verteilung des Fehlergradienten zwischen den Neuronen.
if(CheckPointer(DropOutMultiplier)==POINTER_INVALID) return false; //--- if(!DropOutMultiplier.BufferCreate(OpenCL)) return false;
Nach erfolgreicher Validierung des DropOutMultiplier-Objekts legen wir einen Puffer im GPU-Speicher an und füllen ihn mit Daten.
Nun müssen wir zwei Vektoren elementweise multiplizieren. Kommt Ihnen das nicht bekannt vor? Genau der gleiche Satz steht oben, in der Beschreibung des Vorwärtsdurchlauf. Ja, in der Tat. Im theoretischen Teil haben wir gesehen, dass die Ableitung der mathematischen Funktion Dropout gleich dem steigenden Koeffizienten ist. Daher werden wir beim Rückwärtsdurchlauf auch den Gradienten aus der nächsten Schicht mit dem steigenden Koeffizienten multiplizieren, der in den Maskierungspuffer DropOutMultiplier geschrieben wird. Die Klasse CNeuronDropoutOCL ist also ein einzigartiger Fall, in dem derselbe Kernel sowohl für den Vorwärts- als auch für den Rückwärtsdurchlauf verwendet wird, aber in diesen Fällen werden unterschiedliche Eingabedaten eingespeist: für den Vorwärtsdurchlauf sind es die Ausgabedaten der Neuronen, und für den Rückwärtsdurchlauf ist es der Fehlergradient.
Wir spezifizieren also die Datenpuffer und rufen die Kernel-Ausführung auf. Der Code ist ähnlich wie der Code für den Vorwärtsdurchlauf und bedarf daher keiner zusätzlichen Erklärungen.
uint global_work_offset[1]= {0}; uint global_work_size[1]; int i=Neurons()%4; global_work_size[0]=(Neurons()-i)/4+(i>0 ? 1 : 0); if(!OpenCL.SetArgumentBuffer(def_k_Dropout,def_k_dout_input,Gradient.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_Dropout,def_k_dout_map,DropOutMultiplier.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_Dropout,def_k_dout_out,NeuronOCL.getGradientIndex())) return false; if(!OpenCL.SetArgument(def_k_Dropout,def_k_dout_dimension,Neurons())) return false; ResetLastError(); if(!OpenCL.Execute(def_k_Dropout,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Dropout: %d",GetLastError()); return false; } if(!NeuronOCL.getGradient().BufferRead()) return false; DropOutMultiplier.BufferFree(); //--- return true; }
Der gesamte Code aller Klassen und Methoden befindet sich in der Anlage.
2.4. Methoden zum Speichern und Laden von Daten
Schauen wir uns die Methoden an, die das Dropout-Objekt der neuronalen Schicht speichern und laden. Es besteht keine Notwendigkeit, das Maskenpuffer-Objekt zu speichern, da bei jedem Trainingszyklus eine neue Maske generiert wird. In der Initialisierungsmethode der Klasse CNeuronDropoutOCL wurde nur eine Variable hinzugefügt: die Wahrscheinlichkeit des Ausschlusses eines Neurons, die gespeichert werden soll.
In der Methode Save rufen wir die entsprechende Methode der Elternklasse auf. Nach erfolgreicher Beendigung speichern wir die angegebene Wahrscheinlichkeit des Ausscheidens eines Neurons.
bool CNeuronDropoutOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false; //--- if(FileWriteDouble(file_handle,OutProbability)<=0) return false; //--- return true; }
In der Methode Laden werden wir Daten von der Festplatte lesen und alle Elemente der Klasse wiederherstellen. Daher ist der Algorithmus dieser Methode ein wenig komplizierter als der von Save.
In Analogie zur Speichermethode der Klasse rufen wir die gleiche Methode wie die der Elternklasse auf. Nach ihrer Fertigstellung berechnen wir die Neuronen-Ausfallwahrscheinlichkeit. Damit ist die Speichermethode abgeschlossen, aber wir müssen die fehlenden Elemente wiederherstellen. Basierend auf der Neuronen-Ausfallwahrscheinlichkeit berechnen wir die Anzahl der auszuschließenden Neuronen und den Wert des ansteigenden Koeffizienten, der auch als Wert für die Initialisierung des Maskierungsvektors dient.
bool CNeuronDropoutOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false; //--- OutProbability=FileReadDouble(file_handle); OutNumber=(int)(Neurons()*OutProbability); dInitValue=1/(1-OutProbability); if(CheckPointer(DropOutMultiplier)==POINTER_INVALID) DropOutMultiplier=new CBufferDouble(); if(!DropOutMultiplier.BufferInit(Neurons()+1,dInitValue)) return false; //--- return true; }
Jetzt, nach der Berechnung, können wir den Maskierungsvektor wiederherstellen. Wir prüfen die Gültigkeit des Zeigers auf das Datenpuffer-Objekt in DropOutMultiplier und legen ggf. ein neues Objekt an. Dann initialisieren wir den Maskierungspuffer mit Initialwerten.
2.5. Änderungen in den Basisklassen des neuronalen Netzwerks
Auch diese neue Klasse sollte korrekt in den Bibliotheksbetrieb eingefügt werden. Beginnen wir mit der Deklaration von Makro-Ersetzungen für die Arbeit mit dem neuen Kernel. Außerdem müssen wir die Identifikationskonstante für die neue Klasse festlegen.
#define def_k_Dropout 23 ///< Index of the kernel for Dropout process (#Dropout) #define def_k_dout_input 0 ///< Inputs Tensor #define def_k_dout_map 1 ///< Map Tensor #define def_k_dout_out 2 ///< Out Tensor #define def_k_dout_dimension 3 ///< Dimension of Inputs #define defNeuronDropoutOCL 0x7890 ///<Dropout neuron OpenCL \details Identified class #CNeuronDropoutOCL
Dann fügen wir in der Methode zur Beschreibung der neuronalen Schicht eine neue Variable hinzu, um die Ausfallwahrscheinlichkeit der Neuronen zu erfassen.
class CLayerDescription : public CObject { public: /** Constructor */ CLayerDescription(void); /** Destructor */~CLayerDescription(void) {}; //--- int type; ///< Type of neurons in layer (\ref ObjectTypes) int count; ///< Number of neurons int window; ///< Size of input window int window_out; ///< Size of output window int step; ///< Step size int layers; ///< Layers count ENUM_ACTIVATION activation; ///< Type of activation function (#ENUM_ACTIVATION) ENUM_OPTIMIZATION optimization; ///< Type of optimization method (#ENUM_OPTIMIZATION) double probability; ///< Probability of neurons shutdown, only Dropout used };
In der Methode zur Erstellung des neuronalen Netzwerks CNet::CNet fügen wir im Block zur Erstellung und Initialisierung von Schichten den Code zur Initialisierung einer neuen Schicht hinzu (im folgenden Code hervorgehoben).
for(int i=0; i<total; i++) { prev=desc; desc=Description.At(i); if((i+1)<total) { next=Description.At(i+1); if(CheckPointer(next)==POINTER_INVALID) return; } else next=NULL; int outputs=(next==NULL || (next.type!=defNeuron && next.type!=defNeuronBaseOCL) ? 0 : next.count); temp=new CLayer(outputs); int neurons=(desc.count+(desc.type==defNeuron || desc.type==defNeuronBaseOCL ? 1 : 0)); if(CheckPointer(opencl)!=POINTER_INVALID) { CNeuronBaseOCL *neuron_ocl=NULL; CNeuronConvOCL *neuron_conv_ocl=NULL; CNeuronAttentionOCL *neuron_attention_ocl=NULL; CNeuronMLMHAttentionOCL *neuron_mlattention_ocl=NULL; CNeuronDropoutOCL *dropout=NULL; switch(desc.type) { case defNeuron: case defNeuronBaseOCL: neuron_ocl=new CNeuronBaseOCL(); if(CheckPointer(neuron_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_ocl.Init(outputs,0,opencl,desc.count,desc.optimization)) { delete neuron_ocl; delete temp; return; } neuron_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_ocl)) { delete neuron_ocl; delete temp; return; } neuron_ocl=NULL; break; //--- case defNeuronConvOCL: neuron_conv_ocl=new CNeuronConvOCL(); if(CheckPointer(neuron_conv_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_conv_ocl.Init(outputs,0,opencl,desc.window,desc.step,desc.window_out,desc.count,desc.optimization)) { delete neuron_conv_ocl; delete temp; return; } neuron_conv_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_conv_ocl)) { delete neuron_conv_ocl; delete temp; return; } neuron_conv_ocl=NULL; break; //--- case defNeuronAttentionOCL: neuron_attention_ocl=new CNeuronAttentionOCL(); if(CheckPointer(neuron_attention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_attention_ocl.Init(outputs,0,opencl,desc.window,desc.count,desc.optimization)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_attention_ocl)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl=NULL; break; //--- case defNeuronMHAttentionOCL: neuron_attention_ocl=new CNeuronMHAttentionOCL(); if(CheckPointer(neuron_attention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_attention_ocl.Init(outputs,0,opencl,desc.window,desc.count,desc.optimization)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_attention_ocl)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl=NULL; break; //--- case defNeuronMLMHAttentionOCL: neuron_mlattention_ocl=new CNeuronMLMHAttentionOCL(); if(CheckPointer(neuron_mlattention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_mlattention_ocl.Init(outputs,0,opencl,desc.window,desc.window_out,desc.step,desc.count,desc.layers,desc.optimization)) { delete neuron_mlattention_ocl; delete temp; return; } neuron_mlattention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_mlattention_ocl)) { delete neuron_mlattention_ocl; delete temp; return; } neuron_mlattention_ocl=NULL; break; //--- case defNeuronDropoutOCL: dropout=new CNeuronDropoutOCL(); if(CheckPointer(dropout)==POINTER_INVALID) { delete temp; return; } if(!dropout.Init(outputs,0,opencl,desc.count,desc.probability,desc.optimization)) { delete dropout; delete temp; return; } if(!temp.Add(dropout)) { delete dropout; delete temp; return; } dropout=NULL; break; //--- default: return; break; } }
Vergessen wir nicht, in der gleichen Methode einen neuen Kernel zu deklarieren.
opencl.SetKernelsCount(24); opencl.KernelCreate(def_k_FeedForward,"FeedForward"); opencl.KernelCreate(def_k_CalcOutputGradient,"CalcOutputGradient"); opencl.KernelCreate(def_k_CalcHiddenGradient,"CalcHiddenGradient"); opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum"); opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam"); opencl.KernelCreate(def_k_AttentionGradients,"AttentionInsideGradients"); opencl.KernelCreate(def_k_AttentionOut,"AttentionOut"); opencl.KernelCreate(def_k_AttentionScore,"AttentionScore"); opencl.KernelCreate(def_k_CalcHiddenGradientConv,"CalcHiddenGradientConv"); opencl.KernelCreate(def_k_CalcInputGradientProof,"CalcInputGradientProof"); opencl.KernelCreate(def_k_FeedForwardConv,"FeedForwardConv"); opencl.KernelCreate(def_k_FeedForwardProof,"FeedForwardProof"); opencl.KernelCreate(def_k_MatrixSum,"SumMatrix"); opencl.KernelCreate(def_k_Matrix5Sum,"Sum5Matrix"); opencl.KernelCreate(def_k_UpdateWeightsConvAdam,"UpdateWeightsConvAdam"); opencl.KernelCreate(def_k_UpdateWeightsConvMomentum,"UpdateWeightsConvMomentum"); opencl.KernelCreate(def_k_Normilize,"Normalize"); opencl.KernelCreate(def_k_NormilizeWeights,"NormalizeWeights"); opencl.KernelCreate(def_k_ConcatenateMatrix,"ConcatenateBuffers"); opencl.KernelCreate(def_k_DeconcatenateMatrix,"DeconcatenateBuffers"); opencl.KernelCreate(def_k_MHAttentionGradients,"MHAttentionInsideGradients"); opencl.KernelCreate(def_k_MHAttentionScore,"MHAttentionScore"); opencl.KernelCreate(def_k_MHAttentionOut,"MHAttentionOut"); opencl.KernelCreate(def_k_Dropout,"Dropout");
Die gleiche neue Kernel-Deklaration muss der Methode zum Lesen des vortrainierten neuronalen Netzes von der Festplatte hinzugefügt werden - CNet::Load.
In Bezug auf den Prozess des Ladens eines vortrainierten neuronalen Netzes müssen wir auch die Methode CLayer::CreateElement anpassen, die ein Element der Schicht des neuronalen Netzes erstellt, indem wir den entsprechenden Code für die Erstellung des Dropout-Elements hinzufügen. Die Änderungen sind unten hervorgehoben.
bool CLayer::CreateElement(int index) { if(index>=m_data_max) return false; //--- bool result=false; CNeuronBase *temp=NULL; CNeuronProof *temp_p=NULL; CNeuronBaseOCL *temp_ocl=NULL; CNeuronConvOCL *temp_con_ocl=NULL; CNeuronAttentionOCL *temp_at_ocl=NULL; CNeuronMLMHAttentionOCL *temp_mlat_ocl=NULL; CNeuronDropoutOCL *temp_drop_ocl=NULL; if(iFileHandle<=0) { temp=new CNeuron(); if(CheckPointer(temp)==POINTER_INVALID || !temp.Init(iOutputs,index,SGD)) return false; result=true; } else { int type=FileReadInteger(iFileHandle); switch(type) { case defNeuron: temp=new CNeuron(); if(CheckPointer(temp)==POINTER_INVALID) result=false; result=temp.Init(iOutputs,index,ADAM); break; case defNeuronProof: temp_p=new CNeuronProof(); if(CheckPointer(temp_p)==POINTER_INVALID) result=false; if(temp_p.Init(iOutputs,index,1,1,1,ADAM)) { temp=temp_p; result=true; } break; case defNeuronConv: temp_p=new CNeuronConv(); if(CheckPointer(temp_p)==POINTER_INVALID) result=false; if(temp_p.Init(iOutputs,index,1,1,1,ADAM)) { temp=temp_p; result=true; } break; case defNeuronLSTM: temp_p=new CNeuronLSTM(); if(CheckPointer(temp_p)==POINTER_INVALID) result=false; if(temp_p.Init(iOutputs,index,1,1,1,ADAM)) { temp=temp_p; result=true; } break; case defNeuronBaseOCL: if(CheckPointer(OpenCL)==POINTER_INVALID) return false; temp_ocl=new CNeuronBaseOCL(); if(CheckPointer(temp_ocl)==POINTER_INVALID) result=false; if(temp_ocl.Init(iOutputs,index,OpenCL,1,ADAM)) { m_data[index]=temp_ocl; return true; } break; case defNeuronConvOCL: if(CheckPointer(OpenCL)==POINTER_INVALID) return false; temp_con_ocl=new CNeuronConvOCL(); if(CheckPointer(temp_con_ocl)==POINTER_INVALID) result=false; if(temp_con_ocl.Init(iOutputs,index,OpenCL,1,1,1,1,ADAM)) { m_data[index]=temp_con_ocl; return true; } break; case defNeuronAttentionOCL: if(CheckPointer(OpenCL)==POINTER_INVALID) return false; temp_at_ocl=new CNeuronAttentionOCL(); if(CheckPointer(temp_at_ocl)==POINTER_INVALID) result=false; if(temp_at_ocl.Init(iOutputs,index,OpenCL,1,1,ADAM)) { m_data[index]=temp_at_ocl; return true; } break; case defNeuronMHAttentionOCL: if(CheckPointer(OpenCL)==POINTER_INVALID) return false; temp_at_ocl=new CNeuronMHAttentionOCL(); if(CheckPointer(temp_at_ocl)==POINTER_INVALID) result=false; if(temp_at_ocl.Init(iOutputs,index,OpenCL,1,1,ADAM)) { m_data[index]=temp_at_ocl; return true; } break; case defNeuronMLMHAttentionOCL: if(CheckPointer(OpenCL)==POINTER_INVALID) return false; temp_mlat_ocl=new CNeuronMLMHAttentionOCL(); if(CheckPointer(temp_mlat_ocl)==POINTER_INVALID) result=false; if(temp_mlat_ocl.Init(iOutputs,index,OpenCL,1,1,1,1,0,ADAM)) { m_data[index]=temp_mlat_ocl; return true; } break; case defNeuronDropoutOCL: if(CheckPointer(OpenCL)==POINTER_INVALID) return false; temp_drop_ocl=new CNeuronDropoutOCL(); if(CheckPointer(temp_drop_ocl)==POINTER_INVALID) result=false; if(temp_drop_ocl.Init(iOutputs,index,OpenCL,1,0.1,ADAM)) { m_data[index]=temp_drop_ocl; return true; } break; default: result=false; break; } } if(result) m_data[index]=temp; //--- return (result); }
Die neue Klasse sollte zu den Dispatcher-Methoden der Basisklasse CNeuronBaseOCL hinzugefügt werden.
Der Vorwärtsdurchlauf CNeuronBaseOCL::FeedForward.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; }
Die Methode der Weiterleitung des Fehlergradienten CNeuronBaseOCL::calcHiddenGradients.
bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; CNeuronAttentionOCL *at=NULL; CNeuronMLMHAttentionOCL *mlat=NULL; CNeuronConvOCL *conv=NULL; CNeuronDropoutOCL *dropout=NULL; switch(TargetObject.Type()) { case defNeuronBaseOCL: temp=TargetObject; return calcHiddenGradients(temp); break; case defNeuronConvOCL: conv=TargetObject; temp=GetPointer(this); return conv.calcInputGradients(temp); break; case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: at=TargetObject; temp=GetPointer(this); return at.calcInputGradients(temp); break; case defNeuronMLMHAttentionOCL: mlat=TargetObject; temp=GetPointer(this); return mlat.calcInputGradients(temp); break; case defNeuronDropoutOCL: dropout=TargetObject; temp=GetPointer(this); return dropout.calcInputGradients(temp); break; } //--- return false; }
Und überraschenderweise ist hier die Methode zur Aktualisierung der Gewichte CNeuronBaseOCL::UpdateInputWeights.
bool CNeuronBaseOCL::UpdateInputWeights(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: temp=SourceObject; return updateInputWeights(temp); break; } //--- return false; }
Auch wenn die oben genannten Änderungen geringfügig oder unbedeutend erscheinen mögen, führt das Fehlen mindestens einer von ihnen zu einem fehlerhaften Betrieb des gesamten neuronalen Netzwerks.
Der gesamte Code aller Klassen und Methoden befindet sich in der Anlage.
3. Tests
Um die Nachfolge und Vererbung zu erhalten, verwenden wir einen Expert Advisor aus dem Artikel 11, dem 4 Dropout-Layer hinzugefügt wurden:
- 1 nach den Anfangsdaten,
- 1 nach dem eingebetteten Schicht,
- 1 nach dem Aufmerksamkeitsblock,
- 1 nach der ersten vollständig verbundenen Schicht.
Die Struktur des neuronalen Netzes ist im folgenden Code beschrieben.
//--- 0 CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBaseOCL; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 1 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronDropoutOCL; desc.probability=0.2; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 2 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronConvOCL; desc.window=12; desc.step=12; desc.window_out=24; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 3 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronDropoutOCL; desc.probability=0.2; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 4 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronMLMHAttentionOCL; desc.window=24; desc.window_out=4; desc.step=8; //heads desc.layers=5; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 5 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronDropoutOCL; desc.probability=0.2; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 6 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 7 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuronDropoutOCL; desc.probability=0.2; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 8 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 9 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; desc.activation=SIGMOID; desc.optimization=ADAM;
Der Expert Advisor wurde auf EURUSD mit dem H1-Zeitrahmen getestet, historische Daten der letzten 20 Candlesticks werden in das neuronale Netzwerk eingespeist. Das Testen aller Architekturen auf ähnlichen Datensätzen ermöglicht die Minimierung des Einflusses externer Faktoren, sowie die Bewertung der Leistung verschiedener Architekturen unter ähnlichen Bedingungen.
Beim Vergleich zweier Lerndiagramme des neuronalen Netzes mit und ohne Dropout kann man sehen, dass die ersten 30 Epochen der Fehlerlinien des neuronalen Netzes fast parallel waren, während das neuronale Netz ohne Dropout etwas bessere Ergebnisse zeigte. Aber nach der 33. Epoche gibt es einen Rückgang dieses Parameters, den der Expert Advisor mit Dropout zeigt. Nach der 35. Epoche zeigt Dropout das beste Ergebnis, es gibt eine Tendenz zur Fehlerabnahme. Der Expert Advisor ohne Dropout hält den Fehler weiterhin auf dem gleichen Niveau.
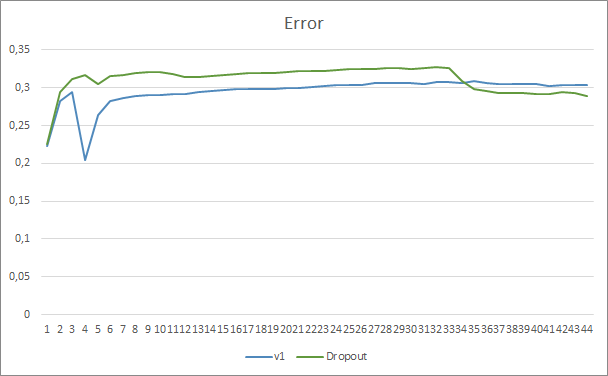
Das Diagramm der verpassten Muster zeigt auch, dass der Expert Advisor mit der Dropout-Technologie besser abschneidet. Dieses Diagramm liefert noch mehr Details. Der Expert Advisor, der Dropout verwendet, zeigt sofort eine Tendenz zur Abnahme der Gaps. Im Gegensatz dazu erhöht der Expert Advisor ohne Dropout allmählich die Bereiche mit verpassten Mustern.
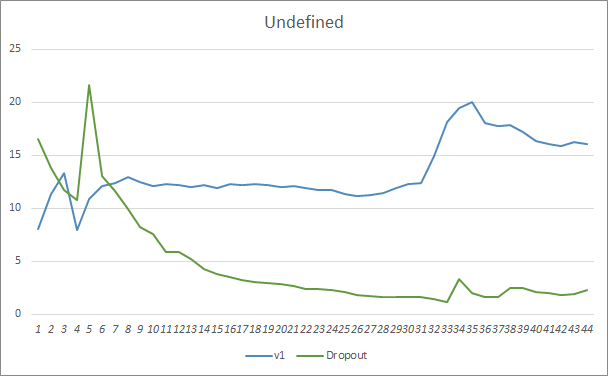
Die Diagramme der prognostizierten Treffer der beiden Expert Advisors liegen recht nahe beieinander. Nach 44 Epochen des Trainings ist der EA mit Dropout nur um 0,5 % besser.
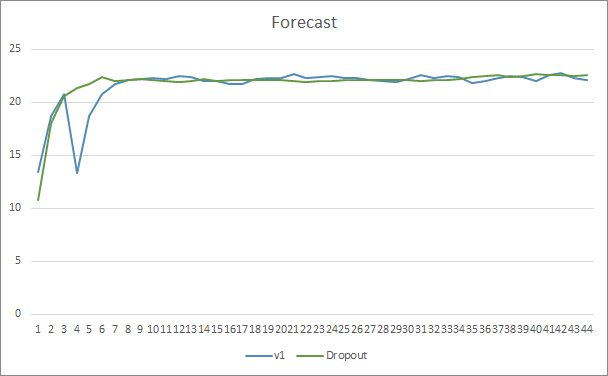
Schlussfolgerung
In diesem Artikel haben wir uns mit Methoden zur Erhöhung der Konvergenz von neuronalen Netzen beschäftigt und eine dieser Methoden, Dropout, kennengelernt. Die Methode wurde zu einem unserer früheren Expert Advisors hinzugefügt. Die Effizienz dieser Methode wurde in den EA-Tests gezeigt. Natürlich kann die Verwendung dieser Methode die Trainingskosten des neuronalen Netzes erhöhen. Aber diese Kosten werden durch die erhöhte Effizienz des Endergebnisses abgedeckt.
Ich lade jeden ein, diese Methode auszuprobieren und ihre Effektivität zu bewerten.
Referenzen
- Neuronale Netze leicht gemacht
- Neuronale Netze leicht gemacht (Teil 2): Netzwerktraining und Tests
- Neuronale Netze leicht gemacht (Teil 3): Convolutional Neurale Netzwerke
- Neuronale Netze leicht gemacht (Teil 4): Rekurrente Netze
- Neuronale Netze leicht gemacht (Teil 5): Parallele Berechnungen mit OpenCL
- Neuronale Netze leicht gemacht (Teil 6): Experimentieren mit der Lernrate des neuronalen Netzwerks
- Neuronale Netze leicht gemacht (Teil 7): Adaptive Optimierungsverfahren
- Neuronale Netze leicht gemacht (Teil 8): Attention-Mechanismen
- Neuronale Netze leicht gemacht (Teil 9): Dokumentation der Arbeit
- Neuronale Netze leicht gemacht (Teil 10): Multi-Head Attention
- Neuronale Netze leicht gemacht (Teil 11): Ein Blick auf GPT
- Verbesserung von neuronalen Netzwerken durch Verhinderung der Co-Adaptation von Merkmalsdetektoren (auf Englisch)
- Statistische Schätzungen
…
Die Programme dieses Artikels
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Fractal_OCL_AttentionMLMH.mq5 | Expert Advisor | Ein Expert Advisor mit dem klassifizierenden neuronalen Netz (3 Neuronen in der Ausgabeschicht) unter Verwendung der GTP-Architektur, mit 5 Attention-Schichten |
| 2 | Fractal_OCL_AttentionMLMH_d.mq5 | Expert Advisor | Ein Expert Advisor mit dem klassifizierenden neuronalen Netz (3 Neuronen in der Ausgabeschicht) unter Verwendung der GTP-Architektur, mit 5 Aufmerksamkeitsschichten + Dropout |
| 3 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek mit Klassen zum Erstellen eines neuronalen Netzwerks |
| 4 | NeuroNet.cl | Bibliothek | Die Bibliothek mit dem Programm-Code für OpenCL |
| 5 | NN.chm | HTML Hilfe | Eine kompilierte CHM-Hilfedatei |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/9112
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Brute-Force-Ansatz zur Mustersuche (Teil IV): Minimale Funktionalität
Brute-Force-Ansatz zur Mustersuche (Teil IV): Minimale Funktionalität
 Maschinelles Lernen für Grid- und Martingale-Handelssysteme. Würden Sie darauf wetten?
Maschinelles Lernen für Grid- und Martingale-Handelssysteme. Würden Sie darauf wetten?
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Ich nehme an, dass ohne OCL nichts funktioniert? Schade, ich bin kein Gamer und die Karte ist alt....