Neuronale Netzwerke: Von der Theorie zur Praxis
4 946
0
Einleitung
Heutzutage hat sicherlich jeder Trader schon einmal etwas von einem neuronalen Netzwerk gehört - und weiß, wie cool es ist, diese zu benutzen. Die Mehrheit scheint zu glauben, dass es sich bei all jenen, die mit neuronalen Netzwerken operieren, um irgendwelche Übermenschen handeln würde. Mithilfe des vorliegenden Artikels verbinde ich die Absicht, Ihnen die Architektur eines neuronalen Netzwerks samt seiner Applikationen und praktischen Nutzanwendungen näherzubringen.
Das Konzept eines neuronalen Netzwerks
Künstliche neuronale Netzwerke zählen zu den Bereichen der Künstlichen Intelligenz-Forschung, in denen der Versuch unternommen wird, ein menschliches Nervensystem - samt seiner Befähigung zu lernen und zu adaptieren - zu simulieren.
Kurioserweise bestehen künstliche neuronale Netzwerke aus künstlichen Neuronen.
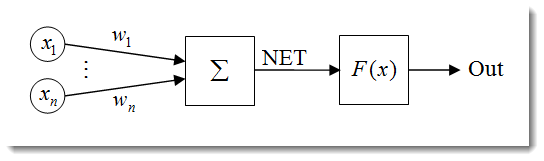
Abb. 1. Das künstliche Neuronenmodell
Die Struktur eines Neurons kann als eine Komposition folgender Einheiten dargestellt werden:
- Eingaben
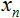; - Gewichte
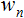; - Übertragungsfunktion
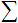und Net Input 
; - Aktivierungsfunktion
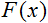; - Output
.
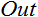Neuronale Netzwerke weisen eine ganze Reihe an Eigenschaften auf, von denen die wichtigste die ist, dass es lernfähig ist. Der Lernprozess basiert letztendlich darauf, die Gewichte zu verändern .
hier sehen wir den Net Input eines Neurons.
Der Net Input wird dann durch die Aktivierungsfunktion - auf die ich später noch genauer eingehen werde - in den Output transformiert. Zusammengefasst ist ein neuronales Netzwerk also eine Art von Blackbox, die Signale als Inputs erhält und Resultate ausgibt.
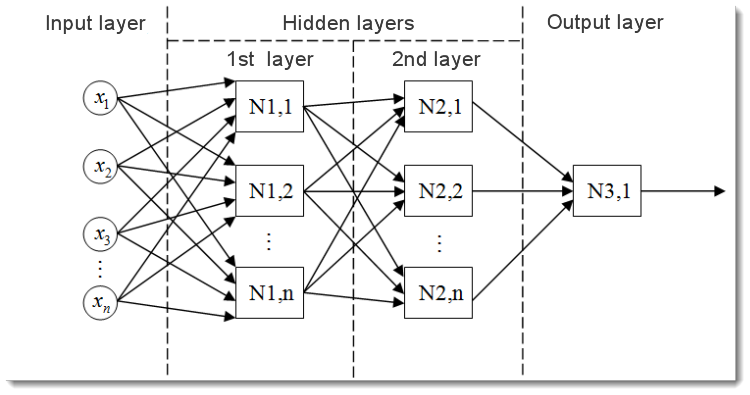
Abb. 2. Das Modell eines mehrschichtigen neuronalen Netzwerks
Hier können wir ein mehrschichtiges neuronales Netzwerk betrachten. Dieses enthält folgende Komponenten:
- Die Input-Schicht dient dazu, die Daten über das Netzwerk zu verteilen. Sie führt allerdings selbst keine Berechnungen durch. Die Outputs dieser Schicht senden Signale an die nächste Schicht (ausgeblendet oder Output);
- Die Output-Schicht, enthält normalerweise ein (manchmal auch mehr) Neuron(en) und generiert den Output des gesamten neuronalen Netzwerks. Dieses Signal bildet die Grundlage für die zukünftige Steuerlogik des Expert Advisors;
- Die ausgeblendeten Schichten sind Schichten eines Standardneurons, die Signale von der Input- zur Output-Schicht senden. Dessen Input ist der Output der vorherigen Schicht, während dessen Output als Input der nächsten Schicht fungiert.
Dieses Beispiel handelte von einem neuronalen Netzwerk mit zwei ausgeblendeten Schichten. Allerdings kann es durchaus auch neuronale Netzwerke mit mehr ausgeblendeten Schichten geben.
Normalisierung der Eingabedaten
Die Normalisierung der Eingabedaten ist ein Prozess, bei dem alle Eingabedaten normalisiert werden. Falls diese Normalisierung nicht durchgeführt wird, werden diese Daten einen zusätzlichen, zu falschen Entscheidungen führenden Effekt auf das Neuron ausüben. Mit anderen Worten: Wie können wir Werte miteinander vergleichen, die verschiedene Größenordnungen aufweisen?
Die Normalisierungsformel sieht in ihrer Standardform folgendermaßen aus:
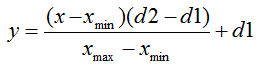
wobei gilt:
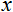- der zu normierender Wert;
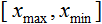- х-Wertebereich;
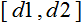- Bereich, bis zu dem der x-Wert reduziert werden soll.
Lassen Sie mich das an einem Beispiel erklären:
Nehmen wir an, wir haben die Eingabedaten n mit dem Bereich [0,10], so gilt 
= 0 und 
= 10. Nun reduzieren wir die Daten auf den Bereich [0,1], so erhalten wir 
= 0 und 
= 1. Setzen wir nun diese Werte in die Formel ein, so können wir normierte Werte für jedes beliebige x der Eingabedaten n ermitteln.
Und so sieht das Ganze aus, wenn es in MQL5 implementiert wird:
double d1=0.0; double d2=1.0; double x_min=iMA_buf[ArrayMinimum(iMA_buf)]; double x_max=iMA_buf[ArrayMaximum(iMA_buf)]; for(int i=0;i<ArraySize(iMA_buf);i++) { inputs[i]=(((iMA_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; }
Zunächst spezifizieren wir das obere und untere Limit des Output-Werts, wodurch wir die Werte für das Indikator-Minimum und -Maximum erhalten (Daten vom Indikator zu kopieren, wird hier weggelassen, aber beispielsweise die 10 letzten Werte möglich). Schließlich normalisieren wir ein jedes Input-Element (Indikatorwerte der verschiedenen Balken) und speichern die Ergebnisse in einem Array für den späteren Gebrauch.
Aktivierungsfunktionen
Die Aktivierungsfunktion ist eine Funktion, die den Output eines Neurons berechnet. Der Input, den es erhält, repräsentiert die Summe aller Input-Produkte und ihrer entsprechenden Gewichte (kurz: gewichtete Summe).
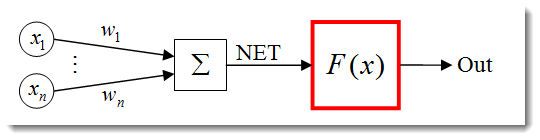
Abb. 3. Das künstliche neuronale Netzwerk mit einer skizzierten Aktivierungsfunktion.
Die Aktivierungsformel sieht in ihrer Standardform folgendermaßen aus:
wobei gilt:
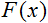- Ist die Aktivierungsfunktion;
- ist die gewichtete Summe, die in der ersten Phase der Output-Berechnung eines Neurons erhalten wird;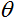
Ist ein Schwellenwert der Aktivierungsfunktion. Dieser spielt lediglich für die Hard Threshold-Funktion eine Bedeutung und ist in anderen Funktion gleich 0.
Zu den Haupttypen von Aktivierungsfunktionen zählen:
-
Die Sprung- oder Hard Threshold-Funktion.
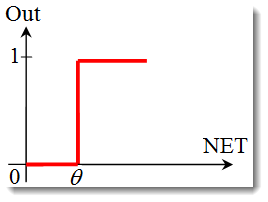
Diese Funktion wird durch die folgende Formel beschrieben:
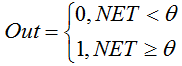
Falls die gewichtete Summe kleiner als der spezifizierte Wert ist, so gibt die Aktivierungsfunktion 0 zurück. Ist die gewichtete Summe größer, so gibt sie 1 zurück.
-
Die Sigmoidfunktion.
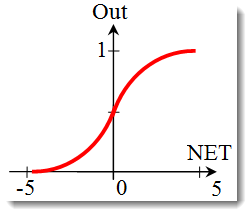
Die die Sigmoidfunktion beschreibende Formel sieht wie folgt aus:
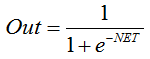
Sie wird oft bei mehrschichtigen neuronalen Netzwerken und anderen Netzwerken mit kontinuierlichen Signalen verwendet. Die Glätte als auch die Kontinuität der Funktion sind sehr positive Eigenschaften.
-
Der Tangens Hyperbolicus.
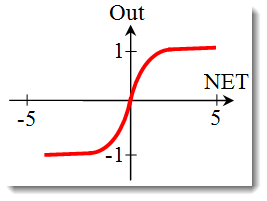
Formel:
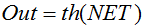
Oder
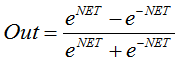
Eine Funktion, die ebenfalls sehr oft in Verbindung mit Netzwerken mit kontinuierlichem Signal verwendet wird. Ihre Eigenheit: Sie kann negative Werte ausgeben.
Die Form einer Aktivierungsfunktion ändern
Im vorhergehenden Teil haben wir uns mit den Aktivierungsfunktionstypen auseinandergesetzt. Allerdings gibt es noch eine weitere wichtige Sache zu diskutieren - die Steigung einer Funktion (Hard Threshold-unktionen ausgenommen). Sehen wir uns die Sigmoidfunktion noch einmal genauer an.
Der Funktionsgraph weist darauf hin, dass die Funktion über dem Wertebereich [-5,5] glatt wird. Lassen Sie uns die Existenz eines Netzwerks annehmen, das aus einem Neuron mit 10 Inputs und einem Output besteht. Nun wollen wir die oberen und unteren Variablenwerte berechnen . Jeder Input wird einen normalisierten Wert - z.B. im Bereich [-1,1] - annehmen (wie bereits in Normalisierung der Eingabedaten erwähnt).
Wir werden die negativen Eingabewerte verwenden, da es sich um eine - selbst bei einem negativen Argument - differenzierbare Funktion handelt. Die Gewichte werden dabei demselben Bereich entnommen. Durch alle möglichen Input- beziehungsweise Gewicht-Kombinationen erhalten wir die Extremwerte im Bereich von [-10,10]:
In MQL5 wird die Formel folgendermaßen aussehen:
for(int n=0; n<10; n++) { NET+=Xn*Wn; }
Nun müssen wir die Aktivierungsfunktion im identifizierten Bereich zeichnen. Die Sigmoidfunktion soll uns an dieser Stelle als Beispiel dienen. Der einfachste Weg ist dabei die Verwendung von Excel.
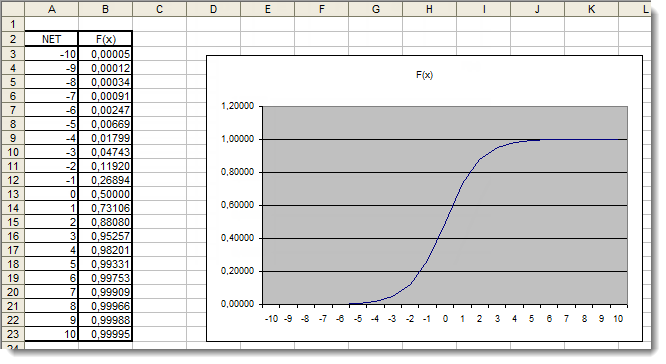
Abb. 4. Der Excel-Graph einer Sigmoidfunktion
Hieran können wir klar erkennen, dass ein Argumentwert außerhalb des Bereichs [-5,5] keinerlei Effekt auf die Ergebnisse ausübt. Dies deutet darauf hin, dass der Wertebereich unvollständig ist. Lassen Sie uns versuchen, dies zu beheben. Wir werden dem Argument einen zusätzlichen Koeffizienten hinzufügen, der es uns erlaubt, den Wertebereich zu vergrößern.
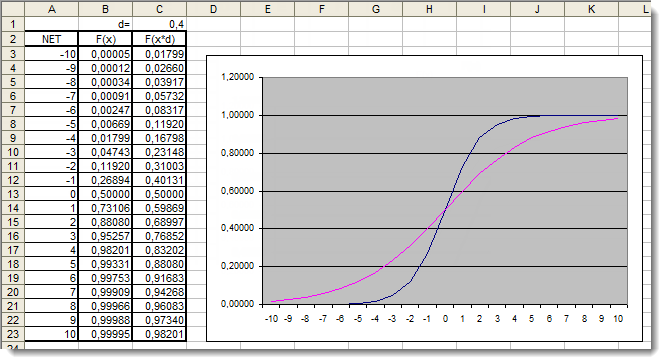
Abb. 5. Der Excel-Graph der Sigmoidfunktion mit zusätzlichem Koeffizienten
Lassen Sie uns nun noch einmal einen Blick auf die Graphen werfen. Wir haben einen zusätzlichen Koeffizienten (d=0.4) hinzugefügt, der die Form der Funktion verändert hat. Vergleicht man die Tabellenwerte, so scheinen sie jetzt wesentlich gleichmäßiger verteilt zu sein. Die Ergebnisse können also wie folgt ausgedrückt werden:
for(int n=0; n<10; n++) { NET+=Xn*Wn; } NET*=0.4;
Lassen Sie uns erneut die hyperbolische Tangensfunktion betrachten. Dabei wollen wir - im Gegensatz zu vorherigen Funktionen - auf die Theorie verzichten und uns direkt der Praxis widmen. Der einzige Unterschied besteht darin, dass der Output im Bereich [-1,1] liegen kann. Ebenso kann die gewichtete Summe Werte im Bereich [-10,10] annehmen.
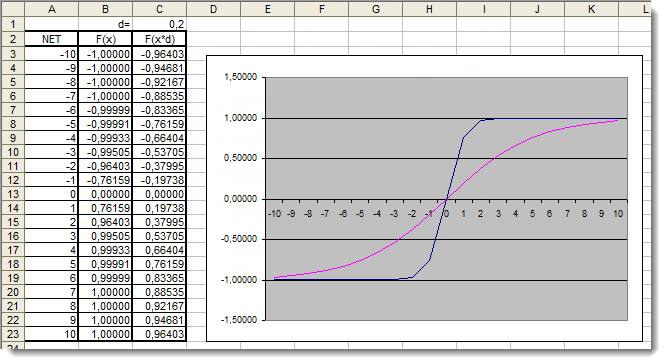
Abb. 6. Der Excel-Graph der hyperbolischen Tangensfunktion mit zusätzlichem Koeffizienten
Der Graph zeigt, dass die Form der Funktion aufgrund der Verwendung des zusätzlichen Koeffizienten d=0.2 verbessert worden ist. Die Ergebnisse können also wie folgt ausgedrückt werden:
for(int n=0;n<10;n++) { NET+=Xn*Wn; } NET*=0.2;
Auf diese Weise können Sie die Form einer jeden Aktivierungsfunktion ändern beziehungsweise verbessern.
Anwendung
Lassen Sie uns nun zur praktischen Anwendung kommen. Zunächst werden wir versuchen, die Berechnungen des Net Inputs des Neurons zu implementieren. Daraufhin fügen wir die Aktivierungsfunktion hinzu. Erinnern wir uns noch einmal an die Formel zur Berechnung des Net Inputs eines Neurons:
double NET; double x[3]; double w[3]; int OnInit() { x[0]=0.1; // set the input value х1 x[1]=0.8; // set the input value х2 x[2]=0.5; // set the input value х3 w[0]=0.5; // set the weight value w1 w[1]=0.6; // set the weight value w2 w[2]=0.3; // set the weight value w3 for(int n=0;n<3;n++) { NET+=x[n]*w[n]; // add the weighted net input values together } }
Sehen wir es uns ein wenig genau an:
- Wir haben damit begonnen, eine Variable, um den Net Input des Neurons zu speichern, als auch zwei Arrays zu definieren: Eingaben 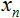und Gewichte ;
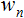- Diese Variablen wurden bereits zu Anfang definiert, unabhängig aller Funktionen, um ihnen eine globale Reichweite zu verleihen (Zugriff innerhalb des gesamten Programms möglich);
- In der OnInit()-Initialisierungsfunktion (jeder andere Funktion wäre ebenso denkbar) haben wir das Input- sowie das Gewicht-Array befüllt.
- Hierauf folgte die Summing Loop, n<3 , da wir nur drei Eingaben und drei entsprechende Gewichte haben.
- Dann haben wir gewichtete Eingabewerte hinzugefügt und haben diese in der Variable gespeichert.
Die erste Aufgabe ist somit beendet - und wir haben eine Summe erhalten. Jetzt ist die Aktivierungsfunktion dran. Unten befindet sich der Code zur Berechnung von Aktivierungsfunktionen (siehe Aktivierungsfunktionen).
Der Graph einer Sprung- oder Hard Threshold-Funktion
double Out; if(NET>=x) Out=1; else Out=0;
Die Sigmoidfunktion
double Out = 1/(1+exp(-NET));
Die hyperbolische Tangensfunktion
double Out = (exp(NET)-exp(-NET))/(exp(NET)+exp(-NET));
Die „Endmontage“
Um die Implementation einfach zu gestalten, werden wir uns ein Netzwerk vornehmen, das nur ein einziges Neuron aufweist. Die Bezeichnung Netzwerk mag bei der Verwendung nur eines einzigen Neurons eventuell ein wenig gewagt erscheinen, allerdings geht es uns an dieser Stelle ums Prinzip. Denn schließlich besteht ein mehrschichtiges neuronales Netzwerk aus den selben Neuronen, wobei der Output der vorherigen Neuronenschicht als Input für die nachfolgende fungiert.
Wir werden eine leicht modifizierte Version des Expert Advisors verwenden (Entwicklung und Einführung: „Schnelleinstieg oder Kurzanleitung für Anfänger" Wir werden daher beispielsweise den Trendindikator des Gleitenden Durchschnittswerts durch den Relative-Strength-Index-Oszillator ersetzen. Informationen betreffend die Parameter eines Indikators und ihre Sequenz finden sich in der eingebauten Hilfe.
//+------------------------------------------------------------------+ //| neuro-example.mq5 | //| Copyright 2012, MetaQuotes Software Corp. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2012, MetaQuotes Software Corp." #property link "http://www.mql5.com" #property version "1.00" //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> //include the library for execution of trades #include <Trade\PositionInfo.mqh> //include the library for obtaining information on positions //--- weight values input double w0=0.5; input double w1=0.5; input double w2=0.5; input double w3=0.5; input double w4=0.5; input double w5=0.5; input double w6=0.5; input double w7=0.5; input double w8=0.5; input double w9=0.5; int iRSI_handle; // variable for storing the indicator handle double iRSI_buf[]; // dynamic array for storing indicator values double inputs[10]; // array for storing inputs double weight[10]; // array for storing weights double out; // variable for storing the output of the neuron string my_symbol; // variable for storing the symbol ENUM_TIMEFRAMES my_timeframe; // variable for storing the time frame double lot_size; // variable for storing the minimum lot size of the transaction to be performed CTrade m_Trade; // entity for execution of trades CPositionInfo m_Position; // entity for obtaining information on positions //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int OnInit() { //--- save the current chart symbol for further operation of the EA on this very symbol my_symbol=Symbol(); //--- save the current time frame of the chart for further operation of the EA on this very time frame my_timeframe=PERIOD_CURRENT; //--- save the minimum lot of the transaction to be performed lot_size=SymbolInfoDouble(my_symbol,SYMBOL_VOLUME_MIN); //--- apply the indicator and get its handle iRSI_handle=iRSI(my_symbol,my_timeframe,14,PRICE_CLOSE); //--- check the availability of the indicator handle if(iRSI_handle==INVALID_HANDLE) { //--- no handle obtained, print the error message into the log file, complete handling the error Print("Failed to get the indicator handle"); return(-1); } //--- add the indicator to the price chart ChartIndicatorAdd(ChartID(),0,iRSI_handle); //--- set the iRSI_buf array indexing as time series ArraySetAsSeries(iRSI_buf,true); //--- place weights into the array weight[0]=w0; weight[1]=w1; weight[2]=w2; weight[3]=w3; weight[4]=w4; weight[5]=w5; weight[6]=w6; weight[7]=w7; weight[8]=w8; weight[9]=w9; //--- return 0, initialization complete return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- delete the indicator handle and deallocate the memory space it occupies IndicatorRelease(iRSI_handle); //--- free the iRSI_buf dynamic array of data ArrayFree(iRSI_buf); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- variable for storing the results of working with the indicator buffer int err1=0; //--- copy data from the indicator array to the iRSI_buf dynamic array for further work with them err1=CopyBuffer(iRSI_handle,0,1,10,iRSI_buf); //--- in case of errors, print the relevant error message into the log file and exit the function if(err1<0) { Print("Failed to copy data from the indicator buffer"); return; } //--- double d1=0.0; //lower limit of the normalization range double d2=1.0; //upper limit of the normalization range double x_min=iRSI_buf[ArrayMinimum(iRSI_buf)]; //minimum value over the range double x_max=iRSI_buf[ArrayMaximum(iRSI_buf)]; //maximum value over the range //--- In the loop, fill in the array of inputs with the pre-normalized indicator values for(int i=0;i<ArraySize(inputs);i++) { inputs[i]=(((iRSI_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; } //--- store the neuron calculation result in the out variable out=CalculateNeuron(inputs,weight); //--- if the output value of the neuron is less than 0.5 if(out<0.5) { //--- if the position for this symbol already exists if(m_Position.Select(my_symbol)) { //--- and this is a Sell position, then close it if(m_Position.PositionType()==POSITION_TYPE_SELL) m_Trade.PositionClose(my_symbol); //--- or else, if this is a Buy position, then exit if(m_Position.PositionType()==POSITION_TYPE_BUY) return; } //--- if we got here, it means there is no position; then we open it m_Trade.Buy(lot_size,my_symbol); } //--- if the output value of the neuron is equal to or greater than 0.5 if(out>=0.5) { //--- if the position for this symbol already exists if(m_Position.Select(my_symbol)) { //--- and this is a Buy position, then close it if(m_Position.PositionType()==POSITION_TYPE_BUY) m_Trade.PositionClose(my_symbol); //--- or else, if this is a Sell position, then exit if(m_Position.PositionType()==POSITION_TYPE_SELL) return; } //--- if we got here, it means there is no position; then we open it m_Trade.Sell(lot_size,my_symbol); } } //+------------------------------------------------------------------+ //| Neuron calculation function | //+------------------------------------------------------------------+ double CalculateNeuron(double &x[],double &w[]) { //--- variable for storing the weighted sum of inputs double NET=0.0; //--- Using a loop we obtain the weighted sum of inputs based on the number of inputs for(int n=0;n<ArraySize(x);n++) { NET+=x[n]*w[n]; } //--- multiply the weighted sum of inputs by the additional coefficient NET*=0.4; //--- send the weighted sum of inputs to the activation function and return its value return(ActivateNeuron(NET)); } //+------------------------------------------------------------------+ //| Activation function | //+------------------------------------------------------------------+ double ActivateNeuron(double x) { //--- variable for storing the activation function results double Out; //--- sigmoid Out=1/(1+exp(-x)); //--- return the activation function value return(Out); } //+------------------------------------------------------------------+
Zunächst einmal müssen wir unser Netzwerk trainieren. Lassen Sie uns hierfür die Gewichte optimieren.
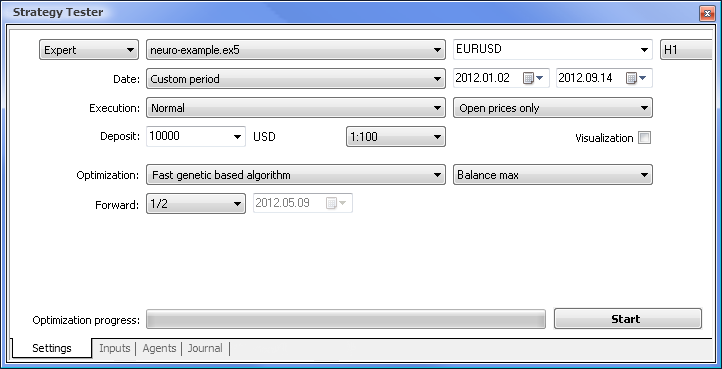
Abb. 7. Strategietester mit dem erforderlichen Set an Parametern
Wir werden die Optimierung anhand folgender Parameter vornehmen:
- Datum - z.B. seit dem Anfang des Jahres; Je länger der Zeitrahmen, umso geringer das Auftreten einer Kurvenanpassung und umso bessere Ergebnisse.
- Ausführung - normal, nur Eröffnungskurse. Es gibt keinen Grund für einen Test, der alle Modi umfasst, da unser EA lediglich die letzten 10 Indikatorwerte benötigt (Währungswert ausgenommen).
- Optimierung kann so eingestellt werden, dass sie den langsamen vollständigen Algorithmus verwendet. Eine genetische Optimierung verspricht hingegen schnellere Resultate, was besonders bei der Bewertung eines Algorithmus Vorteile bietet. Falls das Ergebnis zufriedenstellend ausfällt, können Sie ferner versuchen, den langsamen vollständigen Algorithmus zu verwenden, um noch genauere Ergebnisse zu erzielen.
- Vorwärts von 1/2 erlaubt es Ihnen zu beurteilen, wie lange Ihr EA die erhaltenen Resultate generieren kann, bis die nächste Optimierung fällig wird.
- Zeitrahmen und Währungspaar können nach eigenem Ermessen gewählt werden.
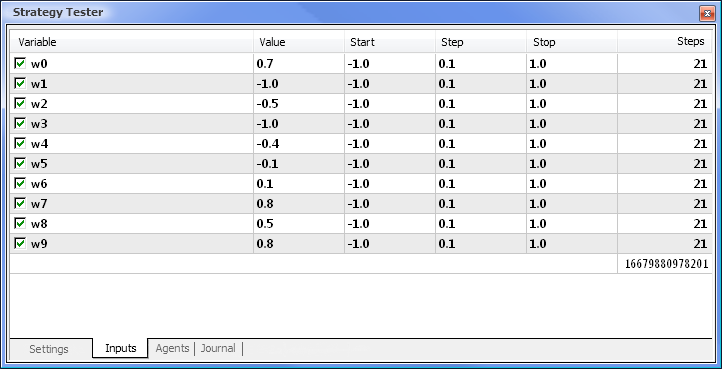
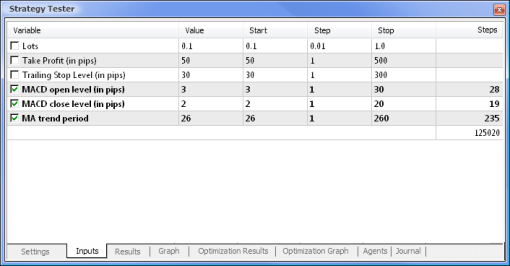
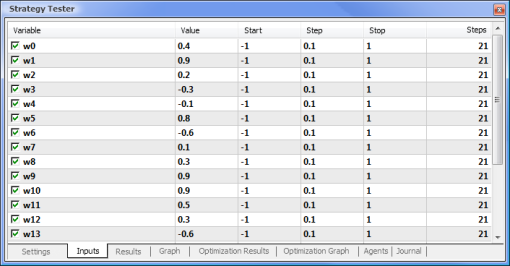
Abb. 8. Optimierung der Parameter und ihrer entsprechenden Bereiche
Die Optimierung wird unter Berücksichtigung aller Gewichte und ihrer Bereiche durchgeführt. Starten Sie die Optimierung, indem Sie in den Einstellungsreiter zurückkehren und den Start-Button drücken.
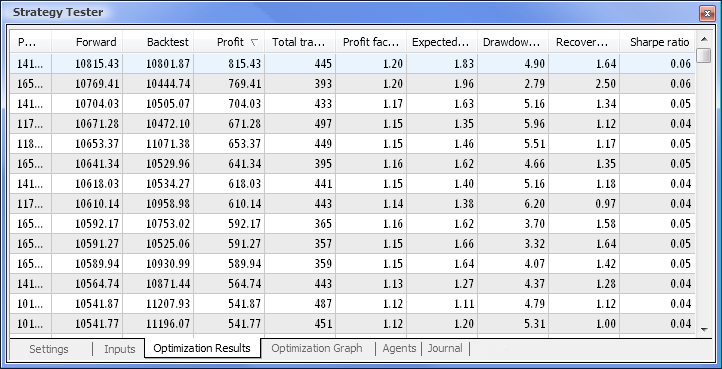
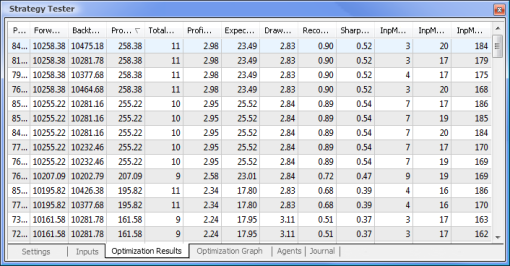
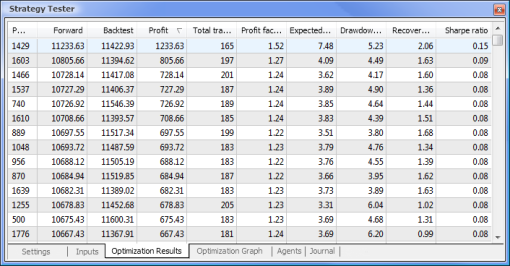
Abb. 9. Infolge der Optimierung erhaltene Daten
Nachdem die Optimierung abgeschlossen ist, wählen wir den erfolgreichen Test mit dem maximalen Profitwert im Optimierungsergebnisse-Reiter aus (um nach Parametern zu sortieren, klicken Sie bitte auf den entsprechenden Spaltenkopf). Sie können danach auch andere Parameter auswerten und den entsprechenden erfolgreichen Test auswählen, falls gewünscht.
Mit einem Doppelklick auf den benötigten Vorgang initiieren Sie einen Test der Ergebnisse, die im Ergebnis- beziehungsweise Graphen-Reiter angezeigt werden.
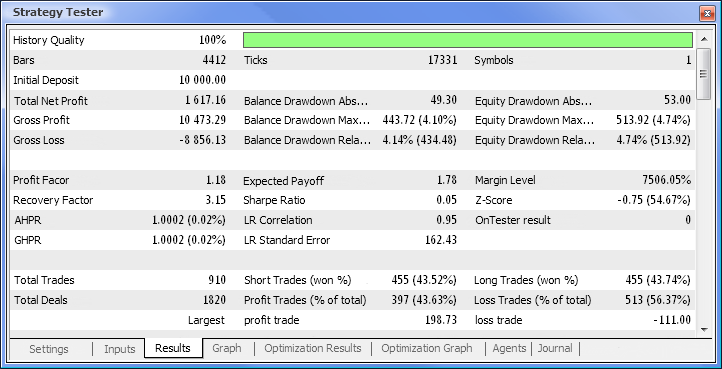
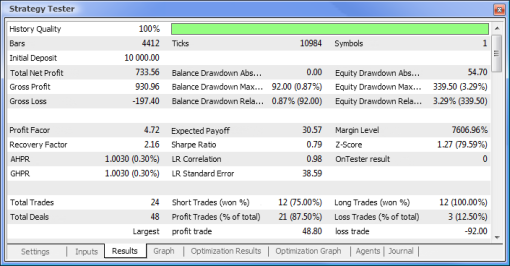
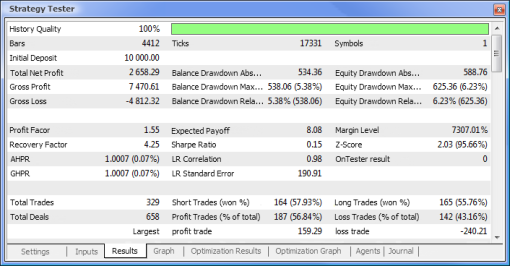
Abb. 10. Testbericht
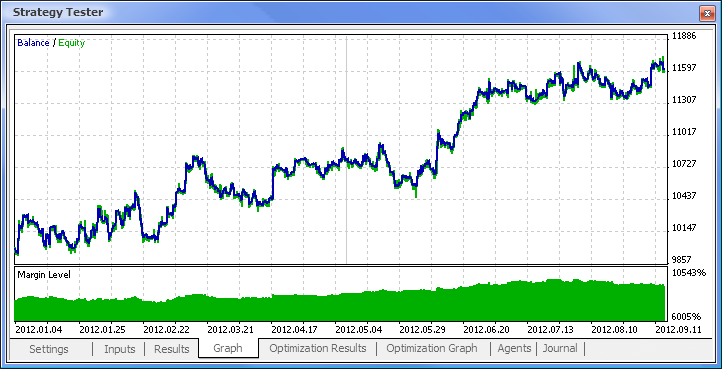
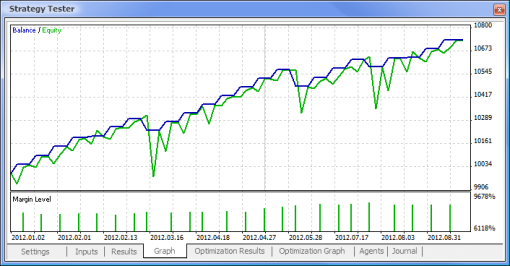
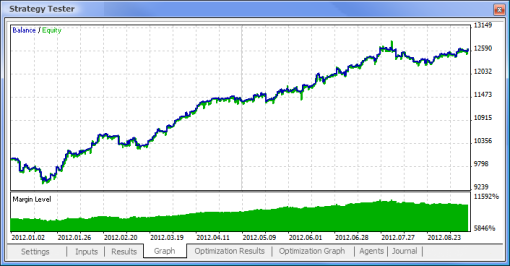
Abb. 11. Bilanzchart
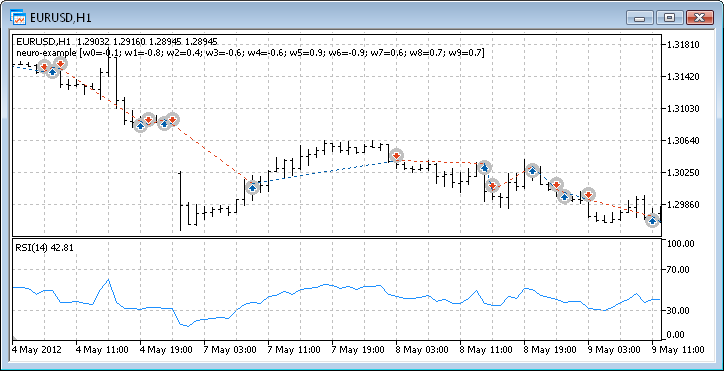
Abb. 12. Trading-Performance des Expert Advisors
Nun liegen uns also endlich die finalen Ergebnisse vor - und die sind für den Anfang gar nicht übel. Bedenken Sie an dieser Stelle bitte, dass wir nur ein Neuron zur Verfügung hatten. Das Beispiel war zweifellos äußerst primitiv, dennoch lässt sich nicht leugnen, dass sich selbst damit Profite machen lassen.
Vorteile eines neuronalen Netzwerks
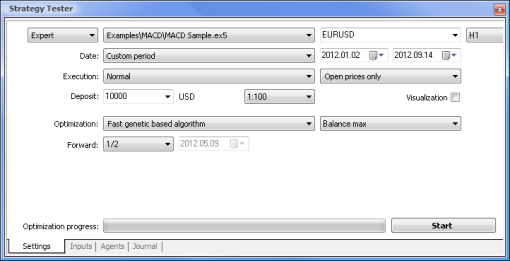
Lassen Sie uns nun einen EA, der sich einer normalen Logik bedient, und einen, der auf ein neuronales Netzwerk zurückgreifen kann, miteinander vergleichen. Wir werden die Optimierungs- und Testergebnisse eines herkömmlichen, mit dem Terminal ausgelieferten MACD-EAs und eines EAs, der auf einem neuronalen Netzwerk basiert, miteinander vergleichen.
Take Profit und Trailing Stop-Werte werden bei der Optimierung nicht berücksichtigt, da sie dem neuronalen Netzwerk-EA nicht zur Verfügung stehen. Beide zu testende Expert Advisors basieren auf dem MACD-Indikator (Moving Average Convergence-Divergence) und den folgenden Parametern:
- Zeitraum für den schnellen gleitenden Durchschnittswert: 12;
- Zeitraum für den langsamen gleitenden Durchschnittswert: 26;
- Zeitraum für die durchschnittliche Differenz: 9;
- Preistyp: Schlussnotierung.
Sie haben ferner die Möglichkeit, das benötigte Währungspaar und den Zeitraum zu ändern. Wir werden dies im vorliegenden Fall jedoch nicht tun: EURUSD, H1. Die Testperiode ist in beiden Fällen identisch: die Eröffnungskurse seit dem Anfang des Jahres.
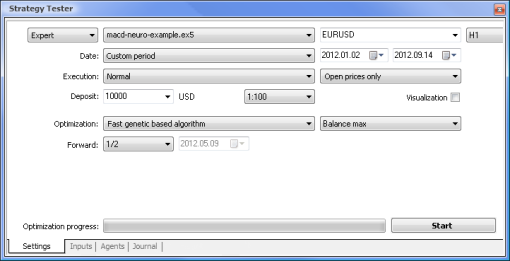
| MACD-Probe | MACD-Neuro-Probe |
|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Lassen Sie uns nun die Schlüsseleigenschaften der zu testenden EAs betrachten:
| Eigenschaft | MACD-Probe | MACD-Neuro-Probe |
|---|---|---|
| Gesamtnettogewinn: | 733,56 | 2 658,29 |
| Absoluter Wertverlust des Kontos: | 0,00 | 534,36 |
| Maximaler Wertverlust des Kapitals: | 339,50 (3,29%) | 625,36 (6,23%) |
| Profit Factor | 4,72 | 1,55 |
| Recovery Factor | 2,16 | 4,25 |
| Expected Payoff | 30,57 | 8,08 |
| Sharpe Ratio | 0,79 | 0,15 |
| Trades insgesamt: | 24 | 329 |
| Abschlüsse insgesamt: | 48 | 658 |
| Gewinn (in % aller Abschlüsse) | 21 (87,50%) | 187 (56,84%) |
| Durchschnittlicher Abschluss mit Gewinn | 44,33 | 39,95 |
| Durchschnittliche ununterbrochene Gewinne | 5 | 2 |
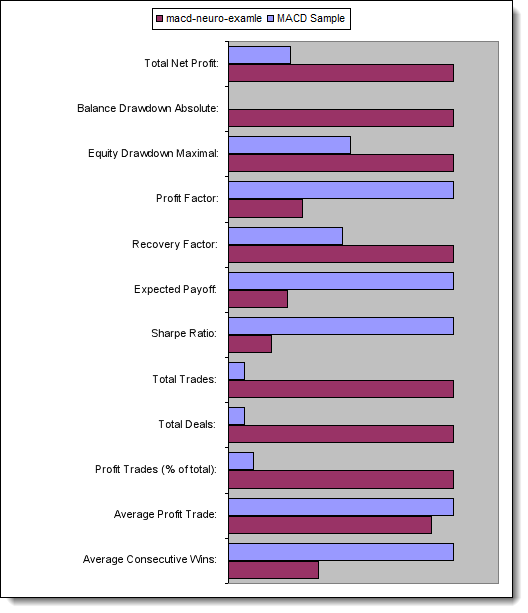
Abb. 13. Vergleich der Schlüsseleigenschaften
Fazit
Dieser Artikel hat die wichtigste Punkte abgedeckt, die Sie wissen müssen, wenn Sie einen EA konzipieren wollen, der auf ein neuronales Netzwerk zurückgreift. Wir haben die Struktur eines Neurons als auch eines neuronalen Netzwerks kennengelernt, es wurden Aktivierungsfunktionen und Methoden umrissen, mit denen man ihre Form verändern kann, als auch der Prozess einer Optimierung sowie einer Normalisierung von Eingabedaten skizziert. Außerdem haben wir einen EA, der sich einer normalen Logik bedient, mit einem, der auf einer neuronalen Netzwerk-Logik basiert, vergleichen.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/497
Wie man einen Handelsroboter via MetaTrader Market ersteht
Statistische Carry Trade-Strategie
Wie erstelle ich MetaTrader 5-Angebote für andere Applikationen
Entdecken der Trading-Strategieklassen der Standard Library - Anpassungsstrategien
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.