Neuronale Netze leicht gemacht
3 206
1
Inhaltsverzeichnis
- Einführung
- 1. Prinzipien des Aufbaus von AI-Netzwerken
- 2. Die Struktur eines künstlichen Neurons
- 3. Trainieren des Netzwerks
- 4. Aufbau eines eigenen neuronalen Netzes mit MQL
- Schlussfolgerung
- Referenzen
- Programme, die im diesem Artikel verwendet werden
Einführung
Die künstliche Intelligenz deckt zunehmend verschiedene Aspekte unseres Lebens ab. Es erscheinen viele neue Veröffentlichungen, in denen es heißt, dass "das neuronale Netz wurde trainiert,..". Dennoch wird die künstliche Intelligenz immer noch mit etwas Fantastischem assoziiert. Die Idee scheint sehr kompliziert, übernatürlich und unerklärlich zu sein. Deshalb kann ein solches Wunder auf dem neuesten Stand der Technik nur von einer Gruppe von Wissenschaftlern geschaffen werden. Es scheint, dass ein ähnliches Programm nicht mit unserem Heim-PC entwickelt werden kann. Aber glauben Sie mir, es ist nicht so schwierig. Versuchen wir zu verstehen, was die neuronalen Netze sind und wie sie im Handel eingesetzt werden können.
1. Prinzipien des Aufbaus von AI-Netzwerken
Die folgende Definition der Neuronalen Netze bietet Wikipedia:
Künstliche neuronale Netze, auch künstliche neuronale Netzwerke, kurz: KNN (englisch artificial neural network, ANN), sind Netze aus künstlichen Neuronen .. [die ein] biologisches Vorbild [haben]. Eine KNN basiert auf einer Anzahl von miteinander verbundenen Einheiten oder Knoten, die künstliche Neuronen genannt werden und die Neuronen in einem biologischen Gehirn nachempfunden sind.
Das heißt, ein neuronales Netzwerk ist eine Einheit, die aus künstlichen Neuronen besteht, zwischen denen eine organisierte Beziehung besteht. Diese Beziehungen sind ähnlich wie bei einem biologischen Gehirn.
Die Abbildung unten zeigt das Bild eines einfachen Neuronalen Netzes. Hier zeigen Kreise die Neuronen an und Linien visualisieren die Verbindungen zwischen den Neuronen. Die Neuronen befinden sich in Schichten, die in drei Gruppen unterteilt sind. Blau zeigt die Schicht der Eingangsneuronen an, die für die Eingabe der Quellinformationen bestimmt sind. Grün und blau sind Ausgangsneuronen, die das Ergebnis der Operation des neuronalen Netzes ausgeben. Dazwischen befinden sich graue Neuronen, die eine verborgene Schicht bilden.
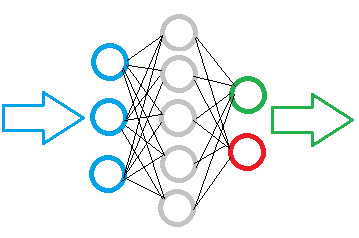
Trotz der Schichten ist das gesamte Netzwerk aus denselben Neuronen aufgebaut, die mehrere Elemente für die Eingangssignale und nur ein Element für das Ergebnis haben. Die Eingangsdaten werden innerhalb des Neurons verarbeitet und dann wird ein einfaches logisches Ergebnis ausgegeben. Dieses kann zum Beispiel ja oder nein sein. Wenn das Ergebnis auf den Handel angewandt wird, kann es als Handelssignal oder als Handelsrichtung ausgegeben werden.
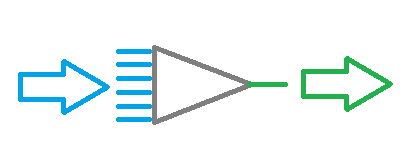
Die Ausgangsinformation wird in die Eingangsneuronenschicht eingegeben, dann wird sie verarbeitet und das Verarbeitungsergebnis dient als Quellinformation für die Neuronen der nächsten Schicht. Die Operationen werden von einer Schicht zur anderen wiederholt, bis die Schicht der Ausgangsneuronen erreicht ist. So werden die Ausgangsdaten von einer Schicht zur anderen verarbeitet und gefiltert, und danach wird ein Ergebnis erzeugt.
Abhängig von der Komplexität der Aufgabe und den erstellten Modellen kann die Anzahl der Neuronen in jeder Schicht variieren. Einige Netzwerkvariationen können mehrere verborgene Schichten enthalten. Ein solch fortschrittliches neuronales Netzwerk kann komplexere Probleme lösen. Dies würde jedoch mehr Rechenressourcen erfordern.
Daher ist es bei der Erstellung eines neuronalen Netzwerkmodells notwendig, die zu verarbeitende Datenmenge und das gewünschte Ergebnis zu definieren. Dies beeinflusst die Anzahl der benötigten Neuronen in den Modellschichten.
Wenn wir ein Datenarray mit 10 Elementen in ein neuronales Netzwerk eingeben müssen, dann sollte die Eingangsnetzwerkschicht 10 Neuronen enthalten. Dies ermöglicht die Übernahme aller 10 Elemente des Datenarrays. Zusätzliche Eingabe-Neuronen sind.
Die Qualität der Ausgangsneuronen wird durch das erwartete Ergebnis bestimmt. Um ein eindeutiges logisches Ergebnis zu erhalten, reicht ein Ausgangsneuron aus. Wenn Sie Antworten auf mehrere Fragen erhalten möchten, erstellen Sie für jede der Fragen ein Neuron.
Die verborgenen Schichten dienen als analytisches Zentrum, das die empfangenen Informationen verarbeitet und analysiert. Daher hängt die Anzahl der Neuronen in der Schicht von der Variabilität der Daten der vorherigen Schicht ab, d.h. jedes Neuron schlägt eine bestimmte Hypothese von Ereignissen vor.
Die Anzahl der verborgenen Schichten wird durch eine kausale Beziehung zwischen den Quelldaten und dem erwarteten Ergebnis bestimmt. Wenn wir zum Beispiel ein Modell für die "5-Warum"-Technik erstellen wollen, ist eine logische Lösung die Verwendung von 4 verborgenen Schichten, die zusammen mit der Ausgabeschicht die Möglichkeit bieten, den Quelldaten 5 Fragen zu stellen.
Zusammenfassung:
- ein neuronales Netz wird aus denselben Neuronen aufgebaut, daher reicht eine Klasse von Neuronen aus, um ein Modell zu erstellen;
- die Neuronen im Modell sind in Schichten organisiert;
- der Datenfluss im neuronalen Netz ist als serielle Datenübertragung durch alle Schichten des Modells, von den Eingangs- bis zu den Ausgangsneuronen, implementiert;
- die Anzahl der Eingangsneuronen hängt von der Menge der pro Durchgang analysierten Daten ab, während die Anzahl der Ausgangsneuronen von der resultierenden Datenmenge abhängt;
- da am Ausgang ein logisches Ergebnis gebildet wird, sollten die dem neuronalen Netz gestellten Fragen die Möglichkeit bieten, eine eindeutige Antwort zu geben.
2. Die Struktur eines künstlichen Neurons
Nachdem wir nun die Struktur des neuronalen Netzes betrachtet haben, wollen wir zur Schaffung eines künstlichen Neuronenmodells übergehen. Alle mathematischen Berechnungen und die Entscheidungsfindung werden innerhalb dieses Neurons durchgeführt. Hier stellt sich eine Frage: Wie können wir viele verschiedene Lösungen auf der Grundlage derselben Quelldaten und unter Verwendung derselben Formel implementieren? Die Lösung liegt in der Veränderung der Verbindungen zwischen den Neuronen. Für jede Verbindung wird ein Gewichtskoeffizient bestimmt. Dieser Gewichtungskoeffizient legt fest, wie viel Einfluss der Eingabewert auf das Ergebnis haben wird.
Das mathematische Modell eines Neurons besteht aus zwei Funktionen. Zunächst werden die Produkte der Eingabedaten durch ihre Gewichtskoeffizienten zusammengefasst.
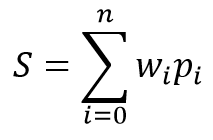
Basierend auf dem empfangenen Wert wird das Ergebnis in der sogenannten Aktivierungsfunktion berechnet. In der Praxis werden verschiedene Varianten der Aktivierungsfunktion verwendet. Die am häufigsten verwendeten sind folgende:
- Sigmoid-Funktion — der Bereich der Rückgabewerte von "0" bis "1".
- Hyperbolische Tangente — der Bereich der Rückgabewerte von "-1" bis "1"
Die Wahl der Aktivierungsfunktion hängt von den zu lösenden Problemen ab. Wenn wir beispielsweise eine logische Antwort als Ergebnis der Quelldatenverarbeitung erwarten, ist eine Sigmoid-Funktion vorzuziehen. Für Handelszwecke ziehe ich es vor, die hyperbolische Tangente zu verwenden. Der Wert "-1" entspricht dem Verkaufssignal, "1" entspricht dem Kaufsignal. Ein mittleres Ergebnis zeigt die Unsicherheit an.
3. Trainieren des Netzwerks
Wie oben erwähnt, hängt die Ergebnisvariabilität jedes einzelnen Neurons und des gesamten neuronalen Netzes von den gewählten Gewichten für die Verbindungen zwischen den Neuronen ab. Das Problem der Gewichtsbestimmung wird als Lernen des neuronalen Netzes bezeichnet.
Ein Netzwerk kann nach verschiedenen Algorithmen und Methoden trainiert werden:
- Überwachtes Lernen;
- Unbeaufsichtigtes Lernen;
- Verstärkungslernen
Die Lernmethode hängt von den Quelldaten und den für das neuronale Netz festgelegten Aufgaben ab.
Überwachtes Lernen wird eingesetzt, wenn ein ausreichender Satz von Ausgangsdaten mit den entsprechenden richtigen Antworten auf die gestellten Fragen vorliegt. Während des Lernprozesses werden die Ausgangsdaten in das Netzwerk eingegeben und die Ausgabe mit der bekannten richtigen Antwort verifiziert. Danach werden die Gewichte angepasst, um den Fehler zu reduzieren.
Unüberwachtes Lernen wird verwendet, wenn es einen Satz von Ausgangsdaten ohne die entsprechenden richtigen Antworten gibt. Bei dieser Methode sucht das neuronale Netzwerk nach ähnlichen Datensätzen und ermöglicht die Aufteilung der Quelldaten in ähnliche Gruppen.
Verstärkungslernen wird verwendet, wenn es keine richtigen Antworten gibt, wir aber das gewünschte Ergebnis kennen. Während des Lernprozesses werden die Quelldaten in das Netzwerk eingegeben, das dann versucht, das Problem zu lösen. Nach der Verifizierung des Ergebnisses wird ein Feedback als eine gewisse Belohnung gesendet. Während des Lernprozesses versucht das Netzwerk, die maximale Belohnung zu erhalten.
In diesem Artikel verwenden wir überwachtes Lernen. Als Beispiel verwende ich den Algorithmus der back propagation. Dieser Ansatz ermöglicht ein kontinuierliches Training des neuronalen Netzes in Echtzeit.
Die Methode basiert auf der Verwendung des Ergebnisfehlers des neuronalen Netzes zur Korrektur seiner Gewichte. Der Lernalgorithmus besteht aus zwei Stufen. Zuerst berechnet das Netzwerk auf der Grundlage der Eingangsdaten den resultierenden Wert, der dann mit dem Referenzwert verifiziert und ein Fehler berechnet wird. Dann wird ein rückwärts durch das Netz gegangen, und gemäß des Fehlers alle Gewichtungsfaktoren angepasst werden. Dies ist ein interaktiver Ansatz, bei dem das Netzwerk Schritt für Schritt trainiert wird. Nach dem Lernen anhand historischer Daten kann das Netzwerk im Online-Modus weiter trainiert werden.
Die Methode der back propagation verwendet einen stochastischen Gradientenabfall, der es erlaubt, ein akzeptables Fehlerminimum zu erreichen. Die Möglichkeit, das Netzwerk im Online-Modus weiter zu trainieren, erlaubt es, dieses Minimum über ein langes Zeitintervall beizubehalten.
4. Aufbau eines eigenen neuronalen Netzes mit MQL
Kommen wir nun zum praktischen Teil des Artikels. Zur besseren Visualisierung der Funktionsweise von neuronalen Netzen (NN) erstellen wir ein Beispiel, bei dem wir nur die Sprache MQL5 verwenden, ohne Bibliotheken von Drittanbietern. Beginnen wir mit der Erstellung der Klassen, die Daten über elementare Verbindungen zwischen Neuronen speichern.
4.1. Verbindungen
Erstellen wir zunächst die Klasse СConnection, um den Gewichtskoeffizienten einer Verbindung zu speichern. Sie wird von der Klasse CObject abgeleitet. Die Klasse wird zwei Variablen vom Typ double enthalten: "weight" zur Speicherung des Gewichts und deltaWeight, in der wir den Wert der letzten Gewichtsänderung (die beim Lernen verwendet wird) speichern werden. Um die Notwendigkeit zu vermeiden, zusätzliche Methoden für die Arbeit mit Variablen zu verwenden, sollten diese 'public' sein. Die Anfangswerte für die Variablen werden im Klassenkonstruktor festgelegt.
class СConnection : public CObject { public: double weight; double deltaWeight; СConnection(double w) { weight=w; deltaWeight=0; } ~СConnection(){}; //--- methods for working with files virtual bool Save(const int file_handle); virtual bool Load(const int file_handle); };
Um die Speicherung weiterer Informationen über Verbindungen zu ermöglichen, werden wir eine Methode zum Speichern von Daten in eine Datei (Save) und zum Lesen dieser Daten (Load) erstellen. Die Methoden basieren auf einem klassischen Schema: Das Datei-Handle wird in den Methodenparametern übernommen, dann verifiziert und die Daten werden geschrieben (oder in der Load-Methode gelesen).
bool СConnection::Save(const int file_handle) { if(file_handle==INVALID_HANDLE) return false; //--- if(FileWriteDouble(file_handle,weight)<=0) return false; if(FileWriteDouble(file_handle,deltaWeight)<=0) return false; //--- return true; }
Der nächste Schritt ist das Erstellen eines Arrays zum Speichern von Gewichten: CArrayCon basierend auf CArrayObj. Hier überschreiben wir zwei virtuelle Methoden, CreateElement und Type. Die erste wird zur Erstellung eines neuen Elements verwendet, und die zweite identifiziert unsere Klasse.
class CArrayCon : public CArrayObj { public: CArrayCon(void){}; ~CArrayCon(void){}; //--- virtual bool CreateElement(const int index); virtual int Type(void) const { return(0x7781); } };
In den Parametern der Methoden CreateElement, die ein neues Element erzeugt, übergeben wir den Index dieses neuen Elements. Wir überprüfen die Gültigkeit in der Methode, die Größe des Datenspeicher-Arrays und passen die Größe gegebenenfalls an. Dann erzeugen wir eine neue Instanz der Klasse СConnection, indem wir eine zufällige Anfangsgewichtung angeben.
bool CArrayCon::CreateElement(const int index) { if(index<0) return false; //--- if(m_data_max<index+1) { if(ArrayResize(m_data,index+10)<=0) return false; m_data_max=ArraySize(m_data)-1; } //--- m_data[index]=new СConnection(MathRand()/32767.0); if(!CheckPointer(m_data[index])!=POINTER_INVALID) return false; m_data_total=MathMax(m_data_total,index); //--- return (true); }
4.2. Ein Neuron
Der nächste Schritt ist die Schaffung eines künstlichen Neurons. Wie bereits erwähnt, verwende ich die hyperbolische Tangentenfunktion zur Aktivierung für mein Neuron. Der Bereich der resultierenden Werte liegt zwischen "-1" und "1". "-1" zeigt ein Verkaufssignal an und "1" bedeutet ein Kaufsignal.
Ähnlich wie die vorherige Klasse CConnection wird die Klasse der künstlichen Neuronen CNeuron von der Klasse CObject abgeleitet. Ihre Struktur ist jedoch etwas komplizierter.
class CNeuron : public CObject { public: CNeuron(uint numOutputs,uint myIndex); ~CNeuron() {}; void setOutputVal(double val) { outputVal=val; } double getOutputVal() const { return outputVal; } void feedForward(const CArrayObj *&prevLayer); void calcOutputGradients(double targetVals); void calcHiddenGradients(const CArrayObj *&nextLayer); void updateInputWeights(CArrayObj *&prevLayer); //--- methods for working with files virtual bool Save(const int file_handle) { return(outputWeights.Save(file_handle)); } virtual bool Load(const int file_handle) { return(outputWeights.Load(file_handle)); } private: double eta; double alpha; static double activationFunction(double x); static double activationFunctionDerivative(double x); double sumDOW(const CArrayObj *&nextLayer) const; double outputVal; CArrayCon outputWeights; uint m_myIndex; double gradient; };
Wir übergeben in den Parametern des Klassenkonstruktors die Anzahl der ausgehenden Neuronenverbindungen und die Ordnungszahl des Neurons in der Schicht (wird für die spätere Identifizierung des Neurons verwendet). Wir deklarieren im Methodenrumpf Konstanten, speichern die erhaltenen Daten und erstellen ein Array von ausgehenden Verbindungen.
CNeuron::CNeuron(uint numOutputs, uint myIndex) : eta(0.15), // net learning rate alpha(0.5) // momentum { for(uint c=0; c<numOutputs; c++) { outputWeights.CreateElement(c); } m_myIndex=myIndex; }
Die Methoden setOutputVal und getOutputVal werden verwendet, um auf den resultierenden Wert des Neurons zuzugreifen. Dieser resultierende Wert des Neurons wird mit der feedForward-Methode berechnet. Die vorherige Schicht von Neuronen wird als Parameter in diese Methode eingegeben.
void CNeuron::feedForward(const CArrayObj *&prevLayer) { double sum=0.0; int total=prevLayer.Total(); for(int n=0; n<total && !IsStopped(); n++) { CNeuron *temp=prevLayer.At(n); double val=temp.getOutputVal(); if(val!=0) { СConnection *con=temp.outputWeights.At(m_myIndex); sum+=val * con.weight; } } outputVal=activationFunction(sum); }
Der Methodenkörper enthält eine Schleife durch alle Neuronen der Vorgängerschicht. Die Produkte aus den resultierenden Neuronenwerten und Gewichten werden ebenfalls im Methodenkörper summiert. Nach der Berechnung der Summe wird der resultierende Neuronenwert in der Methode activationFunction berechnet (die Aktivierungsfunktion des Neurons ist wie in einer separaten Methode implementiert).
double CNeuron::activationFunction(double x) { //output range [-1.0..1.0] return tanh(x); }
Der nächste Methodenblock wird vom Lernen des NNs verwendet. Wir erstellen eine Methode zur Berechnung einer Ableitung für die Aktivierungsfunktion, activationFunctionDerivative. Dies ermöglicht die Bestimmung einer erforderlichen Änderung der Summierungsfunktion, um den Fehler des resultierenden Neuronenwertes auszugleichen.
double CNeuron::activationFunctionDerivative(double x) { return 1/MathPow(cosh(x),2); }
Als Nächstes erstellen wir zwei Gradientenberechnungsmethoden für die Gewichtsanpassung. Wir müssen 2 Methoden erstellen, da der Fehler des resultierenden Wertes für die Neuronen der Ausgabeschicht und die der verborgenen Schichten auf unterschiedliche Weise berechnet wird. Für die Ausgabeschicht wird der Fehler als Differenz zwischen dem resultierenden und dem Referenzwert berechnet. Für die Neuronen der verborgenen Schicht wird der Fehler als Summe der Gradienten aller Neuronen der nachfolgenden Schicht berechnet, die auf der Grundlage der Gewichte der Verbindungen zwischen den Neuronen gewichtet werden. Diese Berechnung ist als separate Methode sumDOW implementiert.
void CNeuron::calcHiddenGradients(const CArrayObj *&nextLayer) { double dow=sumDOW(nextLayer); gradient=dow*CNeuron::activationFunctionDerivative(outputVal); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CNeuron::calcOutputGradients(double targetVals) { double delta=targetVals-outputVal; gradient=delta*CNeuron::activationFunctionDerivative(outputVal); }
Der Gradient wird dann durch Multiplikation des Fehlers mit der Ableitung der Aktivierungsfunktion bestimmt.
Betrachten wir die Methode sumDOW genauer, die den Neuronenfehler für die verdeckte Schicht bestimmt. Die Methode erhält als Parameter einen Zeiger auf die nächste Schicht von Neuronen. Im Körper der Methode wird zunächst der Wert der resultierende 'Summe' auf Null gesetzt, dann wird eine Schleife durch alle Neuronen der nächsten Schicht implementiert und das Produkt aus Neuronengradienten und dem Gewicht seiner Verbindung summiert.
double CNeuron::sumDOW(const CArrayObj *&nextLayer) const { double sum=0.0; int total=nextLayer.Total()-1; for(int n=0; n<total; n++) { СConnection *con=outputWeights.At(n); CNeuron *neuron=nextLayer.At(n); sum+=con.weight*neuron.gradient; } return sum; }
Sobald die oben genannten Vorbereitungsarbeiten abgeschlossen sind, brauchen wir nur noch die Methode updateInputWeights zu erstellen, mit der die Gewichte neu berechnet werden können. In meinem Modell speichert ein Neuron die ausgehende Gewichte, so dass die Methode zur Aktualisierung der Gewichte die vorherige Schicht von Neuronen in Parametern erhält.
void CNeuron::updateInputWeights(CArrayObj *&prevLayer) { int total=prevLayer.Total(); for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron= prevLayer.At(n); СConnection *con=neuron.outputWeights.At(m_myIndex); con.weight+=con.deltaWeight=eta*neuron.getOutputVal()*gradient + alpha*con.deltaWeight; } }
Der Methodenkörper enthält eine Schleife durch alle Neuronen der vorherigen Schicht, wobei die Anpassung der Gewichte den Einfluss auf das aktuelle Neuron anzeigt.
Bitte beachten Sie, dass die Gewichtsanpassung mit zwei Koeffizienten durchgeführt wird: eta (um die Reaktion auf die aktuelle Abweichung zu reduzieren) und alpha (Trägheitskoeffizient). Dieser Ansatz ermöglicht eine gewisse Mittelung des Einflusses einer Reihe von nachfolgenden Lerniterationen und filtert die Rauschdaten heraus.
4.3. Neuronales Netz
Nachdem wir das künstliche Neuron geschaffen haben, müssen wir die geschaffenen Objekte zu einer einzigen Einheit, dem neuronalen Netz, zusammenfügen. Die daraus resultierenden Objekte müssen flexibel sein und die Erstellung von neuronalen Netzen verschiedener Konfigurationen ermöglichen. Dadurch können wir die resultierende Lösung für verschiedene Aufgaben verwenden.
Wie bereits oben erwähnt, besteht ein neuronales Netz aus Schichten von Neuronen. Daher besteht der erste Schritt darin, Neuronen zu einer Schicht zusammenzufassen. Erstellen wir die Klasse CLayer. Die grundlegenden Methoden darin werden von CArrayObj abgeleitet.
class CLayer: public CArrayObj { private: uint iOutputs; public: CLayer(const int outputs=0) { iOutputs=outpus; }; ~CLayer(void){}; //--- virtual bool CreateElement(const int index); virtual int Type(void) const { return(0x7779); } };
Stellen Sie in den Parametern der Initialisierungsmethode der Klasse CLayer die Anzahl der Elemente der nächsten Schicht ein. Schreiben wir außerdem zwei virtuelle Methoden neu: CreateElement (Erstellung eines neuen Neurons der Schicht) und Type (Methode zur Objektidentifizierung).
Wenn Sie ein neues Neuron erstellen, geben Sie seinen Index in den Parametern der Methode an. Die Gültigkeit des erhaltenen Index wird im Methodenrumpf überprüft. Dann wird die Größe des Arrays für die Speicherung von Zeigern auf Neuron-Objektinstanzen überprüft und die Array-Größe gegebenenfalls erhöht. Danach erstellen wir das Neuron. Wenn die neue Neuroneninstanz erfolgreich erstellt wurde, setzen wir ihren Anfangswert und ändern die Anzahl der Objekte im Array. Dann verlassen wir die Methode mit 'true'.
bool CLayer::CreateElement(const uint index) { if(index<0) return false; //--- if(m_data_max<index+1) { if(ArrayResize(m_data,index+10)<=0) return false; m_data_max=ArraySize(m_data)-1; } //--- CNeuron *neuron=new CNeuron(iOutputs,index); if(!CheckPointer(neuron)!=POINTER_INVALID) return false; neuron.setOutputVal((neuronNum%3)-1) //--- m_data[index]=neuron; m_data_total=MathMax(m_data_total,index); //--- return (true); }
Erstellen wir mit einem ähnlichen Ansatz die Klasse CArrayLayer zum Speichern der Zeiger auf unsere Netzwerkschichten.
class CArrayLayer : public CArrayObj { public: CArrayLayer(void){}; ~CArrayLayer(void){}; //--- virtual bool CreateElement(const uint neurons, const uint outputs); virtual int Type(void) const { return(0x7780); } };
Der Unterschied zur vorherigen Klasse erscheint in der Methode CreateElement, die ein neues Array-Element erstellt. In diesen Methodenparametern geben Sie die Anzahl der Neuronen in der aktuellen und den weiteren zu erstellenden Schichten an. Wir überprüfen im Methodenkörper die Anzahl der Neuronen in der Schicht. Wenn keine Neuronen in der erstellten Schicht vorhanden sind, verlassen wir die Methode mit 'false'. Dann prüfen wir, ob es notwendig ist, die Größe des Arrays, das die Zeiger speichert, zu ändern. Danach können Objektinstanzen erstellt werden: Wir erstellen eine neue Schicht und implementieren eine Schleife, die Neuronen erzeugt. Wir überprüfen das erzeugte Objekt bei jedem Schritt. Im Falle eines Fehlers verlassen wir das Objekt mit dem Wert 'false'. Nachdem alle Elemente erstellt wurden, speichern wir einen Zeiger auf die erstellte Schicht im Array und verlassen das Array mit 'true'.
bool CArrayLayer::CreateElement(const uint neurons, const uint outputs) { if(neurons<=0) return false; //--- if(m_data_max<=m_data_total) { if(ArrayResize(m_data,m_data_total+10)<=0) return false; m_data_max=ArraySize(m_data)-1; } //--- CLayer *layer=new CLayer(outputs); if(!CheckPointer(layer)!=POINTER_INVALID) return false; for(uint i=0; i<neurons; i++) if(!layer.CreatElement(i)) return false; //--- m_data[m_data_total]=layer; m_data_total++; //--- return (true); }
Das Erstellen separater Klassen für die Schicht und die Anordnung der Schichten ermöglicht das Erstellen verschiedener neuronaler Netze mit unterschiedlichen Konfigurationen, ohne dass die Klassen geändert werden müssen. Dies ist eine flexible Einheit, die die Eingabe der gewünschten Anzahl von Schichten und Neuronen pro Schicht ermöglicht.
Betrachten wir nun die Klasse CNet, die ein neuronales Netz erzeugt.
class CNet { public: CNet(const CArrayInt *topology); ~CNet(){}; void feedForward(const CArrayDouble *inputVals); void backProp(const CArrayDouble *targetVals); void getResults(CArrayDouble *&resultVals); double getRecentAverageError() const { return recentAverageError; } bool Save(const string file_name, double error, double undefine, double forecast, datetime time, bool common=true); bool Load(const string file_name, double &error, double &undefine, double &forecast, datetime &time, bool common=true); //--- static double recentAverageSmoothingFactor; private: CArrayLayer layers; double recentAverageError; };
Wir haben in den oben genannten Klassen bereits eine Menge der erforderlichen Arbeit implementiert, und daher enthält die Klasse des neuronalen Netzes selbst ein Minimum an Variablen und Methoden. Der Klassencode enthält nur zwei statistische Variablen zur Berechnung und Speicherung des durchschnittlichen Fehlers (recentAverageSmoothingFactor und recentAverageError) sowie einen Zeiger auf das Array der 'Schichten', das die Netzwerkschichten enthält.
Betrachten wir die Methoden dieser Klasse im Detail. In den Parametern des Klassenkonstruktors wird ein Zeiger auf das int Datenarray übergeben. Die Anzahl der Elemente in dem Array gibt die Anzahl der Schichten an, während jedes Element des Arrays die Anzahl der Neuronen in der entsprechenden Schicht enthält. Somit kann diese universelle Klasse verwendet werden, um ein neuronales Netz beliebiger Komplexitätsstufe zu erstellen.
CNet::CNet(const CArrayInt *topology) { if(CheckPointer(topology)==POINTER_INVALID) return; //--- int numLayers=topology.Total(); for(int layerNum=0; layerNum<numLayers; layerNum++) { uint numOutputs=(layerNum==numLayers-1 ? 0 : topology.At(layerNum+1)); if(!layers.CreateElement(topology.At(layerNum), numOutputs)) return; } }
Wir überprüfen in der Methode die Gültigkeit des übergebenen Zeigers und implementieren eine Schleife, um Schichten im neuronalen Netz zu erzeugen. Für die Ausgangsebene wird ein Nullwert der ausgehenden Verbindungen angegeben.
Die Methode FeedForward wird zur Berechnung des Wertes des neuronalen Netzwerks verwendet. In den Parametern erhält die Methode ein Array von Eingabewerten, auf deren Grundlage die resultierenden Werte des neuronalen Netzes berechnet werden.
void CNet::feedForward(const CArrayDouble *inputVals) { if(CheckPointer(inputVals)==POINTER_INVALID) return; //--- CLayer *Layer=layers.At(0); if(CheckPointer(Layer)==POINTER_INVALID) { return; } int total=inputVals.Total(); if(total!=Layer.Total()-1) return; //--- for(int i=0; i<total && !IsStopped(); i++) { CNeuron *neuron=Layer.At(i); neuron.setOutputVal(inputVals.At(i)); } //--- total=layers.Total(); for(int layerNum=1; layerNum<total && !IsStopped(); layerNum++) { CArrayObj *prevLayer = layers.At(layerNum - 1); CArrayObj *currLayer = layers.At(layerNum); int t=currLayer.Total()-1; for(int n=0; n<t && !IsStopped(); n++) { CNeuron *neuron=currLayer.At(n); neuron.feedForward(prevLayer); } } }
In der Methode überprüfen wir die Gültigkeit des Empfangszeigers und der Nullschicht unseres Netzwerks. Dann stellen wir die erhaltenen Anfangswerte als die resultierenden Werte der Nullschicht-Neuronen ein und implementieren eine Doppelschleife mit einer phasenweisen Neuberechnung der resultierenden Werte der Neuronen im gesamten neuronalen Netzwerk, von der ersten verborgenen Schicht bis zu den Ausgangsneuronen.
Das Ergebnis erhalten wir durch die Methode getResults, die eine Schleife enthält, die die resultierenden Werte der Neuronen der Ausgabeschicht sammelt.
void CNet::getResults(CArrayDouble *&resultVals) { if(CheckPointer(resultVals)==POINTER_INVALID) { resultVals=new CArrayDouble(); } resultVals.Clear(); CArrayObj *Layer=layers.At(layers.Total()-1); if(CheckPointer(Layer)==POINTER_INVALID) { return; } int total=Layer.Total()-1; for(int n=0; n<total; n++) { CNeuron *neuron=Layer.At(n); resultVals.Add(neuron.getOutputVal()); } }
Der Lernprozess des neuronalen Netzes ist in der Methode BackProp implementiert. Die Methode erhält eine Reihe von Referenzwerten in Form von Parametern. Im Körper der Methode wird die Gültigkeit des empfangenen Arrays überprüft und der mittlere quadratische Fehler der resultierenden Schicht berechnet. Dann werden in der Schleife die Gradienten der Neuronen in allen Schichten neu berechnet. Danach aktualisieren wir in der letzten Schicht der Methode die Gewichte der Verbindungen zwischen den Neuronen auf der Grundlage der zuvor berechneten Gradienten.
void CNet::backProp(const CArrayDouble *targetVals) { if(CheckPointer(targetVals)==POINTER_INVALID) return; CArrayObj *outputLayer=layers.At(layers.Total()-1); if(CheckPointer(outputLayer)==POINTER_INVALID) return; //--- double error=0.0; int total=outputLayer.Total()-1; for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=outputLayer.At(n); double delta=targetVals[n]-neuron.getOutputVal(); error+=delta*delta; } error/= total; error = sqrt(error); recentAverageError+=(error-recentAverageError)/recentAverageSmoothingFactor; //--- for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=outputLayer.At(n); neuron.calcOutputGradients(targetVals.At(n)); } //--- for(int layerNum=layers.Total()-2; layerNum>0; layerNum--) { CArrayObj *hiddenLayer=layers.At(layerNum); CArrayObj *nextLayer=layers.At(layerNum+1); total=hiddenLayer.Total(); for(int n=0; n<total && !IsStopped();++n) { CNeuron *neuron=hiddenLayer.At(n); neuron.calcHiddenGradients(nextLayer); } } //--- for(int layerNum=layers.Total()-1; layerNum>0; layerNum--) { CArrayObj *layer=layers.At(layerNum); CArrayObj *prevLayer=layers.At(layerNum-1); total=layer.Total()-1; for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=layer.At(n); neuron.updateInputWeights(prevLayer); } } }
Um zu vermeiden, dass das System im Falle eines Programmneustarts erneut trainiert werden muss, erstellen wir die Methode 'Save' zum Speichern von Daten in einer lokalen Datei und die Methode 'Load' zum Laden der gespeicherten Daten aus der Datei.
Der vollständige Code aller Klassenmethoden ist in der Anlage verfügbar.
Schlussfolgerung
Dieser Artikel sollte zeigen, wie ein neuronales Netzwerk zu Hause erstellt werden kann. Natürlich ist dies nur die Spitze des Eisbergs. Der Artikel betrachtet nur eine der möglichen Versionen, nämlich das Perceptron, das Frank Rosenblatt bereits 1957 eingeführt hat. Seit der Einführung des Modells sind mehr als 60 Jahre vergangen, und eine Vielzahl weiterer Modelle ist erschienen. Das Perceptron-Modell ist jedoch immer noch brauchbar und liefert gute Ergebnisse — Sie können das Modell selbst testen. Wer sich tiefer in die Idee der künstlichen Intelligenz vertiefen möchte, sollte einschlägiges Material lesen, denn es ist unmöglich, alles auch nur in einer Reihe von Artikeln zu behandeln.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zum Erstellen eines neuronalen Netzes (ein Perceptron) |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/7447
Bibliothek für ein leichtes und schnelles Entwickeln vom Programmen für den MetaTrader (Teil XXIX): Schwebende Handelsanfrage - die Klasse der Anfrageobjekte
Bibliothek für ein leichtes und schnelles Entwickeln vom Programmen für den MetaTrader (Teil XXVIII): Schließen, Entfernen und Ändern von schwebenden Handelsanfragen
Bibliothek für ein leichtes und schnelles Entwickeln vom Programmen für den MetaTrader (Teil XXX): Schwebende Handelsanfragen - die Verwaltung der Anfrageobjekte
Bibliothek für ein leichtes und schnelles Entwickeln vom Programmen für den MetaTrader (Teil XXVII): Arbeiten mit Handelsanfragen - platzieren von Pending-Orders
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Hi Dmitriy Gizlyk,
your article "Neural Network Made Easy" is great!
Could you give an example where you use your classes?
For example, a simple task such as: A neural network that can convert from binary numbers to decimal numbers?