
Neuronale Netze im Handel: Optimierung des Transformers für Zeitreihenprognosen (LSEAttention)
Einführung
Multivariate Zeitreihenprognosen spielen in vielen Bereichen (Finanzen, Gesundheitswesen usw.) eine entscheidende Rolle, wenn es darum geht, zukünftige Werte auf der Grundlage historischer Daten vorherzusagen. Eine besondere Herausforderung stellt diese Aufgabe bei langfristigen Prognosen dar, die Modelle erfordern, die in der Lage sind, Merkmalskorrelationen und langfristige Abhängigkeiten in multivariaten Zeitreihendaten wirksam zu erfassen. In jüngster Zeit hat sich die Forschung zunehmend auf die Nutzung der Transformer-Architektur für die Zeitreihenprognose konzentriert, da diese über einen leistungsfähigen Selbstaufmerksamkeitsmechanismus (Self-Attention) verfügt, der sich durch die Modellierung komplexer zeitlicher Interaktionen auszeichnet. Trotz ihres Potenzials stützen sich jedoch viele moderne Methoden für multivariate Zeitreihenprognosen immer noch stark auf lineare Modelle, was Bedenken hinsichtlich der tatsächlichen Wirksamkeit von Transformers in diesem Zusammenhang aufkommen lässt.
Der Selbstaufmerksamkeitsmechanismus, der den Kern der Transformer-Architektur bildet, ist wie folgt definiert:
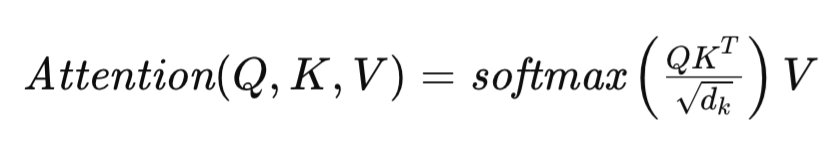
wobei Q, K und V die Matrizen von Query (Abfrage), Key (Schlüssel) bzw. Value (Wert) darstellen und dk die Dimensionalität der Vektoren bezeichnet, die jedes Sequenzelement beschreiben. Diese Formulierung ermöglicht es dem Transformer, die Relevanz verschiedener Elemente in der Eingabesequenz dynamisch zu bewerten, wodurch die Modellierung komplexer Abhängigkeiten innerhalb der Daten erleichtert wird.
Es wurden verschiedene Anpassungen der Transformer-Architektur vorgeschlagen, um ihre Leistung bei langfristigen Zeitreihenprognosen zu verbessern. Zum Beispiel FEDformer, ein fortschrittliches Fourier-Modul, das eine lineare Komplexität sowohl in der Zeit als auch im Raum erreicht, was die Skalierbarkeit und Effizienz bei langen Eingabesequenzen erheblich verbessert.
PatchTST hingegen gibt die punktuelle Aufmerksamkeit zugunsten einer Darstellung auf Patch-Ebene auf und konzentriert sich auf zusammenhängende Segmente statt auf einzelne Zeitschritte. Dieser Ansatz ermöglicht es dem Modell, umfangreichere semantische Informationen in multivariaten Zeitreihen zu erfassen, was für eine effektive Langzeitprognose entscheidend ist.
In Bereichen wie dem Computersehen und der Verarbeitung natürlicher Sprache können Aufmerksamkeitsmatrizen unter einem Entropie- oder Rangkollaps leiden. Dieses Problem wird bei der Zeitreihenprognose aufgrund der häufigen Schwankungen, die zeitbasierte Daten aufweisen, noch verschärft, was häufig zu einer erheblichen Verschlechterung der Modellleistung führt. Die dem Entropiekollaps zugrunde liegenden Ursachen sind nach wie vor nur unzureichend bekannt, was die Notwendigkeit weiterer Untersuchungen zu den Mechanismen und Auswirkungen auf die Modellgeneralisierung unterstreicht. Diese Herausforderungen stehen im Mittelpunkt des Papiers mit dem Titel „LSEAttention is All You Need for Time Series Forecasting“ (LSEAttention ist alles, was Sie für Zeitreihenprognosen benötigen).
1. Der LSEAttention-Algorithmus
Das Ziel der multivariaten Zeitreihenprognose ist die Schätzung der wahrscheinlichsten zukünftigen Werte P für jeden der KanäleC, dargestellt als Tensor Y ∈ RC×P. Diese Vorhersage basiert auf historischen Zeitreihendaten der Länge L mit C Kanälen, die in der Eingangsmatrix X ∈ RC×L gekapselt sind. Die Aufgabe besteht im Training eines Vorehrsagemodells fωRC×L →RC×P, parametrisiert durch ω, das den mittleren quadratischen Fehler (MSE) zwischen vorhergesagten und tatsächlichen Werten minimiert.
Transformer stützen sich in hohem Maße auf punktuelle Mechanismen der Selbstaufmerksamkeit, um zeitliche Zusammenhänge zu erfassen. Diese Abhängigkeit kann jedoch zu einem Phänomen führen, das als Aufmerksamkeitskollaps bekannt ist, bei dem die Aufmerksamkeitsmatrizen über verschiedene Eingabesequenzen hinweg zu nahezu identischen Werten konvergieren. Dies führt zu einer schlechten Verallgemeinerung der Daten durch das Modell.
Die Autoren der Methode LSEAttention ziehen eine Analogie zwischen den über die Funktion Softmax berechneten Abhängigkeits-Koeffizienten und der Operation Log-Sum-Exp (LSE). Sie stellen die Hypothese auf, dass numerische Instabilität in dieser Formulierung die Ursache für den Zusammenbruch der Aufmerksamkeit sein könnte.
Die Zustandszahl einer Funktion spiegelt ihre Empfindlichkeit gegenüber kleinen Eingangsschwankungen wider. Eine hohe Zustandszahl zeigt an, dass selbst kleine Störungen im Eingang zu erheblichen Abweichungen im Ausgang führen können.
Im Zusammenhang mit Aufmerksamkeitsmechanismen kann sich eine solche Instabilität als Überaufmerksamkeit oder Entropiekollaps manifestieren, gekennzeichnet durch Aufmerksamkeitsmatrizen mit extrem hohen Diagonalwerten (was auf einen Überlauf hinweist) und sehr niedrigen Off-Diagonalwerten (was auf einen Unterlauf hinweist).
Um diese Probleme zu lösen, schlagen die Autoren das Modul LSEAttention den Trick vor, Log-Sum-Exp (LSE) mit der Aktivierungsfunktion GELU (Gaussian Error Linear Unit) zu integrieren. Der LSE-Trick mildert die durch Über- und Unterlauf verursachte numerische Instabilität durch Normalisierung. Die Softmax-Funktion kann mit LSE wie folgt umformuliert werden:
![]()
wobei der Exponent von LSE (x) die Exponentialwerte der Funktion log-sum-exp angibt, was die numerische Stabilität erhöht.
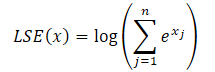
Unter Verwendung der Exponenteneigenschaften kann jeder Exponentialterm als Produkt zweier Exponentialterme ausgedrückt werden.
![]()
wobei a eine Konstante ist, die zur Normalisierung dient. In der Praxis wird in der Regel der Höchstwert als Konstante verwendet. Setzt man das Produkt der Exponenten in die LSE-Formel ein und nimmt den Gesamtwert außerhalb des Summenzeichens, erhält man:
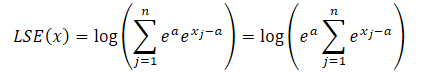
Der Logarithmus eines Produkts wird zu einer Summe von Logarithmen, und der natürliche Logarithmus eines Exponentialwerts ist gleich dem Exponenten. Dadurch lässt sich der dargestellte Ausdruck vereinfachen:
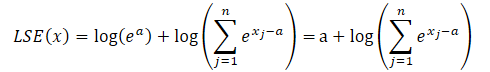
Wir setzen den resultierenden Ausdruck in die Softmax-Funktion ein und nutzen die Exponentialeigenschaft:
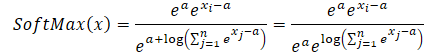
Wie Sie feststellen können, hebt sich der Exponentialwert der Konstante, die Zähler und Nenner gemeinsam haben, auf. Der Exponent des natürlichen Logarithmus ist gleich dem logarithmischen Ausdruck. So erhalten wir einen numerisch stabilen Softmax-Ausdruck.
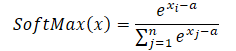
Wenn man den Maximalwert als Konstante verwendet (a = max(x)), erhält man immer x-a kleiner oder gleich 0. In diesem Fall liegt der Exponentialwert von x-a im Bereich von 0 bis 1, 0 nicht eingeschlossen. Dementsprechend liegt der Nenner der Funktion im Bereich (1, n].
Darüber hinaus schlagen die Autoren von LSEAttention die Verwendung der Aktivierungsfunktion GELU vor, die eine glattere probabilistische Aktivierung ermöglicht. Dies trägt dazu bei, Extremwerte in der logarithmischen Wahrscheinlichkeit vor der Anwendung der Exponentialfunktion zu stabilisieren, wodurch abrupte Übergänge in den Aufmerksamkeitswerten abgemildert werden. Durch die Annäherung der Funktion ReLU durch eine glatte Kurve, die die kumulative Verteilungsfunktion (CDF) der Standardnormalverteilung einbezieht, reduziert GELU die starken Verschiebungen in den Aktivierungen, die bei der traditionellen ReLU auftreten können. Diese Eigenschaft ist besonders vorteilhaft für die Stabilisierung von Transformer-basierten Aufmerksamkeitsmechanismen, bei denen plötzliche Aktivierungsspitzen zu numerischer Instabilität und Gradientenexplosionen führen können.
Die GELU-Funktion ist formell wie folgt definiert:
![]()
wobei Φ(x) die CDF der Standardnormalverteilung darstellt. Diese Formulierung stellt sicher, dass GELU die Eingabewerte in Abhängigkeit von ihrer Größe unterschiedlich stark skaliert und so die Verstärkung von Extremwerten unterdrückt. Die sanfte, probabilistische Natur von GELU ermöglicht einen allmählichen Übergang der Eingangsaktivierungen, was wiederum große Gradientenschwankungen während des Trainings abmildert.
Diese Eigenschaft wird besonders wertvoll, wenn sie mit dem Tricj von Log-Sum-Exp (LSE) kombiniert wird, der die Softmax-Funktion auf eine numerisch stabile Weise normalisiert. Zusammen verhindern LSE und GELU wirksam Über- und Unterlauf bei den exponentiellen Operationen von Softmax, was zu einem stabilisierten Bereich von Aufmerksamkeitsgewichten führt. Diese Synergie erhöht die Robustheit von Transformer-Modellen, indem sie eine gut verteilte Verteilung der Aufmerksamkeitskoeffizienten auf die Token gewährleistet. Letztendlich führt dies zu stabileren Gradienten und einer besseren Konvergenz beim Training.
In traditionellen Transformer-Architekturen ist die Aktivierungsfunktion ReLU (Rectified Linear Unit), die im Block des Vorwärtsdurchlauf-Netzwerks (FFN) verwendet wird, anfällig für das Problem des „sterbenden ReLU“, bei dem Neuronen inaktiv werden können, indem sie für alle negativen Eingangswerte Null ausgeben. Dies führt dazu, dass die Gradienten für diese Neuronen gleich Null sind, was ihr Lernen effektiv stoppt und zur Instabilität des Trainings beiträgt.
Um dieses Problem zu lösen, wird die Funktion parametrische ReLU (PReLU) als Alternative verwendet. PReLU führt eine erlernbare Steigung für negative Eingänge ein, die eine Ausgabe ungleich Null ermöglicht, selbst wenn der Eingang negativ ist. Diese Anpassung entschärft nicht nur das ReLU-Problem, sondern ermöglicht auch einen sanfteren Übergang zwischen negativen und positiven Aktivierungen und verbessert so die Fähigkeit des Modells, über den gesamten Eingaberaum hinweg zu lernen. Das Vorhandensein von Nicht-Null-Gradienten für negative Werte unterstützt einen besseren Gradientenfluss, der für das Training tieferer Architekturen unerlässlich ist. Folglich trägt die Verwendung von PReLU zur allgemeinen Stabilität des Trainings bei und hilft, aktive Repräsentationen aufrechtzuerhalten, was letztendlich zu einer verbesserten Modellleistung führt.
In die Architektur des „LSEAttention Time Series Transformer“ (LATST) integrieren die Autoren auch eine invertierbare Datennormalisierung, die sich als besonders effektiv erweist, wenn es darum geht, Verteilungsdiskrepanzen zwischen Trainings- und Testdaten bei Zeitreihenprognosen zu beheben.
Die Architektur behält den traditionellen zeitlichen Selbstaufmerksamkeits-Mechanismus bei, der in das Modul LSEAttention eingebettet ist.
Insgesamt besteht die LATST-Architektur aus einer einschichtigen Transformer-Struktur, die mit Substitutionsmodulen erweitert wurde und adaptives Lernen ermöglicht, während die Zuverlässigkeit der Aufmerksamkeitsmechanismen erhalten bleibt. Dieses Design erleichtert die effiziente Modellierung zeitlicher Abhängigkeiten und steigert die Leistung bei Zeitreihenprognosen. Die Originalvisualisierung des Rahmens finden Sie unten.
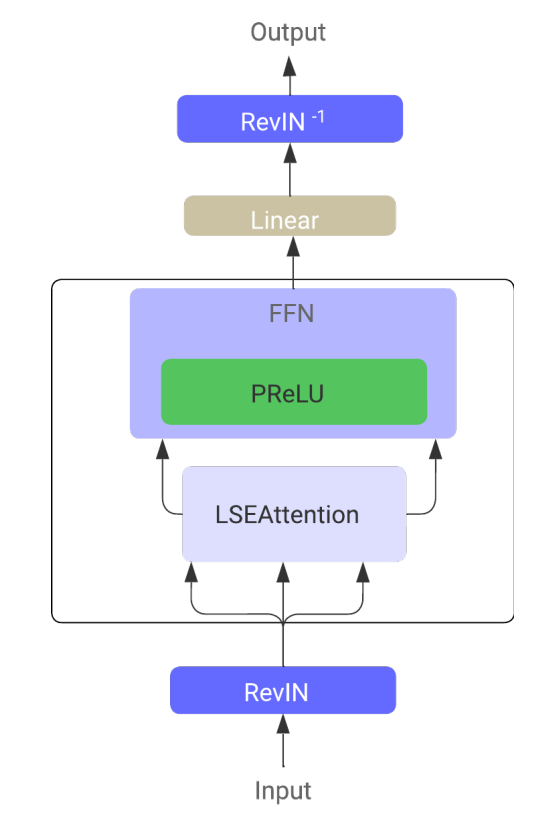
2. Die Implementation in MQL5
Nachdem wir die theoretischen Aspekte von LSEAttention besprochen haben, wenden wir uns nun dem praktischen Teil unserer Arbeit zu, in dem wir eine mögliche Implementierung der vorgeschlagenen Techniken mit MQL5 untersuchen. Es ist wichtig zu beachten, dass sich diese Umsetzung erheblich von früheren unterscheidet. Insbesondere werden wir kein neues Objekt erstellen, um die vorgeschlagenen Methoden zu implementieren. Stattdessen werden wir sie in bereits entwickelte Klassen integrieren.
2.1 Anpassen der Softmax-Schicht
Betrachten wir die Klasse CNeuronSoftMaxOCL, die die Softmax-Funktionsschicht behandelt. Diese Klasse wird sowohl als eigenständige Komponente unseres Modells als auch als Teil verschiedener Frameworks ausgiebig genutzt. Zum Beispiel haben wir das Objekt CNeuronSoftMaxOCL beim Aufbau eines Pooling-Moduls auf der Grundlage von Abhängigkeitsmustern (CNeuronMHAttentionPooling), das wir in mehreren aktuellen Studien eingesetzt haben. Daher ist es logisch, numerisch stabile Softmax-Berechnungen in diesen Klassenalgorithmus einzubauen.
Um dies zu erreichen, werden wir das Verhalten des SoftMax_FeedForward-Kernels ändern. Der Kernel erhält Zeiger auf zwei Datenpuffer als Parameter: einen für die Eingabewerte und einen für die Ausgabeergebnisse.
__kernel void SoftMax_FeedForward(__global float *inputs, __global float *outputs) { const uint total = (uint)get_local_size(0); const uint l = (uint)get_local_id(0); const uint h = (uint)get_global_id(1);
Wir planen die Ausführung des Kernels in einem zweidimensionalen Aufgabenraum. Die Größe der ersten Dimension entspricht der Anzahl der zu normalisierenden Werte innerhalb einer unitären Sequenz. In der zweiten Dimension geben wir die Anzahl der unitären Sequenzen (oder Normalisierungsköpfe) an. Dabei fassen wir die Ströme in Arbeitsgruppen innerhalb einzelner unitären Sequenzen zusammen.
Innerhalb des Kernelkörpers identifizieren wir zunächst den aktuellen Thread im Aufgabenraum über alle Dimensionen hinweg.
Anschließend deklarieren wir ein lokales Speicherfeld, das den Datenaustausch innerhalb der Arbeitsgruppe erleichtern soll.
__local float temp[LOCAL_ARRAY_SIZE];
Als Nächstes definieren wir konstante Offsets in den globalen Datenpuffern, die auf die entsprechenden Elemente zeigen.
const uint ls = min(total, (uint)LOCAL_ARRAY_SIZE); uint shift_head = h * total;
Um die Zugriffe auf den globalen Speicher zu minimieren, kopieren wir die Eingabewerte in lokale Variablen und validieren die resultierenden Werte.
float inp = inputs[shift_head + l]; if(isnan(inp) || isinf(inp) || inp<-120.0f) inp = -120.0f;
Es ist erwähnenswert, dass wir die Eingabewerte auf einen unteren Schwellenwert von -120 begrenzen, der dem kleinsten im Format float darstellbaren Exponentenwert nahe kommt. Dies dient als zusätzliche Maßnahme, um einen Unterlauf zu verhindern. Wir legen keine Obergrenze für die Werte fest, da ein möglicher Überlauf durch Subtraktion des Höchstwertes ausgeglichen wird.
Als Nächstes ermitteln wir den Höchstwert innerhalb der aktuellen Einheitsfolge. Dies wird durch eine Schleife erreicht, die die Maximalwerte jeder Untergruppe in der Arbeitsgruppe sammelt und in Elementen des lokalen Speicherarrays speichert.
for(int i = 0; i < total; i += ls) { if(l >= i && l < (i + ls)) temp[l] = (i > 0 ? fmax(inp, temp[l]) : inp); barrier(CLK_LOCAL_MEM_FENCE); }
Anschließend wird über das lokale Array iteriert, um das globale Maximum der aktuellen Arbeitsgruppe zu ermitteln.
uint count = min(ls, (uint)total); do { count = (count + 1) / 2; if(l < ls) temp[l] = (l < count && (l + count) < total ? fmax(temp[l + count],temp[l]) : temp[l]); barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); float max_value = temp[0]; barrier(CLK_LOCAL_MEM_FENCE);
Der ermittelte Maximalwert wird in einer lokalen Variablen gespeichert, und wir stellen in dieser Phase die Synchronisierung der Threads sicher. Es ist von entscheidender Bedeutung, dass alle Threads in der Arbeitsgruppe den korrekten Maximalwert beibehalten, bevor eine Änderung der Elemente des lokalen Speicherarrays erfolgt.
Nun wird der Maximalwert von jeder ursprünglichen Eingabe subtrahiert. Auch hier prüfen wir, ob die untere Grenze erreicht ist. Da die Subtraktion eines positiven Maximums das Ergebnis über den gültigen Bereich hinausschieben kann. Anschließend wird der Exponentialwert des angepassten Wertes berechnet.
inp = fmax(inp - max_value, -120); float inp_exp = exp(inp); if(isinf(inp_exp) || isnan(inp_exp)) inp_exp = 0;
In zwei aufeinander folgenden Schleifen summieren wir die resultierenden Exponentiale in der gesamten Arbeitsgruppe. Die Schleifenstruktur ist ähnlich wie bei der Berechnung des Höchstwertes. Wir ändern einfach die Operation im Körper der Schleifen entsprechend.
for(int i = 0; i < total; i += ls) { if(l >= i && l < (i + ls)) temp[l] = (i > 0 ? temp[l] : 0) + inp_exp; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)total); do { count = (count + 1) / 2; if(l < ls) temp[l] += (l < count && (l + count) < total ? temp[l + count] : 0); if(l + count < ls) temp[l + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Nachdem wir alle erforderlichen Werte erhalten haben, können wir nun die endgültigen Werte von Softmax berechnen, indem wir jedes Exponential durch die Summe der Exponentiale innerhalb der Arbeitsgruppe dividieren.
//--- float sum = temp[0]; outputs[shift_head+l] = inp_exp / (sum + 1.2e-7f); }
Das Ergebnis dieser Operation wird in das entsprechende Element im globalen Ergebnispuffer geschrieben.
Es ist wichtig hervorzuheben, dass die Änderungen, die während des Vorwärtsdurchlaufs an der Berechnung Softmax vorgenommen werden, keine Änderungen an den Rückwärtsdurchlauf-Algorithmen erfordern. Wie in den mathematischen Ableitungen, die weiter oben in diesem Artikel vorgestellt wurden, gezeigt wurde, ändert die Anwendung des LSE-Tricks nichts an der endgültigen Ausgabe der Softmax-Funktion. Folglich bleibt der Einfluss der Eingabedaten auf das Endergebnis unverändert. So können wir den bestehenden Algorithmus für die Gradientenfehlerverteilung ohne Änderungen weiter verwenden.
2.2 Modifizierung des Moduls der Relativen Aufmerksamkeit
Es ist wichtig zu beachten, dass der Algorithmus Softmax nicht immer als eigenständige Schicht verwendet wird. In fast allen Versionen unserer Implementierungen, die verschiedene Blockdesigns der Selbstaufmerksamkeit beinhalten, ist die Logik direkt in einen einheitlichen Aufmerksamkeitskern eingebettet. Untersuchen wir das Modul CNeuronRelativeSelfAttention. Hier ist der gesamte Algorithmus für den modifizierten Selbstaufmerksamkeits-Mechanismus im Kernel von MHRelativeAttentionOut implementiert. Und natürlich wollen wir einen stabilen Trainingsprozess für alle Modellarchitekturen gewährleisten. Daher müssen wir Softmax in all diese Kernel numerisch stabil implementieren. Wann immer es möglich ist, behalten wir die bestehenden Kernel-Parameter und die Taskspace-Konfiguration bei. Dieser Ansatz wurde auch bei der Aktualisierung des Kerns von MHRelativeAttentionOut verwendet.
Beachten Sie jedoch, dass alle Änderungen an den Kernel-Parametern oder am Task-Space-Layout in allen Wrapper-Methoden des Hauptprogramms, das diesen Kernel zur Ausführung auffordert, berücksichtigt werden müssen. Andernfalls kann es zu kritischen Laufzeitfehlern beim Kernel-Dispatch kommen. Dies gilt nicht nur für Änderungen des globalen Aufgabenbereichs, sondern auch für Änderungen der Arbeitsgruppengröße.
__kernel void MHRelativeAttentionOut(__global const float *q, ///<[in] Matrix of Querys __global const float *k, ///<[in] Matrix of Keys __global const float *v, ///<[in] Matrix of Values __global const float *bk, ///<[in] Matrix of Positional Bias Keys __global const float *bv, ///<[in] Matrix of Positional Bias Values __global const float *gc, ///<[in] Global content bias vector __global const float *gp, ///<[in] Global positional bias vector __global float *score, ///<[out] Matrix of Scores __global float *out, ///<[out] Matrix of attention const int dimension ///< Dimension of Key ) { //--- init const int q_id = get_global_id(0); const int k_id = get_local_id(1); const int h = get_global_id(2); const int qunits = get_global_size(0); const int kunits = get_local_size(1); const int heads = get_global_size(2);
Innerhalb des Kernelkörpers identifizieren wir wie zuvor den aktuellen Thread innerhalb des Aufgabenraums und definieren alle notwendigen Dimensionen.
Als Nächstes deklarieren wir eine Reihe von erforderlichen Konstanten, einschließlich der Offsets in den globalen Datenpuffern und der Hilfswerte.
const int shift_q = dimension * (q_id * heads + h); const int shift_kv = dimension * (heads * k_id + h); const int shift_gc = dimension * h; const int shift_s = kunits * (q_id * heads + h) + k_id; const int shift_pb = q_id * kunits + k_id; const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE); float koef = sqrt((float)dimension);
Wir definieren auch ein lokales Speicherfeld für den Datenaustausch zwischen den einzelnen Arbeitsgruppen.
__local float temp[LOCAL_ARRAY_SIZE];
Zur Berechnung der Aufmerksamkeitswerte nach dem einfachen Algorithmus der Selbstaufmerksamkeit wird zunächst ein Punktprodukt zwischen den entsprechenden Vektoren der Tensoren Query und Key gebildet. Die Autoren des R-MAT-Rahmens fügen jedoch kontextabhängige und globale Verzerrungsterme hinzu. Da alle Vektoren gleich lang sind, können diese Operationen in einer einzigen Schleife durchgeführt werden, wobei die Anzahl der Iterationen der Vektorgröße entspricht. Innerhalb des Schleifenkörpers führen wir eine elementweise Multiplikation gefolgt von einer Summierung durch.
//--- score float sc = 0; for(int d = 0; d < dimension; d++) { float val_q = q[shift_q + d]; float val_k = k[shift_kv + d]; float val_bk = bk[shift_kv + d]; sc += val_q * val_k + val_q * val_bk + val_k * val_bk + gc[shift_q + d] * val_k + gp[shift_q + d] * val_bk; } sc = sc / koef;
Die resultierende Punktzahl wird mit der Quadratwurzel aus der Dimensionalität des Vektors skaliert. Nach Ansicht der Autoren des einfachen Transformers verbessert dieser Vorgang die Stabilität des Modells. Wir halten an dieser Praxis fest.
Die sich daraus ergebenden Werte werden dann mit Hilfe von Softmax in Wahrscheinlichkeiten umgewandelt. Hier fügen wir Operationen ein, um die numerische Stabilität zu gewährleisten. Zunächst ermitteln wir den Maximalwert unter den Aufmerksamkeitswerten innerhalb jeder Arbeitsgruppe. Zu diesem Zweck werden die Threads in Untergruppen aufgeteilt, von denen jede ihr lokales Maximum in ein Element des lokalen Speicherfelds schreibt.
//--- max value for(int cur_k = 0; cur_k < kunits; cur_k += ls) { if(k_id >= cur_k && k_id < (cur_k + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_k == 0 ? sc : fmax(temp[shift_local], sc)); } barrier(CLK_LOCAL_MEM_FENCE); }
Anschließend wird eine Schleife über das Array gelegt, um den globalen Höchstwert zu ermitteln.
uint count = min(ls, (uint)kunits); //--- do { count = (count + 1) / 2; if(k_id < ls) temp[k_id] = (k_id < count && (k_id + count) < kunits ? fmax(temp[k_id + count], temp[k_id]) : temp[k_id]); barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Der aktuelle Aufmerksamkeitswert wird dann angepasst, indem dieser Maximalwert abgezogen wird, bevor die Exponentialfunktion angewendet wird. Auch hier müssen wir Threads synchronisieren. Denn im nächsten Schritt werden wir die Werte der lokalen Array-Elemente ändern und riskieren, den Wert des maximalen Elements zu überschreiben, bevor er von allen Threads der Arbeitsgruppe verwendet wird.
sc = exp(fmax(sc - temp[0], -120)); if(isnan(sc) || isinf(sc)) sc = 0; barrier(CLK_LOCAL_MEM_FENCE);
Als nächsten Schritt müssen wir die Summe der erhaltenen Exponentialwerte innerhalb der Arbeitsgruppe berechnen. Dazu verwenden wir wie zuvor einen Algorithmus aus zwei aufeinanderfolgenden Zyklen.
//--- sum of exp for(int cur_k = 0; cur_k < kunits; cur_k += ls) { if(k_id >= cur_k && k_id < (cur_k + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_k == 0 ? 0 : temp[shift_local]) + sc; } barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k_id < ls) temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0); if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Nun können wir die Aufmerksamkeitswerte in Wahrscheinlichkeiten umwandeln, indem wir jeden Wert durch die Gesamtsumme dividieren.
//--- score float sum = temp[0]; if(isnan(sum) || isinf(sum) || sum <= 1.2e-7f) sum = 1; sc /= sum; score[shift_s] = sc; barrier(CLK_LOCAL_MEM_FENCE);
Die resultierenden Wahrscheinlichkeiten werden in die entsprechenden Elemente des globalen Ausgabepuffers geschrieben, und wir synchronisieren die Ausführung der Threads innerhalb der Arbeitsgruppe.
Schließlich berechnen wir die gewichtete Summe der Werte des Tensors der Elemente für jedes Element der Eingabesequenz. Wir werden die Werte auf der Grundlage der oben berechneten Aufmerksamkeitskoeffizienten gewichten. Innerhalb eines Elements der Sequenz wird diese Operation durch Multiplikation des Vektors der Aufmerksamkeitskoeffizienten mit dem Wertetensor dargestellt, zu dem die Autoren des Rahmens von R-MAT einen globalen Verzerrungstensor hinzugefügt haben.
Dies wird mit Hilfe eines Schleifensystems realisiert, wobei die äußere Schleife über die letzte Dimension des Wertetensors iteriert.
//--- out for(int d = 0; d < dimension; d++) { float val_v = v[shift_kv + d]; float val_bv = bv[shift_kv + d]; float val = sc * (val_v + val_bv); if(isnan(val) || isinf(val)) val = 0;
Innerhalb der Schleife berechnet jeder Thread seinen Beitrag zum entsprechenden Element, und diese Beiträge werden mithilfe von verschachtelten sequenziellen Reduktionsschleifen innerhalb der Arbeitsgruppe aggregiert.
//--- sum of value for(int cur_v = 0; cur_v < kunits; cur_v += ls) { if(k_id >= cur_v && k_id < (cur_v + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_v == 0 ? 0 : temp[shift_local]) + val; } barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k_id < count && (k_id + count) < kunits) temp[k_id] += temp[k_id + count]; if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Die Summe wird dann von einem der Threads in das entsprechende Element des globalen Ergebnispuffers geschrieben.
//--- if(k_id == 0) out[shift_q + d] = (isnan(temp[0]) || isinf(temp[0]) ? 0 : temp[0]); barrier(CLK_LOCAL_MEM_FENCE); } }
Danach synchronisieren wir die Threads erneut, bevor wir zur nächsten Schleifeniteration übergehen.
Wie bereits erwähnt, haben die Änderungen an Softmax keinen Einfluss auf die Abhängigkeit der Ergebnisse von den Eingabedaten. Daher können wir die bestehenden Backpropagation-Algorithmen ohne Änderungen wiederverwenden.
2.3 GELU Aktivierungsfunktion
Neben der numerischen Stabilisierung von Softmax empfehlen die Autoren des Rahmens von LSEAttention auch die Verwendung der Aktivierungsfunktion GELU. Die Autoren haben zwei Versionen dieser Funktion vorgeschlagen. Eine davon wird im Folgenden vorgestellt.
![]()
Die Implementierung dieser Aktivierungsfunktion ist recht einfach. Wir fügen einfach die neue Variante zu unserem bestehenden Aktivierungsfunktions-Handler hinzu.
float Activation(const float value, const int function) { if(isnan(value) || isinf(value)) return 0; //--- float result = value; switch(function) { case 0: result = tanh(clamp(value, -20.0f, 20.0f)); break; case 1: //Sigmoid result = 1 / (1 + exp(clamp(-value, -20.0f, 20.0f))); break; case 2: //LReLU if(value < 0) result *= 0.01f; break; case 3: //SoftPlus result = (value >= 20.0f ? 1.0f : (value <= -20.0f ? 0.0f : log(1 + exp(value)))); break; case 4: //GELU result = value / (1 + exp(clamp(-1.702f * value, -20.0f, 20.0f))); break; default: break; } //--- return result; }
Hinter der scheinbaren Einfachheit des Vorwärtsdurchlaufs verbirgt sich jedoch die komplexere Aufgabe der Implementierung des Rückwärtsdurchlauf. Das liegt daran, dass die Ableitung von GELU von der ursprünglichen Eingabe und der Sigmoidfunktion abhängt. Beide sind in unserer Standardimplementierung nicht vorhanden.
![]()
Außerdem ist es nicht möglich, die Ableitung der GELU-Funktion allein auf der Grundlage des Ergebnisses des Vorwärtsdurchlaufs genau auszudrücken. Daher mussten wir auf bestimmte Heuristiken und Näherungswerte zurückgreifen.
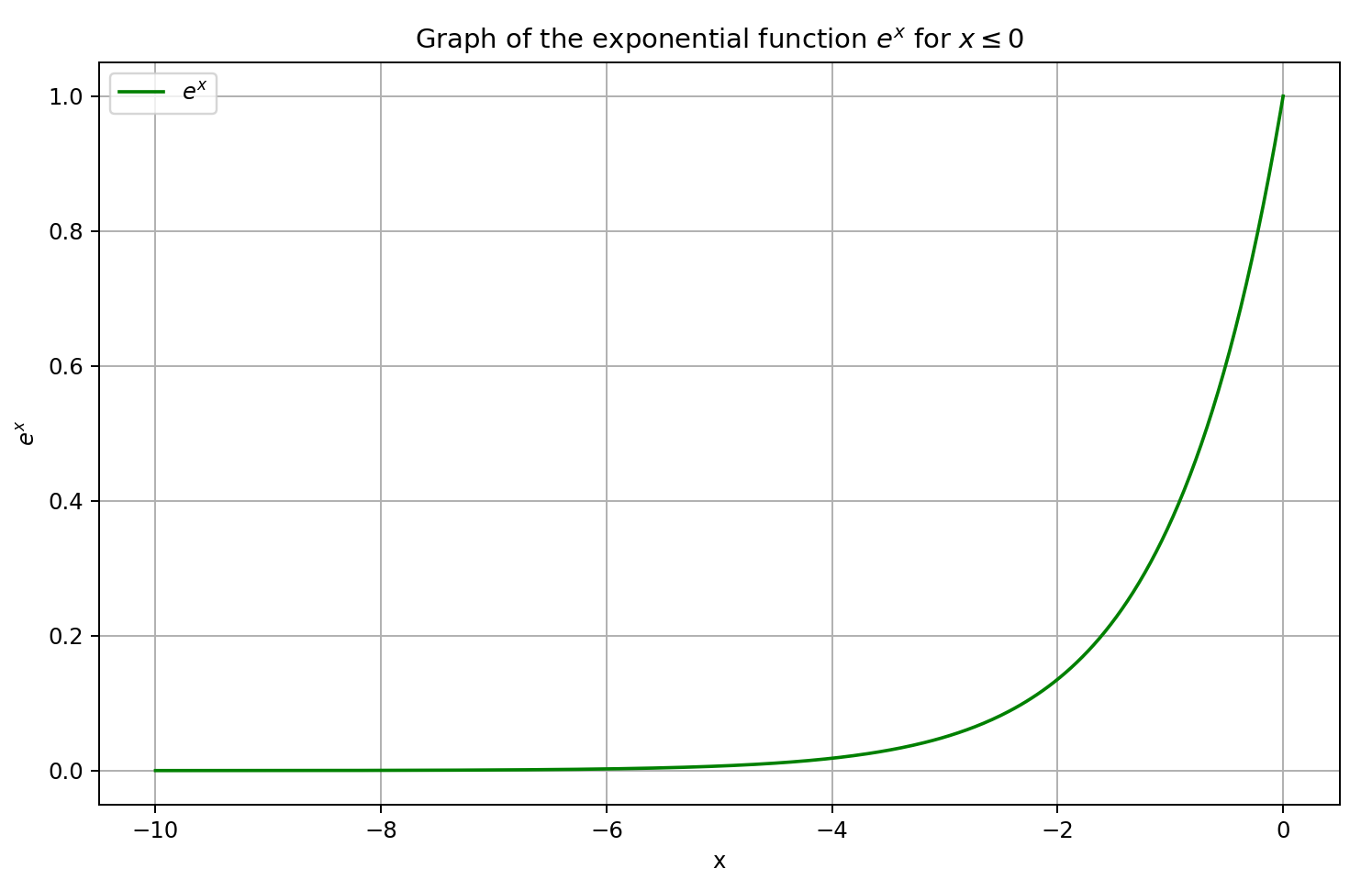
Erinnern wir uns zunächst an die Form der sigmoiden Funktion.
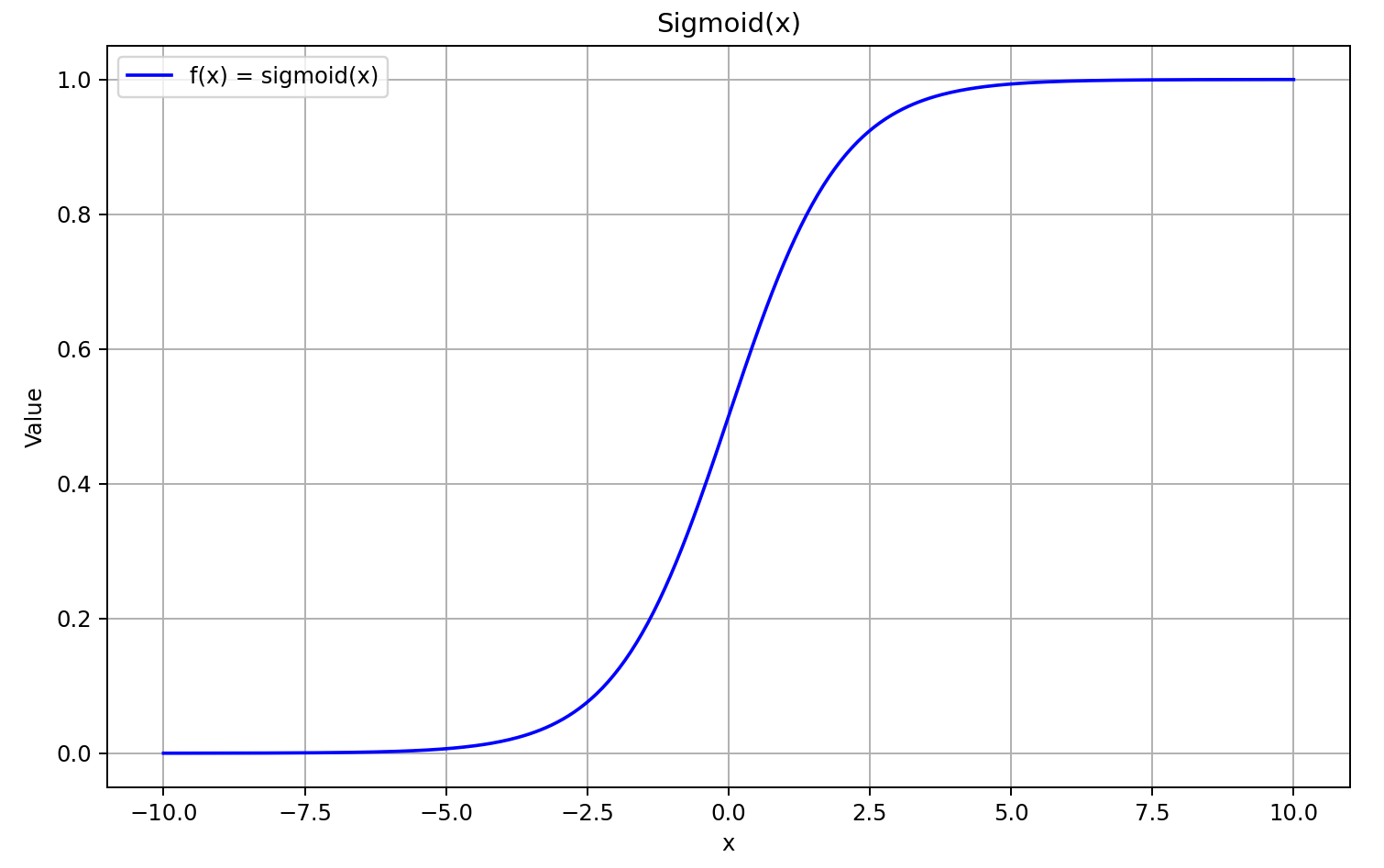
Für Eingabewerte über 5 nähert sich das Sigmoid der Zahl 1, für Eingaben unter -5 der Zahl 0. Daher tendiert die Ableitung von GELU für ausreichend negative Werte von X gegen 0, da der linke Faktor der Ableitungsgleichung gegen Null geht. Für große positive Werte von X tendiert die Ableitung gegen 1, da beide multiplikativen Faktoren gegen 1 konvergieren. Dies wird durch die unten stehende Grafik bestätigt.
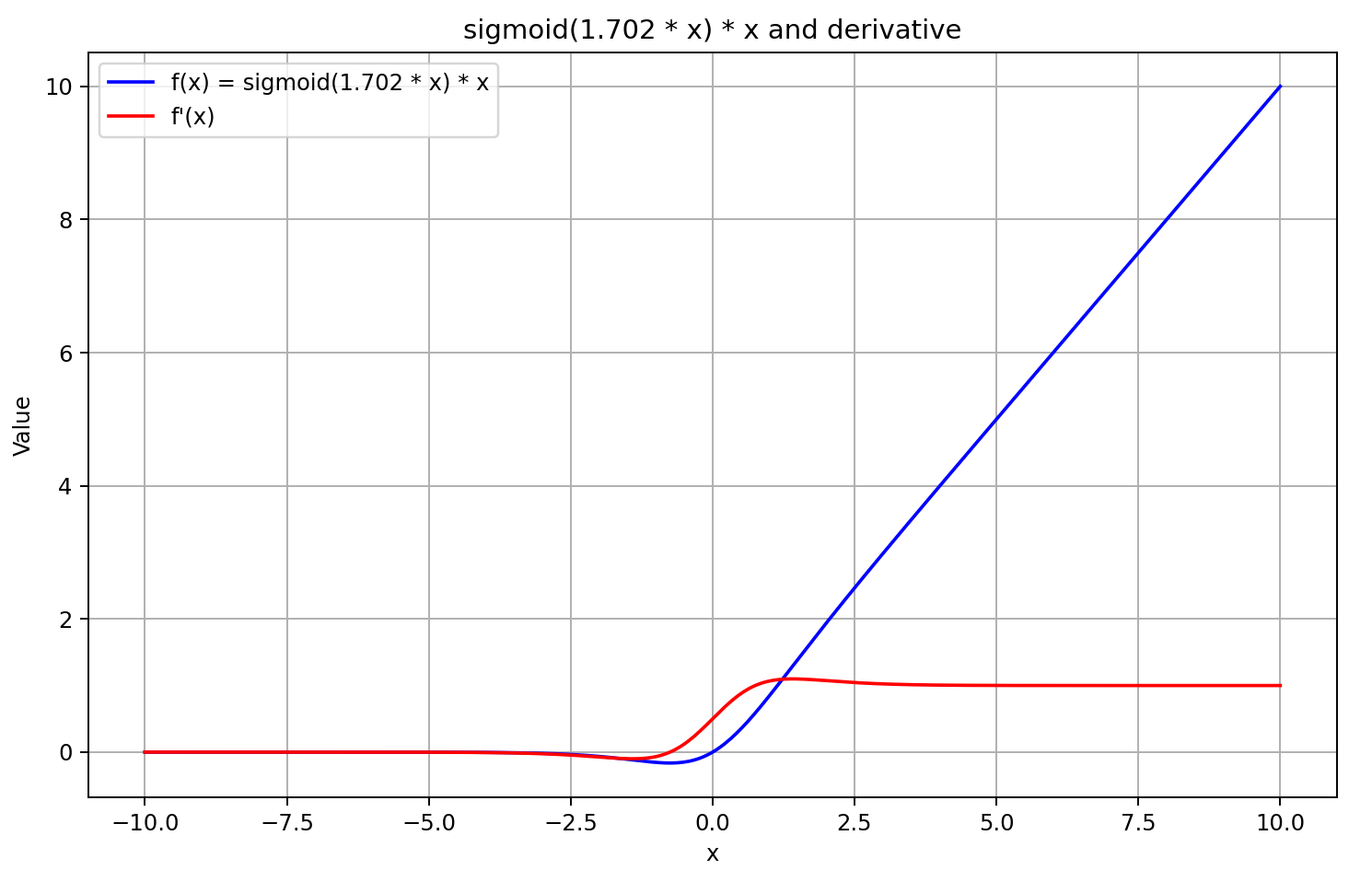
Ausgehend von diesem Verständnis nähern wir uns der Ableitung als dem Sigmoid des mit 5 multiplizierten Ergebnisses des Feedforward-Passes. Diese Methode bietet eine schnelle Berechnung und liefert eine gute Annäherung für Ausgaben von GELU größer oder gleich 0. Bei negativen Ausgangswerten wird die Ableitung jedoch auf 0,5 festgelegt, sodass das Modell nicht weiter trainiert werden kann. In Wirklichkeit sollte sich die Ableitung dem Wert 0 annähern, wodurch die Ausbreitung des Fehlergradienten effektiv blockiert wird.
![]()
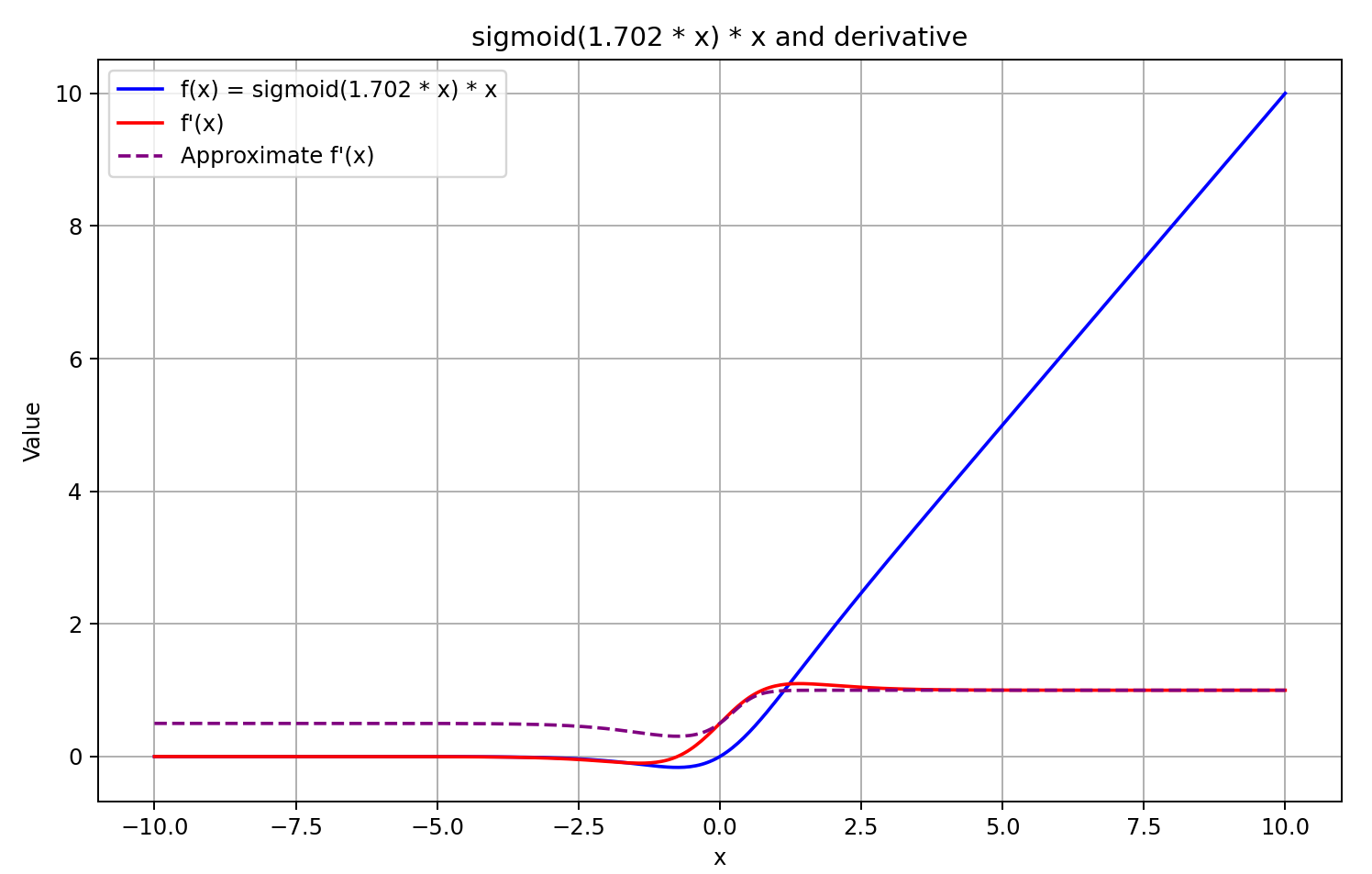
Die Entscheidung ist gefallen. Lassen Sie uns mit der Umsetzung beginnen. Zu diesem Zweck haben wir die Funktion zur Berechnung der Ableitung um einen weiteren Fall erweitert.
float Deactivation(const float grad, const float inp_value, const int function) { float result = grad; //--- if(isnan(inp_value) || isinf(inp_value) || isnan(grad) || isinf(grad)) result = 0; else switch(function) { case 0: //TANH result = clamp(grad + inp_value, -1.0f, 1.0f) - inp_value; result *= 1.0f - pow(inp_value, 2.0f); break; case 1: //Sigmoid result = clamp(grad + inp_value, 0.0f, 1.0f) - inp_value; result *= inp_value * (1.0f - inp_value); break; case 2: //LReLU if(inp_value < 0) result *= 0.01f; break; case 3: //SoftPlus result *= Activation(inp_value, 1); break; case 4: //GELU if(inp_value < 0.9f) result *= Activation(5 * inp_value, 1); break; default: break; } //--- return clamp(result, -MAX_GRAD, MAX_GRAD); }
Beachten Sie, dass wir die Aktivierungsableitung nur dann berechnen, wenn das Ergebnis des Vorwärtsdurchlauf kleiner als 0,9 ist. In allen anderen Fällen wird angenommen, dass die Ableitung 1 ist, was auch richtig ist. Auf diese Weise lässt sich die Anzahl der Operationen während der Gradientenfortpflanzung verringern.
Die Autoren des Frameworks schlagen vor, die Funktion GELU als Nichtlinearität zwischen den Schichten im Block vonFeedForward zu verwenden. In unserer Klasse CNeuronRMAT wird dieser Block durch ein rückgekoppeltes Faltungsmodul implementiert CResidualConv. Wir ändern die Aktivierungsfunktion, die zwischen den Schichten innerhalb dieses Moduls verwendet wird. Dieser Vorgang wird in der Initialisierungsmethode der Klasse durchgeführt. Die spezifische Aktualisierung ist im Code unterstrichen.
bool CResidualConv::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_out, uint count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * count, optimization_type, batch)) return false; //--- if(!cConvs[0].Init(0, 0, OpenCL, window, window, window_out, count, optimization, iBatch)) return false; if(!cNorm[0].Init(0, 1, OpenCL, window_out * count, iBatch, optimization)) return false; cNorm[0].SetActivationFunction(GELU); if(!cConvs[1].Init(0, 2, OpenCL, window_out, window_out, window_out, count, optimization, iBatch)) return false; if(!cNorm[1].Init(0, 3, OpenCL, window_out * count, iBatch, optimization)) return false; cNorm[1].SetActivationFunction(None); //--- ........ ........ ........ //--- return true; }
Damit haben wir die Implementierung der von den Autoren des Rahmens von LSEAttention vorgeschlagenen Techniken abgeschlossen. Der vollständige Code aller Änderungen ist im Anhang zu finden, ebenso wie der vollständige Code aller Programme, die bei der Erstellung dieses Artikels verwendet wurden.
Es ist anzumerken, dass alle Programme zur Interaktion mit der Umgebung und zur Schulung der Modelle vollständig aus dem vorherigen Artikel übernommen wurden. Auch die Modellarchitektur wurde nicht verändert. Umso interessanter ist es, die Auswirkungen der eingeführten Optimierungen zu bewerten, da der einzige Unterschied in den algorithmischen Verbesserungen liegt.
3. Tests
In diesem Artikel haben wir Optimierungstechniken für den einfachen Algorithmus des Transformers implementiert, wie er von den Autoren des Rahmens von LSEAttention für die Zeitreihenprognose vorgeschlagen wurde. Wie bereits erwähnt, unterscheidet sich diese Arbeit von unseren früheren Studien. Wir haben keine neuen neuronalen Schichten geschaffen, wie es früher der Fall war. Stattdessen haben wir die vorgeschlagenen Verbesserungen in bereits implementierte Komponenten integriert. Im Wesentlichen haben wir das im vorigen Artikel implementierte Rahmen von HypDiff genommen und algorithmische Optimierungen eingebaut, die die Modellarchitektur nicht verändert haben. Wir haben auch die Aktivierungsfunktion in FeedForward geändert. Diese Anpassungen betrafen in erster Linie die internen Berechnungsmechanismen, indem sie die numerische Stabilität verbesserten. Natürlich sind wir daran interessiert, wie sich diese Änderungen auf die Ergebnisse der Modellschulung auswirken.
Um einen fairen Vergleich zu gewährleisten, haben wir den Trainingsalgorithmus des Modells HypDiff vollständig repliziert. Es wurde derselbe Trainingsdatensatz verwendet. Dieses Mal haben wir jedoch keine iterativen Aktualisierungen der Trainingsmenge vorgenommen. Dies kann zwar die Trainingsleistung etwas beeinträchtigen, ermöglicht aber einen genauen Vergleich des Modells vor und nach der Algorithmusoptimierung.
Die Modelle wurden anhand realer historischer Daten aus dem ersten Quartal 2024 bewertet. Die Testergebnisse werden im Folgenden vorgestellt.
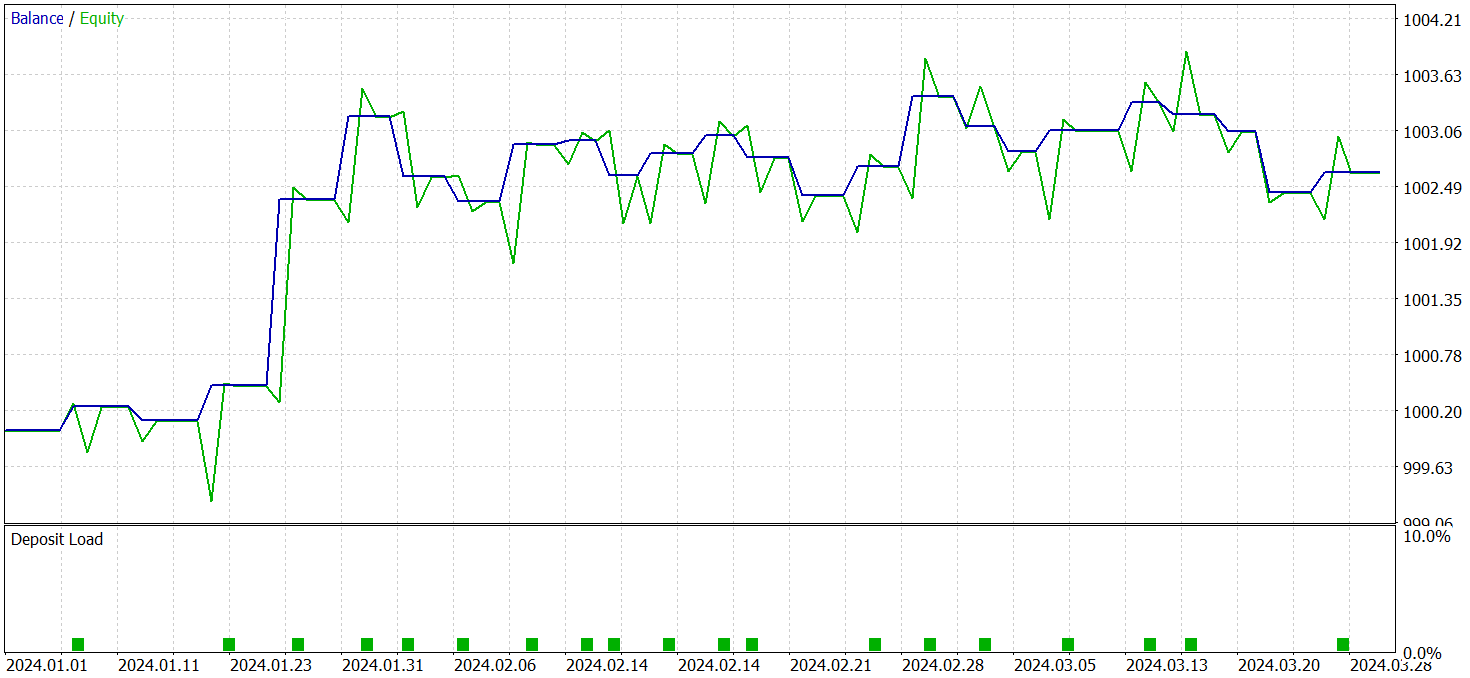
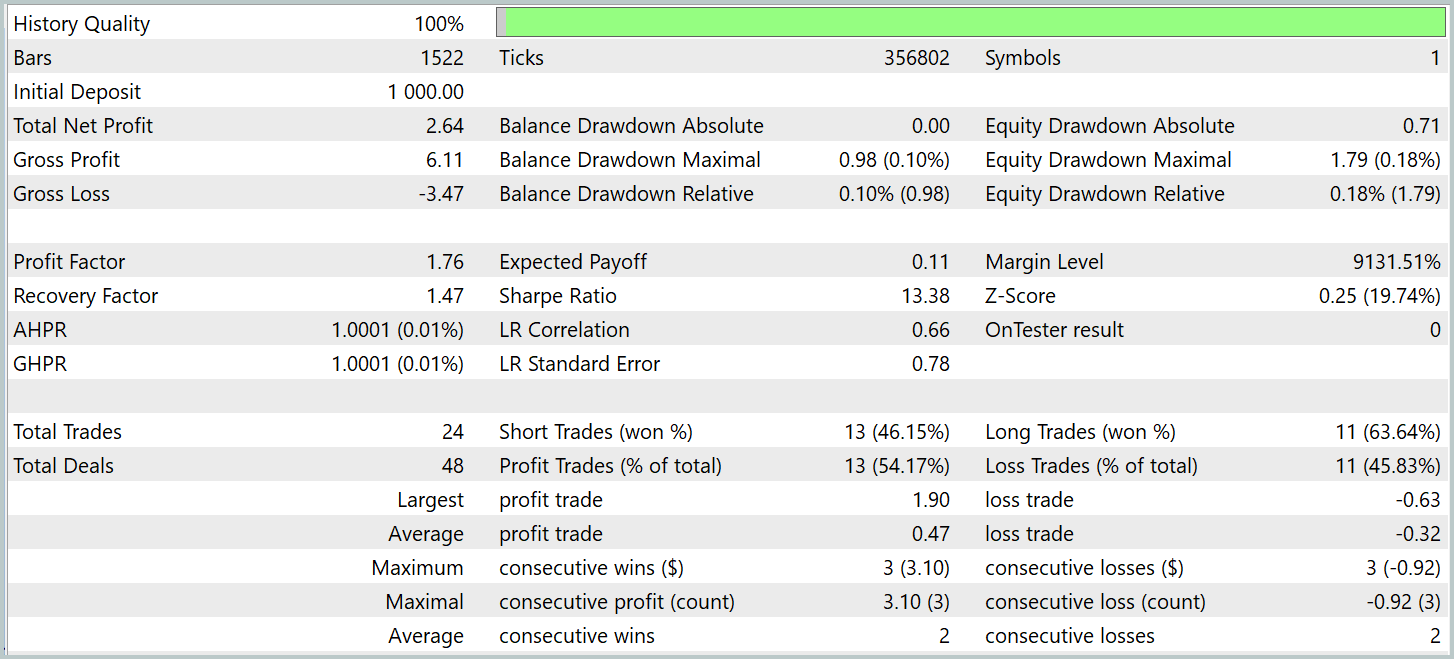
Es ist anzumerken, dass die Leistung des Modells vor und nach der Änderung recht ähnlich war. Während des Testzeitraums führte das aktualisierte Modell 24 Handelsgeschäfte aus. Die Abweichung vom Basismodell betrug nur ein Handelsgeschäft, was innerhalb der Fehlermarge liegt. Beide Modelle erzielten 13 gewinnbringende Abschlüsse. Die einzige sichtbare Verbesserung war das Ausbleiben eines Rückgangs im Februar.
Schlussfolgerung
Die Methode LSEAttention stellt eine Weiterentwicklung von Aufmerksamkeitsmechanismen dar, die besonders effektiv bei Aufgaben ist, die eine hohe Widerstandsfähigkeit gegenüber Rauschen und Datenvariabilität erfordern. Der Hauptvorteil von LSEAttention liegt in der Verwendung der logarithmischen Glättung, die über die Funktion Log-Sum-Exp realisiert wird. Dadurch kann das Modell Probleme mit numerischem Überlauf und verschwindenden Gradienten vermeiden, die bei tiefen neuronalen Netzen kritisch sind.
Im praktischen Teil haben wir die vorgeschlagenen Ansätze in MQL5 implementiert, indem wir sie in bereits entwickelte Module integriert haben. Wir haben die Modelle anhand echter historischer Daten trainiert und getestet. Aus den Testergebnissen lässt sich schließen, dass diese Methoden die Stabilität des Modellbildungsprozesses verbessern.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Expert Advisor zum Sammeln von Beispielen |
| 2 | ResearchRealORL.mq5 | Expert Advisor | Expert Advisor für das Sammeln von Beispielen nach der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modellausbildung Expert Advisor |
| 4 | Test.mq5 | Expert Advisor | Modellprüfung Expert Advisor |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Bibliothek | OpenCL-Programmcode-Bibliothek |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16360
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Entwicklung eines Expert Advisors für mehrere Währungen (Teil 20): Ordnung in den Ablauf der automatischen Projektoptimierungsphasen bringen (I)
Entwicklung eines Expert Advisors für mehrere Währungen (Teil 20): Ordnung in den Ablauf der automatischen Projektoptimierungsphasen bringen (I)
 Von der Grundstufe bis zur Mittelstufe: Rekursion
Von der Grundstufe bis zur Mittelstufe: Rekursion
 Gleitender Durchschnitt in MQL5 von Anfang an: Schlicht und einfach
Gleitender Durchschnitt in MQL5 von Anfang an: Schlicht und einfach
 Training eines mehrschichtigen Perzeptrons unter Verwendung des Levenberg-Marquardt-Algorithmus
Training eines mehrschichtigen Perzeptrons unter Verwendung des Levenberg-Marquardt-Algorithmus
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.