
Maschinelles Lernen für Grid- und Martingale-Handelssysteme. Würden Sie darauf wetten?
Einführung
Wir haben uns intensiv mit verschiedenen Ansätzen zum Einsatz von maschinellem Lernen beschäftigt, die darauf abzielen, Muster im Devisenmarkt zu finden. Sie wissen bereits, wie man Modelle trainiert und implementiert. Aber es gibt eine große Anzahl von Handelsansätzen, von denen fast jeder durch die Anwendung moderner maschineller Lernalgorithmen verbessert werden kann. Einer der beliebtesten Algorithmen ist das Grid und/oder Martingale. Bevor ich diesen Artikel geschrieben habe, habe ich eine kleine Sondierungsanalyse durchgeführt und im Internet nach den entsprechenden Informationen gesucht. Überraschenderweise hat dieser Ansatz wenig bis gar keine Verbreitung im globalen Netzwerk. Ich habe eine kleine Umfrage unter den Community-Mitgliedern zu den Aussichten einer solchen Lösung gemacht, und die Mehrheit hat geantwortet, dass sie gar nicht wüssten, wie man dieses Thema angehen könnte, aber die Idee selbst klang interessant. Dabei scheint die Idee selbst recht einfach zu sein.
Lassen Sie uns eine Reihe von Experimenten durchführen, die zwei Ziele verfolgen. Erstens werden wir versuchen zu beweisen, dass dies nicht so schwierig ist, wie es auf den ersten Blick erscheinen mag. Zweitens werden wir versuchen, herauszufinden, ob dieser Ansatz anwendbar und effektiv ist.
Kennzeichnung der Deals
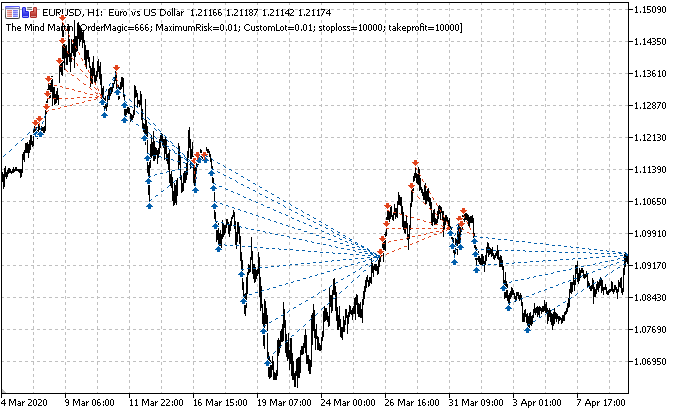
Die Hauptaufgabe besteht darin, die Deals korrekt zu definieren. Erinnern wir uns daran, wie dies für einzelne Positionen in früheren Artikeln gemacht wurde. Wir setzen einen zufälligen oder deterministischen Horizont von Deals, zum Beispiel 15 Bars. Wenn der Markt in diesen 15 Bars gestiegen ist, wurde das Geschäft als Kaufen gekennzeichnet, andernfalls als Verkaufen. Eine ähnliche Logik wird für ein Gitter von Anforderungen verwendet, aber hier ist es notwendig, den Gesamtgewinn/-verlust für eine Gruppe von offenen Positionen zu berücksichtigen. Dies kann mit einem einfachen Beispiel veranschaulicht werden. Der Autor hat sein Bestes versucht, das Bild zu zeichnen.
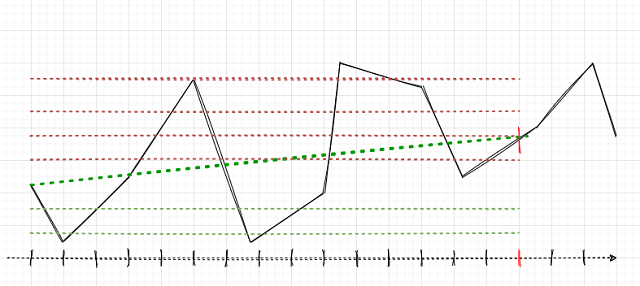
Nehmen wir an, dass der Handelshorizont 15 (fünfzehn) Bars beträgt (auf der herkömmlichen Zeitskala mit einem senkrechten roten Strich markiert). Wenn eine einzelne Position verwendet wird, wird sie als Kauf (Buy, schräge grüne gestrichelte Linie) gekennzeichnet, da der Markt von einem Punkt zum anderen gewachsen ist. Der Markt wird hier als schwarze gestrichelte Kurve dargestellt.
Bei einer solchen Beschriftung werden zwischenzeitliche Marktschwankungen ignoriert. Wenn wir ein Raster von Anforderungen (rote und grüne horizontale Linien) anwenden, dann ist es notwendig, den Gesamtgewinn für alle ausgelösten schwebenden Anforderungen einschließlich der ganz am Anfang geöffneten Anforderung zu berechnen (Sie können eine Position öffnen und das Raster in derselben Richtung platzieren, oder optional kann ein Raster von schwebenden Anforderungen sofort platziert werden, ohne eine Position zu öffnen). Diese Kennzeichnung wird in einem gleitenden Fenster fortgesetzt, für die gesamte Tiefe der Lernhistorie. Die Aufgabe von ML (maschinelles Lernen) ist es, die ganze Vielfalt der Situationen zu verallgemeinern und effizient auf neue Daten vorauszusagen (wenn möglich).
In diesem Fall kann es mehrere Optionen für die Auswahl der Handelsrichtung und für die Beschriftung der Daten geben. Die Auswahlaufgabe ist hier sowohl philosophisch als auch experimentell.
- Auswahl nach dem maximalen Gesamtgewinn. Wenn ein Verkaufs-Gitter mehr Gewinn generiert, wird dieses Gitter beschriftet.
- Gewichtete Auswahl zwischen der Anzahl der offenen Anforderungen und dem Gesamtgewinn. Wenn der durchschnittliche Gewinn für jede offene Anforderung im Raster höher ist als der der gegenüberliegenden Seite, dann wird diese Seite ausgewählt.
- Auswahl nach der maximalen Anzahl der ausgelösten Anforderungen. Da der gewünschte Roboter das Raster handeln soll, erscheint diese Option sinnvoll. Wenn die Anzahl der ausgelösten Anforderungen maximal ist und die Gesamtposition im Gewinn ist, dann wird diese Seite ausgewählt. Die Seite bedeutet hier die Richtung des Gitters (verkaufen oder kaufen).
Diese drei Kriterien scheinen für den Anfang ausreichend zu sein. Lassen Sie uns das erste im Detail betrachten, da es das einfachste ist und auf maximalen Gewinn abzielt.
Kennzeichnung von Deals im Code
Erinnern wir uns nun daran, wie die Deals in den vorherigen Artikeln beschriftet wurden.
def add_labels(dataset, min, max): labels = [] for i in range(dataset.shape[0]-max): rand = random.randint(min, max) curr_pr = dataset['close'][i] future_pr = dataset['close'][i + rand] if future_pr + MARKUP < curr_pr: labels.append(1.0) elif future_pr - MARKUP > curr_pr: labels.append(0.0) else: labels.append(2.0) dataset = dataset.iloc[:len(labels)].copy() dataset['labels'] = labels dataset = dataset.dropna() dataset = dataset.drop( dataset[dataset.labels == 2].index).reset_index(drop=True) return dataset
Dieser Code muss für ein normales und ein Martingale-Gitter verallgemeinert werden. Ein weiteres spannendes Feature ist, dass die Gitter mit unterschiedlicher Anzahl von Anforderungen, mit unterschiedlichen Abständen zwischen den Anforderungen und sogar Martingale (Losgrößenerhöhung) verwendet werden können.
Dazu fügen wir globale Variablen hinzu, die später verwendet und optimiert werden können.
GRID_SIZE = 10 GRID_DISTANCES = np.full(GRID_SIZE, 0.00200) GRID_COEFFICIENTS = np.linspace(1, 3, num= GRID_SIZE)
Die Variable GRID_SIZE enthält die Anzahl der Aufträge in beide Richtungen.
GRID_DISTANCES legt den Abstand zwischen den Aufträgen fest. Der Abstand kann fest oder variabel (für alle Aufträge unterschiedlich) sein. Dadurch wird die Flexibilität des Handelssystems erhöht.
Die Variable GRID_COEFFICIENTS enthält Multiplikatoren für die Losgrößen (lots) für jeden Auftrag. Wenn sie konstant sind, wird das System ein regelmäßiges Raster erstellen. Wenn die Losgröße unterschiedlich sind, dann wird es ein Martingale oder Anti-Martingale, oder ein anderer Name, der für ein Gitter mit unterschiedlichen Losgrößen-Multiplikatoren gilt.
Für diejenigen unter Ihnen, die neu in der Bibliothek numpy sind:
- np.full füllt ein Array mit einer bestimmten Anzahl von identischen Werten
- np.linspace füllt ein Array mit der angegebenen Anzahl der Werte, die gleichmäßig zwischen zwei reellen Zahlen verteilt sind. Im obigen Beispiel wird GRID_COEFFICIENTS folgendes enthalten.
array([1. , 1.22222222, 1.44444444, 1.66666667, 1.88888889, 2.11111111, 2.33333333, 2.55555556, 2.77777778, 3. ])
Dementsprechend ist der erste Losgrößenmultiplikator gleich eins, so dass diese Losgröße der in den Parametern des Handelssystems angegebenen Basislosgröße entspricht. Multiplikatoren von 1 bis 3 werden nacheinander für weitere Gitteraufträge verwendet. Um dieses Gitter mit einem festen Multiplikator für alle Aufträge zu verwenden, rufen Sie np.full auf.
Die Abrechnung von getriggerten und nicht getriggerten Aufträgen kann etwas knifflig sein, und deshalb müssen wir eine Art Datenstruktur erstellen. Ich habe mich dafür entschieden, ein Register zu erstellen, in dem die Aufträge und Positionen für jeden einzelnen Fall (Beispiel) festgehalten werden. Stattdessen könnten wir ein Data Class-Objekt, einen Pandas Data Frame oder ein numpy-strukturiertes Array verwenden. Die letzte Lösung wäre vielleicht die schnellste, aber hier ist sie nicht entscheidend.
Ein Register, das Informationen über einen Auftrag speichert, wird bei jeder Iteration des Hinzufügens einer Probe zum Trainingssatz erstellt. Dies bedarf vielleicht einiger Erklärung. Das Register Grid_stats enthält alle erforderlichen Informationen über das aktuelle Auftragsgitter von seiner Öffnung bis zur Schließung.
def add_labels(dataset, min, max, distances, coefficients): labels = [] for i in range(dataset.shape[0]-max): rand = random.randint(min, max) all_pr = dataset['close'][i:i + rand + 1] grid_stats = {'up_range': all_pr[0] - all_pr.min(), 'dwn_range': all_pr.max() - all_pr[0], 'up_state': 0, 'dwn_state': 0, 'up_orders': 0, 'dwn_orders': 0, 'up_profit': all_pr[-1] - all_pr[0] - MARKUP, 'dwn_profit': all_pr[0] - all_pr[-1] - MARKUP } for i in np.nditer(distances): if grid_stats['up_state'] + i <= grid_stats['up_range']: grid_stats['up_state'] += i grid_stats['up_orders'] += 1 grid_stats['up_profit'] += (all_pr[-1] - all_pr[0] + grid_stats['up_state']) \ * coefficients[int(grid_stats['up_orders']-1)] grid_stats['up_profit'] -= MARKUP * coefficients[int(grid_stats['up_orders']-1)] if grid_stats['dwn_state'] + i <= grid_stats['dwn_range']: grid_stats['dwn_state'] += i grid_stats['dwn_orders'] += 1 grid_stats['dwn_profit'] += (all_pr[0] - all_pr[-1] + grid_stats['dwn_state']) \ * coefficients[int(grid_stats['dwn_orders']-1)] grid_stats['dwn_profit'] -= MARKUP * coefficients[int(grid_stats['dwn_orders']-1)] if grid_stats['up_profit'] > grid_stats['dwn_profit'] and grid_stats['up_profit'] > 0: labels.append(0.0) continue elif grid_stats['dwn_profit'] > 0: labels.append(1.0) continue labels.append(2.0) dataset = dataset.iloc[:len(labels)].copy() dataset['labels'] = labels dataset = dataset.dropna() dataset = dataset.drop( dataset[dataset.labels == 2].index).reset_index(drop=True) return dataset
Die Variable all_pr enthält die Preise, vom aktuellen bis zu einem zukünftigen. Sie wird benötigt, um das Gitter selbst zu berechnen. Um das Gitter aufzubauen, wollen wir die Preisbereiche vom ersten bis zum letzten Bar kennen. Diese Werte sind in den Register-Einträgen 'up_range' und 'dwn_range' enthalten. Die Variablen 'up_profit' und 'dwn_profit' enthalten den endgültigen Gewinn aus der Verwendung des Gitters "Kaufen" oder "Verkaufen" im aktuellen Verlaufssegment. Diese Werte werden mit dem Gewinn aus einem Marktgeschäft initialisiert, das zu Beginn geöffnet wurde. Dann werden sie mit den Geschäften summiert, die gemäß dem Gitter geöffnet wurden, wenn schwebende Aufträge ausgelöst wurden.
Jetzt müssen wir eine Schleife durch alle GRID_DISTANCES machen und prüfen, ob die schwebenden Limit-Aufträge ausgelöst haben. Wenn ein Auftrag im Bereich von up_range oder dwn_range liegt, dann hat der Auftrag ausgelöst. In diesem Fall inkrementieren wir die entsprechenden up_state und dwn_state Zähler, die den Pegel des zuletzt aktivierten Auftrags speichern. Bei der nächsten Iteration wird zu diesem Pegel der Abstand zum neuen Auftrag im Gitter addiert - liegt dieser Auftrag im Preisbereich, dann hat er auch ausgelöst.
Für alle ausgelösten Aufträge werden zusätzliche Informationen geschrieben. Zum Beispiel wird der Gewinn eines schwebenden Auftrags zum Gesamtwert addiert. Bei Kaufpositionen wird dieser Gewinn nach der folgenden Formel berechnet. Hier wird der Eröffnungskurs der Position vom letzten Kurs (zu dem die Position geschlossen werden soll) subtrahiert, der Abstand zum ausgewählten schwebenden Auftrag aus der Serie addiert und das Ergebnis mit dem Losgrößenmultiplikator für diesen Auftrag im Gitter multipliziert. Eine umgekehrte Berechnung wird für Verkaufsaufträge verwendet. Der kumulierte Aufschlag wird zusätzlich berechnet.
grid_stats['up_profit'] += (all_pr[-1] - all_pr[0] + grid_stats['up_state']) \ * coefficients[int(grid_stats['up_orders']-1)] grid_stats['up_profit'] -= MARKUP * coefficients[int(grid_stats['up_orders']-1)]
Der nächste Codeblock prüft den Gewinn für Kauf- und Verkaufs-Gitter. Wenn der Gewinn unter Berücksichtigung der kumulierten Aufschläge größer als Null und maximal ist, dann wird die entsprechende Probe zum Trainingsdatensatz hinzugefügt. Wenn keine der Bedingungen erfüllt ist, wird die Markierung 2.0 hinzugefügt - die mit dieser Markierung versehenen Proben werden aus dem Trainingsdatensatz entfernt, da sie als uninformativ angesehen werden. Diese Bedingungen können später geändert werden, je nach den gewünschten Optionen zur Erstellung von Gittern.
Aufrüstung des Testers für die Arbeit mit dem Gitter für Aufträge
Um den Gewinn aus dem Handel mit dem Gitter korrekt zu berechnen, müssen wir den Strategietester modifizieren. Ich habe mich dafür entschieden, ihn ähnlich wie den Tester von MetaTrader 5 zu gestalten, so dass er sequenziell eine Schleife durch die Historie der Kurse durchläuft und Positionen öffnet und schließt, als ob es sich um einen echten Handel handeln würde. Dies verbessert das Verständnis des Codes und vermeidet den Blick in die Zukunft. Ich werde mich auf die wichtigsten Punkte des Codes konzentrieren. Ich werde hier nicht die alte Tester-Version zur Verfügung stellen, aber Sie können sie in meinen früheren Artikeln finden. Ich vermute, dass einige Leser den folgenden Code nicht verstehen werden, da sie schnell den Gral erreichen möchten, ohne auf Details einzugehen. Die wichtigsten Punkte sollten jedoch geklärt sein.
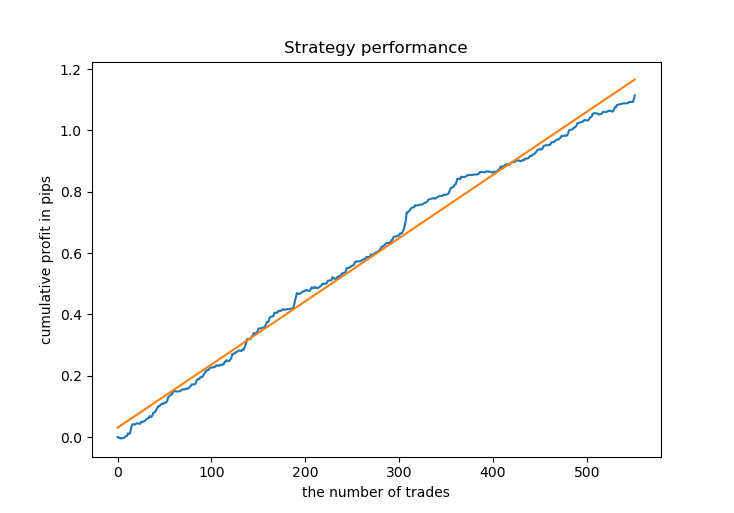
def tester(dataset, markup, distances, coefficients, plot=False): last_deal = int(2) all_pr = np.array([]) report = [0.0] for i in range(dataset.shape[0]): pred = dataset['labels'][i] all_pr = np.append(all_pr, dataset['close'][i]) if last_deal == 2: last_deal = 0 if pred <= 0.5 else 1 continue if last_deal == 0 and pred > 0.5: last_deal = 1 up_range = all_pr[0] - all_pr.min() up_state = 0 up_orders = 0 up_profit = (all_pr[-1] - all_pr[0]) - markup report.append(report[-1] + up_profit) up_profit = 0 for d in np.nditer(distances): if up_state + d <= up_range: up_state += d up_orders += 1 up_profit += (all_pr[-1] - all_pr[0] + up_state) \ * coefficients[int(up_orders-1)] up_profit -= markup * coefficients[int(up_orders-1)] report.append(report[-1] + up_profit) up_profit = 0 all_pr = np.array([dataset['close'][i]]) continue if last_deal == 1 and pred < 0.5: last_deal = 0 dwn_range = all_pr.max() - all_pr[0] dwn_state = 0 dwn_orders = 0 dwn_profit = (all_pr[0] - all_pr[-1]) - markup report.append(report[-1] + dwn_profit) dwn_profit = 0 for d in np.nditer(distances): if dwn_state + d <= dwn_range: dwn_state += d dwn_orders += 1 dwn_profit += (all_pr[0] + dwn_state - all_pr[-1]) \ * coefficients[int(dwn_orders-1)] dwn_profit -= markup * coefficients[int(dwn_orders-1)] report.append(report[-1] + dwn_profit) dwn_profit = 0 all_pr = np.array([dataset['close'][i]]) continue y = np.array(report).reshape(-1, 1) X = np.arange(len(report)).reshape(-1, 1) lr = LinearRegression() lr.fit(X, y) l = lr.coef_ if l >= 0: l = 1 else: l = -1 if(plot): plt.figure(figsize=(12,7)) plt.plot(report) plt.plot(lr.predict(X)) plt.title("Strategy performance") plt.xlabel("the number of trades") plt.ylabel("cumulative profit in pips") plt.show() return lr.score(X, y) * l
Historisch gesehen sind Gitter-Händler nur an der Saldenkurve (balance) interessiert, während sie die Kapitalkurve (equity) ignorieren. Wir werden uns also an diese Tradition halten und unser komplexes Prüfgerät nicht übermäßig kompliziert gestalten. Wir werden nur die Saldokurve anzeigen. Außerdem kann die Kapitalkurve immer im MetaTrader 5-Terminal angezeigt werden.
Wir gehen in einer Schleife durch alle Kurse und tragen sie in das Array all_pr ein. Weiter gibt es drei oben markierte Optionen. Da dieser Tester bereits in früheren Artikeln betrachtet wurde, erkläre ich hier nur die Optionen zum Schließen des Auftragsgitters, wenn ein gegenteiliges Signal erscheint. Genau wie bei der Kennzeichnung der Geschäfte speichert die Variable up_range den Bereich der iterierten Preise bis zum Zeitpunkt des Schließens der offenen Positionen. Als Nächstes wird der Gewinn der ersten (vom Markt eröffneten) Position berechnet. Dann prüft der Zyklus auf das Vorhandensein von ausgelösten schwebenden Aufträgen. Wenn es welche gibt, wird ihr Ergebnis zum Saldograph hinzugefügt. Das Gleiche wird für Verkaufsaufträge/-positionen durchgeführt. Somit spiegelt der Saldograph alle geschlossenen Positionen wider und nicht den Gesamtgewinn nach Gruppe.
Testen neuer Methoden für die Arbeit mit Auftragsgittern
Die Datenaufbereitung für maschinelles Lernen ist uns bereits vertraut. Zuerst erhalten Sie Preise und einen Satz von Merkmalen, dann kennzeichnen Sie die Daten (erstellen Kauf- und Verkaufsbeschriftungen), und dann überprüfen Sie die Kennzeichnung im benutzerdefinierten Tester.
# Get prices and labels and test it pr = get_prices(START_DATE, END_DATE) pr = add_labels(pr, 15, 15, GRID_DISTANCES, GRID_COEFFICIENTS) tester(pr, MARKUP, GRID_DISTANCES, GRID_COEFFICIENTS, plot=True)
Nun müssen wir das CatBoost-Modell trainieren und es auf neuen Daten testen. Ich habe mich wieder für das Training auf synthetischen Daten entschieden, die mit dem Gaußschen Mischungsmodell erzeugt wurden, da es gut funktioniert.
# Learn and test CatBoost model gmm = mixture.GaussianMixture( n_components=N_COMPONENTS, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]]) res = [] for i in range(10): res.append(brute_force(10000)) print('Iteration: ', i, 'R^2: ', res[-1][0]) res.sort() test_model(res[-1])
In diesem Beispiel werden wir zehn Modelle auf 10.000 generierten Stichproben trainieren und das beste durch einen R^2-Score auswählen. Der Lernprozess läuft folgendermaßen ab.
Iteration: 0 R^2: 0.8719436661855786 Iteration: 1 R^2: 0.912006346274096 Iteration: 2 R^2: 0.9532278725035132 Iteration: 3 R^2: 0.900845571741786 Iteration: 4 R^2: 0.9651728908727953 Iteration: 5 R^2: 0.966531822300101 Iteration: 6 R^2: 0.9688263099200539 Iteration: 7 R^2: 0.8789927823514787 Iteration: 8 R^2: 0.6084261786804662 Iteration: 9 R^2: 0.884741078512629
Die meisten Modelle haben einen hohen Wert für R^2 auf neuen Daten, was auf eine hohe Stabilität des Modells hinweist. Hier ist das resultierende Saldenkurve der Trainingsdaten und mit Daten außerhalb der Trainingsperiode.
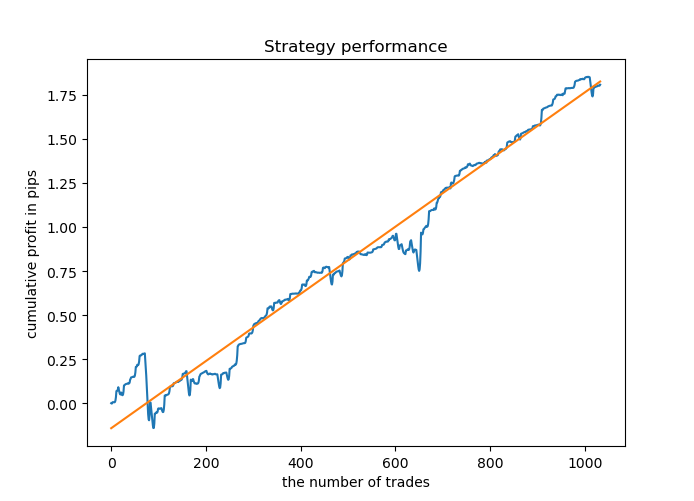
Sieht gut aus. Jetzt können wir das trainierte Modell in MetaTrader 5 exportieren und sein Ergebnis im Terminal-Tester überprüfen. Vor dem Testen ist es notwendig, den Trading Expert Advisor und die Include-Datei vorzubereiten. Jedes trainierte Modell wird seine eigene Datei haben, so dass es einfach ist, sie zu speichern und zu ändern.
Exportieren des CatBoost-Modells nach MQL5
Rufen Sie die folgende Funktion auf, um das Modell zu exportieren.
export_model_to_MQL_code(res[-1][1])
Die Funktion wurde leicht modifiziert. Die Erklärung dieser Änderung folgt weiter unten.
def export_model_to_MQL_code(model):
model.save_model('catmodel.h',
format="cpp",
export_parameters=None,
pool=None)
# add variables
code = '#include <Math\Stat\Math.mqh>'
code += '\n'
code += 'int MAs[' + str(len(MA_PERIODS)) + \
'] = {' + ','.join(map(str, MA_PERIODS)) + '};'
code += '\n'
code += 'int grid_size = ' + str(GRID_SIZE) + ';'
code += '\n'
code += 'double grid_distances[' + str(len(GRID_DISTANCES)) + \
'] = {' + ','.join(map(str, GRID_DISTANCES)) + '};'
code += '\n'
code += 'double grid_coefficients[' + str(len(GRID_COEFFICIENTS)) + \
'] = {' + ','.join(map(str, GRID_COEFFICIENTS)) + '};'
code += '\n'
# get features
code += 'void fill_arays( double &features[]) {\n'
code += ' double pr[], ret[];\n'
code += ' ArrayResize(ret, 1);\n'
code += ' for(int i=ArraySize(MAs)-1; i>=0; i--) {\n'
code += ' CopyClose(NULL,PERIOD_CURRENT,1,MAs[i],pr);\n'
code += ' double mean = MathMean(pr);\n'
code += ' ret[0] = pr[MAs[i]-1] - mean;\n'
code += ' ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
code += ' ArraySetAsSeries(features, true);\n'
code += '}\n\n'
# add CatBosst
code += 'double catboost_model' + '(const double &features[]) { \n'
code += ' '
with open('catmodel.h', 'r') as file:
data = file.read()
code += data[data.find("unsigned int TreeDepth")
:data.find("double Scale = 1;")]
code += '\n\n'
code += 'return ' + \
'ApplyCatboostModel(features, TreeDepth, TreeSplits , BorderCounts, Borders, LeafValues); } \n\n'
code += 'double ApplyCatboostModel(const double &features[],uint &TreeDepth_[],uint &TreeSplits_[],uint &BorderCounts_[],float &Borders_[],double &LeafValues_[]) {\n\
uint FloatFeatureCount=ArrayRange(BorderCounts_,0);\n\
uint BinaryFeatureCount=ArrayRange(Borders_,0);\n\
uint TreeCount=ArrayRange(TreeDepth_,0);\n\
bool binaryFeatures[];\n\
ArrayResize(binaryFeatures,BinaryFeatureCount);\n\
uint binFeatureIndex=0;\n\
for(uint i=0; i<FloatFeatureCount; i++) {\n\
for(uint j=0; j<BorderCounts_[i]; j++) {\n\
binaryFeatures[binFeatureIndex]=features[i]>Borders_[binFeatureIndex];\n\
binFeatureIndex++;\n\
}\n\
}\n\
double result=0.0;\n\
uint treeSplitsPtr=0;\n\
uint leafValuesForCurrentTreePtr=0;\n\
for(uint treeId=0; treeId<TreeCount; treeId++) {\n\
uint currentTreeDepth=TreeDepth_[treeId];\n\
uint index=0;\n\
for(uint depth=0; depth<currentTreeDepth; depth++) {\n\
index|=(binaryFeatures[TreeSplits_[treeSplitsPtr+depth]]<<depth);\n\
}\n\
result+=LeafValues_[leafValuesForCurrentTreePtr+index];\n\
treeSplitsPtr+=currentTreeDepth;\n\
leafValuesForCurrentTreePtr+=(1<<currentTreeDepth);\n\
}\n\
return 1.0/(1.0+MathPow(M_E,-result));\n\
}'
file = open('C:/Users/dmitrievsky/AppData/Roaming/MetaQuotes/Terminal/D0E8209F77C8CF37AD8BF550E51FF075/MQL5/Include/' +
str(SYMBOL) + '_cat_model_martin' + '.mqh', "w")
file.write(code)
file.close()
print('The file ' + 'cat_model' + '.mqh ' + 'has been written to disc')
Die Gitter-Einstellungen, die beim Training verwendet wurden, werden jetzt gespeichert. Sie werden auch im Handel verwendet.
Der Gleitende Durchschnitt aus dem Standardpaket des Terminals und die Indikatorpuffer werden nicht mehr verwendet. Stattdessen werden alle Elemente im Funktionskörper berechnet. Beim Hinzufügen von Originalmerkmalen sollten diese auch in der Exportfunktion hinzugefügt werden.
Grün markiert ist der Pfad zum Include-Ordner Ihres Terminals. Er ermöglicht das Speichern der .mqh-Datei und das Verbinden mit dem Expert Advisor.
Sehen wir uns die .mqh-Datei selbst an (das CatBoost-Modell wird hier weggelassen)
#include <Math\Stat\Math.mqh> int MAs[14] = {5,25,55,75,100,125,150,200,250,300,350,400,450,500}; int grid_size = 10; double grid_distances[10] = {0.003,0.0035555555555555557,0.004111111111111111,0.004666666666666666,0.005222222222222222, 0.0057777777777777775,0.006333333333333333,0.006888888888888889,0.0074444444444444445,0.008}; double grid_coefficients[10] = {1.0,1.4444444444444444,1.8888888888888888,2.333333333333333, 2.7777777777777777,3.2222222222222223,3.6666666666666665,4.111111111111111,4.555555555555555,5.0}; void fill_arays( double &features[]) { double pr[], ret[]; ArrayResize(ret, 1); for(int i=ArraySize(MAs)-1; i>=0; i--) { CopyClose(NULL,PERIOD_CURRENT,1,MAs[i],pr); double mean = MathMean(pr); ret[0] = pr[MAs[i]-1] - mean; ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); } ArraySetAsSeries(features, true); }
Wie man sehen kann, wurden alle Einstellungen des Gitters gespeichert und das Modell ist einsatzbereit. Sie müssen es nur noch mit dem Expert Advisor verbinden.
#include <EURUSD_cat_model_martin.mqh> Nun möchte ich die Logik erklären, nach der der Expert Advisor die Signale verarbeitet. Als Beispiel wird die Funktion OnTick() verwendet. Der Bot verwendet die MT4Orders Bibliothek, die zusätzlich heruntergeladen werden müsste.
void OnTick() { //--- if(!isNewBar()) return; TimeToStruct(TimeCurrent(), hours); double features[]; fill_arays(features); if(ArraySize(features) !=ArraySize(MAs)) { Print("No history available, will try again on next signal!"); return; } double sig = catboost_model(features); // Close positions by an opposite signal if(count_market_orders(0) || count_market_orders(1)) for(int b = OrdersTotal() - 1; b >= 0; b--) if(OrderSelect(b, SELECT_BY_POS) == true) { if(OrderType() == 0 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic && sig > 0.5) if(OrderClose(OrderTicket(), OrderLots(), OrderClosePrice(), 0, Red)) { } if(OrderType() == 1 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic && sig < 0.5) if(OrderClose(OrderTicket(), OrderLots(), OrderClosePrice(), 0, Red)) { } } // Delete all pending orders if there are no pending orders if(!count_market_orders(0) && !count_market_orders(1)) { for(int b = OrdersTotal() - 1; b >= 0; b--) if(OrderSelect(b, SELECT_BY_POS) == true) { if(OrderType() == 2 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic ) if(OrderDelete(OrderTicket())) { } if(OrderType() == 3 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic ) if(OrderDelete(OrderTicket())) { } } } // Open positions and pending orders by signals if(countOrders() == 0 && CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_BUY)) { double l = LotsOptimized(); if(sig < 0.5) { OrderSend(Symbol(),OP_BUY,l, Ask, 0, Bid-stoploss*_Point, Ask+takeprofit*_Point, NULL, OrderMagic); double p = Ask; for(int i=0; i<grid_size; i++) { p = NormalizeDouble(p - grid_distances[i], _Digits); double gl = NormalizeDouble(l * grid_coefficients[i], 2); OrderSend(Symbol(),OP_BUYLIMIT,gl, p, 0, p-stoploss*_Point, p+takeprofit*_Point, NULL, OrderMagic); } } else { OrderSend(Symbol(),OP_SELL,l, Bid, 0, Ask+stoploss*_Point, Bid-takeprofit*_Point, NULL, OrderMagic); double p = Ask; for(int i=0; i<grid_size; i++) { p = NormalizeDouble(p + grid_distances[i], _Digits); double gl = NormalizeDouble(l * grid_coefficients[i], 2); OrderSend(Symbol(),OP_SELLLIMIT,gl, p, 0, p+stoploss*_Point, p-takeprofit*_Point, NULL, OrderMagic); } } } }
Die Funktion fill_arrays bereitet Besonderheiten für das CatBoost-Modell vor und füllt das Array features. Dann wird dieses Array der Funktion catboost_model() übergeben, die ein Signal im Bereich von 0;1 zurückgibt.
Wie Sie am Beispiel der Kaufaufträge sehen können, wird hier die Variable grid_size verwendet. Sie zeigt die Anzahl der schwebenden Aufträge an, die sich in einem Abstand von grid_distances befinden. Die Standard-Losgröße wird mit dem Koeffizienten aus dem Array grid_coefficients multipliziert, der der Auftragsnummer entspricht.
Nachdem der Bot kompiliert ist, können wir zum Testen übergehen.
Testen des Bots im MetaTrader 5 Tester
Die Tests sollten mit dem Zeitrahmen durchgeführt werden, mit dem der Bot trainiert wurde. In diesem Fall ist es H1. Es kann mit den Eröffnungspreisen getestet werden, da der Bot eine explizite die Eröffnungspreise der Bars verwendet. Da jedoch ein Gitter verwendet wird, kann M1 OHLC für eine höhere Genauigkeit gewählt werden.
Dieser spezielle Bot wurde in der folgenden Periode trainiert:
START_DATE = datetime(2020, 5, 1) TSTART_DATE = datetime(2019, 1, 1) FULL_DATE = datetime(2018, 1, 1) END_DATE = datetime(2022, 1, 1)
- Das Intervall vom fünften Monat des Jahres 2020 bis zum heutigen Tag ist ein Trainingszeitraum, der 50/50 in Trainings- und Validierungs-Teilstichproben aufgeteilt wird.
- Ab dem 1. Monat des Jahres 2019 wurde das Modell nach R^2 bewertet und das beste Modell ausgewählt.
- Ab dem 1. Monat des Jahres 2018 wurde das Modell in einem nutzerdefinierten Tester getestet.
- Für das Training wurden synthetische Daten verwendet (generiert durch das Gaußsche Mischverteilung).
- Das CatBoost-Modell hat eine starke Regularisierung, die hilft, eine Überanpassung an die Trainingsstichprobe zu vermeiden.
All diese Faktoren deuten darauf hin (was auch durch den Nutzer-Tester bestätigt wird), dass wir ein bestimmtes Muster im Intervall von 2018 bis heute gefunden haben.
Schauen wir uns an, wie es im MetaTrader 5 Strategietester aussieht.
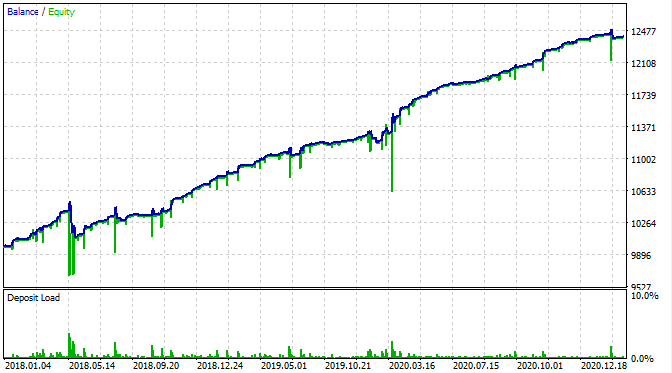
Mit der Ausnahme, dass wir jetzt Kapitalrückgang sehen können, sieht die Saldenkurve genauso aus wie in meinem Nutzer-Tester. Das ist eine gute Nachricht. Stellen wir sicher, dass der Bot genau das Gitter handelt und nichts anderes.
Hier ist das Testergebnis im Intervall von 2015.
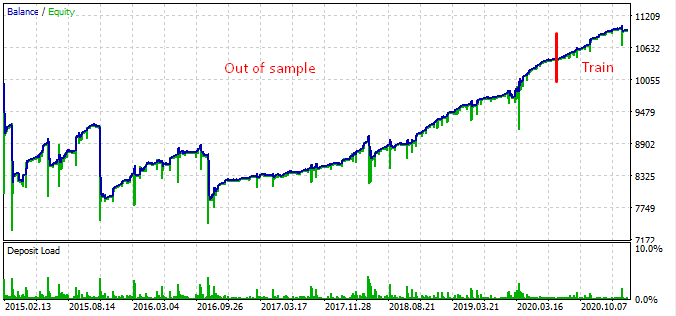
Laut der Grafik funktioniert das gefundene Muster von Ende 2016 bis zum heutigen Tag, im restlichen Intervall schlägt es fehl. In diesem Fall ist die anfängliche Losgröße minimal, was dem Bot geholfen hat, zu überleben. Zumindest wissen wir, dass der Bot seit Anfang 2017 effektiv ist. Auf dieser Grundlage können wir das Risiko erhöhen, um die Rentabilität zu steigern. Der Roboter zeigt beeindruckende Ergebnisse: 1600% in 3 Jahren mit einem Drawdown von 40%, bei einem hypothetischen Risiko, die gesamte Einlage zu verlieren.
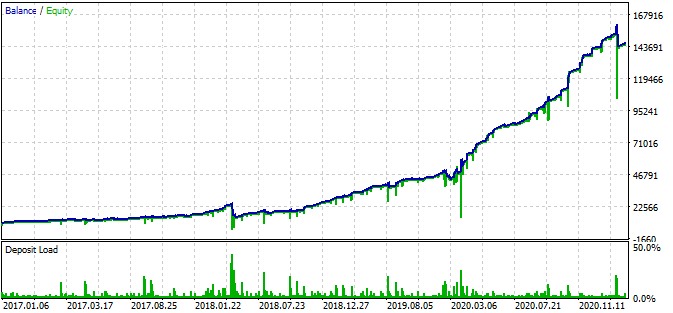
Außerdem verwendet der Bot Stop-Loss und Take-Profit für jede Position. SL und TP können auf Kosten der Performance eingesetzt werden, begrenzen aber das Risiko.
Bitte beachten Sie, dass ich ein recht aggressives Gitter verwendet habe.
GRID_COEFFICIENTS = np.linspace(1, 5, num= GRID_SIZE)
array([1. , 1.44444444, 1.88888889, 2.33333333, 2.77777778, 3.22222222, 3.66666667, 4.11111111, 4.55555556, 5. ])
Der letzte Multiplikator ist gleich fünf. Das bedeutet, dass die Losgröße des letzten Auftrags in der Serie fünfmal höher ist als die anfängliche Losgröße, was zusätzliche Risiken mit sich bringt. Sie können moderatere Modi wählen.
Warum hat der Bot in der Zeit ab 2016 und früher aufgehört zu funktionieren? Ich habe keine sinnvolle Antwort auf diese Frage. Es scheint, dass es lange siebenjährige Zyklen auf dem Forex-Markt gibt oder kürzere, deren Muster in keiner Weise miteinander verbunden sind. Dies ist ein separates Thema, das eine genauere Untersuchung erfordert.
Schlussfolgerung
In diesem Artikel habe ich versucht, die Technik zu beschreiben, die verwendet werden kann, um ein Boosting-Modell oder ein neuronales Netzwerk für den Martingale-Handel zu trainieren. Der Artikel enthält eine fertige Lösung, mit der Sie Ihre eigenen Handelsroboter erstellen können.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/8826
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Neuronale Netze leicht gemacht (Teil 12): Dropout
Neuronale Netze leicht gemacht (Teil 12): Dropout
 Der selbstanpassenden Algorithmus (Teil IV): Zusätzliche Funktionen und Tests
Der selbstanpassenden Algorithmus (Teil IV): Zusätzliche Funktionen und Tests
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
In außergewöhnlichen Zeiten, in denen die Zentralbanken Geld drucken wie nie zuvor, ist es sehr wahrscheinlich, dass viele Vermögenswerte in eine Richtung (nach oben) tendieren. Mit Backtesting der letzten 3 Jahre ist dieses Handelssystem anfällig für ein höheres Risiko, sobald die Zentralbanken die Zinsen anheben müssen (Sie können argumentieren, dass dies nie passiert, aber können Sie dies zu 100% garantieren?)
Dann werden die Auszahlungen höher sein als die in dem Artikel genannten ~40 %. Für jeden ernsthaften Anleger sind solche Risiken nicht akzeptabel.
Vielen Dank für Ihren interessanten Artikel.
Kann ich daraus schließen, dass Ihr System den Schritt und den Martingale-Koeffizienten automatisch an die Marktbedingungen anpasst, oder müssen Sie Backtests in Python durchführen und die Include-Datei regelmäßig generieren.
Nochmals vielen Dank.
Das Martingale-System ist gut, um kurzfristig etwas Geld zu verdienen (hoffentlich), aber langfristig gehen Sie bankrott. Ganz gleich, wie kompliziert Ihre Wahl ist.
Einverstanden. Grid, Hedging, Martingale sind beliebt für ihre schnelle und regelmäßige Rentabilität. Sie sind auch verantwortlich für alle Beschwerden gegen EA als Betrug, wegen der Margin-Call setzt es eine Konstante zu sein.
Es handelt sich um ein logisches und mathematisches Problem, und derjenige, der es - auf die eine oder andere Weise - lösen kann, wird eine Menge Geld verdienen!
According to the graph, the found pattern works from the end of 2016 to the present day, in the rest interval it fails.Hier ist ein weiterer Versuch mit maschinellem Lernen ...
Seit vielen Jahren habe ich einen Quellcode eines EAs, der diese Techniken verwendet, von Zeit zu Zeit, wenn ich eine Idee habe, probiere ich es aus ... 😉