Neuronale Netze leicht gemacht (Teil 11): Ein Blick auf GPT
1 007
0
Inhaltsverzeichnis
- Einführung
- 1. Verstehen der GPT-Modelle
- 2. Unterschiede zwischen GPT und dem zuvor betrachteten Transformer
- 3. Umsetzung
- 3.1. Erstellen einer neuen Klasse für unser Modell
- 3.2. Feed-Forward (Vorwärtskopplung)
- 3.3. Feed-Backward (Rückwärtskopplung)
- 3.4. Änderungen in den Basisklassen des neuronalen Netzwerks
- 4. Tests
- Schlussfolgerung
- Referenzen
- Die Programme dieses Artikels
Einführung
Im Juni 2018 präsentierte OpenAI das neuronale Netzwerkmodell GPT (Generative Pre-trained Transformer), das sofort die besten Ergebnisse in einer Reihe von Sprachtests zeigte. GDP-2 erschien 2019, und GPT-3 wurde im Mai 2020 vorgestellt. Diese Modelle demonstrierten die Fähigkeit des neuronalen Netzwerks, zusammenhängenden Text zu generieren. Weitere Experimente betrafen die Fähigkeit, Musik und Bilder zu generieren. Der Hauptnachteil solcher Modelle hängt mit den Rechenressourcen zusammen, die sie benötigen. Es dauerte einen Monat, um das erste GPT auf einer Maschine mit 8 GPUs zu trainieren. Dieser Nachteil kann teilweise durch die Möglichkeit kompensiert werden, vortrainierte Modelle zu verwenden, um neue Probleme zu lösen. Es sind jedoch erhebliche Ressourcen erforderlich, um das Modell in Anbetracht seiner Größe funktionsfähig zu halten.
1. Verstehen der GPT-Modelle
Konzeptionell werden GPT-Modelle auf der Basis des zuvor betrachteten Transformers aufgebaut. Die Hauptidee besteht darin, ein unüberwachtes Vortraining eines Modells mit einer großen Datenmenge durchzuführen und dann eine Feinabstimmung mit einer relativ kleinen Menge von markierten Daten vorzunehmen.
Der Grund für das zweistufige Training ist die Modellgröße. Moderne Deep-Machine-Learning-Modelle wie GPT beinhalten eine große Anzahl von Parametern, bis zu Hunderten von Millionen. Daher erfordert das Training solcher neuronaler Netze eine große Trainingsstichprobe. Bei der Verwendung von überwachtem Lernen wäre die Erstellung eines gelabelten Trainingssets arbeitsintensiv. Gleichzeitig gibt es viele verschiedene digitalisierte und nicht gekennzeichnete Texte im Internet, die sich hervorragend für das unüberwachte Modelltraining eignen. Statistiken zeigen jedoch, dass die Ergebnisse des unüberwachten Lernens dem überwachten Lernen unterlegen sind. Daher wird das Modell nach dem unüberwachten Training auf einer relativ kleinen Stichprobe von gelabelten Daten feinabgestimmt.
Unüberwachtes Lernen ermöglicht es dem GPT, das Sprachmodell zu erlernen, während weiteres Training auf gelabelten Daten das Modell für bestimmte Aufgaben abstimmt. Auf diese Weise kann ein vortrainiertes Modell repliziert und für verschiedene Sprachaufgaben feinabgestimmt werden. Die Einschränkung basiert auf der Sprache des ursprünglichen Datensatzes für unüberwachtes Lernen.
Die Praxis hat gezeigt, dass dieser Ansatz bei einer Vielzahl von Sprachproblemen gute Ergebnisse liefert. Zum Beispiel ist das GPT-3-Modell in der Lage, kohärente Texte zu einem bestimmten Thema zu generieren. Es ist jedoch zu beachten, dass das angegebene Modell 175 Milliarden Parameter enthält und auf einem 570 GB großen Datensatz vortrainiert wurde.
Obwohl GPT-Modelle für die Verarbeitung natürlicher Sprache entwickelt wurden, haben sie sich auch bei Aufgaben der Musik- und Bilderzeugung bewährt.
Theoretisch können GPT-Modelle mit jeder beliebigen Sequenz von digitalisierten Daten verwendet werden. Die einzige Voraussetzung ist die ausreichende Menge an Daten und Ressourcen für das unüberwachte Vorlernen.
2. Unterschiede zwischen GPT und dem zuvor betrachteten Transformer
Betrachten wir, was die GPT-Modelle von den bisher betrachteten Transformern unterscheidet. Zunächst einmal verwenden die GPT-Modelle keinen Encoder, da sie nur einen Decoder verwenden. Da es keinen Encoder gibt, verfügen die Modelle auch nicht mehr über die innere Schicht Encoder-Decoder Self-Attention. Die folgende Abbildung zeigt einen GPT-Transformer-Block.
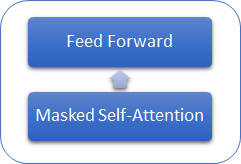
Ähnlich wie beim klassischen Transformer sind die Blöcke in GPT-Modellen übereinander aufgebaut. Und jeder Block hat seine eigenen Gewichtsmatrizen für den Attention-Mechanismus und voll verbundene Feed Forward-Schichten. Die Anzahl der Blöcke bestimmt die Modellgröße. Der Blockstapel kann recht groß sein. GPT-1 und das kleinste GPT-2 (GPT-2 Small) haben 12 Blöcke; GPT-2 Extra Large hat 48 davon, während GPT-3 96 Blöcke hat.
Ähnlich wie traditionelle Sprachmodelle erlaubt GPT nur das Auffinden von Beziehungen zu vorhergehenden Elementen der Sequenz, kann aber nicht in die Zukunft schauen. Aber im Gegensatz zum Transformer verwendet GPT keine Maskierung von Elementen — stattdessen nimmt es Änderungen am Rechenprozess vor. GPT setzt die Attention-Verhältnisse in der Score-Matrix für nachfolgende Elemente zurück.
Gleichzeitig kann GPT als ein autoregressives Modell eingestuft werden. Bei jeder Iteration wird ein Sequenz-Token erzeugt. Das resultierende Token wird zur Eingangssequenz hinzugefügt und in das Modell für die nächste Iteration eingespeist.
Wie beim klassischen Transformer werden für jedes Token innerhalb des Self-Attention-Mechanismus drei Vektoren erzeugt: eine Abfrage, ein Schlüssel und ein Wert. Im autoregressiven Modell, in dem sich bei jeder neuen Iteration die Eingabesequenz nur um 1 Token ändert, müssen die Vektoren nicht für jedes Token neu berechnet werden. Daher berechnet jede Schicht in GPT die Vektoren nur für neue Elemente der Sequenz und berechnet sie für jedes Element der Sequenz. Jeder Transformer-Block speichert seine Vektoren zur späteren Verwendung.
Dieser Ansatz ermöglicht es dem Modell, Texte Wort für Wort zu generieren, bevor es das endgültige Token erhält.
Natürlich verwenden GPT-Modelle den Multi-Head Attention-Mechanismus.
3. Umsetzung
Bevor wir loslegen, wollen wir kurz den Algorithmus wiederholen:
- Eine Eingangssequenz von Token wird in den Transformer-Block eingespeist.
- Für jedes Token werden drei Vektoren berechnet (query, key, value [Abfrage, Schlüssel, Wert]), indem der Token-Vektor mit der entsprechenden Matrix der Gewichte W, die trainiert wird, multipliziert wird.
- Durch Multiplikation von 'query' und 'key' werden Abhängigkeiten zwischen den Sequenzelementen ermittelt. In diesem Schritt wird der Vektor 'query' jedes Elements der Sequenz mit den 'key'-Vektoren des aktuellen und aller vorherigen Elemente der Sequenz multipliziert.
- Die Matrix der erhaltenen Attention-Scores wird mit Hilfe der SoftMax-Funktion im Kontext jeder Abfrage normalisiert. Für die nachfolgenden Elemente der Sequenz wird ein Attention-Score von Null gesetzt.
- Durch Multiplikation der normalisierten Attention-Scores mit den 'value'-Vektoren der entsprechenden Elemente der Sequenz und anschließender Addition der resultierenden Vektoren erhalten wir den durch attention korrigierten Wert für jedes Element der Sequenz (Z).
- Als Nächstes bestimmen wir den gewichteten Z-Vektor, der auf den Ergebnissen aller Attention-Heads basiert. Dazu werden die korrigierten 'value'-Vektoren aller Attention Heads zu einem einzigen Vektor konkateniert und dann mit der zu trainierenden W0-Matrix multipliziert.
- Der resultierende Tensor wird zur Eingabesequenz hinzugefügt und normalisiert.
- Auf den Multi-Heads-Self-Attention-Mechanismus folgen zwei voll verbundene Schichten des Feed Forward-Blocks. Die erste (versteckte) Schicht enthält 4-mal so viele Neuronen wie die Eingangssequenz mit der ReLU-Aktivierungsfunktion. Die Dimension der zweiten Schicht ist gleich der Dimension der Eingabesequenz, und die Neuronen verwenden die Aktivierungsfunktion nicht.
- Das Ergebnis der vollverknüpften Schichten wird mit dem Tensor aufsummiert, der in den Feed Forward-Block eingespeist wird. Der resultierende Tensor wird dann normalisiert.
Eine Sequenz für alle Self-Attention Heads (Selbstaufmerksamkeitsköpfe). Außerdem sind die Aktionen in 2-5 für jeden Attention Head identisch.
Als Ergebnis der Schritte 3 und 4 erhalten wir eine quadratische Matrix Score, deren Größe der Anzahl der Elemente in der Sequenz entspricht, in der die Summe aller Elemente im Kontext jeder 'query' "1" ist.
3.1. Erstellen einer neuen Klasse für unser Modell.
Um unser Modell zu implementieren, erstellen wir eine neue Klasse CNeuronMLMHAttentionOCL, die auf der Basisklasse CNeuronBaseOCL basiert. Ich bin bewusst einen Schritt zurück gegangen und habe die zuvor erstellten Attention-Klassen nicht verwendet. Das liegt daran, dass wir uns jetzt mit neuen Prinzipien zur Erzeugung von Multi-Head Self-Attention beschäftigen. Vorher, in Artikel 10, haben wir die Klasse CNeuronMHAttentionOCL erstellt, die eine sequentielle Neuberechnung von 4 Attention-Threads ermöglichte. Die Anzahl der Threads war in den Methoden hart kodiert, so dass eine Änderung der Anzahl der Threads einen erheblichen Aufwand erfordern würde, der mit Änderungen im Code der Klasse und ihrer Methoden verbunden ist.
Ein Vorbehalt. Wie oben erwähnt, verwendet das GPT-Modell einen Stapel identischer Transformer-Blöcke mit denselben (unveränderlichen) Hyperparametern, wobei der einzige Unterschied in den zu trainierenden Matrizen besteht. Daher habe ich mich entschlossen, einen Multi-Layer-Block zu erstellen, der es ermöglicht, Modelle mit Hyperparametern zu erstellen, die beim Erstellen einer Klasse übergeben werden können. Dazu gehört auch die Anzahl der Wiederholungen von Transformer-Blöcken im Stack.
Als Ergebnis haben wir eine Klasse, die fast das gesamte Modell auf der Grundlage einiger weniger angegebener Parameter erstellen kann. Im 'protected'-Block der neuen Klasse deklarieren wir also fünf Variablen, um die Blockparameter zu speichern:
| iLayers | die Anzahl der Transformerblöcke im Modell |
| iHeads | die Anzahl der Self-Attention-Heads |
| iWindow | die Größe des Eingabefensters (1 Eingabesequenz-Token) |
| iWindowKey | die Dimensionen der internen Vektoren Query, Key, Value |
| iUnits | die Anzahl der Elemente (Token) in der Eingabesequenz |
Wir deklarieren außerdem im 'protected'-Block 6 Arrays, um eine Kollektion von Puffern für unsere Tensoren und Trainingsgewichtsmatrizen zu speichern:
| QKV_Tensors | das Array zum Speichern der Tensoren Query, Key, Value und deren Gradienten |
| QKV_Weights | das Array zum Speichern einer Kollektion der von Gewichtungsmatrizen Wq, Wk, Wv und deren Moment-Matrizen |
| S_Tensors | das Array zum Speichern einer Kollektion von Score-Matrizen und deren Gradienten |
| AO_Tensors | das Array zum Speichern von Ausgangstensoren des Self-Attention-Mechanismus und deren Gradienten |
| FF_Tensors | das Array zum Speichern von Eingangs-, Hidden- und Ausgangstensoren des Feed-Forward-Blocks und deren Gradienten |
| FF_Weights | das Array zum Speichern der Gewichtsmatrizen des Feed Forward-Blocks und deren Momente. |
Wir werden die Methoden der Klasse später bei der Implementierung berücksichtigen.
class CNeuronMLMHAttentionOCL : public CNeuronBaseOCL { protected: uint iLayers; ///< Number of inner layers uint iHeads; ///< Number of heads uint iWindow; ///< Input window size uint iUnits; ///< Number of units uint iWindowKey; ///< Size of Key/Query window //--- CCollection *QKV_Tensors; ///< The collection of tensors of Queries, Keys and Values CCollection *QKV_Weights; ///< The collection of Matrix of weights to previous layer CCollection *S_Tensors; ///< The collection of Scores tensors CCollection *AO_Tensors; ///< The collection of Attention Out tensors CCollection *FF_Tensors; ///< The collection of tensors of Feed Forward output CCollection *FF_Weights; ///< The collection of Matrix of Feed Forward weights ///\ingroup neuron_base_ff virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); ///< \brief Feed Forward method of calling kernel ::FeedForward().@param NeuronOCL Pointer to previos layer. virtual bool ConvolutionForward(CBufferDouble *weights, CBufferDouble *inputs,CBufferDouble *outputs, uint window, uint window_out, ENUM_ACTIVATION activ); ///< \brief Convolution Feed Forward method of calling kernel ::FeedForwardConv(). virtual bool AttentionScore(CBufferDouble *qkv, CBufferDouble *scores, bool mask=true); ///< \brief Multi-heads attention scores method of calling kernel ::MHAttentionScore(). virtual bool AttentionOut(CBufferDouble *qkv, CBufferDouble *scores, CBufferDouble *out); ///< \brief Multi-heads attention out method of calling kernel ::MHAttentionOut(). virtual bool SumAndNormilize(CBufferDouble *tensor1, CBufferDouble *tensor2, CBufferDouble *out); ///< \brief Method sum and normalize 2 tensors by calling 2 kernels ::SumMatrix() and ::Normalize(). ///\ingroup neuron_base_opt virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); ///< Method for updating weights.\details Calling one of kernels ::UpdateWeightsMomentum() or ::UpdateWeightsAdam() in depends on optimization type (#ENUM_OPTIMIZATION).@param NeuronOCL Pointer to previos layer. virtual bool ConvolutuionUpdateWeights(CBufferDouble *weights, CBufferDouble *gradient, CBufferDouble *inputs, CBufferDouble *momentum1, CBufferDouble *momentum2, uint window, uint window_out); ///< Method for updating weights in convolution layer.\details Calling one of kernels ::UpdateWeightsConvMomentum() or ::UpdateWeightsConvAdam() in depends on optimization type (#ENUM_OPTIMIZATION). virtual bool ConvolutionInputGradients(CBufferDouble *weights, CBufferDouble *gradient, CBufferDouble *inputs, CBufferDouble *inp_gradient, uint window, uint window_out, uint activ); ///< Method of passing gradients through a convolutional layer. virtual bool AttentionInsideGradients(CBufferDouble *qkv,CBufferDouble *qkv_g,CBufferDouble *scores,CBufferDouble *scores_g,CBufferDouble *gradient); ///< Method of passing gradients through attention layer. public: /** Constructor */CNeuronMLMHAttentionOCL(void); /** Destructor */~CNeuronMLMHAttentionOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint layers, ENUM_OPTIMIZATION optimization_type); ///< Method of initialization class.@param[in] numOutputs Number of connections to next layer.@param[in] myIndex Index of neuron in layer.@param[in] open_cl Pointer to #COpenCLMy object.@param[in] window Size of in/out window and step.@param[in] units_countNumber of neurons.@param[in] optimization_type Optimization type (#ENUM_OPTIMIZATION)@return Boolen result of operations. virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); ///< Method to transfer gradients to previous layer @param[in] prevLayer Pointer to previous layer. //--- virtual int Type(void) const { return defNeuronMLMHAttentionOCL; }///< Identificator of class.@return Type of class //--- methods for working with files virtual bool Save(int const file_handle); ///< Save method @param[in] file_handle handle of file @return logical result of operation virtual bool Load(int const file_handle); ///< Load method @param[in] file_handle handle of file @return logical result of operation };
Im Klassenkonstruktor setzen wir die Anfangswerte der Klassenhyperparameter und initialisieren die Arrays der Kollektion.
CNeuronMLMHAttentionOCL::CNeuronMLMHAttentionOCL(void) : iLayers(0), iHeads(0), iWindow(0), iWindowKey(0), iUnits(0) { QKV_Tensors=new CCollection(); QKV_Weights=new CCollection(); S_Tensors=new CCollection(); AO_Tensors=new CCollection(); FF_Tensors=new CCollection(); FF_Weights=new CCollection(); }
Entsprechend löschen wir die Arrays der Kollektion im Destruktor der Klasse.
CNeuronMLMHAttentionOCL::~CNeuronMLMHAttentionOCL(void) { if(CheckPointer(QKV_Tensors)!=POINTER_INVALID) delete QKV_Tensors; if(CheckPointer(QKV_Weights)!=POINTER_INVALID) delete QKV_Weights; if(CheckPointer(S_Tensors)!=POINTER_INVALID) delete S_Tensors; if(CheckPointer(AO_Tensors)!=POINTER_INVALID) delete AO_Tensors; if(CheckPointer(FF_Tensors)!=POINTER_INVALID) delete FF_Tensors; if(CheckPointer(FF_Weights)!=POINTER_INVALID) delete FF_Weights; }
Die Initialisierung der Klasse zusammen mit dem Aufbau des Modells wird in der Methode Init durchgeführt. Der Methode werden folgende Parametern übergeben:
| numOutputs | die Anzahl der Elemente in der nachfolgenden Schicht, um Verknüpfungen zu erstellen |
| myIndex | Neuronenindex in der Schicht |
| open_cl | der Zeiger auf das OpenCL-Objekt |
| window | die Größe des Eingangsfensters (Eingangssequenz-Token) |
| window_key | die Dimensionen der internen Vektoren Query, Key, Value |
| heads | die Anzahl der Self-Attention-Köpfe (Threads) |
| units_count | die Anzahl der Elemente in der Eingabesequenz |
| layers | die Anzahl der Blöcke (Schichten) im Modellstapel |
| optimization_type | die Methode der Parameteroptimierung beim Training |
bool CNeuronMLMHAttentionOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window,uint window_key,uint heads,uint units_count,uint layers,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronBaseOCL::Init(numOutputs,myIndex,open_cl,window*units_count,optimization_type)) return false; //--- iWindow=fmax(window,1); iWindowKey=fmax(window_key,1); iUnits=fmax(units_count,1); iHeads=fmax(heads,1); iLayers=fmax(layers,1);
Zu Beginn der Methode initialisieren wir die übergeordnete Klasse, indem wir die entsprechende Methode aufrufen. Vergessen wir nicht, dass wir keine grundlegenden Prüfungen zur Validierung des erhaltenen OpenCL-Objektzeigers und der Eingangssequenzgröße durchführen, da diese Prüfungen bereits in der Methode der Elternklasse implementiert sind.
Nach erfolgreicher Initialisierung der Elternklasse speichern wir die Hyperparameter in den entsprechenden Variablen.
Als Nächstes berechnen wir die Größen der zu erzeugenden Tensoren. Bitte beachten Sie den zuvor modifizierten Ansatz zur Organisation von Multi-Head Attention. Wir werden keine separaten Arrays für die Vektoren 'query', 'key' und 'value' anlegen - sie werden in einem Array zusammengefasst. Außerdem werden wir keine separaten Arrays für jeden Attention-Heads erstellen. Stattdessen werden wir gemeinsame Arrays für QKV (Query + Key + Value), Scores und Ausgaben des Selbstaufmerksamkeitsmechanismus erstellen. Die Elemente werden in Sequenzen auf der Ebene der Indizes im Tensor unterteilt. Natürlich ist dieser Ansatz schwieriger zu verstehen. Es kann auch schwieriger sein, das gewünschte Element im Tensor zu finden. Aber es erlaubt, das Modell je nach Anzahl der Attention-Heads flexibel zu gestalten und die gleichzeitige Neuberechnung aller Attention-Heads durch Parallelisierung von Threads auf der Kernel-Ebene zu organisieren.
Die Größe des Tensors QKV_Tensor (num) ist definiert als das Produkt aus den drei Größen des internen Vektors (query + key + value) und der Anzahl der Heads. Die Größe der verketteten Matrix der Gewichte QKV_Weight ist definiert als das Produkt der drei Größen des Eingangssequenz-Tokens, erhöht um das Offset-Element, um die Größe des internen Vektors und die Anzahl der Attention-Heads. Berechnen wir auf ähnliche Weise die Größen der übrigen Tensoren.
uint num=3*iWindowKey*iHeads*iUnits; //Size of QKV tensor uint qkv_weights=3*(iWindow+1)*iWindowKey*iHeads; //Size of weights' matrix of QKV tensor uint scores=iUnits*iUnits*iHeads; //Size of Score tensor uint mh_out=iWindowKey*iHeads*iUnits; //Size of multi-heads self-attention uint out=iWindow*iUnits; //Size of our tensor uint w0=(iWindowKey+1)*iHeads*iWindow; //Size W0 tensor uint ff_1=4*(iWindow+1)*iWindow; //Size of weights' matrix 1-st feed forward layer uint ff_2=(4*iWindow+1)*iWindow; //Size of weights' matrix 2-nd feed forward layer
Nachdem wir die Größen aller Tensoren bestimmt haben, führen wir eine Schleife mit der Anzahl der Attention-Schichten im Block aus, um die erforderlichen Tensoren zu erzeugen. Beachten Sie, dass innerhalb des Schleifenkörpers zwei verschachtelte Schleifen existieren. Die erste Schleife erzeugt Arrays für die value-Tensoren und deren Gradienten. Die zweite erzeugt Arrays für die weight-Matrizen und deren Momente. Beachten Sie, dass für die letzte Schicht keine neuen Arrays für den Ausgangstensor des Feed Forward-Blocks und seinen Gradienten erstellt werden. Stattdessen werden der Kollektion Zeiger auf die Ausgabe- und Gradienten-Arrays der Elternklasse hinzugefügt. Ein solch einfacher Schritt vermeidet eine unnötige Iteration, bei der Werte zwischen den Arrays übertragen werden, und eliminiert unnötigen Speicherverbrauch.
for(uint i=0; i<iLayers; i++) { CBufferDouble *temp=NULL; for(int d=0; d<2; d++) { //--- Initialize QKV tensor temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(num,0)) return false; if(!QKV_Tensors.Add(temp)) return false; //--- Initialize scores temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(scores,0)) return false; if(!S_Tensors.Add(temp)) return false; //--- Initialize multi-heads attention out temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(mh_out,0)) return false; if(!AO_Tensors.Add(temp)) return false; //--- Initialize attention out temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(out,0)) return false; if(!FF_Tensors.Add(temp)) return false; //--- Initialize Feed Forward 1 temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(4*out,0)) return false; if(!FF_Tensors.Add(temp)) return false; //--- Initialize Feed Forward 2 if(i==iLayers-1) { if(!FF_Tensors.Add(d==0 ? Output : Gradient)) return false; continue; } temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(out,0)) return false; if(!FF_Tensors.Add(temp)) return false; } //--- Initialize QKV weights temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Reserve(qkv_weights)) return false; for(uint w=0; w<qkv_weights; w++) { if(!temp.Add(GenerateWeight())) return false; } if(!QKV_Weights.Add(temp)) return false; //--- Initialize Weights0 temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Reserve(w0)) return false; for(uint w=0; w<w0; w++) { if(!temp.Add(GenerateWeight())) return false; } if(!FF_Weights.Add(temp)) return false; //--- Initialize FF Weights temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Reserve(ff_1)) return false; for(uint w=0; w<ff_1; w++) { if(!temp.Add(GenerateWeight())) return false; } if(!FF_Weights.Add(temp)) return false; //--- temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Reserve(ff_2)) return false; for(uint w=0; w<ff_1; w++) { if(!temp.Add(GenerateWeight())) return false; } if(!FF_Weights.Add(temp)) return false; //--- for(int d=0; d<(optimization==SGD ? 1 : 2); d++) { temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(qkv_weights,0)) return false; if(!QKV_Weights.Add(temp)) return false; temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(w0,0)) return false; if(!FF_Weights.Add(temp)) return false; //--- Initialize FF Weights temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(ff_1,0)) return false; if(!FF_Weights.Add(temp)) return false; temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(ff_2,0)) return false; if(!FF_Weights.Add(temp)) return false; } } //--- return true; }
Als Ergebnis erhalten wir für jede Schicht die folgende Matrix von Tensoren.
| QKV_Tensor |
|
| S_Tensors |
|
| AO_Tensors |
|
| FF_Tensors |
|
| QKV_Weights |
|
| FF_Weights |
|
Nach dem Erstellen der Array-Kollektionen verlassen Sie die Methode mit 'true'. Der gesamte Code aller Klassen und Methoden befindet sich in der Anlage.
3.2. Vorwärtsdurchgang.
Der Feed-forward-Durchgang ist traditionell in der feedForward-Methode organisiert, die als Parameter einen Zeiger auf die vorherige Schicht des neuronalen Netzes erhält. Zu Beginn der Methode wird die Gültigkeit des empfangenen Zeigers überprüft.
bool CNeuronMLMHAttentionOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL)==POINTER_INVALID) return false;
Als Nächstes wollen wir eine Schleife organisieren, um alle Ebenen unseres Blocks neu zu berechnen. Im Gegensatz zu den zuvor beschriebenen analogen Methoden anderer Klassen, ist diese Methode eine Top-Level-Methode. Die organisierten Operationen sind auf die Vorbereitung der Daten und den Aufruf von Hilfsmethoden reduziert (die Logik dieser Methoden wird weiter unten beschrieben).
Zu Beginn der Schleife erhalten wir aus der Kollektion den Eingangsdatenpuffer der Tensoren QKV und QKV_Weights, der der aktuellen Schicht entspricht. Dann rufen wir ConvolutionForward auf, um die Vektoren Query, Key und Value zu berechnen.
for(uint i=0; (i<iLayers && !IsStopped()); i++) { //--- Calculate Queries, Keys, Values CBufferDouble *inputs=(i==0? NeuronOCL.getOutput() : FF_Tensors.At(6*i-4)); CBufferDouble *qkv=QKV_Tensors.At(i*2); if(IsStopped() || !ConvolutionForward(QKV_Weights.At(i*(optimization==SGD ? 2 : 3)),inputs,qkv,iWindow,3*iWindowKey*iHeads,None)) return false;
Ich bin auf ein Problem gestoßen, als ich die Attention-Ebenen erhöht habe. Irgendwann bekam ich den Fehler 5113 ERR_OPENCL_TOO_MANY_OBJECTS. Also musste ich darüber nachdenken, alle Tensoren dauerhaft im GPU-Speicher zu speichern. Deshalb gebe ich nach Beendigung der Operationen die Puffer frei, die in diesem Schritt nicht mehr verwendet werden. Vergessen Sie in Ihrem Code nicht, die letzten Daten der freigegebenen Puffer aus dem GPU-Speicher zu lesen. In der in diesem Artikel vorgestellten Klasse werden die Pufferdaten in Kernel-Initialisierungsmethoden gelesen, die wir etwas später besprechen werden.
CBufferDouble *temp=QKV_Weights.At(i*(optimization==SGD ? 2 : 3)); temp.BufferFree();
Attention-Scores und gewichtete Vektoren der Werte des Self-Attention-Mechanismus werden auf ähnliche Weise berechnet, indem entsprechende Methoden aufgerufen werden.
//--- Score calculation temp=S_Tensors.At(i*2); if(IsStopped() || !AttentionScore(qkv,temp,true)) return false; //--- Multi-heads attention calculation CBufferDouble *out=AO_Tensors.At(i*2); if(IsStopped() || !AttentionOut(qkv,temp,out)) return false; qkv.BufferFree(); temp.BufferFree();
Nach der Berechnung der Multi-Heads-Self-Attention wird der verkettete Attention-Output auf die Größe der Eingangssequenz reduziert, zwei Vektoren addiert und das Ergebnis normalisiert.
//--- Attention out calculation temp=FF_Tensors.At(i*6); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i*(optimization==SGD ? 6 : 9)),out,temp,iWindowKey*iHeads,iWindow,None)) return false; out.BufferFree(); //--- Sum and normalize attention if(IsStopped() || !SumAndNormilize(temp,inputs,temp)) return false; if(i>0) inputs.BufferFree();
Auf den Self-Attention-Mechanismus im Transformer folgt der Feed Forward-Block, der aus zwei vollständig verbundenen Schichten besteht. Dann wird das Ergebnis zur Eingangssequenz addiert. Der endgültige Tensor wird normalisiert und in die nächste Schicht eingespeist. In unserem Fall schließen wir den Zyklus.
//--- Feed Forward inputs=temp; temp=FF_Weights.At(i*(optimization==SGD ? 6 : 9)); temp.BufferFree(); temp=FF_Tensors.At(i*6+1); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i*(optimization==SGD ? 6 : 9)+1),inputs,temp,iWindow,4*iWindow,LReLU)) return false; out=FF_Weights.At(i*(optimization==SGD ? 6 : 9)+1); out.BufferFree(); out=FF_Tensors.At(i*6+2); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i*(optimization==SGD ? 6 : 9)+2),temp,out,4*iWindow,iWindow,activation)) return false; temp.BufferFree(); temp=FF_Weights.At(i*(optimization==SGD ? 6 : 9)+2); temp.BufferFree(); //--- Sum and normalize out if(IsStopped() || !SumAndNormilize(out,inputs,out)) return false; inputs.BufferFree(); } //--- return true; }
Der vollständige Code der Methode ist im Anhang unten zu finden. Betrachten wir nun Hilfsmethoden, die von der FeedForward-Methode aufgerufen werden. Die erste Methode, die wir aufrufen, ist ConvolutionForward. Sie wird viermal pro einem Zyklus der FeedForward-Methode aufgerufen. Im Methodenkörper wird der Kernel für den Vorwärtsdurchgang der Convolutional-Schicht aufgerufen. Diese Methode spielt in diesem Fall die Rolle einer voll verbundenen Schicht für jedes einzelne Token der Eingabesequenz. Die Lösung wurde im Artikel 8 ausführlicher besprochen. Im Gegensatz zu der zuvor beschriebenen Lösung erhält die neue Methode in Parametern Zeiger auf Puffer, um Daten an den OpenCL-Kernel zu übergeben. Daher prüfen wir zu Beginn der Methode die Gültigkeit der erhaltenen Zeiger.
bool CNeuronMLMHAttentionOCL::ConvolutionForward(CBufferDouble *weights, CBufferDouble *inputs,CBufferDouble *outputs, uint window, uint window_out, ENUM_ACTIVATION activ) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(weights)==POINTER_INVALID || CheckPointer(inputs)==POINTER_INVALID || CheckPointer(outputs)==POINTER_INVALID) return false;
Als Nächstes erstellen wir Puffer im GPU-Speicher und übergeben ihnen die notwendigen Informationen.
if(!weights.BufferCreate(OpenCL)) return false; if(!inputs.BufferCreate(OpenCL)) return false; if(!outputs.BufferCreate(OpenCL)) return false;
Es folgt der in Artikel 8 beschriebene Code, ohne Änderungen. Der aufgerufene Kernel wird so verwendet, wie er ist, ohne Änderungen.
uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=outputs.Total()/window_out; OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_w,weights.GetIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_i,inputs.GetIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_o,outputs.GetIndex()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_inputs,inputs.Total()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_step,window); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_window_in,window); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffс_window_out,window_out); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_activation,(int)activ); if(!OpenCL.Execute(def_k_FeedForwardConv,1,global_work_offset,global_work_size)) { printf("Error of execution kernel FeedForwardConv: %d",GetLastError()); return false; } //--- return outputs.BufferRead(); }
Weiter im Code der feedForward-Methode kommt der Aufruf der AttentionScore-Methode, die einen Kernel aufruft, um Attention-Scores zu berechnen und zu normalisieren - diese resultierenden Werte werden dann in die Score-Matrix geschrieben. Für diese Methode wurde ein neuer Kernel geschrieben; er wird später betrachtet, nachdem wir die Methode selbst betrachtet haben.
Wie die vorherige Methode erhält AttentionScore die Zeiger auf die anfänglichen Datenpuffer und Aufzeichnungen der erhaltenen Werte in den Parametern. Zu Beginn der Methode prüfen wir also die Gültigkeit der erhaltenen Zeiger.
bool CNeuronMLMHAttentionOCL::AttentionScore(CBufferDouble *qkv, CBufferDouble *scores, bool mask=true) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(qkv)==POINTER_INVALID || CheckPointer(scores)==POINTER_INVALID) return false;
Der oben beschriebenen Logik folgend, wollen wir Puffer für den Datenaustausch mit der GPU erstellen.
if(!qkv.BufferCreate(OpenCL)) return false; if(!scores.BufferCreate(OpenCL)) return false;
Nach den Vorarbeiten gehen wir zur Spezifikation der Kernel-Parameter über. Die Threads dieses Kernels werden in zwei Dimensionen erstellt: im Kontext der Eingangssequenzelemente und im Kontext der Attention-Heads. Dies ermöglicht eine parallele Berechnung für alle Elemente der Sequenz und alle Attention-Heads.
uint global_work_offset[2]= {0,0}; uint global_work_size[2]; global_work_size[0]=iUnits; global_work_size[1]=iHeads; OpenCL.SetArgumentBuffer(def_k_MHAttentionScore,def_k_mhas_qkv,qkv.GetIndex()); OpenCL.SetArgumentBuffer(def_k_MHAttentionScore,def_k_mhas_score,scores.GetIndex()); OpenCL.SetArgument(def_k_MHAttentionScore,def_k_mhas_dimension,iWindowKey); OpenCL.SetArgument(def_k_MHAttentionScore,def_k_mhas_mask,(int)mask);
Danach geht es direkt weiter zum Kernelaufruf. Die Berechnungsergebnisse werden in den Puffer 'score' eingelesen.
if(!OpenCL.Execute(def_k_MHAttentionScore,2,global_work_offset,global_work_size)) { printf("Error of execution kernel MHAttentionScore: %d",GetLastError()); return false; } //--- return scores.BufferRead(); }
Betrachten wir die Logik des aufgerufenen MHAttentionScore-Kernels. Wie oben gezeigt, erhält der Kernel in den Parametern einen Zeiger auf das qkv-Quelldaten-Array und ein Array zur Aufnahme der resultierenden Scores. Außerdem erhält der Kernel in den Parametern die Größe der internen Vektoren (Query, Key) und ein Flag zur Aktivierung des Maskierungsalgorithmus für nachfolgende Elemente.
Zunächst erhalten wir die Ordnungszahlen der zu verarbeitenden Abfrage q und des Attention-Heads h. Außerdem erhalten wir die Dimension der Anzahl von Abfragen und Attention-Heads.
__kernel void MHAttentionScore(__global double *qkv, ///<[in] Matrix of Querys, Keys, Values __global double *score, ///<[out] Matrix of Scores int dimension, ///< Dimension of Key int mask ///< 1 - calc only previous units, 0 - calc all ) { int q=get_global_id(0); int h=get_global_id(1); int units=get_global_size(0); int heads=get_global_size(1);
Bestimmen wir auf der Grundlage der erhaltenen Daten die Verschiebung in den Arrays für 'query' und 'score'.
int shift_q=dimension*(h+3*q*heads); int shift_s=units*(h+q*heads);
Berechnen wir außerdem einen Score-Korrekturkoeffizienten.
double koef=sqrt((double)dimension); if(koef<1) koef=1;
Die Berechnung der Attention-Werte erfolgt in einer Schleife, in der wir durch die Schlüssel der gesamten Folge von Elementen im entsprechenden Attention-Heads iterieren.
Prüfen Sie zu Beginn der Schleife die Bedingung für die Verwendung des Attention-Mechanismus. Wenn diese Funktionalität aktiviert ist, prüfen wir die Seriennummer des Schlüssels. Wenn der aktuelle Schlüssel dem nächsten Element der Sequenz entspricht, schreiben wir den Wert Null in das Array 'score' und gehen zum nächsten Element.
double sum=0; for(int k=0;k<units;k++) { if(mask>0 && k>q) { score[shift_s+k]=0; continue; }
Wenn der Attention-Score für die analysierte Taste berechnet wird, dann organisieren wir eine verschachtelte Schleife, um das Produkt der beiden Vektoren zu berechnen. Vergessen wir nicht, dass der Schleifenkörper zwei Berechnungszweige hat: einen mit Vektorberechnungen und den anderen ohne solche Berechnungen. Der erste Zweig wird verwendet, wenn es 4 oder mehr Elemente von der aktuellen Position im Schlüsselvektor bis zu dessen letztem Element gibt; der zweite Zweig wird für die letzten nicht-mehrfachen 4 Elemente des Schlüsselvektors verwendet.
double result=0; int shift_k=dimension*(h+heads*(3*k+1)); for(int i=0;i<dimension;i++) { if((dimension-i)>4) { result+=dot((double4)(qkv[shift_q+i],qkv[shift_q+i+1],qkv[shift_q+i+2],qkv[shift_q+i+3]), (double4)(qkv[shift_k+i],qkv[shift_k+i+1],qkv[shift_k+i+2],qkv[shift_k+i+3])); i+=3; } else result+=(qkv[shift_q+i]*qkv[shift_k+i]); }
Gemäß dem Transformer-Algorithmus werden die Attention-Scores mit der SoftMax-Funktion normalisiert. Um diese Funktion zu implementieren, werden wir das Ergebnis des Produkts der Vektoren durch den Korrekturkoeffizienten dividieren und den Exponenten für den resultierenden Wert bestimmen. Das Berechnungsergebnis soll in das entsprechende Element des 'Score'-Tensors geschrieben und zur Summe der Exponenten addiert werden.
result=exp(clamp(result/koef,-30.0,30.0)); if(isnan(result)) result=0; score[shift_s+k]=result; sum+=result; }
Auf ähnliche Weise werden wir die Exponenten für alle Elemente berechnen. Um die Normalisierung von SoftMax der Attention-Scores abzuschließen, organisieren wir einen weiteren Zyklus, in dem alle Elemente des 'Score'-Tensors durch die zuvor berechnete Summe der Exponenten geteilt werden.
for(int k=0;(k<units && sum>1);k++) score[shift_s+k]/=sum; }
Am Ende der Schleife wird der Kernel verlassen.
Fahren wir mit der feedForward-Methode fort und betrachten die Hilfsmethode AttentionOut. Die Methode erhält als Parameter die Zeiger auf drei Tensoren: QKV, Scores und Out. Die Struktur der Methode ist ähnlich wie die zuvor betrachteten. Sie startet die MHAttentionOut-Kernels in zwei Dimensionen: Sequenzelemente und Attention-Heads.
bool CNeuronMLMHAttentionOCL::AttentionOut(CBufferDouble *qkv, CBufferDouble *scores, CBufferDouble *out) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(qkv)==POINTER_INVALID || CheckPointer(scores)==POINTER_INVALID || CheckPointer(out)==POINTER_INVALID) return false; uint global_work_offset[2]= {0,0}; uint global_work_size[2]; global_work_size[0]=iUnits; global_work_size[1]=iHeads; if(!qkv.BufferCreate(OpenCL)) return false; if(!scores.BufferCreate(OpenCL)) return false; if(!out.BufferCreate(OpenCL)) return false; //--- OpenCL.SetArgumentBuffer(def_k_MHAttentionOut,def_k_mhao_qkv,qkv.GetIndex()); OpenCL.SetArgumentBuffer(def_k_MHAttentionOut,def_k_mhao_score,scores.GetIndex()); OpenCL.SetArgumentBuffer(def_k_MHAttentionOut,def_k_mhao_out,out.GetIndex()); OpenCL.SetArgument(def_k_MHAttentionOut,def_k_mhao_dimension,iWindowKey); if(!OpenCL.Execute(def_k_MHAttentionOut,2,global_work_offset,global_work_size)) { printf("Error of execution kernel MHAttentionOut: %d",GetLastError()); return false; } //--- return out.BufferRead(); }
MHAttentionOut wurde wie der vorherige Kernel unter Berücksichtigung der Multi-Head Attention neu geschrieben. Er verwendet einen einzigen Puffer für die Tensoren der Abfragen, Schlüssel und Werte. Der Kernel erhält als Parameter die Zeiger auf die Tensoren Scores, QKV, Out und die Größe des Wertevektors. Der erste und zweite Puffer liefern die Originaldaten, der letzte wird für die Aufzeichnung des Ergebnisses verwendet.
Wir bestimmen außerdem zu Beginn des Kernels die Ordnungszahlen der zu verarbeitenden Abfrage q und des Attention-Head h sowie die Dimension der Anzahl der Abfragen und Attention-Heads.
__kernel void MHAttentionOut(__global double *scores, ///<[in] Matrix of Scores __global double *qkv, ///<[in] Matrix of Values __global double *out, ///<[out] Output tensor int dimension ///< Dimension of Value ) { int u=get_global_id(0); int units=get_global_size(0); int h=get_global_id(1); int heads=get_global_size(1);
Bestimmen wir als Nächstes die Position des gewünschten Attention-Values und des ersten Elementes des zu analysierenden Ausgangswertvektors. Zusätzlich berechnen wir die Länge des Vektors von einem Element im QKV-Tensor - dieser Wert wird zur Bestimmung der Verschiebung im QKV-Tensor verwendet.
int shift_s=units*(h+heads*u); int shift_out=dimension*(h+heads*u); int layer=3*dimension*heads;
Wir werden verschachtelte Schleifen für die Hauptberechnungen implementieren. Die äußere Schleife läuft über die Größe des Wertevektors, die innere Schleife über die Anzahl der Elemente in der ursprünglichen Folge. Zu Beginn der äußeren Schleife deklarieren wir eine Variable für die Berechnung des resultierenden Wertes und initialisieren sie mit einem Nullwert. Die innere Schleife beginnt mit der Definition einer Verschiebung für den Wertevektor. Beachten Sie, dass der Schritt der inneren Schleife gleich 4 ist, da wir später Vektorberechnungen verwenden werden.
for(int d=0;d<dimension;d++) { double result=0; for(int v=0;v<units;v+=4) { int shift_v=dimension*(h+heads*(3*v+2))+d;
Wie beim Kernel MHAttentionScore wollen wir die Berechnungen in zwei Threads aufteilen: einen mit Vektorberechnungen und
der andere ohne sie. Der zweite Thread wird nur für die letzten Elemente verwendet, in Fällen, in denen die Sequenzlänge kein Vielfaches von 4 ist.h
if((units-v)>4) { result+=dot((double4)(scores[shift_s+v],scores[shift_s+v+1],scores[shift_s+v+1],scores[shift_s+v+3]), (double4)(qkv[shift_v],qkv[shift_v+layer],qkv[shift_v+2*layer],qkv[shift_v+3*layer])); } else for(int l=0;l<(int)fmin((double)(units-v),4.0);l++) result+=scores[shift_s+v+l]*qkv[shift_v+l*layer]; } out[shift_out+d]=result; } }
Nach dem Verlassen der geschachtelten Schleife schreiben Sie den resultierenden Wert in das entsprechende Element des Ausgangstensors.
Weiterhin wird in der Methode feedForward die oben beschriebene ConvolutionForward-Methode verwendet. Der vollständige Code aller Methoden und Funktionen steht im Anhang zur Verfügung.
3.3. Feed-Backward.
Wie in allen bisher betrachteten Klassen enthält der Feed-Backward-Prozess zwei Teilprozesse: die Propagierung des Fehlergradienten und die Aktualisierung der Gewichte. Der erste Teil ist in der Methode calcInputGradients implementiert, der zweite in updateInputWeights.
Der Aufbau der Methode calcInputGradients ist ähnlich dem von feedForward. Die Methode erhält als Parameter einen Zeiger auf die vorherige Schicht des neuronalen Netzes, an die der Fehlergradient übergeben werden soll. Überprüfen wir also zu Beginn der Methode die Gültigkeit des erhaltenen Zeigers.
bool CNeuronMLMHAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
Dann fixieren wir den Tensor des Gradienten, den wir von der nächsten Neuronenschicht erhalten, und organisieren eine Schleife über alle inneren Schichten, um den Fehlergradienten sequentiell zu berechnen. Da es sich um einen Feed-Backward-Prozess handelt, iteriert die Schleife in umgekehrter Reihenfolge über die inneren Schichten.
for(int i=(int)iLayers-1; (i>=0 && !IsStopped()); i--) { //--- Passing gradient through feed forward layers if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i*(optimization==SGD ? 6 : 9)+2),out_grad,FF_Tensors.At(i*6+1),FF_Tensors.At(i*6+4),4*iWindow,iWindow,None)) return false; CBufferDouble *temp=FF_Weights.At(i*(optimization==SGD ? 6 : 9)+2); temp.BufferFree(); temp=FF_Tensors.At(i*6+1); temp.BufferFree(); temp=FF_Tensors.At(i*6+3); if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i*(optimization==SGD ? 6 : 9)+1),FF_Tensors.At(i*6+4),FF_Tensors.At(i*6),temp,iWindow,4*iWindow,LReLU)) return false;
Berechnen wir zu Beginn der Schleife die Fehlergradientenfortpflanzung durch die vollständig verbundenen Schichten von Neuronen des Feed-Forward-Blocks des Transformers. Diese Iteration wird von der Methode ConvolutionInputGradients durchgeführt. Geben Sie die Puffer nach Beendigung der Methode frei.
Da unser Algorithmus den Datenfluss durch den gesamten Prozess implementiert, sollte der gleiche Prozess für den Fehlergradienten implementiert werden. Der vom Feed-Forward-Block erhaltene Fehlergradient wird also mit dem von der vorherigen Schicht von Neuronen erhaltenen Fehlergradienten aufsummiert. Um das Risiko eines "explodierenden Gradienten" zu eliminieren, normalisieren Sie die Summe der beiden Vektoren. Alle diese Operationen werden in der Methode SumAndNormilize durchgeführt. Geben Sie die Puffer nach Beendigung der Methode frei.
//--- Sum and normalize gradients if(IsStopped() || !SumAndNormilize(out_grad,temp,temp)) return false; if(i!=(int)iLayers-1) out_grad.BufferFree(); out_grad=temp; temp=FF_Weights.At(i*(optimization==SGD ? 6 : 9)+1); temp.BufferFree(); temp=FF_Tensors.At(i*6+4); temp.BufferFree(); temp=FF_Tensors.At(i*6); temp.BufferFree();
Im weiteren Verlauf des Algorithmus wollen wir den Fehlergradienten durch die Attention-Heads teilen. Dies geschieht durch den Aufruf der Methode ConvolutionInputGradients für die W0-Matrix.
//--- Split gradient to multi-heads if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i*(optimization==SGD ? 6 : 9)),out_grad,AO_Tensors.At(i*2),AO_Tensors.At(i*2+1),iWindowKey*iHeads,iWindow,None)) return false; temp=FF_Weights.At(i*(optimization==SGD ? 6 : 9)); temp.BufferFree(); temp=AO_Tensors.At(i*2); temp.BufferFree();
Die weitere Gradientenausbreitung entlang der Attention-Heads wird in der Methode AttentionInsideGradients organisiert.
if(IsStopped() || !AttentionInsideGradients(QKV_Tensors.At(i*2),QKV_Tensors.At(i*2+1),S_Tensors.At(i*2),S_Tensors.At(i*2+1),AO_Tensors.At(i*2+1))) return false; temp=QKV_Tensors.At(i*2); temp.BufferFree(); temp=S_Tensors.At(i*2); temp.BufferFree(); temp=S_Tensors.At(i*2+1); temp.BufferFree(); temp=AO_Tensors.At(i*2+1); temp.BufferFree();
Am Ende der Schleife berechnen wir den Fehlergradienten, der an die vorherige Schicht übergeben wurde. Hier wird der von der vorherigen Iteration erhaltene Fehlergradient durch den verketteten Tensor QKV_Weights geleitet, und dann wird der erhaltene Vektor mit dem Fehlergradienten aus dem Feed-Forward-Block des Selbstbeobachtungsmechanismus summiert und das Ergebnis normalisiert, um explodierende Gradienten zu eliminieren.
CBufferDouble *inp=NULL; if(i==0) { inp=prevLayer.getOutput(); temp=prevLayer.getGradient(); } else { temp=FF_Tensors.At(i*6-1); inp=FF_Tensors.At(i*6-4); } if(IsStopped() || !ConvolutionInputGradients(QKV_Weights.At(i*(optimization==SGD ? 2 : 3)),QKV_Tensors.At(i*2+1),inp,temp,iWindow,3*iWindowKey*iHeads,None)) return false; //--- Sum and normalize gradients if(IsStopped() || !SumAndNormilize(out_grad,temp,temp)) return false; out_grad.BufferFree(); if(i>0) out_grad=temp; temp=QKV_Weights.At(i*(optimization==SGD ? 2 : 3)); temp.BufferFree(); temp=QKV_Tensors.At(i*2+1); temp.BufferFree(); } //--- return true; }
Vergessen wir nicht, die verwendeten Datenpuffer wieder freizugeben, und, dass die Datenpuffer der vorherigen Schicht im GPU-Speicher belassen werden.
Lassen Sie uns einen Blick auf die aufgerufenen Methoden werfen. Wie man sehen kann, ist die am häufigsten aufgerufene Methode ConvolutionInputGradients, die auf einer ähnlichen Methode der Faltungsschicht basiert und für die aktuelle Aufgabe optimiert ist. Die Methode erhält als Parameter Zeiger auf Tensoren der Gewichte, des Gradienten der nächsten Schicht, der Ausgabedaten der vorhergehenden Schicht und des Tensors zur Speicherung des Iterationsergebnisses. Außerdem erhält die Methode als Parameter die Größe des Eingangs- und Ausgangsdatenfensters und die verwendete Aktivierungsfunktion.
bool CNeuronMLMHAttentionOCL::ConvolutionInputGradients(CBufferDouble *weights, CBufferDouble *gradient, CBufferDouble *inputs, CBufferDouble *inp_gradient, uint window, uint window_out, uint activ) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(weights)==POINTER_INVALID || CheckPointer(gradient)==POINTER_INVALID || CheckPointer(inputs)==POINTER_INVALID || CheckPointer(inp_gradient)==POINTER_INVALID) return false;
Am Anfang der Methode prüfen wir die Gültigkeit der erhaltenen Zeiger und legen die Datenpuffer im Speicher der GPU an.
if(!weights.BufferCreate(OpenCL)) return false; if(!gradient.BufferCreate(OpenCL)) return false; if(!inputs.BufferCreate(OpenCL)) return false; if(!inp_gradient.BufferCreate(OpenCL)) return false;
Nach dem Anlegen von Datenpuffern implementieren wir den Aufruf des entsprechenden OpenCL-Programmkerns. Hier verwenden wir einen Convolutional-Netzwerk-Kernel ohne Änderungen.
//--- uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=inputs.Total(); OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv,def_k_chgc_matrix_w,weights.GetIndex()); OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv,def_k_chgc_matrix_g,gradient.GetIndex()); OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv,def_k_chgc_matrix_o,inputs.GetIndex()); OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv,def_k_chgc_matrix_ig,inp_gradient.GetIndex()); OpenCL.SetArgument(def_k_CalcHiddenGradientConv,def_k_chgc_outputs,gradient.Total()); OpenCL.SetArgument(def_k_CalcHiddenGradientConv,def_k_chgc_step,window); OpenCL.SetArgument(def_k_CalcHiddenGradientConv,def_k_chgc_window_in,window); OpenCL.SetArgument(def_k_CalcHiddenGradientConv,def_k_chgc_window_out,window_out); OpenCL.SetArgument(def_k_CalcHiddenGradientConv,def_k_chgc_activation,activ); //Comment(com+"\n "+(string)__LINE__+"-"__FUNCTION__); if(!OpenCL.Execute(def_k_CalcHiddenGradientConv,1,global_work_offset,global_work_size)) { printf("Error of execution kernel CalcHiddenGradientConv: %d",GetLastError()); return false; } //--- return inp_gradient.BufferRead(); }
Die Methode AttentionInsideGradients, die ebenfalls von der Methode ConvolutionInputGradients aufgerufen wird, ist nach einem ähnlichen Algorithmus aufgebaut. Den Code der Methode entnehmen Sie bitte dem Anhang. Werfen wir nun einen Blick auf den OpenCL-Programmkern, der von der angegebenen Methode aufgerufen wird, da alle Berechnungen im Kernel durchgeführt werden.
Der MHAttentionInsideGradients-Kernel wird von Threads in zwei Dimensionen gestartet: Elemente der Sequenz und Attention-Heads. Der Kernel erhält in Parametern Zeiger auf den verketteten QKV-Tensor und den Tensor seiner Gradienten, den Scores-Matrix-Tensor und seine Gradienten, den Fehlergradiententensor aus der vorherigen Iteration und die Größe des Schlüsselvektors.
__kernel void MHAttentionInsideGradients(__global double *qkv,__global double *qkv_g, __global double *scores,__global double *scores_g, __global double *gradient, int dimension) { int u=get_global_id(0); int h=get_global_id(1); int units=get_global_size(0); int heads=get_global_size(1); double koef=sqrt((double)dimension); if(koef<1) koef=1;
Zu Beginn der Methode erhalten wir die Ordnungszahlen des bearbeiteten Sequenzelements und des Attention-Heads sowie deren Größe. Außerdem berechnen wir den Aktualisierungskoeffizienten der Scores-Matrix.
Dann organisieren wir eine Schleife zur Berechnung des Fehlergradienten für die Scores-Matrix. Durch das Setzen einer Barriere nach der Schleife können wir den Berechnungsprozess über alle Threads hinweg synchronisieren. Der Algorithmus wechselt erst nach der vollständigen Neuberechnung der Gradienten der Scores-Matrix zum nächsten Block von Operationen.
//--- Calculating score's gradients uint shift_s=units*(h+u*heads); for(int v=0;v<units;v++) { double s=scores[shift_s+v]; if(s>0) { double sg=0; int shift_v=dimension*(h+heads*(3*v+2)); int shift_g=dimension*(h+heads*v); for(int d=0;d<dimension;d++) sg+=qkv[shift_v+d]*gradient[shift_g+d]; scores_g[shift_s+v]=sg*(s<1 ? s*(1-s) : 1)/koef; } else scores_g[shift_s+v]=0; } barrier(CLK_GLOBAL_MEM_FENCE);
Implementieren wir eine weitere Schleife, um die Fehlergradienten für die Abfragen, Schlüssel- und Wertvektoren zu berechnen.
//--- Calculating gradients for Query, Key and Value uint shift_qg=dimension*(h+3*u*heads); uint shift_kg=dimension*(h+(3*u+1)*heads); uint shift_vg=dimension*(h+(3*u+2)*heads); for(int d=0;d<dimension;d++) { double vg=0; double qg=0; double kg=0; for(int l=0;l<units;l++) { uint shift_q=dimension*(h+3*l*heads)+d; uint shift_k=dimension*(h+(3*l+1)*heads)+d; uint shift_g=dimension*(h+heads*l)+d; double sg=scores_g[shift_s+l]; kg+=sg*qkv[shift_q]; qg+=sg*qkv[shift_k]; vg+=gradient[shift_g]*scores[shift_s+l]; } qkv_g[shift_qg+d]=qg; qkv_g[shift_kg+d]=kg; qkv_g[shift_vg+d]=vg; } }
Der vollständige Code aller Methoden und Funktionen steht im Anhang zur Verfügung.
Die Gewichte werden in der Methode updateInputWeights aktualisiert, die nach den Prinzipien der zuvor besprochenen Methoden feedForward und calcInputGradients aufgebaut ist. Nur die eine Hilfsmethode ConvolutuionUpdateWeights, die die Gewichte des Convolutional-Netzwerks aktualisiert, wird innerhalb dieser Methode sequentiell aufgerufen.
bool CNeuronMLMHAttentionOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL)==POINTER_INVALID) return false; CBufferDouble *inputs=NeuronOCL.getOutput(); for(uint l=0; l<iLayers; l++) { if(IsStopped() || !ConvolutuionUpdateWeights(QKV_Weights.At(l*(optimization==SGD ? 2 : 3)),QKV_Tensors.At(l*2+1),inputs,(optimization==SGD ? QKV_Weights.At(l*2+1) : QKV_Weights.At(l*3+1)),(optimization==SGD ? NULL : QKV_Weights.At(l*3+2)),iWindow,3*iWindowKey*iHeads)) return false; if(l>0) inputs.BufferFree(); CBufferDouble *temp=QKV_Weights.At(l*(optimization==SGD ? 2 : 3)); temp.BufferFree(); temp=QKV_Tensors.At(l*2+1); temp.BufferFree(); if(optimization==SGD) { temp=QKV_Weights.At(l*2+1); } else { temp=QKV_Weights.At(l*3+1); temp.BufferFree(); temp=QKV_Weights.At(l*3+2); temp.BufferFree(); } //--- if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l*(optimization==SGD ? 6 : 9)),FF_Tensors.At(l*6+3),AO_Tensors.At(l*2),(optimization==SGD ? FF_Weights.At(l*6+3) : FF_Weights.At(l*9+3)),(optimization==SGD ? NULL : FF_Weights.At(l*9+6)),iWindowKey*iHeads,iWindow)) return false; temp=FF_Weights.At(l*(optimization==SGD ? 6 : 9)); temp.BufferFree(); temp=FF_Tensors.At(l*6+3); temp.BufferFree(); temp=AO_Tensors.At(l*2); temp.BufferFree(); if(optimization==SGD) { temp=FF_Weights.At(l*6+3); temp.BufferFree(); } else { temp=FF_Weights.At(l*9+3); temp.BufferFree(); temp=FF_Weights.At(l*9+6); temp.BufferFree(); } //--- if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l*(optimization==SGD ? 6 : 9)+1),FF_Tensors.At(l*6+4),FF_Tensors.At(l*6),(optimization==SGD ? FF_Weights.At(l*6+4) : FF_Weights.At(l*9+4)),(optimization==SGD ? NULL : FF_Weights.At(l*9+7)),iWindow,4*iWindow)) return false; temp=FF_Weights.At(l*(optimization==SGD ? 6 : 9)+1); temp.BufferFree(); temp=FF_Tensors.At(l*6+4); temp.BufferFree(); temp=FF_Tensors.At(l*6); temp.BufferFree(); if(optimization==SGD) { temp=FF_Weights.At(l*6+4); temp.BufferFree(); } else { temp=FF_Weights.At(l*9+4); temp.BufferFree(); temp=FF_Weights.At(l*9+7); temp.BufferFree(); } //--- if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l*(optimization==SGD ? 6 : 9)+2),FF_Tensors.At(l*6+5),FF_Tensors.At(l*6+1),(optimization==SGD ? FF_Weights.At(l*6+5) : FF_Weights.At(l*9+5)),(optimization==SGD ? NULL : FF_Weights.At(l*9+8)),4*iWindow,iWindow)) return false; temp=FF_Weights.At(l*(optimization==SGD ? 6 : 9)+2); temp.BufferFree(); temp=FF_Tensors.At(l*6+5); if(temp!=Gradient) temp.BufferFree(); temp=FF_Tensors.At(l*6+1); temp.BufferFree(); if(optimization==SGD) { temp=FF_Weights.At(l*6+5); temp.BufferFree(); } else { temp=FF_Weights.At(l*9+5); temp.BufferFree(); temp=FF_Weights.At(l*9+8); temp.BufferFree(); } inputs=FF_Tensors.At(l*6+2); } //--- return true; }
Der gesamte Code aller Klassen und Methoden befindet sich in der Anlage.
3.4. Änderungen in den Basisklassen des neuronalen Netzwerks
Wie in allen vorherigen Artikeln nehmen wir nach dem Erstellen einer neuen Klasse Änderungen in der Basisklasse vor, um den ordnungsgemäßen Betrieb unseres Netzwerks sicherzustellen.
Fügen wir einen neuen Klassenbezeichner hinzu.
#define defNeuronMLMHAttentionOCL 0x7889 ///<Multilayer multi-headed attention neuron OpenCL \details Identified class #CNeuronMLMHAttentionOCL
Außerdem fügen wir im Block für die Definitionen Konstanten für die Arbeit mit den neuen Kerneln des OpenCL-Programms hinzu.
#define def_k_MHAttentionScore 20 ///< Index of the kernel of the multi-heads attention neuron to calculate score matrix (#MHAttentionScore) #define def_k_mhas_qkv 0 ///< Matrix of Queries, Keys, Values #define def_k_mhas_score 1 ///< Matrix of Scores #define def_k_mhas_dimension 2 ///< Dimension of Key #define def_k_mhas_mask 3 ///< 1 - calc only previous units, 0 - calc all //--- #define def_k_MHAttentionOut 21 ///< Index of the kernel of the multi-heads attention neuron to calculate multi-heads out matrix (#MHAttentionOut) #define def_k_mhao_score 0 ///< Matrix of Scores #define def_k_mhao_qkv 1 ///< Matrix of Queries, Keys, Values #define def_k_mhao_out 2 ///< Matrix of Outputs #define def_k_mhao_dimension 3 ///< Dimension of Key //--- #define def_k_MHAttentionGradients 22 ///< Index of the kernel for gradients calculation process (#AttentionInsideGradients) #define def_k_mhag_qkv 0 ///< Matrix of Queries, Keys, Values #define def_k_mhag_qkv_g 1 ///< Matrix of Gradients to Queries, Keys, Values #define def_k_mhag_score 2 ///< Matrix of Scores #define def_k_mhag_score_g 3 ///< Matrix of Scores Gradients #define def_k_mhag_gradient 4 ///< Matrix of Gradients from previous iteration #define def_k_mhag_dimension 5 ///< Dimension of Key
Außerdem fügen wir die Deklaration neuer Kernel im Konstruktor der Klasse Neuronales Netzwerk hinzu
//--- create kernels opencl.SetKernelsCount(23); opencl.KernelCreate(def_k_FeedForward,"FeedForward"); opencl.KernelCreate(def_k_CalcOutputGradient,"CalcOutputGradient"); opencl.KernelCreate(def_k_CalcHiddenGradient,"CalcHiddenGradient"); opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum"); opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam"); opencl.KernelCreate(def_k_AttentionGradients,"AttentionInsideGradients"); opencl.KernelCreate(def_k_AttentionOut,"AttentionOut"); opencl.KernelCreate(def_k_AttentionScore,"AttentionScore"); opencl.KernelCreate(def_k_CalcHiddenGradientConv,"CalcHiddenGradientConv"); opencl.KernelCreate(def_k_CalcInputGradientProof,"CalcInputGradientProof"); opencl.KernelCreate(def_k_FeedForwardConv,"FeedForwardConv"); opencl.KernelCreate(def_k_FeedForwardProof,"FeedForwardProof"); opencl.KernelCreate(def_k_MatrixSum,"SumMatrix"); opencl.KernelCreate(def_k_Matrix5Sum,"Sum5Matrix"); opencl.KernelCreate(def_k_UpdateWeightsConvAdam,"UpdateWeightsConvAdam"); opencl.KernelCreate(def_k_UpdateWeightsConvMomentum,"UpdateWeightsConvMomentum"); opencl.KernelCreate(def_k_Normilize,"Normalize"); opencl.KernelCreate(def_k_NormilizeWeights,"NormalizeWeights"); opencl.KernelCreate(def_k_ConcatenateMatrix,"ConcatenateBuffers"); opencl.KernelCreate(def_k_DeconcatenateMatrix,"DeconcatenateBuffers"); opencl.KernelCreate(def_k_MHAttentionGradients,"MHAttentionInsideGradients"); opencl.KernelCreate(def_k_MHAttentionScore,"MHAttentionScore"); opencl.KernelCreate(def_k_MHAttentionOut,"MHAttentionOut");
und erstellen einen neuen Neuronentyp im Konstruktor des neuronalen Netzwerks.
case defNeuronMLMHAttentionOCL: neuron_mlattention_ocl=new CNeuronMLMHAttentionOCL(); if(CheckPointer(neuron_mlattention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_mlattention_ocl.Init(outputs,0,opencl,desc.window,desc.window_out,desc.step,desc.count,desc.layers,desc.optimization)) { delete neuron_mlattention_ocl; delete temp; return; } neuron_mlattention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_mlattention_ocl)) { delete neuron_mlattention_ocl; delete temp; return; } neuron_mlattention_ocl=NULL; break;
Wir werden auch die Verarbeitung der neuen Klasse von Neuronen zu den Dispatch-Methoden der Basisklasse von Neuronen CNeuronBaseOCL hinzufügen.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; } bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; CNeuronAttentionOCL *at=NULL; CNeuronMLMHAttentionOCL *mlat=NULL; CNeuronConvOCL *conv=NULL; switch(TargetObject.Type()) { case defNeuronBaseOCL: temp=TargetObject; return calcHiddenGradients(temp); break; case defNeuronConvOCL: conv=TargetObject; temp=GetPointer(this); return conv.calcInputGradients(temp); break; case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: at=TargetObject; temp=GetPointer(this); return at.calcInputGradients(temp); break; case defNeuronMLMHAttentionOCL: mlat=TargetObject; temp=GetPointer(this); return mlat.calcInputGradients(temp); break; } //--- return false; } bool CNeuronBaseOCL::UpdateInputWeights(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: temp=SourceObject; return updateInputWeights(temp); break; } //--- return false; }
Der gesamte Code aller Klassen und Methoden befindet sich in der Anlage.
4. Tests
Es wurden zwei Expert Advisors erstellt, um die neue Architektur zu testen: Fractal_OCL_AttentionMLMH und Fractal_OCL_AttentionMLMH_v2. Diese EAs wurden auf Basis des EAs aus dem vorherigen Artikel erstellt, lediglich der Attention-Block wurde ersetzt. Der Fractal_OCL_AttentionMLMH EA hat einen 5-Schicht-Block mit 8 Self-Attention-Heads. Der zweite EA verwendet einen 12-Schicht-Block mit 12 Heads für die Self-Attention.
Die neue Klasse des neuronalen Netzwerks wurde auf demselben Datensatz getestet, der in den vorherigen Tests verwendet wurde: EURUSD mit dem H1-Zeitrahmen, historische Daten der letzten 20 Candlesticks wurden in das neuronale Netz eingespeist.
Die Testergebnisse haben die Vermutung bestätigt, dass mehr Parameter eine längere Trainingsperiode erfordern. In den ersten Trainingsepochen zeigt ein Expert Advisor mit weniger Parametern stabilere Ergebnisse. Mit zunehmender Dauer des Trainings zeigt ein Expert Advisor mit einer großen Anzahl von Parametern jedoch bessere Werte. Im Allgemeinen sank der Fehler von Fractal_OCL_AttentionMLMH_v2 nach 33 Epochen unter das Fehlerniveau des Fractal_OCL_AttentionMLMH EA und blieb weiterhin niedrig.
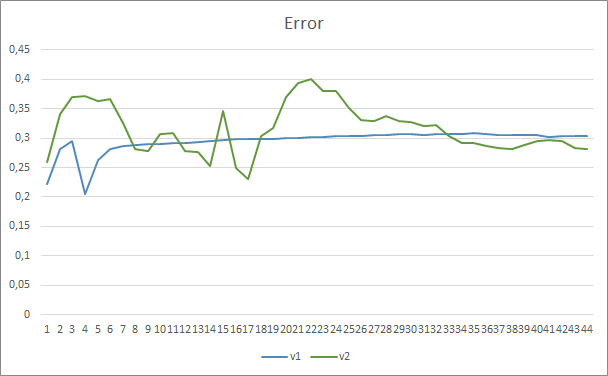
Der Parameter für verpasste Muster zeigte ähnliche Ergebnisse. Zu Beginn des Trainings verpassten die nicht abgestimmten Parameter von Fractal_OCL_AttentionMLMH_v2 mehr als 50 % der Muster. Im weiteren Verlauf des Trainings nahm dieser Wert jedoch ab und stabilisierte sich nach 27 Epochen bei 3-5 %, während der EA mit weniger Parametern glattere Ergebnisse zeigte, aber gleichzeitig 10-16 % der Muster verfehlte.
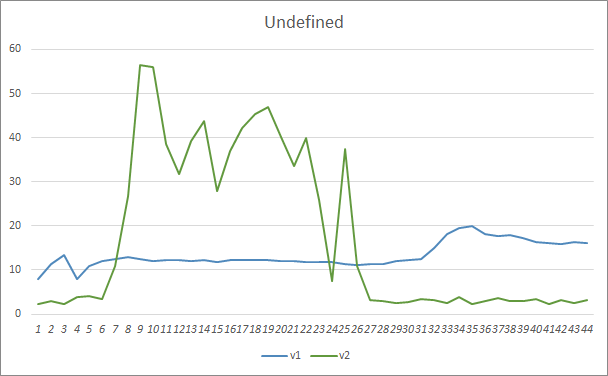
In Bezug auf die Genauigkeit der Mustervorhersage zeigten beide Expert Advisors gleichmäßige Ergebnisse auf dem Niveau von 22-23 %.
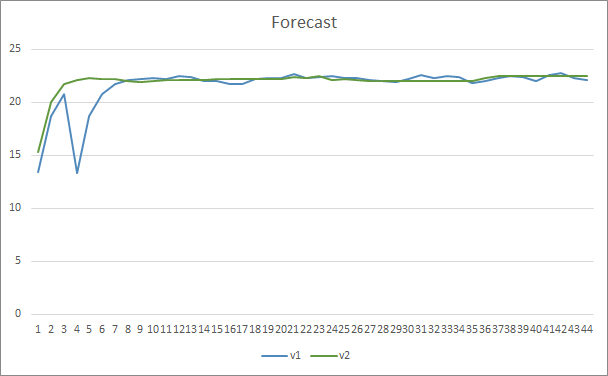
Schlussfolgerung
In diesem Artikel haben wir eine neue Klasse von Attention-Neuronen geschaffen, die den von OpenAI vorgestellten GPT-Architekturen ähneln. Natürlich ist es unmöglich, diese Architekturen in ihrer vollen Form zu wiederholen und zu trainieren, da ihr Training und Betrieb zeit- und ressourcenintensiv ist. Das von uns erstellte Objekt kann jedoch gut in neuronalen Netzen für die Erstellung von Handelsrobotern verwendet werden.
Referenzen
- Neuronale Netze leicht gemacht
- Neuronale Netze leicht gemacht (Teil 2): Netzwerktraining und Tests
- Neuronale Netze leicht gemacht (Teil 3): Convolutional Neurale Netzwerke
- Neuronale Netze leicht gemacht (Teil 4): Rekurrente Netze
- Neuronale Netze leicht gemacht (Teil 5): Parallele Berechnungen mit OpenCL
- Neuronale Netze leicht gemacht (Teil 6): Experimentieren mit der Lernrate des neuronalen Netzwerks
- Neuronale Netze leicht gemacht (Teil 7): Adaptive Optimierungsverfahren
- Neuronale Netze leicht gemacht (Teil 8): Attention-Mechanismen
- Neuronale Netze leicht gemacht (Teil 9): Dokumentation der Arbeit
- Neuronale Netze leicht gemacht (Teil 10): Multi-Head Attention
- Improving Language Understanding with Unsupervised Learning (Verbesserung des Sprachverständnisses durch unüberwachtes Lernen)
- Better Language Models and Their Implications (Bessere Sprachmodelle und ihre Implikationen)
- How GPT3 Works - Visualizations and Animations (Wie GPT3 arbeitet - Visualisierung und Animation)
…
Die Programme dieses Artikels
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Fractal_OCL_AttentionMLMH.mq5 | Expert Advisor | Ein Expert Advisor mit dem klassifizierenden neuronalen Netz (3 Neuronen in der Ausgabeschicht) unter Verwendung der GTP-Architektur, mit 5 Attention-Schichten |
| 2 | Fractal_OCL_AttentionMLMH_v2.mq5 | Expert Advisor | Ein Expert Advisor mit dem neuronalen Klassifikationsnetz (3 Neuronen in der Ausgabeschicht) unter Verwendung der GTP-Architektur, mit 12 Attention-Schichten |
| 3 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek mit Klassen zum Erstellen eines neuronalen Netzwerks |
| 4 | NeuroNet.cl | Bibliothek | Die Bibliothek mit dem Programm-Code für OpenCL |
| 5 | NN.chm | HTML Hilfe | Die kompilierte CHM-Datei. |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/9025
Nützliche und exotische Techniken für den automatisierten Handel
Preise in der DoEasy-Bibliothek (Teil 63): Markttiefe und deren abstrakte Anforderungsklasse
Der selbstanpassenden Algorithmus (Teil IV): Zusätzliche Funktionen und Tests
Preise in der DoEasy-Bibliothek (Teil 62): Aktualisieren der Tick-Serien in Echtzeit, Vorbereitung für die Arbeit mit Markttiefe
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.