Neuronale Netze im Handel: Verbesserung des Wirkungsgrads des Transformers durch Verringerung der Schärfe (SAMformer)

Einführung

Die multivariate Zeitreihenprognose ist eine klassische Aufgabe des maschinellen Lernens, bei der es darum geht, Zeitreihendaten zu analysieren, um zukünftige Trends auf der Grundlage historischer Muster vorherzusagen. Aufgrund von Merkmalskorrelationen und langfristigen zeitlichen Abhängigkeiten ist dies ein besonders schwieriges Problem. Dieses Lernproblem tritt häufig bei realen Anwendungen auf, bei denen Beobachtungen sequentiell gesammelt werden (z. B. medizinische Daten, Stromverbrauch, Aktienkurse).

In jüngster Zeit haben Transformer-basierte Architekturen bahnbrechende Leistungen bei der Verarbeitung natürlicher Sprache und bei Computer-Vision-Aufgaben erzielt. Transformer sind besonders effektiv bei der Arbeit mit sequentiellen Daten, was sie zu einer natürlichen Ergänzung für Zeitreihenprognosen macht. Multivariate Zeitreihenprognosen auf dem neuesten Stand der Technik werden jedoch häufig noch mit einfacheren MLP-basierten Modellen erstellt.

Neuere Studien zur Anwendung von Transformers auf Zeitreihendaten haben sich in erster Linie auf die Optimierung von Aufmerksamkeitsmechanismen konzentriert, um quadratische Rechenkosten zu reduzieren, oder auf die Zerlegung von Zeitreihen, um die zugrunde liegenden Muster besser zu erfassen. Allerdings haben die Autoren des Artikels „SAMformer: Unlocking the Potential of Transformers in Time Series Forecasting with Sharpness-Aware Minimization and Channel-Wise Attention“ heben ein kritisches Problem hervor: die Trainingsinstabilität von Transformers in Ermangelung großer Datenmengen.

Sowohl in der Computer Vision als auch im NLP wurde beobachtet, dass Aufmerksamkeitsmatrizen unter einem Kollaps von Entropie oder Rang leiden können. Es wurden mehrere Ansätze vorgeschlagen, um diese Probleme zu entschärfen. Bei der Vorhersage von Zeitreihen bleibt jedoch die Frage offen, wie Transformer-Architekturen effektiv und ohne Überanpassung trainiert werden können. Die Autoren wollen zeigen, dass die Behebung von Trainingsinstabilitäten die Leistung von Transformer bei der langfristigen multivariaten Vorhersage erheblich verbessern kann, im Gegensatz zu den bisherigen Vorstellungen über ihre Grenzen.

1. Der Algorithmus von SAMformer

Der Schwerpunkt liegt auf der Langzeitprognose in einem multivariaten System bei einer D-dimensionalen Zeitreihe der Länge L (dem Rückblickfenster). Die Eingabedaten werden als eine Matrix 𝐗 ∈ RD×L dargestellt. Das Ziel ist die Vorhersage der nächsten H-Werte (der Prognosehorizont), bezeichnet als 𝐘 ∈ RD×H. Ausgehend von einem Trainingssatz, der aus N Beobachtungen besteht, besteht das Ziel darin, ein Prognosemodell f𝝎: RD×L→RD×L mit den Parametern 𝝎, die den mittleren quadratischen Fehler (MSE) auf den Trainingsdaten minimiert.

Jüngste Ergebnisse zeigen, dass Transformer genauso gut abschneiden wie einfache lineare neuronale Netze, die darauf trainiert sind, Eingangsdaten direkt in Prognosewerte zu projizieren. Um dieses Phänomen zu untersuchen, verwendet SAMformer ein generatives Modell, das eine synthetische Regressionsaufgabe simuliert, die die Zeitreihenprognose nachahmt. Die Autoren verwenden ein lineares Modell, um aus zufälligen Eingabedaten Zeitserienfortsetzungen zu generieren, und fügen der Ausgabe eine kleine Menge Rauschen hinzu. Auf diese Weise entstanden 15.000 Input-Output-Paare, die in 10.000 für das Training und 5.000 für die Validierung aufgeteilt wurden.

Auf der Grundlage dieses generativen Ansatzes haben die Autoren von SAMformer eine Transformer-Architektur entwickelt, die in der Lage ist, die Vorhersageaufgabe effizient und ohne unnötige Komplexität zu bewältigen. Um dies zu erreichen, vereinfachten sie den konventionellen Transformer-Encoder, indem sie nur den Selbstaufmerksamkeits-Block, gefolgt von einer Residualverbindung, beibehalten. Anstelle eines FeedForward-Blocks wird direkt eine lineare Schicht für die Vorhersage der nachfolgenden Werte verwendet.

Es ist wichtig anzumerken, dass der SAMformer kanalweise Aufmerksamkeit verwendet, was die Aufgabe vereinfacht und das Risiko einer Überparametrisierung verringert, da die Aufmerksamkeitsmatrix aufgrund von L>D deutlich kleiner wird. Außerdem ist die kanalbezogene Aufmerksamkeit in diesem Fall besser geeignet, da die Datengenerierung einem Identifikationsprozess folgt.

Um die Rolle der Aufmerksamkeit bei der Lösung dieser Aufgabe zu verstehen, schlagen die Autoren ein Modell namens Random Transformer vor. Bei diesem Modell wird nur die Vorhersageschicht optimiert, während die Parameter des Selbstaufmerksamkeitsblocks während des Trainings zufällig initialisiert werden. Dadurch wird der Transformer gezwungen, sich wie ein lineares Modell zu verhalten. Ein Vergleich der mit diesen beiden Modellen erzielten lokalen Minima, die mit der Adam-Methode optimiert wurden, mit einem Oracle-Modell (das der Lösung der kleinsten Quadrate entspricht) ist in der nachstehenden Abbildung dargestellt (wie im Originalartikel).

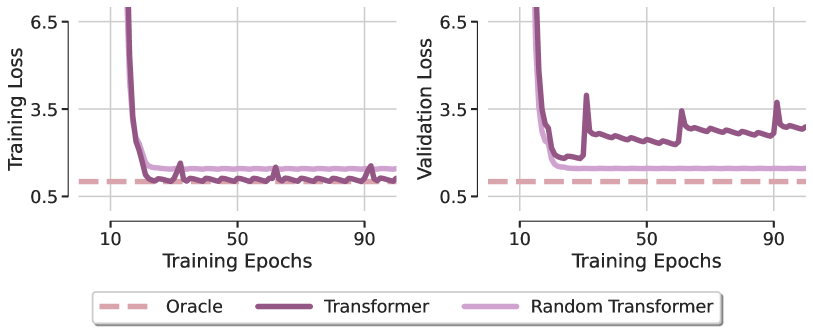
Die erste überraschende Erkenntnis ist, dass keines der beiden Transformer-Modelle in der Lage ist, die lineare Abhängigkeit der synthetischen Regressionsaufgabe wiederherzustellen, was deutlich macht, dass die Optimierung selbst bei einer so einfachen Architektur mit günstigem Design einen klaren Mangel an Generalisierung aufweist. Diese Beobachtung gilt für verschiedene Optimierer und Lernrateneinstellungen. Daraus schließen die Autoren von SAMformer, dass die begrenzten Generalisierungsfähigkeiten von Transformers in erster Linie auf Trainingsschwierigkeiten innerhalb des Aufmerksamkeitsmoduls zurückzuführen sind.

Um dieses Phänomen besser zu verstehen, visualisierten die Autoren von SAMformer die Aufmerksamkeitsmatrizen zu verschiedenen Trainingsepochen und stellten fest, dass die Aufmerksamkeitsmatrix unmittelbar nach der ersten Epoche einer Identitätsmatrix ähnelte und sich danach nur noch wenig veränderte, insbesondere da die Softmax-Funktion die Unterschiede zwischen den Aufmerksamkeitswerten verstärkte. Dieses Verhalten zeigt den Beginn eines Entropie-Kollapses in der Aufmerksamkeit, der zu einer vollwertigen Aufmerksamkeitsmatrix führt, die die Autoren als eine der Ursachen für die Trainingsstarrheit des Transformers identifizieren.

Die Autoren von SAMformer beobachteten auch eine Beziehung zwischen dem Entropie-Kollaps und der Schärfe der Verlustlandschaft des Transformers. Im Vergleich zum Zufalls-Transformer konvergiert der Standard-Transformer zu einem schärferen Minimum und weist eine deutlich geringere Entropie auf (da die Aufmerksamkeitsgewichte im Zufalls-Transformer bei der Initialisierung festgelegt werden, bleibt seine Entropie während des gesamten Trainings konstant). Diese pathologischen Muster deuten darauf hin, dass Transformer aufgrund des doppelten Effekts eines Entropiekollapses und scharfer Verlustlandschaften während des Trainings unterdurchschnittlich abschneiden.

Jüngste Studien haben bestätigt, dass die Verlustlandschaft von Transformers tatsächlich schärfer ist als die anderer Architekturen. Dies könnte eine Erklärung für die Instabilität beim Training und die geringere Leistung von Transformers sein, insbesondere wenn es auf kleineren Datensätzen trainiert wird.

Um diese Herausforderungen zu bewältigen und die Generalisierung und Trainingsstabilität zu verbessern, verfolgen die Autoren von SAMformer zwei Ansätze. Bei der ersten handelt es sich um die schärfebewusste Minimierung (Sharpness-Aware Minimization, SAM), bei der das Trainingsziel wie folgt geändert wird:

wobei ρ>0 ein Hyperparameter ist und 𝝎 die Modellparameter darstellt.

Der zweite Ansatz führt eine Neuparametrisierung aller Gewichtsmatrizen durch spektrale Normalisierung zusammen mit einem zusätzlichen trainierbaren Skalar, bekannt als σReparam, ein.

Die Ergebnisse zeigen, dass die vorgeschlagene Lösung das gewünschte Ziel erreicht hat. Bemerkenswerterweise gelingt dies allein mit SAM, da die Methode σReparam trotz Erhöhung der Entropie der Aufmerksamkeitsmatrix nicht annähernd optimale Ergebnisse erzielt. Darüber hinaus ist die mit SAM erreichte Schärfe um mehrere Größenordnungen geringer als die eines Standard-Transformers, während die Aufmerksamkeitsentropie unter SAM mit der des Basis-Transformers vergleichbar bleibt, mit nur einem bescheidenen Anstieg in den späteren Phasen des Trainings. Dies zeigt, dass der Entropiekollaps in diesem Szenario harmlos ist.

Das SAMformer-Framework umfasst außerdem die Reversible Instance Normalization (RevIN). Diese Methode hat sich bei der Behandlung von Verteilungsverschiebungen zwischen Trainings- und Testdaten in Zeitreihen bewährt. Wie die obige Untersuchung zeigt, wird das Modell mithilfe von SAM optimiert, wobei es auf flachere lokale Minima ausgerichtet wird. Insgesamt ergibt sich daraus ein vereinfachtes Transformermodell mit einem einzigen Encoder-Block, wie in der folgenden Abbildung dargestellt (Originalvisualisierung der Autoren).

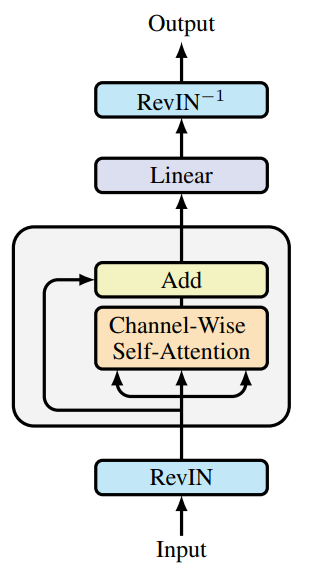
Es ist wichtig zu betonen, dass SAMformer die kanalweise Aufmerksamkeit beibehält, die durch eine D×D-Matrix dargestellt wird, im Gegensatz zur räumlichen (oder zeitlichen) Aufmerksamkeit, die sich in anderen Modellen typischerweise auf eine L×L-Matrix stützt. Diese Konstruktion bietet zwei entscheidende Vorteile:

• Permutationsinvarianz der Merkmale, wodurch die Notwendigkeit einer Positionskodierung entfällt, die normalerweise vor der Aufmerksamkeitsschicht angewendet wird;
• Geringere Rechenzeit und Speicherkomplexität, da D≤L in den meisten realen Datensätzen.

Die kanalweise Aufmerksamkeit lernt den durchschnittlichen Einfluss jedes Merkmals auf die anderen über alle Zeitschritte hinweg.

2. Die Implementation in MQL5

Nachdem wir uns mit den theoretischen Aspekten des Rahmens von SAMformer beschäftigt haben, gehen wir nun zu seiner praktischen Umsetzung mit MQL5 über. An diesem Punkt ist es wichtig, genau zu definieren, was wir in unseren Modellen umsetzen wollen und wie. Schauen wir uns die von den Autoren von SAMformer vorgeschlagenen Komponenten genauer an:

• Trimmen des Transformer-Encoders bis zum Selbstaufmerksamkeits-Block mit einer Restverbindung;
• Kanalbezogene Aufmerksamkeit;
• Umkehrbare Normalisierung (RevIN);
• SAM-Optimierung.

Ein interessanter Aspekt ist das Trimmen des Encoders. In der Praxis liegt der Hauptwert jedoch in der Reduzierung der Anzahl der trainierbaren Parameter. Das Verhalten des Modells wird nicht davon beeinflusst, ob wir die neuronalen Schichten als Teil des FeedForward-Blocks des Encoders oder als Vorhersageschicht nach der Aufmerksamkeit bezeichnen, wie es im ursprünglichen Rahmen geschieht.

Um die kanalweise Aufmerksamkeit zu implementieren, genügt es, die Eingangsdaten zu transponieren, bevor sie in den Aufmerksamkeitsblock eingespeist werden. Dieser Schritt erfordert keine strukturellen Änderungen des Modells.

Wir sind bereits vertraut mit der Reversiblen Instanznormalisierung (RevIN). Die verbleibende Aufgabe ist die Implementierung der SAM-Optimierung, die nach Parametersätzen sucht, die in Nachbarschaften mit gleichmäßig niedrigen Verlustwerten liegen.

Der SAM-Optimierungsalgorithmus umfasst mehrere Schritte. Zunächst wird ein Vorwärtsdurchlauf durchgeführt, um die Verlustgradienten in Bezug auf die Modellparameter zu ermitteln. Diese Gradienten werden dann normalisiert und zu den aktuellen Parametern addiert und mit einem Schärfekoeffizienten skaliert. Ein zweiter Vorwärtsdurchlauf wird mit diesen verzerrten Parametern durchgeführt, und die neuen Gradienten werden berechnet. Anschließend werden die ursprünglichen Gewichte wiederhergestellt, indem die zuvor hinzugefügte Störung abgezogen wird. Und schließlich aktualisieren wir die Parameter mit einem Standardoptimierer - SGD oder Adam. Die Autoren von SAMformer empfehlen Letzteren.

Ein wichtiges Detail ist, dass die Autoren von SAMformer die Gradienten für das gesamte Modell normalisieren. Dies kann sehr rechenintensiv sein. Daher ist es wichtig, die Anzahl der Modellparameter zu reduzieren. Infolgedessen wird es zu einer praktischen Notwendigkeit, die internen Schichten zu reduzieren und die Anzahl der Aufmerksamkeitsköpfe zu verringern. Das haben die Autoren von SAMformer getan.

In unserer Implementierung weichen wir jedoch leicht davon ab: Wir führen die Gradienten-Normalisierung auf der Ebene der einzelnen neuronalen Schichten durch. Außerdem normalisieren wir die Gradienten separat für jede Parametergruppe, die zur Ausgabe eines einzelnen Neurons beiträgt. Wir beginnen diese Implementierung mit der Entwicklung neuer Kernel auf der Seite von OpenCL des Programms.

2.1 Erweitern des OpenCL-Programms

Wie Sie vielleicht aus unserer bisherigen Arbeit wissen, verwenden wir hauptsächlich zwei Arten von neuronalen Schichten: voll verknüpfte Schichten und Faltungsschichten. Alle unsere Aufmerksamkeitsmodule sind aus Faltungsschichten aufgebaut, die ohne Überlappung angewendet werden, um einzelne Elemente in der Sequenz zu analysieren und zu transformieren. Daher haben wir uns entschieden, diese beiden Schichttypen durch SAM-Optimierung zu verbessern. Auf der Seite von OpenCL erstellen wir Kernel zur Normalisierung des Fehlergradienten und zur Erstellung der verzerrten Gewichtungskoeffizienten ω+ε.

Wir beginnen mit der Erstellung eines Kerns für die vollständig verbundene Schicht CalcEpsilonWeights. Dieser Kernel erhält Zeiger auf vier Datenpuffer und einen Schärfe-Dispersions-Koeffizienten. Drei Puffer nehmen die Eingangsdaten auf, während der vierte für die Speicherung der Ausgangsergebnisse vorgesehen ist. 

__kernel void CalcEpsilonWeights(__global const float *matrix_w,
                                 __global const float *matrix_g,
                                 __global const float *matrix_i,
                                 __global float *matrix_epsw,
                                 const float rho
                                )
  {
   const size_t inp = get_local_id(0);
   const size_t inputs = get_local_size(0) - 1;
   const size_t out = get_global_id(1);

Wir planen, diesen Kernel in einem zweidimensionalen Aufgabenraum aufzurufen und die Threads nach der ersten Dimension zu gruppieren. Innerhalb des Kernelkörpers identifizieren wir sofort den aktuellen Ausführungsthread in allen Dimensionen des Aufgabenraums.

Als Nächstes deklarieren wir ein lokales Speicherarray auf dem Gerät, um den Datenaustausch zwischen Threads innerhalb derselben Arbeitsgruppe zu erleichtern.

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((int)inputs, (int)LOCAL_ARRAY_SIZE);

Im folgenden Schritt berechnen wir den Gradienten des Fehlers für jedes analysierte Element als Produkt der entsprechenden Elemente in den Eingangs- und Ausgangsgradientenpuffern. Wir skalieren dieses Ergebnis dann mit dem absoluten Wert des zugehörigen Parameters. Dadurch wird der Einfluss von Parametern erhöht, die einen größeren Beitrag zum Ergebnis der Ebene leisten.

   const int shift_w = out * (inputs + 1) + inp;
   const float w =IsNaNOrInf(matrix_w[shift_w],0);
   float grad = fabs(w) * IsNaNOrInf(matrix_g[out],0) * (inputs == inp ? 1.0f : IsNaNOrInf(matrix_i[inp],0));

Schließlich berechnen wir die L2-Norm der resultierenden Gradienten. Dabei werden die Quadrate der berechneten Werte innerhalb der Arbeitsgruppe summiert, wobei das lokale Speicherarray und zwei Reduktionsschleifen verwendet werden, wie dies auch in unseren früheren Implementierungen der Fall war.

   const int local_shift = inp % ls;
   for(int i = 0; i <= inputs; i += ls)
     {
      if(i <= inp && inp < (i + ls))
         temp[local_shift] = (i == 0 ? 0 : temp[local_shift]) + IsNaNOrInf(grad * grad,0);
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   int count = ls;
   do
     {
      count = (count + 1) / 2;
      if(inp < count)
         temp[inp] += ((inp + count) < inputs ? IsNaNOrInf(temp[inp + count],0) : 0);
      if(inp + count < inputs)
         temp[inp + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Die Quadratwurzel der akkumulierten Summe stellt die L2-Norm der Gradienten dar. Mit diesem Wert berechnen wir den angepassten Parameterwert.

   float norm = sqrt(IsNaNOrInf(temp[0],0));
   float epsw = IsNaNOrInf(w * w * grad * rho / (norm + 1.2e-7), w);
//---
   matrix_epsw[shift_w] = epsw;
  }

Anschließend speichern wir den resultierenden Wert im entsprechenden Element des globalen Ergebnispuffers.

Ein ähnlicher Ansatz wird verwendet, um den CalcEpsilonWeightsConv-Kernel zu konstruieren, der die anfängliche Parameteranpassung für Faltungsschichten durchführt. Wie Sie jedoch wissen, haben Faltungsschichten ihre eigenen Merkmale. Sie enthalten in der Regel weniger Parameter, aber jeder Parameter interagiert mit mehreren Elementen der Eingabedatenschicht und trägt zu den Werten mehrerer Elemente im Ergebnispuffer bei. Folglich wird der Gradient für jeden Parameter durch Aggregation seines Einflusses aus mehreren Elementen des Ausgabepuffers berechnet.

Dieses faltungsspezifische Verhalten wirkt sich auch auf die Kernelparameter aus. Hier erscheinen zwei zusätzliche Konstanten, die die Größe der Eingabesequenz und die Schrittweite des Eingabefensters definieren.

__kernel void CalcEpsilonWeightsConv(__global const float *matrix_w,
                                     __global const float *matrix_g,
                                     __global const float *matrix_i,
                                     __global float *matrix_epsw,
                                     const int inputs,
                                     const float rho,
                                     const int step
                                    )
  {
//---
   const size_t inp = get_local_id(0);
   const size_t window_in = get_local_size(0) - 1;
   const size_t out = get_global_id(1);
   const size_t window_out = get_global_size(1);
   const size_t v = get_global_id(2);
   const size_t variables = get_global_size(2);

Außerdem erweitern wir den Aufgabenraum auf drei Dimensionen. Die erste Dimension entspricht dem Eingangsdatenfenster, das um einen Offset erweitert wird. Die zweite Dimension stellt die Anzahl der Faltungsfilter dar. Die dritte Dimension gibt die Anzahl der unabhängigen Eingangssequenzen an. Wie zuvor gruppieren wir die Arbeitsgänge nach der ersten Dimension in Arbeitsgruppen.

Innerhalb des Kernels identifizieren wir den aktuellen Ausführungsthread über alle Task-Raum-Dimensionen hinweg. Anschließend wird ein lokales Speicherarray im OpenCL-Kontext initialisiert, um die Inter-Thread-Kommunikation innerhalb der Arbeitsgruppe zu erleichtern.

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((int)(window_in + 1), (int)LOCAL_ARRAY_SIZE);

Als Nächstes berechnen wir die Anzahl der Elemente pro Filter im Ausgangspuffer und bestimmen die entsprechenden Offsets in den Datenpuffern.

   const int shift_w = (out + v * window_out) * (window_in + 1) + inp;
   const int total = (inputs - window_in + step - 1) / step;
   const int shift_out = v * total * window_out + out;
   const int shift_in = v * inputs + inp;
   const float w = IsNaNOrInf(matrix_w[shift_w], 0);

An dieser Stelle speichern wir auch den aktuellen Wert des zu analysierenden Parameters in einer lokalen Variablen. Diese Optimierung reduziert die Anzahl der Zugriffe auf den globalen Speicher in späteren Schritten.

Im nächsten Schritt wird der Gradientenbeitrag aller Elemente des Ausgangspuffers erfasst, die durch den zu analysierenden Parameter beeinflusst wurden.

   float grad = 0;
   for(int t = 0; t < total; t++)
     {
      if(inp != window_in && (inp + t * step) >= inputs)
         break;
      float g = IsNaNOrInf(matrix_g[t * window_out + shift_out],0);
      float i = IsNaNOrInf(inp == window_in ? 1.0f : matrix_i[t * step + shift_in],0);
      grad += IsNaNOrInf(g * i,0);
     }

Anschließend skalieren wir den gesammelten Gradienten um den absoluten Wert des Parameters.

   grad *= fabs(w);

Anschließend wenden wir den zuvor beschriebenen zweistufigen Reduktionsalgorithmus an, um die Quadrate der Gradienten innerhalb der Arbeitsgruppe zu summieren.

   const int local_shift = inp % ls;
   for(int i = 0; i <= inputs; i += ls)
     {
      if(i <= inp && inp < (i + ls))
         temp[local_shift] = (i == 0 ? 0 : temp[local_shift]) + IsNaNOrInf(grad * grad,0);
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   int count = ls;
   do
     {
      count = (count + 1) / 2;
      if(inp < count)
         temp[inp] += ((inp + count) < inputs ? IsNaNOrInf(temp[inp + count],0) : 0);
      if(inp + count < inputs)
         temp[inp + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Die Quadratwurzel der resultierenden Summe ergibt die gewünschte L2-Norm der Fehlergradienten.

   float norm = sqrt(IsNaNOrInf(temp[0],0));
   float epsw = IsNaNOrInf(w * w * grad * rho / (norm + 1.2e-7),w);
//---
   matrix_epsw[shift_w] = epsw;
  }

Anschließend berechnen wir den angepassten Parameterwert und speichern ihn im entsprechenden Element des Ergebnispuffers.

Damit ist unsere Implementierungs-Arbeit auf Seiten von OpenCL abgeschlossen. Der vollständige Code ist in der beigefügten Datei zu finden.

2.2 Vollständig vernetzte Schicht mit SAM-Optimierung

Nachdem wir die Arbeit auf der Seite von OpenCL abgeschlossen haben, gehen wir zu unserer Bibliotheksimplementierung über, wo wir das Objekt für eine vollständig verbundene Schicht mit integrierter SAM-Optimierung erstellen - CNeuronBaseSAMOCL. Die Struktur der neuen Klasse ist unten dargestellt.

class CNeuronBaseSAMOCL  :  public CNeuronBaseOCL
  {
protected:
   float             fRho;
   CBufferFloat      cWeightsSAM;
   //---
   virtual bool      calcEpsilonWeights(CNeuronBaseSAMOCL *NeuronOCL);
   virtual bool      feedForwardSAM(CNeuronBaseSAMOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronBaseSAMOCL(void) {};
                    ~CNeuronBaseSAMOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint numNeurons, float rho, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual int       Type(void)        const    {  return defNeuronBaseSAMOCL;      }
   virtual int       Activation(void)  const    {  return (fRho == 0 ? (int)None : (int)activation);   }
   virtual int       getWeightsSAMIndex(void)   {  return cWeightsSAM.GetIndex();   }
   //---
   virtual CLayerDescription* GetLayerInfo(void);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Wie Sie aus der Struktur ersehen können, wird die Hauptfunktionalität von der Basisschicht abgeleitet, die vollständig verbunden ist. Im Grunde genommen ist diese Klasse eine Kopie der Basisebene, wobei die Methode zur Parameteraktualisierung überschrieben wurde, um die Optimierungslogik von SAM zu integrieren.

Das heißt, wir haben eine Wrapper-Methode calcEpsilonWeights hinzugefügt, um eine Schnittstelle zum entsprechenden Kernel zu schaffen, der zuvor beschrieben wurde, und wir haben auch eine modifizierte Version der Methode für den Vorwärtsdurchlauf erstellt, die einen geänderten Gewichtspuffer namens feedForwardSAM verwendet.

Es ist erwähnenswert, dass die Autoren im ursprünglichen Rahmen von SAMformer ε auf die Modellparameter anwandten und es anschließend subtrahierten, um den ursprünglichen Zustand wiederherzustellen. Wir sind das anders angegangen. Wir speichern die verzerrten Parameter in einem separaten Puffer. Dadurch konnte der Schritt der Subtraktion ε umgangen und die Gesamtausführungszeit verkürzt werden. Aber das Wichtigste zuerst.

Der Puffer für die verzerrten Modellparameter wird statisch deklariert, sodass wir den Konstruktor und den Destruktor leer lassen können. Die Initialisierung aller deklarierten und geerbten Objekte wird in der Methode Init durchgeführt.

bool CNeuronBaseSAMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, 
                             float rho, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch))
      return false;

In den Methodenparametern erhalten wir die wichtigsten Konstanten, die die Architektur des erstellten Objekts bestimmen. Innerhalb der Methode rufen wir sofort die Init-Methode der übergeordneten Klasse auf, die die Validierung und Initialisierung der geerbten Komponenten implementiert.

Sobald die übergeordnete Methode erfolgreich abgeschlossen ist, wird der Koeffizient des Schärfenradius‘ in einer internen Variablen gespeichert.

   fRho = fabs(rho);
   if(fRho == 0 || !Weights)
      return true;

Anschließend prüfen wir den Wert des Schärfekoeffizienten und das Vorhandensein einer Parametermatrix. Ist der Koeffizient gleich „0“ oder ist die Parametermatrix nicht vorhanden (d. h. die Schicht hat keine ausgehenden Verbindungen), wird die Methode erfolgreich beendet. Andernfalls müssen wir einen Puffer für die alternativen Parameter anlegen. Strukturell ist er identisch mit dem Hauptgewichtspuffer, wird aber in dieser Phase mit Nullwerten initialisiert.

   if(!cWeightsSAM.BufferInit(Weights.Total(), 0) ||
      !cWeightsSAM.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Damit ist die Methode abgeschlossen.

Wir empfehlen Ihnen, die Wrapper-Methoden für das Einreihen von OpenCL-Kernel selbst zu überprüfen. Ihr Code ist in der Anlage enthalten. Kommen wir nun zur Aktualisierungsmethode für die Parameter: updateInputWeights.

bool CNeuronBaseSAMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;
   if(NeuronOCL.Type() != Type() || fRho == 0)
      return CNeuronBaseOCL::updateInputWeights(NeuronOCL);

Diese Methode erhält wie üblich einen Zeiger auf das Eingabedatenobjekt. Wir validieren den Zeiger sofort, da jede weitere Operation zu kritischen Fehlern führen würde, wenn der Zeiger ungültig ist.

Wir überprüfen auch den Typ des Eingabedatenobjekts, da er in diesem Zusammenhang wichtig ist. Außerdem muss der Schärfekoeffizient größer als „0“ sein. Andernfalls degeneriert die SAM-Logik zu einer Standardoptimierung. Dann rufen wir die entsprechende Methode der übergeordneten Klasse auf.

Sobald diese Prüfungen bestanden sind, fahren wir mit der Ausführung der Operationen der SAM-Methode fort. Es sei daran erinnert, dass der SAM-Algorithmus einen vollständigen Vorwärts- und Rückwärtsdurchlauf umfasst, bei dem die Fehlergradienten nach der Störung der Parameter mit ε verteilt werden. Wir haben jedoch bereits festgestellt, dass unsere SAM-Implementierung auf der Ebene einer einzigen Schicht arbeitet. Das wirft die Frage auf: Woher bekommen wir die Zielwerte für jede Schicht?

Auf den ersten Blick scheint die Lösung einfach zu sein - man addiert einfach das Ergebnis des letzten Vorwärtsdurchlauf mit dem Fehlergradienten. Aber es gibt einen Vorbehalt. Wenn der Gradient von der nachfolgenden Schicht weitergegeben wird, wird er normalerweise durch die Ableitung der Aktivierungsfunktion angepasst. Eine einfache Summierung würde also das Ergebnis verfälschen. Eine Möglichkeit wäre die Implementierung eines Mechanismus, der die Gradientenkorrektur auf der Grundlage der Aktivierungsableitung umkehrt. Wir haben jedoch eine einfachere und effizientere Lösung gefunden: Wir überschreiben die Rückgabemethode der Aktivierungsfunktion, sodass die Methode Null zurückgibt, wenn der Schärfekoeffizient Null ist. Auf diese Weise erhalten wir den rohen Fehlergradienten aus der nächsten Schicht, der nicht durch die Aktivierungsableitung verändert wurde. Wir können also das Ergebnis des Vorwärtsdurchlauf und den Fehlergradienten addieren. Die Summe dieser beiden Werte ergibt das effektive Ziel für die zu analysierende Schicht.

   if(!SumAndNormilize(Gradient, Output, Gradient, 1, false, 0, 0, 0, 1))
      return false;

Als Nächstes rufen wir die Wrapper-Methode auf, um die angepassten Modellparameter zu erhalten.

   if(!calcEpsilonWeights(NeuronOCL))
      return false;

Und wir führen einen Vorwärtsdurchlauf mit verzerrten Parametern durch.

   if(!feedForwardSAM(NeuronOCL))
      return false;

Zu diesem Zeitpunkt enthält der Fehlergradientenpuffer die Zielwerte, während der Ergebnispuffer die durch die verzerrten Parameter erzeugte Ausgabe enthält. Um die Abweichung zwischen diesen Werten zu ermitteln, rufen wir einfach die Methode der übergeordneten Klasse zur Berechnung der Abweichung von den Sollwerten auf.

   float error = 1;
   if(!calcOutputGradients(Gradient, error))
      return false;

Jetzt müssen wir nur noch die Modellparameter auf der Grundlage des aktualisierten Fehlergradienten aktualisieren. Dies geschieht durch den Aufruf der entsprechenden Methode der übergeordneten Klasse.

   return CNeuronBaseOCL::updateInputWeights(NeuronOCL);
  }

Ein paar Worte zu den Dateiverarbeitungsmethoden. Um Speicherplatz zu sparen, haben wir uns entschieden, den Puffer für die verzerrten Gewichte cWeightsSAM nicht zu speichern. Die Aufbewahrung der Daten hat keinen praktischen Wert, da dieser Puffer nur bei der Aktualisierung der Parameter relevant ist. Sie wird bei jedem Aufruf überschrieben. Die Größe der gespeicherten Daten erhöht sich also nur um ein Element vom Typ float (den Koeffizienten).

bool CNeuronBaseSAMOCL::Save(const int file_handle)
  {
   if(!CNeuronBaseOCL::Save(file_handle))
      return false;
   if(FileWriteFloat(file_handle, fRho) < INT_VALUE)
      return false;
//---
   return true;
  }

Andererseits ist der cWeightsSAM-Puffer nach wie vor notwendig, um die geforderte Funktionalität zu erfüllen. Seine Größe ist entscheidend, da er alle Parameter der aktuellen Ebene aufnehmen muss. Daher müssen wir sie neu erstellen, wenn wir ein zuvor gespeichertes Modell laden. In der Datenlademethode rufen wir zunächst die entsprechende Methode der Basisklasse auf.

bool CNeuronBaseSAMOCL::Load(const int file_handle)
  {
   if(!CNeuronBaseOCL::Load(file_handle))
      return false;

Als Nächstes wird geprüft, ob die Datei einen Inhalt hat, der über die Grundstruktur hinausgeht, und falls ja, wird der Schärfekoeffizient eingelesen.

   if(FileIsEnding(file_handle))
      return false;
   fRho = FileReadFloat(file_handle);

Anschließend wird überprüft, ob der Schärfekoeffizient ungleich Null ist, und sichergestellt, dass eine gültige Parametermatrix existiert (Hinweis: Bei Schichten ohne ausgehende Verbindungen kann der Zeiger ungültig sein).

   if(fRho == 0 || !Weights)
      return true;

Wenn eine der beiden Prüfungen fehlschlägt, wird die Parameteroptimierung zu einfachen Methoden degradiert, und es besteht keine Notwendigkeit, einen Puffer mit angepassten Parametern neu zu erstellen. Daher beenden wir die Methode erfolgreich.

Es ist anzumerken, dass das Scheitern dieser Prüfung für die SAM-Optimierung entscheidend ist, nicht aber für den Betrieb des Modells als Ganzes. Daher wird das Programm mit den grundlegenden Optimierungsmethoden fortgesetzt.

Wenn die Erstellung eines Puffers erforderlich ist, wird zunächst der vorhandene Puffer gelöscht. Wir verzichten absichtlich darauf, das Ergebnis des Löschvorgangs zu überprüfen. Dies liegt daran, dass es Situationen geben kann, in denen der Puffer beim Laden noch nicht vorhanden ist. 

   cWeightsSAM.BufferFree();

Anschließend initialisieren wir einen neuen Puffer geeigneter Größe mit Nullwerten und erstellen seine OpenCL-Kopie.

   if(!cWeightsSAM.BufferInit(Weights.Total(), 0) ||
      !cWeightsSAM.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Dieses Mal validieren wir die Ausführung dieser Operationen, da ihr Erfolg für den weiteren Betrieb des Modells entscheidend ist. Nach Abschluss des Vorgangs wird der Status an die aufrufende Funktion zurückgegeben.

Damit ist unsere Diskussion über die Implementierung der vollständig vernetzten Schicht mit Optimierungsunterstützung durch SAM (CNeuronBaseSAMOCL) abgeschlossen. Den vollständigen Quellcode für diese Klasse und ihre Methoden finden Sie im beigefügten Anhang.

Leider haben wir die Volumengrenze für diesen Artikel erreicht, aber wir haben die Arbeit noch nicht abgeschlossen. Im nächsten Artikel werden wir die Implementierung fortsetzen und uns die Faltungsschicht mit der Implementierung der SAM-Funktionalität ansehen. Wir werden uns auch die Anwendung der vorgeschlagenen Technologien in der Transformer-Architektur ansehen und natürlich die Leistung der vorgeschlagenen Ansätze an realen historischen Daten testen.

Schlussfolgerung

SAMformer bietet eine effektive Lösung für die zentralen Nachteile von Transformer-Modellen bei der Langzeitprognose von multivariaten Zeitreihen, wie z.B. die Komplexität des Trainings und die schlechte Generalisierung auf kleinen Datensätzen. Durch die Verwendung einer flachen Architektur und einer auf Schärfe ausgerichteten Optimierung vermeidet SAMformer nicht nur schlechte lokale Minima, sondern übertrifft auch die modernsten Methoden. Außerdem werden weniger Parameter verwendet. Die von den Autoren vorgestellten Ergebnisse bestätigen sein Potenzial als universelles Werkzeug für Zeitreihenaufgaben.

Im praktischen Teil unseres Artikels haben wir unsere Vision der vorgeschlagenen Ansätze unter Verwendung von MQL5 entwickelt. Aber unsere Arbeit ist noch nicht abgeschlossen. Im nächsten Artikel werden wir den praktischen Wert der vorgeschlagenen Ansätze für die Lösung unserer Probleme bewerten.

Referenzen

SAMformer: Unlocking the Potential of Transformers in Time Series Forecasting with Sharpness-Aware Minimization and Channel-Wise Attention

Sharpness-Aware Minimization for Efficiently Improving Generalization

Andere Artikel dieser Serie

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	Expert Advisor zum Sammeln von Beispielen
2	ResearchRealORL.mq5	Expert Advisor	Expert Advisor für das Sammeln von Beispielen nach der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modellausbildung Expert Advisor
4	StudyEncoder.mq5	Expert Advisor	Trainings-EA der Kodierung
5	Test.mq5	Expert Advisor	Modellprüfung Expert Advisor
6	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
7	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
8	NeuroNet.cl	Bibliothek	OpenCL-Programmcode-Bibliothek