
Redes neuronales: así de sencillo (Parte 12): Dropout
Contenido
- Introducción
- 1. El Dropout como método para aumentar la convergencia de las redes neuronales
- 2. Implementación
- 2.1. Creando una nueva clase para nuestro modelo
- 2.2. Propagación hacia delante
- 2.3. Propagación inversa
- 2.4. Métodos para guardar y cargar datos
- 2.5. Cambios puntuales en las clases básicas de la red neronal
- 3. Simulación
- Conclusión
- Enlaces
- Programas utilizados en el artículo
Introducción
Desde el comienzo de esta serie de artículos, hemos avanzado mucho en el estudio de varios modelos de redes neuronales. Pero el proceso de entrenamiento siempre ha tenido lugar sin nuestra participación. Al mismo tiempo, siempre sentimos el deseo de ayudar de alguna forma a la red neuronal a mejorar los resultados de su aprendizaje, la llamada convergencia de la red neuronal. En este artículo, proponemos analizar uno de estos métodos: el Dropout (dilución).
1. El Dropout como método para aumentar la convergencia de las redes neuronales
Al entrenar una red neuronal, suministramos un gran número de características a la entrada de cada neurona, y resulta difícil valorar el impacto de cada una de ellas. Como resultado, los errores de algunas neuronas se suavizan con los valores correctos de otras y los errores se acumulan en la salida de la red neuronal. Como resultado, el entrenamiento se detiene en un cierto mínimo local con un error considerable. Este efecto se denominó adaptación conjunta de características, cuando la influencia de cada característica, por así decirlo, se ajusta al entorno. Sería mejor para nosotros lograr el efecto contrario, es decir, descomponer el entorno en características aparte y valorar la influencia de cada una por separado.
Para combatir la compleja adaptación conjunta de características, en julio de 2012, un grupo de científicos de la Universidad de Toronto propuso excluir aleatoriamente algunas de las neuronas en el proceso de aprendizaje[12]. La disminución en el número de características durante el entrenamiento aumentará la importancia de cada una, mientras que el cambio constante en la composición cuantitativa y cualitativa de las características reducirá el riesgo de su adaptación conjunta. Este método se llama Dropout o dilución. Algunas personas comparan la aplicación de este método con los árboles de decisión, porque, admitámoslo, excluyendo algunas de las neuronas, en cada iteración del entrenamiento obtenemos una nueva red neuronal con nuestros propios coeficientes de peso. Y, según, las reglas de la combinatoria, la variabilidad de tales redes resulta bastante alta.
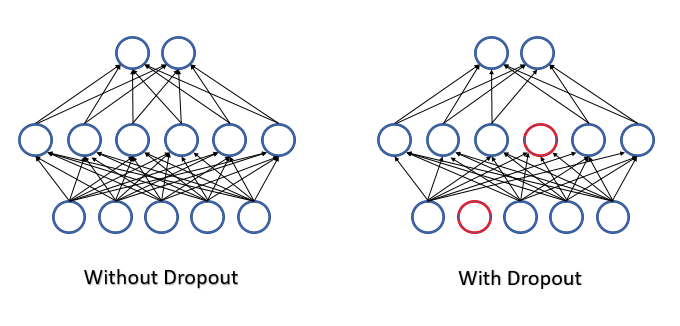
Durante el funcionamiento de la red neuronal, se valoran todas las características y neuronas, consiguiendo así la evaluación más precisa e independiente del estado actual del entorno analizado.
Los autores de la solución, en el artículo [12], indican la posibilidad de usar el método para mejorar la calidad de los modelos previamente entrenados.
Al describir la solución propuesta desde el punto de vista de las matemáticas, podemos decir que cada neurona individual se descarta del proceso con una cierta probabilidad especificada p. O bien que la neurona participará en el proceso de aprendizaje de la red neuronal con una probabilidad q=1-p.
Para determinar la lista de neuronas descartadas, se usa un generador de números pseudoaleatorios con distribución normal. Este enfoque permite conseguir una exclusión de neuronas lo más uniforme posible. En la práctica, generaremos un vector con un tamaño igual a la secuencia de entrada. Para las características usadas en el vector, escribiremos "1", y para los elementos excluidos, pondremos "0".
No obstante, la exclusión de las características analizadas indudablemente provoca una disminución en la cantidad a la entrada de la función de activación neuronal. Para compensar este efecto, multiplicaremos el valor de cada característica por el coeficiente 1/q. Resulta fácil ver que este coeficiente hará aumentar los valores, ya que la probabilidad q se encontará siempre en el intervalo de 0 a 1.
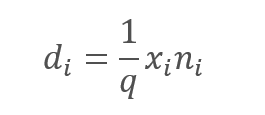 ,
,
donde:
d — son los elementos del vector de resultados del Dropout,
q — es la probabilidad de usar una neurona en el proceso de aprendizaje,
x - son los elementos del vector de enmascaramiento,
n - son los elementos de la secuencia de entrada.
En la propagación inversa, durante el proceso de aprendizaje, el gradiente de error se multiplica por la derivada de la función mostrada anteriormente. Como podremos ver con facilidad, en el caso del Dropout, la propagación inversa será similar a la propagación hacia adelante utilizando el vector de enmascaramiento de la propagación hacia adelante.
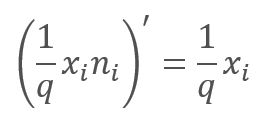
Durante el funcionamiento de la red neuronal, el vector de enmascaramiento se rellena con "1", lo cual permite que los valores se transmitan sin problemas en ambas direcciones.
En la práctica, el coeficiente 1/q es constante durante todo el entrenamiento, por lo que podemos calcular fácilmente este coeficiente una vez y anotarlo en lugar de "1" en el tensor de enmascaramiento. Así, descartaremos las operaciones de recálculo del coeficiente y su multiplicación por el "1" de la máscara en cada iteración de entrenamiento.
2. Implementación
Una vez estudiados los aspectos teóricos, procedemos a analizar las opciones disponibles para implementar este método en nuestra biblioteca. Lo primero que nos encontramos es la implementación de dos algoritmos diferentes. Uno para el proceso de entrenamiento, y otro para las pruebas y la explotación. Por consiguiente, necesitaremos indicarle explícitamente a la neurona con qué algoritmo trabajar en cada caso individual. Para ello, al nivel de la neurona básica, introduciremos la bandera bTrain, a la que asignaremos el valor true durante el entrenamiento y false durante la prueba.
class CNeuronBaseOCL : public CObject { protected: bool bTrain; ///< Training Mode Flag
Para controlar los valores de las banderas, crearemos métodos auxiliares.
virtual void TrainMode(bool flag) { bTrain=flag; }///< Set Training Mode Flag virtual bool TrainMode(void) { return bTrain; }///< Get Training Mode Flag
La introducción de la bandera y los métodos al nivel de la neurona básica se realiza a propósito. Esto nos permitirá usar desarrollos de Dropout en implementaciones futuras.
2.1. Creando una nueva clase para nuestro modelo
Para implementar el algoritmo Dropout, crearemos una nueva clase CNeuronDropoutOCL, que incluiremos en nuestro modelo como una capa aparte. La nueva clase heredará directamente de la clase de neurona básica CNeuronBaseOCL. En el bloque protected, declaramos las variables:
- OutProbability — probabilidad indicada de exclusión de neuronas.
- OutNumber — número de neuronas excluidas.
- dInitValue — valor para inicializar el vector de enmascaramiento, en la parte teórica de este artículo, nombramos este coeficiente 1/q.
También declaramos dos punteros a las clases:
- DropOutMultiplier — vector de enmascaramiento.
- PrevLayer — puntero al objeto de la capa anterior, lo utilizaremos durante las pruebas y la aplicación práctica.
class CNeuronDropoutOCL : public CNeuronBaseOCL { protected: CNeuronBaseOCL *PrevLayer; double OutProbability; double OutNumber; CBufferDouble *DropOutMultiplier; double dInitValue; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); ///<\brief Feed Forward method of calling kernel ::FeedForward().@param NeuronOCL Pointer to previos layer. virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) {return true;} ///< Method for updating weights.@param NeuronOCL Pointer to previos layer. //--- int RND(void) { xor128; return (int)((double)(Neurons()-1)/UINT_MAX*rnd_w); } ///< Generates a random neuron position to turn off public: CNeuronDropoutOCL(void); ~CNeuronDropoutOCL(void); //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons,double out_prob, ENUM_OPTIMIZATION optimization_type); ///< Method of initialization class.@param[in] numOutputs Number of connections to next layer.@param[in] myIndex Index of neuron in layer.@param[in] open_cl Pointer to #COpenCLMy object. //#param[in] numNeurons Number of neurons in layer #param[in] out_prob Probability of neurons shutdown @param optimization_type Optimization type (#ENUM_OPTIMIZATION)@return Boolen result of operations. //--- virtual int getOutputIndex(void) { return (bTrain ? Output.GetIndex() : PrevLayer.getOutputIndex()); } ///< Get index of output buffer @return Index virtual int getGradientIndex(void) { return (bTrain ? Gradient.GetIndex() : PrevLayer.getGradientIndex()); } ///< Get index of gradient buffer @return Index //--- virtual int getOutputVal(double &values[]) { return (bTrain ? Output.GetData(values) : PrevLayer.getOutputVal(values)); } ///< Get values of output buffer @param[out] values Array of data @return number of items virtual int getOutputVal(CArrayDouble *values) { return (bTrain ? Output.GetData(values) : PrevLayer.getOutputVal(values)); } ///< Get values of output buffer @param[out] values Array of data @return number of items virtual int getGradient(double &values[]) { return (bTrain ? Gradient.GetData(values) : PrevLayer.getGradient(values)); } ///< Get values of gradient buffer @param[out] values Array of data @return number of items virtual CBufferDouble *getOutput(void) { return (bTrain ? Output : PrevLayer.getOutput()); } ///< Get pointer of output buffer @return Pointer to object virtual CBufferDouble *getGradient(void) { return (bTrain ? Gradient : PrevLayer.getGradient()); } ///< Get pointer of gradient buffer @return Pointer to object //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); ///< Method to transfer gradient to previous layer by calling kernel ::CalcHiddenGradient(). @param NeuronOCL Pointer to next layer. //--- virtual bool Save(int const file_handle);///< Save method @param[in] file_handle handle of file @return logical result of operation virtual bool Load(int const file_handle);///< Load method @param[in] file_handle handle of file @return logical result of operation //--- virtual int Type(void) const { return defNeuronDropoutOCL; }///< Identificator of class.@return Type of class };
La lista de métodos de clase resulta bastante familiar, y todos ellos redefinen los métodos de la clase principal. La excepción a esta regla es el método RND, diseñado para generar números pseudoaleatorios de distribución uniforme. El algoritmo para este método lo hemos tomado prestado del artículo [13]. Para obtener los máximos valores aleatorios en todos los objetos de nuestra red neuronal, el generador de secuencias pseudoaleatorias se implementa como una macrosustitución usando variables globales.
#define xor128 rnd_t=(rnd_x^(rnd_x<<11)); \ rnd_x=rnd_y; \ rnd_y=rnd_z; \ rnd_z=rnd_w; \ rnd_w=(rnd_w^(rnd_w>>19))^(rnd_t^(rnd_t>>8)) uint rnd_x=MathRand(), rnd_y=MathRand(), rnd_z=MathRand(), rnd_w=MathRand(), rnd_t=0;
El algoritmo propuesto genera una secuencia de números enteros en el intervalo [0,UINT_MAX=4294967295]. Por consiguiente, en el método generador de la secuencia pseudoaleatoria, tras ejecutar la macro, el valor resultante se normaliza hasta el tamaño de la secuencia.
int RND(void) { xor128; return (int)((double)(Neurons()-1)/UINT_MAX*rnd_w); }
Si el lector está familiarizado con publicaciones anteriores de esta serie de artículos, podrá notar que no hemos redefinido previamente los métodos para trabajar con los búferes de datos de las clases de otros objetos. No olvidemos que estos métodos se usan para intercambiar datos entre las capas de una red neuronal cuando las neuronas acceden a los datos de la capa anterior o posterior.
Hemos tomado esta decisión para intentar optimizar el funcionamiento de la red neuronal durante su aplicación práctica. Repetimos: la capa de Dropout se usa solo para entrenar la red neuronal. Durante las pruebas y la aplicación práctica, el algoritmo de exclusión de neuronas permanecerá desactivado. Después de redefinir los métodos para acceder a los búferes de datos, hemos organizado la omisión de la capa de Dropout. Todos los métodos redefinidos se basan en el mismo principio. En lugar de copiar los datos, organizamos la sustitución de los búferes de la capa de Dropout por los búferes de la capa anterior. Así, en el modo de aplicación práctica, la velocidad de una red neuronal con una capa de Dropout será comparable a la velocidad de una red similar sin Dropout; en esta caso, obtendremos todas las ventajas derivadas de la excluisión de neuronas a la hora de entrenar la red.
virtual int getOutputIndex(void) { return (bTrain ? Output.GetIndex() : PrevLayer.getOutputIndex()); }
Podrá familiarizarse con el código completo de todos los métodos y clases en los anexos.
2.2. Propagación hacia delante
Para no romper la tradición, vamos a organizar la propagación hacia delante en el método feedForward. Al inicio del método, verificamos la validez del puntero a la capa anterior de la red neuronal y el puntero al objeto OpenCL obtenido en los parámetros. Luego guardaremos la función de activación usada en la capa anterior y el puntero al objeto de la propia capa anterior. Para el modo de aplicación práctica de la red neuronal, aquí finaliza la propagación hacia delante de la capa de Dropout. Además, al acceder desde la siguiente capa, se activará el mecanismo de sustitución de los búferes de datos, descrito anteriormente.
bool CNeuronDropoutOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- activation=(ENUM_ACTIVATION)NeuronOCL.Activation(); PrevLayer=NeuronOCL; if(!bTrain) return true;
Las posteriores iteraciones solo serán relevantes para el modo de entrenamiento de la red neuronal. Primero, formaremos un vector de enmascaramiento en el que definiremos las neuronas que se desactivarán en este paso. A continuación, escribimos la máscara en el búfer DropOutMultiplier, verificamos la presencia del objeto anteriormente creado y, si es necesario, creamos uno nuevo. Después, inicializamos el búfer con los valores iniciales. Para reducir los cálculos, inicializaremos el búfer directamente con el factor de aumento 1/q.
if(CheckPointer(DropOutMultiplier)==POINTER_INVALID) DropOutMultiplier=new CBufferDouble(); if(!DropOutMultiplier.BufferInit(NeuronOCL.Neurons(),dInitValue)) return false; for(int i=0;i<OutNumber;i++) { uint p=RND(); double val=DropOutMultiplier.At(p); if(val==0 || val==DBL_MAX) { i--; continue; } if(!DropOutMultiplier.Update(RND(),0)) return false; }
Después de inicializar el búfer, organizamos un ciclo con un número de repeticiones igual al número de neuronas a excluir y reemplazamos con valores cero los elementos elegidos al azar del búfer. Para evitar el riesgo de escribir "0" dos veces en una celda, organizaremos una verificación adicional dentro de nuestro ciclo.
Después de generar la máscara, creamos un búfer directamente en la memoria de la GPU y transferimos los datos.
if(!DropOutMultiplier.BufferCreate(OpenCL)) return false;
Ahora tenemos que realizar la multiplicación por elementos de los dos vectores. El resultado de esta operación será la salida de la capa de Dropout. La operación de multiplicación de los vectores se realiza usando OpenCL en la GPU. La forma más eficaz de multiplicar los elementos será usar operaciones vectoriales. En nuestro caso, hemos usado en el kernel OpenCL las variables del tipo double4, dado que es un vector de 4 elementos. Por consiguiente, el número de hilos iniciados será 4 veces menor que la cantidad de elementos en los vectores.
uint global_work_offset[1]= {0}; uint global_work_size[1]; int i=Neurons()%4; global_work_size[0]=(Neurons()-i)/4+(i>0 ? 1 : 0);
A continuación, indicamos los búferes y las variables de los datos iniciales e iniciamos la ejecución del kernel.
if(!OpenCL.SetArgumentBuffer(def_k_Dropout,def_k_dout_input,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_Dropout,def_k_dout_map,DropOutMultiplier.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_Dropout,def_k_dout_out,Output.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_Dropout,def_k_dout_dimension,Neurons())) return false; ResetLastError(); if(!OpenCL.Execute(def_k_Dropout,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Dropout: %d",GetLastError()); return false; }
Al final del método, obtenemos el resultado de las operaciones en el kernel y eliminamos el búfer de enmascaramiento de la memoria de la GPU.
if(!Output.BufferRead()) return false; DropOutMultiplier.BufferFree(); //--- return true; }
Después de terminar las operaciones, salimos del método con el resultado true.
La descripción del método de propagación hacia delante sin considerar las operaciones en el lado de la GPU estará incompleta. Veamos el código del kernel.
__kernel void Dropout (__global double *inputs, ///<[in] Input matrix __global double *map, ///<[in] Dropout map matrix __global double *out, ///<[out] Output matrix int dimension ///< Dimension of matrix )
En los parámetros, el kernel recibe los punteros a los dos tensores entrantes con los datos iniciales y al tensor de resultados, así como la dimensión de los vectores.
Directamente en el código del kernel, según el número de hilo, determinamos los elementos para la multiplicación y luego dividimos el código en dos ramas. Primero, la principal: utilizando operaciones vectoriales, multiplicamos los 4 elementos consecutivos y escribimos los datos obtenidos en los elementos correspondientes del búfer de resultados.
{
const int i=get_global_id(0)*4;
if(i+3<dimension)
{
double4 k=(double4)(inputs[i],inputs[i+1],inputs[i+2],inputs[i+3])*(double4)(map[i],map[i+1],map[i+2],map[i+3]);
out[i]=k.s0;
out[i+1]=k.s1;
out[i+2]=k.s2;
out[i+3]=k.s3;
}
else
for(int k=i;k<min(dimension,i+4);k++)
out[i+k]=(inputs[i+k]*map[i+k]);
}
La segunda rama se incluye solo en los casos en que el número de elementos en los tensores no es múltiplo de 4 y los elementos restantes se multiplican en un bucle. Podemos ver fácilmente que en este ciclo no habrá más de 3 iteraciones, y que no resultará crítico en cuanto al tiempo de cálculo.
Podrá familiarizarse con el código completo de todas las clases y sus métodos en los anexos.
2.3. Propagación inversa
La propagación inversa en todas las neuronas analizadas anteriormente se ha dividido en 2 métodos:
- calcInputGradients — transmisión del gradiente de error a la capa anterior.
- updateInputWeights — actualización de los coeficientes de peso de la capa neuronal.
En el caso del Dropout, carecemos del tensor de peso, pero para mantener la estructura general de los objetos, aun así anularemos el método updateInputWeights, que, sin embargo, siempre retornará en este caso el valor true.
virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) {return true;} ///< Method for updating weights.
Veamos la implementación del método calcInputGradients. Este obtiene en los parámetros el puntero a la capa anterior. Al inicio del método, verificamos la validez del puntero recibido y el puntero al objeto OpenCL. A continuación, al igual que en la propagación hacia delante, dividimos el algoritmo en el proceso de entrenamiento y el proceso de aplicación práctica. En el modo de prueba o aplicación práctica, en este punto, salimos del método, es decir, gracias a nuestra sustitución de los búferes de datos, la capa neuronal posterior ha escrito el gradiente directamente en el búfer de la capa anterior, omitiendo iteraciones innecesarias en la capa de Dropout.
bool CNeuronDropoutOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- if(!bTrain) return true;
En el modo de entrenamiento, la transmisión del gradiente tomará un camino distinto, y el algoritmo mostrado a continuación resultará relevante solo durante el entrenamiento de la red neuronal. Al igual que en el método de propagación hacia delante, verificamos la validez del puntero al búfer de enmascaramiento DropOutMultiplier, solo que, a diferencia de la propagación hacia delante, un error de verificación no creará un nuevo búfer, sino que provocará que el método salga con el resultado false. Esto se debe a que la propagación inversa utiliza la máscara generada por la propagación hacia delante. Este enfoque asegura la comparabilidad de los datos y la distribución correcta del gradiente de error entre las neuronas.
if(CheckPointer(DropOutMultiplier)==POINTER_INVALID) return false; //--- if(!DropOutMultiplier.BufferCreate(OpenCL)) return false;
Después de verificar con éxito el objeto DropOutMultiplier, creamos un búfer en la memoria de la GPU y lo rellenamos con datos.
Ahora tenemos que realizar la multiplicación por elementos de los dos vectores. ¿No le recuerda nada? Más arriba, en la descripción de la propagación hacia delante, hemos mostrado exactamente la misma oración. Sí, realmente. En la parte teórica, hemos mostrado que la derivada de la función matemática de Dropout es igual al coeficiente de aumento. Por consiguiente, durante la propagación inversa, también multiplicaremos el gradiente de la capa posterior por el coeficiente de aumento registrado en el búfer de enmascaramiento DropOutMultiplier. Por consiguiente, la clase CNeuronDropoutOCL será ese caso único en el que usaremos el mismo kernel para la propagación hacia delante y la propagación inversa, solo que suministrando datos diferentes a la entrada: para la propagación hacia delante, serán los datos de salida de las neuronas, para la propagación inversa, el gradiente de error.
Y así sucesivamente, indicaremos los búferes de datos y llamaremos a la ejecución del kernel. El código que mostramos es similar al código de la propagación hacia delante, por lo que no requerirá explicaciones adicionales.
uint global_work_offset[1]= {0}; uint global_work_size[1]; int i=Neurons()%4; global_work_size[0]=(Neurons()-i)/4+(i>0 ? 1 : 0); if(!OpenCL.SetArgumentBuffer(def_k_Dropout,def_k_dout_input,Gradient.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_Dropout,def_k_dout_map,DropOutMultiplier.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_Dropout,def_k_dout_out,NeuronOCL.getGradientIndex())) return false; if(!OpenCL.SetArgument(def_k_Dropout,def_k_dout_dimension,Neurons())) return false; ResetLastError(); if(!OpenCL.Execute(def_k_Dropout,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Dropout: %d",GetLastError()); return false; } if(!NeuronOCL.getGradient().BufferRead()) return false; DropOutMultiplier.BufferFree(); //--- return true; }
Podrá familiarizarse con el código completo de todas las clases y sus métodos en los anexos.
2.4. Métodos para guardar y cargar datos
Vamos a detenernos un poco en los métodos encargados de guardar y cargar el objeto de capa neuronal Dropout. No necesitamos guardar el objeto de búfer de máscara, ya que una nueva máscara se genera en cada ciclo de entrenamiento. En el método de inicialización de la clase CNeuronDropoutOCL, solo hemos añadido una variable: la probabilidad de excluir una neurona, que debemos guardar.
De esta forma, en el método de guardado Save, llamaremos al método del mismo nombre de la clase padre, y tras finalizarlo con éxito, guardaremos la probabilidad indicada de excluir neuronas.
bool CNeuronDropoutOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false; //--- if(FileWriteDouble(file_handle,OutProbability)<=0) return false; //--- return true; }
En el método de carga de la clase Load, debemos leer los datos del disco y restablecer todos los elementos de la clase, por lo que el algoritmo del método resultará un poco más complejo que el método de guardado.
Repitiendo el código del método de guardado de clases, llamamos al método homónimo de la clase padre. Una vez completado, calculamos la probabilidad de excluisión de las neuronas. En este punto, el método de guardado ha finalizado, pero necesitamos restablecer los elementos faltantes. Partiendo de la probabilidad de exclusión de las neuronas, calcularemos el número de neuronas a excluir y el valor del coeficiente de aumento, que también servirá como valor para inicializar el vector de enmascaramiento.
bool CNeuronDropoutOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false; //--- OutProbability=FileReadDouble(file_handle); OutNumber=(int)(Neurons()*OutProbability); dInitValue=1/(1-OutProbability); if(CheckPointer(DropOutMultiplier)==POINTER_INVALID) DropOutMultiplier=new CBufferDouble(); if(!DropOutMultiplier.BufferInit(Neurons()+1,dInitValue)) return false; //--- return true; }
Después de realizar los cálculos, restableceremos el vector de enmascaramiento. Vamos a verificar la validez del puntero al objeto de búfer de datos en DropOutMultiplier; de ser necesario, crearemos un nuevo objeto. Luego inicializaremos el vector de enmascaramiento con los valores iniciales.
2.5. Cambios puntuales en las clases básicas de la red neronal
Y como siempre, tras crear una nueva clase, necesitaremos acoplarla correctamente al funcionamiento de nuestra biblioteca. Lo primero que haremos es declarar las macrosustituciones para trabajar con el nuevo kernel, y también establecer la constante de identificación para la nueva clase.
#define def_k_Dropout 23 ///< Index of the kernel for Dropout process (#Dropout) #define def_k_dout_input 0 ///< Inputs Tensor #define def_k_dout_map 1 ///< Map Tensor #define def_k_dout_out 2 ///< Out Tensor #define def_k_dout_dimension 3 ///< Dimension of Inputs
#define defNeuronDropoutOCL 0x7890 ///<Dropout neuron OpenCL \details Identified class #CNeuronDropoutOCL
A continuación, en el método encargado de describir la capa neuronal, añadiremos una nueva variable para registrar la probabilidad de exclusión de las neuronas.
class CLayerDescription : public CObject { public: /** Constructor */ CLayerDescription(void); /** Destructor */~CLayerDescription(void) {}; //--- int type; ///< Type of neurons in layer (\ref ObjectTypes) int count; ///< Number of neurons int window; ///< Size of input window int window_out; ///< Size of output window int step; ///< Step size int layers; ///< Layers count ENUM_ACTIVATION activation; ///< Type of activation function (#ENUM_ACTIVATION) ENUM_OPTIMIZATION optimization; ///< Type of optimization method (#ENUM_OPTIMIZATION) double probability; ///< Probability of neurons shutdown, only Dropout used };
En el método para crear la red neuronal CNet::CNet, en el bloque encargado de crear e inicializar las capas, añadimos el código de inicialización para una nueva capa (en el código a continuación se destaca con un fondo coloreado).
for(int i=0; i<total; i++) { prev=desc; desc=Description.At(i); if((i+1)<total) { next=Description.At(i+1); if(CheckPointer(next)==POINTER_INVALID) return; } else next=NULL; int outputs=(next==NULL || (next.type!=defNeuron && next.type!=defNeuronBaseOCL) ? 0 : next.count); temp=new CLayer(outputs); int neurons=(desc.count+(desc.type==defNeuron || desc.type==defNeuronBaseOCL ? 1 : 0)); if(CheckPointer(opencl)!=POINTER_INVALID) { CNeuronBaseOCL *neuron_ocl=NULL; CNeuronConvOCL *neuron_conv_ocl=NULL; CNeuronAttentionOCL *neuron_attention_ocl=NULL; CNeuronMLMHAttentionOCL *neuron_mlattention_ocl=NULL; CNeuronDropoutOCL *dropout=NULL; switch(desc.type) { case defNeuron: case defNeuronBaseOCL: neuron_ocl=new CNeuronBaseOCL(); if(CheckPointer(neuron_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_ocl.Init(outputs,0,opencl,desc.count,desc.optimization)) { delete neuron_ocl; delete temp; return; } neuron_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_ocl)) { delete neuron_ocl; delete temp; return; } neuron_ocl=NULL; break; //--- case defNeuronConvOCL: neuron_conv_ocl=new CNeuronConvOCL(); if(CheckPointer(neuron_conv_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_conv_ocl.Init(outputs,0,opencl,desc.window,desc.step,desc.window_out,desc.count,desc.optimization)) { delete neuron_conv_ocl; delete temp; return; } neuron_conv_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_conv_ocl)) { delete neuron_conv_ocl; delete temp; return; } neuron_conv_ocl=NULL; break; //--- case defNeuronAttentionOCL: neuron_attention_ocl=new CNeuronAttentionOCL(); if(CheckPointer(neuron_attention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_attention_ocl.Init(outputs,0,opencl,desc.window,desc.count,desc.optimization)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_attention_ocl)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl=NULL; break; //--- case defNeuronMHAttentionOCL: neuron_attention_ocl=new CNeuronMHAttentionOCL(); if(CheckPointer(neuron_attention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_attention_ocl.Init(outputs,0,opencl,desc.window,desc.count,desc.optimization)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_attention_ocl)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl=NULL; break; //--- case defNeuronMLMHAttentionOCL: neuron_mlattention_ocl=new CNeuronMLMHAttentionOCL(); if(CheckPointer(neuron_mlattention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_mlattention_ocl.Init(outputs,0,opencl,desc.window,desc.window_out,desc.step,desc.count,desc.layers,desc.optimization)) { delete neuron_mlattention_ocl; delete temp; return; } neuron_mlattention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_mlattention_ocl)) { delete neuron_mlattention_ocl; delete temp; return; } neuron_mlattention_ocl=NULL; break; //--- case defNeuronDropoutOCL: dropout=new CNeuronDropoutOCL(); if(CheckPointer(dropout)==POINTER_INVALID) { delete temp; return; } if(!dropout.Init(outputs,0,opencl,desc.count,desc.probability,desc.optimization)) { delete dropout; delete temp; return; } if(!temp.Add(dropout)) { delete dropout; delete temp; return; } dropout=NULL; break; //--- default: return; break; } }
No debemos olvidarnos de declarar un nuevo kernel con el mismo método.
opencl.SetKernelsCount(24); opencl.KernelCreate(def_k_FeedForward,"FeedForward"); opencl.KernelCreate(def_k_CalcOutputGradient,"CalcOutputGradient"); opencl.KernelCreate(def_k_CalcHiddenGradient,"CalcHiddenGradient"); opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum"); opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam"); opencl.KernelCreate(def_k_AttentionGradients,"AttentionInsideGradients"); opencl.KernelCreate(def_k_AttentionOut,"AttentionOut"); opencl.KernelCreate(def_k_AttentionScore,"AttentionScore"); opencl.KernelCreate(def_k_CalcHiddenGradientConv,"CalcHiddenGradientConv"); opencl.KernelCreate(def_k_CalcInputGradientProof,"CalcInputGradientProof"); opencl.KernelCreate(def_k_FeedForwardConv,"FeedForwardConv"); opencl.KernelCreate(def_k_FeedForwardProof,"FeedForwardProof"); opencl.KernelCreate(def_k_MatrixSum,"SumMatrix"); opencl.KernelCreate(def_k_Matrix5Sum,"Sum5Matrix"); opencl.KernelCreate(def_k_UpdateWeightsConvAdam,"UpdateWeightsConvAdam"); opencl.KernelCreate(def_k_UpdateWeightsConvMomentum,"UpdateWeightsConvMomentum"); opencl.KernelCreate(def_k_Normilize,"Normalize"); opencl.KernelCreate(def_k_NormilizeWeights,"NormalizeWeights"); opencl.KernelCreate(def_k_ConcatenateMatrix,"ConcatenateBuffers"); opencl.KernelCreate(def_k_DeconcatenateMatrix,"DeconcatenateBuffers"); opencl.KernelCreate(def_k_MHAttentionGradients,"MHAttentionInsideGradients"); opencl.KernelCreate(def_k_MHAttentionScore,"MHAttentionScore"); opencl.KernelCreate(def_k_MHAttentionOut,"MHAttentionOut"); opencl.KernelCreate(def_k_Dropout,"Dropout");
Tenemos que añadir una declaración similar del nuevo kernel al método para leer una red neuronal previamente entrenada desde el disco CNet::Load.
Continuando con el tema del proceso de carga de una red neuronal previamente entrenada, también deberemos ajustar el método encargado de crear un elemento de la capa de red neuronal CLayer::CreateElement, añadiendo allí el código para crear el elemento Dropout. Hemos destacado los cambios con un fondo coloreado.
bool CLayer::CreateElement(int index) { if(index>=m_data_max) return false; //--- bool result=false; CNeuronBase *temp=NULL; CNeuronProof *temp_p=NULL; CNeuronBaseOCL *temp_ocl=NULL; CNeuronConvOCL *temp_con_ocl=NULL; CNeuronAttentionOCL *temp_at_ocl=NULL; CNeuronMLMHAttentionOCL *temp_mlat_ocl=NULL; CNeuronDropoutOCL *temp_drop_ocl=NULL; if(iFileHandle<=0) { temp=new CNeuron(); if(CheckPointer(temp)==POINTER_INVALID || !temp.Init(iOutputs,index,SGD)) return false; result=true; } else { int type=FileReadInteger(iFileHandle); switch(type) { case defNeuron: temp=new CNeuron(); if(CheckPointer(temp)==POINTER_INVALID) result=false; result=temp.Init(iOutputs,index,ADAM); break; case defNeuronProof: temp_p=new CNeuronProof(); if(CheckPointer(temp_p)==POINTER_INVALID) result=false; if(temp_p.Init(iOutputs,index,1,1,1,ADAM)) { temp=temp_p; result=true; } break; case defNeuronConv: temp_p=new CNeuronConv(); if(CheckPointer(temp_p)==POINTER_INVALID) result=false; if(temp_p.Init(iOutputs,index,1,1,1,ADAM)) { temp=temp_p; result=true; } break; case defNeuronLSTM: temp_p=new CNeuronLSTM(); if(CheckPointer(temp_p)==POINTER_INVALID) result=false; if(temp_p.Init(iOutputs,index,1,1,1,ADAM)) { temp=temp_p; result=true; } break; case defNeuronBaseOCL: if(CheckPointer(OpenCL)==POINTER_INVALID) return false; temp_ocl=new CNeuronBaseOCL(); if(CheckPointer(temp_ocl)==POINTER_INVALID) result=false; if(temp_ocl.Init(iOutputs,index,OpenCL,1,ADAM)) { m_data[index]=temp_ocl; return true; } break; case defNeuronConvOCL: if(CheckPointer(OpenCL)==POINTER_INVALID) return false; temp_con_ocl=new CNeuronConvOCL(); if(CheckPointer(temp_con_ocl)==POINTER_INVALID) result=false; if(temp_con_ocl.Init(iOutputs,index,OpenCL,1,1,1,1,ADAM)) { m_data[index]=temp_con_ocl; return true; } break; case defNeuronAttentionOCL: if(CheckPointer(OpenCL)==POINTER_INVALID) return false; temp_at_ocl=new CNeuronAttentionOCL(); if(CheckPointer(temp_at_ocl)==POINTER_INVALID) result=false; if(temp_at_ocl.Init(iOutputs,index,OpenCL,1,1,ADAM)) { m_data[index]=temp_at_ocl; return true; } break; case defNeuronMHAttentionOCL: if(CheckPointer(OpenCL)==POINTER_INVALID) return false; temp_at_ocl=new CNeuronMHAttentionOCL(); if(CheckPointer(temp_at_ocl)==POINTER_INVALID) result=false; if(temp_at_ocl.Init(iOutputs,index,OpenCL,1,1,ADAM)) { m_data[index]=temp_at_ocl; return true; } break; case defNeuronMLMHAttentionOCL: if(CheckPointer(OpenCL)==POINTER_INVALID) return false; temp_mlat_ocl=new CNeuronMLMHAttentionOCL(); if(CheckPointer(temp_mlat_ocl)==POINTER_INVALID) result=false; if(temp_mlat_ocl.Init(iOutputs,index,OpenCL,1,1,1,1,0,ADAM)) { m_data[index]=temp_mlat_ocl; return true; } break; case defNeuronDropoutOCL: if(CheckPointer(OpenCL)==POINTER_INVALID) return false; temp_drop_ocl=new CNeuronDropoutOCL(); if(CheckPointer(temp_drop_ocl)==POINTER_INVALID) result=false; if(temp_drop_ocl.Init(iOutputs,index,OpenCL,1,0.1,ADAM)) { m_data[index]=temp_drop_ocl; return true; } break; default: result=false; break; } } if(result) m_data[index]=temp; //--- return (result); }
Y, por supuesto, vamos añadir la nueva clase a los métodos de despacho de la clase básica CNeuronBaseOCL.
Propagación hacia delante CNeuronBaseOCL::FeedForward.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; }
El método de propagación del gradiente de error es CNeuronBaseOCL::calcHiddenGradients.
bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; CNeuronAttentionOCL *at=NULL; CNeuronMLMHAttentionOCL *mlat=NULL; CNeuronConvOCL *conv=NULL; CNeuronDropoutOCL *dropout=NULL; switch(TargetObject.Type()) { case defNeuronBaseOCL: temp=TargetObject; return calcHiddenGradients(temp); break; case defNeuronConvOCL: conv=TargetObject; temp=GetPointer(this); return conv.calcInputGradients(temp); break; case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: at=TargetObject; temp=GetPointer(this); return at.calcInputGradients(temp); break; case defNeuronMLMHAttentionOCL: mlat=TargetObject; temp=GetPointer(this); return mlat.calcInputGradients(temp); break; case defNeuronDropoutOCL: dropout=TargetObject; temp=GetPointer(this); return dropout.calcInputGradients(temp); break; } //--- return false; }
Y, por extraño que parezca, también tenemos el método de actualización de coeficientes de peso CNeuronBaseOCL::UpdateInputWeights.
bool CNeuronBaseOCL::UpdateInputWeights(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: temp=SourceObject; return updateInputWeights(temp); break; } //--- return false; }
Recordemos: no importa cómo de puntuales e insignificantes puedan parecer los cambios anteriores, la ausencia de al menos uno de ellos hará que toda la red neuronal funcione de forma incorrecta.
Podrá familiarizarse con el código completo de todas las clases y sus métodos en los anexos.
3.Prueba
Respetando los principios de sucesión y herencia, el asesor del artículo [11] nos ha servido como base para poner a prueba el método, al que hemos añadido 4 capas de Dropout:
- después de los datos iniciales,
- después de la capa de incrustación,
- después del bloque de atención,
- después de la primera capa completamente conectada.
En el código a continuación, describimos la estructura de la red neuronal.
//--- 0 CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBaseOCL; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 1 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronDropoutOCL; desc.probability=0.2; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 2 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronConvOCL; desc.window=12; desc.step=12; desc.window_out=24; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 3 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronDropoutOCL; desc.probability=0.2; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 4 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronMLMHAttentionOCL; desc.window=24; desc.window_out=4; desc.step=8; //heads desc.layers=5; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 5 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronDropoutOCL; desc.probability=0.2; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 6 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 7 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuronDropoutOCL; desc.probability=0.2; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 8 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 9 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; desc.activation=SIGMOID; desc.optimization=ADAM;
Hemos puesto a prueba el asesor en el instrumento EURUSD, con el marco temporal H1, suministrando los datos históricos de las últimas 20 velas a la entrada de la red neuronal. La simulación de todas las arquitecturas en conjuntos de datos similares nos permite minimizar la influencia de factores externos y valorar el rendimiento de varias arquitecturas en condiciones semejantes.
Al comparar los gráficos de entrenamiento de una red neuronal con y sin Dropout, podemos ver que las primeras 30 épocas, las líneas de error de la red neuronal han sido casi paralelas, mientras que la red neuronal sin Dropout ha mostrado resultados ligeramente superiores. Pero, después de la 33ª época, observamos una reducción en el indicador del asesor experto que usa Dropout. Y después de la 35ª época, el Dropout muestra el mejor resultado, pues existe una tendencia a que el indicador disminuya. Al mismo tiempo, el asesor experto sin Dropout sigue manteniendo el error al mismo nivel.
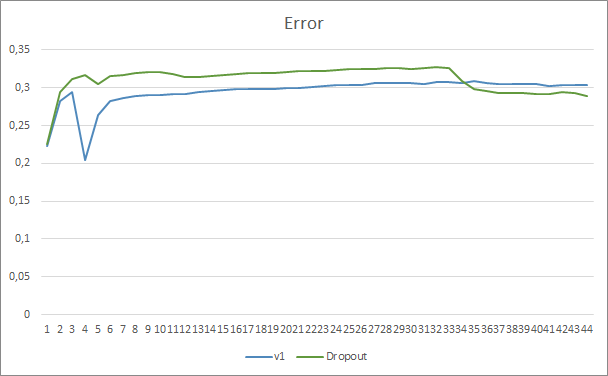
El gráfico de omisión de patrones también muestra las ventajas del asesor experto al usar la tecnología de Dropout. Y este gráfico resulta más elocuente. Con un inicio peor, el asesor experto que usa Dropout muestra inmediatamente una tendencia a reducir las omisiones, mientras que el asesor experto sin Dropout aumenta paulatinamente las omisiones.
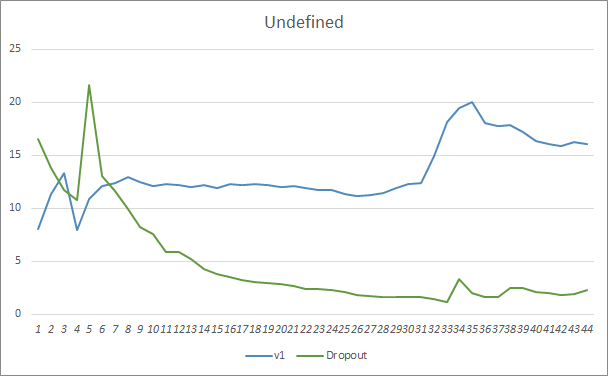
Los gráficos del nivel de acierto de los patrones predichos de ambos asesores expertos se encuentran bastante cerca y prácticamente se entrelazan. Después de 44 épocas de entrenamiento, la ventaja del asesor experto con Dropout es solo del 0.5%.
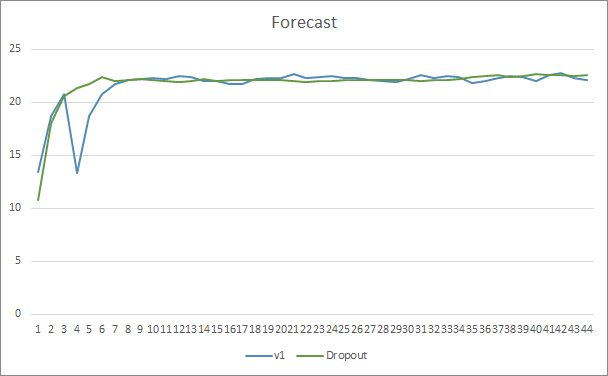
Conclusión
En este artículo, hemos comenzado a analizar los métodos para aumentar la convergencia de las redes neuronales, y también nos hemos familiarizado con uno de esos métodos, el Dropout. Tras añadirlo a uno de los asesores expertos creados anteriormente, hemos visto su efectividad en las simulaciones. Obviamente, el uso de este método puede incrementar los costes derivados del entrenamiento de una red neuronal, pero estos se amortizarán gracias al aumento de la eficiencia del resultado final.
Animamos al lector a probar este método en sus diseños y valorar su efectividad.
Enlaces
- Redes neuronales: así de sencillo
- Redes neuronales: así de sencillo (Parte 2): Entrenamiento y prueba de la red
- Redes neuronales: así de sencillo (Parte 3): Redes convolucionales
- Redes neuronales: así de sencillo (Parte 4): Redes recurrentes
- Redes neuronales: así de sencillo (Parte 5): Cálculos multihilo en OpenCL
- Redes neuronales: así de sencillo (Parte 6): Experimentos con la tasa de aprendizaje de la red neuronal
- Redes neuronales: así de sencillo (Parte 7): Métodos de optimización adaptativos
- Redes neuronales: así de sencillo (Parte 8): Mecanismos de atención
- Redes neuronales: así de sencillo (Parte 9): Documentamos el trabajo realizado
- Redes neuronales: así de sencillo (Parte 10): Multi-Head Attention (atención multi-cabeza)
- Redes neuronales: así de sencillo (Parte 11): Variaciones de GTP
- Improving neural networks by preventing co-adaptation of feature detectors
- Valoraciones estadísticas
…
Programas utilizados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Fractal_OCL_AttentionMLMH.mq5 | Asesor | Asesor con la red neuronal de clasificación (3 neuronas en la capa de salida) con uso de la arquitectura GPT, 5 capas de atención |
| 2 | Fractal_OCL_AttentionMLMH_d.mq5 | Asesor | Asesor con la red neuronal de clasificación (3 neuronas en la capa de salida) con uso de la arquitectura GPT, 5 capas de atención + Dropout |
| 3 | NeuroNet.mqh | Biblioteca de clase | Biblioteca de clases para crear la red neuronal |
| 4 | NeuroNet.cl | Biblioteca | Biblioteca de código del programa OpenCL |
| 5 | NN.chm | Guía de ayuda de HTML | Archivo CHM compilado de ayuda sobre la biblioteca. |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/9112
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Aprendizaje de máquinas en sistemas comerciales con cuadrícula y martingale. ¿Apostaría por ello?
Aprendizaje de máquinas en sistemas comerciales con cuadrícula y martingale. ¿Apostaría por ello?
 Aproximación por fuerza bruta a la búsqueda de patrones (Parte IV): Funcionalidad mínima
Aproximación por fuerza bruta a la búsqueda de patrones (Parte IV): Funcionalidad mínima
 Técnicas útiles y exóticas para el comercio automático
Técnicas útiles y exóticas para el comercio automático
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
¿Supongo que nada funciona sin OCL? Que pena, no soy gamer y la tarjeta es old....