Neuronale Netze leicht gemacht (Teil 8): Attention-Mechanismen
1 442
0
Inhalt
- Einführung
- 1. Aufmerksamkeitsmechanismen
- 2. Der Algorithmus der Self-Attention
- 3. Umsetzung
- 3.1. Erweiterung des Convolutional Layers
- 3.2. Klasse der Self-Attention
- 3.3. Feed-Forward der Self-Attention
- 3.4. Feed-Backward der Self-Attention
- 3.5. Änderungen in den Basisklassen des neuronalen Netzwerks
- 4. Tests
- Schlussfolgerungen
- Referenzen
- Die Programme dieses Artikels
Einführung
In früheren Artikeln haben wir bereits verschiedene Möglichkeiten zur Organisation neuronaler Netze getestet. Dazu gehören Convolutional-Netze [3], die für Bildverarbeitungsalgorithmen verwendet werden, sowie rekurrente neuronale Netze [4], die für die Arbeit mit Sequenzen verwendet werden, bei denen nicht nur die Werte wichtig sind, sondern auch ihre Position im Quelldatensatz.
Voll verbundene und Convolutional neuronale Netze haben eine feste Größe der Eingangssequenz. Rekurrente neuronale Netze ermöglichen eine leichte Erweiterung der analysierten Sequenz, indem sie versteckte Zustände aus vorherigen Iterationen übernehmen. Aber auch ihre Effektivität nimmt mit zunehmender Sequenzgröße ab. Im Jahr 2014 wurde der erste Attention-Mechanismus für die maschinelle Übersetzung vorgestellt. Der Zweck des Mechanismus war es, die für das Zielübersetzungswort relevantesten Blöcke des Ausgangssatzes (Kontext) zu bestimmen und hervorzuheben. Ein solcher intuitiver Ansatz hat die Qualität der von neuronalen Netzen übersetzten Texte deutlich verbessert.
1. Aufmerksamkeitsmechanismen
Bei der Analyse des Kerzenchart eines Symbols definieren wir Trends und Tendenzen, und bestimmen auch deren Handelsbereiche. Das heißt, wir wählen einige Objekte aus dem Gesamtbild aus und richten unsere Aufmerksamkeit auf sie. Wir verstehen, dass die Objekte das zukünftige Preisverhalten beeinflussen. Um einen solchen Ansatz zu implementieren, haben die Entwickler bereits 2014 den ersten Algorithmus vorgeschlagen, der Abhängigkeiten zwischen den Elementen der Eingangs- und Ausgangssequenzen analysiert und hervorhebt [8]. Der vorgeschlagene Algorithmus wird "Generalized Attention Mechanism" genannt. Er wurde ursprünglich für den Einsatz in maschinellen Übersetzungsmodellen mit rekurrenten Netzen als Lösung für das Problem des Langzeitgedächtnisses bei der Übersetzung langer Sätze vorgeschlagen. Dieser Ansatz verbesserte die Ergebnisse der zuvor betrachteten rekurrenten neuronalen Netze, die auf LSTM-Blöcken basieren, erheblich [4].
Das klassische maschinelle Übersetzungsmodell mit rekurrenten Netzen besteht aus zwei Blöcken, dem Encoder und dem Decoder. Der erste Block kodiert die Eingabesequenz in der Ausgangssprache in einen Kontextvektor, und der zweite Block dekodiert den resultierenden Kontext in eine Sequenz von Wörtern in der Zielsprache. Wenn die Länge der Eingabesequenz zunimmt, nimmt der Einfluss der ersten Wörter auf den endgültigen Satzkontext ab. Infolgedessen nimmt die Qualität der Übersetzung ab. Durch die Verwendung von LSTM-Blöcken wurden die Fähigkeiten des Modells zwar leicht erhöht, sie blieben aber dennoch begrenzt.
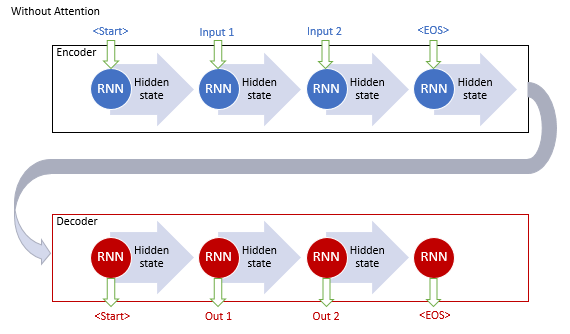
Die Autoren des allgemeinen Attention-Mechanismus schlugen vor, eine zusätzliche Schicht zu verwenden, um die versteckten Zustände aller rekurrenten Blöcke der Eingangssequenz zu akkumulieren. Außerdem sollte der Mechanismus während der Sequenzdekodierung den Einfluss jedes Elements der Eingangssequenz auf das aktuelle Wort der Ausgangssequenz bewerten und dem Dekoder den relevantesten Teil des Kontexts vorschlagen.
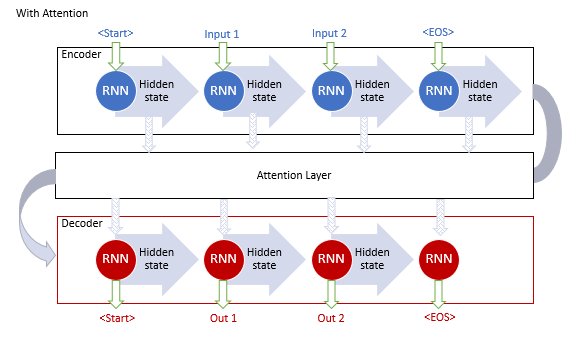
Dieser Betriebsalgorithmus des Mechanismus umfasste die folgenden Iterationen:
1. Erzeugung von versteckten Zuständen des Encoders und deren Akkumulation im Attention-Block.
2. Auswertung der paarweisen Abhängigkeiten zwischen den versteckten Zuständen jedes Encoder-Elements und dem letzten versteckten Zustand des Decoders.
3. Kombinieren der resultierenden Scores zu einem einzigen Vektor und Normalisieren mit der Softmax-Funktion.
4. Berechnung des Kontextvektors durch Multiplikation aller versteckten Zustände des Encoders mit ihren entsprechenden Alignment-Scores.
5. Dekodierung des Kontextvektors und Kombination des resultierenden Wertes mit dem vorherigen Zustand des Dekoders.
Alle Iterationen werden wiederholt, bis das Satzende-Signal empfangen wird.
Der vorgeschlagene Mechanismus ermöglichte die Lösung des Problems mit einer begrenzten Länge der Eingabesequenz und sorgte für die Verbesserung der Qualität der maschinellen Übersetzung durch rekurrente neuronale Netze. Die Methode wurde populär und es wurden weitere Varianten erstellt. Im Jahr 2012 schlug Minh-Thang Luong in seinem Artikel [9] eine neue Variante der Attention-Methode vor. Die Hauptunterschiede des neuen Ansatzes waren die Verwendung von drei Funktionen zur Berechnung des Grades der Abhängigkeiten und der Punkt der Verwendung des Attention-Mechanismus im Decoder.
Die oben beschriebenen Modelle verwenden rekurrente Blöcke, die rechenintensiv zu trainieren sind. Im Juni 2017 wurde im Artikel [10] eine weitere Variante vorgeschlagen. Dabei handelte es sich um eine neue Architektur des neuronalen Netzwerks Transformer, die keine rekurrenten Blöcke verwendete, sondern einen neuen Algorithmus für Self-Attention (Selbst-Aufmerksamkeit). Anders als der zuvor beschriebene Algorithmus analysiert Self-Attention paarweise Abhängigkeiten innerhalb einer Sequenz. Transformer zeigte beim Testen bessere Ergebnisse. Heute werden dieses Modell und seine Derivate in vielen Modellen verwendet, einschließlich GPT-2 und GPT-3. Betrachten wir den Algorithmus Self-Attention etwas genauer.
2. Der Algorithmus der Self-Attention
Die Transformer-Architektur basiert auf sequentiellen Encoder- und Decoder-Blöcken mit einer ähnlichen Architektur. Jeder der Blöcke umfasst mehrere identische Schichten mit unterschiedlichen Gewichtsmatrizen.
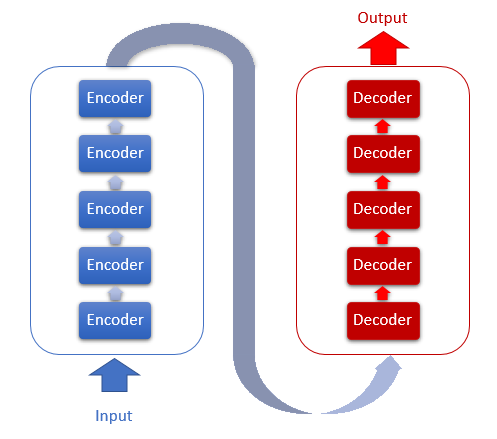
Jede Encoder-Schicht enthält 2 innere Schichten: Self-Attention und Feed Forward. Die Feed Forward-Schicht enthält zwei vollständig verbundene Schichten von Neuronen mit der ReLU-Aktivierungsfunktion auf der inneren Schicht. Jede Schicht wird auf alle Elemente der Sequenz mit den gleichen Gewichten angewendet, was gleichzeitige unabhängige Berechnungen für alle Elemente der Sequenz in parallelen Threads ermöglicht.
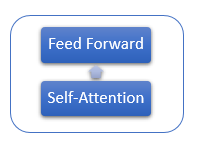
Die Decoder-Schicht ist ähnlich aufgebaut, hat aber zusätzlich eine Self-Attention, die die Abhängigkeiten zwischen den Eingangs- und Ausgangssequenzen analysiert.
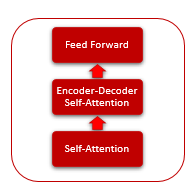
Der Mechanismus der Self-Attention selbst umfasst mehrere iterative Aktionen, die für jedes Element der Sequenz angewendet werden.
1. Zunächst werden die Vektoren Query, Key und Value berechnet. Diese Vektoren erhält man durch Multiplikation jedes Elements der Sequenz mit der entsprechenden Matrix WQ, WK und WV.
2. Als Nächstes werden die paarweisen Abhängigkeiten zwischen den Elementen der Sequenz bestimmt. Dazu wird der Query-Vektor mit den Key-Vektoren aller Elemente der Sequenz multipliziert. Diese Iteration wird für den Query-Vektor jedes Elements der Sequenz wiederholt. Als Ergebnis dieser Iteration erhalten wir eine Score-Matrix der Größe N*N, wobei N die Größe der Sequenz ist.
3. Der nächste Schritt besteht darin, den resultierenden Wert durch die Quadratwurzel der Dimension des Key-Vektors zu teilen und ihn durch die Softmax-Funktion im Kontext jeder Abfrage zu normalisieren. So erhalten wir die Koeffizienten der paarweisen Interdependenz zwischen den Elementen der Sequenz.
4. Multiplizieren wir jeden Wertvektor mit dem entsprechenden Interdependenzkoeffizienten, um den angepassten Elementwert zu erhalten. Der Zweck dieser Iteration ist es, sich auf relevante Elemente zu konzentrieren und den Einfluss irrelevanter Werte zu reduzieren.
5. Als Nächstes werden alle angepassten Wertvektoren für jedes Element summiert. Das Ergebnis dieser Operation ist der Vektor der Ausgangswerte der Self-Attention-Schicht.
Die Ergebnisse der Iterationen jeder Schicht werden zur Eingabesequenz addiert und mit der Formel normalisiert.
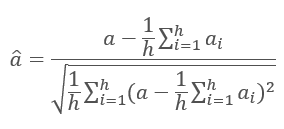
Die Normalisierung von Schichten des neuronalen Netzes wird in dem Artikel [11] ausführlicher behandelt.
3. Umsetzung
Ich schlage vor, den Mechanismus der Self-Attention in unserer Implementierung zu verwenden. Betrachten wir die Möglichkeiten der Implementierung.
3.1. Erweiterung des Convolutional Layers
Wir beginnen mit der ersten Aktion des Algorithmus der Self-Attention — der Berechnung der Vektoren Query, Key und Value. Geben Sie eine Datenmatrix ein, die Features für jeden Bar der analysierten Sequenz enthält. Nehmen Sie die Features eines Candlesticks einzeln und multiplizieren Sie sie mit der Gewichtsmatrix, um einen Vektor zu erhalten. Dies ähnelt einer Convolutional Schicht, wie sie im Artikel [3] betrachtet wurde. Allerdings ist in diesem Fall die Ausgabe keine Zahl, sondern ein Vektor mit fester Größe. Um dieses Problem zu lösen, erweitern wir die Klasse CNeuronConvOCL, die für den Betrieb einer Convolutional Schicht des neuronalen Netzes zuständig ist. Wir fügen die Variable iWindowOut hinzu, die die Größe der Ausgabevektoren speichern wird. Implementieren wir entsprechende Änderungen in den Methoden der Klasse.
class CNeuronConvOCL : public CNeuronProofOCL { protected: uint iWindowOut; //--- CBufferDouble *WeightsConv; CBufferDouble *DeltaWeightsConv; CBufferDouble *FirstMomentumConv; CBufferDouble *SecondMomentumConv; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronConvOCL(void) : iWindowOut(1) { activation=LReLU; } ~CNeuronConvOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window, uint step, uint window_out, uint units_count, ENUM_OPTIMIZATION optimization_type); //--- virtual bool SetGradientIndex(int index) { return Gradient.BufferSet(index); } //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); virtual int Type(void) const { return defNeuronConvOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); };
Fügen wir im OpenCL-Kernel FeedForwardConv einen Parameter zur Ermittlung der Größe des Ausgangsvektors hinzu. Außerdem ergänzen wir die Berechnung des Offsets des verarbeiteten Segments des Ausgangsvektors im allgemeinen Vektor, am Ausgang der Convolutional Schicht, und implementieren eine zusätzliche Schleife durch Elemente der Ausgangsschicht.
__kernel void FeedForwardConv(__global double *matrix_w, __global double *matrix_i, __global double *matrix_o, int inputs, int step, int window_in, int window_out, uint activation) { int i=get_global_id(0); int w_in=window_in; int w_out=window_out; double sum=0.0; double4 inp, weight; int shift_out=w_out*i; int shift_in=step*i; for(int out=0;out<w_out;out++) { int shift=(w_in+1)*out; int stop=(w_in<=(inputs-shift_in) ? w_in : (inputs-shift_in)); for(int k=0; k<=stop; k=k+4) { switch(stop-k) { case 0: inp=(double4)(1,0,0,0); weight=(double4)(matrix_w[shift+k],0,0,0); break; case 1: inp=(double4)(matrix_i[shift_in+k],1,0,0); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],0,0); break; case 2: inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],1,0); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],0); break; case 3: inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],matrix_i[shift_in+k+2],1); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]); break; default: inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],matrix_i[shift_in+k+2],matrix_i[shift_in+k+3]); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]); break; } sum+=dot(inp,weight); } switch(activation) { case 0: sum=tanh(sum); break; case 1: sum=1/(1+exp(-clamp(sum,-50.0,50.0))); break; case 2: if(sum<0) sum*=0.01; break; default: break; } matrix_o[out+shift_out]=sum; } }
Vergessen wir nicht, beim Aufruf dieses Kernels die Übergabe eines zusätzlichen Parameters zu aktivieren.
bool CNeuronConvOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=Output.Total()/iWindowOut; OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_w,WeightsConv.GetIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_i,NeuronOCL.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_o,Output.GetIndex()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_inputs,NeuronOCL.Neurons()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_step,iStep); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_window_in,iWindow); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffс_window_out,iWindowOut); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_activation,(int)activation); if(!OpenCL.Execute(def_k_FeedForwardConv,1,global_work_offset,global_work_size)) { printf("Error of execution kernel FeedForwardProof: %d",GetLastError()); return false; } //--- return Output.BufferRead(); }
Ähnliche Änderungen wurden in Kernel und in Methoden zur Neuberechnung von Gradienten (calcInputGradients) und zur Aktualisierung der Gewichtsmatrix (updateInputWeights) implementiert. Der vollständige Code aller Methoden und Funktionen steht im Anhang zur Verfügung.
3.2. Klasse der Self-Attention
Der vollständige Code aller Methoden und Funktionen steht im Anhang zur Verfügung. Dazu legen wir die Klasse CNeuronAttentionOCL an. Da sich alle unsere Operationen für jedes Element wiederholen und unabhängig voneinander ausgeführt werden, wollen wir einige der Operationen in die modernisierten Convolutional Schichten verlagern. Innerhalb unseres Attention-Blocks erstellen wir die Convolutional Schichten Querys, Keys, Values, die für die Erzeugung der entsprechenden Vektoren sowie für die Übergabe der Gradienten und die Aktualisierung der Gewichtsmatrix zuständig sein werden. Der FeedForward-Block wird ebenfalls mit den Convolutional Schichten FF1 und FF2 realisiert. Die Werte der Score-Matrix werden im Puffer Scores gespeichert; die Ergebnisse der Attention-Methode werden in der inneren Neuronenschicht der Basisklasse AttentionOut gespeichert.
Hier achten wir auf den Unterschied zwischen der Ausgabe des Aufmerksamkeitsalgorithmus und der Ausgabe der gesamten Klasse der Self-Attention. Erstere entsteht nach der Ausführung des Self-Attention-Algorithmus durch Anpassung der Werte der Value-Vektoren; sie wird in AttentionOut gespeichert. Der zweite entsteht nach der Verarbeitung von FeedForward - er wird im Ausgabepuffer der Basisklasse gespeichert.
class CNeuronAttentionOCL : public CNeuronBaseOCL { protected: CNeuronConvOCL *Querys; CNeuronConvOCL *Keys; CNeuronConvOCL *Values; CBufferDouble *Scores; CNeuronBaseOCL *AttentionOut; CNeuronConvOCL *FF1; CNeuronConvOCL *FF2; //--- uint iWindow; uint iUnits; //--- virtual bool feedForward(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *prevLayer); public: CNeuronAttentionOCL(void) : iWindow(1), iUnits(0) {}; ~CNeuronAttentionOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); //--- virtual int Type(void) const { return defNeuronAttentionOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); };
In den Variablen iWindows und iUnits werden wir die Größe des Ausgabefensters bzw. die Anzahl der Elemente in der Ausgabereihenfolge speichern.
Die Klasse wird in der Methode Init initialisiert. Die Methode erhält als Parameter die Ordnungszahl des Elements, einen Zeiger auf das Objekt COpenCL, die Fenstergröße, die Anzahl der Elemente und die Optimierungsmethode. Am Anfang der Methode rufen Sie die entsprechende Methode der Elternklasse auf.
bool CNeuronAttentionOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window,uint units_count,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronBaseOCL::Init(numOutputs,myIndex,open_cl,units_count*window,optimization_type)) return false;
Deklarieren und initialisieren wir anschließend die Instanzen der Klasse des Convolutional Netzes zur Berechnung der Vektoren Querys, Keys und Values.
//--- if(CheckPointer(Querys)==POINTER_INVALID) { Querys=new CNeuronConvOCL(); if(CheckPointer(Querys)==POINTER_INVALID) return false; if(!Querys.Init(0,0,open_cl,window,window,window,units_count,optimization_type)) return false; Querys.SetActivationFunction(TANH); } //--- if(CheckPointer(Keys)==POINTER_INVALID) { Keys=new CNeuronConvOCL(); if(CheckPointer(Keys)==POINTER_INVALID) return false; if(!Keys.Init(0,1,open_cl,window,window,window,units_count,optimization_type)) return false; Keys.SetActivationFunction(TANH); } //--- if(CheckPointer(Values)==POINTER_INVALID) { Values=new CNeuronConvOCL(); if(CheckPointer(Values)==POINTER_INVALID) return false; if(!Values.Init(0,2,open_cl,window,window,window,units_count,optimization_type)) return false; Values.SetActivationFunction(None); }
Weiter im Algorithmus deklarieren wir den Scores-Puffer. Achten wir auf die Größe des Puffers - er muss genügend Speicherplatz haben, um eine quadratische Matrix zu speichern, deren Seiten der Anzahl der Elemente in der Sequenz entsprechen.
if(CheckPointer(Scores)==POINTER_INVALID) { Scores=new CBufferDouble(); if(CheckPointer(Scores)==POINTER_INVALID) return false; } if(!Scores.BufferInit(units_count*units_count,0.0)) return false; if(!Scores.BufferCreate(OpenCL)) return false;
Deklarieren wir außerdem die AttentionOut-Schicht der Neuronen. Diese Schicht dient als Puffer für die Speicherung der Ergebnisse der Self-Attention. Gleichzeitig wird sie als Eingangsschicht für den FeedForward-Block verwendet. Ihre Größe entspricht dem Produkt aus der Fensterbreite und der Anzahl der Elemente.
if(CheckPointer(AttentionOut)==POINTER_INVALID) { AttentionOut=new CNeuronBaseOCL(); if(CheckPointer(AttentionOut)==POINTER_INVALID) return false; if(!AttentionOut.Init(0,3,open_cl,window*units_count,optimization_type)) return false; AttentionOut.SetActivationFunction(None); }
Wir initialisieren zwei Instanzen der Convolutional Schicht, um den FeedForward-Block zu implementieren. Beachten Sie, dass die erste Instanz (versteckte Schicht) ein 2-fach breiteres Fenster ausgibt und eine LReLU-Aktivierungsfunktion (ReLU mit "Leckage") besitzt. Für die zweite Schicht (FF2) ersetzen wir den Gradientenpuffer durch den Gradientenpuffer der Elternklasse mit der Methode SetGradientIndex. Durch das Kopieren des Puffers entfällt das Kopieren von Daten.
if(CheckPointer(FF1)==POINTER_INVALID) { FF1=new CNeuronConvOCL(); if(CheckPointer(FF1)==POINTER_INVALID) return false; if(!FF1.Init(0,4,open_cl,window,window,window*2,units_count,optimization_type)) return false; FF1.SetActivationFunction(LReLU); } //--- if(CheckPointer(FF2)==POINTER_INVALID) { FF2=new CNeuronConvOCL(); if(CheckPointer(FF2)==POINTER_INVALID) return false; if(!FF2.Init(0,5,open_cl,window*2,window*2,window,units_count,optimization_type)) return false; FF2.SetActivationFunction(None); FF2.SetGradientIndex(Gradient.GetIndex()); }
Speichern wir die wichtigsten Parameter am Ende der Methode.
iWindow=window; iUnits=units_count; activation=FF2.Activation(); //--- return true; }
3.3. Feed-Forward der Self-Attention
Betrachten wir als Nächstes die feedForward-Methode der Klasse CNeuronAttentionOCL. Die Methode erhält als Parameter einen Zeiger auf die vorherige Schicht des neuronalen Netzes. Überprüfen wir also zunächst die Gültigkeit des empfangenen Zeigers.
bool CNeuronAttentionOCL::feedForward(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
Wir normalisieren vor der weiteren Verarbeitung der Daten die Eingangsdaten. Dieser Schritt wird vom Self-Attention-Mechanismus des Autors nicht vorgesehen. Ich habe ihn jedoch aufgrund von Testergebnissen hinzugefügt, um einen Überlauf während der Normalisierungsphase der Score-Matrix zu verhindern. Es wurde ein spezieller Kernel erstellt, um die Daten zu normalisieren. Er wird in der feedForward-Methode aufgerufen.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=1;
OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getOutputIndex());
OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons());
if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Normalize: %d",GetLastError());
return false;
}
if(!prevLayer.Output.BufferRead())
return false;
}
Lassen Sie uns einen Blick in den Normalisierungskern werfen. Am Anfang des Kerns berechnen wir den Offset zum ersten Element der normalisierten Sequenz. Dann berechnen wir den Durchschnittswert für die normalisierte Sequenz und die Standardabweichung. Am Ende des Kerns aktualisieren wir die Daten im Puffer.
__kernel void Normalize(__global double *buffer, int dimension) { int n=get_global_id(0); int shift=n*dimension; double mean=0; for(int i=0;i<dimension;i++) mean+=buffer[shift+i]; mean/=dimension; double variance=0; for(int i=0;i<dimension;i++) variance+=pow(buffer[shift+i]-mean,2); variance=sqrt(variance/dimension); for(int i=0;i<dimension;i++) buffer[shift+i]=(buffer[shift+i]-mean)/(variance==0 ? 1 : variance); }
Nachdem wir die Quelldaten normalisiert haben, berechnen wir die Vektoren Querys, Keys und Values. Dazu rufen wir die Methode FeedForward der entsprechenden Instanz der Klasse Convolutional Schicht auf (diese Methode wurde bereits früher betrachtet).
if(CheckPointer(Querys)==POINTER_INVALID || !Querys.FeedForward(prevLayer)) return false; if(CheckPointer(Keys)==POINTER_INVALID || !Keys.FeedForward(prevLayer)) return false; if(CheckPointer(Values)==POINTER_INVALID || !Values.FeedForward(prevLayer)) return false;
Im weiteren Verlauf des Self-Attention-Algorithmus wird die Score-Matrix berechnet. Die Berechnungen werden auf einer GPU mit OpenCL durchgeführt. Implementieren wir den Kernel-Aufruf in der Hauptprogramm-Methode. Die Anzahl der aufgerufenen Threads ist gleich der Anzahl der Einheiten in der Klasse. Jeder Thread wird in seiner Fenstergröße arbeiten. Mit anderen Worten: Jeder Thread nimmt seinen eigenen Query-Vektor eines Elements und gleicht ihn mit den Key-Vektoren aller Elemente der Sequenz ab.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_querys,Querys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_keys,Keys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_score,Scores.GetIndex());
OpenCL.SetArgument(def_k_AttentionScore,def_k_as_dimension,iWindow);
if(!OpenCL.Execute(def_k_AttentionScore,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel AttentionScore: %d",GetLastError());
return false;
}
if(!Scores.BufferRead())
return false;
}
Wir bestimmen zu Beginn des Kerns die Offsets des Anfangselements mit Hilfe der Arrays 'querys' und 'score', berechnen den Koeffizienten, um die erhaltenen Werte zu reduzieren und setzen die Variable zur Berechnung des Betrags, den wir bei der Normalisierung der Werte benötigen, auf Null. Als nächstes implementieren wir eine Schleife über alle Elemente der Schlüsselmatrix, während der Berechnung der entsprechenden Abhängigkeiten. Bitte beachten Sie, dass der von uns betrachtete Kernel die Schritte zur Berechnung der Score-Matrix und zur Normalisierung kombiniert. Daher sollten wir nach der Berechnung der Produkte aus den Vektoren Query und Key den resultierenden Wert durch einen Koeffizienten teilen und den Exponenten des erhaltenen Wertes berechnen. Der resultierende Exponent sollte in einer Matrix gespeichert und zur Summe addiert werden. Am Ende der Schleife implementieren wir die zweite Schleife, in der alle in der vorherigen Schleife gespeicherten Werte durch die berechnete Summe der Exponenten geteilt werden. Die Kernel-Ausgabe wird die berechnete und normalisierte Score-Matrix enthalten.
__kernel void AttentionScore(__global double *querys, __global double *keys, __global double *score, int dimension) { int q=get_global_id(0); int shift_q=q*dimension; int units=get_global_size(0); int shift_s=q*units; double koef=sqrt((double)(units*dimension)); if(koef<1) koef=1; double sum=0; for(int k=0;k<units;k++) { double result=0; int shift_k=k*dimension; for(int i=0;i<dimension;i++) result+=(querys[shift_q+i]*keys[shift_k+i]); result=exp(result/koef); score[shift_s+k]=result; sum+=result; } for(int k=0;k<units;k++) score[shift_s+k]/=sum; }
Betrachten wir weiter den Self-Attention-Algorithmus. Nach der Normalisierung der Score-Matrix ist es notwendig, die Wertevektoren für die erhaltenen Werte zu korrigieren und die erhaltenen Vektoren im Kontext der Elemente der Eingangssequenz zu summieren. Am Ausgang des Self-Attention-Blocks werden die erhaltenen Werte summiert und zur Eingangssequenz hinzugefügt. Alle diese Iterationen werden im nächsten AttentionOut-Kernel zusammengeführt. Der Kernelaufruf ist im Hauptprogrammcode implementiert. Vergessen wir nicht, dass dieser Kernel mit einer Menge von Threads auf zwei Arten ausgeführt wird: nach Elementen der Sequenz (iUnits) und nach der Anzahl der Merkmale für jedes Element (iWindow). Die resultierenden Werte werden im Ausgabepuffer der AttentionOut-Schicht gespeichert.
{
uint global_work_offset[2]={0,0};
uint global_work_size[2];
global_work_size[0]=iUnits;
global_work_size[1]=iWindow;
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_scores,Scores.GetIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_inputs,prevLayer.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_values,Values.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_out,AttentionOut.getOutputIndex());
if(!OpenCL.Execute(def_k_AttentionOut,2,global_work_offset,global_work_size))
{
printf("Error of execution kernel Attention Out: %d",GetLastError());
return false;
}
double temp[];
if(!AttentionOut.getOutputVal(temp))
return false;
}
Bestimmen wir im Kernelkörper den Offset für das verarbeitete Element in den Vektoren der Eingangs- und Ausgangssequenzen. Dann organisieren wir eine Schleife, um die Produkte von Scores durch die entsprechenden Value-Werte zu summieren. Sobald die zyklischen Iterationen abgeschlossen sind, addieren wir die resultierende Summe zu dem Eingangsvektor, den wir von der vorherigen Schicht des neuronalen Netzes erhalten haben. Schreiben wir das Ergebnis in den Ausgangspuffer.
__kernel void AttentionOut(__global double *scores, __global double *values, __global double *inputs, __global double *out) { int units=get_global_size(0); int u=get_global_id(0); int d=get_global_id(1); int dimension=get_global_size(1); int shift=u*dimension+d; double result=0; for(int i=0;i<units;i++) result+=scores[u*units+i]*values[i*dimension+d]; out[shift]=result+inputs[shift]; }
An diesem Punkt kann der Self-Attention-Algorithmus als abgeschlossen betrachtet werden. Jetzt müssen wir die resultierenden Daten nur noch mit der oben beschriebenen Methode normalisieren. Der einzige Unterschied besteht im Normalisierungspuffer.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=1;
OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,AttentionOut.getOutputIndex());
OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,AttentionOut.Neurons());
if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Normalize: %d",GetLastError());
return false;
}
double temp[];
if(!AttentionOut.getOutputVal(temp))
return false;
}
Des Weiteren durchlaufen wir nach dem Transformer-Encoder-Algorithmus jedes Element der Sequenz durch ein vollverknüpftes neuronales Netz mit einer versteckten Schicht. Dabei wird auf alle Elemente der Sequenz die gleiche Gewichtsmatrix angewendet. Ich habe diesen Prozess unter Verwendung einer modernisierten Convolutional Schicht Klasse implementiert. Im Methodencode rufe ich sequentiell die FeedForward-Methoden der entsprechenden Instanzen der Convolutional Klasse auf.
if(!FF1.FeedForward(AttentionOut)) return false; if(!FF2.FeedForward(FF1)) return false;
Um das Feed-Forward-Verfahren zu vervollständigen, ist es notwendig, die Ergebnisse des vollständig verbundenen Netzwerkdurchlaufs mit den Ergebnissen des Self-Attention-Mechanismus zu summieren. Zu diesem Zweck habe ich einen Kernel der Addition zweier Vektoren erstellt, der am Ende des Feed-Forward-Verfahrens aufgerufen wird.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,FF2.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,Output.GetIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
if(!Output.BufferRead())
return false;
}
//---
return true;
}
Innerhalb des Kerns wird eine einfache Schleife mit elementweiser Summierung der eingehenden Vektorwerte organisiert.
__kernel void SumMatrix(__global double *matrix1, __global double *matrix2, __global double *matrix_out, int dimension) { const int i=get_global_id(0)*dimension; for(int k=0;k<dimension;k++) matrix_out[i+k]=matrix1[i+k]+matrix2[i+k]; }
Der vollständige Code aller Methoden und Funktionen steht im Anhang zur Verfügung.
3.4. Feed-Backward der Self-Attention
Auf den Feed-Forward-Durchgang folgt Feed-Backward, bei dem der Fehler in niedrigere Ebenen des neuronalen Netzes eingespeist wird und die Gewichtsmatrix angepasst wird, um optimale Ergebnisse auszuwählen. Die Klasse erhält den Fehlergradienten von der oberen vollverknüpften Schicht des neuronalen Netzes, wobei die in Artikel 5 beschriebene Elternklassenmethode verwendet wird. Der weitere Mechanismus für die Zuführung des Fehlergradienten ist stark verbesserungswürdig, was auf die Komplexität der internen Architektur zurückzuführen ist.
Um den Fehlergradienten an die inneren Convolutional Schichten und an die vorherige neuronale Schicht des Netzes zu übergeben, erstellen wir die Methode calcInputGradients. Die Methode erhält als Parameter einen Zeiger auf die vorhergehende Schicht von Neuronen. Wie immer überprüfen Sie zuerst die Gültigkeit des empfangenen Zeigers. Dann rufen wir in umgekehrter Reihenfolge nacheinander die Methoden der Convolutional Schichten des Feed Forward FF2 und FF1 Blocks auf. Wir verwenden die Puffersubstitution, so dass die innere FF2-Schicht den Fehlergradienten direkt von der nächsten neuronalen Netzschicht unter Verwendung der Methoden der übergeordneten Klasse erhält.
bool CNeuronAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- if(!FF2.calcInputGradients(FF1)) return false; if(!FF1.calcInputGradients(AttentionOut)) return false;
Da wir am Ausgang des Feed-Forward-Durchgangs die Ergebnisse von Feed Forward und Self-Attention aufsummiert haben, kommt auch der Fehlergradient in zwei Zweigen. Daher wird der aus FF1 erhaltene Fehlergradient mit dem aus der nächsten Schicht des neuronalen Netzes erhaltenen Fehlergradienten aufsummiert. Der Vektorsummen-Kernel ist oben beschrieben. Fügen wir also seinen Aufruf hinzu.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,Gradient.GetIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
double temp[];
if(AttentionOut.getGradient(temp)<=0)
return false;
}
Im nächsten Schritt propagieren Sie den Fehlergradienten auf Querys, Keys und Values. Der Fehlergradient wird an die Vektoren im Kernel AttentionIsideGradients übergeben. Rufen wir ihn in der folgenden Methode mit einem Satz von Threads in zwei Dimensionen auf.
{
uint global_work_offset[2]={0,0};
uint global_work_size[2];
global_work_size[0]=iUnits;
global_work_size[1]=iWindow;
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_gradient,AttentionOut.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys,Keys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys_g,Keys.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys,Querys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys_g,Querys.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values,Values.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values_g,Values.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_scores,Scores.GetIndex());
if(!OpenCL.Execute(def_k_AttentionGradients,2,global_work_offset,global_work_size))
{
printf("Error of execution kernel AttentionGradients: %d",GetLastError());
return false;
}
double temp[];
if(Keys.getGradient(temp)<=0)
return false;
}
Der Kernel erhält Zeiger auf Datenpuffer in Parametern. Die Dimensionen werden zu Beginn des Kernels durch die Anzahl der laufenden Threads bestimmt. Dann berechnen wir den Korrekturfaktor und laufen in einer Schleife über alle Elemente der Sequenz. Innerhalb der Schleife berechnen wir zunächst den Fehlergradienten auf den Value-Vektor, indem wir den Gradientenvektor mit dem entsprechenden Score-Vektor multiplizieren. Beachten Sie, dass der Fehlergradient durch 2 geteilt wird. Das liegt daran, dass wir ihn im vorherigen Schritt aufsummiert und damit den Fehler verdoppelt haben. Jetzt teilen wir ihn durch zwei, um einen Durchschnittswert zu erhalten.
__kernel void AttentionIsideGradients(__global double *querys,__global double *querys_g, __global double *keys,__global double *keys_g, __global double *values,__global double *values_g, __global double *scores, __global double *gradient) { int u=get_global_id(0); int d=get_global_id(1); int units=get_global_size(0); int dimension=get_global_size(1); double koef=sqrt((double)(units*dimension)); if(koef<1) koef=1; //--- double vg=0; double qg=0; double kg=0; for(int iu=0;iu<units;iu++) { double g=gradient[iu*dimension+d]/2; double sc=scores[iu*units+u]; vg+=sc*g;
Organisieren wir als Nächstes eine verschachtelte Schleife, um den Gradienten an den Elementen der Score-Matrix zu definieren. Danach berechnen Sie den Gradienten der Elemente der Vektoren Querys und Keys. Am Ende der externen Schleife weisen Sie die berechneten Gradienten den entsprechenden globalen Puffern zu.
//--- double sqg=0; double skg=0; for(int id=0;id<dimension;id++) { sqg+=values[iu*dimension+id]*gradient[u*dimension+id]/2; skg+=values[u*dimension+id]*gradient[iu*dimension+id]/2; } qg+=(scores[u*units+iu]==0 || scores[u*units+iu]==1 ? 0.0001 : scores[u*units+iu]*(1-scores[u*units+iu]))*sqg*keys[iu*dimension+d]/koef; //--- kg+=(scores[iu*units+u]==0 || scores[iu*units+u]==1 ? 0.0001 : scores[iu*units+u]*(1-scores[iu*units+u]))*skg*querys[iu*dimension+d]/koef; } int shift=u*dimension+d; values_g[shift]=vg; querys_g[shift]=qg; keys_g[shift]=kg; }
Als Nächstes müssen wir die Fehlergradienten aus den Vektoren Querys, Keys und Values übergeben. Achten Sie darauf, dass, da alle Vektoren durch Multiplikation der gleichen Ausgangsdaten mit verschiedenen Matrizen erhalten werden, auch die Fehlergradienten aufsummiert werden sollten. Ich habe keinen separaten Puffer zum Aufsummieren von Fehlergradienten vorgesehen. Das Aufsummieren von Werten bei der Berechnung von Gradienten erfordert jedoch eine zusätzliche Komplikation des Codes, mit der Verfolgung der Puffer-Nullstellung. Ich entschied mich, bestehende Methoden zur Berechnung von Fehlergradienten zu verwenden und die Werte im Gradientenpuffer der Ebene AttentionOut weiter zu akkumulieren.
if(!Querys.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- if(!Keys.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- if(!Values.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,prevLayer.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow+1); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(prevLayer.getGradient(temp)<=0) return false; } //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=1; OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getGradientIndex()); OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons()); if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Normalize: %d",GetLastError()); return false; } double temp[]; if(prevLayer.getGradient(temp)<=0) return false; } //--- return true; }
Nach dem Einspeisen des Fehlergradienten in die vorherige Schichtstufe korrigieren wir die Gewichtsmatrizen in der Methode updateInputWeights. Die Methode ist recht einfach. Sie ruft entsprechende Methoden von verschachtelten Convolutional Schichten auf.
bool CNeuronAttentionOCL::updateInputWeights(CNeuronBaseOCL *prevLayer) { if(!Querys.UpdateInputWeights(prevLayer)) return false; if(!Keys.UpdateInputWeights(prevLayer)) return false; if(!Values.UpdateInputWeights(prevLayer)) return false; if(!FF1.UpdateInputWeights(AttentionOut)) return false; if(!FF2.UpdateInputWeights(FF1)) return false; //--- return true; }
3.5. Änderungen in den Basisklassen des neuronalen Netzwerks
Wir haben die Arbeit mit der Klasse unseres Attention-Blocks abgeschlossen. Nehmen wir nun noch einige Ergänzungen zu den Basisklassen unseres neuronalen Netzes vor. Zunächst fügen wir dem define-Block Konstanten für die Arbeit mit neuen Kerneln hinzu.
#define def_k_FeedForwardConv 7 #define def_k_ffc_matrix_w 0 #define def_k_ffc_matrix_i 1 #define def_k_ffc_matrix_o 2 #define def_k_ffc_inputs 3 #define def_k_ffc_step 4 #define def_k_ffc_window_in 5 #define def_k_ffс_window_out 6 #define def_k_ffc_activation 7 //--- #define def_k_CalcHiddenGradientConv 8 #define def_k_chgc_matrix_w 0 #define def_k_chgc_matrix_g 1 #define def_k_chgc_matrix_o 2 #define def_k_chgc_matrix_ig 3 #define def_k_chgc_outputs 4 #define def_k_chgc_step 5 #define def_k_chgc_window_in 6 #define def_k_chgc_window_out 7 #define def_k_chgc_activation 8 //--- #define def_k_UpdateWeightsConvMomentum 9 #define def_k_uwcm_matrix_w 0 #define def_k_uwcm_matrix_g 1 #define def_k_uwcm_matrix_i 2 #define def_k_uwcm_matrix_dw 3 #define def_k_uwcm_inputs 4 #define def_k_uwcm_learning_rates 5 #define def_k_uwcm_momentum 6 #define def_k_uwcm_window_in 7 #define def_k_uwcm_window_out 8 #define def_k_uwcm_step 9 //--- #define def_k_UpdateWeightsConvAdam 10 #define def_k_uwca_matrix_w 0 #define def_k_uwca_matrix_g 1 #define def_k_uwca_matrix_i 2 #define def_k_uwca_matrix_m 3 #define def_k_uwca_matrix_v 4 #define def_k_uwca_inputs 5 #define def_k_uwca_l 6 #define def_k_uwca_b1 7 #define def_k_uwca_b2 8 #define def_k_uwca_window_in 9 #define def_k_uwca_window_out 10 #define def_k_uwca_step 11 //--- #define def_k_AttentionScore 11 #define def_k_as_querys 0 #define def_k_as_keys 1 #define def_k_as_score 2 #define def_k_as_dimension 3 //--- #define def_k_AttentionOut 12 #define def_k_aout_scores 0 #define def_k_aout_values 1 #define def_k_aout_inputs 2 #define def_k_aout_out 3 //--- #define def_k_MatrixSum 13 #define def_k_sum_matrix1 0 #define def_k_sum_matrix2 1 #define def_k_sum_matrix_out 2 #define def_k_sum_dimension 3 //--- #define def_k_AttentionGradients 14 #define def_k_ag_querys 0 #define def_k_ag_querys_g 1 #define def_k_ag_keys 2 #define def_k_ag_keys_g 3 #define def_k_ag_values 4 #define def_k_ag_values_g 5 #define def_k_ag_scores 6 #define def_k_ag_gradient 7 //--- #define def_k_Normilize 15 #define def_k_norm_buffer 0 #define def_k_norm_dimension 1
Fügen wir außerdem eine Konstante der neuen Klasse von Neuros hinzu.
#define defNeuronAttentionOCL 0x7887
In der Klasse CLayerDescription, die die Schichten des neuronalen Netzes beschreibt, fügen wir ein Feld zur Angabe der Anzahl der Neuronen im Ausgangsvektorfenster hinzu.
class CLayerDescription : public CObject { public: CLayerDescription(void); ~CLayerDescription(void) {}; //--- int type; int count; int window; int window_out; int step; ENUM_ACTIVATION activation; ENUM_OPTIMIZATION optimization; };
Fügen wir im Konstruktor der Netzwerk-Klasse CNet neue Klassen hinzu, um eine Instanz der Klasse zu initialisieren, die mit OpenCL arbeitet.
CNet::CNet(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
..........
..........
..........
//---
next=Description.At(1);
if(next.type==defNeuron || next.type==defNeuronBaseOCL || next.type==defNeuronConvOCL || next.type==defNeuronAttentionOCL)
{
opencl=new COpenCLMy();
if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true))
delete opencl;
}
else
{
if(CheckPointer(opencl)!=POINTER_INVALID)
delete opencl;
}
Weiters ergänzen wir im Konstruktorkörper Code, um die neue Klasse des Attention-Neurons zu initialisieren.
if(CheckPointer(opencl)!=POINTER_INVALID) { CNeuronBaseOCL *neuron_ocl=NULL; CNeuronConvOCL *neuron_conv_ocl=NULL; CNeuronAttentionOCL *neuron_attention_ocl=NULL; switch(desc.type) { case defNeuron: case defNeuronBaseOCL: neuron_ocl=new CNeuronBaseOCL(); if(CheckPointer(neuron_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_ocl.Init(outputs,0,opencl,desc.count,desc.optimization)) { delete neuron_ocl; delete temp; return; } neuron_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_ocl)) { delete neuron_ocl; delete temp; return; } neuron_ocl=NULL; break; case defNeuronConvOCL: neuron_conv_ocl=new CNeuronConvOCL(); if(CheckPointer(neuron_conv_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_conv_ocl.Init(outputs,0,opencl,desc.window,desc.step,desc.window_out,desc.count,desc.optimization)) { delete neuron_conv_ocl; delete temp; return; } neuron_conv_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_conv_ocl)) { delete neuron_conv_ocl; delete temp; return; } neuron_conv_ocl=NULL; break; case defNeuronAttentionOCL: neuron_attention_ocl=new CNeuronAttentionOCL(); if(CheckPointer(neuron_attention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_attention_ocl.Init(outputs,0,opencl,desc.window,desc.count,desc.optimization)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_attention_ocl)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl=NULL; break; default: return; break; } }
Wir fügen auch die Initialisierung von neuen Kerneln am Ende des Konstruktors hinzu
if(CheckPointer(opencl)==POINTER_INVALID) return; //--- create kernels opencl.SetKernelsCount(16); opencl.KernelCreate(def_k_FeedForward,"FeedForward"); opencl.KernelCreate(def_k_CalcOutputGradient,"CalcOutputGradient"); opencl.KernelCreate(def_k_CalcHiddenGradient,"CalcHiddenGradient"); opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum"); opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam"); opencl.KernelCreate(def_k_AttentionGradients,"AttentionIsideGradients"); opencl.KernelCreate(def_k_AttentionOut,"AttentionOut"); opencl.KernelCreate(def_k_AttentionScore,"AttentionScore"); opencl.KernelCreate(def_k_CalcHiddenGradientConv,"CalcHiddenGradientConv"); opencl.KernelCreate(def_k_CalcInputGradientProof,"CalcInputGradientProof"); opencl.KernelCreate(def_k_FeedForwardConv,"FeedForwardConv"); opencl.KernelCreate(def_k_FeedForwardProof,"FeedForwardProof"); opencl.KernelCreate(def_k_MatrixSum,"SumMatrix"); opencl.KernelCreate(def_k_UpdateWeightsConvAdam,"UpdateWeightsConvAdam"); opencl.KernelCreate(def_k_UpdateWeightsConvMomentum,"UpdateWeightsConvMomentum"); opencl.KernelCreate(def_k_Normilize,"Normalize"); //--- return; }
und die Verarbeitung der neuen Klasse von Neuronen in den Dispatcher-Methoden der Klasse CNeuronBase.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; } bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; CNeuronAttentionOCL *at=NULL; CNeuronConvOCL *conv=NULL; switch(TargetObject.Type()) { case defNeuronBaseOCL: temp=TargetObject; return calcHiddenGradients(temp); break; case defNeuronConvOCL: conv=TargetObject; temp=GetPointer(this); return conv.calcInputGradients(temp); break; case defNeuronAttentionOCL: at=TargetObject; temp=GetPointer(this); return at.calcInputGradients(temp); break; } //--- return false; }
Der vollständige Code aller Methoden und Funktionen steht im Anhang zur Verfügung.
4. Tests
Nach all den oben genannten Änderungen können wir die neue Klasse von Neuronen zum neuronalen Netzwerk hinzufügen und die neue Architektur testen. Ich habe einen Test-EA Fractal_OCL_Attention erstellt, der sich von den vorherigen EAs nur durch die Architektur des neuronalen Netzwerks unterscheidet. Auch hier besteht die erste Schicht aus Basisneuronen zum Schreiben der Ausgangsdaten und enthält 12 Features für jeden historischen Balken. Die zweite Schicht ist als modifizierte Convolutional Schicht mit einer sigmoidalen Aktivierungsfunktion und einem ausgehenden Fenster von 36 Neuronen deklariert. Diese Schicht übernimmt die Funktion der Einbettung und Normalisierung der Originaldaten. Darauf folgen zwei Schichten eines Encoders mit einem Self-Attention-Mechanismus. Drei vollständig verbundene Schichten von Neuronen vervollständigen das neuronale Netzwerk.
CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBaseOCL; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronConvOCL; desc.window=12; desc.step=12; desc.window_out=36; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- bool result=true; for(int i=0; (i<2 && result); i++) { desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronAttentionOCL; desc.window=36; desc.optimization=ADAM; desc.activation=None; result=Topology.Add(desc); } if(!result) { delete Topology; return INIT_FAILED; } //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; desc.activation=SIGMOID; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED;
Der vollständige Code des EAs befindet sich im Anhang.
Das Testen des EA wurde unter den gleichen Bedingungen durchgeführt: EURUSD, H1-Zeitrahmen, Daten von 20 aufeinanderfolgenden Kerzen werden in das Netzwerk eingespeist, und das Training wird anhand der Historie der letzten zwei Jahre durchgeführt, wobei die Parameter durch die Adam-Methode aktualisiert werden.
Der Expert Advisor wurde mit Zufallsgewichten im Bereich von -1 bis 1 initialisiert, wobei Nullwerte ausgeschlossen wurden. Nach einem Test über 25 Epochen zeigte der EA einen Fehler von 35-36% mit einer Trefferquote von 22-23%x
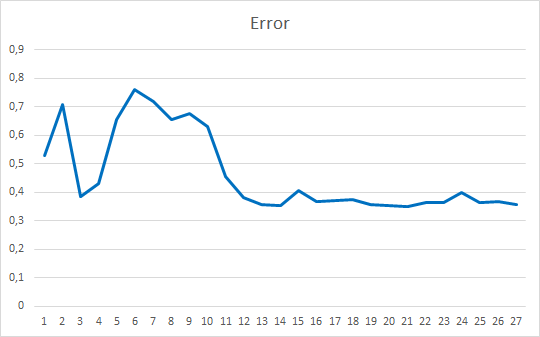
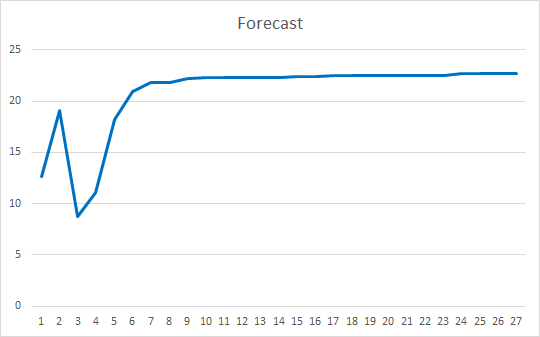
Schlussfolgerungen
In diesem Artikel haben wir Attention-Mechanismen betrachtet. Wir haben einen Self-Attention-Block erstellt und seinen Betrieb an historischen Daten getestet. Der resultierende Expert Advisor zeigte recht glatte Ergebnisse in Bezug auf die Reduzierung des Fehlers im Betrieb des neuronalen Netzes und in Bezug auf das "Treffen" der vorhergesagten Ergebnisse. Die erzielten Ergebnisse zeigen, dass es möglich ist, diesen Ansatz zu verwenden. Es ist jedoch zusätzliche Arbeit erforderlich, um die Ergebnisse zu verbessern. Als weitere Entwicklungsmöglichkeit kann man die Verwendung mehrerer paralleler Threads der Attention mit unterschiedlichen Gewichten in Betracht ziehen. Im Artikel 10 wird dieser Ansatz als "Multi had Attention" bezeichnet.
Referenzen
- Neuronale Netze leicht gemacht
- Neuronale Netze leicht gemacht (Teil 2): Netzwerktraining und Tests
- Neuronale Netze leicht gemacht (Teil 3): Convolutional Neurale Netzwerke
- Neuronale Netze leicht gemacht (Teil 4): Rekurrente Netze
- Neuronale Netze leicht gemacht (Teil 5): Parallele Berechnungen mit OpenCL
- Neuronale Netze leicht gemacht (Teil 6): Experimentieren mit der Lernrate des neuronalen Netzwerks
- Neuronale Netze leicht gemacht (Teil 7): Adaptive Optimierungsverfahren
- Neural Machine Translation by Jointly Learning to Align and Translate
- Effective Approaches to Attention-based Neural Machine Translation
- Attention Is All You Need
- Layer Normalization
Die Programme dieses Artikels
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Fractal_OCL_Attention.mq5 | Expert Advisor | Ein Expert Advisor mit dem neuronalen Klassifizierungsnetzwerk (3 Neuronen in der Ausgabeschicht), das den Mechanismus der Self-Attention verwendet |
| 2 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek mit Klassen zum Erstellen eines neuronalen Netzwerks |
| 3 | NeuroNet.cl | Bibliothek | Die Bibliothek mit dem Programm-Code für OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/8765
Zeitreihen in der Bibliothek DoEasy (Teil 59): Objekt zum Speichern der Daten eines Ticks
Verwendung von Tabellenkalkulationen zur Erstellung von Handelsstrategien
Entwicklung eines selbstanpassenden Algorithmus (Teil I): Finden eines Grundmusters
Zeitreihen in der Bibliothek DoEasy (Teil 58): Zeitreihen der Datenpuffer von Indikatoren
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.