
Neuronale Netze leicht gemacht (Teil 3): Convolutional Neurale Netzwerke
Inhalt
- Einführung
- 1. Charakteristische Merkmale von Convolutional Netzen
- 2. Trainingsprinzipien der Neuronen in Convolutional-Layern
- 3. Aufbau eines Convolutional Neuronalen Netzwerks
- 3.1. Basisklasse der Neuronen
- 3.2. Das Element des Subsampling-Layer
- 3.3. Das Element des Convolutional-Layers
- 3.4. Erstellen einer Convolutional Neuronalen Netzwerks
- 4. Tests
- Schlussfolgerung
- Liste der Referenzen
- Programme, die im diesem Artikel verwendet werden
Einführung
Als Fortsetzung des Themas Neuronale Netze schlage ich vor, Convolutional Neurale Netzwerke (faltende Neuronale Netzwerke) zu besprechen. Diese Neuronalen Netze werden normalerweise bei Problemen im Zusammenhang mit der Objekterkennung in Foto- und Videobildern eingesetzt. Es wird angenommen, dass Convolutional Neuronale Netzwerke resistent gegen Zoomen, wechselnde Winkel und andere räumliche Bildverzerrungen sind. Ihre Architektur erlaubt es, Objekte überall in der Szene gleichermaßen erfolgreich zu erkennen. Bei der Anwendung auf den Handel möchte ich Convolutional Neuronale Netzwerk verwenden, um das Erkennen von Handelsmustern in einem Kurschart zu verbessern.
1. Charakteristische Merkmale von Convolutional Netzen
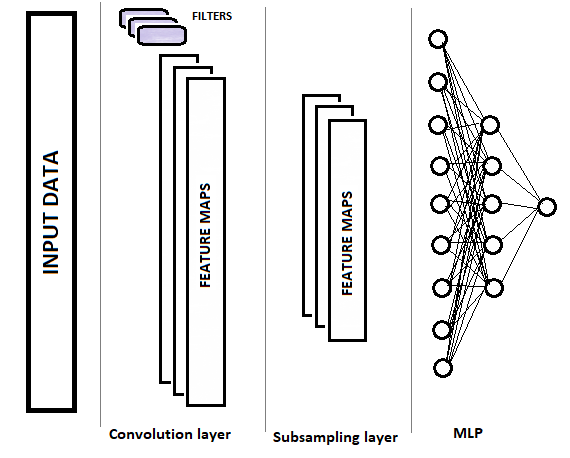
Convolutional Netzwerke haben im Vergleich zu einem vollverknüpften Perzeptron zwei neue Layer-Typen (Schichttypen): Convolutional (faltend, Filter) und Subsampling (teilweises Abtasten). Diese Layer wechseln sich mit dem Zweck ab, die Hauptkomponenten auszuwählen und Rauschen in den Quelldaten zu eliminieren, während die Datendimension (Volumen) reduziert wird. Diese Daten werden dann in ein vollständig verbundenes Perzeptron zur Entscheidungsfindung eingegeben. Die Struktur eines Convolutional Neuronalen Netzes ist in der folgenden Abbildung grafisch dargestellt. Je nach Aufgabenstellung können wir nacheinander mehrere Gruppen von abwechselnden Convolutional-Layern und Subsample-Layern verwenden.
1.1. Convolutional-Layer
Der Convolution-Layer ist für das Erkennen von Objekten im Quelldatenfeld zuständig. Dieser Layer führt sequentielle Operationen der mathematischen Faltung der Originaldaten durch, wobei ein kleines Muster (Filter) als Convolutional-Kernel dient.
Die Faltung (Convolution) ist eine Operation der Funktionalanalysis auf zwei Funktionen (f und g), die eine dritte Funktion entsprechend der Kreuzkorrelationsfunktion f(x) und g(-x) erzeugt. Die Faltungsoperation kann als "Ähnlichkeit" einer Funktion mit einer umgekehrten und verschobenen Kopie einer anderen interpretiert werden (Wikipedia).
Mit anderen Worten, der Convolutional-Layer sucht nach einem Musterelement in der gesamten Originalprobe. Bei jeder Iteration wird das Muster entlang des ursprünglichen Datenfeldes mit einem bestimmten Schritt verschoben, dessen Größe von "1" bis zur Mustergröße reichen kann. Wenn die Schrittgröße der Verschiebung kleiner als die Mustergröße ist, wird eine solche Faltung als überlappend bezeichnet.
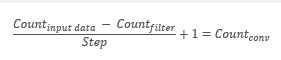
Die Faltungsoperation erzeugt bei jeder Iteration ein Array von Features, die die "Ähnlichkeit" der Originaldaten mit dem gewünschten Muster zeigen. Aktivierungsfunktionen werden verwendet, um die Daten zu normalisieren. Die resultierende Array-Größe wird kleiner sein als das ursprüngliche Daten-Array. Die Anzahl solcher Arrays ist gleich der Anzahl der Filter.
Ein wichtiger Punkt ist, dass die Muster nicht beim Entwurf eines Neuronalen Netzes festgelegt werden, sondern dass sie im Lernprozess ausgewählt werden.
1.2. Subsampling-Layer
Der nächste Subsampling-Layer dient dazu, die Dimension des Feature-Arrays zu reduzieren und Rauschen zu filtern. Die Verwendung dieser Iteration ergibt sich aus der Annahme, dass das Vorhandensein von Ähnlichkeit zwischen den Originaldaten und dem Muster primär ist, während die genauen Koordinaten des Merkmals im Originaldaten-Array nicht so wichtig sind. Dies bietet eine Lösung für das Skalierungsproblem, da es eine gewisse Variabilität im Abstand zwischen den gewünschten Objekten zulässt.
In diesem Stadium werden die Daten verdichtet, indem der Maximal- oder Durchschnittswert innerhalb eines bestimmten "Fensters" gehalten wird. So wird für jedes Daten-"Fenster" nur ein Wert gespeichert. Die Operationen werden iterativ durchgeführt, und das Fenster wird bei jeder neuen Iteration um einen bestimmten Schritt verschoben. Die Datenverdichtung wird für jedes Feature-Array separat durchgeführt.
Häufig werden Subsample-Layer mit einem Fenster und einem Schritt gleich 2 verwendet - dies ermöglicht die Halbierung der Dimension des Eigenschafts-Arrays. Es können jedoch auch größere Fenster verwendet werden, während die Verdichtungsiterationen mit Überlappung (wenn die Schrittweite kleiner als die Fenstergröße ist) oder ohne Überlappung durchgeführt werden können.
Der Subsample-Layer gibt Feature-Arrays mit einer kleineren Dimension aus.
Je nach Komplexität der Probleme ist es möglich, eine oder mehrere Gruppen aus dem Convolutional- und Subsample-Layer nach dem Subsample-Layer zu verwenden. Deren Konstruktionsprinzipien und Funktionalität entsprechen dem oben beschriebenen Layer. Im allgemeinen Fall werden nach einer oder mehreren Gruppen der Faltung + Verdichtung die für alle Filter erhaltenen Merkmalsarrays zu einem einzigen Vektor zusammengefasst und in ein mehrschichtiges Perzeptron eingespeist, damit das Neuronale Netz eine Entscheidung treffen kann (der Aufbau des mehrschichtigen Perzeptrons wird im ersten Teil dieser Artikelserie ausführlich beschrieben).
2. Trainingsprinzipien der Neuronen in Convolutional-Layern
Convolutional Neuronale Netzwerk werden mit der Backpropagation-Methode trainiert, die in früheren Artikeln besprochen wurde. Dies ist eine der überwachten Lernmethoden. Sie besteht darin, dass der Fehlergradient von der Ausgangsschicht der Neuronen über die versteckten Schichten bis zur Eingangsschicht der Neuronen absteigt, wobei eine Gewichtskorrektur in Richtung des Antigradienten erfolgt.
Das Training des mehrschichtigen Perzeptrons wurde im ersten Artikel erläutert, daher verzichte ich hier auf eine Erklärung. Besprechen wir das Training von Neuronen der Subsample- und der Convolutional-Layer.
Im Subsample-Layer wird der Fehlergradient für jedes Element des Eigenschafts-Arrays berechnet, ähnlich wie die Gradienten der Neuronen von vollständig verbundenen Perceptrons. Der Algorithmus zur Übertragung des Gradienten in den vorherigen Layer hängt von der angewandten Verdichtungsoperation ab. Wenn nur der Maximalwert verwendet wird, wird der gesamte Gradient dem Neuron mit dem Maximalwert zugeführt (für alle anderen Elemente innerhalb des Verdichtungsfensters wird ein Nullgradient gesetzt). Wenn die Operation der Mittelwertbildung innerhalb des Fensters verwendet wird, dann wird der Gradient gleichmäßig auf alle Elemente innerhalb des Fensters verteilt.
Die Verdichtungsoperation verwendet keine Gewichte, deshalb wird im Lernprozess nichts angepasst.
Beim Training der Neuronen des Convolutional-Layers sind die Berechnungen etwas komplexer. Der Fehlergradient wird für jedes Element des Feature-Arrays berechnet und den entsprechenden Neuronen des vorherigen Layers zugeführt. Der Trainingsprozess des Convolutional-Layers basiert auf Faltung und inversen Faltungsoperationen.
Um den Fehlergradienten vom Subsample-Layer an den Convolutional-Layer weiterzuleiten, werden die Kanten des Arrays der Fehlergradienten, die vom Subsample Layer erhalten wurden, zuerst mit Nullelementen ergänzt und dann wird das resultierende Array mit dem um 180° gedrehten Convolutional-Kernel gefaltet. Die Ausgabe ist ein Array von Fehlergradienten mit der Dimension gleich dem Eingangsdatenarray, in dem die Gradientenindizes dem Index des entsprechenden Neurons vor dem Convoluitonal-Layer entsprechen.
Das Delta der Gewichte erhält man durch Faltung der Matrix der Eingangswerte mit der Matrix der Fehlergradienten dieses Layers, die um 180° gedreht ist. Dies ergibt ein Array von Deltas mit einer Größe, die dem Convolutional-Kernel entspricht. Die resultierenden Deltas müssen um die Ableitung der Aktivierungsfunktion des Convolutional-Layers und den Lernfaktor angepasst werden. Danach werden die Gewichte des Convolutional-Kernels um den Wert der angepassten Deltas verändert.
Das klingt vielleicht ziemlich schwer verständlich. Ich werde versuchen, einige Momente in der detaillierten Code-Analyse unten zu klären.
3. Aufbau eines Convolutional Neuronalen Netzwerks
Das Convolutional Neuronale Netzwerk besteht aus drei Arten von neuronalen Layern (faltend, subsampled und vollständig verbunden) mit unterschiedlichen Klassen von Neuronen und verschiedenen Funktionen für den Vorwärts- und Rückwärtsdurchgang. Gleichzeitig müssen wir alle Neuronen zu einem einzigen Netzwerk zusammenfassen und den Aufruf der Datenverarbeitungsmethode organisieren, die dem verarbeiteten Neuron entspricht. Ich denke, der einfachste Weg, diesen Prozess zu organisieren, ist die Verwendung von Klassenvererbung und Funktionsvirtualisierung.
Lassen Sie uns zunächst die Klassenvererbungsstruktur aufbauen.
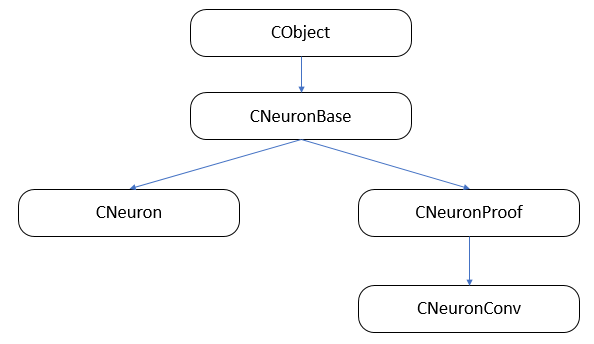
3.1. Basisklasse der Neuronen.
Im ersten Artikel haben wir die Layer-Klasse CLayer als Nachkomme von CArrayObj angelegt, einer dynamischen Array-Klasse zur Speicherung von Zeigern auf Objekte der Klasse CObject. Daher müssen alle Neuronen von dieser Klasse abgeleitet werden. Erstellen wir die Klasse CNeuronBase auf der Grundlage der Klasse CObject. Deklarieren wir im Klassenkörper die Variablen, die allen Typen von Neuronen gemeinsam sind, und erstellen Vorlagen für die Hauptmethoden. Alle Methoden der Klasse werden als virtuell deklariert, um eine weitere Neudefinition zu ermöglichen.
class CNeuronBase : public CObject { protected: double eta; double alpha; double outputVal; uint m_myIndex; double gradient; CArrayCon *Connections; //--- virtual bool feedForward(CLayer *prevLayer) { return false; } virtual bool calcHiddenGradients( CLayer *&nextLayer) { return false; } virtual bool updateInputWeights(CLayer *&prevLayer) { return false; } virtual double activationFunction(double x) { return 1.0; } virtual double activationFunctionDerivative(double x) { return 1.0; } virtual CLayer *getOutputLayer(void) { return NULL; } public: CNeuronBase(void); ~CNeuronBase(void); virtual bool Init(uint numOutputs, uint myIndex); //--- virtual void setOutputVal(double val) { outputVal=val; } virtual double getOutputVal() { return outputVal; } virtual void setGradient(double val) { gradient=val; } virtual double getGradient() { return gradient; } //--- virtual bool feedForward(CObject *&SourceObject); virtual bool calcHiddenGradients( CObject *&TargetObject); virtual bool updateInputWeights(CObject *&SourceObject); //--- virtual bool Save( int const file_handle); virtual bool Load( int const file_handle) { return(Connections.Load(file_handle)); } //--- virtual int Type(void) const { return defNeuronBase; } };
Variablen- und Methodennamen sind die gleichen wie zuvor beschrieben. Besprechen wir die Methoden feedForward(CObject *&SourceObject), сalcHiddenGradients(CObject *&TargetObject) und updateInputWeights(CObject *&SourceObject), in denen die Arbeits für die Arbeit mit vollständig verbundenen und Convolutional-Layern verteilt wird.
3.1.1. Vorwärtsdurchgang.
Die Methode feedForward(CObject *&SourceObject) wird während eines Vorwärtsdurchgangs aufgerufen, um den resultierenden Neuronenwert zu berechnen. Bei einem Vorwärtsdurchgang übernimmt jedes Neuron in vollverknüpften Layern die Werte aller Neuronen des vorherigen Layers und muss den gesamten vorherigen Layer als Eingabe erhalten. In den Convolutional- und Subsampled-Layern wird nur ein Teil der Daten, die sich auf diesen Filter beziehen, dem Neuron zugeführt. Bei der besprochenen Methode wird der Algorithmus auf der Grundlage des Typs der in den Parametern erhaltenen Klasse ausgewählt.
Überprüfen wir zunächst die Gültigkeit des in den Methodenparametern erhaltenen Objektzeigers.
bool CNeuronBase::feedForward(CObject *&SourceObject) { bool result=false; //--- if(CheckPointer(SourceObject)==POINTER_INVALID) return result;
Da Klasseninstanzen nicht innerhalb des Selektionsoperators deklariert werden können, müssen wir im Vorfeld Templates vorbereiten.
CLayer *temp_l; CNeuronProof *temp_n;
Als Nächstes prüfen wir im Auswahloperator den Typ des in den Parametern empfangenen Objekts. Wenn ein Zeiger auf eine Schicht von Neuronen empfangen wird, dann ist die vorherige Schicht voll verbunden und wir müssen daher eine Methode für die Arbeit mit voll verbundenen Schichten aufrufen (ausführlich beschrieben im ersten Artikel). Wenn es sich um ein Neuron einer Faltungs- oder einer Subsample-Schicht handelt, dann erhalten wir zuerst eine Schicht von Ausgangsneuronen dieses Filters und verwenden dann eine Methode, die eine voll verbundene Schicht verarbeitet, in die wir eine Schicht von Neuronen des aktuellen Filters eingeben sollten, und das Verarbeitungsergebnis muss in der Variablen result gespeichert werden (weitere Details über die Struktur der Neuronen in den Faltungsschichten und Subsample-Schichten werden weiter unten beschrieben). Nach der Operation verlassen wir die Methode und übergeben das Operationsergebnis.
switch(SourceObject.Type()) { case defLayer: temp_l=SourceObject; result=feedForward(temp_l); break; case defNeuronConv: case defNeuronProof: temp_n=SourceObject; result=feedForward(temp_n.getOutputLayer()); break; } //--- return result; }
3.1.2. Berechnung des Fehlergradienten.
Ähnlich wie bei einem Vorwärtsdurchgang wurde ein Dispatcher (Verteiler) erstellt, um die Funktion zur Berechnung eines Fehlergradienten auf den versteckten Layern des Neuronalen Netzes aufzurufen - сalcHiddenGradients(CObject*&TargetObject). Die Logik und Struktur der Methode sind ähnlich wie oben beschrieben. Zunächst wird die Gültigkeit des empfangenen Zeigers überprüft. Anschließend deklarieren wir die Variablen, um Zeiger auf die entsprechenden Objekte zu speichern. Anschließend wählen wir in der Selektionsfunktion die passende Methode entsprechend dem empfangenen Objekttyp aus. Unterschiede ergeben sich, wenn in den Parametern ein Zeiger auf ein Element eines Convolutional oder Subsample Layers übergeben wird. Die Berechnung des Fehlergradienten durch solche Neuronen ist anders und gilt nicht für alle Neuronen des vorherigen Layers, sondern nur für Neuronen innerhalb des Abtastfensters. Deshalb wurde die Gradientenberechnung in der Methode calcInputGradients auf diese Neuronen übertragen. Auch gibt es Unterschiede in den Methoden zur Berechnung pro Layer oder für ein bestimmtes Neuron. Daher wird die gewünschte Methode je nach Typ des Objekts, von dem sie aufgerufen wird, aufgerufen.
bool CNeuronBase::calcHiddenGradients(CObject *&TargetObject) { bool result=false; //--- if(CheckPointer(TargetObject)==POINTER_INVALID) return result; //--- CLayer *temp_l; CNeuronProof *temp_n; switch(TargetObject.Type()) { case defLayer: temp_l=TargetObject; result=calcHiddenGradients(temp_l); break; case defNeuronConv: case defNeuronProof: switch(Type()) { case defNeuron: temp_n=TargetObject; result=temp_n.calcInputGradients(GetPointer(this),m_myIndex); break; default: temp_n=GetPointer(this); temp_l=temp_n.getOutputLayer(); temp_n=TargetObject; result=temp_n.calcInputGradients(temp_l); break; } break; } //--- return result; }
Die Verteilung durch updateInputWeights(CObject *&SourceObject), die alle Gewichte aktualisiert, basiert auf den oben genannten Prinzipien. Der vollständige Code ist im Anhang verfügbar.
3.2. Die Elemente des Subsampling-Layers.
Der Hauptbaustein des Subsample-Layers ist die Klasse CNeuronProof, die von der zuvor beschriebenen Basisklasse CNeuronBase abgeleitet wurde. Für jeden Filter im Subsample-Layer wird eine Instanz dieser Klasse erzeugt. Daher werden zusätzliche Variablen (iWindow und iStep) eingeführt, um die Größe des Verdichtungsfensters und den Verschiebungsschritt zu speichern. Wir fügen auch einen inneren Layer mit Neuronen zum Speichern von Feature-Arrays, Fehlergradienten und ggf. Gewichten für die Weitergabe von Features an ein voll verbundenes Perzeptron hinzu. Außerdem fügen wir eine Methode hinzu, um bei Bedarf einen Zeiger auf die innere Schicht der Neuronen zu erhalten.
class CNeuronProof : public CNeuronBase { protected: CLayer *OutputLayer; int iWindow; int iStep; virtual bool feedForward(CLayer *prevLayer); virtual bool calcHiddenGradients( CLayer *&nextLayer); public: CNeuronProof(void){}; ~CNeuronProof(void); virtual bool Init(uint numOutputs,uint myIndex,int window, int step, int output_count); //--- virtual CLayer *getOutputLayer(void) { return OutputLayer; } virtual bool calcInputGradients( CLayer *prevLayer) ; virtual bool calcInputGradients( CNeuronBase *prevNeuron, uint index) ; //--- methods for working with files virtual bool Save( int const file_handle) { return(CNeuronBase::Save(file_handle) && OutputLayer.Save(file_handle)); } virtual bool Load( int const file_handle) { return(CNeuronBase::Load(file_handle) && OutputLayer.Load(file_handle)); } virtual int Type(void) const { return defNeuronProof; } };
Vergessen wir nicht, die Logik für die in der Basisklasse deklarierten virtuellen Funktionen neu zu definieren.
3.2.1. Vorwärtsdurchgang.
Die Methode FeedForward wird angewendet, um das Rauschen herauszufiltern und die Dimension des Eigenschafts-Arrays zu reduzieren. In der beschriebenen Lösung wird die Funktion des arithmetischen Mittels zur Verdichtung der Daten verwendet. Lassen Sie uns den Code der Methode genauer betrachten. Zu Beginn der Methode wird die Relevanz des erhaltenen Zeigers auf den vorherigen Layer der Neuronen überprüft.
bool CNeuronProof::feedForward(CLayer *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
Dann durchlaufen wir durch alle Neuronen des in den Parametern erhaltenen Layers in einer Schleife mit einem vorgegebenen Schritt.
int total=prevLayer.Total()-iWindow+1; CNeuron *temp; for(int i=0;(i<=total && result);i+=iStep) {
Wir erstellen in der Schleife eine verschachtelte Schleife zur Berechnung der Summe der Ausgangswerte der Neuronen des vorherigen Layers innerhalb des angegebenen Verdichtungsfensters.
double sum=0; for(int j=0;j<iWindow;j++) { temp=prevLayer.At(i+j); if(CheckPointer(temp)==POINTER_INVALID) continue; sum+=temp.getOutputVal(); }
Nach der Berechnung der Summe verwenden wir das entsprechende Neuron des inneren Layers, das die resultierenden Daten speichert, und schreiben das Verhältnis der erhaltenen Summe zur Fenstergröße in seinen resultierenden Wert. Dieses Verhältnis wird das arithmetische Mittel für das aktuelle Verdichtungsfenster sein.
temp=OutputLayer.At(i/iStep); if(CheckPointer(temp)==POINTER_INVALID) return false; temp.setOutputVal(sum/iWindow); } //--- return true; }
Nach dem Durchlaufen aller Neuronen ist die Methode abgeschlossen.
3.2.2. Berechnung des Fehlergradienten.
In dieser Klasse werden zwei Methoden zur Berechnung des Fehlergradienten erstellt: calcHiddenGradients und calcInputGradients. Die erste Klasse sammelt Daten über die Fehlergradienten des nachfolgenden Layers und berechnet den Gradienten für die Elemente des aktuellen Layers. Die zweite Klasse verwendet die in der ersten Methode erhaltenen Daten und verteilt den Fehler auf die vorherigen Layer-Elemente.
Überprüfen wir wiederum die Gültigkeit des erhaltenen Zeigers zu Beginn der Methode calcHiddenGradients. Überprüfen wir zusätzlich den Zustand des inneren Layers der Neuronen.
bool CNeuronProof::calcHiddenGradients( CLayer *&nextLayer) { if(CheckPointer(nextLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID || OutputLayer.Total()<=0) return false;
Dann durchlaufen wir in einer Schleife alle Neuronen des inneren Layers und rufen eine Methode zur Berechnung des Fehlergradienten auf.
gradient=0; int total=OutputLayer.Total(); CNeuron *temp; for(int i=0;i<total;i++) { temp=OutputLayer.At(i); if(CheckPointer(temp)==POINTER_INVALID) return false; temp.setGradient(temp.sumDOW(nextLayer)); } //--- return true; }
Bitte beachten Sie, dass diese Methode korrekt funktioniert, wenn sie von einem vollständig verbundenen Layer von Neuronen gefolgt wird. Folgt ein Convolutional- oder Subsampling-Layer, verwenden wir die Methode calcInputGradients des nächsten Layer Neurons.
Die Methode calcInputGradients erhält als Parameter einen Zeiger auf den vorherigen Layer. Vergessen wir nicht, die Gültigkeit des Zeigers zu Beginn der Methode zu überprüfen.
bool CNeuronProof::calcInputGradients(CLayer *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID) return false;
Prüfen wir dann den Typ des ersten erhaltenen Elements in den Layer-Parametern. Wenn der resultierende Verweis auf einen Subsample- oder Convolutional-Layer zeigt, dann fordern wir eine Referenz auf den inneren Layer der Neuronen an, der dem Filter entspricht.
if(prevLayer.At(0).Type()!=defNeuron) { CNeuronProof *temp=prevLayer.At(m_myIndex); if(CheckPointer(temp)==POINTER_INVALID) return false; prevLayer=temp.getOutputLayer(); if(CheckPointer(prevLayer)==POINTER_INVALID) return false; }
Als Nächstes wird eine Schleife durch alle Neuronen des vorherigen Layers durchgeführt, wobei die Gültigkeit der Referenz auf das verarbeitete Neuron überprüft wird.
CNeuronBase *prevNeuron, *outputNeuron; int total=prevLayer.Total(); for(int i=0;i<total;i++) { prevNeuron=prevLayer.At(i); if(CheckPointer(prevNeuron)==POINTER_INVALID) continue;
Bestimmen wir, welche Neuronen des inneren Layers von dem verarbeiteten Neuron betroffen sind.
double prev_gradient=0; int start=i-iWindow+iStep; start=(start-start%iStep)/iStep; double stop=(i-i%iStep)/iStep+1;
Berechnen wir in einer Schleife den Fehlergradienten für das bearbeitete Neuron und speichern das Ergebnis. Die Methode endet nach Abarbeitung aller Neuronen des vorherigen Layers.
for(int out=(int)fmax(0,start);out<(int)fmin(OutputLayer.Total(),stop);out++) { outputNeuron=OutputLayer.At(out); if(CheckPointer(outputNeuron)==POINTER_INVALID) continue; prev_gradient+=outputNeuron.getGradient()/iWindow; } prevNeuron.setGradient(prev_gradient); } //--- return true; }
Die gleichnamige Methode, die einen separaten Neuronengradienten berechnet, hat eine ähnliche Struktur. Der Unterschied ist, dass der externe Zyklus, der Neuronen iteriert, ausgeschlossen ist. Stattdessen wird ein Neuron durch einen Index aufgerufen.
Da im Subsample Layer keine Gewichte verwendet werden, kann die Methode der Gewichtsaktualisierung weggelassen werden. Wenn wir die Struktur der Neuronenklassen beibehalten wollen, können wir eine leere Methode erstellen, die beim Aufruf true erzeugt.
Der komplette Code aller Methoden und Funktionen ist im Anhang verfügbar.
3.3. Das Element des Convolutional-Layers.
Der Convolutional-Layer wird mit den Objekten der Klasse CNeuronConv aufgebaut, die von der Klasse CNeuronProof abgeleitet wird. Als Aktivierungsfunktion für diesen Typ von Neuronen habe ich die parametrische ReLU gewählt. Diese Funktion ist einfacher zu berechnen als der hyperbolische Tangens, der in voll verbundenen Perceptron-Neuronen verwendet wird. Führen wir eine zusätzliche Variable param ein, um die Funktion zu berechnen.
class CNeuronConv : public CNeuronProof { protected: double param; //PReLU param virtual bool feedForward(CLayer *prevLayer); virtual bool calcHiddenGradients(CLayer *&nextLayer); virtual double activationFunction(double x); virtual bool updateInputWeights(CLayer *&prevLayer); public: CNeuronConv() : param(0.01) { }; ~CNeuronConv(void) { }; //--- virtual bool calcInputGradients(CLayer *prevLayer) ; virtual bool calcInputGradients(CNeuronBase *prevNeuron, uint index) ; virtual double activationFunctionDerivative(double x); virtual int Type(void) const { return defNeuronConv; } };
Die Vorwärts- und Rückwärts-Durchgangsmethoden basieren auf ähnlichen Algorithmen wie die Klasse CNeuron Proof. Der Unterschied liegt in der Verwendung der Aktivierungsfunktion und der Gewichtskoeffizienten. Daher werde ich sie nicht im Detail beschreiben. Besprechen wir die Gewichtsanpassungsmethode updateInputWeights.
Die Methode erhält einen Zeiger auf den vorherigen Layer der Neuronen. Auch hier überprüfen wir zu Beginn der Methode die Gültigkeit des Zeigers und den Zustand des inneren Layers.
bool CNeuronConv::updateInputWeights(CLayer *&prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID) return false;
Erstellen wir anschließend eine Schleife über alle Gewichte. Vergessen wir nicht, die Gültigkeit des erhaltenen Objektzeigers zu prüfen.
CConnection *con; for(int n=0; n<iWindow && !IsStopped(); n++) { con=Connections.At(n); if(CheckPointer(con)==POINTER_INVALID) continue;
Berechnen wir danach die Faltung des Eingangsdaten-Arrays mit dem Array der um 180° gedrehten Fehlergradienten des inneren Layers. Dies geschieht in einer Schleife durch alle Elemente des inneren Layers, multipliziert mit den Elementen des Eingangsdaten-Arrays nach folgendem Schema:
- das erste Element des Eingangsdaten-Arrays (mit einer Verschiebung um die Anzahl der Schritte, die der Ordnungszahl des Gewichts entspricht), multipliziert mit dem letzten Element des Fehlergradienten-Arrays,
- das zweite Element des Eingangsdaten-Arrays (mit einer Verschiebung um die Anzahl der Schritte, die gleich der Ordnungszahl des Gewichts ist), multipliziert mit dem vorletzten Element des Fehlergradienten-Arrays,
- und so weiter, bis das Element mit dem Index gleich der Anzahl der Elemente im Array des inneren Layers (mit einer Verschiebung um die Anzahl der Schritte gleich der Ordnungszahl der Gewichtung) mit dem ersten Element des Fehlergradienten-Arrays multipliziert ist.
Dann ermitteln wir die Summe der resultierenden Produkte.
double delta=0; int total_i=OutputLayer.Total(); CNeuron *prev, *out; for(int i=0;i<total_i;i++) { prev=prevLayer.At(n*iStep+i); out=OutputLayer.At(total_i-i-1); if(CheckPointer(prev)==POINTER_INVALID || CheckPointer(out)==POINTER_INVALID) continue; delta+=prev.getOutputVal()*out.getGradient(); }
Die berechnete Summe der Produkte dient als Grundlage für die Anpassung der Gewichte. Gewichte unter Berücksichtigung der eingestellten Trainingsgeschwindigkeit anpassen.
con.weight+=con.deltaWeight=(delta!=0 ? eta*delta : 0)+(con.deltaWeight!=0 ? alpha*con.deltaWeight : 0); } //--- return true; }
Nachdem wir alle Gewichte angepasst haben, beenden wir die Methode.
Die Klasse CNeuron ist im ersten Artikel ausführlich beschrieben. Sie hat sich nicht wesentlich verändert, so dass ich ihre Beschreibung hier nicht wiederhole.
3.4. Erstellen einer Klasse für das Convolutional Neuronale Netzwerk.
Nachdem nun alle Bausteine erstellt wurden, können wir mit dem Bau eines Hauses beginnen. Wir werden eine Klasse des Convolutional Neuronalen Netzwerks erstellen, die alle Arten von Neuronen in einer klaren Struktur zusammenfasst und die Arbeit unseres Neuronalen Netzwerks organisiert. Die erste Frage, die sich bei der Erstellung dieser Klasse stellt, ist, wie man die gewünschte Netzwerkstruktur einstellt. Im Falle eines vollständig verbundenen Perzeptrons haben wir ein Array von Elementen mit einer Information über die Anzahl der Neuronen in jedem Layer übergeben. Nun benötigen wir weitere Informationen, um den gewünschten Layer des Netzes zu erzeugen. Legen wir eine kleine Klasse CLayerDescription an, die den Aufbau des Layers beschreibt. Diese Klasse enthält keine Methoden (außer dem Konstruktor und Destruktor) und nur Variablen zur Angabe des Typs der Neuronen in der Schicht, der Anzahl dieser Neuronen, der Fenstergröße und des Schrittes für die Neuronen in der Convolutional- und Subsample-Layers. Ein Zeiger auf ein Array von Klassen mit der Beschreibung von Layern wird in den Parametern des Konstruktors der Klasse der Convolutional Netzwerke übergeben.
class CLayerDescription : public CObject { public: CLayerDescription(void); ~CLayerDescription(void){}; //--- int type; int count; int window; int step; }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CLayerDescription::CLayerDescription(void) : type(defNeuron), count(0), window(1), step(1) {}
Besprechen wir die Struktur der Klasse CNetConvolution des Convolutional Neuronalen Netzwerkes. Die Klasse enthält:
- Layers — ein Array von Layern;
- recentAverageError — aktueller Netzwerkfehler;
- recentAverageSmoothingFactor — Fehler des Mittelungsfaktors;
- CNetConvolution — Klassenkonstruktor;
- ~CNetConvolution — Klassendestruktor;
- feedForward — Methode zur direkten Weitergabe;
- backProp — Methode für den Rückwärtsdurchgang;
- getResults — Methode zum Abrufen der Ergebnisse des letzten Vorwärtsdurchgangs;
- getRecentAverageError — Methode zum Abrufen des aktuellen Netzwerkfehlers;
- Save und Load — Methoden zum Speichern und Laden der zuvor erstellten und trainierten Methode.
class CNetConvolution { public: CNetConvolution(CArrayObj *Description); ~CNetConvolution(void) { delete layers; } bool feedForward( CArrayDouble *inputVals); void backProp( CArrayDouble *targetVals); void getResults(CArrayDouble *&resultVals) ; double getRecentAverageError() { return recentAverageError; } bool Save( string file_name, double error, double undefine, double forecast, datetime time, bool common=true); bool Load( string file_name, double &error, double &undefine, double &forecast, datetime &time, bool common=true); //--- static double recentAverageSmoothingFactor; virtual int Type(void) const { return defNetConv; } private: CArrayLayer *layers; double recentAverageError; };
Die Methodennamen und Konstruktionsalgorithmen ähneln denen für ein vollständig verbundenes Perzeptron, die im ersten Artikel beschrieben wurden. Lassen Sie uns nur auf die Hauptmethoden der Klasse eingehen.
3.4.1. Konstruktor der Klasse Convolutional Neuronales Netzwerk.
Besprechen wir den Klassenkonstruktor. Der Konstruktor erhält als Parameter einen Zeiger auf ein Array von Layer-Beschreibungen zum Aufbau eines Netzwerks. Wir müssen also die Gültigkeit des empfangenen Zeigers überprüfen, die Anzahl der Layer bestimmen und eine neue Instanz des Layer-Arrays erstellen.
CNetConvolution::CNetConvolution(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
int total=Description.Total();
if(total<=0)
return;
//---
layers=new CArrayLayer();
if(CheckPointer(layers)==POINTER_INVALID)
return;
Als Nächstes deklarieren wir die internen Variablen.
CLayer *temp; CLayerDescription *desc=NULL, *next=NULL, *prev=NULL; CNeuronBase *neuron=NULL; CNeuronProof *neuron_p=NULL; int output_count=0; int temp_count=0;
Damit sind die Vorbereitungsarbeiten abgeschlossen. Gehen wir direkt zur zyklischen Erzeugung von Layern des Neuronalen Netzes über. Zu Beginn des Zyklus lesen wir die Informationen über den aktuellen und den nächsten Layer.
for(int i=0;i<total;i++) { prev=desc; desc=Description.At(i); if((i+1)<total) { next=Description.At(i+1); if(CheckPointer(next)==POINTER_INVALID) return; } else next=NULL;
Zählen wir die Anzahl der Ausgangsverbindungen für den Layer und erzeugen eine neue Instanz der Klasse der neuronalen Schicht. Beachten Sie, dass die Anzahl der Verbindungen am Ausgang des Layers nur vor dem vollständig verbundenen Layer angegeben werden sollte, ansonsten wird Null angegeben. Das liegt daran, dass die Faltungsneuronen die Eingangsgewichte selbst speichern, während der Subsample Layer diese gar nicht verwendet.
int outputs=(next==NULL || next.type!=defNeuron ? 0 : next.count); temp=new CLayer(outputs);
Anschließend werden die Neuronen erzeugt, wobei der Algorithmus nach dem Typ der Neuronen im Layer unterteilt. Für voll verbundene Layer wird eine neue Neuroneninstanz erzeugt und initialisiert. Bitte beachten Sie, dass bei vollverknüpften Layern zusätzlich zu der in der Beschreibung angegebenen Anzahl ein weiteres Neuron erzeugt wird. Dieses Neuron wird als Bayes'scher Bias verwendet.
for(int n=0;n<(desc.count+(i>0 && desc.type==defNeuron ? 1 : 0));n++) { switch(desc.type) { case defNeuron: neuron=new CNeuron(); if(CheckPointer(neuron)==POINTER_INVALID) { delete temp; delete layers; return; } neuron.Init(outputs,n); break;
Wir erstellen eine neue Neuroneninstanz für den Faltungs-Layer. Zählen wir die Anzahl der Ausgangselemente anhand der Informationen über den vorherigen Layer und initialisieren das neu erstellte Neuron.
case defNeuronConv: neuron_p=new CNeuronConv(); if(CheckPointer(neuron_p)==POINTER_INVALID) { delete temp; delete layers; return; } if(CheckPointer(prev)!=POINTER_INVALID) { if(prev.type==defNeuron) { temp_count=(int)((prev.count-desc.window)%desc.step); output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } else if(n==0) { temp_count=(int)((output_count-desc.window)%desc.step); output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } } if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count)) neuron=neuron_p; break;
Ein ähnlicher Algorithmus wird auf die Neuronen im Subsample-Layer angewendet.
case defNeuronProof: neuron_p=new CNeuronProof(); if(CheckPointer(neuron_p)==POINTER_INVALID) { delete temp; delete layers; return; } if(CheckPointer(prev)!=POINTER_INVALID) { if(prev.type==defNeuron) { temp_count=(int)((prev.count-desc.window)%desc.step); output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } else if(n==0) { temp_count=(int)((output_count-desc.window)%desc.step); output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } } if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count)) neuron=neuron_p; break; }
Nachdem das Neuron deklariert und initialisiert wurde, fügen wir es dem neuronalen Layer hinzu.
if(!temp.Add(neuron)) { delete temp; delete layers; return; } neuron=NULL; }
Wenn der Zyklus zur Erzeugung von Neuronen für die nächste Schicht abgeschlossen ist, fügen wir die Schicht dem Speicher hinzu. Wir beenden die Methode, nachdem wir alle Layer erzeugt haben.
if(!layers.Add(temp)) { delete temp; delete layers; return; } } //--- return; }
3.4.2. Die Vorwärtspropagationsverfahren für das Convolutional Neuronale Netzwerk
Der gesamte Betrieb des Neuronalen Netzes ist in der Methode für den Vorwärtsdurchgang FeedForward organisiert. Diese Methode erhält in Parametern die ursprünglichen Daten für die Analyse (in unserem Fall sind diese Daten Informationen aus dem Preisdiagramm und den Indikatoren). Zunächst prüfen wir die Gültigkeit des empfangenen Verweises auf das Datenarray und den Initialisierungszustand des Neuronalen Netzes.
bool CNetConvolution::feedForward(CArrayDouble *inputVals) { if(CheckPointer(layers)==POINTER_INVALID || CheckPointer(inputVals)==POINTER_INVALID || layers.Total()<=1) return false;
Als Nächstes deklarieren wir die Hilfsvariablen und übergeben die empfangenen externen Daten an den Input Layer des Neuronalen Netzwerks.
CLayer *previous=NULL; CLayer *current=layers.At(0); int total=MathMin(current.Total(),inputVals.Total()); CNeuronBase *neuron=NULL; for(int i=0;i<total;i++) { neuron=current.At(i); if(CheckPointer(neuron)==POINTER_INVALID) return false; neuron.setOutputVal(inputVals.At(i)); }
Nachdem wir die Quelldaten in das Neuronale Netzwerk geladen haben, führen wir eine Schleife durch alle neuronalen Layer, vom Eingang des Neuronalen Netzwerks bis zu seinem Ausgang.
CObject *temp=NULL; for(int l=1;l<layers.Total();l++) { previous=current; current=layers.At(l); if(CheckPointer(current)==POINTER_INVALID) return false;
Wir führen innerhalb der gestarteten Schleife eine verschachtelte Schleife für jeden Layer aus, um über alle Neuronen im Layer zu iterieren und ihre Werte neu zu berechnen. Bitte beachten Sie, dass bei vollständig verbundenen neuronalen Layern der Wert des letzten Neurons nicht neu berechnet wird. Wie oben erwähnt, wird dieses Neuron als Bayes'scher Bias verwendet und daher wird nur sein Gewicht verwendet.
total=current.Total(); if(current.At(0).Type()==defNeuron) total--; //--- for(int n=0;n<total;n++) { neuron=current.At(n); if(CheckPointer(neuron)==POINTER_INVALID) return false;
Außerdem hängt die Wahl der Methode von der Art der Neuronen im vorherigen Layer ab. Bei vollständig verbundenen Layern rufen wir die Vorwärtspropagationsmethode auf und geben in ihren Parametern einen Verweis auf den vorherigen Layer an.
if(previous.At(0).Type()==defNeuron) { temp=previous; if(!neuron.feedForward(temp)) return false; continue; }
Wenn zuvor ein Convolutional- oder Subsample-Layer vorhanden war, prüfen wir den neu berechneten Neuronentyp. Fassen wir für ein Neuron einer vollverknüpften Schicht die inneren Schichten aller Neuronen der vorherigen Schicht zu einer einzigen Schicht zusammen und rufen dann die Vorwärtspropagationsmethode des aktuellen Neurons auf, mit einer Referenz auf die in den Parametern angegebene Gesamtschicht der Neuronen.
if(neuron.Type()==defNeuron) { if(n==0) { CLayer *temp_l=new CLayer(total); if(CheckPointer(temp_l)==POINTER_INVALID) return false; CNeuronProof *proof=NULL; for(int p=0;p<previous.Total();p++) { proof=previous.At(p); if(CheckPointer(proof)==POINTER_INVALID) return false; temp_l.AddArray(proof.getOutputLayer()); } temp=temp_l; } if(!neuron.feedForward(temp)) return false; if(n==total-1) { CLayer *temp_l=temp; temp_l.FreeMode(false); temp_l.Shutdown(); delete temp_l; } continue; }
Sobald die Schleife durch alle Neuronen dieses Layers beendet ist, löschen wir das gesamte Layer-Objekt. Hier ist es notwendig, das Layer-Objekt zu löschen, ohne Objekte von Neuronen zu löschen, die in diesem Layer enthalten sind, da dieselben Objekte weiterhin in unseren Convolutional- und Subsampled-Layers verwendet werden. Dazu setzen wir das Flag m_free_mode auf den Zustand false und löschen dann das Objekt.
Wenn wir ein Element einer Convolutional- und Subsampled-Layers vor uns haben, rufen wir die direkte Ausbreitungsmethode mit der Übertragung der Parameter der Verknüpfung zum vorherigen Element des entsprechenden Filters auf.
temp=previous.At(n); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!neuron.feedForward(temp)) return false; } } //--- return true; }
Nach der Iteration über alle Neuronen und Layer beenden wir die Methode.
3.4.3. Die Rückwärtspropagationsmethode des Convolutional Neuronalen Netzwerks.
Das Neuronale Netz wird mit der Rückwärtspropagationsmethode backProp trainiert. Sie implementiert die Methode der Rückwärts-Fehlerfortpflanzung vom Output Layer des Neuronalen Netzes zu seinen Eingängen. Die Methode erhält also die aktuellen Daten in Parametern.
Überprüfen wir zu Beginn der Methode die Gültigkeit des Zeigers auf das Zeigerwertobjekt.
void CNetConvolution::backProp(CArrayDouble *targetVals) { if(CheckPointer(targetVals)==POINTER_INVALID) return;
Dann berechnen wir den Effektivwert des Fehlers am Ausgang des Vorwärtsdurchgangs des Neuronalen Netzwerks im Vergleich zu den tatsächlichen Daten und berechnen die Fehlergradienten der Neuronen des Output-Layers.
CLayer *outputLayer=layers.At(layers.Total()-1); if(CheckPointer(outputLayer)==POINTER_INVALID) return; //--- double error=0.0; int total=outputLayer.Total()-1; for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=outputLayer.At(n); double target=targetVals.At(n); double delta=(target>1 ? 1 : target<-1 ? -1 : target)-neuron.getOutputVal(); error+=delta*delta; neuron.calcOutputGradients(targetVals.At(n)); } error/= total; error = sqrt(error); recentAverageError+=(error-recentAverageError)/recentAverageSmoothingFactor;
Als Nächstes wird eine Rückwärtsschleife durch alle Layer des Neuronalen Netzwerks organisiert. Hier führen wir eine verschachtelte Schleife durch alle Neuronen des entsprechenden Layers aus, um die Fehlergradienten der Neuronen der versteckten Layer neu zu berechnen.
CNeuronBase *neuron=NULL; CObject *temp=NULL; for(int layerNum=layers.Total()-2; layerNum>0; layerNum--) { CLayer *hiddenLayer=layers.At(layerNum); CLayer *nextLayer=layers.At(layerNum+1); total=hiddenLayer.Total(); for(int n=0; n<total && !IsStopped(); ++n) {
Ähnlich wie bei der Vorwärtspropagationsmethode wird die erforderliche Methode zur Aktualisierung der Fehlergradienten anhand der Typen des aktuellen Neurons und der Neuronen des nächsten Layers ausgewählt. Als Nächstes folgt eine vollständig verbundene Schicht von Neuronen, dann rufen wir die Methode calcHiddenGradients des analysierten Neurons auf, wobei wir den Zeiger auf das Objekt des nächsten Layers des Neuronalen Netzes in Parametern übergeben.
neuron=hiddenLayer.At(n); if(nextLayer.At(0).Type()==defNeuron) { temp=nextLayer; neuron.calcHiddenGradients(temp); continue; }
Wenn danach ein Convolutional- oder Subsample-Layer folgt, dann prüfen wir den Typ des aktuellen Neurons. Als Nächstes werden alle Filter des nächsten Layers in einer Schleife durchlaufen, wobei die Neuberechnung des Fehlergradienten für jeden Filter für ein bestimmtes Neuron gestartet wird. Dann werden die resultierenden Gradienten aufsummiert. Wenn der aktuelle Layer ebenfalls ein Convolutional- oder Subsampled-Layer ist, bestimmen wir den Fehlergradienten mit dem entsprechenden Filter.
if(neuron.Type()==defNeuron) { double g=0; for(int i=0;i<nextLayer.Total();i++) { temp=nextLayer.At(i); neuron.calcHiddenGradients(temp); g+=neuron.getGradient(); } neuron.setGradient(g); continue; } temp=nextLayer.At(n); neuron.calcHiddenGradients(temp); } }
Nachdem alle Gradienten aktualisiert worden sind, führen wir ähnliche Schleifen mit der gleichen Verzweigungslogik aus, um die Neuronengewichte zu aktualisieren. Wir beenden die Methode nach dem Aktualisieren der Gewichte.
for(int layerNum=layers.Total()-1; layerNum>0; layerNum--) { CLayer *layer=layers.At(layerNum); CLayer *prevLayer=layers.At(layerNum-1); total=layer.Total()-(layer.At(0).Type()==defNeuron ? 1 : 0); int n_conv=0; for(int n=0; n<total && !IsStopped(); n++) { neuron=layer.At(n); if(CheckPointer(neuron)==POINTER_INVALID) return; if(neuron.Type()==defNeuronProof) continue; switch(prevLayer.At(0).Type()) { case defNeuron: temp=prevLayer; neuron.updateInputWeights(temp); break; case defNeuronConv: case defNeuronProof: if(neuron.Type()==defNeuron) { for(n_conv=0;n_conv<prevLayer.Total();n_conv++) { temp=prevLayer.At(n_conv); neuron.updateInputWeights(temp); } } else { temp=prevLayer.At(n); neuron.updateInputWeights(temp); } break; default: temp=NULL; break; } } } }
Der komplette Code aller Methoden und Klassen befindet sich im Anhang.
4. Tests
Lassen Sie uns den Klassifizierungs-Expert Advisor aus dem zweiten Artikel innerhalb dieser Serie verwenden, um die Funktionsweise des Convolutional Neuronalen Netzwerkes zu testen. Der Zweck des Neuronalen Netzwerks ist es, zu lernen, ein Fraktal auf der aktuellen Kerze vorherzusagen. Zu diesem Zweck füttern wir das Neuronale Netzwerk mit Informationen über die letzten N Candlestick-Formationen und mit Daten von 4 Oszillatoren für denselben Zeitraum.
Erstellen wir im Convolutional-Layer des Neuronalen Netzwerks 4 Filter, die nach Mustern in den gesamten Preisenn der Kerzen und Oszillatorwerten für die analysierte Kerze suchen werden. Das Filterfenster und der Filterschritt werden der Datenmenge pro Kerzen-Beschreibung entsprechen. Mit anderen Worten, es werden alle Informationen über jede Kerze mit einem bestimmten Muster verglichen und der Konvergenzwert wird zurückgegeben. Dieser Ansatz erlaubt es, die Ausgangsdaten mit neuen Informationen über die Kerzen zu ergänzen (z. B. weitere Indikatoren für die Analyse hinzuzufügen usw.), ohne dass es zu einem signifikanten Leistungsverlust kommt.
Die Größe des Eigenschafts-Arrays wird im Subsampling-Layer reduziert, ebenso werden die Ergebnisse durch Mittelwertbildung geglättet.
Der EA selbst erforderte ein Minimum an Änderungen. Die Änderung betrifft die Klasse des Neuronalen Netzwerks, nämlich die Deklaration von Variablen und die Erzeugung einer Instanz.
CNetConvolution *Net;
Weitere Änderungen betreffen den Teil, der die Struktur des Neuronalen Netzes in der Funktion OnInit festlegt. Der Test wurde mit einem Netzwerk mit einem Convolutional- und einem Subsampling-Layer mit jeweils 4 Filtern durchgeführt. Die Struktur der vollverknüpften Layer wurde nicht geändert (dies geschah absichtlich, um die Auswirkungen der Convolutional-Layer auf den Betrieb des gesamten Netzwerks zu bewerten).
Net=new CNetConvolution(NULL); ResetLastError(); if(CheckPointer(Net)==POINTER_INVALID || !Net.Load(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false)) { printf("%s - %d -> Error of read %s prev Net %d",__FUNCTION__,__LINE__,FileName+".nnw",GetLastError()); CArrayObj *Topology=new CArrayObj(); if(CheckPointer(Topology)==POINTER_INVALID) return INIT_FAILED; //--- CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuron; if(!Topology.Add(desc)) return INIT_FAILED; //--- int filters=4; desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=filters; desc.type=defNeuronConv; desc.window=12; desc.step=12; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=filters; desc.type=defNeuronProof; desc.window=3; desc.step=2; if(!Topology.Add(desc)) return INIT_FAILED; //--- int n=1000; bool result=true; for(int i=0;(i<4 && result);i++) { desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=n; desc.type=defNeuron; result=(Topology.Add(desc) && result); n=(int)MathMax(n*0.3,20); } if(!result) { delete Topology; return INIT_FAILED; } //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; if(!Topology.Add(desc)) return INIT_FAILED; delete Net; Net=new CNetConvolution(Topology); delete Topology; if(CheckPointer(Net)==POINTER_INVALID) return INIT_FAILED; dError=-1; dUndefine=0; dForecast=0; dtStudied=0; }
Der Rest des Codes des Expert Advisors blieb unverändert.
Die Tests wurden mit dem EURUSD-Paar mit dem H1-Zeitrahmen durchgeführt. Zwei Expert Advisors, einer mit einem Convolutional Neuronalen Netzwerks und der andere mit einem voll verbundenen Netzwerk, wurden gleichzeitig auf verschiedenen Charts desselben Symbols im selben Terminal gestartet. Die Parameter der voll verbundenen Layer des Convolutional Neuronalen Netzwerks stimmen mit den Parametern des voll verbundenen Netzwerks des zweiten Expert Advisors überein, d. h. wir haben einfach Convolutional- und Subsampled-Layer zu einem zuvor erstellten Netzwerk hinzugefügt.
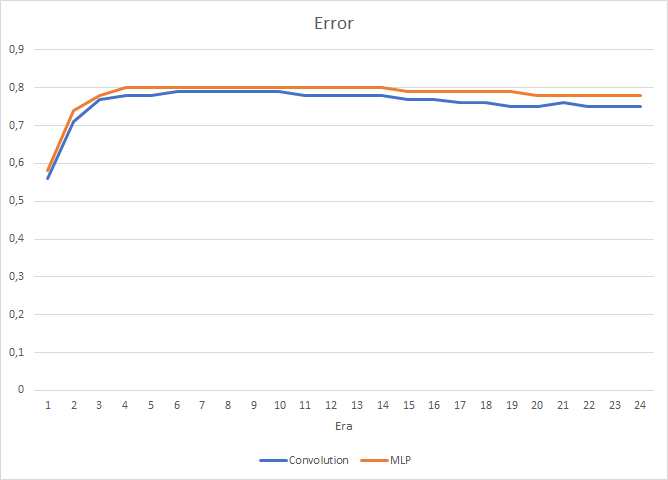
Die Tests zeigen einen kleinen Leistungszuwachs des Convolutional Neuronalen Netzwerkes. Trotz der Hinzufügung von zwei Layern betrug die durchschnittliche Trainingszeit für eine Epoche (basierend auf den Ergebnissen von 24 Epochen) des Convolutional Neuronalen Netzwerkes 2 Stunden 4 Minuten und die des voll verbundenen Netzwerks 2 Stunden 10 Minuten.
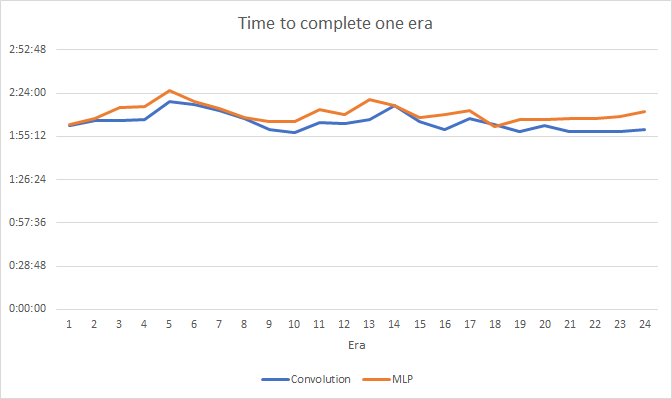
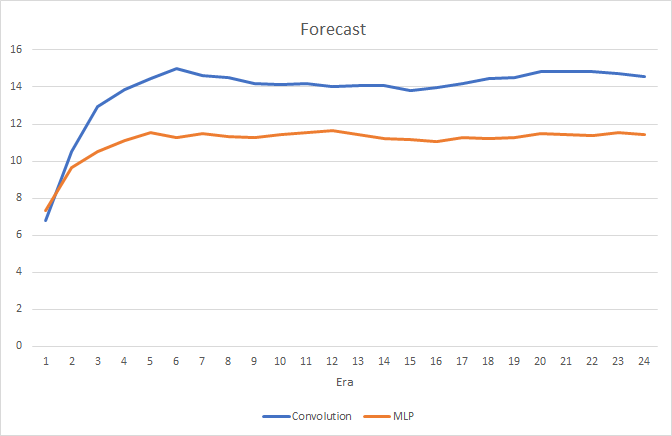
Das Convolutional Neuronale Netzwerk zeigt etwas bessere Ergebnisse in Bezug auf Vorhersagefehler und "Zieltreffer".
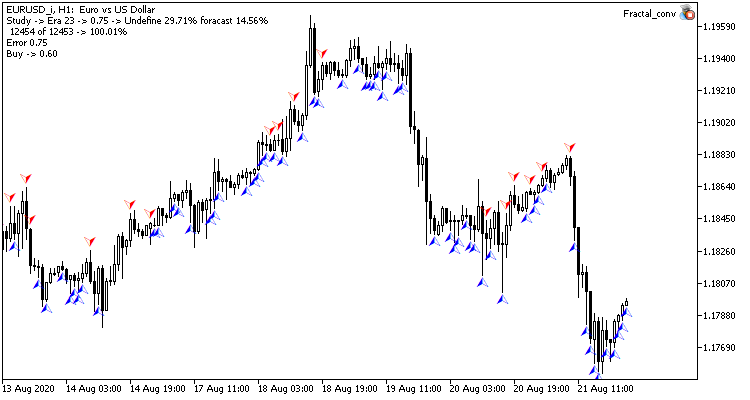
Optisch kann man sehen, dass die Signale im Diagramm des Convolutional Neuronalen Netzwerks weniger häufig erscheinen, aber sie sind näher am Ziel.
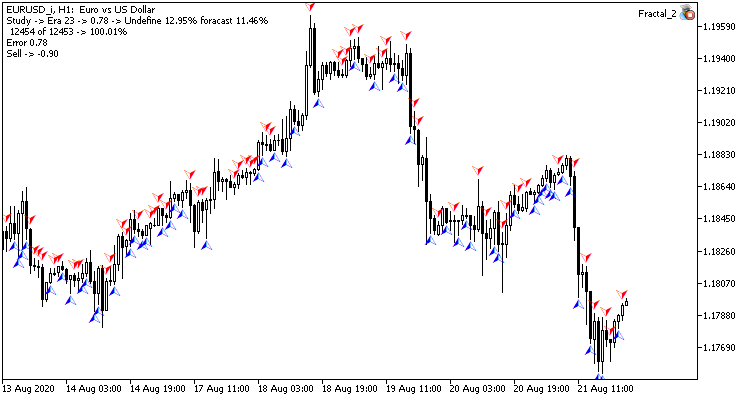
Schlussfolgerung
In diesem Artikel haben wir die Möglichkeit des Einsatzes von Convolutional Neuronalen Netzwerkes in Finanzmärkten untersucht. Tests haben gezeigt, dass wir durch ihre Verwendung die Ergebnisse eines vollständig verbundenen Neuronalen Netzwerks verbessern können. Dies kann mit der Vorverarbeitung der Daten zusammenhängen, die wir in das voll verbundene Perzeptron einspeisen. Die Originaldaten werden in den Convolutional- und Subsampled-Layern gefiltert, um Rauschen zu entfernen, was die Qualität der Quelldaten und die Qualität des Neuronalen Netzwerks verbessert. Darüber hinaus trägt die reduzierte Dimensionalität dazu bei, die Anzahl der Perceptron-Verbindungen mit den Originaldaten zu verringern, was zu einer Leistungssteigerung führt.
Liste der Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Fractal.mq5 | Expert Advisor | Ein Expert Advisor mit der Regression durch ein Neuronales Netz (1 Neuron in der Ausgabeschicht) |
| 2 | Fractal_2.mq5 | Expert Advisor | Ein Expert Advisor mit der Klassifikation durch ein Neuronales Netz (3 Neuron in der Ausgabeschicht) |
| 3 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zum Erstellen eines Neuronalen Netzes (ein Perceptron) |
| 4 | Fractal_conv.mq5 | Expert Advisor | Ein Expert Advisor mit einem Convolutional Neuronalen Netzwerk (3 Neuronen im Output Layer) |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/8234
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Parallele Partikelschwarmoptimierung
Parallele Partikelschwarmoptimierung
 Grundlegende Mathematik hinter dem Forex-Handel
Grundlegende Mathematik hinter dem Forex-Handel
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Der Artikel ist sicherlich interessant. Vor allem in Bezug auf die Tatsache, dass alles in MQL implementiert ist und keine Bibliotheken erforderlich sind. Ich hoffe, dass es eine Fortsetzung geben wird. Das Testen des Expert Advisors hat leider noch nicht zu positiven Ergebnissen geführt.
Neuer Artikel Neuronale Netze leicht gemacht (Teil 3): Convolutional networks wurde veröffentlicht:
Autor: Dmitriy Gizlyk
Hallo. Vielen Dank für das hier. Ich habe eine Frage an Sie. Wie erhalten Sie die Pixelwerte für das Diagramm oder das Bild? Ich habe nachgeschaut, kann aber keine Erklärung finden, wie man die Pixelwerte des Diagramms ableitet, um sie in der Eingangsfaltungsschicht zu verwenden.
Hallo, Sie haben Recht. Die Faltungsschicht nimmt keine Pixel aus dem Diagramm. Meine Idee war eine andere. Ich nehme Daten von verschiedenen Indikatoren und historischen Kursen und gebe sie in den Input des neuronalen Netzwerks ein. Die Faltungsschicht sucht nach Mustern in diesen Daten und gibt einen Wert für jede Kerze zurück.
Hallo, Sie haben Recht. Die Faltungsebene nimmt keine Pixel aus dem Diagramm. Meine Idee war eine andere. Ich nehme Daten von verschiedenen Indikatoren und historischen Kursen und gebe sie in den Input des neuronalen Netzwerks ein. Die Faltungsschicht sucht nach Mustern in diesen Daten und gibt einen Wert für jede Kerze zurück.
Ich verstehe, danke.