
Neuronale Netze im Handel: Knotenadaptive Graphendarstellung mit NAFS
Einführung
In den letzten Jahren wurde das Lernen von Graphenrepräsentationen in verschiedenen Anwendungsszenarien, wie z. B. Knotencluster, Linkvorhersage, Knotenklassifizierung und Graphenklassifizierung, weit verbreitet. Das Ziel des Lernens von Graphdarstellungen ist es, Graphinformationen in Knoteneinbettungen zu kodieren. Traditionelle Methoden zum Erlernen von Graphdarstellungen haben sich in erster Linie darauf konzentriert, Informationen über die Graphstruktur zu erhalten. Diesen Methoden sind jedoch zwei wesentliche Grenzen gesetzt:
- Flache Architektur. Während Graph Convolutional Networks (GCNs) mehrere Schichten verwenden, um tiefe strukturelle Informationen zu erfassen, führt die Erhöhung der Anzahl der Schichten oft zu einer Überglättung, was zu ununterscheidbaren Knoteneinbettungen führt.
- Schlechte Skalierbarkeit. GNN-basierte Methoden zum Erlernen von Graphenrepräsentationen können bei großen Graphen aufgrund der hohen Rechenkosten und des erheblichen Speicherverbrauchs nicht skalieren.
Die Autoren des Artikels „NAFS: A Simple yet Tough-to-beat Baseline for Graph Representation Learning“ haben sich zum Ziel gesetzt, diese Probleme zu lösen, indem sie eine neuartige Methode zur Darstellung von Graphen einführen, die auf einer einfachen Glättung von Merkmalen und einer anschließenden adaptiven Kombination basiert. Die Methode NAFS (Node-Adaptive Feature Smoothing) erzeugt überlegene Knoteneinbettungen, indem sie sowohl die Strukturinformationen des Graphen als auch die Knotenmerkmale integriert. Ausgehend von der Beobachtung, dass verschiedene Knoten sehr unterschiedliche „Glättungsgeschwindigkeiten“ aufweisen, glättet NAFS adaptiv die Merkmale jedes Knotens, indem es sowohl Nachbarschaftsinformationen niedriger als auch hoher Ordnung verwendet. Darüber hinaus werden Merkmalsensembles verwendet, um geglättete Merkmale zu kombinieren, die mit verschiedenen Glättungsoperatoren extrahiert wurden. Da NAFS keine Training erfordert, reduziert es die Schulungskosten erheblich und lässt sich effizient auf große Graphen skalieren.
1. Der NAFS-Algorithmus
Viele Forscher haben vorgeschlagen, die Glättung und Transformation von Merkmalen innerhalb jeder GCN-Schicht zu trennen, um eine skalierbare Knotenklassifizierung zu ermöglichen. Konkret werden in einem Vorverarbeitungsschritt zunächst die Merkmale geglättet, und dann werden die verarbeiteten Merkmale in einen einfachen MLP eingespeist, um die endgültigen Knotenbeschriftungen vorherzusagen.
Solche entkoppelten GNNs bestehen aus zwei Teilen: Merkmalsglättung und MLP-Training. Die Phase der Merkmalsglättung kombiniert strukturelle Graphinformationen mit Knotenmerkmalen, um informativere Eingaben für den nachfolgenden MLP zu erzeugen. Beim Training lernt der MLP nur aus diesen geglätteten Merkmalen.
Ein anderer Zweig der GNN-Forschung trennt ebenfalls Glättung und Transformation, verfolgt aber einen anderen Ansatz. Rohe Knotenmerkmale werden zunächst in ein MLP eingespeist, um Zwischeneinbettungen zu erzeugen. Anschließend werden personalisierte Propagierungsoperationen auf diese Einbettungen angewandt, um endgültige Vorhersagen zu erhalten. Dieser GNN-Zweig muss jedoch in jeder Trainingsepoche rekursive Propagierungsoperationen durchführen, was ihn für große Graphen unpraktisch macht.
Der einfachste Weg zur Erfassung umfangreicher struktureller Informationen besteht darin, mehrere GNN-Schichten übereinander zu legen. Die wiederholte Glättung von Merkmalen in GNN-Modellen führt jedoch zu ununterscheidbaren Knoteneinbettungen - dem bekannten Problem der Überglättung.
Die quantitative Analyse zeigt empirisch, dass der Grad eines Knotens bei der Bestimmung seiner optimalen Glättungsstufe eine wichtige Rolle spielt. Intuitiv sollten Knoten mit hohem Grad im Vergleich zu Knoten mit niedrigem Grad weniger Glättungsschritte durchlaufen.
Während die Anwendung der Merkmalsglättung in entkoppelten GNNs ein skalierbares Training für große Graphen ermöglicht, führt eine undifferenzierte Glättung über alle Knoten zu suboptimalen Einbettungen. Knoten mit unterschiedlichen strukturellen Eigenschaften erfordern unterschiedliche Glättungsraten. Daher sollte eine knotenadaptive Merkmalsglättung verwendet werden, um die individuellen Glättungsanforderungen jedes Knotens zu erfüllen.
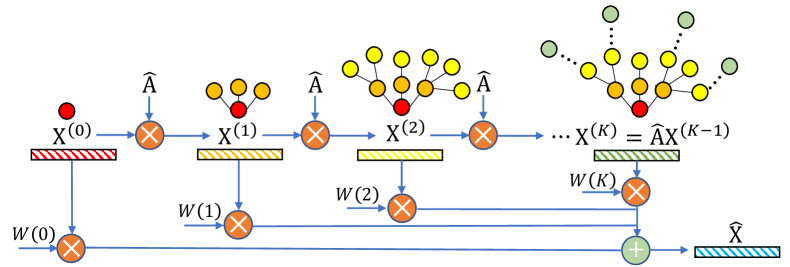
Bei sequentieller Anwendung, 𝐗l=Â𝐗l−1, akkumuliert die geglättete Knoteneinbettungsmatrix 𝐗l−1 mit zunehmendem l eine tiefere Strukturinformation. Die mehrskaligen Knoteneinbettungsmatrizen {𝐗0, 𝐗1, …, 𝐗K} (wobei K die maximale Glättungsstufe ist) werden dann zu einer einheitlichen Matrix Ẋ zusammengeführt, die sowohl lokale als auch globale Nachbarschaftsinformationen kombiniert.
Die Analyse der Autoren von NAFS zeigt, dass die Geschwindigkeit, mit der jeder Knoten einen stabilen Zustand erreicht, stark variiert. Daher ist eine individuelle Knotenanalyse erforderlich. Zu diesem Zweck führt NAFS das Konzept des Glättungsgewichts ein, das auf der Grundlage des Abstands zwischen den lokalen und geglätteten Merkmalsvektoren eines Knotens berechnet wird. Auf diese Weise kann der Glättungsprozess für jeden Knoten individuell angepasst werden.
Eine effektivere Alternative besteht darin, die Glättungsmatrix  durch Kosinusähnlichkeit zu ersetzen. Eine höhere Kosinusähnlichkeit zwischen dem lokalen und dem geglätteten Merkmalsvektor eines Knotens zeigt an, dass der Knoten vi weiter vom Gleichgewicht entfernt ist, und dass [Âk𝐗]i intuitiv mehr aktuelle Informationen enthält. Daher sollten für den Knoten vi die geglätteten Merkmale mit höherer Kosinusähnlichkeit mehr zu seiner endgültigen Einbettung beitragen.
Verschiedene Glättungsoperatoren fungieren effektiv als unterschiedliche Wissensextraktoren. Dies ermöglicht die Erfassung von Graphenstrukturen über verschiedene Skalen und Dimensionen hinweg. Um dies zu erreichen, werden bei Feature-Ensemble-Operationen mehrere Wissensextraktoren eingesetzt. Diese Extraktoren werden im Prozess der Merkmalsglättung verwendet, um verschiedene geglättete Merkmale zu erzeugen.
NAFS erzeugt Knoteneinbettungen ohne jegliches Training und ist daher äußerst effizient und skalierbar. Darüber hinaus ermöglicht die knotenadaptive Strategie der Merkmalsglättung die Erfassung tiefer struktureller Informationen.
Die Autoren haben die Methode NAFS wie folgt visualisiert.
2. Die Implementation in MQL5
Nachdem wir die theoretischen Aspekte von NAFS behandelt haben, gehen wir nun zu seiner praktischen Umsetzung mit MQL5 über. Bevor wir zur eigentlichen Umsetzung übergehen, sollten wir die wichtigsten Phasen des Rahmens klar umreißen.
- Konstruktion der Matrix für die Darstellung von Knoten in mehreren Maßstäben.
- Berechnung der Glättungsgewichte auf der Grundlage der Kosinusähnlichkeit zwischen dem Merkmalsvektor des Knotens und seinen geglätteten Darstellungen.
- Berechnung des gewichteten Durchschnitts für die endgültige Einbettung.
Es ist erwähnenswert, dass einige dieser Operationen mit den bestehenden Funktionen unserer Bibliothek implementiert werden können. Die Berechnung der Kosinusähnlichkeit und des gewichteten Mittelwerts kann beispielsweise effizient durch Matrixmultiplikation erfolgen. Die Softmax-Schicht kann bei der Bestimmung der Glättungskoeffizienten helfen.
Die verbleibende Frage ist die Konstruktion der Knotenrepräsentationsmatrix mit mehreren Skalen.
2.1 Multiskalige Knotenrepräsentationsmatrix
Um die Matrix für die Repräsentation der Knoten in mehreren Maßstäben zu erstellen, verwenden wir eine einfache Mittelung der Merkmale einzelner Knoten mit den entsprechenden Merkmalen ihrer unmittelbaren Nachbarn. Das Mehrskalenverhalten wird durch die Anwendung von Mittelungsfenstern unterschiedlicher Größe erreicht.
In unseren Arbeiten implementieren wir wichtige Berechnungen im OpenCL-Kontext. Folglich wird auch der Prozess der Matrixerstellung an das parallele Rechnen delegiert. Zu diesem Zweck werden wir einen neuen Kernel im OpenCL-Programm FeatureSmoothing erstellen.
__kernel void FeatureSmoothing(__global const float *feature, __global float *outputs, const int smoothing ) { const size_t pos = get_global_id(0); const size_t d = get_global_id(1); const size_t total = get_global_size(0); const size_t dimension = get_global_size(1);
In den Kernelparametern erhalten wir Zeiger auf zwei Datenpuffer (die Quelldaten und die Ergebnisse) sowie eine Konstante, die die Anzahl der Glättungsskalen angibt. In diesem Fall wird keine spezifische Schrittweite für die Glättungsskala festgelegt, da sie als „1“ angenommen wird. Das Mittelungsfenster erweitert sich um 2 Elemente. Denn wir erweitern sie gleichermaßen vor und nach dem Zielelement.
Es ist wichtig zu beachten, dass die Anzahl der Glättungsskalen nicht negativ sein kann. Ist dieser Wert gleich Null, werden die Quelldaten einfach unverändert weitergegeben.
Wir planen, diesen Kernel in einem zweidimensionalen Aufgabenraum auszuführen, der aus völlig unabhängigen Threads besteht, ohne lokale Arbeitsgruppen zu bilden. Die erste Dimension entspricht der Größe der zu analysierenden Quellsequenz, während die zweite Dimension die Anzahl der Merkmale in dem Vektor darstellt, der jedes Sequenzelement beschreibt.
Innerhalb des Kernelkörpers identifizieren wir den aktuellen Thread sofort anhand aller Dimensionen des Aufgabenraums und bestimmen ihre jeweilige Größe.
Anhand der gewonnenen Daten berechnen wir die Offsets in den Datenpuffern.
const int shift_input = pos * dimension + d; const int shift_output = dimension * pos * smoothing + d;
Damit ist die Vorbereitungsphase abgeschlossen, und wir können direkt mit der Erstellung der multiskaligen Darstellungen beginnen. Der erste Schritt besteht darin, die Quelldaten zu kopieren, die der Darstellung mit Mittelwertbildung auf Nullniveau entsprechen.
float value = feature[shift_input]; if(isinf(value) || isnan(value)) value = 0; outputs[shift_output] = value;
Anschließend wird eine Schleife zur Berechnung der Mittelwerte der einzelnen Merkmale innerhalb des Mittelungsfensters eingerichtet. Wie Sie sich vorstellen können, müssen dazu alle Werte innerhalb des Fensters summiert und die Summe anschließend durch die Anzahl der in die Summierung einbezogenen Elemente geteilt werden.
Es ist wichtig zu beachten, dass alle Mittelungsfenster für verschiedene Skalen um dasselbe analysierte Element zentriert sind. Folglich enthält jede nachfolgende Skala alle Elemente der vorherigen Skala. Wir machen uns diese Eigenschaft zunutze, um die Zugriffe auf den teuren globalen Speicher zu minimieren: Bei jeder Iteration addieren wir nur die neu hinzugekommenen Werte zu der zuvor akkumulierten Summe und dividieren dann die aktuelle akkumulierte Summe durch die Anzahl der Elemente im aktuellen Mittelungsfenster.
for(int s = 1; s <= smoothing; s++) { if((pos - s) >= 0) { float temp = feature[shift_input - s * dimension]; if(isnan(temp) || isinf(temp)) temp = 0; value += temp; } if((pos + s) < total) { float temp = feature[shift_input + s * dimension]; if(isnan(temp) || isinf(temp)) temp = 0; value += temp; } float factor = 1.0f / (min((int)total, (int)(pos + s)) - max((int)(pos - s), 0) + 1); if(isinf(value) || isnan(value)) value = 0; float out = value * factor; if(isinf(out) || isnan(out)) out = 0; outputs[shift_output + s * dimension] = out; } }
Es ist auch erwähnenswert (auch wenn es etwas kontraintuitiv klingen mag), dass nicht alle Mittelungsfenster innerhalb der gleichen Skala die gleiche Größe haben. Dies ist auf Randelemente in der Sequenz zurückzuführen, bei denen das Mittelungsfenster auf beiden Seiten über die Sequenzgrenzen hinausgeht. Daher berechnen wir bei jeder Iteration die tatsächliche Anzahl der Elemente, die an der Mittelwertbildung beteiligt sind.
In ähnlicher Weise konstruieren wir den Algorithmus zur Ausbreitung des Fehlergradienten durch die oben beschriebenen Operationen im Kernel von FeatureSmoothingGradient, den Sie sich am besten selbst ansehen. Den vollständigen Programmcode für OpenCL finden Sie im Anhang.
2.2 Aufbau der NAFS-Klasse
Nachdem wir die notwendigen Ergänzungen am OpenCL-Programm vorgenommen haben, gehen wir zur Hauptanwendung über, wo wir eine neue Klasse für die adaptive Knoteneinbettung erstellen werden: CNeuronNAFS. Die Struktur der neuen Klasse ist unten dargestellt.
class CNeuronNAFS : public CNeuronBaseOCL { protected: uint iDimension; uint iSmoothing; uint iUnits; //--- CNeuronBaseOCL cFeatureSmoothing; CNeuronTransposeOCL cTranspose; CNeuronBaseOCL cDistance; CNeuronSoftMaxOCL cAdaptation; //--- virtual bool FeatureSmoothing(const CNeuronBaseOCL *neuron, const CNeuronBaseOCL *smoothing); virtual bool FeatureSmoothingGradient(const CNeuronBaseOCL *neuron, const CNeuronBaseOCL *smoothing); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return true; } public: CNeuronNAFS(void) {}; ~CNeuronNAFS(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint step, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronNAFS; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Wie man sieht, deklariert die Struktur der neuen Klasse drei Variablen und vier interne Schichten. Wir werden ihre Funktionalität während der Implementierung der Algorithmen innerhalb der überschriebenen virtuellen Methoden überprüfen.
Wir haben auch zwei Wrapper-Methoden für die gleichnamigen Kernel in dem zuvor beschriebenen OpenCL-Programm. Sie werden mit dem Standard-Kernelaufruf-Algorithmus erstellt. Sie können den Code selbst im Anhang finden.
Alle internen Objekte der neuen Klasse werden statisch deklariert, sodass wir den Konstruktor und Destruktor der Klasse „leer“ lassen können. Die Initialisierung dieser deklarierten und geerbten Objekte wird in der Methode Init durchgeführt.
bool CNeuronNAFS::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint dimension, uint smoothing, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, dimension * units_count, optimization_type, batch)) return false;
In den Methodenparametern erhalten wir die wichtigsten Konstanten, mit denen wir die Architektur des zu erstellenden Objekts eindeutig bestimmen können. Dazu gehören:
- dimension - die Größe des Merkmalsvektors, der ein einzelnes Sequenzelement beschreibt;
- smoothing - Anzahl der Glättungsskalen (wenn auf Null gesetzt, werden die Quelldaten direkt kopiert);
- units_count – die Größe der zu analysierenden Sequenz.
Beachten Sie, dass alle Parameter vom Typ Ganzzahl ohne Vorzeichen sind. Auf diese Weise wird die Möglichkeit ausgeschlossen, negative Parameterwerte zu erhalten.
Innerhalb der Methode rufen wir wie üblich zunächst die gleichnamige Methode der Elternklasse auf, die bereits die Parametervalidierung und die Initialisierung der geerbten Objekte übernimmt. Es wird davon ausgegangen, dass die Größe des Ergebnistensors der Größe des Eingabetensors entspricht und als Produkt aus der Anzahl der Elemente in der analysierten Sequenz und der Größe des Merkmalsvektors für ein einzelnes Element berechnet wird.
Nach erfolgreicher Ausführung der übergeordneten Klassenmethode speichern wir die extern bereitgestellten Parameter in internen Variablen mit entsprechenden Namen.
iDimension = dimension; iSmoothing = smoothing; iUnits = units_count;
Als Nächstes gehen wir zur Initialisierung der deklarierten Objekte über. Zunächst deklarieren wir die interne Ebene für die Speicherung der Multiskalen-Knotenrepräsentationsmatrix. Seine Größe muss ausreichen, um die gesamte Matrix zu speichern. Daher ist sie (iSmoothing + 1) mal größer als die Größe der Originaldaten.
if(!cFeatureSmoothing.Init(0, 0, OpenCL, (iSmoothing + 1) * iUnits * iDimension, optimization, iBatch)) return false; cFeatureSmoothing.SetActivationFunction(None);
Nach der Konstruktion der Multiskalendarstellungen (in unserem Fall handelt es sich um Kerzen-Muster in verschiedenen Maßstäben) müssen wir die Kosinusähnlichkeit zwischen diesen Darstellungen und dem Merkmalsvektor des analysierten Balkens berechnen. Dazu multiplizieren wir den Eingabetensor mit dem Tensor der Multiskalen-Knotenrepräsentation. Bevor wir diese Multiplikation durchführen können, müssen wir jedoch zunächst den Tensor der Multiskalendarstellung transponieren.
if(!cTranspose.Init(0, 1, OpenCL, (iSmoothing + 1)*iUnits, iDimension, optimization, iBatch)) return false; cTranspose.SetActivationFunction(None);
Die Operation der Matrixmultiplikation wurde bereits in unserer Basisklasse für neuronale Schichten implementiert und von der übergeordneten Klasse geerbt. Um die Ergebnisse dieser Operation zu speichern, initialisieren wir das interne Objekt cDistance.
if(!cDistance.Init(0, 2, OpenCL, (iSmoothing + 1)*iUnits, optimization, iBatch)) return false; cDistance.SetActivationFunction(None);
Ich möchte Sie daran erinnern, dass die Multiplikation zweier Vektoren, die in die gleiche Richtung zeigen, positive Werte ergibt, während entgegengesetzte Richtungen negative Werte ergeben. Wenn der analysierte Balken mit dem allgemeinen Trend übereinstimmt, ist das Ergebnis der Multiplikation zwischen dem Merkmalsvektor des Balkens und den geglätteten Werten eindeutig positiv. Umgekehrt ist das Ergebnis negativ, wenn der Balken dem allgemeinen Trend entgegengesetzt ist. Bei gleichbleibenden Marktbedingungen wird der geglättete Wertvektor nahe bei Null liegen. Folglich geht auch das Multiplikationsergebnis gegen Null. Um die resultierenden Werte zu normalisieren und die adaptiven Einflusskoeffizienten für jede Skala zu berechnen, verwenden wir die Softmax-Funktion.
if(!cAdaptation.Init(0, 3, OpenCL, cDistance.Neurons(), optimization, iBatch)) return false; cAdaptation.SetActivationFunction(None); cAdaptation.SetHeads(iUnits);
Um nun die endgültige Einbettung für den analysierten Knoten (Balken) zu berechnen, multiplizieren wir den adaptiven Koeffizientenvektor jedes Knotens mit der entsprechenden Multiskalen-Darstellungsmatrix. Das Ergebnis dieser Operation wird in den Puffer der Schnittstelle für den Datenaustausch mit der nachfolgenden, von der übergeordneten Klasse geerbten Schicht geschrieben. Daher erstellen wir kein zusätzliches internes Objekt. Stattdessen deaktivieren wir einfach die Aktivierungsfunktion, schließen die Initialisierungsmethode ab und geben das logische Ergebnis der Operation an das aufrufende Programm zurück.
SetActivationFunction(None); //--- return true; }
Nachdem die Initialisierung des neuen Objekts abgeschlossen ist, werden in der Methode feedForward die Vorwärtsdurchgangs-Algorithmen konstruiert. In den Methodenparametern erhalten wir einen Zeiger auf das Quelldatenobjekt.
bool CNeuronNAFS::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!FeatureSmoothing(NeuronOCL, cFeatureSmoothing.AsObject())) return false;
Aus diesen Daten konstruieren wir zunächst den Multiskalen-Repräsentationstensor, indem wir die Wrapper-Methode für den zuvor beschriebenen Kernel FeatureSmoothing aufrufen.
if(!FeatureSmoothing(NeuronOCL, cFeatureSmoothing.AsObject())) return false;
Wie in der Beschreibung des Initialisierungsalgorithmus erläutert, wird die resultierende Matrix der Knotenrepräsentation in mehreren Maßstäben transponiert.
if(!cTranspose.FeedForward(cFeatureSmoothing.AsObject())) return false;
Anschließend multiplizieren wir ihn mit dem Eingabetensor, um die Kosinus-Ähnlichkeitskoeffizienten zu erhalten.
if(!MatMul(NeuronOCL.getOutput(), cTranspose.getOutput(), cDistance.getOutput(), 1, iDimension, iSmoothing + 1, iUnits)) return false;
Diese Koeffizienten werden dann mit der Softmax-Funktion normalisiert.
if(!cAdaptation.FeedForward(cDistance.AsObject())) return false;
Schließlich multiplizieren wir den resultierenden Tensor der adaptiven Koeffizienten mit der zuvor gebildeten Multiskalen-Darstellungsmatrix.
if(!MatMul(cAdaptation.getOutput(), cFeatureSmoothing.getOutput(), Output, 1, iSmoothing + 1, iDimension, iUnits)) return false; //--- return true; }
Als Ergebnis dieses Vorgangs erhalten wir die endgültigen Knoteneinbettungen, die im Schnittstellenpuffer der neuronalen Schicht innerhalb des Modells gespeichert werden. Die Methode schließt mit der Rückgabe des logischen Ergebnisses der Operation an das aufrufende Programm ab.
Der nächste Entwicklungsschritt ist die Implementierung der Rückwärtsdurchlauf-Algorithmen für unsere neue NAFS-Rahmenklasse. Dabei gibt es zwei wesentliche Merkmale zu beachten. Erstens enthält unser neues Objekt, wie im theoretischen Teil erwähnt, keine trainierbaren Parameter. Dementsprechend überschreiben wir die Methode updateInputWeights mit einem Fragment, das immer ein positives Ergebnis liefert.
virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return true; }
Besondere Aufmerksamkeit verdient jedoch die Methode calcInputGradients. Trotz der Einfachheit des Vorwärtsdurchlaufs werden sowohl die Eingabedaten als auch die Multiskalen-Darstellungsmatrix zweimal verwendet. Um den Fehlergradienten zurück auf die Ebene der Eingabedaten zu propagieren, müssen wir ihn daher sorgfältig durch alle Informationspfade des konstruierten Algorithmus leiten.
bool CNeuronNAFS::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Die Methode erhält als Parameter einen Zeiger auf das Objekt der vorherigen Schicht, das die propagierten Fehlergradienten erhält. Diese Gradienten müssen im Verhältnis zum Einfluss der einzelnen Datenelemente auf das Endergebnis des Modells verteilt werden. Im Methodenrumpf wird zunächst die Gültigkeit des empfangenen Zeigers überprüft, da eine Fortsetzung mit einer ungültigen Referenz alle nachfolgenden Operationen sinnlos machen würde.
Zunächst muss der von der nachfolgenden Schicht erhaltene Fehlergradient auf die adaptiven Koeffizienten und die Multiskalen-Darstellungsmatrix verteilt werden. Wir planen jedoch auch, den Gradienten durch den Informationspfad der adaptiven Koeffizienten zurück in die Multiskalen-Darstellungsmatrix zu propagieren. In diesem Stadium speichern wir also den Gradienten des Tensors der Multiskalendarstellung in einem temporären Puffer.
if(!MatMulGrad(cAdaptation.getOutput(), cAdaptation.getGradient(), cFeatureSmoothing.getOutput(), cFeatureSmoothing.getPrevOutput(), Gradient, 1, iSmoothing + 1, iDimension, iUnits)) return false;
Als Nächstes behandeln wir den Informationsfluss der adaptiven Koeffizienten. Hier propagieren wir den Fehlergradienten zurück zum Kosinus-Ähnlichkeitstensor, indem wir die Gradientenverteilungsmethode des entsprechenden Objekts aufrufen.
if(!cDistance.calcHiddenGradients(cAdaptation.AsObject())) return false;
Im folgenden Schritt verteilen wir den Fehlergradienten zwischen den Eingabedaten und dem transponierten Multiskalendarstellungstensor. Auch hier gehen wir davon aus, dass der Gradient über einen zweiten Informationspfad auf die Ebene der Eingangsdaten übertragen wird. Daher speichern wir in dieser Phase den entsprechenden Gradienten in einem temporären Puffer.
if(!MatMulGrad(NeuronOCL.getOutput(), PrevOutput, cTranspose.getOutput(), cTranspose.getGradient(), cDistance.getGradient(), 1, iDimension, iSmoothing + 1, iUnits)) return false;
Anschließend transponieren wir den Gradiententensor der Multiskalendarstellung und summieren ihn mit den zuvor gespeicherten Daten.
if(!cFeatureSmoothing.calcHiddenGradients(cTranspose.AsObject()) || !SumAndNormilize(cFeatureSmoothing.getGradient(), cFeatureSmoothing.getPrevOutput(), cFeatureSmoothing.getGradient(), iDimension, false, 0, 0, 0, 1) ) return false;
Schließlich propagieren wir den akkumulierten Fehlergradienten auf die Ebene der Eingangsdaten. Zunächst wird der Fehlergradient aus der Multiskalen-Darstellungsmatrix übergeben.
if(!FeatureSmoothingGradient(NeuronOCL, cFeatureSmoothing.AsObject()) || !SumAndNormilize(NeuronOCL.getGradient(), cFeatureSmoothing.getPrevOutput(), NeuronOCL.getGradient(), iDimension, false, 0, 0, 0, 1) || !DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), NeuronOCL.getGradient(), (ENUM_ACTIVATION)NeuronOCL.Activation()) ) return false; //--- return true; }
Dann fügen wir die zuvor gespeicherten Daten hinzu und wenden die Ableitung der Aktivierungsfunktion an, um den Gradienten der Eingabeschicht anzupassen. Die Methode schließt mit der Rückgabe des logischen Ergebnisses der Operation an das aufrufende Programm ab.
Damit ist die Beschreibung der Methoden der Klasse CNeuronNAFS abgeschlossen. Der vollständige Quellcode für diese Klasse und alle ihre Methoden ist im Anhang enthalten.
2.3 Modellarchitektur
Ein paar Worte sollten über die Architektur der trainierbaren Modelle gesagt werden. Wir haben das neue adaptive Objekt für das Glätten der Eigenschaften in das Environment State Encoder Modell integriert. Das Modell selbst wurde aus dem vorherigen Artikel entwickelt, der dem AMCT gewidmet ist. Das neue Modell nutzt also Ansätze aus Beiden. Die Modellarchitektur wird in der Methode CreateEncoderDescriptions implementiert.
Wir beginnen mit der Erstellung einer vollständig verknüpften Schicht, um die Quelldaten in das Modell einzugeben. Dabei bleiben wir unseren allgemeinen Modelldesignprinzipien treu.
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } //--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Es ist anzumerken, dass der NAFS-Algorithmus eine adaptive Glättung direkt auf die rohen Eingabedaten anwenden kann. Wir dürfen jedoch nicht vergessen, dass unser Modell unbearbeitete Rohdaten direkt vom Handelsterminal erhält. Infolgedessen können die zu analysierenden Merkmale sehr unterschiedliche Werteverteilungen aufweisen. Um die negativen Auswirkungen dieses Faktors zu minimieren, haben wir immer eine Normalisierungsschicht verwendet. Und wir wenden hier den gleichen Ansatz an.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Nach der Normalisierung wenden wir die adaptive Merkmalsglättungsschicht an. Diese spezifische Reihenfolge wird für Ihre eigenen Experimente empfohlen, da signifikante Unterschiede in den einzelnen Merkmalsverteilungen sonst dazu führen können, dass bestimmte Merkmale mit höheren Amplitudenwerten bei der Berechnung der adaptiven Aufmerksamkeitskoeffizienten für die Glättungsskalen dominieren.
Die meisten Parameter für das neue Objekt passen in die bereits bekannte Beschreibungsstruktur der neuronalen Schichten.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronNAFS; descr.count = HistoryBars; descr.window = BarDescr; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM;
In diesem Fall verwenden wir 5 Mittelungsskalen, was der Bildung von Fenstern {1, 3, 5, 7, 9, 11} entspricht.
descr.window_out = 5; if(!encoder.Add(descr)) { delete descr; return false; }
Die übrige Architektur des Encoders bleibt unverändert und umfasst die AMCT-Schicht.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronAMCT; descr.window = BarDescr; // Window (Indicators to bar) { int temp[] = {HistoryBars, 50}; // Bars, Properties if(ArrayCopy(descr.units, temp) < (int)temp.Size()) return false; } descr.window_out = EmbeddingSize / 2; // Key Dimension descr.layers = 5; // Layers descr.step = 4; // Heads descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Daran schließt sich eine vollständig verknüpfte Schicht zur Dimensionalitätsreduktion an.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Die Architekturen der Modelle Akteur und Kritiker bleiben ebenfalls unverändert. Zusammen mit ihnen haben wir die Programme für die Interaktion mit der Umwelt und die Trainingsmodelle aus unserer früheren Arbeit übernommen. Den vollständigen Code finden Sie im Anhang. Der Anhang enthält auch den vollständigen Code aller bei der Erstellung des Artikels verwendeten Programme.
3. Tests
In den vorangegangenen Abschnitten haben wir umfangreiche Arbeit geleistet, um die von den Autoren des NAFS-Rahmens vorgeschlagenen Methoden mit MQL5 zu implementieren. Jetzt ist es an der Zeit, ihre Wirksamkeit für unsere spezifischen Aufgaben zu bewerten. Zu diesem Zweck werden wir die Modelle, die diese Ansätze verwenden, auf realen EURUSD-Daten für das gesamte Jahr 2023 trainieren. Für den Handel verwenden wir historische Daten aus dem H1-Zeitrahmen.
Wie zuvor wird das Modell offline trainiert, wobei der Trainingsdatensatz regelmäßig aktualisiert wird, um seine Relevanz innerhalb des Wertebereichs zu erhalten, der sich aus der aktuellen Politik des Akteurs ergibt.
Wir haben bereits erwähnt, dass das neue Environment State Encoder-Modell auf dem kontrastiven Muster-Transformer aufbaut. Um die Ergebnisse besser vergleichen zu können, haben wir die Tests mit dem neuen Modell unter vollständiger Beibehaltung der Testparameter des Basismodells durchgeführt. Die Testergebnisse für die ersten drei Monate des Jahres 2024 sind nachstehend aufgeführt.
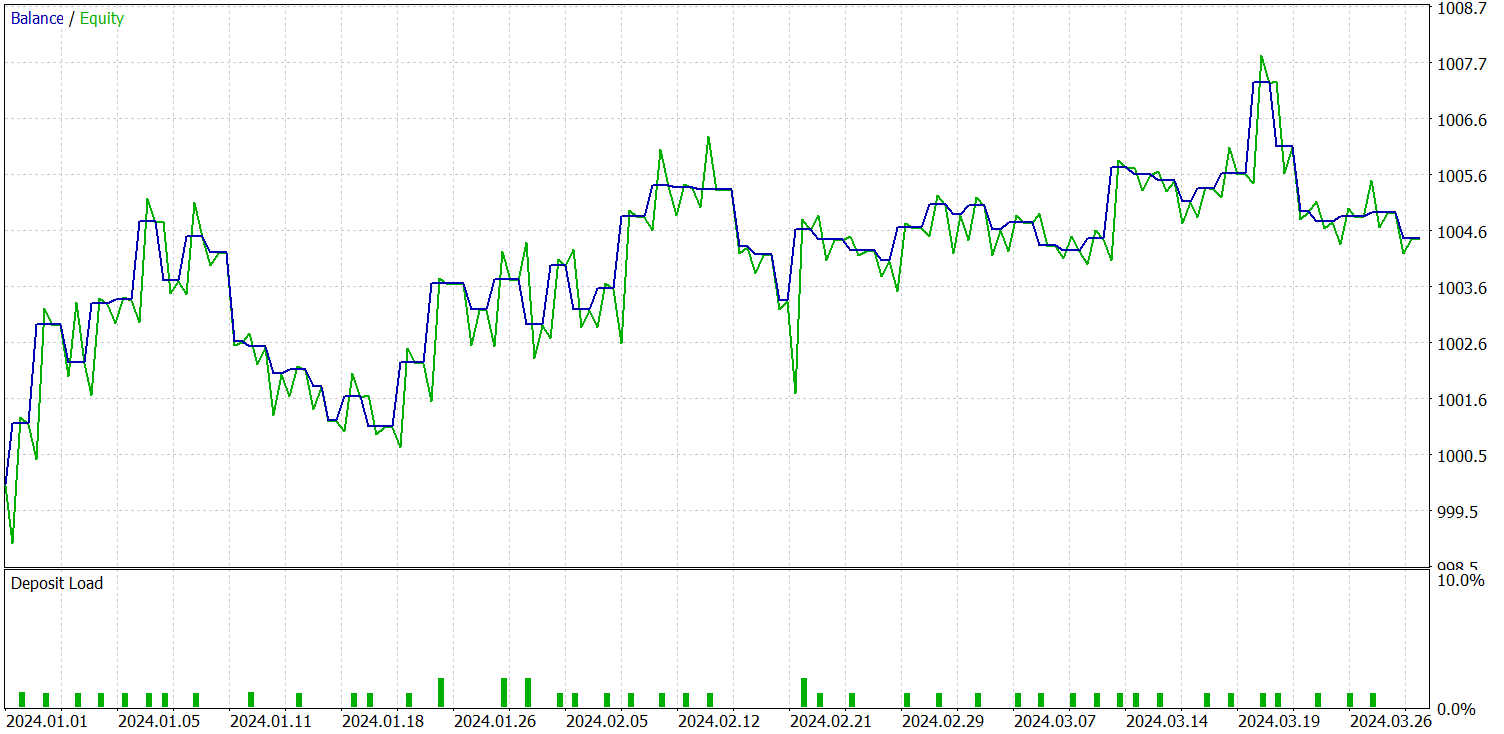
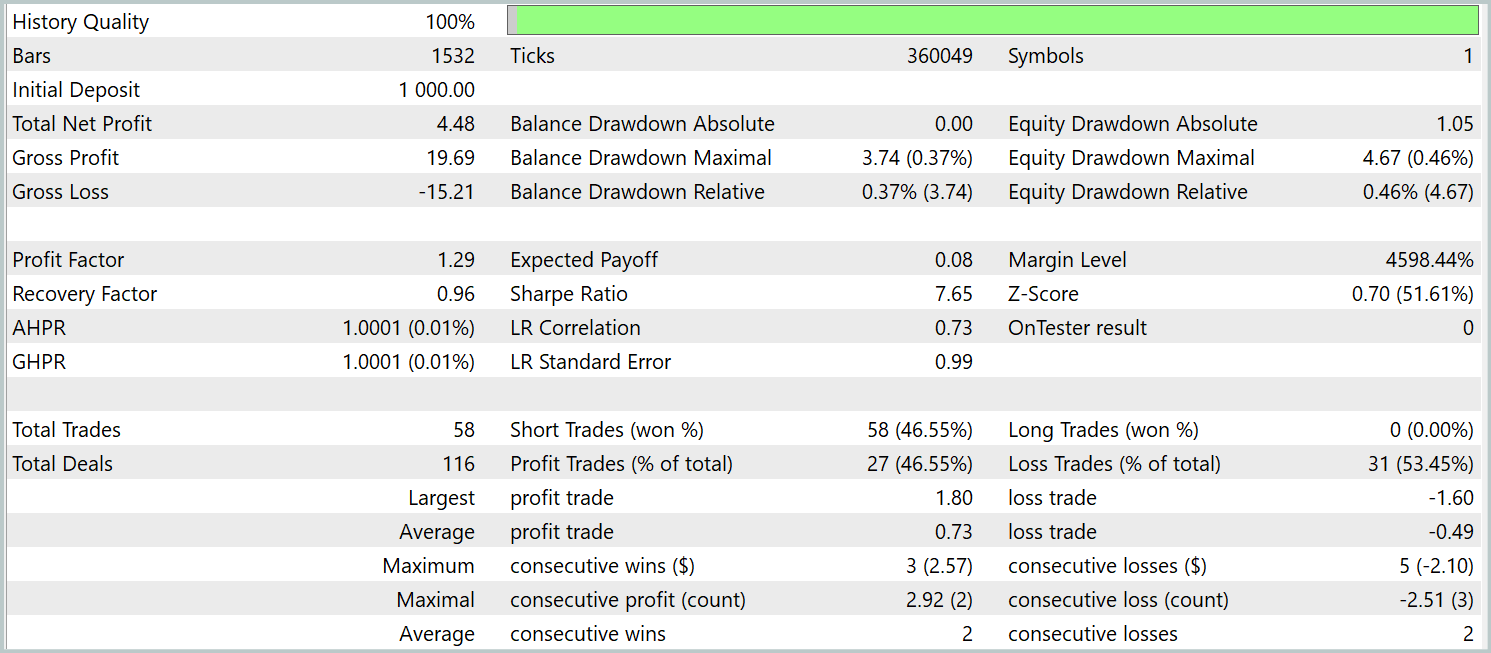
Der Vergleich der Testergebnisse zwischen dem aktuellen Modell und dem Basismodell ergibt auf den ersten Blick ein gemischtes Bild. Einerseits beobachten wir einen Rückgang des Gewinnfaktors von 1,4 auf 1,29. Dank einer 2,5-fachen Steigerung der Anzahl der Handelsgeschäfte stieg der Gesamtgewinn im gleichen Testzeitraum proportional an.
Darüber hinaus zeigt das neue Modell im Gegensatz zum Basismodell während des gesamten Testzeitraums einen konstanten Aufwärtstrend der Bilanz. Es wurden jedoch nur Verkäufe ausgeführt. Dies könnte darauf zurückzuführen sein, dass bei den geglätteten Werten der Schwerpunkt stärker auf globalen Trends liegt. Infolgedessen können einige lokale Trends bei der Rauschfilterung ignoriert werden.
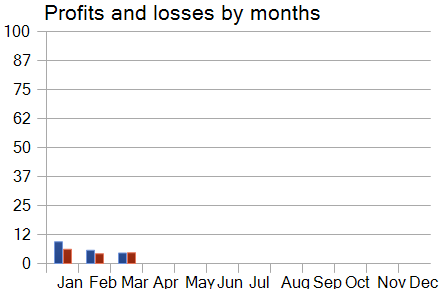
Bei der Analyse der monatlichen Leistungskurve des Modells lässt sich jedoch ein allmählicher Rückgang der Rentabilität im Laufe der Zeit feststellen. Diese Beobachtung stützt die im vorangegangenen Artikel aufgestellte Hypothese, dass die Repräsentativität des Trainingsdatensatzes mit zunehmender Länge des Testzeitraums abnimmt.
Schlussfolgerung
In diesem Artikel haben wir die Methode NAFS (Node-Adaptive Feature Smoothing) untersucht, die einen einfachen, aber effektiven nicht-parametrischen Ansatz für die Konstruktion von Knotenrepräsentationen in Graphen darstellt, ohne dass ein Parametertraining erforderlich ist. Sie kombiniert geglättete Nachbarmerkmale und erzeugt durch die Verwendung von Ensembles verschiedener Glättungsstrategien robuste und informative endgültige Einbettungen.
Auf der praktischen Seite haben wir unsere Interpretation der vorgeschlagenen Methoden in MQL5 implementiert, die konstruierten Modelle auf realen historischen Daten trainiert und sie auf Out-of-Sample-Datensätzen getestet. Auf der Grundlage unserer Experimente können wir feststellen, dass die vorgeschlagenen Ansätze Potenzial aufweisen. Sie können mit anderen Frameworks kombiniert werden. Außerdem kann ihre Integration die Effizienz der Basismodelle verbessern.
Referenzen
- NAFS: A Simple yet Tough-to-beat Baseline for Graph Representation Learning
- Andere Artikel dieser Serie
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA zum Sammeln von Beispielen |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | Test.mq5 | Expert Advisor | Modelltraining EA |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Bibliothek | OpenCL-Programmcode-Bibliothek |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16243
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 SQLite-Fähigkeiten in MQL5: Beispiel für ein Dashboard mit Handelsstatistiken nach Symbolen und magischen Zahlen
SQLite-Fähigkeiten in MQL5: Beispiel für ein Dashboard mit Handelsstatistiken nach Symbolen und magischen Zahlen
 Neuronale Netze im Handel: Der Contrastive Muster-Transformer (letzter Teil)
Neuronale Netze im Handel: Der Contrastive Muster-Transformer (letzter Teil)
 Optimierungsmethoden der ALGLIB-Bibliothek (Teil II)
Optimierungsmethoden der ALGLIB-Bibliothek (Teil II)
 Optimierungsmethoden der ALGLIB-Bibliothek (Teil I)
Optimierungsmethoden der ALGLIB-Bibliothek (Teil I)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.