
Neuronale Netze im Handel: Hyperbolisches latentes Diffusionsmodell (letzter Teil)
Einführung
Ein hyperbolischer geometrischer Raum ist in der Lage, diskrete baumartige oder hierarchische Strukturen darzustellen, die für eine Vielzahl von Graphenlernaufgaben geeignet sind. Es birgt auch ein erhebliches Potenzial für die Lösung des Problems der strukturellen Anisotropie in nicht-euklidischen Räumen während latenter Graphendiffusionsprozesse. Die hyperbolische Geometrie integriert die Winkel- und Radialdimensionen der Polarkoordinaten und ermöglicht geometrische Messungen mit physikalischer Semantik und Interpretierbarkeit.
In diesem Zusammenhang stellt der Rahmen von HypDiff eine fortschrittliche Methode zur Erzeugung von hyperbolischem Gauß-Rauschen dar, die das Problem der additiven Störungen in Gauß-Verteilungen im hyperbolischen Raum wirksam löst. Die Autoren des Rahmens führten geometrische Beschränkungen ein, die auf der Winkelähnlichkeit basieren und im Prozess der anisotropen Diffusion angewandt werden, um die lokale Struktur der Graphen zu erhalten.
Die Originalvisualisierung des Rahmens finden Sie unten.
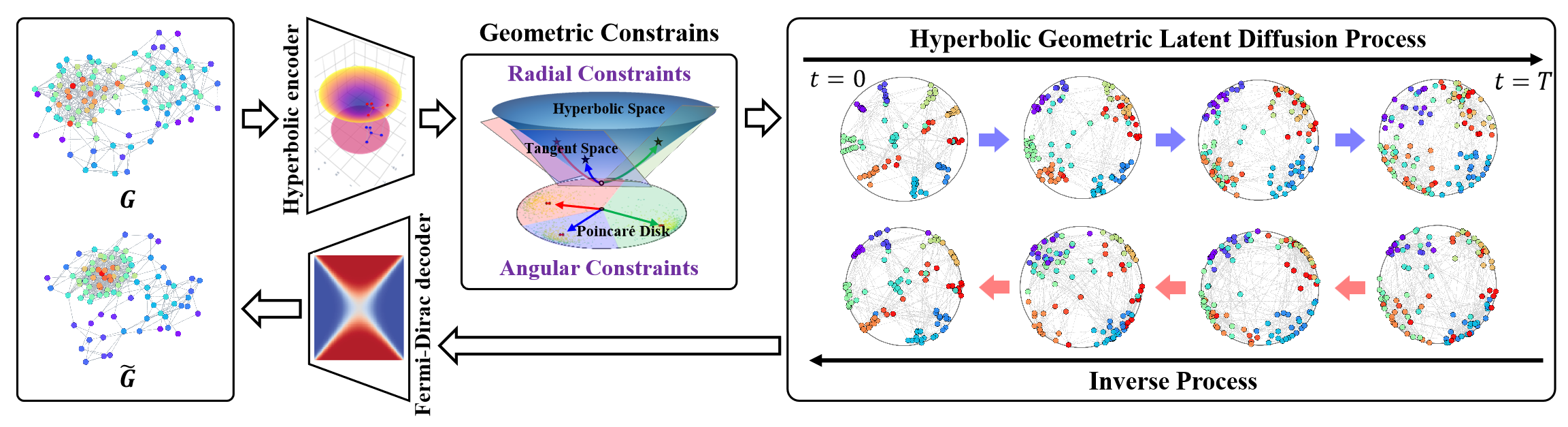
Im letzten Artikel haben wir begonnen, die vorgeschlagenen Ansätze in MQL5 zu implementieren. Der Umfang der Arbeiten ist jedoch recht umfangreich. Wir konnten nur die Implementierungsblöcke auf der OpenCL-Programmseite abdecken. In diesem Artikel werden wir die begonnene Arbeit fortsetzen und die Implementierung des Rahmens von HypDiff zu einem logischen Abschluss bringen. Dennoch werden wir bei unserer Implementierung gewisse Abweichungen vom ursprünglichen Algorithmus einführen, die wir im Laufe der Entwicklung des Algorithmus diskutieren werden.
1. Datenprojektion in den hyperbolischen Raum
Unsere Arbeit auf der OpenCL-Programmseite begann mit der Entwicklung von Kerneln für die Vorwärts- und Rückwärtsdurchläufe der Projektion der Originaldaten in den hyperbolischen Raum (HyperProjection bzw. HyperProjectionGrad). Ebenso werden wir mit der Implementierung des Rahmens von HypDiff auf der Seite des Hauptprogramms beginnen, indem wir die Algorithmen für diese Funktionalität konstruieren. Zu diesem Zweck wird eine neue Klasse, CNeuronHyperProjection, geschaffen, deren Struktur im Folgenden dargestellt wird.
class CNeuronHyperProjection : public CNeuronBaseOCL { protected: uint iWindow; uint iUnits; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) { return true; } public: CNeuronHyperProjection(void) : iWindow(-1), iUnits(-1) {}; ~CNeuronHyperProjection(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronHyperProjection; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); };
In der vorgestellten Struktur sehen wir die Deklaration von zwei internen Variablen, die zur Speicherung von Konstanten verwendet werden, die die Architektur des Objekts definieren, zusammen mit der bekannten Reihe von überschreibbaren Methoden. Es ist jedoch zu beachten, dass die Methode zur Aktualisierung der Modellparameter updateInputWeights als positiver „Platzhalter“ implementiert ist. Dies geschieht absichtlich. Die von uns entwickelten Projektionskernel für die Vorwärts- und Rückwärtsdurchläufe implementieren einen explizit definierten Algorithmus, der keine trainierbaren Parameter enthält. Dennoch ist das Vorhandensein einer Methode zur Aktualisierung der Parameter Voraussetzung für das korrekte Funktionieren unseres Modells. Daher sind wir gezwungen, die angegebene Methode zu überschreiben, damit sie immer ein positives Ergebnis liefert.
Da es keine neu deklarierten internen Objekte gibt, können wir den Konstruktor und den Destruktor der Klasse leer lassen. Die Initialisierung von geerbten Objekten und internen Variablen wird in der Init-Methode durchgeführt.
Der Algorithmus der Initialisierungsmethode ist recht einfach. Wie üblich enthalten seine Parameter die wichtigsten Konstanten, die zur eindeutigen Identifizierung der Architektur des zu erstellenden Objekts erforderlich sind.
bool CNeuronHyperProjection::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, (window + 1)*units_count, optimization_type, batch)) return false; iWindow = window; iUnits = units_count; //--- return true; }
Im Hauptteil der Methode rufen wir sofort die gleichnamige Methode der übergeordneten Klasse auf und übergeben ihr den entsprechenden Teil der empfangenen Parameter. Wie Sie wissen, implementiert die übergeordnete Klasse bereits die Logik zur Validierung dieser Parameter und zur Initialisierung der geerbten Objekte. Alles, was wir tun müssen, ist, das logische Ergebnis der Ausführung der übergeordneten Methode zu überprüfen. Danach speichern wir die vom externen Programm erhaltenen Architekturkonstanten in den internen Variablen.
Das war's. Wir haben keine neuen internen Objekte deklariert, und die geerbten Objekte werden in der Methode der Elternklasse initialisiert. Es bleibt nur noch, das Ergebnis der Operationen an das aufrufende Programm zurückzugeben und die Methode zu beenden.
Was die Methoden der Vorwärts- und Rückwärtsdurchläufe dieser Klasse betrifft, schlage ich vor, dass Sie sie selbst überprüfen. Beide sind einfache „Wrapper“, die die entsprechenden Kernel des OpenCL-Programms aufrufen. Ähnliche Methoden wurden in unserer Artikelserie bereits mehrfach beschrieben. Ich denke, die Logik der Umsetzung wird Ihnen klar sein. Der vollständige Code dieser Klasse und alle ihre Methoden sind im Anhang zu finden.
2. Projektion auf tangentiale Ebenen
Nach der Projektion der Originaldaten in den hyperbolischen Raum erfordert der Rahmen HypDiff die Konstruktion eines Encoders zur Erzeugung hyperbolischer Knoteneinbettungen. Wir planen, diese Funktionalität mit bestehenden Komponenten aus unserer Bibliothek zu implementieren. Die sich ergebenden Einbettungen werden auf Tangentialebenen projiziert, die den Zentroiden k entsprechen. Wir haben die Projektionsalgorithmen für die Tangentenabbildung und die entsprechende Gradientenrückverteilung bereits auf der OpenCL-Seite über die LogMap- bzw. LogMapGrad-Kernel implementiert. Die Frage der Zentroiden bleibt jedoch ungelöst.
Es ist anzumerken, dass die Autoren von HypDiff in der Phase der Datenaufbereitung Zentroiden aus dem Trainingsdatensatz definiert haben. Leider ist ein solcher Ansatz für unsere Zwecke nicht geeignet. Und das liegt nicht nur an der Arbeitsintensität. Diese Methode eignet sich nicht für die Analyse im Kontext der dynamischen Finanzmärkte. Bei der technischen Analyse von Kursbewegungen haben die sich abzeichnenden Muster oft Vorrang vor bestimmten Kurswerten. Für ähnliche Marktsituationen, die über verschiedene Zeiträume hinweg beobachtet werden, können unterschiedliche Schwerpunkte relevant sein. Daraus schließen wir, dass es notwendig ist, ein dynamisches Modell für die Anpassung oder Generierung von Zentroiden und deren Parametern zu schaffen. In unserer Implementierung haben wir uns für ein Modell zur Erzeugung von Schwerpunkten entschieden, das auf Einbettungen der Originaldaten basiert. Daher haben wir uns entschieden, die Prozesse der Schwerpunktbildung und der Datenprojektion auf die entsprechenden Tangentialebenen in einer einzigen Klasse zu kombinieren: CNeuronHyperboloide. Seine Struktur wird im Folgenden dargestellt.
class CNeuronHyperboloids : public CNeuronBaseOCL { protected: uint iWindows; uint iUnits; uint iCentroids; //--- CLayer cHyperCentroids; CLayer cHyperCurvatures; //--- int iProducts; int iDistances; int iNormes; //--- virtual bool LogMap(CNeuronBaseOCL *featers, CNeuronBaseOCL *centroids, CNeuronBaseOCL *curvatures, CNeuronBaseOCL *outputs); virtual bool LogMapGrad(CNeuronBaseOCL *featers, CNeuronBaseOCL *centroids, CNeuronBaseOCL *curvatures, CNeuronBaseOCL *outputs); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronHyperboloids(void) : iWindows(0), iUnits(0), iCentroids(0), iProducts(-1), iDistances(-1), iNormes(-1) {}; ~CNeuronHyperboloids(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint centroids, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronHyperboloids; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); virtual void TrainMode(bool flag); };
In der vorgestellten Struktur der neuen Klasse können wir die Deklaration von zwei dynamischen Arrays und sechs Variablen beobachten, die in zwei Gruppen unterteilt sind.
Die dynamischen Arrays sollen Zeiger auf die neuronalen Schichtobjekte von zwei verschachtelten Modellen speichern. In unserer Implementierung haben wir beschlossen, die Funktion zur Generierung von Schwerpunktparametern in zwei separate Modelle aufzuteilen. Das erste Modell ist für die Generierung der Koordinaten der Zentroiden im hyperbolischen Raum zuständig. Der zweite liefert die Krümmungsparameter des Raums an den entsprechenden Punkten.
Auch die Gruppierung der internen Variablen folgt einer logischen Erklärung. Eine Gruppe enthält die Architekturparameter des zu erstellenden Objekts, die wir vom externen Programm erhalten. Die zweite Gruppe besteht aus Variablen, die Zeiger auf Puffer für Zwischenwerte speichern, die ausschließlich im OpenCL-Kontext erstellt werden, ohne Daten in den Hauptspeicher des Systems zu kopieren.
Alle internen Objekte werden statisch deklariert, was es uns ermöglicht, den Konstruktor und Destruktor der Klasse leer zu lassen. Die Initialisierung aller geerbten und deklarierten Objekte ist in der Methode Init implementiert.
bool CNeuronHyperboloids::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint centroids, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window*units_count*centroids, optimization_type, batch)) return false;
Wie üblich enthalten die Methodenparameter eine Reihe von Konstanten, die die Architektur des zu erstellenden Objekts eindeutig definieren. Dazu gehören:
- units_count - die Anzahl der Elemente in der zu analysierenden Sequenz;
- window - die Größe des Einbettungsvektors für ein einzelnes Element der analysierten Sequenz;
- centroids - die Anzahl der Zentroide, die das Modell für eine umfassende Analyse der Originaldaten erzeugt.
Im Methodenhauptteil rufen wir, unserem bewährten Ansatz folgend, die gleichnamige Methode der Elternklasse auf, um die geerbten Objekte und Variablen zu initialisieren. An dieser Stelle sei angemerkt, dass im Gegensatz zum ursprünglichen Algorithmus von HypDiff bei unserer Implementierung die einzelnen Elemente der Eingabesequenz nicht bestimmten Zentroiden zugeordnet werden. Um das Modell mit möglichst vielen Informationen zu versorgen, erzeugen wir stattdessen Projektionen der gesamten Sequenz auf alle Tangentialebenen. Natürlich erhöht sich dadurch die Größe des resultierenden Tensors im Verhältnis zur Anzahl der erzeugten Zentroiden. Daher geben wir beim Aufruf der Initialisierungsmethode der Elternklasse das Produkt aller drei extern bereitgestellten Konstanten als Größe der erstellten Ebene an.
Sobald die übergeordnete Methode erfolgreich abgeschlossen ist, was durch ihren booleschen logischen Rückgabewert angezeigt wird, speichern wir die erhaltenen Konstanten in den internen Variablen.
iWindows = window; iUnits = units_count; iCentroids = centroids;
Im nächsten Schritt werden wir unsere dynamischen Arrays vorbereiten, um Zeiger auf die Objekte der Modelle zur Erzeugung der Schwerpunktparameter zu speichern.
cHyperCentroids.Clear(); cHyperCurvatures.Clear(); cHyperCentroids.SetOpenCL(OpenCL); cHyperCurvatures.SetOpenCL(OpenCL);
Dann gehen wir direkt zur Initialisierung der Modellobjekte über. Zunächst initialisieren wir das Modell, das für die Generierung der Schwerpunktkoordinaten zuständig ist.
Ziel ist es, ein lineares Modell zu konstruieren, das nach der Analyse der Eingabedaten eine Reihe von Koordinaten für die relevanten Zentroiden liefert. Die Verwendung von vollständig verknüpften Schichten zu diesem Zweck führt jedoch zu einer großen Anzahl von trainierbaren Parametern und einem erhöhten Rechenaufwand. Die Verwendung von Faltungsschichten ermöglicht es uns, sowohl die Anzahl der trainierbaren Parameter als auch den Umfang der Berechnungen zu reduzieren. Darüber hinaus scheint die Anwendung von Faltungsschichten auf einzelne univariate Sequenzen ein logischer Ansatz zu sein. Um dies zu realisieren, müssen wir zunächst die Eingabedaten entsprechend transponieren.
CNeuronTransposeOCL *transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, 0, OpenCL, iUnits, iWindows, optimization, iBatch) || !cHyperCentroids.Add(transp)) { delete transp; return false; } transp.SetActivationFunction(None);
Anschließend fügen wir eine Faltungsschicht hinzu, um die Dimensionen der univariaten Sequenzen zu reduzieren.
CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, 1, OpenCL, iUnits, iUnits, iCentroids, iWindows, 1, optimization, iBatch) || !cHyperCentroids.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(TANH);
In dieser Ebene verwenden wir einen gemeinsamen Satz von Parametern für alle univariaten Sequenzen. Am Ausgang der Schicht wenden wir die hyperbolische Tangensfunktion als Aktivierungsfunktion an, um Nichtlinearität einzuführen.
Dann fügen wir eine weitere Faltungsschicht hinzu, ohne Aktivierungsfunktion, aber mit unterschiedlichen trainierbaren Parametern für jede univariate Sequenz.
conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, 2, OpenCL, iCentroids, iCentroids, iCentroids, 1, iWindows, optimization, iBatch) || !cHyperCentroids.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None);
Infolgedessen bilden die beiden sequentiellen Faltungsschichten für jede univariate Reihe in der Eingabesequenz einen eigenen MLP. Jede solche MLP erzeugt eine Koordinate für die erforderliche Anzahl von Zentroiden. Mit anderen Worten, wir haben für jede Dimension des Koordinatenraums eine MLP entwickelt, die zusammen den gesamten Koordinatensatz für die angegebene Anzahl von Zentroiden erzeugt.
Jetzt müssen wir nur noch die erzeugten Schwerpunktkoordinaten in ihre ursprüngliche Darstellung zurückbringen. Um dies zu erreichen, fügen wir eine weitere Datenumsetzungsebene hinzu.
transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, 3, OpenCL, iWindows, iCentroids, optimization, iBatch) || !cHyperCentroids.Add(transp)) { delete transp; return false; } transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
Als Nächstes gehen wir zur Konstruktion der Objekte für das zweite Modell über, das die Krümmungsparameter des hyperbolischen Raums an den Schwerpunkten bestimmen wird. Die Krümmungsparameter werden auf der Grundlage der erzeugten Schwerpunktkoordinaten abgeleitet. Es ist vernünftig anzunehmen, dass der Krümmungsparameter nur von den spezifischen Koordinaten abhängt. Denn wir erwarten, dass das Modell während des Trainings eine interne Repräsentation des hyperbolischen Raums bildet und dies in seinen gelernten Parametern widerspiegelt. Daher verwenden wir im Modell der Krümmungsparameter keine Transpositionsschichten mehr. Stattdessen erstellen wir einfach einen eigenen MLP für jeden Schwerpunkt, der aus zwei aufeinanderfolgenden Faltungsschichten besteht.
conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, 4, OpenCL, iWindows, iWindows, iWindows, iCentroids, 1, optimization, iBatch) || !cHyperCurvatures.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(TANH); //--- conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, 5, OpenCL, iWindows, iWindows, 1, 1, iCentroids, optimization, iBatch) || !cHyperCurvatures.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None);
Hier verwenden wir auch die hyperbolische Tangensfunktion, um Nichtlinearität zwischen den Schichten des Modells einzuführen.
In diesem Stadium schließen wir die Initialisierung der Modellobjekte ab, die für die Generierung der Schwerpunktparameter verantwortlich sind. Was bleibt, ist die Vorbereitung der Objekte, die zur Unterstützung der Kernel für die Projektion von Daten auf Tangentialebenen und die Verteilung von Gradientenfehlern erforderlich sind. An dieser Stelle möchte ich Sie daran erinnern, dass wir während der Entwicklung der oben genannten Kernel über die Erstellung von Zwischenspeichern für Zwischenergebnisse gesprochen haben. Dabei handelt es sich um drei Datenpuffer, die jeweils ein Element pro Paar von „Centroid - Sequence Element“ enthalten.
Diese Puffer werden ausschließlich zur Übertragung von Informationen des Kernels des Vorwärtsdurchlaufs zum Gradientenverteilungskernel verwendet. Dementsprechend ist ihre Erstellung nur im Rahmen von OpenCL gerechtfertigt. Mit anderen Worten: Die Zuweisung dieser Puffer im Systemspeicher und das Kopieren von Daten zwischen dem OpenCL-Kontext und dem Hauptspeicher wäre überflüssig. Ebenso ist es nicht erforderlich, diese Puffer bei der Speicherung von Modellparametern zu speichern, da sie bei jedem Vorwärtsdurchlauf aktualisiert werden. Daher deklarieren wir auf der Seite des Hauptprogramms nur Variablen, die Zeiger auf diese Datenpuffer enthalten.
Wir müssen jedoch noch die Puffer für den Kontext von OpenCL erstellen. Zu diesem Zweck wird zunächst die erforderliche Größe der Datenpuffer bestimmt. Wie bereits erwähnt, haben alle drei Puffer die gleiche Größe.
uint size = iCentroids * iUnits * sizeof(float); iProducts = OpenCL.AddBuffer(size, CL_MEM_READ_WRITE); if(iProducts < 0) return false; iDistances = OpenCL.AddBuffer(size, CL_MEM_READ_WRITE); if(iDistances < 0) return false; iNormes = OpenCL.AddBuffer(size, CL_MEM_READ_WRITE); if(iNormes < 0) return false; //--- return true; }
Als Nächstes erstellen wir die Datenpuffer im OpenCL-Speicher und speichern die resultierenden Zeiger in den entsprechenden Variablen. Wie immer überprüfen wir die Gültigkeit des empfangenen Zeigers.
Sobald alle Objekte initialisiert sind, geben wir das logische Ergebnis der Operation an den Aufrufer zurück und beenden die Ausführung der Methode.
Der nächste Schritt unserer Arbeit ist die Entwicklung der Algorithmen der Vorwärtsdurchläufe für unsere Klasse CNeuronHyperboloids. An dieser Stelle sei erwähnt, dass die Methoden LogMap und LogMapGrad Wrapper für den Aufruf der entsprechenden OpenCL-Kernel sind. Wir überlassen es Ihnen, diese auf eigene Faust zu erkunden.
Schauen wir uns die Methode feedForward an. In den Parametern dieser Methode erhalten wir einen Zeiger auf das Objekt der neuronalen Schicht, das den Tensor der ursprünglichen Daten enthält.
bool CNeuronHyperboloids::feedForward(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *prev = NeuronOCL; CNeuronBaseOCL *centroids = NULL; CNeuronBaseOCL *curvatures = NULL;
Und im Hauptteil der Methode leisten wir zunächst ein wenig Vorarbeit: Wir deklarieren lokale Variablen für die vorübergehende Speicherung von Zeigern auf Objekte der internen neuronalen Schichten. Einer von ihnen wird der empfangene Zeiger auf das Eingangsdatenobjekt zugewiesen. Die beiden anderen werden vorerst leer bleiben.
Beachten Sie, dass wir an dieser Stelle die Gültigkeit des empfangenen Eingangsdatenzeigers nicht überprüfen. Die Methode greift während ihrer Ausführung nicht direkt auf die Datenpuffer dieses Objekts zu. Daher wäre eine solche Kontrolle unnötig.
Als Nächstes werden die Schwerpunktkoordinaten für den aktuellen Satz von Eingabedaten erzeugt. Zu diesem Zweck wird eine Schleife über die Objekte des entsprechenden internen Modells gezogen.
//--- Centroids for(int i = 0; i < cHyperCentroids.Total(); i++) { centroids = cHyperCentroids[i]; if(!centroids || !centroids.FeedForward(prev)) return false; prev = centroids; }
Innerhalb des Schleifenkörpers rufen wir nacheinander Zeiger auf die Objekte der neuronalen Schicht ab und überprüfen ihre Gültigkeit. Anschließend rufen wir die feedForward-Methode des abgerufenen internen Objekts auf und übergeben ihm den entsprechenden Eingangsdatenzeiger aus der entsprechenden lokalen Variablen. Nach erfolgreicher Ausführung des Vorwärtsdurchlaufs der internen Schicht wird dieses Objekt zur Quelle der Eingabedaten für die nächste Schicht des Modells. Daher speichern wir seinen Zeiger in der lokalen Eingangsdatenvariablen.
Beachten Sie, dass diese lokale Variable ursprünglich den Zeiger auf das vom externen Programm empfangene Eingabedatenobjekt enthielt. Deshalb haben wir sie bei der ersten Iteration unserer Schleife als Eingabedaten verwendet. Das bedeutet, dass die Gültigkeit des externen Datenzeigers in der feedForward-Methode der internen Modellschicht überprüft wird. Auf diese Weise werden alle Kontrollpunkte durchgesetzt, und der Datenfluss vom Eingabeobjekt bleibt erhalten.
Wir organisieren eine ähnliche Schleife, um die Krümmungsparameter des hyperbolischen Raums an den Schwerpunktpunkten zu bestimmen. Beachten Sie, dass nach Abschluss der Iterationen der vorherigen Schleife die lokalen Variablen prev und centroids beide auf das letzte Schichtobjekt des Modells zur Erzeugung von Schwerpunktkoordinaten zeigen. Da die Krümmungsparameter auf der Grundlage der Schwerpunktkoordinaten bestimmt werden sollen, können wir getrost mit der Variable prev arbeiten.
//--- Curvatures for(int i = 0; i < cHyperCurvatures.Total(); i++) { curvatures = cHyperCurvatures[i]; if(!curvatures || !curvatures.FeedForward(prev)) return false; prev = curvatures; }
Sobald alle erforderlichen Parameter der Zentroiden erfolgreich ermittelt wurden, können wir die Projektion der Eingabedaten auf die entsprechenden Tangentialebenen durchführen. Um dies zu erreichen, rufen wir die Wrapper-Methode für den LogMap-Kernel auf, die im vorherigen Artikel vorgestellt wurde.
if(!LogMap(NeuronOCL, centroids, curvatures, AsObject())) return false; //--- return true; }
Beachten Sie, dass wir den Zeiger auf das aktuelle Objekt als die ergebnisempfangende Entität übergeben. Auf diese Weise können wir die Operationsergebnisse in den Schnittstellenpuffern unserer Klasse speichern, auf die spätere neuronale Schichten des Modells zugreifen werden.
Jetzt müssen wir nur noch das logische Ergebnis der Operationen an den Aufrufer zurückgeben und die Weiterleitungsmethode abschließen.
Nach der Implementierung der Methoden für den Vorwärtsdurchlauf gehen wir zur Entwicklung der Algorithmen des Rückwärtsdurchlaufs über. Hier schlage ich vor, dass wir uns auf die Methode calcInputGradients konzentrieren, die die Gradientenverteilung behandelt. Die Methode updateInputWeights wird Ihnen zur unabhängigen Überprüfung überlassen.
Wie üblich erhält die Methode calcInputGradients einen Zeiger auf das Objekt der vorhergehenden Schicht, in dessen Puffer wir den Fehlergradienten übertragen sollen, der auf der Grundlage des Einflusses der Eingabedaten auf die endgültige Ausgabe des Modells berechnet wurde.
bool CNeuronHyperboloids::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
Diesmal prüfen wir sofort, ob der empfangene Zeiger korrekt ist. Denn wenn wir einen falschen Zeiger erhalten, verlieren alle weiteren Operationen sofort ihren Sinn.
Genau wie im Vorwärtsdurchlauf deklarieren wir lokale Variablen, um Zeiger auf interne Modellobjekte vorübergehend zu speichern. Dieses Mal werden wir jedoch sofort die Zeiger auf die letzten Schichten der internen Modelle extrahieren.
CObject *next = NULL; CNeuronBaseOCL *centroids = cHyperCentroids[-1]; CNeuronBaseOCL *curvatures = cHyperCurvatures[-1];
Danach rufen wir die Wrapper-Methode des Gradientenverteilungskerns durch die Operationen der Projektion der Originaldaten auf die Tangentialebenen auf.
if(!LogMapGrad(prevLayer, centroids, curvatures, AsObject())) return false;
Dann verteilen wir den Fehlergradienten entsprechend dem internen Modell zur Bestimmung der Krümmung des Hyperraums an den Schwerpunktpunkten, wodurch ein Zyklus der umgekehrten Enumeration der neuronalen Schichten des Modells entsteht.
//--- Curvatures for(int i = cHyperCurvatures.Total() - 2; i >= 0; i--) { next = curvatures; curvatures = cHyperCurvatures[i]; if(!curvatures || !curvatures.calcHiddenGradients(next)) return false; }
Und dann müssen wir den Fehlergradienten vom Modell zur Krümmungsbestimmung an das Modell zur Erzeugung von Schwerpunktkoordinaten weitergeben. Hier ist jedoch festzustellen, dass der Puffer der letzten Schicht des Modells zur Erzeugung von Schwerpunktkoordinaten bereits einen Fehlergradienten aus den Operationen zur Projektion der Daten auf Tangentialebenen enthält. Und wir wollen diese Werte bewahren. In solchen Fällen müssen wir Zeiger auf Datenpuffer ersetzen. Zunächst speichern wir den aktuellen Zeiger auf den Fehlergradientenpuffer der letzten Schicht des Modells zur Erzeugung von Schwerpunktkoordinaten in einer lokalen Variablen und passen die Werte bei Bedarf durch die Ableitung der Aktivierungsfunktion der neuronalen Schicht an.
CBufferFloat *temp = centroids.getGradient(); if(centroids.Activation()!=None) if(!DeActivation(centroids.getOutput(),temp,temp,centroids.Activation())) return false; if(!centroids.SetGradient(centroids.getPrevOutput(), false) || !centroids.calcHiddenGradients(curvatures.AsObject()) || !SumAndNormilize(temp, centroids.getGradient(), temp, iWindows, false, 0, 0, 0, 1) || !centroids.SetGradient(temp, false) ) return false;
Dann ersetzen wir ihn vorübergehend durch einen unbenutzten Puffer der entsprechenden Größe. Wir nennen die Methode der Fehlergradientenverteilung für die letzte Schicht des Modells zur Erzeugung von Schwerpunktkoordinaten und übergeben ihr die erste Schicht des Modells zur Bestimmung der Hyperspace-Krümmung an den Schwerpunktpunkten als nachfolgendes Objekt. Wir summieren die Werte der beiden Datenpuffer und setzen ihre Zeiger auf ihren ursprünglichen Zustand zurück. Vergessen wir nicht, die Ausführung von Vorgängen zu kontrollieren.
Nun, da wir den Gesamtfehlergradienten im Puffer der letzten Schicht des Modells zur Bestimmung der Schwerpunktkoordinaten haben, können wir eine Schleife für die Rückwärtsiteration durch die neuronalen Schichten des Modells erstellen. In dieser Schleife organisieren wir die Verteilung des Fehlergradienten zwischen den Schichten des Modells in Abhängigkeit von ihrem Beitrag zum Endergebnis.
//--- Centroids for(int i = cHyperCentroids.Total() - 2; i >= 0; i--) { next = centroids; centroids = cHyperCentroids[i]; if(!centroids || !centroids.calcHiddenGradients(next)) return false; }
Schließlich propagieren wir den akkumulierten Fehlergradienten auf die Ebene der Eingangsdaten. Aber auch hier stellt sich die Frage nach der Beibehaltung des zuvor aufgelaufenen Fehlergradienten. Wir ersetzen also das Eingangsdatenobjekt durch Datenpuffer.
temp = prevLayer.getGradient(); if(prevLayer.Activation()!=None) if(!DeActivation(prevLayer.getOutput(),temp,temp,prevLayer.Activation())) return false; if(!prevLayer.SetGradient(prevLayer.getPrevOutput(), false) || !prevLayer.calcHiddenGradients(centroids.AsObject()) || !SumAndNormilize(temp, prevLayer.getGradient(), temp, iWindows, false, 0, 0, 0, 1) || !prevLayer.SetGradient(temp, false) ) return false; //--- return true; }
Dann geben wir das Ergebnis der Operationen an den Aufrufer zurück und beenden die Methode.
Damit ist unser Überblick über die Implementierung von Methoden in unserer neuen Klasse CNeuronHyperboloids abgeschlossen. Den vollständigen Code dieser Klasse und alle ihre Methoden finden Sie im Anhang.
3. Aufbau des Rahmens von HypDiff
Wir haben die Entwicklung der einzelnen neuen Komponenten des Rahmens von HypDiff abgeschlossen und sind nun in der Lage, ein einheitliches Objekt zu konstruieren, das die Top-Level-Implementierung des Frameworks darstellt. Um dies zu erreichen, erstellen wir eine neue Klasse CNeuronHypDiff mit der unten dargestellten Struktur.
class CNeuronHypDiff : public CNeuronRMAT { public: CNeuronHypDiff(void) {}; ~CNeuronHypDiff(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, uint centroids, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronHypDiff; } //--- virtual uint GetWindow(void) const override { CNeuronRMAT* neuron = cLayers[1]; return (!neuron ? 0 : neuron.GetWindow() - 1); } virtual uint GetUnits(void) const override { CNeuronRMAT* neuron = cLayers[1]; return (!neuron ? 0 : neuron.GetUnits()); } };
Wie aus der Struktur der neuen Klasse ersichtlich ist, wird ihre Kernfunktionalität von der Klasse CNeuronRMAT Objekt geerbt. Dieses Basisobjekt bietet Funktionen für die Organisation des Betriebs eines kleinen linearen Modells, was für die Implementierung des HypDiff Rahmenwerks ausreicht. Daher reicht es in diesem Stadium aus, die Objektinitialisierungsmethode zu überschreiben und die richtige Architektur für das eingebettete Modell festzulegen. Alle anderen Prozesse sind bereits durch die Methoden der übergeordneten Klasse abgedeckt.
In den Parametern der Initialisierungsmethode erhalten wir die primären Konstanten, die eine eindeutige Interpretation der Architektur des zu erstellenden Objekts ermöglichen.
bool CNeuronHypDiff::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, uint centroids, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
Innerhalb des Methodenkörpers rufen wir sofort die entsprechende Methode des Basisobjekts der neuronalen Schicht auf, in dem die Initialisierung der Kernschnittstellen implementiert ist. Wir vermeiden in diesem Stadium absichtlich den Aufruf der Initialisierungsmethode der direkten übergeordneten Klasse, da sich die Architektur des eingebetteten Modells, das wir erstellen, erheblich unterscheidet.
Als Nächstes bereiten wir das geerbte dynamische Array für die Speicherung von Zeigern auf die internen Objekte vor.
cLayers.Clear(); cLayers.SetOpenCL(OpenCL); int layer = 0;
Dann gehen wir direkt zum Aufbau der internen Architektur des Rahmens von HypDiff über.
Die in das Modell eingegebenen Daten werden zunächst in den hyperbolischen Raum projiziert. Zu diesem Zweck fügen wir eine Instanz der zuvor erstellten Klasse CNeuronHyperProjection hinzu.
//--- Projection CNeuronHyperProjection *lorenz = new CNeuronHyperProjection(); if(!lorenz || !lorenz.Init(0, layer, OpenCL, window, units_count, optimization, iBatch) || !cLayers.Add(lorenz)) { delete lorenz; return false; } layer++;
Das System HypDiff erfordert dann einen hyperbolischen Encoder, der Einbettungen für die Knoten des analysierten Graphen erzeugt. Die Autoren des ursprünglichen Rahmens verwendeten für diese Phase graphneuronale Modelle in Kombination mit Faltungsschichten. In unserer Implementierung werden wir die graphischen neuronalen Netze durch einen Transformer ersetzen, der eine relative Positionskodierung verwendet.
//--- Encoder CNeuronRMAT *rmat = new CNeuronRMAT(); if(!rmat || !rmat.Init(0, layer, OpenCL, window + 1, window_key, units_count, heads, layers, optimization, iBatch) || !cLayers.Add(rmat)) { delete rmat; return false; } layer++; //--- CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer, OpenCL, window + 1, window + 1, 2 * window, units_count, 1, optimization, iBatch) || !cLayers.Add(conv)) { delete conv; return false; } layer++; conv.SetActivationFunction(TANH); //--- conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer, OpenCL, 2 * window, 2 * window, 3, units_count, 1, optimization, iBatch) || !cLayers.Add(conv)) { delete conv; return false; } layer++;
Bei der Projektion der resultierenden Einbettungen auf die Tangentialebenen ist zu beachten, dass wir die Menge der verarbeiteten Informationen deutlich erhöhen, indem wir Projektionen auf alle Tangentialebenen unter Verwendung des gesamten Datenbestands durchführen. Um die negativen Auswirkungen dieses Ansatzes teilweise abzumildern, reduzieren wir die Dimensionen der Einbettung der einzelnen Knoten.
Die resultierenden Dateneinbettungen müssen dann auf die Tangentialebenen der Zentroiden projiziert werden. Die Funktionalität zur Erzeugung von Schwerpunkten und zur Projektion von Eingabedaten auf die entsprechenden Tangentenräume wurde bereits in der Klasse CNeuronHyperboloids implementiert. An diesem Punkt genügt es, eine Instanz dieses Objekts in unser lineares Modell aufzunehmen.
//--- LogMap projecction CNeuronHyperboloids *logmap = new CNeuronHyperboloids(); if(!logmap || !logmap.Init(0, layer, OpenCL, 3, units_count, centroids, optimization, iBatch) || !cLayers.Add(logmap)) { delete logmap; return false; } layer++;
Am Ausgang erhalten wir Projektionen der Eingabedaten auf mehrere Ebenen. Diese können nun mit dem gerichteten Diffusionsalgorithmus verarbeitet werden, der ursprünglich für euklidische Modelle entwickelt wurde. In unserer Implementierung haben wir die CNeuronDiffusion Objekt für diesen Zweck.
//--- Diffusion model CNeuronDiffusion *diff = new CNeuronDiffusion(); if(!diff || !diff.Init(0, layer, OpenCL, 3, window_key, heads, units_count*centroids, 2, layers, optimization, iBatch) || !cLayers.Add(diff)) { delete diff; return false; } layer++;
Ein wichtiger Aspekt dabei ist, dass wir die verschiedenen Projektionen eines einzelnen Sequenzelements nicht zu einer einzigen Einheit zusammengefasst haben. Im Gegenteil, unser Diffusionsmodell behandelt jede Projektion als ein unabhängiges Objekt. Auf diese Weise kann das Modell lernen, verschiedene Projektionen derselben Sequenz zu korrelieren und eine volumetrische Darstellung der zugrunde liegenden Daten zu erstellen.
Ein weiteres erwähnenswertes Detail ist die Injektion von Rauschen. Wir haben uns entschieden, das Modell nicht dadurch zu verkomplizieren, dass wir versuchen, das Rauschen bei Projektionen desselben Sequenzelements abzugleichen. Schon das Hinzufügen von Rauschen bedeutet eine Art Unschärfe der ursprünglichen Eingaben in einer gewissen Umgebung. Durch die Einführung von unterschiedlichem Rauschen in verschiedenen Projektionen erreichen wir eine volumetrische Unschärfe.
Am Ausgang des Diffusionsmodells erwarten wir eine entrauschte Darstellung der Eingabedaten über mehrere Projektionen. Und hier weicht unsere Implementierung am deutlichsten vom ursprünglichen HypDiff-Rahmen ab. Im Original führten die Autoren eine inverse Projektion zurück in den hyperbolischen Raum durch und verwendeten einen Fermi-Dirac-Decoder, um die ursprüngliche Graphendarstellung zu rekonstruieren. Unser Ziel ist es, eine informative latente Repräsentation der Eingabedaten zu erhalten, die an ein Akteursmodell weitergegeben werden kann, um eine profitable Strategie für das Verhalten unseres Agenten zu lernen. Daher wenden wir anstelle der Dekodierung eine abhängigkeitsbasierte Pooling-Schicht an, um eine einheitliche Darstellung für jedes Sequenzelement abzuleiten.
//--- Pooling CNeuronMHAttentionPooling *pooling = new CNeuronMHAttentionPooling(); if(!pooling || !pooling.Init(0, layer, OpenCL, 3, units_count, centroids, optimization, iBatch) || !cLayers.Add(pooling)) { delete pooling; return false; } layer++;
Ändern Sie die Größe des Ergebnistensors auf die Ebene der Eingabedaten.
//--- Resize to source size conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer, OpenCL, 3, 3, window, units_count, 1, optimization, iBatch) || !cLayers.Add(conv)) { delete conv; return false; }
Jetzt müssen wir nur noch die Zeiger der Schnittstellendatenpuffer mit den entsprechenden Puffern der letzten Schicht unseres Modells ersetzen. Und dann schließen wir die Arbeit der Initialisierungsmethode unserer Klasse ab.
//--- if(!SetOutput(conv.getOutput(), true) || !SetGradient(conv.getGradient(), true)) return false; //--- return true; }
Damit ist die Umsetzung unserer eigenen Interpretation des Rahmens von HypDiff mit MQL5 abgeschlossen. Der vollständige Quellcode für alle in diesem Artikel behandelten Klassen und Methoden ist im Anhang verfügbar. Sie finden dort auch den Code für die Programme zur Interaktion mit der Umgebung und zum Training der Modelle, die unverändert aus früheren Arbeiten übernommen wurden.
Ein paar abschließende Bemerkungen zur Architektur der trainierbaren Modelle. Die Architekturen der Modelle Akteur (Actor) und Kritiker (Critic) bleiben unverändert. Allerdings haben wir das Modell des Umgebungszustands-Encoders leicht verändert. Die Eingabedaten für dieses Modell werden wie zuvor über eine Batch-Normalisierungsschicht einer ersten Vorverarbeitung unterzogen.
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } //--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Danach werden sie sofort in unser hyperbolisches latentes Diffusionsmodell übernommen.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronHypDiff; descr.count = HistoryBars; descr.window = BarDescr; descr.window_out = BarDescr; descr.layers=2; descr.step=10; // centroids { int temp[] = {4}; // Heads if(ArrayCopy(descr.heads, temp) < (int)temp.Size()) return false; } descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Der oben beschriebene Algorithmus des hyperbolischen latenten Diffusionsmodells ist ein recht komplexer und umfassender Prozess. Daher haben wir eine weitere Datenverarbeitung ausgeschlossen. Wir haben nur eine vollständig verknüpfte Schicht verwendet, um die Daten auf die erforderliche Tensorgröße zu reduzieren, die in das Akteurs-Modell eingegeben wird.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
An dieser Stelle schließen wir die Implementierung des Rahmens von HypDiff ab und gehen zur am meisten erwarteten Phase über - der praktischen Evaluierung der Ergebnisse auf realen historischen Daten.
4. Tests
Wir haben den Rahmen von HypDiff mit MQL5 implementiert und gehen nun zur letzten Phase über - dem Training der Modelle und der Evaluierung der daraus resultierenden Akteurspolitik. Wir folgen dem in früheren Arbeiten beschriebenen Trainingsalgorithmus und trainieren gleichzeitig drei Modelle: den State Encoder (Zustand-Encoder), den Actor (Akteur) und den Critic (Kritiker). Der Encoder analysiert das Marktumfeld. Der Akteur trifft seine Handelsentscheidungen auf der Grundlage der erlernten Strategie. Der Kritiker bewertet die Aktionen des Akteurs und leitet die Verfeinerung der Politik an.
Das Training wird mit realen historischen Daten für das gesamte Jahr 2023 für das Instrument EURUSD mit dem Zeitrahmen H1 durchgeführt. Alle Indikatorparameter wurden auf ihre Standardwerte gesetzt.
Der Trainingsprozess ist iterativ und beinhaltet regelmäßige Aktualisierungen des Trainingsdatensatzes.
Um die Wirksamkeit der trainierten Politik zu überprüfen, verwenden wir historische Daten für das erste Quartal 2024. Die Testergebnisse sind wie folgt:
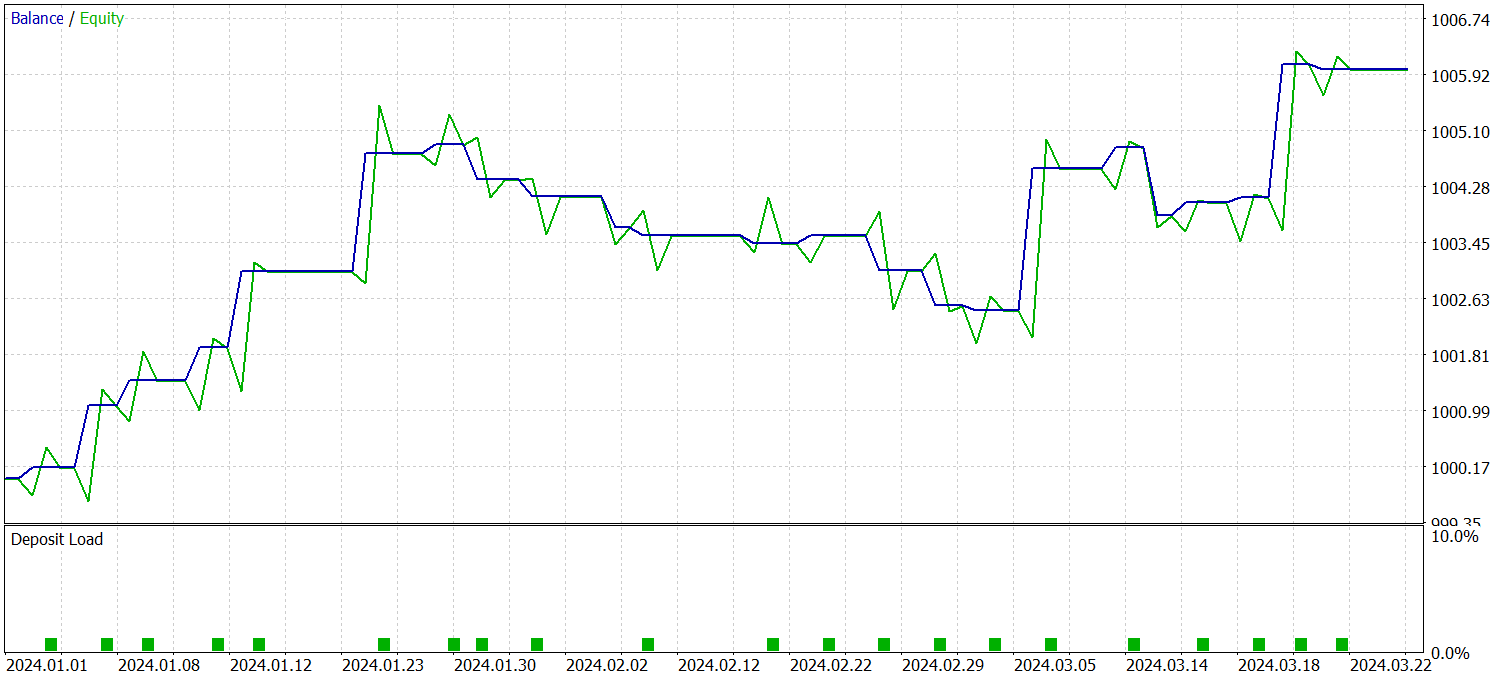
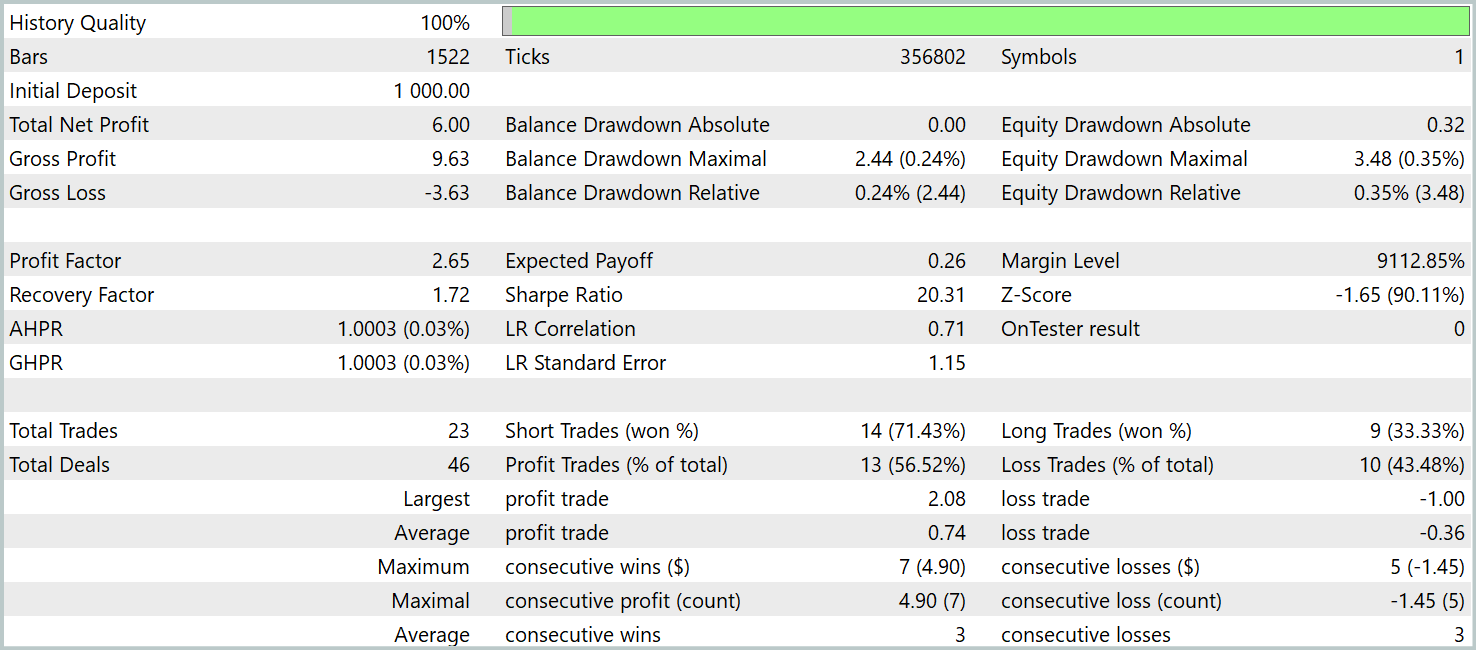
Wie die Daten zeigen, hat das Modell während des Testzeitraums erfolgreich einen Gewinn erzielt. Im Laufe von drei Monaten wurden insgesamt 23 Handelsgeschäfte getätigt, was eine relativ geringe Zahl ist. Über 56 % der Handelsgeschäfte wurden mit Gewinn abgeschlossen. Sowohl der maximale als auch der durchschnittliche Gewinn pro Handelsgeschäft sind etwa doppelt so hoch wie die entsprechenden Verluste.
Einen noch aussagekräftigeren Einblick bietet jedoch eine detaillierte Aufschlüsselung der Handelsgeschäfte. Von den drei Testmonaten war das Modell nur in zwei Monaten rentabel. Der Februar war völlig unrentabel. Im Januar 2024 waren 7 von 8 Handelsgeschäften gewinnbringend - der einzige Verlust entstand beim letzten Handelsgeschäft des Monats. Dieses Ergebnis bestätigt die zuvor aufgestellte Hypothese über die begrenzte Repräsentativität einer einjährigen Ausbildungsstichprobe nach dem ersten Monat der Einführung des Modells.
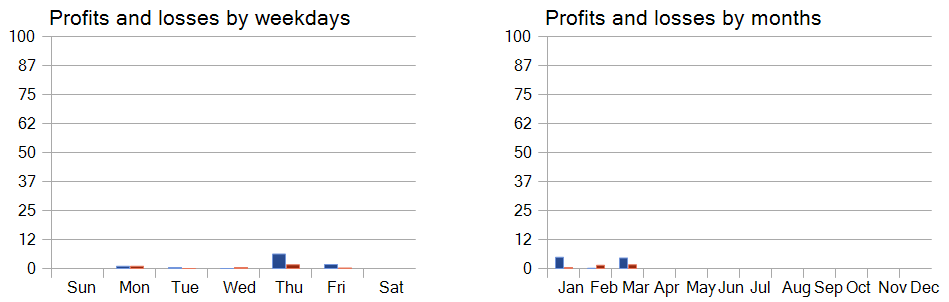
Eine Performance-Analyse über die Wochentage hinweg zeigt auch eine deutliche Präferenz für den Handel an Donnerstagen und Freitagen.
Schlussfolgerung
Die Anwendung der hyperbolischen Geometrie hilft bei der Bewältigung von Herausforderungen, die sich aus dem inhärenten Konflikt zwischen der diskreten Natur von grafisch strukturierten Daten und der kontinuierlichen Natur von Diffusionsmodellen ergeben. Der Rahmen von HypDiff führt eine verbesserte Methode zur Erzeugung von hyperbolischem Gauß-Rauschen ein, die Probleme im Zusammenhang mit additiven Inkonsistenzen von Gauß-Verteilungen im hyperbolischen Raum beseitigt. Um die lokale Struktur während der anisotropen Diffusion zu erhalten, werden geometrische Beschränkungen auf der Grundlage der Winkelähnlichkeit eingeführt.
Im praktischen Teil unserer Arbeit haben wir unsere Interpretation dieser Methoden mit MQL5 implementiert und die Modelle mit Hilfe der vorgeschlagenen Techniken auf realen historischen Daten trainiert. Wir haben die vom Akteur erlernte Strategie auch anhand von Daten außerhalb des Trainingssatzes bewertet. Die Ergebnisse zeigen das Potenzial der vorgeschlagenen Methoden und weisen auf mögliche Wege zur Verbesserung der Modellleistung hin.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA zum Sammeln von Beispielen |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | Test.mq5 | Expert Advisor | Modelltraining EA |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Bibliothek | OpenCL-Programmcode-Bibliothek |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16323
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Training eines mehrschichtigen Perzeptrons unter Verwendung des Levenberg-Marquardt-Algorithmus
Training eines mehrschichtigen Perzeptrons unter Verwendung des Levenberg-Marquardt-Algorithmus
 Von der Grundstufe bis zur Mittelstufe: Union (II)
Von der Grundstufe bis zur Mittelstufe: Union (II)
 Von der Grundstufe bis zur Mittelstufe: Rekursion
Von der Grundstufe bis zur Mittelstufe: Rekursion
 Nichtlineare Regressionsmodelle an der Börse
Nichtlineare Regressionsmodelle an der Börse
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Lesen Sie den neuen Artikel: Neuronale Netze im Handel: Hyperbolisches latentes Diffusionsmodell (letzter Teil).
Autor: Dmitriy Gizlyk