
Neuronale Netze leicht gemacht (Teil 2): Netzwerktraining und Tests
Inhalt
- Einführung
- 1. Definition des Problems
- 2. Modellprojekt eines Neuronalen Netzwerks
- 2.1. Bestimmung der Anzahl von Neuronen in der Eingangsschicht
- 2.2. Verdeckte Schichten entwerfen
- 2.3. Bestimmung der Anzahl von Neuronen in der Ausgabeschicht
- 3. Programmierung
- 3.1. Vorbereitung
- 3.2. Initialisierung von Klassen
- 3.3. Training des Neuronalen Netzes
- 3.4. Verbesserung der Gradientenberechnungsmethode
- 4. Tests
- Schlussfolgerung
- Programme, die im diesem Artikel verwendet werden
Einführung
Im vorherigen Artikel mit dem Titel Neuronale Netze leicht gemacht befassten wir uns mit den Konstruktionsprinzipien für CNet für die Arbeit mit vollständig verbundenen Neuronalen Netzen unter Verwendung von MQL5. In diesem Artikel werde ich ein Beispiel für die Verwendung dieser Klasse in einem Expert Advisor demonstrieren und die Klasse unter realen Bedingungen bewerten.
1. Definition des Problems
Bevor wir mit der Schaffung unseres Expert Advisors beginnen, ist es notwendig, die Ziele und Vorgaben zu definieren, die wir für unser neues Neuronales Netz festlegen werden. Natürlich ist das gemeinsame Ziel eines jeden Expert Advisors auf den Finanzmärkten die Gewinnerzielung. Dieser Zweck ist jedoch sehr allgemein. Wir müssen spezifischere Aufgaben für das Neuronale Netz festlegen. Darüber hinaus müssen wir verstehen, wie wir zukünftige Ergebnisse des Neuronalen Netzes auswerten können.
Ein weiterer wichtiger Moment ist, dass die zuvor geschaffene K CNet die Prinzipien des überwachten Lernens anwendet, und deshalb benötigt sie gekennzeichnete Daten für das Trainingsset.
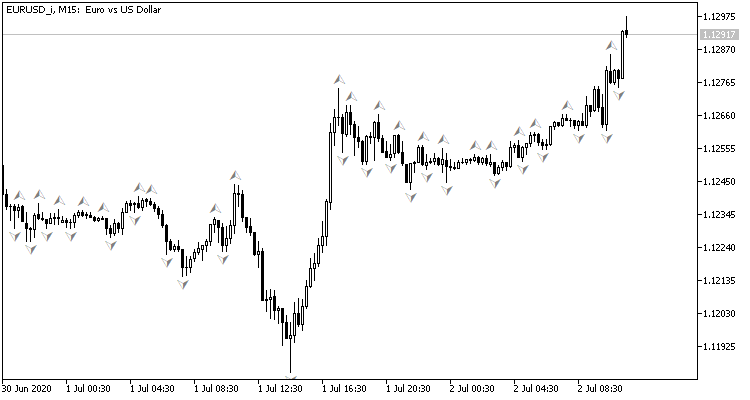
Wenn man sich das Preischart ansieht, wäre der natürliche Wunsch, Handelsoperationen zu Preisspitzen auszuführen, was durch den Standard-Fraktalindikator von Bill Williams gezeigt werden kann. Das Problem mit dem Indikator ist, dass er die Spitzen durch 3 Kerzen bestimmt und immer ein um 1 Kerze verzögertes Signal erzeugt, das sich dann als entgegengesetztes Signal herausstellen kann. Was wäre, wenn wir das Neuronale Netz so einstellen, dass es die Drehpunkte bestimmt, bevor die dritte Kerze gebildet wird? Dieser Ansatz würde mindestens eine vorherige Kerze der Bewegung in Handelsrichtung ergeben.
Dies bezieht sich auf den Trainingssatz:
- Im direkten Durchlauf geben wir die aktuelle Marktsituation in das Neuronale Netz ein, und der Ausgang wird eine Schätzung der Wahrscheinlichkeit einer Spitzenbildung für die letzte geschlossene Kerze sein.
- Im umgekehrten Durchgang, nach der Bildung der nächsten Kerze, prüfen wir, ob auf der vorherigen Kerze ein Fraktal vorhanden war und geben das Ergebnis zur Anpassung der Gewichte ein.
Um die Ergebnisse der Netzwerkoperationen zu bewerten, können wir den mittleren quadratischen Vorhersagefehler, den Prozentsatz der korrekten Fraktalvorhersagen und den Prozentsatz der nicht erkannten Fraktale verwenden.
Jetzt müssen wir bestimmen, welche Daten in unser Neuronales Netz eingegeben werden sollen. Erinnern Sie sich daran, was Sie tun, wenn Sie versuchen, die Marktsituation auf der Grundlage des Charts zu beurteilen?
Zunächst einmal wird einem unerfahrenen Händler empfohlen, die Trendrichtung anhand des Charts visuell zu bewerten. Daher müssen wir Informationen über Preisbewegungen digitalisieren und in das Neuronale Netz eingeben. Ich schlage vor, Daten über Eröffnungs- und Schlusskurse, Höchst- und Tiefstpreise, Volumen und Formationszeit einzugeben.
Eine weitere beliebte Methode zur Bestimmung des Trends ist die Verwendung von Oszillatorindikatoren. Die Verwendung solcher Indikatoren ist bequem, weil Indikatoren normalisierte Daten ausgeben. Ich beschloss, für das Experiment vier Standardindikatoren zu verwenden: RCI, CCI, ATR und MACD, alle mit Standardparametern. Ich habe keine zusätzliche Analyse zur Auswahl der Indikatoren und ihrer Parameter durchgeführt.
Jemand mag sagen, dass die Verwendung von Indikatoren bedeutungslos ist, da ihre Daten aus der Neuberechnung der Preisdaten von Kerzen aufgebaut sind, die wir bereits in das Neuronale Netz eingeben. Aber das stimmt nicht ganz. Indikatorwerte werden durch die Berechnung von Daten aus mehreren Kerzen ermittelt, was eine gewisse Erweiterung der analysierten Stichprobe ermöglicht. Der Trainingsprozess des Neuronalen Netzes wird bestimmen, wie sie sich auf das Ergebnis auswirken.
Um die Marktdynamik beurteilen zu können, werden wir die gesamte Information über einen bestimmten historischen Zeitraum in das Neuronale Netz eingeben.
2. Modellprojekt eines Neuronalen Netzwerks
2.1. Bestimmung der Anzahl von Neuronen in der Eingangsschicht
Hier müssen wir die Anzahl der Neuronen in der Eingangsschicht verstehen. Um dies zu tun, werten Sie die Anfangsinformationen zu jeder Kerze aus und multiplizieren Sie diese mit der Tiefe der analysierten Historie.
Eine Vorverarbeitung der Indikatordaten ist nicht erforderlich, da sie normalisiert sind und die entsprechende Anzahl von Indikatorpuffern bekannt ist (die 4 oben genannten Indikatoren haben zusammen 5 Werte). Um diese Indikatoren in der Input-Schicht zu erhalten, müssen wir daher für jede analysierte Kerze 5 Neuronen erstellen.
Bei den Preisdaten der Kerze ist die Situation etwas anders. Wenn wir die Trendrichtung und -stärke visuell aus einem Chart bestimmen, analysieren wir zunächst die Richtung und Größe der Kerze. Erst danach, wenn wir zur Bestimmung der Trendrichtung und der wahrscheinlichen Umkehrpunkte kommen, achten wir auf das Preisniveau des analysierten Symbols. Daher ist es notwendig, diese Daten zu normalisieren, bevor sie in das Neuronale Netz eingegeben werden. Ich persönlich gebe die Differenz von Schluss-, Höchst- und Tiefstkurs zum Eröffnungskurs der beschriebenen Kerze ein. Bei diesem Ansatz reicht es aus, drei Neuronen zu beschreiben, wobei das Vorzeichen des ersten Neurons die Richtung der Kerze bestimmt.
Es gibt eine Menge verschiedener Materialien, die den Einfluss verschiedener Zeitfaktoren auf die Währungsvolatilität beschreiben. Zum Beispiel beeinflussen die Jahreszeit, Unterschiede in der Dynamik nach Wochen und Tagen sowie europäische, amerikanische und asiatische Handelssitzungen die Währungskurse auf unterschiedliche Weise. Um solche Faktoren zu analysieren, geben Sie Monat, Stunde und Wochentag der Kerzenbildung in das Neuronale Netz ein. Ich habe die Zeit und das Datum der Kerzenbildung bewusst in Komponenten aufgeteilt, da dies dem Neuronalen Netz ermöglicht, zu verallgemeinern und Abhängigkeiten zu finden.
Lassen Sie uns zusätzlich Informationen über Volumina einbeziehen. Wenn Ihr Broker Daten über reale Volumina liefert, geben wir diese Volumina an; andernfalls geben wir Tick-Volumina an.
Wir benötigen also 12 Neuronen, um jede Kerze zu beschreiben. Wenn Sie diese Zahl mit der analysierten Historietiefe multiplizieren, erhalten Sie die Größe der Eingabeschicht des Neuronalen Netzes.
2.2. Verdeckte Schichten entwerfen
Der nächste Schritt ist die Vorbereitung der verdeckten Schichten unseres Neuronalen Netzes. Die Auswahl einer Netzwerkstruktur (Anzahl der Schichten und Neuronen) ist eine der schwierigsten Aufgaben. Das einschichtige Perceptron eignet sich gut für die lineare Trennung von Klassen. Netzwerke mit zwei Schichten können nichtlinearen Grenzen folgen. Netzwerke aus drei Schichten ermöglichen die Beschreibung komplexer, mehrfach verbundener Bereiche. Wenn wir die Anzahl der Schichten erhöhen, wird die Klasse der Funktionen erweitert, aber dies führt zu einer schlechteren Konvergenz und höheren Trainingskosten. Die Anzahl der Neuronen in jeder Schicht muss der erwarteten Variabilität der Funktionen genügen. Tatsächlich sind sehr einfache Netzwerke nicht in der Lage, das Verhalten unter realen Bedingungen mit der erforderlichen Genauigkeit zu simulieren, während zu komplexe Netzwerke darauf trainiert werden, nicht nur die Zielfunktion, sondern auch das Rauschen zu wiederholen.
Im ersten Artikel erwähnte ich die Methode der "5-Warums". Nun schlage ich vor, dieses Experiment fortzusetzen und ein Netzwerk mit 4 verdeckten Schichten zu schaffen. Ich setze die Anzahl der Neuronen in der ersten verdeckten Schicht auf 1000. Es ist jedoch auch möglich, eine gewisse Abhängigkeit von der Tiefe des analysierten Zeitraums herzustellen. Durch Anwendung der Pareto-Regel werden wir die Anzahl der Neuronen in jeder nachfolgenden Schicht um 70% reduzieren. Darüber hinaus wird folgende Einschränkung verwendet: Die Anzahl der Neuronen in der verdeckten Schicht darf nicht weniger als 20 betragen.
2.3. Bestimmung der Anzahl von Neuronen in der Ausgabeschicht
Die Anzahl der Neuronen in der Ausgangsschicht hängt von der Aufgabe und dem Lösungsansatz ab. Um Regressionsprobleme zu lösen, genügt es, ein Neuron zu haben, das den erwarteten Wert produziert. Zur Lösung von Klassifizierungsproblemen benötigen wir eine Anzahl von Neuronen, die der erwarteten Anzahl von Klassen entspricht - jedes der Neuronen wird die Wahrscheinlichkeit erzeugen, das ursprüngliche Objekt jeder Klasse zuzuordnen. In der Praxis wird die Klasse eines Objekts durch die maximale Wahrscheinlichkeit bestimmt.
Für unseren Fall schlage ich vor, 2 Varianten des Neuronalen Netzes zu erstellen und ihre Anwendbarkeit für unser Problem in der Praxis zu bewerten. Im ersten Fall wird die Ausgabeschicht ein Neuron haben. Werte im Bereich von 0,5...1,0 entsprechen einem Kauffraktal, -0,5...-1,0 entsprechen einem Verkaufssignal, und Werte im Bereich von -0,5...0,5 bedeuten, dass kein Signal vorhanden ist. In dieser Lösung wird der hyperbolische Tangens als Aktivierungsfunktion verwendet - er kann Ausgabewerte im Bereich von -1,0 bis +1,0 haben.
Im zweiten Fall werden 3 Neuronen in der Ausgabeschicht erzeugt (Kauf, Verkauf, kein Signal). In dieser Variante werden wir das Neuronale Netz trainieren, um ein Ergebnis im Bereich 0.0 zu erhalten ... 1.0. Hier ist das Ergebnis die Wahrscheinlichkeit für das Auftreten eines Fraktals. Das Signal wird entsprechend der maximalen Wahrscheinlichkeit bestimmt, und seine Richtung wird entsprechend dem Index des Neurons mit der höchsten Wahrscheinlichkeit bestimmt.
3. Programmierung
3.1. Vorbereitung
Jetzt ist es Zeit zu programmieren. Binden wir zunächst die erforderlichen Bibliotheken ein:
- NeuroNet.mqh — eine Bibliothek zum Erstellen eines Neuronalen Netzes aus dem vorherigen Artikel
- SymbolInfo.mqh — Standardbibliothek für den Empfang von Symboldaten
- TimeSeries.mqh — Standardbibliothek für die Arbeit mit Zeitreihen
- Volumes.mqh — Standardbibliothek für den Empfang von Volumendaten
- Oscilators.mqh — Standardbibliothek mit Oszillatorklassen
#include "NeuroNet.mqh" #include <Trade\SymbolInfo.mqh> #include <Indicators\TimeSeries.mqh> #include <Indicators\Volumes.mqh> #include <Indicators\Oscilators.mqh>
Der nächste Schritt ist das Schreiben der Programmparameter, mit denen Neuronales Netz und Indikatorparameter eingestellt werden.
//+------------------------------------------------------------------+ //| input parameters | //+------------------------------------------------------------------+ input int StudyPeriod = 10; //Study period, years input uint HistoryBars = 20; //Depth of history ENUM_TIMEFRAMES TimeFrame = PERIOD_CURRENT; //--- input group "---- RSI ----" input int RSIPeriod = 14; //Period input ENUM_APPLIED_PRICE RSIPrice = PRICE_CLOSE; //Applied price //--- input group "---- CCI ----" input int CCIPeriod = 14; //Period input ENUM_APPLIED_PRICE CCIPrice = PRICE_TYPICAL; //Applied price //--- input group "---- ATR ----" input int ATRPeriod = 14; //Period //--- input group "---- MACD ----" input int FastPeriod = 12; //Fast input int SlowPeriod = 26; //Slow input int SignalPeriod= 9; //Signal input ENUM_APPLIED_PRICE MACDPrice = PRICE_CLOSE; //Applied price
Als Nächstes deklarieren wir globalen Variablen - ihre Verwendung wird später erklärt.
CSymbolInfo *Symb; CiOpen *Open; CiClose *Close; CiHigh *High; CiLow *Low; CiVolumes *Volumes; CiTime *Time; CNet *Net; CArrayDouble *TempData; CiRSI *RSI; CiCCI *CCI; CiATR *ATR; CiMACD *MACD; //--- double dError; double dUndefine; double dForecast; double dPrevSignal; datetime dtStudied; bool bEventStudy;
Damit sind die Vorbereitungsarbeiten abgeschlossen. Fahren wir nun mit der Initialisierung der Klassen fort.
3.2 Initialisierung von Klassen
Die Initialisierung von Klassen wird in der Funktion OnInit durchgeführt. Zuerst erstellen wir eine Instanz der Klasse CSymbolInfo für die Arbeit mit Symbolen und aktualisieren die Daten über das Chart-Symbol.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Symb=new CSymbolInfo(); if(CheckPointer(Symb)==POINTER_INVALID || !Symb.Name(_Symbol)) return INIT_FAILED; Symb.Refresh();
Erstellen wir dann Zeitreiheninstanzen. Wir prüfen jedes Mal, wenn wir eine Klasseninstanz anlegen, ob sie erfolgreich angelegt wurde, und initialisieren sie. Im Falle eines Fehlers verlassen Sie die Funktion mit dem Ergebnis INIT_FAILED.
Open=new CiOpen(); if(CheckPointer(Open)==POINTER_INVALID || !Open.Create(Symb.Name(),TimeFrame)) return INIT_FAILED; //--- Close=new CiClose(); if(CheckPointer(Close)==POINTER_INVALID || !Close.Create(Symb.Name(),TimeFrame)) return INIT_FAILED; //--- High=new CiHigh(); if(CheckPointer(High)==POINTER_INVALID || !High.Create(Symb.Name(),TimeFrame)) return INIT_FAILED; //--- Low=new CiLow(); if(CheckPointer(Low)==POINTER_INVALID || !Low.Create(Symb.Name(),TimeFrame)) return INIT_FAILED; //--- Volumes=new CiVolumes(); if(CheckPointer(Volumes)==POINTER_INVALID || !Volumes.Create(Symb.Name(),TimeFrame,VOLUME_TICK)) return INIT_FAILED; //--- Time=new CiTime(); if(CheckPointer(Time)==POINTER_INVALID || !Time.Create(Symb.Name(),TimeFrame)) return INIT_FAILED;
In diesem Beispiel werden die Tickvolumina verwendet. Wenn wir echte Volumina verwenden wollen, dann ersetzen wir "VOLUME_TICK" durch "VOLUME_REAL" beim Aufruf der Methode Volumes.Creare.
Nachdem wir die Zeitreihe deklariert haben, erstellen wir auf ähnliche Weise die Instanzen der Klassen für die Arbeit mit Indikatoren.
RSI=new CiRSI(); if(CheckPointer(RSI)==POINTER_INVALID || !RSI.Create(Symb.Name(),TimeFrame,RSIPeriod,RSIPrice)) return INIT_FAILED; //--- CCI=new CiCCI(); if(CheckPointer(CCI)==POINTER_INVALID || !CCI.Create(Symb.Name(),TimeFrame,CCIPeriod,CCIPrice)) return INIT_FAILED; //--- ATR=new CiATR(); if(CheckPointer(ATR)==POINTER_INVALID || !ATR.Create(Symb.Name(),TimeFrame,ATRPeriod)) return INIT_FAILED; //--- MACD=new CiMACD(); if(CheckPointer(MACD)==POINTER_INVALID || !MACD.Create(Symb.Name(),TimeFrame,FastPeriod,SlowPeriod,SignalPeriod,MACDPrice)) return INIT_FAILED;
Jetzt können wir direkt mit der Klasse des Neuronalen Netzes arbeiten. Erstellen wir zunächst eine Klasseninstanz. Bei der Initialisierung der Klasse CNet übergeben die Konstruktorparameter eine Referenz auf ein Array mit der Spezifikation der Netzwerkstruktur. Bitte beachten Sie, dass der Prozess des Netzwerktrainings Rechenressourcen verbraucht und viel Zeit in Anspruch nimmt. Daher wäre es falsch, das Netzwerk nach jedem Start neu zu trainieren. Ich mache Folgendes: Zuerst deklariere ich die Netzwerkinstanz ohne Angabe der Struktur und versuche, ein zuvor trainiertes Netzwerk von einem lokalen Speicher hochzuladen (der Dateiname wird in #define angegeben).
#define FileName Symb.Name()+"_"+EnumToString((ENUM_TIMEFRAMES)Period())+"_"+IntegerToString(HistoryBars,3)+"fr_ea" ... ... ... ... Net=new CNet(NULL); ResetLastError(); if(CheckPointer(Net)==POINTER_INVALID || !Net.Load(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false)) { printf("%s - %d -> Error of read %s prev Net %d",__FUNCTION__,__LINE__,FileName+".nnw",GetLastError());
Wenn zuvor trainierte Daten nicht geladen werden konnten, wird eine Meldung mit dem Fehlercode in das Protokoll gedruckt, und die Erstellung eines neuen, nicht trainierten Netzwerks beginnt. Zuerst deklarieren wir eine Instanz der Klasse CArrayInt, und geben dort die Struktur des Neuronalen Netzes an. Die Anzahl der Elemente gibt die Anzahl der Schichten des neuronalen Netzes an, und der Wert der Elemente gibt die Anzahl der Neuronen in der entsprechenden Schicht an.
CArrayInt *Topology=new CArrayInt(); if(CheckPointer(Topology)==POINTER_INVALID) return INIT_FAILED;
Wie bereits früher erwähnt, benötigen wir 12 Neuronen in der Eingangsschicht, um jede Kerze zu beschreiben. Wir schreiben daher das Produkt von 12 durch die Tiefe der analysierten Geschichte in das erste Array-Element.
if(!Topology.Add(HistoryBars*12)) return INIT_FAILED;
Dann beschreiben wir die verdeckten Schichten. Wir haben festgestellt, dass es 4 verdeckte Schichten mit 1000 Neuronen in der ersten verdeckten Schicht geben wird. Dann wird die Anzahl der Neuronen in jeder folgenden Schicht um 70% verringert, aber jede Schicht wird mindestens 20 Neuronen haben. Die Daten werden in einer Schleife zu einem Array hinzugefügt.
int n=1000; bool result=true; for(int i=0;(i<4 && result);i++) { result=(Topology.Add(n) && result); n=(int)MathMax(n*0.3,20); } if(!result) { delete Topology; return INIT_FAILED; }
Geben Sie in der Ausgabeschicht 1 an, um ein Regressionsmodell zu erstellen.
if(!Topology.Add(1)) return INIT_FAILED;
Wenn wir ein Klassifikationsmodell verwenden würden, müssten wir für das Ausgangsneuron 3 angeben.
Als Nächstes löschen wir die zuvor erstellten Klasseninstanz von CNet und erstellen eine neue, in der die Struktur des zu erstellenden Neuronalen Netzes angegeben ist. Nach der Erstellung einer neuen Instanz des Neuronalen Netzes löschen wir die Klasse der Netzstruktur, da sie nicht weiter verwendet wird.
delete Net; Net=new CNet(Topology); delete Topology; if(CheckPointer(Net)==POINTER_INVALID) return INIT_FAILED;
Wir legen die Anfangswerte der Variablen fest, um statistische Daten zu sammeln:
- dError - Standardabweichung (Fehler)
- dUndefine - Prozentsatz der undefinierten Fraktale
- dForecast - Prozentsatz der korrekt vorhergesagten Fraktale
- dtStudied - das Datum der letzten Kerze des Trainings.
dError=-1; dUndefine=0; dForecast=0; dtStudied=0; }
Vergessen wir nicht, dass wir die Struktur des neuronalen Netzes festlegen, eine neue Instanz der Klasse des neuronalen Netzes erstellen und die statistischen Variablen nur dann initialisieren müssen, wenn es kein zuvor trainiertes neuronales Netz gibt, das von einem lokalen Speicher geladen werden kann.
Erstellen wir am Ende der Funktion OnInit eine Instanz der Klasse CArrayDouble(), die für den Datenaustausch mit dem Neuronalen Netz verwendet wird, und starten den Trainingsprozess für das Neuronale Netz.
Ich möchte hier noch eine weitere Lösung vorstellen. MQL5 kennt keine asynchronen Funktionsaufrufe. Wenn wir die Lernfunktion explizit von der OnInit-Funktion aufrufen, betrachtet das Terminal den Programminitialisierungsprozess als unvollständig, bis das Training abgeschlossen ist. Aus diesem Grund erstellen wir, anstatt die Funktion direkt aufzurufen, ein benutzerdefiniertes Ereignis, während die Training-Funktion von der Funktion OnChartEvent aufgerufen wird. Beim Erstellen eines Ereignisses, geben wir den Tag des Trainingsbeginns im Parameter lparam an. Dieser Ansatz ermöglicht es uns, einen Funktionsaufruf durchzuführen und die Funktion OnInit zu vervollständigen.
TempData=new CArrayDouble(); if(CheckPointer(TempData)==POINTER_INVALID) return INIT_FAILED; //--- bEventStudy=EventChartCustom(ChartID(),1,(long)MathMax(0,MathMin(iTime(Symb.Name(),PERIOD_CURRENT,(int)(100*Net.recentAverageSmoothingFactor*(dForecast>=70 ? 1 : 10))),dtStudied)),0,"Init"); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| ChartEvent function | //+------------------------------------------------------------------+ void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam) { //--- if(id==1001) { Train(lparam); bEventStudy=false; OnTick(); } }
Vergessen wir nicht, den Speicher in der Funktion OnDeinit zu löschen.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- if(CheckPointer(Symb)!=POINTER_INVALID) delete Symb; //--- if(CheckPointer(Open)!=POINTER_INVALID) delete Open; //--- if(CheckPointer(Close)!=POINTER_INVALID) delete Close; //--- if(CheckPointer(High)!=POINTER_INVALID) delete High; //--- if(CheckPointer(Low)!=POINTER_INVALID) delete Low; //--- if(CheckPointer(Time)!=POINTER_INVALID) delete Time; //--- if(CheckPointer(Volumes)!=POINTER_INVALID) delete Volumes; //--- if(CheckPointer(RSI)!=POINTER_INVALID) delete RSI; //--- if(CheckPointer(CCI)!=POINTER_INVALID) delete CCI; //--- if(CheckPointer(ATR)!=POINTER_INVALID) delete ATR; //--- if(CheckPointer(MACD)!=POINTER_INVALID) delete MACD; //--- if(CheckPointer(Net)!=POINTER_INVALID) delete Net; if(CheckPointer(TempData)!=POINTER_INVALID) delete TempData; }
3.3. Training des Neuronalen Netzes
Um das Neuronale Netz zu trainieren, erstellen wir die Funktion Train. Das Startdatum der Trainingsperiode wird an die Funktionsparameter übergeben.
void Train(datetime StartTrainBar=0)
Wir deklarieren lokale Variablen am Anfang der Funktion:
- count - Zählen von Lernepochen
- prev_un - Prozentsatz der nicht erkannten Fraktale in der vorangegangenen Epoche
- prev_for - Prozentsatz der korrekten fraktalen "Vorhersagen" in der vorangegangenen Epoche
- prev_er - Fehler der vorherigen Epoche
- bar_time - Neuberechnung des Datums der Bar
- stop - Flag für die Kontrolle des Aufrufs einer erzwungenen Programmbeendigung.
int count=0; double prev_up=-1; double prev_for=-1; double prev_er=-1; datetime bar_time=0; bool stop=IsStopped(); MqlDateTime sTime;
Prüfen wir als Nächstes, ob das in den Funktionsparametern erhaltene Datum nicht über den ursprünglich angegebenen Trainingszeitraum hinausgeht.
MqlDateTime start_time; TimeCurrent(start_time); start_time.year-=StudyPeriod; if(start_time.year<=0) start_time.year=1900; datetime st_time=StructToTime(start_time); dtStudied=MathMax(StartTrainBar,st_time);
Das Training des Neuronalen Netzes wird in der Do-while-Schleife durchgeführt. Berechnen Sie zu Beginn der Schleife die Anzahl der historischen Balken für das Training des Neuronalen Netzes neu und speichern Sie die vorherige Durchlauf-Statistik.
do { int bars=(int)MathMin(Bars(Symb.Name(),TimeFrame,dtStudied,TimeCurrent())+HistoryBars,Bars(Symb.Name(),TimeFrame)); prev_un=dUndefine; prev_for=dForecast; prev_er=dError; ENUM_SIGNAL bar=Undefine;
Dann passen wir die Größe der Puffer an und laden die erforderlichen, historischen Daten.
if(!Open.BufferResize(bars) || !Close.BufferResize(bars) || !High.BufferResize(bars) || !Low.BufferResize(bars) || !Time.BufferResize(bars) || !RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars) || !Volumes.BufferResize(bars)) break; Open.Refresh(OBJ_ALL_PERIODS); Close.Refresh(OBJ_ALL_PERIODS); High.Refresh(OBJ_ALL_PERIODS); Low.Refresh(OBJ_ALL_PERIODS); Volumes.Refresh(OBJ_ALL_PERIODS); Time.Refresh(OBJ_ALL_PERIODS); RSI.Refresh(OBJ_ALL_PERIODS); CCI.Refresh(OBJ_ALL_PERIODS); ATR.Refresh(OBJ_ALL_PERIODS); MACD.Refresh(OBJ_ALL_PERIODS);
Das Flag wird zur Kontrolle der erzwungenen Programmbeendigung aktualisiert und es wird ein neues Flag deklarierte, das anzeigt, dass die Lernepoche vorüber ist (add_loop).
stop=IsStopped(); bool add_loop=false;
Wir organisieren einen verschachtelten Trainingszyklus durch alle historischen Daten. Zu Beginn des Zyklus prüfen wir, ob das Ende der historischen Daten erreicht ist. Falls erforderlich, ändern wir das Flag add_loop. Außerdem wird der aktuelle Stand des Trainings des Neuronalen Netzes auf dem Chart mit Hilfe von Kommentaren angezeigt. Dies hilft bei der Überwachung des Trainingsprozesses.
for(int i=(int)(bars-MathMax(HistoryBars,0)-1); i>=0 && !stop; i--) { if(i==0) add_loop=true; string s=StringFormat("Study -> Era %d -> %.2f -> Undefine %.2f%% foracast %.2f%%\n %d of %d -> %.2f%% \nError %.2f\n%s -> %.2f",count,dError,dUndefine,dForecast,bars-i+1,bars,(double)(bars-i+1.0)/bars*100,Net.getRecentAverageError(),EnumToString(DoubleToSignal(dPrevSignal)),dPrevSignal); Comment(s);
Prüfen wir dann, ob der vorhergesagte Systemzustand im vorherigen Schritt des Zyklus berechnet wurde. Wenn ja, dann passen wir die Gewichte in Richtung des richtigen Wertes an. Dazu löschen wir den Inhalt der TempData-Matrix, prüfen, ob das Fraktal auf der vorherigen Kerze gebildet wurde, und fügen einen korrekten Wert zur TempData-Matrix hinzu (unten ist der Code für ein Neuronales Netz der Regression mit einem Neuron in der Ausgabeschicht). Danach rufen wir die Methode BackProp des Neuronalen Netzes auf und übergeben eine Referenz auf das Array TempData als Parameter. Wir aktualisieren die statistischen Daten in dForecast (Prozentsatz der korrekt vorhergesagten Fraktale) und dUndefine (Prozentsatz der nicht erkannten Fraktale).
if(i<(int)(bars-MathMax(HistoryBars,0)-1) && i>1 && Time.GetData(i)>dtStudied && dPrevSignal!=-2) { TempData.Clear(); bool sell=(High.GetData(i+2)<High.GetData(i+1) && High.GetData(i)<High.GetData(i+1)); bool buy=(Low.GetData(i+2)<Low.GetData(i+1) && Low.GetData(i)<Low.GetData(i+1)); TempData.Add(buy && !sell ? 1 : !buy && sell ? -1 : 0); Net.backProp(TempData); if(DoubleToSignal(dPrevSignal)!=Undefine) { if(DoubleToSignal(dPrevSignal)==DoubleToSignal(TempData.At(0))) dForecast+=(100-dForecast)/Net.recentAverageSmoothingFactor; else dForecast-=dForecast/Net.recentAverageSmoothingFactor; dUndefine-=dUndefine/Net.recentAverageSmoothingFactor; } else { if(sell || buy) dUndefine+=(100-dUndefine)/Net.recentAverageSmoothingFactor; } }
Nach der Anpassung der Neuronales-Netz-Gewichtskoeffizienten berechnen wir die Wahrscheinlichkeit eines fraktalen Entstehens auf dem aktuellen historischen Balken (wenn i gleich 0 ist, wird die Wahrscheinlichkeit einer Fraktalbildung auf dem aktuellen Balken berechnet). Dazu löschen wir das Array TempData und fügen die aktuellen Daten für die Eingabeschicht des Neuronalen Netzes hinzu. Wenn das Hinzufügen von Daten fehlschlägt oder nicht genügend Daten vorhanden sind, verlassen wir die Schleife.
TempData.Clear(); int r=i+(int)HistoryBars; if(r>bars) continue; //--- for(int b=0; b<(int)HistoryBars; b++) { int bar_t=r+b; double open=Open.GetData(bar_t); TimeToStruct(Time.GetData(bar_t),sTime); if(open==EMPTY_VALUE || !TempData.Add(Close.GetData(bar_t)-open) || !TempData.Add(High.GetData(bar_t)-open) || !TempData.Add(Low.GetData(bar_t)-open) || !TempData.Add(Volumes.Main(bar_t)/1000) || !TempData.Add(sTime.mon) || !TempData.Add(sTime.hour) || !TempData.Add(sTime.day_of_week) || !TempData.Add(RSI.Main(bar_t)) || !TempData.Add(CCI.Main(bar_t)) || !TempData.Add(ATR.Main(bar_t)) || !TempData.Add(MACD.Main(bar_t)) || !TempData.Add(MACD.Signal(bar_t))) break; } if(TempData.Total()<(int)HistoryBars*12) break;
Nach der Vorbereitung der Anfangsdaten führen wir die Methode FeedForward aus und schreiben die Ergebnisse des Neuronalen Netzes in die Variable dPrevSignal. Unten sehen wir den Code für ein neuronales Netz mit einem Neuron in der Ausgabeschicht. Darunter befindet sich der Code für ein klassifizierendes neuronales Netz mit drei Neuronen in der Ausgabeschicht.
Net.feedForward(TempData);
Net.getResults(TempData);
dPrevSignal=TempData[0];
Um die Funktionsweise des Neuronalen Netzes auf einem Chart zu visualisieren, zeigen wir die Kennzeichnung der vorhergesagten Fraktale für die letzten 200 Kerzen an.
bar_time=Time.GetData(i); if(i<200) { if(DoubleToSignal(dPrevSignal)==Undefine) DeleteObject(bar_time); else DrawObject(bar_time,dPrevSignal,High.GetData(i),Low.GetData(i)); }
Aktualisieren wir am Ende des historischen Datenzyklus das Flag für den erzwungenen Programmabbruch.
stop=IsStopped();
}
Sobald das Neuronale Netz mit allen verfügbaren historischen Daten trainiert wurde, erhöhen wir den Zähler der Trainingsepochen und speichern den aktuellen Zustand des Neuronalen Netzes in einer lokalen Datei. Wir werden dies beim nächsten Start des Neuronalen Netzes die Daten verwenden können.
if(add_loop) count++; if(!stop) { dError=Net.getRecentAverageError(); if(add_loop) { Net.Save(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false); printf("Era %d -> error %.2f %% forecast %.2f",count,dError,dForecast); } }
Am Ende geben wir die Bedingungen für das Verlassen der Trainingsphase an. Die Bedingungen können wie folgt lauten: Es wird ein Signal mit der Wahrscheinlichkeit empfangen, das Ziel über einem vorgegebenen Niveau zu erreichen; der Zielfehlerparameter ist erreicht; oder wenn sich die statistischen Daten nach einer Trainingsepoche nicht oder nur unwesentlich ändern (das Training wird bei einem lokalen Minimum abgebrochen). Sie können Ihre eigenen Bedingungen zum Verlassen des Trainingsprozesses definieren.
} while((!(DoubleToSignal(dPrevSignal)!=Undefine || dForecast>70) || !(dError<0.1 && MathAbs(dError-prev_er)<0.01 && MathAbs(dUndefine-prev_up)<0.1 && MathAbs(dForecast-prev_for)<0.1)) && !stop);
Wir sichern die Zeit der letzten Kerze des Trainings, bevor wir die Trainingsfunktion verlassen.
if(count>0) { dtStudied=bar_time; } }
3.4. Verbesserung der Gradientenberechnungsmethode
Ich möchte Ihre Aufmerksamkeit auf den folgenden Aspekt lenken, den ich während des Testprozesses gefunden habe. Beim Training eines Neuronalen Netzes kam es in einigen Fällen zu einem unkontrollierten Anstieg der Gewichtskoeffizienten von Neuronen verdeckter Schichten, wodurch die maximal zulässigen Variablenwerte überschritten wurden und infolgedessen das gesamte Neuronale Netz gelähmt wurde. Dies geschah, als der nachfolgende Schichtfehler die Neuronen aufforderte, Werte auszugeben, die über den Bereich der möglichen Werte der Aktivierungsfunktion hinausgingen. Die Lösung, die ich fand, bestand darin, die Zielwerte der Neuronen zu normalisieren. Der korrigierte Code der Gradientenberechnungsmethode ist unten dargestellt.
void CNeuron::calcOutputGradients(double targetVals) { double delta=(targetVals>1 ? 1 : targetVals<-1 ? -1 : targetVals)-outputVal; gradient=(delta!=0 ? delta*CNeuron::activationFunctionDerivative(targetVals) : 0); }
Der vollständige Code aller Methoden und Funktionen steht im Anhang zur Verfügung.
4. Tests
Das Test-Training des Neuronalen Netzes wurde auf dem EURUSD-Paar im H1-Zeitrahmen durchgeführt. Daten von 20 Kerzen wurden in das neuronale Netz eingegeben. Das Training wurde mit den letzten 2 Jahren durchgeführt. Um die Ergebnisse zu überprüfen, startete ich beide zwei Expert Advisors auf zwei Charts desselben Terminals: ein EA mit Regression Neuronales Netz (Fractal - mit 1 Neuron in der Ausgabeschicht) und Klassifikation Neuronales Netz (Fractal_2 - mit 3 Neuronen in der Ausgabeschicht).
Die erste Trainingsepoche mit 12432 Balken dauerte 2 Stunden und 20 Minuten. Beide EAs schnitten ähnlich ab, mit einer Trefferquote von knapp über 6%.
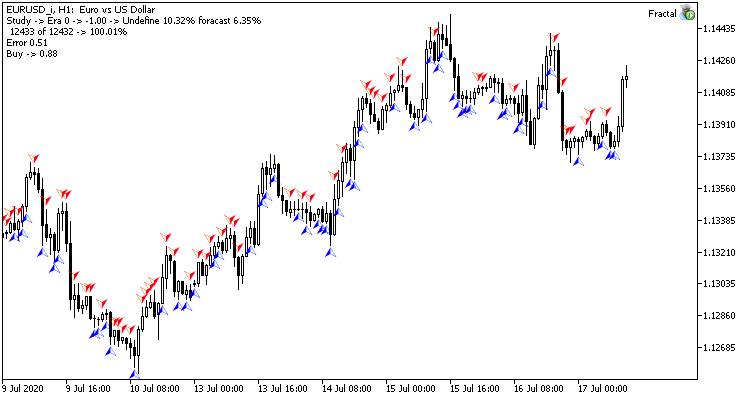
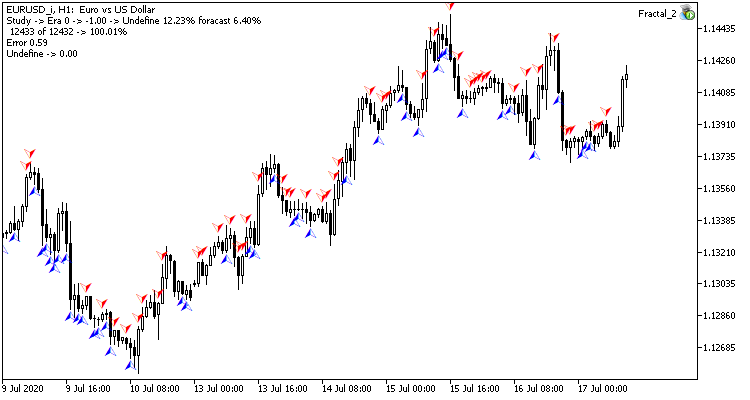
Die erste Epoche hängt stark von den Gewichten des Neuronalen Netzes ab, die in der Anfangsphase zufällig ausgewählt wurden.
Nach 35 Epochen Training nahm der Unterschied in der Statistik leicht zu - das Regressionsmodell des Neuronalen Netzes schnitt besser ab:
| Wert | Regression Neuronales Netz | Klassifikation Neuronales Netz |
|---|---|---|
| Mittlerer quadratischer Fehler | 0.68 | 0.78 |
| Trefferwahrscheinlichkeit | 12.68% | 11.22% |
| Nicht erkannte Fraktale | 20.22% | 24.65% |
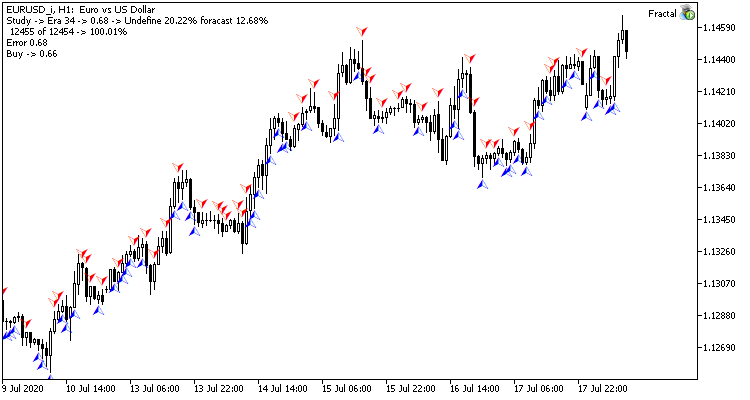
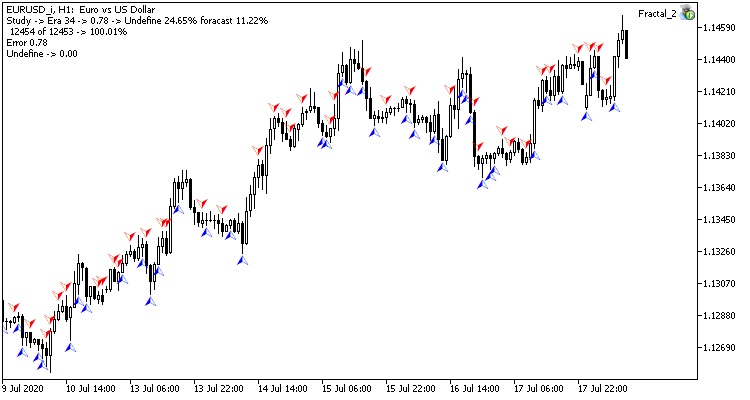
Die Testergebnisse zeigen, dass beide Varianten der Organisation des Neuronalen Netzes ähnliche Ergebnisse in Bezug auf Trainingszeit und Vorhersagegenauigkeit erzielen. Gleichzeitig zeigen die erzielten Ergebnisse, dass das Neuronale Netz zusätzliche Zeit und Ressourcen für das Training benötigt. Wenn Sie die Lerndynamik des neuronalen Netzes analysieren möchten, sehen Sie sich bitte die Screenshots der einzelnen Lernepochen im Anhang an.
Schlussfolgerung
In diesem Artikel haben wir den Prozess der Erstellung, des Trainings und des Testens von Neuronalen Netzen betrachtet. Die erzielten Ergebnisse zeigen, dass es ein Potenzial für den Einsatz dieser Technologie gibt. Der Prozess des Trainings von Neuronalen Netzen verbraucht jedoch eine Menge an Rechenressourcen und nimmt viel Zeit in Anspruch.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| Experts\NeuroNet_DNG\ | |||
| 1 | Fractal.mq5 | Expert Advisor | Ein Expert Advisor mit der Regression durch ein Neuronales Netz (1 Neuron in der Ausgabeschicht) |
| 2 | Fractal_2.mq5 | Expert Advisor | Ein Expert Advisor mit der Klassifikation durch ein Neuronales Netz (3 Neuron in der Ausgabeschicht) |
| 3 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zum Erstellen eines neuronalen Netzes (ein Perceptron) |
| Files\ | |||
| 4 | Fractal | Verzeichnis | Enthält Screenshots, die das Testen des Neuronalen Netzes der Regression zeigen |
| 5 | Fractal_2 | Verzeichnis | Enthält Screenshots, die das Testen des Neuronalen Netzes der Klassifikation zeigen |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/8119
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Nutzerdefinierte Symbole: Praktische Grundlagen
Nutzerdefinierte Symbole: Praktische Grundlagen
 Was ist ein Trend und basiert die Marktstruktur auf einem Trend oder einer Seitwärtsbewegung?
Was ist ein Trend und basiert die Marktstruktur auf einem Trend oder einer Seitwärtsbewegung?
 Der Algorithmus CatBoost von Yandex für das maschinelle Lernen, Kenntnisse von Python- oder R sind nicht erforderlich
Der Algorithmus CatBoost von Yandex für das maschinelle Lernen, Kenntnisse von Python- oder R sind nicht erforderlich
 Diskretisierung von Preisreihen, Zufallskomponente und das Rauschen
Diskretisierung von Preisreihen, Zufallskomponente und das Rauschen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Danke, Dmitriy.
Was für ein fantastischer Artikel (und der vorangegangene Artikel)! Ich war auf der Suche nach etwas, um mich zu starten, einige Code, den ich anpassen kann, und das ist perfekt. Ich bin neu bei MQL5, aber ich lerne bereits beim Lesen des Codes. Beim Kompilieren hatte ich die gleichen zwei Fehler wie ein anderer Poster, aber dank der Antwort von Dmitriy konnte ich NeuroNet.mqh bearbeiten und eine erfolgreiche Kompilierung erhalten.
Hat jemand den Code geschrieben, um Bestellungen aufzugeben? Möchten Sie ihn teilen?
Wie könnten wir auch die Vorhersage einbeziehen, welche Parameter für die Positionseröffnung am besten funktionieren würden, wie z. B. Volumen, Sl und Tp?
Ich finde es toll, dass sowohl das Beispiel als auch die Bibliothek nur etwa 500 Codezeilen umfassen. Das ist eine überschaubare Größe zum Lernen und Anpassen.
Ich glaube, ich habe das Problem gefunden, dass die Beschriftungen der vorhergesagten Fraktale für das neuronale Regressionsnetzwerk (Fractal) nicht angezeigt werden.
Im Artikel steht folgendes:
Die Variable i durchläuft die Kerzen. Dieser Code ist im neuronalen Klassifizierungsnetz (Fractal_2) korrekt, obwohl dort der Test i<300 ist.
Im neuronalen Regressionsnetzwerk (Fractal) wird jedoch count als Testvariable verwendet, und der Test ist ">".
Count scheint die Era-Zahl zu sein. Das würde bedeuten, dass alle relevanten Kerzen beschriftet würden, nicht nur die der letzten 200 und erst nach 200 Epochen. Ich nehme an, dass dies ein Fehler ist.
Ist das richtig?
Eine großartige Lernerfahrung.
Guten Morgen
Vielen Dank für diesen Artikel, allerdings bin ich beim Kompilieren von Fractal_2.mq5 und Fractal.mq5 auf einen Compilerfehler gestoßen. Das Problem war "void feedForward(const CArrayObj *&prevLayer);" und ich habe es in "void feedForward(const CArrayObj *prevLayer);" geändert. Ist diese Änderung korrekt?
Mit freundlichen Grüßen
Mit freundlichen Grüßen
Hallo, ja, Sie können es verwenden.