Von der Grundstufe bis zur Mittelstufe: Rekursion

Einführung

Die hier vorgestellten Materialien sind ausschließlich für Bildungszwecke bestimmt. Die Anwendung sollte unter keinen Umständen zu einem anderen Zweck als zum Erlernen und Beherrschen der vorgestellten Konzepte verwendet werden.

Im vorherigen Artikel Von der Grundstufe zur Mittelstufe: Union (II) haben wir untersucht, wie Unions verwendet werden können, um ein Problem zu lösen, von dem viele behaupten, dass es mit reiner und einfacher MQL5 unmöglich ist.

Obwohl viele von Ihnen, liebe Leserinnen und Leser, annehmen könnten, dass diese Art von Aufgabe nur von sehr erfahrenen Programmierern bewältigt werden kann, ist das, was wir dort behandelt haben, aus meiner Sicht und nach meinem Verständnis grundlegendes Material. Es ist für jeden Anfänger im Programmieren durchaus machbar.

Wir treten jetzt in eine Phase ein, in der sich die Dinge rasch ausweiten und zahlreiche Möglichkeiten für die Anwendung und Erforschung bieten. Auch wenn viele immer noch zögern, sich in eine Programmierung zu stürzen, die kühn oder fortgeschritten erscheinen mag, beweist das, was wir bisher behandelt haben, dass es tatsächlich möglich ist, eine Vielzahl von Lösungen zu programmieren, solange wir Ereignisse vorerst nicht berühren, da wir noch nicht behandelt haben, wie man richtig damit arbeitet und sie implementiert.

Es sollte noch einmal betont werden, dass MetaTrader 5 eine ereignisgesteuerte Plattform ist, und die darauf laufenden Anwendungen sind ebenfalls ereignisgesteuert - mit Ausnahme von zwei Typen, die normalerweise nicht auf Ereignisse angewiesen sind. Dabei handelt es sich um Skripte, die als Anhänge beigefügt wurden, und um Dienste. Wir werden uns zu einem späteren Zeitpunkt mit den Dienstleistungen befassen, da die Arbeit mit ihnen ein tieferes Verständnis der Funktionsweise des MetaTrader 5 erfordert. Meiner Meinung nach sind Dienstleistungen die fortschrittlichste Art von Anwendungen, die man für den MetaTrader 5 erstellen kann.

Neben diesen beiden Typen gibt es auch Indikatoren und Expert Advisors. Beide Typen sind für die ereignisgesteuerte Programmierung konzipiert. An dieser Stelle ist es noch nicht angebracht, sie im Detail zu erörtern. Es gibt jedoch noch einige andere Themen, die ich als grundlegend für den Aufbau einer soliden Grundlage für jeden angehenden Fachmann in der Programmierung für Finanzmärkte betrachte.

Ich erwähne dies, weil viele glauben, dass sie bereit sind, in den Beruf einzusteigen, aber wenn sie auf die Probe gestellt werden, scheitern sie kläglich und beschuldigen oft die Welt, ungerecht zu sein. Die Wahrheit ist jedoch, dass sie einfach nicht angemessen auf die Herausforderungen vorbereitet waren, die ein kompetenter Programmierer mit Leichtigkeit, Geschwindigkeit und Effizienz bewältigen kann.

Eine besondere Art von Schleife

In mehreren Artikeln habe ich Befehle für die Arbeit mit Schleifen erklärt. In MQL5, wie auch in vielen anderen Sprachen, gibt es im Allgemeinen drei Typen. Die ersten und meiner Meinung nach einfachsten sind „while“ und „do...while“. Darüber hinaus gibt es noch die „for“-Schleife. Es gibt jedoch noch eine vierte Möglichkeit, Schleifen zu erstellen, die in fast jeder Programmiersprache verfügbar ist. Das einzige Programm, an das ich mich erinnere, das dies nicht unterstützt, ist BASIC. Das liegt daran, dass BASIC keine strukturierte Sprache ist, die für die Arbeit mit Funktionen und Prozeduren entwickelt wurde. Aber das ist hier irrelevant, da wir mit MQL5 arbeiten, einer strukturierten Sprache, die Funktionen und Prozeduren vollständig unterstützt. Und damit sind wir bei der vierten Form der Schleifenbildung angelangt.

Typischerweise werden Schleifen auf zwei Arten erstellt: mit Hilfe spezieller Schleifen-Kontrollstrukturen oder mit Hilfe von Funktionen oder Prozeduren. Ja, lieber Leser, es mag seltsam klingen, eine Funktion oder Prozedur zu verwenden, um eine Schleife zu erstellen. Doch das ist viel häufiger der Fall, als Sie vielleicht denken.

Wenn wir Schleifenkonstrukte verwenden, um Wiederholungen zu erstellen, sprechen wir von iterativer Programmierung. Wenn wir Funktionen oder Prozeduren für denselben Zweck verwenden, nennt man das rekursive Programmierung. Die Erstellung und Anwendung von Rekursionen ist etwas, das jeder Anfänger lernen sollte - rekursive Schleifen sind in vielen Fällen leichter zu verstehen.

Warum bringe ich das jetzt erst zur Sprache? Denn die effektive Verwendung von Rekursionen in Ihrem Code erfordert ein solides Verständnis einiger Schlüsselkonzepte: die „if“-Anweisung, die richtige Verwendung von Variablen und Konstanten, das Verständnis von Lebensdauer und Wertübertragung und - am wichtigsten - ein gutes Verständnis von Datentypen und ihren Grenzen. Je nachdem, was Sie tun, ist es wichtig, den am besten geeigneten Typ zu wählen. Auf diese Weise können Sie Mehrdeutigkeiten vermeiden, die rekursive Operationen behindern könnten.

Bedenken Sie Folgendes: Im Gegensatz zu iterativen Schleifen, die sich in der Regel in der Nähe des Codes befinden, an dem Sie gerade arbeiten, kann sich der Schlüsselteil einer rekursiven Schleife in einer Funktion oder Prozedur befinden, die weit von dem entfernt ist, was Sie gerade lesen. Und wenn ein Fehler oder eine Störung auftritt, müssen Sie oft den gesamten Code zurückverfolgen, um den Ursprungspunkt zu finden, an dem alles wieder beginnt. Dies ist nicht immer eine Aufgabe, die Anfänger bewältigen können, da es sich um eine Rekursion handelt. Auf den ersten Blick sieht es nicht nach einer Schleife aus, aber genau das ist es auch. Nur eine besondere Art von Schleife.

Um dies besser zu verstehen, sollten wir uns ein praktisches Beispiel ansehen. Doch zuvor noch ein letzter Hinweis: Jede iterative Schleife kann in eine rekursive Schleife umgeschrieben werden, und jede rekursive Schleife kann in eine iterative Schleife umgeschrieben werden. Die Schwierigkeit, das eine in das andere umzuwandeln, hängt jedoch von der Art der Schleife selbst ab. Iterative Schleifen haben im Allgemeinen eine bessere Leistung während der Ausführung. Rekursive Schleifen sind oft einfacher zu programmieren. Das eine kompensiert also das andere. Der Zeitaufwand für die Umwandlung einer rekursiven Schleife in eine iterative Schleife ist den Leistungsgewinn möglicherweise nicht wert. Daher gilt die Faustregel, dass man sich um Einfachheit und minimale Kosten bemüht. In diesem Sinne, fangen wir an.

Wir beginnen mit einem sehr einfachen Beispiel, um zu verstehen, wie dies in der Praxis funktioniert. Hier ist sie.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Recursive(5);
07. }
08. //+------------------------------------------------------------------+
09. void Recursive(uchar arg)
10. {
11.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
12.     arg--;
13.     if (arg > 0)
14.         Recursive(arg);
15.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
16. }
17. //+------------------------------------------------------------------+

Code 01

Wenn dieser Code 01 ausgeführt wird, führt er zu dem in der folgenden Abbildung dargestellten Ergebnis.

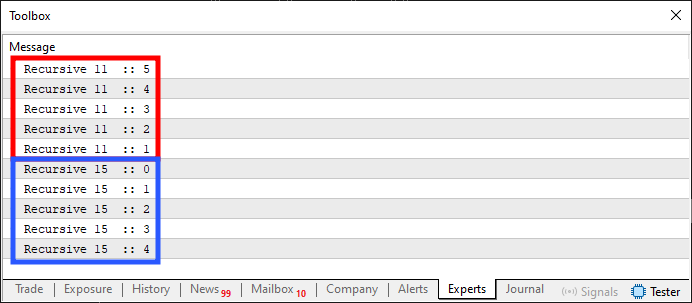
Abbildung 01

Aber was ist das für ein Wahnsinn? Nun, genau das ist es, was eine rekursive Routine tut. Das mag auf den ersten Blick etwas verrückt erscheinen, aber oft ist es genau das, was wir wollen. Sie werden feststellen, dass die in Abbildung 01 gezeigte Ausgabe auch mit herkömmlichen Schleifen hätte erzeugt werden können. In diesem Fall wurde sie jedoch mit Hilfe eines Konzepts erstellt, das als Rekursion bekannt ist. Das heißt, wenn eine Funktion oder Prozedur sich selbst oder eine andere Funktion oder Prozedur mit der Absicht aufruft, eine Schleife zwischen ihnen zu bilden. Viele Menschen assoziieren Rekursion ausschließlich mit einer einzelnen Funktion oder Prozedur, die sich selbst aufruft. Aber das ist nicht unbedingt der Fall. Die einzige Voraussetzung ist, dass eine Schleife gebildet wird, ohne dass ein Standardschleifenbefehl verwendet wird. Ein weiteres interessantes Beispiel für eine Rekursion ist unten dargestellt:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Print("Result: ", Fibonacci(7));
07. }
08. //+------------------------------------------------------------------+
09. uint Fibonacci(uint arg)
10. {
11.     if (arg <= 1)
12.         return arg;
13. 
14.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
15. 
16.     return Fibonacci(arg - 1) + Fibonacci(arg - 2);
17. }
18. //+------------------------------------------------------------------+

Code 02

Dies ist vielleicht das klassischste Beispiel, das beim Studium der Rekursion verwendet wird. Das liegt daran, dass Code 02 deutlich zeigt, wie Rekursion funktioniert. Wenn sie ausgeführt wird, ergibt sich das unten dargestellte Ergebnis:

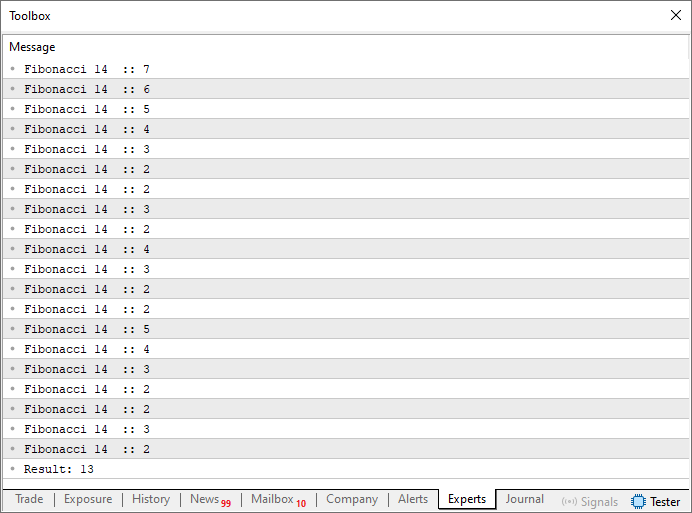
Abbildung 02

Mit anderen Worten: Der siebte Wert in der Fibonacci-Folge ist dreizehn. Und in der Tat, wenn Sie mit der Reihenfolge vertraut sind, wissen Sie, dass dies richtig ist. Aber wie genau hat es dieser Code geschafft, den siebten Wert zu berechnen? Um ehrlich zu sein, ist es vielleicht nicht sofort klar, wie das möglich ist. Nun, lieber Leser, der Schlüssel liegt in Zeile 16, die die minimale Faktorisierung enthält, die zur Berechnung einer Fibonacci-Zahl erforderlich ist. Wenn Sie den mathematischen Ausdruck zur Berechnung der Fibonacci-Werte nachschlagen, werden Sie etwas finden, das der folgenden Abbildung ähnelt.

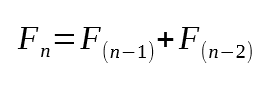
Abbildung 03

Schauen Sie sich jetzt noch einmal Zeile 16 an. Kannst du die Ähnlichkeit zwischen dem mathematischen Ausdruck in Bild 03 und dem, was in Zeile 16 steht, erkennen? Genau das ist die Grundlage einer rekursiven Routine. Das heißt, wir zerlegen das Problem so lange, bis wir einen Punkt erreichen, an dem die Antwort auf einen bekannten Mindestwert konvergiert. Und wie hoch ist dieser Mindestwert? Im Fall der Fibonacci-Folge ist dieser Wert entweder Null oder Eins. Das überprüfen wir in Zeile 11.

Beachten Sie dies: Wie bei Code 01 gab es zunächst einen Countdown (eine absteigende Sequenz), gefolgt von einem scheinbar aufsteigenden Countdown (eine aufsteigende Sequenz). Dasselbe Muster findet sich auch im Code 02, allerdings in zwei unterschiedlichen Phasen. In der ersten Stufe wird der Wert von arg - 1 berechnet. Es wird eine Reihe von Funktionsaufrufen durchgeführt, bis schließlich Zeile 12 erreicht wird. Bei jedem Aufruf wird Zeile 14 ausgeführt und der aktuelle Wert von arg ausgegeben. Infolgedessen beobachten wir zunächst eine absteigende Reihenfolge um eine Einheit pro Schritt. Sobald alle diese Aufrufe zurückkehren, ruft sich die Funktion erneut auf, diesmal mit einer Verringerung um zwei Einheiten. Ich verstehe, dass dies immer noch recht kompliziert erscheinen mag. Um die Dinge einfacher zu visualisieren und besser zu verstehen, wie Code 02 das Ergebnis erfolgreich berechnet, werden wir einige Teile davon ändern. Die aktualisierte Fassung ist unten abgebildet:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Print("Result: ", Fibonacci(5, 0, 0));
07. }
08. //+------------------------------------------------------------------+
09. uint Fibonacci(uint arg, uint call, int who)
10. {
11.     uint value = 0;
12. 
13.     Print(__FUNCTION__, " ", __LINE__, " Entry point [ ", call," ]  ARG: ", arg, " WHO: ", who);
14. 
15.     if (arg <= 1)
16.     {
17.         Print(__FUNCTION__, " ", __LINE__, " Number Callback [ ", call," ]  ARG: ", arg, " WHO: ", who);
18. 
19.         return arg;
20.     }
21. 
22.     value += Fibonacci(arg - 1, call + 1, 1);
23. 
24.     Print(__FUNCTION__, " ", __LINE__, " Value = ", value, "  >> New call with arg: ", arg);
25. 
26.     value += Fibonacci(arg - 2, call + 1, 2);
27. 
28.     Print(__FUNCTION__, " ", __LINE__, " General Return = ", value);
29. 
30.     return value;
31. }
32. //+------------------------------------------------------------------+

Code 03

An dieser Stelle muss ich mich bei allen entschuldigen. Aber leider gibt es keinen einfacheren Weg, um zu erklären, was hier vor sich geht. Die Ausgabe der Ausführung von Code 03 ist unten dargestellt:

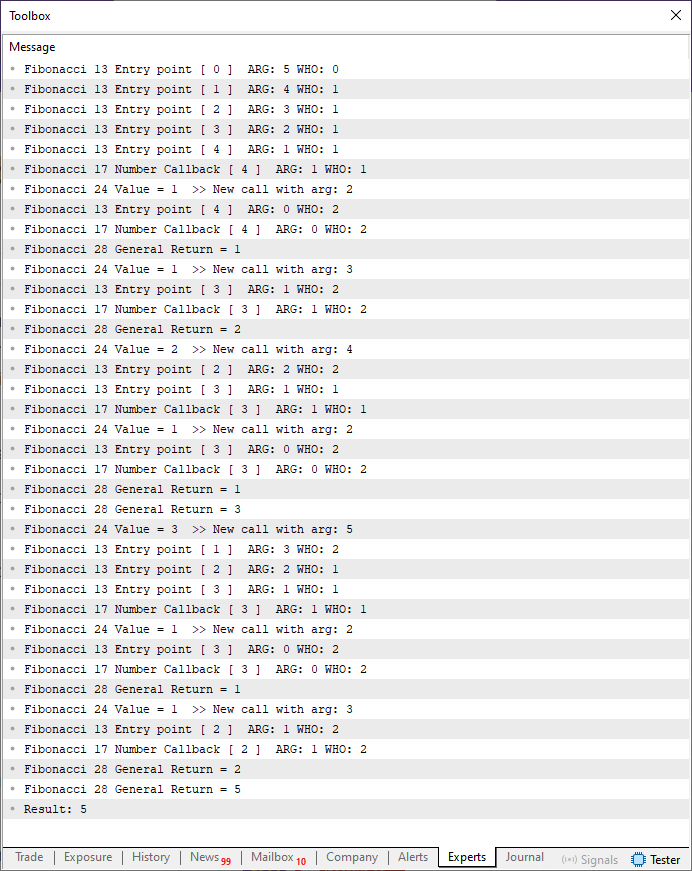
Abbildung 04

Ich weiß, dass Abbildung 04 ziemlich lang ist. Beachten Sie jedoch, dass ich den Funktionsaufruf von der Berechnung von sieben Elementen auf fünf geändert habe. Dies mag zwar nicht viel erscheinen, reduziert aber die Menge der zu analysierenden Informationen erheblich. Dennoch gibt es etwas sehr Wichtiges zu beachten. Jedes Mal, wenn Zeile 13 ausgeführt wird, geben wir die Funktion ein. Das kann zu einer sofortigen Rückkehr oder einem weiteren rekursiven Aufruf führen. Ein Detail, das auf den ersten Blick verwirrend erscheinen mag, ist die Bedingung in Zeile 11. Viele könnten denken, dass dies das Endergebnis beeinträchtigen würde. Aber wenn Sie das glauben, bedeutet das wahrscheinlich, dass Sie noch nicht ganz verstanden haben, was die Rekursion eigentlich mit einer Funktion oder Prozedur macht.

Das ist genau der Grund, warum ich Abbildung 04 so detailliert wie möglich darstelle. Ich möchte Ihnen helfen, wirklich zu sehen, was passiert und wie der Code 02 das richtige Ergebnis berechnet.

Da die folgenden Ausführungen Ihre volle Aufmerksamkeit erfordern, bitte ich Sie, liebe Leserin, lieber Leser, alle Ablenkungen zu beseitigen, bevor Sie fortfahren. Rekursive Funktionen oder Prozeduren können verwirrend sein, vor allem, wenn man ihnen zum ersten Mal beim Programmieren begegnet.

Anhand von Abbildung 04 wollen wir nun verstehen, was wirklich vor sich geht. Erstens: Wenn Zeile 6 ausgeführt wird, rufen wir die Fibonacci-Funktion auf, als wäre sie eine Schleife. Keine iterative Schleife, sondern eine rekursive Schleife. Dies ist der erste wichtige Punkt, den Sie verstehen müssen.

Der nächste Punkt ist die Erkenntnis, dass eine einschränkende Bedingung notwendig ist, so wie wir es bei Code 01 gesehen haben. Jede Schleife, die eine Rekursion verwendet, muss eine Abbruchbedingung haben. In diesem Fall wird diese Bedingung in Zeile 15 festgelegt. Ich weiß, dass zuvor erwähnt wurde, dass die Rekursion auf einen einfachen Ausdruck reduziert werden sollte, aber die Rolle der Begrenzung der Rekursion ist nicht mit diesem Ausdruck verbunden. Dies sind unterschiedliche Konzepte. Dies ist ein wichtiger Moment. Lassen Sie mich das klarstellen: 

Die Rekursion entsteht durch die Umsetzung eines minimalen mathematischen Ausdrucks. Was die Rekursion begrenzt, ist die Bedingung, die verhindert, dass sie zu einer Endlosschleife wird.

In Code 04 befindet sich die einschränkende Bedingung also in Zeile 15. Der rekursive Mechanismus wird durch die Zeilen 22 und 26 geschaffen. In Code 02 ist die einschränkende Bedingung Zeile 11, und die Rekursion wird durch Zeile 16 ausgelöst.

Schauen wir uns nun an, wie das funktioniert. Unser erstes Argument ist 5. Das löst Zeile 13 aus, und dann Zeile 22. In dieser Zeile wird die Funktion erneut aufgerufen, wobei man bis zur Zeile 9 zurückgeht und eine Schleife erzeugt. Aber Achtung: Bei diesem Aufruf in Zeile 22 wird das Argument um eins reduziert. Unser Aufrufstapel wird also aufgebaut - Aufruf nach Aufruf - bis Zeile 15 wahr wird.

An diesem Punkt passiert etwas Interessantes. Es ist der vierte Aufruf, und die Werte der Argumente nehmen ab. Wenn Zeile 15 wahr wird, wird Zeile 17 ausgeführt, die uns den aktuellen Argumentwert anzeigt und wie oft die Funktion aufgerufen wurde. Da das Argument nun 1 ist, geben wir diesen Wert an den Aufrufer zurück. Aber der Anrufer ist nicht die Zeile 6, sondern die Zeile 22. Denken Sie daran, dass wir mehrere Anrufe gestapelt haben. Nun beginnen wir mit dem Abwickeln des Stapels. Der erste zurückgegebene Wert ist 1 und wird der Variablen Value hinzugefügt. Diese Variable verliert ihren Wert zwischen den Aufrufen nicht, da sie akkumuliert und bei jeder Rückkehr einen neuen Wert aufbaut. Um dies besser zu verstehen, müssen Sie wissen, wie ein Aufrufstapel funktioniert, aber das ist jetzt ein fortgeschritteneres Thema. Machen Sie sich keine Sorgen, Sie können den Kerngedanken der Rekursion immer noch nachvollziehen. Man muss nur vorsichtig sein.

Wir haben jetzt also den ersten Rückgabewert berechnet. Wie der Ausdruck in Abbildung 03 zeigt, müssen wir jedoch noch einen weiteren rekursiven Aufruf machen. Aus diesem Grund wird in Zeile 26 ein neuer Aufruf gemacht. Und genau hier wird es knifflig.

Der Aufruf in Zeile 22 reduziert den Wert jedes Mal um 1. Aber wenn arg 1 erreicht hat und die Funktion zurückkehrt, ist arg im vorherigen Aufruf (der aus Zeile 22) immer noch 2. Wenn wir also zu Zeile 24 kommen, obwohl arg beim letzten Aufruf 1 war, haben wir jetzt arg = 2.

Dies mag zunächst verwirrend sein. Aus diesem Grund verwende ich das einfachste Beispiel für eine Rekursion: Fibonacci. Deshalb haben wir uns den Code 01 angesehen, bei dem wir zuerst einen Countdown und dann so etwas wie einen Count-up sahen. Das Hochzählen geschah nur, weil wir die Werte zuvor gestapelt hatten. Als wir also begannen, diese Werte abzuwickeln, entstand die Illusion einer aufsteigenden Folge, obwohl sie nicht direkt implementiert war. Dieses Verhalten ist lediglich ein Nebeneffekt der Art und Weise, wie rekursive Aufrufe gestapelt und zurückgegeben werden.

Gut, lassen Sie uns vorsichtig vorgehen. In Zeile 26 ist arg in diesem Moment 2. Bei einer Verringerung um 2 wird er zu 0. Das führt dazu, dass Zeile 15 true zurückgibt, und die Funktion gibt 0 zurück. In Zeile 28 wird also ein Rückgabewert von 1 ausgegeben. Das ist der Fibonacci-Wert für das erste Element.

Denken Sie daran, dass wir fünf Anrufe gestapelt haben und nur von einem zurückgekommen sind. Zurück in Zeile 22 wird Value also zu 1. Aber war es nicht schon 1? Nein, lieber Leser. Das war in der vorherigen Aufforderung. Jetzt sind wir wieder bei Zeile 22, wo Value 0 war. Jetzt wird es 1. Wir führen dann Zeile 24 aus. Wenn wir einen weiteren Anruf abwickeln, ist arg jetzt 2. Dieser Moment tritt in Zeile 24 auf. Bitte befolgen Sie die Reihenfolge der Maßnahmen sorgfältig. Wir subtrahieren also 2 (in Zeile 26), wodurch das an die Funktion übergebene Argument 0 wird. Und who ist immer noch 2. Das liegt daran, dass wir die Funktion in Zeile 26 aufrufen.

Da arg 0 ist, ist Zeile 15 wahr und gibt in Zeile 19 0 zurück. Zurück in Zeile 26 addieren wir dieses Ergebnis (0) zu unserem früheren Wert (1). Der Wert ist jetzt also 1. Das ist die zweite Fibonacci-Zahl.

Nun kehren wir zu Zeile 22 zurück - wir haben nur zwei von fünf Aufrufen abgewickelt. Dieses Mal ist Value gleich 1 und arg gleich 3. Das ist der interessante Teil: arg = 3. Die Subtraktion von 2 (Zeile 26) ergibt 1, also wird die Funktion mit arg = 1 aufgerufen. Das löst Zeile 15 aus, die 1 zurückgibt. Jetzt ist der Wert 2.

Das ist die dritte Fibonacci-Zahl. Abwickeln einer weiteren Ebene: Zurück zu Zeile 22, Value = 2, arg = 4. Was passiert, wenn Zeile 26 ausgeführt wird? Haben Sie es erraten? Die Funktion wird erneut aufgerufen, aber mit arg = 2. Denken Sie daran, dass wir vor dem Aufruf der Funktion in Zeile 26 2 subtrahieren.

Da arg an dieser Stelle also 2 ist, schlägt Zeile 15 fehl und Zeile 22 wird erneut ausgeführt. Nur ist in diesem Moment die Variable Wert Null und nicht 2. Dieser andere Wert wurde auf dem Stapel gespeichert. Da arg = 2 ist und wir vor dem Aufruf eins subtrahieren müssen, wird in Zeile 15 arg gleich eins sein und eins zurückgegeben. In Zeile 22 ist nun Wert = 1, also wird Zeile 26 ausgeführt. An dieser Stelle wird beim Subtrahieren von 2 von arg die Funktion aufgerufen und 2 subtrahiert. Das Ergebnis ist Null. Und in Zeile 30 wird der Wert 1 zurückgegeben, aber wohin geht er zurück? Damit kehren Sie zur Zeile 26 zurück, in der der Aufruf erfolgte. Denken Sie daran, dass der Wert derzeit 2 beträgt. Da es eine Rückgabe gab, ist der Wert jetzt 3. Wir haben also gerade das vierte Element der Folge berechnet. Nur einer fehlt. (Gelächter)

Ich kann mir vorstellen, dass sich Ihr Gehirn in diesem Moment wie ein Knoten anfühlt - so viele Anrufe, so viele Rückmeldungen. Aber für das letzte Element lassen wir die Wiederholung weg. Sie haben bereits alle notwendigen Mechanismen kennengelernt. In Zeile 26 ist nun arg = 5 und Value = 3. Da arg zur Hälfte abgezogen werden muss, wird eine neue Reihe von Aufrufen durchgeführt. Ich denke, wir haben bereits alles erklärt, was Sie verstehen müssen.

Wichtig ist, was wir zu Beginn dieses Artikels gesagt haben: Rekursion ist einfach zu programmieren, aber langsamer in der Ausführung. Deshalb können wir eine gleichwertige iterative Version zur Berechnung der Fibonacci-Zahlen erstellen. Dies führt zu einer besseren Leistung, obwohl der Code etwas komplexer wird.

Um das zu beweisen, schauen wir uns nun an, wie dieselbe Berechnung mit Iteration statt Rekursion durchgeführt werden könnte. Es gibt viele Möglichkeiten, dies zu tun. Im Folgenden wird ein solcher Ansatz vorgestellt:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     const uchar who = 6;
07. 
08.     Print("Result: ", Fibonacci_Recursive(who));
09.     Print("Result: ", Fibonacci_Interactive(who));
10. }
11. //+------------------------------------------------------------------+
12. uint Fibonacci_Recursive(uint arg)
13. {
14.     if (arg <= 1)
15.         return arg;
16. 
17.     return Fibonacci_Recursive(arg - 1) +  Fibonacci_Recursive(arg - 2);
18. }
19. //+------------------------------------------------------------------+
20. uint Fibonacci_Interactive(uint arg)
21. {
22.     uint v, i, c;
23. 
24.     for (c = 0, i = 0, v = 1; c < arg; i += v, c += 2)
25.         v += i;
26. 
27.     return (c == arg ? i : v);
28. }
29. //+------------------------------------------------------------------+

Code 04

Beachten Sie, dass wir hier mit beiden Ansätzen für Schleifen arbeiten. Das erste ist die Rekursion, das zweite die Iteration. Nun frage ich Sie: Welches ist für Sie leichter zu verstehen? Was glauben Sie, welche Lösung ist schneller, was die Ausführungszeit betrifft? Berücksichtigen Sie dabei, was Sie bereits über die beiden Methoden zur Durchführung der gleichen Art von Berechnung wissen.

Da ich weiß, dass einige Leser die iterative Funktion, die ab Zeile 20 implementiert wird, etwas ungewöhnlich finden könnten, möchte ich kurz erklären, wie sie funktioniert.

In Zeile 22 deklarieren wir die Variablen, die wir benötigen. In Zeile 24 wird dann die Hauptschleife der Berechnung eingeleitet. An dieser Stelle wird es interessant. Beachten Sie, dass wir die Werte initialisieren, bevor wir irgendwelche Berechnungen durchführen. Jetzt kommt ein wichtiger Punkt: Wenn das gesuchte Element ungerade ist (erstes, drittes, fünftes, siebtes Element usw.), enthält die Variable v das richtige Ergebnis. Ist das gesuchte Element jedoch gerade, wird der richtige Wert in der Variablen i gespeichert. Warum?

Der Grund dafür ist, dass die Zählervariable c bei jeder Iteration um zwei erhöht wird, um zu verhindern, dass das richtige Ergebnis überschritten wird. Und da bei jeder Iteration der vorherige Wert zu einem neuen addiert wird und wir die Werte zwischen i und v nicht vertauschen, ergibt sich dieser kleine Unterschied in unserer iterativen Funktion. Es ist möglich, dies auf eine Weise zu implementieren, die dieses spezielle Problem vermeidet, aber ich halte das für unnötig. Die Schleifeninteraktion zeigt mir bereits den aktuellen und den nächsten Wert an. Daher muss ich nur einen ternären Operator anwenden, um das richtige Ergebnis zu erhalten. Ohne diese kleine Anpassung könnten wir am Ende entweder auf das nächste oder das vorherige Element in der Sequenz zeigen, je nachdem, ob die Eingabe (oder das gesuchte Element) ungerade oder gerade ist und ob wir den Wert von i oder v zurückgeben.

Um zu zeigen, dass dieser Code 04 tatsächlich funktioniert, haben wir seine Ausgabe gleich unten eingefügt. Um andere Werte zu testen und beide Arten der Berechnung der Fibonacci-Folge zu vergleichen, ändern Sie einfach die Konstante in Zeile sechs. Aber bedenken Sie, dass die Fibonacci-Folge sehr schnell wächst. Und da es aufgrund der im Code verwendeten Typen Einschränkungen gibt, sollten Sie nicht zu weit gehen, indem Sie Werte zu weit unten in der Sequenz abfragen, da dies zu unerwarteten Ergebnissen oder sogar Fehlern führen kann.

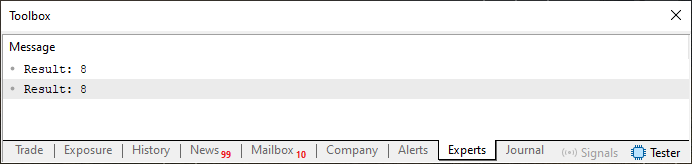
Abbildung 05

Es gibt Möglichkeiten, diese Beschränkungen zu überwinden, sodass wir jede Zahl im Rahmen der Speicherkapazität eines Computers berechnen können. Dies ist jedoch ein fortgeschrittenes Thema, das meiner Meinung nach für einen geeigneteren Zeitpunkt aufgespart werden sollte. Aber nur um Ihre Neugier zu wecken: Was glauben Sie, wie Programmierer den Wert von π (Pi) oder andere irrationale Konstanten mit Tausenden von Nachkommastellen berechnen können? Schließlich sind die in den meisten Programmiersprachen verwendeten Standarddatentypen nicht annähernd in der Lage, diesen Grad an Präzision zu erreichen.

Wie ich bereits erwähnt habe, erfordert dieses Thema ein fortgeschritteneres Verständnis. Nicht, dass es mit dem bisher vermittelten Wissen völlig unerreichbar wäre, denn das ist es nicht. In der Tat ist es möglich, solche Berechnungen mit den Konzepten durchzuführen, die wir hier besprochen haben, einschließlich der Rekursion. Die Umsetzung würde jedoch viel mehr Aufwand bedeuten, da man verschiedene Komponenten an Formate anpassen müsste, die nicht sofort intuitiv sind.

Abschließende Überlegungen

Dieser Artikel soll ein leistungsfähiges und wirklich unterhaltsames Programmierkonzept vorstellen. Aber es ist ein Thema, das mit Vorsicht und Respekt angegangen werden muss. Ein schlechtes Verständnis oder ein falscher Gebrauch der Rekursion kann relativ einfache Programme in unnötig komplexe Programme verwandeln. Wenn sie jedoch richtig und in den richtigen Situationen eingesetzt wird, wird die Rekursion zu einem mächtigen Verbündeten bei der Lösung von Problemen, die sonst wesentlich schwieriger oder zeitaufwändiger wären.

Generell sollten Sie, wann immer es möglich ist, Rekursionen verwenden, insbesondere bei mathematischen Ausdrücken, die sich nicht so leicht iterativ lösen lassen. Aber bedenken Sie: Die hohen Kosten mehrerer rekursiver Aufrufe können Ihr Programm verlangsamen. Wenn die Leistung ein Problem wird, sollten Sie Ihre rekursive Logik in eine iterative Schleife umschreiben. Obwohl der Entwurf anfänglich komplexer ist, sind iterative Lösungen in der Regel viel schneller in der Ausführung, insbesondere bei großen Datensätzen oder Sequenzen, die transformiert werden müssen.