Neuronale Netze leicht gemacht (Teil 7): Adaptive Optimierungsverfahren
1 023
0
Inhalt
- Einführung
- 1. Besonderheiten der adaptiven Optimierungsverfahren
- 1.1. Adaptive Gradientenmethode (AdaGrad)
- 1.2. RMSProp-Verfahren
- 1.3. Die Methode Adadelta
- 1.4. Die Methode Adaptive-Moment-Schätzung (Adam)
- 2. Umsetzung
- 2.1. Aufbau des OpenCL-Kernels
- 2.2. Änderungen im Code der Neuronenklasse des Hauptprogramms
- 2.3. Änderungen im Code der Klasse, die OpenCL nicht verwendet
- 2.4. Änderungen im Code der Klasse des neuronalen Netzwerk des Hauptprogramms
- 3. Tests
- Schlussfolgerungen
- Referenzen
- Programme, die im diesem Artikel verwendet werden
Einführung
In früheren Artikeln haben wir verschiedene Arten von Neuronen verwendet, aber wir haben immer den stochastischen Gradientenabstieg verwendet, um das neuronale Netz zu trainieren. Diese Methode kann wohl als grundlegend bezeichnet werden, und ihre Variationen werden in der Praxis sehr häufig verwendet. Es gibt jedoch noch viele andere Trainingsmethoden für neuronale Netze. Heute schlage ich vor, adaptive Lernmethoden zu betrachten. Diese Methodenfamilie ermöglicht die Änderung der Lernrate der Neuronen während des Trainings des neuronalen Netzes.
1. Besonderheiten der adaptiven Optimierungsverfahren
Sie wissen, dass nicht alle Merkmale, die in ein neuronales Netzwerk eingespeist werden, den gleichen Effekt auf das Endergebnis haben. Einige Parameter können viel Rauschen enthalten und sich häufiger als andere ändern, mit unterschiedlichen Amplituden. Stichproben anderer Parameter können seltene Werte enthalten, die beim Training des neuronalen Netzes mit einer festen Lernrate unbemerkt bleiben können. Einer der Nachteile des bisher betrachteten stochastischen Gradientenabstiegsverfahrens ist die Nichtverfügbarkeit von Optimierungsmechanismen auf solchen Proben. Infolgedessen kann der Lernprozess an einem lokalen Minimum stoppen. Dieses Problem kann durch adaptive Methoden für das Training neuronaler Netze gelöst werden. Diese Methoden erlauben die dynamische Änderung der Lernrate im Trainingsprozess des neuronalen Netzes. Es gibt eine Reihe von solchen Methoden und deren Variationen. Betrachten wir die populärsten von ihnen.
1.1. Adaptive Gradientenmethode (AdaGrad)
Die Adaptive Gradientenmethode wurde 2011 vorgestellt. Sie ist eine Variante der stochastischen Gradientenabstiegsmethode. Wenn wir die mathematischen Formeln dieser Methoden vergleichen, können wir leicht einen Unterschied feststellen: Die Lernrate in AdaGrad wird durch die Quadratwurzel der Summe der Quadrate der Gradienten für alle vorherigen Trainingsiterationen geteilt. Dieser Ansatz erlaubt es, die Lernrate von häufig aktualisierten Parametern zu reduzieren.
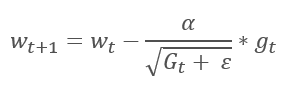
Der Hauptnachteil dieser Methode ergibt sich aus der Formel: Die Summe der Quadrate der Gradienten kann nur wachsen und somit tendiert die Lernrate gegen 0. Dies führt letztlich zum Abbruch des Trainings.
Die Verwendung dieser Methode erfordert zusätzliche Berechnungen und die Zuweisung von zusätzlichem Speicher, um die Summe der Quadrate der Gradienten für jedes Neuron zu speichern.
1.2. RMSProp-Verfahren
Die logische Weiterführung von AdaGrad ist die Methode RMSProp. Um das Absinken der Lernrate auf 0 zu vermeiden, wurde im Nenner der Formel zur Aktualisierung der Gewichte die Summe der Quadrate der vergangenen Gradienten durch das exponentielle Mittel der quadrierten Gradienten ersetzt. Dieser Ansatz eliminiert das konstante und unendliche Wachstum des Wertes im Nenner. Außerdem schenkt er den neuesten Werten des Gradienten, die den aktuellen Zustand des Modells charakterisieren, mehr Aufmerksamkeit.
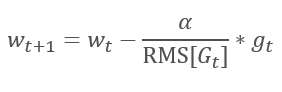
1.3. Die Methode Adadelta
Die adaptive Methode Adadelta wurde fast gleichzeitig mit RMSProp vorgestellt. Diese Methode ist ähnlich und verwendet einen exponentiellen Mittelwert der Summe der quadrierten Gradienten im Nenner der Formel, die für die Aktualisierung der Gewichte verwendet wird. Aber im Gegensatz zu RMSProp verzichtet diese Methode vollständig auf die Lernrate in der Aktualisierungsformel und ersetzt sie durch einen exponentiellen Mittelwert der Summe der Quadrate der vorherigen Änderungen des analysierten Parameters.
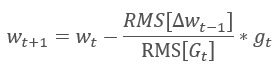
Dieser Ansatz erlaubt es, die Lernrate aus der Formel für die Aktualisierung der Gewichte zu entfernen und einen hoch adaptiven Lernalgorithmus zu erstellen. Diese Methode erfordert jedoch zusätzliche Iterationen der Berechnungen und die Zuweisung von Speicher für die Speicherung eines zusätzlichen Wertes in jedem Neuron.
1.4. Die Methode Adaptive-Moment-Schätzung (Adam)
Im Jahr 2014 schlugen Diederik P. Kingma und Jimmy Lei Ba die Adaptive Moment Estimation Method (Adam) vor. Laut den Autoren kombiniert die Methode die Vorteile der AdaGrad- und RMSProp-Methoden und funktioniert gut für das Online-Training. Diese Methode zeigt konstant gute Ergebnisse mit verschiedenen Stichproben. Sie wird oft zur standardmäßigen Verwendung in verschiedenen Paketen empfohlen.
Die Methode basiert auf der Berechnung des exponentiellen Durchschnitts der Gradienten m und des exponentiellen Durchschnitts der quadrierten Gradienten v. Jeder exponentielle Mittelwert hat einen eigenen Hyperparameter ß, der einer Glättungslänge entspricht.
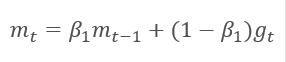
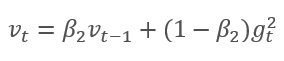
Die Autoren schlagen vor, ß1 bei 0,9 und ß2 bei 0,999 zu verwenden. In diesem Fall werden m0 und v0 Null. Mit diesen Parametern liefern die oben vorgestellten Formeln zu Beginn des Trainings Werte nahe 0, so dass die Lernrate zu Beginn gering sein wird. Um den Lernprozess zu beschleunigen, schlagen die Autoren vor, das erhaltene Moment zu korrigieren.
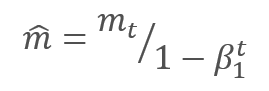
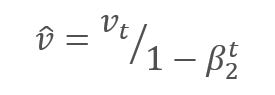
Die Parameter werden aktualisiert, indem das Verhältnis des korrigierten Gradientenmoments m zur Quadratwurzel des korrigierten Moments des quadrierten Gradienten v angepasst wird. Um eine Division durch Null zu vermeiden, wird die Konstante Ɛ nahe 0 zum Nenner addiert. Das resultierende Verhältnis wird um den Lernfaktor α korrigiert, der in diesem Fall die obere Grenze des Lernschritts ist. Die Autoren schlagen vor, α standardmäßig auf 0,001 zu setzen.
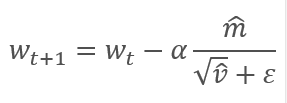
2. Umsetzung
Nachdem wir die theoretischen Aspekte betrachtet haben, können wir zur praktischen Implementierung übergehen. Ich schlage vor, die Adam-Methode mit den von den Autoren angebotenen Standard-Hyperparametern zu implementieren. Weiterhin können Sie andere Variationen von Hyperparametern ausprobieren.
Das früher erstellte neuronale Netz verwendet zum Training den stochastischen Gradientenabstieg, für den wir bereits den Backpropagation-Algorithmus implementiert haben. Die vorhandene Backpropagation-Funktionalität kann für die Implementierung der Adam-Methode verwendet werden. Wir müssen nur noch den Algorithmus zur Aktualisierung der Gewichte implementieren. Diese Funktionalität wird von der Methode updateInputWeights ausgeführt, die in jeder Klasse von Neuronen implementiert ist. Natürlich werden wir den zuvor erstellten Algorithmus des stochastischen Gradientenabstiegs nicht löschen. Wir erstellen einen alternativen Algorithmus, der die Wahl der zu verwendenden Trainingsmethode ermöglicht.
2.1. Aufbau des OpenCL-Kernels
Betrachten wir die Implementierung der Adam-Methode für die Klasse CNeuronBaseOCL. Erstellen Sie zunächst den UpdateWeightsAdam-Kernel, um die Methode in OpenCL zu implementieren. Dem Kernel werden als Parameter Zeiger auf die folgenden Matrizen übergeben:
- Matrix der Gewichte — matrix_w,
- Matrix der Fehlergradienten — matrix_g,
- Matrix der Eingangsdaten — matrix_i,
- Matrix der exponentiellen Mittelwerte der Gradienten — matrix_m,
- Matrix der exponentiellen Mittelwerte der quadrierten Gradienten — matrix_v.
__kernel void UpdateWeightsAdam(__global double *matrix_w, __global double *matrix_g, __global double *matrix_i, __global double *matrix_m, __global double *matrix_v, int inputs, double l, double b1, double b2)
Übergeben Sie zusätzlich in den Kernel-Parametern die Größe des Eingangsdaten-Arrays und die Hyperparameter des Adam-Algorithmus.
Zu Beginn des Kerns erhalten Sie die fortlaufenden Nummern des Datenstroms in zwei Dimensionen, die jeweils die Nummern der Neuronen der aktuellen und der vorherigen Schicht angeben. Bestimmen Sie anhand der erhaltenen Nummern die Anfangsnummer des verarbeiteten Elements in den Puffern. Achten Sie darauf, dass die resultierende Streamnummer in der zweiten Dimension mit "4" multipliziert wird. Das liegt daran, dass wir, um die Anzahl der Streams und die Gesamtausführungszeit des Programms zu reduzieren, Vektorberechnungen mit 4-Element-Vektoren verwenden werden.
{
int i=get_global_id(0);
int j=get_global_id(1);
int wi=i*(inputs+1)+j*4;
Nachdem Sie die Position der verarbeiteten Elemente in Datenpuffern bestimmt haben, deklarieren Sie Vektorvariablen und füllen diese mit den entsprechenden Werten. Verwenden Sie die vorher beschriebene Methode und füllen Sie die fehlenden Daten in den Vektoren mit Nullen.
double4 m, v, weight, inp; switch(inputs-j*4) { case 0: inp=(double4)(1,0,0,0); weight=(double4)(matrix_w[wi],0,0,0); m=(double4)(matrix_m[wi],0,0,0); v=(double4)(matrix_v[wi],0,0,0); break; case 1: inp=(double4)(matrix_i[j],1,0,0); weight=(double4)(matrix_w[wi],matrix_w[wi+1],0,0); m=(double4)(matrix_m[wi],matrix_m[wi+1],0,0); v=(double4)(matrix_v[wi],matrix_v[wi+1],0,0); break; case 2: inp=(double4)(matrix_i[j],matrix_i[j+1],1,0); weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],0); m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],0); v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],0); break; case 3: inp=(double4)(matrix_i[j],matrix_i[j+1],matrix_i[j+2],1); weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],matrix_w[wi+3]); m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],matrix_m[wi+3]); v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],matrix_v[wi+3]); break; default: inp=(double4)(matrix_i[j],matrix_i[j+1],matrix_i[j+2],matrix_i[j+3]); weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],matrix_w[wi+3]); m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],matrix_m[wi+3]); v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],matrix_v[wi+3]); break; }
Der Gradientenvektor ergibt sich durch Multiplikation des Gradienten des aktuellen Neurons mit dem Eingangsdatenvektor.
double4 g=matrix_g[i]*inp;
Als Nächstes werden die exponentiellen Mittelwerte des Gradienten und des quadrierten Gradienten berechnet.
double4 mt=b1*m+(1-b1)*g; double4 vt=b2*v+(1-b2)*pow(g,2)+0.00000001;
Berechnen Sie die Deltas der Parameteränderungen.
double4 delta=l*mt/sqrt(vt);
Beachten Sie, dass wir die empfangenen Momente im Kernel nicht angepasst haben. Dieser Schritt wird hier absichtlich weggelassen. Da ß1 und ß2 für alle Neuronen gleich sind und t, das ist hier die Anzahl der Iterationen der Neuronen-Parameter-Updates, ebenfalls für alle Neuronen gleich ist, wird auch der Korrekturfaktor für alle Neuronen gleich sein. Deshalb werden wir den Faktor nicht für jedes Neuron neu berechnen, sondern ihn einmal im Hauptprogrammcode berechnen und den um diesen Wert bereinigten Lernkoeffizienten an den Kernel übergeben.
Nach der Berechnung der Deltas müssen wir nur noch die Gewichtskoeffizienten anpassen und die berechneten Momente in den Puffern aktualisieren. Dann verlassen Sie den Kernel.
switch(inputs-j*4) { case 2: matrix_w[wi+2]+=delta.s2; matrix_m[wi+2]=mt.s2; matrix_v[wi+2]=vt.s2; case 1: matrix_w[wi+1]+=delta.s1; matrix_m[wi+1]=mt.s1; matrix_v[wi+1]=vt.s1; case 0: matrix_w[wi]+=delta.s0; matrix_m[wi]=mt.s0; matrix_v[wi]=vt.s0; break; default: matrix_w[wi]+=delta.s0; matrix_m[wi]=mt.s0; matrix_v[wi]=vt.s0; matrix_w[wi+1]+=delta.s1; matrix_m[wi+1]=mt.s1; matrix_v[wi+1]=vt.s1; matrix_w[wi+2]+=delta.s2; matrix_m[wi+2]=mt.s2; matrix_v[wi+2]=vt.s2; matrix_w[wi+3]+=delta.s3; matrix_m[wi+3]=mt.s3; matrix_v[wi+3]=vt.s3; break; } };
Dieser Code hat einen weiteren Trick. Achten Sie auf die umgekehrte Reihenfolge von case im Operator switch. Außerdem wird break nur nach case 0 und default verwendet. Dieser Ansatz erlaubt es, die Duplizierung von gleichem Code für alle Varianten zu vermeiden.
2.2. Änderungen im Code der Neuronenklasse des Hauptprogramms
Nachdem wir den Kernel erstellt haben, müssen wir Änderungen am Code des Hauptprogramms vornehmen. Zunächst fügen wir die Konstanten des 'define'-Blocks für die Arbeit mit dem Kernel hinzu.
#define def_k_UpdateWeightsAdam 4 #define def_k_uwa_matrix_w 0 #define def_k_uwa_matrix_g 1 #define def_k_uwa_matrix_i 2 #define def_k_uwa_matrix_m 3 #define def_k_uwa_matrix_v 4 #define def_k_uwa_inputs 5 #define def_k_uwa_l 6 #define def_k_uwa_b1 7 #define def_k_uwa_b2 8
Erstellen Sie die Enumeration, um Trainingsmethoden anzugeben und fügen Sie den Enumerationen die Momentpuffer hinzu.
enum ENUM_OPTIMIZATION { SGD, ADAM }; //--- enum ENUM_BUFFERS { WEIGHTS, DELTA_WEIGHTS, OUTPUT, GRADIENT, FIRST_MOMENTUM, SECOND_MOMENTUM };
Fügen Sie dann im Hauptteil der Klasse CNeuronBaseOCL die Puffer zum Speichern von Momenten, exponentiellen Durchschnittskonstanten, Trainings-Iterationszähler und eine Variable zum Speichern der Trainingsmethode hinzu.
class CNeuronBaseOCL : public CObject { protected: ......... ......... .......... CBufferDouble *FirstMomentum; CBufferDouble *SecondMomentum; //--- ......... ......... const double b1; const double b2; int t; //--- ......... ......... ENUM_OPTIMIZATION optimization;
Im Klassenkonstruktor setzen Sie die Werte der Konstanten und initialisieren die Puffer.
CNeuronBaseOCL::CNeuronBaseOCL(void) : alpha(momentum), activation(TANH), optimization(SGD), b1(0.9), b2(0.999), t(1) { OpenCL=NULL; Output=new CBufferDouble(); PrevOutput=new CBufferDouble(); Weights=new CBufferDouble(); DeltaWeights=new CBufferDouble(); Gradient=new CBufferDouble(); FirstMomentum=new CBufferDouble(); SecondMomentum=new CBufferDouble(); }
Vergessen Sie nicht, das Löschen von Pufferobjekten in den Destruktor der Klasse aufzunehmen.
CNeuronBaseOCL::~CNeuronBaseOCL(void) { if(CheckPointer(Output)!=POINTER_INVALID) delete Output; if(CheckPointer(PrevOutput)!=POINTER_INVALID) delete PrevOutput; if(CheckPointer(Weights)!=POINTER_INVALID) delete Weights; if(CheckPointer(DeltaWeights)!=POINTER_INVALID) delete DeltaWeights; if(CheckPointer(Gradient)!=POINTER_INVALID) delete Gradient; if(CheckPointer(FirstMomentum)!=POINTER_INVALID) delete FirstMomentum; if(CheckPointer(SecondMomentum)!=POINTER_INVALID) delete SecondMomentum; OpenCL=NULL; }
Fügen Sie in den Parametern der Klasseninitialisierungsfunktion eine Trainingsmethode hinzu und initialisieren Sie, abhängig von der angegebenen Trainingsmethode, die Puffer. Wenn der stochastische Gradientenabstieg für das Training verwendet wird, initialisieren Sie den Puffer der Deltas und entfernen Sie die Puffer der Momente. Wenn die Methode Adam verwendet wird, initialisieren Sie die Momentenpuffer und löschen den Puffer der Deltas.
bool CNeuronBaseOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint numNeurons, ENUM_OPTIMIZATION optimization_type) { if(CheckPointer(open_cl)==POINTER_INVALID || numNeurons<=0) return false; OpenCL=open_cl; optimization=optimization_type; //--- .................... .................... .................... .................... //--- if(numOutputs>0) { if(CheckPointer(Weights)==POINTER_INVALID) { Weights=new CBufferDouble(); if(CheckPointer(Weights)==POINTER_INVALID) return false; } int count=(int)((numNeurons+1)*numOutputs); if(!Weights.Reserve(count)) return false; for(int i=0;i<count;i++) { double weigh=(MathRand()+1)/32768.0-0.5; if(weigh==0) weigh=0.001; if(!Weights.Add(weigh)) return false; } if(!Weights.BufferCreate(OpenCL)) return false; //--- if(optimization==SGD) { if(CheckPointer(DeltaWeights)==POINTER_INVALID) { DeltaWeights=new CBufferDouble(); if(CheckPointer(DeltaWeights)==POINTER_INVALID) return false; } if(!DeltaWeights.BufferInit(count,0)) return false; if(!DeltaWeights.BufferCreate(OpenCL)) return false; if(CheckPointer(FirstMomentum)==POINTER_INVALID) delete FirstMomentum; if(CheckPointer(SecondMomentum)==POINTER_INVALID) delete SecondMomentum; } else { if(CheckPointer(DeltaWeights)==POINTER_INVALID) delete DeltaWeights; //--- if(CheckPointer(FirstMomentum)==POINTER_INVALID) { FirstMomentum=new CBufferDouble(); if(CheckPointer(FirstMomentum)==POINTER_INVALID) return false; } if(!FirstMomentum.BufferInit(count,0)) return false; if(!FirstMomentum.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(SecondMomentum)==POINTER_INVALID) { SecondMomentum=new CBufferDouble(); if(CheckPointer(SecondMomentum)==POINTER_INVALID) return false; } if(!SecondMomentum.BufferInit(count,0)) return false; if(!SecondMomentum.BufferCreate(OpenCL)) return false; } } else { if(CheckPointer(Weights)!=POINTER_INVALID) delete Weights; if(CheckPointer(DeltaWeights)!=POINTER_INVALID) delete DeltaWeights; } //--- return true; }
Nehmen Sie außerdem Änderungen an der Gewichtungsaktualisierungsmethode updateInputWeights vor. Erstellen Sie zunächst einen Verzweigungsalgorithmus in Abhängigkeit von der Trainingsmethode.
bool CNeuronBaseOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; uint global_work_offset[2]={0,0}; uint global_work_size[2]; global_work_size[0]=Neurons(); global_work_size[1]=NeuronOCL.Neurons(); if(optimization==SGD) {
Für den stochastischen Gradientenabstieg verwenden Sie den gesamten Code so, wie er ist.
OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_w,NeuronOCL.getWeightsIndex()); OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_g,getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_i,NeuronOCL.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_dw,NeuronOCL.getDeltaWeightsIndex()); OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_inputs,NeuronOCL.Neurons()); OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_learning_rates,eta); OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_momentum,alpha); ResetLastError(); if(!OpenCL.Execute(def_k_UpdateWeightsMomentum,2,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateWeightsMomentum: %d",GetLastError()); return false; } }
Setzen Sie im Adam-Methodenzweig Datenaustauschpuffer für den entsprechenden Kernel.
else { if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_w,NeuronOCL.getWeightsIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_g,getGradientIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_i,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_m,NeuronOCL.getFirstMomentumIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_v,NeuronOCL.getSecondMomentumIndex())) return false;
Dann passen Sie die Lernrate für die aktuelle Iteration des Trainings an.
double lt=eta*sqrt(1-pow(b2,t))/(1-pow(b1,t));
Setzen Sie nun die Hyperparameter.
if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_inputs,NeuronOCL.Neurons())) return false; if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_l,lt)) return false; if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_b1,b1)) return false; if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_b2,b2)) return false;
Da wir Vektorwerte für Berechnungen im Kernel verwendet haben, reduzieren Sie die Anzahl der Threads in der zweiten Dimension um das Vierfache.
uint rest=global_work_size[1]%4; global_work_size[1]=(global_work_size[1]-rest)/4 + (rest>0 ? 1 : 0);
Wenn die Vorarbeiten erledigt sind, rufen Sie den Kernel auf und erhöhen den Trainingsiterationenzähler.
ResetLastError(); if(!OpenCL.Execute(def_k_UpdateWeightsAdam,2,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateWeightsAdam: %d",GetLastError()); return false; } t++; }
Lesen Sie nach der Verzweigung, unabhängig von der Trainingsmethode, die neu berechneten Gewichte. Wie ich im vorigen Artikel erklärt habe, muss der Puffer auch bei versteckten Schichten gelesen werden, da diese Operation nicht nur Daten liest, sondern auch die Ausführung des Kernels startet.
//--- return NeuronOCL.Weights.BufferRead(); }
Zusätzlich zu den Ergänzungen des Algorithmus zur Berechnung der Trainingsmethode ist es notwendig, die Methoden zum Speichern und Laden von Informationen über die bisherigen Trainingsergebnisse der Neuronen anzupassen. Implementieren Sie in der Methode Save das Speichern der Trainingsmethode und fügen Sie den Zähler der Trainingsiterationen hinzu.
bool CNeuronBaseOCL::Save(const int file_handle) { if(file_handle==INVALID_HANDLE) return false; if(FileWriteInteger(file_handle,Type())<INT_VALUE) return false; //--- if(FileWriteInteger(file_handle,(int)activation,INT_VALUE)<INT_VALUE) return false; if(FileWriteInteger(file_handle,(int)optimization,INT_VALUE)<INT_VALUE) return false; if(FileWriteInteger(file_handle,(int)t,INT_VALUE)<INT_VALUE) return false;
Das Speichern von Puffern, die für beide Trainingsmethoden gleich sind, hat sich nicht geändert.
if(CheckPointer(Output)==POINTER_INVALID || !Output.BufferRead() || !Output.Save(file_handle)) return false; if(CheckPointer(PrevOutput)==POINTER_INVALID || !PrevOutput.BufferRead() || !PrevOutput.Save(file_handle)) return false; if(CheckPointer(Gradient)==POINTER_INVALID || !Gradient.BufferRead() || !Gradient.Save(file_handle)) return false; //--- if(CheckPointer(Weights)==POINTER_INVALID) { FileWriteInteger(file_handle,0); return true; } else FileWriteInteger(file_handle,1); //--- if(CheckPointer(Weights)==POINTER_INVALID || !Weights.BufferRead() || !Weights.Save(file_handle)) return false;
Danach erstellen Sie für jede Trainingsmethode einen Verzweigungsalgorithmus, wobei Sie bestimmte Puffer speichern.
if(optimization==SGD) { if(CheckPointer(DeltaWeights)==POINTER_INVALID || !DeltaWeights.BufferRead() || !DeltaWeights.Save(file_handle)) return false; } else { if(CheckPointer(FirstMomentum)==POINTER_INVALID || !FirstMomentum.BufferRead() || !FirstMomentum.Save(file_handle)) return false; if(CheckPointer(SecondMomentum)==POINTER_INVALID || !SecondMomentum.BufferRead() || !SecondMomentum.Save(file_handle)) return false; } //--- return true; }
Nehmen Sie ähnliche Änderungen in der gleichen Reihenfolge in der Methode Load vor.
Der vollständige Code aller Methoden und Funktionen steht im Anhang zur Verfügung.
2.3. Änderungen im Code der Klasse, die OpenCL nicht verwendet
Um die gleichen Betriebsbedingungen für alle Klassen zu erhalten, wurden ähnliche Änderungen an den Klassen vorgenommen, die in reinem MQL5 ohne Verwendung von OpenCL arbeiten.
Fügen Sie zunächst der Klasse CConnection die Variablen zum Speichern von Momentdaten hinzu und setzen Sie die Anfangswerte im Klassenkonstruktor.
class CConnection : public CObject { public: double weight; double deltaWeight; double mt; double vt; CConnection(double w) { weight=w; deltaWeight=0; mt=0; vt=0; }
Außerdem ist es notwendig, die Methoden, die Verbindungsdaten speichern und laden, um die Verarbeitung neuer Variablen zu erweitern.
bool CConnection::Save(int file_handle) { ........... ........... ........... if(FileWriteDouble(file_handle,mt)<=0) return false; if(FileWriteDouble(file_handle,vt)<=0) return false; //--- return true; } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CConnection::Load(int file_handle) { ............ ............ ............ mt=FileReadDouble(file_handle); vt=FileReadDouble(file_handle); //--- return true; }
Fügen Sie als Nächstes der Neuronenklasse CNeuronBase Variablen hinzu, um das Optimierungsverfahren und den Zähler der Aktualisierungsiterationen der Waage zu speichern.
class CNeuronBase : public CObject { protected: ......... ......... ......... ENUM_OPTIMIZATION optimization; const double b1; const double b2; int t;
Dann muss auch die Initialisierungsmethode der Neuronen geändert werden. Fügen Sie den Methodenparametern eine Variable zur Angabe des Optimierungsverfahrens hinzu und implementieren Sie deren Speicherung in der oben definierten Variable.
bool CNeuronBase::Init(uint numOutputs,uint myIndex, ENUM_OPTIMIZATION optimization_type) { optimization=optimization_type;
Danach erstellen wir den Algorithmus, der nach dem Optimierungsverfahren verzweigt, in die Methode updateInputWeights. Berechnen Sie vor der Schleife durch die Verbindungen die angepasste Lernrate neu und erstellen Sie in einer Schleife zwei Zweige zur Berechnung der Gewichte.
bool CNeuron::updateInputWeights(CLayer *&prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- double lt=eta*sqrt(1-pow(b2,t))/(1-pow(b1,t)); int total=prevLayer.Total(); for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron= prevLayer.At(n); CConnection *con=neuron.Connections.At(m_myIndex); if(CheckPointer(con)==POINTER_INVALID) continue; if(optimization==SGD) con.weight+=con.deltaWeight=(gradient!=0 ? eta*neuron.getOutputVal()*gradient : 0)+(con.deltaWeight!=0 ? alpha*con.deltaWeight : 0); else { con.mt=b1*con.mt+(1-b1)*gradient; con.vt=b2*con.vt+(1-b2)*pow(gradient,2)+0.00000001; con.weight+=con.deltaWeight=lt*con.mt/sqrt(con.vt); t++; } } //--- return true; }
Fügen Sie die Verarbeitung von neuen Variablen zu den Speicher- und Lademethoden hinzu.
Der vollständige Code aller Methoden ist im Anhang unten zu finden.
2.4. Änderungen im Code der Klasse des neuronalen Netzwerk des Hauptprogramms
Zusätzlich zu den Änderungen in den Neuronenklassen sind auch Änderungen an anderen Objekten in unserem Code erforderlich. Zunächst einmal müssen wir Informationen über die Trainingsmethode vom Hauptprogramm an das Neuron übergeben. Die Daten aus dem Hauptprogramm werden über die Klasse CLayerDescription an die Klasse des neuronalen Netzwerks übergeben. Dieser Klasse sollte eine geeignete Methode hinzugefügt werden, um Informationen über die Trainingsmethode zu übergeben.
class CLayerDescription : public CObject { public: CLayerDescription(void); ~CLayerDescription(void) {}; //--- int type; int count; int window; int step; ENUM_ACTIVATION activation; ENUM_OPTIMIZATION optimization; };
Nehmen Sie nun die letzten Ergänzungen am Konstruktor der Klasse CNet des Neuronalen Netzes vor. Fügen Sie hier eine Angabe des Optimierungsverfahrens bei der Initialisierung der Netzwerkneuronen hinzu, erhöhen Sie die Anzahl der verwendeten OpenCL-Kernel und deklarieren Sie einen neuen Optimierungskernel - Adam. Nachfolgend finden Sie den geänderten Konstruktorcode mit hervorgehobenen Änderungen.
CNet::CNet(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
int total=Description.Total();
if(total<=0)
return;
//---
layers=new CArrayLayer();
if(CheckPointer(layers)==POINTER_INVALID)
return;
//---
CLayer *temp;
CLayerDescription *desc=NULL, *next=NULL, *prev=NULL;
CNeuronBase *neuron=NULL;
CNeuronProof *neuron_p=NULL;
int output_count=0;
int temp_count=0;
//---
next=Description.At(1);
if(next.type==defNeuron || next.type==defNeuronBaseOCL)
{
opencl=new COpenCLMy();
if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true))
delete opencl;
}
else
{
if(CheckPointer(opencl)!=POINTER_INVALID)
delete opencl;
}
//---
for(int i=0; i<total; i++)
{
prev=desc;
desc=Description.At(i);
if((i+1)<total)
{
next=Description.At(i+1);
if(CheckPointer(next)==POINTER_INVALID)
return;
}
else
next=NULL;
int outputs=(next==NULL || (next.type!=defNeuron && next.type!=defNeuronBaseOCL) ? 0 : next.count);
temp=new CLayer(outputs);
int neurons=(desc.count+(desc.type==defNeuron || desc.type==defNeuronBaseOCL ? 1 : 0));
if(CheckPointer(opencl)!=POINTER_INVALID)
{
CNeuronBaseOCL *neuron_ocl=NULL;
switch(desc.type)
{
case defNeuron:
case defNeuronBaseOCL:
neuron_ocl=new CNeuronBaseOCL();
if(CheckPointer(neuron_ocl)==POINTER_INVALID)
{
delete temp;
return;
}
if(!neuron_ocl.Init(outputs,0,opencl,desc.count,desc.optimization))
{
delete temp;
return;
}
neuron_ocl.SetActivationFunction(desc.activation);
if(!temp.Add(neuron_ocl))
{
delete neuron_ocl;
delete temp;
return;
}
neuron_ocl=NULL;
break;
default:
return;
break;
}
}
else
for(int n=0; n<neurons; n++)
{
switch(desc.type)
{
case defNeuron:
neuron=new CNeuron();
if(CheckPointer(neuron)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
neuron.Init(outputs,n,desc.optimization);
neuron.SetActivationFunction(desc.activation);
break;
case defNeuronConv:
neuron_p=new CNeuronConv();
if(CheckPointer(neuron_p)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
if(CheckPointer(prev)!=POINTER_INVALID)
{
if(prev.type==defNeuron)
{
temp_count=(int)((prev.count-desc.window)%desc.step);
output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
else
if(n==0)
{
temp_count=(int)((output_count-desc.window)%desc.step);
output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
}
if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count,desc.optimization))
neuron=neuron_p;
break;
case defNeuronProof:
neuron_p=new CNeuronProof();
if(CheckPointer(neuron_p)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
if(CheckPointer(prev)!=POINTER_INVALID)
{
if(prev.type==defNeuron)
{
temp_count=(int)((prev.count-desc.window)%desc.step);
output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
else
if(n==0)
{
temp_count=(int)((output_count-desc.window)%desc.step);
output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
}
if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count,desc.optimization))
neuron=neuron_p;
break;
case defNeuronLSTM:
neuron_p=new CNeuronLSTM();
if(CheckPointer(neuron_p)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
output_count=(next!=NULL ? next.window : desc.step);
if(neuron_p.Init(outputs,n,desc.window,1,output_count,desc.optimization))
neuron=neuron_p;
break;
}
if(!temp.Add(neuron))
{
delete temp;
delete layers;
return;
}
neuron=NULL;
}
if(!layers.Add(temp))
{
delete temp;
delete layers;
return;
}
}
//---
if(CheckPointer(opencl)==POINTER_INVALID)
return;
//--- create kernels
opencl.SetKernelsCount(5);
opencl.KernelCreate(def_k_FeedForward,"FeedForward");
opencl.KernelCreate(def_k_CaclOutputGradient,"CaclOutputGradient");
opencl.KernelCreate(def_k_CaclHiddenGradient,"CaclHiddenGradient");
opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum");
opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam");
//---
return;
}
Der gesamte Code aller Klassen und Methoden befindet sich in der Anlage.
3. Tests
Das Testen der Optimierung durch das Adam-Verfahren wurde unter den gleichen Bedingungen durchgeführt, die in früheren Tests verwendet wurden: Symbol EURUSD, Zeitrahmen H1, Daten von 20 aufeinanderfolgenden Kerzen werden in das Netzwerk eingespeist, und das Training wird mit der Historie der letzten zwei Jahre durchgeführt. Zum Testen wurde der Expert Advisor Fractal_OCL_Adam erstellt. Dieser Expert Advisor wurde auf Basis des Fractal_OCL EA erstellt, indem das Optimierungsverfahren Adam bei der Beschreibung des neuronalen Netzwerks in der OnInit-Funktion des Hauptprogramms angegeben wurde.
desc.count=(int)HistoryBars*12; desc.type=defNeuron; desc.optimization=ADAM;
Die Anzahl der Schichten und Neuronen hat sich nicht geändert.
Der Expert Advisor wurde mit Zufallsgewichten im Bereich von -1 bis 1 initialisiert, wobei Nullwerte ausgeschlossen wurden. Während des Testens, bereits nach der 2. Trainingsepoche, stabilisierte sich der Fehler des neuronalen Netzes um 30 %. Wie Sie sich vielleicht erinnern, wenn Sie mit der Methode des stochastischen Gradientenabstiegs lernen, stabilisierte sich der Fehler nach der 5. Testepoche
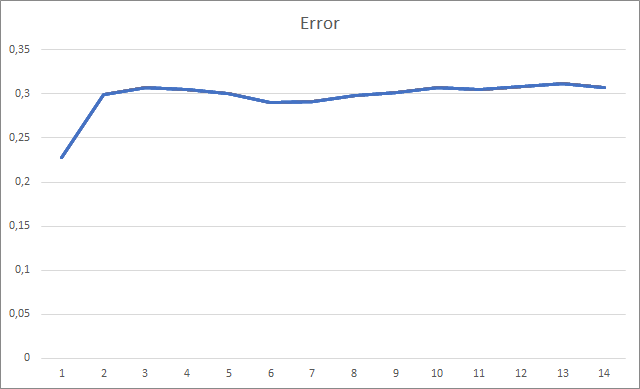
Die Grafik der verpassten Fraktale zeigt einen allmählichen Anstieg des Wertes während des gesamten Trainings. Nach 12 Trainingsepochen ist jedoch eine allmähliche Abnahme der Wertzuwachsrate zu erkennen. Der Wert war nach der 14. Epoche gleich 72,5 %. Beim Training eines ähnlichen neuronalen Netzes mit der stochastischen Gradientenabstiegsmethode lag der Prozentsatz der fehlenden Fraktale nach 10 Epochen bei 97-100 % mit unterschiedlichen Lernraten.
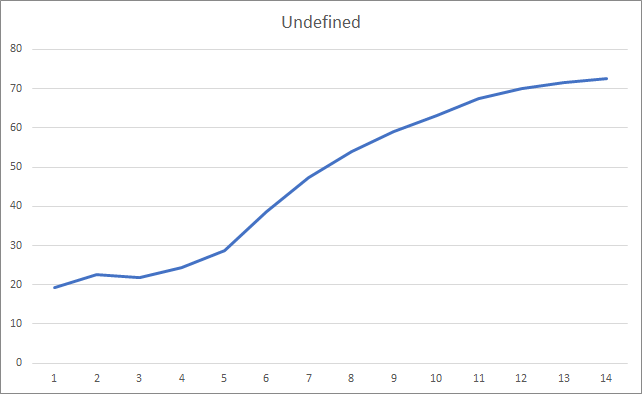
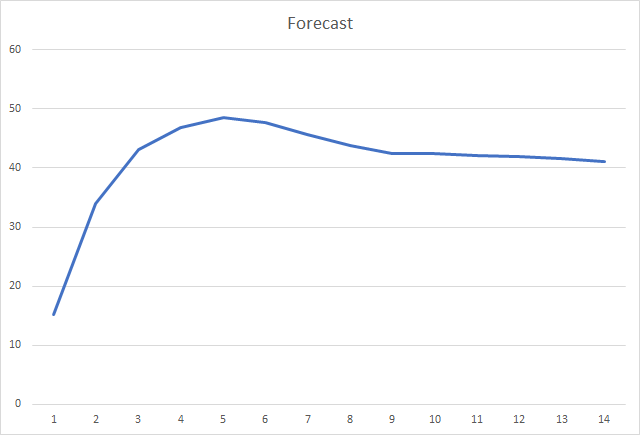
Und die wahrscheinlich wichtigste Metrik ist der Prozentsatz der korrekt definierten Fraktale. Nach der 5. Lernepoche erreichte der Wert 48,6 % und sank dann allmählich auf 41,1 %. Bei der Methode des stochastischen Gradientenabstiegs lag der Wert nach 90 Epochen nicht über 10 %.
Schlussfolgerungen
Der Artikel betrachtete adaptive Verfahren zur Optimierung von Parametern neuronaler Netze. Wir haben das Optimierungsverfahren Adam zu dem zuvor erstellten neuronalen Netzwerkmodell hinzugefügt. Beim Testen wurde das neuronale Netz mit der Adam-Methode trainiert. Die Ergebnisse übertreffen die Ergebnisse, die zuvor beim Training eines ähnlichen neuronalen Netzes mit der Methode des stochastischen Gradientenabstiegs erzielt wurden.
Die geleistete Arbeit zeigt unsere Fortschritte auf dem Weg zum Ziel.
Referenzen
- Neuronale Netze leicht gemacht
- Neuronale Netze leicht gemacht (Teil 2): Netzwerktraining und Tests
- Neuronale Netze leicht gemacht (Teil 3): Convolutional Neurale Netzwerke
- Neuronale Netze leicht gemacht (Teil 4): Rekurrente Netze
- Neuronale Netze leicht gemacht (Teil 5): Parallele Berechnungen mit OpenCL
- Neuronale Netze leicht gemacht (Teil 6): Experimentieren mit der Lernrate des neuronalen Netzwerks
- Adam: Eine stochastische Optimierungsmethode
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Fractal_OCL_Adam.mq5 | Expert Advisor | Ein EA mit dem klassifizierenden neuronalen Netz (3 Neuronen in der Ausgabeschicht), unter Verwendung von OpenCL und der Adam-Trainingsmethode |
| 2 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek mit Klassen zum Erstellen eines neuronalen Netzwerks |
| 3 | NeuroNet.cl | Bibliothek | Die Bibliothek mit dem Programm-Code für OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/8598
Wie kann man $1.000.000 durch algorithmischen Handel verdienen? Nutzen Sie die Dienste von MQL5.com!
Analysieren von Charts mit den Level von DeMark Sequential und Murray-Gann
Websockets für MetaTrader 5
Gradient Boosting beim transduktiven und aktiven maschinellen Lernen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.