
Neuronale Netze leicht gemacht (Teil 10): Multi-Head Attention
Inhaltsverzeichnis
- Einführung
- 1. Multi-Head Attention
- 2. Ein bisschen Mathe
- 3. Positionsbezogene Kodierung
- 4. Umsetzung
- 4.1. Verzicht auf die Verwendung des Key-Tensors
- 4.2. Die Klasse für Multi-Head Attention
- 4.3. Vorwärtskopplung
- 4.4. Rückwärtskopplung
- 4.5. Änderungen in den Basisklassen des neuronalen Netzwerks
- 5. Tests
- Schlussfolgerung
- Referenzen
- Die Programme dieses Artikels
Einführung
In dem Artikel "Neuronale Netze leicht gemacht (Teil 8): Attention-Mechanismen" haben wir den Selbstaufmerksamkeitsmechanismus und eine Variante seiner Implementierung besprochen. In der Praxis verwenden moderne neuronale Netzarchitekturen die Multi-Head-Attention (mehrfache Aufmerksamkeit). Dieser Mechanismus impliziert den Start mehrerer paralleler Selbstaufmerksamkeits-Threads mit unterschiedlichen Gewichten. Eine solche Lösung sollte die Verbindungen zwischen verschiedenen Elementen der Sequenz besser aufdecken. Lassen Sie uns versuchen, eine ähnliche Architektur zu implementieren und die Ergebnisse dieser beiden Methoden zu vergleichen.
1. Multi-Head Attention
Der Self-Attention-Algorithmus verwendet drei trainierte Gewichtsmatrizen (Wq, Wk und Wv). Die Matrixdaten werden verwendet, um 3 Entitäten zu erhalten: Query, Key und Value (Abfrage, Schlüssel und Wert). Die ersten beiden Entitäten definieren die paarweise Beziehung zwischen den Elementen der Sequenz, und die letzte Entität definiert den Kontext des analysierten Elements.
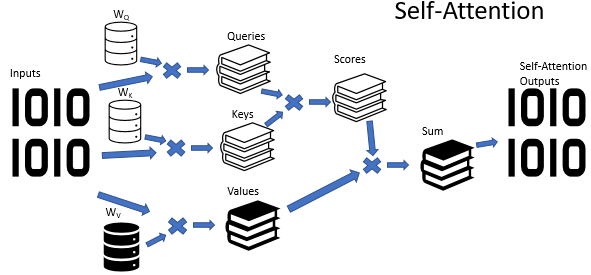
Es ist kein Geheimnis, dass die Situationen nicht immer eindeutig sind. Im Gegenteil, es scheint, dass eine Situation in den meisten Fällen aus verschiedenen Blickwinkeln interpretiert werden kann. So können die Schlussfolgerungen je nach gewähltem Blickwinkel völlig gegensätzlich sein. Es ist wichtig, in solchen Situationen alle möglichen Varianten zu berücksichtigen und erst nach sorgfältiger Analyse eine Entscheidung zu treffen. Zur Lösung solcher Probleme wurde der Multi-Head Attention Mechanismus vorgeschlagen. Jeder "Kopf" (head) hat seine eigene Meinung, während die Entscheidung durch eine ausgewogene Abstimmung getroffen wird.
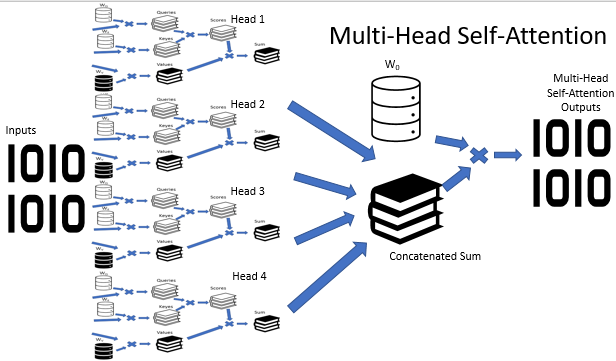
Die Multi-Head-Attention-Architektur impliziert die parallele Verwendung mehrerer Self-Attention-Threads mit unterschiedlicher Gewichtung, was eine vielseitige Analyse einer Situation imitiert. Die Ergebnisse der Operation der Self-Attention-Threads werden zu einem einzigen Tensor verkettet. Das Endergebnis des Algorithmus wird durch Multiplikation des Tensors mit der W0-Matrix gefunden, deren Parameter während des Trainingsprozesses des neuronalen Netzes ausgewählt werden. Die gesamte Architektur ersetzt den Self-Attention-Block im Encoder und Decoder der Transformer-Architektur.
2. Ein bisschen Mathe
Die folgende Formel kann eine mathematische Beschreibung des Self-Attention-Algorithmus liefern:
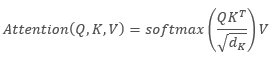 ,
,
wobei "Q" der Abfrage-Tensor, "K" der Key-Tensor, "V" der Value-Tensor und "d" die Dimension eines Key-Vektors ist.
Der Reihe nach
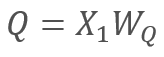 und
und 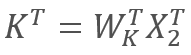 ,
,
wobei X1 und X2 die Elemente der Sequenz sind; Wq und Wk sind Matrizen der Gewichte der Abfragen (query) bzw. Schlüssel (key). Somit ergibt sich folgendes:
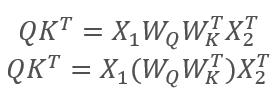
Durch die Assoziativitätseigenschaft der Matrizen können wir zunächst die Gewichtsmatrizen Wq und Wk multiplizieren. Wie Sie sehen, hängt das Produkt der Gewichtsmatrizen nicht von der Eingabesequenz ab und ist für alle Iterationen eines bestimmten Self-Attention-Blocks gleich (dies gilt natürlich bis zur nächsten Aktualisierung der Matrixparameter). Um also Rechenoperationen zu reduzieren, können wir eine Zwischenmatrix einmal für einen bestimmten Ansatz berechnen und sie dann für andere Berechnungen verwenden.
Wir können sogar noch weiter gehen und eine Matrix statt zwei trainieren. Kurioserweise ist es jedoch nicht immer möglich, die Anzahl der Operationen zu reduzieren, indem man nur eine Matrix trainiert. Zum Beispiel kann bei großen Dimensionen des Eingangssequenzvektors die Dimension durch die Matrizen Wq und Wk reduziert werden. In diesem Fall, wenn die Länge der Eingangsvektoren X1 und X2 100 Elemente beträgt, enthält die einzelne Matrix 10K Elemente (100*100). Wenn die Dimension durch die Matrizen Wq und Wk um den Faktor 10 reduziert wird, haben wir zwei Matrizen mit jeweils 1K Elementen (100*10). Daher sollten Sie eine Lösung sorgfältig auswählen und dabei die Netzwerkleistung und die Qualität der Betriebsergebnisse berücksichtigen.
3. Positionsbezogene Kodierung
Achten Sie beim Arbeiten mit Zeitreihen auch auf den Abstand zwischen den Elementen der Sequenz. Der Aufmerksamkeitsalgorithmus führt eine paarweise Überprüfung der Abhängigkeiten zwischen den Elementen der Sequenz durch, wobei für alle Elemente der Sequenz die gleichen Matrizen verwendet werden. Dabei hängt die gegenseitige Beeinflussung von Zeitreihenelementen stark vom zeitlichen Abstand zwischen ihnen ab. Daher ist eine weitere akute Frage die nach einem Positionskodierungsalgorithmus.
Ein idealer Positionskodierungsalgorithmus sollte mehrere Kriterien erfüllen:
- Jedes Element der Sequenz muss einen eindeutigen Code erhalten
- Der Schritt zwischen zwei aufeinanderfolgenden Elementen muss konstant sein
- Das Modell sollte leicht anzupassen und für Sequenzen beliebiger Länge zu verallgemeinern sein
- Das Modell muss deterministisch sein
Die Autoren der Transformer-Architektur schlugen vor, für die Kodierung einer Sequenz nicht ein separates Element zu verwenden, sondern einen ganzen Vektor mit einer Dimension, die der Dimension eines Elements der Eingangssequenz entspricht. Hier wird Sinus verwendet, um gerade Elemente des Vektors zu beschreiben, und Kosinus wird für ungerade Elemente verwendet. Bitte beachten Sie, dass das Sequenzelement kein bestimmtes Arrayelement ist, sondern ein Vektor, der den Zustand einer einzelnen Position beschreibt. In unserem Fall ist es ein Vektor, der eine Kerze beschreibt.
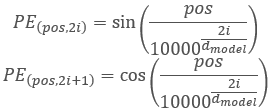 ,
,
wobei 'pos' die Position eines Sequenzelements ist, 'i' die Position des Elements im Vektor von einem Positionselement, 'd' die Dimension des Vektors von einem Sequenzelement ist.
Diese Lösung erlaubt es, die Positionen für jedes Element der Sequenz festzulegen, sowie den Abstand zwischen ihnen zu bestimmen.
Direkt in der Transformer-Architektur liegt die Positionskodierung außerhalb ihres Bereichs. Sie wird durchgeführt, indem der Tensor für die Positionskodierung zum Tensor der Eingangssequenz hinzugefügt wird, bevor die Daten in den ersten Encoder eingegeben werden. Es stellen sich zwei Fragen:
- Warum Addition anstelle von Vektorverkettung?
- Wie stark verzerrt die Addition von Tensoren die Originaldaten?
Die Verkettung würde die Datendimension und damit die Anzahl der Iterationen erhöhen. Dies würde die Gesamtleistung des Systems verringern. Der zweite Aspekt einer solchen Lösung ist, dass die Addition von Vektoren es erlaubt, nicht nur den Vektor eines einzelnen Sequenzelements zu positionieren, sondern jedes Element des Vektors. Dies ermöglicht hypothetisch die Analyse von Abhängigkeiten nicht nur zwischen den Elementen einer Sequenz, sondern auch zwischen deren einzelnen Komponenten.
Was die Datenverzerrung betrifft, so weiß das neuronale Netz nichts über die Bedeutung der einzelnen Elemente und wird auf Daten mit zusätzlicher Kodierung trainiert, d. h. es analysiert nicht jedes Element und seine Position separat. Wenn wir z.B. den gleichen Doji an der 2. und 20. Position sehen, dann würden wir wahrscheinlich das nächstgelegene bevorzugen. Für ein neuronales Netzwerk mit Positionskodierung werden dies völlig unterschiedliche Signale sein, die entsprechend der beim Training gesammelten Daten verarbeitet werden.
4. Umsetzung
Besprechen wir nun die Umsetzung der oben genannten Lösungen. In der bisherigen Implementierung des Self-Attention-Algorithmus war die Dimension für die Vektoren Queries und Keys ähnlich der Eingabesequenz. Daher habe ich den Algorithmus zunächst neu aufgebaut, um eine Matrix zu trainieren.
4.1. Verzicht auf die Verwendung des Key-Tensors
Die praktische Lösung ist ganz einfach. In der Methode CNeuronAttentionOCL::feedForward habe ich den Aufruf der ähnlichen Methode der Convolutional-Schicht von Key auskommentiert. Außerdem habe ich die Convolutional-Schicht von Key durch die vorherige neuronale Schicht im Kernelaufruf der Score-Berechnung ersetzt. Die Änderungen im Code der Methode sind unten hervorgehoben.
bool CNeuronAttentionOCL::feedForward(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=1; OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getOutputIndex()); OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons()); if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Normalize: %d",GetLastError()); return false; } if(!prevLayer.Output.BufferRead()) return false; } //--- if(CheckPointer(Querys)==POINTER_INVALID || !Querys.FeedForward(prevLayer)) return false; //if(CheckPointer(Keys)==POINTER_INVALID || !Keys.FeedForward(prevLayer)) // return false; if(CheckPointer(Values)==POINTER_INVALID || !Values.FeedForward(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_querys,Querys.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_keys,prevLayer.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_score,Scores.GetIndex()); OpenCL.SetArgument(def_k_AttentionScore,def_k_as_dimension,iWindow); if(!OpenCL.Execute(def_k_AttentionScore,1,global_work_offset,global_work_size)) { printf("Error of execution kernel AttentionScore: %d",GetLastError()); return false; } if(!Scores.BufferRead()) return false; } //--- Further code has no changes
Ähnliche Änderungen wurden in der Backpropagation-Methode CNeuronAttentionOCL::calcInputGradients implementiert. Achten Sie darauf, dass der erste Teil der Fehlergradienten früher in den Puffer der vorhergehenden Schicht geschrieben wird, dann beginnt der Prozess der Gradientenakkumulation früher. Die Änderungen sind im untenstehenden Code hervorgehoben.
bool CNeuronAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- if(!FF2.calcInputGradients(FF1)) return false; if(!FF1.calcInputGradients(AttentionOut)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,Gradient.GetIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.5); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- { uint global_work_offset[2]={0,0}; uint global_work_size[2]; global_work_size[0]=iUnits; global_work_size[1]=iWindow; OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_gradient,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys,prevLayer.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys_g,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys,Querys.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys_g,Querys.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values,Values.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values_g,Values.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_scores,Scores.GetIndex()); if(!OpenCL.Execute(def_k_AttentionGradients,2,global_work_offset,global_work_size)) { printf("Error of execution kernel AttentionGradients: %d",GetLastError()); return false; } double temp[]; if(Querys.getGradient(temp)<=0) return false; } //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,1.0); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- if(!Querys.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,1.0); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } ////--- // if(!Keys.calcInputGradients(prevLayer)) // return false; ////--- // { // uint global_work_offset[1]={0}; // uint global_work_size[1]; // global_work_size[0]=iUnits; // OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); // OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); // OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); // OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); // OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,1.0); // if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) // { // printf("Error of execution kernel MatrixSum: %d",GetLastError()); // return false; // } // double temp[]; // if(AttentionOut.getGradient(temp)<=0) // return false; // } //--- Further code has no changes
Ich habe auch die Aktualisierung der Gewichte der Convolutional-Schicht Key in der Methode CNeuronAttentionOCL::updateInputWeights auskommentiert, ebenso wie die Deklaration dieses Objekts im Allgemeinen.
Der vollständige Code aller Methoden und Funktionen steht im Anhang zur Verfügung.
4.2. Die Klasse für Multi-Head Attention
Die Konstruktion der Multi-Head-Attention ist in einer eigenen Klasse CNeuronMHAttentionOCL implementiert, die auf der Elternklasse CNeuronAttentionOCL basiert. Wir deklarieren im Block protected zusätzliche Instanzen der Convolutional-Schichten Querys und Values, entsprechend der Anzahl der Aufmerksamkeitsköpfe. Im Beispiel werden vier heads verwendet. Wir fügen außerdem den Puffer Scores und die voll verbundene Schicht AttentionOut für jeden Attention-Head hinzu. Zusätzlich benötigen wir eine voll verbundene Schicht, um die Daten der Aufmerksamkeitsköpfe zu verketten - AttentionConcatenate - und eine Convolutional-Schicht Weights0, die es erlauben würde, die gewichtete Abstimmung zu imitieren und die Dimension des Ergebnistensors zu reduzieren.
class CNeuronMHAttentionOCL : public CNeuronAttentionOCL { protected: CNeuronConvOCL *Querys2; ///< Convolution layer for Querys Head 2 CNeuronConvOCL *Querys3; ///< Convolution layer for Querys Head 3 CNeuronConvOCL *Querys4; ///< Convolution layer for Querys Head 4 CNeuronConvOCL *Values2; ///< Convolution layer for Values Head 2 CNeuronConvOCL *Values3; ///< Convolution layer for Values Head 3 CNeuronConvOCL *Values4; ///< Convolution layer for Values Head 4 CBufferDouble *Scores2; ///< Buffer for Scores matrix Head 2 CBufferDouble *Scores3; ///< Buffer for Scores matrix Head 3 CBufferDouble *Scores4; ///< Buffer for Scores matrix Head 4 CNeuronBaseOCL *AttentionOut2; ///< Layer of Self-Attention Out CNeuronBaseOCL *AttentionOut3; ///< Layer of Self-Attention Out CNeuronBaseOCL *AttentionOut4; ///< Layer of Self-Attention Out CNeuronBaseOCL *AttentionConcatenate;///< Layer of Concatenate Self-Attention Out CNeuronConvOCL *Weights0; ///< Convolution layer for Weights0 //--- virtual bool feedForward(CNeuronBaseOCL *prevLayer); ///< Feed Forward method.@param prevLayer Pointer to previous layer. virtual bool updateInputWeights(CNeuronBaseOCL *prevLayer); ///< Method for updating weights.@param prevLayer Pointer to previous layer. /// Method to transfer gradients inside Head Self-Attention virtual bool calcHeadGradient(CNeuronConvOCL *query, CNeuronConvOCL *value, CBufferDouble *score, CNeuronBaseOCL *attention, CNeuronBaseOCL *prevLayer); public: /** Constructor */CNeuronMHAttentionOCL(void){}; /** Destructor */~CNeuronMHAttentionOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type); ///< Method of initialization class.@param[in] numOutputs Number of connections to next layer.@param[in] myIndex Index of neuron in layer.@param[in] open_cl Pointer to #COpenCLMy object.@param[in] window Size of in/out window and step.@param[in] units_countNumber of neurons.@param[in] optimization_type Optimization type (#ENUM_OPTIMIZATION)@return Boolean result of operations. virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); ///< Method to transfer gradients to previous layer @param[in] prevLayer Pointer to previous layer. //--- virtual int Type(void) const { return defNeuronMHAttentionOCL; }///< Identificator of class.@return Type of class //--- methods for working with files virtual bool Save(int const file_handle); ///< Save method @param[in] file_handle handle of file @return logical result of operation virtual bool Load(int const file_handle); ///< Load method @param[in] file_handle handle of file @return logical result of operation };
Die Klassenmethoden schreiben die virtuellen Methoden der Elternklasse um. Wahrscheinlich kann sie bereits jetzt standardmäßig aufgerufen werden. Die einzige Ausnahme ist die Methode calcHeadGradient, die Iterationen der Fehlergradientenausbreitung beschreibt, die für jeden head wiederholt werden.
Lassen wir den Klassenkonstruktor leer und verlagern die Initialisierung von neuen Objekten in die Initialisierungsmethode Init. Wir implementieren im Destruktor der Klasse das Löschen von Objektinstanzen, die von dieser Klasse erzeugt und im "protected"-Block deklariert wurden.
CNeuronMHAttentionOCL::~CNeuronMHAttentionOCL(void) { if(CheckPointer(Querys2)!=POINTER_INVALID) delete Querys2; if(CheckPointer(Querys3)!=POINTER_INVALID) delete Querys3; if(CheckPointer(Querys4)!=POINTER_INVALID) delete Querys4; if(CheckPointer(Values2)!=POINTER_INVALID) delete Values2; if(CheckPointer(Values3)!=POINTER_INVALID) delete Values3; if(CheckPointer(Values4)!=POINTER_INVALID) delete Values4; if(CheckPointer(Scores2)!=POINTER_INVALID) delete Scores2; if(CheckPointer(Scores3)!=POINTER_INVALID) delete Scores3; if(CheckPointer(Scores4)!=POINTER_INVALID) delete Scores4; if(CheckPointer(Weights0)!=POINTER_INVALID) delete Weights0; if(CheckPointer(AttentionOut2)!=POINTER_INVALID) delete AttentionOut2; if(CheckPointer(AttentionOut3)!=POINTER_INVALID) delete AttentionOut3; if(CheckPointer(AttentionOut4)!=POINTER_INVALID) delete AttentionOut4; if(CheckPointer(AttentionConcatenate)!=POINTER_INVALID) delete AttentionConcatenate; }
Die Methode Init ist analog zur Methode der Elternklasse aufgebaut. Am Anfang der Methode rufen Sie die entsprechende Methode der Elternklasse auf.
bool CNeuronMHAttentionOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window,uint units_count,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronAttentionOCL::Init(numOutputs,myIndex,open_cl,window,units_count,optimization_type)) return false;
Dann initialisieren wir Instanzen der Instanzen cer Convolutional-Schicht Querys. Bitte beachten Sie, dass wir die Objekte ab dem zweiten Kopf initialisieren, da die Instanzen aller Objekte für den ersten Kopf in der Elternklasse initialisiert werden.
if(CheckPointer(Querys2)==POINTER_INVALID) { Querys2=new CNeuronConvOCL(); if(CheckPointer(Querys2)==POINTER_INVALID) return false; if(!Querys2.Init(0,6,open_cl,window,window,window,units_count,optimization_type)) return false; Querys2.SetActivationFunction(None); } //--- if(CheckPointer(Querys3)==POINTER_INVALID) { Querys3=new CNeuronConvOCL(); if(CheckPointer(Querys3)==POINTER_INVALID) return false; if(!Querys3.Init(0,7,open_cl,window,window,window,units_count,optimization_type)) return false; Querys3.SetActivationFunction(None); } //--- if(CheckPointer(Querys4)==POINTER_INVALID) { Querys4=new CNeuronConvOCL(); if(CheckPointer(Querys4)==POINTER_INVALID) return false; if(!Querys4.Init(0,8,open_cl,window,window,window,units_count,optimization_type)) return false; Querys4.SetActivationFunction(None); }
Wir initialisieren auf ähnliche Weise die Klasseninstanzen für Values und Scores für AttentionOut.
if(CheckPointer(Values2)==POINTER_INVALID) { Values2=new CNeuronConvOCL(); if(CheckPointer(Values2)==POINTER_INVALID) return false; if(!Values2.Init(0,9,open_cl,window,window,window,units_count,optimization_type)) return false; Values2.SetActivationFunction(None); } //--- if(CheckPointer(Values3)==POINTER_INVALID) { Values3=new CNeuronConvOCL(); if(CheckPointer(Values3)==POINTER_INVALID) return false; if(!Values3.Init(0,10,open_cl,window,window,window,units_count,optimization_type)) return false; Values3.SetActivationFunction(None); } //--- if(CheckPointer(Values4)==POINTER_INVALID) { Values4=new CNeuronConvOCL(); if(CheckPointer(Values4)==POINTER_INVALID) return false; if(!Values4.Init(0,11,open_cl,window,window,window,units_count,optimization_type)) return false; Values4.SetActivationFunction(None); } //--- if(CheckPointer(Scores2)==POINTER_INVALID) { Scores2=new CBufferDouble(); if(CheckPointer(Scores2)==POINTER_INVALID) return false; } if(!Scores2.BufferInit(units_count*units_count,0.0)) return false; if(!Scores2.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(Scores3)==POINTER_INVALID) { Scores3=new CBufferDouble(); if(CheckPointer(Scores3)==POINTER_INVALID) return false; } if(!Scores3.BufferInit(units_count*units_count,0.0)) return false; if(!Scores3.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(Scores4)==POINTER_INVALID) { Scores4=new CBufferDouble(); if(CheckPointer(Scores4)==POINTER_INVALID) return false; } if(!Scores4.BufferInit(units_count*units_count,0.0)) return false; if(!Scores4.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(AttentionOut2)==POINTER_INVALID) { AttentionOut2=new CNeuronBaseOCL(); if(CheckPointer(AttentionOut2)==POINTER_INVALID) return false; if(!AttentionOut2.Init(0,12,open_cl,window*units_count,optimization_type)) return false; AttentionOut2.SetActivationFunction(None); } //--- if(CheckPointer(AttentionOut3)==POINTER_INVALID) { AttentionOut3=new CNeuronBaseOCL(); if(CheckPointer(AttentionOut3)==POINTER_INVALID) return false; if(!AttentionOut3.Init(0,13,open_cl,window*units_count,optimization_type)) return false; AttentionOut3.SetActivationFunction(None); } //--- if(CheckPointer(AttentionOut4)==POINTER_INVALID) { AttentionOut4=new CNeuronBaseOCL(); if(CheckPointer(AttentionOut4)==POINTER_INVALID) return false; if(!AttentionOut4.Init(0,14,open_cl,window*units_count,optimization_type)) return false; AttentionOut4.SetActivationFunction(None); }
Initialisierung der Schicht für die Datenverkettung AttentionConcatenate. Dies ist eine voll verkettete Schicht, die nur für die Datenübertragung verwendet wird. Daher ist die Anzahl der ausgehenden Verbindungen gleich "0". Die Größe der Schicht muss ausreichen, um die Ausgangsdaten aller vier Attention Heads zu speichern. Wir geben die Anzahl der Neuronen in der Schicht gleich dem Produkt aus vier Fenstern der Ausgabeschicht eines Kopfes durch die Anzahl der Elemente in der Folge an.
if(CheckPointer(AttentionConcatenate)==POINTER_INVALID) { AttentionConcatenate=new CNeuronBaseOCL(); if(CheckPointer(AttentionConcatenate)==POINTER_INVALID) return false; if(!AttentionConcatenate.Init(0,15,open_cl,4*window*units_count,optimization_type)) return false; AttentionConcatenate.SetActivationFunction(None); }
Am Ende der Methode initialisieren wir die Convolutional-Schicht Weights0. Der Zweck der Schicht ist die Auswahl einer optimalen Strategie auf der Grundlage der von allen Aufmerksamkeitsköpfen empfangenen Daten. Die Dimension der Ausgabedaten wird auf die Dimension der Originaldaten reduziert, die in den Multi-Head Attention-Block eingegeben werden. Wir geben bei der Initialisierung einer Schicht die Größe des Eingangsfensters und des Schritts gleich den vier Datenfenstern der vorherigen Schicht an, und die Größe des Ausgangsfensters gleich dem Datenfenster der vorherigen Schicht.
if(CheckPointer(Weights0)==POINTER_INVALID) { Weights0=new CNeuronConvOCL(); if(CheckPointer(Weights0)==POINTER_INVALID) return false; if(!Weights0.Init(0,16,open_cl,4*window,4*window,window,units_count,optimization_type)) return false; Weights0.SetActivationFunction(None); } //--- return true; }
Der vollständige Code aller Methoden und Funktionen steht im Anhang zur Verfügung.
4.3. Vorwärtskopplung
Der Feed-Forward-Algorithmus wurde hauptsächlich unter Verwendung des zuvor erstellten OpenCL-Programms konstruiert. Die einzige Ausnahme ist die Erstellung eines Kerns, der die Daten von 4 Tensoren von jedem Aufmerksamkeitskopf zu einem einzigen Tensor verkettet. Der Kernel erhält als Parameter: Zeiger auf Datenpuffer und die jeweiligen Fenstergrößen der Puffer, sowie einen Zeiger auf den Ergebnistensor. Die detaillierten Fenstergrößen nach Eingangsdatenpuffern wurden hinzugefügt, um die Verkettung von Tensoren unterschiedlicher Größe mit verschiedenen Fenstergrößen zu ermöglichen.
__kernel void ConcatenateBuffers(__global double *input1, int window1, __global double *input2, int window2, __global double *input3, int window3, __global double *input4, int window4, __global double *output)
Im Hauptteil des Kernels werden die Daten aus den Eingangsarrays elementweise in das Ausgangsarray kopiert. Der Algorithmus ist recht einfach, so dass ich denke, dass der beigefügte Code leicht zu verstehen ist.
In der Klasse CNeuronMHAttentionOCL ist das Feed Forward in der Methode feedForward implementiert. Zu Beginn der Methode wird die Gültigkeit der empfangenen Verknüpfung zur vorhergehenden Schicht überprüft und die Eingangsdaten normalisiert.
bool CNeuronMHAttentionOCL::feedForward(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=1; OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getOutputIndex()); OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons()); if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Normalize: %d",GetLastError()); return false; } if(!prevLayer.Output.BufferRead()) return false; }
Then call appropriate convolutional layer methods and recalculate the values of the Querys and Values tensors for all Attention-Heads.
if(CheckPointer(Querys)==POINTER_INVALID || !Querys.FeedForward(prevLayer)) return false; if(CheckPointer(Querys2)==POINTER_INVALID || !Querys2.FeedForward(prevLayer)) return false; if(CheckPointer(Querys3)==POINTER_INVALID || !Querys3.FeedForward(prevLayer)) return false; if(CheckPointer(Querys4)==POINTER_INVALID || !Querys4.FeedForward(prevLayer)) return false; if(CheckPointer(Values)==POINTER_INVALID || !Values.FeedForward(prevLayer)) return false; if(CheckPointer(Values2)==POINTER_INVALID || !Values2.FeedForward(prevLayer)) return false; if(CheckPointer(Values3)==POINTER_INVALID || !Values3.FeedForward(prevLayer)) return false; if(CheckPointer(Values4)==POINTER_INVALID || !Values4.FeedForward(prevLayer)) return false;
Anschließend berechnen wir die attention für jeden head neu. Der Algorithmus ist ähnlich dem der Elternklasse, der im Artikel 8 beschrieben wird. Im Folgenden finden Sie den Code für einen Attention-Head. Bei den anderen ist der Code identisch, es werden nur die Zeiger auf die Objekte des entsprechenden Attention-Heads geändert.
//--- Scores Head 1 { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_querys,Querys.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_keys,prevLayer.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_score,Scores.GetIndex()); OpenCL.SetArgument(def_k_AttentionScore,def_k_as_dimension,iWindow); if(!OpenCL.Execute(def_k_AttentionScore,1,global_work_offset,global_work_size)) { printf("Error of execution kernel AttentionScore: %d",GetLastError()); return false; } if(!Scores.BufferRead()) return false; } //--- { uint global_work_offset[2]={0,0}; uint global_work_size[2]; global_work_size[0]=iUnits; global_work_size[1]=iWindow; OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_scores,Scores.GetIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_inputs,prevLayer.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_values,Values.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_out,AttentionOut.getOutputIndex()); if(!OpenCL.Execute(def_k_AttentionOut,2,global_work_offset,global_work_size)) { printf("Error of execution kernel Attention Out: %d",GetLastError()); return false; } double temp[]; if(!AttentionOut.getOutputVal(temp)) return false; }
Nachdem wir die Attention für jeden head berechnet haben, verketten wir die Ergebnisse mit dem zuvor geschriebenen Kernel zu einem einzigen Tensor.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_ConcatenateMatrix,def_k_conc_input1,AttentionOut.getOutputIndex());
OpenCL.SetArgument(def_k_ConcatenateMatrix,def_k_conc_window1,iWindow);
OpenCL.SetArgumentBuffer(def_k_ConcatenateMatrix,def_k_conc_input2,AttentionOut2.getOutputIndex());
OpenCL.SetArgument(def_k_ConcatenateMatrix,def_k_conc_window2,iWindow);
OpenCL.SetArgumentBuffer(def_k_ConcatenateMatrix,def_k_conc_input3,AttentionOut3.getOutputIndex());
OpenCL.SetArgument(def_k_ConcatenateMatrix,def_k_conc_window3,iWindow);
OpenCL.SetArgumentBuffer(def_k_ConcatenateMatrix,def_k_conc_input4,AttentionOut4.getOutputIndex());
OpenCL.SetArgument(def_k_ConcatenateMatrix,def_k_conc_window4,iWindow);
OpenCL.SetArgumentBuffer(def_k_ConcatenateMatrix,def_k_conc_out,AttentionConcatenate.getOutputIndex());
if(!OpenCL.Execute(def_k_ConcatenateMatrix,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Concatenate Matrix: %d",GetLastError());
return false;
}
double temp[];
if(!AttentionConcatenate.getOutputVal(temp))
return false;
}
Wir führen das Ergebnis der Tensorkonkatenation durch die Convolutional-Schicht Weights0, um die Größe des Arbeitsergebnisses der Multi-Head Attention zu reduzieren.
if(CheckPointer(Weights0)==POINTER_INVALID || !Weights0.FeedForward(AttentionConcatenate)) return false;
Dann wird das erhaltene Ergebnis mit den Daten der vorherigen Schicht gemittelt und das Ergebnis normalisiert.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,Weights0.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,Weights0.getOutputIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.5);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
if(!Output.BufferRead())
return false;
}
//---
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=1;
OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,Weights0.getOutputIndex());
OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,Weights0.Neurons());
if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Normalize: %d",GetLastError());
return false;
}
double temp[];
if(!Weights0.getOutputVal(temp))
return false;
}
Dann übergeben wir, ähnlich wie bei der übergeordneten Klasse, das Ergebnis durch den FeedForward-Block.
if(!FF1.FeedForward(Weights0)) return false; if(!FF2.FeedForward(FF1)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,Weights0.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,FF2.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,Output.GetIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.5); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } if(!Output.BufferRead()) return false; } //--- return true; }
Der vollständige Code aller Methoden und Funktionen steht im Anhang zur Verfügung.
4.4. Rückwärtskopplung
Der Prozess der Rückwärtskopplung enthält zwei Teilprozesse: die Weitergabe des Fehlergradienten eine Ebene tiefer und die Aktualisierung der Gewichtsmatrizen. Die Gewichte werden mit den zuvor erstellten OpenCL-Kerneln aktualisiert, während wir für die back propagation einige Änderungen vornehmen müssen.
Zunächst einmal müssen wir den Fehlergradienten über die Attention-Heads propagieren. Um diese Funktion auszuführen, erstellen wir den Kernel DeconcatenateBuffers. Wir übergeben dem Kernel Zeiger auf die Puffer für die Gradientenpropagierung, Fenstergrößen für jeden Puffer und einen Zeiger auf den Puffer der Gradienten, die von der vorherigen Iteration empfangen wurden, ein.
__kernel void DeconcatenateBuffers(__global double *output1, int window1, __global double *output2, int window2, __global double *output3, int window3, __global double *output4, int window4, __global double *inputs)
Am Kernelanfang definieren wir die Ordnungszahl des Sequenzelements und die erste Positionsverschiebung für den ursprünglichen Tensor und den ersten Tensor der Attention-Heads.
{
int n=get_global_id(0);
int shift=n*(window1+window2+window3+window4);
int shift_out=n*window1;
Anschließend verschließen wir in einer Schleife den Vektor der Fehlergradienten für den ersten Aufmerksamkeitskopf.
for(int i=0;i<window1;i++) output1[shift_out+i]=inputs[shift+i];
Wenn der Zyklus endet, passen wir die Position des Zeigers im ursprünglichen Tensor an und ermitteln die erste Positionsverschiebung im Puffer des zweiten Attention-Heads. Dann führen wir einen Datenkopierzyklus für den zweiten Aufmerksamkeitskopf durch. Die Vorgänge werden für jeden Attention-Head wiederholt.
//--- Head 2 shift+=window1; shift_out=n*window2; for(int i=0;i<window2;i++) output2[shift_out+i]=inputs[shift+i]; //--- Head 3 shift+=window2; shift_out=n*window3; for(int i=0;i<window3;i++) output3[shift_out+i]=inputs[shift+i]; //--- Head 4 shift+=window3; shift_out=n*window4; for(int i=0;i<window4;i++) output4[shift_out+i]=inputs[shift+i]; }
Später, nach der Berechnung der Fehlergradienten für jeden Attention-Head, ist es notwendig, die Gradienten in einem einzigen Datenpuffer auf der vorherigen Schicht des neuronalen Netzes zu kombinieren. Technisch gesehen könnten wir den Kernel SumMatrix verwenden, indem wir die Gradienten aller Attention-Heads paarweise addieren. Aber diese Lösung ist in Bezug auf die Leistung nicht optimal. Erstellen wir also einen anderen Kernel - Sum5Matrix. In den Kernelparametern übergeben wir Zeiger auf die Datenpuffer (5 Eingänge und 1 Ausgang), die Größe des Datenfensters und einen Multiplikator (den Summenkorrekturfaktor). Vielleicht muss ich noch erklären, warum es 5 Eingangspuffer mit 4 Attention-Heads gibt. Der fünfte Puffer wird zum Durchreichen des Fehlergradienten verwendet, um das Risiko des schwindenden Gradienten zu minimieren.
__kernel void Sum5Matrix(__global double *matrix1, ///<[in] First matrix __global double *matrix2, ///<[in] Second matrix __global double *matrix3, ///<[in] Third matrix __global double *matrix4, ///<[in] Fourth matrix __global double *matrix5, ///<[in] Fifth matrix __global double *matrix_out, ///<[out] Output matrix int dimension, ///< Dimension of matrix double multiplyer ///< Multiplyer for output )
Wir definieren im Hauptteil des Kernels die Verschiebung des ersten Elements der verarbeiteten Vektoren in den Sequenzen und starten den Zyklus zur Summierung der Gradienten. Die Multiplikation der Summe der Fehlergradienten mit 0,2 ermöglicht es, die Werte des übertragenen Fehlers über die vorherige Schicht des neuronalen Netzes zu mitteln. Der Multiplikator wiederum ist absichtlich in Parametern implementiert, um die Auswahl seines Wertes bei der Abstimmung des Algorithmus zu ermöglichen.
{
const int i=get_global_id(0)*dimension;
for(int k=0;k<dimension;k++)
matrix_out[i+k]=(matrix1[i+k]+matrix2[i+k]+matrix3[i+k]+matrix4[i+k]+matrix5[i+k])*multiplyer;
}
In der Klasse CNeuronMHAttentionOCL erhält jeder Unterprozess seine Methode. Die Fehlergradienten-Propagation wird von der Methode calcInputGradients durchgeführt. Die Methode erhält als Parameter einen Zeiger auf das Objekt der vorherigen Schicht des neuronalen Netzes. Prüfung der Gültigkeit des Zeigers zu Beginn der Methode.
bool CNeuronMHAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
Dann berechnen wir die Fehlergradienten durch den FeedForward-Block, indem wir geeignete Methoden der Convolutional-Schichten FF1 und FF2 verwenden.
if(!FF2.calcInputGradients(FF1)) return false; if(!FF1.calcInputGradients(Weights0)) return false;
Führen wir den Fehlergradienten um den FeedForward-Block herum und speichern den durchschnittlichen Fehlerwert im Gradientenpuffer der Schicht Weights0.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,Weights0.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,Gradient.GetIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,Weights0.getGradientIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.5);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
double temp[];
if(Weights0.getGradient(temp)<=0)
return false;
}
Jetzt ist es Zeit für die Fehlerpropagation durch Attention-Heads. Wir müssen die Größe des Gradiententensors auf die Größe des verketteten Aufmerksamkeitspuffers erhöhen. Um dies zu tun, übergeben wir den Fehlergradienten durch die Convolutional-Schicht Weights0, indem wir die entsprechende Methode der Convolutional-Schicht aufrufen.
if(!Weights0.calcInputGradients(AttentionConcatenate)) return false;
Nachdem wir einen ausreichend großen Tensor von Fehlergradienten erhalten haben, können wir den Fehler auf die Puffer der Attention-Heads verteilen. Verwenden wir nun den oben erstellten Dekonkatenationskern.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_DeconcatenateMatrix,def_k_dconc_output1,AttentionOut.getGradientIndex());
OpenCL.SetArgument(def_k_DeconcatenateMatrix,def_k_dconc_window1,iWindow);
OpenCL.SetArgumentBuffer(def_k_DeconcatenateMatrix,def_k_dconc_output2,AttentionOut2.getGradientIndex());
OpenCL.SetArgument(def_k_DeconcatenateMatrix,def_k_dconc_window2,iWindow);
OpenCL.SetArgumentBuffer(def_k_DeconcatenateMatrix,def_k_dconc_output3,AttentionOut3.getGradientIndex());
OpenCL.SetArgument(def_k_DeconcatenateMatrix,def_k_dconc_window3,iWindow);
OpenCL.SetArgumentBuffer(def_k_DeconcatenateMatrix,def_k_dconc_output4,AttentionOut4.getGradientIndex());
OpenCL.SetArgument(def_k_DeconcatenateMatrix,def_k_dconc_window4,iWindow);
OpenCL.SetArgumentBuffer(def_k_DeconcatenateMatrix,def_k_dconc_inputs,AttentionConcatenate.getGradientIndex());
if(!OpenCL.Execute(def_k_DeconcatenateMatrix,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Deconcatenate Matrix: %d",GetLastError());
return false;
}
double temp[];
if(AttentionConcatenate.getGradient(temp)<=0)
return false;
}
Die Berechnung des Fehlergradienten innerhalb eines Attention-Head ist in einer eigenen Methode calcHeadGradient implementiert. Hier rufen wir diese Methode für jeden Aufmerksamkeitsfaden auf.
if(!calcHeadGradient(Querys,Values,Scores,AttentionOut,prevLayer)) return false; if(!calcHeadGradient(Querys2,Values2,Scores2,AttentionOut2,prevLayer)) return false; if(!calcHeadGradient(Querys3,Values3,Scores3,AttentionOut3,prevLayer)) return false; if(!calcHeadGradient(Querys4,Values4,Scores4,AttentionOut4,prevLayer)) return false;
Am Ende der Methode summieren wir die Fehlergradienten aller Attention-Heads und übergeben das Ergebnis an die vorherige Schicht des neuronalen Netzes.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix1,AttentionOut.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix2,AttentionOut2.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix3,AttentionOut3.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix4,AttentionOut4.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix5,Weights0.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix_out,prevLayer.getGradientIndex());
OpenCL.SetArgument(def_k_Matrix5Sum,def_k_sum5_dimension,iWindow);
OpenCL.SetArgument(def_k_Matrix5Sum,def_k_sum5_multiplyer,0.2);
if(!OpenCL.Execute(def_k_Matrix5Sum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Matrix5Sum: %d",GetLastError());
return false;
}
double temp[];
if(prevLayer.getGradient(temp)<=0)
return false;
}
//---
return true;
}
Werfen wir einen Blick auf die Methode calcHeadGradient. Die Methode erhält als Parameter Zeiger auf innere neuronale Schichten 'query', 'value', 'score', 'attention', bezogen auf den besprochenen Attention-Head, und einen Zeiger auf die vorherige neuronale Schicht.
bool CNeuronMHAttentionOCL::calcHeadGradient(CNeuronConvOCL *query,CNeuronConvOCL *value,CBufferDouble *score,CNeuronBaseOCL *attention,CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
Der Methodenkörper beginnt mit der Überprüfung der Gültigkeit des Zeigers auf die vorherige neuronale Schicht. Um den Fehlergradienten über innere Schichten zu verteilen, rufen wir den Kernel AttentionInsideGradients auf, der im Artikel 8 besprochen wurde.
{
uint global_work_offset[2]={0,0};
uint global_work_size[2];
global_work_size[0]=iUnits;
global_work_size[1]=iWindow;
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_gradient,attention.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys,prevLayer.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys_g,prevLayer.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys,query.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys_g,query.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values,value.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values_g,value.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_scores,score.GetIndex());
if(!OpenCL.Execute(def_k_AttentionGradients,2,global_work_offset,global_work_size))
{
printf("Error of execution kernel AttentionGradients: %d",GetLastError());
return false;
}
double temp[];
if(query.getGradient(temp)<=0)
return false;
}
Dieses Beispiel zeigt das Training einer Matrix, ohne Unterteilung in 'query' und 'key'. Daher werden die Puffer der vorherigen Schicht anstelle der Puffer der Key-Schicht angegeben. Um den Fehlergradienten, der auf der vorherigen Schicht gewonnen wurde, bei der Berechnung auf anderen inneren Schichten nicht zu überschreiben, übertragen wir die Daten in den AttentionOut-Tensor des aktuellen Attention-Head. Ich habe keinen separaten Tensor für das Kopieren von Daten zwischen Puffern vorgesehen. Diese Operation wurde mit dem Additionskern SumMatrix für zwei Matrizen durchgeführt. Da wir nur eine Matrix haben, geben wir in den Zeigern der beiden Tensoren die vorherige Schicht an. Um die Duplizierung von Werten zu vermeiden, verwenden wir einen Multiplikator von 0,5.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,prevLayer.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,attention.getGradientIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.5);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
double temp[];
if(attention.getGradient(temp)<=0)
return false;
}
Berechnen wir als Nächstes den Fehlergradienten, der durch die Abfrageebene verläuft, indem wir die entsprechende Methode der 'query'-Schicht aufrufen. Das Ergebnis wird mit dem bei der vorherigen Iteration erhaltenen Gradienten aufsummiert. Bei diesem Schritt wird der Multiplikator gleich 1 verwendet. Der erhöhte Gradient wird im nächsten Schritt gemittelt.
if(!query.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,attention.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,attention.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,1.0); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(attention.getGradient(temp)<=0) return false; }
Am Ende der Methode berechnen wir wieder den Gradienten über die 'value'-Schicht und summieren ihn mit den zuvor erhaltenen Gradienten. Der Gradient über den gesamten Attention-Head kann mit dem Multiplikator von 0,33 gemittelt werden.
if(!value.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,attention.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,attention.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow+1); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.33); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(prevLayer.getGradient(temp)<=0) return false; } //--- return true; }
Nach der Neuberechnung der Fehlergradienten aktualisieren wir die Gewichte aller inneren Schichten. Wir schreiben in die Methode updateInputWeights einen sequentiellen Aufruf der relevanten Methoden aller inneren neuronalen Schichten.
bool CNeuronMHAttentionOCL::updateInputWeights(CNeuronBaseOCL *prevLayer) { if(!Querys.UpdateInputWeights(prevLayer) || !Querys2.UpdateInputWeights(prevLayer) || !Querys3.UpdateInputWeights(prevLayer) || !Querys4.UpdateInputWeights(prevLayer)) return false; //--- if(!Values.UpdateInputWeights(prevLayer) || !Values2.UpdateInputWeights(prevLayer) || !Values3.UpdateInputWeights(prevLayer) || !Values4.UpdateInputWeights(prevLayer)) return false; if(!Weights0.UpdateInputWeights(AttentionConcatenate)) return false; if(!FF1.UpdateInputWeights(Weights0)) return false; if(!FF2.UpdateInputWeights(FF1)) return false; //--- return true; }
Der vollständige Code aller Methoden und Funktionen steht im Anhang zur Verfügung.
4.5. Änderungen in den Basisklassen des neuronalen Netzwerks
Nach der Implementierung des Multi-Head Attention-Algorithmus müssen wir den Positional Encoder implementieren. Dieser Prozess ist in der Methode CNet::feedForward der Klasse "Neuronales Netzwerk" enthalten. Für die Implementierung wurden der Methode zwei Parameter hinzugefügt: window und tem. Das erste gibt die Größe des Datenfensters an und das zweite ist dafür zuständig, dass die Funktion aktiviert/deaktiviert werden muss.
bool CNet::feedForward(CArrayDouble *inputVals,int window=1,bool tem=true)
Im Baustein zur Einspeisung der Eingangsdaten in das Netzwerk wird der eigentliche Prozess implementiert. Deklarieren wir zunächst 2 interne Variablen, pos (Position in der Sequenz) und dim (die Ordnungszahl des Elements innerhalb des Datenfensters). Wir ermitteln die Ordnungszahl des Elements innerhalb des Datenfensters und verwenden dazu den Rest, der sich aus der Division der Ordnungszahl des Elements im Quelldatentensor durch die Fenstergröße ergibt. Die Position in der Folge wird durch das ganzzahlige Ergebnis der Division der Element-Ordnungszahl im Quelldatentensor durch die Fenstergröße bestimmt. Fügen wir dann beim Speichern der Ausgangsdaten in den Tensor des eingegebenen neuronalen Netzes das Ergebnis der Berechnung mit den in Abschnitt 3 dieses Artikels angegebenen Formeln hinzu.
CNeuronBaseOCL *neuron_ocl=current.At(0); double array[]; int total_data=inputVals.Total(); if(ArrayResize(array,total_data)<0) return false; for(int d=0;d<total_data;d++) { int pos=d; int dim=0; if(window>1) { dim=d%window; pos=(d-dim)/window; } array[d]=inputVals.At(d)+(tem ? (dim%2==0 ? sin(pos/pow(10000,(2*dim+1)/(window+1))) : cos(pos/pow(10000,(2*dim+1)/(window+1)))) : 0); } if(!opencl.BufferWrite(neuron_ocl.getOutputIndex(),array,0,0,total_data)) return false;
Jetzt ist es notwendig, einige zusätzliche Änderungen für die normale Funktion des neuronalen Netzwerks vorzunehmen. Hinzufügen der Konstanten für die Arbeit mit neuen Kerneln zum Definitionsblock.
#define def_k_ConcatenateMatrix 17 ///< Index of the Multi Head Attention Neuron Concatenate Output kernel (#ConcatenateBuffers) #define def_k_conc_input1 0 ///< Matrix of Buffer 1 #define def_k_conc_window1 1 ///< Window of Buffer 1 #define def_k_conc_input2 2 ///< Matrix of Buffer 2 #define def_k_conc_window2 3 ///< Window of Buffer 2 #define def_k_conc_input3 4 ///< Matrix of Buffer 3 #define def_k_conc_window3 5 ///< Window of Buffer 3 #define def_k_conc_input4 6 ///< Matrix of Buffer 4 #define def_k_conc_window4 7 ///< Window of Buffer 4 #define def_k_conc_out 8 ///< Output tensor //--- #define def_k_DeconcatenateMatrix 18 ///< Index of the Multi Head Attention Neuron Deconcatenate Output kernel (#DeconcatenateBuffers) #define def_k_dconc_output1 0 ///< Matrix of Buffer 1 #define def_k_dconc_window1 1 ///< Window of Buffer 1 #define def_k_dconc_output2 2 ///< Matrix of Buffer 2 #define def_k_dconc_window2 3 ///< Window of Buffer 2 #define def_k_dconc_output3 4 ///< Matrix of Buffer 3 #define def_k_dconc_window3 5 ///< Window of Buffer 3 #define def_k_dconc_output4 6 ///< Matrix of Buffer 4 #define def_k_dconc_window4 7 ///< Window of Buffer 4 #define def_k_dconc_inputs 8 ///< Input tensor //--- #define def_k_Matrix5Sum 19 ///< Index of the kernel for calculation Sum of 2 matrix with multiplyer (#SumMatrix) #define def_k_sum5_matrix1 0 ///< First matrix #define def_k_sum5_matrix2 1 ///< Second matrix #define def_k_sum5_matrix3 2 ///< Third matrix #define def_k_sum5_matrix4 3 ///< Fourth matrix #define def_k_sum5_matrix5 4 ///< Fifth matrix #define def_k_sum5_matrix_out 5 ///< Output matrix #define def_k_sum5_dimension 6 ///< Dimension of matrix #define def_k_sum5_multiplyer 7 ///< Multiplyer for output
Hinzufügen einer neuen Konstanten zur Identifizierung der neuen Klasse
#define defNeuronMHAttentionOCL 0x7888 ///<Multi-Head Attention neuron OpenCL \details Identified class #CNeuronAttentionOCL
Hinzufügen einer neuen Klasse im Konstruktor der Klasse des neuronalen Netzwerks zum OpenCL-Klasseninitialisierungsblock.
next=Description.At(1); if(next.type==defNeuron || next.type==defNeuronBaseOCL || next.type==defNeuronConvOCL || next.type==defNeuronAttentionOCL || next.type==defNeuronMHAttentionOCL) { opencl=new COpenCLMy(); if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true)) delete opencl; }
Fügen wir einen neuen Typ von Neuronen im Block Initialisierung von Neuronen im Netzwerk hinzu.
case defNeuronMHAttentionOCL: neuron_attention_ocl=new CNeuronMHAttentionOCL(); if(CheckPointer(neuron_attention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_attention_ocl.Init(outputs,0,opencl,desc.window,desc.count,desc.optimization)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_attention_ocl)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl=NULL; break;
Deklaration des neuen Kernels.
if(CheckPointer(opencl)==POINTER_INVALID) return; //--- create kernels opencl.SetKernelsCount(20); opencl.KernelCreate(def_k_FeedForward,"FeedForward"); opencl.KernelCreate(def_k_CalcOutputGradient,"CalcOutputGradient"); opencl.KernelCreate(def_k_CalcHiddenGradient,"CalcHiddenGradient"); opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum"); opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam"); opencl.KernelCreate(def_k_AttentionGradients,"AttentionInsideGradients"); opencl.KernelCreate(def_k_AttentionOut,"AttentionOut"); opencl.KernelCreate(def_k_AttentionScore,"AttentionScore"); opencl.KernelCreate(def_k_CalcHiddenGradientConv,"CalcHiddenGradientConv"); opencl.KernelCreate(def_k_CalcInputGradientProof,"CalcInputGradientProof"); opencl.KernelCreate(def_k_FeedForwardConv,"FeedForwardConv"); opencl.KernelCreate(def_k_FeedForwardProof,"FeedForwardProof"); opencl.KernelCreate(def_k_MatrixSum,"SumMatrix"); opencl.KernelCreate(def_k_Matrix5Sum,"Sum5Matrix"); opencl.KernelCreate(def_k_UpdateWeightsConvAdam,"UpdateWeightsConvAdam"); opencl.KernelCreate(def_k_UpdateWeightsConvMomentum,"UpdateWeightsConvMomentum"); opencl.KernelCreate(def_k_Normilize,"Normalize"); opencl.KernelCreate(def_k_NormilizeWeights,"NormalizeWeights"); opencl.KernelCreate(def_k_ConcatenateMatrix,"ConcatenateBuffers"); opencl.KernelCreate(def_k_DeconcatenateMatrix,"DeconcatenateBuffers");
Hinzufügen einer neuen Klasse zur Verteilmethode der Klasse CNeuronBaseOCL. Die Änderungen sind im untenstehenden Code hervorgehoben.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; } bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; CNeuronAttentionOCL *at=NULL; CNeuronConvOCL *conv=NULL; switch(TargetObject.Type()) { case defNeuronBaseOCL: temp=TargetObject; return calcHiddenGradients(temp); break; case defNeuronConvOCL: conv=TargetObject; temp=GetPointer(this); return conv.calcInputGradients(temp); break; case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: at=TargetObject; temp=GetPointer(this); return at.calcInputGradients(temp); break; } //--- return false; } bool CNeuronBaseOCL::UpdateInputWeights(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: temp=SourceObject; return updateInputWeights(temp); break; } //--- return false; }
Der vollständige Code aller Methoden und Funktionen steht im Anhang zur Verfügung.
5. Tests
Der Expert Advisor Fractal_OCL_AttentionMHTE wurde zum Testen der neuen Architektur erstellt. Dieser Expert Advisor wurde auf der Grundlage des Expert Advisors Fractal_OCL_Attention aus Artikel 8 erstellt. Er unterscheidet sich vom vorherigen EA nur durch den Klassentyp der Attention-Neuronen und durch die Verwendung des Mechanismus zur Kodierung der Position von Eingangsdatenelementen.
CArrayObj *Topology=new CArrayObj(); if(CheckPointer(Topology)==POINTER_INVALID) return INIT_FAILED; //--- CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBaseOCL; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronConvOCL; desc.window=12; desc.step=12; desc.window_out=36; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- bool result=true; for(int i=0; (i<2 && result); i++) { desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronMHAttentionOCL; desc.window=36; desc.optimization=ADAM; desc.activation=None; result=Topology.Add(desc); } if(!result) { delete Topology; return INIT_FAILED; } //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; desc.activation=SIGMOID; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; delete Net; Net=new CNet(Topology); delete Topology;
Für die Reinheit des Experiments habe ich parallel zwei Expert Advisors (Self-Attention und Multi-Head Attention) getestet. Die Tests wurden unter den gleichen Bedingungen durchgeführt: EURUSD, H1-Zeitrahmen, Daten von 20 aufeinanderfolgenden Kerzen werden in das Netzwerk eingespeist, und das Training wird mit der Historie der letzten zwei Jahre durchgeführt, wobei die Parameter durch die Adam-Methode aktualisiert werden.
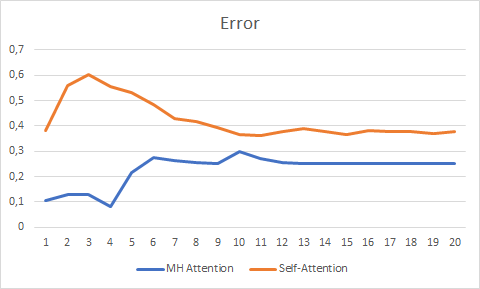
Das Testen über 20 Epochen zeigte den Vorteil der Multi-Head-Attention, die eine glattere Fehleränderungskurve hatte und sich mit dem Fehler von 0,25 gegenüber 0,37 für Self-Attention stabilisierte.
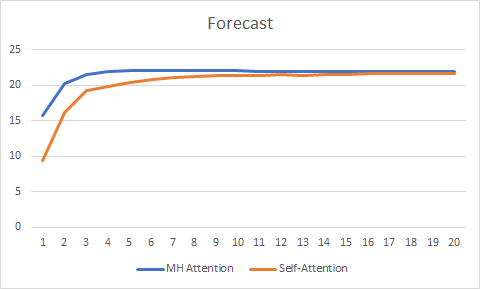
Die Prognosekurve hat ebenfalls die bessere Leistung der Multi-Head Attention Technologie gezeigt, wenn auch nicht so signifikant.
Der vollständige Code aller Klassen und Expert Advisors ist im Anhang verfügbar.
Schlussfolgerung
In diesem Artikel haben wir die Implementierung des Multi-Head Attention-Algorithmus erklärt und vergleichende Tests mit der Single-Head Self-Attention-Architektur durchgeführt. Bei gleichen Testbedingungen hat die Multi-Head Attention bessere Ergebnisse erzielt. Es ist jedoch zu beachten, dass die Verbesserung der Netzwerkqualität einen zusätzlichen Rechenaufwand erfordert.
Referenzen
- Neuronale Netze leicht gemacht
- Neuronale Netze leicht gemacht (Teil 2): Netzwerktraining und Tests
- Neuronale Netze leicht gemacht (Teil 3): Convolutional Neurale Netzwerke
- Neuronale Netze leicht gemacht (Teil 4): Rekurrente Netze
- Neuronale Netze leicht gemacht (Teil 5): Parallele Berechnungen mit OpenCL
- Neuronale Netze leicht gemacht (Teil 6): Experimentieren mit der Lernrate des neuronalen Netzwerks
- Neuronale Netze leicht gemacht (Teil 7): Adaptive Optimierungsverfahren
- Neuronale Netze leicht gemacht (Teil 8): Attention-Mechanismen
- Neuronale Netze leicht gemacht (Teil 9): Dokumentation der Arbeit
- Attention Is All You Need
- Multi-Head Attention: Collaborate Instead of Concatenate
Die Programme dieses Artikels
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Fractal_OCL_Attention.mq5 | Expert Advisor | Ein Expert Advisor mit dem neuronalen Klassifizierungsnetzwerk (3 Neuronen in der Ausgabeschicht), das den Mechanismus der Self-Attention verwendet |
| 2 | Fractal_OCL_AttentionMHTE.mq5 | Expert Advisor | Ein Expert Advisor mit dem neuronalen Klassifizierungsnetzwerk (3 Neuronen in der Ausgabeschicht) unter Verwendung des Multi-Head Attention-Mechanismus |
| 3 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek mit Klassen zum Erstellen eines neuronalen Netzwerks |
| 4 | NeuroNet.cl | Bibliothek | Die Bibliothek mit dem Programm-Code für OpenCL |
| 5 | NN.chm | HTML Hilfe | Die konvertierte HTML-Hilfedatei. |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/8909
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Praktische Anwendung von Neuronalen Netzen im Handel (Teil 2). Computerbilder
Praktische Anwendung von Neuronalen Netzen im Handel (Teil 2). Computerbilder
 Entwicklung eines selbstanpassenden Algorithmus (Teil II): Effizienzverbesserungen
Entwicklung eines selbstanpassenden Algorithmus (Teil II): Effizienzverbesserungen
 Entwicklung eines selbstanpassenden Algorithmus (Teil III): Verzicht auf Optimierung
Entwicklung eines selbstanpassenden Algorithmus (Teil III): Verzicht auf Optimierung
 Brute-Force-Ansatz zur Mustersuche (Teil III): Neue Horizonte
Brute-Force-Ansatz zur Mustersuche (Teil III): Neue Horizonte
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Ausschuss der fortschrittlichsten GPU-basierten NS-Architekturen, hat Python das überhaupt? )
schade, dass ich die üblichen Transformatoren aus Artikel 8 noch nicht ganz durchschaut habe ))