Neuronale Netze im Handel: Direktionale Diffusionsmodelle (DDM)

Einführung

Unüberwachtes Repräsentationslernen mit Hilfe von Diffusionsmodellen hat sich zu einem wichtigen Forschungsgebiet im Bereich des Computersehens entwickelt. Experimentelle Ergebnisse verschiedener Forscher bestätigen die Wirksamkeit von Diffusionsmodellen beim Erlernen sinnvoller visueller Darstellungen. Die Rekonstruktion von Daten, die durch unterschiedliche Rauschpegel verzerrt sind, bietet eine geeignete Grundlage für das Modell, um komplexe visuelle Konzepte zu erfassen. Darüber hinaus hat sich gezeigt, dass sich die Leistung von Diffusionsmodellen verbessern lässt, wenn beim Training ein bestimmtes Ausmaß des Rauschens gegenüber anderen bevorzugt werden.

Die Autoren des Artikels „Directional Diffusion Models for Graph Representation Learning“ schlagen vor, Diffusionsmodelle für das unüberwachte Lernen von Graphenrepräsentationen zu verwenden. Allerdings stießen sie in der Praxis auf die Grenzen von einfachen Diffusionsmodellen. Ihre Experimente ergaben, dass Daten in Graphenstrukturen häufig ausgeprägte anisotrope und gerichtete Muster aufweisen, die in Bilddaten weniger ausgeprägt sind. Herkömmliche Diffusionsmodelle, die sich auf einen isotropen Vorwärtsdiffusionsprozess stützen, neigen zu einer raschen Abnahme des internen Signal-Rausch-Verhältnisses (SNR), wodurch sie für die Erfassung anisotroper Strukturen weniger geeignet sind. Um dieses Problem zu lösen, haben die Autoren neue Ansätze entwickelt, die solche gerichteten Strukturen effizient erfassen können. Dazu gehören gerichtete Diffusionsmodelle, die das Problem des sich schnell verschlechternden SNR entschärfen. Der vorgeschlagene Rahmen bezieht datenabhängiges und richtungsabhängiges Rauschen in den Vorwärtsdiffusionsprozess ein. Die vom Entrauschungsmodell erzeugten Zwischenaktivierungen erfassen effektiv wertvolle semantische und topologische Informationen, die für nachgelagerte Aufgaben entscheidend sind.

Daher bieten direktionale Diffusionsmodelle einen vielversprechenden generativen Ansatz für das Lernen von Graphendarstellungen. Die experimentellen Ergebnisse der Autoren zeigen, dass diese Modelle sowohl das kontrastive Lernen als auch traditionelle generative Methoden übertreffen. Insbesondere bei Graphenklassifizierungsaufgaben übertreffen direktionale Diffusionsmodelle sogar die grundlegenden überwachten Lernmodelle, was das erhebliche Potenzial diffusionsbasierter Methoden beim Lernen von Graphenrepräsentationen unterstreicht.

Die Anwendung von Diffusionsmodellen im Handelskontext eröffnet neue Möglichkeiten, die Darstellung und Analyse von Marktdaten zu verbessern. Insbesondere direktionale Diffusionsmodelle können sich als besonders nützlich erweisen, da sie anisotrope Datenstrukturen berücksichtigen können. Finanzmärkte sind häufig durch asymmetrische und direktionale Bewegungen gekennzeichnet, und Modelle, die direktionales Rauschen berücksichtigen, können strukturelle Muster sowohl in Trend- als auch in Korrekturphasen besser erkennen. Diese Fähigkeit ermöglicht die Identifizierung versteckter Abhängigkeiten und saisonaler Trends.

1. Der DDM-Algorithmus

Es gibt erhebliche strukturelle Unterschiede zwischen Daten in Diagrammen und in Bildern. Beim einfachen Forward-Diffusion-Verfahren wird isotropes Gaußsches Rauschen iterativ zu den Originaldaten hinzugefügt, bis die Daten vollständig in weißes Rauschen umgewandelt sind. Dieser Ansatz ist geeignet, wenn die Daten isotropen Verteilungen folgen, da er einen Datenpunkt allmählich zu Rauschen degradiert und gleichzeitig verrauschte Stichproben über einen breiten Bereich von Signal-Rausch-Verhältnissen (SNR) erzeugt. Bei anisotropen Datenverteilungen kann das Hinzufügen von isotropem Rauschen jedoch schnell die zugrunde liegende Struktur verfälschen und zu einem schnellen Abfall des SNR auf Null führen.

Infolgedessen gelingt es den Entrauschungsmodellen nicht, aussagekräftige und diskriminierende Merkmalsrepräsentationen zu erlernen, die für nachgelagerte Aufgaben effektiv genutzt werden können. Im Gegensatz dazu reduzieren Directional Diffusion Models (DDMs), die einen datenabhängigen und richtungsabhängigen Vorwärtsdiffusionsprozess beinhalten, das SNR langsamer. Diese allmähliche Verschlechterung ermöglicht die Extraktion feinkörniger Merkmalsdarstellungen bei unterschiedlichen SNR-Werten, wobei wichtige Informationen über anisotrope Strukturen erhalten bleiben. Die extrahierten Informationen können dann für nachgelagerte Aufgaben wie die Klassifizierung von Graphen und Knoten verwendet werden.

Bei der Erzeugung von gerichtetem Rauschen wird das ursprüngliche isotrope Gaußsche Rauschen durch zwei zusätzliche Bedingungen in anisotropes Rauschen umgewandelt. Diese Einschränkungen sind wesentlich für die Verbesserung der Leistung von Diffusionsmodellen.

Es sei Gt = (A, Xt), das den Arbeitszustand im t-ten Schritt des Vorwärtsdiffusionsprozesses repräsentiert, wobei 𝐗t = {xt,1, xt,2, …, xt,N} die untersuchten Merkmale bezeichnet.

Dabei ist x0,i der rohe Merkmalsvektor des Knotens i, μ ∈ ℛ und σ ∈ ℛ stellen den Mittelwert- und Standardabweichungstensor der Dimension d der Merkmale über alle N Knoten dar. Und ⊙ bezeichnet die elementweise Multiplikation. Während des Mini-Batch-Trainings werden μ und σ anhand von Graphen innerhalb des Batches berechnet. Der Parameter ɑt steht für den festen Varianzplan und wird durch eine abnehmende Folge {β ∈ (0, 1)} parametrisiert.

Verglichen mit dem reinen Diffusionsprozess gibt es bei direktionalen Diffusionsmodellen zwei wesentliche Beschränkungen: Man verwandelt das datenunabhängige Gaußsche Rauschen in anisotropes, chargenspezifisches Rauschen. Bei dieser Einschränkung wird jede Koordinate des Rauschvektors gezwungen, dem empirischen Mittelwert und der Standardabweichung der entsprechenden Koordinate in den tatsächlichen Daten zu entsprechen. Dadurch wird der Diffusionsprozess auf die lokale Umgebung der Charge beschränkt, was eine übermäßige Divergenz verhindert und die lokale Kohärenz erhält. Eine weitere Bedingung ist die Einführung einer Winkelrichtung, die das Rauschen ε in dieselbe Hyperebene des Objekts x0,i dreht, wobei seine Richtungseigenschaften erhalten bleiben. Dies trägt dazu bei, dass die innere Struktur der Daten während des gesamten Vorwärtsdiffusionsprozesses erhalten bleibt.

Diese beiden Einschränkungen wirken zusammen, um sicherzustellen, dass der Vorwärtsdiffusionsprozess die zugrunde liegende Datenstruktur respektiert und eine schnelle Signalverschlechterung verhindert. Infolgedessen nimmt das Signal-Rausch-Verhältnis langsamer ab, sodass direktionale Diffusionsmodelle aussagekräftige Merkmalsdarstellungen über einen Bereich von SNR-Werten extrahieren können. Dies verbessert die Leistung nachgelagerter Aufgaben, indem es robustere und informativere Einbettungen liefert.

Die Autoren der Methode verfolgen die gleiche Trainingsstrategie wie bei einfachen Diffusionsmodellen, indem sie ein Rauschmodell fθ trainieren, um den umgekehrten Diffusionsprozess zu approximieren. Da jedoch die Umkehrung des Vorwärtsprozesses mit direktionalem Rauschen nicht in geschlossener Form ausgedrückt werden kann, wird das Entrauschungsmodell fθ trainiert, um die ursprüngliche Sequenz direkt vorherzusagen.

Die Originalvisualisierung des Directional Diffusion Models Frameworks, wie es von den Autoren vorgestellt wurde, ist unten zu sehen.

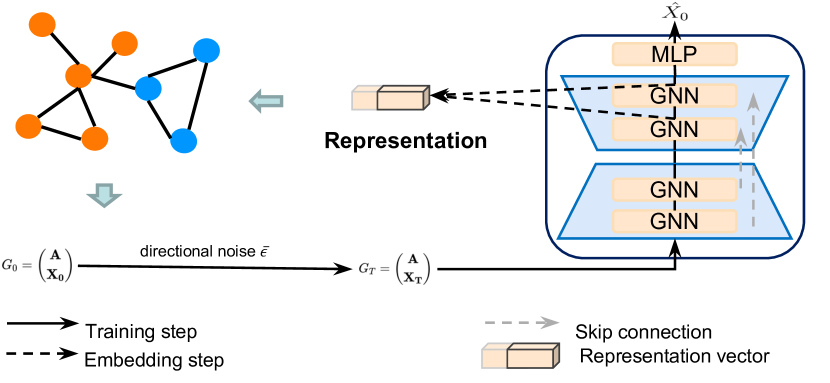
2. Die Implementation in MQL5

Nach der Betrachtung der theoretischen Aspekte der Methode der Directional Diffusion Models gehen wir zum praktischen Teil unseres Artikels über, in dem wir die vorgeschlagenen Ansätze in MQL5 implementieren.

Wir werden unsere Arbeit in zwei Hauptabschnitte unterteilen. In der ersten Phase fügen wir den zu analysierenden Daten Richtungsrauschen hinzu, und in der zweiten Phase implementieren wir den Rahmen innerhalb einer einzigen Klassenstruktur.

2.1 Hinzufügen von Richtungsrauschen

Bevor wir beginnen, wollen wir den Algorithmus für die Erzeugung von Richtungsrauschen besprechen. Zunächst benötigen wir ein Rauschen aus einer Normalverteilung, das wir mit den Standardbibliotheken von MQL5 leicht erhalten können.

Als Nächstes müssen wir dieses isotrope Rauschen in anisotropes, datenabhängiges Rauschen umwandeln, und zwar nach der von den Autoren des Frameworks beschriebenen Methode. Zu diesem Zweck müssen wir den Mittelwert und die Varianz für jedes Merkmal berechnen. Bei näherer Betrachtung ähnelt dies der Aufgabe, die wir bereits bei der Entwicklung der Batch-Normalisierungsschicht CNeuronBatchNormOCL. Der Batch-Normalisierungsalgorithmus standardisiert die Daten auf einen Mittelwert von Null und eine Einheitsvarianz. Während der Verschiebungs- und Skalierungsphase ändert sich jedoch die Datenverteilung. Theoretisch könnten wir diese statistischen Informationen aus der Normalisierungsschicht selbst extrahieren. Tatsächlich haben wir bei der Entwicklung der Klasse der inversen Normalisierung bereits ein Verfahren zur Ermittlung der Parameter der ursprünglichen Verteilung eingeführt CNeuronRevINDenormOCL. Dieser Ansatz würde jedoch die Flexibilität und Allgemeinheit unseres Rahmens einschränken.

Um diese Einschränkung zu überwinden, haben wir einen stärker integrierten Ansatz gewählt. Wir haben die Hinzufügung von Richtungsrauschen mit dem Prozess der Datennormalisierung selbst kombiniert. Dies wirft eine wichtige Frage auf: An welchem Punkt sollte das Rauschen hinzugefügt werden?

Wir können Rauschen VOR der Normalisierung hinzufügen. Dies würde jedoch den Normalisierungsprozess selbst verzerren. Das Hinzufügen von Rauschen verändert die Datenverteilung. Daher würde die Anwendung der Normalisierung mit dem zuvor berechneten Mittelwert und der Varianz zu einer verzerrten Verteilung führen. Dies wäre ein unerwünschtes Ergebnis.

Die zweite Möglichkeit besteht darin, am Ausgang der Normalisierungsschicht Rauschen hinzuzufügen. In diesem Fall müssten wir das Gaußsche Rauschen um die Skalierungs- und Verschiebungsfaktoren anpassen. Betrachtet man jedoch die obigen Formeln des ursprünglichen Algorithmus, so stellt man fest, dass diese Anpassung zu einer Verzerrung führt und sich das Rauschen in Richtung des mittleren Offsets verschiebt. Mit zunehmendem Offset kommt es daher zu schrägem, asymmetrischem Rauschen. Auch dies ist unerwünscht.

Nach Abwägung der Vor- und Nachteile haben wir uns für eine andere Strategie entschieden: Wir fügen das Rauschen zwischen dem Normalisierungsschritt und der Skalierungs-/Offset-Anwendung hinzu. Bei diesem Ansatz wird davon ausgegangen, dass die normalisierten Daten bereits einen Mittelwert von Null und eine Einheitsvarianz haben. Dies ist genau die Verteilung, die wir zur Erzeugung des Rauschens verwendet haben. Anschließend werden die verrauschten Daten in die Skalierungs- und Verschiebungsphase eingespeist, sodass das Modell geeignete Parameter lernen kann.

Dies wird die Umsetzungsstrategie sein. Wir können mit dem praktischen Teil der Arbeit beginnen. Der Algorithmus wird auf der OpenCL-Seite implementiert. Zu diesem Zweck erstellen wir einen neuen Kernel namens BatchFeedForwardAddNoise. Es ist erwähnenswert, dass die Logik dieses Kerns weitgehend auf dem Vorwärtsdurchlauf der Stapelnormalisierungsschicht basiert. Wir erweitern es jedoch um einen Puffer für Daten mit Gaußschem Rauschen und einen Skalierungsfaktor für Abweichungen, der als ɑ bezeichnet wird.

__kernel void BatchFeedForwardAddNoise(__global const float *inputs, __global float *options,
                                       __global const float *noise, __global float *output,
                                       const int batch, const int optimization, 
                                       const int activation, const float alpha)
  {
   if(batch <= 1)
      return;
   int n = get_global_id(0);
   int shift = n * (optimization == 0 ? 7 : 9);

Im Hauptteil der Methode wird zunächst die Größe des Normalisierungsstapels geprüft, der größer als „1“ sein muss. Dann bestimmen wir den Offset in den Datenpuffern anhand der aktuellen Thread-ID.

Als Nächstes wird geprüft, ob der Normalisierungsparameterpuffer reelle Zahlen enthält. Falsche Elemente werden durch Nullwerte ersetzt.

   for(int i = 0; i < (optimization == 0 ? 7 : 9); i++)
     {
      float opt = options[shift + i];
      if(isnan(opt) || isinf(opt))
         options[shift + i] = 0;
     }

Anschließend normalisieren wir die Originaldaten gemäß dem Basiskernel-Algorithmus.

   float inp = inputs[n];
   float mean = (batch > 1 ? (options[shift] * ((float)batch - 1.0f) + inp) / ((float)batch) : inp);
   float delt = inp - mean;
   float variance = options[shift + 1] * ((float)batch - 1.0f) + pow(delt, 2);
   if(batch > 0)
      variance /= (float)batch;
   float nx = (variance > 0 ? delt / sqrt(variance) : 0);

In diesem Stadium erhalten wir normalisierte Ausgangsdaten mit einem Mittelwert von Null und einer Einheitsvarianz. Hier fügen wir das Rauschen hinzu, nachdem wir zuvor seine Richtung angepasst haben.

   float noisex = sqrt(alpha) * nx + sqrt(1-alpha) * fabs(noise[n]) * sign(nx);

Dann führen wir den Skalierungs- und Verschiebungsalgorithmus durch und speichern die Ergebnisse in den entsprechenden Datenpuffern, ähnlich wie bei der Implementierung des Spenderkerns. Diesmal werden jedoch Skalierung und Offset auf die verrauschten Werte angewendet.

   float gamma = options[shift + 3];
   if(gamma == 0 || isinf(gamma) || isnan(gamma))
     {
      options[shift + 3] = 1;
      gamma = 1;
     }
   float betta = options[shift + 4];
   if(isinf(betta) || isnan(betta))
     {
      options[shift + 4] = 0;
      betta = 0;
     }
//---
   options[shift] = mean;
   options[shift + 1] = variance;
   options[shift + 2] = nx;
   output[n] = Activation(gamma * noisex + betta, activation);
  }

Wir haben den Vorwärtsdurchlauf-Algorithmus implementiert. Was ist mit dem Rückwärtsdurchlauf? An dieser Stelle ist anzumerken, dass wir uns zur Durchführung der Rückwärtsdurchlauf-Operationen für die vollständige Implementierung der Algorithmen der Batch-Normalisierungsschicht entschieden haben. Tatsache ist, dass wir das Rauschen selbst nicht trainieren. Daher wird der Fehlergradient direkt und vollständig auf die ursprünglichen Eingabedaten übertragen. Der Skalierungsfaktor ɑ, den wir zuvor eingeführt haben, dient lediglich dazu, den Bereich um die Originaldaten herum leicht zu verwischen. Folglich können wir diesen Faktor vernachlässigen und die Fehlergradienten in voller Übereinstimmung mit dem Standard-Batch-Normalisierungsalgorithmus an die Eingabe weiterleiten.

Damit ist unsere Arbeit an der OpenCL-Seite der Implementierung abgeschlossen. Der vollständige Quellcode ist im Anhang enthalten. Wir gehen nun zur MQL5-Seite der Implementierung über. Hier werden wir eine neue Klasse namens CNeuronBatchNormWithNoise erstellen. Wie der Name schon sagt, wird der größte Teil der Kernfunktionalität direkt von der Batch-Normalisierungsklasse geerbt. Die einzige Methode, die überschrieben werden muss, ist der Vorwärtsdurchlauf. Die Struktur der neuen Klasse ist unten dargestellt.

class CNeuronBatchNormWithNoise  :  public CNeuronBatchNormOCL
  {
protected:
   CBufferFloat      cNoise;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   
public:
                     CNeuronBatchNormWithNoise(void) {};
                    ~CNeuronBatchNormWithNoise(void) {};
   //---
   virtual int       Type(void) const   {  return defNeuronBatchNormWithNoise;    }
  };

Wie Sie vielleicht bemerkt haben, haben wir versucht, die Entwicklung unserer neuen Klasse CNeuronBatchNormWithNoise so einfach wie möglich zu gestalten. Um die erforderliche Funktionalität zu ermöglichen, benötigen wir jedoch einen Puffer zur Übertragung des Rauschens, das auf der Hauptseite erzeugt und an OpenCL übergeben wird. Wir haben uns bewusst dafür entschieden, die Objektinitialisierungsmethode oder die Dateimethoden nicht zu überschreiben. Es gibt keinen praktischen Grund, das zufällig erzeugte Rauschen beizubehalten. Stattdessen werden alle damit zusammenhängenden Vorgänge innerhalb der Methode feedForward implementiert. Diese Methode erhält einen Zeiger auf das Eingangsdatenobjekt als Parameter.

bool CNeuronBatchNormWithNoise::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!bTrain)
      return CNeuronBatchNormOCL::feedForward(NeuronOCL);

Achten Sie darauf, dass das Rauschen nur während der Trainingsphase hinzugefügt wird. Dadurch kann das Modell sinnvolle Strukturen in den Eingabedaten lernen. In der Praxis soll das Modell als Filter fungieren, der sinnvolle Muster aus realen Daten herausfiltert, die naturgemäß ein gewisses Maß an Rauschen oder Inkonsistenz enthalten können. Daher wird in diesem Stadium kein künstliches Rauschen hinzugefügt. Stattdessen führen wir die Standardnormalisierung über die Funktionalität der übergeordneten Klasse durch.

Der folgende Code wird nur während des Modelltrainings ausgeführt. Zunächst wird die Relevanz des empfangenen Zeigers auf das Quelldatenobjekt geprüft.

if(!OpenCL || !NeuronOCL)
   return false;

Und dann speichern wir sie in einer internen Variablen.

PrevLayer = NeuronOCL;

Danach überprüfen wir die Größe des Normalisierungspakets. Und wenn er nicht größer als 1 ist, dann synchronisieren wir einfach die Aktivierungsfunktionen und beenden die Methode mit einem positiven Ergebnis. Denn in diesem Fall ist das Ergebnis des Normalisierungsalgorithmus gleich den Originaldaten. Um zusätzliche Operationen zu vermeiden, werden wir die empfangenen Ausgangsdaten einfach an die nächste Schicht weitergeben.

if(iBatchSize <= 1)
  {
   activation = (ENUM_ACTIVATION)NeuronOCL.Activation();
   return true;
  }

Wenn alle oben genannten Kontrollpunkte erfolgreich durchlaufen wurden, erzeugen wir zunächst Rauschen aus einer Normalverteilung.

double random[];
if(!Math::MathRandomNormal(0, 1, Neurons(), random))
   return false;

Danach müssen wir sie an OpenCL übergeben. Aber wir haben die Objektinitialisierungsmethode nicht außer Kraft gesetzt. Wir überprüfen also zunächst unseren Datenpuffer, um sicherzustellen, dass er genügend Elemente enthält und der zuvor erstellte Puffer im Kontext steht.

if(cNoise.Total() != Neurons() ||
   cNoise.GetOpenCL() != OpenCL)
  {
   cNoise.BufferFree();
   if(!cNoise.AssignArray(random))
      return false;
   if(!cNoise.BufferCreate(OpenCL))
      return false;
  }

Wenn wir an einem der Prüfpunkte einen negativen Wert erhalten, ändern wir die Puffergröße und erstellen einen neuen Zeiger im Kontext von OpenCL.

Ansonsten kopieren wir die Daten einfach in den Puffer und verschieben sie in den Kontextspeicher von OpenCL.

else
  {
   if(!cNoise.AssignArray(random))
      return false;
   if(!cNoise.BufferWrite())
      return false;
  }

Als Nächstes passen wir die tatsächliche Batch-Größe an und bestimmen den Rauschpegel der Originaldaten nach dem Zufallsprinzip.

iBatchCount = MathMin(iBatchCount, iBatchSize);
float noise_alpha = float(1.0 - MathRand() / 32767.0 * 0.01);

Nachdem wir nun alle erforderlichen Daten vorbereitet haben, müssen wir sie nur noch an die Parameter unseres soeben erstellten Kernels übergeben.

uint global_work_offset[1] = {0};
uint global_work_size[1];
global_work_size[0] = Neurons();
int kernel = def_k_BatchFeedForwardAddNoise;
ResetLastError();
if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_inputs, NeuronOCL.getOutputIndex()))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_noise, cNoise.GetIndex()))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_options, BatchOptions.GetIndex()))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_output, Output.GetIndex()))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_activation, int(activation)))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_alpha, noise_alpha))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_batch, iBatchCount))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_optimization, int(optimization)))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
//---
if(!OpenCL.Execute(kernel, 1, global_work_offset, global_work_size))
  {
   printf("Error of execution kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                GetLastError(), __LINE__);
   return false;
  }
   iBatchCount++;
//---
   return true;
  }

Und wir stellen den Kernel in die Ausführungswarteschlange. Außerdem kontrollieren wir die Vorgänge bei jedem Schritt. Am Ende der Methode geben wir das logische Ergebnis der Operationen an den Aufrufer zurück.

Damit ist unsere neue Klasse CNeuronBatchNormWithNoise abgeschlossen. Der vollständige Code ist in der beigefügten Datei enthalten.

2.2 Die Klasse des Frameworks DDM

Wir haben ein Objekt zum Hinzufügen von Richtungsrauschen zu den ursprünglichen Eingabedaten implementiert. Und nun gehen wir dazu über, unsere Interpretation des Rahmens für gerichtete Diffusionsmodelle aufzubauen.

Wir verwenden die Struktur der von den Autoren des Rahmens vorgeschlagenen Ansätze. Im Zusammenhang mit unseren spezifischen Problemen lassen wir jedoch einige Abweichungen zu. In unserer Implementierung verwenden wir ebenfalls die von den Autoren der Methode vorgeschlagene U-förmige Architektur, ersetzen jedoch die Transformer-Encoderblöcke durch Graph Neural Networks (GNN). Darüber hinaus speisen die Autoren der Methode bereits verrauschten Input in das Modell ein, während wir das Rauschen im Modell selbst hinzufügen. Aber das Wichtigste zuerst.

Um unsere Lösung zu implementieren, erstellen wir eine neue Klasse namens CNeuronDiffusion. Als übergeordnetes Objekt verwenden wir einen U-förmigen Transformer. Die Struktur der neuen Klasse ist unten dargestellt.

class CNeuronDiffusion  : public CNeuronUShapeAttention
  {
protected:
   CNeuronBatchNormWithNoise  cAddNoise;
   CNeuronBaseOCL             cResidual;
   CNeuronRevINDenormOCL      cRevIn;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronDiffusion(void) {};
                    ~CNeuronDiffusion(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint heads, uint units_count, 
                          uint layers, uint inside_bloks, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronDiffusion;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

In der vorgestellten Klassenstruktur haben wir drei neue statische Objekte deklariert, mit deren Zweck wir uns bei der Implementierung der Klassenmethoden vertraut machen werden. Um die grundlegende Architektur des Geräuschfiltermodells aufzubauen, werden wir geerbte Objekte verwenden.

Alle Objekte werden als statisch deklariert, was es uns ermöglicht, den Konstruktor und den Destruktor der Klasse leer zu lassen. Die Initialisierung von Objekten wird in der Methode Init durchgeführt.

In den Methodenparametern erhalten wir die wichtigsten Konstanten, die die Architektur des erstellten Objekts bestimmen. Es sei darauf hingewiesen, dass wir in diesem Fall die Struktur der Parameter aus der Methode der Elternklasse vollständig und unverändert übernommen haben.

bool CNeuronDiffusion::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                            uint window, uint window_key, uint heads, 
                            uint units_count, uint layers, uint inside_bloks, 
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

Bei der Konstruktion neuer Algorithmen werden wir jedoch die Reihenfolge, in der die geerbten Objekte verwendet werden, leicht ändern. Deshalb rufen wir im Hauptteil der Methode die entsprechende Methode der Basisklasse auf, in der nur die wichtigsten Schnittstellen initialisiert werden.

Als Nächstes initialisieren wir das Normalisierungsobjekt der ursprünglichen Eingabedaten mit dem Zusatz von Rauschen. Wir werden dieses Objekt für die Erstverarbeitung der Eingabedaten verwenden.

if(!cAddNoise.Init(0, 0, OpenCL, window * units_count, iBatch, optimization))
   return false;

Dann bauen wir die U-förmige Transformer-Struktur. Hier verwenden wir zunächst den mehrköpfigen Aufmerksamkeitsblock.

if(!cAttention[0].Init(0, 1, OpenCL, window, window_key, heads, units_count, layers, optimization, iBatch))
   return false; 

Darauf folgt eine Faltungsschicht zur Dimensionalitätsreduktion.

if(!cMergeSplit[0].Init(0, 2, OpenCL, 2 * window, 2 * window, window, (units_count + 1) / 2, optimization, 
                                                                                                  iBatch))
   return false;

Dann bilden wir immer wieder Nackenobjekte (cNeck).

 if(inside_bloks > 0)
   {
    CNeuronDiffusion *temp = new CNeuronDiffusion();
    if(!temp)
       return false;
    if(!temp.Init(0, 3, OpenCL, window, window_key, heads, (units_count + 1) / 2, layers, inside_bloks - 1, 
                                                                                     optimization, iBatch))
      {
       delete temp;
       return false;
      }
    cNeck = temp;
   }
 else
   {
   CNeuronConvOCL *temp = new CNeuronConvOCL();
   if(!temp)
      return false;
   if(!temp.Init(0, 3, OpenCL, window, window, window, (units_count + 1) / 2, optimization, iBatch))
     {
      delete temp;
         return false;
     }
   cNeck = temp;
     }

An dieser Stelle sei darauf hingewiesen, dass wir die Architektur des Modells etwas verkompliziert haben. Dies hat auch das Problem, das das Modell lösen soll, verkompliziert. Der Punkt ist, dass wir als Nackenobjekt immer wieder ähnliche Richtungsdiffusionsobjekte hinzufügen. Das bedeutet, dass jede neue Schicht den ursprünglichen Eingabedaten Rauschen hinzufügt. Daher lernt das Modell, mit Daten zu arbeiten und sie aus stark verrauschten Daten wiederherzustellen.

Dieser Ansatz steht nicht im Widerspruch zur Idee der Diffusionsmodelle, die im Wesentlichen generative Modelle sind. Sie wurden geschaffen, um iterativ Daten aus Rauschen zu erzeugen. Es ist jedoch auch möglich, Objekte der übergeordneten Klasse im Nacken des Modells zu verwenden.

Als Nächstes fügen wir einen zweiten Aufmerksamkeitsblock zu unserem Rauschunterdrückungsmodell hinzu.

if(!cAttention[1].Init(0, 4, OpenCL, window, window_key, heads, (units_count + 1) / 2, layers, optimization,
                                                                                                     iBatch))
   return false;

Wir fügen auch eine Faltungsschicht hinzu, um die Dimensionalität der Eingabedaten wiederherzustellen.

if(!cMergeSplit[1].Init(0, 5, OpenCL, window, window, 2 * window, (units_count + 1) / 2, optimization, iBatch))
   return false;

Entsprechend der Architektur des U-förmigen Transformers ergänzen wir das erzielte Ergebnis durch Residual-Verbindungen. Um sie zu schreiben, werden wir eine grundlegende neuronale Schicht erstellen.

if(!cResidual.Init(0, 6, OpenCL, Neurons(), optimization, iBatch))
   return false;
if(!cResidual.SetGradient(cMergeSplit[1].getGradient(), true))
   return false;

Danach synchronisieren wir die Gradientenpuffer der Residual-Verbindungs- und Dimensionalitätswiederherstellungsschicht.

Als Nächstes fügen wir eine umgekehrte Normalisierungsschicht hinzu, die von den Autoren des Frameworks nicht erwähnt wird, sich aber aus der Logik der Methode ergibt.

if(!cRevIn.Init(0, 7, OpenCL, Neurons(), 0, cAddNoise.AsObject()))
   return false;

In der ursprünglichen Version des Frameworks wird nämlich keine Datennormalisierung verwendet. Es wird davon ausgegangen, dass der Algorithmus aufbereitete Graphdaten verwendet, die von Graphennetzwerken verarbeitet werden. Am Ausgang des Modells werden also entrauschte Originaldaten erwartet. Während des Trainingsprozesses wird der Fehler bei der Datenwiederherstellung minimiert. Bei unserer Lösung haben wir die Daten normalisiert. Um die Ergebnisse mit den wahren Werten vergleichen zu können, müssen wir die Daten daher in die ursprüngliche Darstellung zurückversetzen. Dieser Vorgang wird von der Ebene der inversen Normalisierung durchgeführt.

Nun müssen wir die Datenpuffer ersetzen, um unnötige Kopiervorgänge zu vermeiden, und das logische Ergebnis der Methodenoperationen an das aufrufende Programm zurückgeben.

   if(!SetOutput(cRevIn.getOutput(), true))
      return false;
//---
   return true;
  }

Beachten Sie jedoch, dass wir in diesem Fall nur den Zeiger des Ausgabepuffers austauschen. Der Fehlergradientenpuffer ist davon nicht betroffen. Wir werden die Gründe für diese Entscheidung bei der Untersuchung der Rückwärtsdurchlauf-Algorithmen erörtern.

Doch betrachten wir zunächst die Methode feedForward.

bool CNeuronDiffusion::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cAddNoise.FeedForward(NeuronOCL))
      return false;

In den Methodenparametern erhalten wir einen Zeiger auf das Eingabedatenobjekt, den wir sofort an die gleichnamige Methode der internen Rauschadditionsschicht übergeben.

Dem ersten Aufmerksamkeitsblock werden die mit Rauschen versehenen Eingänge zugeführt.

if(!cAttention[0].FeedForward(cAddNoise.AsObject()))
   return false;

Danach ändern wir die Datendimension und übergeben sie an das Nackenobjekt.

if(!cMergeSplit[0].FeedForward(cAttention[0].AsObject()))
   return false;
if(!cNeck.FeedForward(cMergeSplit[0].AsObject()))
   return false;

Die aus dem Nacken gewonnenen Ergebnisse werden in den zweiten Aufmerksamkeitsblock eingespeist.

if(!cAttention[1].FeedForward(cNeck))
   return false;

Danach stellen wir die Dimensionalität der Daten wieder auf das ursprüngliche Niveau her und summieren sie mit den durch Rauschen hinzugefügten Daten.

if(!cMergeSplit[1].FeedForward(cAttention[1].AsObject()))
   return false;
if(!SumAndNormilize(cAddNoise.getOutput(), cMergeSplit[1].getOutput(), cResidual.getOutput(),
                                                                        1, true, 0, 0, 0, 1))
   return false;

Am Ende der Methode werden die Daten in den ursprünglichen Verteilungsunterraum zurückgeführt.

   if(!cRevIn.FeedForward(cResidual.AsObject()))
      return false;
//---
   return true;
  }

Danach müssen wir nur noch das logische Ergebnis der Ausführung der Operation an die aufrufende Funktion zurückgeben.

Ich glaube, die Logik der Methode feedForward ist ziemlich einfach. Komplexer wird es jedoch bei der Gradientenfortpflanzungsmethode calcInputGradients. An dieser Stelle müssen wir uns daran erinnern, dass wir mit einem Diffusionsmodell arbeiten.

bool CNeuronDiffusion::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!prevLayer)
      return false;

Genau wie beim Vorwärtsdurchlauf erhält die Methode einen Zeiger auf das Quelldatenobjekt. Dieses Mal müssen wir jedoch den Fehlergradienten entsprechend dem Einfluss, den die Eingabedaten auf die Ausgabe des Modells hatten, zurückgeben. Wir beginnen mit der Validierung des empfangenen Zeigers, da weitere Operationen sonst sinnlos wären.

Ich möchte Sie auch daran erinnern, dass wir bei der Initialisierung die Zeiger der Gradientenpuffer absichtlich nicht ersetzt haben. Zu diesem Zeitpunkt existiert der Fehlergradient aus der nächsten Schicht nur noch im entsprechenden Schnittstellenpuffer. Diese Entscheidung ermöglicht es uns, unser zweites Hauptziel zu erreichen - das Training des Diffusionsmodells. Wie im theoretischen Teil dieses Artikels erwähnt, werden Diffusionsmodelle trainiert, um Eingabedaten aus Rauschen zu rekonstruieren. Wir berechnen also die Abweichung zwischen dem Ausgang des Vorwärtsdurchlaufs und den ursprünglichen Eingangsdaten (ohne Rauschen).

float error = 1;
if(!cRevIn.calcOutputGradients(prevLayer.getOutput(), error) ||
   !SumAndNormilize(cRevIn.getGradient(), Gradient, cRevIn.getGradient(), 1, false, 0, 0, 0, 1))
   return false;

Wir wollen jedoch einen Filter konfigurieren, der in der Lage ist, sinnvolle Strukturen im Kontext der Hauptaufgabe zu extrahieren. Daher fügen wir dem Rekonstruktionsgradienten den Fehlergradienten hinzu, den wir entlang des Hauptpfads erhalten haben und der den Vorhersagefehler des Hauptmodells anzeigt.

Als Nächstes propagieren wir den kombinierten Fehlergradienten bis hinunter zur Verbindungsschicht der Residuen.

if(!cResidual.calcHiddenGradients(cRevIn.AsObject()))
   return false;

In diesem Stadium verwenden wir die Puffersubstitution und fahren fort, den Gradienten durch den zweiten Aufmerksamkeitsblock zurückzupropagieren.

if(!cAttention[1].calcHiddenGradients(cMergeSplit[1].AsObject()))
   return false;

Von dort aus wird der Fehlergradient weiter durch den Rest des Netzes propagiert: den Nacken, die Dimensionenreduktionsschicht, den ersten Aufmerksamkeitsblock und schließlich die Rauschinjektionsschicht.

if(!cNeck.calcHiddenGradients(cAttention[1].AsObject()))
   return false;
if(!cMergeSplit[0].calcHiddenGradients(cNeck.AsObject()))
   return false;
if(!cAttention[0].calcHiddenGradients(cMergeSplit[0].AsObject()))
   return false;
if(!cAddNoise.calcHiddenGradients(cAttention[0].AsObject()))
   return false;

Hier müssen wir anhalten und den Gradienten des Residual-Verbindungsfehlers hinzufügen.

if(!SumAndNormilize(cAddNoise.getGradient(), cResidual.getGradient(), cAddNoise.getGradient(), 1, 
                                                                             false, 0, 0, 0, 1))
   return false;

Schließlich wird der Gradient zurück zur Eingabeschicht propagiert und das Ergebnis der Operation an die aufrufende Funktion zurückgegeben.

   if(!prevLayer.calcHiddenGradients(cAddNoise.AsObject()))
      return false;
//---
   return true;
  }

Damit ist der Überblick über die algorithmische Implementierung von Methoden innerhalb der Klasse Directional Diffusion Framework abgeschlossen. Den vollständigen Quellcode aller Methoden finden Sie im Anhang. Die Programme für die Ausbildung und die Interaktion mit der Umwelt, die wir unverändert aus unserer früheren Arbeit übernommen haben, sind ebenfalls enthalten.

Die Modellarchitekturen selbst wurden ebenfalls aus dem vorherigen Artikel übernommen. Die einzige Änderung besteht darin, dass die adaptive Graphenrepräsentationsschicht im Umgebungscodierer durch eine trainierbare Richtungsdiffusionsschicht ersetzt wurde.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronDiffusion;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.window_out = BarDescr;
   descr.layers=2;
   descr.step=3;
   {
      int temp[] = {4};                                  // Heads
      if(ArrayCopy(descr.heads, temp) < (int)temp.Size())
         return false;
   }
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Die vollständige Architektur der Modelle finden Sie in den beigefügten Dateien.

Kommen wir nun zur letzten Phase unserer Arbeit - der Bewertung der Wirksamkeit der umgesetzten Ansätze anhand von Daten aus der Praxis.

3. Tests

Wir haben beträchtliche Anstrengungen unternommen, um die Methoden der gerichteten Diffusion mit MQL5 zu implementieren. Jetzt ist es an der Zeit, ihre Leistung in realen Handelsszenarien zu bewerten. Zu diesem Zweck haben wir unsere Modelle mit den vorgeschlagenen Ansätzen auf realen EURUSD-Daten aus dem Jahr 2023 trainiert. Für den Trainingsprozess wurden historische Daten im H1-Zeitrahmen verwendet.

Wie in früheren Arbeiten verwendeten wir eine Offline-Trainingsstrategie mit regelmäßigen Aktualisierungen des Trainingsdatensatzes, um ihn an die aktuelle Politik des Akteurs anzupassen.

Wie bereits erwähnt, basiert die Architektur des neuen Zustandscodierers weitgehend auf dem in unserem vorherigen Artikel vorgestellten Modell. Um einen fairen Leistungsvergleich zu ermöglichen, haben wir die Testparameter des neuen Modells mit denen des Basismodells identisch gehalten. Die Bewertungsergebnisse für die ersten drei Monate des Jahres 2024 sind nachstehend aufgeführt.

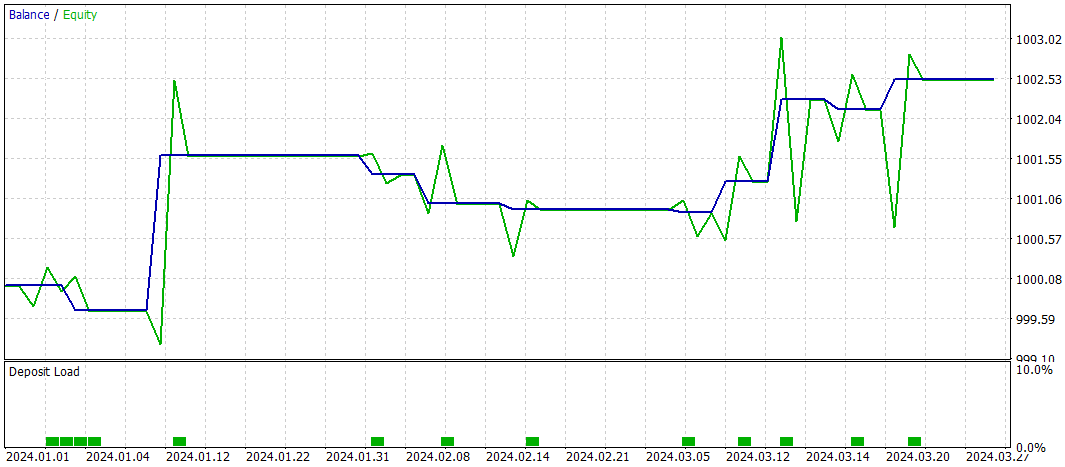
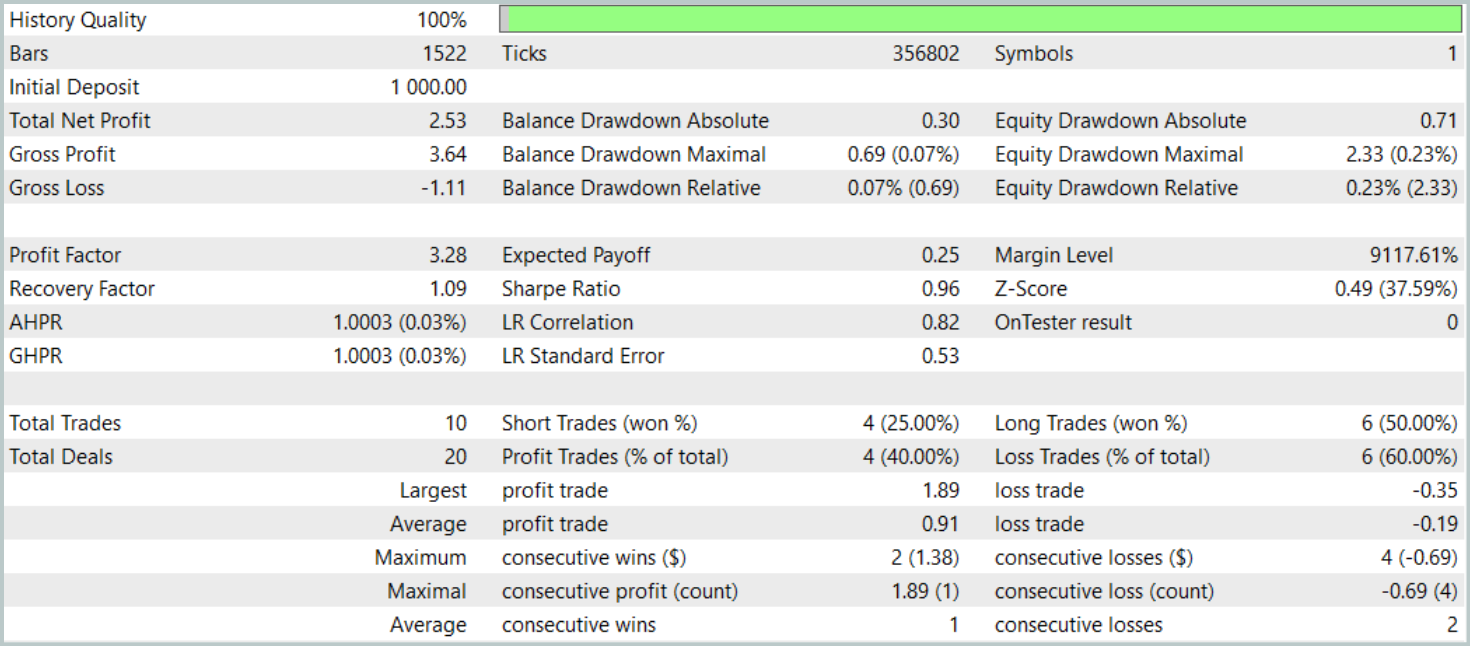
Während des Testzeitraums führte das Modell nur 10 Handelsgeschäfte aus. Dies ist eine auffallend niedrige Frequenz. Außerdem waren nur 4 dieser Handelsgeschäfte gewinnbringend. Kein beeindruckendes Ergebnis. Allerdings waren sowohl der durchschnittliche als auch der maximale Gewinn pro Gewinngeschäft etwa fünfmal so hoch wie bei den Verlustgeschäften. Im Ergebnis erreichte das Modell einen Gewinnfaktor von 3,28.

Im Allgemeinen wies das Modell ein gutes Gewinn-Verlust-Verhältnis auf, allerdings deutet die begrenzte Anzahl von Handelsgeschäften darauf hin, dass wir die Handelsfrequenz erhöhen sollten. Idealerweise ohne Kompromisse bei der Handelsqualität.

Schlussfolgerung

Direktionale Diffusionsmodelle (DDMs) bieten ein vielversprechendes Werkzeug für die Analyse und Darstellung von Marktdaten in Handelsanwendungen. Angesichts der Tatsache, dass die Finanzmärkte aufgrund komplexer struktureller Beziehungen und externer makroökonomischer Faktoren häufig anisotrope und gerichtete Muster aufweisen. Herkömmliche Diffusionsmodelle, die auf isotropen Prozessen beruhen, können diese Nuancen nicht wirksam erfassen. DDMs hingegen passen sich durch die Verwendung von Richtungsrauschen an die Richtungsabhängigkeit der Daten an und ermöglichen eine bessere Identifizierung wichtiger Muster und Trends selbst in Umgebungen mit hohem Rauschen und hoher Volatilität.

Im praktischen Teil haben wir unsere Vision der vorgeschlagenen Ansätze mit MQL5 umgesetzt. Wir haben die Modelle auf realen historischen Marktdaten trainiert und ihre Leistung auf Out-of-Sample-Daten bewertet. Auf der Grundlage der experimentellen Ergebnisse kommen wir zu dem Schluss, dass DDMs ein großes Potenzial aufweisen. Unsere derzeitige Implementierung bedarf jedoch noch weiterer Optimierung.

Referenzen

• Directional diffusion models for graph representation learning
• Andere Artikel dieser Serie

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	EA zum Sammeln von Beispielen
2	ResearchRealORL.mq5	Expert Advisor	EA zum Sammeln von Beispielen mit der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modelltraining EA
4	Test.mq5	Expert Advisor	Modelltraining EA
5	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
6	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
7	NeuroNet.cl	Bibliothek	OpenCL-Programmcode-Bibliothek