MetaTrader 5 / Handelssysteme
English Русский 中文 Español 日本語 Português
preview
Neuronale Netze leicht gemacht (Teil 4): Rekurrente Netze

Neuronale Netze leicht gemacht (Teil 4): Rekurrente Netze

MetaTrader 5 — Handelssysteme | 23 Dezember 2020, 10:32
1 133 0
Dmitriy Gizlyk
Dmitriy Gizlyk

Inhalt


Einführung

Wir fahren mit der Untersuchung Neuronaler Netze fort. Wir haben zuvor das Multilayer Perceptron und die Convolutionalen Neuronalen Netze besprochen. Sie alle arbeiten mit statischen Daten im Rahmen von Markov-Prozessen, wonach der nachfolgende Zustand des Systems nur von seinem aktuellen Zustand und nicht vom Zustand des Systems in der Vergangenheit abhängt. Ich schlage nun vor, Rekurrente Neuronale Netze zu betrachten. Dies ist ein spezieller Typ von Neuronalen Netzen, der für die Arbeit mit Zeitsequenzen entwickelt wurde und als führend in diesem Bereich gilt.


1. Charakteristische Merkmale Rekurrenter Neuronaler Netze

Alle zuvor besprochenen Typen von Neuronalen Netzwerken arbeiten mit einer vorgegebenen Datenmenge. In unserem Fall ist es jedoch schwierig, die ideale Menge an analysierten Daten für Preisdiagramme zu bestimmen. Verschiedene Muster können in verschiedenen Zeitintervallen auftreten. Auch die Intervalle selbst sind nicht immer statisch und können je nach der aktuellen Situation variieren. Manche Ereignisse mögen auf dem Markt selten sein, aber sie treten mit einer hohen Wahrscheinlichkeit auf. Es ist gut, wenn das Ereignis innerhalb des analysierten Datenfensters liegt. Wenn es außerhalb der analysierten Reihe liegt, wird das Neuronale Netzwerk es ignorieren, auch wenn der Markt gerade in diesem Moment eine Reaktion auf dieses Ereignis ausarbeitet. Eine Vergrößerung des analysierten Fensters führt zu einem Anstieg des Verbrauchs von Rechenressourcen und benötigt mehr Zeit, um eine Entscheidung zu treffen.

Um dieses Problem bei der Arbeit mit Zeitreihen zu lösen, wurden Rekurrente Neuronen in Neuronalen Netzwerken vorgeschlagen. Dies ist ein Versuch, ein Kurzzeitgedächtnis in Neuronalen Netzen zu implementieren, bei dem der aktuelle Zustand des Systems zusammen mit dem vorherigen Zustand desselben Neurons in ein Neuron eingespeist wird. Dieses Verfahren basiert auf der Annahme, dass der Wert am Ausgang des Neurons den Einfluss aller Faktoren (einschließlich seines vorherigen Zustands) berücksichtigt und es im nächsten Schritt "sein ganzes Wissen" auf seinen zukünftigen Zustand überträgt. Dies ist ähnlich wie bei uns, wenn wir auf der Grundlage unserer früheren Erfahrungen und früher durchgeführten Handlungen handeln. Die Gedächtnisdauer und ihr Einfluss auf den aktuellen Neuronenzustand hängen von den Gewichten ab.

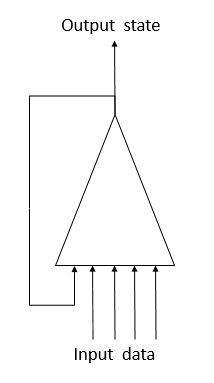
Leider hat eine solch einfache Lösung auch ihre Nachteile. Dieser Ansatz erlaubt das Speichern des "Gedächtnisses" für ein kurzes Zeitintervall. Die zyklische Multiplikation des Signals mit einem Faktor kleiner als 1 und die Anwendung der Neuronen-Aktivierungsfunktion führen zu einer allmählichen Abschwächung des Signals, wenn die Anzahl der Zyklen steigt. Um dieses Problem zu lösen, schlugen Sepp Hochreiter und Jürgen Schmidhuber 1997 die Verwendung der Long Short-Term Memory (LSTM) Architektur vor. Der LTSM-Algorithmus gilt als eine der besten Lösungen für die Probleme der Zeitreihenklassifizierung und -prognose, bei denen signifikante Ereignisse zeitlich getrennt sind und sich über Zeitintervalle erstrecken.

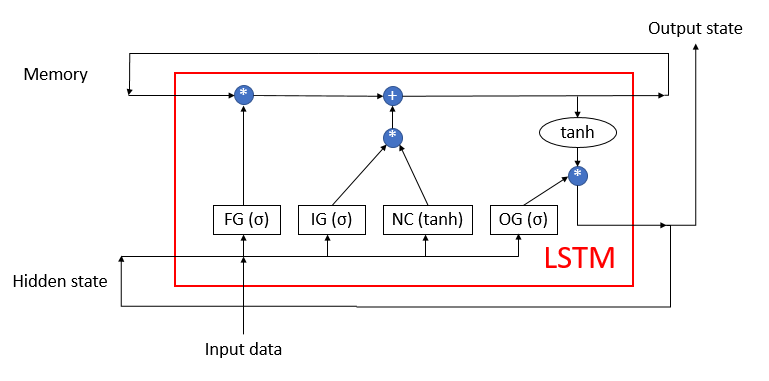
Das LSTM kann kaum als Neuron bezeichnet werden. Es ist bereits ein Neuronales Netzwerk mit 3 Eingangskanälen und 3 Ausgangskanälen. Der Datenaustausch mit der Außenwelt erfolgt nur über zwei Kanäle (einer für die Eingabe, der andere für die Ausgabe). Die restlichen vier Kanäle sind paarweise für den zyklischen Informationsaustausch geschlossen (Gedächtnis und verborgener Zustand).

Der LSTM-Block enthält zwei Hauptdatenströme, die durch 4 vollständig verbundene neuronale Schichten miteinander verbunden sind. Alle neuronalen Schichten enthalten die gleiche Anzahl von Neuronen, die der Größe des Ausgangsdatenstroms und des Gedächtnisdatenstroms entspricht. Betrachten wir den Algorithmus im Detail.

Der Gedächtnisdatenstrom wird verwendet, um wichtige Informationen zu speichern und über die Zeit zu übertragen. Er wird zunächst mit Nullwerten initialisiert und wird dann während des Betriebs des Neuronalen Netzes aufgefüllt. Dies kann mit einem Menschen verglichen werden, der ohne Wissen geboren wird und im Laufe seines Lebens lernt.

Der Strom des Hidden state (verborgen Zustandes) ist für die Übertragung des Ausgangssystemzustands über die Zeit vorgesehen. Die Größe des Datenkanals ist gleich dem Datenkanal "Memory" (Gedächtnis).

Die Kanäle Eingangsdaten und Ausgangsdaten sind für den Austausch von Informationen mit der Außenwelt vorgesehen.

Drei Datenströme werden in den Algorithmus eingespeist:

  • Input data (Eingangsdaten) beschreiben den aktuellen Zustand des Systems.
  • Memory und Hidden state werden vom vorherigen Zustand empfangen.

Zu Beginn des Algorithmus werden die Informationen aus Eingabedaten und Hidden state zu einem einzigen Datenfeld zusammengefasst, das dann an alle 4 versteckten neuronale Schichten des LSTM geleitet wird. 

Die erste neuronale Schicht, "Forget gate", bestimmt, welche der empfangenen Daten im Gedächtnis vergessen werden können und welche erinnert werden sollen. Sie ist als vollverknüpfte neuronale Schicht mit einer sigmoidalen Aktivierungsfunktion implementiert. Die Anzahl der Neuronen in der Schicht entspricht der Anzahl der Gedächtniszellen im Memory-Stream. Jedes Neuron der Schicht empfängt am Eingang das gesamte Array der Eingangsdaten und des Hidden State Streams und gibt eine Zahl im Bereich von 0 (komplett vergessen) bis 1 (im Gedächtnis speichern) aus. Das elementweise Produkt der Ausgangsdaten der neuronalen Schicht mit dem Gedächtnisstrom ergibt das korrigierte Gedächtnis.

Im nächsten Schritt bestimmt der Algorithmus, welche der in diesem Schritt erhaltenen Daten im Gedächtnis abgelegt werden sollen. Zu diesem Zweck werden die folgenden zwei neuronalen Schichten verwendet:

  • Neuer Inhalt — eine vollständig verbundene neuronale Schicht mit einer hyperbolischen Tangens als Aktivierungsfunktion. Sie normalisiert die empfangenen Informationen im Bereich von -1 bis 1.
  • Eingabetor — eine voll verbundene neuronale Schicht mit Sigmoid als Aktivierungsfunktion. Es ist ähnlich wie das Forget gate und bestimmt, welche neuen Daten gespeichert werden sollen.

Das elementweise Produkt aus Neuem Inhalt und Eingabetor wird zu den Werten der Gedächtniszellen addiert. Als Ergebnis dieser Operationen erhalten wir einen aktualisierten Gedächtniszustand, der dann in den nächsten Iterationszyklus eingegeben wird.

Nach der Aktualisierung des Gedächtnisses sollen die Werte des Ausgangsstroms erzeugt werden. Hier wird, ähnlich wie beim Forget-Gate und Input-Gate, das Output-Gate berechnet und der aktuelle Gedächtniswert mit Hilfe des hyperbolischen Tangens normalisiert. Das elementweise Produkt der beiden empfangenen Datensätze ergibt das Array der Output-Signale, das vom LSTM nach außen ausgegeben wird. Das gleiche Datenarray wird dem nächsten Iterationszyklus als Hidden State Stream übergeben.


2. Trainingsprinzipien Rekurrenter Netze

Rekurrente Neuronale Netze werden mit der bereits bekannten Backpropagation-Methode trainiert. Ähnlich wie beim Training von Convolutionalen Neuronalen Netzen wird die zyklische Natur des Prozesses in der Zeit in ein mehrschichtiges Perzeptron zerlegt. Jedes Zeitintervall in einem solchen Perceptron fungiert als eine versteckte Schicht. Allerdings wird für alle Schichten eines solchen Perzeptrons eine Matrix von Gewichten verwendet. Um die Gewichte anzupassen, nehmen wir daher die Summe der Gradienten für alle Schichten und berechnen das Delta der Gewichte einmal für den Gesamtgradienten über alle Schichten.


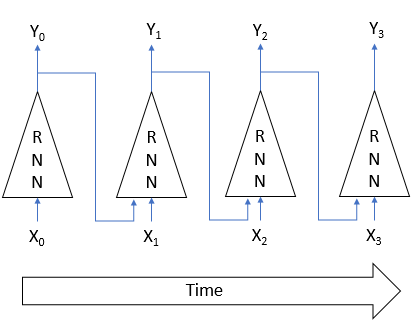
3. Aufbau eines Rekurrenten Neuronalen Netzes

Wir werden den LSTM-Block verwenden, um unser Rekurrentes Neuronales Netz aufzubauen. Beginnen wir mit dem Erstellen der Klasse CNeuronLSTM. Um die Klassenvererbungsstruktur, die im vorherigen Artikel erstellt wurde, beizubehalten, werden wir die neue Klasse von der Klasse KNeuronProof ableiten.

class CNeuronLSTM    :  public CNeuronProof
  {
protected:
   CLayer            *ForgetGate;
   CLayer            *InputGate;
   CLayer            *OutputGate;
   CLayer            *NewContent;
   CArrayDouble      *Memory;
   CArrayDouble      *Input;
   CArrayDouble      *InputGradient;
   //---
   virtual bool      feedForward(CLayer *prevLayer);
   virtual bool      calcHiddenGradients(CLayer *&nextLayer);
   virtual bool      updateInputWeights(CLayer *&prevLayer);
   virtual bool      updateInputWeights(CLayer *gate, CArrayDouble *input_data);
   virtual bool      InitLayer(CLayer *layer, int numOutputs, int numOutputs);
   virtual CArrayDouble *CalculateGate(CLayer *gate, CArrayDouble *sequence);

public:
                     CNeuronLSTM(void);
                    ~CNeuronLSTM(void);
   virtual bool      Init(uint numOutputs,uint myIndex,int window, int step, int units_count);
   //---
   virtual CLayer    *getOutputLayer(void)  { return OutputLayer;  }
   virtual bool      calcInputGradients(CLayer *prevLayer) ;
   virtual bool      calcInputGradients(CNeuronBase *prevNeuron, uint index) ;
   //--- methods for working with files
   virtual bool      Save( int const file_handle);
   virtual bool      Load( int const file_handle);
   virtual int       Type(void)   const   {  return defNeuronLSTM;   }
  };

Die Elternklasse enthält eine Schicht von Ausgangsneuronen OutputLayer. Fügen wir 4 neuronale Schichten hinzu, die für den Betrieb des Algorithmus erforderlich sind: ForgetGate, InputGate, OutputGate und NewContent. Außerdem werden 3 Arrays hinzugefügt, um "Gedächtnis"-Daten zu speichern, um Eingangsdaten und verborgener Zustand zu kombinieren, sowie den Fehlergradienten der Eingangsdaten. Der Name und die Funktionalität der Methoden der Klasse entsprechen denen, die schon früher betrachtet wurden. Ihre Codes weisen jedoch einige Unterschiede auf, die für den Betrieb des Algorithmus erforderlich sind. Lassen Sie uns die Hauptmethoden genauer betrachten.

3.1. Methode zur Initialisierung der Klasse.

Die Klasseninitialisierungsmethode erhält in den Parametern die Grundinformationen über den zu erstellenden Block. Die Namen der Methodenparameter wurden von der Basisklasse geerbt, aber einige von ihnen haben jetzt eine andere Bedeutung:

  • numOutputs — die Anzahl der ausgehenden Verbindungen. Sie wird verwendet, wenn der LSTM-Block-Schicht eine vollständig verbundene Schicht folgt.
  • myIndex — Index eines Neurons in der Schicht. Er wird zur Blockidentifikation verwendet.
  • window — Größe des Eingangsdatenkanals.
  • step — nicht verwendet.
  • units_count  — die Breite des Ausgangskanals und die Anzahl der Neuronen in den verborgenen Schichten des Blocks. Alle neuronalen Schichten eines Blocks enthalten die gleiche Anzahl von Neuronen. 

bool CNeuronLSTM::Init(uint numOutputs,uint myIndex,int window,int step,int units_count)
  {
   if(units_count<=0)
      return false;
//--- Init Layers
   if(!CNeuronProof::Init(numOutputs,myIndex,window,step,units_count))
      return false;
   if(!InitLayer(ForgetGate,units_count,window+units_count))
      return false;
   if(!InitLayer(InputGate,units_count,window+units_count))
      return false;
   if(!InitLayer(OutputGate,units_count,window+units_count))
      return false;
   if(!InitLayer(NewContent,units_count,window+units_count))
      return false;
   if(!Memory.Reserve(units_count))
      return false;
   for(int i=0; i<units_count; i++)
      if(!Memory.Add(0))
         return false;
//---
   return true;
  }

Innerhalb der Methode prüfen wir zunächst, ob in jeder neuronalen Schicht des Blocks mindestens ein Neuron angelegt wurde. Dann rufen wir die entsprechende Methode der Basisklasse auf. Nach dem erfolgreichen Abschluss der Methode initialisieren wir die versteckten Schichten des Blocks, wobei die Operationen, die sich für jede Schicht wiederholen, in einer separaten Methode InitLayer bereitgestellt werden. Sobald die Initialisierung der neuronalen Schichten abgeschlossen ist, wird das Gedächtnis-Array mit Nullwerten initialisiert.

Die Methode InitLayer zur Initialisierung der neuronalen Schicht erhält als Parameter einen Zeiger auf das Objekt der initialisierten neuronalen Schicht, die Anzahl der Neuronen in der Schicht und die Anzahl der ausgehenden Verbindungen. Zu Beginn der Methode wird die Gültigkeit des empfangenen Zeigers überprüft. Wenn der Zeiger ungültig ist, erzeugen wir eine neue Instanz der Klasse der neuronalen Schicht. Wenn der Zeiger gültig ist, löschen wir die Schicht der Neuronen.

bool CNeuronLSTM::InitLayer(CLayer *layer,int numUnits, int numOutputs)
  {
   if(CheckPointer(layer)==POINTER_INVALID)
     {
      layer=new CLayer(numOutputs);
      if(CheckPointer(layer)==POINTER_INVALID)
         return false;
     }
   else
      layer.Clear();

Wir füllen die Schicht mit der gewünschten Anzahl von Neuronen. Wenn in einer der Methodenstufen ein Fehler auftritt, verlassen wir die Funktion mit dem Ergebnis false.

   if(!layer.Reserve(numUnits))
      return false;
//---
   CNeuron *temp;
   for(int i=0; i<numUnits; i++)
     {
      temp=new CNeuron();
      if(CheckPointer(temp)==POINTER_INVALID)
         return false;
      if(!temp.Init(numOutputs+1,i))
         return false;
      if(!layer.Add(temp))
         return false;
     }
//---
   return true;
  }

Nach erfolgreicher Beendigung aller Iterationen verlassen wir die Methode mit dem Ergebnis true.

3.2. Vorwärtsdurchgang.

Der Vorwärtsdurchgang ist in der Methode feedForward implementiert. Die Methode erhält als Parameter einen Zeiger auf die vorherige neuronale Schicht. Zu Beginn der Methode wird die Gültigkeit des empfangenen Zeigers und die Verfügbarkeit der Neuronen in der vorherigen Schicht überprüft. Überprüfen wir auch die Gültigkeit des für die Eingabedaten verwendeten Arrays. Wenn das Objekt noch nicht erstellt wurde, erstellen wir eine neue Instanz der Klasse. Wenn bereits ein Objekt vorhanden ist, löschen wir das Array.

bool CNeuronLSTM::feedForward(CLayer *prevLayer)
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID || prevLayer.Total()<=0)
      return false;
   CNeuronBase *temp;
   CConnection *temp_con;
   if(CheckPointer(Input)==POINTER_INVALID)
     {
      Input=new CArrayDouble();
      if(CheckPointer(Input)==POINTER_INVALID)
         return false;
     }
   else
      Input.Clear();

Als Nächstes kombinieren wir die Daten des aktuellen Systemzustands mit den Daten über den Zustand im vorherigen Zeitintervall in einem einzigen Eingangsdaten-Array Input. 

   int total=prevLayer.Total();
   if(!Input.Reserve(total+OutputLayer.Total()))
      return false;
   for(int i=0; i<total; i++)
     {
      temp=prevLayer.At(i);
      if(CheckPointer(temp)==POINTER_INVALID || !Input.Add(temp.getOutputVal()))
         return false;
     }
   total=OutputLayer.Total();
   for(int i=0; i<total; i++)
     {
      temp=OutputLayer.At(i);
      if(CheckPointer(temp)==POINTER_INVALID || !Input.Add(temp.getOutputVal()))
         return false;
     }
   int total_data=Input.Total();

Berechnen wir den Wert des Gates. Ähnlich wie bei der Initialisierung verschieben wir die für jedes Tor wiederholten Operationen in eine eigene Methode CalculateGate. Rufen wir hier diese Methode auf und tragen darin den Zeiger auf das bearbeitete Gate und das anfängliche Datenarray ein.

//--- Calculated forget gate
   CArrayDouble *forget_gate=CalculateGate(ForgetGate,Input);
   if(CheckPointer(forget_gate)==POINTER_INVALID)
      return false;
//--- Calculated input gate
   CArrayDouble *input_gate=CalculateGate(InputGate,Input);
   if(CheckPointer(input_gate)==POINTER_INVALID)
      return false;
//--- Calculated output gate
   CArrayDouble *output_gate=CalculateGate(OutputGate,Input);
   if(CheckPointer(output_gate)==POINTER_INVALID)
      return false;

Berechnen und normalisieren der eingehenden Daten in das Array new_content.

//--- Calculated new content
   CArrayDouble *new_content=new CArrayDouble();
   if(CheckPointer(new_content)==POINTER_INVALID)
      return false;
   total=NewContent.Total();
   for(int i=0; i<total; i++)
     {
      temp=NewContent.At(i);
      if(CheckPointer(temp)==POINTER_INVALID)
         return false;
      double val=0;
      for(int c=0; c<total_data; c++)
        {
         temp_con=temp.Connections.At(c);
         if(CheckPointer(temp_con)==POINTER_INVALID)
            return false;
         val+=temp_con.weight*Input.At(c);
        }
      val=TanhFunction(val);
      temp.setOutputVal(val);
      if(!new_content.Add(val))
         return false;
     }

Berechnen wir schließlich, nach allen Zwischenberechnungen, das Gedächtnisarray "memory" und ermitteln die Ausgangsdaten.

//--- Calculated output sequences
   for(int i=0; i<total; i++)
     {
      double value=Memory.At(i)*forget_gate.At(i)+new_content.At(i)*input_gate.At(i);
      if(!Memory.Update(i,value))
         return false;
      temp=OutputLayer.At(i);
      value=TanhFunction(value)*output_gate.At(i);
      temp.setOutputVal(value);
     }

Löschen wir dann die Zwischendaten-Arrays und beenden die Methode mit true.

   delete forget_gate;
   delete input_gate;
   delete new_content;
   delete output_gate;
//---
   return true;
  }

In der obigen Methode CalculateGate wird die Matrix der Gewichte mit dem Ausgangsdatenvektor multipliziert, gefolgt von einer Datennormalisierung durch die Sigmoid-Aktivierungsfunktion. Diese Methode erhält als Parameter 2 Zeiger auf Objekte der neuronalen Schicht und die ursprüngliche Datensequenz. Überprüfen wir zunächst die Gültigkeit der erhaltenen Zeiger.

CArrayDouble *CNeuronLSTM::CalculateGate(CLayer *gate,CArrayDouble *sequence)
  {
   CNeuronBase *temp;
   CConnection *temp_con;
   CArrayDouble *result=new CArrayDouble();
   if(CheckPointer(gate)==POINTER_INVALID)
      return NULL;

Als Nächstes implementieren wir eine Schleife über alle Neuronen. 

   int total=gate.Total();
   int total_data=sequence.Total();
   for(int i=0; i<total; i++)
     {
      temp=gate.At(i);
      if(CheckPointer(temp)==POINTER_INVALID)
        {
         delete result;
         return NULL;
        }

Nach der Überprüfung der Gültigkeit des Zeigers auf das Neuron-Objekt implementieren wir eine verschachtelte Schleife über alle Gewichte des Neurons, während wir die Summe der Produkte der Gewichte mit dem entsprechenden Element im Ausgangsdaten-Array berechnen.

      double val=0;
      for(int c=0; c<total_data; c++)
        {
         temp_con=temp.Connections.At(c);
         if(CheckPointer(temp_con)==POINTER_INVALID)
           {
            delete result;
            return NULL;
           }
         val+=temp_con.weight*(sequence.At(c)==DBL_MAX ? 1 : sequence.At(c));
        }

Die resultierende Summe der Produkte wird durch die Aktivierungsfunktion geleitet. Das Ergebnis wird in den Ausgang des Neurons geschrieben und dem Array hinzugefügt. Nach erfolgreicher Iteration über alle Neuronen in der Schicht verlassen wir die Methode, indem wir ein Array mit Ergebnissen zurückgeben. Wenn in irgendeinem Berechnungsschritt ein Fehler aufgetreten ist, gibt die Methode einen leeren Wert zurück.

      val=SigmoidFunction(val);
      temp.setOutputVal(val);
      if(!result.Add(val))
        {
         delete result;
         return NULL;
        }
     }
//---
   return result;
  }

3.3. Berechnung des Fehlergradienten.

Fehlergradienten werden in der Methode calcHiddenGradients berechnet, die in den Parametern einen Zeiger auf die nächste Schicht von Neuronen erhält. Überprüfen wir zu Beginn der Methode die Relevanz des zuvor angelegten Objekts, das zum Speichern der Folge von Fehlergradienten verwendet wird, zu den Originaldaten. Wenn das Objekt noch nicht vorhanden ist, legen wir eine neue Instanz an. Wenn bereits ein Objekt vorhanden ist, löschen wir das Array. Deklarieren wir außerdem interne Variablen und Klasseninstanzen.

bool CNeuronLSTM::calcHiddenGradients(CLayer *&nextLayer)
  {
   if(CheckPointer(InputGradient)==POINTER_INVALID)
     {
      InputGradient=new CArrayDouble();
      if(CheckPointer(InputGradient)==POINTER_INVALID)
         return false;
     }
   else
      InputGradient.Clear();
//---
   int total=OutputLayer.Total();
   CNeuron *temp;
   CArrayDouble *MemoryGradient=new CArrayDouble();
   CNeuron *gate;
   CConnection *con;

Berechnen wir anschließend den Fehlergradienten für die Ausgangsschicht der Neuronen, die aus der nächsten neuronalen Schicht stammen.

   for(int i=0; i<total; i++)
     {
      temp=OutputLayer.At(i);
      if(CheckPointer(temp)==POINTER_INVALID)
         return false;
      temp.setGradient(temp.sumDOW(nextLayer));
     }

Wir erweitern den resultierenden Gradienten auf alle inneren neuronalen Schichten des LSTMs.

   if(CheckPointer(MemoryGradient)==POINTER_INVALID)
      return false;
   if(!MemoryGradient.Reserve(total))
      return false;
   for(int i=0; i<total; i++)
     {
      temp=OutputLayer.At(i);
      gate=OutputGate.At(i);
      if(CheckPointer(gate)==POINTER_INVALID)
         return false;
      double value=temp.getGradient()*gate.getOutputVal();
      value=TanhFunctionDerivative(Memory.At(i))*value;
      if(i>=MemoryGradient.Total())
        {
         if(!MemoryGradient.Add(value))
            return false;
        }
      else
        {
         value=MemoryGradient.At(i)+value;
         if(!MemoryGradient.Update(i,value))
            return false;
        }
      gate.setGradient(gate.getOutputVal()!=0 && temp.getGradient()!=0 ? temp.getGradient()*temp.getOutputVal()*SigmoidFunctionDerivative(gate.getOutputVal())/gate.getOutputVal() : 0);
      //--- Calcculated gates and new content gradients
      gate=ForgetGate.At(i);
      if(CheckPointer(gate)==POINTER_INVALID)
         return false;
      gate.setGradient(gate.getOutputVal()!=0 && value!=0? value*SigmoidFunctionDerivative(gate.getOutputVal()) : 0);
      gate=InputGate.At(i);
      temp=NewContent.At(i);
      if(CheckPointer(gate)==POINTER_INVALID)
         return false;
      gate.setGradient(gate.getOutputVal()!=0 && value!=0 ? value*temp.getOutputVal()*SigmoidFunctionDerivative(gate.getOutputVal()) : 0);
      temp.setGradient(temp.getOutputVal()!=0 && value!=0 ? value*gate.getOutputVal()*TanhFunctionDerivative(temp.getOutputVal()) : 0);
     }

Nachdem wir die Gradienten auf den inneren neuronalen Schichten berechnet haben, berechnen wir den Fehlergradienten für die Sequenz der Anfangsdaten.

//--- Calculated input gradients
   int total_inp=temp.getConnections().Total();
   for(int n=0; n<total_inp; n++)
     {
      double value=0;
      for(int i=0; i<total; i++)
        {
         temp=ForgetGate.At(i);
         con=temp.getConnections().At(n);
         value+=temp.getGradient()*con.weight;
         //---
         temp=InputGate.At(i);
         con=temp.getConnections().At(n);
         value+=temp.getGradient()*con.weight;
         //---
         temp=OutputGate.At(i);
         con=temp.getConnections().At(n);
         value+=temp.getGradient()*con.weight;
         //---
         temp=NewContent.At(i);
         con=temp.getConnections().At(n);
         value+=temp.getGradient()*con.weight;
        }
      if(InputGradient.Total()>=n)
        {
         if(!InputGradient.Add(value))
            return false;
        }
      else
         if(!InputGradient.Update(n,value))
            return false;
     }

Nachdem alle Gradienten berechnet wurden, löschen wir nicht benötigte Objekte und beenden die Methode mit true.

   delete MemoryGradient;
//---
   return true;
  }

Bitte beachten Sie den folgenden Punkt: Im theoretischen Teil habe ich die Notwendigkeit erwähnt, die Sequenz in der Zeit durchzugehen und die Fehlergradienten in jedem Zeitabschnitt zu berechnen. Dies wurde hier nicht gemacht, da der verwendete Trainingskoeffizient viel kleiner als 1 ist, und der Einfluss des Fehlergradienten auf die vorherigen Zeitintervalle so klein sein wird, dass er ignoriert werden kann, um die Gesamtleistung des Algorithmus zu verbessern. 

3.4. Aktualisieren der Gewichte.

Nachdem wir die Fehlergradienten erhalten haben, müssen wir natürlich die Gewichte aller Neuronalen LSTM-Schichten korrigieren. Diese Aufgabe wird in der Methode updateInputWeights implementiert, die als Parameter einen Zeiger auf die vorherige neuronale Schicht erhält. Bitte beachten Sie, dass die Eingabe eines Zeigers auf die vorherige Schicht nur implementiert ist, um die Vererbungsstruktur zu erhalten.

Überprüfen wir zu Beginn der Methode die Gültigkeit des empfangenen Zeigers und die Verfügbarkeit des Anfangsdatenarrays. Nach erfolgreicher Validierung der Zeiger fahren wir mit der Anpassung der Gewichte der inneren neuronalen Schichten fort. Auch hier werden die sich wiederholenden Aktionen in eine separate Methode updateInputWeights ausgelagert, in deren Parametern wir Zeiger auf eine bestimmte neuronale Schicht und ein Anfangsdatenarray übergeben. Hier wird die Hilfsmethode nacheinander für jede neuronale Schicht aufgerufen.

bool CNeuronLSTM::updateInputWeights(CLayer *&prevLayer)
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(Input)==POINTER_INVALID)
      return false;
//---
   if(!updateInputWeights(ForgetGate,Input) || !updateInputWeights(InputGate,Input) || !updateInputWeights(OutputGate,Input)
      || !updateInputWeights(NewContent,Input))
     {
      return false;
     }
//---
   return true;
  }

Betrachten wir die Operationen, die in der Methode updateInputWeights(CLayer *gate,CArrayDouble *input_data) method durchgeführt werden. Prüfen wir zu Beginn der Methode die Gültigkeit der in den Parametern erhaltenen Zeiger und deklarieren die internen Variablen.

bool CNeuronLSTM::updateInputWeights(CLayer *gate,CArrayDouble *input_data)
  {
   if(CheckPointer(gate)==POINTER_INVALID || CheckPointer(input_data)==POINTER_INVALID)
      return false;
   CNeuronBase *neuron;
   CConnection *con;
   int total_n=gate.Total();
   int total_data=input_data.Total();

Wir erstellen verschachtelten Schleifen, um über alle Neuronen in der Schicht und Gewichte in Neuronen zu iterieren, um die Gewichtsmatrix zu korrigieren. Die Formel für die Korrektur der Gewichte ist die gleiche, die bereits für CNeuron::updateInputWeights(CArrayObj *&prevLayer) besprochen wurde. Allerdings können wir hier nicht die zuvor erstellte Methode verwenden, weil wir damals die Neuronenverbindungen zur Verbindung mit der nächsten Schicht verwendet haben, während sie jetzt zur Verbindung mit der vorherigen Schicht verwendet werden.

   for(int n=0; n<total_n; n++)
     {
      neuron=gate.At(n);
      if(CheckPointer(neuron)==POINTER_INVALID)
         return false;
      for(int i=0; i<total_data; i++)
        {
         con=neuron.getConnections().At(i);
         if(CheckPointer(con)==POINTER_INVALID)
            return false;
         double data=input_data.At(i);
         con.weight+=con.deltaWeight=(neuron.getGradient()!=0 && data!=0 ? eta*neuron.getGradient()*(data!=DBL_MAX ? data : 1) : 0)+alpha*con.deltaWeight;
        }
     }
//---
   return true;
  }

Nach dem Aktualisieren der Gewichtsmatrix verlassen wir die Methode mit true.

Nachdem wir die Klasse erstellt haben, wollen wir kleine Anpassungen an den Verteilern der Basisklasse CNeuronBase vornehmen, damit diese die Instanzen der neuen Klasse korrekt behandeln können. Der vollständige Code aller Methoden und Funktionen steht im Anhang zur Verfügung.


4. Tests

Der neu erstellte LSTM-Block wurde unter den gleichen Bedingungen getestet, die wir im vorherigen Artikel für das Testen von Convolutional Netzen verwendet haben. Zum Testen wurde der Fractal_LSTM Expert Advisor erstellt. Im Wesentlichen ist dies der gleiche Fractal_conv aus dem vorherigen Artikel. Aber in der Funktion OnInit, im Block zur Angabe der Netzwerkstruktur, wurden die Convolutional- und die Subsample-Schicht durch eine Schicht aus 4 LSTM-Blöcken ersetzt (in Analogie zu den 4 Filtern des Faltungsnetzes).

      //---
      desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=4;
      desc.type=defNeuronLSTM;
      desc.window=(int)HistoryBars*12;
      desc.step=(int)HistoryBars/2;
      if(!Topology.Add(desc))
         return INIT_FAILED;

Es wurden keine weiteren Änderungen am EA-Code vorgenommen. Sie finden den gesamten EA-Code und die Klassen im Anhang.

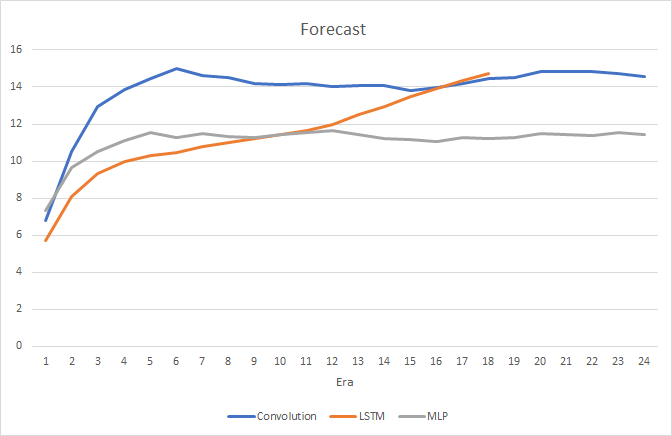
Natürlich haben sich die Verwendung von 4 internen neuronalen Schichten in jedem LSTM-Block und die Komplexität des Algorithmus selbst auf die Leistung ausgewirkt, und so ist die Geschwindigkeit eines solchen Neuronalen Netzes etwas geringer als die des zuvor betrachteten Convolutional Netzes. Allerdings ist der mittlere quadratische Fehler des Rekurrenten Netzes viel geringer.


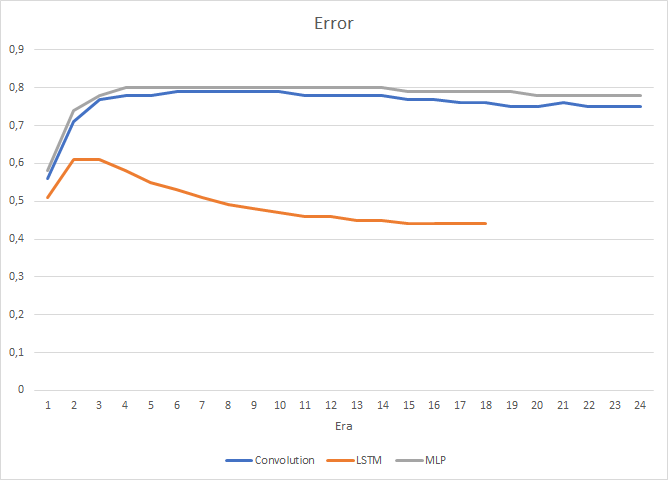
Beim Training des Rekurrenten Neuronalen Netzes weist die Kurve der Zieltreffergenauigkeit einen ausgeprägten, fast geraden Aufwärtstrend auf.

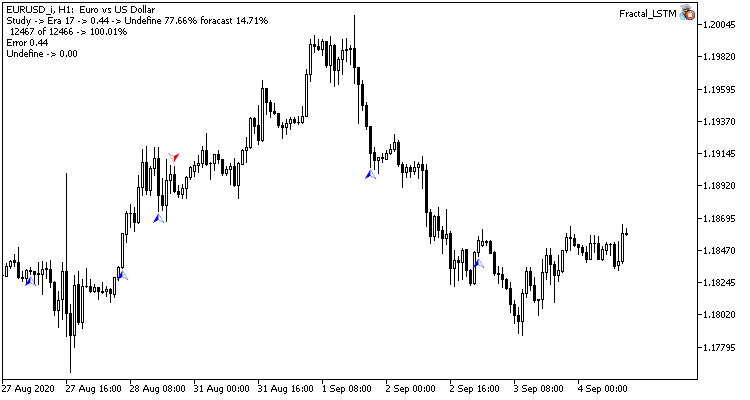
Nur wenige Zeiger auf die vorhergesagten Fraktale sind im Kurschart sichtbar. In den vorherigen Tests war der Kurschart voll mit vorhergesagten Kennzeichen.

Testen eines Rekurrenten Neuronalen Netzes

Schlussfolgerung

In diesem Artikel haben wir den Algorithmus von Rekurrenten Neuronalen Netzen untersucht, einen LSTM-Block gebaut und die Funktionsweise des erstellten Neuronalen Netzes anhand realer Daten getestet. Im Vergleich zu den bisher betrachteten Typen Neuronaler Netze sind Rekurrente Netze ressourcen- und arbeitsintensiver, sowohl während eines Feed-Forward-Durchgangs als auch des Lernprozesses. Dennoch zeigen sie bessere Ergebnisse, was durch durchgeführte Tests bestätigt wurde.

Links

  1. Neuronale Netze leicht gemacht
  2. Neuronale Netze leicht gemacht (Teil 2): Netzwerktraining und Tests
  3. Neuronale Netze leicht gemacht (Teil 3): Convolutional Neurale Netzwerke
  4. Understanding LSTM Networks

Programme, die im diesem Artikel verwendet werden

# Name Typ Beschreibung
1 Fractal.mq5   Expert Advisor  Ein Expert Advisor mit der Regression durch ein Neuronales Netz (1 Neuron in der Ausgabeschicht)
2 Fractal_2.mq5  Expert Advisor  Ein Expert Advisor mit der Klassifikation durch ein Neuronales Netz (3 Neuron in der Ausgabeschicht)
3 NeuroNet.mqh  Klassenbibliothek  Eine Bibliothek von Klassen zum Erstellen eines Neuronalen Netzes (ein Perceptron)
4 ractal_conv.mq5  Expert Advisor  Ein Expert Advisor mit einem Convolutional Neuronalen Netzwerk (3 Neuronen im Output Layer)
5 Fractal_LSTM.mq5   Expert Advisor  Ein Expert Advisor mit dem Rekurrenten Neuronalen Netz (3 Neuronen in der Ausgangsschicht)


Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/8385

Beigefügte Dateien |
ZIP herunterladen
MQL5.zip (32.06 KB)
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum
Zeitreihen in der Bibliothek DoEasy (Teil 54): Abgeleitete Klassen des abstrakten Basisindikators Zeitreihen in der Bibliothek DoEasy (Teil 54): Abgeleitete Klassen des abstrakten Basisindikators
Der Artikel betrachtet das Erstellen von Klassen von abgeleiteten Objekten des abstrakten Basisindikators. Solche Objekte ermöglichen den Zugriff auf die Funktionen der Erstellung von Indikator-EAs, das Sammeln und Abrufen von Datenwertstatistiken verschiedener Indikatoren und Preise. Außerdem wird eine Kollektion von Indikatorobjekten erstellt, von der aus der Zugriff auf die Eigenschaften und Daten jedes im Programm erstellten Indikators möglich sein wird.
Grid und Martingale: was sind sie und wie verwendet man sie? Grid und Martingale: was sind sie und wie verwendet man sie?
In diesem Artikel werde ich versuchen, im Detail zu erklären, was Grid und Martingale sind, sowie was sie gemeinsam haben. Außerdem werde ich versuchen zu analysieren, wie praktikabel diese Strategien wirklich sind. Der Artikel enthält mathematische und praktische Teile.
Neuronale Netze leicht gemacht (Teil 5): Parallele Berechnungen mit OpenCL Neuronale Netze leicht gemacht (Teil 5): Parallele Berechnungen mit OpenCL
Wir haben bereits einige Arten von Implementierungen neuronaler Netze besprochen. In den betrachteten Netzwerken werden die gleichen Operationen für jedes Neuron wiederholt. Ein logischer weiterer Schritt ist die Nutzung der parallelen Berechnung, die die moderne Technologie bietet, um den Lernprozess des neuronalen Netzwerks zu beschleunigen. Eine der möglichen Implementierungen wird in diesem Artikel beschrieben.
Brute-Force-Ansatz zur Mustersuche Brute-Force-Ansatz zur Mustersuche
In diesem Artikel werden wir nach Marktmustern suchen, Expert Advisors basierend auf den identifizierten Mustern erstellen und prüfen, wie lange diese Muster gültig bleiben, wenn sie überhaupt ihre Gültigkeit behalten.