
Neuronale Netze im Handel: Der Contrastive Muster-Transformer (letzter Teil)
Einführung
Der Transformer Atom-Motif Contrastive (AMCT) kann als ein System betrachtet werden, das die Genauigkeit der Vorhersage von Markttrends und -mustern durch die Integration von zwei Analyseebenen verbessert: atomare Elemente und komplexe Strukturen. Der Kerngedanke ist, dass Kerzen und die aus ihnen gebildeten Muster verschiedene Darstellungen desselben Marktszenarios sind. Dies ermöglicht einen natürlichen Abgleich der beiden Darstellungen während des Modelltrainings. Durch die Extraktion zusätzlicher Informationen, die diesen verschiedenen Darstellungsebenen eigen sind, kann die Qualität der erstellten Prognosen erheblich verbessert werden.
Darüber hinaus erzeugen ähnliche Marktmuster, die über verschiedene Zeitrahmen oder Instrumente hinweg beobachtet werden, in der Regel ähnliche Signale. Die Anwendung von Methoden des kontrastiven Lernens ermöglicht daher die Identifizierung von Schlüsselmustern und verbessert die Qualität ihrer Interpretation. Zur genaueren Identifizierung von Mustern, die bei der Bestimmung von Markttrends eine entscheidende Rolle spielen, haben die Entwickler des Frameworks AMCT einen eigenschaftsspezifischen Aufmerksamkeitsmechanismus eingeführt, der Kreuzaufmerksamkeits-Techniken beinhaltet.
Die Originalvisualisierung des Frameworks von Atom-Motif Contrastive Transformer, wie sie von den Autoren vorgestellt wurde, ist unten zu sehen.
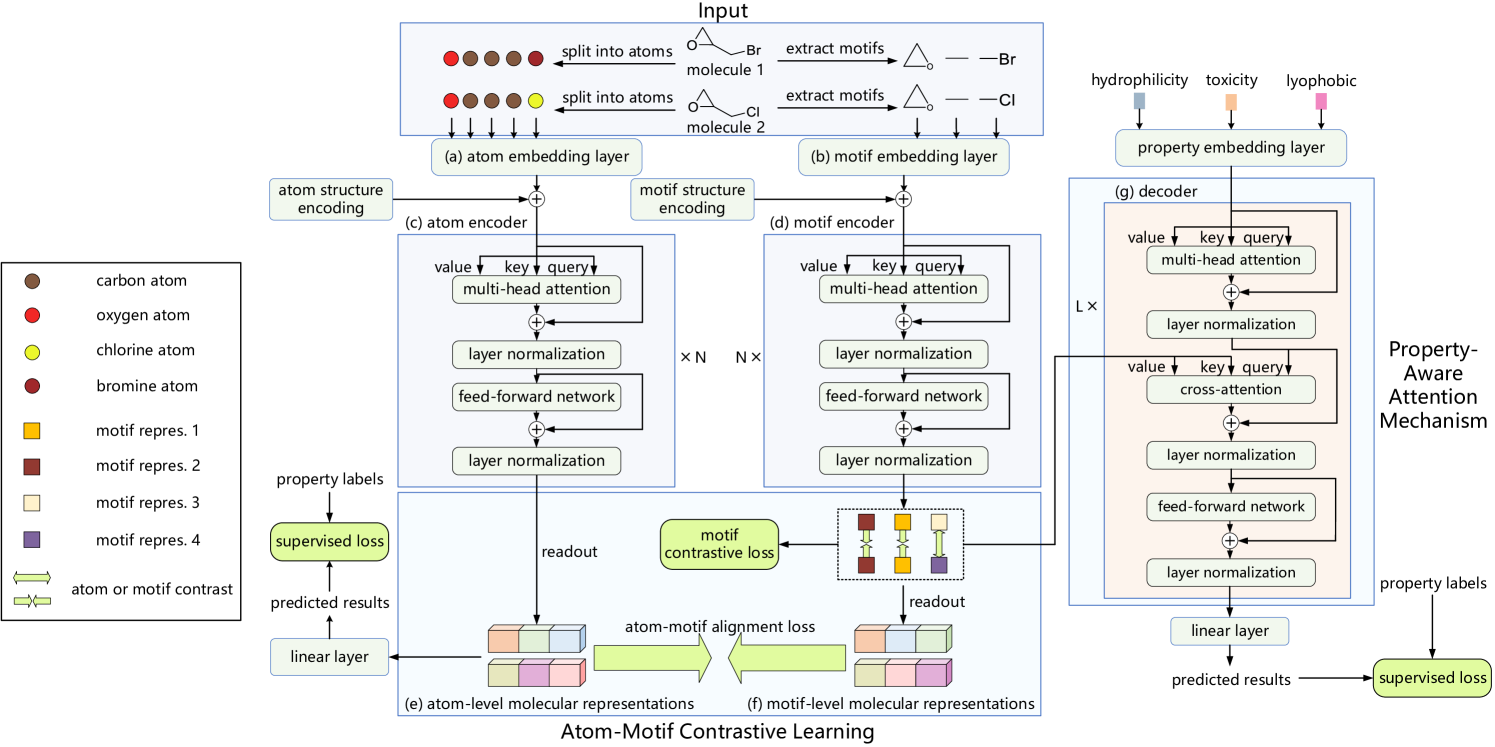
Im vorangegangenen Artikel haben wir die Implementierung von Kerzen- und Muster-Pipelines besprochen und auch eine relative Kreuzaufmerksamkeits-Klasse konstruiert, die wir im Modul zur Analyse der Abhängigkeiten zwischen Marktszenario-Eigenschaften und Kerzen-Mustern verwenden wollen. Heute werden wir diese Arbeit fortsetzen.
1. Analyse der Abhängigkeiten zwischen Eigenschaften und Motiven
Schauen wir uns das Modul, das für die Analyse der Abhängigkeiten zwischen Eigenschaften und Motiven zuständig ist, genauer an. Eine der wichtigsten Fragen dabei ist: Was genau verstehen wir unter „Eigenschaften“? Auf den ersten Blick mag dies eine einfache Frage sein, doch in der Praxis erweist sie sich als recht komplex. Die Autoren des Frameworks AMCT verwendeten ursprünglich verschiedene chemische Eigenschaften, die sie in molekularen Strukturen erkennen und analysieren wollten. Aber wie können wir „Eigenschaften“ im Kontext von Marktszenarien definieren - und noch wichtiger, wie können wir sie genau beschreiben?
Nehmen wir zum Beispiel das Konzept des Trends. In der klassischen technischen Analyseliteratur werden Trends in der Regel in drei Typen eingeteilt: Aufwärtstrend, Abwärtstrend und Seitwärtstrend. Es stellt sich jedoch die Frage, ob diese Klassifizierung für eine eingehende Analyse ausreicht. Wie können wir die Dynamik der Preisbewegung und die Stärke eines Trends genau beschreiben?
Noch mehr Fragen ergeben sich bei der Auswahl von Eigenschaften, die eine Marktsituation im Zusammenhang mit der Lösung konkreter praktischer Aufgaben charakterisieren.
Wenn wir noch keine klare Lösung für dieses Problem haben, sollten wir es aus einem anderen Blickwinkel angehen. Anstatt die Markteigenschaften manuell zu definieren, können wir dem Modell erlauben, sie selbständig aus dem Trainingsdatensatz zu erlernen und so die für die jeweilige Aufgabe relevanten Merkmale zu identifizieren. Ähnlich wie bei den sprachlichen Primitiven, die in der RefMask3D erlernt werden, werden wir einen erlernbaren Tensor von Eigenschaften erzeugen, der auf die Lösung eines bestimmten angewandten Problems zugeschnitten ist. Diesen Algorithmus implementieren wir in der Klasse CNeuronPropertyAwareAttention, deren Struktur im Folgenden dargestellt wird.
class CNeuronPropertyAwareAttention : public CNeuronRMAT { protected: CBufferFloat cTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronPropertyAwareAttention(void) {}; ~CNeuronPropertyAwareAttention(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint properties, uint units_count, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronPropertyAwareAttention; } };
Wir verwenden CNeuronRMAT als übergeordnete Klasse, die einen linearen Modellalgorithmus implementiert. Wie Sie vielleicht wissen, sind die internen Komponenten unserer übergeordneten Klasse in einem einzigen dynamischen Array gekapselt. Dieses Design ermöglicht es uns, die interne Architektur zu ändern, ohne neue Mitgliedsobjekte in der Klassenstruktur zu deklarieren. Es ist lediglich erforderlich, die Initialisierungsmethode des virtuellen Objekts zu überschreiben, in der die erforderliche Abfolge der internen Komponenten erstellt wird. Die einzige Einschränkung ist, dass die Architektur linear bleiben muss.
Leider erfüllt die Kreuzaufmerksamkeits-Architektur die Linearitätsanforderung nicht vollständig, da sie mit zwei separaten Eingangsquellen arbeitet. Daher müssen wir die virtuellen Methoden sowohl für den Vorwärts- als auch für den Rückwärtsdurchlauf außer Kraft setzen. Schauen wir uns die in diesen überschriebenen Methoden implementierten Algorithmen genauer an.
In der Methode Init, die ein neues Objekt initialisiert, erhalten wir Konstanten, die die Architektur des zu erstellenden Objekts eindeutig definieren.
bool CNeuronPropertyAwareAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint properties, uint units_count, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * properties, optimization_type, batch)) return false;
Im Hauptteil der Methode rufen wir sofort die entsprechende Methode der Basisklasse der vollständig verknüpften neuronalen Schicht,CNeuronBaseOCL, auf.
Es ist wichtig zu beachten, dass wir in diesem Fall die Methode von der neuronalen Basisschicht aus aufrufen, nicht von der direkten übergeordneten Klasse. Denn unser Ziel ist es, nur die Basisschnittstellen zu initialisieren. Die Reihenfolge der internen Komponenten wird in unserer Implementierung völlig neu definiert.
Als Nächstes bereiten wir ein dynamisches Array vor, um Zeiger auf die internen Komponenten zu speichern.
cLayers.Clear(); cLayers.SetOpenCL(OpenCL);
Wir deklarieren auch lokale Variablen, um die Zeiger auf die Objekte, die wir erstellen werden, vorübergehend zu speichern.
CNeuronBaseOCL *neuron=NULL; CNeuronRelativeSelfAttention *self_attention = NULL; CNeuronRelativeCrossAttention *cross_attention = NULL; CResidualConv *ff = NULL;
Damit sind die vorbereitenden Arbeiten abgeschlossen und wir können mit der Konstruktion der Abfolge der internen Objekte beginnen. Zunächst erstellen wir 2 aufeinanderfolgende, voll verknüpfte Schichten, um einen trainierbaren Einbettungstensor von Merkmalen zu erzeugen, die die Marktsituation charakterisieren können.
int idx = 0; neuron = new CNeuronBaseOCL(); if (!neuron || !neuron.Init(window * properties, idx, OpenCL, 1, optimization, iBatch) || !cLayers.Add(neuron)) return false; CBufferFloat *temp = neuron.getOutput(); if (!temp.Fill(1)) return false; idx++; neuron = new CNeuronBaseOCL(); if (!neuron || !neuron.Init(0, idx, OpenCL, window * properties, optimization, iBatch) || !cLayers.Add(neuron)) return false;
Hier wenden wir Ansätze an, die in unseren früheren Arbeiten erfolgreich validiert worden sind. Die erste Schicht enthält ein einzelnes Neuron mit einem festen Wert von 1. Die zweite neuronale Schicht erzeugt die erforderliche Folge von Einbettungen, die anhand der Basisfunktionalität des erstellten Objekts trainiert wird. Zeiger auf beide Objekte werden in der Reihenfolge ihres Aufrufs zu unserem dynamischen Array hinzugefügt.
Wir fahren dann fort, eine Struktur zu konstruieren, die einem einfachen Transformer-Decoder sehr ähnlich ist. Die einzige Änderung besteht darin, dass wir die Standard-Aufmerksamkeitsmodule durch Äquivalente ersetzen, die eine relative positionsbezogene Kodierung der analysierten Sequenzstruktur unterstützen. Dazu erstellen wir eine Schleife mit der Anzahl der Iterationen, die der angegebenen Anzahl der internen Schichten entspricht.
for (uint i = 0; i < layers; i++) { idx++; self_attention = new CNeuronRelativeSelfAttention(); if (!self_attention || !self_attention.Init(0, idx, OpenCL, window, window_key, properties, heads, optimization, iBatch) || !cLayers.Add(self_attention) ) { delete self_attention; return false; }
Innerhalb des Schleifenkörpers erstellen und initialisieren wir zunächst eine relative Selbstaufmerksamkeitsschicht, die die Abhängigkeiten zwischen den Einbettungen der erlernbaren Eigenschaften analysiert, die die Marktsituation im Kontext der zu lösenden Aufgabe charakterisieren. Daher wird die Länge der zu analysierenden Sequenz durch den Parameter Eigenschaften bestimmt. Ein Zeiger auf das neu erstellte Objekt wird dann zu unserem dynamischen Array hinzugefügt.
Als Nächstes erstellen wir eine relative Kreuzaufmerksamkeits-Ebene.
idx++; cross_attention = new CNeuronRelativeCrossAttention(); if (!cross_attention || !cross_attention.Init(0, idx, OpenCL, window, window_key, properties, heads, window, units_count, optimization, iBatch) || !cLayers.Add(cross_attention) ) { delete cross_attention; return false; }
Auch hier dienen die Einbettungen der Eigenschaften als primärer Eingabestrom, der die Form des Ergebnistensors bestimmt. Folglich wird die Länge der Sequenz im Vorwärtsdurchlauf-Block ebenfalls gleich der Anzahl der generierten Eigenschaften gesetzt.
idx++; ff = new CResidualConv(); if (!ff || !ff.Init(0, idx, OpenCL, window, window, properties, optimization, iBatch) || !cLayers.Add(ff) ) { delete ff; return false;}
}
Wir fügen Zeiger auf diese neu erstellten Objekte in das dynamische Array ein und fahren mit der nächsten Iteration der Schleife fort.
Sobald die erforderliche Anzahl von Iterationen erfolgreich abgeschlossen ist, enthält unser dynamisches Array alle Objekte, die für die korrekte Implementierung des Moduls benötigt werden, das die Abhängigkeiten zwischen den erlernbaren Eigenschaften und den erkannten Mustern analysiert. Der letzte Schritt besteht darin, die Datenpufferzeiger zu ersetzen, was es uns ermöglicht, die Anzahl der Operationen während des Modelltrainings erheblich zu reduzieren.
if (!SetOutput(ff.getOutput()) || !SetGradient(ff.getGradient())) return false; //--- return true;}
Wir schließen die Methode ab, indem wir ein boolesches Ergebnis, das den Erfolg der Operationen anzeigt, an das aufrufende Programm zurückgeben.
Sobald die Initialisierung des neuen Objekts unserer Klasse abgeschlossen ist, fahren wir mit der Implementierung des Vorwärtsdurchlauf-Algorithmus fort, der in der Methode feedForward definiert ist. Es ist wichtig zu beachten, dass die Methode des Vorwärtsdurchlaufs nur einen einzigen Zeiger auf das Eingangsdatenobjekt erhält, obwohl unsere Blockarchitektur ein Kreuzaufmerksamkeits-Modul enthält. Der Grund dafür ist, dass die zweite Eingabequelle (die „properties“) intern von den Objekten unserer Klasse erzeugt wird.
bool CNeuronPropertyAwareAttention::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Im Hauptteil der Methode wird sofort die Relevanz des empfangenen Zeigers geprüft. Da dieses Objekt als zusätzliche Datenquelle verwendet werden soll, greifen wir direkt auf seine Datenpuffer zu. Ein ungültiger Zeiger in dieser Phase könnte zu einem kritischen Fehler führen.
Wir deklarieren eine lokale Variable, um den Zeiger auf das Eingabeobjekt vorübergehend zu speichern.
CNeuronBaseOCL *neuron = NULL;
Beachten Sie, dass wir diese Variable mit dem Basistyp unserer neuronalen Schichten deklarieren. Dieser Basistyp dient als gemeinsamer Vorfahre für alle unsere internen Objekte der neuronalen Schicht. Dadurch können wir einen Zeiger auf eine der internen Komponenten in der deklarierten Variablen speichern und ihre Basisschnittstellen und überschriebenen Methoden verwenden.
Anschließend arbeiten wir mit unserem Modell zur Erzeugung von Eigenschaftseinbettungen. Seine Objekte werden in den ersten beiden Elementen unseres dynamischen Arrays gespeichert. Die erste neuronale Schicht enthält einen festen Wert, sodass wir sofort die Vorwärtsdurchlauf-Methode des zweiten Objekts aufrufen und den Zeiger auf die erste Schicht als Eingabe übergeben.
if (bTrain) { neuron = cLayers[1]; if (!neuron || !neuron.FeedForward(cLayers[0])) return false; }
Allerdings rufen wir die Vorwärtsdurchlauf-Methode der zweiten Schicht nur während des Trainings auf, da das Modell in dieser Phase lernt, aus den Trainingsdaten die für die aktuelle Aufgabe relevanten Eigenschaftseinbettungen zu extrahieren. Bei der operativen Anwendung verwenden wir stattdessen die zuvor erlernten Eigenschaftseinbettungen. Dadurch bleibt der Output dieser Schicht konstant. Außerdem muss der Einbettungstensor nicht bei jedem Durchgang neu generiert werden. Das Überspringen dieses Schrittes im realen Betrieb verringert die Entscheidungslatenz des Modells.
Danach durchlaufen wir einfach die verbleibenden internen Schichten und rufen nacheinander deren Vorwärtsdurchlauf-Methoden auf. Als Eingaben liefern wir die Ausgabe der vorherigen Schicht zusammen mit dem Ergebnispuffer des in den Methodenparametern erhaltenen Eingabeobjekts.
for (int i = 2; i < cLayers.Total(); i++) { neuron = cLayers[i]; if (!neuron.FeedForward(cLayers[i - 1], NeuronOCL.getOutput())) return false; } //--- return true; }
Die primäre Datenquelle ist hier die Ausgabe der vorherigen Ebene. Dies ist der Hauptdatenstrom, durch den die Einbettungen der erlernbaren Eigenschaften von Marktsituationen geleitet werden. Diese Einbettungen werden von allen Aufmerksamkeitsmodulen und dem Block von FeedForward im Decoder verarbeitet. Die Mustereinbettungen, die als Parameter in die Methode eingehen, stellen Muster dar, die in der Beschreibung der analysierten Marktsituation erkannt wurden. Sie heben die Eigenschaften hervor, die für den aktuellen Kontext am wichtigsten sind. Als Ergebnis gibt der Decoder eine verfeinerte Darstellung der Marktsituation als eine Reihe von Eigenschaften aus, wobei die wichtigsten Merkmale im Vordergrund stehen.
Nach Abschluss aller Iterationen der Schleife gibt die Vorwärtsdurchlauf-Methode einen booleschen Wert an die aufrufende Funktion zurück, der den Erfolg der Operation angibt.
Als Nächstes müssen wir das Rückwärtsdurchlauf-Verfahren konstruieren. Die Methode updateInputWeights, die die Modellparameter aktualisiert, ist recht einfach. Wir rufen einfach die entsprechende Methode für jedes interne Objekt der Reihe nach auf. Die Methode calcInputGradients, mit der die Fehlergradienten verteilt werden, enthält jedoch ein differenzierteres Detail.
Wie Sie wissen, muss der Gradientenverteilungsalgorithmus den Informationsfluss des Vorwärtsdurchlauf-Durchlaufs genau widerspiegeln, jedoch in umgekehrter Reihenfolge, indem er den Fehlergradienten auf alle Komponenten auf der Grundlage ihres Beitrags zur endgültigen Ausgabe verteilt. Wenn ein Objekt als Datenquelle für mehrere Informationsflüsse dient, muss es seinen Anteil am Fehlergradienten von jedem Fluss erhalten.
Werfen Sie einen weiteren Blick auf die Implementierung der Vorwärtsdurchläufe. Der Zeiger des Mustereinbettungsobjekts wird als Parameter an alle internen neuronalen Schichten des Decoders übergeben. Die Module der Selbstaufmerksamkeit und des Vorwärtsdurchlaufs ignorieren dies natürlich, da sie keine zweite Eingangsquelle verwenden. Die Kreuzaufmerksamkeits-Module werden diese Einbettungen jedoch in jeder internen Schicht des Decoders nutzen. Daher müssen wir während der Fehlerrückverfolgung die entsprechenden Anteile des Fehlergradienten aus jedem Kreuzaufmerksamkeits-Modul akkumulieren und die Summe auf das Mustereinbettungsobjekt anwenden.
Die Methode erhält einen Zeiger auf das Mustereinbettungsobjekt als einen ihrer Parameter. Der erste Schritt im Methodenrumpf besteht darin, den Zeiger zu validieren, um sicherzustellen, dass er auf dem neuesten Stand ist und sicher verwendet werden kann.
bool CNeuronPropertyAwareAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Als Nächstes müssen wir einige vorbereitende Arbeiten erledigen. Hier prüfen wir zunächst, ob ein zuvor initialisierter Hilfsdatenpuffer vorhanden ist, in den wir planen, die Zwischenwerte der Fehlergradienten zu schreiben. Wir müssen auch darauf achten, dass die Größe ausreichend ist. Im Falle eines negativen Ergebnisses wird an einem beliebigen Kontrollpunkt ein neuer Datenpuffer von ausreichender Größe initialisiert.
if (cTemp.GetIndex() < 0 || cTemp.Total() < NeuronOCL.Neurons()) { cTemp.BufferFree(); if (!cTemp.BufferInit(NeuronOCL.Neurons(), 0) || !cTemp.BufferCreate(OpenCL)) return false; }
Dann setzen wir den in den Objektparametern erhaltenen Fehlergradientenpuffer zurück.
if (!NeuronOCL.getGradient() || !NeuronOCL.getGradient().Fill(0)) return false;
In der Regel führen wir diesen Vorgang nicht durch, da wir bei der Durchführung von Operationen zur Verteilung von Fehlergradienten die zuvor gespeicherten Werte durch neue Werte ersetzen. Dies ist eine gute Lösung für lineare Modelle. Andererseits zwingt uns eine solche Implementierung dazu, nach Umgehungsmöglichkeiten zu suchen, wenn wir Fehlergradienten von mehreren Pfaden sammeln.
Nach erfolgreichem Abschluss der Vorbereitungsarbeiten führen wir eine Rückwärtsschleife durch die internen Schichten unseres Blocks durch, um den Fehlergradienten auf sie zu verteilen.
CNeuronBaseOCL *neuron = NULL; for (int i = cLayers.Total() - 2; i > 0; i--) { neuron = cLayers[i]; if (!neuron.calcHiddenGradients(cLayers[i + 1], NeuronOCL.getOutput(), GetPointer(cTemp), (ENUM_ACTIVATION)NeuronOCL.Activation())) return false;
Im Hauptteil der Schleife rufen wir die Methode zur Verteilung des Fehlergradienten für jede interne Schicht auf und übergeben ihr die entsprechenden Parameter. Anstelle des Standard-Gradientenpuffers übergeben wir jedoch einen Zeiger auf unseren temporären Datenspeicherpuffer. Sobald die Methode der internen Komponente erfolgreich ausgeführt wurde, überprüfen wir den Typ der neuronalen Schicht. Wie wir wissen, verwenden nicht alle internen Ebenen eine zweite Datenquelle. Wenn die aktuelle Schicht als Kreuzaufmerksamkeits-Modul identifiziert wird, akkumulieren wir den mit der zweiten Eingangsquelle verbundenen Fehlergradienten im Puffer des Mustereinbettungsobjekts und summieren ihn mit den zuvor gesammelten Werten.
if (neuron.Type() == defNeuronRelativeCrossAttention) { if (!SumAndNormilize(NeuronOCL.getGradient(), GetPointer(cTemp), NeuronOCL.getGradient(), 1, false, 0, 0, 0, 1)) return false; } //--- return true;}
Nachdem alle Iterationen der Schleife erfolgreich abgeschlossen wurden, geben wir ein boolsches Ergebnis der Operation an die aufrufende Funktion zurück und beenden die Ausführung der Methode.
Damit ist die Implementierung des eigenschaftsbasierten Aufmerksamkeitsblocks abgeschlossen. Der vollständige Quellcode für diese Klasse und alle ihre Methoden ist im Anhang enthalten.
2. Der AMCT-Rahmen
Wir haben bedeutende Fortschritte gemacht und einzelne Bausteine implementiert, die den Atom-Motif Contrastive Transformer (AMCT) bilden. Nun ist es an der Zeit, diese Module in eine kohärente Architektur zu integrieren. Zu diesem Zweck erstellen wir ein Objekt namens CNeuronAMCT. Seine Struktur ist unten dargestellt.
class CNeuronAMCT : public CNeuronBaseOCL { protected: CNeuronRMAT cAtomEncoder; CNeuronMotifEncoder cMotifEncoder; CLayer cMotifProjection; CNeuronPropertyAwareAttention cPropertyDecoder; CLayer cPropertyProjection; CNeuronBaseOCL cConcatenate; CNeuronMHAttentionPooling cPooling; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronAMCT(void) {}; ~CNeuronAMCT(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint properties, uint units_count, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronAMCT; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
In der dargestellten Struktur sehen wir die Deklaration der Objekte, die wir implementiert haben, und zwei zusätzliche dynamische Arrays. Wir werden etwas später auf ihre Funktionalität eingehen. Alle Objekte werden als statisch deklariert, was es uns ermöglicht, den Konstruktor und den Destruktor der Klasse leer zu lassen. Die Initialisierung sowohl geerbter als auch neu deklarierter Mitglieder wird in der Methode Init durchgeführt.
In den Parametern der Initialisierungsmethode erhalten wir die wichtigsten Konstanten, mit denen wir die Architektur des zu erstellenden Objekts eindeutig bestimmen können.
bool CNeuronAMCT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint properties, uint units_count, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
Im Methodenrumpf rufen wir sofort die gleichnamige Methode der übergeordneten Klasse auf und übergeben ihr einen Teil der erhaltenen Parameter.
Sie haben wahrscheinlich bemerkt, dass die Struktur dieses Objekts keine internen Variablen zur Speicherung der empfangenen Parameterwerte enthält. Alle Konstanten, die die Architektur unserer Klasse definieren, werden ausschließlich für die Initialisierung interner Objekte verwendet, und die erforderlichen Werte werden in diesen Objekten gespeichert. Sowohl bei der Vorwärts- als auch bei der Rückwärtsdurchlauf-Methode interagieren wir nur mit diesen internen Komponenten. Daher vermeiden wir die Einführung unnötiger Variablen auf Klassenebene.
Als Nächstes gehen wir zur Initialisierung der internen Objekte über. Wir beginnen mit der Initialisierung von zwei Pipelines: eine für Kerzen und die andere für Muster.
int idx = 0; if (!cAtomEncoder.Init(0, idx, OpenCL, window, window_key, units_count, heads, layers, optimization, iBatch)) return false; idx++; if (!cMotifEncoder.Init(0, idx, OpenCL, window, window_key, units_count, heads, layers, optimization, iBatch)) return false;
Trotz der architektonischen Unterschiede zwischen diesen Pipelines arbeiten beide mit derselben Eingabedatenquelle, und in diesem Stadium erhalten sie identische Initialisierungsparameter.
Von diesen beiden Pipelines erwarten wir zwei Darstellungen der analysierten Marktsituation: auf der Ebene der Kerzenständer und auf der Ebene der Muster. Der AMCT-Rahmen schlägt vor, diese Darstellungen aufeinander abzustimmen, um ihr gegenseitiges Verständnis zu bereichern und zu verfeinern. Es ist jedoch wichtig zu beachten, dass sich die Dimensionen der Ausgabetensoren der beiden Pipelines unterscheiden. Dieser Umstand erschwert den Anpassungsprozess erheblich. Um dieses Problem zu lösen, verwenden wir ein leichtes Skalierungsmodell, um die Ausgabe der Muster-Pipeline zu transformieren. Zeiger auf diese Skalierungsmodellobjekte werden in einem dynamischen Array namens cMotifProjection gespeichert.
Wir beginnen mit der Initialisierung dieses dynamischen Arrays.
cMotifProjection.Clear(); cMotifProjection.SetOpenCL(OpenCL);
Wir bestimmen die Länge der Musterfolge. Wie Sie wissen, erhalten wir am Ende der Muster-Pipeline einen verketteten Tensor von Einbettungen zweier Ebenen.
int motifs = int(cMotifEncoder.Neurons() / window);
Man beachte, dass sich die Darstellungstensoren nur in der Länge ihrer Sequenzen unterscheiden. Die Vektorgröße, die jedes Sequenzelement beschreibt, bleibt gleich. Daher ist es durchaus sinnvoll, dass der Skalierungsprozess auf einzelne univariate Sequenzen innerhalb des Tensors wirkt. Zu diesem Zweck transponieren wir zunächst den Repräsentationstensor der Musterebene.
idx++; CNeuronTransposeOCL *transp = new CNeuronTransposeOCL(); if (!transp || !transp.Init(0, idx, OpenCL, motifs, window, optimization, iBatch) || !cMotifProjection.Add(transp)) return false;
Dann wenden wir eine Faltungsschicht an, um diese univariaten Sequenzen zu skalieren.
idx++; CNeuronConvOCL *conv = new CNeuronConvOCL(); if (!conv || !conv.Init(0, idx, OpenCL, motifs, motifs, units_count, 1, window, optimization, iBatch) || !cMotifProjection.Add(conv)) return false; conv.SetActivationFunction((ENUM_ACTIVATION)cAtomEncoder.Activation());
Achten Sie darauf, dass die Größe des Eingabefensters und seine Schrittweite gleich der Länge der Sequenz in der Darstellung auf Musterebene sind. In der Zwischenzeit wird die Anzahl der Filter so festgelegt, dass sie der Sequenzlänge der Kerzen-Darstellung entspricht.
Ein weiterer wichtiger Aspekt ist, wie wir die Sequenzlänge und die Anzahl der univariaten Sequenzen definieren. In diesem Fall legen wir fest, dass die Eingabesequenz aus einem einzigen Element besteht. Die Anzahl der univariaten Sequenzen entspricht der Vektorgröße eines einzelnen Sequenzelements aus der Eingabe. Diese Konfiguration ermöglicht es uns, jeder unitären Sequenz der Eingabedaten individuelle lernfähige Gewichtsmatrizen für die Skalierung zuzuweisen. Mit anderen Worten: Jedes Element der ursprünglichen Eingabesequenz wird mit einer eigenen Matrix skaliert. Dies ermöglicht einen flexibleren und besser abgestimmten Transformationsprozess.
Außerdem müssen die Aktivierungsfunktionen zwischen der Ausgabe der Faltungsskalierungsschicht und der Repräsentationspipeline auf Kerzen-Ebene synchronisiert werden.
Anschließend werden die skalierten Daten mit Hilfe einer Datentranspositionsebene in ihr ursprüngliches Layout zurückverwandelt.
idx++; transp = new CNeuronTransposeOCL(); if (!transp || !transp.Init(0, idx, OpenCL, window, units_count, optimization, iBatch) || !cMotifProjection.Add(transp)) return false; transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
Als Nächstes initialisieren wir den Kreuzaufmerksamkeits-Block für Eigenschaften und Muster, der eine Darstellung des analysierten Marktzustands auf der Ebene der Eigenschaften ausgeben soll.
idx++; if (!cPropertyDecoder.Init(0, idx, OpenCL, window, window_key, properties, motifs, heads, layers, optimization, iBatch)) return false;
Und jetzt sind wir am entscheidenden Punkt angelangt. Am Ende der drei Hauptblöcke erhalten wir drei verschiedene Darstellungen eines einzigen Marktszenarios, das wir analysieren. Außerdem ist jede dieser Darstellungen als Tensor mit verschiedenen Dimensionen strukturiert. Und wie geht es weiter? Wie können wir sie nutzen, um praktische Probleme zu lösen? Welche sollten wir wählen, um die höchste Vorhersagequalität zu erreichen?
Ich denke, wir sollten alle drei Darstellungen verwenden. Wir haben das Skalierungsmodell für die Musterdarstellung bereits initialisiert. Nun werden wir ein analoges Modell für die Skalierung der eigenschaftsbasierten Darstellung erstellen. Zeiger auf diese Skalierungsmodell-Objekte werden in dem dynamischen Array cPropertyProjection gespeichert.
cPropertyProjection.Clear(); cPropertyProjection.SetOpenCL(OpenCL); idx++; transp = new CNeuronTransposeOCL(); if (!transp || !transp.Init(0, idx, OpenCL, properties, window, optimization, iBatch) || !cPropertyProjection.Add(transp)) return false; idx++; conv = new CNeuronConvOCL(); if (!conv || !conv.Init(0, idx, OpenCL, properties, properties, units_count, 1, window, optimization, iBatch) || !cPropertyProjection.Add(conv)) return false; conv.SetActivationFunction((ENUM_ACTIVATION)cAtomEncoder.Activation()); idx++; transp = new CNeuronTransposeOCL(); if (!transp || !transp.Init(0, idx, OpenCL, window, units_count, optimization, iBatch) || !cPropertyProjection.Add(transp)) return false; transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
Die drei Darstellungen, die auf eine einheitliche Dimensionalität gebracht wurden, werden zu einem einzigen Tensor verkettet.
idx++; if (!cConcatenate.Init(0, idx, OpenCL, 3 * window * units_count, optimization, iBatch)) return false;
Wir haben einen verketteten Tensor erhalten, der drei verschiedene Perspektiven auf eine einzige Marktsituation kombiniert. Erinnert Sie das nicht an die Ergebnisse der Mehrkopfaufmerksamkeit? Wir haben im Grunde die Ergebnisse von drei Köpfen, und um die endgültigen Werte abzuleiten, verwenden wir eine abhängigkeitsbasierte Pooling-Schicht.
idx++; if(!cPooling.Init(0, idx, OpenCL, window, units_count, 3, optimization, iBatch)) return false;
Als Nächstes ersetzen wir einfach die Datenpuffer in den geerbten Schnittstellen durch die entsprechenden Pooling-Objekte. Auf diese Weise können wir unnötige Datenkopien vermeiden.
if (!SetOutput(cPooling.getOutput(), true) || !SetGradient(cPooling.getGradient(), true)) return false; //--- return true; }
Wir schließen dann die Initialisierungsmethode ab, indem wir einen booleschen Status an das aufrufende Programm zurückgeben, der den Erfolg anzeigt.
Nachdem wir die Initialisierungsmethode unseres Objekts abgeschlossen haben, fahren wir mit der Organisation der Prozesse der Vorwärtsdurchläufe fort. Wie üblich ist der Algorithmus des Vorwärtsdurchlaufs in der Methode feedForward implementiert.
bool CNeuronAMCT::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cAtomEncoder.FeedForward(NeuronOCL)) return false; if(!cMotifEncoder.FeedForward(NeuronOCL)) return false;
Unter den Methodenparametern erhalten wir einen Zeiger auf das Rohdatenobjekt, das wir sofort an unsere beiden Darstellungspipelines weitergeben: die Kerzen-Ebene und die Musterebene.
Die Ausgabe der Muster-Pipeline wird an das Modul für die übergreifende Bearbeitung von Eigenschaften und Mustern weitergeleitet.
if(!cPropertyDecoder.FeedForward(cMotifEncoder.AsObject())) return false;
In diesem Stadium haben wir drei verschiedene Darstellungen der analysierten Marktsituation. Wir bringen sie auf eine einheitliche Datenskala. Zu diesem Zweck wird zunächst eine Skalierung der Darstellung auf Musterebene vorgenommen.
//--- Motifs projection CNeuronBaseOCL *prev = cMotifEncoder.AsObject(); CNeuronBaseOCL *current = NULL; for(int i = 0; i < cMotifProjection.Total(); i++) { current = cMotifProjection[i]; if(!current || !current.FeedForward(prev, NULL)) return false; prev = current; }
Anschließend führen wir ein analoges Skalierungsverfahren für die Darstellung auf Eigenschaftsebene durch.
//--- Property projection prev = cPropertyDecoder.AsObject(); for(int i = 0; i < cPropertyProjection.Total(); i++) { current = cPropertyProjection[i]; if(!current || !current.FeedForward(prev, NULL)) return false; prev = current; }
Nun können wir die drei Darstellungen zu einem einzigen Tensor zusammenfassen.
//--- Concatenate uint window = cAtomEncoder.GetWindow(); uint units = cAtomEncoder.GetUnits(); prev = cMotifProjection[cMotifProjection.Total() - 1]; if(!Concat(cAtomEncoder.getOutput(), prev.getOutput(), current.getOutput(), cConcatenate.getOutput(), window, window, window, units)) return false;
Wir verwenden eine Pooling-Ebene, um eine gewichtete Aggregation der Ergebnisse aus diesen drei Darstellungen zu berechnen.
//--- Out if(!cPooling.FeedForward(cConcatenate.AsObject())) return false; //--- return true; }
Dank der Ersetzung der Pufferzeiger während der Initialisierung vermeiden wir das Kopieren von Daten in die Puffer der Klassenschnittstelle. Wir schließen die Methode einfach ab und geben dem Aufrufer ein boolesches Erfolgsflag zurück.
Der nächste Schritt ist die Entwicklung der Rückwärtsdurchlauf-Methoden. Algorithmisch von besonderem Interesse ist die Gradientenverteilungsmethode calcInputGradients. Die verzweigte Abhängigkeitsstruktur zwischen Informationsflüssen, wie sie von den Autoren von AMCT vorgeschlagen wurde, beeinflusst diesen Methodenalgorithmus stark. Schauen wir uns die Umsetzung im Detail an.
Wie üblich erhält die Methode einen Zeiger auf das Objekt der vorhergehenden Schicht, in das der Fehlergradient entsprechend dem Beitrag der Eingabedaten zum Endergebnis propagiert werden muss.
bool CNeuronAMCT::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Wir überprüfen sofort die Gültigkeit des Zeigers, da jede weitere Operation sinnlos wird, wenn er ungültig ist.
Anschließend verteilen wir den Fehlergradienten sequentiell auf die internen Objekte. Dank der Pufferzeiger, die die Schnittstellenpuffer ersetzen, müssen keine Daten von externen Schnittstellen in interne Objekte kopiert werden. Wir können also sofort damit beginnen, den Fehlergradienten auf interne Objekte zu verteilen. Wir beginnen mit der Berechnung des Fehlergradienten am verketteten Tensor, der die drei Perspektiven des analysierten Umweltzustands darstellt.
if(!cConcatenate.calcHiddenGradients(cPooling.AsObject())) return false;
Anschließend übertragen wir den Fehlergradienten auf die einzelnen Pipelines. Der Gradient für die Kerzen-Darstellung wird sofort an den Encoder weitergeleitet. Die beiden anderen werden an ihre jeweiligen Skalierungsmodelle weitergeleitet.
uint window = cAtomEncoder.GetWindow(); uint units = cAtomEncoder.GetUnits(); CNeuronBaseOCL *motifs = cMotifProjection[cMotifProjection.Total() - 1]; CNeuronBaseOCL *prop = cPropertyProjection[cPropertyProjection.Total() - 1]; if (!motifs || !prop || !DeConcat(cAtomEncoder.getGradient(), motifs.getGradient(), prop.getGradient(), cConcatenate.getGradient(), window, window, window, units)) return false;
Als Nächstes passen wir die Fehlergradienten der einzelnen Repräsentationen entsprechend ihrer Aktivierungsfunktionen an.
if (cAtomEncoder.Activation() != None) { if (!DeActivation(cAtomEncoder.getOutput(), cAtomEncoder.getGradient(), cAtomEncoder.getGradient(), cAtomEncoder.Activation())) return false; if (motifs.Activation() != None) { if (!DeActivation(motifs.getOutput(), motifs.getGradient(), motifs.getGradient(), motifs.Activation())) return false; if (prop.Activation() != None) { if (!DeActivation(prop.getOutput(), prop.getGradient(), prop.getGradient(), prop.Activation())) return false;
Wir fügen auch den Fehlergradienten hinzu, der sich aus dem Abgleich zwischen der Kerzen- und der Musterdarstellung ergibt.
if(!motifs.calcAlignmentGradient(cAtomEncoder.AsObject(), true)) return false;
Anschließend verteilen wir die Fehlergradienten durch die Skalierungsmodelle und iterieren dabei rückwärts durch ihre neuronalen Schichten.
for (int i = cMotifProjection.Total() - 2; i >= 0; i--) { motifs = cMotifProjection[i]; if (!motifs || !motifs.calcHiddenGradients(cMotifProjection[i + 1])) return false; }
for (int i = cPropertyProjection.Total() - 2; i >= 0; i--) { prop = cPropertyProjection[i]; if (!prop || !prop.calcHiddenGradients(cPropertyProjection[i + 1])) return false; }
Der Fehlergradient aus dem Eigenschaftsskalierungsmodell wird an das Kreuzaufmerksamkeits-Modul für Eigenschaften und Muster und anschließend an den Muster- Encoder weitergegeben.
if (!cPropertyDecoder.calcHiddenGradients(cPropertyProjection[0]) || !cMotifEncoder.calcHiddenGradients(cPropertyDecoder.AsObject())) return false;
Es ist zu beachten, dass die Ausgaben des Musterkodierers auch im Skalierungsmodell für die Musterdarstellung verwendet werden. Daher müssen wir den Fehlergradienten dieses sekundären Informationsflusses einbeziehen. Dazu speichern wir zunächst den Zeiger auf den Fehlergradientenpuffer des Muster-Encoders in einer lokalen Variablen. Dann ersetzen wir ihn durch den „Spender“-Puffer.
Als Spenderobjekt haben wir die Verkettungsebene der drei Darstellungen gewählt. Sein Fehlergradient wurde bereits auf die entsprechenden Informationsströme verteilt. Da diese Schicht keine lernbaren Parameter hat, können wir ihren Puffer sicher löschen. Außerdem hat diese Ebene die größte Puffergröße aller internen Objekte in unserem Block, was sie zum optimalen Spenderkandidaten macht.
Nach der Ersetzung des Puffers wird der Fehlergradient aus dem Skalierungsmodell abgerufen. Wir summieren auch die Gradienten aus beiden Informationsströmen und stellen die ursprünglichen Pufferzeiger wieder her. Und schließlich propagieren wir den Fehlergradienten auf die Ebene der Eingangsdaten.
CBufferFloat *temp = cMotifEncoder.getGradient(); if (!cMotifEncoder.SetGradient(cConcatenate.getGradient(), false) || !cMotifEncoder.calcHiddenGradients(cMotifProjection[0]) || !SumAndNormilize(temp, cMotifEncoder.getGradient(), temp, window, false, 0, 0, 0, 1) || !cMotifEncoder.SetGradient(temp, false) || !NeuronOCL.calcHiddenGradients(cMotifEncoder.AsObject())) return false;
Eine ähnliche Situation ergibt sich auf der Ebene der Eingabedaten: Der vom Muster-Encoder empfangene Fehlergradient muss um den Beitrag ergänzt werden, der durch die Kerzen-Encoder Pipeline kommt. Wir wiederholen den Trick der Zeigerersetzung für ein anderes Pufferobjekt entsprechend.
temp = NeuronOCL.getGradient(); if (!NeuronOCL.SetGradient(cConcatenate.getGradient(), false) || !NeuronOCL.calcHiddenGradients(cAtomEncoder.AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, window, false, 0, 0, 0, 1) || !NeuronOCL.SetGradient(temp, false)) return false; //--- return true; }
Nachdem der Fehlergradient nun vollständig auf alle Modellkomponenten und Eingabedaten verteilt wurde, schließt die Methode mit der Rückgabe eines booleschen Ergebnisses an den Aufrufer ab.
Ich möchte zwei wichtige Punkte bei dieser Umsetzung hervorheben. Erstens wird bei der Ersetzung des Pufferzeigers der ursprüngliche Pufferzeiger immer vorher gespeichert. Beim Aufruf der Zeigerersatzmethode setzen wir explizit ein Flag auf false, das die Löschung des zuvor gespeicherten Pufferobjekts verhindert. Auf diese Weise bleibt der Puffer erhalten und sein Zeiger kann später wiederhergestellt werden. Wenn wir true wie in der Initialisierungsmethode verwenden würden, hätten wir das vorhandene Pufferobjekt gelöscht, was bei künftigen Zugriffen zu kritischen Fehlern führen würde.
Zweitens zur Architektur der Methode: Der vorgestellte Algorithmus implementiert nicht das kontrastive Repräsentationslernen für Muster, wie es von den Autoren von AMCT vorgeschlagen wurde. Es sei jedoch daran erinnert, dass wir die Diversifizierung der Repräsentation in das Objekt der relativen Kreuzaufmerksamkeit integriert haben. Wir haben also den Punkt der Injektion des kontrastiven Lernfehlers effektiv verlagert.
Damit ist der Überblick über die algorithmische Konstruktion des Atom-Motif Contrastive Transformer abgeschlossen. Der vollständige Quellcode für alle vorgestellten Klassen und Methoden ist im Anhang verfügbar. Dort finden Sie auch den vollständigen Code für die Programme zur Interaktion mit der Umgebung und zum Modelltraining. Sie wurden alle unverändert aus früheren Werken übernommen. Dazu gehören auch Programme zur Interaktion mit der Umgebung und Trainingsskripte. Hier haben wir eine Ebene ersetzt.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronAMCT; descr.window = BarDescr; // Window (Indicators to bar) { int temp[] = {HistoryBars, 100}; // Bars, Properties if(ArrayCopy(descr.units, temp) < (int)temp.Size()) return false; } descr.window_out = EmbeddingSize / 2; // Key Dimension descr.layers = 5; // Layers descr.step = 4; // Heads descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Eine vollständige Beschreibung der Architektur der trainierbaren Modelle finden Sie im Anhang.
3. Tests
Wir haben umfangreiche Arbeiten zur Implementierung des Atom-Motif Contrastive Transformer in MQL5 abgeschlossen, und es ist an der Zeit, die Wirksamkeit unserer Ansätze in der Praxis zu bewerten. Zu diesem Zweck trainieren wir das Modell mit neuen Objekten auf realen historischen Daten, gefolgt von einer Validierung der trainierten Strategie im Strategy Tester von MetaTrader 5 über einen Zeitraum außerhalb des Trainingssets.
Wie üblich wird das Modelltraining offline auf einem vorab gesammelten Trainingsdatensatz durchgeführt, der das gesamte Jahr 2023 abdeckt. Das Training ist iterativ, und nach mehreren Iterationen wird der Trainingsdatensatz aktualisiert. Dies ermöglicht die genaueste Bewertung der Handlungen des Agenten gemäß der aktuellen Politik.
Während des Trainings erhielten wir ein Modell, das sowohl in den Trainings- als auch in den Testdatensätzen Gewinne erzielen konnte. Es gibt jedoch einen Vorbehalt. Das daraus resultierende Modell führt nur sehr wenige Handelsgeschäfte aus. Wir haben den Testzeitraum sogar auf drei Monate verlängert. Die Testergebnisse sind wie folgt:
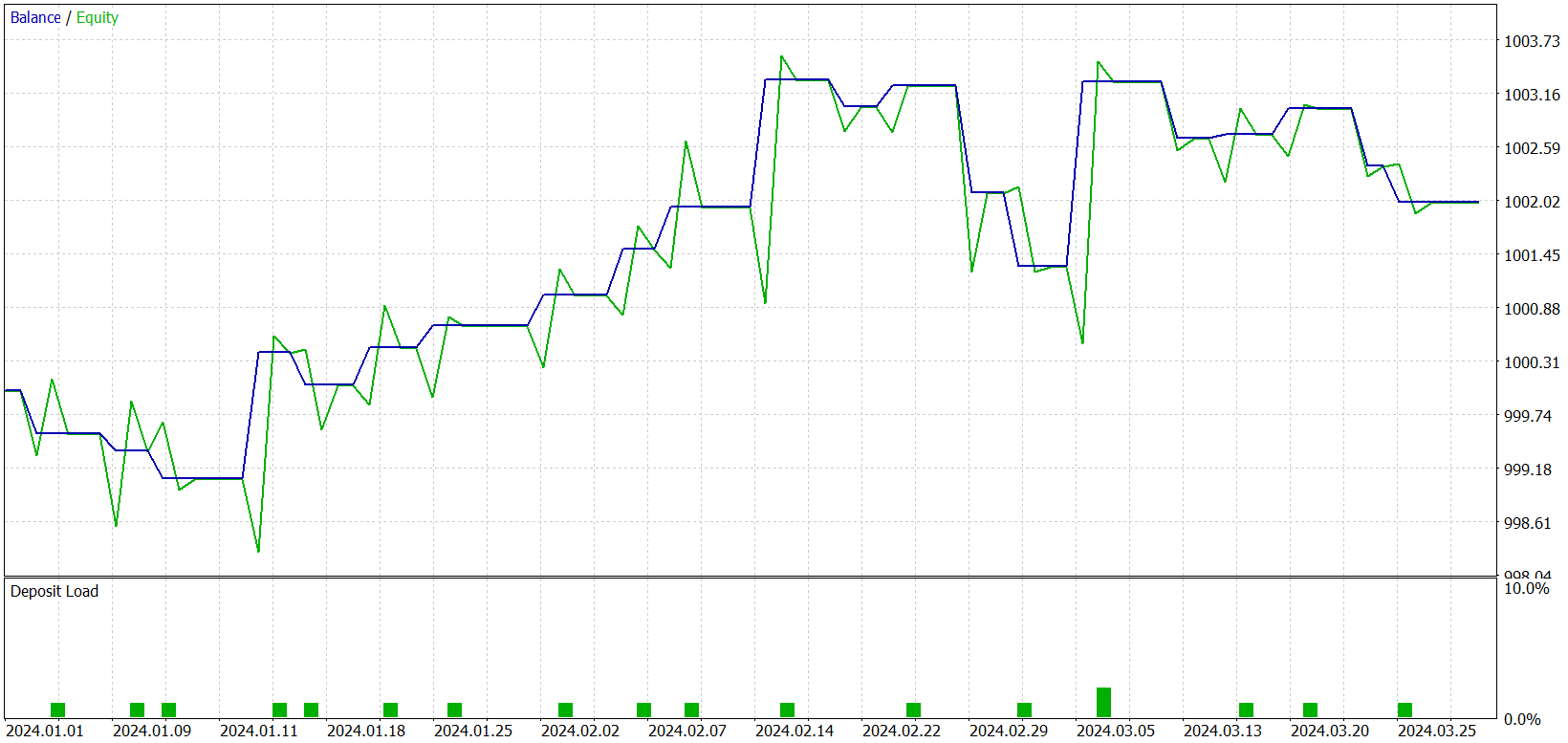
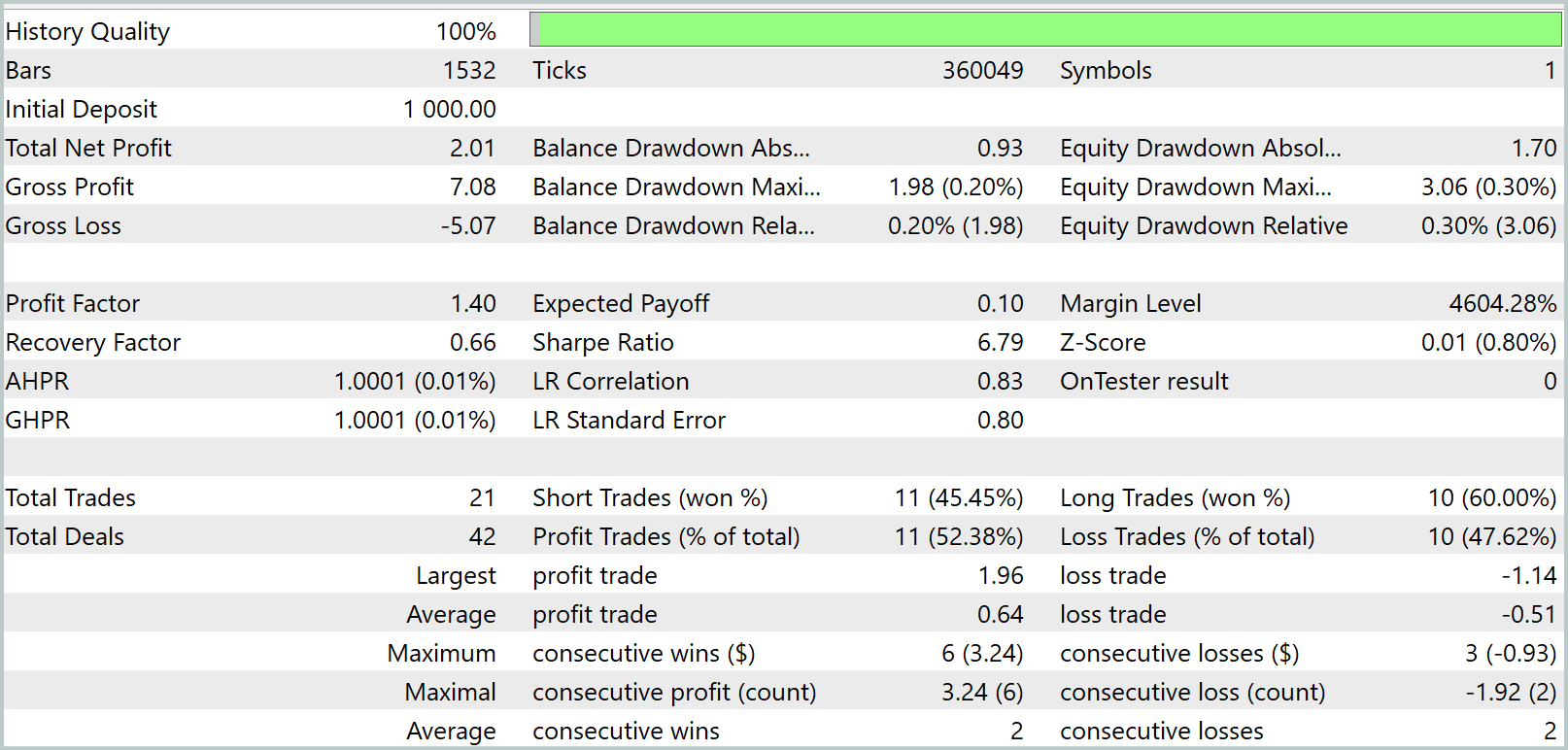
Wie aus den Ergebnissen ersichtlich ist, führte das Modell während des dreimonatigen Testzeitraums nur 21 Handelsgeschäfte aus, von denen etwas mehr als die Hälfte gewinnbringend abgeschlossen wurden. Betrachtet man das Schaubild des Saldos, so stellt man in den ersten anderthalb Monaten einen anfänglichen Anstieg fest, gefolgt von einer Seitwärtsbewegung. Dies ist ein durchaus erwartetes Verhalten. Unser Modell sammelt nur Statistiken von Marktzuständen, die im Trainingsdatensatz vorhanden sind. Wie bei jedem statistischen Modell müssen die Trainingsdaten repräsentativ sein. Aus der Saldenkurve können wir schließen, dass ein einjähriger Trainingsdatensatz eine Repräsentativität für etwa 1,2 bis 1,5 Monate in die Zukunft bietet.
Es kann also angenommen werden, dass das Training des Modells auf einem Zehnjahresdatensatz ein Modell mit stabiler Leistung über ein Jahr hinweg hervorbringen kann. Darüber hinaus sollte ein größerer Trainingssatz die Identifizierung einer größeren Anzahl von Schlüsselmustern und erlernbaren Eigenschaften ermöglichen, was die Handelshäufigkeit erhöhen könnte. Um diese Hypothesen zu bestätigen oder zu widerlegen, sind jedoch weitere Arbeiten mit dem Modell erforderlich.
Schlussfolgerung
In den letzten beiden Artikeln haben wir den Atom-Motif Contrastive Transformer (AMCT) untersucht, der auf den Konzepten der atomaren Elemente (Kerzen) und Motive (Muster) beruht. Die Hauptidee der Methode ist die Anwendung kontrastiven Lernens, um informative und nicht-informative Muster auf mehreren Ebenen zu unterscheiden: von elementaren Komponenten bis hin zu komplexen Strukturen. Dadurch kann das Modell nicht nur lokale Preisbewegungen erfassen, sondern auch signifikante Muster erkennen, die zusätzliche Erkenntnisse für eine genauere Prognose des Marktverhaltens liefern. Die Architektur des Transformers, die diesem Rahmen zugrunde liegt, identifiziert effektiv langfristige Abhängigkeiten und komplizierte Beziehungen zwischen Kerzen und Mustern.
Im praktischen Teil haben wir unsere Interpretation dieser Ansätze in MQL5 implementiert, die Modelle trainiert und Tests mit realen historischen Daten durchgeführt. Leider ist das resultierende Modell nur spärlich mit Handelsaktivitäten ausgestattet. Nichtsdestotrotz gibt es ein offensichtliches Potenzial, das wir in zukünftigen Studien weiter ausbauen wollen.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA zum Sammeln von Beispielen |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | Test.mq5 | Expert Advisor | Modelltraining EA |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Bibliothek | OpenCL-Programmcode-Bibliothek |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16192
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Neuronale Netze im Handel: Knotenadaptive Graphendarstellung mit NAFS
Neuronale Netze im Handel: Knotenadaptive Graphendarstellung mit NAFS
 Optimierungsmethoden der ALGLIB-Bibliothek (Teil I)
Optimierungsmethoden der ALGLIB-Bibliothek (Teil I)
 SQLite-Fähigkeiten in MQL5: Beispiel für ein Dashboard mit Handelsstatistiken nach Symbolen und magischen Zahlen
SQLite-Fähigkeiten in MQL5: Beispiel für ein Dashboard mit Handelsstatistiken nach Symbolen und magischen Zahlen
 Entwicklung eines Expert Advisors für mehrere Währungen (Teil 19): In Python implementierte Stufen erstellen
Entwicklung eines Expert Advisors für mehrere Währungen (Teil 19): In Python implementierte Stufen erstellen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.