MetaTrader 5 / Sistemas comerciales
English Русский 中文 Deutsch 日本語 Português
preview
Redes neuronales: así de sencillo (Parte 4): Redes recurrentes

Redes neuronales: así de sencillo (Parte 4): Redes recurrentes

MetaTrader 5 — Sistemas comerciales | 18 enero 2021, 14:49
1 180 0
Dmitriy Gizlyk
Dmitriy Gizlyk

Contenido


Introducción

Continuamos estudiando las redes neuronales. En artículos anteriores, hemos analizado el perceptrón multicapa y las redes neuronales convolucionales. Todos ellos trabajan con datos estáticos dentro de los procesos de Márkov, cuando el estado posterior de un sistema depende solo de su estado actual, y no del estado del sistema en el pasado. Ahora, proponemos analizar las redes neuronales recurrentes. Se trata de un tipo especial de redes neuronales diseñadas para trabajar con secuencias temporales, y actualmente es el líder en esta rama.


1. Particularidades distintivas de las redes neuronales recurrentes

Los tipos de redes neuronales que hemos analizado anteriormente funcionan con una cantidad de datos predefinida. En nuestro caso, al trabajar con gráficos de precios, resulta difícil decir cuál será el tamaño ideal de los datos analizados. Pueden aparecer diferentes patrones en distintos intervalos temporales. Además, en sí mismos, dichos intervalos no son siempre estáticos, y pueden cambiar según la situación actual. Algunos eventos pueden ser raros en el mercado, aunque se procesen con un alto grado de probabilidad. Y sería bueno si este evento permaneciera dentro de la ventana analizada. Pero, tan pronto como sale de ella, la red neuronal ya no lo tiene en cuenta. Aunque, posiblemente, en dicho momento el mercado procese una reacción a este evento. Un aumento de la ventana analizada implica un incremento del consumo de recursos informáticos y, por consiguiente, ocupará más tiempo tomar una decisión.

Para solucionar este problema al trabajar con las series temporales, hemos propuesto usar neuronas recurrentes en las redes neuronales. Es un intento de implementar la memoria a corto plazo en las redes neuronales, cuando, a la entrada de una neurona, junto con la información sobre el estado actual del sistema, se suministra el estado anterior de la misma neurona. Esta decisión se basa en el supuesto de que el valor a la salida de la neurona toma en consideración la influencia de todos los factores (incluido su estado anterior), transmitiendo en el siguiente salto "todo su conocimiento" a su estado futuro. Por analogía con el ser humano, cuando este realiza sus acciones en función de su experiencia y las acciones que ha realizado anteriormente. La duración de dicha memoria y su efecto sobre el estado actual de la neurona dependerán de los coeficientes de peso.

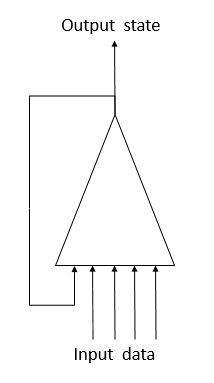
Por desgracia, esta secilla solución no está libre de inconvenientes. Este enfoque nos permite ahorrar "memoria" durante un breve intervalo temporal. La multiplicación cíclica de la señal por un factor inferior a "1" y el uso de la función de activación neuronal provocan una atenuación gradual de la señal con un aumento en el número de estos ciclos. Para solucionar este problema, en 1997, Sepp Hochreiter y Jürgen Schmidhuber propusieron el uso de la arquitectura de "memoria larga a corto plazo" (Long short-term memory - LSTM). Hasta ahora, el algoritmo de LTSM se considera uno de los mejores para resolver problemas de clasificación y pronóstico de series temporales, cuando los eventos significativos están separados en el tiempo y se prolongan por un cierto espacio de tiempo.

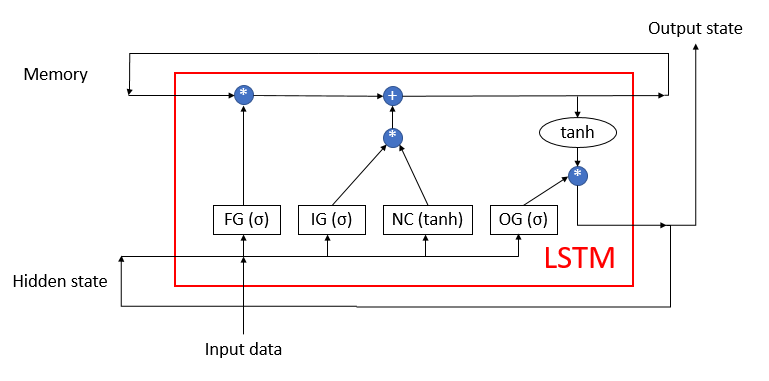
La LSTM no se puede denominar como neurona. Más bien sería una red neuronal con 3 canales de entrada y 3 canales de salida. De estos canales, solo 2 se usan para intercambiar datos con los mundos circundantes (uno para la entrada y otro para la salida). Los otros cuatro canales se cierran en pares para intercambiar información cíclicamente ("Memory" - memoria y "Hidden state" - estado oculto).

El bloque de LSTM contiene 2 flujos de información principales, interconectados por 4 capas neuronales completamente conectadas. Todas las capas neuronales contienen la misma cantidad de neuronas, igual al tamaño del flujo de salida y del flujo de memoria. Vamos a echar un vistazo más detallado al algoritmo.

El flujo de datos de la memoria se usa para guardar y transmitir información importante a lo largo del tiempo. En la etapa inicial, se inicializa con valores cero y se rellena durante el funcionamiento de la red neuronal. Podemos comparar el proceso con el aprendizaje de una persona viva que nace sin conocimientos y adquiere estos a lo largo de su vida.

El flujo Hiden state (estado oculto) se encarga de transferir a lo largo del tiempo el estado de salida del sistema. El tamaño del canal de datos es igual al canal de datos de la "memoria".

Los canales Input data (datos de entrada) y Output state (estado de salida) se encargan de intercambiar información con el mundo exterior.

La entrada del algoritmo recibe 3 flujos de datos:

  • Input data: describe el estado actual del sistema.
  • Memory y Hidden state: obtenemos del estado anterior.

Al inicio de la operación del algoritmo, la información de Input data y Hidden state se combina en una única matriz de datos, que posteriormente se suministra a las 4 capas neuronales ocultas de LSTM. 

La primera capa neuronal Forget gate (puerta de olvido) determina qué información entre la recibida en la memoria puede olvidarse y cuál debe recordarse. Se organiza como una capa neural completamente conectada con una función de activación sigmoidea. El número de neuronas en la capa se corresponde con el número de celdas de memoria en el flujo de memoria. Cada neurona de la capa obtiene en la entrada la matriz total de datos de los flujos Input data y Hidden state, generando en la salida un número dentro del intervalo entre 0 (olvidar por completo) y 1 (guardar en la memoria). El producto por elementos de la salida de la capa neuronal con flujo de memoria retorna la memoria corregida.

En el siguiente salto, el algoritmo determina qué información entre la obtenida en este salto debe guardarse en la memoria. Para ello, se usan 2 capas neuronales:

  • New Content (nuevo contenido): capa neuronal completamente conectada con una tangente hiperbólica como función de activación que normaliza la información recibida en el rango de -1 a 1.
  • Input gate (puerta de entrada): capa neural completamente conectada con una sigmoide como función de activación. Es similar a Forget gate y determina qué nueva información se debe recordar.

El producto de los elementos de New Content e Input gate se suma a los valores de las celdas de memoria. Como resultado de estas operaciones, obtenemos un estado de memoria actualizado, que posteriormente es transmitido a la entrada del siguiente ciclo de iteración.

Tras actualizar la memoria, generamos los valores del flujo de salida. Para hacerlo, de forma similar a Forget gate e Input gate, recalculamos Output gate (puerta de la señal de salida), y luego normalizamos el valor de la memoria actual utilizando la tangente hiperbólica. El producto por elementos de los dos conjuntos de datos obtenidos proporciona la matriz de señales de salida, que se envía después desde la LSTM al mundo exterior. Esta misma matriz de datos se transmite al siguiente ciclo de iteración como una secuencia del estado oculto.


2. Principios de aprendizaje de las redes neuronales recurrentes

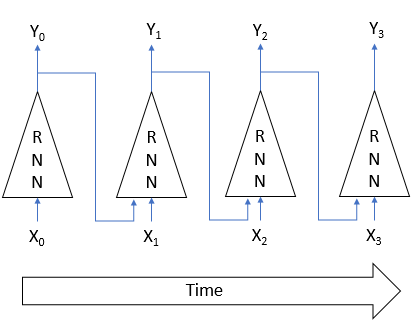
El entrenamiento de las redes neuronales recurrentes se realiza con el ya conocido método de propagación inversa del error. De forma similar al entrenamiento de las redes neuronales convolucionales, la naturaleza cíclica del proceso a lo largo del tiempo se descompone en un perceptrón multicapa. En un perceptrón así, cada intervalo temporal funciona como una capa oculta. Para todas las capas de dicho perceptrón, solo se usa una matriz de coeficientes de peso. Por consiguiente, para ajustar los pesos, tomaremos la suma de los gradientes para todas las capas, calculando el delta de los coeficientes de peso una vez para el gradiente total en todas las capas.


3. Construyendo una red neuronal recurrente

Para construir nuestra red neuronal recurrente, utilizaremos bloques de LSTM. Para ello, empezaremos creando la clase CNeuronLSTM. Para conservar la estructura de herencia de clases que creamos en el artículo anterior, crearemos una nueva clase heredada de la clase CNeuronProof.

class CNeuronLSTM    :  public CNeuronProof
  {
protected:
   CLayer            *ForgetGate;
   CLayer            *InputGate;
   CLayer            *OutputGate;
   CLayer            *NewContent;
   CArrayDouble      *Memory;
   CArrayDouble      *Input;
   CArrayDouble      *InputGradient;
   //---
   virtual bool      feedForward(CLayer *prevLayer);
   virtual bool      calcHiddenGradients(CLayer *&nextLayer);
   virtual bool      updateInputWeights(CLayer *&prevLayer);
   virtual bool      updateInputWeights(CLayer *gate, CArrayDouble *input_data);
   virtual bool      InitLayer(CLayer *layer, int numOutputs, int numOutputs);
   virtual CArrayDouble *CalculateGate(CLayer *gate, CArrayDouble *sequence);

public:
                     CNeuronLSTM(void);
                    ~CNeuronLSTM(void);
   virtual bool      Init(uint numOutputs,uint myIndex,int window, int step, int units_count);
   //---
   virtual CLayer    *getOutputLayer(void)  { return OutputLayer;  }
   virtual bool      calcInputGradients(CLayer *prevLayer) ;
   virtual bool      calcInputGradients(CNeuronBase *prevNeuron, uint index) ;
   //--- methods for working with files
   virtual bool      Save( int const file_handle);
   virtual bool      Load( int const file_handle);
   virtual int       Type(void)   const   {  return defNeuronLSTM;   }
  };

La clase padre ya contiene la capa de neuronas de salida OutputLayer. Vamos a añadir 4 capas neuronales adicionales que necesitamos para el funcionamiento del algoritmo: ForgetGate, InputGate, OutputGate y NewContent. También añadiremos 3 matrices para guardar los datos de la "memoria", combinando Input data y Hidden state, así como un gradiente con los datos entrantes erróneos. El nombre y la funcionalidad de los métodos de clase se corresponden con los analizados anteriormente. No obstante, hay en su código diferencias necesarias para que el algoritmo funcione. Vamos a analizar con más detalle los métodos principales.

3.1. Método de inicialización de la clase.

El método de inicialización de clases en los parámetros recibe la información principal sobre el bloque creado. Los nombres de los parámetros del método se han conservado respecto a la clase básico, pero algunos tienen ahora un significado diferente:

  • numOutputs — número de conexiones salientes. Se usa cuando una capa completamente conectada sigue a una capa de bloques de LSTM;
  • myIndex  — índice de la neurona en la capa. Se utiliza para identificar un bloque;
  • window  — tamaño del canal de datos de entrada;
  • step  — no se usa;
  • unit_count  — ancho del canal de salida y cantidad de neuronas en las capas ocultas del bloque. Todas las capas neuronales de un bloque tienen el mismo número de neuronas. 

bool CNeuronLSTM::Init(uint numOutputs,uint myIndex,int window,int step,int units_count)
  {
   if(units_count<=0)
      return false;
//--- Init Layers
   if(!CNeuronProof::Init(numOutputs,myIndex,window,step,units_count))
      return false;
   if(!InitLayer(ForgetGate,units_count,window+units_count))
      return false;
   if(!InitLayer(InputGate,units_count,window+units_count))
      return false;
   if(!InitLayer(OutputGate,units_count,window+units_count))
      return false;
   if(!InitLayer(NewContent,units_count,window+units_count))
      return false;
   if(!Memory.Reserve(units_count))
      return false;
   for(int i=0; i<units_count; i++)
      if(!Memory.Add(0))
         return false;
//---
   return true;
  }

Dentro del método, primero verificamos que se cree al menos una neurona en las capas neuronales del bloque. A continuación, llamamos al método correspondiente de la clase básica. Una vez haya finalizado con éxito, inicializamos las capas ocultas del bloque; las operaciones repetidas para cada capa serán enviadas al método separado InitLayer. Después de completar la inicialización de las capas neuronales, inicializamos la matriz de memoria con valores cero.

El método de inicialización de la capa neuronal InitLayer en los parámetros obtiene un puntero al objeto de la capa neuronal inicializada, el número de neuronas en la capa y el número de conexiones salientes. Al comienzo del método, comprobamos que el puntero resultante sea válido. Si el puntero no es válido, creamos una nueva instancia de la clase de capa neuronal. Si el puntero es válido, limpiamos la capa neuronal.

bool CNeuronLSTM::InitLayer(CLayer *layer,int numUnits, int numOutputs)
  {
   if(CheckPointer(layer)==POINTER_INVALID)
     {
      layer=new CLayer(numOutputs);
      if(CheckPointer(layer)==POINTER_INVALID)
         return false;
     }
   else
      layer.Clear();

A continuación, llenamos la capa con el número necesario de neuronas. Si surge un error en cualquiera de las etapas del método, salimos de la función con el resultado false.

   if(!layer.Reserve(numUnits))
      return false;
//---
   CNeuron *temp;
   for(int i=0; i<numUnits; i++)
     {
      temp=new CNeuron();
      if(CheckPointer(temp)==POINTER_INVALID)
         return false;
      if(!temp.Init(numOutputs+1,i))
         return false;
      if(!layer.Add(temp))
         return false;
     }
//---
   return true;
  }

Tras completar con éxito todas las iteraciones, salimos del método con el resultado true.

3.2. Propagación hacia delante.

La propagación hacia delante se implementa en el método feedForward. En los parámetros, el método obtiene un puntero a la capa neuronal anterior. Al comienzo del método, verificamos la validez del puntero recibido, y también si hay neuronas en la capa anterior. Asimismo, comprobamos la validez de la matriz para los datos de entrada. Si el objeto aún no ha sido creado, creamos una nueva instancia de la clase. Si ya existe un objeto creado, borramos la matriz.

bool CNeuronLSTM::feedForward(CLayer *prevLayer)
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID || prevLayer.Total()<=0)
      return false;
   CNeuronBase *temp;
   CConnection *temp_con;
   if(CheckPointer(Input)==POINTER_INVALID)
     {
      Input=new CArrayDouble();
      if(CheckPointer(Input)==POINTER_INVALID)
         return false;
     }
   else
      Input.Clear();

A continuación, combinamos en una única matriz de datos de entrada Input los datos sobre el estado actual del sistema y los datos sobre el estado en el intervalo temporal anterior. 

   int total=prevLayer.Total();
   if(!Input.Reserve(total+OutputLayer.Total()))
      return false;
   for(int i=0; i<total; i++)
     {
      temp=prevLayer.At(i);
      if(CheckPointer(temp)==POINTER_INVALID || !Input.Add(temp.getOutputVal()))
         return false;
     }
   total=OutputLayer.Total();
   for(int i=0; i<total; i++)
     {
      temp=OutputLayer.At(i);
      if(CheckPointer(temp)==POINTER_INVALID || !Input.Add(temp.getOutputVal()))
         return false;
     }
   int total_data=Input.Total();

Luego, calculamos nuevamente el valor de las puertas. Al igual que sucede en el proceso de inicialización, trasladamos las operaciones repetidas para cada puerta al método separado CalculateGate. Aquí, llamamos a este método pasando los punteros a la puerta procesada y la matriz de datos iniciales.

//--- Calculated forget gate
   CArrayDouble *forget_gate=CalculateGate(ForgetGate,Input);
   if(CheckPointer(forget_gate)==POINTER_INVALID)
      return false;
//--- Calculated input gate
   CArrayDouble *input_gate=CalculateGate(InputGate,Input);
   if(CheckPointer(input_gate)==POINTER_INVALID)
      return false;
//--- Calculated output gate
   CArrayDouble *output_gate=CalculateGate(OutputGate,Input);
   if(CheckPointer(output_gate)==POINTER_INVALID)
      return false;

A continuación, calculamos y normalizamos los datos entrantes en la matriz new_content.

//--- Calculated new content
   CArrayDouble *new_content=new CArrayDouble();
   if(CheckPointer(new_content)==POINTER_INVALID)
      return false;
   total=NewContent.Total();
   for(int i=0; i<total; i++)
     {
      temp=NewContent.At(i);
      if(CheckPointer(temp)==POINTER_INVALID)
         return false;
      double val=0;
      for(int c=0; c<total_data; c++)
        {
         temp_con=temp.Connections.At(c);
         if(CheckPointer(temp_con)==POINTER_INVALID)
            return false;
         val+=temp_con.weight*Input.At(c);
        }
      val=TanhFunction(val);
      temp.setOutputVal(val);
      if(!new_content.Add(val))
         return false;
     }

Y finalmente, después de realizar todos los cálculos intermedios, recalculamos la matriz de "memoria" y determinamos los datos de salida.

//--- Calculated output sequences
   for(int i=0; i<total; i++)
     {
      double value=Memory.At(i)*forget_gate.At(i)+new_content.At(i)*input_gate.At(i);
      if(!Memory.Update(i,value))
         return false;
      temp=OutputLayer.At(i);
      value=TanhFunction(value)*output_gate.At(i);
      temp.setOutputVal(value);
     }

Luego borramos las matrices de los datos intermedios y salimos del método con el resultado true.

   delete forget_gate;
   delete input_gate;
   delete new_content;
   delete output_gate;
//---
   return true;
  }

En el método CalculateGate, que hemos mencionado anteriormente, la matriz de coeficientes de peso se multiplica por el vector de datos originales, normalizándose posteriormente los datos con una función de activación sigmoidea. En los parámetros, este método recibe 2 punteros a objetos de la capa neuronal y la secuencia de datos original. Antes que nada, verificamos la validez de los punteros obtenidos.

CArrayDouble *CNeuronLSTM::CalculateGate(CLayer *gate,CArrayDouble *sequence)
  {
   CNeuronBase *temp;
   CConnection *temp_con;
   CArrayDouble *result=new CArrayDouble();
   if(CheckPointer(gate)==POINTER_INVALID)
      return NULL;

A continuación, organizamos un ciclo para iterar por todas las neuronas. 

   int total=gate.Total();
   int total_data=sequence.Total();
   for(int i=0; i<total; i++)
     {
      temp=gate.At(i);
      if(CheckPointer(temp)==POINTER_INVALID)
        {
         delete result;
         return NULL;
        }

Tras verificar en la secuencia la validez del puntero al objeto de neurona, organizamos un ciclo anidado para iterar por todos los coeficientes de peso de la neurona, calculando la suma de los productos de esta última por el elemento correspondiente en la matriz de datos inicial.

      double val=0;
      for(int c=0; c<total_data; c++)
        {
         temp_con=temp.Connections.At(c);
         if(CheckPointer(temp_con)==POINTER_INVALID)
           {
            delete result;
            return NULL;
           }
         val+=temp_con.weight*(sequence.At(c)==DBL_MAX ? 1 : sequence.At(c));
        }

La suma de productos resultante se pasa por la función de activación. El resultado se escribe en la salida de la neurona y se añade a la matriz. Después de iterar con éxito por todas las neuronas de la capa, salimos del método retornando una matriz de resultados. Si surge un error en cualquier etapa de los cálculos, el método retornará un valor vacío.

      val=SigmoidFunction(val);
      temp.setOutputVal(val);
      if(!result.Add(val))
        {
         delete result;
         return NULL;
        }
     }
//---
   return result;
  }

3.3. Calculando el gradiente de error.

El cálculo de los gradientes de error se realiza en el método calcHiddenGradients, que obtiene en los parámetros un puntero a la siguiente capa de neuronas. Al inicio del método, comprobamos la relevancia del objeto creado previamente para guardar la secuencia de gradientes de error respecto a los datos originales. Si el objeto aún no ha sido creado, creamos una nueva instancia del mismo. Si existe un objeto creado con anterioridad, borramos la matriz de datos. También declararemos las variables internas y las instancias de las clases.

bool CNeuronLSTM::calcHiddenGradients(CLayer *&nextLayer)
  {
   if(CheckPointer(InputGradient)==POINTER_INVALID)
     {
      InputGradient=new CArrayDouble();
      if(CheckPointer(InputGradient)==POINTER_INVALID)
         return false;
     }
   else
      InputGradient.Clear();
//---
   int total=OutputLayer.Total();
   CNeuron *temp;
   CArrayDouble *MemoryGradient=new CArrayDouble();
   CNeuron *gate;
   CConnection *con;

A continuación, calculamos el gradiente de error para la capa de salida de neuronas que nos ha llegado de la siguiente capa neuronal.

   for(int i=0; i<total; i++)
     {
      temp=OutputLayer.At(i);
      if(CheckPointer(temp)==POINTER_INVALID)
         return false;
      temp.setGradient(temp.sumDOW(nextLayer));
     }

Extendemos el gradiente resultante a todas las capas internas de LSTM.

   if(CheckPointer(MemoryGradient)==POINTER_INVALID)
      return false;
   if(!MemoryGradient.Reserve(total))
      return false;
   for(int i=0; i<total; i++)
     {
      temp=OutputLayer.At(i);
      gate=OutputGate.At(i);
      if(CheckPointer(gate)==POINTER_INVALID)
         return false;
      double value=temp.getGradient()*gate.getOutputVal();
      value=TanhFunctionDerivative(Memory.At(i))*value;
      if(i>=MemoryGradient.Total())
        {
         if(!MemoryGradient.Add(value))
            return false;
        }
      else
        {
         value=MemoryGradient.At(i)+value;
         if(!MemoryGradient.Update(i,value))
            return false;
        }
      gate.setGradient(gate.getOutputVal()!=0 && temp.getGradient()!=0 ? temp.getGradient()*temp.getOutputVal()*SigmoidFunctionDerivative(gate.getOutputVal())/gate.getOutputVal() : 0);
      //--- Calcculated gates and new content gradients
      gate=ForgetGate.At(i);
      if(CheckPointer(gate)==POINTER_INVALID)
         return false;
      gate.setGradient(gate.getOutputVal()!=0 && value!=0? value*SigmoidFunctionDerivative(gate.getOutputVal()) : 0);
      gate=InputGate.At(i);
      temp=NewContent.At(i);
      if(CheckPointer(gate)==POINTER_INVALID)
         return false;
      gate.setGradient(gate.getOutputVal()!=0 && value!=0 ? value*temp.getOutputVal()*SigmoidFunctionDerivative(gate.getOutputVal()) : 0);
      temp.setGradient(temp.getOutputVal()!=0 && value!=0 ? value*gate.getOutputVal()*TanhFunctionDerivative(temp.getOutputVal()) : 0);
     }

Tras calcular los gradientes en las capas neuronales internas, calculamos el gradiente de error para la secuencia de datos iniciales.

//--- Calculated input gradients
   int total_inp=temp.getConnections().Total();
   for(int n=0; n<total_inp; n++)
     {
      double value=0;
      for(int i=0; i<total; i++)
        {
         temp=ForgetGate.At(i);
         con=temp.getConnections().At(n);
         value+=temp.getGradient()*con.weight;
         //---
         temp=InputGate.At(i);
         con=temp.getConnections().At(n);
         value+=temp.getGradient()*con.weight;
         //---
         temp=OutputGate.At(i);
         con=temp.getConnections().At(n);
         value+=temp.getGradient()*con.weight;
         //---
         temp=NewContent.At(i);
         con=temp.getConnections().At(n);
         value+=temp.getGradient()*con.weight;
        }
      if(InputGradient.Total()>=n)
        {
         if(!InputGradient.Add(value))
            return false;
        }
      else
         if(!InputGradient.Update(n,value))
            return false;
     }

Una vez calculados todos los gradientes, eliminamos los objetos innecesarios y salimos del método con el resultado true.

   delete MemoryGradient;
//---
   return true;
  }

Querríamos llamar la atención del lector sobre el siguiente punto: en la parte teórica, hemos hablado sobre la necesidad de desplegar la secuencia en el tiempo y recalcular los gradientes de error en cada etapa temporal. Esto no lo hemos hecho aquí, ya que el coeficiente de entrenamiento es muy inferior a 1, y el efecto del gradiente de error en los intervalos temporales anteriores será tan insignificante que podríamos despreciarlo para mejorar el rendimiento general del algoritmo. 

3.4. Actualizando los coeficientes de peso.

Resulta totalmente natural que después de obtener los gradientes de error, corrijamos los coeficientes de peso de todas las capas neuronales de LSTM. Esta tarea se resuelve en el método updateInputWeights, que recibe en sus parámetros un puntero a la capa neuronal anterior. Debemos destacar de inmediato que la transmisión del puntero a la capa anterior en los parámetros se ha realizado solo para conservar la estructura de herencia.

Al comienzo del método, comprobamos la validez del puntero obtenido y la presencia de la matriz de datos inicial. Tras verificar con éxito los punteros, corregimos directamente los coeficientes peso de las capas neuronales internas. Como antes, movemos las acciones repetidas al método aparte updateInputWeights, con los punteros a la capa neuronal específica y a la matriz de datos iniciales en los parámetros. Aquí, llamamos por turno al método auxiliar para cada capa neuronal.

bool CNeuronLSTM::updateInputWeights(CLayer *&prevLayer)
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(Input)==POINTER_INVALID)
      return false;
//---
   if(!updateInputWeights(ForgetGate,Input) || !updateInputWeights(InputGate,Input) || !updateInputWeights(OutputGate,Input)
      || !updateInputWeights(NewContent,Input))
     {
      return false;
     }
//---
   return true;
  }

Vamos a echar un vistazo a las operaciones realizadas en el método updateInputWeights (CLayer *gate, CArrayDouble *input_data). Al comienzo del método, verificamos la validez de los punteros recibidos en los parámetros y declaramos las variables internas.

bool CNeuronLSTM::updateInputWeights(CLayer *gate,CArrayDouble *input_data)
  {
   if(CheckPointer(gate)==POINTER_INVALID || CheckPointer(input_data)==POINTER_INVALID)
      return false;
   CNeuronBase *neuron;
   CConnection *con;
   int total_n=gate.Total();
   int total_data=input_data.Total();

A continuación, organizamos ciclos anidados para iterar por todas las neuronas de la capa y los pesos de las neuronas, corrigiendo las matrices de pesos. La fórmula para corregir los pesos es la misma que analizamos anteriormente para CNeuron::updateInputWeights(CArrayObj *&prevLayer). La imposibilidad de utilizar el método anteriormente creado se debe solo al hecho de que anteriormente usamos las conexiones de la neurona para conectarnos con la siguiente capa, y ahora las usamos para conectarnos con la capa anterior.

   for(int n=0; n<total_n; n++)
     {
      neuron=gate.At(n);
      if(CheckPointer(neuron)==POINTER_INVALID)
         return false;
      for(int i=0; i<total_data; i++)
        {
         con=neuron.getConnections().At(i);
         if(CheckPointer(con)==POINTER_INVALID)
            return false;
         double data=input_data.At(i);
         con.weight+=con.deltaWeight=(neuron.getGradient()!=0 && data!=0 ? eta*neuron.getGradient()*(data!=DBL_MAX ? data : 1) : 0)+alpha*con.deltaWeight;
        }
     }
//---
   return true;
  }

Después de actualizar la matriz de pesos, salimos del método con el resultado true.

Tras crear la clase, realizamos pequeñas correcciones en los despachadores de la clase básica CNeuronBase, para que puedan procesar correctamente las instancias de la nueva clase. Podrá familiarizarse con el código de todos los métodos y funciones en los anexos.


4. Simulación

Las pruebas del bloque de LSTM que hemos creado se han realizado en las mismas condiciones que las pruebas de las redes convolucionales anteriores. Para realizar dichas pruebas, hemos creado el asesor experto Fractal_LSTM. En esencia, se trata del mismo Fractal_conv del artículo anterior, salvo que en la función OnInit, en el bloque donde se establece la estructura de la red neuronal, las capas convolucional y de submuestreo son reemplazadas por una capa de 4 bloques de LSTM (por analogía con los 4 filtros de la red convolucional).

      //---
      desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=4;
      desc.type=defNeuronLSTM;
      desc.window=(int)HistoryBars*12;
      desc.step=(int)HistoryBars/2;
      if(!Topology.Add(desc))
         return INIT_FAILED;

No hemos realizado otros cambios en el código del asesor. Podrá encontrar el código completo del asesor y las clases en el archivo adjunto.

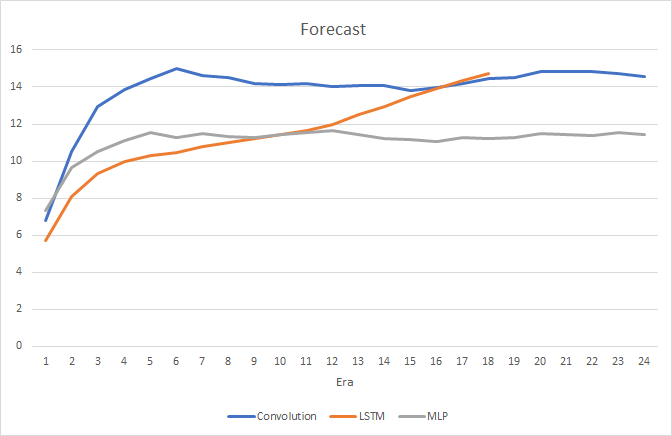
Parece bastante natural que la presencia de las 4 capas neuronales internas en cada bloque de LSTM y la complejidad del algoritmo en sí influyan en el rendimiento: la velocidad de dicha red neuronal resulta algo menor que en la red convolucional analizada anteriormente. Pero, en este caso, además, el error cuadrático medio de la red recurrente es mucho menor.


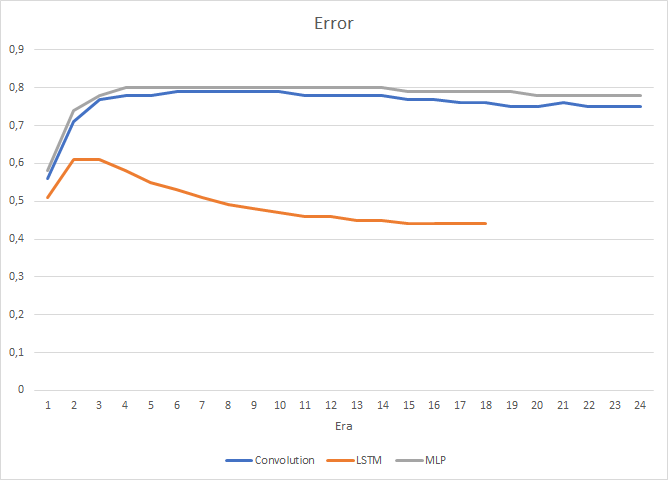
Al mismo tiempo, durante el entrenamiento de la red neuronal recurrente, el gráfico que muestra la precisión de los aciertos tiene una pronunciada tendencia ascendente, casi en línea recta.

En el gráfico de precios, solo se ven los indicadores raros en los fractales predichos. No olvidemos que durante las pruebas anteriores el gráfico de precios estaba totalmente sembrado de etiquetas.

Simulación de la red neuronal recurrente

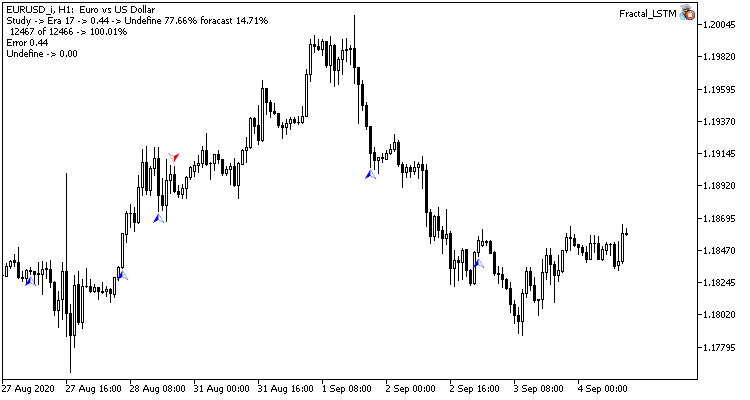
Conclusión

En este artículo, hemos analizado el algoritmo de funcionamiento de las redes neuronales recurrentes, hemos construido un bloque de LSTM y hemos puesto a prueba el funcionamiento de una red neuronal construida sobre datos reales. En comparación con los tipos de redes neuronales analizados anteriormente, las redes recurrentes resultan tremendamente laboriosas tanto en lo que respecta a la propagación hacia delante, como en el proceso de entrenamiento. Pero, al mismo tiempo, demuestran mejores resultados, y así lo confirman las simulaciones realizadas.

Enlaces

  1. Redes neuronales: así de sencillo
  2. Redes neuronales: así de sencillo (Parte 2): Entrenamiento y prueba de la red
  3. Redes neuronales: así de sencillo (Parte 3): Redes convolucionales
  4. Understanding LSTM Networks

Programas utilizados en el artículo

# Nombre Tipo Descripción
1 Fractal.mq5   Asesor  Asesor con la red neuronal de regresión (1 neurona en la capa de salida)
2 Fractal_2.mq5  Asesor  Asesor con la red neuronal de clasificación (3 neuronas en la capa de salida)
3 NeuroNet.mqh  Biblioteca de clase  Biblioteca de clases para crear la red neuronal (perceptrón)
4 Fractal_conv.mq5  Asesor  Asesor con la red neuronal convolucional de clasificación (3 neuronas en la capa de salida)
5 Fractal_LSTM.mq5   Asesor  Asesor con la red neuronal recurriente de clasificación (3 neuronas en la capa de salida)


Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/8385

Archivos adjuntos |
Descargar ZIP
MQL5.zip (32.06 KB)
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores
Gradient boosting en el aprendizaje de máquinas transductivo y activo Gradient boosting en el aprendizaje de máquinas transductivo y activo
En este artículo, el lector podrá familiarizarse con los métodos de aprendizaje automático activo basados en datos reales, descubriendo además cuáles son sus ventajas y desventajas. Puede que estos métodos terminen por ocupar un lugar en su arsenal de modelos de aprendizaje automático. El término transducción fue introducido por Vladímir Naúmovich Vápnik, el inventor de la máquina de vectores de soporte (SVM).
Redes neuronales: así de sencillo (Parte 3): Redes convolucionales Redes neuronales: así de sencillo (Parte 3): Redes convolucionales
Continuando el tema de la redes neuronales, proponemos al lector analizar las redes neuronales convolucionales. Este tipo de redes neuronales ha sido desarrollado para buscar objetos en una imagen. Asimismo, analizaremos cómo nos pueden ayudar al operar en los mercados financieros.
¿Cómo ganar $1 000 000 en el trading algorítmico? ¡En los servicios de MQL5.com! ¿Cómo ganar $1 000 000 en el trading algorítmico? ¡En los servicios de MQL5.com!
Todo tráder llega al mercado con el objetivo de ganar su primer millón de dólares. ¿Cómo podemos conseguirlo sin grandes riesgos y sin capital inicial? Los servicios MQL5 ofrecen estas posibilidades a los desarrolladores y tráders en cualquier país del mundo.
Optimización móvil continua (Parte 8): Mejorando el programa y corrigiendo los errores encontrados Optimización móvil continua (Parte 8): Mejorando el programa y corrigiendo los errores encontrados
A petición de los usuarios y lectores del presente ciclo de artículos, el programa ha sido modificado, y ahora podemos decir que el este artículo contiene la nueva versión del autooptimizador. Asimismo, hemos introducido en el autooptimizador tanto las mejoras solicitadas, como algunas nuevas cuya idea surgió durante la corrección del programa.