Redes neuronales en el trading: Transformer parámetro-eficiente con atención segmentada (PSformer)

Introducción

La predicción de series temporales multidimensionales supone una importantísima tarea en el aprendizaje profundo de modelos con aplicaciones en diversos campos, como la meteorología, la energía, la detección de anomalías y el análisis financiero. Con el desarrollo de las técnicas de inteligencia artificial, se han realizado importantes esfuerzos para crear modelos innovadores que mejoren la calidad de la predicción. Los modelos basados en la arquitectura del Transformer, que han demostrado su eficacia en el procesamiento del lenguaje natural y la visión por computadora, resultan especialmente atractivos. Además, los modelos a gran escala previamente entrenados basados en la arquitectura del Transformer han demostrado sus ventajas en la previsión de series temporales, confirmando que el aumento del número de parámetros y la cantidad de datos de entrenamiento puede mejorar significativamente las capacidades del modelo.

Por otra parte, muchos modelos lineales sencillos también muestran resultados competitivos en comparación con modelos más complejos basados en la arquitectura del Transformer. Probablemente, la clave de su éxito a la hora de pronosticar series temporales resida en la baja complejidad de los modelos, lo cual reduce la probabilidad de sobreentrenamiento con datos ruidosos o irrelevantes. Así, incluso con datos limitados, estos modelos pueden captar representaciones sólidas de la información de manera eficaz.

Para superar las limitaciones relacionadas con el modelado de dependencias a largo plazo y captar relaciones temporales complejas PatchTST procesa los datos utilizando técnicas de conmutación para extraer la semántica local, lo que proporciona un rendimiento excepcional. Sin embargo, usa construcciones independientes del canal y tiene un potencial significativo para mejorar aún más el rendimiento del modelado. Además, los retos exclusivos de la modelización multidimensional de series temporales, en la que las dimensiones temporal y espacial difieren sustancialmente de otros tipos de datos, ofrecen muchas oportunidades sin explotar.

Una manera de reducir la complejidad de los modelos en el aprendizaje profundo es utilizar un enfoque de compartición de parámetros (PS), capaz de reducir significativamente el número de parámetros del modelo y aumentar la eficiencia computacional. En las redes convolucionales, los filtros comparten los pesos entre posiciones espaciales, identificando características locales con menos parámetros. Del mismo modo, los modelos LSTM usan matrices de pesos comunes para los pasos temporales, gestionan la memoria y regulan el flujo de información. En el procesamiento del lenguaje natural, la capacidad de compartir parámetros se ve reforzada por los pesos compartidos entre las capas del Transformer, lo cual reduce la redundancia de parámetros al tiempo que preserva el rendimiento.

En el entrenamiento multitarea se aplica el método Task Adaptive Parameter Sharing (TAPS): un ajuste selectivo de los niveles específicos de la tarea usados en el aprendizaje multitarea para maximizar la compartición de parámetros entre tareas y lograr un aprendizaje eficiente con cambios mínimos específicos de la tarea. Las investigaciones apuntan al potencial de la compartición de parámetros para reducir el tamaño de los modelos, mejorar la generalizabilidad y reducir el riesgo de sobreentrenamiento en diversas tareas.

Los autores del artículo "PSformer: Parameter-efficient Transformer with Segment Attention for Time Series Forecasting" exploran el desarrollo de modelos innovadores basados en Transformers para resolver problemas de previsión de series temporales multidimensionales considerando el concepto de compartición de parámetros.

Así, proponen un modelo de codificador basado en la arquitectura del Transformer con una estructura de atención segmentada de dos niveles, donde cada nivel del modelo incluye un bloque con parámetros comunes. Este bloque contiene tres capas completamente conectadas con enlace residual para mantener bajo el número total de parámetros, lo que permite un intercambio eficaz de información entre las partes del modelo. Para centrar la atención en los segmentos, se utiliza una técnica de parcheado que divide la serie de variables en parches individuales. A continuación, los parches que se hallan en la misma posición en distintas variables se combinan en segmentos. Como resultado, cada segmento supone una extensión espacial de un único parche variable, lo que permite dividir una serie temporal multidimensional en múltiples segmentos.

Dentro de cada segmento, la atención se centra en mejorar la detección de las relaciones espaciotemporales localizadas, mientras que la integración de la información entre segmentos contribuye a la precisión global de las predicciones. La aplicación del método de optimización SAM permite a los autores del framework reducir aún más el sobreentrenamiento sin perder eficacia en el entrenamiento. Extensos experimentos realizados por los creadores del PSformer sobre datos de previsión de series temporales a largo plazo demuestran el alto rendimiento de la arquitectura propuesta. El PSformer compite con modelos avanzados y obtiene los mejores resultados en 6 de las 8 tareas clave de previsión de series temporales.

El algoritmo PSformer

La serie temporal multidimensional X ∈ RM×L contiene M variables y la ventana de análisis retrospectivo es L. La longitud de la secuencia L se divide uniformemente en N parches no solapados de tamaño P. Entonces P(i) de M variables forma el i-ésimo segmento, denotando un segmento transversal de longitud C (C=M×P).

Los componentes clave del framework PSformer propuesto son el bloque de atención a los segmentos (SegAtt) y el bloque de compartición de parámetros (PS). El codificador PSformer sirve de base del modelo y contiene tanto el módulo de atención a los segmentos como la unidad PS. El bloque PS proporciona parámetros para todas las capas del codificador usando la técnica de compartición de parámetros.

Al igual que otras arquitecturas de previsión de series temporales, los autores del PSformer utilizan el método de RevIN, que elimina eficazmente el problema del desplazamiento de la distribución.

La atención espaciotemporal a (SegAtt) combina parches de diferentes canales en la misma posición en un segmento y establece relaciones espaciotemporales entre diferentes segmentos. En concreto, las series temporales originales X ∈ RM×L se dividen primero en parches, donde L=P×N, y después se transforman en X ∈ R(M×P)×N, fusionando las mediciones de M y P. Así, los datos iniciales adoptan la forma X ∈ RC×N(C=M×P), lo que facilita la posterior fusión de información entre canales.

En este espacio transformado, los datos de origen son procesados por dos módulos consecutivos con la misma arquitectura y separados por ReLU. Cada uno de estos módulos contiene un bloque de compartición de parámetros y, otro bloque que ya nos resulta familiar, de Self-Attention. Mientras que el cálculo de las matrices 𝑸uery ∈ RC×N, 𝑲ey ∈ RC×N y 𝑽alue ∈ RC×N incluye transformaciones no lineales de los datos de origen Xin según los segmentos en N, la atención escalada en forma de producto escalar distribuye principalmente la atención a través de toda la dimensionalidad C, permitiendo que el modelo se centre en las dependencias entre segmentos espaciales y temporales a través de canales y tiempo.

Este mecanismo garantiza la integración de la información procedente de distintos segmentos mediante el cálculo de Q, K y V. También capta las dependencias espaciotemporales localizadas dentro de segmentos individuales, prestando atención a la estructura interna de cada segmento. También capta las dependencias a largo plazo entre segmentos en grandes pasos temporales. El resultado final es Xout ∈ RC×Ncompletando el proceso de atención.

El PSformer propone la implementación de un nuevo bloque Parameter Shared Block (PS Block), que consta de 3 capas completamente conectadas con enlace residual. En concreto, utilizaremos 3 representaciones lineales entrenables Wj ∈ RN×N с j ∈ {1, 2, 3}. Los resultados de las dos primeras capas se calcularán del siguiente modo:

Aquí podemos observar una estructura similar al bloque FeedForward con enlaces residuales. Este resultado intermedio 𝑿out se usa como dato de entrada para la tercera transformación:

Así, el bloque PS en su conjunto puede expresarse de la siguiente manera:

La estructura del bloque PS permite realizar transformaciones no lineales manteniendo la trayectoria de transformación lineal. Aunque las 3 capas del bloque PS tienen parámetros diferentes, todo el bloque PS se reutiliza en distintas posiciones del codificador PSformer, lo que garantiza que los mismos parámetros de bloque 𝑾S sean comunes a todas estas posiciones. En concreto, el bloque PS utiliza parámetros comunes en 3 partes de cada codificador PSformer, incluidos los 2 módulos de atención a segmentos espaciotemporales y el último bloque PS. Esta estrategia de compartición de parámetros reduce el número total de parámetros al tiempo que mantiene la expresividad del modelo.

El mecanismo SegAtt de dos etapas puede compararse con el bloque FeedForward del Transformer vainilla, en el que un MLP se sustituye por operaciones de atención. Asimismo, se añaden enlaces residuales entre los datos originales y el resultado, tras lo cual el resultado pasa al bloque PS final.

A continuación, se aplica una transformación de dimensionalidad para obtener 𝑿o⁢ut ∈ RM×L, donde C=M×P y L=P×N.

Tras pasar por n capas del codificador del PSformer, se realiza la transformación final de los datos al horizonte de planificación F.

donde 𝑿pred ∈ RM×F y 𝑾F ∈ RL×F son una representación lineal.

A continuación se muestra la visualización del framework PSformer realizada por el autor.

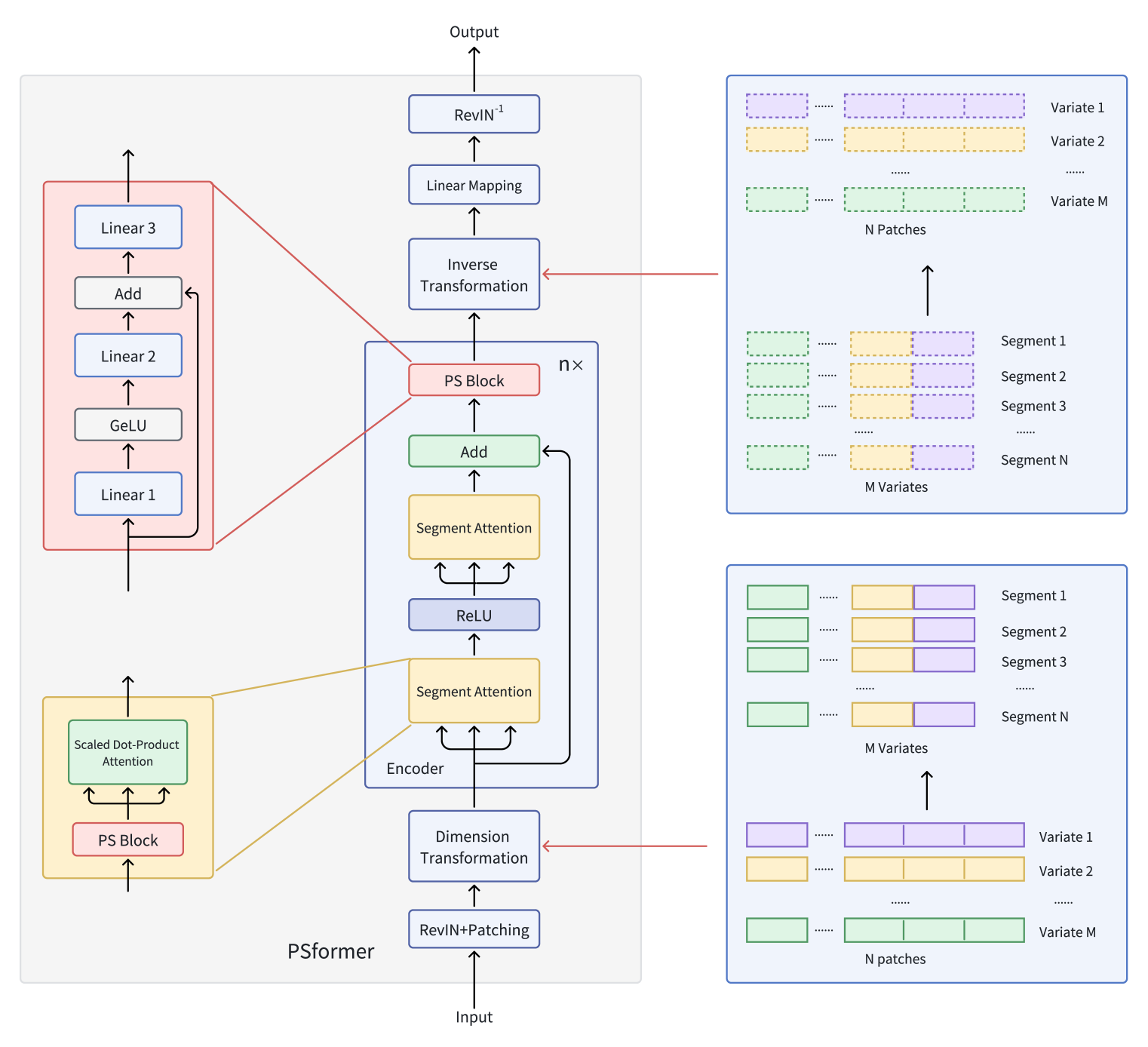
Implementación con MQL5

Tras repasar los aspectos teóricos del framework PSformer, vamos a pasar a la aplicación práctica de nuestra visión de los enfoques propuestos mediante MQL5. Y lo que más nos interesa a nosotros es el algoritmo que implementa el bloque de compartición de parámetros (PS).

Parameter Shared Block

Como ya hemos mencionado, el bloque de compartición de parámetros en la aplicación del autor consta de 3 capas completamente conectadas cuyos parámetros se aplican a todos los segmentos analizados. No hay nada difícil para nosotros aquí. Ya hemos usado muchas veces capas convolucionales con ventanas de análisis de datos no solapadas en casos similares. La dificultad reside en otra parte: el mecanismo para compartir parámetros entre varios bloques.

Por un lado, por supuesto, podemos usar el mismo bloque varias veces dentro de una misma capa. Pero en tal caso, nos enfrentamos al problema de guardar datos para las operaciones de pasada inversa. Al fin y al cabo, cuando volvamos a usar el objeto para realizar operaciones de pasada directa, almacenaremos en el búfer de resultados nuevos datos que sustituirán los resultados de la anterior llamada al método de pasada directa. En un algoritmo normal que utilice la capa neuronal, esto no tiene nada de malo, ya que estaremos alternando constantemente entre pasadas directas e inversas. Y después de realizar las operaciones de la siguiente pasada inversa, podremos sustituir sin problemas los resultados de la pasada directa anterior. Al fin y al cabo, ya no los necesitaremos. No obstante, si se infringen las alternancias de las pasadas directa e inversa, se planteará la cuestión del almacenamiento de todos los datos necesarios para la correcta ejecución de la funcionalidad de la siguiente pasada inversa.

Vale la pena añadir que, en una implementación de este tipo, necesitaremos guardar no solo los resultados a la salida del bloque, sino también todos los valores intermedios. O bien recalcularlos, lo que aumentaría la complejidad computacional del modelo. Además, necesitaremos un mecanismo para sincronizar los búferes en los distintos segmentos a fin de graduar correctamente el error.

Obviamente, hacer realidad los requisitos anteriores exigirá modificar nuestras interfaces para el intercambio de datos entre las capas neuronales. Y esto implicará cambios más globales en la funcionalidad de nuestra biblioteca.

La segunda opción consiste en encontrar un mecanismo para compartir al completo un único búfer de parámetros entre varias capas neuronales idénticas. Y debemos decir que esta opción tampoco está exenta de escollos.

Permítame recordarle que al analizar el framework Deep Deterministic Policy Gradien ya hemos implementado un algoritmo para la actualización suave de los parámetros del modelo objetivo. Sin embargo, copiar la configuración (después de cada actualización) resulta bastante costoso. Por lo tanto, será deseable que realicemos la sustitución de los búferes por matrices de parámetros en sus objetos de compartición.

Aquí, además de la propia matriz de parámetros, también tendremos que organizar la compartición de los búferes de momentos utilizados en el proceso de actualización de los parámetros. De hecho, el uso de búferes de momentos separados en diferentes etapas puede desplazar el vector de actualización de parámetros hacia una de las capas internas.

Hay otro punto que debemos considerar. En una implementación de este tipo, nos enfrentamos a una situación en la que los parámetros de capa al ejecutar las operaciones de pasada inversa son diferentes de los utilizados en la pasada directa. Como esto puede parecer extraño, vamos a desglosar un ejemplo sencillo de 2 capas consecutivas con compartición de parámetros. En la pasada directa, ambas capas utilizan los parámetros W, y en las salidas obtenemos O1 y O2, respectivamente. Cuando los gradientes de error se distribuyen a nivel de los resultados de cada capa, tenemos un desplazamiento de G1 y G2, respectivamente. Sobre el proceso de distribución del gradiente de error no tenemos ninguna duda. En esta fase, los parámetros del modelo permanecen inalterados y todos los gradientes de error se corresponden con los de la pasada directa W. Pero en cuanto ajustemos los parámetros de una de las capas, por ejemplo de la segunda, obtendremos los parámetros ajustados de W'. E inmediatamente nos enfrentaremos al problema del desajuste entre los gradientes de error y los parámetros. Obviamente, el uso directo de un gradiente de error inadecuado puede distorsionar el proceso de aprendizaje.

Una de las opciones para resolver este problema sería determinar los valores objetivo para una capa en particular usando como base los resultados de la última pasada directa y el gradiente de error, con la posterior ejecución de operaciones de pasada directa con los parámetros actuales y el cálculo del gradiente de error correcto. ¿No le recuerda esto al algoritmo de optimización SAM que hemos analizado en artículos anteriores? De hecho, si añadimos al algoritmo de resolución de problemas presentado anteriormente el ajuste de los parámetros antes de realizar una pasada directa repetida, obtendremos un algoritmo de optimización de SAM completo.

Los autores del framework PSformer proponen usar la optimización de SAM. Y esto nos permite aceptar los riesgos derivados del uso de gradientes de error inadecuados porque se recalculan antes de actualizar los parámetros. Sin embargo, en otro caso, podría ser un problema grave.

Considerando todo lo anterior, hemos decidido utilizar la segunda opción para aplicar el compartición de parámetros.

Como ya hemos mencionado, el bloque PS utiliza 3 capas completamente conectadas que sustituiremos por capas convolucionales. Por ello, comenzaremos la implementación del algoritmo de compartición de parámetros precisamente con el objeto de capa convolucional CNeuronConvSAMOCL.

Aquí vale la pena señalar que en la capa convolucional de compartición de parámetros, solo intercambiamos los punteros a los búferes de parámetros y momentos. Al mismo tiempo, los búferes restantes y los valores de las variables internas deberán corresponderse con la dimensionalidad de la matriz de parámetros. Obviamente, en este caso tendremos que cambiar el método de inicialización del objeto. Pero primero crearemos 2 métodos auxiliares: InitBufferLike y ReplaceBuffer.

El primer método creará un nuevo búfer lleno de valores cero según el patrón proporcionado. Su algoritmo es bastante simple. En los parámetros obtendremos los 2 punteros a los objetos de búfer de datos. Primero comprobaremos la relevancia del puntero al búfer de muestra (master). Disponer de un puntero actualizado a este búfer resultará fundamental para las operaciones posteriores. Por lo tanto, si obtenemos un resultado negativo, finalizaremos el método con el resultado false.

bool CNeuronConvSAMOCL::InitBufferLike(CBufferFloat *&buffer, CBufferFloat *master)
  {
   if(!master)
      return false;

Tras pasar con éxito el primer punto de control, comprobaremos la relevancia del puntero al búfer que estamos creando. Pero aquí, si tenemos un resultado negativo, simplemente crearemos una nueva instancia del objeto.

   if(!buffer)
     {
      buffer = new CBufferFloat();
      if(!buffer)
         return false;
     }

Y no nos olvidaremos de comprobar si el nuevo búfer se ha creado correctamente.

A continuación, inicializaremos un búfer del tamaño requerido con valores cero.

   if(!buffer.BufferInit(master.Total(), 0))
      return false;

Y crearemos una copia del mismo en el contexto OpenCL.

   if(!buffer.BufferCreate(master.GetOpenCL()))
      return false;
//---
   return true;
  }

A continuación, finalizaremos el método retornando el resultado lógico de las operaciones al programa que realiza la llamada.

El segundo método ReplaceBuffer realiza una operación de intercambio de punteros en el búfer indicado. A primera vista, no necesitamos un método completo para asignar un puntero a un objeto a una variable interna. Sin embargo, en el cuerpo del método, comprobaremos los búferes de datos excesivos y, de ser necesario, los eliminaremos, lo cual nos permitirá hacer un uso más eficiente de la memoria, tanto de la RAM como del contexto OpenCL.

void CNeuronConvSAMOCL::ReplaceBuffer(CBufferFloat *&buffer, CBufferFloat *master)
  {
   if(buffer==master)
     return;
   if(!!buffer)
     {
      buffer.BufferFree();
      delete buffer;
     }
//---
   buffer = master;
  }

Tras crear los métodos auxiliares, procederemos a construir un nuevo algoritmo para inicializar un objeto de capa convolucional según el copiado de los punteros de los búferes de parámetros del objeto-imagen InitPS. En los parámetros del método, en lugar de la serie de constantes que definen la arquitectura del objeto, obtendremos únicamente el puntero al objeto-imagen que usaremos como modelo al crear un nuevo objeto.

bool CNeuronConvSAMOCL::InitPS(CNeuronConvSAMOCL *master)
  {
   if(!master ||
      master.Type() != Type()
     )
      return false;

En el cuerpo del método comprobaremos la corrección del puntero recibido y la correspondencia de los tipos de objeto.

Además, no construiremos una serie completa de métodos de la clase padre, sino que simplemente transferiremos los valores de todos los parámetros heredados del objeto-imagen.

   alpha = master.alpha;
   iBatch = master.iBatch;
   t = master.t;
   m_myIndex = master.m_myIndex;
   activation = master.activation;
   optimization = master.optimization;
   iWindow = master.iWindow;
   iStep = master.iStep;
   iWindowOut = master.iWindowOut;
   iVariables = master.iVariables;
   bTrain = master.bTrain;
   fRho = master.fRho;

 A continuación, crearemos unos búferes de resultados y gradientes de error similares a los del objeto-imagen.

   if(!InitBufferLike(Output, master.Output))
      return false;
   if(!!master.getPrevOutput())
      if(!InitBufferLike(PrevOutput, master.getPrevOutput()))
         return false;
   if(!InitBufferLike(Gradient, master.Gradient))
      return false;

Después, trasladaremos los punteros primero a los búferes de parámetros de peso y sus momentos heredados de la capa completamente conectada básica.

   ReplaceBuffer(Weights, master.Weights);
   ReplaceBuffer(DeltaWeights, master.DeltaWeights);
   ReplaceBuffer(FirstMomentum, master.FirstMomentum);
   ReplaceBuffer(SecondMomentum, master.SecondMomentum);

Repetiremos la misma operación para los búferes de los parámetros de la capa convolucional y sus momentos.

   ReplaceBuffer(WeightsConv, master.WeightsConv);
   ReplaceBuffer(DeltaWeightsConv, master.DeltaWeightsConv);
   ReplaceBuffer(FirstMomentumConv, master.FirstMomentumConv);
   ReplaceBuffer(SecondMomentumConv, master.SecondMomentumConv);

A continuación, solo tendremos que crear búferes de los parámetros ajustados. No obstante, conviene recordar que, en determinadas condiciones, puede ser posible que no se creen los dos búferes de parámetros corregidos. El búfer de parámetros corregidos de una capa completamente conectada solo se creará si hay enlaces salientes. Por ello, primero comprobaremos el tamaño de este búfer en el objeto-imagen. Y crearemos un búfer similar solo de ser necesario.

   if(master.cWeightsSAM.Total() > 0)
     {
      CBufferFloat *buf = GetPointer(cWeightsSAM);
      if(!InitBufferLike(buf, GetPointer(master.cWeightsSAM)))
         return false;
     }

De lo contrario, eliminaremos este búfer, reduciendo así el consumo de memoria.

   else
     {
      cWeightsSAM.BufferFree();
      cWeightsSAM.Clear();
     }

El búfer de parámetros corregidos de los enlaces entrantes se creará si el coeficiente del área de desenfoque es superior a "0".

   if(fRho > 0)
     {
      CBufferFloat *buf = GetPointer(cWeightsSAMConv);
      if(!InitBufferLike(buf, GetPointer(master.cWeightsSAMConv)))
         return false;
     }

De lo contrario, simplemente eliminaremos este búfer.

   else
     {
      cWeightsSAMConv.BufferFree();
      cWeightsSAMConv.Clear();
     }

Claro que, técnicamente, en lugar del factor de desenfoque, podríamos comprobar el tamaño del búfer de los parámetros ajustados de los enlaces entrantes del objeto-imagen. Al igual que hicimos para el búfer de parámetros ajustados de enlaces salientes. Pero sabemos que cuando el factor de desenfoque es mayor que "0", este búfer debe estar ahí. Y de esta forma incorporaremos controles adicionales. Después de todo, si intentamos crear un búfer de longitud cero, obtendremos un error y detendremos el proceso de inicialización. Esto ayudará a eliminar errores más graves en lo sucesivo.

Al final del método de inicialización, trasladaremos todos los objetos a un único contexto OpenCL y finalizaremos el método devolviendo el resultado lógico de las operaciones al programa que realiza llamada.

   SetOpenCL(master.OpenCL);
//---
   return true;
  }

Una vez realizados los cambios en el objeto de capa convolucional, pasaremos a la siguiente fase de nuestro trabajo. Y en este punto crearemos directamente el bloque de compartición de parámetros (PS). Para ello, crearemos un nuevo objeto CNeuronPSBlock. Como hemos mencionado en la parte teórica, el bloque de compartición de parámetros constará de 3 capas consecutivas de transformación lineal de datos. En este caso, cada capa tiene una matriz cuadrada de parámetros que indicará la conservación de las dimensionalidades de los tensores a la entrada y a la salida tanto del bloque en su conjunto como de las capas internas. Entre las dos primeras capas se creará una no linealidad utilizando la función de activación GELU. Y tras la segunda capa, se añadirá un enlace residual con los datos de origen.

Para implementar el algoritmo propuesto, crearemos 2 capas convolucionales internas en el cuerpo de nuestro nuevo objeto, y como última capa convolucional utilizaremos directamente la estructura de nuestra clase, cuya funcionalidad básica heredaremos de la capa convolucional. Y puesto que utilizaremos la optimización de SAM en el proceso de entrenamiento, también usaremos las capas convolucionales correspondientes al construir la arquitectura de los objetos. A continuación, le mostraremos la estructura de la nueva clase.

class CNeuronPSBlock :  public CNeuronConvSAMOCL
  {
protected:
   CNeuronConvSAMOCL acConvolution[2];
   CNeuronBaseOCL    cResidual;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronPSBlock(void) {};
                    ~CNeuronPSBlock(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_out, uint units_count, 
                          uint variables, float rho, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   virtual bool      InitPS(CNeuronPSBlock *master);
   //---
   virtual int       Type(void)   const         {  return defNeuronPSBlock;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual CLayerDescription* GetLayerInfo(void);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Como puede ver, la estructura presentada del nuevo objeto declara 2 métodos de inicialización. Y esto no es casualidad. El primer método de inicialización Init supone un medio básico para inicializar un objeto cuya arquitectura se especifica explícitamente en los parámetros del método. El segundo método InitPS, similar al método de capa convolucional homónimo, creará un nuevo objeto a imagen y semejanza del objeto-imagen obtenido en los parámetros. Y al inicializar un nuevo objeto, se copiarán los punteros a las búferes de parámetros y sus momentos. Le propongo analizar con detalle el algoritmo para construir los métodos anteriores.

Como ya hemos mencionado anteriormente, en los parámetros del método Init obtenemos una serie de constantes que nos permiten definir de forma inequívoca la arquitectura del objeto que estamos creando.

bool CNeuronPSBlock::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_out, uint units_count,
                          uint variables, float rho,
                          ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronConvSAMOCL::Init(numOutputs, myIndex, open_cl, window, window, window_out,
                               units_count, variables, rho, optimization_type, batch))
      return false;

Y en el cuerpo del método transmitiremos directamente todos los parámetros recibidos al método homónimo de la clase padre. Como sabrá, el método de la clase padre ya ha organizado los puntos de control necesarios para los parámetros recibidos y los algoritmos para inicializar los objetos heredados.

Como ya hemos mencionado, todas las capas convolucionales del bloque de compartición de parámetros tienen la misma dimensionalidad. Por lo tanto, al inicializar la primera capa convolucional anidada, transmitiremos los mismos parámetros.

   if(!acConvolution[0].Init(0, 0, OpenCL, iWindow, iWindow, iWindowOut, units_count,
                             iVariables, fRho, optimization, iBatch))
      return false;
   acConvolution[0].SetActivationFunction(GELU);

Y añadiremos la función de activación sugerida por los autores del framework.

No obstante, dejaremos que el usuario cambie las dimensiones del tensor a la salida del bloque. Por lo tanto, al inicializar la segunda capa convolucional anidada, destinada a añadir los enlaces residuales, para obtener una dimensionalidad de los resultados igual a la de los datos originales, intercambiaremos los parámetros de la ventana de los datos analizados y el número de filtros.

   if(!acConvolution[1].Init(0, 1, OpenCL, iWindowOut, iWindowOut, iWindow, units_count,
                             iVariables, fRho, optimization, iBatch))
      return false;
   acConvolution[1].SetActivationFunction(None);

Aquí no utilizaremos la función de activación.

A continuación, añadiremos una capa neuronal básica para almacenar los datos de los enlaces residuales. Su tamaño se corresponderá con el búfer de resultados de la segunda capa convolucional anidada.

   if(!cResidual.Init(0, 2, OpenCL, acConvolution[1].Neurons(), optimization, iBatch))
      return false;
   if(!cResidual.SetGradient(acConvolution[1].getGradient(), true))
      return false;
   cResidual.SetActivationFunction(None);

E inmediatamente implementaremos la sustitución del búfer del gradiente de error, lo que nos permitirá reducir las operaciones de copiado de datos en el proceso de pasada inversa.

Ahora solo tendremos que desactivar explícitamente la función de activación de nuestro bloque de compartición de parámetros y finalizar el método pasando el resultado lógico de las operaciones al programa que realiza la llamada.

   SetActivationFunction(None);
//---
   return true;
  }

El algoritmo del segundo método de inicialización parece un poco más sencillo. En los parámetros del método obtendremos el puntero al objeto-imagen y lo transmitiremos inmediatamente al método homónimo de la clase padre.

Aquí deberemos prestar atención a la diferencia entre los tipos de parámetros recibidos en el método actual y la clase padre. Por lo tanto, especificaremos explícitamente el tipo de objeto que vamos a transmitir.

bool CNeuronPSBlock::InitPS(CNeuronPSBlock *master)
  {
   if(!CNeuronConvSAMOCL::InitPS((CNeuronConvSAMOCL*)master))
      return false;

En el cuerpo de la clase padre ya están organizados los puntos de control necesarios. Así como el copiado de constantes, la creación de nuevos búferes y el guardado de los punteros a los búferes de parámetros y sus momentos.

A continuación, organizaremos un ciclo en el que llamaremos a los métodos homónimos para las capas convolucionales anidadas, copiando los datos de los objetos-imagen correspondientes.

   for(int i = 0; i < 2; i++)
      if(!acConvolution[i].InitPS(master.acConvolution[i].AsObject()))
         return false;

La capa de almacenamiento de resultados de los enlaces residuales no contendrá parámetros entrenados y su tamaño será igual al búfer de resultados de la segunda capa convolucional anidada. Por lo tanto, hemos transferido completamente el algoritmo para inicializar este objeto del método de inicialización principal.

   if(!cResidual.Init(0, 2, OpenCL, acConvolution[1].Neurons(), optimization, iBatch))
      return false;
   if(!cResidual.SetGradient(acConvolution[1].getGradient(), true))
      return false;
   cResidual.SetActivationFunction(None);
//---
   return true;
  }

Y no nos olvidaremos de sustituir los punteros por el búfer de gradiente de error.

Tras considerar los métodos de inicialización de un objeto, que en este caso son dos, pasaremos a la construcción de los algoritmos de pasada directa. Aquí todo será bastante trivial. En los parámetros del método obtendremos el puntero al objeto de datos de origen, que pasaremos inmediatamente al método homónimo de la primera capa convolucional interna.

bool CNeuronPSBlock::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!acConvolution[0].FeedForward(NeuronOCL))
      return false;

Luego encadenaremos los resultados en la siguiente capa convolucional. Después, sumaremos los valores obtenidos con los datos de origen. La suma de los valores se almacenará en el búfer de la capa de enlaces residuales.

   if(!acConvolution[1].FeedForward(acConvolution[0].AsObject()))
      return false;
   if(!SumAndNormilize(NeuronOCL.getOutput(), acConvolution[1].getOutput(), cResidual.getOutput(),
                                                                       iWindow, true, 0, 0, 0, 1))
      return false;

Aquí cabe señalar que, a diferencia del algoritmo del autor, normalizaremos el tensor residual. Y solo entonces pasaremos a la última capa convolucional, cuya funcionalidad se ejecutará mediante la funcionalidad heredada de la clase padre.

   if(!CNeuronConvSAMOCL::feedForward(cResidual.AsObject()))
      return false;
//---
   return true;
  }

Y finalizaremos el método devolviendo el resultado lógico de las operaciones al programa que realiza la llamada.

El método de distribución de gradientes de error calcInputGradients será igual de sencillo, pero no estará exento de matices. En los parámetros del método obtendremos el puntero al objeto de capa neuronal con los datos de origen al que pasaremos el gradiente de error.

bool CNeuronPSBlock::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
     return false;

En el cuerpo del método comprobamos directamente la relevancia del puntero recibido, porque de lo contrario las operaciones posteriores carecerán de sentido.

A continuación, pasaremos sucesivamente los gradientes por todas las capas convolucionales en orden inverso.

   if(!CNeuronConvSAMOCL::calcInputGradients(cResidual.AsObject()))
      return false;
   if(!acConvolution[0].calcHiddenGradients(acConvolution[1].AsObject()))
      return false;
   if(!NeuronOCL.calcHiddenGradients(acConvolution[0].AsObject()))
      return false;

Nótese que en el código presentado, no existe la transferencia del gradiente de error desde el objeto de enlace residual a la segunda capa convolucional interna. Sin embargo, gracias a la sustitución de punteros del búfer de datos que organizamos anteriormente, la transferencia de información se ha completado.

Después de pasar el gradiente de error a la capa de datos de origen desde la línea troncal de la capa convolucional, tendremos que añadir el gradiente de error a lo largo de la línea troncal de los enlaces residuales. Y aquí se podrían dar dos situaciones, dependiendo de la función de activación del objeto de datos de origen.

Quiero recordar que pasaremos el gradiente de error al objeto de enlace residual sin corregir la derivada de la función de activación. Hemos señalado explícitamente la falta de esta para dicho objeto.

Por lo tanto, siempre que el objeto de datos de origen no tenga función de activación, solo tendremos que sumar los valores correspondientes de los dos búferes.

   if(NeuronOCL.Activation() == None)
     {
      if(!SumAndNormilize(NeuronOCL.getGradient(), cResidual.getGradient(), NeuronOCL.getGradient(),
                                                                        iWindow, false, 0, 0, 0, 1))
         return false;
     }

De lo contrario, primero corregiremos el gradiente de error resultante mediante la derivada de la función de activación de los datos de origen en el búfer libre. Y, a continuación, sumaremos los resultados obtenidos con los acumulados previamente en el búfer del objeto de datos de origen.

   else
     {
      if(!DeActivation(NeuronOCL.getOutput(), cResidual.getGradient(), cResidual.getPrevOutput(), 
                                                                           NeuronOCL.Activation()) ||
         !SumAndNormilize(NeuronOCL.getGradient(), cResidual.getPrevOutput(), NeuronOCL.getGradient(),
                                                                          iWindow, false, 0, 0, 0, 1))
         return false;
     }
//---
   return true;
  }

A continuación, finalizaremos el método.

Debemos decir unas palabras sobre el método de actualización de los parámetros del bloque updateInputWeights. Aquí no tendremos dificultades para construir el algoritmo: bastará con llamar a los métodos homónimos de la clase padre y a los objetos anidados que contienen los parámetros a entrenar.

bool CNeuronPSBlock::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!CNeuronConvSAMOCL::updateInputWeights(cResidual.AsObject()))
      return false;
   if(!acConvolution[1].UpdateInputWeights(acConvolution[0].AsObject()))
      return false;
   if(!acConvolution[0].UpdateInputWeights(NeuronOCL))
      return false;
//---
   return true;
  }

Sin embargo, el uso de enfoques de optimización de SAM impone estrictas restricciones a la secuencia de operaciones. La cuestión es que durante la optimización de SAM, realizaremos una segunda pasada directa con parámetros ajustados. Como resultado, cambiaremos los datos del búfer de resultados. Esto no tiene una importancia crítica a la hora de optimizar los parámetros de la capa actual, pero afecta a la actualización de los parámetros de la capa siguiente. Al fin y al cabo, usamos los resultados de la pasada directa de la capa anterior para ajustar sus parámetros. Por lo tanto, en este caso, será importante que realicemos los ajustes de los parámetros en el orden inverso al de los objetos internos. Esto nos permitirá ajustar los parámetros de la capa antes de modificar los valores en el búfer de resultados del objeto anterior.

Con esto concluye nuestra revisión de los algoritmos de los bloques de compartición de parámetros CNeuronPSBlock. Podrá leer el código completo de esta clase y todos sus métodos por sí mismo en el archivo adjunto.

Nuestro trabajo aún no ha terminado, pero ya casi hemos agotado el volumen del presente artículo. Así que nos tomaremos un breve descanso y continuaremos el trabajo iniciado en el próximo artículo.

Conclusión

En este artículo, nos hemos familiarizado con el framework PSformer, cuyos autores destacan la alta precisión en la previsión de series temporales y la eficiencia en el uso de recursos computacionales. Las principales características arquitectónicas del PSformer son el bloque de compartición de parámetros (PS) y la atención a los segmentos espaciotemporales (SegAtt). Su uso permite modelar eficazmente las dependencias locales y globales de las series temporales y reducir el número de parámetros sin perder calidad en las previsiones.

En la parte práctica del artículo, hemos empezado a aplicar nuestra propia visión de los enfoques propuestos utilizando herramientas MQL5. Sin embargo, nuestro trabajo aún no ha concluido. En el próximo artículo continuaremos el trabajo iniciado, además de evaluar la eficacia de los enfoques propuestos para resolver nuestros problemas con datos históricos reales.

Enlaces

PSformer: Parameter-efficient Transformer with Segment Attention for Time Series Forecasting

Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	StudyEncoder.mq5	Asesor	Asesor de entrenamiento del Codificador
5	Test.mq5	Asesor	Asesor para la prueba de modelos
6	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
7	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
8	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL