Redes neuronales en el trading: Conjunto de agentes con uso de mecanismos de atención (Final)

Introducción

La gestión de portafolios de instrumentos financieros desempeña un papel importante en las decisiones de inversión encaminadas a aumentar la rentabilidad y reducir los riesgos reasignando dinámicamente el capital entre activos. En el artículo "Developing an attention-based ensemble learning framework for financial portfolio optimisation" se propone el innovador framework adaptativo multiagente MASAAT, que combina mecanismos de atención y análisis de series temporales. El enfoque propuesto genera múltiples agentes comerciales que analizan de forma cruzada los cambios direccionales en los precios de los activos a diferentes niveles de detalle. Esta solución nos permite revisar la estructura del portafolio de inversiones para equilibrar de forma eficaz los rendimientos y los riesgos en unos mercados financieros muy volátiles.

Para captar cambios sustanciales en los precios, los agentes usan filtros de movimiento direccional con diferentes umbrales. De esta forma, se extraen las principales características de tendencia de las series temporales de precios analizadas, lo cual mejora la comprensión de las transiciones del mercado de distinta intensidad. El enfoque propuesto introduce una nueva técnica para generar tokens de secuencias que permite a los módulos de análisis transversal basados en la atención (CSA) y de análisis temporal (TA) detectar eficazmente diversas correlaciones. En concreto, al reconstruir los mapas de características, los tokens de secuencia del módulo CSA se generan según el rendimiento de los activos individuales optimizado mediante la aplicación de mecanismos de atención. Al mismo tiempo, los tokens del módulo TA se construyen a partir de las características de los puntos temporales, lo que nos permite destacar relaciones significativas entre momentos individuales en el tiempo.

Los agentes MASAAT combinan las estimaciones de correlación de activos y puntos temporales recogidas en los módulos CSA y TA usando un mecanismo de atención, con el objetivo de encontrar correlaciones para cada activo respecto a cada punto temporal durante el periodo de observación.

A continuación le mostramos la visualización del framework MASAAT realizada por el autor.

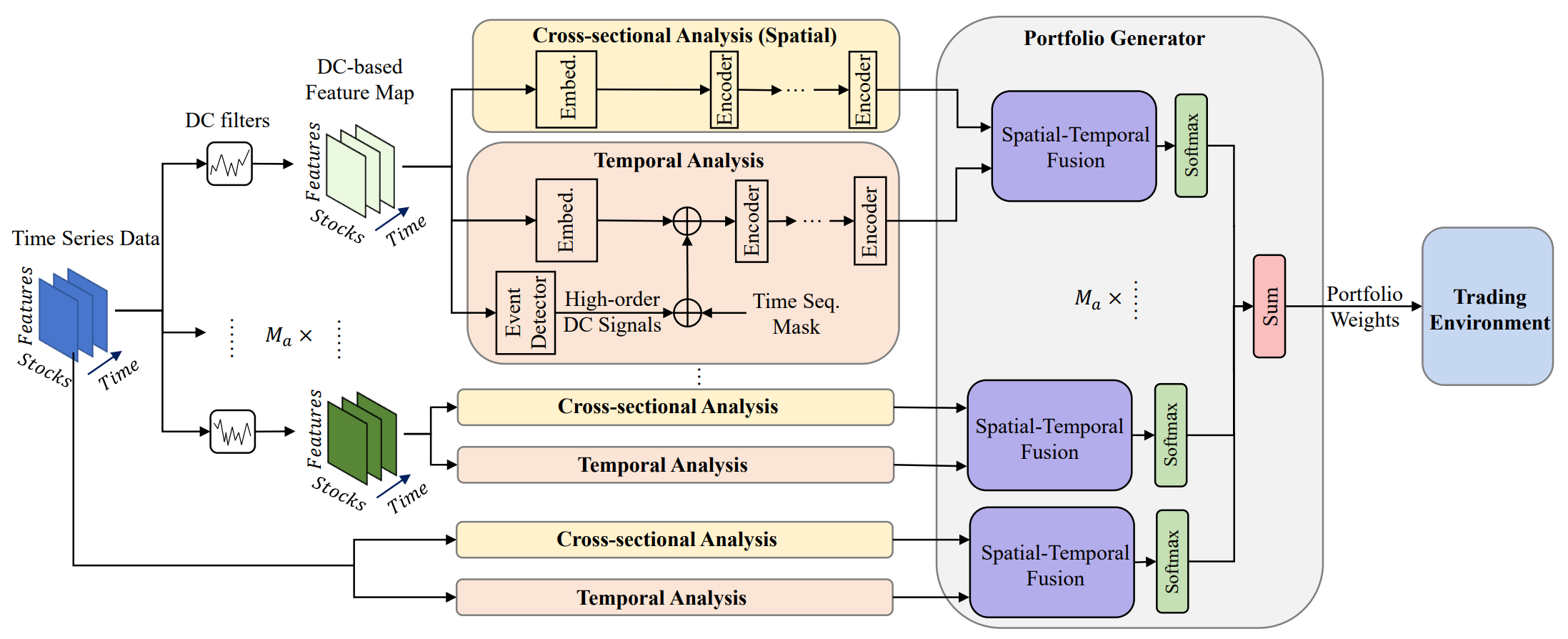
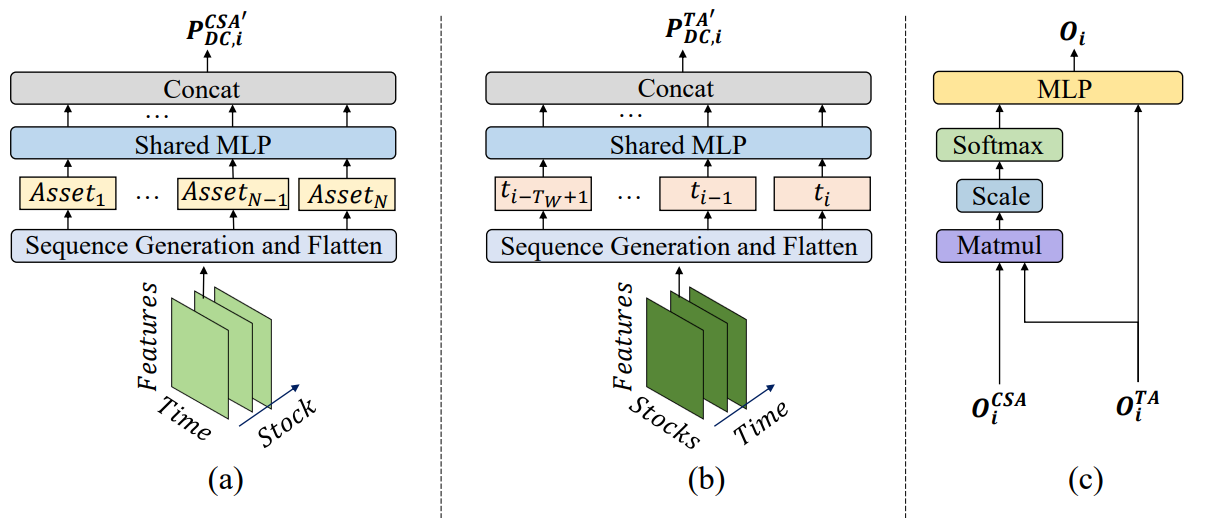
El framework MASAAT tiene una marcada estructura de bloques. Esto nos permite implementar cada bloque como una clase independiente y luego combinar los objetos creados en una estructura única. En el último artículo ya presentamos los algoritmos necesarios para implementar un objeto multiagente de transformación paralela de las series temporales multimodales analizadas en representaciones lineales por trozos de diferentes escalas CNeuronPLRMultiAgentsOCL. Asimismo, analizamos el algoritmo del módulo de atención transversal de activos CSACNeuronCrossSectionalAnalysis. En este artículo continuaremos el trabajo iniciado.

Módulo de análisis temporal

En el artículo anterior, finalizamos el análisis del objeto CNeuronCrossSectionalAnalysis, en el marco del cual se implementa la funcionalidad del módulo CSA. Paralelamente, el módulo de análisis temporal TA trabaja en la estructura del framework MASAAT. Dicho módulo organiza la búsqueda de dependencias entre puntos temporales individuales de la secuencia multimodal analizada. Un examen detallado de la estructura de estos dos módulos revela su casi total coincidencia. En este caso, además, realizan un análisis cruzado de los datos de origen. En otras palabras, observan la secuencia analizada desde distintos ángulos.

La solución obvia aquí consiste en transponer la secuencia original antes de pasar los datos a la entrada del objeto CNeuronCrossSectionalAnalysis creado previamente. Y aquí nos enfrentamos a la necesidad de transponer dos dimensiones en un tensor tridimensional. No olvidemos que debemos realizar el análisis paralelo de varias secuencias temporales multimodales. Más concretamente, cada agente analizará una escala diferente de la representación lineal por trozos de la secuencia multimodal original. Como consecuencia, a la entrada del objeto, planeamos recibir un tensor tridimensional [Agente, Activo, Tiempo], y para analizar las dependencias de los puntos temporales, tendremos que transponer los datos de origen de las dos últimas dimensiones. Esta funcionalidad aún no está disponible en nuestra biblioteca, lo que significa que dependerá de nosotros crearla.

El problema de la transposición del tensor tridimensional de las dos últimas dimensiones puede abordarse de diferentes formas. Obviamente, la primera solución consiste en resolver el problema, como se dice, "frontalmente", es decir, creando un nuevo kernel en el lado del programa OpenCL, seguido de la construcción de una nueva clase en el lado del programa principal para servir a este kernel. Esta es probablemente la solución más eficiente en cuanto a la utilización de recursos informáticos. Pero, al mismo tiempo, es la más laboriosa para el programador. Así, hemos decidido facilitar un poco la vida del programador a expensas de los recursos informáticos y organizar el proceso mediante tres capas de transposición consecutivas creadas previamente. Más concretamente, primero utilizaremos la capa de transposición de una matriz bidimensional combinando las dos últimas dimensiones en una sola:

[Agente, [Activo, Tiempo]] → [[Tiempo, Activo], Agente]

A continuación, utilizaremos el objeto CNeuronTransposeRCDOCL para transponer el tensor 3D de las dos primeras dimensiones:

[Tiempo, Activo, Agente] → [Activo, Tiempo, Agente]

Por último, reutilizaremos la capa de transposición de matrices para devolver la dimensión de los agentes al primer lugar combinando las otras dos dimensiones en una sola:

[[Activo, Tiempo], Agente] → [Agente, [Tiempo, Activo]]

Luego organizaremos el proceso descrito dentro de una nueva clase CNeuronTransposeVRCOCL, cuya estructura se indica a continuación.

class CNeuronTransposeVRCOCL  :  public CNeuronTransposeOCL
  {
protected:
   CNeuronTransposeOCL     cTranspose;
   CNeuronTransposeRCDOCL  cTransposeRCD;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;

public:
                     CNeuronTransposeVRCOCL(void) {};
                    ~CNeuronTransposeVRCOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint variables, uint count, uint window, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)  const override    {  return defNeuronTransposeVRCOCL; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Utilizaremos la capa de transposición de matrices 2D como objeto padre, que actúa simultáneamente como último paso de la transposición de datos. Esto nos permitirá declarar solo dos objetos estáticos en el cuerpo de la nueva clase. La inicialización de todos los objetos se realizará en el método Init, en cuyos parámetros obtendremos las tres dimensionalidades del tensor transpuesto.

bool CNeuronTransposeVRCOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                  uint variables, uint count, uint window,
                                  ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronTransposeOCL::Init(numOutputs, myIndex, open_cl, count * window, variables, optimization_type, batch))
      return false;

En el cuerpo del método llamaremos al método homónimo de la clase padre. Sin embargo, aquí cabe señalar que utilizaremos el objeto padre para la permutación final de los datos. Por lo tanto, deberemos transmitir los parámetros correctos al llamar a un método de la clase padre. En este caso, la primera dimensión se definirá como el producto de las dos últimas dimensiones del tensor original. La dimensión restante, creo, resulta obvia.

Tras ejecutar con éxito las operaciones del método de la clase padre, inicializaremos los objetos internos. Primero inicializaremos la capa de transposición primaria de la matriz. Sus parámetros serán los inversos del método ejecutado anteriormente de la clase padre.

   if(!cTranspose.Init(0, 0, OpenCL, variables, count * window, optimization, iBatch))
      return false;

Y a continuación, inicializaremos el objeto de transposición de las dos primeras dimensiones del tensor tridimensional. Aquí es donde intercambiaremos las medidas de activo y tiempo.

   if(!cTransposeRCD.Init(0, 1, OpenCL, count, window, variables, optimization, iBatch))
      return false;
//---
   return true;
  }

Solo nos quedará devolver el resultado lógico de las operaciones al programa que realiza la llamada y finalizar el método.

El método de inicialización presentado es bastante sencillo y directo. Lo mismo puede decirse de los demás métodos de la clase presentada de transposición tensorial tridimensional. Por ejemplo, en el método feedForward, llamaremos secuencialmente a los métodos homónimos de los objetos internos, mientras que el método homónimo de la clase padre completará el trabajo.

bool CNeuronTransposeVRCOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;
   if(!cTransposeRCD.FeedForward(cTranspose.AsObject()))
      return false;
//---
   return CNeuronTransposeOCL::feedForward(cTransposeRCD.AsObject());
  }

Le sugiero que leas usted mismo los algoritmos de los métodos de pasada inversa en el archivo adjunto. Además, el objeto no contendrá parámetros entrenables.

Y ahora que tenemos el objeto de transposición de datos necesario, podremos proceder a la implementación del módulo de análisis temporal TA, cuyos algoritmos implementaremos en la clase CNeuronTemporalAnalysis. La funcionalidad de la nueva clase será lo más sencilla posible. Solo transpondremos los datos de origen y luego utilizaremos las herramientas del módulo de atención transversal de activos. Más abajo le mostramos la estructura del nuevo objeto.

class CNeuronTemporalAnalysis :  public CNeuronCrossSectionalAnalysis
  {
protected:
   CNeuronTransposeVRCOCL  cTranspose;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronTemporalAnalysis(void) {};
                    ~CNeuronTemporalAnalysis(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint heads, uint heads_kv,
                          uint units_count, uint layers, uint layers_to_one_kv,
                          uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) override;
   //---
   virtual int       Type(void)   const override   {  return defNeuronTemporalAnalysis;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Utilizaremos como clase padre el objeto del módulo de atención transversal de activos. Como se ha mencionado anteriormente, planeamos usar la funcionalidad de este objeto para implementar el algoritmo principal. Simplemente añadiremos un objeto de transposición interna del tensor tridimensional sobre las dos últimas dimensiones. La inicialización de los objetos nuevos y heredados se realizará en el método Init, que heredará completamente la estructura de parámetros del método similar de la clase padre.

bool CNeuronTemporalAnalysis::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                   uint window, uint window_key, uint heads, uint heads_kv,
                                   uint units_count, uint layers, uint layers_to_one_kv, uint variables,
                                   ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronCrossSectionalAnalysis::Init(numOutputs, myIndex, open_cl, 3 * units_count, window_key, heads, heads_kv,
                                           window / 3, layers, layers_to_one_kv, variables, optimization_type, batch))
      return false;

En el cuerpo del método llamaremos inmediatamente al método homónimo de la clase padre, transmitiéndole todos los parámetros recibidos.

Y aquí deberemos prestar atención a algunos matices de nuestra aplicación. En primer lugar, en los parámetros externos, obtendremos las dimensionalidades de los datos de origen. Y quiero recordarles que se supone que debemos transponer el tensor tridimensional de los datos de origen de las dos últimas dimensiones. Por lo tanto, al transmitir los parámetros al método de inicialización de la clase padre, intercambiaremos el sitio de las dimensiones especificadas.

En segundo lugar, deberemos recordar la estructura de los datos de origen a obtener. A la entrada de este objeto supondremos que se suministran los resultados del bloque multiagente de detección de tendencias. Esto significa que cada vez, suministraremos a la entrada del modelo el tensor de la representación lineal por trozos de la serie temporal multimodal. La variante de representación lineal por trozos de la serie temporal que hemos implementado implica la selección de 3 elementos para preservar los parámetros de un segmento dirigido de la serie temporal unitaria. La lógica nos dice que durante su análisis deberemos considerarlos como un todo. Por lo tanto, aumentaremos el tamaño de la ventana analizada en un factor de 3 y, en consecuencia, disminuiremos en un factor de 3 la longitud de la secuencia.

Una vez las operaciones del método de inicialización de la clase padre hayan tenido éxito, llamaremos al método homónimo del objeto interno de transposición del tensor tridimensional.

   if(!cTranspose.Init(0, 0, OpenCL,variables, units_count, window, optimization_type, batch))
      return false;
//---
   return true;
  }

Y finalizaremos el método devolviendo el resultado lógico de las operaciones al programa que realiza la llamada.

Los algoritmos para los métodos de pasada directa e inversa del objeto CNeuronTemporalAnalysis son trivialmente simples. Por lo tanto, no nos detendremos ahora a analizarlos; el lector podrá estudiarlos por su propia cuenta. El código completo de esta clase y todos sus métodos se encuentran en el archivo adjunto al artículo.

Módulo de generación de portafolios

A la salida de los bloques CSA y TA, obtendremos datos de origen enriquecidos con información sobre las dependencias entre activos y puntos temporales, respectivamente. Esta información se combinará usando un mecanismo de atención para que cada agente forme su propia versión de un portafolio de inversión. Más concretamente, en primer lugar, cada agente generará sus propias incorporaciones de activos dependientes del tiempo y, a continuación, utilizando una capa completamente conectada, se generará un vector de distribución proporcional del paquete de inversiones, donde la suma de todos los elementos del vector será igual a 1.

Permítame recordarle la representación matemática de la función de generación del paquete de inversión:

A partir de las propuestas del paquete de inversión, se elaborará la presentación final del mismo.

Aquí nos desviaremos un poco de la presentación que hace el autor del framework MASAAT. Aunque, todo hay que decirlo, nuestra digresión será más lógica que matemática. En la práctica, al repetir la función anterior en su totalidad, la idea de los resultados obtenidos cambiará ligeramente.

La cuestión es que nuestra tarea será algo distinta de la resuelta por los autores del framework. A la salida del modelo nos gustaría obtener un vector de acciones del Agente con la indicación de la dirección de la transacción y su volumen, así como los niveles de stop-loss y take-profit. Al mismo tiempo, para determinar el volumen de operaciones, además de los datos sobre la dinámica del instrumento financiero analizado, necesitaremos información sobre el estado de la cuenta, ausente en los datos de origen. Por lo tanto, a la salida de nuestro objeto de implementación de los enfoques del framework MASAAT, esperamos obtener algún estado oculto que contenga una incorporación con un análisis exhaustivo de la situación actual del mercado.

La parte final de la funcionalidad del framework MASAAT se implementará en el objeto CNeuronPortfolioGenerator, cuya estructura se muestra a continuación.

class CNeuronPortfolioGenerator  :  public CNeuronBaseOCL
  {
protected:
   uint              iAssets;
   uint              iTimePoints;
   uint              iAgents;
   uint              iDimension;
   //---
   CNeuronBaseOCL          cAssetTime[2];
   CNeuronTransposeVRCOCL  cTransposeVRC;
   CNeuronSoftMaxOCL       cSoftMax;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)  override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override { return false; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                                                   CBufferFloat *SecondGradient, 
                                                ENUM_ACTIVATION SecondActivation = None) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronPortfolioGenerator(void) {};
                    ~CNeuronPortfolioGenerator(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint assets, uint time_points, uint dimension,
                          uint agents,  uint projection,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const override   {  return defNeuronPortfolioGenerator;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

En la estructura de la nueva clase declararemos varios objetos internos, cuya funcionalidad conoceremos durante la implementación de los métodos. Luego declararemos todos los objetos internos de forma estática, lo cual nos permitirá dejar el constructor y el destructor de la clase vacíos. La inicialización de todos los objetos internos declarados y heredados se realizará en el método Init. Y aquí, todo sea dicho, hay una serie de matices a considerar.

bool CNeuronPortfolioGenerator::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                     uint assets, uint time_points, uint dimension,
                                     uint agents, uint projection,
                                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(assets <= 0 || time_points <= 0 || dimension <= 0 || agents <= 0)
      return false;

En los parámetros del método, tenemos varios parámetros cuyo significado requiere explicación:

• assets — número de activos analizados en el módulo CSA;
• time_points — número de puntos temporales analizados en el módulo TA;
• dimension — dimensionalidad del vector de incorporación de un elemento de la secuencia analizada (común para los módulos CSA y TA);
• agents — número de agentes;
• projection — tamaño de la proyección del estado analizado a la salida del módulo.

En el cuerpo del método, comprobaremos directamente los valores de los parámetros. Todos ellos deberán ser al menos mayores que "0". Y luego llamaremos al método de inicialización de la clase padre, transmitiéndole la dimensionalidad de la proyección del estado analizado. Este es el tipo de tensor que esperamos obtener a la salida del módulo.

   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, projection, optimization_type, batch))
      return false;

Una vez ejecutadas con éxito las operaciones del método de la clase padre, almacenaremos los valores de los parámetros externos en las variables internas.

   iAssets = assets;
   iTimePoints = time_points;
   iDimension = dimension;
   iAgents = agents;

Después, inicializaremos los objetos internos. Y aquí debemos remitirnos a la fórmula presentada anteriormente. Esta implica que utilizaremos dos veces los resultados del módulo de análisis temporal de TA. La primera vez en versión transpuesta y la segunda no.

Me gustaría recordarle que la salida del módulo TA es un tensor tridimensional con dimensionalidades [Agente, Tiempo, Incorporación]. Por lo tanto, en este caso, necesitaremos utilizar el objeto de transposición del tensor tridimensional de las dos últimas dimensiones.

   if(!cTransposeVRC.Init(0, 0, OpenCL, iAgents, iTimePoints, iDimension, optimization, iBatch))
      return false;

A continuación, multiplicaremos los resultados del módulo CSA por los datos transpuestos del módulo TA. El método de multiplicación de matrices lo heredaremos de la clase padre. Pero para registrar los resultados, inicializaremos la capa interna completamente conectada.

   if(!cAssetTime[0].Init(0, 1, OpenCL, iAssets * iTimePoints * iAgents, optimization, iBatch))
      return false;
   cAssetTime[0].SetActivationFunction(None);

Luego normalizaremos los valores obtenidos con la función SoftMax.

   if(!cSoftMax.Init(0, 2, OpenCL, cAssetTime[0].Neurons(), optimization, iBatch))
      return false;
   cSoftMax.SetHeads(iAssets * iAgents);

Obsérvese que la normalización de los datos se realizará de acuerdo con los activos de cada agente. Por lo tanto, especificaremos el número de cabezas de normalización como el producto del número de activos por el número de agentes.

Los coeficientes normalizados, obtenidos como resultado de esta operación, representarán los pesos de atención asignados a cada punto temporal a nivel de cada activo, separados por agente. Multiplicando la matriz de estos coeficientes por los resultados del módulo TA, obtendremos las incorporaciones de los activos analizados. Para escribir estas incorporaciones, inicializaremos una capa completamente conectada.

   if(!cAssetTime[1].Init(Neurons(), 3, OpenCL, iAssets * iDimension * iAgents, optimization, iBatch))
      return false;
   cAssetTime[1].SetActivationFunction(None);
//---
   return true;
  }

Para proyectar el conjunto de incorporaciones recibidas de todos los agentes en una única representación del estado del entorno analizado, utilizaremos una capa completamente conectada. Y aquí deberemos prestar atención al hecho de que es precisamente el objeto de la capa completamente conectada lo que hemos utilizado como padre. Aprovechando este hecho, no crearemos una capa interna adicional completamente conectada. Su funcionalidad será realizada por las herramientas heredadas del padre. Solo especificaremos en la última capa interna el número de enlaces salientes al nivel del tamaño de la proyección obtenido del programa externo.

Y después de inicializar con éxito todos los objetos internos, finalizaremos el método, devolviendo previamente los resultados de las operaciones al programa que realiza la llamada.

En la siguiente etapa de nuestro trabajo, procederemos a la construcción de los algoritmos de pasada directa en el método feedForward. Debemos señalar que en este caso estaremos tratando con dos fuentes de datos de origen. Al hacerlo, tendremos presente el doble uso de los resultados del módulo de análisis temporal. Y esta circunstancia nos obligará a utilizar precisamente este flujo de información como nuestro principal flujo de información.

bool CNeuronPortfolioGenerator::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   if(!SecondInput)
      return false;
//---
   if(!cTransposeVRC.FeedForward(NeuronOCL))
      return false;

En el cuerpo del método, comprobaremos si el puntero a la segunda fuente de datos está actualizado y transpondremos la primera. Y tras el trabajo preparatorio, pasaremos a los cálculos directos. Primero multiplicaremos el tensor de la segunda fuente de datos de origen por el tensor transpuesto de la primera.

   if(!MatMul(SecondInput, cTransposeVRC.getOutput(), cAssetTime[0].getOutput(), iAssets, iDimension, 
                                                                                 iTimePoints, iAgents))
      return false;

Los resultados se normalizarán usando la función SoftMax.

   if(!cSoftMax.FeedForward(cAssetTime[0].AsObject()))
      return false;

Y multiplicaremos por los datos de origen del flujo de información principal.

   if(!MatMul(cSoftMax.getOutput(), NeuronOCL.getOutput(), cAssetTime[1].getOutput(), iAssets, iTimePoints,
                                                                                      iDimension, iAgents))
      return false;

Y ahora tendremos que proyectar los datos obtenidos en el subespacio especificado utilizando la clase padre.

   return CNeuronBaseOCL::feedForward(cAssetTime[1].AsObject());
  }

Después devolveremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.

Una vez completado el trabajo de organización de los procesos de pasada directa, pasaremos a la construcción de los algoritmos de la pasada inversa. Y aquí veremos en primer lugar el método de distribución del gradiente de error calcInputGradients.

bool CNeuronPortfolioGenerator::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                     CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!NeuronOCL || !SecondGradient || !SecondInput)
      return false;

En los parámetros del método, obtendremos los punteros a los objetos de datos de origen y los gradientes de error correspondientes para ambos flujos de información. Y en el cuerpo del método comprobaremos directamente la corrección de los punteros recibidos. De lo contrario, todas las operaciones posteriores carecerán de sentido.

Como usted ya sabrá, la propagación del gradiente de error se realiza de acuerdo con el flujo de información de la pasada directa, solo que en la dirección opuesta. Las operaciones de este método comenzarán con una llamada al método homónimo de distribución del gradiente del error de la clase padre hasta el objeto interior.

   if(!CNeuronBaseOCL::calcInputGradients(cAssetTime[1].AsObject()))
      return false;

Y entonces llamaremos al método de distribución del gradiente de error para la operación de multiplicación de matrices donde pasaremos los datos a la capa de datos de origen y a la capa interna SoftMax.

   if(!MatMulGrad(cSoftMax.getOutput(), cSoftMax.getGradient(),
                  NeuronOCL.getOutput(), cTransposeVRC.getPrevOutput(),
                  cAssetTime[1].getGradient(),
                  iAssets, iTimePoints, iDimension, iAgents))
      return false;

Sin embargo, deberemos recordar que al nivel de datos de origen del flujo principal, el gradiente de error tendrá que proceder de dos flujos de información. Por lo tanto, guardaremos los valores obtenidos en esta etapa en el búfer libre de transposición de datos.

A continuación, pasaremos el gradiente de error a través de la capa de la función SoftMax hasta el nivel de los coeficientes no normalizados.

   if(!cAssetTime[0].calcHiddenGradients(cSoftMax.AsObject()))
      return false;

Y luego distribuiremos el gradiente de error resultante al nivel de la segunda fuente de datos y nuestra capa de transposición.

   if(!MatMulGrad(SecondInput, SecondGradient,
                  cTransposeVRC.getOutput(), cTransposeVRC.getGradient(),
                  cAssetTime[0].getGradient(),
                  iAssets, iDimension, iTimePoints, iAgents))
      return false;

Aquí comprobaremos directamente la función de activación de la segunda fuente de datos y, de ser necesario, corregiremos el gradiente de error resultante mediante la derivada correspondiente.

   if(SecondActivation != None)
      if(!DeActivation(SecondInput, SecondGradient, SecondGradient, SecondActivation))
         return false;

En este paso, pasaremos el gradiente de error al nivel del módulo CSA (en este caso, se tratará de la segunda fuente de los datos de origen). Ya solo queda por finalizar la transmisión del gradiente de error al módulo de atención temporal (la principal fuente de datos de origen). Este recibirá datos de dos flujos de información: de los coeficientes de atención y directamente de los resultados. Los datos de ambos flujos de datos se encuentran ahora en búferes diferentes del objeto de transposición de datos. El búfer de gradiente principal contendrá los valores transpuestos del flujo de información de los coeficientes de atención. Aprovecharemos la funcionalidad básica del objeto de transposición del tensor tridimensional y los bajaremos hasta el nivel de los datos de origen.

   if(!NeuronOCL.calcHiddenGradients(cTransposeVRC.AsObject()) ||
      !SumAndNormilize(NeuronOCL.getGradient(), cTransposeVRC.getPrevOutput(), NeuronOCL.getGradient(),
                                                                        iDimension, false, 0, 0, 0, 1))
      return false;

A continuación, sumaremos los datos de los dos flujos de información. Y al final de las operaciones del método, ajustaremos el gradiente de error obtenido usando la derivada de la función de activación del flujo de información principal.

   if(NeuronOCL.Activation() != None)
      if(!DeActivation(NeuronOCL.getOutput(), cTransposeVRC.getPrevOutput(), cTransposeVRC.getPrevOutput(), 
                                                                                   NeuronOCL.Activation()))
         return false;
//---
   return true;
  }

Y saldremos del método pasando el resultado lógico de las operaciones al programa que realiza la llamada.

Le sugiero que se familiarice con el método de actualización de los parámetros del modelo. En el archivo adjunto se incluye el código completo de la clase CNeuronPortfolioGenerator, así como todos sus métodos.

Creación del framework MASAAT

Ya hemos implementado el funcionamiento de los bloques individuales del framework MASAAT; ahora es el momento de ensamblarlos en una estructura de framework unificada. Realizaremos este trabajo como parte de la clase CNeuronMASAAT. Y como el objeto padre para ella, hemos elegido CNeuronPortfolioGenerator, que supone el último bloque de nuestra implementación de los enfoques del framework MASAAT. Esto nos permitirá no declarar este módulo entre los objetos internos de nuestra clase, mientras que toda la funcionalidad necesaria será heredada del objeto padre. A continuación, le mostraremos la estructura de la nueva clase.

class CNeuronMASAAT  :  public CNeuronPortfolioGenerator
  {
protected:
   CNeuronTransposeOCL              cTranspose;
   CNeuronPLRMultiAgentsOCL         cPLR;
   CNeuronBaseOCL                   cConcat;
   CNeuronCrossSectionalAnalysis    cCrossSectionalAnalysis;
   CNeuronTemporalAnalysis          cTemporalAnalysis;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)  override
     { return        feedForward(NeuronOCL); }
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                       CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override
     { return        calcInputGradients(NeuronOCL); }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMASAAT(void)  {};
                    ~CNeuronMASAAT(void)  {};
   //---
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint heads, uint units_cout,
                          uint layers, vector<float> &min_distance, uint projection,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const override   {  return defNeuronMASAAT;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

En la estructura presentada de la nueva clase podemos ver la declaración de todos los objetos creados anteriormente. Y no resulta difícil adivinar que el algoritmo de todos los métodos de esta clase se construirá sobre la llamada consecutiva de los métodos homónimos de los objetos internos. Nos familiarizaremos con la secuencia de sus llamadas durante la implementación de los métodos.

Todos los objetos internos se declararán estáticamente, lo que nos permitirá dejar "vacíos" el constructor y el destructor de nuestra clase. La inicialización de todos los objetos declarados y heredados se realizará, como siempre, en el método Init.

bool CNeuronMASAAT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                         uint window, uint window_key, uint heads, uint units_cout,
                         uint layers, vector<float> &min_distance, uint projection,
                         ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronPortfolioGenerator::Init(numOutputs, myIndex, open_cl, window, units_cout / 3,
                                       window_key, (uint)min_distance.Size() + 1, projection, optimization_type, batch))
      return false;

En los parámetros de este método obtendremos las constantes básicas que indicarán la estructura de los datos de origen y definirán la arquitectura del objeto a inicializar.

En el cuerpo del método, como viene siendo tradicional, llamaremos directamente al método homónimo de la clase padre, en el que ya se ha organizado el proceso de inicialización de los objetos heredados y de las interfaces básicas. Sin embargo, tenga en cuenta que en este caso usaremos la clase padre como un bloque funcional completo de los algoritmos a construir. Y este será el módulo que utilizaremos en la salida de nuestra implementación del framework MASAAT. Así que deberemos anticiparnos mentalmente un poco para definir los parámetros de inicialización del objeto padre.

Así pues, tenemos previsto introducir los resultados de nuestros módulos CSA y TA en la entrada del objeto padre. En ellos, el número de activos a analizar será igual al tamaño de la ventana de datos de entrada, y se espera que el número de puntos temporales sea el mismo que la longitud de la secuencia de datos de entrada. Pero espere, estamos planeando transformar la secuencia temporal multimodal original en una representación lineal por trozos. Por consiguiente, el número de puntos temporales será 3 veces menor. Como resultado, al pasar los parámetros a un método de la clase padre, dividiremos el tamaño de la secuencia original por 3.

Continuando con el análisis de los parámetros del método padre y llegamos al número de agentes. Como hemos comentado antes, al construir un objeto multiagente para transformar una serie temporal en una representación lineal por trozos, el número de agentes viene determinado por la longitud del vector de desviaciones límite de los indicadores. Pero si nos fijamos en el análisis realizado por los autores del MASAAT sobre el impacto de los componentes individuales del framework en el resultado, descubriremos que utilizar una representación lineal por trozos de la serie temporal junto con la original permite mejorar el rendimiento del modelo. Por lo tanto, aumentaremos el número de agentes en 1. Este último trabajará con la representación original de la serie temporal analizada.

Transmitiremos el resto de los parámetros sin cambios.

Tras ejecutar con éxito las operaciones del método de la clase padre, procederemos a inicializar los objetos recién declarados. Y aquí inicializaremos primero el objeto de transposición de los datos de origen.

   if(!cTranspose.Init(0, 0, OpenCL, units_cout, window, optimization, iBatch))
      return false;

A continuación, inicializaremos un objeto multiagente para transformar la secuencia analizada en una representación lineal por trozos.

   if(!cPLR.Init(0, 1, OpenCL, window, units_cout, false, min_distance, optimization, iBatch))
      return false;

Y concatenaremos los resultados de la transformación con los datos de origen. Para ello, inicializaremos una capa completamente conectada del tamaño adecuado.

   if(!cConcat.Init(0, 2, OpenCL, cTranspose.Neurons() + cPLR.Neurons(), optimization, iBatch))
      return false;

Y todo lo que deberemos hacer es inicializar los objetos de los módulos CSA y TA. Ambos módulos trabajarán con la misma fuente de datos, por lo que recibirán los mismos parámetros.

   if(!cCrossSectionalAnalysis.Init(0, 3, OpenCL, units_cout, window_key, heads, heads / 2, window, layers, 1, 
                                                                                 iAgents, optimization, iBatch))
      return false;
   if(!cTemporalAnalysis.Init(0, 4, OpenCL, units_cout, window_key, heads, heads / 2, window, layers, 1, 
                                                                                  iAgents, optimization, iBatch))
      return false;
//---
   return true;
  }

Y después de inicializar con éxito todos los objetos internos, devolveremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.

A continuación, construiremos el algoritmo de pasada directa en el método feedForward. Aquí todo resultará bastante sencillo. En los parámetros del método obtendremos el puntero al objeto de datos de origen, que pasaremos directamente al método homónimo del objeto de transposición de datos.

bool CNeuronMASAAT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;

A continuación, convertiremos los datos de origen resultantes en diversas variantes de una representación lineal por trozos de la serie temporal y concatenaremos los valores resultantes con los datos de origen, usando únicamente su forma transpuesta.

   if(!cPLR.FeedForward(cTranspose.AsObject()))
      return false;
   if(!Concat(cTranspose.getOutput(), cPLR.getOutput(), cConcat.getOutput(), cTranspose.Neurons(), cPLR.Neurons(), 1))
      return false;

Luego pasaremos los datos así preparados a los módulos CSA y TA, y transmitiremos los resultados obtenidos al método homónimo de la clase padre.

   if(!cCrossSectionalAnalysis.FeedForward(cConcat.AsObject()))
      return false;
   if(!cTemporalAnalysis.FeedForward(cConcat.AsObject()))
      return false;
//---
   return CNeuronPortfolioGenerator::feedForward(cTemporalAnalysis.AsObject(), cCrossSectionalAnalysis.getOutput());
  }

A continuación, finalizaremos el método retornando el resultado lógico de las operaciones al programa que realiza la llamada.

La aparente simplicidad del método de pasada directa oculta la ramificación de los flujos de información. Nótese que usamos dos veces los datos de origen transpuestos y el tensor concatenado. Esto conlleva algunas complicaciones a la hora de organizar el proceso de distribución del gradiente de error en el método calcInputGradients.

En los parámetros del método de distribución del gradiente de error, obtendremos el puntero al objeto de datos de origen al que vamos a pasar el gradiente de error. En el cuerpo del método comprobaremos directamente la relevancia del puntero obtenido.

bool CNeuronMASAAT::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!prevLayer)
      return false;

Después llamaremos al método de la clase padre para distribuir el gradiente de error entre los módulos CSA y TA según su influencia en el resultado del modelo.

   if(!CNeuronPortfolioGenerator::calcInputGradients(cTemporalAnalysis.AsObject(),
         cCrossSectionalAnalysis.getOutput(),
         cCrossSectionalAnalysis.getGradient(),
         (ENUM_ACTIVATION)cCrossSectionalAnalysis.Activation()))
      return false;

Ambos módulos trabajarán con datos tensoriales concatenados. Por lo tanto, tendremos que transferir el gradiente de error sobre los dos flujos de información al nivel del tensor concatenado. En primer lugar, transmitiremos el gradiente de error de un módulo.

   if(!cConcat.calcHiddenGradients(cCrossSectionalAnalysis.AsObject()))
      return false;

Y entonces usaremos el truco de la sustitución del búfer de gradiente de error y obtendremos los valores del segundo flujo de información seguido de la suma de la información de las dos fuentes.

   CBufferFloat *grad = cConcat.getGradient();
   if(!cConcat.SetGradient(cConcat.getPrevOutput(), false) ||
      !cConcat.calcHiddenGradients(cTemporalAnalysis.AsObject()) ||
      !SumAndNormilize(grad, cConcat.getGradient(), grad, 1, 0, 0, 0, 0, 1) ||
      !cConcat.SetGradient(grad, false))
      return false;

Después distribuiremos el gradiente de error del tensor concatenado entre los objetos de concatenación. Al mismo tiempo, deberemos recordar que hemos previsto un flujo de información distinto para transferir los datos al nivel del objeto de transposición de los datos de origen. Por lo tanto, en esta fase usaremos un búfer de datos libre.

   if(!DeConcat(cTranspose.getPrevOutput(), cPLR.getGradient(), cConcat.getGradient(), cTranspose.Neurons(), 
                                                                                         cPLR.Neurons(), 1))
      return false;

Y antes de continuar con el proceso de distribución del gradiente de error entre los objetos, comprobaremos si necesitamos ajustar la derivada de la función de activación correspondiente.

   if(cPLR.Activation() != None)
      if(!DeActivation(cPLR.getOutput(), cPLR.getGradient(), cPLR.getGradient(), cPLR.Activation()))
         return false;

En el siguiente paso, transmitiremos el gradiente de error a través del objeto de transformación multiagente a la representación lineal por trozos de la serie temporal, y luego sumaremos los valores de los dos flujos de información.

   if(!cTranspose.calcHiddenGradients(cPLR.AsObject()) ||
      !SumAndNormilize(cTranspose.getGradient(), cTranspose.getPrevOutput(), cTranspose.getGradient(), iDimension, 
                                                                                               false, 0, 0, 0, 1))
      return false;

De ser necesario, ajustaremos el gradiente de error usando la derivada de la función de activación y lo pasaremos al nivel de datos de origen.

   if(cTranspose.Activation() != None)
      if(!DeActivation(cTranspose.getOutput(), cTranspose.getGradient(), cTranspose.getGradient(), 
                                                                         cTranspose.Activation()))
         return false;
   if(!prevLayer.calcHiddenGradients(cTranspose.AsObject()))
      return false;
//---
   return true;
  }

Cuando el método finalice, pasaremos el resultado lógico de las operaciones al programa que realiza la llamada.

Con esto concluiremos nuestro análisis de los algoritmos para aplicar los enfoques del framework MASAAT. Encontrará el código completo de todas las clases presentadas y sus métodos en el archivo adjunto. Allí también encontrará todos los programas utilizados en la preparación del artículo, así como las arquitecturas de los modelos. Solo nos detendremos un momento en la arquitectura de los modelos. Nuestra aplicación del framework MASAAT la hemos implementado en el modelo del Actor. No vamos a entrar ahora de lleno en la arquitectura del modelo. Es prácticamente idéntica a la de trabajos anteriores. Analizaremos solo la declaración de una nueva capa.

En el array dinámico de dimensionalidades de la ventana, especificaremos el tamaño de la ventana de datos analizados y la longitud del tensor de estado oculto obtenido a la salida de la capa. 

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMASAAT;
//--- Windows
     {
      int temp[] = {BarDescr, LatentCount};
      if(ArrayCopy(descr.windows, temp) < (int)temp.Size())
         return false;
     }

Asimismo, crearemos los valores umbral para nuestros 3 agentes como una progresión geométrica.

//--- Min Distance
     {
      vector<float> ones = vector<float>::Ones(3);
      vector<float> cs = ones.CumSum() - 1;
      descr.radius = pow(ones * 2, cs) * 0.01f;
     }

Los demás parámetros tendrán los valores habituales.

   descr.window_out = 32;
   descr.count = HistoryBars;
   descr.step = 4;               //Heads
   descr.layers = 3;             //Layers
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

La arquitectura completa de los modelos, como ya hemos dicho, figura en los anexos.

Simulación

Nuestro trabajo de aplicación de los enfoques propuestos por los autores del framework MASAAT con ayuda de MQL5 ha llegado a su conclusión lógica. Ahora pasaremos a la etapa de mayor responsabilidad: la evaluación de la eficacia de los enfoques aplicados sobre datos históricos reales.

Debemos subrayar de inmediato que lo que estamos evaluando son los enfoques *aplicados*, no el framework MASAAT tal y como lo presenta el autor, puesto que la versión original del framework se ha modificado durante el proceso de aplicación.

Los modelos se han entrenado con los datos históricos de 2023 para el instrumento financiero EURUSD y el marco temporal H1. Todos los parámetros de los indicadores analizados se han utilizado al nivel de los ajustes por defecto.

Para la fase de entrenamiento inicial, hemos utilizado una muestra de entrenamiento recogida de estudios anteriores, y actualizada periódicamente durante el entrenamiento del modelo para adaptarse a la estrategia actual del Actor.

Tras varias rondas de entrenamiento y actualización de la muestra, hemos obtenido una política que demuestra rentabilidad tanto en la muestra de entrenamiento como en la de prueba.

Las pruebas de la política final entrenada se han realizado con los datos históricos de enero de 2024 con todos los demás parámetros intactos. Ahora le presentamos los resultados de las pruebas.

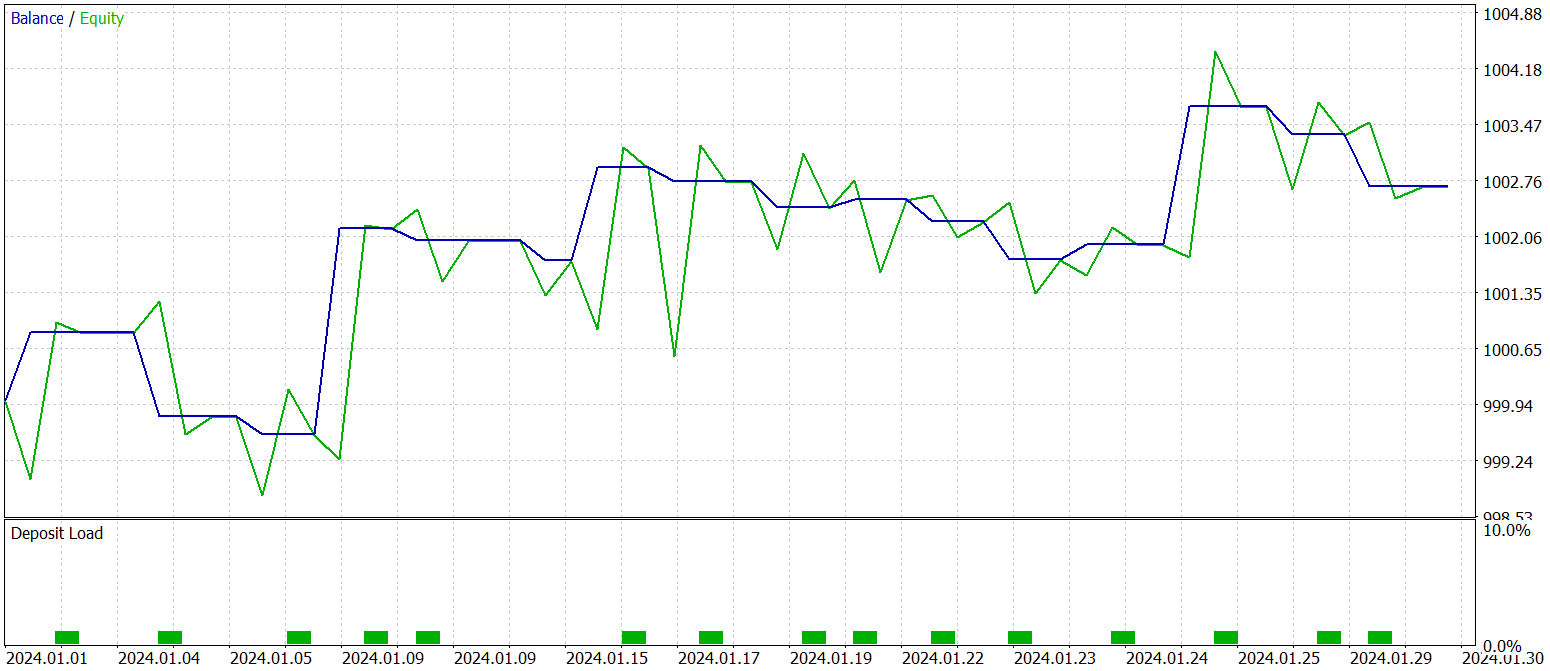
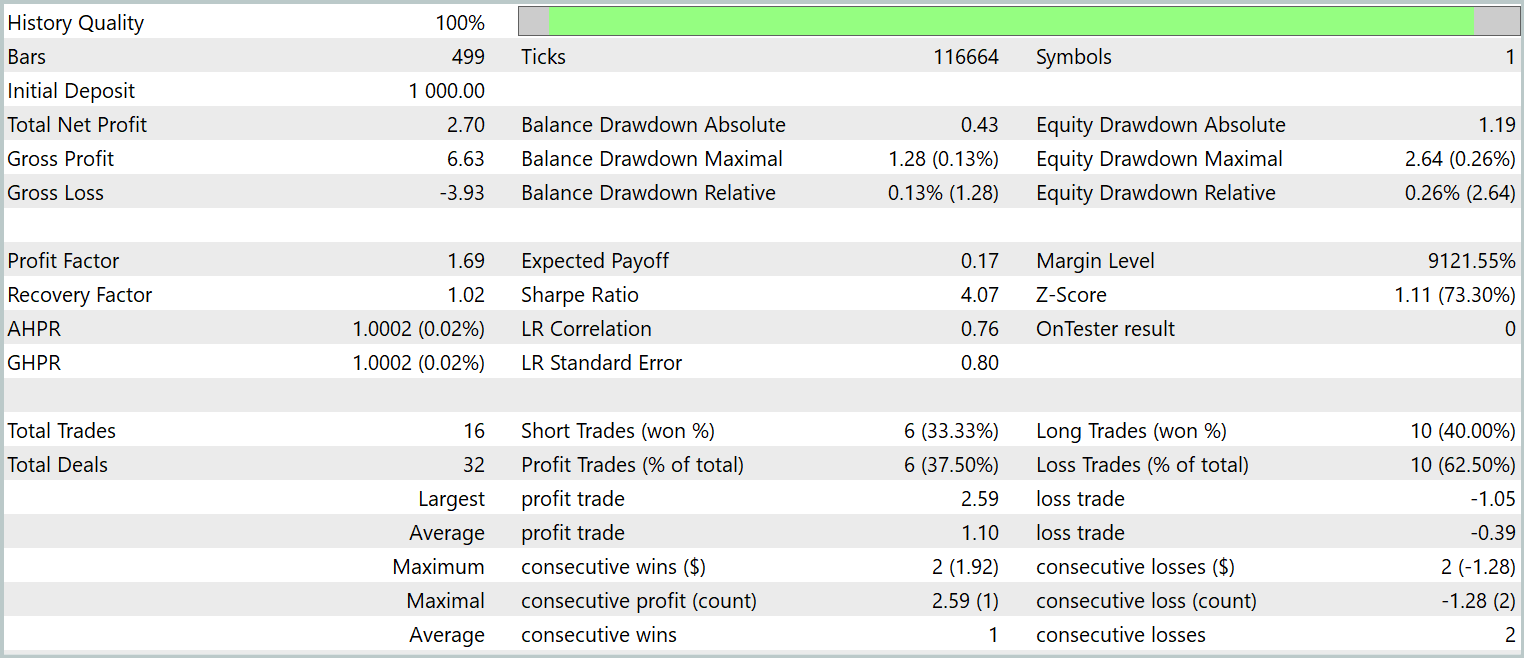
Como se desprende de los datos presentados, el modelo ha realizado 16 transacciones comerciales durante el periodo de prueba. Y solo algo más de un tercio de ellas se han cerrado con beneficios. Sin embargo, la transacción rentable máxima supera en 2,5 veces el mismo indicador de las transacciones deficitarias. Y en la media de las transacciones, lo supera en el triple. Como consecuencia, vemos una clara tendencia al alza en el balance.

Conclusión

En este artículo, hemos analizado el framework adaptativo multiagente MASAAT, desarrollado para la optimización de portafolios de inversión. El MASAAT combina mecanismos de atención y análisis de series temporales. Este framework usa un conjunto de agentes comerciales para analizar los datos de precios de forma multifacética, lo cual nos ayuda a reducir el sesgo en las decisiones comerciales generadas. Cada agente aplica un mecanismo de análisis cruzado basado en la atención para identificar correlaciones entre activos y puntos temporales dentro del periodo observado. A continuación, la información resultante se combinará con la ayuda del módulo de fusión espaciotemporal, lo cual posibilitará una integración eficaz de los datos y la mejora de las estrategias comerciales.

En la parte práctica, hemos implementado nuestra propia visión de los enfoques propuestos utilizando herramientas MQL5. Asimismo, hemos implementado los enfoques propuestos en el modelo y hemos entrenado este con datos históricos reales. Los resultados de las pruebas del modelo entrenado muestran el potencial de los planteamientos propuestos.

Enlaces

• Developing An Attention-Based Ensemble Learning Framework for Financial Portfolio Optimisation
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL