Redes neuronales: así de sencillo (Parte 2): Entrenamiento y prueba de la red

Contenido

• Introducción
• 1. Formulando la tarea
• 2. Proyectando el modelo de red neuronal
• 2.1. Definiendo el número de neuronas de la capa de entrada
• 2.2. Proyectando las capas ocultas
• 2.3. Definiendo el número de neuronas de la capa oculta
• 3. Programación
• 3.1. Preparando el trabajo
• 3.2. Inicializando las clases
• 3.3. Entrenando la red neuronal
• 3.4. Mejorando el método de cálculo del gradiente
• 4.Simulación
• Conclusión
• Programas utilizados en el artículo

Introducción

En el artículo anterior, titulado Redes neuronales: así de sencillo, analizamos los principios de construcción de CNet para operar con redes neuronales completamente conectadas usando MQL5. En el presente artículo, mostraremos un ejemplo de uso de esta clase en un asesor experto y valoraremos la clase en condiciones reales.

1. Formulando la tarea

Antes de comenzar a construir nuestro asesor experto, tenemos que definir los objetivos y tareas a establecer para nuestra nueva red neuronal. Obviamente, el objetivo general de cualquier asesor en los mercados financieros es conseguir beneficios. No obstante, se trata de un objetivo bastante general. Tenemos que concretar las tareas para nuestra red neuronal. Asismismo, deberemos comprender cómo valoraremos los resultados de la red neuronal.

Y otro aspecto importante: la clase CNet que hemos creado anteriormente se basa en los principios del aprendizaje supervisado, que implica la existencia de datos etiquetados para el conjunto de entrenamiento.

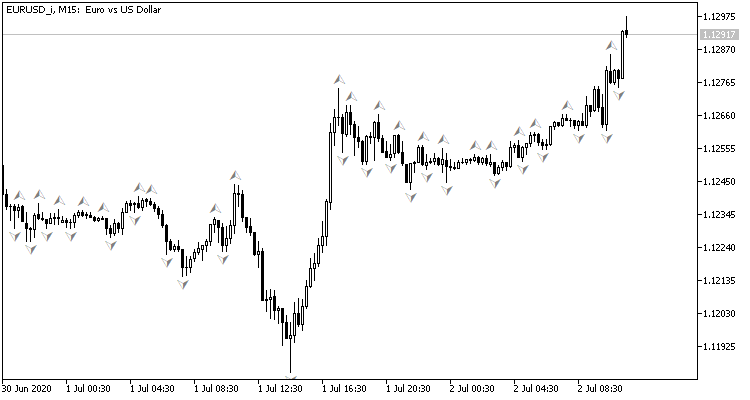
Si miramos el gráfico de una pareja de divisas, el deseo natural sería ejecutar transacciones comerciales en los picos de los precios, lo cual puede mostrarse con el indicador fractal estándar de Bill Williams. El problema con dicho indicador es que indica los picos de 3 velas, y siempre genera una señal retrasada en 1 vela, en la cual puede llegar a formarse finalmente una señal opuesta. ¿Qué ocurrirá si ajustamos la red neuronal para determinar los puntos de viraje antes de que se forme la tercera vela? Al menos, este enfoque nos daría una vela del movimiento en la dirección de la transacción.

De esta forma, resolveríamos el problema con el conjunto de entrenamiento:

• Para la propagación hacia delante, suministraremos a la entrada de la red neuronal la situación actual del mercado, mientras que a la salida se generará una valoración de la probabilidad de la formación de picos en la última vela cerrada.
• Para la propagación inversa, después de que se forme la próxima vela, comprobaremos si había un fractal en la vela anterior y suministraremos el resultado para ajustar los pesos. 

Para valorar los resultados del funcionamiento de la red, podemos usar el error medio cuadrático de la predicción, el porcentaje de predicción correcta de fractales y el porcentaje de fractales restantes.

Ahora, nos queda por responder a la pregunta: ¿qué tipo de datos iniciales suministraremos a la entrada de nuestra red neuronal? Además, debemos recordar lo que hacemos nosotros mismos cuando intentamos valorar la situación del mercado en el gráfico.

Lo primero que se recomienda a un tráder principiante es valorar visualmente la dirección de la tendencia en el gráfico. Por consiguiente, debemos digitalizar y transmitir la información sobre los movimientos de los precios a la entrada de la red neuronal. En nuestro caso, proponemos transmitir la información sobre los precios de apertura y cierre, los precios máximos y mínimos, los volúmenes y el tiempo de formación. 

Otra forma, probablemente la más popular de determinar la tendencia y su fuerza, son los indicadores de oscilador. También conviene utilizar estos indicadores porque el resultado de estos está normalizado. Sin pensarlo demasiado, seleccionamos para el experimento 4 indicadores estándar RCI, CCI, ATR y MACD, con parámetros estándar. No realizamos ningún análisis adicional sobre los indicadores elegidos y los parámetros seleccionados.

Quizás algún lector afirme que el uso de indicadores no tiene sentido, ya que sus datos se construyen recalculando los datos de los precios de las velas que ya hemos transmitido a la entrada de la red neuronal. Pero esto no es del todo correcto. Los valores de los indicadores se determinan calculando los datos de varias velas, lo cual permite ampliar un tanto la muestra analizada. Asignaremos la tarea "determinar su influencia en el resultado" al proceso de entrenamiento de la red neuronal.

Para poder valorar la dinámica del mercado, suministraremos a la red neuronal toda la información durante un periodo histórico determinado.

2. Proyectando el modelo de red neuronal

2.1. Definiendo el número de neuronas de la capa de entrada

Para comenzar a proyectar la propia red neuronal, deberemos entender el número de neuronas existente en la capa de entrada. Para ello, valoraremos la información inicial en cada vela y la multiplicaremos por la profundidad de la historia analizada.

No necesitamos preprocesar los datos del indicador, pues están normalizados y conocemos el número de búferes de indicador (los 4 indicadores mencionados anteriormente suman 5 valores). Por consiguiente, para recibir los datos de estos indicadores en la capa de entrada, necesitaremos crear 5 neuronas por cada vela analizada.

Con los datos de los precios de las velas, la situación cambia un poco. Al determinar visualmente la dirección de la tendencia y la fuerza de la misma a partir de un gráfico, primero analizamos la dirección y el tamaño de la vela. Solo después de ello, cuando determinemos la dirección de la tendencia y los probables puntos de viraje, prestaremos atención al nivel de precio del símbolo analizado. Por eso, debemos normalizar estos datos antes de suministrarlos a la red neuronal. En nuestro caso, hemos suministrado la diferencia de los precios de cierre, máximo y mínimo respecto al precio de apertura de la vela descrita. En este enfoque, solo tenemos que describir las velas de tres neuronas, y el signo de la primera neurona determina la dirección de la vela.

Hay muchas fuentes diferentes que describen la influencia de varios factores temporales sobre la volatilidad de la divisa. Por ejemplo, la temporada, las diferencias en la dinámica por semanas y días, así como las sesiones comerciales europeas, americanas y asiáticas influyen de diferentes maneras en los tipos de cambio. Para analizar estos factores, suministraremos a la entrada de la red neuronal el mes de formación de las velas, la hora y el día de la semana. Hemos dividido a propósito la fecha y hora de la formación de la vela en componentes, para permitir a la red neuronal que generalice y encuentre dependencias.

Además, añadiremos información sobre los volúmenes. Si su bróker ofrece datos sobre los volúmenes reales, los indicaremos, de lo contrario, indicaremos los volúmenes de tick.

Por consiguiente, necesitaremos 12 neuronas para describir cada vela. Multiplicando esta cantidad por la profundidad de la historia analizada, obtendremos el tamaño de la capa de entrada de la red neuronal.

2.2. Proyectando las capas ocultas

El siguiente paso consiste en diseñar las capas ocultas de nuestra red neuronal. La elección de la estructura de la red (el número de capas y neuronas) es una de las tareas más complicadas. El perceptrón simple hace un buen trabajo de separación lineal de clases. Las redes de dos capas pueden seguir límites no lineales tortuosos. Las redes de tres capas permiten describir áreas complejas multiconectadas. Aumentando el número de capas, la clase de funciones que implementa la red se hace más amplia, pero, al mismo tiempo, empeora su convergencia y aumentan los costes de su entrenamiento. El número de neuronas en cada capa debe cumplir con la variabilidad de funciones esperada. De hecho, las redes demasiado sencillas no son capaces de simular con la precisión necesaria el comportamiento en condiciones reales, mientras que las redes demasiado complejas pueden replicar no solo la función objetivo, sino también el ruido.

En el primer artículo, mencionamos el método de los "5 porqués". Ahora, proponemos continuar este experimento y crear una red con 4 capas ocultas. Hemos establecido un número de neuronas en la primera capa oculta igual a 1000. No obstante, también podemos establecer cierta dependencia respecto a la profundidad del periodo analizado. Utilizando la regla de Pareto, reduciremos el número de neuronas en cada capa subsiguiente en un 70%. Además, usaremos la siguiente limitación: el número de neuronas en la capa oculta no deberá ser inferior a 20.

2.3. Definiendo el número de neuronas de la capa oculta

El número de neuronas en la capa de salida dependerá de la tarea y el enfoque para su solución. Para resolver problemas de regresión, bastará con tener una neurona que genere el valor esperado. Para resolver problemas de clasificación, necesitaremos un número de neuronas igual al número esperado de clases; cada una de las neuronas generará la probabilidad de asignación del objeto original a cada clase. En la práctica, la clase de un objeto se determina según la probabilidad máxima.

Para solucionar nuestra tarea, proponemos crear 2 variantes de redes neuronales y valorar en la práctica su aplicabilidad para resolver tareas. En el primer caso, en la capa de salida habrá una neurona. Los valores en el rango 0.5...1.0 se corresponderán con el fractal de compra, en el rango -0.5...-1.0, con el fractal de venta, y en el rango -0.5...0.5, con ninguna señal. Recordemos que la solución ofrecida usa como función de activación una tangente hiperbólica cuyos valores de salida son posibles en el rango de -1.0 a +1.0.

En el segundo caso, crearemos 3 neuronas (compra, venta, sin señal) en la capa de salida. En esta versión, entrenaremos la red neuronal para lograr un resultado en el rango 0.0...1.0, siendo el resultado la probabilidad de un fractal. Asimismo, determinaremos la señal según la probabilidad máxima, y su dirección según el índice neuronal con la máxima probabilidad.

3. Programación

3.1. Preparando el trabajo

Ahora, procederemos a la programación. Primero, añadimos las bibliotecas requeridas:

• NeuroNet.mqh — biblioteca para crear la red neuronal del artículo anterior;
• SymbolInfo.mqh — biblioteca estándar para obtener información sobre el instrumento;
• TimeSeries.mqh — biblioteca estándar para trabajar con series temporales;
• Volumes.mqh — biblioteca estándar para obtener información sobre los volúmenes;
• Oscilators.mqh — biblioteca estándar con las clases de los indicadores de oscilador

#include "NeuroNet.mqh"
#include <Trade\SymbolInfo.mqh>
#include <Indicators\TimeSeries.mqh>
#include <Indicators\Volumes.mqh>
#include <Indicators\Oscilators.mqh>

El siguiente paso consistirá en escribir los parámetros del programa que servirán para configurar la red neuronal y los parámetros del indicador.

//+------------------------------------------------------------------+
//|   input parameters                                               |
//+------------------------------------------------------------------+
input int                  StudyPeriod =  10;            //Study period, years
input uint                 HistoryBars =  20;            //Depth of history
ENUM_TIMEFRAMES            TimeFrame   =  PERIOD_CURRENT;
//---
input group                "---- RSI ----"
input int                  RSIPeriod   =  14;            //Period
input ENUM_APPLIED_PRICE   RSIPrice    =  PRICE_CLOSE;   //Applied price
//---
input group                "---- CCI ----"
input int                  CCIPeriod   =  14;            //Period
input ENUM_APPLIED_PRICE   CCIPrice    =  PRICE_TYPICAL; //Applied price
//---
input group                "---- ATR ----"
input int                  ATRPeriod   =  14;            //Period
//---
input group                "---- MACD ----"
input int                  FastPeriod  =  12;            //Fast
input int                  SlowPeriod  =  26;            //Slow
input int                  SignalPeriod=  9;             //Signal
input ENUM_APPLIED_PRICE   MACDPrice   =  PRICE_CLOSE;   //Applied price

Asimismo, declararemos las variables globales, cuya funcionalidad iremos describiendo a medida que la utilicemos.

CSymbolInfo         *Symb;
CiOpen              *Open;
CiClose             *Close;
CiHigh              *High;
CiLow               *Low;
CiVolumes           *Volumes;
CiTime              *Time;
CNet                *Net;
CArrayDouble        *TempData;
CiRSI               *RSI;
CiCCI               *CCI;
CiATR               *ATR;
CiMACD              *MACD;
//---
double               dError;
double               dUndefine;
double               dForecast;
double               dPrevSignal;
datetime             dtStudied;
bool                 bEventStudy;

Con esto, daremos por finalizado el trabajo preparatorio, por lo que podremos proceder a inicializar las clases.

3.2 Inicializando las clases

Inicializaremos directamente las clases en la función OnInit. Primero, crearemos una instancia de la clase CSymbolInfo para trabajar con los instrumentos y actualizar la información sobre el instrumento del gráfico.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   Symb=new CSymbolInfo();
   if(CheckPointer(Symb)==POINTER_INVALID || !Symb.Name(_Symbol))
      return INIT_FAILED;
   Symb.Refresh();

A continuación, crearemos instancias de las series temporales. Cada vez que creemos una instancia de clase, deberemos comprobar si se ha creado correctamente e inicializarla. En caso de error, saldremos de la función con el resultado INIT_FAILED.

   Open=new CiOpen();
   if(CheckPointer(Open)==POINTER_INVALID || !Open.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;
//---
   Close=new CiClose();
   if(CheckPointer(Close)==POINTER_INVALID || !Close.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;
//---
   High=new CiHigh();
   if(CheckPointer(High)==POINTER_INVALID || !High.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;
//---
   Low=new CiLow();
   if(CheckPointer(Low)==POINTER_INVALID || !Low.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;
//---
   Volumes=new CiVolumes();
   if(CheckPointer(Volumes)==POINTER_INVALID || !Volumes.Create(Symb.Name(),TimeFrame,VOLUME_TICK))
      return INIT_FAILED;
//---
   Time=new CiTime();
   if(CheckPointer(Time)==POINTER_INVALID || !Time.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;

En el ejemplo propuesto, hemos tomado los volúmenes de tick. Si deseamos usar volúmenes reales, reemplazaremos "VOLUME_TICK" por "VOLUME_REAL" al llamar al método Volumes.Creare.

Después de declarar las series temporales, crearemos instancias de las clases para trabajar con los indicadores de manera similar.

   RSI=new CiRSI();      
   if(CheckPointer(RSI)==POINTER_INVALID || !RSI.Create(Symb.Name(),TimeFrame,RSIPeriod,RSIPrice))
      return INIT_FAILED;
//---
   CCI=new CiCCI();      
   if(CheckPointer(CCI)==POINTER_INVALID || !CCI.Create(Symb.Name(),TimeFrame,CCIPeriod,CCIPrice))
      return INIT_FAILED;
//---
   ATR=new CiATR();      
   if(CheckPointer(ATR)==POINTER_INVALID || !ATR.Create(Symb.Name(),TimeFrame,ATRPeriod))
      return INIT_FAILED;
//---
   MACD=new CiMACD();      
   if(CheckPointer(MACD)==POINTER_INVALID || !MACD.Create(Symb.Name(),TimeFrame,FastPeriod,SlowPeriod,SignalPeriod,MACDPrice))
      return INIT_FAILED;

El siguiente paso consistirá en comenzar a trabajar directamente con la clase de la red neuronal. Primero, necesitaremos crear una instancia de la clase. Al inicializar la clase CNet, transmitiremos en los parámetros del constructor una referencia a la matriz con la estructura de red. Aquí, querríamos decir que el entrenamiento de una red neuronal supone un proceso que requiere bastantes recursos tanto computacionales como de tiempo. Por ello, probablemente resultaría incorrecto entrenar nuestra red neuronal de nuevo cada vez que se reinicia el programa. Hemos aplicado un pequeño truco: primero declaramos una instancia de la red sin especificar la estructura, e intentamos cargar la red previamente entrenada desde el repositorio local (hemos sacado el nombre del archivo a #define).

#define FileName        Symb.Name()+"_"+EnumToString((ENUM_TIMEFRAMES)Period())+"_"+IntegerToString(HistoryBars,3)+"fr_ea"
...
...
...
...
   Net=new CNet(NULL);
   ResetLastError();
   if(CheckPointer(Net)==POINTER_INVALID || !Net.Load(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false))
     {
      printf("%s - %d -> Error of read %s prev Net %d",__FUNCTION__,__LINE__,FileName+".nnw",GetLastError());

Si no hemos logrado cargar los datos previamente entrenados, imprimiremos en el diario un mensaje que indicará el código de error e iniciaremos la creación de una nueva red no entrenada. Primero, declararemos una instancia de la clase CArrayInt y especificaremos allí la estructura de la red neuronal. El número de elementos indicará el número de capas de la red neuronal y el valor de los elementos indicará el número de neuronas en la capa correspondiente.

      CArrayInt *Topology=new CArrayInt();
      if(CheckPointer(Topology)==POINTER_INVALID)
         return INIT_FAILED;

Como hemos mencionado antes, en la capa de entrada tendremos 12 neuronas para describir cada vela. Por eso, anotaremos en el primer elemento de la matriz el producto de 12 por la profundidad de la historia analizada.

      if(!Topology.Add(HistoryBars*12))
         return INIT_FAILED;

A continuación, describiremos las capas ocultas. Hemos determinado que habrá 4 capas ocultas con 1000 neuronas en la primera capa oculta. Después, el número de neuronas se reducirá en un 70% en cada capa posterior, pero cada capa tendrá al menos 20 neuronas. Los datos se añadirán a la matriz utilizando un bucle.

      int n=1000;
      bool result=true;
      for(int i=0;(i<4 && result);i++)
        {
         result=(Topology.Add(n) && result);
         n=(int)MathMax(n*0.3,20);
        }
      if(!result)
        {
         delete Topology;
         return INIT_FAILED;
        }

Para construir el modelo de regresión, en la capa de salida indicaremos 1 neurona.

      if(!Topology.Add(1))
         return INIT_FAILED;

En nuestro caso, para el modelo de clasificación necesitaríamos especificar el valor 3 para la neurona de salida.

A continuación, eliminaremos la instancia creada anteriormente de la clase CNet y crearemos una nueva que indique la estructura de la red neuronal que estamos creando. Después de crear la nueva instancia de la red neuronal, eliminaremos la clase de la estructura de red, pues no la usaremos más.

      delete Net;
      Net=new CNet(Topology);
      delete Topology;
      if(CheckPointer(Net)==POINTER_INVALID)
         return INIT_FAILED;

Y estableceremos los valores de las variables para recopilar los datos estadísticos:

• dError — desviación (error) media cuadrática
• dUndefine — porcentaje de fractales no encontrados
• dForecast — porcentaje de fractales correctamente predichos
• dtStudied — fecha de la vela del último entrenamiento.

      dError=-1;
      dUndefine=0;
      dForecast=0;
      dtStudied=0;
     }

Recordemos que necesitamos establecer la estructura de la red neuronal, crear una nueva instancia de la clase de red neuronal e inicializar las variables estadísticas solo si no existe una red neuronal previamente entrenada para cargar desde el repositorio local.
Al final de la función OnInit, crearemos una instancia de la clase CArrayDouble() que se usará para intercambiar datos con la red neuronal e iniciar el proceso de entrenamiento de la misma.

Querríamos compartir aquí una solución más. MQL5 no tiene llamada asíncrona de funciones. Si llamamos de forma explícita a la función de aprendizaje desde la función OnInit, el terminal considerará que el proceso de inicialización del programa no habrá finalizado hasta que se complete el entrenamiento. Por eso, en lugar de llamar directamente a la función, crearemos un evento personalizado, mientras que la función de entrenamiento se llamará desde la función OnChartEvent. Al crear un evento, especificaremos en el parámetro lparam el día de inicio del entrenamiento. Este enfoque nos permitirá efectuar la llamada de la función y completar la función OnInit.

   TempData=new CArrayDouble();
   if(CheckPointer(TempData)==POINTER_INVALID)
      return INIT_FAILED;
//---
   bEventStudy=EventChartCustom(ChartID(),1,(long)MathMax(0,MathMin(iTime(Symb.Name(),PERIOD_CURRENT,(int)(100*Net.recentAverageSmoothingFactor*(dForecast>=70 ? 1 : 10))),dtStudied)),0,"Init");
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| ChartEvent function                                              |
//+------------------------------------------------------------------+
void OnChartEvent(const int id,
                  const long &lparam,
                  const double &dparam,
                  const string &sparam)
  {
//---
   if(id==1001)
     {
      Train(lparam);
      bEventStudy=false;
      OnTick();
     }
  }

No olvidemos limpiar la memoria en la función OnDeinit.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   if(CheckPointer(Symb)!=POINTER_INVALID)
      delete Symb;
//---
   if(CheckPointer(Open)!=POINTER_INVALID)
      delete Open;
//---
   if(CheckPointer(Close)!=POINTER_INVALID)
      delete Close;
//---
   if(CheckPointer(High)!=POINTER_INVALID)
      delete High;
//---
   if(CheckPointer(Low)!=POINTER_INVALID)
      delete Low;
//---
   if(CheckPointer(Time)!=POINTER_INVALID)
      delete Time;
//---
   if(CheckPointer(Volumes)!=POINTER_INVALID)
      delete Volumes;
//---
   if(CheckPointer(RSI)!=POINTER_INVALID)
      delete RSI;
//---
   if(CheckPointer(CCI)!=POINTER_INVALID)
      delete CCI;
//---
   if(CheckPointer(ATR)!=POINTER_INVALID)
      delete ATR;
//---
   if(CheckPointer(MACD)!=POINTER_INVALID)
      delete MACD;
//---
   if(CheckPointer(Net)!=POINTER_INVALID)
      delete Net;
   if(CheckPointer(TempData)!=POINTER_INVALID)
      delete TempData;
  }

3.3. Entrenando la red neuronal

Para entrenar la red neuronal, crearemos la función Train. Transmitiremos a los parámetros de la función la fecha de inicio del periodo de entrenamiento.

void Train(datetime StartTrainBar=0)

Al comienzo de la función, declararemos las variables locales:

• count  — cálculo de las épocas de entrenamiento;
• prev_un  — porcentaje de fractales no reconocidos en la época anterior;
• prev_for  — porcentaje de fractales correctamente "predichos" en la época anterior;
• prev_er  — error de la época anterior;
• bar_time  — fecha de la barra de recálculo;
• stop  — bandera de seguimiento de la llamada de finalización forzosa del programa.

   int count=0;
   double prev_up=-1;
   double prev_for=-1;
   double prev_er=-1;
   datetime bar_time=0;
   bool stop=IsStopped();
   MqlDateTime sTime;

A continuación, comprobamos si la fecha obtenida en los parámetros de la función no supera el periodo de entrenamiento inicialmente indicado.

   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year-=StudyPeriod;
   if(start_time.year<=0)
      start_time.year=1900;
   datetime st_time=StructToTime(start_time);
   dtStudied=MathMax(StartTrainBar,st_time);

El entrenamiento de la red neuronal se organizará en un ciclo do-while. Al comienzo del mismo, volveremos a calcular el número de barras históricas para entrenar la red neuronal y guardaremos las estadísticas de las propagaciones anteriores.

   do
     {
      int bars=(int)MathMin(Bars(Symb.Name(),TimeFrame,dtStudied,TimeCurrent())+HistoryBars,Bars(Symb.Name(),TimeFrame));
      prev_un=dUndefine;
      prev_for=dForecast;
      prev_er=dError;
      ENUM_SIGNAL bar=Undefine;

A continuación, corregiremos el tamaño de los búferes y cargaremos los datos históricos necesarios.

      if(!Open.BufferResize(bars) || !Close.BufferResize(bars) || !High.BufferResize(bars) || !Low.BufferResize(bars) || !Time.BufferResize(bars) ||
         !RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars) || !Volumes.BufferResize(bars))
         break;
      Open.Refresh(OBJ_ALL_PERIODS);
      Close.Refresh(OBJ_ALL_PERIODS);
      High.Refresh(OBJ_ALL_PERIODS);
      Low.Refresh(OBJ_ALL_PERIODS);
      Volumes.Refresh(OBJ_ALL_PERIODS);
      Time.Refresh(OBJ_ALL_PERIODS);
      RSI.Refresh(OBJ_ALL_PERIODS);
      CCI.Refresh(OBJ_ALL_PERIODS);
      ATR.Refresh(OBJ_ALL_PERIODS);
      MACD.Refresh(OBJ_ALL_PERIODS);

Actualizamos la bandera para monitorear la finalización forzosa del programa y declaramos una nueva bandera que indica la superación de la época de aprendizaje (add_loop).

      stop=IsStopped();
      bool add_loop=false;

Y organizamos un ciclo anidado de entrenamiento con iteración de todos los datos históricos. Al inicio del ciclo, comprobaremos si se ha llegado al final de la búsqueda de los datos históricos y, de ser necesario, cambiaremos la bandera add_loop. También mostraremos el estado actual del entrenamiento de la red neuronal usando la funcionalidad de los comentarios. Así, podremos observar el proceso de aprendizaje.

      for(int i=(int)(bars-MathMax(HistoryBars,0)-1); i>=0 && !stop; i--)
        {
         if(i==0)
            add_loop=true;
         string s=StringFormat("Study -> Era %d -> %.2f -> Undefine %.2f%% foracast %.2f%%\n %d of %d -> %.2f%% \nError %.2f\n%s -> %.2f",count,dError,dUndefine,dForecast,bars-i+1,bars,(double)(bars-i+1.0)/bars*100,Net.getRecentAverageError(),EnumToString(DoubleToSignal(dPrevSignal)),dPrevSignal);
         Comment(s);

Luego, comprobamos si el estado previsto del sistema se ha calculado en el paso anterior del ciclo. De ser así, corregiremos los pesos en la dirección del valor correcto. Para eso, borraremos el contenido de la matriz TempData, comprobaremos si el fractal se ha formado en la vela anterior y añadiremos el valor correcto a la matriz TempData (abajo mostramos el código para una red neuronal de regresión con una neurona en la capa de salida). A continuación, llamaremos al método backProp de nuestra red neuronal transfiriendo además como parámetro la referencia a la matriz TempData. Asimismo, actualizaremos los datos estadísticos en las variables dForecast (porcentaje de fractales predichos correctamente) y dUndefine (porcentaje de fractales restantes).

         if(i<(int)(bars-MathMax(HistoryBars,0)-1) && i>1 && Time.GetData(i)>dtStudied && dPrevSignal!=-2)
           {
            TempData.Clear();
            bool sell=(High.GetData(i+2)<High.GetData(i+1) && High.GetData(i)<High.GetData(i+1));
            bool buy=(Low.GetData(i+2)<Low.GetData(i+1) && Low.GetData(i)<Low.GetData(i+1));
            TempData.Add(buy && !sell ? 1 : !buy && sell ? -1 : 0);
            Net.backProp(TempData);
            if(DoubleToSignal(dPrevSignal)!=Undefine)
              {
               if(DoubleToSignal(dPrevSignal)==DoubleToSignal(TempData.At(0)))
                  dForecast+=(100-dForecast)/Net.recentAverageSmoothingFactor;
               else
                  dForecast-=dForecast/Net.recentAverageSmoothingFactor;
               dUndefine-=dUndefine/Net.recentAverageSmoothingFactor;
              }
            else
              {
               if(sell || buy)
                  dUndefine+=(100-dUndefine)/Net.recentAverageSmoothingFactor;
              }
           }

Después de configurar los coeficientes de ponderación de la red neuronal, calcularemos la probabilidad de que aparezca un fractal en la barra histórica actual (si i es igual a "0", se calculará la probabilidad de formación de un fractal en la barra actual). Para hacerlo, borraremos la matriz TempData y le añadiremos los datos actuales para la capa de entrada de la red neuronal. Si se da un error al añadir los datos, o si los datos introducidos son insuficientes, saldremos del ciclo.

         TempData.Clear();
         int r=i+(int)HistoryBars;
         if(r>bars)
            continue;
//---
         for(int b=0; b<(int)HistoryBars; b++)
           {
            int bar_t=r+b;
            double open=Open.GetData(bar_t);
            TimeToStruct(Time.GetData(bar_t),sTime);
            if(open==EMPTY_VALUE || !TempData.Add(Close.GetData(bar_t)-open) || !TempData.Add(High.GetData(bar_t)-open) || !TempData.Add(Low.GetData(bar_t)-open) ||
               !TempData.Add(Volumes.Main(bar_t)/1000) || !TempData.Add(sTime.mon) || !TempData.Add(sTime.hour) || !TempData.Add(sTime.day_of_week) ||
               !TempData.Add(RSI.Main(bar_t)) ||
               !TempData.Add(CCI.Main(bar_t)) || !TempData.Add(ATR.Main(bar_t)) || !TempData.Add(MACD.Main(bar_t)) || !TempData.Add(MACD.Signal(bar_t)))
                  break;
           }
         if(TempData.Total()<(int)HistoryBars*12)
            break;

Después de preparar los datos iniciales, ejecutaremos el método feedForward y escribiremos los resultados de la red neuronal en la variable dPrevSignal. Más abajo mostramos el código para una red neuronal de regresión con una neurona en la capa de salida. El lector podrá encontrar el código para una red neuronal de clasificación con 3 neuronas en la capa de salida en el archivo adjunto al artículo.

         Net.feedForward(TempData);
         Net.getResults(TempData);
         dPrevSignal=TempData[0];

Para visualizar el funcionamiento de la red neuronal en el gráfico, mostraremos las marcas de los fractales pronosticados para las últimas 200 velas.

         bar_time=Time.GetData(i);
         if(i<200)
           {
            if(DoubleToSignal(dPrevSignal)==Undefine)
               DeleteObject(bar_time);
            else
               DrawObject(bar_time,dPrevSignal,High.GetData(i),Low.GetData(i));
           }

Y al final del ciclo de iteración por los datos históricos, actualizaremos la bandera de finalización forzosa del programa.

         stop=IsStopped();
        }

Después de entrenar la red neuronal con todo el volumen de datos históricos, aumentaremos el contador de épocas de entrenamiento y guardaremos el estado actual de la red neuronal en un archivo local para poder cargarlo posteriormente al reiniciar el programa.

      if(add_loop)
         count++;
      if(!stop)
        {
         dError=Net.getRecentAverageError();
         if(add_loop)
           {
            Net.Save(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false);
            printf("Era %d -> error %.2f %% forecast %.2f",count,dError,dForecast);
           }
         }

Finalmente, especificaremos las condiciones para salir del ciclo de formación. Las condiciones pueden ser las siguientes: recibir una señal con la probabilidad de alcanzar el objetivo por encima de un nivel predeterminado; alcanzar el parámetro de error objetivo; o cuando, tras una época de entrenamiento, los datos estadísticos no cambian o cambian de manera insignificante (el entrenamiento se detiene en un mínimo local). O bien podemos definir nuestras propias condiciones para salir del proceso de entrenamiento. 

     }
   while((!(DoubleToSignal(dPrevSignal)!=Undefine || dForecast>70) || !(dError<0.1 && MathAbs(dError-prev_er)<0.01 && MathAbs(dUndefine-prev_up)<0.1 && MathAbs(dForecast-prev_for)<0.1)) && !stop);

Antes de salir de la función de entrenamiento, guardaremos la hora de la última vela de entrenamiento.

   if(count>0)
     {
      dtStudied=bar_time;
     }
  }

3.4. Mejorando el método de cálculo del gradiente.

Querríamos llamar la atención sobre un punto que detectamos durante el proceso de prueba. En algunos casos, al entrenar la red neuronal, se daba un aumento descontrolado de los coeficientes de peso en las neuronas de las capas ocultas, lo que provocaba que se superasen los valores máximos permisibles de las variables y, como consecuencia, se paralizara totalmente la red neuronal. Esta situación se desarrolló en los casos en los que un error de la capa posterior exigía valores de salida de las neuronas que superaban el rango de valores posibles de la función de activación. Hallamos la solución en la normalización de los valores objetivo de las neuronas. A continuación, mostramos el código corregido del método de cálculo de gradiente.

void CNeuron::calcOutputGradients(double targetVals)
  {
   double delta=(targetVals>1 ? 1 : targetVals<-1 ? -1 : targetVals)-outputVal;
   gradient=(delta!=0 ? delta*CNeuron::activationFunctionDerivative(targetVals) : 0);
  }

Podrá familiarizarse con el código de todos los métodos y funciones en los anexos.

4.Simulación

Llevamos a cabo el entrenamiento de prueba de la red neuronal con la pareja EURUSD, en el marco temporal H1. Suministramos a la entrada de la red neuronal los datos de 20 velas. El entrenamiento se realizó durante un periodo que abarcaba los últimos 2 años. Para comprobar los resultados del experimento, iniciamos dos asesores en dos gráficos del mismo terminal: un EA con una red neuronal de regresión (Fractal — con 1 neurona en la capa de salida) y un EA con una red neuronal de clasificación (Fractal_2 — con 3 neuronas en la capa de salida)).

La primera época de entrenamiento con 12432 barras duró 2 horas y 20 minutos. Ambos asesores mostraron resultados similares, con una tasa de acierto de poco más del 6%.

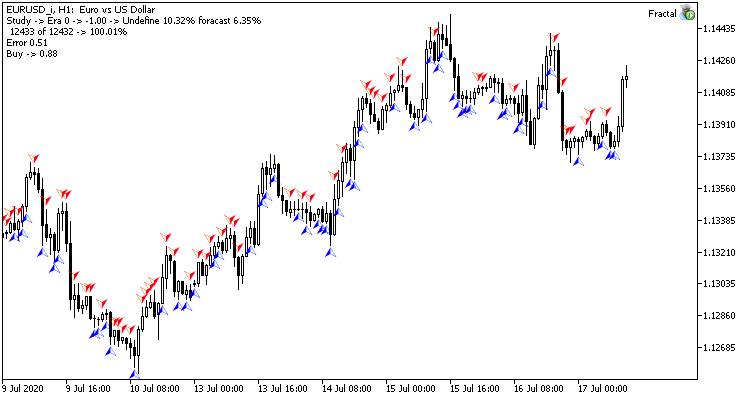
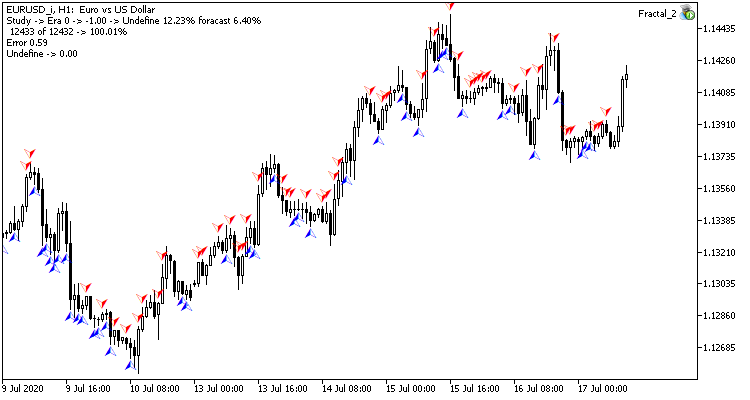
La primera época depende al máximo de los pesos de la red neuronal elegidos al azar en la etapa inicial.

Tras 35 épocas de entrenamiento, la brecha en las estadísticas se amplió levemente a favor del modelo de regresión de la red neuronal:

Índice	Red neuronal de regresión	Red neuronal de clasificación
Error medio cuadrático	0.68	0.78
Porcentaje de "acierto"	12.68%	11.22%
Fractales "omitidos"	20.22%	24.65%

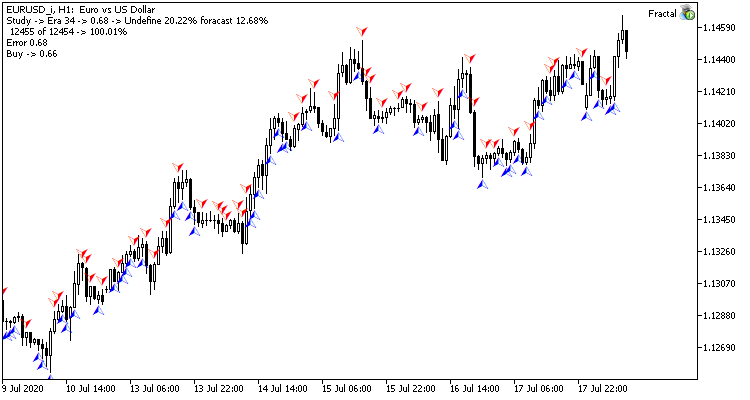
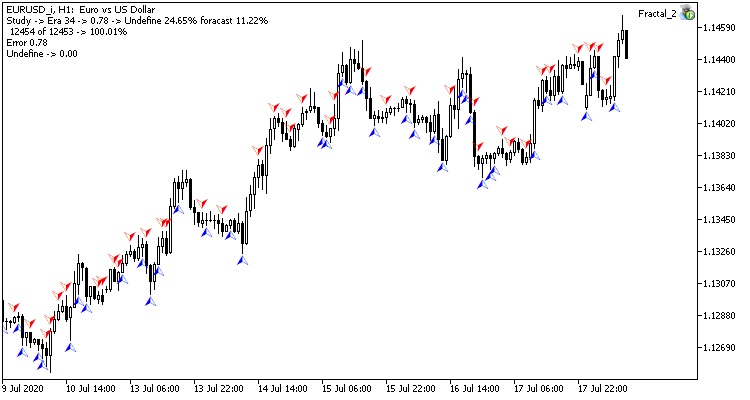
Los resultados de la simulación muestran que ambas variantes de organización de la red neuronal ofrecen resultados semejantes tanto en su tiempo de entrenamiento, como en la precisión de sus predicciones. Asimismo, los indicadores obtenidos muestran la necesidad de gastar tiempo y recursos adicionales para el entrenamiento. Los lectores que deseen analizar la dinámica de aprendizaje de las redes neuronales, podrán estudiar las capturas de pantalla de cada época de entrenamiento en el archivo adjunto.

Conclusión

En el presente artículo, hemos analizado los procesos de construcción, entrenamiento y simulación de una red neuronal. Los resultados obtenidos muestran el potencial disponible para usar esta tecnología. No obstante, el proceso de entrenamiento de las redes neuronales requiere bastantes recursos tanto computacionales como de tiempo.

Programas utilizados en el artículo

#	Nombre	Tipo	Descripción
	Experts\NeuroNet_DNG\
1	Fractal.mq5	Asesor	Asesor con la red neuronal de regresión (1 neurona en la capa de salida)
2	Fractal_2.mq5	Asesor	Asesor con la red neuronal de clasificación (3 neuronas en la capa de salida)
3	NeuroNet.mqh	Biblioteca de clase	Biblioteca de clases para crear la red neuronal (perceptrón)
	Files\
4	Fractal	Directorio	Contiene las capturas de pantalla de la simulación de la red neuronal de regresión
5	Fractal_2	Directorio	Contiene las capturas de pantalla de la simulación de la red neuronal de clasificación