
Redes neuronales: así de sencillo (Parte 10): Multi-Head Attention (atención multi-cabeza)
Contenido
- Introducción
- 1. Multi-Head Attention
- 2. Un poco de matemáticas
- 3. Codificación posicional
- 4. Implementación
- 4.1. Renunciando al uso del Tensor de Claves
- 4.2. La clase Multi-Head Attention
- 4.3. Propagación hacia delante
- 4.4. Propagación inversa
- 4.5. Cambios puntuales en las clases básicas de la red neronal
- 5. Simulación
- Conclusión
- Enlaces
- Programas utilizados en el artículo
Introducción
En el artículo "Redes neuronales: así de sencillo (Parte 8): Mecanismos de Atención", analizamos el mecanismo de auto-atención y una variante de implementación del mismo. En la práctica, las arquitecturas de las redes neurales modernas usan la atención multi-cabeza (Multi-Head Attention). El proceso consiste en el inicio de varios hilos paralelos de auto-atención con diferentes coeficientes de peso. Esta solución debe detectar mejor las conexiones entre los diferentes elementos de la secuencia. Proponemos al lector implementar una arquitectura semejante y comparar en la práctica los resultados del funcionamiento de las dos variantes.
1. Multi-Head Attention
Recordemos un poco: en el algoritmo de Self-Attention se usan 3 matrices entrenadas de los coeficientes de peso (Wq, Wk y Wv). Estas matrices se usan para obtener 3 entidades Query (Solicitud), Key (clave) y Value (Valor). Las dos primeras entidades definen la relación por pares entre los elementos de la secuencia, mientras que la última supone el contexto del elemento analizado.
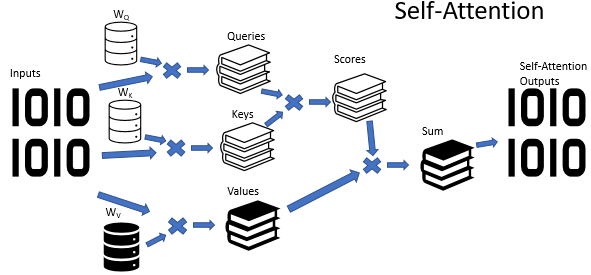
No es un secreto que a veces las situaciones pueden resultar ambiguas. Seguramente, y con aún mayor frecuencia, la misma situación se puede interpretar desde varios puntos de vista. Y desde el punto de vista elegido, las conclusiones pueden resultar absolutamente opuestas. En situaciones así, debemos considerar todas las opciones posibles, y sacar las conclusiones pertinentes solo después de realizar un análisis cuidadoso. Precisamente para resolver tales tareas proponemos la atención multi-cabeza. Aquí, cada "cabeza" tiene su propia opinión, y la decisión se toma tras una votación equilibrada.
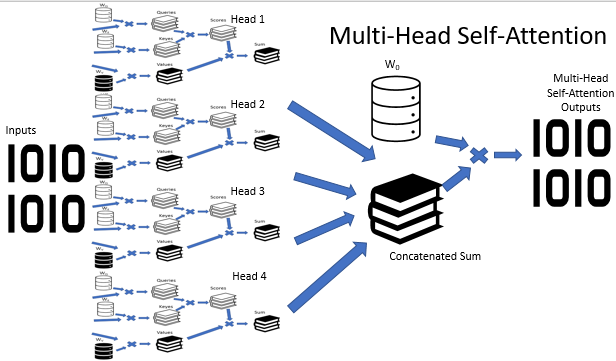
En la arquitectura de Multi-Head Attention, se usan de forma paralela varios hilos de auto-atención con diversos coeficientes de peso que simulan un análisis versátil de la situación. Los resultados del funcionamiento de los hilos de auto-atención se concatenan en un solo tensor. Y el resultado final del algoritmo se determina multiplicando el tensor por la matriz W0, cuyos parámetros se seleccionan durante el entrenamiento de la red neuronal. Toda esta arquitectura sustituye al bloque de Self-Attention en el codificador y el decodificador de la arquitectura del Transformer.
2. Un poco de matemáticas
Al describir el algoritmo de Self-Attention en el lenguaje matemático, obtenemos la fórmula:
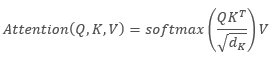 ,
,
donde Q es el tensor de Solicitudes, K es el tensor de Claves, V es el tensor de Valores y d es la dimensión del vector de una clave.
A su vez
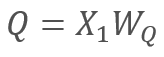 y
y 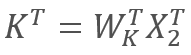 ,
,
donde X1 y X2 son los elementos de la secuencia, y WQ y WK son las matrices de los coeficientes de peso y claves, respectivamente. De esta forma, obtenemos:
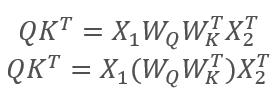
Según las propiedades de las matrices asociativas, podemos multiplicar primero las matrices de los coeficientes de peso WQ y WK. Podemos notar fácilmente que el producto de las matrices de los coeficientes de peso no depende de la secuencia de entrada y es el mismo para todas las iteraciones de un bloque de Self-Attention concreto (claro está, hasta la siguiente actualización de los parámetros de las matrices). A partir de aquí, para reducir el número de operaciones de cálculo, podemos primero calcular de nuevo la matriz intermedia y luego usarla para los cálculos posteriores.
O podemos ir un poco más allá y entrenar una matriz en lugar de dos. Sin embargo, curiosamente, no siempre resulta posible reducir el número de operaciones entrenando una matriz. Por ejemplo, para las grandes dimensiones del vector de secuencia de entrada, podemos reducir la dimensión usando las matrices Wq y Wk. En este caso, si la longitud de los vectores de entrada X1 y X2 es de 100 elementos, una sola matriz contendrá 10k elementos (100*100). Al mismo tiempo, si reducimos la dimensión de las matrices WQ y WK, obtendremos 2 matrices de 1k elementos (100*10). Por consiguiente, debemos decidir con cuidado la ruta que escogemos como solución, considerando la productividad de la red y la calidad de sus resultados.
3. Codificación posicional
Otro punto a considerar a la hora de trabajar con series temporales es la distancia entre los elementos en la secuencia. El algoritmo de atención realiza la verificación interna por pares de las dependencias entre los elementos de secuencia usando las mismas matrices para todos los elementos de la secuencia. Al mismo tiempo, la influencia mutua de los elementos de las series temporales depende en gran medida del intervalo temporal entre ellos. Por consiguiente, la adición de la codificación posicional se convierte en una cuestión acuciante.
El algoritmo de codificación posicional ideal debe cumplir con varios criterios:
- cada elemento de la secuencia debe recibir un código único;
- el salto entre cualquiera de los dos elementos consecutivos debe ser constante;
- el modelo debe ajustarse y generalizarse fácilmente para secuencias de cualquier longitud;
- el modelo debe ser determinado.
Los autores de la arquitectura del Transformer propusieron utilizar una secuencia para codificar no un elemento separado, sino una dimensión completa del vector igual a la dimensión de un elemento de secuencia de entrada. Al mismo tiempo, para describir los elementos pares del vector se usa el seno, mientras que el coseno se usa para los elementos impares. Probablemente, debamos aclarar que aquí no se considera elemento de la secuencia un elemento de matriz específico, sino el vector que describe el estado de una posición aparte. En nuestro caso, será un vector que describe una vela.
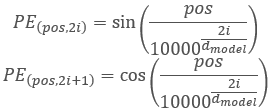 ,
,
Donde "pos" es la posición del elemento de la secuencia, "i" es la posición del elemento en el vector de un elemento de la secuencia, y "d" es la dimensión del vector de un elemento de secuencia.
Esta solución no solo nos permite establecer las posiciones de cada elemento de la secuencia, sino que también determinar la distancia entre ellos.
Directamente en la arquitectura del Transformer, la codificación posicional se realiza más allá de su marco y se ejecuta añadiendo el tensor de codificación posicional al tensor de la secuencia de entrada antes de transferir los datos a la entrada del primer codificador. Podemos plantearnos legítimamente 2 preguntas:
- ¿Por qué sumamos los vectores, y no los concatenamos?
- ¿Cuánto distorsionará la adición de tensores los datos de origen?
La concatentación aumentaría la dimensión de los datos y, por consiguiente, el número de iteraciones. Todo esto reduce el rendimiento general del sistema. El segundo aspecto de esta solución sería que la adición de vectores nos permite posicionar no solo el vector del elemento de la secuencia individual, sino también de cada elemento del vector. Hipotéticamente nos permite analizar las dependencias no solo entre los elementos de la secuencia, sino también entre sus componentes por separado.
Respecto a la distorsión de los datos, la red neuronal no sabe nada sobre el valor de cada elemento y se entrena con la codificación añadida, es decir, no analiza un elemento por separado ni su posición. Por ejemplo, si vemos el mismo doji en la posición 2 y en la 20, entonces, probablemente, le daremos preferencia al más próximo. Para una red neuronal con una codificación posicional, serán señales totalmente distintas y se procesarán según los datos acumulados durante el entrenamiento.
4. Implementación
Vamos a analizar la implementación de las decisiones expuestas anteriormente. En la implementación anterior del algoritmo de Self-Attention para los vectores Query y Keys, usamos una dimensión similar a la secuencia de entrada. Por eso, en primer lugar, reconstruimos el algoritmo para el entrenamiento de una matriz.
4.1. Renunciando al uso del Tensor de Claves
La solución práctica de este problema fue bastante simple. En el método de propagación hacia delante CNeuronAttentionOCL::feedForward comentamos la llamada al método similar de la capa convolucional Key y, al llamar al kernel de cálculo Score, reemplazamos la capa convolucional Key con la capa neuronal anterior. Los cambios en el código del método se destacan más abajo.
bool CNeuronAttentionOCL::feedForward(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=1; OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getOutputIndex()); OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons()); if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Normalize: %d",GetLastError()); return false; } if(!prevLayer.Output.BufferRead()) return false; } //--- if(CheckPointer(Querys)==POINTER_INVALID || !Querys.FeedForward(prevLayer)) return false; //if(CheckPointer(Keys)==POINTER_INVALID || !Keys.FeedForward(prevLayer)) // return false; if(CheckPointer(Values)==POINTER_INVALID || !Values.FeedForward(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_querys,Querys.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_keys,prevLayer.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_score,Scores.GetIndex()); OpenCL.SetArgument(def_k_AttentionScore,def_k_as_dimension,iWindow); if(!OpenCL.Execute(def_k_AttentionScore,1,global_work_offset,global_work_size)) { printf("Error of execution kernel AttentionScore: %d",GetLastError()); return false; } if(!Scores.BufferRead()) return false; } //--- Further code has no changes
De manera similar, también introdujimos cambios en el método de propagación inversa del error CNeuronAttentionOCL::calcInputGradients. Debemos prestar atención, porque, como la primera parte de los gradientes de error en el búfer de la capa anterior se graba antes, el proceso de acumulación de gradientes también comienza antes. Resaltamos los cambios en el texto del código a continuación.
bool CNeuronAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- if(!FF2.calcInputGradients(FF1)) return false; if(!FF1.calcInputGradients(AttentionOut)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,Gradient.GetIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.5); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- { uint global_work_offset[2]={0,0}; uint global_work_size[2]; global_work_size[0]=iUnits; global_work_size[1]=iWindow; OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_gradient,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys,prevLayer.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys_g,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys,Querys.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys_g,Querys.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values,Values.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values_g,Values.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_scores,Scores.GetIndex()); if(!OpenCL.Execute(def_k_AttentionGradients,2,global_work_offset,global_work_size)) { printf("Error of execution kernel AttentionGradients: %d",GetLastError()); return false; } double temp[]; if(Querys.getGradient(temp)<=0) return false; } //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,1.0); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- if(!Querys.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,1.0); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } ////--- // if(!Keys.calcInputGradients(prevLayer)) // return false; ////--- // { // uint global_work_offset[1]={0}; // uint global_work_size[1]; // global_work_size[0]=iUnits; // OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); // OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); // OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); // OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); // OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,1.0); // if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) // { // printf("Error of execution kernel MatrixSum: %d",GetLastError()); // return false; // } // double temp[]; // if(AttentionOut.getGradient(temp)<=0) // return false; // } //--- Further code has no changes
De manera similar, hemos comentado la actualización de los coeficientes de peso de la capa convolucional Key en el método CNeuronAttentionOCL::updateInputWeights, como en general, las declaraciones de este objeto.
El lector podrá familiarizarse con el código de todos los métodos y funciones en los anexos.
4.2. La clase Multi-Head Attention
Hemos sacado la construcción Multi-Head Attention a la clase aparte CNeuronMHAttentionOCL, basada en la clase padre CNeuronAttentionOCL. En el bloque protected, declararemos las instancias adicionales de las capas convolucionales Querys y Values según el número de cabezas de atención. En el ejemplo, usamos 4 cabezas. También añadiremos el búfer Scores y la capa completamente conectada AttentionOut para cada cabeza de atención. Además, necesitamos una capa completamente conectada para concatenar los datos de las cabezas de atención AttentionConcatenate y la capa convolucional Weights0, que permitirá imitar la votación ponderada y reducir la dimensión del tensor de resultados.
class CNeuronMHAttentionOCL : public CNeuronAttentionOCL { protected: CNeuronConvOCL *Querys2; ///< Convolution layer for Querys Head 2 CNeuronConvOCL *Querys3; ///< Convolution layer for Querys Head 3 CNeuronConvOCL *Querys4; ///< Convolution layer for Querys Head 4 CNeuronConvOCL *Values2; ///< Convolution layer for Values Head 2 CNeuronConvOCL *Values3; ///< Convolution layer for Values Head 3 CNeuronConvOCL *Values4; ///< Convolution layer for Values Head 4 CBufferDouble *Scores2; ///< Buffer for Scores matrix Head 2 CBufferDouble *Scores3; ///< Buffer for Scores matrix Head 3 CBufferDouble *Scores4; ///< Buffer for Scores matrix Head 4 CNeuronBaseOCL *AttentionOut2; ///< Layer of Self-Attention Out CNeuronBaseOCL *AttentionOut3; ///< Layer of Self-Attention Out CNeuronBaseOCL *AttentionOut4; ///< Layer of Self-Attention Out CNeuronBaseOCL *AttentionConcatenate;///< Layer of Concatenate Self-Attention Out CNeuronConvOCL *Weights0; ///< Convolution layer for Weights0 //--- virtual bool feedForward(CNeuronBaseOCL *prevLayer); ///< Feed Forward method.@param prevLayer Pointer to previos layer. virtual bool updateInputWeights(CNeuronBaseOCL *prevLayer); ///< Method for updating weights.@param prevLayer Pointer to previos layer. /// Method to transfer gradients inside Head Self-Attention virtual bool calcHeadGradient(CNeuronConvOCL *query, CNeuronConvOCL *value, CBufferDouble *score, CNeuronBaseOCL *attention, CNeuronBaseOCL *prevLayer); public: /** Constructor */CNeuronMHAttentionOCL(void){}; /** Destructor */~CNeuronMHAttentionOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type); ///< Method of initialization class.@param[in] numOutputs Number of connections to next layer.@param[in] myIndex Index of neuron in layer.@param[in] open_cl Pointer to #COpenCLMy object.@param[in] window Size of in/out window and step.@param[in] units_countNumber of neurons.@param[in] optimization_type Optimization type (#ENUM_OPTIMIZATION)@return Boolen result of operations. virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); ///< Method to transfer gradients to previous layer @param[in] prevLayer Pointer to previous layer. //--- virtual int Type(void) const { return defNeuronMHAttentionOCL; }///< Identificator of class.@return Type of class //--- methods for working with files virtual bool Save(int const file_handle); ///< Save method @param[in] file_handle handle of file @return logical result of operation virtual bool Load(int const file_handle); ///< Load method @param[in] file_handle handle of file @return logical result of operation };
El conjunto de métodos de clase reescribe los métodos virtuales de la clase principal, y, probablemente ya podamos llamarlo estándar. La única excepción es el método calcHeadGradient, que describe los iteraciones de la distribución del gradiente de error que se repiten para cada cabeza de atención.
Dejamos el constructor de la clase vacío y transferimos la inicialización de nuevos objetos al método de inicialización Init. En el destructor de clase, organizamos la eliminación de las instancias de los objetos creados por esta clase y declarados en el bloque "protected".
CNeuronMHAttentionOCL::~CNeuronMHAttentionOCL(void) { if(CheckPointer(Querys2)!=POINTER_INVALID) delete Querys2; if(CheckPointer(Querys3)!=POINTER_INVALID) delete Querys3; if(CheckPointer(Querys4)!=POINTER_INVALID) delete Querys4; if(CheckPointer(Values2)!=POINTER_INVALID) delete Values2; if(CheckPointer(Values3)!=POINTER_INVALID) delete Values3; if(CheckPointer(Values4)!=POINTER_INVALID) delete Values4; if(CheckPointer(Scores2)!=POINTER_INVALID) delete Scores2; if(CheckPointer(Scores3)!=POINTER_INVALID) delete Scores3; if(CheckPointer(Scores4)!=POINTER_INVALID) delete Scores4; if(CheckPointer(Weights0)!=POINTER_INVALID) delete Weights0; if(CheckPointer(AttentionOut2)!=POINTER_INVALID) delete AttentionOut2; if(CheckPointer(AttentionOut3)!=POINTER_INVALID) delete AttentionOut3; if(CheckPointer(AttentionOut4)!=POINTER_INVALID) delete AttentionOut4; if(CheckPointer(AttentionConcatenate)!=POINTER_INVALID) delete AttentionConcatenate; }
El método Init se ha construido por analogía con el método de la clase padre. Al inicio del método, llamamos al método homónimo de la clase padre.
bool CNeuronMHAttentionOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window,uint units_count,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronAttentionOCL::Init(numOutputs,myIndex,open_cl,window,units_count,optimization_type)) return false;
A continuación, inicializamos las instancias de las capas convolucionales Querys. Debemos tener en cuenta que inicializamos los objetos partiendo desde la segunda cabeza, ya que las instancias de todos los objetos para la primera cabeza se inicializan en la clase padre.
if(CheckPointer(Querys2)==POINTER_INVALID) { Querys2=new CNeuronConvOCL(); if(CheckPointer(Querys2)==POINTER_INVALID) return false; if(!Querys2.Init(0,6,open_cl,window,window,window,units_count,optimization_type)) return false; Querys2.SetActivationFunction(None); } //--- if(CheckPointer(Querys3)==POINTER_INVALID) { Querys3=new CNeuronConvOCL(); if(CheckPointer(Querys3)==POINTER_INVALID) return false; if(!Querys3.Init(0,7,open_cl,window,window,window,units_count,optimization_type)) return false; Querys3.SetActivationFunction(None); } //--- if(CheckPointer(Querys4)==POINTER_INVALID) { Querys4=new CNeuronConvOCL(); if(CheckPointer(Querys4)==POINTER_INVALID) return false; if(!Querys4.Init(0,8,open_cl,window,window,window,units_count,optimization_type)) return false; Querys4.SetActivationFunction(None); }
Del mismo modo, inicializamos las instancias de las clases Values y Scores para AttentionOut.
if(CheckPointer(Values2)==POINTER_INVALID) { Values2=new CNeuronConvOCL(); if(CheckPointer(Values2)==POINTER_INVALID) return false; if(!Values2.Init(0,9,open_cl,window,window,window,units_count,optimization_type)) return false; Values2.SetActivationFunction(None); } //--- if(CheckPointer(Values3)==POINTER_INVALID) { Values3=new CNeuronConvOCL(); if(CheckPointer(Values3)==POINTER_INVALID) return false; if(!Values3.Init(0,10,open_cl,window,window,window,units_count,optimization_type)) return false; Values3.SetActivationFunction(None); } //--- if(CheckPointer(Values4)==POINTER_INVALID) { Values4=new CNeuronConvOCL(); if(CheckPointer(Values4)==POINTER_INVALID) return false; if(!Values4.Init(0,11,open_cl,window,window,window,units_count,optimization_type)) return false; Values4.SetActivationFunction(None); } //--- if(CheckPointer(Scores2)==POINTER_INVALID) { Scores2=new CBufferDouble(); if(CheckPointer(Scores2)==POINTER_INVALID) return false; } if(!Scores2.BufferInit(units_count*units_count,0.0)) return false; if(!Scores2.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(Scores3)==POINTER_INVALID) { Scores3=new CBufferDouble(); if(CheckPointer(Scores3)==POINTER_INVALID) return false; } if(!Scores3.BufferInit(units_count*units_count,0.0)) return false; if(!Scores3.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(Scores4)==POINTER_INVALID) { Scores4=new CBufferDouble(); if(CheckPointer(Scores4)==POINTER_INVALID) return false; } if(!Scores4.BufferInit(units_count*units_count,0.0)) return false; if(!Scores4.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(AttentionOut2)==POINTER_INVALID) { AttentionOut2=new CNeuronBaseOCL(); if(CheckPointer(AttentionOut2)==POINTER_INVALID) return false; if(!AttentionOut2.Init(0,12,open_cl,window*units_count,optimization_type)) return false; AttentionOut2.SetActivationFunction(None); } //--- if(CheckPointer(AttentionOut3)==POINTER_INVALID) { AttentionOut3=new CNeuronBaseOCL(); if(CheckPointer(AttentionOut3)==POINTER_INVALID) return false; if(!AttentionOut3.Init(0,13,open_cl,window*units_count,optimization_type)) return false; AttentionOut3.SetActivationFunction(None); } //--- if(CheckPointer(AttentionOut4)==POINTER_INVALID) { AttentionOut4=new CNeuronBaseOCL(); if(CheckPointer(AttentionOut4)==POINTER_INVALID) return false; if(!AttentionOut4.Init(0,14,open_cl,window*units_count,optimization_type)) return false; AttentionOut4.SetActivationFunction(None); }
Inicializamos la capa para la concatenación de los datos de AttentionConcatenate. Esta es una capa completamente conectada que se usará solo para transmitir datos, por eso, la cantidad de conexiones salientes será "0". En este caso, el tamaño de la capa deberá ser suficiente para almacenar los datos de salida de las 4 cabezas de atención. Indicaremos un número de neuronas en la capa igual al producto de las 4 ventanas de la capa de salida de una cabeza por el número de elementos en la secuencia.
if(CheckPointer(AttentionConcatenate)==POINTER_INVALID) { AttentionConcatenate=new CNeuronBaseOCL(); if(CheckPointer(AttentionConcatenate)==POINTER_INVALID) return false; if(!AttentionConcatenate.Init(0,15,open_cl,4*window*units_count,optimization_type)) return false; AttentionConcatenate.SetActivationFunction(None); }
Y, para finalizar el método, inicializaremos la capa convolucional Weights0. Su tarea consiste en seleccionar una estrategia óptima basada en los datos obtenidos de todas las cabezas de atención. Esto reducirá la dimensión de los datos de salida hasta la dimensión de los datos originales suministrados a la entrada del bloque Multi-Head Attention. Al inicializar una capa, indicaremos el tamaño de la ventana de entrada y un salto igual a las 4 ventanas de los datos de la capa anterior, así como un tamaño de ventana de salida igual a la ventana de datos de la capa anterior.
if(CheckPointer(Weights0)==POINTER_INVALID) { Weights0=new CNeuronConvOCL(); if(CheckPointer(Weights0)==POINTER_INVALID) return false; if(!Weights0.Init(0,16,open_cl,4*window,4*window,window,units_count,optimization_type)) return false; Weights0.SetActivationFunction(None); } //--- return true; }
El lector podrá familiarizarse con el código de todos los métodos y funciones en los anexos.
4.3. Propagación hacia delante
En su mayor parte, la construcción del algoritmo de propagación hacia adelante se ha realizado usando el programa OpenCL creado previamente. La única excepción ha sido la creación de un kernel para la concatenación de los datos de los 4 tensores de cada cabeza de atención en un solo tensor. En los parámetros, el kernel recibe los punteros a los búferes de los datos iniciales y los tamaños de ventana de cada búfer, así como un puntero al búfer del tensor de resultados. Hemos añadido los detalles de los tamaños de las ventanas usando búferes de datos de entrada para permitir la concatenación de tensores de diferentes tamaños con diferentes tamaños de ventana.
__kernel void ConcatenateBuffers(__global double *input1, int window1, __global double *input2, int window2, __global double *input3, int window3, __global double *input4, int window4, __global double *output)
En el cuerpo del kernel, realizamos el copiado por elementos de los datos de las matrices entrantes en la de salida. El algoritmo es bastante simple, por lo que el lector no encontrará difícil comprender el código en los anexos.
En la clase CNeuronMHAttentionOCL, la propagación hacia delante se organiza en el método feedForward. Al comienzo del método, comprobaremos la validez del enlace a la capa anterior que hemos obtenido y normalizaremos los datos entrantes.
bool CNeuronMHAttentionOCL::feedForward(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=1; OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getOutputIndex()); OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons()); if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Normalize: %d",GetLastError()); return false; } if(!prevLayer.Output.BufferRead()) return false; }
A continuación, llamaremos a los métodos homónimos de las capas convolucionales y recalcularemos los valores de los tensores Querys y Values para todas las cabezas de atención.
if(CheckPointer(Querys)==POINTER_INVALID || !Querys.FeedForward(prevLayer)) return false; if(CheckPointer(Querys2)==POINTER_INVALID || !Querys2.FeedForward(prevLayer)) return false; if(CheckPointer(Querys3)==POINTER_INVALID || !Querys3.FeedForward(prevLayer)) return false; if(CheckPointer(Querys4)==POINTER_INVALID || !Querys4.FeedForward(prevLayer)) return false; if(CheckPointer(Values)==POINTER_INVALID || !Values.FeedForward(prevLayer)) return false; if(CheckPointer(Values2)==POINTER_INVALID || !Values2.FeedForward(prevLayer)) return false; if(CheckPointer(Values3)==POINTER_INVALID || !Values3.FeedForward(prevLayer)) return false; if(CheckPointer(Values4)==POINTER_INVALID || !Values4.FeedForward(prevLayer)) return false;
Luego, recalcularemos la atención de cada cabeza. El algoritmo es similar a la clase principal descrita en el artículo [8]. Más abajo, mostramos el código para una cabeza de atención. Por lo demás, el código es idéntico, solo cambian los punteros a los objetos de la cabeza de atención correspondiente.
//--- Scores Head 1 { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_querys,Querys.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_keys,prevLayer.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_score,Scores.GetIndex()); OpenCL.SetArgument(def_k_AttentionScore,def_k_as_dimension,iWindow); if(!OpenCL.Execute(def_k_AttentionScore,1,global_work_offset,global_work_size)) { printf("Error of execution kernel AttentionScore: %d",GetLastError()); return false; } if(!Scores.BufferRead()) return false; } //--- { uint global_work_offset[2]={0,0}; uint global_work_size[2]; global_work_size[0]=iUnits; global_work_size[1]=iWindow; OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_scores,Scores.GetIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_inputs,prevLayer.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_values,Values.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_out,AttentionOut.getOutputIndex()); if(!OpenCL.Execute(def_k_AttentionOut,2,global_work_offset,global_work_size)) { printf("Error of execution kernel Attention Out: %d",GetLastError()); return false; } double temp[]; if(!AttentionOut.getOutputVal(temp)) return false; }
Después de recalcular la atención para cada cabeza, concatenaremos los resultados en un solo tensor usando el kernel escrito anteriormente.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_ConcatenateMatrix,def_k_conc_input1,AttentionOut.getOutputIndex());
OpenCL.SetArgument(def_k_ConcatenateMatrix,def_k_conc_window1,iWindow);
OpenCL.SetArgumentBuffer(def_k_ConcatenateMatrix,def_k_conc_input2,AttentionOut2.getOutputIndex());
OpenCL.SetArgument(def_k_ConcatenateMatrix,def_k_conc_window2,iWindow);
OpenCL.SetArgumentBuffer(def_k_ConcatenateMatrix,def_k_conc_input3,AttentionOut3.getOutputIndex());
OpenCL.SetArgument(def_k_ConcatenateMatrix,def_k_conc_window3,iWindow);
OpenCL.SetArgumentBuffer(def_k_ConcatenateMatrix,def_k_conc_input4,AttentionOut4.getOutputIndex());
OpenCL.SetArgument(def_k_ConcatenateMatrix,def_k_conc_window4,iWindow);
OpenCL.SetArgumentBuffer(def_k_ConcatenateMatrix,def_k_conc_out,AttentionConcatenate.getOutputIndex());
if(!OpenCL.Execute(def_k_ConcatenateMatrix,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Concatenate Matrix: %d",GetLastError());
return false;
}
double temp[];
if(!AttentionConcatenate.getOutputVal(temp))
return false;
}
Después, transmitimos el resultado de la concatenación de los tensores usando la capa convolucional Weights0 para reducir la dimensión del resultado del funcionamiento de Multi-Head Attention.
if(CheckPointer(Weights0)==POINTER_INVALID || !Weights0.FeedForward(AttentionConcatenate)) return false;
Luego promediamos el resultado obtenido con los datos de la capa anterior y normalizamos el resultado.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,Weights0.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,Weights0.getOutputIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.5);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
if(!Output.BufferRead())
return false;
}
//---
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=1;
OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,Weights0.getOutputIndex());
OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,Weights0.Neurons());
if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Normalize: %d",GetLastError());
return false;
}
double temp[];
if(!Weights0.getOutputVal(temp))
return false;
}
A continuación, por analogía con la clase padre, transmitimos el resultado obtenido a través del bloque FeedForward.
if(!FF1.FeedForward(Weights0)) return false; if(!FF2.FeedForward(FF1)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,Weights0.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,FF2.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,Output.GetIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.5); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } if(!Output.BufferRead()) return false; } //--- return true; }
El lector podrá familiarizarse con el código de todos los métodos y funciones en los anexos.
4.4. Propagación inversa
La propagación inversa contiene dos subprocesos: la transmisión del gradiente de error un nivel hacia abajo y la actualización de las matrices de coeficientes de peso. Y si utilizamos los kernels OpenCL creados previamente para actualizar los pesos, entonces el subproceso de distribución del gradiente de error requerirá mejoras menores.
En primer lugar, tendremos que distribuir el gradiente de error por las cabezas de atención. Para realizar esta función, crearemos el kernel DeconcatenateBuffers. En los parámetros, transmitimos al kernel los punteros a los búferes para distribuir el gradiente, los tamaños de ventana para cada búfer y un puntero al búfer de gradiente obtenido de la iteración anterior.
__kernel void DeconcatenateBuffers(__global double *output1, int window1, __global double *output2, int window2, __global double *output3, int window3, __global double *output4, int window4, __global double *inputs)
Al comienzo del kernel, definimos el número ordinal del elemento procesado de la secuencia y el desplazamiento de la primera posición para el tensor inicial y el tensor de la primera cabeza de atención.
{
int n=get_global_id(0);
int shift=n*(window1+window2+window3+window4);
int shift_out=n*window1;
A continuación, en un ciclo, transmitimos el vector de gradientes de error para la primera cabeza de atención.
for(int i=0;i<window1;i++) output1[shift_out+i]=inputs[shift+i];
Una vez completado el ciclo, corregimos la posición del puntero en el tensor original y determinamos el desplazamiento de la primera posición en el búfer de la segunda cabeza de atención. Después de eso, iniciamos el ciclo de copia de datos ya para la segunda cabeza de atención. Las operaciones se repiten para cada cabeza de atención.
//--- Head 2 shift+=window1; shift_out=n*window2; for(int i=0;i<window2;i++) output2[shift_out+i]=inputs[shift+i]; //--- Head 3 shift+=window2; shift_out=n*window3; for(int i=0;i<window3;i++) output3[shift_out+i]=inputs[shift+i]; //--- Head 4 shift+=window3; shift_out=n*window4; for(int i=0;i<window4;i++) output4[shift_out+i]=inputs[shift+i]; }
Más tarde, tras recalcular los gradientes de error para cada cabeza de atención, necesitaremos combinar los gradientes en un solo búfer de datos en la capa anterior de la red neuronal. Técnicamente, podríamos usar el kernel SumMatrix añadiendo por pares los gradientes de todas las cabezas de atención. Pero esta solución no resultará óptima en cuanto a rendimiento. Por consiguiente, crearemos otro kernel Sum5Matrix. En los parámetros del kernel, transmitimos los punteros a los búferes de datos (5 entrantes y 1 saliente), el tamaño de la ventana de datos y el multiplicador (el factor de corrección de la suma). Probablemente, deberíamos aclarar por qué hay 5 búferes entrantes, si tenemos 4 cabezas de atención. El quinto búfer está diseñado para transmitir el gradiente de error y minimizar el riesgo de desvanecimiento del gradiente.
__kernel void Sum5Matrix(__global double *matrix1, ///<[in] First matrix __global double *matrix2, ///<[in] Second matrix __global double *matrix3, ///<[in] Third matrix __global double *matrix4, ///<[in] Fourth matrix __global double *matrix5, ///<[in] Fifth matrix __global double *matrix_out, ///<[out] Output matrix int dimension, ///< Dimension of matrix double multiplyer ///< Multiplyer for output )
En el cuerpo del kernel, definimos el desplazamiento del primer elemento de los vectores procesados en las secuencias e iniciamos el ciclo de suma de gradientes. La multiplicación la suma de los gradientes de error por un multiplicador igual a 0,2 nos permite promediar los valores del error transmitido sobre la capa anterior de la red neuronal. A su vez, la salida del multiplicador en los parámetros se ha realizado intencionalmente, para asegurar la posibilidad de seleccionar esta durante la configuración del funcionamiento del algoritmo.
{
const int i=get_global_id(0)*dimension;
for(int k=0;k<dimension;k++)
matrix_out[i+k]=(matrix1[i+k]+matrix2[i+k]+matrix3[i+k]+matrix4[i+k]+matrix5[i+k])*multiplyer;
}
En la clase CNeuronMHAttentionOCL, cada subproceso recibirá su propio método. El método calcInputGradients se encarga de propagar el gradiente de error. En los parámetros, el método recibe un puntero al objeto de la capa anterior de la red neuronal, y al comienzo del método, comprueba la validez del puntero recibido.
bool CNeuronMHAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
Luego calculamos los gradientes de error a través del bloque FeedForward, utilizando los métodos homónimos para las capas convolucionales FF1 y FF2.
if(!FF2.calcInputGradients(FF1)) return false; if(!FF1.calcInputGradients(Weights0)) return false;
Y pasamos el gradiente de error alrededor del bloque FeedForward. El valor medio del error lo guardamos en el búfer de gradiente de la capa Weights0.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,Weights0.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,Gradient.GetIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,Weights0.getGradientIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.5);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
double temp[];
if(Weights0.getGradient(temp)<=0)
return false;
}
Ha llegado el momento de distribuir el gradiente de error por las cabezas de atención. Necesitamos aumentar la dimensión del tensor de gradiente hasta el tamaño del búfer de atención concatenado. Para hacer esto, pasaremos el gradiente de error a través de la capa convolucional Weights0 llamando al método correspondiente de la capa convolucional.
if(!Weights0.calcInputGradients(AttentionConcatenate)) return false;
Tras obtener un tensor de gradientes de error de longitud suficiente, podremos distribuir el error entre los búferes de las cabezas de atención. Vamos a usar el kernel de desconcatenación creado arriba.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_DeconcatenateMatrix,def_k_dconc_output1,AttentionOut.getGradientIndex());
OpenCL.SetArgument(def_k_DeconcatenateMatrix,def_k_dconc_window1,iWindow);
OpenCL.SetArgumentBuffer(def_k_DeconcatenateMatrix,def_k_dconc_output2,AttentionOut2.getGradientIndex());
OpenCL.SetArgument(def_k_DeconcatenateMatrix,def_k_dconc_window2,iWindow);
OpenCL.SetArgumentBuffer(def_k_DeconcatenateMatrix,def_k_dconc_output3,AttentionOut3.getGradientIndex());
OpenCL.SetArgument(def_k_DeconcatenateMatrix,def_k_dconc_window3,iWindow);
OpenCL.SetArgumentBuffer(def_k_DeconcatenateMatrix,def_k_dconc_output4,AttentionOut4.getGradientIndex());
OpenCL.SetArgument(def_k_DeconcatenateMatrix,def_k_dconc_window4,iWindow);
OpenCL.SetArgumentBuffer(def_k_DeconcatenateMatrix,def_k_dconc_inputs,AttentionConcatenate.getGradientIndex());
if(!OpenCL.Execute(def_k_DeconcatenateMatrix,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Deconcatenate Matrix: %d",GetLastError());
return false;
}
double temp[];
if(AttentionConcatenate.getGradient(temp)<=0)
return false;
}
El cálculo del gradiente de error dentro de la cabeza de atención se transfiere a un método separado calcHeadGradient, pero aquí solo llamaremos a este método para cada flujo de atención.
if(!calcHeadGradient(Querys,Values,Scores,AttentionOut,prevLayer)) return false; if(!calcHeadGradient(Querys2,Values2,Scores2,AttentionOut2,prevLayer)) return false; if(!calcHeadGradient(Querys3,Values3,Scores3,AttentionOut3,prevLayer)) return false; if(!calcHeadGradient(Querys4,Values4,Scores4,AttentionOut4,prevLayer)) return false;
Al final del método, sumaremos el gradiente de error de todas las cabezas de atención y transferiremos el resultado a la capa anterior de la red neuronal.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix1,AttentionOut.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix2,AttentionOut2.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix3,AttentionOut3.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix4,AttentionOut4.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix5,Weights0.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix_out,prevLayer.getGradientIndex());
OpenCL.SetArgument(def_k_Matrix5Sum,def_k_sum5_dimension,iWindow);
OpenCL.SetArgument(def_k_Matrix5Sum,def_k_sum5_multiplyer,0.2);
if(!OpenCL.Execute(def_k_Matrix5Sum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Matrix5Sum: %d",GetLastError());
return false;
}
double temp[];
if(prevLayer.getGradient(temp)<=0)
return false;
}
//---
return true;
}
Vamos a ver el método calcHeadGradient. En los parámetros, transmitimos al método los punteros a las capas neuronales internas query, value, score y attention relacionadas con la cabeza de atención analizada y un puntero a la capa neuronal anterior.
bool CNeuronMHAttentionOCL::calcHeadGradient(CNeuronConvOCL *query,CNeuronConvOCL *value,CBufferDouble *score,CNeuronBaseOCL *attention,CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
El cuerpo del método se inicia comprobando la validez del puntero a la capa neuronal anterior. Para distribuir el gradiente de error sobre las capas internas, llamaremos al kernel AttentionInsideGradients que analizamos anteriormente en el artículo [8].
{
uint global_work_offset[2]={0,0};
uint global_work_size[2];
global_work_size[0]=iUnits;
global_work_size[1]=iWindow;
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_gradient,attention.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys,prevLayer.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys_g,prevLayer.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys,query.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys_g,query.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values,value.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values_g,value.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_scores,score.GetIndex());
if(!OpenCL.Execute(def_k_AttentionGradients,2,global_work_offset,global_work_size))
{
printf("Error of execution kernel AttentionGradients: %d",GetLastError());
return false;
}
double temp[];
if(query.getGradient(temp)<=0)
return false;
}
Este ejemplo usa el entrenamiento de una matriz, sin dividirla en query y key. Por consiguiente, en lugar de los búferes de la capa de claves, especificaremos los búferes de la capa anterior. Para no sobrescribir el gradiente de error obtenido en la capa anterior al recalcular en otras capas internas, transferiremos los datos al tensor AttentionOut de la cabeza de atención actual, ya elaborado en este paso. No hemos creado un tensor aparte para copiar los datos entre búferes. Realizamos esta operación usando el kernel de adición de 2 matrices SumMatrix. Pero como solo tenemos una matriz, indicaremos la capa anterior en los punteros de ambos tensores. Y para evitar la duplicación de valores, utilizaremos un multiplicador de 0.5.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,prevLayer.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,attention.getGradientIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.5);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
double temp[];
if(attention.getGradient(temp)<=0)
return false;
}
A continuación, recalculamos el gradiente de error que pasa a través de la capa de consultas llamando al método de capa de consulta correspondiente. Luego sumamos el resultado obtenido al gradiente resultante en la iteración anterior. En este salto, utilizaremos un multiplicador de 1, y el gradiente aumentado se promediará en el siguiente salto.
if(!query.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,attention.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,attention.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,1.0); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(attention.getGradient(temp)<=0) return false; }
Para finalizar el método, recalculamos de forma similar el gradiente a través de la capa value y lo sumamos con los gradientes obtenidos previamente. El uso del multiplicador 0.33 nos permite promediar el gradiente de la cabeza de atención en general.
if(!value.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,attention.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,attention.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow+1); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.33); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(prevLayer.getGradient(temp)<=0) return false; } //--- return true; }
Después de recalcular los gradientes de error, actualizamos los pesos de todas las capas internas. A continuación, escribimos en el método updateInputWeights una llamada secuencial de los métodos homónimos de todas las capas neuronales internas.
bool CNeuronMHAttentionOCL::updateInputWeights(CNeuronBaseOCL *prevLayer) { if(!Querys.UpdateInputWeights(prevLayer) || !Querys2.UpdateInputWeights(prevLayer) || !Querys3.UpdateInputWeights(prevLayer) || !Querys4.UpdateInputWeights(prevLayer)) return false; //--- if(!Values.UpdateInputWeights(prevLayer) || !Values2.UpdateInputWeights(prevLayer) || !Values3.UpdateInputWeights(prevLayer) || !Values4.UpdateInputWeights(prevLayer)) return false; if(!Weights0.UpdateInputWeights(AttentionConcatenate)) return false; if(!FF1.UpdateInputWeights(Weights0)) return false; if(!FF2.UpdateInputWeights(FF1)) return false; //--- return true; }
El lector podrá familiarizarse con el código de todos los métodos y funciones en los anexos.
4.5. Cambios puntuales en las clases básicas de la red neronal
Después de implementar el algoritmo de Multi-Head Attention, nos queda aún la cuestión de la implementación del Positional Encoder. Este proceso se ha incluido en el método CNet::feedForward de la clase de red neuronal. Para implementarlo, hemos añadido al método 2 parámetros window y tem. El primero indica el tamaño de la ventana de datos y el segundo se encarga de la necesidad de habilitar/deshabilitar la función.
bool CNet::feedForward(CArrayDouble *inputVals,int window=1,bool tem=true)
El proceso en sí se implementa en el bloque para la transmisión de los datos de origen a la red. Primero, declaramos las 2 variables internas pos (posición en la secuencia) y dim (número ordinal del elemento dentro de la ventana de datos). Con la primera, determinamos el número ordinal del elemento dentro de la ventana de datos. Para hacerlo, tomamos el resto de la división del número ordinal del elemento en el tensor de datos de origen por el tamaño de la ventana. La posición en la secuencia se determina mediante el resultado entero de la división del número ordinal del elemento en el tensor de datos de origen por el tamaño de la ventana. A continuación, al guardar los datos iniciales en el tensor de los datos de entrada de la red neuronal, añadimos el resultado del cálculo usando las fórmulas especificadas en la 3ª sección de este artículo.
CNeuronBaseOCL *neuron_ocl=current.At(0); double array[]; int total_data=inputVals.Total(); if(ArrayResize(array,total_data)<0) return false; for(int d=0;d<total_data;d++) { int pos=d; int dim=0; if(window>1) { dim=d%window; pos=(d-dim)/window; } array[d]=inputVals.At(d)+(tem ? (dim%2==0 ? sin(pos/pow(10000,(2*dim+1)/(window+1))) : cos(pos/pow(10000,(2*dim+1)/(window+1)))) : 0); } if(!opencl.BufferWrite(neuron_ocl.getOutputIndex(),array,0,0,total_data)) return false;
Solo nos queda introducir cambios puntuales en el funcionamiento normal de la red neuronal. Para ello, añadimos al bloque "define" las constantes necesarias para trabajar con los nuevos kernels.
#define def_k_ConcatenateMatrix 17 ///< Index of the Multi Head Attention Neuron Concatenate Output kernel (#ConcatenateBuffers) #define def_k_conc_input1 0 ///< Matrix of Buffer 1 #define def_k_conc_window1 1 ///< Window of Buffer 1 #define def_k_conc_input2 2 ///< Matrix of Buffer 2 #define def_k_conc_window2 3 ///< Window of Buffer 2 #define def_k_conc_input3 4 ///< Matrix of Buffer 3 #define def_k_conc_window3 5 ///< Window of Buffer 3 #define def_k_conc_input4 6 ///< Matrix of Buffer 4 #define def_k_conc_window4 7 ///< Window of Buffer 4 #define def_k_conc_out 8 ///< Output tesor //--- #define def_k_DeconcatenateMatrix 18 ///< Index of the Multi Head Attention Neuron Deconcatenate Output kernel (#DeconcatenateBuffers) #define def_k_dconc_output1 0 ///< Matrix of Buffer 1 #define def_k_dconc_window1 1 ///< Window of Buffer 1 #define def_k_dconc_output2 2 ///< Matrix of Buffer 2 #define def_k_dconc_window2 3 ///< Window of Buffer 2 #define def_k_dconc_output3 4 ///< Matrix of Buffer 3 #define def_k_dconc_window3 5 ///< Window of Buffer 3 #define def_k_dconc_output4 6 ///< Matrix of Buffer 4 #define def_k_dconc_window4 7 ///< Window of Buffer 4 #define def_k_dconc_inputs 8 ///< Input tesor //--- #define def_k_Matrix5Sum 19 ///< Index of the kernel for calculation Sum of 2 matrix with multiplyer (#SumMatrix) #define def_k_sum5_matrix1 0 ///< First matrix #define def_k_sum5_matrix2 1 ///< Second matrix #define def_k_sum5_matrix3 2 ///< Third matrix #define def_k_sum5_matrix4 3 ///< Fourth matrix #define def_k_sum5_matrix5 4 ///< Fifth matrix #define def_k_sum5_matrix_out 5 ///< Output matrix #define def_k_sum5_dimension 6 ///< Dimension of matrix #define def_k_sum5_multiplyer 7 ///< Multiplyer for output
Además, añadimos la constante para identificar la nueva clase.
#define defNeuronMHAttentionOCL 0x7888 ///<Multi-Head Attention neuron OpenCL \details Identified class #CNeuronAttentionOCL
En el constructor de clase de nuestra red neuronal, añadimos una nueva clase al bloque de inicialización de la clase OpenCL.
next=Description.At(1); if(next.type==defNeuron || next.type==defNeuronBaseOCL || next.type==defNeuronConvOCL || next.type==defNeuronAttentionOCL || next.type==defNeuronMHAttentionOCL) { opencl=new COpenCLMy(); if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true)) delete opencl; }
Asimismo, añadimos un nuevo tipo de neuronas en el bloque de inicialización de neuronas en la red.
case defNeuronMHAttentionOCL: neuron_attention_ocl=new CNeuronMHAttentionOCL(); if(CheckPointer(neuron_attention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_attention_ocl.Init(outputs,0,opencl,desc.window,desc.count,desc.optimization)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_attention_ocl)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl=NULL; break;
Después, añadimos la declaración de los nuevos kernels.
if(CheckPointer(opencl)==POINTER_INVALID) return; //--- create kernels opencl.SetKernelsCount(20); opencl.KernelCreate(def_k_FeedForward,"FeedForward"); opencl.KernelCreate(def_k_CalcOutputGradient,"CalcOutputGradient"); opencl.KernelCreate(def_k_CalcHiddenGradient,"CalcHiddenGradient"); opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum"); opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam"); opencl.KernelCreate(def_k_AttentionGradients,"AttentionInsideGradients"); opencl.KernelCreate(def_k_AttentionOut,"AttentionOut"); opencl.KernelCreate(def_k_AttentionScore,"AttentionScore"); opencl.KernelCreate(def_k_CalcHiddenGradientConv,"CalcHiddenGradientConv"); opencl.KernelCreate(def_k_CalcInputGradientProof,"CalcInputGradientProof"); opencl.KernelCreate(def_k_FeedForwardConv,"FeedForwardConv"); opencl.KernelCreate(def_k_FeedForwardProof,"FeedForwardProof"); opencl.KernelCreate(def_k_MatrixSum,"SumMatrix"); opencl.KernelCreate(def_k_Matrix5Sum,"Sum5Matrix"); opencl.KernelCreate(def_k_UpdateWeightsConvAdam,"UpdateWeightsConvAdam"); opencl.KernelCreate(def_k_UpdateWeightsConvMomentum,"UpdateWeightsConvMomentum"); opencl.KernelCreate(def_k_Normilize,"Normalize"); opencl.KernelCreate(def_k_NormilizeWeights,"NormalizeWeights"); opencl.KernelCreate(def_k_ConcatenateMatrix,"ConcatenateBuffers"); opencl.KernelCreate(def_k_DeconcatenateMatrix,"DeconcatenateBuffers");
A continuación, añadimos una nueva clase a los métodos del despachador de la clase CNeuronBaseOCL; los cambios están resaltados.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; }
bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; CNeuronAttentionOCL *at=NULL; CNeuronConvOCL *conv=NULL; switch(TargetObject.Type()) { case defNeuronBaseOCL: temp=TargetObject; return calcHiddenGradients(temp); break; case defNeuronConvOCL: conv=TargetObject; temp=GetPointer(this); return conv.calcInputGradients(temp); break; case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: at=TargetObject; temp=GetPointer(this); return at.calcInputGradients(temp); break; } //--- return false; }
bool CNeuronBaseOCL::UpdateInputWeights(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: temp=SourceObject; return updateInputWeights(temp); break; } //--- return false; }
El lector podrá familiarizarse con el código de todos los métodos y funciones en los anexos.
5. Simulación
Para poner a prueba la nueva arquitectura de la red neuronal, hemos creado el asesor Fractal_Ocl_attrentionMhte. Hemos creado este asesor usando como base el asesor Fractal_OCL_Attention del artículo [8]; se diferencia del asesor principal solo en el tipo de clase de neuronas de atención y en el uso del mecanismo para codificar la posición de los elementos de datos de entrada.
CArrayObj *Topology=new CArrayObj(); if(CheckPointer(Topology)==POINTER_INVALID) return INIT_FAILED; //--- CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBaseOCL; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronConvOCL; desc.window=12; desc.step=12; desc.window_out=36; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- bool result=true; for(int i=0; (i<2 && result); i++) { desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronMHAttentionOCL; desc.window=36; desc.optimization=ADAM; desc.activation=None; result=Topology.Add(desc); } if(!result) { delete Topology; return INIT_FAILED; } //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; desc.activation=SIGMOID; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; delete Net; Net=new CNet(Topology); delete Topology;
Para que el experimento resulte más puro, hemos realizado pruebas paralelas con 2 asesores (Self-Attention y Multi-Head Attention). Hemos realizado la prueba en las mismas condiciones que en los artículos anteriores de este ciclo: instrumento EURUSD, marco temporal H1 y los datos de 20 velas consecutivas; la formación se llevó a cabo utilizando la historia de los últimos 2 años actualizando los parámetros con el método Adam.
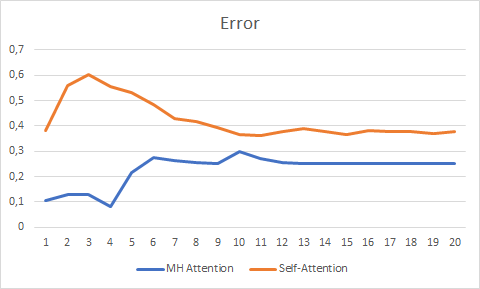
Las pruebas de más de 20 épocas ha mostrado la ventaja de Multi-Head Attention, que representa un gráfico más suave del cambio de error y se estabiliza con un error de 0,25, frente a 0,37 para Self-Attention.
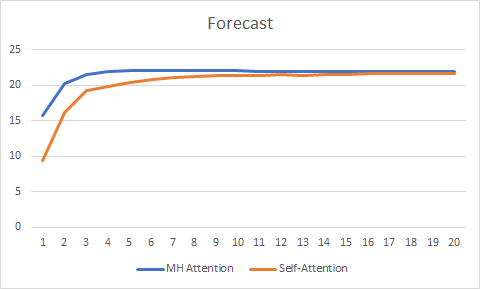
El gráfico las predicciones correctas también ha mostrado las ventajas de la atención multi-cabeza, aunque estas no son tan significativas.
Podrá familiarizarse con el código completo de todos los asesores y clases en los anexos.
Conclusión
En este artículo, hemos analizado la implementación de la arquitectura de Multi-Head Attention y realizado pruebas comparativas con la arquitectura de Self-Attention de una sola cabeza. En iguales condiciones de origen, la atención multi-cabeza ha mostrado mejores resultados. No obstante, debemos considerar que para mejorar la calidad de la red, deberemos pagar costes computacionales adicionales.
Enlaces
- Redes neuronales: así de sencillo
- Redes neuronales: así de sencillo (Parte 2): Entrenamiento y prueba de la red
- Redes neuronales: así de sencillo (Parte 3): Redes convolucionales
- Redes neuronales: así de sencillo (Parte 4): Redes recurrentes
- Redes neuronales: así de sencillo (Parte 5): Cálculos multihilo en OpenCL
- Redes neuronales: así de sencillo (Parte 6): Experimentos con la tasa de aprendizaje de la red neuronal
- Redes neuronales: así de sencillo (Parte 7): Métodos de optimización adaptativos
- Redes neuronales: así de sencillo (Parte 8): Mecanismos de atención
- Redes neuronales: así de sencillo (Parte 9): Documentamos el trabajo realizado
- Attention Is All You Need
- Multi-Head Attention: Collaborate Instead of Concatenate
Programas utilizados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Fractal_OCL_Attention.mq5 | Asesor | Asesor con la red neuronal de clasificación (3 neuronas en la capa de salida) con uso del mecanismo Self-Attention |
| 2 | Fractal_OCL_AttentionMHTE.mq5 | Asesor | Asesor con la red neuronal de clasificación (3 neuronas en la capa de salida) con uso del mecanismo Multi-Head Attention |
| 3 | NeuroNet.mqh | Biblioteca de clase | Biblioteca de clases para crear la red neuronal |
| 4 | NeuroNet.cl | Biblioteca | Biblioteca de código del programa OpenCL |
| 5 | NN.chm | Guía de ayuda de HTML | Archivo convertido de la guía de ayuda HTML. |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/8909
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Aplicación práctica de las redes neuronales en el trading (Parte 2). Visión por computadora
Aplicación práctica de las redes neuronales en el trading (Parte 2). Visión por computadora
 Algoritmo de autoadaptación (Parte IV): Funcionalidad adicional y pruebas
Algoritmo de autoadaptación (Parte IV): Funcionalidad adicional y pruebas
 Aproximación por fuerza bruta a la búsqueda de patrones (Parte II): Nuevos horizontes
Aproximación por fuerza bruta a la búsqueda de patrones (Parte II): Nuevos horizontes
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Comité de las arquitecturas NS más avanzadas basadas en GPU, ¿lo tiene Python? )
es una pena que aún no haya descifrado del todo los transformadores habituales del artículo 8 ))