
Redes neuronales en el trading: Framework comercial híbrido con codificación predictiva (StockFormer)
Introducción
El aprendizaje por refuerzo (Reinforcement Learning, RL) se utiliza cada vez más para resolver problemas complejos en el sector financiero, como el desarrollo de estrategias comerciales y la gestión de portafolios de inversión. Los modelos se entrenan para analizar datos históricos sobre movimientos de precios de instrumentos financieros, volúmenes comerciales e indicadores técnicos. Sin embargo, la mayoría de los métodos existentes presuponen que los datos analizados representan plenamente todas las interdependencias entre activos. En la práctica, esto no siempre es así, y esto es especialmente cierto en el caso de datos de mercado ruidosos y muy volátiles.
Los métodos tradicionales no suelen considerar las previsiones a largo y corto plazo de los rendimientos de los activos, ni sus correlaciones mutuas. Al mismo tiempo, las estrategias de inversión de éxito suelen basarse en un análisis profundo de estos factores. Para modelar dependencias tan complejas, el artículo "StockFormer: Learning Hybrid Trading Machines with Predictive Coding" propone el sistema comercial híbrido StockFormer, que combina las posibilidades del modelado predictivo (predictive coding) con la flexibilidad de los agentes RL. La modelización predictiva, ampliamente usada en los campos del procesamiento del lenguaje natural y la visión por computadora, puede extraer estados ocultos informativos a partir de datos de origen ruidosos, lo que resulta especialmente importante en las aplicaciones financieras.
El framework StockFormer combina tres ramas modificadas de la arquitectura del Transformer, cada una de ellas responsable de estudiar distintos aspectos de la dinámica del mercado:
- tendencias a largo plazo;
- tendencias a corto plazo;
- interdependencias entre activos.
Todas las ramas incorporan el mecanismo "Diversified Multi-Head Attention" (DMH-Attn), que mejora el módulo del Transformer vainilla utilizando bloques FeedForward multicabeza. Esto permite identificar diversos patrones de series temporales en distintos subespacios, conservando la información crítica.
Para optimizar las estrategias comerciales, se combinan de forma adaptativa tres tipos de estados latentes de diferentes ramas usando mecanismos de atención multicabeza en un único subespacio de estados, que luego es utilizado por el agente RL.
Los autores del framework proponen entrenar la política utilizando métodos Actor-Critic. Mientras tanto, la propagación inversa de los gradientes de error del Crítico tiene por objeto mejorar el módulo de codificación predictiva, lo que garantiza una estrecha integración entre las etapas de entrenamiento.
Los experimentos realizados por los autores del framework con tres conjuntos de datos públicos demostraron que StockFormer supera con creces a los métodos existentes tanto en la previsión como en la maximización del rendimiento de las inversiones.
El algoritmo StockFormer
El framework StockFormer resuelve problemas de predicción y toma de decisiones comerciales en los mercados financieros utilizando enfoques de aprendizaje por refuerzo (RL). Uno de los principales problemas de los métodos tradicionales es la falta de un mecanismo eficaz para analizar las relaciones dinámicas entre los activos y sus futuras tendencias. Esto resulta especialmente importante en los mercados financieros, donde los cambios pueden producirse de forma rápida e impredecible. El StockFormer utiliza dos pasos clave para llevar a cabo esta tarea: la codificación predictiva y el entrenamiento de estrategias comerciales.
En la primera etapa, el StockFormer entrena el modelo utilizando métodos de aprendizaje autosupervisado para extraer eficazmente patrones ocultos de los datos del mercado, incluso en presencia de ruido. Esto permite al modelo considerar las tendencias a corto y largo plazo, así como las interdependencias entre activos. Con este planteamiento, el modelo extrae importantes estados ocultos que se aplican en el siguiente paso para tomar decisiones comerciales.
La diversidad de patrones temporales entre las secuencias de múltiples activos en los mercados financieros aumenta sustancialmente la dificultad de extraer pronósticos eficaces de los datos de origen. Para resolver este problema, los autores del framework StockFormer modernizan el módulo de atención multicabeza del Transformer vainilla sustituyendo el único bloque FeedForward(FFN) por un grupo de bloques similares. Sin cambiar el número total de parámetros, dicho mecanismo mejora la capacidad de la atención multicabeza para descomponer las características, lo que facilita el modelado de diversos patrones temporales en distintos subespacios.
Este módulo modificado se denomina "Módulo de atención multicabeza diversificada" (Diversified Multi-Head Attention — DMH-Attn). Para las entidades Query, Key y Value de dimensionalidad dmodel, el proceso en el módulo de atención multicabeza diversificada puede representarse como sigue: primero dividimos las características de salida Z de la atención multicabeza en h grupos a lo largo de la dimensión del canal, donde h será el número de cabezas de atención paralelas, y después, aplicamos un FFN aparte a cada grupo de características divididas en Z:
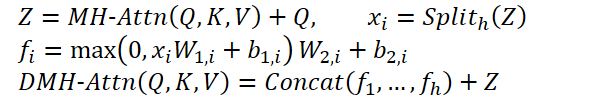
Donde MH-Attn indica la atención multicabeza. Y 𝑓𝑖 son las características de salida de cada cabeza FFN que contiene dos proyecciones lineales con activación ReLU entre ellas.
Cada rama del modelo del Transformer modernizado en StockFormer se divide en dos módulos: un codificador y un decodificador. Ambos módulos se usan durante el entrenamiento de la codificación predictiva con distintos fines, sin embargo, solo el codificador se utiliza en la optimización de estrategias. El modelo utiliza L capas de codificador y M capas de decodificador. Las representaciones latentes obtenidas en la última capa del codificador XLenc sirven como una de las entradas de cada capa del decodificador. El proceso de cálculo en la l-ésima capa del codificador y la m-ésima capa del decodificador puede escribirse como sigue:
- capa del codificador:
![]()
- capa del decodificador:
![]()
Aquí Xl,enc y Xm,dec son los resultados de las capas del codificador y el decodificador, respectivamente. A las entradas para la primera capa del codificador y el decodificador suministramos los datos de origen con las incorporaciones posicionales añadidas. Y los resultados de la última capa de decodificador se pasan a la capa de proyección, que genera el resultado final para la tarea de codificación predictiva.
El módulo de extracción de interdependencias está diseñado para identificar correlaciones dinámicas entre series temporales. En cada paso temporal t, el módulo usa los mismos datos de entrada para el codificador y el decodificador. Los autores del framework utilizan indicadores técnicos como MACD, RSI y SMA para trabajar con datos bursátiles como estadísticas.
En el proceso de entrenamiento, los datos de origen se dividen en dos partes:
- Matriz de covarianza. Matriz de covarianza entre secuencias de precios de cierre diarios de todos los activos para un periodo fijo de tiempo hasta el momento t.
- Estadísticas enmascaradas. En esta parte, la mitad de las series temporales se seleccionan aleatoriamente y sus estadísticas originales se enmascaran con ceros. En la fase de prueba, se usarán los datos completos sin enmascaramiento.
El objetivo principal del módulo de extracción de interdependencias consiste en recuperar las estadísticas enmascaradas basándose en la matriz de covarianzas y en las restantes estadísticas visibles. Este método de codificación predictiva hace que el codificador del Transformer aprenda a identificar las dependencias entre las series temporales analizadas.
Los módulos de previsión a corto y largo plazo del StockFormer tienen por objeto prever las tasas de rendimiento de cada activo en distintos horizontes temporales.
La tarea del módulo de previsión a corto plazo consiste en prever la tasa de rendimiento del activo para el día siguiente (H = 1). Para ello, se introducen a la entrada del codificador las estadísticas analizadas para T días. El decodificador recibe los mismos valores solo en el punto temporal analizado.
El módulo de previsión a largo plazo funciona de forma similar, pero con un horizonte de planificación de las tasas de rendimiento de los activos para un periodo más largo, lo que anima al modelo a captar la dinámica del mercado en un horizonte temporal más largo.
Para entrenar los módulos de previsión a corto y largo plazo se usa una función de pérdida combinada que incluye el error de regresión y el error de clasificación de las acciones. El primero minimiza la diferencia entre los rendimientos previstos y reales, mientras que el error de clasificación garantiza que se dé prioridad a los activos con mayor rendimiento.
De este modo, las dos ramas del modelo ayudan al StockFormer a captar la dinámica del mercado en distintos horizontes temporales, lo que permite al agente RL tomar decisiones comerciales más precisas e informadas.
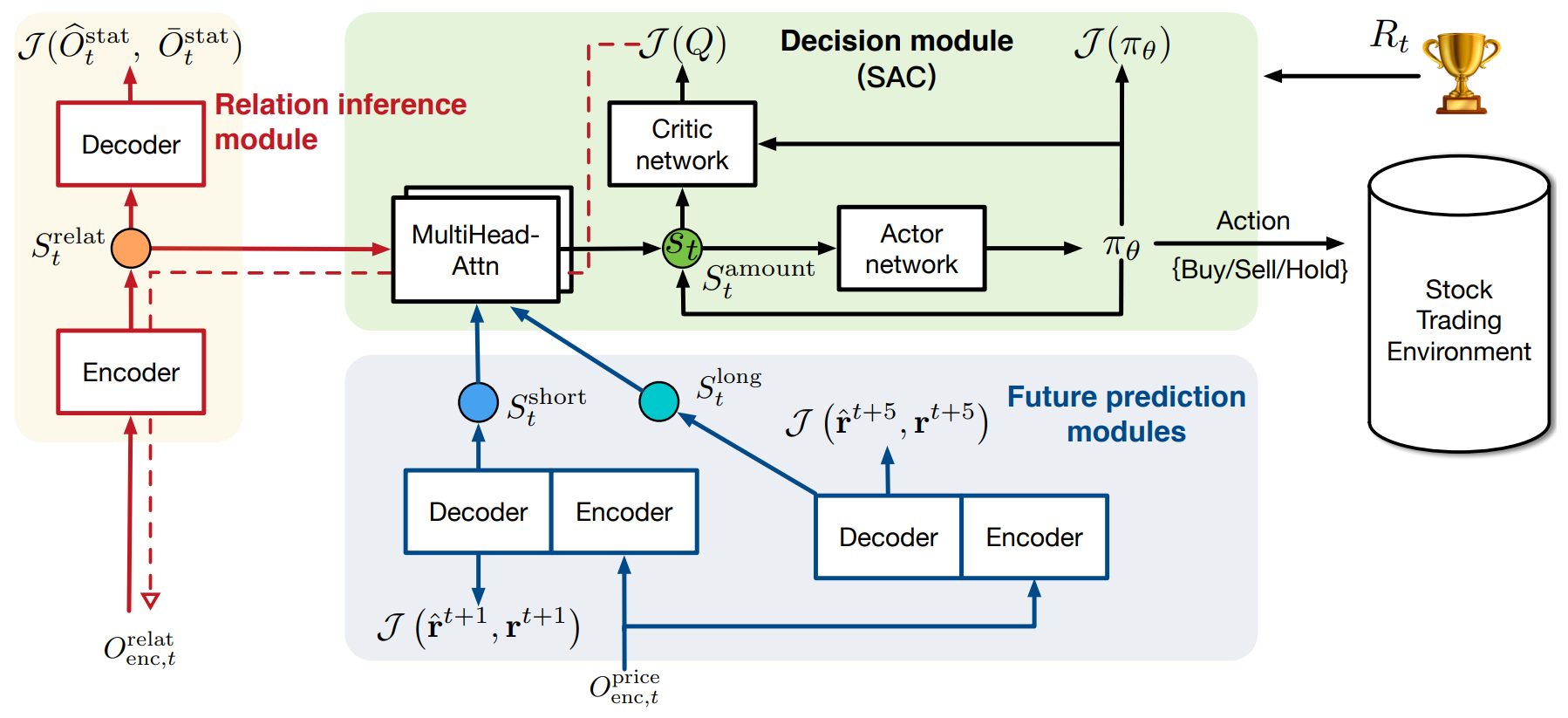
En la segunda etapa del entrenamiento, el StockFormer combina los tres tipos de representaciones latentes srelat,t, slong,t, sshort,t en un único espacio de estados St utilizando una cascada de bloques de atención multicabeza. En un primer momento, se realiza la fusión de las previsiones a corto y largo plazo. En este caso, la representación de la previsión a largo plazo actúa como Query, puesto que es menos susceptible al ruido a corto plazo. Los resultados de este trabajo se asignan al estado latente de las interdependencias de los activos, que se utilizan como Key y Value del siguiente módulo de atención.
A continuación, el modelo se entrena para determinar la estrategia comercial óptima usando el enfoque Actor-Crítico. Una de las principales ventajas del StockFormer es la integración de las fases de codificación predictiva y optimización de políticas. Las puntuaciones del Crítico ayudan a mejorar la calidad de la extracción de las representaciones latentes, lo que permite al modelo analizar las relaciones entre activos con mayor profundidad y hacer frente al ruido de los datos de origen.
A continuación le mostramos la visualización del framework StockFormer por parte del autor.
Implementación con MQL5
Tras repasar los aspectos teóricos del framework StockFormer, podemos implementar nuestra propia visión de los planteamientos propuestos usando MQL5. Y como podemos ver en la descripción teórica presentada del framework, el principal cambio de diseño en la arquitectura de los módulos de atención utilizados es la introducción del bloque FeedForward multicabeza. Pondremos en marcha este bloque en la primera fase de nuestro trabajo.
En la implementación del bloque FeedForward multicabeza propuesto por los autores del framework StockFormer, los resultados del bloque de Self-Attention multicabeza para cada elemento de la secuencia se dividen en h grupos iguales, y a cada grupo se le aplica un MLP diferente con parámetros de entrenamiento únicos.
Tenga en cuenta que el enfoque para formar cabezas aquí es distinto del bloque de atención multicabeza que utilizamos anteriormente. En Multy-Head Self-Attention, formamos múltiples variantes de las entidades Query, Key y Value basadas en una única incorporación de un elemento de secuencia. En este caso, los autores del StockFormer proponen particionar directamente el vector de descripción de un único elemento de la secuencia en varios grupos iguales de elementos. Luego se aplica un MLP diferente a cada grupo. Este enfoque, por supuesto, permite organizar múltiples cabezas sin aumentar los parámetros entrenados. Y en la salida obtenemos un tensor con la misma dimensionalidad, sin necesidad de una capa de proyección, como se organiza en MH Self-Attention. Sin embargo, esto no nos permite usar las capas convolucionales existentes como hacíamos anteriormente. Y debemos encontrar alguna solución alternativa.
Por una parte, podríamos pensar en opciones de transposición del tensor 3D para "ajustar" la solución usando una capa de convolución con análisis independiente de secuencias unitarias. Pero somos conscientes de que habrá bastantes capas de este tipo en el StockFormer. En consecuencia, la transposición de los datos antes y después del bloque FeedForward en cada capa aumentará sustancialmente el tiempo de entrenamiento y ejecución del modelo. Por ello, se decidió crear una versión multicabeza de la capa de convolución. Pero antes de empezar a trabajar en la construcción de un nuevo objeto en el lado del programa principal, tendremos que trabajar un poco con nuestro programa OpenCL.
Incorporación del programa OpenCL
Comenzaremos nuestro trabajo construyendo el kernel de pasada directa de nuestra nueva capa convolucional multicabeza FeedForwardMHConv. Debemos decir que tomamos prestada la estructura de los parámetros y parte del algoritmo de un kernel similar de una capa convolucional existente, e introducimos el identificador de cabezas de convolución y su número total como una dimensión adicional del espacio de tareas.
__kernel void FeedForwardMHConv(__global float *matrix_w, __global float *matrix_i, __global float *matrix_o, const int inputs, const int step, const int window_in, const int window_out, const int activation ) { const size_t i = get_global_id(0); const size_t h = get_global_id(1); const size_t v = get_global_id(2); const size_t total = get_global_size(0); const size_t heads = get_global_size(1);
En el cuerpo del kernel, realizamos la identificación del flujo actual en todas las dimensiones del espacio de tareas. Y luego determinamos las dimensiones de cada cabeza de convolución en la entrada y la salida de la capa y el desplazamiento en los búferes de datos globales hasta los elementos analizados.
const int window_in_h = (window_in + heads - 1) / heads; const int window_out_h = (window_out + heads - 1) / heads; const int shift_out = window_out * i + window_out_h * h; const int shift_in = step * i + window_in_h * h; const int shift_var_in = v * inputs; const int shift_var_out = v * window_out * total; const int shift_var_w = v * window_out * (window_in_h + 1); const int shift_w_h = h * window_out_h * (window_in_h + 1);
Una vez realizado el trabajo preparatorio, procedemos a construir las operaciones del algoritmo de convolución de los datos de origen con el filtro entrenado. Dentro de un mismo flujo, realizaremos operaciones de convolución de una cabeza de datos de origen con el filtro correspondiente. Para ello organizaremos un sistema de ciclos anidados. El ciclo exterior enumera los elementos de la capa de resultados del elemento analizado según la cabeza de convolución correspondiente.
float sum = 0; float4 inp, weight; int stop = (window_in_h <= (inputs - shift_in) ? window_in_h : (inputs - shift_in)); //--- for(int out = 0; (out < window_out_h && (window_out_h * h + out) < window_out); out++) { int shift = (window_in_h + 1) * out + shift_w_h;
Y en el cuerpo del ciclo externo definimos primero el desplazamiento en el búfer de los parámetros a entrenar. Y, a continuación, organizamos un ciclo de iteración de los elementos de la ventana de datos de origen.
for(int k = 0; k <= stop; k += 4) { switch(stop - k) { case 0: inp = (float4)(1, 0, 0, 0); weight = (float4)(matrix_w[shift_var_w + shift + window_in_h], 0, 0, 0); break; case 1: inp = (float4)(matrix_i[shift_var_in + shift_in + k], 1, 0, 0); weight = (float4)(matrix_w[shift_var_w + shift + k], matrix_w[shift_var_w + shift + window_in_h], 0, 0); break; case 2: inp = (float4)(matrix_i[shift_var_in + shift_in + k], matrix_i[shift_var_in + shift_in + k + 1], 1, 0); weight = (float4)(matrix_w[shift_var_w + shift + k], matrix_w[shift_var_w + shift + k + 1], matrix_w[shift_var_w + shift + window_in_h], 0); break; case 3: inp = (float4)(matrix_i[shift_var_in + shift_in + k], matrix_i[shift_var_in + shift_in + k + 1], matrix_i[shift_var_in + shift_in + k + 2], 1); weight = (float4)(matrix_w[shift_var_w + shift + k], matrix_w[shift_var_w + shift + k + 1], matrix_w[shift_var_w + shift + k + 2], matrix_w[shift_var_w + shift + shift_w_h]); break; default: inp = (float4)(matrix_i[shift_var_in + shift_in + k], matrix_i[shift_var_in + shift_in + k + 1], matrix_i[shift_var_in + shift_in + k + 2], matrix_i[shift_var_in + shift_in + k + 3]); weight = (float4)(matrix_w[shift_var_w + shift + k], matrix_w[shift_var_w + shift + k + 1], matrix_w[shift_var_w + shift + k + 2], matrix_w[shift_var_w + shift + k + 3]); break; }
Para optimizar los procesos computacionales de las operaciones de convolución, aprovecharemos la multiplicación incorporada de variables vectoriales, pues permiten un uso más eficiente de los recursos de la CPU. Por lo tanto, primero transferimos los datos de los búferes externos a las variables vectoriales locales y, a continuación, efectuamos la multiplicación vectorial y pasamos a la siguiente iteración del ciclo anidado.
sum += IsNaNOrInf(dot(inp, weight), 0);
}
Una vez ejecutadas todas las iteraciones del ciclo anidado, realizamos las operaciones de la función de activación y almacenamos el valor obtenido en el elemento correspondiente del búfer de resultados. Y pasamos a la siguiente iteración del ciclo exterior.
sum = IsNaNOrInf(sum, 0); //--- matrix_o[shift_var_out + out + shift_out] = Activation(sum, activation);; } }
Cuando todas las iteraciones del sistema de ciclos se hayan completado, todos los valores necesarios se almacenarán en el búfer de resultados, y finalizaremos el kernel.
A continuación, pasaremos a la construcción de algoritmos de pasada inversa. Y aquí debemos decir que ya no podemos introducir el identificador de la cabeza de convolución como una dimensión del espacio de tareas.
Recordemos que durante la ejecución del algoritmo de distribución del gradiente de error, recopilamos los valores de la influencia de cada elemento de los datos originales en el resultado. Y en el caso de que el tamaño de paso de la ventana de convolución analizada sea menor que su tamaño, los elementos de los datos de origen pueden influir en los elementos del tensor de resultados de distintas cabezas de convolución.
Por consiguiente, en este caso introducimos el número de cabezas de atención como un parámetro externo adicional del kernel CalcHiddenGradientMHConv. Y determinamos el identificador de una cabeza de convolución concreta durante la recogida de gradientes de error.
__kernel void CalcHiddenGradientMHConv(__global float *matrix_w, __global float *matrix_g, __global float *matrix_o, __global float *matrix_ig, const int outputs, const int step, const int window_in, const int window_out, const int activation, const int shift_out, const int heads ) { const size_t i = get_global_id(0); const size_t inputs = get_global_size(0); const size_t v = get_global_id(1);
En el cuerpo del kernel, identificamos el flujo actual en el espacio de tareas bidimensional que apunta al elemento de datos de origen y al identificador de secuencia unitaria. Después definimos los valores de las constantes, entre las que se encuentran los desplazamientos en los búferes de datos, así como las dimensionalidades de la ventana y el número de filtros para una cabeza de convolución.
const int shift_var_in = v * inputs; const int shift_var_out = v * outputs; const int shift_var_w = v * window_out * (window_in + 1); const int window_in_h = (window_in + heads - 1) / heads; const int window_out_h = (window_out + heads - 1) / heads;
Aquí es donde definimos el rango de la ventana de resultados que se ve influido por el elemento analizado de los datos de origen.
float sum = 0; float out = matrix_o[shift_var_in + i]; const int w_start = i % step; const int start = max((int)((i - window_in + step) / step), 0); int stop = (w_start + step - 1) / step; stop = min((int)((i + step - 1) / step + 1), stop) + start; if(stop > (outputs / window_out)) stop = outputs / window_out;
Tras el trabajo preparatorio, procederemos a recopilar los gradientes de error de todos los elementos dependientes del tensor de resultados. Para ello, organizaremos un sistema de ciclos. El ciclo exterior iterará los elementos dependientes dentro de la ventana previamente definida.
for(int k = start; k < stop; k++) { int head = (k % window_out) / window_out_h;
En el cuerpo del ciclo externo, primero definimos una cabeza de convolución para un elemento individual del tensor de resultados y, a continuación, organizamos un ciclo de enumeración de filtros anidado.
for(int h = 0; h < window_out_h; h ++) { int shift_g = k * window_out + head * window_out_h + h; int shift_w = (stop - k - 1) * step + (i % step) / window_in_h + head * (window_in_h + 1) + h * (window_in_h + 1); if(shift_g >= outputs || shift_w >= (window_in_h + 1) * window_out) break; float grad = matrix_g[shift_out + shift_g + shift_var_out]; sum += grad * matrix_w[shift_w + shift_var_w]; } }
Precisamente en el cuerpo del ciclo anidado recopilamos el gradiente de error a través de todos los filtros de una cabeza de convolución y procedemos a la siguiente iteración del sistema de ciclo.
Tras recoger con éxito los gradientes de error de todos los elementos dependientes, corregimos el valor recopilado mediante la derivada de la función de activación y almacenamos el resultado obtenido en el elemento del búfer de datos correspondiente.
matrix_ig[shift_var_in + i] = Deactivation(sum, out, activation); }
Con esto completaremos las operaciones del kernel de la distribución del gradiente de error. Le sugiero que se familiarice con el kernel de actualización de los parámetros del modelo. El código completo del programa OpenCL se encuentra en el archivo adjunto al artículo. Ahora pasaremos a la siguiente etapa de nuestro trabajo: la construcción del objeto de capa neuronal de convolución multicabeza en el lado del programa principal.
La capa de convolución multicabeza
Para implementar la funcionalidad de la convolución en el lado del programa principal, crearemos un nuevo objeto CNeuronMHConvOCL. Y, como no resulta difícil de adivinar, utilizaremos una capa de convolución existente como clase padre. Más abajo le mostramos la estructura del nuevo objeto.
class CNeuronMHConvOCL : public CNeuronConvOCL { protected: uint iHeads; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronMHConvOCL(void) : iHeads(1) {}; ~CNeuronMHConvOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint step, uint window_out, uint units_count, uint variables, uint heads, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const override { return defNeuronMHConvOCL; } //--- methods for working with files virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; };
En la estructura de objetos presentada, solo declaramos una variable interna para almacenar un número determinado de cabezas de convolución. Todos los demás objetos y variables necesarios para organizar los procesos los heredaremos de la clase padre. Además, redefiniremos los métodos de pasada directa e inversa, que son "envoltorios" para llamar a los kernels anteriores. El algoritmo para colocar los kernels en la cola de ejecución sigue siendo el mismo. Por consiguiente, no nos detendremos a analizar los métodos anteriores. En el marco de este artículo le propongo aclarar solo el método de inicialización del nuevo objeto Init que hemos creado casi "desde cero".
Solo hemos añadido un elemento a la estructura de parámetros del método de inicialización, encargada de transmitir el número de cabezas de convolución del programa que realiza la llamada.
bool CNeuronMHConvOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint step, uint window_out, uint units_count, uint variables, uint heads, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronProofOCL::Init(numOutputs, myIndex, open_cl, window, step, units_count * window_out * variables, ADAM, batch)) return false;
En el cuerpo del método, llamamos directamente al método homónimo de la capa de submuestreo, que en este caso es el objeto antecesor. Y luego guardamos los valores de los parámetros externos en variables locales.
iWindowOut = window_out; iVariables = variables; iHeads = MathMax(MathMin(heads, window), 1);
A continuación, tenemos que inicializar el tensor de parámetros entrenados con valores aleatorios. Pero antes, debemos definir la dimensionalidad de este tensor. Esta depende del número de filas unitarias de la secuencia multimodal analizada, del número total de filtros y del tamaño de la ventana analizada de una cabeza de convolución.
const int window_h = int((iWindow + heads - 1) / heads); const int count = int((window_h + 1) * iWindowOut * iVariables);
Nótese que hablamos del número total de filtros de todas las cabezas de convolución, pero estamos utilizando la ventana analizada de una sola cabeza. No resulta difícil adivinar que el número de parámetros entrenados para una cabeza de convolución será igual al producto del número de filtros de un cabeza por el tamaño de la ventana de los datos de origen que analiza, más un elemento de sesgo bayesiano (Fi * (Wi + 1)). Entonces, para obtener el número total de parámetros de una secuencia unitaria, solo hay que multiplicar el valor obtenido por el número de cabezas de convolución (Fi * (Wi + 1) * H). Y, obviamente, el número de filtros de una cabeza de convolución multiplicado por el número de cabezas nos dará el número total de filtros especificados por el usuario.
A continuación, comprobamos la relevancia del puntero al objeto de búfer de parámetros entrenados y, si es necesario, creamos un nuevo objeto.
if(!WeightsConv) { WeightsConv = new CBufferFloat(); if(!WeightsConv) return false; }
Luego reservamos el número necesario de elementos en el búfer y organizamos un ciclo de rellenado del búfer con valores aleatorios.
if(!WeightsConv.Reserve(count)) return false; float k = (float)(1 / sqrt(window_h + 1)); for(int i = 0; i < count; i++) { if(!WeightsConv.Add((GenerateWeight() * 2 * k - k) * WeightsMultiplier)) return false; } if(!WeightsConv.BufferCreate(OpenCL)) return false;
Después de rellenar con éxito el búfer con valores aleatorios, lo transferiremos a la memoria contextual OpenCL. Aquí también crearemos los búferes de momentos, rellenándolos con valores cero.
if(!FirstMomentumConv) { FirstMomentumConv = new CBufferFloat(); if(!FirstMomentumConv) return false; } if(!FirstMomentumConv.BufferInit(count, 0.0)) return false; if(!FirstMomentumConv.BufferCreate(OpenCL)) return false; //--- if(!SecondMomentumConv) { SecondMomentumConv = new CBufferFloat(); if(!SecondMomentumConv) return false; } if(!SecondMomentumConv.BufferInit(count, 0.0)) return false; if(!SecondMomentumConv.BufferCreate(OpenCL)) return false; if(!!DeltaWeightsConv) delete DeltaWeightsConv; //--- return true; }
Con esto concluye nuestra revisión de los métodos del objeto de capa de convolución multicabeza CNeuronMHConvOCL. Podrá ver el código completo de la clase anterior y todos sus métodos en el archivo adjunto.
El bloque multicabeza FeedForward
Ya hemos creado el primer "ladrillo" en el camino hacia la construcción del framework StockFormer. Ahora usaremos este para crear un bloque FeedForward multicabeza dentro del nuevo objeto CNeuronMHFeedForward, cuya estructura se muestra a continuación.
class CNeuronMHFeedForward : public CNeuronBaseOCL { protected: CNeuronMHConvOCL acConvolutions[2]; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronMHFeedForward(void) {}; ~CNeuronMHFeedForward(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_out, uint units_count, uint variables, uint heads, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const override { return defNeuronMHFeedForward; } //--- methods for working with files virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual void SetOpenCL(COpenCLMy *obj) override; };
En la estructura del nuevo objeto, declaramos un array de dos capas internas de convolución multicabeza y redefinimos el ya conocido conjunto de métodos virtuales. Los objetos internos se declaran de forma estática, lo que permite dejar vacíos el constructor y el destructor de la clase. La inicialización de todos los objetos declarados y heredados se realizará en el método Init.
bool CNeuronMHFeedForward::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_out, uint units_count, uint variables, uint heads, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables, optimization_type, batch)) return false;
En los parámetros del método de inicialización, obtenemos constantes que definen la arquitectura del objeto a crear. Parte de los parámetros recibidos se transmite al método homónimo de la clase padre para inicializar las interfaces básicas heredadas.
Después inicializamos la primera capa de convolución especificando GELU como su función de activación.
if(!acConvolutions[0].Init(0, 0, OpenCL, window, window, window_out, units_count, variables, heads, optimization, iBatch)) return false; acConvolutions[0].SetActivationFunction(GELU);
A continuación, inicializamos la segunda capa de convolución sin la función de activación.
if(!acConvolutions[1].Init(0, 1, OpenCL, window_out, window_out, window, units_count, variables, heads, optimization, iBatch)) return false; acConvolutions[1].SetActivationFunction(None);
Nótese que cuando llamamos al método de inicialización de la segunda capa de convolución, reordenamos los parámetros del número de filtros y la ventana de datos de origen analizados.
La salida del bloque FeedForward usa enlaces residuales de normalización de datos, por lo que no redefiniremos el búfer de interfaz de resultados de nuestro bloque. Sin embargo, redefiniremos el búfer de gradiente de error, lo cual permitirá la transferencia directa de gradientes desde las interfaces al búfer correspondiente de la segunda capa convolucional.
if(!SetGradient(acConvolutions[1].getGradient(), true)) return false; SetActivationFunction(None); //--- return true; }
También desactivaremos la función de activación de nuestro bloque y finalizaremos el método devolviendo el resultado lógico de las operaciones al programa que realiza la llamada.
Una vez finalizado el trabajo de inicialización del nuevo objeto, podemos construir el algoritmo de pasada directa dentro del método feedForward. Y debemos decir que en este caso su realización no plantea dificultades. Solo tenemos que llamar secuencialmente a los métodos homónimos de la capa de convolución interna.
bool CNeuronMHFeedForward::feedForward(CNeuronBaseOCL *NeuronOCL) { CObject *prev = NeuronOCL; for(uint i = 0; i < acConvolutions.Size(); i++) { if(!acConvolutions[i].FeedForward(prev)) return false; prev = GetPointer(acConvolutions[i]); }
Y a continuación sumar los valores obtenidos a los datos originales normalizando los resultados dentro de los elementos individuales de la secuencia multimodal analizada.
if(!SumAndNormilize(NeuronOCL.getOutput(), acConvolutions[acConvolutions.Size() - 1].getOutput(), Output, acConvolutions[0].GetWindow(), true, 0, 0, 0, 1)) return false; //--- return true; }
Y finalizaremos el método devolviendo el resultado lógico de las operaciones al programa que realiza la llamada.
El algoritmo del método de distribución del gradiente de error calcInputGradients es un poco más complicado, debido a la necesidad de realizar gradientes en dos flujos de información.
bool CNeuronMHFeedForward::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
En los parámetros del método obtendremos el puntero al objeto de datos iniciales, en cuyo búfer debemos pasar el gradiente de error en un volumen igual a la influencia de los datos iniciales en el resultado final del modelo. En el cuerpo del método comprobaremos directamente la relevancia del puntero obtenido.
Tras pasar con éxito el bloque de control, organizaremos un ciclo de iteración inversa de las capas de convolución internas con sucesivas llamadas a sus métodos homónimos.
for(int i = (int)acConvolutions.Size() - 2; i >= 0; i--) { if(!acConvolutions[i].calcHiddenGradients(acConvolutions[i + 1].AsObject())) return false; }
La distribución del gradiente de error a lo largo de la línea troncal de objetos internos va seguida de su transmisión a la capa de datos de origen. Esta operación completa las operaciones del flujo de información principal.
if(!NeuronOCL.calcHiddenGradients(acConvolutions[0].AsObject())) return false;
A continuación, deberemos ejecutar el gradiente de error en el segundo flujo de información. También en este caso, el algoritmo se divide en dos ramas de operaciones, dependiendo de la presencia de la función de activación de los datos de origen. Si no hay una función de activación, bastará con sumar el gradiente de error acumulado al nivel de los datos de origen con los valores similares a la salida de nuestro bloque.
if(NeuronOCL.Activation() == None) { if(!SumAndNormilize(NeuronOCL.getGradient(), Gradient, NeuronOCL.getGradient(), acConvolutions[0].GetWindow(), false, 0, 0, 0, 1)) return false; } else { if(!DeActivation(NeuronOCL.getOutput(), NeuronOCL.getPrevOutput(), Gradient, NeuronOCL.Activation()) || !SumAndNormilize(NeuronOCL.getGradient(), NeuronOCL.getPrevOutput(), NeuronOCL.getGradient(), acConvolutions[0].GetWindow(), false, 0, 0, 0, 1)) return false; } //--- return true; }
De lo contrario, primero necesitaremos ajustar el gradiente de error del nivel de resultados de nuestro bloque usando la derivada de la función de activación de los datos originales. Y solo entonces realizaremos la operación de suma de los datos de sus dos flujos de información.
Ahora todo lo que deberemos hacer es devolver el resultado lógico de la ejecución al programa que realiza la llamada y finalizar el método.
Le propongo estudiar por sí mismo el método de ajuste de parámetros del bloque entrenado para reducir el error global del modelo updateInputWeights. Su algoritmo es bastante sencillo: nos limitaremos a llamar secuencialmente los métodos homónimos de los objetos internos. El código completo del objeto del bloque multicabeza FeedForwardCNeuronMHFeedForward y todos sus métodos se encuentran en el artículo adjunto.
El decodificador de atención multicabeza diversificada
Tras crear el bloque multicabeza FeedForward, pasaremos a construir los objetos de codificador y decodificador de atención multicabeza diversificada. Para construir los algoritmos de los módulos anteriores, crearemos los nuevos objetos CNeuronDMHAttention y CNeuronCrossDMHAttention, respectivamente. La estructura de la construcción de objetos es bastante semejante. Este último se caracteriza por disponer de un bloque interno de atención cruzada y trabajar con dos fuentes de datos de origen. En el marco de este trabajo le propongo detenernos en a analizar los algoritmos de construcción del decodificador, como objeto más complejo. Después de repasarlos, creo que no debería tener problemas para entender los algoritmos del codificador.
Como objeto padre en ambos casos utilizaremos CNeuronRMAT, dentro del cual se organiza el algoritmo del modelo secuencial.
class CNeuronCrossDMHAttention : public CNeuronRMAT { protected: //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override; virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer) override { return false; } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override; public: CNeuronCrossDMHAttention(void) {}; ~CNeuronCrossDMHAttention(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint window_cross, uint units_cross, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronCrossDMHAttention; } };
En la estructura del objeto decodificador solo se aprecia la redefinición de los métodos virtuales. La estructura de los objetos internos se establece en el método de inicialización Init, en cuyos parámetros obtendremos las constantes básicas que definen la arquitectura del objeto.
bool CNeuronCrossDMHAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint window_cross, uint units_cross, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
En el cuerpo del método, primero llamamos al método homónimo del objeto básico de la capa completamente conectada para inicializar las interfaces heredadas.
Y luego borramos el array dinámico de almacenamiento de los punteros a los objetos internos del módulo y creamos algunas variables locales para el almacenamiento temporal de datos.
cLayers.Clear(); cLayers.SetOpenCL(OpenCL); CNeuronRelativeSelfAttention *attention = NULL; CNeuronRelativeCrossAttention *cross = NULL; CNeuronMHFeedForward *conv = NULL; bool use_self = units_count > 0; int layer = 0;
Aquí termina el trabajo preparatorio, así que podemos organizar un ciclo con un número de iteraciones igual al número dado de capas internas del decodificador de atención múltiple diversificada.
for(uint i = 0; i < layers; i++) { if(use_self) { attention = new CNeuronRelativeSelfAttention(); if(!attention || !attention.Init(0, layer, OpenCL, window, window_key, units_count, heads, optimization, iBatch) || !cLayers.Add(attention) ) { delete attention; return false; } layer++; }
En el cuerpo del ciclo, primero creamos un bloque de Self-Attention relativa para analizar las dependencias en los datos de origen del flujo principal. Tenga en cuenta, sin embargo, que el bloque de Self-Attention solo se crea cuando la longitud de la secuencia del flujo principal de origen es superior a "1". De lo contrario, no tendremos datos para buscar dependencias.
A continuación, vamos añadir un módulo de atención cruzada relativa.
cross = new CNeuronRelativeCrossAttention(); if(!cross || !cross.Init(0, layer, OpenCL, window, window_key, units_count, heads, window_cross, units_cross, optimization, iBatch) || !cLayers.Add(cross) ) { delete cross; return false; } layer++;
Y finalizando cada capa interna del decodificador tenemos un bloque FeedForward multicabeza. Después de lo cual podemos pasar a la siguiente iteración del ciclo.
conv = new CNeuronMHFeedForward(); if(!conv || !conv.Init(0, layer, OpenCL, window, 2 * window, units_count, 1, heads, optimization, iBatch) || !cLayers.Add(conv) ) { delete conv; return false; } layer++; }
Una vez finalizada la inicialización del ámbito completo de los objetos internos, sustituiremos los punteros a los objetos de interfaz y finalizaremos el método devolviendo el resultado lógico de las operaciones al programa que realiza la llamada.
SetOutput(conv.getOutput(), true); SetGradient(conv.getGradient(), true); //--- return true; }
El algoritmo del método feedForward no contiene momentos complicados y consta de sucesivas llamadas a los métodos homónimos de los objetos internos. Le sugiero que lo estudie por sí mismo. Sin embargo, le propongo dedicar un momento a examinar el algoritmo de distribución del gradiente de error calcInputGradients.
bool CNeuronCrossDMHAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1) { if(!NeuronOCL || !SecondInput || !SecondGradient) return false;
En los parámetros del método obtenemos los punteros a los objetos de los datos de origen y sus gradientes de error, en los que tenemos que escribir los resultados de las operaciones. Por lo tanto, en el cuerpo del método comprobaremos directamente la relevancia de los punteros recibidos.
Además, cabe señalar que la segunda fuente de datos de origen, como parte de las operaciones de pasada directa, es igualmente utilizada por los módulos de atención cruzada de todas las capas internas del decodificador. En consecuencia, deberemos recopilar el gradiente de error de todos los flujos de información y, como viene siendo habitual, en este caso necesitaremos un búfer de almacenamiento interno, que no hemos creado como parte del nuevo objeto. Así que utilizaremos uno de los búferes no usados heredados de la clase padre.
Primero comprobaremos el tamaño del búfer heredado y lo ajustaremos de ser necesario.
if(PrevOutput.Total() != SecondGradient.Total()) { PrevOutput.BufferFree(); if(!PrevOutput.BufferInit(SecondGradient.Total(), 0) || !PrevOutput.BufferCreate(OpenCL)) return false; }
Y luego rellenaremos con valores cero el búfer de gradiente de error para la segunda fuente de datos. Esta operación es necesaria para evitar la suma de los gradientes de la pasada actual con los gradientes acumulados anteriormente.
if(!SecondGradient.Fill(0)) return false;
Vamos a crear variables locales para el almacenamiento temporal de datos.
CObject *next = cLayers[-1]; CNeuronBaseOCL *current = NULL;
Con esto completaremos la fase preparatoria y podremos crear un ciclo de objetos internos de iteración inversa.
for(int i = cLayers.Total() - 2; i >= 0; i--) { current = cLayers[i]; if(!current || !current.calcHiddenGradients(next, SecondInput, PrevOutput, SecondActivation)) return false; if(next.Type() == defNeuronCrossDMHAttention) if(!SumAndNormilize(SecondGradient, PrevOutput, SecondGradient, 1, false, 0, 0, 0, 1)) return false; next = current; }
En el cuerpo del ciclo, llamaremos secuencialmente a los métodos homónimos de los objetos internos, y comprobamos constantemente el tipo de objeto que realiza la distribución del gradiente de error. En el caso del bloque de atención cruzada, añadiremos el gradiente de error resultante de la segunda fuente de datos a los valores acumulados anteriormente.
Una vez ejecutadas con éxito todas las iteraciones del ciclo, realizaremos la transferencia del gradiente de error a la capa de datos de origen de la línea troncal principal.
if(!NeuronOCL.calcHiddenGradients(next, SecondInput, PrevOutput, SecondActivation)) return false; if(next.Type() == defNeuronCrossDMHAttention) if(!SumAndNormilize(SecondGradient, PrevOutput, SecondGradient, 1, false, 0, 0, 0, 1)) return false; //--- return true; }
Al mismo tiempo, comprobaremos el tipo del objeto de distribución del gradiente de error y, de ser necesario, añadiremos el gradiente del segundo flujo de información a los datos acumulados anteriormente. Después, todo lo que deberemos hacer es finalizar el método devolviendo el resultado lógico de las operaciones al programa que realiza la llamada.
Con esto concluiremos nuestro análisis de los algoritmos para construir los métodos decodificadores para la atención multicabeza diversificada. Podrá ver el código completo de este objeto y todos sus métodos en el archivo adjunto. Allí también encontrará el código completo de todos los objetos presentados en este artículo.
Pues bien, ya hemos implementado la principal unidad arquitectónica del framework StockFormer: un módulo diversificado de atención multicabeza en forma de codificador y decodificador de arquitectura del Transformer. Sin embargo, los autores del StockFormer proponen un proceso de aprendizaje en dos niveles con un complejo mecanismo de interacción de los modelos entrenados. Hablaremos de ello en el próximo artículo.
Conclusión
Hoy nos hemos familiarizado con el framework StockFormer, cuyos autores proponen un enfoque innovador para entrenar estrategias comerciales en los mercados financieros. El StockFormer combina métodos de codificación predictiva y aprendizaje profundo con el aprendizaje por refuerzo. Su principal ventaja reside en su capacidad para formar políticas flexibles que consideren las dependencias dinámicas entre varios activos, además de predecir su comportamiento a corto y largo plazo.
La codificación predictiva de tres ramas permite extraer representaciones latentes relacionadas con las tendencias a corto plazo, la dinámica a largo plazo y las interdependencias entre activos, mientras que el mecanismo de atención multicabeza en cascada permite integrar eficazmente distintos tipos de representaciones en un único espacio de estados.
En la parte práctica del artículo, hemos implementado con la ayuda de MQL5 la modificación vainilla del algoritmo del Transformer propuesta por los autores del método y la hemos integrado en los módulos del codificador y el decodificador de la atención multicabeza diversificada. En el próximo artículo, continuaremos el trabajo iniciado y hablaremos de la arquitectura de los modelos entrenados, así como del proceso de entrenamiento de los mismos.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study1.mq5 | Asesor | Asesor de entrenamiento del aprendizaje predictivo |
| 4 | Study2.mq5 | Asesor | Asesor de entrenamiento de la política |
| 5 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 6 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 7 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16686
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Solicitudes en Connexus (Parte 6): Creación de una solicitud y respuesta HTTP
Solicitudes en Connexus (Parte 6): Creación de una solicitud y respuesta HTTP
 Desarrollo de un kit de herramientas para el análisis de la acción del precio (Parte 1): Proyector de gráficos
Desarrollo de un kit de herramientas para el análisis de la acción del precio (Parte 1): Proyector de gráficos
 Algoritmo de Tribu Artificial (Artificial Tribe Algorithm, ATA)
Algoritmo de Tribu Artificial (Artificial Tribe Algorithm, ATA)
 Redes neuronales en el trading: Conjunto de agentes con uso de mecanismos de atención (Final)
Redes neuronales en el trading: Conjunto de agentes con uso de mecanismos de atención (Final)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso