Redes neuronales: así de sencillo

Contenido

• Introducción
• 1. Principios de construcción de las redes neuronales artificiales
• 2. Construcción de las neuronas artificiales
• 3. Entrenando la red
• 4. Construyendo nuestra propia red con los recursos de MQL
• 4.1. Conexiones
• 4.2. La neurona
• 4.3. La red neuronal
• Conclusión
• Enlaces
• Programas usados en el artículo

Introducción

La inteligencia artifical cada vez abarca un mayor número de aspectos de nuestra vida diaria. Cada vez con más frecuencia escuchamos en las noticias "una red neuronal ha sido entrenada para ..." Y cada vez que hablamos de inteligencia artificial, nos hacemos ideas fantásticas e improbables. Parece un tema complejo, sobrenatural e inexplicable, que la creación de semejante milagro solo está al alcance de un grupo slectos de científicos. Y claro está que nosotros solo podemos maravillarnos, ya que nunca lograríamos repetir algo incluso semejante en nuestra computadora doméstica. Pues créaselo: "no es tan malo el Diablo como lo pintan". Vamos a intentar aclarar qué son las redes neuronales y cómo podemos aplicarlas a nuestro trading.

1. Principios de construcción de las redes neuronales artificiales

En la Wikipedia encontramos la siguiente definición de lo que es una red neuronal:

"Las redes neuronales artificiales (también conocidas como sistemas conexionistas) son un modelo computacional vagamente inspirado en el comportamiento observado en su homólogo biológico. Consiste en un conjunto de unidades, llamadas neuronas artificiales, conectadas entre sí para transmitirse señales."

Es decir, una red neuronal artificial es una cierta entidad que consta de una matriz de neuronas artificiales con una conexión organizada entre las mismas. En este caso, además, la organización de la interacción mutua de las neuronas se ha creado a imagen y semejanza del cerebro de un organismo vivo.

En la figura de abajo podemos el esquema de una red neuronal simple. En esta, las neuronas están marcadas con círculos, mientras que las conexiones entre las mismas se muestran con líneas. Como podemos ver por la figura, las neuronas se disponen en capas que se dividen en 3 grupos. En color azul se marca la capa de las neuronas de entrada, a las que se suministra la información original. En color verde y rojo se marcan las neuronas de salida, que generan el resultado del trabajo de la red neuronal. Entre ellas se ubican las neuronas grises, que forman la llamada capa oculta. 

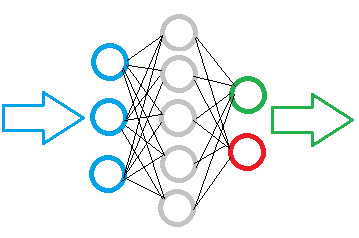
A pesar de la diferencia entre las capas, la red neuronal al completo está construida a partir de neuronas iguales, que tienen varios elementos para las señales de entrada y solo uno para la generación del resultado. Dentro de una neurona se organiza el procesamiento de la información entrante y la generación de un resultado lógico sencillo. Por ejemplo, "Sí" o "No". Con respecto al tema del trading, puede ser, por ejemplo, una señal de transacción o su dirección.

La información original llega a la capa de neuronas de entrada, donde es procesada. A continuación el resultado del funcionamiento de las neuronas se convierte en información de origen para las neuronas de la siguiente capa. La operación se repite de una capa a otra, hasta alcanzar la capa de las neuronas de salida. De esta manera, la información original se procesa y filtra de capa en capa, generando un cierto resultado en la capa de salida.

Dependiendo de la complejidad de las traeas a resolver y de los módulos creados, el número de neuronas en cada capa puede variar. Asimsimo, se pueden dar variaciones de redes neuronales con diferentes capas ocultas. Todo esto hace la red neuronal más complicada, lo que permite resolver tareas más complejas. Pero, al mismo tiempo, también demanda mayores recursos computacionales.

Por eso, al crear nuestro modelo de red neuronal, debemos entender claramente qué tipo de información y en qué volumen vamos a procesar, y también el resultado que esperamos. De ello depende el número de neuronas necesarias en las capas del modelo.

Si queremos suministrar a la entrada de la red una cierta matriz de datos de 10 elementos, la capa de entrada deberá contener 10 neuronas Esto nos permitirá tomar la matriz de datos completa. Las neuronas de entrada sobrantes solo servirán de lastre.

El número de neuronas de salida es determinado por el resultado esperado. Para obtener un resultado lógico único, basta con una neurona de salida. Si necesitamos obtener respuesta a varias preguntas, tendremos que crear una neurona para cada pregunta.

Las capas ocultas de la red neuronal son un cierto centro analítico que procesa y analiza la información obtenida. Por consiguiente, el número de neuronas en la capa depende de la variabilidad de los datos de la capa siguiente, es decir, cada neurona presupone una cierta hipótesis de desarrollo de los eventos.

El número de capas ocultas es determinado por la relación causa-efecto entre los datos roiginales y el resultado esperado. Por ejemplo, si construimos nuestro modelo aplicado a la técnica de los "5 porqués", lo lógico será usar 4 capas ocultas, que sumadas a la capa de salida, darán la posibilidad de asignar 5 preguntas a los datos originales.

En conclusión:

• la red neuronal se construye a partir de neuronas iguales, por consiguiente, para construir un modelo, bastará con crear una clase de neuronas;
• las neuronas en el modelo se organizan en capas;
• el flujo de información en la red neuronal está organizado en forma de transmisión consecutiva de datos a través de todas las capas del modelo, desde las neuronas de entrada hacia las de salida;
• el número de neuronas de entrada viene condicionado por el volumen de la información en una propagación, mientras que el número de neuronas de salida viene condicionado por el volumen de los datos resultantes;
• dado que en la salida de la neurona se genera un cierto resultado lógico, las preguntas planteadas a la red neuronal también deberán presuponer una respuesta unívoca.

2. Construcción de las neuronas artificiales

Una vez nos hemos hecho una idea de la estructura de la red neuronal, vamos a analizar la construcción del modelo de neurona artificial. Y es que precisamente en sus núcleos se realizan los cálculos matemáticos y se toman las decisiones. Y aquí nos surge la pregunta: ¿de qué forma implementar la multitud de posibles decisiones a partir de ciertos datos originales, usando una sola fórmula matemática? Hemos hallado la solución en el cambio de las conexiones entre las neuronas. Para cada conexión se determina un cierto coeficiente de peso que determina la influencia de este valor de entrada en el resultado de la decisión adoptada.

El modelo matemático de la neurona consta de dos funciones. En primer lugar, se suman los productos de los datos de entrada y sus coeficientes de peso.

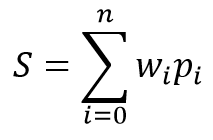
A continuación, basándonos en los valores obtenidos, se calcula el valor resultante en la llamada función de activación. En la práctica, se aplican diferentes variantes de la función de activación, pero las más extendidas son las siguientes:

• Función sigmoide — intervalo de valores retornados de "0" a "1"
• Tangente hiperbólica — intervalo de valores retornados de "-1" a "1" 

La elección de la función de activación depende de las tareas a resolver. Así, si como resultado del procesamiento de los datos originales esperamos obtener una respuesta lógica, se dará preferencia a la función sigmoide. En el contexto del trading, preferimos usar la tangente hiperbólica, donde el valor "-1" se corresponde con la señal de venta, y el valor "1", con la señal de compra. El resultado entre los valores umbral indica cierta incertidumbre.

3. Entrenando la red

Como hemos dicho anteriormente, la variabilidad de los resultados de cada neurona y red neuronal depende en general de los coeficientes de peso seleccionados para las conexiones entre neuronas. La resolución de la tarea de seleccionar los coeficientes de peso correctos se llama entrenamiento de la red neuronal.

Para entrenar una red neuronal, existen diferentes algoritmos y métodos:

• Entrenamiento supervisado;
• Entrenamiento no supervisado;
• Entrenamiento con refuerzo.

El método de entrenamiento se determina a partir de los datos originales y las tareas planteadas a la red neuronal.

El entrenamiento supervisado se usa cuando existe una cantidad suficiente de datos originales con sus correspondientes respuestas correctas a las preguntas planteadas. Durante el entrenamiento, primero se suministran los datos originales a la entrada de la red neuronal, y después, se compara el resultado en la salida de la red con la respuesta correcta conocida de antemano. A continuación, se corrigen los pesos hacia el lado de la reducción del error.

El entrenamiento no supervisado se usa cuando disponemos de una matriz de datos originales y no disponemos de respuestas correctas a las tareas planteadas. En este entrenamiento, la red neuronal busca conjuntos semejantes de datos y permite dividir los datos originales en grupos similares.

El entrenamiento con refuerzo se aplica cuando no hay respuestas correctas, pero tenemos una idea de lo que debemos obtener como resultado. Durante el entrenamiento, suministramos los datos originales a la entrada de la red neuronal, y la red trata de resolver la tarea. Después de comprobar el resultado, se produce la retroalimentación de la red en forma de determinada recompensa. Durante el entrenamiento, la red neuronal trata de conseguir la máxima recompensa.

En este artículo, vamos a usar el entrenamiento supervisado. Como ejemplo, hemos elegido el método de propagación inversa del error. Este enfoque nos permitirá organizar un entrenamiento constante de la red neuronal en tiempo real.

En la base de este método se encuentra el uso del error de salida de la red neuronal para la corrección de sus pesos. El propio algoritmo de entranamiento consta de dos etapas. Al principio, usando como base los datos de entrada, se calcula el valor resultante de la red neuronal, que se compara con el valor patrón, corrigiendo luego el error. A continuación, se realiza una pasada inversa con propagación del error desde la salida de la red hacia sus entradas, corrigiendo todos los coeficientes de peso. Este enfoque es iterativo, es decir, el entrenamiento de la red se realiza paso a paso, lo que permite, tras realizar el entrenamiento con datos históricos, pasar al entrenamiento de la red en el modo online.

El método de propagación inversa del error usa un descenso de gradiente estocástico, lo que permite alcanzar un mínimo aceptable del error, y, gracias a la posibilidad de entrenar una red neuronal online, mantener este mínimo por un intervalo de tiempo prolongado.

4. Construyendo nuestra propia red con los recursos de MQL

Después de asimilar la teoría del funcionamiento de las redes neuronales, vamos a pasar a la parte práctica del artículo. Para mostrar mejor el algoritmo de trabajo de la red neuronal, proponemos al lector crear un ejemplo usando solo los recursos del lenguaje MQL5, sin utilizar bibliotecas aparte. Comenzaremos el trabajo creando las clases para guardar los datos sobre las conexiones elementales entre neuronas.

4.1. Conexiones

En primer lugar, vamos a crear la clase СConnection para guardar el coeficiente de peso de una conexión. La crearemos como heredera de la clase CObject. Esta clase contendrá dos variables del tipo double: weight para guardar el valor inmediato del coeficiente de peso y deltaWeight, en el que guardaremos la magnitud del último cambio del coeficiente de peso (se usa durante el entrenamiento). Para no usar métodos adicionales al trabajar con las variables, los haremos públicos. El valor inicial de las variables se establecerá en el constructor de la clase. 

class СConnection : public CObject
  {
public:
   double            weight;
   double            deltaWeight;
                     СConnection(double w) { weight=w; deltaWeight=0; }
                    ~СConnection(){};
   //--- methods for working with files
   virtual bool      Save(const int file_handle);
   virtual bool      Load(const int file_handle);
  };

Asimismo, para que sea posible guardar posteriormente la información sobre las conexiones, crearemos el método de guardado de datos en el archivo Save, y el método de lectura posterior en el archivo Load. Estos métodos se han construido según un esquema clásico con obtención del manejador del archivo en los parámetros del método. Comprobamos su consistencia y registramos los datos (o los leemos en el método Load).

bool СConnection::Save(const int file_handle)
  {
   if(file_handle==INVALID_HANDLE)
      return false;
//---
   if(FileWriteDouble(file_handle,weight)<=0)
      return false;
   if(FileWriteDouble(file_handle,deltaWeight)<=0)
      return false;
//---
   return true;
  }

El siguiente paso consistirá en crear la matriz para guardar los pesos CArrayCon, basada en la clase CArrayObj. Aquí, redefinimos los dos métodos virtuales CreateElement y Type. El primero se usará para crear un nuevo elemento, mientras que el segundo identificará nuestra clase.

class CArrayCon  :    public CArrayObj
  {
public:
                     CArrayCon(void){};
                    ~CArrayCon(void){};
   //---
   virtual bool      CreateElement(const int index);
   virtual int       Type(void) const { return(0x7781); }
   };

En los parámetros del método para crear un nuevo elemento CreateElement, transmitiremos el índice del elemento creado. En el propio método, comprobaremos su autenticidad, comprobando asimismo el tamaño de la matriz de guardado de datos y modificándolo en caso necesario. A continuación, crearemos un nuevo ejemplar de la clase СConnection, estableciendo el peso inicial de la magnitud aleatoria.

bool CArrayCon::CreateElement(const int index)
  {
   if(index<0)
      return false;
//---
   if(m_data_max<index+1)
     {
      if(ArrayResize(m_data,index+10)<=0)
         return false;
      m_data_max=ArraySize(m_data)-1;
     }
//---
   m_data[index]=new СConnection(MathRand()/32767.0);
   if(!CheckPointer(m_data[index])!=POINTER_INVALID)
      return false;
   m_data_total=MathMax(m_data_total,index);
//---
   return (true);
  }

4.2. La neurona

El siguiente paso consistirá en crear una neurona artificial. Como ya hemos escrito antes, nosotros utilizamos la tangente hiperbólica como función de activación para nuestra neurona. El intervalo de los valores resultantes de esta función se encuentra entre "-1" y "1". El valor "-1" da una señal de venta, y el valor "1", de compra.

La clase de la neurona CNeuron, al igual que en el anterior elemento СConnection, la crearemos como heredera de la clase CObject, pero su estructura será un poco más complicada. 

class CNeuron  :  public CObject
  {
public:
                     CNeuron(uint numOutputs,uint myIndex);
                    ~CNeuron() {};
   void              setOutputVal(double val) { outputVal=val; }
   double            getOutputVal() const { return outputVal; }
   void              feedForward(const CArrayObj *&prevLayer);
   void              calcOutputGradients(double targetVals);
   void              calcHiddenGradients(const CArrayObj *&nextLayer);
   void              updateInputWeights(CArrayObj *&prevLayer);
   //--- methods for working with files
   virtual bool      Save(const int file_handle)                         { return(outputWeights.Save(file_handle));   }
   virtual bool      Load(const int file_handle)                         { return(outputWeights.Load(file_handle));   }

private:
   double            eta;
   double            alpha;
   static double     activationFunction(double x);
   static double     activationFunctionDerivative(double x);
   double            sumDOW(const CArrayObj *&nextLayer) const;
   double            outputVal;
   CArrayCon         outputWeights;
   uint              m_myIndex;
   double            gradient;
  };

En los parámetros del constructor de la clase, transmitimos el número de conexiones salientes de la neurona y su número ordinal en la capa (será necesario para la posterior identificación de la neurona). En el cuerpo del método, establecemos las constantes, guardamos los datos obtenidos y creamos la matriz de conexiones salientes.

CNeuron::CNeuron(uint numOutputs, uint myIndex)  :  eta(0.15), // net learning rate
                                                    alpha(0.5) // momentum  
  {
   for(uint c=0; c<numOutputs; c++)
     {
      outputWeights.CreateElement(c);
     }

   m_myIndex=myIndex;
  }

Los métodos setOutputVal y getOutputVal sirven para recurrir al valor resultante de la neurona. El propio cálculo del valor resultante de la neurona se realiza en el método feedForward. En los parámetros, este método recibe la capa de neuronas precedente.

void CNeuron::feedForward(const CArrayObj *&prevLayer)
  {
   double sum=0.0;
   int total=prevLayer.Total();
   for(int n=0; n<total && !IsStopped(); n++)
     {
      CNeuron *temp=prevLayer.At(n);
      double val=temp.getOutputVal();
      if(val!=0)
        {
         СConnection *con=temp.outputWeights.At(m_myIndex);
         sum+=val * con.weight;
        }
     }
   outputVal=activationFunction(sum);
  }

En el cuerpo del método, se ha organizado un ciclo de iteración de todas las neuronas de la capa anterior y se han sumado los productos de los valores resultantes de las neuronas con los coeficientes de peso. Después de calcular la suma, se calcula el valor resultante de la neurona en el método activationFunction (la función de activación de la neurona se ha sacado a un método aparte).

double CNeuron::activationFunction(double x)
  {
//output range [-1.0..1.0]
   return tanh(x);
  }

El siguiente bloque de métodos se usa al entrenar la red neuronal. En primer lugar, creamos el método de cálculo de la derivada para la función de activación activationFunctionDerivative. Esto es necesario para determinar qué cambio se necesita en la función que realiza la suma para compensar el valor resultante total de la neurona.

double CNeuron::activationFunctionDerivative(double x)
  {
   return 1/MathPow(cosh(x),2);
  }

A continuación, creamos dos métodos de cálculo de gradiente para corregir los coeficientes de peso. La necesidad de crear estos 2 métodos viene condicionada por la diferencia en el cálculo del error del valor resultante para las neuronas de la capa de salida y las capas ocultas. Para la capa de salida, el error se calcula como la diferencia entre el valor resultante y el valor patrón, al tiempo que para las neuronas de las capas ocultas, el error se calcula como la suma de los gradientes de todas las neuronas de la capa posterior multiplicadas por los coeficientes de peso de las conexiones entre neuronas. Este cálculo se ha sacado al método aparte sumDOW.

void CNeuron::calcHiddenGradients(const CArrayObj *&nextLayer)
  {
   double dow=sumDOW(nextLayer);
   gradient=dow*CNeuron::activationFunctionDerivative(outputVal);
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CNeuron::calcOutputGradients(double targetVals)
  {
   double delta=targetVals-outputVal;
   gradient=delta*CNeuron::activationFunctionDerivative(outputVal);
  }

A continuación, el gradiente se determina como el producto del error por la derivada de la función de activación.

Vamos a ver com más detalle el método para determinar el error de la neurona de la capa oculta sumDOW. En los parámetros, este método recibe el puuntero a la siguiente capa de neuronas. En el cuerpo del método, reseteamos primero la variable final sum, y después organizamos un ciclo de iteración por todas las neuronas de la capa siguiente y sumamos el producto de los gradientes de las neuronas por el coeficiente de peso de la conexión con ella.

double CNeuron::sumDOW(const CArrayObj *&nextLayer) const
  {
   double sum=0.0;
   int total=nextLayer.Total()-1;
   for(int n=0; n<total; n++)
     {
      СConnection *con=outputWeights.At(n);
      CNeuron *neuron=nextLayer.At(n);
      sum+=con.weight*neuron.gradient;
     }
   return sum;
  }

Después de terminar los trabajos preliminares descritos más arriba, solo queda crear el método para recalcular los coeficientes updateInputWeights. En nuestro módulo, la neurona guarda los coeficientes de peso originales, por eso, el método de actualización de los coeficientes de peso obtiene en los parámetros la capa de neuronas anterior.

void CNeuron::updateInputWeights(CArrayObj *&prevLayer)
  {
   int total=prevLayer.Total();
   for(int n=0; n<total && !IsStopped(); n++)
     {
      CNeuron *neuron= prevLayer.At(n);
      СConnection *con=neuron.outputWeights.At(m_myIndex);
      con.weight+=con.deltaWeight=eta*neuron.getOutputVal()*gradient + alpha*con.deltaWeight;
     }
  }

En el cuerpo del método se ha creado un ciclo de iteración por todas las neuronas de la capa anterior con corrección de todos los coeficientes de peso que influyen precisamente sobre la neurona actual.

Debemos prestar atención a que la corrección de los pesos se realiza aplicando dos coeficientes eta (amortigua la reacción a la desviación actual) y alpha (coeficiente de inercia). Este enfoque ayuda en cierta medida a promediar la influencia de varias iteraciones posteriores en el entrenamiento y descartar los datos de ruido.

4.3. La red neuronal

Después de crear la neurona artifical, tenemos que combinar los objetos creados en una sola entidad: la red neuronal. Debemos comprender que los objetos creados tienen que ser flexibles y permitir crear redes neuronales de diferentes configuraciones. Esto nos permitirá sacar partido al fruto de nuestro esfuerzo al resolver diferentes tareas.

Como ya hemos explicado anteriormente, la red neuronal consta de capas de neuronas. Por consiguiente, lo primero que haremos es combinar las neuronas en una capa. Para ello, crearemos la clase CLayer, heredando los métodos principales de la clase CArrayObj.

class CLayer: public CArrayObj
  {
private:
   uint              iOutputs;
public:
                     CLayer(const int outputs=0) { iOutputs=outpus; };
                    ~CLayer(void){};
   //---
   virtual bool      CreateElement(const int index);
   virtual int       Type(void) const { return(0x7779); }
   };

En los parámetros de inicialización de la clase CLayer, establecemos el número de elementos de la capa siguiente. Asimismo, reescribiremos dos métodos virtuales, CreateElement (creación de una nueva neurona de la capa) y Type (método de identificación del objeto).

Al crear una nueva neurona, indicamos su número ordinal en los parámetros del método. En el cuerpo del método, primero comprobamos que el índice obtenido sea válido. A continuación, comprobamos el tamaño de la matriz para guardar los punteros a los ejemplares de los objetos de la neurona, y, si fuera necesario, aumentamos el tamaño de la matriz. A continuación, creamos una nueva neurona. Si tenemos éxito al crear el nuevo ejemplar de neurona, establecemos su valor inicial, cambiamos su número de objetos en la matriz y salimos del método con el resultado true.

bool CLayer::CreateElement(const uint index)
  {
   if(index<0)
      return false;
//---
   if(m_data_max<index+1)
     {
      if(ArrayResize(m_data,index+10)<=0)
         return false;
      m_data_max=ArraySize(m_data)-1;
     }
//---
   CNeuron *neuron=new CNeuron(iOutputs,index);
   if(!CheckPointer(neuron)!=POINTER_INVALID)
      return false;
   neuron.setOutputVal((neuronNum%3)-1)   
//---
   m_data[index]=neuron;
   m_data_total=MathMax(m_data_total,index);
//---
   return (true);
  }

Con un enfoque análogo, creamos la clase CArrayLayer, destinada a guardar los punteros a las capas de nuestra red.

class CArrayLayer  :    public CArrayObj
  {
public:
                     CArrayLayer(void){};
                    ~CArrayLayer(void){};
   //---
   virtual bool      CreateElement(const uint neurons, const uint outputs);
   virtual int       Type(void) const { return(0x7780); }
   };

La diferencia con la clase anterior se puede ver en las especificaciones del método de creación del nuevo elemento de la matriz CreateElement. En los parámetros de este método transmitimos el número de neuronas en la capa creada y en la siguiente. En el cuerpo del método, comprobamos el número de neuronas en la capa creada. Si no existen neuronas en la capa creada, salimos del método con el valor false. A continuación, comprobamos si es necesario cambiar el tamaño de la matriz para guaradar los punteros. Después, pasamos directamente a la creación de los ejemplares de los objetos: creamos una nueva capa y organizamos un ciclo por la creación de neuronas. En cada paso, comprobamos el objeto creado. Si surge algún error, salimos del método con el valor false. Tras crear todos los elementos, guardamos en la matriz el puntero a la capa creada y salimos del método con el resultado true.

bool CArrayLayer::CreateElement(const uint neurons, const uint outputs)
  {
   if(neurons<=0)
      return false;
//---
   if(m_data_max<=m_data_total)
     {
      if(ArrayResize(m_data,m_data_total+10)<=0)
         return false;
      m_data_max=ArraySize(m_data)-1;
     }
//---
   CLayer *layer=new CLayer(outputs);
   if(!CheckPointer(layer)!=POINTER_INVALID)
      return false;
   for(uint i=0; i<neurons; i++)
      if(!layer.CreatElement(i))
         return false;
//---
   m_data[m_data_total]=layer;
   m_data_total++;
//---
   return (true);
  }

La creación de clases aparte para una capa y para la matriz de capas nos permite crear redes neuronales de diferentes configuraciones sin cambiar las propias clases. Hemos obtenido una entidad bastante flexible, que nos permite establecer desde fuera tanto el número de capas, como el número de neuronas en cada capa.

Finalmente, pasamos a la creación de la clase de nuestra red neuronal CNet.

class CNet
  {
public:
                     CNet(const CArrayInt *topology);
                    ~CNet(){};
   void              feedForward(const CArrayDouble *inputVals);
   void              backProp(const CArrayDouble *targetVals);
   void              getResults(CArrayDouble *&resultVals);
   double            getRecentAverageError() const { return recentAverageError; }
   bool              Save(const string file_name, double error, double undefine, double forecast, datetime time, bool common=true);
   bool              Load(const string file_name, double &error, double &undefine, double &forecast, datetime &time, bool common=true);
//---
   static double     recentAverageSmoothingFactor;
private:
   CArrayLayer       layers;
   double            recentAverageError;
  };

Gracias al trabajo realizado, la propia clase de la red neuronal contiene el mínimo posible de variables y métodos. En el código mostrado, solo hay dos variables estáticas para el cálculo y el guardado del error medio (recentAverageSmoothingFactor y recentAverageError) y un puntero a la matriz de capas de nuestra red neuronal layers.

Vamos a ver con más detalle los métodos de esta clase. En los parámetros del constructor de la clase, transmitimos el puntero a la matriz de datos de tipo int. El número de elementos en la matriz indica el número de capas en la red neuronal creada, mientras que cada elemento de la matriz contiene el número de neuronas en la capa correspondiente. De esta manera, hacemos de nuestra clase una clase universal, capaz de crear una red neuronal de prácticamente cualquier nivel de dificultad.

CNet::CNet(const CArrayInt *topology)
  {
   if(CheckPointer(topology)==POINTER_INVALID)
      return;
//---
   int numLayers=topology.Total();
   for(int layerNum=0; layerNum<numLayers; layerNum++) 
     {
      uint numOutputs=(layerNum==numLayers-1 ? 0 : topology.At(layerNum+1));
      if(!layers.CreateElement(topology.At(layerNum), numOutputs))
         return;
     }
  }

En el cuerpo del método, comprobamos si el puntero transmitido es válido y organizamos un ciclo por la creación de las capas de la red neuronal. Debemos decir que para la capa de neuronas de salida, se indica un número de conexiones de salida igual a cero.

El método feedForward ha sido pensado para calcular los valores de la red neuronal. En los parámetros, el método obtiene la matriz de valores de entrada sobre cuya base se calcularán los valores resultantes de la red neuronal.

void CNet::feedForward(const CArrayDouble *inputVals)
  {
   if(CheckPointer(inputVals)==POINTER_INVALID)
      return;
//---
   CLayer *Layer=layers.At(0);
   if(CheckPointer(Layer)==POINTER_INVALID)
     {
      return;
     }
   int total=inputVals.Total();
   if(total!=Layer.Total()-1)
      return;
//---
   for(int i=0; i<total && !IsStopped(); i++) 
     {
      CNeuron *neuron=Layer.At(i);
      neuron.setOutputVal(inputVals.At(i));
     }
//---
   total=layers.Total();
   for(int layerNum=1; layerNum<total && !IsStopped(); layerNum++) 
     {
      CArrayObj *prevLayer = layers.At(layerNum - 1);
      CArrayObj *currLayer = layers.At(layerNum);
      int t=currLayer.Total()-1;
      for(int n=0; n<t && !IsStopped(); n++) 
        {
         CNeuron *neuron=currLayer.At(n);
         neuron.feedForward(prevLayer);
        }
     }
  }

En el cuerpo del método, comprobamos si el puntero obtenido y la capa cero de nuestra red son válidos. A continuación, establecemos los datos originales como valores resultantes de las neuronas de la capa cero y organizamos un ciclo doble con recálculo por etapas de los valores resultantes de las neuronas por toda la red neuronal desde la primera capa oculta hasta las capas de salida.

Para obtener el propio resultado, tenemos el método getResults, en el que se organiza un ciclo de recopilación de los resultados desde las neuronas de la capa de salida.

void CNet::getResults(CArrayDouble *&resultVals)
  {
   if(CheckPointer(resultVals)==POINTER_INVALID)
     {
      resultVals=new CArrayDouble();
     }
   resultVals.Clear();
   CArrayObj *Layer=layers.At(layers.Total()-1);
   if(CheckPointer(Layer)==POINTER_INVALID)
     {
      return;
     }
   int total=Layer.Total()-1;
   for(int n=0; n<total; n++)
     {
      CNeuron *neuron=Layer.At(n);
      resultVals.Add(neuron.getOutputVal());
     }
  }

El proceso de entrenamiento de la red neuronal está construido en el método backProp. El método obtiene en los parámetros la matriz de los valores patrón. En el cuerpo del método, comprobamos si la matriz obtenida es válida y calculamos el error medio cuadrático de la capa resultante. A continuación, recalculamos los gradientes de las neuronas en todas las capas. Después de ello, actualizamos en el ciclo del método los coeficientes de peso de las conexiones entre neuronas usando como base los gradientes calculados anteriormente.

void CNet::backProp(const CArrayDouble *targetVals)
  {
   if(CheckPointer(targetVals)==POINTER_INVALID)
      return;
   CArrayObj *outputLayer=layers.At(layers.Total()-1);
   if(CheckPointer(outputLayer)==POINTER_INVALID)
      return;
//---
   double error=0.0;
   int total=outputLayer.Total()-1;
   for(int n=0; n<total && !IsStopped(); n++)
     {
      CNeuron *neuron=outputLayer.At(n);
      double delta=targetVals[n]-neuron.getOutputVal();
      error+=delta*delta;
     }
   error/= total;
   error = sqrt(error);

   recentAverageError+=(error-recentAverageError)/recentAverageSmoothingFactor;
//---
   for(int n=0; n<total && !IsStopped(); n++)
     {
      CNeuron *neuron=outputLayer.At(n);
      neuron.calcOutputGradients(targetVals.At(n));
     }
//---
   for(int layerNum=layers.Total()-2; layerNum>0; layerNum--)
     {
      CArrayObj *hiddenLayer=layers.At(layerNum);
      CArrayObj *nextLayer=layers.At(layerNum+1);
      total=hiddenLayer.Total();
      for(int n=0; n<total && !IsStopped();++n)
        {
         CNeuron *neuron=hiddenLayer.At(n);
         neuron.calcHiddenGradients(nextLayer);
        }
     }
//---
   for(int layerNum=layers.Total()-1; layerNum>0; layerNum--)
     {
      CArrayObj *layer=layers.At(layerNum);
      CArrayObj *prevLayer=layers.At(layerNum-1);
      total=layer.Total()-1;
      for(int n=0; n<total && !IsStopped(); n++)
        {
         CNeuron *neuron=layer.At(n);
         neuron.updateInputWeights(prevLayer);
        }
     }
  }

Para reentrenar nuestra red neuronal al reiniciar el programa, vamos a crear dos métodos: uno para guardar los datos en el archivo local Save y otro para cargar posteriormente los datos desde el archivo Load.

El lector podrá leer con más detalle el código de todos los métodos de la clase en los anexos.

Conclusión

En el presente artículo, hemos tratado de mostrar cómo se puede crear una red neuronal para nuestras propias necesidades en condiciones domésticas. Claro que solo hemos visto la punta del iceberg. En el artículo solo hemos analizado una de las posibles variantes: el perceptrón propuesto por  Frank Rosenblatt en el lejano 1957. Desde entonces, han pasado más de 60 años y han aparecido otros modelos. Pero este modelo sigue siendo útil y ofrece buenos resultados, como podrá comprobar el lector por sí mismo. Recomendamos a aquellos que quieran profundizar en el tema de la inteligencia artificial que recurran a la bibliografía correspondiente, dado que describir el amplio trabajo de los científicos, incluso en una serie completa de artículos, resulta casi imposible.

Enlaces

1. Wikipedia
2. Perceptrón

Programas usados en el artículo:

#	Nombre	Tipo	Descripción
1	NeuroNet.mqh	Biblioteca de clase	Biblioteca de clases para crear la red neuronal (perceptrón)