Redes neuronales en el trading: Conjunto de agentes con mecanismos de atención (MASAAT)

Introducción

La gestión de portafolios de instrumentos financieros supone un aspecto clave de las decisiones de inversión, cuyo objetivo consiste en aumentar la rentabilidad minimizando los riesgos mediante la asignación dinámica de capital entre activos. La alta volatilidad de los mercados financieros, donde los precios de los activos dependen de muchos factores, dificulta la gestión de un portafolio óptimo que cumpla dos objetivos contrapuestos: maximizar los beneficios y minimizar los riesgos. Los modelos financieros tradicionales desarrollados con diversos principios de inversión a menudo resultan eficaces en un solo mercado y pueden fallar en condiciones de mercado dinámicas y complejas.

Recientemente, el énfasis se ha desplazado hacia la aplicación de métodos de aprendizaje automático al análisis de series de precios no estacionarias. Entre ellas destacan las estrategias de aprendizaje profundo y aprendizaje por refuerzo, que han demostrado un éxito significativo en las finanzas computacionales. Sin embargo, los datos de precios en los mercados financieros con frecuencia representan series temporales ruidosas, lo que dificulta la extracción de información que indique tendencias futuras.

Una de las soluciones a estos problemas se presenta en el artículo "Developing an attention-based ensemble learning framework for financial portfolio optimisation". Sus autores propusieron una innovadora estructura comercial adaptativa con mecanismos de atención integrados y análisis de series temporales (Multi-Agent and Self-Adaptive portfolio optimisation framework integrated with Attention mechanisms and Time series — MASAAT). Dentro del framework presentado se crean múltiples agentes para monitorear y analizar los cambios direccionales en los precios de los activos en varios niveles de detalle, con el objetivo de revisar cuidadosamente los portafolios para equilibrar los rendimientos generales y los riesgos de inversión en mercados financieros altamente volátiles.

Al usar filtros de movimiento direccional que utilizan diferentes umbrales para capturar cambios de precios significativos, los agentes primero extraen características de tendencia de las series temporales de los precios regulares, intentando mantenerse al tanto de las transiciones del estado del mercado desde diferentes perspectivas. Este enfoque ofrece una nueva forma de generación de tokens en una secuencia, de modo que el módulo de análisis transversal basado en la atención (CSA) y el módulo de análisis temporal (TA) de los agentes construidos dentro del framework propuesto puedan captar eficazmente las correlaciones entre activos y las dependencias entre puntos temporales. Específicamente, al reconstruir mapas de características, el token de secuencia en el módulo CSA se basa en las características de los activos individuales, con el objetivo de optimizar la integración de puntajes de atención entre los activos, mientras que el token de secuencia en el módulo TA se basa en características de puntos temporales individuales, tratando de extraer la relevancia entre los puntos temporales actuales y anteriores.

Además, la información sobre las dependencias de los activos y los puntos temporales se combina en un bloque de atención espaciotemporal. Con una clara separación de las funcionalidades entre los módulos CSA y TA,, los agentes tienen más información para analizar continuamente las tendencias de los activos y sugerir portafolios adaptados a sus perspectivas específicas. Finalmente, las portafolios propuestos proporcionados por diferentes agentes se combinan en un nuevo portafolio de conjunto para responder rápidamente a las condiciones actuales del mercado. Incluso si un solo agente no logra evaluar las tendencias del mercado y genera ofertas desplazadas, el framework MASAAT propuesto integrado con múltiples agentes aún puede ajustar de forma adaptativa el portafolio final para reducir los efectos negativos.

El algoritmo MASAAT

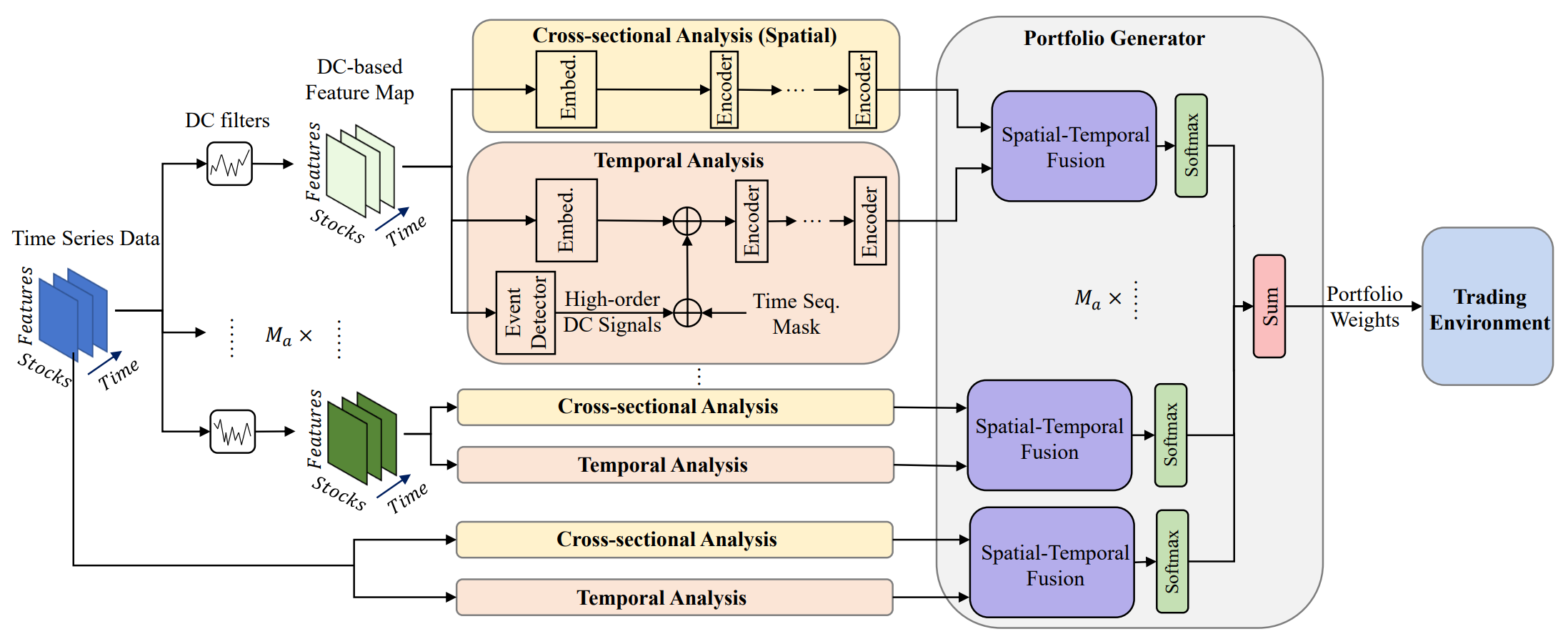
El framework MASAAT aplica múltiples filtros de detección de movimiento direccional respecto a los diferentes umbrales para capturar cambios significativos en los precios de los activos de campos receptivos multiescala para analizar el posible impacto en los futuros movimientos de los precios. En particular, los campos receptivos representan diferentes niveles de fluctuaciones de los precios de los activos, lo cual permite a los agentes percibir intuitivamente los estados dinámicos del mercado a través de diferentes filtros. Además, al reconstruir las funciones de movimiento direccional orientado a la actividad en el módulo CSA y los puntos de tendencia orientados al tiempo en el módulo TA como tokens de secuencia, el esquema multiagente MASAAT puede recopilar simultáneamente información espacial y temporal en diferentes grados de cambio de precios. Esto ayuda a determinar la dirección y la escala de las tendencias futuras. De forma similar, los datos de origen de las series de precios se transformarán directamente en características de precios orientadas a activos y puntos temporales, con la posterior extracción de información transversal y específica del tiempo de los módulos CSA y TA.

Merece la pena señalar que los módulos CSA y TA se basan en codificadores con mecanismos de Self-Attention, en los que los puntajes de atención se calculan sobre una secuencia global en todos los tokens para que la medida de similitud de todos los activos se pueda calcular de manera justa, mientras que las redes neuronales basadas en la convolución resultan muy sensibles a la posición relativa de los activos en los mapas de características y se centran en las regiones locales según el tamaño del núcleo de convolución. Por otra parte, gracias a los puntajes de atención que indican la similitud de los tokens, las señales comerciales generadas por el framework propuesto pueden ser más explicables. Posteriormente, utilizando el mecanismo de atención en el bloque espacio-temporal para construir un mapeo entre la secuencia de activos y la secuencia de puntos temporales históricos, los agentes comerciales generan incorporaciones que representan los puntajes de atención de cada activo en cada punto temporal dentro de una ventana de observación dada, y luego proponen sus opciones de portafolio de inversión. El generador de portafolio añade todas las propuestas de diferentes agentes para crear un nuevo portafolio revisado que se adapte al entorno financiero actual.

Digamos que N es el número de activos en el portafolio, M es el número de características de observación de los mercados financieros y Ma es el número de agentes comerciales. Para una profundidad dada de la historia analizada, el agente primero observa las características del precio 𝐏 ∈ RN×M×Tw durante el periodo de observación Tw. Luego, las funciones basadas en tendencias 𝐏DC={𝐏DC,1, 𝐏DC,2,…,𝐏DC,𝐌a} ∈ RMa, 𝐏DC,i ∈ RN×M×Tw se obtienen usando filtros de movimiento direccional. Como hemos mencionado antes, el método 𝐏DC,i se transformará en 𝐏DC,i,CSA ∈ RN×MTw para el módulo CSA y 𝐏DC,i,TA ∈ RTw×NM para el módulo ТА, seguido de un análisis de dependencia en el codificador del Transformer. De manera similar, la serie de precios original 𝐏 se transformará en 𝐏CSA ∈ RN×MTw y 𝐏TA ∈ RTw×NM.

Después de analizar las dependencias entre tokens en la secuencia proporcionada, los módulos CSA y TA retornarán las incorporaciones orientadas de los activos 𝐎CSA ∈ RN×D y los puntos temporales 𝐎TA ∈ RTw×D, donde D será el tamaño del vector de una incorporación. Posteriormente, estas incorporaciones se combinarán para crear un nuevo portafolio, y luego se integrarán aún más con los resultados de otros agentes para obtener el vector final de dependencias W𝐭 y ajustar el portafolio.

Tras realizar operaciones comerciales, la recompensa rt se recopilará y almacenará en el búfer de reproducción de experiencias Ď, junto con W𝐭, 𝐏 y 𝐏DC. Además, la política del actor π se actualizará iterativamente a medida que explore el búfer de reproducción de experiencias Ď utilizando el método de gradiente de políticas.

Como los rendimientos más altos suelen venir acompañados de mayores riesgos, la diversificación de los riesgos de inversión es una tarea importante pero compleja en la que los tráders deben asignar los pesos correspondientes a activos de diferente naturaleza para la cobertura. Por ello, estudiar constantemente las correlaciones entre activos ayudará a los agentes a gestionar mejor los riesgos en condiciones de alta turbulencia.

Las funciones de tendencia originales se transformarán para generar los tokens de secuencia correspondientes antes de aprender las correlaciones entre activos utilizando codificadores basados en Self-Attention. El vector de atención optimizado medirá la correlación entre dos activos diferentes, en la que dos activos con vectores de atención similares implican propiedades más relevantes.

Además de investigar la correlación entre dos activos, el framework MASAAT intenta investigar la relevancia de los puntos temporales dentro de un periodo de observación dado para predecir la tendencia de precios en diferentes niveles. El análisis temporal analiza un punto temporal como un token en una secuencia para estudiar las correlaciones entre puntos temporales utilizando los codificadores del Transformer. Como consecuencia, los patrones de tendencia subyacentes de dos puntos temporales se considerarán similares cuando sus vectores de atención estén cerca.

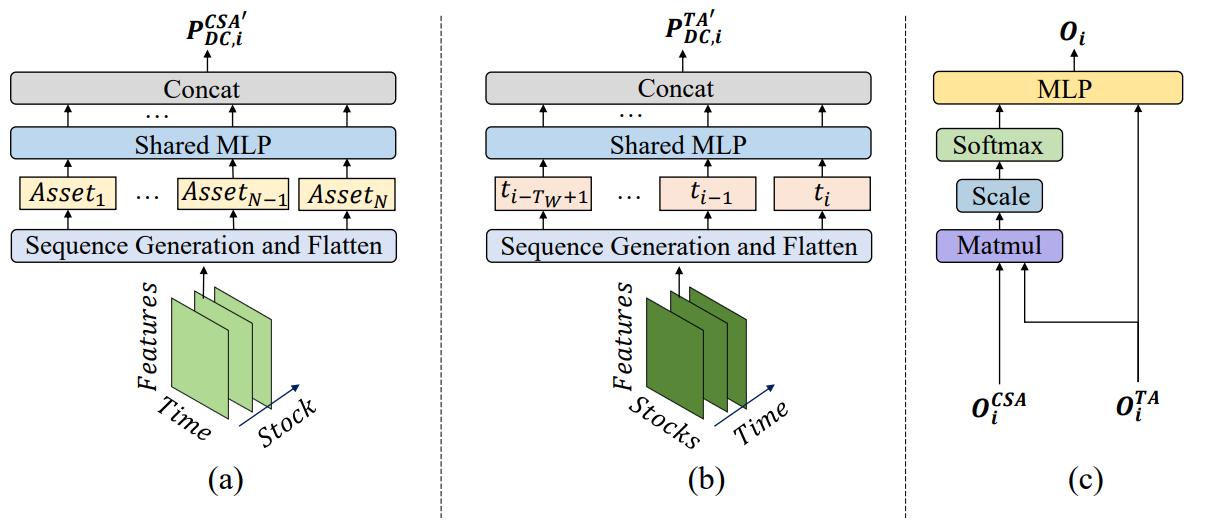
Después de recopilar información de los módulos CSA y TA, los agentes MASAAT combinan las puntuaciones de activos y puntos temporales utilizando un mecanismo de atención, intentando obtener las puntuaciones de atención de cada activo para cada punto temporal durante el periodo de observación. El resultado, construido como un portafolio propuesto de cada agente, se puede representar como:

donde 𝐕i y bi son los parámetros de MLP estudiados.

Los resultados de cada agente comercial, referentes a varios niveles de detalle de los cambios de precios, se combinarán para crear un nuevo portafolio para responder al mercado financiero actual. En comparación con el portafolio obtenido de un solo agente, los agentes múltiples MASAAT ofrecen varios portafolios potenciales según las observaciones de las características del mercado desde diferentes perspectivas. Esto puede ampliar las capacidades del sistema para gestionar diferentes mercados financieros, especialmente cuando el mercado resulta muy volátil.

A continuación le presentamos la visualización del autor del framework MASAAT.

Implementación con MQL5

Tras revisar los aspectos teóricos del framework MASAAT propuesto, vamos a pasar a la parte práctica de nuestro artículo, en la que consideraremos una opción para implementar nuestra propia visión de los enfoques propuestos utilizando MQL5. Como habrá notado, el MASAAT es un framework integral. Y para dividir claramente la funcionalidad entre bloques individuales, crearemos una estructura de bloques del framework en forma de objetos separados, cada uno de los cuales realizará parte de la funcionalidad de MASAAT.

Comenzaremos nuestro trabajo construyendo un mecanismo para determinar las tendencias. Cabe decir que la determinación de tendencias locales se puede manejar perfectamente con una capa de representación lineal por partes de una serie temporal. Pero hay un matiz a considerar: el objeto que construimos anteriormente solo puede desempeñar el papel de un agente. Y para implementar el framework MASAAT, necesitaremos proporcionarle al usuario una funcionalidad flexible para crear modelos con diferentes números de agentes.

Obviamente, podemos crear un array dinámico con punteros a varios objetos de la representación lineal por partes de la serie temporal analizada con diferentes valores umbral de los cambios de características almacenados en ella. Pero en esta versión terminaran funcionando de forma secuencial, y esta no es la mejor opción. Por lo tanto, crearemos un nuevo objeto en el que organizaremos el funcionamiento paralelo de los agentes de detección de tendencias. Pero primero necesitaremos crear los kernels correspondientes en el lado del programa OpenCL.

Programas complementarios de OpenCL

Al intentar modernizar los kernels existentes de representación lineal por partes de series temporales, nos enfrentamos a la necesidad de reemplazar el número discreto del valor umbral del cambio de una característica con un vector de valores que contenga niveles de umbral para cada agente. Un cambio de este tipo requeriría no solo la modificación del algoritmo del kernel, sino que también provocaría una revisión completa de la estructura de los objetos que trabajan con él. Por consiguiente, hemos decidido crear nuevos kernels de pasada directa e inversa; tomaremos prestado parte de su algoritmo de los ya existentes.

Para organizar la pasada directa, hemos creado el kernel PLRMultiAgents. En los parámetros del kernel obtendremos los cuatro punteros a los búferes de datos. De estos, dos búferes contienen los valores iniciales en forma de series temporales analizadas, así como los valores umbral de los cambios de características para cada agente. En los otros dos anotaremos los resultados del análisis y las banderas que indican la presencia de un extremo.

__kernel void PLRMultiAgents(__global const float *inputs,
                             __global float *outputs,
                             __global int *isttp,
                             const int transpose,
                             __global const float *min_step
                            )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);
   const size_t a = get_global_id(2);
   const size_t agents = get_global_size(2);

Planeamos implementar este kernel en un espacio de tareas tridimensional. En la primera dimensión indicaremos el tamaño de la secuencia que estamos analizando. La segunda dimensión determinará el número de filas unitarias en la secuencia multimodal, mientras que el último se corresponderá con el número de agentes. En el cuerpo del kernel, identificaremos directamente el flujo actual en todas las dimensiones del espacio de tareas. Después de esto, determinaremos el desplazamiento en los búferes de datos.

//--- constants
   const int shift_in = ((bool)transpose ? (i * variables + v) : (v * lenth + i));
   const int step_in = ((bool)transpose ? variables : 1);
   const int shift_ag = a * lenth * variables;

Aquí vale la pena señalar que todos los agentes analizarán una secuencia multimodal. Por lo tanto, el ID del agente solo influirá en el desplazamiento en los búferes de resultados y los valores de desviación del umbral de precio.

Después de un pequeño trabajo preparatorio, pasaremos a la búsqueda de extremos. Cada flujo determinará la presencia de un punto de reversión de tendencia en la posición del elemento actual. Los puntos extremos de la serie temporal analizada recibirán automáticamente el estatus de punto de reversión de tendencia, ya que son a priori los puntos extremos del segmento.

//--- look for ttp
   float value = IsNaNOrInf(inputs[shift_in], 0);
   bool bttp = false;
   if(i == 0 || i == lenth - 1)
      bttp = true;

En otros casos, primero buscaremos la desviación más cercana de los valores de la serie analizada por el valor mínimo requerido al elemento actual en la secuencia unitaria analizada. En el proceso, mantendremos los valores mínimo y máximo dentro del rango probado.

   else
     {
      float prev = value;
      int prev_pos = i;
      float max_v = value;
      float max_pos = i;
      float min_v = value;
      float min_pos = i;
      while(fmax(fabs(prev - max_v), fabs(prev - min_v)) < min_step[a] && prev_pos > 0)
        {
         prev_pos--;
         prev = IsNaNOrInf(inputs[shift_in - (i - prev_pos) * step_in], 0);
         if(prev >= max_v && (prev - min_v) < min_step[a])
           {
            max_v = prev;
            max_pos = prev_pos;
           }
         if(prev <= min_v && (max_v - prev) < min_step[a])
           {
            min_v = prev;
            min_pos = prev_pos;
           }
        }

Luego, de forma similar, buscaremos el elemento subsiguiente más cercano con la desviación mínima requerida.

      float next = value;
      int next_pos = i;
      while(fmax(fabs(next - max_v), fabs(next - min_v)) < min_step[a] && next_pos < (lenth - 1))
        {
         next_pos++;
         next = IsNaNOrInf(inputs[shift_in + (next_pos - i) * step_in], 0);
         if(next > max_v && (next - min_v) < min_step[a])
           {
            max_v = next;
            max_pos = next_pos;
           }
         if(next < min_v && (max_v - next) < min_step[a])
           {
            min_v = next;
            min_pos = next_pos;
           }
        }

Y luego comprobaremos la presencia de un extremo en la posición analizada.

      if(
         (value >= prev && value > next) ||
         (value > prev && value == next) ||
         (value <= prev && value < next) ||
         (value < prev && value == next)
      )
         if(max_pos == i || min_pos == i)
            bttp = true;
     }

Tenga en cuenta que durante la búsqueda de elementos con la desviación mínima requerida, hemos recopilado un cierto pasillo de valores de varios elementos de la secuencia que pueden formar una cierta meseta del extremo. Por consiguiente, un elemento recibirá una bandera de punto de reversión de tendencia solo si es un extremo en dicho pasillo. Si hay varios elementos con el mismo valor, asignaremos la bandera de extremo al primero de ellos.

Luego guardaremos la bandera resultante y eliminaremos el búfer de resultados. Al mismo tiempo, sincronizaremos los flujos del grupo de trabajo.

   isttp[shift_in + shift_ag] = (int)bttp;
   outputs[shift_in + shift_ag] = 0;
   barrier(CLK_LOCAL_MEM_FENCE);

Las operaciones posteriores se realizarán únicamente mediante flujos en los que esté definido el punto de reversión de tendencia. Las demás simplemente no cumplen las condiciones establecidas y prácticamente finalizan las operaciones.

Primero determinaremos la posición del extremo actual. Para ello, contaremos el número de extremos según las banderas guardadas antes de la posición analizada y guardaremos prudentemente la posición del extremo anterior en el búfer de datos de origen en una variable local.

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int prev_ttp = 0;
   if(bttp)
     {
      pos = 0;
      for(int p = 0; p < i; p++)
        {
         int current_in = ((bool)transpose ? (p * variables + v) : (v * lenth + p));
         if((bool)isttp[current_in + shift_ag])
           {
            pos++;
            prev_ttp = p;
            prev_in = current_in;
           }
        }
     }

Luego determinaremos los parámetros de la aproximación lineal de la tendencia del segmento actual.

//--- cacl tendency
   if(pos > 0 && pos < (lenth / 3))
     {
      float sum_x = 0;
      float sum_y = 0;
      float sum_xy = 0;
      float sum_xx = 0;
      int dist = i - prev_ttp;
      for(int p = 0; p < dist; p++)
        {
         float x = (float)(p);
         float y = IsNaNOrInf(inputs[prev_in + p * step_in], 0);
         sum_x += x;
         sum_y += y;
         sum_xy += x * y;
         sum_xx += x * x;
        }
      float slope = IsNaNOrInf((dist * sum_xy - sum_x * sum_y) / (dist > 1 ? (dist * sum_xx - sum_x * sum_x) : 1), 0);
      float intercept = IsNaNOrInf((sum_y - slope * sum_x) / dist, 0);

Después de esto, guardaremos los valores obtenidos en el búfer de resultados.

      int shift_out = ((bool)transpose ? ((pos - 1) * 3 * variables + v) : (v * lenth + (pos - 1) * 3)) + shift_ag;
      outputs[shift_out] = slope;
      outputs[shift_out + step_in] = intercept;
      outputs[shift_out + 2 * step_in] = ((float)dist) / lenth;
     }

Permítame recordarle que cada segmento obtenido se caracterizará por 3 parámetros:

• slope — ángulo de inclinación de la línea de tendencia;
• intercept — desplazamiento de la línea de tendencia en el subespacio de los datos de origen;
• dist — longitud del segmento.

El almacenamiento de la longitud de la secuencia como un valor entero no es la mejor opción en este caso. Al fin y al cabo, resulta deseable disponer de un formato de representación de datos normalizado para que el modelo funcione de forma eficaz. Por ello, convertiremos el tamaño del segmento entero en una fracción de la longitud de la secuencia unitaria que estamos analizando. Para ello, dividiremos el número de elementos del segmento por el número de elementos de toda la secuencia de la serie temporal unitaria. Y para evitar caer en la "trampa de las operaciones con enteros", primero convertiremos el número de elementos del segmento del tipo int al tipo float.

Además, crearemos una rama de operaciones aparte para el último segmento. La cuestión es que en esta etapa no sabemos el número de segmentos que se formarán en un momento concreto. Hipotéticamente, con fluctuaciones significativas en los elementos de una serie temporal y un valor umbral pequeño, existe la posibilidad de obtener puntos de reversión de tendencia en cada elemento de la serie temporal. Resulta poco probable que se produzca este giro de los acontecimientos, pero no nos gustaría que el volumen de datos aumentara. Al mismo tiempo, tampoco querríamos perder datos.

Por lo tanto, partiremos de un conocimiento a priori de la representación de series temporales en MQL5 y una comprensión de la estructura de los datos analizados: los últimos datos en el tiempo estarán al comienzo de nuestra serie temporal. A estos les prestaremos más atención. Los datos al final de la secuencia analizada tienen una mayor profundidad histórica y es probable que ejerzan menos influencia en los eventos posteriores. Aunque no excluiremos dichas dependencias.

Como resultado, para registrar los resultados del trabajo de cada agente, usaremos un tamaño de búfer de datos similar al tamaño del tensor de los valores de la serie temporal original. Esto nos permite escribir un número de segmentos 3 veces menor que la longitud de la secuencia (3 elementos para escribir 1 segmento). Esperamos que este volumen resulte más que suficiente. Sin embargo, iremos a lo seguro y, si hay más segmentos, para evitar la pérdida de datos, combinaremos los datos de los últimos segmentos en uno solo.

   else
     {
      if(pos == (lenth / 3))
        {
         float sum_x = 0;
         float sum_y = 0;
         float sum_xy = 0;
         float sum_xx = 0;
         int dist = lenth - prev_ttp;
         for(int p = 0; p < dist; p++)
           {
            float x = (float)(p);
            float y = IsNaNOrInf(inputs[prev_in + p * step_in], 0);
            sum_x += x;
            sum_y += y;
            sum_xy += x * y;
            sum_xx += x * x;
           }
         float slope = IsNaNOrInf((dist * sum_xy - sum_x * sum_y) / (dist > 1 ? (dist * sum_xx - sum_x * sum_x) : 1),0);
         float intercept = IsNaNOrInf((sum_y - slope * sum_x) / dist, 0);
         int shift_out = ((bool)transpose ? ((pos - 1) * 3 * variables + v) : (v * lenth + (pos - 1) * 3)) + shift_ag;
         outputs[shift_out] = slope;
         outputs[shift_out + step_in] = intercept;
         outputs[shift_out + 2 * step_in] = IsNaNOrInf((float)dist / lenth, 0);
        }
     }
  }

En la mayoría de los casos, sin embargo, esperaremos menos segmentos, y entonces los últimos elementos de nuestro búfer de resultados se rellenarán con valores cero.

Como puede ver, en el algoritmo de pasada directa no utilizamos parámetros entrenables. Por lo tanto, el algoritmo completo de pasada inversa se reducirá a la distribución del gradiente de error, que implementaremos en el kernel PLRMultiAgentsGradient.

Resulta importante recordar aquí que todos los agentes analizarán la misma serie temporal. Por consiguiente, a nivel de datos de origen necesitaremos recopilar el gradiente de error de todos los agentes. Esperamos usar un número relativamente pequeño de agentes. Por ello, no complicaremos demasiado la lógica del kernel. En lugar de ello, hemos transferido casi por completo el algoritmo de kernel de distribución del gradiente de error de un solo agente implementado previamente. Solo agregaremos un parámetro para especificar el número de agentes y en el cuerpo del kernel organizaremos un ciclo para recopilar los gradientes de error de todos los agentes. Le sugiero dejar este kernel para el estudio independiente. Encontrará el código completo del programa OpenCL en el archivo adjunto.

El objeto de mecanismo de detección de tendencias

Una vez hemos completado el trabajo en el lado OpenCL del programa, pasaremos a nuestra biblioteca principal e implementaremos el algoritmo de detección de tendencias de múltiples agentes en el objeto CNeuronPLRMultiAgentsOCL. Como habrá podido observar, prácticamente estamos complementando el objeto de representación lineal por partes de una serie temporal. Por eso lo hemos elegido como clase padre. Más abajo resumiremos la estructura del nuevo objeto.

class CNeuronPLRMultiAgentsOCL  :  public CNeuronPLROCL
  {
protected:
   int               iAgents;
   CBufferFloat      cMinDistance;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);

public:
                     CNeuronPLRMultiAgentsOCL(void)  : iAgents(1) {};
                    ~CNeuronPLRMultiAgentsOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window_in, uint units_count, bool transpose,
                          vector<float> &min_distance,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronPLRMultiAgentsOCL;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

En la nueva clase, declararemos una constante para el número de agentes utilizados (iAgents) y un búfer para almacenar los valores umbral de los cambios de características en la serie temporal analizada (cMinDistance).

El uso de una declaración estática de objetos internos nos permitirá dejar el constructor y el destructor de la clase vacíos, mientras que la inicialización de todos los objetos declarados y heredados se realizará en el método Init.

bool CNeuronPLRMultiAgentsOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                    uint window_in, uint units_count, bool transpose,
                                    vector<float> &min_distance,
                                    ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   iAgents = (int)min_distance.Size();
   if(iAgents <= 0)
      return false;

Tenga en cuenta que en los parámetros del método solo pasaremos el vector de valores umbral. En este caso no indicaremos el número de agentes utilizados. Determinaremos su número según el tamaño del vector resultante de valores umbral. De esta forma reduciremos el número de parámetros externos del método y garantizaremos que el valor del parámetro y la longitud del búfer coincidan.

En el cuerpo del método, después de guardar el número de agentes en una variable interna y verificar la corrección del valor (se necesita al menos un agente para el funcionamiento normal), llamaremos al método de inicialización del objeto básico, en cuyo cuerpo se llevará a cabo la inicialización de las interfaces principales.

   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_in * units_count * iAgents, optimization_type, batch))
      return false;

Tenga en cuenta que estamos utilizando el método de inicialización del objeto básico, no la clase padre directa. Esto se debe a que aumentaremos el tamaño del búfer de resultados proporcionalmente al número de agentes. Sin embargo, ahora tendremos que inicializar también los objetos heredados.

Primero, guardaremos los valores de los parámetros recibidos en variables heredadas.

   iVariables = (int)window_in;
   iCount = (int)units_count;
   bTranspose = transpose;

Y luego inicializaremos el búfer de banderas de presencia de extremos.

   icIsTTP = OpenCL.AddBuffer(sizeof(int) * Neurons(), CL_MEM_READ_WRITE);
   if(icIsTTP < 0)
      return false;

Tenga en cuenta que los valores del búfer de banderas de extremos se redefinen después de cada pase directa, mientras que el tamaño de este búfer será igual al tamaño de los resultados. Obviamente, no necesitaremos almacenar los valores del búfer especificado, por lo que lo crearemos solo en la memoria de contexto OpenCL. Aquí solo guardaremos un puntero al búfer creado.

A continuación inicializaremos el búfer de umbral.

   if(!cMinDistance.AssignArray(min_distance) ||
      !cMinDistance.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Después de eso, finalizaremos el trabajo del método pasando el resultado lógico de las operaciones al programa que realiza la llamada.

Además, hemos redefinido los métodos de pasada directa e inversa. Sin embargo, estos métodos solo llamarán a los kernels mencionados anteriormente. El algoritmo de los métodos no presenta ninguna dificultad, por lo que le sugiero que lo estudie por su cuenta.

Con esto concluirá nuestro trabajo con el objeto de detección de tendencias locales multiagente CNeuronPLRMultiAgentsOCL. Podrá ver el código completo de sus métodos en el archivo adjunto.

Módulo atención transversal de activos (CSA)

Después de obtener una representación lineal por partes y en múltiples escalas de la serie temporal analizada, cada agente tomará su propia escala y realizará su análisis exhaustivo. El framework MASAAT permite el análisis de series temporales en dos proyecciones: activos y puntos temporales.

El análisis de series temporales en el framework MASAAT será procesado por el módulo de atención transversal de activos, que implementaremos como un objeto CNeuronCrossSectionalAnalysis. Pero antes de comenzar con la implementación, hablaremos un poco sobre el algoritmo de construcción del módulo CSA.

Como se indica en la descripción teórica del framework MASAAT, en el módulo CSA se utilizará un codificador con un mecanismo de Self-Attention para analizar las dependencias entre activos. Nuestra biblioteca contiene bastantes implementaciones de estos codificadores. Sin embargo, existe un matiz a considerar en el funcionamiento en paralelo de varios agentes, cuando cada agente analiza las dependencias solo en un área separada de los datos de origen. Pero si lo pensamos bien, podemos encontrar uno como este.

Por ejemplo, el bloque de análisis independiente de canales individuales CNeuronMVMHAttentionMLKV, que implementamos como parte del trabajo en el framework InjectTST. No es una mala solución. Pero en su forma pura, este bloque funciona en un plano ligeramente distinto: puede analizar dependencias en diferentes escalas de un activo, y necesitamos encontrar dependencias entre activos dentro de una escala. Por lo tanto, antes de introducir los datos de origen en el bloque de análisis independiente de canales individuales, necesitaremos transponer el tensor tridimensional analizado a lo largo de las dos primeras dimensiones. Por cierto, nuestra biblioteca también tiene una capa de transposición de este tipo (CNeuronTransposeRCDOCL).

Parece que ya nos hemos decidido con el codificador. Sin embargo, antes de introducir datos en el codificador, deberemos crear incorporaciones de trayectoria para cada activo. Los autores del framework proponen usar para esto un MLP cuyos parámetros sean los mismos para todos los activos. Al igual que antes en casos similares, utilizaremos capas convolucionales. Siendo más concretos, añadiremos solo una capa convolucional con GELU como función de activación. Y el papel de la segunda capa de MLP para generar las incorporaciones lo realizará la capa interna del codificador, responsable de la formación de las entidades Query, Key y Value.

Entonces, ya hemos decidido la estructura de nuestro módulo CSA. En él usaremos sucesivamente una capa de transposición de datos, una capa de incorporación convolucional y un bloque de análisis de canal independiente. Pero vamos a pensar un poco: ¿quizás sería mejor poner primero una capa convolucional y luego transponer los datos? El resultado de las operaciones no cambiará. La pregunta se relaciona más con la eficacia de la solución.

En la entrada del módulo CSA introduciremos una determinada representación de la serie temporal de movimientos de precios de los activos analizados. Por consiguiente, a medida que aumente la profundidad de la historia analizada, también aumentará el volumen de datos de origen. Y como usaremos una representación lineal por partes de la serie temporal, esperamos que una parte significativa de los datos originales se llene con valores cero. Esto nos permitirá usar incorporaciones mucho más pequeñas. Esto significa que al instalar una capa de transposición después de la capa de incorporación convolucional, podremos reducir significativamente el tamaño del tensor transpuesto, lo cual reducirá el número de operaciones y aumentará la eficiencia del modelo.

Una vez definidos los principales aspectos clave de la implementación, podremos pasar a trabajar en la construcción de un nuevo objeto CNeuronCrossSectionalAnalysis, cuya estructura se presenta a continuación.

class CNeuronCrossSectionalAnalysis :  public CNeuronMVMHAttentionMLKV
  {
protected:
   CNeuronConvOCL          cEmbeding;
   CNeuronTransposeRCDOCL  cTransposeRCD;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronCrossSectionalAnalysis(void) {};
                    ~CNeuronCrossSectionalAnalysis(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint heads, uint heads_kv,
                          uint units_count, uint layers, uint layers_to_one_kv,
                          uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) override;
   //---
   virtual int       Type(void)   const override   {  return defNeuronCrossSectionalAnalysis;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Tenga en cuenta que usaremos el bloque de análisis de canal independiente como clase principal. Esta solución nos permitirá no incluir este bloque en el número de objetos internos, sino implementar la funcionalidad necesaria utilizando recursos heredados. Declararemos los objetos restantes de forma estática, lo cual nos permitirá dejar el constructor y el destructor de la clase vacíos. La inicialización de todos los objetos se realizará en el método Init, que heredará por completo la estructura de parámetros del método homónimo de la clase padre.

bool CNeuronCrossSectionalAnalysis::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                         uint window, uint window_key, uint heads, uint heads_kv,
                                         uint units_count, uint layers, uint layers_to_one_kv, uint variables,
                                         ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronMVMHAttentionMLKV::Init(numOutputs, myIndex, open_cl, window_key, window_key, heads, heads_kv,
                                      variables, layers, layers_to_one_kv, units_count, optimization_type, batch))
      return false;

En el cuerpo del método, como es habitual, primero llamaremos al método homónimo de la clase padre. Pero aquí hay un matiz que no debemos soslayar. Durante la implementación de la funcionalidad del módulo CSA, planeamos utilizar completamente todos los métodos heredados. Como parte de la pasada directa, planeamos suministrar a la entrada del método de la clase principal incorporaciones transpuestas de los datos de origen. Por lo tanto, al llamar al método de inicialización de la clase padre, cambiaremos el tamaño de la ventana de datos de origen a la dimensionalidad de la incorporación e intercambiaremos los parámetros de la longitud de la secuencia analizada con el número de variables independientes.

Una vez completadas con éxito las operaciones de inicialización de los objetos de la clase padre, inicializaremos secuencialmente la capa de transposición e incorporación convolucional de los datos.

   if(!cEmbeding.Init(0, 0, OpenCL, window, window, window_key, units_count, variables, optimization, iBatch))
      return false;
   cEmbeding.SetActivationFunction(GELU);
   if(!cTransposeRCD.Init(0,1,OpenCL,variables,units_count,window_key,optimization,iBatch))
      return false;

Después de esto, necesitaremos deshabilitar forzosamente la función de activación y finalizar el método, retornando previamente el resultado lógico de las operaciones al programa que realiza la llamada.

   SetActivationFunction(None);
//---
   return true;
  }

A continuación, implementaremos el algoritmo de pasada directa de nuestro módulo CSA en el método feedForward. Debemos decir que no esperamos ninguna complicación aquí. En los parámetros del método, obtendremos el puntero al objeto de datos de origen, que pasaremos inmediatamente al método homónimo de la capa de incorporación convolucional.

bool CNeuronCrossSectionalAnalysis::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cEmbeding.FeedForward(NeuronOCL))
      return false;
   if(!cTransposeRCD.FeedForward(cEmbeding.AsObject()))
     return false;
//---
   return CNeuronMVMHAttentionMLKV::feedForward(cTransposeRCD.AsObject());
  }

Transpondremos los resultados del procesamiento de los datos de origen mediante una capa convolucional y los pasaremos al método homónimo de la clase padre. Después de esto, finalizaremos el funcionamiento del método, retornando el resultado lógico de las operaciones al programa que realiza la llamada.

El algoritmo de los métodos de pasada inversa también es muy simple. Por lo tanto, podrá revisarlo por su propia cuenta. Ya hemos finalizado el trabajo sobre el objeto CNeuronCrossSectionalAnalysis. Podrá familiarizarse con el código completo de todos sus métodos en el archivo adjunto.

Por hoy, hemos agotado el alcance del presente artículo, así que podemos dar nuestra jornada de trabajo por finalizada. Sin embargo, el trabajo aún no ha terminado. Haremos una breve pausa y llegaremos a su conclusión lógica en el próximo artículo.

Conclusión

En este artículo, hemos presentado una estructura adaptativa multiagente para la optimización de portafolios de inversión con mecanismos integrados de atención y análisis de series temporales, llamada MASAAT. Esta explota un conjunto de agentes comerciales para analizar los datos de precios desde diferentes perspectivas, lo cual ayudará a reducir el sesgo en las acciones comerciales generadas. El análisis cruzado, basado en mecanismos de atención, se usa en cada agente para capturar las correlaciones entre activos y puntos temporales durante el periodo de observación desde diferentes perspectivas, y se ve seguido de un módulo de fusión espacio-temporal que intenta combinar la información obtenida.

En la parte práctica del artículo hemos comenzado la implementación de nuestra propia visión de los enfoques propuestos utilizando herramientas MQL5. En el próximo artículo continuaremos el trabajo iniciado.  También probaremos la eficacia de la solución construida con datos históricos reales.

Enlaces

• Developing An Attention-Based Ensemble Learning Framework for Financial Portfolio Optimisation
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL