Redes neuronales: así de sencillo (Parte 8): Mecanismos de atención
1 773
0
Contenido
- Introducción
- 1. Mecanismos de atención
- 2. Algoritmo de Self-Attention
- 3. Implementación
- 3.1. Modernizando la capa convolucional
- 3.2. Clase de bloque de Self-Attention
- 3.3. Propagación hacia delante de Self-Attention
- 3.4. Propagación inversa de Self-Attention
- 3.5. Cambios puntuales en las clases básicas de la red neronal
- 4. Simulación
- Conclusión
- Enlaces
- Programas utilizados en el artículo
Introducción
En artículos anteriores, ya hemos puesto a prueba diferentes variantes para organizar las redes neuronales, incluyendo las redes convolucionales [3], adoptadas de algoritmos de procesamiento de imágenes y las redes neuronales recurrentes [4], usadas para trabajar con secuencias en las que son importantes tanto los propios valores como su lugar en el conjunto de datos original.
Las redes neuronales convolucionales y totalmente conectadas tienen un tamaño fijo de secuencia de entrada. Las redes neuronales recurrentes nos permiten ampliar ligeramente la secuencia analizada transmitiendo los estados ocultos de las iteraciones anteriores. Pero su efectividad también se reduce con el aumento de la secuencia. En 2014, en la esfera de la traducción de programas, se propuso la utilización del primer mecanismo de atención, diseñado para determinar y resaltar programáticamente los bloques de la oración (contexto) original con mayor relevancia para la palabra de destino de la traducción. Un enfoque tan comprensible a nivel intuitivo para las personas ha permitido mejorar significativamente la calidad de la traducción de textos con la ayuda de redes neuronales.
1. Mecanismos de atención
Analizando el gráfico de velas del movimiento de un instrumento, podemos destacar las tendencias y definir los rangos comerciales, es decir, podemos destacar algunos objetos en el cuadro general, para luego concentrar nuestra atención en ellos. Podemos entender intuitivamente que los objetos influyen en el futuro comportamiento de los precios en diversos grados. Para implementar tal enfoque, en septiembre de 2014 se propuso el primer algoritmo capaz de analizar y aislar las dependencias entre los elementos de las secuencias de entrada y salida [8]. El algoritmo propuesto se denominó "mecanismo de atención generalizada". Inicialmente, se propuso su utilización en modelos de traducción automática usando redes recurrentes y resolvió el problema de la memoria a largo plazo en la traducción de oraciones largas. Este enfoque superó significativamente los resultados de las redes neuronales recurrentes previamente analizadas, basadas en bloques de LSTM [4].
El modelo clásico de traducción automática con uso de redes recurrentes consta de dos bloques, Encoder y Decoder. El primero codifica la secuencia de entrada en el idioma de origen en un vector de contexto y el segundo decodifica el contexto resultante en una secuencia de palabras en el idioma de destino. Al aumentar la longitud de la secuencia de entrada, la influencia de las primeras palabras en el contexto final de la oración se reduce y, como consecuencia, también lo hace la calidad de la traducción. El uso de bloques de LSTM aumentó ligeramente las capacidades del modelo, pero aún así, permanecieron limitadas.
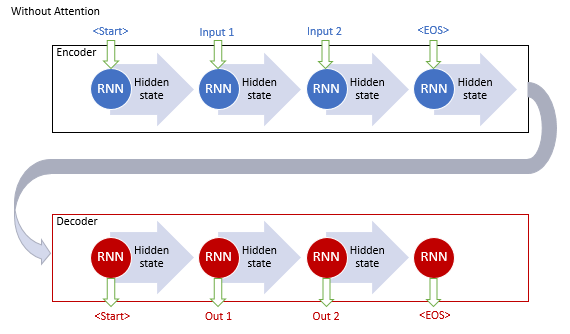
Los autores del mecanismo de atención general propusieron entonces usar una capa adicional para acumular los estados ocultos de todos los bloques recurrentes de la secuencia de entrada. Además, durante la decodificación de la secuencia, el mecanismo debería valorar la influencia de cada elemento de la secuencia de entrada en la palabra actual de la secuencia de salida y sugerir al decodificador la parte más relevante del contexto.
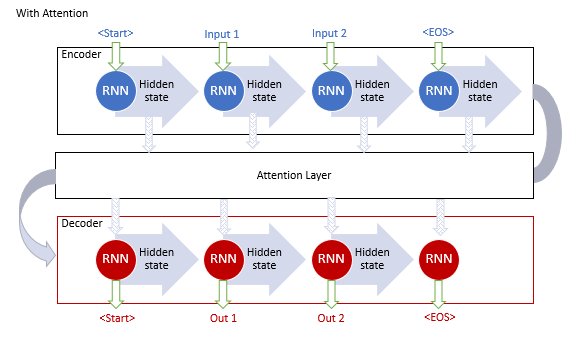
Este algoritmo operativo del mecanismo incluía las siguientes iteraciones:
1. Creación de estados ocultos del Encoder y acumulación de los mismos en el bloque de atención.
2. Valoración de las dependencias por pares entre los estados ocultos de cada elemento del Encoder y el último estado oculto del Decoder.
3. Las valoraciones obtenidas se combinan en un solo vector y se normalizan utilizando la función Softmax.
4. Cálculo del vector de contexto multiplicando todos los estados ocultos del Encoder por sus correspondientes puntuaciones de alineación.
5. Decodificación del vector de contexto y combinación del valor resultante con el estado anterior del Decoder.
Todas las iteraciones se repiten hasta que se reciba la señal de fin de frase.
El mecanismo ofrecido permitió solucionar el problema relacionado con la longitud limitada de la secuencia de entrada e hizo posible mejorar la calidad de la traducción automática usando redes neuronales recurrentes. El método se popularizó, generando además diversas variaciones. En 2012, Minh-Thang Luong en su artículo [9] propuso una nueva variación del método de atención. Las principales diferencias del nuevo enfoque eran la utilización de tres funciones para calcular el grado de dependencia y el punto de uso del mecanismo de atención en el Decoder.
Los modelos descritos anteriormente usaban bloques recurrentes que cuestan mucho entrenar. En junio de 2017, en el artículo [10], se mostró una nueva arquitectura de la red neuronal Transformer, en la que se abandonaba el uso de bloques recurrentes y se ofrecía un nuevo algoritmo de atención, Self-Attention. . A diferencia del descrito anteriormente, el algoritmo de Self-Attention analiza las dependencias emparejadas dentro de una secuencia. En las pruebas, Transformer mostró los mejores resultados, y hoy este modelo y sus derivados se usan en muchos modelos, incluidos el GPT-2 y el GPT-3. Vamos a analizar con mayor detalle el algoritmo de Self-Attention.
2. Algoritmo de Self-Attention
La arquitectura de Transformer se basa en bloques secuenciales de Encoder y Decoder con una arquitectura similar. Cada uno de los bloques incluye varias capas idénticas con diferentes matrices de peso.
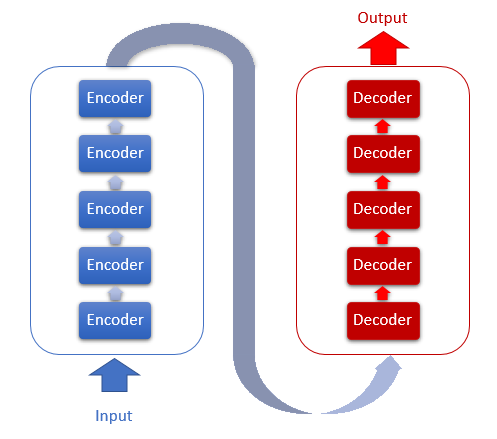
Cada capa del Encoder contiene 2 capas internas: Self-Attention y Feed Forward. La capa Feed Forward incluye 2 capas de neuronas completamente conectadas con la función de activación ReLU en la capa interna. Cada capa se aplica a todos los elementos de la secuencia con los mismos coeficientes de peso, lo cual posibilita realizar cálculos simultáneos e independientes para todos los elementos de la secuencia en flujos paralelos.
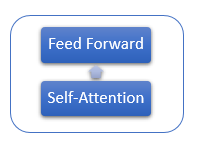
La capa Decoder tiene una estructura similar, pero se añade otra capa de Self-Attention que analiza las dependencias entre las secuencias de entrada y salida.
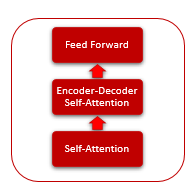
El propio mecanismo de Self-Attention incluye varias acciones iterativas que se usan para cada elemento de la secuencia.
1. Primero, calculamos los vectores Query (consulta), Key (clave) y Value (valor). Estos vectores se obtienen multiplicando cada elemento de la secuencia por la matriz WQ, WK y WV correspondiente.
2. A continuación, determinamos las dependencias por pares entre los elementos de la secuencia. Para hacerlo, multiplicamos el vector Query por los vectores Key de todos los elementos de la secuencia. Esta iteración se repite para el vector Query de cada elemento de la secuencia. Como resultado de esta iteración, obtendremos una matriz Score con un tamaño N*N, donde N será el tamaño de la secuencia.
3. En la siguiente etapa, dividimos el valor resultante por la raíz cuadrada de la dimensión del vector Key y los normalizamos con la función Softmax en el contexto de cada Query. Así, obtenemos los coeficientes de interdependencia por pares entre los elementos de la secuencia.
4. A continuación, multiplicamos cada vector Value por el coeficiente de interdependencia correspondiente para obtener el valor ajustado del elemento. El propósito de esta iteración es concentrarse en los elementos relevantes y reducir la influencia de los valores irrelevantes.
5. Después, sumamos todos los vectores Value ajustados para cada elemento. El resultado de esta operación será el vector de valores de salida de la capa de Self-Attention.
Los resultados de las iteraciones de cada capa se añaden a la secuencia de entrada y se normalizan utilizando la fórmula.
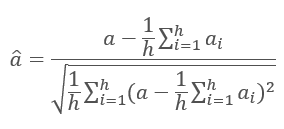
Si quiere encontrar más información sobre la normalización de las capas de las redes neuronales, consulte el artículo [11].
3. Implementación
En nuestro desarrollo, proponemos implementar el mecanismo de Self-Attention. Vamos a analizar las opciones de implementación.
3.1. Modernizando la capa convolucional
En primer lugar, analizaremos la primera acción del algoritmo de Self-Attention: el cálculo de los vectores Query, Key y Value. En la entrada, recibimos una matriz de datos que contiene las características para cada barra de la secuencia analizada. Luego, tomamos por turno los signos de una vela y, multiplicándolos por la matriz de pesos, obtenemos un vector. En opinión del autor, esto es muy semejante a la capa convolucional analizada en el artículo [3]. Solo que en la salida debe encontrarse no un número, sino un vector de longitud fija. Para solucionar este problema, vamos a modernizar la clase CNeuronConvOCL, encargada del funcionamiento de la capa convolucional de la red neuronal. Para ello, añadimos la variable iWindowOut, en la cual guardaremos el tamaño del vector de salida, y realizamos los ajustes necesarios a los métodos de la clase.
class CNeuronConvOCL : public CNeuronProofOCL { protected: uint iWindowOut; //--- CBufferDouble *WeightsConv; CBufferDouble *DeltaWeightsConv; CBufferDouble *FirstMomentumConv; CBufferDouble *SecondMomentumConv; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronConvOCL(void) : iWindowOut(1) { activation=LReLU; } ~CNeuronConvOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window, uint step, uint window_out, uint units_count, ENUM_OPTIMIZATION optimization_type); //--- virtual bool SetGradientIndex(int index) { return Gradient.BufferSet(index); } //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); virtual int Type(void) const { return defNeuronConvOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); };
En el kernel OpenCL FeedForwardConv, añadimos un parámetro para obtener el tamaño del vector de salida. A continuación, agregamos el cálculo del desplazamiento de la parte procesada del vector de salida en el vector común en la salida de la capa convolucional y organizamos un ciclo adicional para iterar sobre los elementos del vector de salida.
__kernel void FeedForwardConv(__global double *matrix_w, __global double *matrix_i, __global double *matrix_o, int inputs, int step, int window_in, int window_out, uint activation) { int i=get_global_id(0); int w_in=window_in; int w_out=window_out; double sum=0.0; double4 inp, weight; int shift_out=w_out*i; int shift_in=step*i; for(int out=0;out<w_out;out++) { int shift=(w_in+1)*out; int stop=(w_in<=(inputs-shift_in) ? w_in : (inputs-shift_in)); for(int k=0; k<=stop; k=k+4) { switch(stop-k) { case 0: inp=(double4)(1,0,0,0); weight=(double4)(matrix_w[shift+k],0,0,0); break; case 1: inp=(double4)(matrix_i[shift_in+k],1,0,0); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],0,0); break; case 2: inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],1,0); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],0); break; case 3: inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],matrix_i[shift_in+k+2],1); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]); break; default: inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],matrix_i[shift_in+k+2],matrix_i[shift_in+k+3]); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]); break; } sum+=dot(inp,weight); } switch(activation) { case 0: sum=tanh(sum); break; case 1: sum=1/(1+exp(-clamp(sum,-50.0,50.0))); break; case 2: if(sum<0) sum*=0.01; break; default: break; } matrix_o[out+shift_out]=sum; } }
No olvide añadir la transmisión del parámetro adicional al llamar a este kernel.
bool CNeuronConvOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=Output.Total()/iWindowOut; OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_w,WeightsConv.GetIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_i,NeuronOCL.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_o,Output.GetIndex()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_inputs,NeuronOCL.Neurons()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_step,iStep); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_window_in,iWindow); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffс_window_out,iWindowOut); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_activation,(int)activation); if(!OpenCL.Execute(def_k_FeedForwardConv,1,global_work_offset,global_work_size)) { printf("Error of execution kernel FeedForwardProof: %d",GetLastError()); return false; } //--- return Output.BufferRead(); }
Hemos realizado cambios semejantes en los métodos de recálculo de los kernels y gradientes (calcInputGradients) y en la actualización de la matriz de coeficientes de peso (updateInputWeights). Podrá familiarizarse con el código de todos los métodos y funciones en los anexos.
3.2. Clase de bloque de Self-Attention
Ahora, vamos a comenzar a implementar el método de Self-Attention. Para describirlo, crearemos la clase CNeuronAttentionOCL. Dado que todas nuestras operaciones se repiten para cada elemento y se realizan de forma independiente, transferiremos algunas de las operaciones a las capas convolucionales modernizadas. Así, creamos dentro de nuestro bloque de atención las capas convolucionales Querys, Keys, Values, que se encargarán de crear los vectores correspondientes, así como de transferir los gradientes y actualizar la matriz de pesos. También organizamos el bloque FeedForward utilizando las capas convolucionales FF1 y FF2. Los valores de la matriz Score se guardarán en el búfer Scores y los resultados del método de atención en la capa de neuronas interna de la clase básica AttentionOut.
En este lugar, deberemos prestar atención a la diferencia que hay entre la salida del algoritmo de atención y la salida de toda nuestra clase de Self-Attention. La primera se obtiene después de ejecutar el algoritmo de Self-Attention ajustando los valores de los vectores Value y guardar estos en AttentionOut; el segundo, tras procesar FeedForward y realizar el guardado en el búfer Output de la clase básica.
class CNeuronAttentionOCL : public CNeuronBaseOCL { protected: CNeuronConvOCL *Querys; CNeuronConvOCL *Keys; CNeuronConvOCL *Values; CBufferDouble *Scores; CNeuronBaseOCL *AttentionOut; CNeuronConvOCL *FF1; CNeuronConvOCL *FF2; //--- uint iWindow; uint iUnits; //--- virtual bool feedForward(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *prevLayer); public: CNeuronAttentionOCL(void) : iWindow(1), iUnits(0) {}; ~CNeuronAttentionOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); //--- virtual int Type(void) const { return defNeuronAttentionOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); };
En las variables iWindows e iUnits, guardamos el tamaño de la ventana de salida y el número de elementos en la secuencia de salida, respectivamente.
La clase se inicializará en el método Init. En los parámetros, transmitimos al método el número ordinal del elemento, un puntero al objeto COpenCL, el tamaño de la ventana, el número de elementos y el método de optimización. Al comienzo del método, llamamos al método análogo de la clase principal.
bool CNeuronAttentionOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window,uint units_count,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronBaseOCL::Init(numOutputs,myIndex,open_cl,units_count*window,optimization_type)) return false;
Luego, declaramos e inicializamos las instancias de la clase de red convolucional para calcular los vectores Querys, Keys y Values.
//--- if(CheckPointer(Querys)==POINTER_INVALID) { Querys=new CNeuronConvOCL(); if(CheckPointer(Querys)==POINTER_INVALID) return false; if(!Querys.Init(0,0,open_cl,window,window,window,units_count,optimization_type)) return false; Querys.SetActivationFunction(TANH); } //--- if(CheckPointer(Keys)==POINTER_INVALID) { Keys=new CNeuronConvOCL(); if(CheckPointer(Keys)==POINTER_INVALID) return false; if(!Keys.Init(0,1,open_cl,window,window,window,units_count,optimization_type)) return false; Keys.SetActivationFunction(TANH); } //--- if(CheckPointer(Values)==POINTER_INVALID) { Values=new CNeuronConvOCL(); if(CheckPointer(Values)==POINTER_INVALID) return false; if(!Values.Init(0,2,open_cl,window,window,window,units_count,optimization_type)) return false; Values.SetActivationFunction(None); }
Avanzando por el algoritmo, declaramos el búfer Scores. Preste atención al tamaño del búfer: debe contener suficiente memoria para almacenar una matriz cuadrada con los lados iguales al número de elementos en la secuencia.
if(CheckPointer(Scores)==POINTER_INVALID) { Scores=new CBufferDouble(); if(CheckPointer(Scores)==POINTER_INVALID) return false; } if(!Scores.BufferInit(units_count*units_count,0.0)) return false; if(!Scores.BufferCreate(OpenCL)) return false;
Asimismo, declaramos la capa de neuronas AttentionOut. Esta capa nos servirá como búfer para almacenar los resultados de Self-Attention. Al mismo tiempo, la usaremos como capa de entrada para el bloque FeedForward. Su tamaño es igual al producto del ancho de la ventana por el número de elementos.
if(CheckPointer(AttentionOut)==POINTER_INVALID) { AttentionOut=new CNeuronBaseOCL(); if(CheckPointer(AttentionOut)==POINTER_INVALID) return false; if(!AttentionOut.Init(0,3,open_cl,window*units_count,optimization_type)) return false; AttentionOut.SetActivationFunction(None); }
A continuación, inicializamos dos instancias de la capa convolucional para implementar el bloque FeedForward. Tenga en cuenta que la primera instancia (la capa oculta) retorna en la salida una ventana 2 veces más ancha y tiene una función de activación LReLU (ReLU con "fuga"). Para la segunda capa (FF2), sustituimos el búfer de gradiente por el búfer de gradiente de la clase principal usando el método SetGradientIndex. La sustitución del búfer nos ayudará a evitar la necesidad de copiar datos.
if(CheckPointer(FF1)==POINTER_INVALID) { FF1=new CNeuronConvOCL(); if(CheckPointer(FF1)==POINTER_INVALID) return false; if(!FF1.Init(0,4,open_cl,window,window,window*2,units_count,optimization_type)) return false; FF1.SetActivationFunction(LReLU); } //--- if(CheckPointer(FF2)==POINTER_INVALID) { FF2=new CNeuronConvOCL(); if(CheckPointer(FF2)==POINTER_INVALID) return false; if(!FF2.Init(0,5,open_cl,window*2,window*2,window,units_count,optimization_type)) return false; FF2.SetActivationFunction(None); FF2.SetGradientIndex(Gradient.GetIndex()); }
Y al final del método, almacenamos los parámetros clave.
iWindow=window; iUnits=units_count; activation=FF2.Activation(); //--- return true; }
3.3. Propagación hacia delante de Self-Attention
En la siguiente etapa, analizaremos el método feedForward de la clase CNeuronAttentionOCL. En los parámetros, el método recibe un puntero a la capa anterior de la red neuronal. En primer lugar, verificamos la validez del puntero recibido.
bool CNeuronAttentionOCL::feedForward(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
Antes de seguir procesando los datos, normalizamos los datos de entrada. Este paso no está previsto por el mecanismo de Self-Attention del autor, pero se ha añadido según los resultados de la prueba para evitar el desbordamiento en la etapa de normalización de la matriz Score. Para normalizar los datos, hemos creado un kernel especial, que llamaremos en el método feedForward.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=1;
OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getOutputIndex());
OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons());
if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Normalize: %d",GetLastError());
return false;
}
if(!prevLayer.Output.BufferRead())
return false;
}
Echemos un vistazo al interior del kernel de normalización. Al comienzo del kernel, calculamos el desplazamiento hasta el primer elemento de la secuencia normalizada. A continuación, calculamos el valor promedio de la secuencia normalizada y la desviación estándar. Al final del kernel, actualizamos los datos en el búfer.
__kernel void Normalize(__global double *buffer, int dimension) { int n=get_global_id(0); int shift=n*dimension; double mean=0; for(int i=0;i<dimension;i++) mean+=buffer[shift+i]; mean/=dimension; double variance=0; for(int i=0;i<dimension;i++) variance+=pow(buffer[shift+i]-mean,2); variance=sqrt(variance/dimension); for(int i=0;i<dimension;i++) buffer[shift+i]=(buffer[shift+i]-mean)/(variance==0 ? 1 : variance); }
Después de normalizar los datos iniciales, calculamos los vectores Querys, Keys y Values. Para hacerlo, llamamos al método FeedForward de la instancia correspondiente de la clase de capa convolucional (ya lo hemos analizado anteriormente).
if(CheckPointer(Querys)==POINTER_INVALID || !Querys.FeedForward(prevLayer)) return false; if(CheckPointer(Keys)==POINTER_INVALID || !Keys.FeedForward(prevLayer)) return false; if(CheckPointer(Values)==POINTER_INVALID || !Values.FeedForward(prevLayer)) return false;
Continuando con el algoritmo de Self-Attention, calculamos la matriz Score. También realizamos los cálculos en una GPU usando OpenCL. En el método del programa principal, organizamos una llamada al kernel. El número de hilos llamados será igual al número de unidades en la clase, y cada hilo funcionará dentro del tamaño de su ventana. En otras palabras, cada hilo tomará su propio vector Query de un elemento y lo opondrá a los vectores Key de todos los elementos de la secuencia.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_querys,Querys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_keys,Keys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_score,Scores.GetIndex());
OpenCL.SetArgument(def_k_AttentionScore,def_k_as_dimension,iWindow);
if(!OpenCL.Execute(def_k_AttentionScore,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel AttentionScore: %d",GetLastError());
return false;
}
if(!Scores.BufferRead())
return false;
}
Al comienzo del kernel, determinamos los desplazamientos del elemento inicial usando las matrices Query y Score. Vamos a calcular el coeficiente para reducir los valores obtenidos y poner a cero la variable para calcular la cantidad que necesitamos al normalizar los valores. A continuación, organizaremos un ciclo para iterar sobre todos los elementos de la matriz de claves calculando las dependencias correspondientes. Debemos señalar que el kernel en cuestión ha combinado las etapas de cálculo y normalización de la matriz Score. Por consiguiente, tras calcular los productos de los vectores Query y Key, dividimos el valor resultante por un coeficiente y calculamos el exponente del valor resultante. Guardamos el exponente resultante en la matriz y lo añadimos a la suma. Al final del ciclo, organizamos un segundo ciclo en el que dividimos todos los valores guardados en el ciclo anterior por la suma calculada de exponentes. A la salida del kernel, obtenemos la matriz Score recalculada y normalizada.
__kernel void AttentionScore(__global double *querys, __global double *keys, __global double *score, int dimension) { int q=get_global_id(0); int shift_q=q*dimension; int units=get_global_size(0); int shift_s=q*units; double koef=sqrt((double)(units*dimension)); if(koef<1) koef=1; double sum=0; for(int k=0;k<units;k++) { double result=0; int shift_k=k*dimension; for(int i=0;i<dimension;i++) result+=(querys[shift_q+i]*keys[shift_k+i]); result=exp(result/koef); score[shift_s+k]=result; sum+=result; } for(int k=0;k<units;k++) score[shift_s+k]/=sum; }
Continuamos con el algoritmo de Self-Attention. Después de normalizar la matriz Score, nos queda ajustar los vectores de valores para los valores obtenidos y sumar los vectores obtenidos en el contexto de los elementos de la secuencia de entrada. A la salida del bloque de Self-Attention, los valores obtenidos se suman a la secuencia de entrada. Todas estas iteraciones se combinan en el siguiente kernel AttentionOut. En el código del programa principal, organizamos la llamada de este kernel. No olvide que iniciaremos este kernel con un conjunto de hilos en dos cambios: según los elementos de la secuencia (iUnits) y según el número de características para cada elemento (iWindow). Guardaremos los valores obtenidos en el búfer de salida de la capa AttentionOut.
{
uint global_work_offset[2]={0,0};
uint global_work_size[2];
global_work_size[0]=iUnits;
global_work_size[1]=iWindow;
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_scores,Scores.GetIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_inputs,prevLayer.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_values,Values.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_out,AttentionOut.getOutputIndex());
if(!OpenCL.Execute(def_k_AttentionOut,2,global_work_offset,global_work_size))
{
printf("Error of execution kernel Attention Out: %d",GetLastError());
return false;
}
double temp[];
if(!AttentionOut.getOutputVal(temp))
return false;
}
En el cuerpo del núcleo, determinamos el desplazamiento del elemento procesado en los vectores de las secuencias de entrada y salida. Luego, organizamos un ciclo para sumar los productos de los coeficientes Score a los valores Value correspondientes. En cuanto se han completado las iteraciones cíclicas, añadimos la suma resultante al vector de entrada recibido de la capa anterior de la red neuronal. El resultado lo escribimos en el búfer de salida.
__kernel void AttentionOut(__global double *scores, __global double *values, __global double *inputs, __global double *out) { int units=get_global_size(0); int u=get_global_id(0); int d=get_global_id(1); int dimension=get_global_size(1); int shift=u*dimension+d; double result=0; for(int i=0;i<units;i++) result+=scores[u*units+i]*values[i*dimension+d]; out[shift]=result+inputs[shift]; }
Con esto, podemos considerar completado el algoritmo de Self-Attention. Ahora, solo necesitamos normalizar los datos resultantes utilizando el método descrito anteriormente. La única diferencia está en el búfer de normalización.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=1;
OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,AttentionOut.getOutputIndex());
OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,AttentionOut.Neurons());
if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Normalize: %d",GetLastError());
return false;
}
double temp[];
if(!AttentionOut.getOutputVal(temp))
return false;
}
Además, según el algoritmo del codificador de Transformer, pasamos cada elemento de la secuencia a través de una red neuronal completamente conectada con una capa oculta. En este proceso, se aplica la misma matriz de coeficientes de peso a todos los elementos de la secuencia. Hemos implementado este proceso usando una clase de capa convolucional modernizada. En el código del método, llamamos secuencialmente a los métodos FeedForward de las instancias correspondientes de la clase convolucional.
if(!FF1.FeedForward(AttentionOut)) return false; if(!FF2.FeedForward(FF1)) return false;
Para completar el proceso de propagación hacia delante, nos queda añadir los resultados de la pasada de la red completamente conectada a los resultados del mecanismo de Self-Attention. Con este objetivo, hemos creado un kernel para sumar los dos vectores, que llamaremos al final de nuestro método de propagación hacia delante.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,FF2.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,Output.GetIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
if(!Output.BufferRead())
return false;
}
//---
return true;
}
Dentro del kernel, organizamos un ciclo simple con la suma por elementos de los valores vectoriales entrantes.
__kernel void SumMatrix(__global double *matrix1, __global double *matrix2, __global double *matrix_out, int dimension) { const int i=get_global_id(0)*dimension; for(int k=0;k<dimension;k++) matrix_out[i+k]=matrix1[i+k]+matrix2[i+k]; }
Podrá familiarizarse con el código de todos los métodos y funciones en los anexos.
3.4. Propagación inversa de Self-Attention
Tras la propagación hacia delante, viene la propagación inversa, durante la cual el error se transmite a las capas inferiores de la red neuronal y se corrigen las matrices de peso para seleccionar los resultados óptimos. Desde la capa superior completamente conectada de la red neuronal, nuestra clase recibe el gradiente de error utilizando el método de la clase padre descrito en el artículo [5]. El mecanismo adicional para transmitir el gradiente de error requiere una mejora significativa, dada la complejidad de la arquitectura interna.
Para transmitir el gradiente de error a las capas convolucionales internas y a la capa neuronal anterior de nuestra red, creamos el método calcInputGradients. En los parámetros, el método recibe un puntero a la capa neuronal anterior. A continuación, como de costumbre, verificamos de inmediato la validez del enlace recibido. Luego, en orden inverso, llamamos secuencialmente a los métodos del mismo nombre de las capas convolucionales del bloque Feed Forward, FF2 y FF1. Debemos recordar que, gracias a la sustitución del búfer, nuestra capa FF2 interna recibe el gradiente de error directamente de la siguiente capa de la red neuronal, usando para ello los métodos de la clase principal.
bool CNeuronAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- if(!FF2.calcInputGradients(FF1)) return false; if(!FF1.calcInputGradients(AttentionOut)) return false;
Como en la salida de la propagación hacia delante hemos sumado los resultados de Feed Forward y Self-Attention, el gradiente de error también se presentará en dos ramas. Por consiguiente, el gradiente de error obtenido de FF1 se sumará al gradiente de error obtenido de la siguiente capa de la red neuronal. El kernel de suma vectorial se ha descrito arriba. Aquí solo añadiremos su llamada.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,Gradient.GetIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
double temp[];
if(AttentionOut.getGradient(temp)<=0)
return false;
}
En el siguiente paso, propagamos el gradiente de error a Querys, Keys y Values. El gradiente de error se transmitirá a los vectores en el kernel AttentionIsideGradients, mientras que en el siguiente método organizaremos su llamada con un conjunto de hilos en dos dimensiones.
{
uint global_work_offset[2]={0,0};
uint global_work_size[2];
global_work_size[0]=iUnits;
global_work_size[1]=iWindow;
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_gradient,AttentionOut.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys,Keys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys_g,Keys.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys,Querys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys_g,Querys.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values,Values.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values_g,Values.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_scores,Scores.GetIndex());
if(!OpenCL.Execute(def_k_AttentionGradients,2,global_work_offset,global_work_size))
{
printf("Error of execution kernel AttentionGradients: %d",GetLastError());
return false;
}
double temp[];
if(Keys.getGradient(temp)<=0)
return false;
}
En los parámetros, el kernel recibe los punteros a los búferes de datos; el tamaño de las dimensiones se determinará al inicio del kernel según el número de hilos en ejecución. A continuación, calculamos el coeficiente de corrección y organizamos un ciclo para iterar sobre todos los elementos de la secuencia. Dentro del ciclo, primero calculamos el gradiente de error en el vector Value multiplicando el vector de gradiente por el vector Score correspondiente. No olvide que estamos dividiendo el gradiente de error por 2. Esto se debe a que, habiéndolo sumado en el paso anterior, duplicamos el error, mientras que dividiendo por dos, tomamos el valor promedio en el cálculo.
__kernel void AttentionIsideGradients(__global double *querys,__global double *querys_g, __global double *keys,__global double *keys_g, __global double *values,__global double *values_g, __global double *scores, __global double *gradient) { int u=get_global_id(0); int d=get_global_id(1); int units=get_global_size(0); int dimension=get_global_size(1); double koef=sqrt((double)(units*dimension)); if(koef<1) koef=1; //--- double vg=0; double qg=0; double kg=0; for(int iu=0;iu<units;iu++) { double g=gradient[iu*dimension+d]/2; double sc=scores[iu*units+u]; vg+=sc*g;
Después, organizamos un ciclo anidado para definir el gradiente en los elementos de la matriz Score. Luego, calculamos el gradiente de los elementos de los vectores Querys y Keys. Al final del ciclo externo, asignamos los gradientes calculados a los búferes globales correspondientes.
//--- double sqg=0; double skg=0; for(int id=0;id<dimension;id++) { sqg+=values[iu*dimension+id]*gradient[u*dimension+id]/2; skg+=values[u*dimension+id]*gradient[iu*dimension+id]/2; } qg+=(scores[u*units+iu]==0 || scores[u*units+iu]==1 ? 0.0001 : scores[u*units+iu]*(1-scores[u*units+iu]))*sqg*keys[iu*dimension+d]/koef; //--- kg+=(scores[iu*units+u]==0 || scores[iu*units+u]==1 ? 0.0001 : scores[iu*units+u]*(1-scores[iu*units+u]))*skg*querys[iu*dimension+d]/koef; } int shift=u*dimension+d; values_g[shift]=vg; querys_g[shift]=qg; keys_g[shift]=kg; }
A continuación, tenemos que transmitir los gradientes de error de los vectores Querys, Keys y Values. Aquí, cabe señalar que, como todos los vectores se obtienen multiplicando los mismos datos iniciales por diferentes matrices, también tendremos que sumar los gradientes de error. Para acumular gradientes de error, no hemos asignado un búfer aparte: la suma de los valores al calcular los gradientes requiere de una complicación adicional del código para monitorear los momentos de puesta a cero del búfer. Hemos decidido usar los métodos existentes para calcular los gradientes de error, acumulando posteriormente los valores en el búfer de gradiente de la capa AttentionOut.
if(!Querys.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- if(!Keys.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- if(!Values.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,prevLayer.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow+1); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(prevLayer.getGradient(temp)<=0) return false; } //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=1; OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getGradientIndex()); OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons()); if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Normalize: %d",GetLastError()); return false; } double temp[]; if(prevLayer.getGradient(temp)<=0) return false; } //--- return true; }
Después de transmitir el gradiente de error al nivel de la capa anterior, corregimos las matrices de coeficientes de peso en el método updateInputWeights. La construcción del método es bastante sencilla. En ella solo se llaman los métodos homónimos de las capas convolucionales anidadas.
bool CNeuronAttentionOCL::updateInputWeights(CNeuronBaseOCL *prevLayer) { if(!Querys.UpdateInputWeights(prevLayer)) return false; if(!Keys.UpdateInputWeights(prevLayer)) return false; if(!Values.UpdateInputWeights(prevLayer)) return false; if(!FF1.UpdateInputWeights(AttentionOut)) return false; if(!FF2.UpdateInputWeights(FF1)) return false; //--- return true; }
3.5. Cambios puntuales en las clases básicas de la red neronal
Una vez hemos terminado de trabajar con la clase de nuestro bloque de atención, vamos a realizar pequeñas adiciones a las clases básicas de nuestra red neuronal. En primer lugar, añadimos las constantes al bloque define para trabajar con los nuevos kernels.
#define def_k_FeedForwardConv 7 #define def_k_ffc_matrix_w 0 #define def_k_ffc_matrix_i 1 #define def_k_ffc_matrix_o 2 #define def_k_ffc_inputs 3 #define def_k_ffc_step 4 #define def_k_ffc_window_in 5 #define def_k_ffс_window_out 6 #define def_k_ffc_activation 7 //--- #define def_k_CalcHiddenGradientConv 8 #define def_k_chgc_matrix_w 0 #define def_k_chgc_matrix_g 1 #define def_k_chgc_matrix_o 2 #define def_k_chgc_matrix_ig 3 #define def_k_chgc_outputs 4 #define def_k_chgc_step 5 #define def_k_chgc_window_in 6 #define def_k_chgc_window_out 7 #define def_k_chgc_activation 8 //--- #define def_k_UpdateWeightsConvMomentum 9 #define def_k_uwcm_matrix_w 0 #define def_k_uwcm_matrix_g 1 #define def_k_uwcm_matrix_i 2 #define def_k_uwcm_matrix_dw 3 #define def_k_uwcm_inputs 4 #define def_k_uwcm_learning_rates 5 #define def_k_uwcm_momentum 6 #define def_k_uwcm_window_in 7 #define def_k_uwcm_window_out 8 #define def_k_uwcm_step 9 //--- #define def_k_UpdateWeightsConvAdam 10 #define def_k_uwca_matrix_w 0 #define def_k_uwca_matrix_g 1 #define def_k_uwca_matrix_i 2 #define def_k_uwca_matrix_m 3 #define def_k_uwca_matrix_v 4 #define def_k_uwca_inputs 5 #define def_k_uwca_l 6 #define def_k_uwca_b1 7 #define def_k_uwca_b2 8 #define def_k_uwca_window_in 9 #define def_k_uwca_window_out 10 #define def_k_uwca_step 11 //--- #define def_k_AttentionScore 11 #define def_k_as_querys 0 #define def_k_as_keys 1 #define def_k_as_score 2 #define def_k_as_dimension 3 //--- #define def_k_AttentionOut 12 #define def_k_aout_scores 0 #define def_k_aout_values 1 #define def_k_aout_inputs 2 #define def_k_aout_out 3 //--- #define def_k_MatrixSum 13 #define def_k_sum_matrix1 0 #define def_k_sum_matrix2 1 #define def_k_sum_matrix_out 2 #define def_k_sum_dimension 3 //--- #define def_k_AttentionGradients 14 #define def_k_ag_querys 0 #define def_k_ag_querys_g 1 #define def_k_ag_keys 2 #define def_k_ag_keys_g 3 #define def_k_ag_values 4 #define def_k_ag_values_g 5 #define def_k_ag_scores 6 #define def_k_ag_gradient 7 //--- #define def_k_Normilize 15 #define def_k_norm_buffer 0 #define def_k_norm_dimension 1
Asimismo, añadimos una constante de la nueva clase de neuronas.
#define defNeuronAttentionOCL 0x7887
A continuación, añadimos a CLayerDescription (la clase encargada de describir las capas de la red neuronal) un campo para especificar el número de neuronas en la ventana de vector de salida.
class CLayerDescription : public CObject { public: CLayerDescription(void); ~CLayerDescription(void) {}; //--- int type; int count; int window; int window_out; int step; ENUM_ACTIVATION activation; ENUM_OPTIMIZATION optimization; };
En el constructor de la clase de red neuronal CNet, añadimos las nuevas clases para inicializar una instancia de la clase para trabajar con OpenCL.
CNet::CNet(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
..........
..........
..........
//---
next=Description.At(1);
if(next.type==defNeuron || next.type==defNeuronBaseOCL || next.type==defNeuronConvOCL || next.type==defNeuronAttentionOCL)
{
opencl=new COpenCLMy();
if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true))
delete opencl;
}
else
{
if(CheckPointer(opencl)!=POINTER_INVALID)
delete opencl;
}
A continuación, añadimos en el cuerpo del constructor el código para inicializar la nueva clase de la neurona de atención.
if(CheckPointer(opencl)!=POINTER_INVALID) { CNeuronBaseOCL *neuron_ocl=NULL; CNeuronConvOCL *neuron_conv_ocl=NULL; CNeuronAttentionOCL *neuron_attention_ocl=NULL; switch(desc.type) { case defNeuron: case defNeuronBaseOCL: neuron_ocl=new CNeuronBaseOCL(); if(CheckPointer(neuron_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_ocl.Init(outputs,0,opencl,desc.count,desc.optimization)) { delete neuron_ocl; delete temp; return; } neuron_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_ocl)) { delete neuron_ocl; delete temp; return; } neuron_ocl=NULL; break; case defNeuronConvOCL: neuron_conv_ocl=new CNeuronConvOCL(); if(CheckPointer(neuron_conv_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_conv_ocl.Init(outputs,0,opencl,desc.window,desc.step,desc.window_out,desc.count,desc.optimization)) { delete neuron_conv_ocl; delete temp; return; } neuron_conv_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_conv_ocl)) { delete neuron_conv_ocl; delete temp; return; } neuron_conv_ocl=NULL; break; case defNeuronAttentionOCL: neuron_attention_ocl=new CNeuronAttentionOCL(); if(CheckPointer(neuron_attention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_attention_ocl.Init(outputs,0,opencl,desc.window,desc.count,desc.optimization)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_attention_ocl)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl=NULL; break; default: return; break; } }
Y al final del constructor, añadimos la inicialización de los nuevos kernels.
if(CheckPointer(opencl)==POINTER_INVALID) return; //--- create kernels opencl.SetKernelsCount(16); opencl.KernelCreate(def_k_FeedForward,"FeedForward"); opencl.KernelCreate(def_k_CalcOutputGradient,"CalcOutputGradient"); opencl.KernelCreate(def_k_CalcHiddenGradient,"CalcHiddenGradient"); opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum"); opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam"); opencl.KernelCreate(def_k_AttentionGradients,"AttentionIsideGradients"); opencl.KernelCreate(def_k_AttentionOut,"AttentionOut"); opencl.KernelCreate(def_k_AttentionScore,"AttentionScore"); opencl.KernelCreate(def_k_CalcHiddenGradientConv,"CalcHiddenGradientConv"); opencl.KernelCreate(def_k_CalcInputGradientProof,"CalcInputGradientProof"); opencl.KernelCreate(def_k_FeedForwardConv,"FeedForwardConv"); opencl.KernelCreate(def_k_FeedForwardProof,"FeedForwardProof"); opencl.KernelCreate(def_k_MatrixSum,"SumMatrix"); opencl.KernelCreate(def_k_UpdateWeightsConvAdam,"UpdateWeightsConvAdam"); opencl.KernelCreate(def_k_UpdateWeightsConvMomentum,"UpdateWeightsConvMomentum"); opencl.KernelCreate(def_k_Normilize,"Normalize"); //--- return; }
Asimismo, añadimos a los métodos de administración de la clase CNeuronBase el procesamiento de la nueva clase de neuronas.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; }
bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; CNeuronAttentionOCL *at=NULL; CNeuronConvOCL *conv=NULL; switch(TargetObject.Type()) { case defNeuronBaseOCL: temp=TargetObject; return calcHiddenGradients(temp); break; case defNeuronConvOCL: conv=TargetObject; temp=GetPointer(this); return conv.calcInputGradients(temp); break; case defNeuronAttentionOCL: at=TargetObject; temp=GetPointer(this); return at.calcInputGradients(temp); break; } //--- return false; }
Podrá familiarizarse con el código de todos los métodos y funciones en los anexos.
4. Simulación
Tras realizar todos los cambios anteriores, podemos añadir la nueva clase de neuronas a la red neuronal y poner a prueba la nueva arquitectura. Hemos creado el asesor de prueba Fractal_OCL_Attention, que se diferencia de los asesores anteriores solo en la arquitectura de la red neuronal. Una vez más, la primera capa consta de neuronas las básicas para escribir los datos iniciales, y contiene 12 características para cada barra de la historia. La segunda capa se declara como una capa convolucional modificada con una función de activación sigmoidea y una ventana de salida de 36 neuronas. Esta capa realiza la función de incrustar y normalizar los datos originales. Después siguen las dos capas del codificador con el mecanismo de Self-Attention. Y cierran la red neuronal tres capas de neuronas completamente conectadas.
CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBaseOCL; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronConvOCL; desc.window=12; desc.step=12; desc.window_out=36; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- bool result=true; for(int i=0; (i<2 && result); i++) { desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronAttentionOCL; desc.window=36; desc.optimization=ADAM; desc.activation=None; result=Topology.Add(desc); } if(!result) { delete Topology; return INIT_FAILED; } //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; desc.activation=SIGMOID; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED;
El código completo del asesor se puede encontrar en el archivo adjunto.
Hemos puesto a prueba el asesor experto en las mismas condiciones que en los artículos anteriores de este ciclo: instrumento EURUSD, marco temporal H1 y los datos de 20 velas consecutivas; la formación se llevó a cabo utilizando la historia de los últimos 2 años actualizando los parámetros con el método Adam.
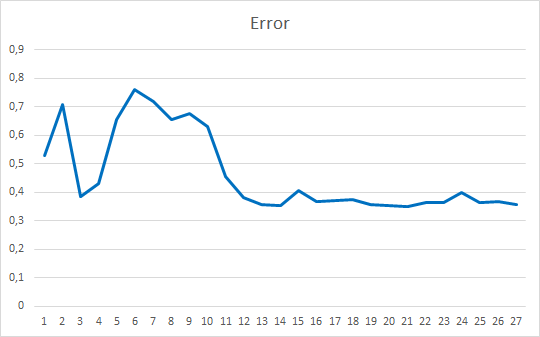
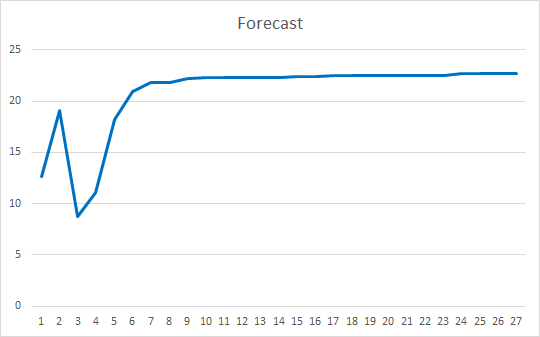
Inicializamos el asesor con pesos aleatorios que van de -1 a 1, excluyendo los valores iguales a cero. Según los resultados de las simulaciones de 25 épocas, el asesor ha mostrado un error del 35-36%, con un acierto del 22-23%.
Conclusión
En este artículo, hemos analizado los mecanismos de atención, creando un bloque de Self-Attention y poniendo a prueba su funcionamiento con datos históricos. El asesor experto construido ha mostrado resultados bastante suaves respecto a la reducción del error en el funcionamiento de la red neuronal y el nivel de "acierto" en los resultados previstos. Los resultados obtenidos indican la posibilidad de usar el enfoque, pero necesitaremos realizar algunos trabajos adicionales para mejorar los resultados. Como opción de desarrollo, podemos considerar la utilización de varios hilos de atención paralelos con diferentes pesos. En el artículo [10], este enfoque se denominará Multi-head attention.
Enlaces
- Redes neuronales: así de sencillo
- Redes neuronales: así de sencillo (Parte 2): Entrenamiento y prueba de la red
- Redes neuronales: así de sencillo (Parte 3): Redes convolucionales
- Redes neuronales: así de sencillo (Parte 4): Redes recurrentes
- Redes neuronales: así de sencillo (Parte 5): Cálculos multihilo en OpenCL
- Redes neuronales: así de sencillo (Parte 6): Experimentos con la tasa de aprendizaje de la red neuronal
- Redes neuronales: así de sencillo (Parte 7): Métodos de optimización adaptativos
- Neural Machine Translation by Jointly Learning to Align and Translate
- Effective Approaches to Attention-based Neural Machine Translation
- Attention Is All You Need
- Layer Normalization
Programas utilizados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Fractal_OCL_Attention.mq5 | Asesor | Asesor con la red neuronal de clasificación (3 neuronas en la capa de salida) con uso del mecanismo Self-Attention |
| 2 | NeuroNet.mqh | Biblioteca de clase | Biblioteca de clases para crear la red neuronal |
| 3 | NeuroNet.cl | Biblioteca | Biblioteca de código del programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/8765
Utilizando hojas de cálculo para construir estrategias comerciales
Perceptrón Multicapa y Algoritmo de Retropropagación
Desarrollando un algoritmo de autoadaptación (Parte I): Encontrando un patrón básico
WebSocket para MetaTrader 5
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso