Redes neuronales: así de sencillo (Parte 7): Métodos de optimización adaptativos
1 080
0
Contenido
- Introducción
- 1. Particularidades distintivas de los métodos de optimización adaptativa
- 1.1. Método de gradiente adaptativo (AdaGrad)
- 1.2. Método RMSProp
- 1.3. Método Adadelta
- 1.4. Método de valoración del momento adaptativo (Adam)
- 2. Implementación
- 2.1. Construyendo el kernel en OpenCL
- 2.2. Cambios en el código de la clase de neurona del programa principal
- 2.3. Cambios en el código de las clases sin usar OpenCL
- 2.4. Cambios en el código de la clase de red neuronal del programa principal
- 3. Simulación
- Conclusión
- Enlaces
- Programas utilizados en el artículo
Introducción
En artículos anteriores, analizamos diferentes tipos de neuronas, utilizando siempre el método de descenso de gradiente estocástico para entrenar la red neuronal. Este método probablemente se pueda llamar básico, y sus diversas variaciones se usan con mucha frecuencia en la práctica. No obstante, no es el único método: existen otras formas de entrenar redes neuronales. Hoy proponemos al lector analizar varios métodos de aprendizaje adaptativo. Esta familia de métodos nos permite modificar la tasa de aprendizaje de las neuronas mientras entrenamos una red neuronal.
1. Particularidades distintivas de los métodos de optimización adaptativa
Como ya sabemos, no todas las funciones introducidas en una red neuronal tienen el mismo efecto en el resultado final. Algunos parámetros pueden contener mucho ruido y cambiar con más frecuencia que otros que tienen diferentes amplitudes. Las muestras de otros parámetros pueden contener valores raros que podemos pasar por alto al entrenar una red neuronal con una tasa de aprendizaje fija. Una de las desventajas del método descenso de gradiente estocástico analizado anteriormente es la ausencia de mecanismos de optimización en tales muestras. Como resultado, el proceso de aprendizaje puede interrumpirse en el mínimo local. Podemos resolver este problema usando métodos adaptativos para entrenar las redes neuronales. Estos métodos nos permiten cambiar de forma dinámica la tasa de aprendizaje durante el entrenamiento de la red neuronal. Existen muchos de estos métodos, y no menos variaciones de los mismos. Vamos a analizar los más populares.
1.1. Método de gradiente adaptativo (AdaGrad)
El método de gradiente adaptativo se presentó en 2011, y supone una variación del método de descenso de gradiente estocástico. Si comparamos las fórmulas matemáticas de ambos métodos, resulta fácil percibir una única diferencia: en AdaGrad, la tasa de aprendizaje se divide por la raíz cuadrada de la suma de los cuadrados de los gradientes para todas las iteraciones de entrenamiento anteriores. Este enfoque reduce la tasa de aprendizaje de los parámetros que se actualizan con frecuencia.
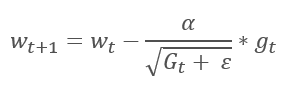
La principal desventaja de este método proviene de su propia fórmula: la suma de los cuadrados de los gradientes solo puede aumentar y, como consecuencia de ello, la tasa de aprendizaje tenderá a "0", lo que en última instancia provocará la interrupción del aprendizaje.
El precio por utilizar este método es la necesidad de realizar cálculos adicionales y de asignar memoria adicional para guardar la suma de los cuadrados de los gradientes para cada neurona.
1.2. Método RMSProp
La continuación lógica del método AdaGrad es el método RMSProp. Para evitar la reducción de la tasa de aprendizaje a "0", se propuso sustituir la suma de los cuadrados de los gradientes en el denominador de la fórmula para actualizar los pesos por la media exponencial de los cuadrados de los gradientes. Este enfoque nos permite evitar el crecimiento constante e infinito del valor en el denominador y, en mayor medida, considerar los últimos valores de gradiente que caracterizan el estado actual del modelo.
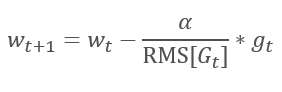
1.3. Método Adadelta
Casi simultáneamente con RMSProp, se expuso otro método de aprendizaje adaptativo muy similar, el método Adadelta. Este método es parecido y usa el promedio exponencial de la suma de los cuadrados de los gradientes en el denominador de la fórmula usada para actualizar los pesos. Pero, a diferencia de RMSProp, este método rechaza por completo la tasa de aprendizaje en la fórmula de actualización y la sustituye por el promedio exponencial de la suma de los cuadrados de los cambios anteriores en el parámetro analizado.
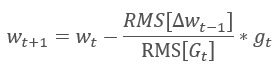
Este enfoque nos permite eliminar la tasa de aprendizaje de la fórmula usada para actualizar los pesos y crear un algoritmo de aprendizaje altamente adaptable. No obstante, este método requiere iteraciones adicionales de los cálculos, así como la asignación de memoria para guardar un valor adicional en cada neurona.
1.4. Método de valoración del momento adaptativo (Adam)
En 2014, Diederik P. Kingma y Jimmy Lei Ba propusieron el método de valoración del momento adaptativo de Adam. Según los autores, el método combina las ventajas de los métodos AdaGrad y RMSProp, y funciona bien con la formación online. Este método muestra resultados buenos y consistentes en diferentes muestras, y recientemente se ha recomendado su utilización por defecto en varios paquetes.
El método se basa en el cálculo de la media exponencial del gradiente m y la media exponencial de los cuadrados del gradiente v. Cada promedio exponencial posee su propio hiperparámetro ß, que determina el periodo de promedio.
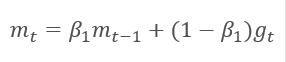
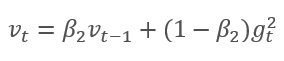
Los autores sugieren utilizar el valor predeterminado ß1 en 0.9 y ß2 en el nivel 0,999. En este caso, m0 y v0 toman valores cero. Con estos parámetros, las fórmulas presentadas anteriormente al inicio del entrenamiento retornan valores cercanos a "0" y, como consecuencia de ello, obtendremos una baja tasa de aprendizaje en la etapa inicial. Para acelerar el aprendizaje, los autores propusieron corregir los momentos obtenidos.
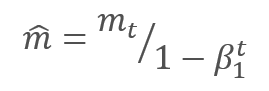
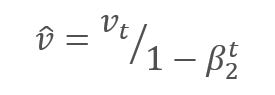
Los parámetros se actualizan corrigiendo la relación del momento corregido del gradiente m respecto a la raíz cuadrada del momento corregido del cuadrado del gradiente v. Para excluir la división por cero, se añade al denominador una constante Ɛ cercana a "0". La relación resultante se corrige con el coeficiente de aprendizaje α, que, en este caso, supone el límite superior del salto de aprendizaje. Por defecto, los autores proponen usar α en el nivel 0,001.
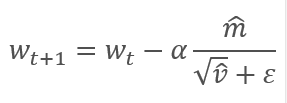
2. Implementación
Una vez analizados los aspectos teóricos, podemos proceder a la implementación práctica. Proponemos implementar el método Adam con los hiperparámetros estándar ofrecidos por los autores. Además, cualquiera puede probar otras variaciones de los hiperparámetros.
La red neuronal construida anteriormente usaba el descenso de gradiente estocástico para el entrenamiento que ya implementamos: el algoritmo de propagación inversa del error. La funcionalidad existente de la propagación inversa se puede usar para implementar el método Adam. Solo necesitamos implementar el algoritmo de actualización de los coeficientes de peso. De esta funcionalidad se encarga el método updateInputWeights, que se implementa en cada clase de neurona. Claro está, no vamos a excluir el algoritmo de descenso de gradiente estocástico creado previamente. Crearemos un algoritmo alternativo que nos permita seleccionar el método de entrenamiento a usar.
2.1. Construyendo el kernel en OpenCL
Vamos a analizar la implementación del método Adam para la clase CNeuronBaseOCL. En primer lugar, creamos el kernel UpdateWeightsAdam para implementar el método en OpenCL. En los parámetros del kernel, transmitiremos los punteros a las matrices de:
- los coeficientes de peso — matrix_w,
- los gradientes de error — matrix_g,
- los datos de entrada — matrix_i,
- las medias exponenciales de los gradientes — matrix_m,
- las medias exponenciales de los cuadrados de los gradientes — matrix_v.
__kernel void UpdateWeightsAdam(__global double *matrix_w, __global double *matrix_g, __global double *matrix_i, __global double *matrix_m, __global double *matrix_v, int inputs, double l, double b1, double b2)
Además, en los parámetros del kernel, transmitiremos el tamaño de la matriz de los datos de entrada y los hiperparámetros del algoritmo Adam.
Al inicio del kernel, obtenemos los números ordinales del hilo en las dos dimensiones, que indicarán los números de las neuronas de las capas actual y anterior, respectivamente. Utilizando los números obtenidos, determinamos el número inicial del elemento procesado en los búferes. Debemos tener en cuenta que el número de hilo resultante en la segunda dimensión se multiplica por "4". Esto se debe a que para reducir el número de hilos y el tiempo total de ejecución del programa, usaremos más cálculos vectoriales con vectores de 4 elementos.
{
int i=get_global_id(0);
int j=get_global_id(1);
int wi=i*(inputs+1)+j*4; Una vez determinada la posición de los elementos procesados en los búferes de datos, declaramos las variables vectoriales y las llenamos con los valores correspondientes. Usamos el método descrito anteriormente y rellenamos con ceros los datos restantes en los vectores.
double4 m, v, weight, inp; switch(inputs-j*4) { case 0: inp=(double4)(1,0,0,0); weight=(double4)(matrix_w[wi],0,0,0); m=(double4)(matrix_m[wi],0,0,0); v=(double4)(matrix_v[wi],0,0,0); break; case 1: inp=(double4)(matrix_i[j],1,0,0); weight=(double4)(matrix_w[wi],matrix_w[wi+1],0,0); m=(double4)(matrix_m[wi],matrix_m[wi+1],0,0); v=(double4)(matrix_v[wi],matrix_v[wi+1],0,0); break; case 2: inp=(double4)(matrix_i[j],matrix_i[j+1],1,0); weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],0); m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],0); v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],0); break; case 3: inp=(double4)(matrix_i[j],matrix_i[j+1],matrix_i[j+2],1); weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],matrix_w[wi+3]); m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],matrix_m[wi+3]); v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],matrix_v[wi+3]); break; default: inp=(double4)(matrix_i[j],matrix_i[j+1],matrix_i[j+2],matrix_i[j+3]); weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],matrix_w[wi+3]); m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],matrix_m[wi+3]); v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],matrix_v[wi+3]); break; }
El vector de gradiente se obtiene multiplicando el gradiente de la neurona actual por el vector de datos de entrada.
double4 g=matrix_g[i]*inp;
Después calculamos las medias exponenciales del gradiente y su cuadrado.
double4 mt=b1*m+(1-b1)*g; double4 vt=b2*v+(1-b2)*pow(g,2)+0.00000001;
Y calculamos los deltas del cambio de los parámetros.
double4 delta=l*mt/sqrt(vt);
Debemos tener en cuenta que no hemos corregido los momentos recibidos en el kernel. Hemos omitido intencionalmente en este paso aquí. Como los coeficientes ß1 y ß2 son iguales para todas las neuronas, y t (que aquí es el número de iteraciones de las actualizaciones de los parámetros de las neuronas) también es igual para todas las neuronas, el factor de corrección también será el mismo para todas las neuronas. Por consiguiente, no recalcularemos el coeficiente para cada neurona, sino que lo calcularemos una vez en el código del programa principal y transmitiremos el coeficiente de aprendizaje ajustado por este valor al kernel.
Tras calcular los deltas, solo necesitamos ajustar los coeficientes de peso y actualizar los momentos calculados en los búferes. Después, salimos del kernel.
switch(inputs-j*4) { case 2: matrix_w[wi+2]+=delta.s2; matrix_m[wi+2]=mt.s2; matrix_v[wi+2]=vt.s2; case 1: matrix_w[wi+1]+=delta.s1; matrix_m[wi+1]=mt.s1; matrix_v[wi+1]=vt.s1; case 0: matrix_w[wi]+=delta.s0; matrix_m[wi]=mt.s0; matrix_v[wi]=vt.s0; break; default: matrix_w[wi]+=delta.s0; matrix_m[wi]=mt.s0; matrix_v[wi]=vt.s0; matrix_w[wi+1]+=delta.s1; matrix_m[wi+1]=mt.s1; matrix_v[wi+1]=vt.s1; matrix_w[wi+2]+=delta.s2; matrix_m[wi+2]=mt.s2; matrix_v[wi+2]=vt.s2; matrix_w[wi+3]+=delta.s3; matrix_m[wi+3]=mt.s3; matrix_v[wi+3]=vt.s3; break; } };
En este código hay otro truco. Preste atención al orden inverso de las variantes case en el operador switch. Además, el operador break solo se usa después de case 0 y default. Este enfoque permite evitar la duplicación del mismo código para todas las variantes.
2.2. Cambios en el código de la clase de neurona del programa principal
Tras construir el kernel, necesitaremos realizar cambios en el código del programa principal. Primero, añadimos al bloque 'define' las constantes para trabajar con el kernel.
#define def_k_UpdateWeightsAdam 4 #define def_k_uwa_matrix_w 0 #define def_k_uwa_matrix_g 1 #define def_k_uwa_matrix_i 2 #define def_k_uwa_matrix_m 3 #define def_k_uwa_matrix_v 4 #define def_k_uwa_inputs 5 #define def_k_uwa_l 6 #define def_k_uwa_b1 7 #define def_k_uwa_b2 8
Creamos las enumeraciones para indicar los modos de entrenamiento y añadimos a las enumeraciones los búferes de momento.
enum ENUM_OPTIMIZATION { SGD, ADAM }; //--- enum ENUM_BUFFERS { WEIGHTS, DELTA_WEIGHTS, OUTPUT, GRADIENT, FIRST_MOMENTUM, SECOND_MOMENTUM };
Luego, directamente en el cuerpo de la clase CNeuronBaseOCL, añadimos los búferes para guardar los momentos, las constantes de las medias exponenciales, el contador de las iteraciones de entrenamiento y la variable para almacenar el método de entrenamiento.
class CNeuronBaseOCL : public CObject { protected: ......... ......... .......... CBufferDouble *FirstMomentum; CBufferDouble *SecondMomentum; //--- ......... ......... const double b1; const double b2; int t; //--- ......... ......... ENUM_OPTIMIZATION optimization;
En el constructor de la clase, establecemos los valores de las constantes e inicializamos los búferes.
CNeuronBaseOCL::CNeuronBaseOCL(void) : alpha(momentum), activation(TANH), optimization(SGD), b1(0.9), b2(0.999), t(1) { OpenCL=NULL; Output=new CBufferDouble(); PrevOutput=new CBufferDouble(); Weights=new CBufferDouble(); DeltaWeights=new CBufferDouble(); Gradient=new CBufferDouble(); FirstMomentum=new CBufferDouble(); SecondMomentum=new CBufferDouble(); }
Y no olvidamos añadir la eliminación de los objetos de búfer en el destructor de la clase.
CNeuronBaseOCL::~CNeuronBaseOCL(void) { if(CheckPointer(Output)!=POINTER_INVALID) delete Output; if(CheckPointer(PrevOutput)!=POINTER_INVALID) delete PrevOutput; if(CheckPointer(Weights)!=POINTER_INVALID) delete Weights; if(CheckPointer(DeltaWeights)!=POINTER_INVALID) delete DeltaWeights; if(CheckPointer(Gradient)!=POINTER_INVALID) delete Gradient; if(CheckPointer(FirstMomentum)!=POINTER_INVALID) delete FirstMomentum; if(CheckPointer(SecondMomentum)!=POINTER_INVALID) delete SecondMomentum; OpenCL=NULL; }
En los parámetros de la función de inicialización de clases, añadimos el modo de entrenamiento y, dependiendo del modo especificado, inicializamos los búferes. Si utilizamos el descenso de gradiente estocástico para el entrenamiento, inicializamos el búfer de deltas y eliminamos los búferes de momento. Si usamos el método Adam, inicializamos los búferes de momento y eliminamos el búfer de deltas.
bool CNeuronBaseOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint numNeurons, ENUM_OPTIMIZATION optimization_type) { if(CheckPointer(open_cl)==POINTER_INVALID || numNeurons<=0) return false; OpenCL=open_cl; optimization=optimization_type; //--- .................... .................... .................... .................... //--- if(numOutputs>0) { if(CheckPointer(Weights)==POINTER_INVALID) { Weights=new CBufferDouble(); if(CheckPointer(Weights)==POINTER_INVALID) return false; } int count=(int)((numNeurons+1)*numOutputs); if(!Weights.Reserve(count)) return false; for(int i=0;i<count;i++) { double weigh=(MathRand()+1)/32768.0-0.5; if(weigh==0) weigh=0.001; if(!Weights.Add(weigh)) return false; } if(!Weights.BufferCreate(OpenCL)) return false; //--- if(optimization==SGD) { if(CheckPointer(DeltaWeights)==POINTER_INVALID) { DeltaWeights=new CBufferDouble(); if(CheckPointer(DeltaWeights)==POINTER_INVALID) return false; } if(!DeltaWeights.BufferInit(count,0)) return false; if(!DeltaWeights.BufferCreate(OpenCL)) return false; if(CheckPointer(FirstMomentum)==POINTER_INVALID) delete FirstMomentum; if(CheckPointer(SecondMomentum)==POINTER_INVALID) delete SecondMomentum; } else { if(CheckPointer(DeltaWeights)==POINTER_INVALID) delete DeltaWeights; //--- if(CheckPointer(FirstMomentum)==POINTER_INVALID) { FirstMomentum=new CBufferDouble(); if(CheckPointer(FirstMomentum)==POINTER_INVALID) return false; } if(!FirstMomentum.BufferInit(count,0)) return false; if(!FirstMomentum.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(SecondMomentum)==POINTER_INVALID) { SecondMomentum=new CBufferDouble(); if(CheckPointer(SecondMomentum)==POINTER_INVALID) return false; } if(!SecondMomentum.BufferInit(count,0)) return false; if(!SecondMomentum.BufferCreate(OpenCL)) return false; } } else { if(CheckPointer(Weights)!=POINTER_INVALID) delete Weights; if(CheckPointer(DeltaWeights)!=POINTER_INVALID) delete DeltaWeights; } //--- return true; }
Y, por supuesto, introducimos los cambios directamente en el método para actualizar los coeficientes de peso updateInputWeights. En primer lugar, creamos un algoritmo de ramificación según el método de entrenamiento.
bool CNeuronBaseOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; uint global_work_offset[2]={0,0}; uint global_work_size[2]; global_work_size[0]=Neurons(); global_work_size[1]=NeuronOCL.Neurons(); if(optimization==SGD) {
Para el descenso de gradiente estocástico, trasladamos todo el código sin cambios.
OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_w,NeuronOCL.getWeightsIndex()); OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_g,getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_i,NeuronOCL.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_dw,NeuronOCL.getDeltaWeightsIndex()); OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_inputs,NeuronOCL.Neurons()); OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_learning_rates,eta); OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_momentum,alpha); ResetLastError(); if(!OpenCL.Execute(def_k_UpdateWeightsMomentum,2,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateWeightsMomentum: %d",GetLastError()); return false; } }
A continuación, en la rama del método Adam, configuramos los búferes de intercambio de datos para el kernel correspondiente.
else { if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_w,NeuronOCL.getWeightsIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_g,getGradientIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_i,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_m,NeuronOCL.getFirstMomentumIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_v,NeuronOCL.getSecondMomentumIndex())) return false;
A continuación, ajustamos la tasa de aprendizaje para la iteración de entrenamiento actual.
double lt=eta*sqrt(1-pow(b2,t))/(1-pow(b1,t));
Y establecemos los hiperparámetros de entrenamiento.
if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_inputs,NeuronOCL.Neurons())) return false; if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_l,lt)) return false; if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_b1,b1)) return false; if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_b2,b2)) return false;
Ahora, debemos recordar que en el kernel hemos usado valores vectoriales para los cálculos, por lo que disminuimos cuatro veces el número de hilos en la segunda dimensión.
uint rest=global_work_size[1]%4; global_work_size[1]=(global_work_size[1]-rest)/4 + (rest>0 ? 1 : 0);
Después de realizar todo el trabajo preparatorio, llamamos directamente al kernel y aumentamos el contador de iteraciones de entrenamiento.
ResetLastError(); if(!OpenCL.Execute(def_k_UpdateWeightsAdam,2,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateWeightsAdam: %d",GetLastError()); return false; } t++; }
Una vez realizada la ramificación, independientemente del método de entrenamiento, leemos los pesos recalculados. Como explicamos en el anterior artículo, el búfer también debe ser leído para las capas ocultas, porque esta operación no solo lee los datos, sino que también inicia la ejecución del kernel.
//--- return NeuronOCL.Weights.BufferRead(); }
Además de completar el algoritmo de cálculo del método de entrenamiento, es necesario ajustar los métodos usados para guardar y cargar la información sobre los resultados del entrenamiento de la neurona anterior. En el método Save, implementamos el guardado del método de entrenamiento y añadimos el contador de iteraciones de entrenamiento.
bool CNeuronBaseOCL::Save(const int file_handle) { if(file_handle==INVALID_HANDLE) return false; if(FileWriteInteger(file_handle,Type())<INT_VALUE) return false; //--- if(FileWriteInteger(file_handle,(int)activation,INT_VALUE)<INT_VALUE) return false; if(FileWriteInteger(file_handle,(int)optimization,INT_VALUE)<INT_VALUE) return false; if(FileWriteInteger(file_handle,(int)t,INT_VALUE)<INT_VALUE) return false;
Además, dejamos sin cambios el guardado de los búferes comunes para ambos métodos de entrenamiento.
if(CheckPointer(Output)==POINTER_INVALID || !Output.BufferRead() || !Output.Save(file_handle)) return false; if(CheckPointer(PrevOutput)==POINTER_INVALID || !PrevOutput.BufferRead() || !PrevOutput.Save(file_handle)) return false; if(CheckPointer(Gradient)==POINTER_INVALID || !Gradient.BufferRead() || !Gradient.Save(file_handle)) return false; //--- if(CheckPointer(Weights)==POINTER_INVALID) { FileWriteInteger(file_handle,0); return true; } else FileWriteInteger(file_handle,1); //--- if(CheckPointer(Weights)==POINTER_INVALID || !Weights.BufferRead() || !Weights.Save(file_handle)) return false;
Luego creamos una ramificación del algoritmo para cada método de entrenamiento preservando los búferes específicos.
if(optimization==SGD) { if(CheckPointer(DeltaWeights)==POINTER_INVALID || !DeltaWeights.BufferRead() || !DeltaWeights.Save(file_handle)) return false; } else { if(CheckPointer(FirstMomentum)==POINTER_INVALID || !FirstMomentum.BufferRead() || !FirstMomentum.Save(file_handle)) return false; if(CheckPointer(SecondMomentum)==POINTER_INVALID || !SecondMomentum.BufferRead() || !SecondMomentum.Save(file_handle)) return false; } //--- return true; }
Después realizamos cambios similares y en la misma secuencia en el método Load.
Podrá familiarizarse con el código de todos los métodos y funciones en los anexos.
2.3. Cambios en el código de las clases sin usar OpenCL
Para mantener el rendimiento de todas las clases en las mismas condiciones, hemos realizado cambios similares en las clases que trabajaban con MQL5 puro sin usar OpenCL.
El primer paso consiste en añadir variables para guardar los datos de los momentos en la clase CConnection y establecer los valores iniciales en el constructor de la clase.
class CConnection : public CObject { public: double weight; double deltaWeight; double mt; double vt; CConnection(double w) { weight=w; deltaWeight=0; mt=0; vt=0; }
También debemos añadir el procesamiento de las nuevas variables a los métodos de guardado y carga de los datos de conexión.
bool CConnection::Save(int file_handle) { ........... ........... ........... if(FileWriteDouble(file_handle,mt)<=0) return false; if(FileWriteDouble(file_handle,vt)<=0) return false; //--- return true; } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CConnection::Load(int file_handle) { ............ ............ ............ mt=FileReadDouble(file_handle); vt=FileReadDouble(file_handle); //--- return true; }
A continuación, añadimos a la clase de neurona CNeuronBase las variables para guardar el método de optimización y el contador de iteraciones para actualizar los pesos.
class CNeuronBase : public CObject { protected: ......... ......... ......... ENUM_OPTIMIZATION optimization; const double b1; const double b2; int t;
Después realizamos las adiciones necesarias al método de inicialización de neuronas. En primer lugar, añadimos a los parámetros del método una variable para indicar el método de optimización y organizar su guardado en la variable definida anteriormente.
bool CNeuronBase::Init(uint numOutputs,uint myIndex, ENUM_OPTIMIZATION optimization_type) { optimization=optimization_type;
Luego creamos una ramificación del algoritmo usando el método de optimización en el método updateInputWeights para actualizar los pesos. Antes del ciclo de iteración de las conexiones, recalculamos el factor de aprendizaje ajustado, y creamos en un ciclo dos ramas para calcular los pesos.
bool CNeuron::updateInputWeights(CLayer *&prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- double lt=eta*sqrt(1-pow(b2,t))/(1-pow(b1,t)); int total=prevLayer.Total(); for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron= prevLayer.At(n); CConnection *con=neuron.Connections.At(m_myIndex); if(CheckPointer(con)==POINTER_INVALID) continue; if(optimization==SGD) con.weight+=con.deltaWeight=(gradient!=0 ? eta*neuron.getOutputVal()*gradient : 0)+(con.deltaWeight!=0 ? alpha*con.deltaWeight : 0); else { con.mt=b1*con.mt+(1-b1)*gradient; con.vt=b2*con.vt+(1-b2)*pow(gradient,2)+0.00000001; con.weight+=con.deltaWeight=lt*con.mt/sqrt(con.vt); t++; } } //--- return true; }
Y añadimos a los métodos de guardado y carga el procesamiento de las nuevas variables.
Podrá encontrar el código completo de todos los métodos en el archivo adjunto.
2.4. Cambios en el código de la clase de red neuronal del programa principal
Además de los cambios efectuados en las clases de neurona, necesitamos realizar cambios en otros objetos de nuestro código. Primero, necesitamos transmitir a la neurona la información sobre el método de entrenamiento del programa principal. Los datos del programa principal se transmiten a la clase de red neuronal a través de la clase CLayerDescription. Asimismo, para transmitir la información sobre el método de entrenamiento, debemos añadir el método apropiado a esta clase.
class CLayerDescription : public CObject { public: CLayerDescription(void); ~CLayerDescription(void) {}; //--- int type; int count; int window; int step; ENUM_ACTIVATION activation; ENUM_OPTIMIZATION optimization; };
Ahora, realizamos las adiciones finales al constructor de la clase de red neuronal CNet. Aquí añadimos la indicación del método de optimización al inicializar las neuronas de la red, incrementamos el número de kernels OpenCL usados y declaramos un nuevo kernel de optimización, Adam. A continuación, mostramos el código del constructor modificado con los cambios resaltados.
CNet::CNet(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
int total=Description.Total();
if(total<=0)
return;
//---
layers=new CArrayLayer();
if(CheckPointer(layers)==POINTER_INVALID)
return;
//---
CLayer *temp;
CLayerDescription *desc=NULL, *next=NULL, *prev=NULL;
CNeuronBase *neuron=NULL;
CNeuronProof *neuron_p=NULL;
int output_count=0;
int temp_count=0;
//---
next=Description.At(1);
if(next.type==defNeuron || next.type==defNeuronBaseOCL)
{
opencl=new COpenCLMy();
if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true))
delete opencl;
}
else
{
if(CheckPointer(opencl)!=POINTER_INVALID)
delete opencl;
}
//---
for(int i=0; i<total; i++)
{
prev=desc;
desc=Description.At(i);
if((i+1)<total)
{
next=Description.At(i+1);
if(CheckPointer(next)==POINTER_INVALID)
return;
}
else
next=NULL;
int outputs=(next==NULL || (next.type!=defNeuron && next.type!=defNeuronBaseOCL) ? 0 : next.count);
temp=new CLayer(outputs);
int neurons=(desc.count+(desc.type==defNeuron || desc.type==defNeuronBaseOCL ? 1 : 0));
if(CheckPointer(opencl)!=POINTER_INVALID)
{
CNeuronBaseOCL *neuron_ocl=NULL;
switch(desc.type)
{
case defNeuron:
case defNeuronBaseOCL:
neuron_ocl=new CNeuronBaseOCL();
if(CheckPointer(neuron_ocl)==POINTER_INVALID)
{
delete temp;
return;
}
if(!neuron_ocl.Init(outputs,0,opencl,desc.count,desc.optimization))
{
delete temp;
return;
}
neuron_ocl.SetActivationFunction(desc.activation);
if(!temp.Add(neuron_ocl))
{
delete neuron_ocl;
delete temp;
return;
}
neuron_ocl=NULL;
break;
default:
return;
break;
}
}
else
for(int n=0; n<neurons; n++)
{
switch(desc.type)
{
case defNeuron:
neuron=new CNeuron();
if(CheckPointer(neuron)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
neuron.Init(outputs,n,desc.optimization);
neuron.SetActivationFunction(desc.activation);
break;
case defNeuronConv:
neuron_p=new CNeuronConv();
if(CheckPointer(neuron_p)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
if(CheckPointer(prev)!=POINTER_INVALID)
{
if(prev.type==defNeuron)
{
temp_count=(int)((prev.count-desc.window)%desc.step);
output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
else
if(n==0)
{
temp_count=(int)((output_count-desc.window)%desc.step);
output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
}
if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count,desc.optimization))
neuron=neuron_p;
break;
case defNeuronProof:
neuron_p=new CNeuronProof();
if(CheckPointer(neuron_p)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
if(CheckPointer(prev)!=POINTER_INVALID)
{
if(prev.type==defNeuron)
{
temp_count=(int)((prev.count-desc.window)%desc.step);
output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
else
if(n==0)
{
temp_count=(int)((output_count-desc.window)%desc.step);
output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
}
if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count,desc.optimization))
neuron=neuron_p;
break;
case defNeuronLSTM:
neuron_p=new CNeuronLSTM();
if(CheckPointer(neuron_p)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
output_count=(next!=NULL ? next.window : desc.step);
if(neuron_p.Init(outputs,n,desc.window,1,output_count,desc.optimization))
neuron=neuron_p;
break;
}
if(!temp.Add(neuron))
{
delete temp;
delete layers;
return;
}
neuron=NULL;
}
if(!layers.Add(temp))
{
delete temp;
delete layers;
return;
}
}
//---
if(CheckPointer(opencl)==POINTER_INVALID)
return;
//--- create kernels
opencl.SetKernelsCount(5);
opencl.KernelCreate(def_k_FeedForward,"FeedForward");
opencl.KernelCreate(def_k_CaclOutputGradient,"CaclOutputGradient");
opencl.KernelCreate(def_k_CaclHiddenGradient,"CaclHiddenGradient");
opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum");
opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam");
//---
return;
} Podrá familiarizarse con el código completo de todas las clases y sus métodos en los anexos.
3. Simulación
Las pruebas de optimización usando el método Adam se realizaron en las mismas condiciones que todas las pruebas anteriores: instrumento EURUSD, marco temporal H1 y los datos de 20 velas consecutivas; la formación se llevó a cabo utilizando la historia de los últimos 2 años. Para la prueba, creamos Fractal_OCL_Adam. Este asesor se creó a partir del asesor experto Fractal_OCL especificando el método de optimización Adam al describir la red neuronal en la función OnInit del programa principal.
desc.count=(int)HistoryBars*12; desc.type=defNeuron; desc.optimization=ADAM;
El número de capas y neuronas se mantuvo sin cambios.
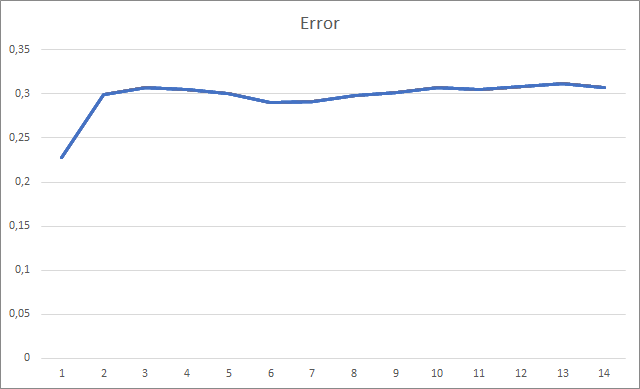
Inicializamos el asesor con pesos aleatorios que iban de -1 a 1, excluyendo los valores cero. Durante las pruebas, literalmente después de la segunda época de entrenamiento, el error de la red neuronal se estabilizó alrededor del 30%. Recordemos que al realizar el entrenamiento usando el método de descenso de gradiente estocástico, el error se estabilizó alrededor del 42% después de la 5ª época de entrenamiento.
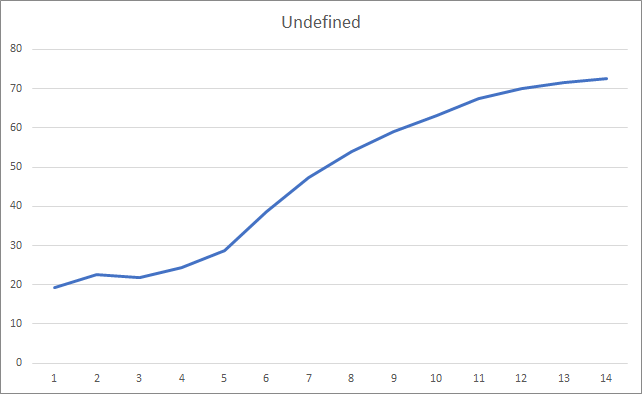
El gráfico de fractales omitidos muestra un aumento paulatino en el indicador a lo largo del entrenamiento. Al mismo tiempo, tras 12 épocas de entrenamiento, observamos una disminución gradual en la tasa de crecimiento del indicador. Después de la 14ª época de formación, el valor de este indicador era del 72,5%. Como comparación, al entrenar una red neuronal similar con el método de descenso de gradiente estocástico, después de 10 épocas de entrenamiento, la proporción de fractales omitidos era del 97-100% con diferentes tasas de aprendizaje.
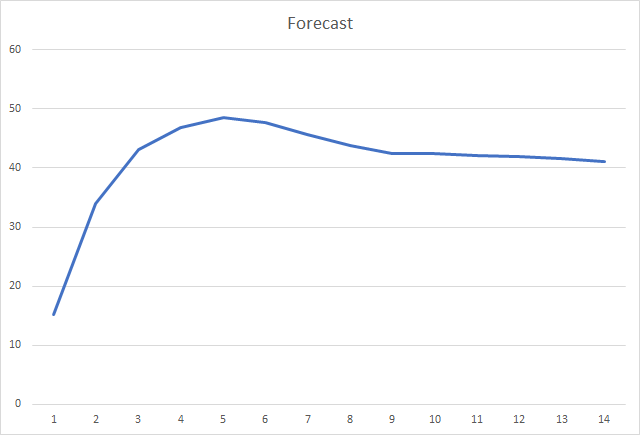
Y, probablemente, el indicador más importante sea la proporción de fractales correctamente definidos. Durante el entrenamiento posterior a la 5ª era, este indicador alcanzó el 48,6%, disminuyendo luego gradualmente hasta el 41,1%. Al realizar el entrenamiento usando el método de descenso de gradiente estocástico, tras 90 épocas de entrenamiento, este indicador no superó el 10%.
Conclusión
El artículo ha analizado las características distintivas de los métodos adaptativos para optimizar los parámetros de las redes neuronales, añadiendo además el modo de optimización Adam al modelo de red neuronal construido previamente. Durante las pruebas, entrenamos la red neuronal mediante el método de Adam y los resultados obtenidos superan los indicadores obtenidos previamente al entrenar una red neuronal similar con el método de descenso de gradiente estocástico.
El trabajo realizado muestra nuestro progreso hacia la meta.
Enlaces
- Redes neuronales: así de sencillo
- Redes neuronales: así de sencillo (Parte 2): Entrenamiento y prueba de la red
- Redes neuronales: así de sencillo (Parte 3): Redes convolucionales
- Redes neuronales: así de sencillo (Parte 4): Redes recurrentes
- Redes neuronales: así de sencillo (Parte 5): Cálculos multihilo en OpenCL
- Redes neuronales: así de sencillo (Parte 6): Experimentos con la tasa de aprendizaje de la red neuronal
- Adam: A Method for Stochastic Optimization
Programas utilizados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Fractal_OCL_Adam.mq5 | Asesor | Asesor con la red neuronal de clasificación (3 neuronas en la capa de salida) con uso de la tecnología OpenCL y el método de entrenamiento Adam. |
| 2 | NeuroNet.mqh | Biblioteca de clase | Biblioteca de clases para crear la red neuronal |
| 3 | NeuroNet.cl | Biblioteca | Biblioteca de código del programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/8598
Remuestreo avanzado y selección de modelos CatBoost con el método de fuerza bruta
Ejemplos de análisis de gráficos utilizando el TD Sequential de DeMark y los niveles de Murray-Gann
Aproximación por fuerza bruta a la búsqueda de patrones (Parte II): Inmersión
Aplicación práctica de las redes neuronales en el trading. Python (Parte I)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso