
Redes neuronales: así de sencillo (Parte 3): Redes convolucionales
Contenido
- Introducción
- 1. Particularidades distintivas de las redes neuronales convolucionales
- 2. Principios de entrenamiento de las neuronas de las capas convolucionales
- 3. Construyendo una red neuronal convolucional
- 3.1. Clase básica de las neuronas
- 3.2. Elemento de la capa de submuestreo
- 3.3. Elemento de la capa convolucional
- 3.4. Creando la clase de red neuronal convolucional
- 4. Simulación
- Conclusión
- Enlaces
- Programas utilizados en el artículo
Introducción
Prosiguiendo con el tema de las redes neuronales, proponemos al lector analizar los principios de funcionamiento y construcción de las redes neuronales convolucionales (Convolutional Neural Network). Este tipo de redes neuronales se usa ampliamente en problemas relacionados con el reconocimiento de objetos en imágenes de fotos y vídeos. Se considera que las redes neuronales convolucionales son resistentes al zoom, los ángulos cambiantes y otras distorsiones de la imagen espacial. La arquitectura de dichas redes permite encontrar objetos con igual éxito en cualquier lugar de una escena. Hablando concretamente de trading, resultaría interesante usar las redes neuronales convolucionalesa aplicadas a la detección de patrones comerciales en un gráfico de precios.
1. Particularidades distintivas de las redes neuronales convolucionales
Las redes convolucionales, en comparación con un perceptrón completamente conectado, poseen dos nuevos tipos de capas: la capa convolucional (filtro) y la capa de submuestreo. Estas capas se alternan para seleccionar los principales componentes y eliminar ruidos en los datos de origen, reduciendo paralelamente la dimensión de los datos (volumen). Luego, dichos datos se introducen en un perceptrón completamente conectado para la toma de decisiones. En la siguiente figura, podemos gráficamente ver la estructura de una red neuronal convolucional. Dependiendo de las tareas, podemos utilizar secuencialmente varios grupos de capas convolucionales y de submuestreo alternas.
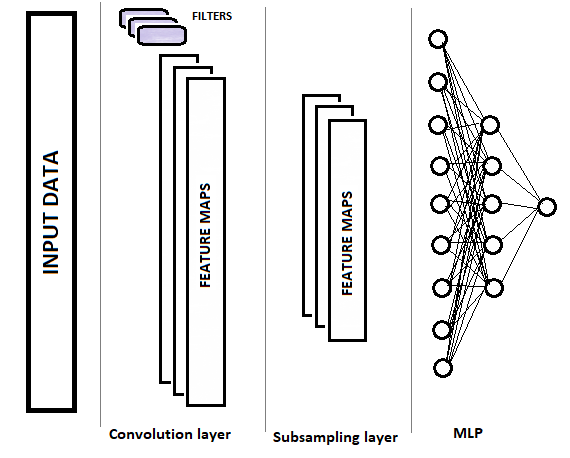
1.1. Capa convolucional
La capa de convolucional es la responsable de reconocer los objetos en la matriz de datos de origen. En esta capa, se realizan las operaciones secuenciales de convolución matemática de los datos originales con un pequeño patrón (filtro) que ejerce de núcleo de convolución.
La convolución supone una operación en el análisis funcional que, al ser aplicada a dos funciones f y g, retorna una tercera función correspondiente a la función de correlación cruzada f(x) y g(-x). La operación de convolución se puede interpretar como la "similitud" de una función con una copia reflejada y desplazada de otra (Wikipedia ).
Dicho de otra form, la capa convolucional busca un elemento de plantilla en toda la muestra original. En este caso, con cada iteración, la plantilla se desplaza a lo largo de la matriz de datos inicial con un salto dado, que puede ir desde "1" hasta el tamaño de la plantilla. Si el tamaño del salto de desplazamiento es inferior al tamaño de la plantilla, dicha convolución se denominará superposición.
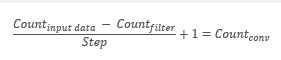
Como resultado de la operación de convolución, obtendremos una serie de características que muestran la "similitud" de los datos iniciales con el patrón necesario en cada iteración. Para normalizar los datos, se usan las funciones de activación. El tamaño de la matriz resultante será inferior al de la matriz de datos inicial; el número de dichas matrices será igual al número de plantillas (filtros).
También es de suma importancia para nosotros que las propias plantillas, en lugar de establecerse al diseñar la red neuronal, sean seleccionadas en el proceso de aprendizaje.
1.2. Capa de submuestreo
La siguiente capa de submuestreo se usa para reducir la dimensión de la matriz de características y filtrar el ruido. La utilización de esta iteración se basa en la suposición de que la similitud entre los datos originales y el patrón es primaria, mientras que las coordenadas exactas de una característica en la matriz de datos original no son tan importantes. Esto permite solucionar el problema del escalado, ya que permite cierta variabilidad en la distancia entre los objetos buscados.
En esta etapa, los datos se compactan conservando el valor máximo o promedio dentro de una "ventana" dada. Por consiguiente, solo se guardará un valor para cada "ventana" de datos. Las operaciones se efectúan de forma iterativa desplazando la ventana en un salto dado con cada nueva iteración. La compactación de datos se lleva a cabo por separado para cada matriz de características.
Con bastante frecuencia, se aplican capas de submuestreo con una ventana y un salto igual a 2; esto nos permite reducir a la mitad la dimensión de la matriz de características. No obstante, podemos utilizar ventanas realmente más grandes, mientras que las iteraciones de compactación se pueden efectuar tanto con superposición (cuando el tamaño del salto es inferior al tamaño de la ventana) como sin ella.
A la salida de la capa de submuestreo, obtenemos matrices de características de una dimensión menor.
Dependiendo de la complejidad de los problemas, podemos usar uno o más grupos de la capa convolucional y de la capa de submuestreo después de esta última. Sus principios de construcción y su funcionalidad se corresponden con la capa que hemos descrito antes. En general, tras uno o varios grupos de convolución + compactación, las matrices de características obtenidas para todos los filtros son recopiladas en un solo vector y suministradas a un perceptrón multicapa para que la red neuronal tome una decisión (describimos con detalle la construcción del perceptrón multicapa en la primera parte de esta serie de artículos).
2. Principios de entrenamiento de las neuronas de las capas convolucionales
El entrenamiento de las redes neuronales convolucionales se realiza con el método de propagación inversa del error que conocemos de publicaciones anteriores. Este método pertenece a los métodos de aprendizaje supervisado y consiste en hacer descender el gradiente de error desde la capa de salida de neuronas a través de las capas ocultas hasta la capa de entrada de neuronas, corrigiendo los coeficientes de ponderación hacia el antigradiente.
Ya hablamos sobre el entrenamiento del perceptrón multicapa en el primer artículo de esta serie, así que no nos detendremos en ello. Vamos a analizar el entrenamiento de neuronas en las capas de submuestreo y convolucionales.
En la capa de submuestreo, el gradiente de error se calcula para cada elemento en la matriz de características por analogía con los gradientes de las neuronas en un perceptrón completamente conectado. El algoritmo para transmitir el gradiente a la capa anterior depende de la operación de compactación usada. Si solo tomamos el valor máximo, el gradiente completo se transmitirá a la neurona con el valor máximo (para los elementos restantes dentro de la ventana de compactación, se establecerá un gradiente cero). Si usamos una operación de promediado dentro de la ventana, el gradiente se distribuirá uniformemente sobre todos los elementos dentro de la ventana.
Como la operación de compactación no utiliza coeficientes de peso, no se corrigirá nada en el proceso de entrenamiento.
Los cálculos son un poco más complicados al entrenar las neuronas de la capa convolucional. El gradiente de error se calcula para cada elemento de la matriz de características y desciende a las neuronas correspondientes de la capa anterior. El proceso de entrenamiento de una capa convolucional se basa en las operaciones de convolución y convolución inversa.
Para transmitir el gradiente de error de la capa de submuestreo a la capa convolucional, los bordes de la matriz de gradientes de error obtenidos de la capa de submuestreo se complementan en primer lugar con elementos cero, y después se realiza la convolución de la matriz resultante con el núcleo de convolución girado 180°. En la salida, obtenemos una matriz de gradientes de error con un tamaño igual a la matriz de datos de entrada, en la que los índices de gradiente corresponderán con el índice de la neurona correspondiente que precede a la capa convolucional.
Para obtener los deltas de los coeficientes de ponderación, se realiza la convolución de la matriz de valores de entrada con la matriz de gradientes de error de esta capa desplegada en 180°. En la salida, obtenemos una matriz de deltas con un tamaño igual al kernel de convolución. Los deltas obtenidos deben corregirse con la derivada de la función de activación de la capa convolucional y el factor de aprendizaje. Tras realizar dichas operaciones, los coeficientes de ponderación del núcleo de convolución se cambian por el valor de los deltas ajustados.
Seguramente, suene bastante complicado de entender. Vamos a tratar de explicar estos puntos al analizar el código con detalle.
3. Construyendo una red neuronal convolucional
La red neuronal convolucional constará de tres tipos de capas neuronales (convolucional, de submuestreo y completamente conectada) con clases distintivas de neuronas y diferentes funciones para la propagación hacia delante y la propagación inversa. Al mismo tiempo, necesitaremos combinar todas las neuronas en una sola red y organizar la llamada al método de procesamiento de datos que corresponda a la neurona procesada. A nuestro juicio, la forma más simple de organizar este proceso es usando la herencia de clases y la virtualización de funciones.
En primer lugar, debemos construir la estructura de herencia de las clases.
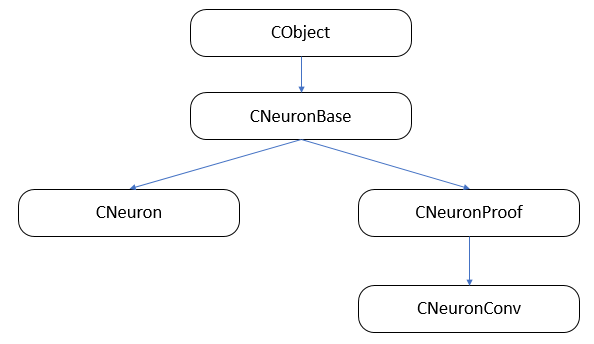
3.1. Clase básica de las neuronas.
En el primer artículo, creamos la clase de capa CLayer como descendiente de CArrayObj, que es una clase de matriz dinámica para almacenar punteros a objetos de la clase CObject. Por consiguiente, todas las neuronas deberán ser heredadas de esta clase. Usando como base la clase CObject, vamos a crear la clase básica CNeuronBase. En el cuerpo de la clase, declaramos las variables comunes a todos los tipos de neuronas y creamos las plantillas para los métodos principales. Asimismo, declaramos todos los métodos de clase como virtuales, para permitir su posterior redefinición.
class CNeuronBase : public CObject { protected: double eta; double alpha; double outputVal; uint m_myIndex; double gradient; CArrayCon *Connections; //--- virtual bool feedForward(CLayer *prevLayer) { return false; } virtual bool calcHiddenGradients( CLayer *&nextLayer) { return false; } virtual bool updateInputWeights(CLayer *&prevLayer) { return false; } virtual double activationFunction(double x) { return 1.0; } virtual double activationFunctionDerivative(double x) { return 1.0; } virtual CLayer *getOutputLayer(void) { return NULL; } public: CNeuronBase(void); ~CNeuronBase(void); virtual bool Init(uint numOutputs, uint myIndex); //--- virtual void setOutputVal(double val) { outputVal=val; } virtual double getOutputVal() { return outputVal; } virtual void setGradient(double val) { gradient=val; } virtual double getGradient() { return gradient; } //--- virtual bool feedForward(CObject *&SourceObject); virtual bool calcHiddenGradients( CObject *&TargetObject); virtual bool updateInputWeights(CObject *&SourceObject); //--- virtual bool Save( int const file_handle); virtual bool Load( int const file_handle) { return(Connections.Load(file_handle)); } //--- virtual int Type(void) const { return defNeuronBase; } };
Los nombres de las variables y los métodos se corresponden con los mencionados anteriormente. Proponemos al lector analizar los métodos feedForward(CObject *&SourceObject), сalcHiddenGradients(CObject *&TargetObject) y updateInputWeights(CObject *&SourceObject), puesto que en los métodos indicados se realiza el despacho para trabajar con las capas convolucionales y las capas completamente conectadas.
3.1.1. Propagación hacia delante.
El método feedForward(CObject *&SourceObject) se llama durante la propagación hacia delante, para calcular el valor de neurona resultante. Durante una propagación hacia adelante, cada neurona en capas completamente conectadas toma los valores de todas las neuronas de la capa anterior y tiene que recibir como entrada la capa anterior al completo. En las capas convolucional y de submuestreo, solo una parte de los datos relacionados con este filtro se suministra a la neurona. En el método analizado, seleccionamos el algoritmo según el tipo de clase obtenida en los parámetros.
Primero, comprobamos la validez del puntero al objeto obtenido en los parámetros del método.
bool CNeuronBase::feedForward(CObject *&SourceObject) { bool result=false; //--- if(CheckPointer(SourceObject)==POINTER_INVALID) return result;
Como resulta imposible declarar instancias de clase dentro del operador select, prepararemos plantillas de antemano.
CLayer *temp_l; CNeuronProof *temp_n;
Después, comprobamos en el operador select el tipo de objeto obtenido en los parámetros. Si obtenemos una referencia a una capa de neuronas, la capa anterior estará completamente conectada y, por consiguiente, llamaremos al método para trabajar con las capas completamente conectadas (que describimos con detalle en el primer artículo). Si estamos tenemos entre manos una neurona de una capa convolucional o de submuestreo, primero obtendremos la capa de neuronas de salida de este filtro y luego usaremos el método para procesar una capa completamente conectada, transmitiéndole en los parámetros la capa de neuronas del filtro actual y guardando el resultado del procesamiento en la variable result (más tarde discutiremos sobre la estructura de las neuronas en las capa convolucional y la de submuestreo). Después realizar el procesamiento, salimos del método transmitiendo el resultado del trabajo.
switch(SourceObject.Type()) { case defLayer: temp_l=SourceObject; result=feedForward(temp_l); break; case defNeuronConv: case defNeuronProof: temp_n=SourceObject; result=feedForward(temp_n.getOutputLayer()); break; } //--- return result; }
3.1.2. Calculando el gradiente de error.
Por analogía con la propagación hacia delante, hemos creado un despachador para llamar a la función que calcula el gradiente de error en las capas ocultas de la red neuronal сalcHiddenGradients (CObject *&TargetObject). La estructura de la construcción y la lógica del método se asemejan a las descritas anteriormente. Primero, comprobamos la validez de la referencia obtenida. A continuación, declaramos las variables para almacenar las referencias a los objetos correspondientes. Y en la función de selección según el tipo de objeto obtenido, seleccionamos el método necesario. Las diferencias comienzan al transmitir una referencia a un elemento de la capa convolucional o de submuestreo en los parámetros. El cálculo del gradiente de error utilizando dichas neuronas es distinto, y no se aplica a todas las neuronas de la capa anterior, sino solo dentro de la ventana de muestreo. Por consiguiente, el cálculo del gradiente se ha trasladado a estas neuronas en el método calcInputGradients. En este caso, además, existen diferencias en los métodos de cálculo por la capa o para una neurona en particular. Por ello, llamaremos al método necesario según el tipo de objeto desde el que se llame.
bool CNeuronBase::calcHiddenGradients(CObject *&TargetObject) { bool result=false; //--- if(CheckPointer(TargetObject)==POINTER_INVALID) return result; //--- CLayer *temp_l; CNeuronProof *temp_n; switch(TargetObject.Type()) { case defLayer: temp_l=TargetObject; result=calcHiddenGradients(temp_l); break; case defNeuronConv: case defNeuronProof: switch(Type()) { case defNeuron: temp_n=TargetObject; result=temp_n.calcInputGradients(GetPointer(this),m_myIndex); break; default: temp_n=GetPointer(this); temp_l=temp_n.getOutputLayer(); temp_n=TargetObject; result=temp_n.calcInputGradients(temp_l); break; } break; } //--- return result; }
El despachador updateInputWeights (CObject *&SourceObject) para la actualización de pesos se construye según los principios descritos anteriormente. Podrá encontrar el código detallado del método en los archivos adjuntos.
3.2. Elemento de la capa de submuestreo.
El componente principal de la capa de submuestreo es la clase CNeuronProof, heredada de la clase básica CNeuronBase descrita anteriormente. Al procesar la arquitectura, hemos tomado la decisión de crear en la capa de submuestreo una instancia de esta clase para cada filtro. Por consiguiente, hemos introducido variables adicionales (iWindow e iStep) para guardar el tamaño de la ventana de compactación y el salto de cambio. También vamos a añadir una capa interna de neuronas para guardar las matrices de características, los gradientes de error y, de ser necesario, los pesos para transmitir las características a un perceptrón completamente conectado. Además, añadiremos un método para obtener el puntero a la capa interna de neuronas según una solicitud.
class CNeuronProof : public CNeuronBase { protected: CLayer *OutputLayer; int iWindow; int iStep; virtual bool feedForward(CLayer *prevLayer); virtual bool calcHiddenGradients( CLayer *&nextLayer); public: CNeuronProof(void){}; ~CNeuronProof(void); virtual bool Init(uint numOutputs,uint myIndex,int window, int step, int output_count); //--- virtual CLayer *getOutputLayer(void) { return OutputLayer; } virtual bool calcInputGradients( CLayer *prevLayer) ; virtual bool calcInputGradients( CNeuronBase *prevNeuron, uint index) ; //--- methods for working with files virtual bool Save( int const file_handle) { return(CNeuronBase::Save(file_handle) && OutputLayer.Save(file_handle)); } virtual bool Load( int const file_handle) { return(CNeuronBase::Load(file_handle) && OutputLayer.Load(file_handle)); } virtual int Type(void) const { return defNeuronProof; } };
No debemos olvidarnos de redefinir la lógica de las funciones virtuales declaradas en la clase básica.
3.2.1. Propagación hacia delante.
El método feedForward se usa para filtrar el ruido y reducir la dimensión de la matriz de características. En la solución descrita, la función de media aritmética se usa para compactar los datos. Vamos a analizar con más detalle el código del método. Al comienzo del método, comprobamos la relevancia del puntero obtenido para la anterior capa de neuronas.
bool CNeuronProof::feedForward(CLayer *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
A continuación, recorremos todas las neuronas de la capa obtenida en los parámetros, con el salto dado.
int total=prevLayer.Total()-iWindow+1; CNeuron *temp; for(int i=0;(i<=total && result);i+=iStep) {
En el cuerpo del ciclo, creamos un ciclo anidado para calcular la suma de los valores de salida de las neuronas de la capa anterior dentro de la ventana de compactación establecida.
double sum=0; for(int j=0;j<iWindow;j++) { temp=prevLayer.At(i+j); if(CheckPointer(temp)==POINTER_INVALID) continue; sum+=temp.getOutputVal(); }
Tras calcular la suma, usaremos la neurona correspondiente de la capa interna que guarda los datos resultantes y escribiremos en su valor resultante la relación entre la suma obtenida y el tamaño de la ventana. Esta relación será la media aritmética de la ventana de compactación actual.
temp=OutputLayer.At(i/iStep); if(CheckPointer(temp)==POINTER_INVALID) return false; temp.setOutputVal(sum/iWindow); } //--- return true; }
Una vez terminada la enumeración de todas las neuronas, el método finalizará.
3.2.2. Calculando el gradiente de error.
Para calcular el gradiente de error en esta clase, hemos creado dos métodos: calcHiddenGradients y calcInputGradients. El primero reúne los datos sobre los gradientes de error de la capa siguiente y calcula el gradiente para los elementos de la capa actual. El segundo, usando como base los datos obtenidos en el primer método, distribuye el error entre los elementos de la capa anterior.
Al inicio del método calcHiddenGradients, como hacemos normalmente, comprobamos la validez de la referencia obtenida en los parámetros. Además, verificamos el estado de la capa de neuronas interna.
bool CNeuronProof::calcHiddenGradients( CLayer *&nextLayer) { if(CheckPointer(nextLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID || OutputLayer.Total()<=0) return false;
Después, utilizando un ciclo, iteramos todas las neuronas de la capa interna y llamamos al método para calcular el gradiente de error.
gradient=0; int total=OutputLayer.Total(); CNeuron *temp; for(int i=0;i<total;i++) { temp=OutputLayer.At(i); if(CheckPointer(temp)==POINTER_INVALID) return false; temp.setGradient(temp.sumDOW(nextLayer)); } //--- return true; }
Querríamos llamar la atención del lector sobre el hecho de que este método funciona correctamente si a continuación sigue una capa de neuronas completamente conectada. Si sigue una capa convolucional o de submuestreo, será necesario usar el método calcInputGradients de la neurona de la capa siguiente.
En los parámetros, el método calcInputGradients obtiene una referencia a la capa anterior. Y de inmediato, al inicio del método, verificamos la validez de esta referencia, el estado de la capa de neuronas interna.
bool CNeuronProof::calcInputGradients(CLayer *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID) return false;
A continuación, comprobamos el tipo del primer elemento obtenido en los parámetros de la capa. Si la referencia obtenida señala a una capa de submuestreo o convolucional, solicitaremos una referencia a la capa interna de neuronas que corresponde al filtro.
if(prevLayer.At(0).Type()!=defNeuron) { CNeuronProof *temp=prevLayer.At(m_myIndex); if(CheckPointer(temp)==POINTER_INVALID) return false; prevLayer=temp.getOutputLayer(); if(CheckPointer(prevLayer)==POINTER_INVALID) return false; }
Después, organizamos un ciclo para iterar por todas las neuronas de la capa anterior, comprobando obligatoriamente la validez de la referencia a la neurona procesada.
CNeuronBase *prevNeuron, *outputNeuron; int total=prevLayer.Total(); for(int i=0;i<total;i++) { prevNeuron=prevLayer.At(i); if(CheckPointer(prevNeuron)==POINTER_INVALID) continue;
A continuación, determinamos qué neuronas de la capa interna se ven influidas por la neurona procesada.
double prev_gradient=0; int start=i-iWindow+iStep; start=(start-start%iStep)/iStep; double stop=(i-i%iStep)/iStep+1;
En un ciclo, calculamos el gradiente de error para la neurona procesada y guardamos el resultado. Tras iterar todas las neuronas de la capa anterior, finalizamos el método.
for(int out=(int)fmax(0,start);out<(int)fmin(OutputLayer.Total(),stop);out++) { outputNeuron=OutputLayer.At(out); if(CheckPointer(outputNeuron)==POINTER_INVALID) continue; prev_gradient+=outputNeuron.getGradient()/iWindow; } prevNeuron.setGradient(prev_gradient); } //--- return true; }
De forma similar, hemos construido un método con el mismo nombre para calcular el gradiente de una neurona individual. La diferencia reside en la exclusión de un ciclo externo para iterar neuronas. En lugar del mismo, se realiza una llamada según el número ordinal de la neurona.
Como los pesos no se usan en la capa de submuestreo, podemos omitir el método para actualizarlos. O, de forma alternativa, para mantener la estructura unificada de las clases de neuronas, podemos crear un método vacío que, cuando sea llamado, retorne el valor true.
El lector podrá familiarizarse con el código de todos los métodos y funciones en los archivos anexos.
3.3. Elemento de la capa convolucional.
Para construir una capa convolucional, utilizaremos los objetos de la clase CNeuronConv, que heredarán de la clase CNeuronProof. Como función de activación para este tipo de neuronas, hemos elegido un ReLU paramétrico. Esta función resulta más fácil de calcular que la tangente hiperbólica usada en las neuronas de un perceptrón completamente conectado. Para calcularla, introduciremos la variable adicional param.
class CNeuronConv : public CNeuronProof { protected: double param; //PReLU param virtual bool feedForward(CLayer *prevLayer); virtual bool calcHiddenGradients(CLayer *&nextLayer); virtual double activationFunction(double x); virtual bool updateInputWeights(CLayer *&prevLayer); public: CNeuronConv() : param(0.01) { }; ~CNeuronConv(void) { }; //--- virtual bool calcInputGradients(CLayer *prevLayer) ; virtual bool calcInputGradients(CNeuronBase *prevNeuron, uint index) ; virtual double activationFunctionDerivative(double x); virtual int Type(void) const { return defNeuronConv; } };
Los métodos de propagación hacia delante e inversa se basan en algoritmos similares a la clase CNeuron Proof. Las únicas diferencias están en el uso de la función de activación y los coeficientes de peso. Por consiguiente, no vemos motivo alguno para analizarlos con detalle. Vamos a echar un vistazo al método para ajustar los pesos updateInputWeights.
En los parámetros, el método obtiene la referencia a la capa de neuronas anterior; inmediatamente después, verificamos la validez de la referencia obtenida y el estado de la capa interna.
bool CNeuronConv::updateInputWeights(CLayer *&prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID) return false;
Acto seguido, creamos un ciclo para iterar por todos los coeficientes de peso y, por supuesto, después de obtener la referencia al siguiente objeto de enlace, verificamos su validez.
CConnection *con; for(int n=0; n<iWindow && !IsStopped(); n++) { con=Connections.At(n); if(CheckPointer(con)==POINTER_INVALID) continue;
Después de ello, calculamos la convolución de la matriz de datos de entrada con la matriz de los gradientes de error de la capa interna rotada 180°. Esto se realiza en un ciclo por todos los elementos de la capa interna, multiplicado por los elementos de la matriz de datos de entrada según el siguiente esquema:
- el primer elemento de la matriz de datos de entrada (con un desplazamiento del número de pasos igual al número ordinal del coeficiente de peso) se multiplica por el último elemento de la matriz de gradiente de error,
- el segundo elemento de la matriz de datos de entrada (con un desplazamiento del número de pasos igual al número ordinal del coeficiente de peso) se multiplica por el penúltimo elemento de la matriz de gradiente de error,
- y así sucesivamente, hasta que el elemento con un índice igual al número de elementos en la matriz de la capa interna con un desplazamiento en un número de pasos igual al número ordinal del coeficiente de peso, se multiplique por el primer elemento de la matriz de gradiente de error.
A continuación, sumamos los productos obtenidos.
double delta=0; int total_i=OutputLayer.Total(); CNeuron *prev, *out; for(int i=0;i<total_i;i++) { prev=prevLayer.At(n*iStep+i); out=OutputLayer.At(total_i-i-1); if(CheckPointer(prev)==POINTER_INVALID || CheckPointer(out)==POINTER_INVALID) continue; delta+=prev.getOutputVal()*out.getGradient(); }
La suma calculada de los productos actúa como base para corregir los coeficientes de peso. Corregimos los coeficientes de peso considerando la velocidad de entrenamiento establecida.
con.weight+=con.deltaWeight=(delta!=0 ? eta*delta : 0)+(con.deltaWeight!=0 ? alpha*con.deltaWeight : 0); } //--- return true; }
Después de ajustar todos los coeficientes de peso, salimos del método.
Ya describimos con detalle la clase CNeuron en el primer artículo de esta serie; no ha cambiado mucho, así que no hablaremos de ella en este artículo.
3.4. Creando la clase de red neuronal convolucional.
Ahora que hemos creado todos los ladrillos, podemos comenzar a construir una casa: para ello, crearemos una clase de red neuronal convolucional que combinará todos los tipos de neuronas en una estructura clara, organizando el trabajo de nuestra red neuronal. La primera cuestión que surge al crear esta clase es cómo establecer la estructura de red necesaria. En un perceptrón completamente conectado, hemos transmitido una matriz de elementos en la que indicamos el número de neuronas en cada capa. Ahora, necesitamos más información para generar la capa de red necesaria. Para ello, crearemos una pequeña clase CLayerDescription para describir la construcción de la capa. Esta clase no contiene ningún método (salvo el constructor y el destructor), en cambio, incluye las variables para especificar el tipo de neuronas en la capa, el número de dichas neuronas, el tamaño de la ventana y el salto para las neuronas en las capas convolucional y de submuestreo. En los parámetros del constructor de la clase de la red neuronal convolucional, transmitimos una referencia a la matriz de clases con la descripción de las capas.
class CLayerDescription : public CObject { public: CLayerDescription(void); ~CLayerDescription(void){}; //--- int type; int count; int window; int step; }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CLayerDescription::CLayerDescription(void) : type(defNeuron), count(0), window(1), step(1) {}
Vamos a analizar la estructura de la clase de red neuronal convolucional CNetConvolution. La clase contiene:
- layers — matriz de capas;
- recentAverageError — error actual de la red;
- recentAverageSmoothingFactor — factor de promediación del error;
- CNetConvolution — constructor de la clase;
- ~CNetConvolution — destructor de la clase;
- feedForward — método de propagación hacia delante;
- backProp — método de propagación inversa;
- getResults — método para obtener los resultados de la última propagación hacia delante;
- getRecentAverageError — método para obtener el error de red actual;
- Save y Load — métodos para guardar y cargar una red previamente creada y entrenada.
class CNetConvolution { public: CNetConvolution(CArrayObj *Description); ~CNetConvolution(void) { delete layers; } bool feedForward( CArrayDouble *inputVals); void backProp( CArrayDouble *targetVals); void getResults(CArrayDouble *&resultVals) ; double getRecentAverageError() { return recentAverageError; } bool Save( string file_name, double error, double undefine, double forecast, datetime time, bool common=true); bool Load( string file_name, double &error, double &undefine, double &forecast, datetime &time, bool common=true); //--- static double recentAverageSmoothingFactor; virtual int Type(void) const { return defNetConv; } private: CArrayLayer *layers; double recentAverageError; };
Los nombres de los métodos y algoritmos de construcción son similares a los descritos anteriormente para un perceptrón completamente conectado en el primer artículo de este ciclo. Vamos a detenernos solo en los métodos principales de la clase.
3.4.1. Constructor de una clase de red neuronal convolucional.
Analicemos el constructor de clase. En los parámetros, el constructor obtiene una referencia a una matriz de descripciones de capas para construir la red. Por consiguiente, comprobamos la validez de la referencia obtenida, determinamos el número de capas a construir y creamos una nueva instancia de la matriz de capas.
CNetConvolution::CNetConvolution(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
int total=Description.Total();
if(total<=0)
return;
//---
layers=new CArrayLayer();
if(CheckPointer(layers)==POINTER_INVALID)
return; A continuación, añadimos las variables internas.
CLayer *temp; CLayerDescription *desc=NULL, *next=NULL, *prev=NULL; CNeuronBase *neuron=NULL; CNeuronProof *neuron_p=NULL; int output_count=0; int temp_count=0;
Con esto, concluimos la etapa preparatoria y procedemos directamente a la generación cíclica de la capa de la red neuronal. Al comienzo del ciclo, leemos información sobre la capa actual y la capa siguiente.
for(int i=0;i<total;i++) { prev=desc; desc=Description.At(i); if((i+1)<total) { next=Description.At(i+1); if(CheckPointer(next)==POINTER_INVALID) return; } else next=NULL;
Calculamos el número de conexiones de salida para la capa y creamos una nueva instancia de la clase de capa neuronal. Debemos considerar que el número de conexiones en la salida de la capa se indica solo antes de la capa completamente conectada; de lo contrario, indicaremos cero. Esto se debe a que las neuronas convolucionales almacenan los propios coeficientes de peso de entrada, mientras que la capa de submuestreo no los utiliza en absoluto.
int outputs=(next==NULL || next.type!=defNeuron ? 0 : next.count); temp=new CLayer(outputs);
A continuación, en el ciclo tiene lugar la generación de neuronas con la división del algoritmo según el tipo de neuronas en la capa creada. Para las capas completamente conectadas, creamos e inicializamos una nueva instancia de una neurona. Debemos considerar que para las capas completamente conectadas se crea una neurona más de las indicadas en la descripción. Esta neurona se usará como sesgo bayesiano.
for(int n=0;n<(desc.count+(i>0 && desc.type==defNeuron ? 1 : 0));n++) { switch(desc.type) { case defNeuron: neuron=new CNeuron(); if(CheckPointer(neuron)==POINTER_INVALID) { delete temp; delete layers; return; } neuron.Init(outputs,n); break;
Para la capa convolucional, creamos una nueva instancia de la neurona. Calculamos el número de elementos de salida según la información sobre la capa anterior e inicializamos la neurona recién creada.
case defNeuronConv: neuron_p=new CNeuronConv(); if(CheckPointer(neuron_p)==POINTER_INVALID) { delete temp; delete layers; return; } if(CheckPointer(prev)!=POINTER_INVALID) { if(prev.type==defNeuron) { temp_count=(int)((prev.count-desc.window)%desc.step); output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } else if(n==0) { temp_count=(int)((output_count-desc.window)%desc.step); output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } } if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count)) neuron=neuron_p; break;
Usamos un algoritmo similar para las neuronas en la capa de submuestreo.
case defNeuronProof: neuron_p=new CNeuronProof(); if(CheckPointer(neuron_p)==POINTER_INVALID) { delete temp; delete layers; return; } if(CheckPointer(prev)!=POINTER_INVALID) { if(prev.type==defNeuron) { temp_count=(int)((prev.count-desc.window)%desc.step); output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } else if(n==0) { temp_count=(int)((output_count-desc.window)%desc.step); output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } } if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count)) neuron=neuron_p; break; }
Después de declarar e inicializar la neurona, la añadimos a la capa neuronal.
if(!temp.Add(neuron)) { delete temp; delete layers; return; } neuron=NULL; }
Tras completar el ciclo de generación de neuronas para la siguiente capa, añadimos la capa al repositorio. Una vez generadas todas las capas, salimos del método.
if(!layers.Add(temp)) { delete temp; delete layers; return; } } //--- return; }
3.4.2. Método de propagación hacia delante de una red neuronal convolucional.
Todo el trabajo de la red neuronal se organiza en el método de propagación hacia adelante feedForward. En los parámetros, este método obtiene los datos iniciales para su análisis (en nuestro caso, se trata de la información del gráfico de precios y los indicadores usados). En primer lugar, comprobamos la validez de la referencia obtenida a la matriz de datos y el estado de inicialización de la red neuronal.
bool CNetConvolution::feedForward(CArrayDouble *inputVals) { if(CheckPointer(layers)==POINTER_INVALID || CheckPointer(inputVals)==POINTER_INVALID || layers.Total()<=1) return false;
A continuación, declaramos las variables auxiliares y transferimos los datos externos recibidos a la capa de entrada de la red neuronal.
CLayer *previous=NULL; CLayer *current=layers.At(0); int total=MathMin(current.Total(),inputVals.Total()); CNeuronBase *neuron=NULL; for(int i=0;i<total;i++) { neuron=current.At(i); if(CheckPointer(neuron)==POINTER_INVALID) return false; neuron.setOutputVal(inputVals.At(i)); }
Tras cargar los datos iniciales en la red neuronal, iniciamos un ciclo de enumeración secuencial de las capas neuronales desde la entrada de la red neuronal hasta su salida.
CObject *temp=NULL; for(int l=1;l<layers.Total();l++) { previous=current; current=layers.At(l); if(CheckPointer(current)==POINTER_INVALID) return false;
Dentro del ciclo iniciado, ponemos en marcha para cada capa un ciclo anidado para iterar sobre todas las neuronas en la capa con un nuevo cálculo de sus valores. Debemos tener en cuenta que para las capas neuronales completamente conectadas, el valor de la última neurona no se calcula de nuevo. Como hemos indicado antes, se utiliza como sesgo bayesiano, y solo utilizaremos su coeficiente de peso.
total=current.Total(); if(current.At(0).Type()==defNeuron) total--; //--- for(int n=0;n<total;n++) { neuron=current.At(n); if(CheckPointer(neuron)==POINTER_INVALID) return false;
Después, la selección del método depende del tipo de neuronas de la capa anterior. Para las capas completamente conectadas, llamaremos al método de propagación hacia delante, indicando en los parámetros la referencia a la capa anterior.
if(previous.At(0).Type()==defNeuron) { temp=previous; if(!neuron.feedForward(temp)) return false; continue; }
Si antes había una capa convolucional o de submuestreo, veremos el tipo de neurona recalculada. Para una neurona de una capa completamente conectada, reuniremos las capas internas de todas las neuronas de la capa anterior en una sola, y luego llamaremos al método de propagación hacia delante de la neurona actual, indicando la referencia a la capa total de neuronas en los parámetros.
if(neuron.Type()==defNeuron) { if(n==0) { CLayer *temp_l=new CLayer(total); if(CheckPointer(temp_l)==POINTER_INVALID) return false; CNeuronProof *proof=NULL; for(int p=0;p<previous.Total();p++) { proof=previous.At(p); if(CheckPointer(proof)==POINTER_INVALID) return false; temp_l.AddArray(proof.getOutputLayer()); } temp=temp_l; } if(!neuron.feedForward(temp)) return false; if(n==total-1) { CLayer *temp_l=temp; temp_l.FreeMode(false); temp_l.Shutdown(); delete temp_l; } continue; }
Tras completar el ciclo de enumeración de todas las neuronas de dicha capa, será necesario eliminar el objeto de la neurona total. En este caso, deberemos eliminar el objeto de capa sin eliminar los objetos neuronales contenidos en dicha capa, es decir, estos objetos se seguirán usando en nuestras capas convolucionales y de submuestreo. Para hacer esto, estableceremos el indicador m_free_mode en el estado false, y solo entonces eliminaremos el objeto.
Si tenemos delante un elemento de una capa convolucional o de submuestreo, llamaremos al método de propagación hacia delante con transmisión en los parámetros de la referencia al elemento anterior del filtro correspondiente.
temp=previous.At(n); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!neuron.feedForward(temp)) return false; } } //--- return true; }
Una vez enumeradas todas las neuronas y capas, saldremos del método.
3.4.3. Método de propagación inversa de una red neuronal convolucional.
La red neuronal se entrena mediante en el método de propagación inversa backProp. En este, se implementa el método de propagación inversa del error desde la capa de salida de la red neuronal hacia sus entradas. Por consiguiente, en los parámetros, este método recibe los datos reales.
Al inicio del método, comprobamos la validez de la referencia al objeto de valor de referencia o valor patrón.
void CNetConvolution::backProp(CArrayDouble *targetVals) { if(CheckPointer(targetVals)==POINTER_INVALID) return;
A continuación, calculamos el error cuadrático medio a la salida de la propagación hacia delante de la red neuronal partiendo de los datos reales, y luego calculamos los gradientes de error de las neuronas de la capa de salida.
CLayer *outputLayer=layers.At(layers.Total()-1); if(CheckPointer(outputLayer)==POINTER_INVALID) return; //--- double error=0.0; int total=outputLayer.Total()-1; for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=outputLayer.At(n); double target=targetVals.At(n); double delta=(target>1 ? 1 : target<-1 ? -1 : target)-neuron.getOutputVal(); error+=delta*delta; neuron.calcOutputGradients(targetVals.At(n)); } error/= total; error = sqrt(error); recentAverageError+=(error-recentAverageError)/recentAverageSmoothingFactor;
El siguiente paso consiste en organizar un ciclo con iteración de todas las capas de la red neuronal en orden inverso; en dicho ciclo, iniciaremos un ciclo anidado con iteración de todas las neuronas de la capa correspondiente para recalcular los gradientes de los errores neuronales en las capas ocultas.
CNeuronBase *neuron=NULL; CObject *temp=NULL; for(int layerNum=layers.Total()-2; layerNum>0; layerNum--) { CLayer *hiddenLayer=layers.At(layerNum); CLayer *nextLayer=layers.At(layerNum+1); total=hiddenLayer.Total(); for(int n=0; n<total && !IsStopped(); ++n) {
Al igual que sucede con la propagación hacia delante, la selección del método necesario para actualizar los gradientes de error se basa en el análisis de los tipos de neurona actual y las neuronas de la siguiente capa. Si a continuación viene una capa de neuronas completamente conectada, llamaremos al método calcHiddenGradients de la neurona analizada, transmitiendo en los parámetros una referencia al objeto de la siguiente capa de la red neuronal.
neuron=hiddenLayer.At(n); if(nextLayer.At(0).Type()==defNeuron) { temp=nextLayer; neuron.calcHiddenGradients(temp); continue; }
Si después sigue una capa convolucional o de submuestreo, entonces comprobaremos el tipo de la neurona actual. Para una neurona completamente conectada, organizaremos un ciclo para iterar por todos los filtros de la siguiente capa, iniciando el recálculo del gradiente de error de cada filtro para dicha neurona, y sumaremos después los gradientes resultantes. En el caso de que la capa actual también sea convolucional o de submuestreo, definiremos el gradiente de error usando el filtro correspondiente.
if(neuron.Type()==defNeuron) { double g=0; for(int i=0;i<nextLayer.Total();i++) { temp=nextLayer.At(i); neuron.calcHiddenGradients(temp); g+=neuron.getGradient(); } neuron.setGradient(g); continue; } temp=nextLayer.At(n); neuron.calcHiddenGradients(temp); } }
Tras actualizar todos los gradientes, ejecutaremos ciclos similares con la misma lógica de ramificación para actualizar los coeficientes de peso de las neuronas. Después de actualizar los pesos, saldremos del método.
for(int layerNum=layers.Total()-1; layerNum>0; layerNum--) { CLayer *layer=layers.At(layerNum); CLayer *prevLayer=layers.At(layerNum-1); total=layer.Total()-(layer.At(0).Type()==defNeuron ? 1 : 0); int n_conv=0; for(int n=0; n<total && !IsStopped(); n++) { neuron=layer.At(n); if(CheckPointer(neuron)==POINTER_INVALID) return; if(neuron.Type()==defNeuronProof) continue; switch(prevLayer.At(0).Type()) { case defNeuron: temp=prevLayer; neuron.updateInputWeights(temp); break; case defNeuronConv: case defNeuronProof: if(neuron.Type()==defNeuron) { for(n_conv=0;n_conv<prevLayer.Total();n_conv++) { temp=prevLayer.At(n_conv); neuron.updateInputWeights(temp); } } else { temp=prevLayer.At(n); neuron.updateInputWeights(temp); } break; default: temp=NULL; break; } } } }
Podrá encontrar el código completo de todos los métodos y clases en el archivo adjunto.
4. Simulación
Para comprobar el funcionamiento de la red neuronal convolucional, hemos utilizado el asesor de clasificación del segundo artículo del presente ciclo. Recordemos que la red neuronal tiene la misión de predecir un fractal en la vela actual. Para ello, suministramos los datos sobre la formación de las últimas N velas y la información de los 4 osciladores para el mismo periodo a la entrada de la red neuronal.
En la capa convolucional de nuestra nueva red neuronal, creamos 4 filtros que buscarán patrones en el conjunto total de datos respecto a la formación de velas y las lecturas de los osciladores en la vela analizada. La ventana y el salto del filtro corresponderán a la cantidad de datos respecto a la descripción de una vela. Dicho de otra forma: vamos a comparar toda la información sobre cada vela con un patrón determinado y a retornar el valor de convergencia. De ser necesario, este enfoque nos permitirá complementar los datos iniciales con nueva información sobre las velas (incluidos indicadores adicionales para el análisis, etcétera) sin sufrir pérdidas significativas de rendimiento.
En la capa de submuestreo, reducimos el tamaño de la matriz de características y suavizamos los resultados promediando los datos.
El propio asesor ha necesitado unos cambios mínimos. Hablamos del cambio de la clase de la red neuronal al declarar variables y la creación de una instancia.
CNetConvolution *Net;
Asimismo, hemos realizado cambios en la parte encargada de establecer la estructura de la red neuronal en la función OnInit. Para las simulaciones, se ha utilizado una red con una capa convolucional y una capa de submuestreo con 4 filtros cada una. La estructura de las capas completamente conectadas se ha mantenido sin cambios (lo hemos hecho así a propósito, para valorar el impacto de las capas convolucionales en el funcionamiento de toda la red).
Net=new CNetConvolution(NULL); ResetLastError(); if(CheckPointer(Net)==POINTER_INVALID || !Net.Load(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false)) { printf("%s - %d -> Error of read %s prev Net %d",__FUNCTION__,__LINE__,FileName+".nnw",GetLastError()); CArrayObj *Topology=new CArrayObj(); if(CheckPointer(Topology)==POINTER_INVALID) return INIT_FAILED; //--- CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuron; if(!Topology.Add(desc)) return INIT_FAILED; //--- int filters=4; desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=filters; desc.type=defNeuronConv; desc.window=12; desc.step=12; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=filters; desc.type=defNeuronProof; desc.window=3; desc.step=2; if(!Topology.Add(desc)) return INIT_FAILED; //--- int n=1000; bool result=true; for(int i=0;(i<4 && result);i++) { desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=n; desc.type=defNeuron; result=(Topology.Add(desc) && result); n=(int)MathMax(n*0.3,20); } if(!result) { delete Topology; return INIT_FAILED; } //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; if(!Topology.Add(desc)) return INIT_FAILED; delete Net; Net=new CNetConvolution(Topology); delete Topology; if(CheckPointer(Net)==POINTER_INVALID) return INIT_FAILED; dError=-1; dUndefine=0; dForecast=0; dtStudied=0; }
El resto del código del asesor se ha mantenido sin cambios.
Las simulaciones se han realizado con la pareja EURUSD, periodo H1. En el mismo terminal, en diferentes gráficos del mismo instrumento, hemos iniciado simultáneamente 2 asesores expertos: con una red neuronal convolucional y con una red totalmente conectada. Los parámetros de las capas completamente conectadas de la red neuronal convolucional son similares a los de la red completamente conectada del segundo asesor experto, es decir, acabamos de añadir capas convolucionales y de submuestreo a una red construida previamente.
Las simulaciones han demostrado un pequeño aumento del rendimiento en la red neuronal convolucional. A pesar de que hemos añadido dos capas, según los resultados de las 24 épocas, el tiempo medio de entrenamiento para una época en la red neuronal convolucional ha sido de 2 horas y 4 minutos, y en la red completamente conectada, de 2 horas y 10 minutos.
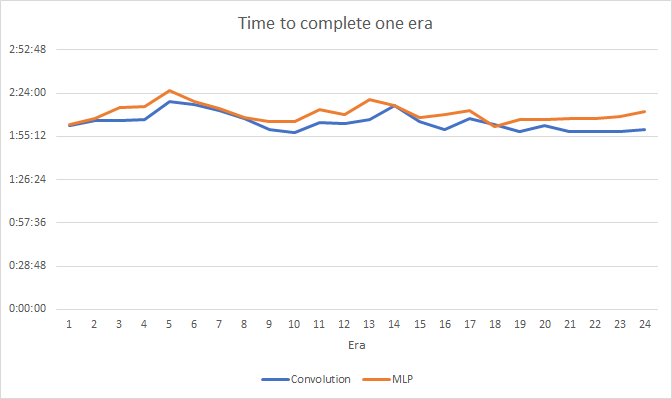
Al mismo tiempo, la red neuronal convolucional ha mostrado resultados ligeramente mejores en cuanto al error de predicción y al "acierto en el blanco".
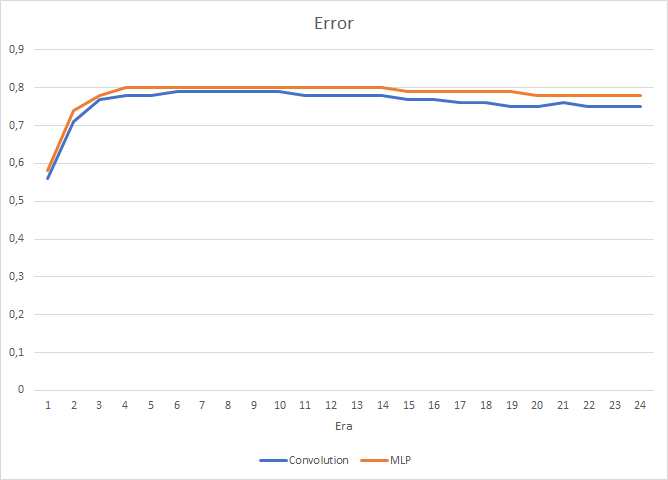
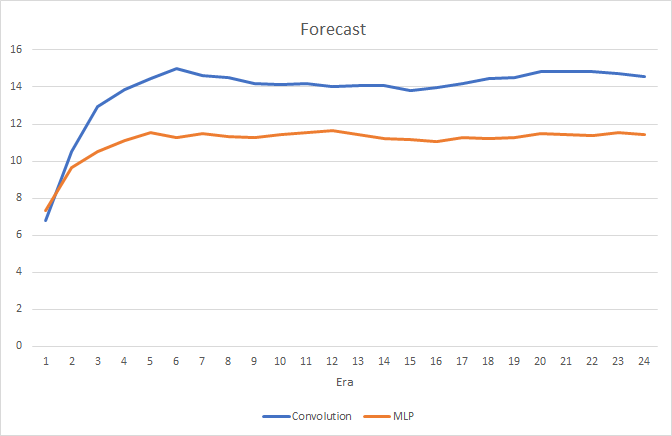
Visualmente, podemos comprender que las señales aparecen con menos frecuencia en el gráfico de la red neuronal convolucional, pero más cerca del objetivo.
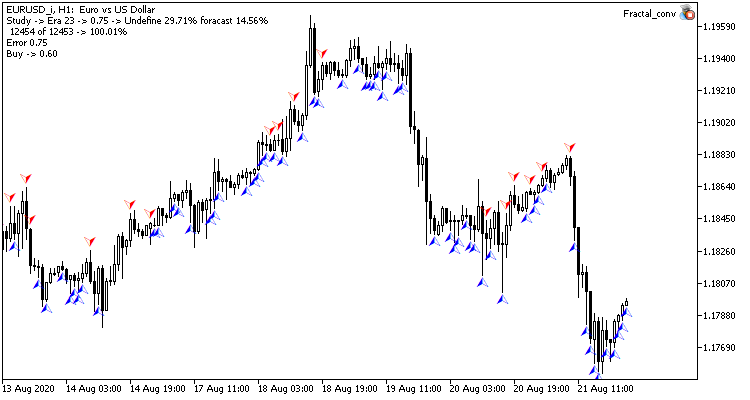
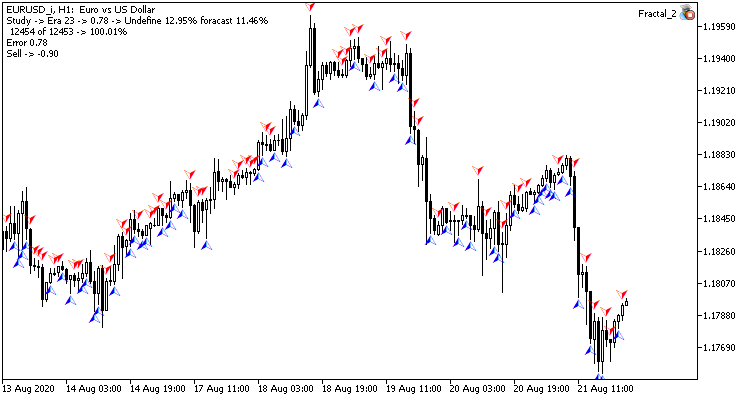
Conclusión
En el presente artículo, hemos analizado la posibilidad de usar redes neuronales convolucionales en los mercados financieros. Y las simulaciones muestran que su utilización puede mejorar los resultados de una red neuronal completamente conectada. En concreto, esto puede deberse al procesamiento preliminar de los datos suministrados a la entrada de un perceptrón completamente conectado. En las capas convolucional y de submuestreo, los datos son filtrados de ruido, lo cual permite mejorar la calidad de los datos iniciales y, como resultado, la calidad de la red neuronal. Asimismo, la reducción de la dimensionalidad ayuda a disminuir el número de conexiones del perceptrón con los datos originales, lo cual aumenta el rendimiento.
Enlaces
- Redes neuronales: así de sencillo
- Redes neuronales: así de sencillo (Parte 2): Entrenamiento y prueba de la red
Programas utilizados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Fractal.mq5 | Asesor | Asesor con la red neuronal de regresión (1 neurona en la capa de salida) |
| 2 | Fractal_2.mq5 | Asesor | Asesor con la red neuronal de clasificación (3 neuronas en la capa de salida) |
| 3 | NeuroNet.mqh | Biblioteca de clase | Biblioteca de clases para crear la red neuronal (perceptrón) |
| 4 | Fractal_conv.mq5 | Asesor | Asesor con la red neuronal convolucional de clasificación (3 neuronas en la capa de salida) |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/8234
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Redes neuronales: así de sencillo (Parte 4): Redes recurrentes
Redes neuronales: así de sencillo (Parte 4): Redes recurrentes
 Gradient boosting en el aprendizaje de máquinas transductivo y activo
Gradient boosting en el aprendizaje de máquinas transductivo y activo
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
El artículo es ciertamente interesante. Especialmente en cuanto al hecho de que todo se implementa en MQL y no se requieren bibliotecas. Espero que haya una secuela. Desafortunadamente, las pruebas del Asesor Experto aún no han dado resultados positivos.
Nuevo artículo Neural networks made easy (Part 3): Se han publicado redes convolucionales:
Autor: Dmitriy Gizlyk
Hola. Gracias por esto. Tengo una pregunta para usted. ¿Cómo se obtienen los valores de píxel para el gráfico o la imagen? He buscado pero no encuentro una explicación de cómo obtener los valores de los píxeles del gráfico para utilizarlos en la capa convolucional de entrada.
Hola, tienes razón. La capa convolucional no toma píxeles del gráfico. Mi idea era otra. Tomo los datos de los indicadores differnet y el precio histórico y lo pongo a la entrada de la red neuronal. La capa de convolución busca patrones de estos datos y devuelve algún valor para cada vela.
Hola, tienes razón. La capa de convolución no toma píxeles del gráfico. Mi idea era otra. Tomo los datos de los indicadores differnet y precio histórico y ponerlo a la entrada de la red neuronal. La capa de convolución busca patrones de estos datos y devuelve algún valor para cada vela.
Entiendo, gracias.