Técnicas útiles y exóticas para el comercio automático

Contenido

• Introducción
• Algoritmo de cierre parcial de posiciones utilizando el movimiento de la última barra
• Algoritmo de variación híbrida del lote
• Principio de promediación
• Señales directas e indirectas sobre la consistencia de una técnica comercial
• Usando las ondas de balance y equidad
• Conclusión

Introducción

Hay muchas técnicas comerciales que, en opinión de sus propios creadores o del público, deberían ser rentables. En este artículo, no analizaremos esas técnicas, ya que existe mucha información sobre ellas en una amplia variedad de recursos, y no podremos ofrecer nada nuevo e interesante con este enfoque. En cambio, hemos decidido recopilar varias técnicas útiles y heterodoxas que resultarían útiles tanto a nivel teórico como práctico. Alguna de estas técnicas podría resultar familiar al lector, o quizá no, pero intentaremos exponer los métodos más interesantes y explicar por qué merece la pena utilizarlos. Además, y lo que es más importante, mostraremos en la práctica cómo pueden ayudarnos dichas técnicas.

Algoritmo de cierre parcial de posiciones utilizando el movimiento de la última barra

Teoría:

Queremos abordar esta cuestión como una técnica comercial que resultará útil en el caso de que hayamos abierto posiciones y no estemos seguros de la dirección que tomará el movimiento posterior de los precios. Un cierre adecuado de la posición por partes puede compensar las pérdidas derivadas de los spreads y, con una buena optimización, generará incluso beneficios.

A nuestro juicio, merece la pena comenzar partiendo de la siguiente consideración: ya hemos entrado en el mercado, pero no sabemos dónde salir. No importa en qué dirección hayamos entrado, todavía tenemos que salir de la posición en algún momento. Algunos jugadores, por supuesto, pueden mantener sus posiciones durante años, pero entonces debemos asumir que el robot operará intensamente y ofrecerá una alta frecuencia de transacciones. Es posible salir de todas a la vez, pero debe hacerse poco a poco. Ya sabemos que la estructura del mercado es plana; hablando en términos sencillos, esto significa que el precio tiende a regresar antes del comienzo de la media onda actual. En otras palabras, un movimiento alcista indica que la probabilidad de continuación es siempre inferior al 50%, lo que a su vez implica que la probabilidad de un movimiento contrario es superior al 50%. Si usamos el cierre completo, podemos omitir todas las ondas y no sacar provecho de ellas, porque no sabemos cuál es la amplitud futura de las estas. El cierre parcial puede librarnos de esta idea. Podremos obtener el máximo beneficio partiendo del hecho de que no conocemos la naturaleza de las futuras ondas.

Ahora que sabemos qué son las ondas y que nunca desaparecerán del mercado, podemos pasar al principio de cierre de posiciones, que implica la obtención de al menos algún beneficio aunque la entrada se realice de forma incorrecta. En realidad, tal mecanismo existe.

Podemos encontrar muchos de estos algoritmos, pero aquí mostraremos solo el más simple y efectivo (en nuestra opinión). Este aprovecha la suposición de que cuanto más grande y poderoso sea el movimiento ocurrido en la vela anterior completamente formada, más probable será que haya un movimiento de retroceso bastante fuerte. En general, ¿por qué necesitamos este mecanismo? La respuesta es elemental: para aumentar los beneficios y reducir las pérdidas. Los impulsos también son ondas. Solo que estas ondas resultan mucho más útiles que las ondas clásicas normales en nuestro concepto habitual. El asunto es que cuanto más fiables sean las ondas más próximas del mercado, y cuanto más poderoso sea el impulso y menor sea el tiempo en que haya sucedido, mayor será la probabilidad de un retroceso en el futuro cercano y mayor resultará la magnitud que esperamos de este retroceso. El asunto es que deberemos conseguir que al aumentar la potencia del impulso, el cierre parcial de la posición resulte aún más fuerte. Vamos a representar la explicación en una figura:

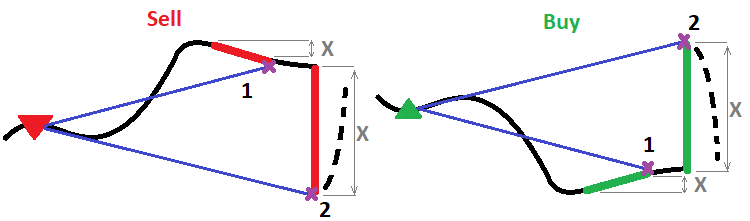
Para calcular el volumen de la parte de la posición que debemos cerrar, podemos usar cualquier función. Mostraremos 2 funciones. Una es lineal y la segunda es de potencia:

• { D } - potencia
• { X } - movimiento de la barra anterior en puntos
• { С } - coeficiente de escala
• { Lc(X) = C * Pow(X , D) } - función de potencia que calcula el lote que se cerrará en la vela actual
• { Lc(X) = C * X } - función lineal que calcula el lote que se cerrará en la vela actual

Si echamos un vistazo más de cerca, veremos que una función lineal representa un caso especial de una función de potencia para "D" = 1, así que podemos ignorarla: solo la hemos mostrado como ejemplo desde donde parte la lógica de pensamiento. Las ideas siempre son sencillas de inicio, pero luego, tras pensarlo bien, conseguimos herramientas mucho más versátiles: solo necesitamos comenzar con algo simple.

Para no establecer directamente estos coeficientes sin pensar en cómo influirán más tarde en el proceso, vamos a introducir varios parámetros de control que determinarán nuestros coeficientes:

• { StartLotsToOnePoint } - cerrar la posición en esta magnitud cuando X = 1 (parámetro de entrada)
• { PointsForEndLots } - movimiento de la vela anterior en la dirección del beneficio para la velocidad final de cierre de una posición  (parámetro de entrada)
• { EndLotsToOnePoint } - cerrar la posición en esta magnitud cuando X = PointsForEndLots  (parámetro de entrada)

Ahora, vamos a crear un sistema de ecuaciones para calcular los coeficientes y conseguir la forma final de nuestra función expresada mediante los parámetros de entrada. Para lograrlo, necesitaremos convertir todas nuestras ideas en expresiones matemáticas:

1. { Lc( 1 ) = StartLotsToOnePoint }
2. { Lc( PointsForEndLots ) = EndLotsToOnePoint }
   

Buenos, ya están listas todas nuestras ecuaciones. Ahora, las escribiremos de forma expandida y comenzaremos a resolverlas, transformándolas gradualmente:

1. { C * Pow(1 , D) = StartLotsToOnePoint }
2. { C * Pow( PointsForEndLots  , D) = EndLotsToOnePoint }
   

De la primera ecuación, podemos encontrar enseguida "C", considerando que la unidad a cualquier potencia es igual a sí misma:

• { C = StartLotsToOnePoint }

Tras dividir ambas partes de la segunda ecuación por "C" y luego encontrar el logaritmo de ambos lados de la ecuación con la base "PointsForEndLots", obtendremos lo siguiente:

• { log( PointsForEndLots ) [ Pow( PointsForEndLots  , D)] = log( PointsForEndLots ) [  EndLotsToOnePoint / C ] }

Teniendo en cuenta que el logaritmo de la base del mismo logaritmo elevado a cualquier potencia es igual a esta misma potencia, ahora podemos resolver nuestra ecuación respecto a la potencia que buscamos:

• { D =  log( PointsForEndLots ) [  EndLotsToOnePoint / C ] }

Hemos encontrado el segundo coeficiente desconocido, pero eso no es todo, porque en MQL4 y MQL5 no existe una función básica que implemente un logaritmo de cualquier base necesaria, solo existe el logaritmo natural. Por consiguiente, tendremos que cambiar la base de nuestro logaritmo al logaritmo natural (el logaritmo natural es un logaritmo con la base expresada como número de Euler). En sí, la ausencia de otros logaritmos en el lenguaje no supone un problema, porque siempre podemos expresar cualquier logaritmo mediante un logaritmo natural. Para cualquier persona un poco versada en matemáticas, esto no supondrá ningún problema. Tras cambiar la base, la fórmula para nuestro coeficiente buscado quedará así:

• { D = ln(  EndLotsToOnePoint / C ) /  ln(  PointsForEndLots  ) }

Sustituyendo ahí el coeficiente "C" ya conocido, obtendremos:

• { D = ln(  EndLotsToOnePoint / StartLotsToOnePoint  ) /  ln(  PointsForEndLots  ) }

Ahora, ya podemos sustituir ambos coeficientes en la plantilla de nuestra función y obtener su forma final:

• { Lc(X) = StartLotsToOnePoint  * Pow( X ,  ln(  EndLotsToOnePoint / StartLotsToOnePoint  ) /  ln(  PointsForEndLots  )  )  }
  

La ventaja de esta función consistirá en que el grado podrá ser tanto igual a la unidad, como mayor o menor que esta, ofreciendo así la máxima flexibilidad para adaptarse a cualquier mercado e instrumento comercial. Si D = 1, obtenemos nuestra función lineal. Si D> 1, la función se ajustará al supuesto de que todas las ondas son escalables y el número de ondas de una cierta amplitud es inversamente proporcional a la amplitud (es decir, si contamos el número de ondas, digamos M5 y H1 para el mismo segmento temporal, resultará que hay 12 veces menos ondas de este tipo en H1, simplemente porque hay 12 veces menos velas de hora que velas de cinco minutos). Si D <1, asumiremos que tenemos más ondas de amplitud que pequeñas, y cuando D> 1, supondremos que las ondas predominantes son de baja amplitud. 

También querríamos señalar que no resulta necesario usar una serie de precios discretizada en forma de barras: podemos trabajar tanto con ticks como con cualquier otro segmento de precios que creamos necesario. Lo único es que, como ya tenemos barras, ¿por qué no usarlas?

Código:

En el código, esta función se verá así:

double CalcCloseLots(double orderlots0,double X)
   {
   double functionvalue;
   double correctedlots;
   if ( X < 0.0 ) return 0.0;
   functionvalue=StartLotsToOnePoint*MathPow(X ,MathLog(EndLotsToOnePoint/StartLotsToOnePoint)/MathLog(PointsForEndLots));
   correctedlots=GetLotAniError(functionvalue);
   if ( correctedlots > orderlots0 ) return orderlots0;
   else return correctedlots;
   }

En color púrpura, destacamos la función que corrige los lotes para que adopten solo el valor correcto; no tiene demasiado sentido mostrar su interior. La función en sí se calcula bajo el operador resaltado en verde, pero forma parte de una función más general que llamaremos aquí:

void PartialCloseType()// close order partially
   {
   bool ord;
   double ValidLot;
   MqlTick TickS;
   SymbolInfoTick(_Symbol,TickS);
            
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
                            
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == _Symbol )
         {
         if ( OrderType() == OP_BUY )
            {
            ValidLot=CalcCloseLots(OrderLots(),(Open[0]-Open[1])/_Point);
            if ( ValidLot > 0.0 ) ord=OrderClose(OrderTicket(),ValidLot,TickS.bid,MathAbs(SlippageMaxClose),Green);
            }
         if ( OrderType() == OP_SELL )
            {
            ValidLot=CalcCloseLots(OrderLots(),(Open[1]-Open[0])/_Point);
            if ( ValidLot > 0.0 ) ord=OrderClose(OrderTicket(),ValidLot,TickS.ask,MathAbs(SlippageMaxClose),Red);
            }         
         break;
         }
      }

Esto también se compilará en MQL5, ya que utilizaremos la biblioteca MT4Orders. Solo queremos aclarar que estas funciones resultan adecuadas para las pruebas: en lo que respecta al comercio real, deberemos someterlas a un análisis minucioso y refinarlas para detectar errores y posibiles omisiones. Para realizar las pruebas necesarias en el simulador de estrategias, en todo caso, las funciones son bastante convenientes.

Probando el asesor:

Para demostrar cómo funciona, hemos escrito una versión del asesor para MetaTrader 4, porque al realizar las pruebas en MetaTrader 5, el spread ocultará todo lo que queremos ver. En su lugar, hemos tomado un spread "1" y abierto posiciones en una dirección aleatoria:

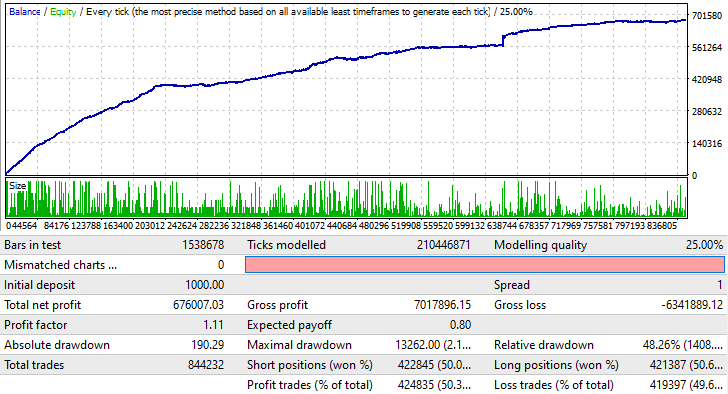
Todo esto funciona de la misma forma para otras parejas de divisas. También funciona con marcos temporales mayores: solo necesitamos un poco de paciencia y encontraremos los ajustes necesarios. No obstante, esta prueba no significa que debamos tomar este asesor ahora e iniciarlo en una cuenta real, supone solo la confirmación de que esta técnica puede resultar beneficiosa si la usamos correctamente. Queremos que el lector entienda que, en este punto, incluso un asesor de este tipo resulta del todo insuficiente para obtener beneficios. Sin embargo, si lo usamos en combinación con una buena señal y un enfoque competente, esta técnica podrá generar beneficios.

Algoritmo de variación híbrida del lote

Al comienzo de la investigación de mercado, nos hacíamos una idea sobre cómo cambiar el factor de beneficio de cualquier sistema hacia valores positivos. De hecho, en esencia, esto significará que cualquier estrategia que no dependa tanto del spread conseguirá una enorme ventaja sobre cualquier otra que tenga un factor de beneficio próximo a uno. ¿Por qué es necesario reforzar precisamente el factor de beneficio? Simple: porque de este indicador dependen tanto la reducción relativa del sistema en su conjunto como la rentabilidad del mismo. Existe un mecanismo así, que veremos a continuación. Pero antes, repaseremos rápidamente las técnicas comerciales más célebres que pueden usar la manipulación de lotes. Existen las siguientes supuestas técnicas para reforzar el factor de beneficio:

• Martingale
• Martingale inverso

De hecho, todo se reduce a dos trucos que todo el mundo sigue discutiendo, pero que no pueden ofrecer otra cosa que decepciones. Se trata de un principio matemático muy simple que ya expusimos en el artículo "Cuadrícula y martingale: ¿qué son y cómo usarlos?". Describe no tanto todos los principios, como lo que estos tienen en común. En general, hablamos de una disminución o un aumento en el lote, dependiendo de ciertas condiciones. Si las condiciones no tienen nada que ver con la naturaleza de la fijación de los precios, entonces dicho sistema será deliberadamente no rentable.

Cualquier estrategia que use la variación de lotes tiene una señal subyacente. Podemos conseguirlo asegurándonos de que los lotes de todas las órdenes sean iguales. Esto es necesario para comprender si la señal subyacente está relacionada con la naturaleza del precio. En la mayoría de los casos, dicha señal ofrecerá una esperanza matemática igual a cero, pero existe un parámetro en esta señal que puede permitirnos usar martingale hacia adelante y hacia atrás al mismo tiempo. Un requisito previo será la existencia de un gran número de ondas de baja amplitud. Si usamos correctamente el martingale y el martingale inverso en conjunto, podremos convertirlos en una especie de mecanismo híbrido que transformará una esperanza matemática cero en una positiva. En la siguiente figura, mostramos el aspecto aproximado de todo esto:

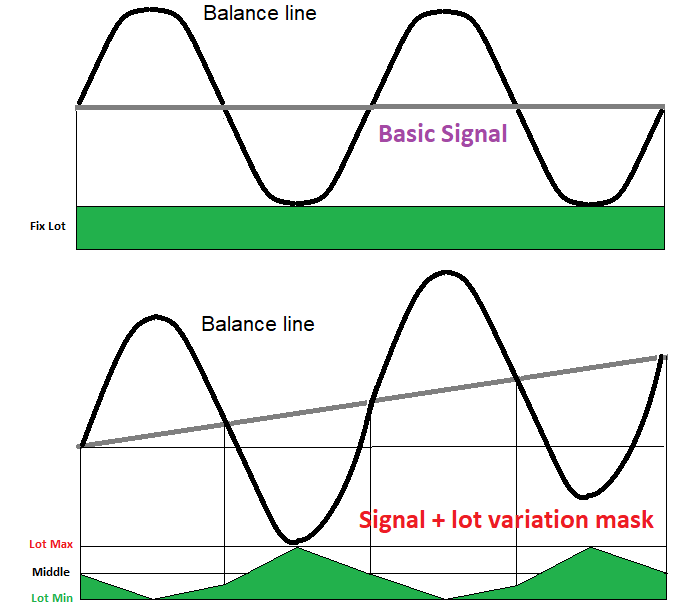
Teoría:

Para que en nuestra cabeza madure un híbrido de este tipo, deberemos asumir que tenemos una cierta línea de balance inicial, y que, sin considerar el margen y la comisión, esta siempre oscilará en torno al nivel del balance inicial, hasta que un día decida dejar de operar con un beneficio positivo o negativo en relación con el balance inicial, o hasta que el sistema liquide lentamente nuestro depósito, consumiéndolo con la ayuda de spreads, comisiones y swaps. Todo esto implica que cualquier línea del balance de una operación aleatoria será, de una u otra forma, un proceso de onda que fluctuará alrededor del saldo inicial.

Usando este hecho como base, podemos dividir la línea de balance toda en secciones ascendentes y descendentes (en la figura, tenemos un cuarto de una onda completa). Si el cuarto de la onda está aumentando, deberemos disminuir los lotes (martingale inverso), si la onda está descendiendo, deberemos aumentarlos (martingale). El único impedimento al aumento infinito de lotes es el hecho de que cualquier cuenta tiene un volumen de posición máximo permitido, e incluso si tal situación fuera posible, el depósito simplemente no nos permitiría abrir posiciones adicionales. En este sentido, resulta evidente que los lotes deberán oscilar en el corredor de valores seleccionado, sin salir del mismo. Por consiguiente, lo que realmente necesitamos es que las ondas no tengan demasiada amplitud y, si existiera tal posibilidad, que haya el mayor número posible de ondas pequeñas y el menor número posible de ondas grandes. Si observamos detenidamente la figura y la máscara de variación del lote a continuación, comprenderemos por qué, usando la variación híbrida, podemos hacer que la línea en relación a la cual ocurren las oscilaciones adquiera una inclinación "hacia arriba", que equivale a una esperanza matemática y un factor de beneficio positivos.

¿Cómo calcular los lotes en este caso? La situación, a primera vista, resulta incomprensible. Obviamente, los lotes pueden alcanzar uno de los límites de nuestro canal y nunca salir de allí. Para ello, deberemos conseguir un mecanismo de retorno al lote original para obtener oscilaciones estables alrededor del valor promedio de los lotes. El único inconveniente de tal sistema, obvio por otra parte, es la intolerancia a las ondas de gran amplitud. En la "sierra", nuestro mecanismo funcionará perfectamente y nos alegrará la vista. Hemos resuelto este problema organizando la función de cálculo del siguiente lote de tal forma que empuje los lotes hacia la parte media cuanto más cerca de uno de los límites se encuentren los lotes de la orden cerrada anterior. Vamos a ilustrar lo dicho en la figura siguiente:

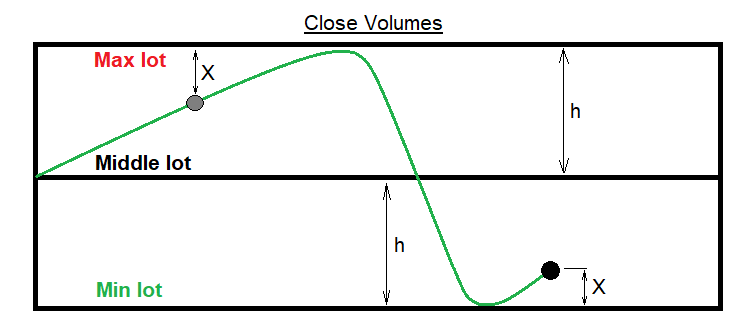
A continuación, vamos a exponer una vista general de una función adecuada para esta tarea, utilizando la notación de la figura. Pero antes, definiremos los parámetros de entrada y las variables auxiliares:

Variables de entrada para controlar la variación del lote híbrido

• { MaxLot } - lote máximo del corredor (parámetro de entrada)
• { MinLot } - lote mínimo del corredor (parámetro de entrada)
• { LotForMultiplier } - lote de referencia para aumentar o disminuir el volumen
• { ProfitForMultiplier } - pérdida o beneficio en puntos para el aumento o disminución de referencia del lote

Variables auxiliares

• { MiddleLot = (MaxLot + MinLot)/2 } - parte media entre el lote mínimo y el máximo
• { h =  (MaxLot - MinLot)/2 } - anchura de la mitad del canal (la necesitaremos para los cálculos)
• { L } - lote de la última transacción de la historia
• { X } - variable auxiliar
• { OrderProfit , OrderComission , OrderSwap , OrderLots } - beneficio sin considerar las comisiones, la comisión y el swap cargados por la orden, y el volumen de cierre de la última orden de la historia (ya los conocemos)
• { TickSize } - aumento en el beneficio de una posición abierta, siempre que su volumen sea igual a 1 lote y el precio se haya movido 1 punto en la dirección que necesitamos
• { PointsProfit = ( OrderProfit + OrderComission + OrderSwap ) / ( OrderLots * TickSize ) } - profit of the last order in history expressed in points

Función para el caso en que los lotes se encuentran por encima o por debajo de la línea central

• { L  >=  MiddleLot  ?  X = MaxLot - L  } - si los lotes se encuentran en la parte superior del corredor, el valor "X" será la distancia hasta el borde superior del canal
• { L  <  MiddleLot  ?  X = L - MinLot } - si los lotes se encuentran en la parte superior del corredor, el valor "X" será la distancia hasta el borde inferior del canal
• { L  >=  MiddleLot & PointsProfit < 0   ?  Lo(X) =  OrderLots - LotForMultiplier * (  PointsProfit / ProfitForMultiplier ) * ( X / h )  } - aumento ralentizado del lote al aproximarse al borde superior del canal
• { L  <  MiddleLot & PointsProfit >= 0   ?  Lo(X) =  OrderLots - LotForMultiplier * (  PointsProfit / ProfitForMultiplier ) * ( X / h )  } - disminución ralentizada del lote al aproximarse al borde inferior del canal
• { L  >=  MiddleLot & PointsProfit >= 0   ?  Lo(X) =  OrderLots - LotForMultiplier * (  PointsProfit / ProfitForMultiplier ) / ( X / h )  )  } - disminución acelerada del lote 
• { L  <  MiddleLot & PointsProfit < 0   ?  Lo(X) =  OrderLots - LotForMultiplier * (  PointsProfit / ProfitForMultiplier ) / ( X / h )  } - aumento acelerado del lote

Resulta bastante difícil digerir estas proporciones en nuestra cabeza, porque son difíciles de leer, pero, en este caso, si intentamos combinar todo en una función continua, obtendremos una estructura tan compleja que nos será imposible trabajar con ella, si es que podemos lograrlo en general. A continuación, mostraremos cómo se verá todo esto en el código, así quedará más claro. Aquí vemos la implementación del código en el estilo MQL4, pero si usamos la famosa y conveniente biblioteca MT4Orders, este código se compilará y funcionará en MQL5:

Código:

double CalcMultiplierLot()
   {
   bool ord;
   double templot=(MaxLot+MinLot)/2.0;
   for ( int i=OrdersHistoryTotal()-1; i>=0; i-- )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_HISTORY );
      if ( ord && OrderSymbol() == CurrentSymbol &&  OrderMagicNumber() == MagicF )
         {
         double PointsProfit=(OrderProfit()+OrderCommission()+OrderSwap())/(OrderLots()*MarketInfo(CurrentSymbol,MODE_TICKVALUE));
         if ( OrderLots() >= (MaxLot+MinLot)/2.0 )
            {
            if ( PointsProfit < 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))*((MaxLot-OrderLots())/((MaxLot-MinLot)/2.0));
            if ( PointsProfit > 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))/((MaxLot-OrderLots())/((MaxLot-MinLot)/2.0)) ;
            if ( PointsProfit == 0.0 ) templot=OrderLots();
            break;
            }
         else
            {
            if ( PointsProfit > 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))*((OrderLots()-MinLot)/((MaxLot-MinLot)/2.0));
            if ( PointsProfit < 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))/((Orderlots()-MinLot)/((MaxLot-MinLot)/2.0));
            if ( PointsProfit == 0.0 ) templot=OrderLots();
            break;
            }
         }
      }
   if ( templot <= MinLot ) templot=(MaxLot+MinLot)/2.0;
   if ( templot >= MaxLot ) templot=(MaxLot+MinLot)/2.0;
         
   return templot;
   }

Hemos probado recientemente esta biblioteca, y resulta especialmente útil cuando necesitamos controlar cada orden abierta. Bueno, este sería el enfoque completo. Resaltamos en amarillo las variables de entrada del algoritmo.

Probando el asesor:

También hemos creado este asesor para MetaTrader 4, por el mismo motivo que en el asesor anterior, porque resultará más fácil ver una mejora en el factor de beneficio:

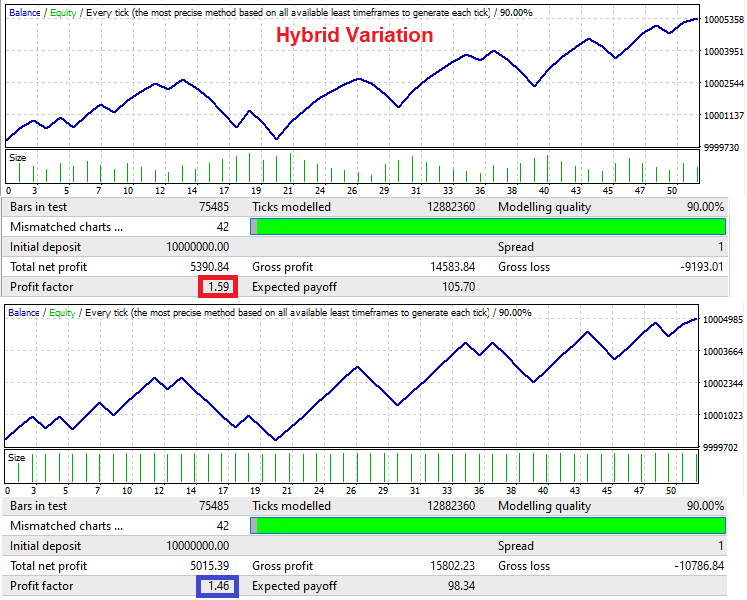
Las señales en este asesor experto se generan por turno. Después de la compra, viene la venta, y después de la venta, la compra, etcétera. Se ha implementado así por simplicidad, solo para demostrar cómo funciona este mecanismo. En la segunda prueba, comerciamos con un lote fijo, mientras que en la primera comerciamos con una variación híbrida del lote. Podemos ver que este sistema ofrecerá una mejora en el factor de beneficio solo si las oscilaciones en el balance de la señal original son mínimas. El sistema no tolerará grandes ondas.

Principio de promediación

El principio de promediado es un algoritmo bastante interesante, aunque no resulta rentable como la cuadrícula de martingale y la pirámide, pero posee una característica muy interesante que nos puede ayudar en el trading de ondas. Si sabemos que el movimiento continuará hasta un cierto nivel y que luego se dará necesariamente un rebote en un cierto número de puntos, en este caso, podremos aplicar el promedio con martingale. Esta técnica funciona especialmente bien con el martingale, porque este nos permite reducir el retroceso necesario, al tiempo que mantiene un factor de beneficio superior a 1.0. 

Este principio explota la suposición de que si el precio no se mueve en la dirección de nuestra posición abierta, tras algún tiempo ciertamente hará retroceder parte de este movimiento. De hecho, este no es siempre el caso, aunque podemos ajustar este algoritmo para muchas herramientas si analizamos la naturaleza de sus ondas. Para rentabilizar este retroceso, tendremos que predecirlo o determinarlo empíricamente.

Esto también funciona con niveles fuertes, porque, con mucha frecuencia, cuando se rompe un nivel, el mercado puede intentar probarlo para la inversión. Si acertamos con la dirección de la primera transacción y el beneficio ha alcanzado el valor necesario, cerraremos la operación con calma y abriremos una nueva en la dirección que nos parezca más atractiva. Si el precio ha ido en la dirección contraria a la que deseábamos, podremos intentar aumentar el volumen de nuestra posición realizando ciertos pasos. Debemos construir la posición con mucho cuidado y precisión, basándonos en el retroceso, que, según creemos, debería suceder. A continuación, ilustraremos lo expuesto con ejemplos de dos situaciones que podrían surgir.

Ejemplo para una serie de órdenes Buy:

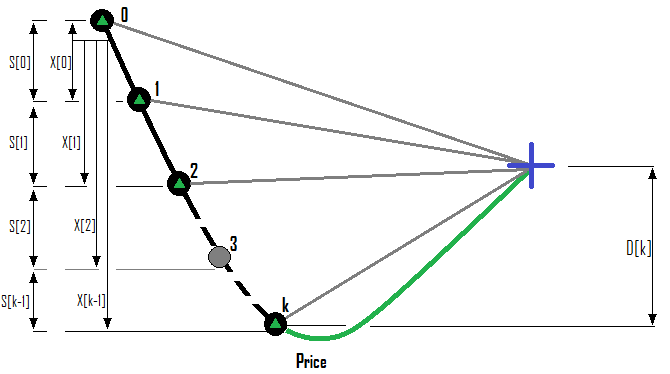
Ejemplo para una serie de órdenes Sell:

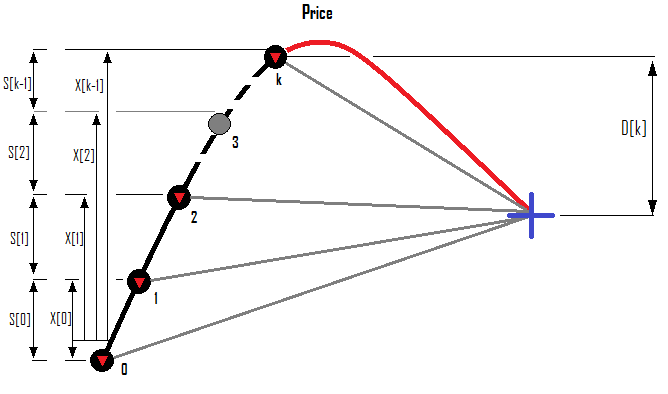
Ahora, mostraremos cómo calcular el beneficio o las pérdidas de todas las órdenes y cómo calcular según la situación actual el lote de la siguiente orden en función del retroceso requerido. Para cerrar un abanico de posiciones, necesitaremos saber por qué debemos construir este abanico y qué condición lo hace útil. A nuestro juicio, resulta mejor usar el "factor de beneficio". Si el abanico es positivo, entonces su factor de beneficio también será positivo. Sería una tontería cerrarlo en cuanto el beneficio total de todas las órdenes sea positivo, porque cualquier oscilación de precio en el servidor o el propio deslizamiento podría redirigir el beneficio en la dirección negativa, y entonces, ¿qué sentido tendría construir estos abanicos? ¿Verdad? Además, el factor de beneficio del ciclo nos dará la oportunidad de ajustar de forma adicional la agresividad de nuestro promedio, que se podrá utilizar al optimizar una estrategia automática o al buscar configuraciones manualmente.

Supongamos que hay un límite en el número máximo de órdenes en una serie, y supongamos igualmente que estamos en alguna situación desconocida, donde ya hemos abierto "k" órdenes, y que sus índices parten desde "0", como en cualquier colección o matriz. Así, el índice de la última orden de la serie será "k-1". Cuando abramos la siguiente orden, su índice será "k", y el número de órdenes será "k+1". Vamos a dotar a nuestras conclusiones de una forma completa en los datos de entrada de la tarea:

• { MaxOrders } - número máximo de órdenes permitidas en una serie
• {  k = 0 ... 1 ... 2 ...  (MaxOrders-1)  } - índice de la siguiente orden de la serie que queremos abrir si no hemos obtenido beneficios del anterior pronóstico
• {  ProfitFactorMax } - factor de beneficio permitido para el cierre
• {  i = 1 ... 1 ... 2 ... k  } - índices de las órdenes ya pendientes del abanico actual y de la siguiente orden que queremos abrir
• {  S[i-1]  } - distancia en puntos desde la orden anterior a la actual
• {  X[i-1]  } - distancia en puntos desde la orden cero en la serie hasta la actual
• {  D[k]  } - retroceso previsto en la dirección deseada en relación con el precio de apertura de la última orden de la serie

De forma adicional, podemos decir que, al referirnos a una orden específica, los lenguajes MQL4 y MQL5 nos ofrecen los siguientes datos necesarios para describir todas las opciones de cálculo:

• {  P[i] } - beneficio de una orden específica excluyendo las comisiones y los swaps
• {  С[i] } - comisión de la orden seleccionada
  
• {  S[i] } - swaps de la orden calculados por la traslado de una posición a través de las 0:00
  
• {  L[i] } - volumen de la orden
  
• {  Sp[i] } - spread al abrir una posición Buy / spread actual para las posiciones Sell
• { TickSize } - aumento en el beneficio de una posición abierta, siempre que su volumen sea igual a 1 lote y el precio se haya movido 1 punto en la dirección que necesitamos

En realidad, no todos estos valores nos resultarán útiles para un uso práctico en el comercio automatizado, pero serán necesarios para resaltar todas las opciones posibles para calcular estos valores. Algunos de estos valores, que son relevantes y se pueden representar en relación al precio, han sido mostrados más arriba en las figuras. Vamos a comenzar con el método de cálculo más simple usado en nuestro código:

Si la primera orden se cierra en positivo, no haremos nada, y en cualquier momento que creamos necesario, abriremos una nueva orden en la dirección necesaria. Si el precio no ha alcanzado el objetivo y se ha dado en la dirección opuesta, deberemos decidir cuántos puntos debe moverse el precio en dicha dirección no rentable para abrir la siguiente orden (S[k-1]). Si el precio ha alcanzado este nivel, deberemos decidir qué retroceso es el adecuado para nosotros (D[k]). Después, deberemos determinar el lote de orden que abriremos ahora para que, considerando un retroceso planificado, obtengamos un factor de beneficio necesario de todas las órdenes superior al valor que hemos seleccionado (ProfitFactorMax). Para hacer esto, primero necesitaremos calcular qué beneficio obtendrán las órdenes ya abiertas que estén ya pendientes, además de las pérdidas y su valor total, lo cual explicaremos después de escribir las fórmulas correspondientes:

Primero, introducimos el valor del beneficio en el futuro para cada orden específica: este consta del beneficio actual y el incremento que recibirá la orden, siempre que suceda el retroceso necesario:

• {  j = 0 ... 1 ... 2 ... k-1 }
  
• {  PF[j] = P[j] + С[j] + S[j] + (D[k] * L[j] * TickSize) } - dicho valor adoptará el beneficio de una orden específica cuando se produzca un retroceso según el escenario planificado
• {  PF[k] = { ( D[k] - Spread[k] ) * L[k] * TickSize } - este valor no se puede calcular, ya que contiene el lote requerido de la posición que queremos abrir, pero esta expresión será necesaria en el futuro
  

En el primer caso, conocemos el valor P[i] y podemos obtenerlo utilizando las funciones integradas del lenguaje, o bien podemos calcularlo nosotros mismos. Mostraremos cómo calcularlo al final, como una adición, ya que los medios del lenguaje nos permiten no recurrir a ello. En cuanto a la última orden de la serie que queremos abrir, en teoría, necesitaríamos añadir allí la comisión y el swap, pero solo podemos obtener la comisión de una orden que esté ya abierta, y todavía no lo hemos hecho. Tampoco podemos determinar el tamaño del swap, ya que no sabemos si la posición cambiará en general a través de las 0:00 o no. Siempre habrá errores. Podemos seleccionar solo aquellas parejas que tienen swaps positivos 

Después, podemos utilizar este beneficio proyectado para dividir las órdenes con beneficios y pérdidas, porque esta es la única forma de calcular el factor de beneficio que darán al final:

• {  i = 0 ... 1 ... 2 ... k } - índices de las órdenes ya abiertas
• {  Pr[i] >= 0, Ls[i]  >= 0 } - introduciremos 2 matrices que adoptarán el beneficio o las pérdidas de la orden, dependiendo de cuál sea su signo, pero estaremos de acuerdo en que el beneficio y las pérdidas tienen un signo "+" (lo necesitaremos para calcular el factor de beneficio)
• {  PF [i] < 0  ?  Pr[i] = 0 & Ls[i] = - PF[i]  } - si el beneficio de la orden es negativo, anotaremos su beneficio como "0" y el propio beneficio con el signo invertido lo escribiremos en la variable de las pérdidas.
• {  PF [i] > 0 ?  Ls[i] = 0 & Pr[i] = PF[i]  } - si el beneficio de la orden es positivo, simplemente lo escribirimos en la matriz correspondiente, estableciendo después como cero el valor de la matriz para las pérdidas.
  

Tras rellenar estas matrices, podremos escribir una fórmula para calcular el beneficio y las pérdidas totales y su resultado.

• { SummProfit = Summ[0,k]( PF[i] ) } - módulo total de beneficio de todas las órdenes rentables
• { SummLoss = Summ[0,k]( Ls [i] ) } - módulo de pérdidas totales de todas las órdenes no rentables
  

Ahora, deberemos escribir la condición para cerrar el ciclo:

• { SummLoss > 0 ?  SummProfit/SummLoss  = ProfitFactorMax }

Para poder utilizar esta ecuación de alguna forma, deberemos comprender que el beneficio de la última orden de la serie es siempre positivo cuando el abanico de posiciones está cerrado. Partiendo de ello, podemos escribir:

• { SummProfit = Summ[0,k-1]( PF[j] )  +  PF[k] }
  

Sustituyendo este valor en la ecuación, obtendremos:

• {  ( Summ[0,k-1]( PF[j] )  +  PF[k] ) /  SummLoss  =  ProfitFactorMax }
  

Ahora, tras resolver esta ecuación para PF[k], obtendremos:

• { PF[k]  =  ProfitFactorMax * SummLoss  -  Summ[0,k-1]( PF[j] ) }
  

Considerando que ya tenemos una fórmula para PF[k], podremos sustituir esta expresión aquí y obtener:

• { ( D[k] - Spread[k] ) * L[k] * TickSize = ProfitFactorMax * SummLoss  -  Summ[0,k-1]( PF[j] ) }
  

Ahora, podemos resolver esta ecuación para L[k] y finalmente obtener la fórmula para calcular el volumen buscado de la posición que queremos abrir:

• { L[k] =  ( ProfitFactorMax * SummLoss  -  Summ[0,k-1]( PF[j] ) )  /  ( ( D[k] - Spread[k] ) *  TickSize ) }
  

Pues bien, eso es todo. Ahora, vamos a ver cómo calcular el valor P[i] sin utilizar para ello funciones integradas.

• { P[i] = ( X[i-1] - Spread[i] ) * L[i] * TickSize + С[j] + S[j] }
  

Calculando el valor de retroceso

Ahora, analizaremos las formas de calcular el retroceso. Usaremos 2 modos. En general, podemos pensar en una gran variedad de estos, pero mostraremos dos de los más útiles, en nuestra opinión. El retroceso se calcula respecto a la distancia que ha recorrido el precio en la dirección incorrecta. Es decir, D[i] y X[i] pueden vincularse con cualquier función que sea positiva en todo el eje positivo "X":

• { D=D(X) }
• { D[k] = D( X[k-1] ) }

Usamos dos funciones para calcular el retroceso. La primera es lineal. La segunda, es una función de potencia. La segunda es más compleja, pero también más interesante. Este es el aspecto de las funciones:

• { D = K * X }
• { D = DMin + C * Pow(S , X) }

Resaltamos a color los coeficientes que seleccionamos. Usando estos coeficientes como base, las funciones comienzan a actuar de forma diferente y, en consecuencia, tenemos la oportunidad de ajustar de manera flexible nuestra estrategia según una pareja de divisas o marco temporal específicos.

1. { K } - coeficiente de retroceso para una función lineal (también se utiliza como parámetro de entrada para un sistema automático) 
   
2. { DMin } - retroceso mínimo permitido (D >= DMin, en el caso de una función de potencia)
   
3. { С } - coeficiente de escalado de la función de potencia
4. { S } - base de exponenciación

Estrictamente hablando, podemos elevar "C" a una potencia, pero todos estaremos de acuerdo en que de esta forma la función resultará más cómoda y legible. También debemos tener en cuenta que las magnitudes "K" y "DMin" son parámetros de entrada, y estos coeficientes los conocemos de inmediato. Lo único que no está claro es cómo calcular los dos coeficientes restantes. Esto es lo que haremos ahora. Para encontrar las 2 incógnitas, necesitaremos un sistema con al menos dos ecuaciones. Tras resolver el sistema, obtendremos los coeficientes requeridos. Para escribir un sistema de este tipo, primero deberemos decidir cómo gestionaremos la apariencia de nuestra función. De hecho, hemos seleccionado la actual forma de la función de potencia precisamente tomando como base la manera más fácil y adecuada de hacer una disminución suave del retroceso. Al final, la elección ha recaído en una función de potencia. Las consideraciones han sido las siguientes:

1. { HalfX } - movimiento del precio para la mitad del retroceso adicional (parámetro de entrada adicional para controlar la función)
2. { D(0) = DMin + K*DMin }
3. { D(HalfX) = DMin + K*DMin/2 }

Por consiguiente, obtendremos el sistema de ecuaciones necesario, que resolveremos acto seguido. En otras palabras, estableceremos el movimiento del precio en dirección a las pérdidas en relación con la primera orden abierta, en la que la adición al retroceso adopta la mitad del valor al principio. Y al principio, esta adición tiene un valor máximo. Como resultado, obtendremos una función que no puede adoptar un valor inferior al retroceso mínimo y que, cuando tienda al infinito, tenderá al retroceso mínimo. Desde un punto de vista matemático, lo escribiremos así:

• { D >= DMin }
  
• { Lim( X -> +infinito ) = DMin }

Ahora, podemos comenzar a resolver nuestro sistema de ecuaciones, pero primero lo reescribimos por completo:

1. { DMin + C * Pow(S , 0) = DMin + K*DMin } 
2. { DMin + C * Pow(S , HalfX) =  DMin + K*DMin/2 }

Partiendo de la primera ecuación, podemos encontrar inmediatamente "C", dado que cualquier número a la potencia cero se convierte en la unidad, descartando así la variable "S". Solo nos queda resolver la ecuación para la variable "C". 

• { С = K * DMin }
  

Ahora que tenemos "C", podemos encontrar la "S" desconocida restante con solo sustituir la expresión anterior por la variable "C":

• { Pow(S , HalfX) = 0.5 }

Para deshacernos de la potencia, tendremos que elevar ambos lados de la ecuación a la potencia inversa a la magnitud de "HalfX", obteniendo así una expresión tan simple que resultará el coeficiente deseado:

• { S = Pow(0.5  , 1/HalfX) }

Ahora, podemos escribir nuestra función de potencia sustituyendo nuestros coeficientes allí, describiendo con ello todo lo necesario para implementar esta estrategia:

• { D(X) = DMin + K *  DMin * Pow( Pow(0.5  , 1/HalfX)  , X ) }

Este será el aspecto de la función en el código:

Código:

double D(double D0,double K0,double H0,double X)
   {
   return D0+(D0*K0)*MathPow(MathPow(0.5,1.0/H0),X);
   }

Vamos a mostrar algunas otras funciones importantes que habrá en el asesor para probar la teoría. Comenzaremos con una función que determina la distancia en puntos desde el precio hasta la orden abierta más cercana de la serie:

double CalculateTranslation()
   {
   bool ord;
   bool bStartDirection;
   bool bFind;
   double ExtremumPrice=0.0;
   
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         if ( OrderType() == OP_SELL ) bStartDirection=false;
         if ( OrderType() == OP_BUY ) bStartDirection=true;
         ExtremumPrice=OrderOpenPrice();
         bFind=true;
         break;
         }
      }      
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
                        
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         if ( OrderType() == OP_SELL && OrderOpenPrice() > ExtremumPrice ) ExtremumPrice=OrderOpenPrice();
         if ( OrderType() == OP_BUY && OrderOpenPrice() < ExtremumPrice ) ExtremumPrice=OrderOpenPrice();
         }
      }
   if ( bFind )
      {
      if ( bStartDirection ) return (ExtremumPrice-Close[0])/_Point;
      else return (Close[0]-ExtremumPrice)/_Point;      
      }   
   else return -1.0;
   }

Necesitaremos esta función para cumplir con el salto requerido entre las órdenes de la serie, que será fijo para nosotros. No debemos olvidar que la matriz "Close[]" no está implementada en MQL5 y debe implementarse de forma independiente, como hemos mostrado en otros artículos. A nuestro juicio, nadie debería tener especiales problemas con ello.

Para calcular las incógnitas "X" y "D" actuales, utilizaremos la siguiente función, que, como todas las que le siguen, no tendrá valores de retorno, si bien escribirá el resultado en las variables globales (puesto que resulta mejor trabajar con órdenes lo mínimo posible y no volver a llamar a esas funciones que trabajan con la historia):

double Xx;//shift of X
double Dd;//desired rollback of D
void CalcXD()//calculate current X and D
   {
   bool ord;
   bool bStartDirection=false;
   bool bFind=false;
   double ExtremumPrice=0.0;
   
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         if ( OrderType() == OP_SELL ) bStartDirection=false;
         if ( OrderType() == OP_BUY ) bStartDirection=true;
         ExtremumPrice=OrderOpenPrice();
         bFind=true;
         break;
         }
      }   
   
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
                        
      if ( OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         if ( OrderType() == OP_SELL && OrderOpenPrice() < ExtremumPrice ) ExtremumPrice=OrderOpenPrice();
         if ( OrderType() == OP_BUY && OrderOpenPrice() > ExtremumPrice ) ExtremumPrice=OrderOpenPrice();
         }
      }
   Xx=0.0;
   Dd=0.0;   
   if ( bFind )
      {
      if ( !bStartDirection ) Xx=(Close[0]-ExtremumPrice)/_Point;
      if ( bStartDirection ) Xx=(ExtremumPrice-Close[0])/_Point;
      if ( MODEE==MODE_SINGULARITY ) Dd=D(DE,KE,XE,Xx);
      else Dd=Xx*KE;
      }      
   }

De nuevo, recordemos que todo este código se encuentra en concordancia total con la librería "MT4Orders" y se compilará en MQL5 sin problemas, como las funciones que daremos a continuación. Resaltamos en amarillo las variables de entrada del algoritmo.

Para calcular el beneficio actual y el proyectado, usaremos 3 variables:

double TotalProfitPoints=0.0;   
double TotalProfit=0;
double TotalLoss=0;   

En ellas, añadiremos los valores de retorno, mientras que las funciones en sí mismas no tendrán valores de retorno para no iterar sobre los órdenes nuevamente en cada caso necesario, puesto que esto ralentiza el funcionamiento del código hasta en decenas de veces.

Este será el aspecto de las dos funciones. Una resulta útil para la condición de cierre, mientras que la segunda sirve para calcular el beneficio previsto de las posiciones que ya están pendientes:

void CalcLP()//calculate losses and profits of all open orders
   {
   bool ord;
   double TempProfit=0.0;
   TotalProfit=0.0;   
   TotalLoss=0.0;    
   TotalProfitPoints=0.0;
   
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
                            
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         TempProfit=OrderProfit()+OrderCommission()+OrderSwap();
         TotalProfitPoints+=(OrderProfit()+OrderCommission()+OrderSwap())/(OrderLots()*SymbolInfoDouble(Symbol(),SYMBOL_TRADE_TICK_VALUE));
         if ( TempProfit >= 0.0 ) TotalProfit+=TempProfit;
         else TotalLoss-=TempProfit;
         }
      }
   }
   
void CalcLPFuture()//calculate losses and profits of all existing orders in the future
   {
   bool ord;
   double TempProfit=0;
   TotalProfit=0;   
   TotalLoss=0;    
    
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
                            
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         TempProfit=OrderProfit()+OrderCommission()+OrderSwap()+(OrderLots()*SymbolInfoDouble(Symbol(),SYMBOL_TRADE_TICK_VALUE)*Dd);
         if ( TempProfit >= 0.0 ) TotalProfit+=TempProfit;
         else TotalLoss-=TempProfit;
         }
      }
   }

También merece la pena mostrar la función de predicado para la condición de cierre de una serie de órdenes:

bool bClose()
   {
   CalcLP();
   if ( TotalLoss != 0.0 && TotalProfit/TotalLoss >= ProfitFactorMin ) return true;
   if ( TotalLoss == 0.0 && TotalProfitPoints >= DE*KE ) return true;
   return false;
   }

Probando el asesor:

Hemos creado un asesor experto basado en este principio para MetaTrader 5, ya que este principio, si se aplica correctamente, puede superar casi cualquier spread, comisión y swap. Al poner a prueba el asesor experto con promediado, obtenemos la siguiente imagen:

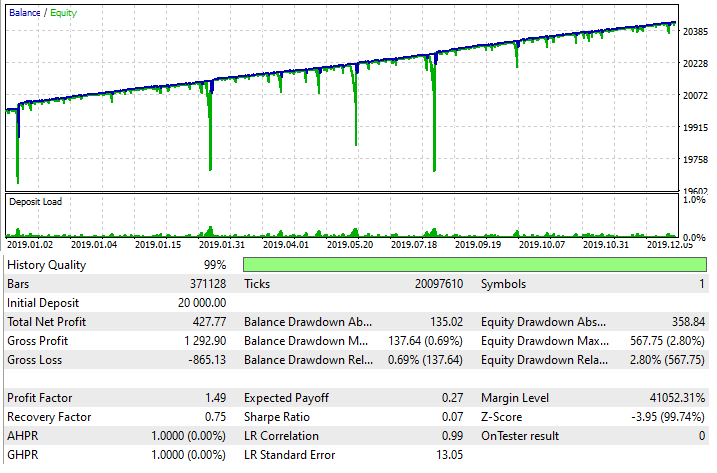
No debemos olvidar que esto es solo un truco comercial que tenemos que usar con mucho cuidado. Sin embargo, resulta muy flexible y se puede usar junto con una amplia variedad de estrategias. Eso sí, rogamos al lector que tenga mucho cuidado al usar esta técnica.

Señales directas e indirectas sobre la consistencia de una técnica comercial

En el marco de este artículo, resultaría útil analizar qué indicadores matemáticos del backtest nos pueden señalar que la técnica que hemos usado refuerza nuestra estrategia, o que una estrategia perdedora se ha convertido en rentable. La cuestión es muy importante, porque una interpretación incorrecta de los resultados del backtest podría decidir si realmente descartamos una técnica de trabajo o dejamos una falsa. Al desarrollar nuevas técnicas comerciales, siempre seguimos dos reglas que posibilitan una detección más probable de las técnicas de trabajo y un descarte más probable de las falsas:

1. El tamaño de la muestra de datos, así como el número de transacciones en el backtest, deben maximizarse para realizar una valoración estadística fiable.
2. Incluso un pequeño cambio en los indicadores del backtest puede indicar cambios positivos.

En muchos casos, podremos aprovechar cualquier cambio positivo y hacer que este resulte beneficioso para el comercio. Al menos, podemos convertir un sistema no rentable en rentable. Existen ventajas innegables, cuya importancia no podemos sobreestimar:

1. Estas técnicas comerciales funcionan en cualquier instrumento comercial.
2. Las técnicas se pueden combinar para crear híbridos.
3. Cuando se aplican correctamente, las posibilidades de obtener beneficios son mayores que las de sufrir pérdidas, incluso si hay spread

Ahora mostraremos específicamente qué indicadores debemos mirar al intentar usar una técnica comercial utilizando como ejemplo la última técnica comercial mencionada en este artículo. Comenzaremos con las métricas del backtest y les mostraremos cómo usar estas para crear métricas sintéticas que ayuden a detectar mejoras.

En primer lugar, merece la pena recurrir a indicadores como:

• El beneficio total del backtest
• La reducción máxima del balance
• La reducción máxima de la equidad

Otras métricas adicionales más precisas que podrían servir de ayuda, pero que no se encuentran en los informes del simulador de estrategias son:

• La reducción promedio del balance
• La reducción promedio de la equidad

¿Por qué estas métricas muestran con tanta precisión cómo de seguro y rentable es un sistema? El asunto es que para cualquier backtest, existen las siguientes identidades matemáticas, como para cualquier sistema comercial que opere en una cuenta demo o real:

• { i = 0 ... 1 ... 2 ... m } - número de la media onda (la media onda es un segmento ascendente de equidad o balance, seguido por uno descendente)
• { j = 0 ... 1 ... 2 ... k } - segmentos de media onda negativos (los segmentos de balance comienzan y terminan en los puntos de apertura y cierre de las posiciones, mientras que los segmentos de equidad comienzan y terminan en otros puntos)
• { OrderProfit[j]-OrderComission[j]-OrderSwap[j] < 0 !  Lim(m --> +infinito) [ Summ(i) [Summ(j) [ OrderProfit[j]-OrderComission[j]-OrderSwap[j] ]] / m  ] = beneficio total sin considerar spreads, comisiones y swaps   } - reducción media de balance del backtest o el comercio
• { SegmentEquity[j]-SegmentComission[j]-SegmentSwap[j] < 0 !  Lim( m --> +infinito ) [ Summ(i) [Summ(j) [ SegmentEquity[j]-SegmentComission[j]-SegmentSwap[j] ]] / m  ] = beneficio total sin considerar spreads, comisiones y swaps      } - reducción media de balance del backtest o el comercio

En otras palabras, la reducción promedio, tanto respecto al balance como a la equidad, con un backtest interminable o un uso interminable de la estrategia en una cuenta demo o real, tiende a la magnitud del balance total si la comisión de la transacción fuera cero. Pero, obviamente, esto resulta cierto solo cuando nuestra estrategia tiene un beneficio positivo pronunciado. Si el beneficio total tiene un signo negativo, entonces podremos escribir fórmulas inversas en las que deberemos sumar no los segmentos negativos, sino los positivos. Pero lo más conveniente, por supuesto, será operar con un backtest positivo y luego aplicarle algunas técnicas. Esto no significa en absoluto que vaya a mostrar beneficios con un backtest global. Solo necesitamos encontrar en la historia segmentos donde la estrategia muestre beneficios, preferiblemente varios. Luego, aplicaremos un enfoque similar. 

Ahora mostraremos cómo, con la ayuda de un martingale simple, podemos reforzar su estabilidad y cambiar ligeramente su rendimiento hacia los beneficios. Usando como base las fórmulas dadas anteriormente, podremos elaborar dichos indicadores sintéticos, que nos permitirán, usando varios segmentos pequeños, sacar una conclusión sobre cómo una técnica comercial influye en la negociación en su conjunto:

Datos de entrada para los indicadores sintéticos:

• { Tp } - beneficio total del backtest o el comercio
• { BdM } -  reducción media del balance
• { EdM } - reducción media de la equidad
• { BdMax } - reducción máxima del balance
• { EdMax } - reducción máxima de la equidad

Resaltamos a color los datos que el backtest no nos puede ofrecer. Podemos, sin embargo, calcular estos datos en el código, o bien mostrarlos después de una transacción o backtest. En nuestro caso, preferimos usar otros datos disponibles. El asunto es que, en la abrumadora mayoría de los casos, cuanto menor sea la reducción promedio, menor será la reducción máxima de ambos valores. Estas magnitudes se relacionan muy estrechamente con las probabilidades, y los cambios en una magnitud generalmente implican un cambio aproximadamente proporcional en la otra. 

Indicadores sintéticos:

• { A = Tp/BdM } - es igual a uno si la estrategia no predice el futuro, y superior a uno, si sabe cómo realizar predicciones y ganar dinero (lo cual equivale a responder a la pregunta sobre su rentabilidad)
• { B = Tp/EdM } - igual que para el indicador anterior
• { C = Tp / BdMax } - si se detecta un aumento en este indicador, podremos decir que la técnica aumenta la efectividad del método (si se da una disminución, en consecuencia, la influencia resultará negativa)
• { D = Tp / EdMax } - igual que para la magnitud anterior

Podemos usar cualquiera de estos 4 criterios. Los 2 primeros son, obviamente, más precisos, pero el backtest no puede ofrecer los datos necesarios para su cálculo, por lo que tendremos que leer los datos de entrada nosotros mismos. Los otros dos son más sencillos; los números que necesitamos para calcularlos se pueden sacar del backtest. Es este último el que usamos, por su disponibilidad y sencillez. A continuación, analizaremos la aplicación de este método, tomando como base un martingale simple que cierra según los stops, y trataremos de reforzar estos indicadores con la ayuda de una última técnica exótica que mostraremos ahora.

Usando las ondas de balance y equidad

Teoría:

En realidad, esta mecánica se puede usar no solo en un martingale, sino también en cualquier otra estrategia que tenga una frecuencia de transacciones lo suficientemente alta. En este ejemplo, utilizaremos un indicador basado en la reducción del balance, porque todo lo relacionado con el balance se considera más sencillo. Vamos a dividir el gráfico de balance en segmentos ascendentes y descendentes. Dos segmentos adyacentes forman una media onda. El número de medias ondas tiende al infinito cuando el número de transacciones tiende al infinito. Pero la muestra final nos basta para hacer el martingale un poco más rentable. Vamos a representar nuestros pensamientos en un esquema:

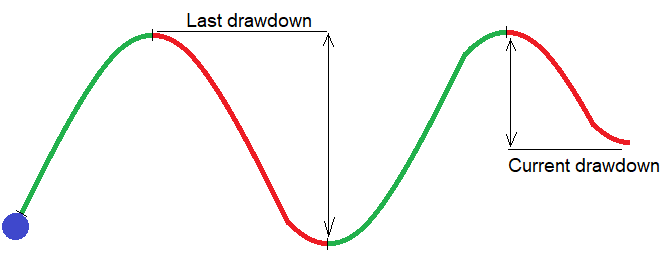
Si miramos la imagen, veremos una media onda formada y recién iniciada. Cualquier gráfico de balance consta de esas medias ondas. Si lo pensamos detenidamente, el tamaño de estas medias ondas oscila constantemente de media onda a media onda, y siempre podemos distinguir grupos de estas medias ondas en el gráfico. En un grupo, el tamaño de estas medias ondas es más pequeño, mientras que en otro resulta más grande. De aquí podemos sacar la conclusión de que, disminuyendo gradualmente los lotes, podemos esperar hasta que aparezca una media onda con una reducción crítica en el grupo actual, y, dado que los lotes de esta reducción crítica serán los mínimos en la serie, esto aumentará los indicadores generales promedio de todos los grupos de ondas. Como resultado, en principio, deberían aumentar los propios indicadores de rendimiento de la prueba original.

Para realizar la implementación, necesitaremos dos parámetros de entrada adicionales para nuestra martingala:

• { DealsMinusToBreak } - número de transacciones perdedoras del ciclo anterior, en el cual restablecemos el lote inicial del ciclo al valor inicial.
• { LotDecrease } - salto para disminuir el lote inicial del ciclo cuando aparece un nuevo ciclo en la historia de transacciones

Estos dos parámetros nos permitirán ofrecer lotes aumentados para los grupos seguros de medias ondas y lotes reducidos para los grupos peligrosos de medias ondas, lo que debería, en teoría, incrementar los indicadores que hemos definido anteriormente.

En el asesor experto de martingale, deberemos introducir el siguiente código, encargado de calcular el lote inicial del siguiente ciclo y también de restablecerlo si fuera necesario:

Código:

double DecreasedLot=Lot;//lot to decrease
double CalcSmartLot()//calculate previous cycle
   {
   bool ord;
   int PrevCycleDeals=0;
   HistorySelect(TimeCurrent()-HistoryDaysLoadI*86400,TimeCurrent());
   for ( int i=HistoryDealsTotal()-1; i>=0; i-- )
      {
      ulong ticket=HistoryDealGetTicket(i);
      ord=HistoryDealSelect(ticket);
      if ( ord && HistoryDealGetString(ticket,DEAL_SYMBOL) == _Symbol 
      && HistoryDealGetInteger(ticket,DEAL_MAGIC) == MagicC 
      && HistoryDealGetInteger(ticket,DEAL_ENTRY) == DEAL_ENTRY_OUT )
         {
         if ( HistoryDealGetDouble(ticket,DEAL_PROFIT) > 0 )
            {
            for ( int j=i+1; j>=0; j-- )//found a profitable deal followed by losing (count them)
                {
                ticket=HistoryDealGetTicket(j);
                ord=HistoryDealSelect(ticket);
                if ( ord && HistoryDealGetString(ticket,DEAL_SYMBOL) == _Symbol 
                && HistoryDealGetInteger(ticket,DEAL_MAGIC) == MagicC 
                && HistoryDealGetInteger(ticket,DEAL_ENTRY) == DEAL_ENTRY_OUT )
                   {
                   if ( HistoryDealGetDouble(ticket,DEAL_PROFIT) < 0 )
                      {
                      PrevCycleDeals++;
                      }
                   else
                      {
                      break;
                      }
                   }                
                }
            break;    
            }
         else
            {
            break;
            }
         }
      }
      
   if ( PrevCycleDeals < DealsMinusToBreak ) DecreasedLot-=LotDecrease;
   else DecreasedLot=Lot;
   if ( DecreasedLot <= 0.0 ) DecreasedLot=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN);

   return DecreasedLot;
   }

Destacamos en amarillo los parámetros de entrada. La función, por supuesto, es una función de prueba y resulta adecuada en esta forma solo para realizar pruebas en el simulador; sin embargo, incluso esto bastará para que llevar a cabo la primera prueba aproximada y simple de esta suposición. En este caso, escribiremos el mínimo necesario debido a las especificidades del artículo, y no mostraremos el resto del código del asesor para no distraer al lector con reflexiones innecesarias, muchas de las cuales, en nuestra opinión, habrá realizado por sí mismo durante la lectura. La misma consideración se aplica al resto de asesores implementados durante la redacción del artículo. Ahora, vamos a probar el martingale habitual. Luego activaremos nuestro nuevo modo y veremos cómo ha influido en los indicadores. Este asesor experto también será diseñado para MetaTrader 5, ya que la señal inicial en él es un martingale normal que muestra la misma imagen con diferentes spreads.

Probando el asesor:

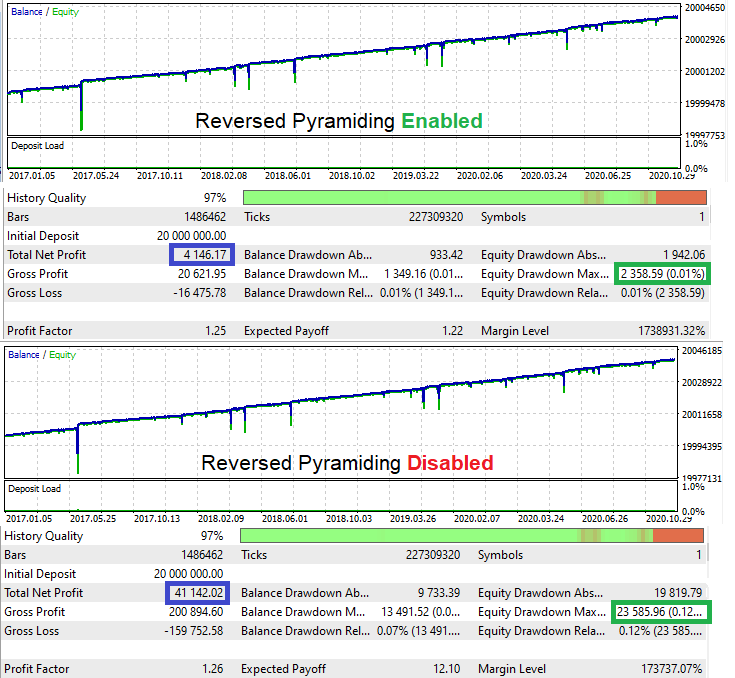
Si calculamos el indicador "D" para la prueba original, adoptará el valor "1.744", y para la prueba con el nuevo modo activado, adoptará "1.758". En otras palabras, la rentabilidad se ha movido ligeramente en la dirección que necesitamos. Obviamente, si realizamos algunas pruebas más, este indicador podría disminuir, pero de media debería darse un aumento en el indicador. Estrictamente hablando, no hemos elegido la lógica de la mejor manera, pero esta resulta suficiente para la demostración.

Conclusión

En el presente artículo, hemos intentado recopilar las técnicas más interesantes y útiles que pueden servir de ayuda a los desarrolladores de sistemas comerciales automatizados. Algunas de estas técnicas, con las mejoras e investigaciones adecuadas, podrían resultar provechosas. Esperamos que este material haya resultado útil y entretenido a los lectores. Todos estos trucos suponen más bien una caja de herramientas que una guía de montaje para conseguir el "Grial". Incluso un conocimiento simple de estas técnicas puede protegernos de inversiones precipitadas o pérdidas críticas. Por otra parte, los más curiosos pueden intentar construir algo más interesante y estable que un sistema comercial convencional basado en el cruzamiento de dos indicadores.