
Redes neuronales en el trading: Modelo adaptativo multiagente (Final)
Introducción
En el artículo anterior, nos familiarizamos con el framework MASA, un sistema multiagente basado en la integración única de agentes que interactúan entre sí. En la arquitectura MASA, un agente RL basado en técnicas de aprendizaje por refuerzo optimiza el rendimiento total de un portafolio de inversiones. Al mismo tiempo, el agente, basándose en un algoritmo alternativo, trata de optimizar la portafolio de inversiones devuelto por el agente RL para minimizar los riesgos potenciales.
Con una clara división de funciones entre los agentes, el modelo aprende y se adapta constantemente al entorno básico del mercado financiero. El esquema multiagente de MASA logra portafolios de inversión más equilibrados, tanto por su rentabilidad como por sus riesgos potenciales.
A continuación le mostramos la visualización del framework MASA por parte del autor.
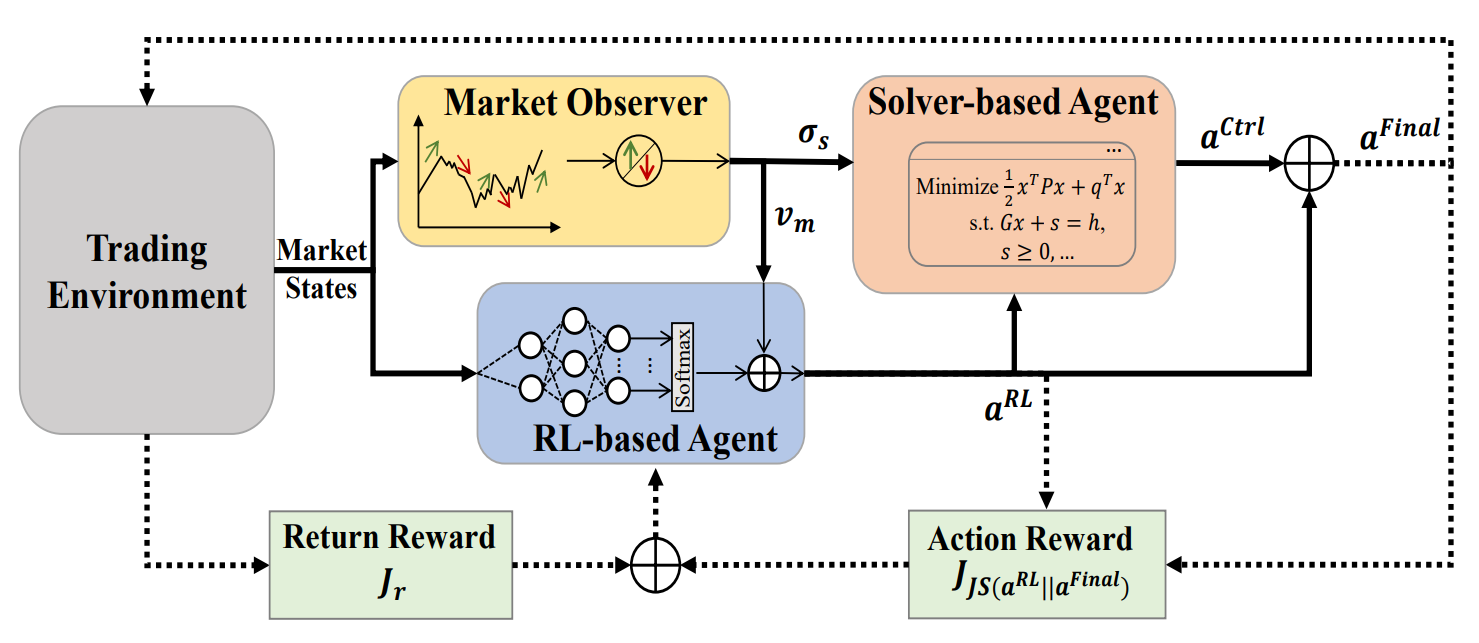
En la parte práctica del artículo anterior presentamos algoritmos para implementar la funcionalidad de agentes individuales del framework MASA, que implementamos como objetos independientes. Continuando por donde lo dejamos.
1. La capa compleja MASA
En el artículo anterior creamos tres agentes distintos, cada uno de los cuales realizaba una función específica dentro del framework MASA. Hoy los combinaremos en un único sistema. Para ello, crearemos un nuevo objeto CNeuronMASA, cuya estructura le presentamos a continuación.
class CNeuronMASA : public CNeuronBaseSAMOCL { protected: CNeuronMarketObserver cMarketObserver; CNeuronRevINDenormOCL cRevIN; CNeuronRLAgent cRLAgent; CNeuronControlAgent cControlAgent; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronMASA(void) {}; ~CNeuronMASA(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers_mo, uint forecast, uint segments_rl, float rho, uint layers_rl, uint n_actions, uint heads_contr, uint layers_contr, int NormLayer, CNeuronBatchNormOCL *normLayer, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronMASA; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; virtual void SetActivationFunction(ENUM_ACTIVATION value) override; //--- virtual int GetNormLayer(void) { return cRevIN.GetNormLayer(); } virtual bool SetNormLayer(int NormLayer, CNeuronBatchNormOCL *normLayer); };
Debo admitir que hay algunos puntos en la estructura presentada de la nueva estructura que merecen cierta atención.
Obviamente, el número relativamente elevado de parámetros del método de inicialización Init llama la atención de inmediato. Y esto se debe a la necesidad de abarcar las necesidades de nuestros tres agentes, cada uno con sus propias características arquitectónicas.
Además, hay un matiz que va en contra del concepto de nuestra biblioteca. El método de pasada directa tiene una única fuente de datos de entrada, lo que resulta coherente con el framework considerado. La situación actual del mercado se suministra a la entrada del agente RL y del agente de supervisión del mercado. Pero aquí, en el método de distribución de gradiente de error, aparecen objetos de una segunda fuente de datos, lo que no se observa ni en el método de pasada adelante ni en la presentación del autor del framework MASA.
Esta solución no estándar se adoptó para organizar un proceso de aprendizaje alternativo para el agente de supervisión del mercado. Para este objetivo, hemos añadido un objeto interno de normalización inversa de datos. Discutiremos esta solución con más detalle durante la construcción de los algoritmos para los métodos de nuestra clase.
Todos los objetos internos de nuestra nueva clase se declararán estáticamente, lo que nos permitirá dejar vacíos el constructor y el destructor del objeto. El proceso inmediato de inicialización de una nueva instancia de la clase se organizará en el método Init. Como ya hemos mencionado, el método de inicialización contiene un gran número de parámetros, pero en realidad estos duplican los parámetros de inicialización de los agentes creados anteriormente.
bool CNeuronMASA::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads_mo, uint layers_mo, uint forecast, uint segments_rl, float rho, uint layers_rl, uint n_actions, uint heads_contr, uint layers_contr, int NormLayer, CNeuronBatchNormOCL *normLayer, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseSAMOCL::Init(numOutputs, myIndex, open_cl, n_actions, rho, optimization_type, batch)) return false;
En el cuerpo de un método, por tradición, llamaremos primero al método homónimo de la clase padre. En este caso, utilizaremos una capa neuronal totalmente conectada con optimización SAM como clase principal.
Y aquí deberemos recordar que el resultado del framework MASA se forma a la salida del agente-controlador en forma de un tensor de acciones. Por consiguiente, especificaremos el tamaño de la capa en el método de inicialización de la clase padre en el nivel del espacio de acción del Actor.
A continuación, llamaremos secuencialmente a los métodos de inicialización de nuestros agentes. En primer lugar, inicializaremos el agente de supervisión del mercado transmitiéndole los parámetros correspondientes.
Recordemos que los agentes de supervisión del mercado reciben como entrada una descripción tensorial de la situación actual del mercado, y como salida devuelven valores de previsión en el formato de la misma secuencia multimodal para un horizonte de planificación determinado.
//--- Market Observation if(!cMarketObserver.Init(0, 0, OpenCL, window, window_key, units_count, heads_mo, layers_mo, forecast, optimization, iBatch)) return false; if(!cRevIN.Init(0, 1, OpenCL, cMarketObserver.Neurons(), NormLayer, normLayer)) return false;
Inmediatamente, inicializaremos una capa de normalización inversa cuyo tamaño será igual a los resultados del agente de supervisión del mercado.
A continuación inicializaremos el agente RL, que recibirá como entrada el mismo tensor que describe la situación actual del mercado, pero devolviendo ya el tensor de acciones del Actor, según la política aprendida.
//--- RL Agent if(!cRLAgent.Init(0, 2, OpenCL, window, units_count, segments_rl, fRho, layers_rl, n_actions, optimization, iBatch)) return false;
Y por último inicializaremos el agente-controlador, que recibirá los resultados de los dos agentes anteriores como entrada y devolverá el tensor corregido de acciones del Actor.
if(!cControlAgent.Init(0, 3, OpenCL, 3, window_key, n_actions / 3, heads_contr, window, forecast, layers_contr, optimization, iBatch)) return false;
Nótese aquí que en nuestra implementación, el agente RL y el agente-controlador miran de forma diferente el tensor de acciones del Actor generado por el agente RL. Y no se trata solo de separar la funcionalidad de los agentes.
La salida del agente RL usa una capa totalmente conectada que genera de forma independiente cada elemento del tensor de acciones del Actor basándose en el análisis de la situación del mercado realizado y en la política de comportamiento aprendida. Sin embargo, tenemos un conocimiento a priori de la exclusión mutua de las acciones multidireccionales (compra y venta de un activo), y los parámetros de transacción en cada dirección ocupan tres elementos en el vector de descripción de la acción.
Dado lo anterior, indicaremos al agente-controlador que el tensor de acciones está representado por una secuencia multimodal en la que cada elemento de la secuencia está descrito por un vector de tres elementos (la dimensionalidad de un vector que describe una transacción). Así, pediremos al agente-controlador que evalúe los riesgos de la transacción en cada dirección individual.
Al final del método de inicialización de nuestro objeto framework MASA, sustituiremos los punteros a los búferes de la interfaz externa y estableceremos la función de activación sigmoidea por defecto.
if(!SetOutput(cControlAgent.getOutput(), true) || !SetGradient(cControlAgent.getGradient(), true)) return false; SetActivationFunction(SIGMOID); //--- return true; }
A continuación, finalizaremos el método de inicialización retornando el resultado lógico de las operaciones al programa que realiza la llamada.
Aquí debemos decir unas palabras sobre la configuración de la función de activación. En la salida de nuestra nueva clase, obtendremos el tensor de acciones del Actor, que primero generará el agente RL y luego ajustará el agente-controlador. Obviamente, el espacio de valores en la salida de ambos agentes y nuestro objeto deberá ser idéntico. Por lo tanto, redefiniremos el método de especificación de la función de activación con el fin de sincronizarlo para todos los objetos mencionados.
void CNeuronMASA::SetActivationFunction(ENUM_ACTIVATION value) { cControlAgent.SetActivationFunction(value); cRLAgent.SetActivationFunction((ENUM_ACTIVATION)cControlAgent.Activation()); CNeuronBaseSAMOCL::SetActivationFunction((ENUM_ACTIVATION)cControlAgent.Activation()); }
Una vez finalizada la inicialización de los objetos, construiremos el algoritmo de pasada directa. Aquí todo será bastante sencillo. Solo llamaremos secuencialmente a los métodos de nuestros agentes homónimos. Primero obtendremos los resultados del análisis del estado actual del mercado y el tensor preliminar de las acciones del Actor.
bool CNeuronMASA::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cMarketObserver.FeedForward(NeuronOCL.AsObject())) return false; if(!cRLAgent.FeedForward(NeuronOCL.AsObject())) return false;
A continuación, transmitiremos los resultados al agente-controlador para que tome una decisión final.
if(!cControlAgent.FeedForward(cRLAgent.AsObject(), cMarketObserver.getOutput())) return false; //--- return true; }
Y por supuesto, antes de que el método termine, devolveremos el resultado lógico de las operaciones al programa que realiza la llamada.
Aquí debemos señalar que en la visualización del autor del framework MASA presentada anteriormente, la formación del vector de acción final como la suma de los resultados del agente RL y el agente de control resulta claramente visible. En nuestra implementación, en cambio, tomaremos los resultados del agente-controlador como valores finales, excluyendo la comunicación residual con el agente RL. Pero aquí debemos recordar la arquitectura de nuestro agente-controlador.
Recordemos que el agente-controlador en nuestra implementación se representará como el decodificador del Transformer. Y, como ya sabrá, la arquitectura del Transformer prevé enlaces residuales tanto en los módulos de atención como en el bloque FeedForward. Por consiguiente, el flujo de información de los enlaces residuales al agente RL ya es inherente a la arquitectura del agente-controlador, y no necesitaremos organizar enlaces residuales adicionales.
Y ahora llegamos a la organización de los procesos de pasada inversa. Para ser más precisos, a la construcción del algoritmo calcInputGradients de distribución de gradientes de error, sobre cuyas soluciones no estándar empezamos a hablar al familiarizarnos con la estructura de la clase CNeuronMASA.
En primer lugar, echaremos un vistazo al rendimiento esperado de nuestros agentes. Dos de ellos retornarán el tensor de acciones del Actor. Así que resultará bastante lógico utilizar durante el aprendizaje un conjunto de acciones óptimas como instrucciones objetivo en el caso del aprendizaje supervisado, o su proyección a recompensas en el caso del aprendizaje con refuerzo.
Sin embargo, seguiremos contando con un agente de supervisión del mercado que retornará los valores previstos de la serie temporal multimodal de las lecturas del instrumento financiero analizado. Y luego está la cuestión del entrenamiento de este agente, o más exactamente la cuestión de la fijación de objetivos. Por supuesto, podemos transmitir el gradiente de error a través del agente-controlador y obtener la influencia del agente de supervisión del mercado en la decisión sobre la corrección de los resultados del agente RL. Pero, ¿hasta qué punto este enfoque se corresponde con la tarea de prever el próximo movimiento del instrumento financiero analizado?
Creo que en este caso resultará más apropiado implementar un entrenamiento aparte para el agente de supervisión del mercado para predecir las próximas series temporales, como hicimos antes para el Codificador de estado de la cuenta. Pero el problema es que el agente de supervisión del mercado es parte integrante de nuestro modelo, y no podemos aislarlo en un proceso de aprendizaje separado. Y en tal caso, surgirá la idea de pasar dos valores objetivo al nivel de la capa. Y esto ya supondrá un cambio fundamental en el algoritmo de nuestra biblioteca. Como se habrá dado cuenta, es un vasto campo por mejorar.
Las soluciones no estándar a menudo nos ayudan a evitar grandes cantidades de trabajo, resolviendo la tarea por así decirlo "con poco daño". ¿Qué le parece si utilizamos el mecanismo de transferencia de objetos de la segunda fuente de datos de origen para dar al objeto dos propósitos? Tomaremos esta idea y redefiniremos el método de distribución del gradiente de error utilizando dos fuentes de datos de entrada, solo que esta vez se utilizarán los búferes del segundo objeto para transferir el tensor de valores objetivo al agente de supervisión del mercado.
bool CNeuronMASA::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1) { if(!NeuronOCL) return false;
Sin embargo, esta idea no está exenta de escollos. Y una de ellos será la comparabilidad de los datos. La cuestión es que, a la entrada del modelo, solemos suministrar los datos de origen sin procesar obtenidos del terminal. Estos se someten a un procesamiento inicial en la capa de normalización por lotes, y todas las demás capas neuronales de nuestro modelo trabajan con datos normalizados. Esto incluye el objeto CNeuronMASA que estamos creando. Y resulta bastante lógico que a la salida del agente de supervisión del mercado obtengamos también una previsión normalizada, con la que le podrá trabajar cómodamente al agente-controlador. Lo único es que solo podemos proporcionar en bruto los valores posteriores objetivo de las series temporales multimodales analizadas. Por lo tanto, añadiremos una capa de normalización inversa de los datos que no utilicemos en el método de pasada directa. Pero para organizar la distribución del gradiente de error, primero añadiremos a los resultados del agente de supervisión del mercado los parámetros estadísticos de la distribución de los datos de origen.
if(!cRevIN.FeedForward(cMarketObserver.AsObject())) return false;
Y de esta forma, ya podremos comparar los valores objetivo con nuestra previsión y distribuir el gradiente de error hasta el agente de supervisión del mercado.
if(!cRevIN.FeedForward(cMarketObserver.AsObject())) return false; float error = 1.0f; if(!cRevIN.calcOutputGradients(SecondGradient, error)) return false; if(!cMarketObserver.calcHiddenGradients(cRevIN.AsObject())) return false;
A continuación, distribuiremos el gradiente de error del agente-controlador entre el agente RL y el agente de supervisión del mercado. Y aquí tendremos que mantener el gradiente de error derivado anteriormente a nivel del agente de supervisión del mercado. Por lo tanto, obtendremos el error de este agente en el búfer auxiliar, después de lo cual, sumaremos los valores obtenidos de los dos flujos de información.
if(!cRLAgent.calcHiddenGradients(cControlAgent.AsObject(), cMarketObserver.getOutput(), cMarketObserver.getPrevOutput(), (ENUM_ACTIVATION)cMarketObserver.Activation()) || !SumAndNormilize(cMarketObserver.getGradient(), cMarketObserver.getPrevOutput(), cMarketObserver.getGradient(), 1, false, 0, 0, 0, 1)) return false;
Otro punto a tener en cuenta serán los resultados del agente RL y del agente-controlador. Ambos agentes retornarán el tensor de acciones del Actor. El primero se basará en los resultados de su propio análisis de la situación actual del mercado. El segundo se realizará después de evaluar los riesgos del tensor de acciones proporcionado, considerando los valores de previsión del próximo movimiento de precios obtenido del agente de supervisión del mercado. En condiciones ideales, los resultados de ambos agentes deberían coincidir. Por ello, para el agente RL, introduciremos un error de desviación de los resultados del agente-controlador.
CBufferFloat *temp = cRLAgent.getGradient(); if(!cRLAgent.SetGradient(cRLAgent.getPrevOutput(), false) || !cRLAgent.calcOutputGradients(cControlAgent.getOutput(), error) || !SumAndNormilize(temp, cRLAgent.getPrevOutput(), temp, 1, false, 0, 0, 0, 1) || !cRLAgent.SetGradient(temp, false)) return false;
Y, obviamente, las operaciones para determinar el error adicional no deberán eliminar el gradiente de error acumulado previamente. Por lo tanto, utilizaremos el algoritmo de sustitución de los búferes de datos y luego sumaremos los valores obtenidos de los dos flujos de información.
Después de distribuir el gradiente de error a los agentes internos, tendremos que transmitirlo a la capa de datos de origen. Aquí también tendremos que ensamblar el gradiente de error a través de dos flujos de información: el del agente RL y el del agente de supervisión del mercado. Al igual que antes, en estos casos, primero transmitiremos el gradiente de error del agente de supervisión del mercado.
if(!NeuronOCL.calcHiddenGradients(cMarketObserver.AsObject())) return false;
Después, realizaremos la sustitución de búferes y haremos descender el gradiente de error del agente RL.
temp = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(NeuronOCL.getPrevOutput(), false) || !NeuronOCL.calcOutputGradients(cRLAgent.getOutput(), error) || !SumAndNormilize(temp, NeuronOCL.getPrevOutput(), temp, 1, false, 0, 0, 0, 1) || !NeuronOCL.SetGradient(temp, false)) return false; //--- return true; }
Luego sumaremos los valores obtenidos de los dos flujos de información y retornaremos los punteros a los búferes de datos al estado inicial.
En esta fase, distribuiremos el gradiente de error entre todos los participantes en el proceso según su influencia en el resultado final del modelo. Ahora solo nos quedará actualizar los parámetros del modelo para minimizar el error. Esta funcionalidad se realizará en el método updateInputWeights. El algoritmo de este método es bastante simple. Solo llamaremos secuencialmente a los métodos internos del agente homónimo. No nos detendremos ahora en su examen detallado. No olvide que nuestros agentes internos explotarán los enfoques de optimización SAM. Esto significa que las llamadas a los métodos internos del agente deberán realizarse en la secuencia inversa a la de la pasada directa.
Con esto concluirá nuestro análisis de los algoritmos de creación de los métodos para la nueva clase CNeuronMASA. Podrá leer el código completo de este objeto y todos sus métodos por sí mismo en el archivo adjunto.
2. Arquitectura de los modelos
Pues bien, una vez finalizado el trabajo de construcción de los nuevos objetos, procederemos a analizar la arquitectura de los modelos entrenados. Y aquí, debemos decirlo, también hemos introducido cambios y algunas soluciones no estándar.
En primer lugar, descartaremos el modelo independiente del Codificador de estados del entorno. Y esto no es de extrañar. En nuestra clase CNeuronMASA, son dos los agentes que realizan el análisis paralelo del estado actual del entorno.
El segundo punto a considerar se refiere a la inclusión de la información sobre la cuenta. Mientras que antes lo transmitíamos al modelo del Actor como una segunda fuente de datos de entrada, ahora ocuparemos este flujo de información con el tensor de los valores objetivo del agente de supervisión del mercado. Por lo tanto, simplemente añadiremos la información del estado de la cuenta al final del tensor de descripción del estado del entorno.
Así, suministraremos a la entrada del Actor un tensor general de datos de entrada que incluirá las descripciones del estado del entorno, así como información del estado de la cuenta.
bool CreateDescriptions(CArrayObj *&actor, CArrayObj *&critic) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } //--- Actor actor.Clear(); //--- if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr + AccountDescr); descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Los datos de origen "brutos" obtenidos se someten a un procesamiento primario en la capa de normalización por lotes.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
A continuación, debemos señalar que el vector de información del estado de la cuenta no cumple la estructura del tensor de descripción del estado del entorno. Su longitud puede ser diferente del tamaño de la descripción de un elemento de la secuencia multimodal de la serie temporal analizada, que no se ajusta a la estructura de los módulos de atención que usaremos a continuación. Por consiguiente, deberemos poner los datos de origen en forma de matriz. Asignaremos esta funcionalidad a una capa de incorporaciones entrenadas.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronEmbeddingOCL; descr.count = 1; descr.window_out = BarDescr; { int temp[HistoryBars + 1]; if(ArrayInitialize(temp, BarDescr) < (HistoryBars + 1)) return false; temp[HistoryBars] = AccountDescr; if(ArrayCopy(descr.windows, temp) < (HistoryBars + 1)) return false; } descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Esta capa descompone un vector de datos de origen en bloques de una longitud determinada y proyecta cada uno de esos bloques en un subespacio de una dimensionalidad determinada, independientemente del tamaño del bloque original. Esto se logra entrenando una matriz de proyección independiente para cada bloque.
Sabemos que la mayor parte del tensor original está representada por los vectores del mismo tipo que describen estados del entorno individuales (barras), y solo se extrae el último elemento (información del estado de la cuenta). Por lo tanto, primero inicializaremos un array de ventanas analizadas de longitud suficiente con valores fijos y, a continuación, cambiaremos solo el tamaño del último elemento de la secuencia analizada.
Tenga en cuenta que en la salida de la capa de incorporación, fijaremos el tamaño de un elemento de secuencia igual al tamaño de una descripción de barra. Este es un punto muy importante. A efectos del análisis de datos, podríamos utilizar cualquier tamaño de un único elemento de secuencia a la salida de la capa de incorporación. Pero nuestro modelo tiene un agente de supervisión del mercado que retorna valores de previsión en la dimensionalidad de los datos de origen. Por ello, resultará bastante lógico que los valores de previsión de las series temporales multimodales analizadas se correspondan con los valores objetivo utilizados en el entrenamiento del modelo. Y estos son idénticos a los datos de origen. Así que el círculo se ha cerrado.
El uso de incorporaciones entrenadas cumple implícitamente la función de la codificación posicional. Como ya hemos mencionado, cada elemento de la secuencia tiene su propia matriz de proyección de datos. Y esto significa que tener dos vectores idénticos en los datos de origen en posiciones diferentes devolverá proyecciones distintas en el subespacio objetivo. Y en el análisis posterior, se distinguirán claramente.
Las incorporaciones resultantes se pasarán a la entrada de nuestro nuevo objeto de framework MASA. Y deberemos considerar varias cosas.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMASA; //--- Windows { int temp[] = {BarDescr, NForecast, 2 * NActions}; if(ArrayCopy(descr.windows, temp) < (int)temp.Size()) return false; } descr.window_out = 32; descr.count = HistoryBars+1; //--- Heads { int temp[] = {4, 4}; if(ArrayCopy(descr.heads, temp) < (int)temp.Size()) return false; } //--- Layers { int temp[] = {3, 3, 3}; if(ArrayCopy(descr.units, temp) < (int)temp.Size()) return false; } descr.window = BarDescr; descr.probability = Rho; descr.step = 1; // Normalization layer descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
En el array dinámico descr.windows, especificaremos los parámetros básicos de las secuencias analizadas por los agentes internos. Aquí especificaremos secuencialmente la dimensionalidad de un elemento de la secuencia de datos de origen, el horizonte de planificación de las series temporales posteriores y el espacio de acción del Actor.
Deberemos prestar especial atención al último parámetro. Al construir la arquitectura de los agentes internos, hablamos de organizar una dependencia directa entre el estado del entorno y la acción generada, lo que elimina la estocasticidad del comportamiento del Actor. Sin embargo, en nuestra implementación, entrenaremos exactamente la política estocástica del Actor. Por ello, estaremos duplicando el espacio de acción obtenido en la salida del framework MASA. Es fácil ver que esto resulta coherente con el enfoque que hemos explotado antes en la organización de las políticas estocásticas. El vector obtenido de la salida del framework MASA lo dividiremos lógicamente en 2 partes iguales que representarán los valores medios y la varianza del espacio de acción del Actor en el estado del entorno analizado. Por eso desactivaremos la activación de esta capa.
Cada módulo de atención que utilizamos usará 4 cabezas cada uno. Y cada Agente incluirá 3 capas internas del Codificador/Decodificador cada una.
Como ya hemos mencionado, pasaremos los resultados del framework MASA a la capa de estado de valencia del Autocodificador, para generar acciones del Actor aleatorias en una distribución determinada.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Proyectaremos el vector de acción resultante en los límites dados utilizando una capa convolucional y una función de activación sigmoidal.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvSAMOCL; descr.count = NActions / 3; descr.window = 3; descr.step = 3; descr.window_out = 3; descr.activation = SIGMOID; descr.optimization = ADAM; descr.probability = Rho; if(!actor.Add(descr)) { delete descr; return false; }
Y en la salida del modelo, utilizaremos una capa de concordancia de frecuencia para hacer coincidir los resultados del modelo con los valores objetivo.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NActions; descr.count = 1; descr.step = int(false); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
A continuación construiremos la arquitectura del Crítico. Aquí podemos decir que la arquitectura del modelo la tomaremos en su mayor parte de artículos anteriores. Sin embargo, la renuncia a un modelo separado de Codificador de estados del entorno nos ha llevado a añadir también al modelo del Crítico un bloque de análisis del estado inicial. Aquí hemos utilizado el framework PSformer para analizar el estado actual. Al mismo tiempo, los datos de origen del Crítico no incluirán información sobre el estado de la cuenta. Mi opinión subjetiva es que esa información no posee ningún valor para el Crítico. La eficacia de la operación dependerá de las condiciones del mercado, no del estado de la cuenta en el momento de la apertura.
Obviamente, aquí podemos argumentar que especificar un volumen excesivamente grande o pequeño puede llevar a un error de ejecución de la transacción y, como resultado, a que no haya posición abierta. Pero la determinación del alcance de la transacción reside en la funcionalidad del Actor. ¿Y debe el Crítico responder a dichas instancias privadas? La cuestión reside en la distribución de la funcionalidad entre los modelos.
La segunda cuestión se encuentra en las posiciones abiertas y las ganancias o pérdidas acumuladas. Se trata del rendimiento de las transacciones anteriores, mientras que el Crítico evalúa la actual. E incluso si asumimos que el Crítico no está evaluando una operación individual sino una política en curso, en este caso, estará evaluando el rendimiento de la política hasta el final del episodio, pero en ningún caso en orden inverso.
Por consiguiente, solo suministraremos información sobre el estado actual del entorno a la entrada del modelo.
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Al igual que antes, los datos de origen "en bruto" serán procesados por la capa de normalización por lotes.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Y se transmitirán a 3 capas consecutivas del framework PSformer.
//--- layer 2 - 4 for(int i = 0; i < 3; i++) { if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronPSformer; descr.window = BarDescr; descr.count = HistoryBars; descr.window_out = Segments; descr.probability = Rho; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } }
A continuación, utilizaremos sucesivamente las capas convolucional y completamente conectada para reducir la dimensionalidad del tensor obtenido.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvSAMOCL; descr.count = HistoryBars; descr.window = BarDescr; descr.step = BarDescr; descr.window_out = int(LatentCount / descr.count); descr.probability = Rho; descr.activation = GELU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseSAMOCL; descr.count = LatentCount; descr.probability = Rho; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Y combinaremos los resultados del análisis del entorno con las acciones del agente en la capa de concatenación de datos.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = LatentCount; descr.step = NActions; descr.activation = GELU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Después vendrá el módulo de decisión, que consta de 4 capas completamente conectadas.
//--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseSAMOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; descr.probability = Rho; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseSAMOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; descr.probability = Rho; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 10 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseSAMOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; descr.probability = Rho; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 11 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseSAMOCL; descr.count = NRewards; descr.activation = None; descr.optimization = ADAM; descr.probability = Rho; if(!critic.Add(descr)) { delete descr; return false; }
Y en la salida, utilizaremos una capa de concordancia de frecuencia de los resultados del modelo con los valores objetivo.
//--- layer 12 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NRewards; descr.count = 1; descr.step = int(false); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
Tras especificar con éxito la arquitectura de los dos modelos entrenados, finalizaremos el método retornando el resultado lógico de las operaciones al programa que realiza la llamada.
3. Programa de entrenamiento de modelos
Ya nos acercamos a la conclusión lógica de nuestro trabajo. Ahora pasaremos a construir el modelo del programa de entrenamiento. Resulta bastante obvio que la exclusión de un modelo entrenado impone su propia huella en el algoritmo de construcción del programa de entrenamiento. Además, al construir el módulo del framework MASA, acordamos utilizar el flujo de información de la segunda fuente de datos como flujo de valores objetivo adicional. Por consiguiente, vamos a no perder el tiempo y a analizar el algoritmo de entrenamiento del modelo que implementaremos en el método Train.
Al igual que antes, primero haremos un poco de trabajo preparatorio. Aquí generaremos un vector de probabilidades para seleccionar trayectorias del búfer de reproducción de experiencias en función del rendimiento de las pasadas.
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9); //--- vector<float> result, target, state; bool Stop = false; //--- uint ticks = GetTickCount();
Y declararemos las variables locales necesarias.
A continuación, organizaremos un ciclo de entrenamiento cuyo número de iteraciones se establecerá con la ayuda de los parámetros externos de nuestro asesor experto.
for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++) { int tr = SampleTrajectory(probability); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast)); if(i <= 0) { iter --; continue; } if(!state.Assign(Buffer[tr].States[i].state) || MathAbs(state).Sum() == 0 || !bState.AssignArray(state)) { iter --; continue; } if(!state.Assign(Buffer[tr].States[i+NForecast].state) || !state.Resize(NForecast*BarDescr) || MathAbs(state).Sum() == 0 || !bForecast.AssignArray(state)) { iter --; continue; }
En el cuerpo del ciclo, muestreamos una única trayectoria y el estado del entorno en ella. E inmediatamente comprobaremos la disponibilidad de los datos históricos y posteriores del estado muestreado para una profundidad de análisis y un horizonte de planificación dados. Si se da un resultado negativo en al menos un punto de control, se muestreará una nueva trayectoria y el estado en esta.
Si disponemos de los datos necesarios, los transferiremos a los búferes correspondientes. A continuación, añadiremos a la descripción del estado del entorno información sobre el estado de la cuenta en el momento del análisis.
//--- Account float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; bState.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); bState.Add(Buffer[tr].States[i].account[1] / PrevBalance); bState.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); bState.Add(Buffer[tr].States[i].account[2]); bState.Add(Buffer[tr].States[i].account[3]); bState.Add(Buffer[tr].States[i].account[4] / PrevBalance); bState.Add(Buffer[tr].States[i].account[5] / PrevBalance); bState.Add(Buffer[tr].States[i].account[6] / PrevBalance);
Y luego añadiremos una marca temporal del estado del entorno analizado.
//--- double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); bState.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); bState.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); bState.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); bState.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
Una vez preparados los datos de entrada, iniciaremos el proceso de entrenamiento del modelo. Y la primera iteración de entrenamiento la realizará el Crítico. A la entrada del modelo introduciremos el estado analizado del entorno y el vector de acciones realmente realizadas por el Actor al momento de recoger la muestra de entrenamiento. Al fin y al cabo, es por estas acciones por las que obtenemos verdaderas recompensas del entorno. Y realizamos las operaciones de pasada directa, evaluando las acciones reales del Actor.
//--- Critic bActions.AssignArray(Buffer[tr].States[i].action); Critic.TrainMode(true); if(!Critic.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)GetPointer(bActions))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Podemos adivinar fácilmente que, como resultado de las operaciones de pasada directa del Crítico, nos gustaría obtener un tensor de recompensas cercano al realmente obtenido del entorno. Por lo tanto, recuperaremos la recompensa real de las acciones realizadas del búfer de reproducción de experiencias y realizaremos las operaciones de pasada inversa del Crítico, minimizando además el error.
result.Assign(Buffer[tr].States[i + 1].rewards); target.Assign(Buffer[tr].States[i + 2].rewards); result = result - target * DiscFactor; Result.AssignArray(result); if(!Critic.backProp(Result, (CBufferFloat *)GetPointer(bActions), (CBufferFloat *)GetPointer(bGradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
A continuación vendrá el proceso de entrenamiento de la política del Actor, que realizaremos en 2 fases. Primero realizaremos una pasada directa del Actor para generar el tensor de acciones.
//--- Actor Policy if(!Actor.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Seguida de la ejecución de las operaciones de pasada directa del Crítico. Solo que esta vez se evaluarán las acciones generadas por el Actor.
Critic.TrainMode(false); if(!Critic.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CNet*)GetPointer(Actor), LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Cabe señalar que en este punto desactivaremos el modo de aprendizaje del Crítico. Esto nos permitirá eliminar el impacto de los valores incorrectos en el estudio de las políticas de recompensa.
Luego comprobaremos el rendimiento de la pasada analizada. Y si la política de comportamiento del Actor al realizar la pasada analizada ha dado un resultado positivo, entonces nosotros, en el estilo del aprendizaje supervisado, aproximaremos la política actual del Actor a una positiva. Esta será la primera etapa de la entrenamiento del Actor.
if(Buffer[tr].States[0].rewards[0] > 0) if(!Actor.backProp(GetPointer(bActions),(CBufferFloat*)GetPointer(bForecast),GetPointer(bGradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
En la segunda etapa del entrenamiento del Actor, ajustaremos el Crítico para aumentar la recompensa y reducir el gradiente de error al nivel de acción del Actor.
Critic.getResults(Result); for(int c = 0; c < Result.Total(); c++) { float value = Result.At(c); if(value >= 0) Result.Update(c, value * 1.01f); else Result.Update(c, value * 0.99f); } if(!Critic.backProp(Result, (CNet *)GetPointer(Actor), LatentLayer) || !Actor.backPropGradient((CBufferFloat*)GetPointer(bForecast),GetPointer(bGradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Así pues, queremos que el Crítico indique al Actor cómo ajustar la política para obtener mayores rendimientos totales. Después, ajustaremos la política del Actor en la dirección establecida.
Ahora todo lo que tendremos que hacer es informar al usuario sobre el progreso del proceso de entrenamiento y pasar a la siguiente iteración del entrenamiento del modelo.
//--- if(GetTickCount() - ticks > 500) { double percent = double(iter) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent, Actor.getRecentAverageError()); str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Critic", percent, Critic.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
Una vez completadas con éxito todas las iteraciones del entrenamiento del modelo, borraremos el campo de comentarios del gráfico del instrumento financiero donde mostramos la información para el usuario.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic", Critic.getRecentAverageError()); ExpertRemove(); //--- }
Luego registraremos los resultados del entrenamiento del modelo e inicializaremos el proceso de finalización del programa.
Con esto concluirá nuestra revisión de los algoritmos para construir el framework MASA y la implementación de los programas de entrenamiento de modelos. Podrá leer su código completo por sí mismo en el archivo adjunto.
4. Simulación
Nuestro trabajo de aplicación de los enfoques propuestos por los autores del framework MASA usando herramientas MQL5 ha llegado a su conclusión lógica. Ahora pasaremos a la fase más emocionante: la evaluación de la eficacia de los enfoques aplicados sobre datos históricos reales.
Es importante señalar que estamos realizando una "evaluación de la eficacia de los enfoques aplicados", no de los enfoques "propuestos". Al fin y al cabo, durante la implementación hemos introducido cambios en la versión del framework del autor.
Los modelos se entrenarán con datos históricos de 2023 y el instrumento financiero EURUSD, marco temporal H1. Los parámetros de todos los indicadores usados se mantienen por defecto.
Para el entrenamiento inicial, hemos utilizado una muestra de entrenamiento recogida en trabajos anteriores, actualizada periódicamente durante el entrenamiento de modelos con objeto de actualizarla para la política actual del Actor.
Tras varios ciclos de entrenamiento de los modelos y después de actualizar la muestra de entrenamiento, hemos obtenido una política que demuestra rentabilidad en las muestras de entrenamiento y prueba.
Las pruebas de la política entrenada se han realizado con los datos históricos de enero de 2024, manteniendo constantes los demás parámetros. A continuación figuran los resultados de la prueba.
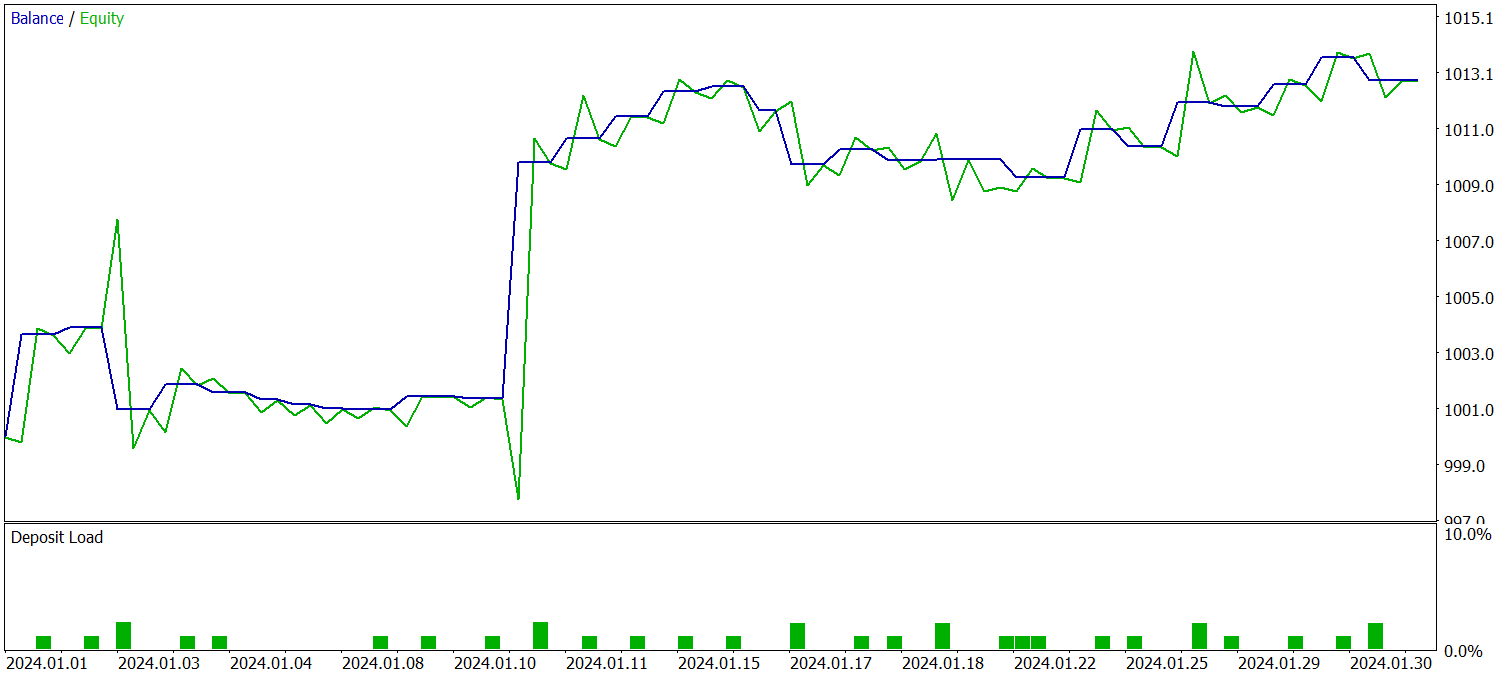
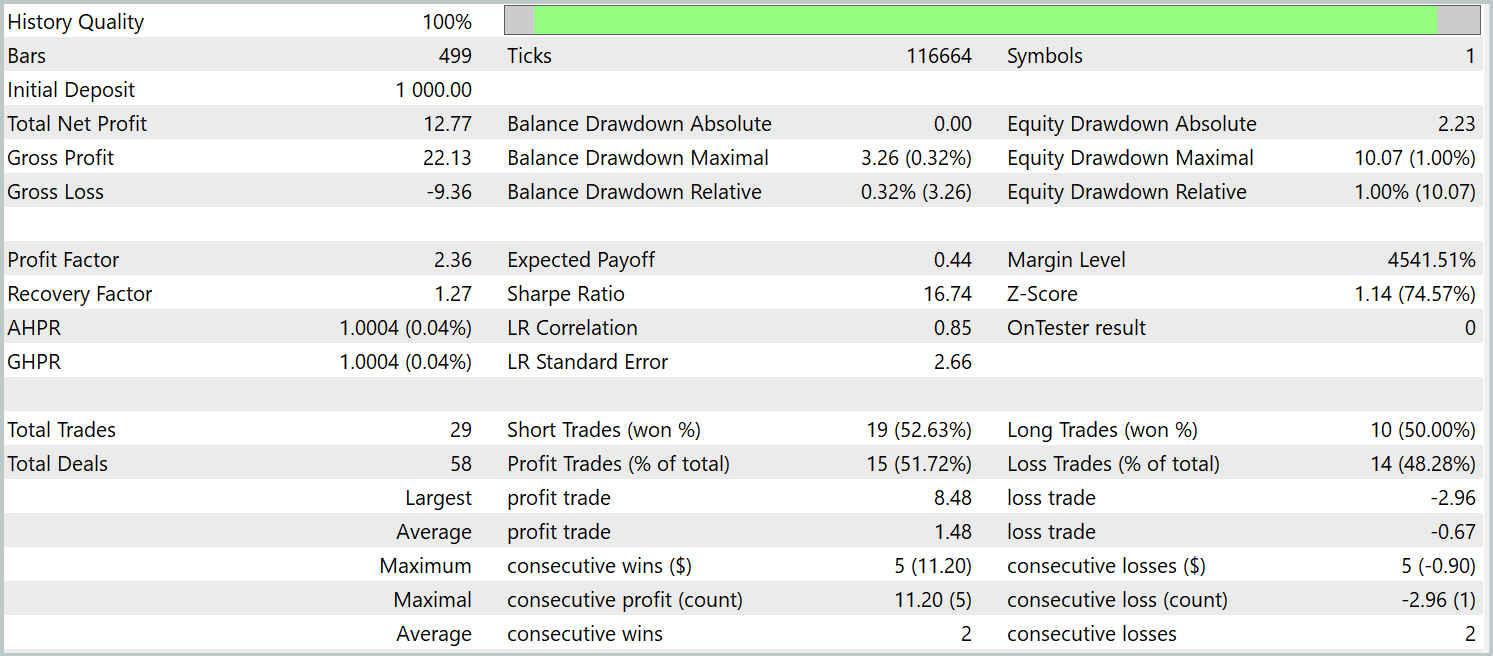
Durante el periodo de prueba, el modelo ha realizado 29 transacciones comerciales, la mitad de las cuales se han cerrado con beneficios. No obstante, gracias a que la media de las transacciones rentables es más de 2 veces superior a la del mismo indicador de las transacciones con pérdidas, tenemos una marcada tendencia al crecimiento de los depósitos. Y esto puede indicar el potencial del framework aplicado.
Conclusión
Hoy nos hemos familiarizado con una metodología innovadora para gestionar portafolios de inversión en mercados financieros inestables: el sistema adaptativo multiagente MASA. Este framework combina eficazmente los puntos fuertes de los algoritmos RL y los métodos de optimización adaptativa para aumentar efectivamente la rentabilidad del modelo junto con la reducción del riesgo.
En la parte práctica, hemos implementado nuestra visión de los enfoques propuestos usando herramientas MQL5. Asimismo, hemos entrenado los modelos con datos históricos reales. Los resultados obtenidos indican el potencial existente de los planteamientos propuestos. No obstante, antes de aplicar el modelo en el comercio real, será necesario introducir una serie de medidas adicionales para su entrenamiento en una muestra más representativa, además de realizar pruebas exhaustivas.
Enlaces
- Developing A Multi-Agent and Self-Adaptive Framework with Deep Reinforcement Learning for Dynamic Portfolio Risk Management
- Otros artículos de la serie
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 5 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 6 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16570
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Creación de un asesor experto MQL5 basado en la estrategia de ruptura del rango diario (Daily Range Breakout)
Creación de un asesor experto MQL5 basado en la estrategia de ruptura del rango diario (Daily Range Breakout)
 Reimaginando las estrategias clásicas en MQL5 (Parte X): ¿Puede la IA impulsar el MACD?
Reimaginando las estrategias clásicas en MQL5 (Parte X): ¿Puede la IA impulsar el MACD?
 Media móvil en MQL5 desde cero: Sencilla y accesible
Media móvil en MQL5 desde cero: Sencilla y accesible
 Redes neuronales en el trading: Modelo adaptativo multiagente (MASA)
Redes neuronales en el trading: Modelo adaptativo multiagente (MASA)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso