From Basic to Intermediate: Recursion

Introduction

The materials presented here are intended for educational purposes only. Under no circumstances should the application be viewed for any purpose other than to learn and master the concepts presented.

In the previous article From Basic to Intermediate: Union (II), we explored how unions could be used to solve a problem that many claim to be impossible using pure and simple MQL5.

Although many of you, dear readers, might assume that this kind of task can only be accomplished by highly experienced programmers, from my perspective and understanding, what we covered there is basic material. It is entirely achievable by any beginner-level programming student.

We're now entering a phase where things start to expand rapidly, presenting numerous possibilities for application and exploration. Even though many are still hesitant to dive into programming that may appear bold or advanced, what we've covered so far proves that it is indeed possible to program a wide variety of solutions, as long as we don't touch events for now, since we haven't yet covered how to properly work with and implement them.

It's worth emphasizing again that MetaTrader 5 is an event-driven platform, and the applications running in it are also event-based - with the exception of two types that typically do not rely on events. These are scripts, which have been included as attachments, and services. We'll explore services at a more appropriate time, as working with them requires a deeper understanding of how MetaTrader 5 operates. In my view, services are the most advanced type of application one can build for use with MetaTrader 5.

Alongside these two types, we also have indicators and Expert Advisors. Both types are designed around event-driven programming. At this point, it's not yet suitable to discuss them in detail. However, there are still several other topics to cover, which I consider fundamental to building a solid foundation for any aspiring professional in programming for financial markets.

I mention this because many believe that they are ready to enter the field, but when put to the test, they fail miserably, often blaming the world for being unfair. The truth, however, is that they were simply not adequately prepared to face the challenges that a competent programmer can handle with ease, speed, and efficiency.

A Special Kind of Loop

Throughout several articles, I've explained commands related to working with loops. In MQL5, as in many other languages, we generally have three types. The first and, in my opinion, the simplest are 'while' and 'do...while'. In addition to those, we also have the 'for' loop. However, there is, in fact, a fourth way to create loops, which is available in nearly every programming language. The only one I recall lacking support for it is BASIC. That's because BASIC is not a structured language designed to work with functions and procedures. But that's irrelevant here, since we're working with MQL5, a structured language that fully supports functions and procedures. And this brings us to the fourth form of looping.

Typically, loops are created in one of two ways: by using dedicated loop control structures or by using functions or procedures. Yes, dear reader, it may sound strange to use a function or procedure to create a loop. Yet it's far more common than you might think.

When we use loop constructs to create repetitions, we refer to this as iterative programming. When we use functions or procedures for the same purpose, it's known as recursive programming. Understanding how to create and apply recursion is something every beginner should learn - recursive loops are, in many cases, easier to understand.

So why am I only bringing this up now? Because using recursion effectively in your code requires a solid understanding of a few key concepts: the 'if' statement, the proper use of variables and constants, understanding lifespan and value transfer, and - most importantly - a strong understanding of data types and their limitations. Depending on what you're doing, selecting the most appropriate type is important. This will help you avoid ambiguity that could hinder recursive operations.

Consider this: unlike iterative loops, which are typically located near the code you're working on, the key part of a recursive loop may reside in a function or procedure far removed from where you're currently reading. And if an error or failure occurs, you'll often need to trace through the entire code to find the origin point where everything starts to return. This isn't always a task beginners can handle, due to the very nature of recursion. It doesn't seem like a loop at first glance, but that's exactly what it is. Just a special kind of loop.

To better understand this, we need to look at a practical example. But before we do, one final note: any iterative loop can be rewritten as a recursive one, and any recursive loop can be rewritten as an iterative one. However, the difficulty of transforming one into the other depends on the nature of the loop itself. In general, iterative loops perform better during execution. Recursive loops are often easier to program. So, one compensates for the other. The time spent converting a recursive loop into an iterative one may not be worth the performance gains. Therefore, the rule of thumb is to aim for simplicity and minimal cost. With that said, let's begin.

We'll start with a very simple example, just to make it easier to understand how this works in practice. Here it is.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Recursive(5);
07. }
08. //+------------------------------------------------------------------+
09. void Recursive(uchar arg)
10. {
11.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
12.     arg--;
13.     if (arg > 0)
14.         Recursive(arg);
15.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
16. }
17. //+------------------------------------------------------------------+

Code 01

When this Code 01 is executed, it will produce the result shown in the image below.

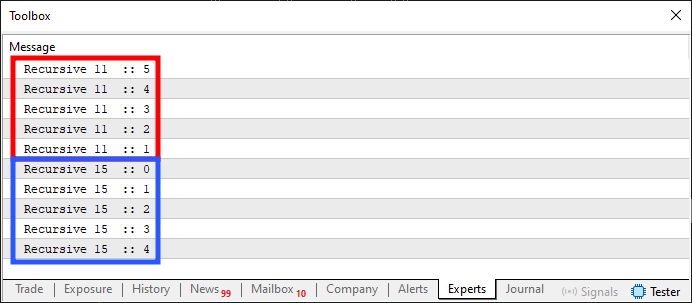
Figure 01

But what kind of madness is this? Well, this is precisely what a recursive routine does. It may seem a bit crazy at first, but often, this is exactly what we want. You'll notice that the same output shown in Figure 01 could have been generated using traditional loops. However, in this case, it was produced using a concept known as recursion. That is, when a function or procedure calls itself or another function or procedure with the intent of forming a loop between them. Many people associate recursion strictly with a single function or procedure calling itself. But that's not necessarily the case. The only requirement is that a loop is formed without using any standard looping command. Another interesting example of recursion is shown below:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Print("Result: ", Fibonacci(7));
07. }
08. //+------------------------------------------------------------------+
09. uint Fibonacci(uint arg)
10. {
11.     if (arg <= 1)
12.         return arg;
13. 
14.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
15. 
16.     return Fibonacci(arg - 1) + Fibonacci(arg - 2);
17. }
18. //+------------------------------------------------------------------+

Code 02

This might be the most classic example used when studying recursion. That's because Code 02 clearly demonstrates how recursion works. When executed, it produces the result shown just below:

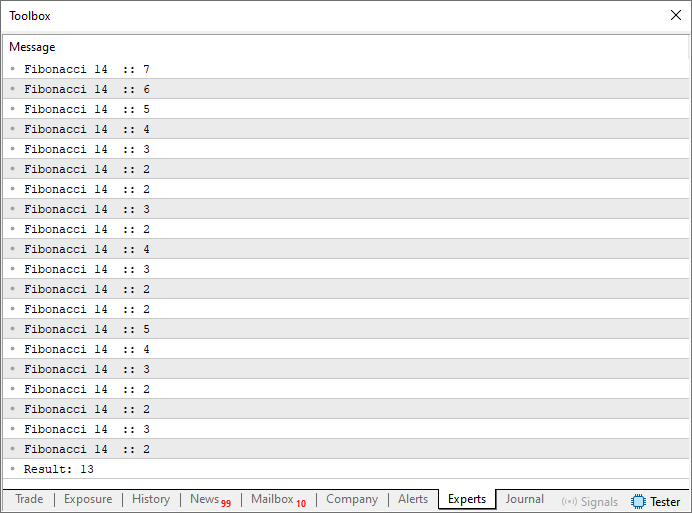
Figure 02

In other words, the seventh value in the Fibonacci sequence is thirteen. And indeed, if you are familiar with the sequence, you know this is correct. But how exactly did this code manage to compute the seventh value? Honestly, it may not be immediately clear how that's possible. Well, dear reader, the key lies in line 16, which contains the minimal factorization required to calculate a Fibonacci number. If you look up the mathematical expression used to compute Fibonacci values, you'll find something resembling what's shown below.

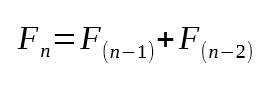
Figure 03

Now, look again at line 16. Can you spot the similarity between the mathematical expression in Image 03 and what's written in line 16? This is precisely the basis of a recursive routine. That is, we keep breaking down the problem until we reach a point where the answer converges to a minimum known value. And what is that minimum value? In the case of the Fibonacci sequence, that value is either zero or one. That's what we're checking in line 11.

Notice this: Just like in Code 01, we first had a countdown (a descending sequence), followed by what seemed like a count-up (an ascending sequence). The same pattern appears here in Code 02, but in two distinct stages. The first stage calculates the value of arg - 1. A series of function calls is made until line 12 is finally reached. With each call, line 14 is executed and prints the current value of arg. As a result, we initially observe a descending sequence by one unit per step. Once all these calls start returning, the function then begins calling itself again, this time with a reduction of two units. I understand this may still seem quite complex. So, to make things easier to visualize and better understand how Code 02 successfully computes the result, we'll modify a few parts of it. The updated version is shown below:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Print("Result: ", Fibonacci(5, 0, 0));
07. }
08. //+------------------------------------------------------------------+
09. uint Fibonacci(uint arg, uint call, int who)
10. {
11.     uint value = 0;
12. 
13.     Print(__FUNCTION__, " ", __LINE__, " Entry point [ ", call," ]  ARG: ", arg, " WHO: ", who);
14. 
15.     if (arg <= 1)
16.     {
17.         Print(__FUNCTION__, " ", __LINE__, " Number Callback [ ", call," ]  ARG: ", arg, " WHO: ", who);
18. 
19.         return arg;
20.     }
21. 
22.     value += Fibonacci(arg - 1, call + 1, 1);
23. 
24.     Print(__FUNCTION__, " ", __LINE__, " Value = ", value, "  >> New call with arg: ", arg);
25. 
26.     value += Fibonacci(arg - 2, call + 1, 2);
27. 
28.     Print(__FUNCTION__, " ", __LINE__, " General Return = ", value);
29. 
30.     return value;
31. }
32. //+------------------------------------------------------------------+

Code 03

At this point, I must apologize to everyone. But unfortunately, there's no easier way to explain what is happening here. The output of executing Code 03 is shown below:

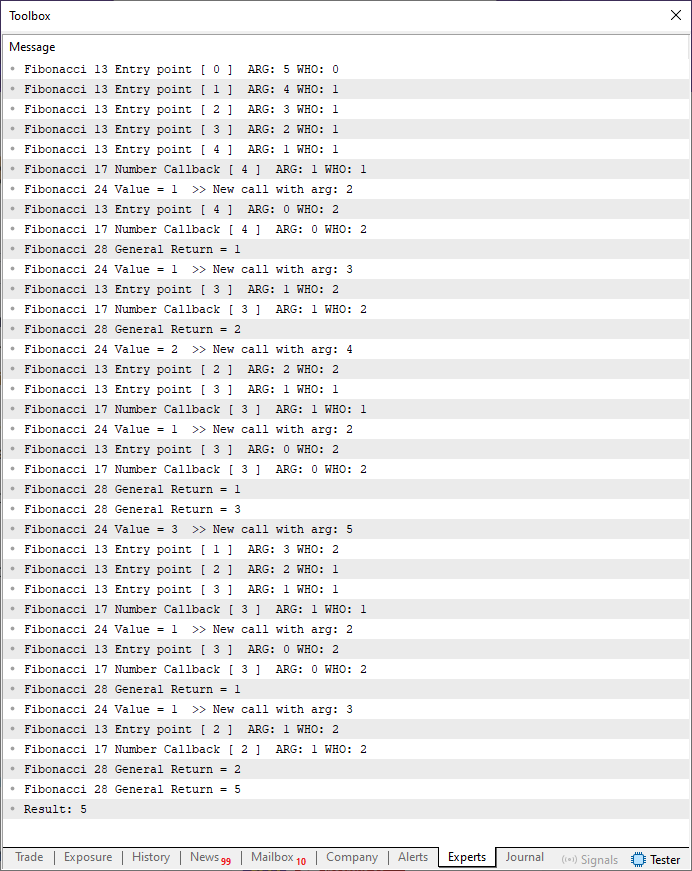
Figure 04

I understand that Figure 04 is quite long. However, note that I've changed the function call from computing seven elements to five. While this may not seem like much, it significantly reduces the amount of information to analyze here. Still, there's something very important to consider. Each time line 13 is executed, we are entering the function. That might lead to an immediate return or another recursive call. One detail that might seem confusing at first is the condition on line 11. Many might think this would interfere with the final result. But if you believe that, it likely means you don't yet fully grasp what recursion actually does to a function or procedure.

That's exactly why I'm showing Figure 04 in as much detail as possible. I want to help you truly see what's happening, and how Code 02 manages to compute the correct result.

Since what follows requires your full attention, I kindly ask you, dear reader, to remove any distractions before continuing. Recursive functions or procedures can become confusing, especially the first time you encounter them in programming.

Now, based on Figure 04, let's understand what's really going on. First, when line 6 is executed, we're calling the Fibonacci function as if it were a loop. Not an iterative loop, but a recursive loop. This is the first key point you must understand.

The next point is recognizing that a limiting condition is necessary, just as we saw in Code 01. Any loop that uses recursion must have a stopping condition. In this case, that condition is set on line 15. I know it was previously mentioned that recursion should be reduced to a simple expression, but the role of limiting recursion is not related to that expression. These are different concepts. This is an important moment. Let me clarify: 

What generates recursion is the implementation of a minimal mathematical expression. What limits recursion is the condition that prevents it from becoming an infinite loop.

So in Code 04, the limiting condition is on line 15. The recursive mechanism is created by lines 22 and 26. In Code 02, the limiting condition is line 11, and recursion is triggered by line 16.

Let's now walk through how this works. Our initial argument is 5. That triggers line 13, and then line 22. This line calls the function again, going back to line 9, creating a loop. But pay attention: during this call on line 22, the argument is reduced by one. So, our call stack starts building - call after call - until line 15 becomes true.

At that point, something interesting happens. It's the fourth call, and the argument values are decreasing. When line 15 becomes true, line 17 is executed, showing us the current argument value and how many times the function has been called. Since the argument is now 1, we return this value to the caller. But the caller is not line 6 - it's line 22. Remember that we've stacked multiple calls. Now we begin unwinding the stack. The first value returned is 1, and it is added to the variable Value. This variable does not lose its value between calls as it accumulates and builds up a new value with each return. To understand this better, you'd need to know how a call stack works, but for now, that's a more advanced topic. Don't worry, as you can still follow along with the core idea of recursion. You just have to be careful.

So, we've now computed the first return value. But, as shown in the expression in Figure 03, we still need to make another recursive call. For this reason, on line 26 we make a new call. And here's where it gets tricky.

The call on line 22 reduced the value by 1 each time. But when arg reached 1, and the function returned, the arg in the previous call (the one from line 22) is still 2. So, when we move to line 24, although arg was 1 in the most recent call, we now have arg = 2.

This might be confusing at first. That's why I'm using the simplest recursion example: Fibonacci. And why we looked at Code 01, where we first saw a countdown, and then what looked like a count-up. That count-up only happened because we had previously stacked values. So when we started unwinding those values, we got the illusion of an ascending sequence, although it wasn't directly implemented. That behavior is purely a side effect of how recursive calls are stacked and returned.

Alright, let's proceed carefully. On line 26, at this moment, arg is 2. When reduced by 2, it becomes 0. That causes line 15 to return true, and the function returns 0. Thus, line 28 prints a return value of 1. That's the Fibonacci value for the first element.

Remember, we stacked five calls and have only returned from one. So now, back in line 22, Value becomes 1. But wasn't it already 1? No, dear reader. That was in the previous call. Now we're back to line 22, where Value was 0. Now it becomes 1. We then execute line 24. As we unwind another call, arg is now 2. This moment occurs in line 24. Please follow the order of actions carefully. So we subtract 2 (on line 26), making the argument passed to the function 0. And WHO is still 2. That's because we're calling the function from line 26.

Since arg is 0, line 15 is true and returns 0 on line 19. Back on line 26, we add this result (0) to our earlier value (1). So now Value is 1. That's the second Fibonacci number.

Now we return to line 22 - we've only unwound two of five calls. This time, Value is 1, and arg is 3. This is the interesting part: arg = 3. Subtracting 2 (line 26) gives 1, so the function is called with arg = 1. That triggers line 15, which returns 1. Now Value is 2.

That's the third Fibonacci number. Unwinding another level: Back to line 22, Value = 2, arg = 4. What happens when line 26 is executed? Did you guess? The function is called again, but with arg = 2. Remember that before calling the function we subtract 2 on line 26.

So, since arg is 2 at this point, line 15 will fail and line 22 will be executed again. Only at this moment the Value variable is zero, not 2. This other value was saved on the stack. Since arg = 2 and we need to subtract one before calling, on line 15 arg will be one and one will be returned. Now on line 22 Value = 1, so line 26 will be executed. At this point, when subtracting 2 from arg, the function is called and 2 is subtracted. This will return zero. And line 30 will return the Value 1, but where will it return to? This will take you back to line 26, which is where that call was made. Remember that Value is currently 2. Since there was one return, the Value is now 3. So we have just calculated the fourth element of the sequence. Only one is missing. (laughs)

At this point, I imagine your brain may feel like it's twisting into knots - so many calls, so many returns. But for the final element, let's skip the repetition. You've already seen all the necessary mechanics. So now, on line 26, arg = 5 and Value = 3. Since arg will need to be subtracted in half, a new series of calls will be made. I think we have already explained everything you need to understand.

What's important is what we said at the beginning of this article: recursion is easy to code, but slower to execute. That's why we can build an equivalent iterative version to compute Fibonacci numbers. This results in better performance, though the code becomes a bit more complex.

To prove it, let's now take a look at how this same computation could be implemented using iteration instead of recursion. There are many ways to do it. Below is one such approach:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     const uchar who = 6;
07. 
08.     Print("Result: ", Fibonacci_Recursive(who));
09.     Print("Result: ", Fibonacci_Interactive(who));
10. }
11. //+------------------------------------------------------------------+
12. uint Fibonacci_Recursive(uint arg)
13. {
14.     if (arg <= 1)
15.         return arg;
16. 
17.     return Fibonacci_Recursive(arg - 1) +  Fibonacci_Recursive(arg - 2);
18. }
19. //+------------------------------------------------------------------+
20. uint Fibonacci_Interactive(uint arg)
21. {
22.     uint v, i, c;
23. 
24.     for (c = 0, i = 0, v = 1; c < arg; i += v, c += 2)
25.         v += i;
26. 
27.     return (c == arg ? i : v);
28. }
29. //+------------------------------------------------------------------+

Code 04

Note that here we are working with both approaches to loops. The first is recursion, and the second is iteration. Now I ask you: which one do you find easier to understand? Based on your answer, which do you believe is faster in terms of execution time? Consider this in light of what you already know about both methods for performing the same type of calculation.

Since I know that some readers may find the iterative function implemented starting at line 20 a bit unusual, let me give a brief explanation of how it works.

In line 22, we declare the variables we need. Then, in line 24, we enter the main loop of the calculation. This is where things get interesting. Notice that we initialize the values before performing any calculations. Now here's a key point: when the element we're looking for is odd (first, third, fifth, seventh element, and so on), the variable v holds the correct result. However, when the sought element is even, the correct value is held by the variable i. Why?

The reason is that the counter variable c is incremented by two each iteration to prevent overshooting the correct result. And since each iteration adds the previous value to a new one, and we're not swapping the values between i and v, this slight distinction arises in our iterative function. It is possible to implement this in a way that avoids this particular issue, but I find that unnecessary. The loop interaction already tells me both the current and next values. Therefore, all I need to do is apply a ternary operator to return the correct result. Without this small adjustment, we might end up pointing either to the next element or the previous one in the sequence, depending on whether the input (or the sought element) is odd or even; and whether we're returning the value of i or v.

To demonstrate that this Code 04 does indeed work, we've included its output immediately below. To test other values and compare both ways of calculating the Fibonacci sequence, simply change the constant in line six. But please remember that the Fibonacci sequence grows very rapidly. And since there are limitations due to the types used in the code, be cautious not to go overboard by requesting values too far down the sequence, doing so may lead to unexpected results or even errors.

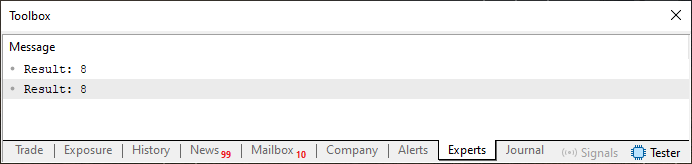
Figure 05

There are ways to overcome these limitations, allowing us to calculate any number within the memory capacity of a computer. However, this is a more advanced topic, and in my opinion, best saved for a more appropriate time. But just to spark your curiosity: how do you think programmers are able to compute the value of π (pi) or other irrational constants with thousands of decimal places? After all, the standard data types used in most programming languages are nowhere near capable of achieving this level of precision.

As I mentioned, this topic requires a more advanced understanding. Not that it's entirely out of reach with the knowledge we've covered so far, because it's not. In fact, yes, it's possible to achieve such computations using the concepts we've discussed here, including recursion. However, implementing it would require much more effort, as you'd need to adapt various components into formats that aren't immediately intuitive.

Final Thoughts

This article aimed to introduce a powerful and genuinely enjoyable programming concept. But it's one that must be approached with care and respect. A poor understanding or misuse of recursion can turn relatively simple programs into needlessly complex ones. However, when used properly and in the right situations, recursion becomes a powerful ally for solving problems that would otherwise be significantly more difficult or time-consuming.

As a general rule, use recursion whenever possible, especially when dealing with mathematical expressions that don't lend themselves easily to iterative solutions. But remember: the heavy cost of multiple recursive calls can slow down your program. When performance becomes an issue, consider rewriting your recursive logic into an iterative loop. Although initially more complex to design, iterative solutions tend to be much faster during execution, especially when dealing with large data sets or sequences requiring transformation.