
Automatisieren von Handelsstrategien in MQL5 (Teil 28): Erstellen eines Price Action Bat Harmonic Patterns mit visuellem Feedback
Einführung
In unserem vorangegangenen Artikel (Teil 27) haben wir ein Harmonic-System für die Krabben-Muster (crab) in MetaQuotes Language 5 (MQL5) entwickelt, das Muster zur Identifizierung von Umkehrpunkten mit hoher Wahrscheinlichkeit und präzisen Fibonacci-Verhältnissen nutzt, den Handel automatisiert und die Muster mit Chart-Objekten visualisiert. In Teil 28 erstellen wir das Harmonic-System der Fledermaus-Muster, die die Auf- und Abwärtsmuster der Fledermaus (bat) anhand von Umkehrpunkten (pivot points) und bestimmten Fibonacci-Retracements erkennen. Das Programm führt Handelsgeschäfte mit berechneten Einstiegs-, Stop-Loss- und mehrstufigen Take-Profit-Punkten aus, die durch visuelle Dreiecke, Trendlinien und Etiketten für eine klare Darstellung von Mustern ergänzt werden. Wir werden die folgenden Themen behandeln:
- Verständnis des Rahmens für harmonische Fledermausmuster
- Implementation in MQL5
- Backtests
- Schlussfolgerung
Am Ende haben Sie eine robuste MQL5-Strategie für den Handel mit harmonischen Fledermausmustern, die Sie nur noch anpassen müssen – legen wir los!
Verständnis des Systems der harmonische Fledermausmuster
Das Fledermausmuster ist eine harmonische Handelsformation, die durch fünf wichtige Umkehr-Punkte – X, A, B, C und D – definiert ist und in zwei Formen existiert: ein Aufwärtsmuster und ein Abwärtsmuster, die beide dazu dienen, potenzielle Marktumkehrungen mit präzisen Messungen durch Fibonacci-Verhältnisse zu identifizieren. Bei einem Aufwärtstrend bildet die Struktur eine Sequenz aus Tief-Hoch-Tief-Hoch-Tief, bei der Punkt X ein tiefer Umkehrpunkt, Punkt A ein hoher Umkehrpunkt, Punkt B ein tiefer Umkehrpunkt (das etwa 0,5 von XA zurückgeht), Punkt C ein hoher Umkehrpunkt (das sich von 0,382 bis 0,886 von AB erstreckt) und Punkt D ein tiefer Umkehrpunkt (das sich von 0,886 von XA erstreckt und über X liegt) ist. Umgekehrt bildet eine Abwärts-Fledermaus eine Sequenz aus Hoch-Tief-Hoch-Tief-Hoch, mit Punkt X als hoher Umkehrpunkt, Punkt A als tiefer Umkehrpunkt, Punkt B als hoher Umkehrpunkt, Punkt C als tiefer Umkehrpunkt und Punkt D als hoher Umkehrpunkt (das sich über 0,886 von XA erstreckt und unter X liegt). Nachfolgend sind die visualisierten Mustertypen aufgeführt.
Harmonisches Aufwärtsmuster der Fledermaus:
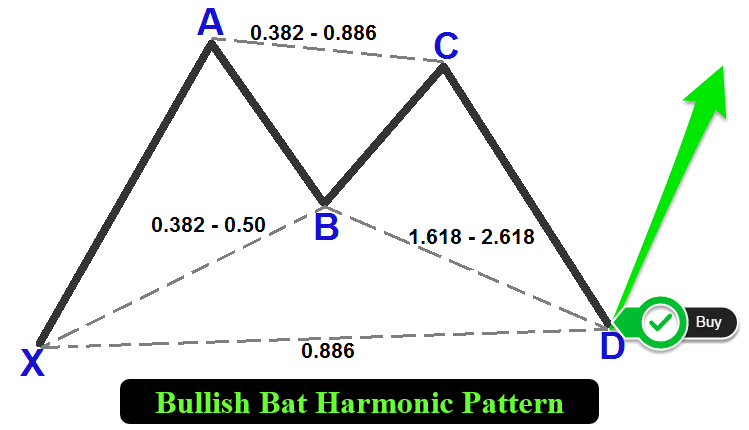
Harmonisches Abwärtsmuster der Fledermaus:
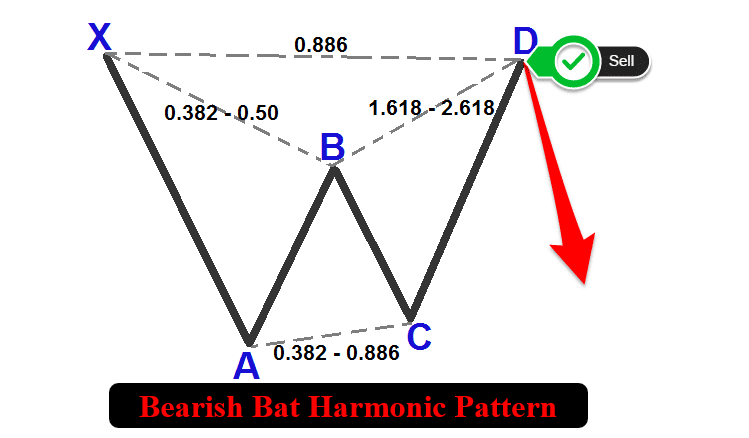
Um die Muster zu erkennen, gehen wir wie folgt strukturiert vor:
- Die Definition der XA-Strecke: Die erste Bewegung von Punkt X zu Punkt A gibt die Richtung des Musters vor (steigend für ein Aufwärtsmuster, fallend für ein Abwärtsmuster) und dient als primäre Referenz für Fibonacci-Berechnungen.
- Die Einrichtung der Strecke AB: Punkt B sollte etwa 0,5 der XA-Strecke zurückgehen, was auf eine moderate Korrektur des anfänglichen Impulses hindeutet.
- Analyse der BC-Strecke: Diese Strecke dürfte sich zwischen 0,382 und 0,886 des AB-Schenkels erstrecken und eine Gegenbewegung auslösen, die die endgültige Umkehrzone einleitet.
- Einstellung der CD-Strecke: Die letzte Strecke sollte sich über 0,886 des XA-Schenkels erstrecken und die potenzielle Umkehrzone bei Punkt D markieren, wo sich das Muster vervollständigt und ein Handelssignal erzeugt wird.
Durch die Anwendung dieser geometrischen und Fibonacci-basierten Kriterien wird unser Handelssystem systematisch gültige Fledermaus-Muster in den Preisdaten erkennen. Sobald ein Muster bestätigt wird, visualisiert der EA die Formation auf dem Chart mit Dreiecken, Trendlinien und Beschriftungen für die Punkte X, A, B, C und D sowie Handelsstufen für Einstieg und Gewinnmitnahme. Dieses Setup ermöglicht die automatische Ausführung von Handelsgeschäften am D-Punkt mit berechneten Stop-Loss- und mehrstufigen Take-Profit-Zonen, wobei die Vorhersagekraft des Musters für Marktumkehrungen genutzt wird. Kommen wir nun zur Umsetzung!
Implementation in MQL5
Um das Programm in MQL5 zu erstellen, öffnen wir den MetaEditor, gehen zum Navigator, suchen den Ordner der Indikatoren, klicken auf die Registerkarte „Neu“ und folgen den Anweisungen, um die Datei zu erstellen. Sobald das erledigt ist, müssen wir in der Programmierumgebung einige globale Variablen deklarieren, die wir im gesamten Programm verwenden werden.
//+------------------------------------------------------------------+ //| Bat Pattern EA.mq5. | //| Copyright 2025, Forex Algo-Trader, Allan. | //| "https://t.me/Forex_Algo_Trader" | //+------------------------------------------------------------------+ #property copyright "Forex Algo-Trader, Allan" #property link "https://t.me/Forex_Algo_Trader" #property version "1.00" #property description "This EA trades based on Bat Strategy" #property strict //--- Include the trading library for order functions #include <Trade\Trade.mqh> //--- Include Trade library CTrade obj_Trade; //--- Instantiate a obj_Trade object //--- Input parameters for user configuration input int PivotLeft = 5; // Number of bars to the left for pivot check input int PivotRight = 5; // Number of bars to the right for pivot check input double Tolerance = 0.10; // Allowed deviation (10% of XA move) input double LotSize = 0.01; // Lot size for new orders input bool AllowTrading = true; // Enable or disable trading //--------------------------------------------------------------------------- //--- Bat pattern definition: // //--- Bullish Bat: //--- Pivots (X-A-B-C-D): X swing low, A swing high, B swing low, C swing high, D swing low. //--- Normally XA > 0; Ideal B = A - 0.5*(A-X); Legs within specified ranges. // //--- Bearish Bat: //--- Pivots (X-A-B-C-D): X swing high, A swing low, B swing high, C swing low, D swing high. //--- Normally XA > 0; Ideal B = A + 0.5*(X-A); Legs within specified ranges. //--------------------------------------------------------------------------- //--- Structure for a pivot point struct Pivot { datetime time; //--- Bar time of the pivot double price; //--- Pivot price (High for swing high, low for swing low) bool isHigh; //--- True if swing high; false if swing low }; //--- Global dynamic array for storing pivots in chronological order Pivot pivots[]; //--- Declare a dynamic array to hold identified pivot points //--- Global variables to lock in a pattern (avoid trading on repaint) int g_patternFormationBar = -1; //--- Bar index where the pattern was formed (-1 means none) datetime g_lockedPatternX = 0; //--- The key X pivot time for the locked pattern bool g_tradeTaken = false; //--- Flag to indicate if a trade has been taken for the current pattern
Um die Grundlage für das Systems der Fledermaus-Muster zu schaffen, das den Handel auf der Grundlage des harmonischen Fledermaus-Musters automatisiert, binden wir zunächst die Bibliothek „<Trade\Trade.mqh>“ ein und instanziieren „obj_Trade“ als CTrade-Objekt, um Handelsoperationen wie die Ausführung von Kauf- und Verkaufsaufträgen zu verwalten. Anschließend definieren wir die Eingabeparameter für die Nutzeranpassung: „PivotLeft“ und „PivotRight“ auf jeweils 5 Balken, um den Rückblickbereich für die Erkennung der Umkehrpunkte festzulegen, „Tolerance“ auf 0,10 für die Fibonacci-Abweichung, „LotSize“ auf 0,01 für das Handelsvolumen und „AllowTrading“ auf true, um den automatischen Handel zu aktivieren.
Als Nächstes definieren wir die Struktur „Pivot“ mit „time“ (datetime), „price“ (double) und „isHigh“ (bool), um Umkehrpunkte zu speichern, deklarieren „Pivots“ als dynamisches Array, um diese Punkte zu halten, und initialisieren die Globals „g_patternFormationBar“ mit -1, um die Musterbildung zu verfolgen, „g_lockedPatternX“ mit 0, um die Zeit des Umkehrpunkts von X zu sperren, und „g_tradetaken“ auf false zu setzen, um mehrere Handelsgeschäfte desselben Musters zu verhindern, wodurch die Grundlage des EA für das Erkennen und den Handel mit Fledermausmustern geschaffen wird. Zur Visualisierung können wir Funktionen zum Zeichnen von Linien, Texten und Dreiecken verwenden.
//+------------------------------------------------------------------+ //| Helper: Draw a filled triangle | //+------------------------------------------------------------------+ void DrawTriangle(string name, datetime t1, double p1, datetime t2, double p2, datetime t3, double p3, color cl, int width, bool fill, bool back) { //--- Attempt to create a triangle object with three coordinate points if(ObjectCreate(0, name, OBJ_TRIANGLE, 0, t1, p1, t2, p2, t3, p3)) { //--- Set the triangle's color ObjectSetInteger(0, name, OBJPROP_COLOR, cl); //--- Set the triangle's line style to solid ObjectSetInteger(0, name, OBJPROP_STYLE, STYLE_SOLID); //--- Set the line width of the triangle ObjectSetInteger(0, name, OBJPROP_WIDTH, width); //--- Determine if the triangle should be filled ObjectSetInteger(0, name, OBJPROP_FILL, fill); //--- Set whether the object is drawn in the background ObjectSetInteger(0, name, OBJPROP_BACK, back); } } //+------------------------------------------------------------------+ //| Helper: Draw a trend line | //+------------------------------------------------------------------+ void DrawTrendLine(string name, datetime t1, double p1, datetime t2, double p2, color cl, int width, int style) { //--- Create a trend line object connecting two points if(ObjectCreate(0, name, OBJ_TREND, 0, t1, p1, t2, p2)) { //--- Set the trend line's color ObjectSetInteger(0, name, OBJPROP_COLOR, cl); //--- Set the trend line's style (solid, dotted, etc.) ObjectSetInteger(0, name, OBJPROP_STYLE, style); //--- Set the width of the trend line ObjectSetInteger(0, name, OBJPROP_WIDTH, width); } } //+------------------------------------------------------------------+ //| Helper: Draw a dotted trend line | //+------------------------------------------------------------------+ void DrawDottedLine(string name, datetime t1, double p, datetime t2, color lineColor) { //--- Create a horizontal trend line at a fixed price level with dotted style if(ObjectCreate(0, name, OBJ_TREND, 0, t1, p, t2, p)) { //--- Set the dotted line's color ObjectSetInteger(0, name, OBJPROP_COLOR, lineColor); //--- Set the line style to dotted ObjectSetInteger(0, name, OBJPROP_STYLE, STYLE_DOT); //--- Set the line width to 1 ObjectSetInteger(0, name, OBJPROP_WIDTH, 1); } } //+------------------------------------------------------------------+ //| Helper: Draw anchored text label (for pivots) | //| If isHigh is true, anchor at the bottom (label appears above); | //| if false, anchor at the top (label appears below). | //+------------------------------------------------------------------+ void DrawTextEx(string name, string text, datetime t, double p, color cl, int fontsize, bool isHigh) { //--- Create a text label object at the specified time and price if(ObjectCreate(0, name, OBJ_TEXT, 0, t, p)) { //--- Set the text of the label ObjectSetString(0, name, OBJPROP_TEXT, text); //--- Set the color of the text ObjectSetInteger(0, name, OBJPROP_COLOR, cl); //--- Set the font size for the text ObjectSetInteger(0, name, OBJPROP_FONTSIZE, fontsize); //--- Set the font type and style ObjectSetString(0, name, OBJPROP_FONT, "Arial Bold"); //--- Anchor the text depending on whether it's a swing high or low if(isHigh) ObjectSetInteger(0, name, OBJPROP_ANCHOR, ANCHOR_BOTTOM); else ObjectSetInteger(0, name, OBJPROP_ANCHOR, ANCHOR_TOP); //--- Center-align the text ObjectSetInteger(0, name, OBJPROP_ALIGN, ALIGN_CENTER); } }
Um eine übersichtliche Darstellung des Musters und seiner Schlüsselebenen zu erstellen, entwickeln wir die Funktion „DrawTriangle“, die ObjectCreate verwendet, um ein gefülltes Dreieck (OBJ_TRIANGLE) mit drei Punkten zu zeichnen, die durch Zeiten („t1“, „t2“, „t3“) und Preise („p1“, „p2“, „p3“), wobei OBJPROP_COLOR auf die angegebene Farbe, „OBJPROP_STYLE“ auf „STYLE_SOLID“, „OBJPROP_WIDTH“ auf die angegebene Breite, „OBJPROP_FILL“ zum Aktivieren oder Deaktivieren der Füllung und „OBJPROP_BACK“ zum Einstellen der Hintergrund- oder Vordergrundplatzierung mit der Funktion ObjectSetInteger gesetzt werden. Anschließend erstellen wir die Funktion „DrawTrendLine“, die eine Trendlinie („OBJ_TREND“) zwischen zwei Punkten im gleichen Format wie für Dreiecke zeichnet.
Als Nächstes implementieren wir die Funktion „DrawDottedLine“, die eine horizontale gepunktete Linie erzeugt und deren Eigenschaften ebenfalls definiert. Zuletzt entwickeln wir die Funktion „DrawTextEx“, die eine Kennzeichnung (OBJ_TEXT) an den Koordinaten („t“, „p“) erstellt, wobei „OBJPROP_TEXT“ der angegebenen Text zugewiesen wird, „OBJPROP_COLOR“, „OBJPROP_FONTSIZE“ und der OBJPROP_FONT auf „Arial Bold“ eingestellt wird und mit Hilfe von ObjectSetString und „ObjectSetInteger“, Verankerung nach oben für Hochs oder nach unten für Tiefs basierend auf „isHigh“ mit „OBJPROP_ANCHOR“ und Zentrierung mit der Eigenschaft „OBJPROP_ALIGN“. Wir können nun mit OnTick fortfahren und versuchen, die Umkehrpunkte zu finden, die wir später zur Identifizierung von Mustern verwenden können. Hier ist die Logik, mit der wir das erreichen.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Declare a static variable to store the time of the last processed bar static datetime lastBarTime = 0; //--- Get the time of the current confirmed bar datetime currentBarTime = iTime(_Symbol, _Period, 1); //--- If the current bar time is the same as the last processed, exit if(currentBarTime == lastBarTime) return; //--- Update the last processed bar time lastBarTime = currentBarTime; //--- Clear the pivot array for fresh analysis ArrayResize(pivots, 0); //--- Get the total number of bars available on the chart int barsCount = Bars(_Symbol, _Period); //--- Define the starting index for pivot detection (ensuring enough left bars) int start = PivotLeft; //--- Define the ending index for pivot detection (ensuring enough right bars) int end = barsCount - PivotRight; //--- Loop through bars from 'end-1' down to 'start' to find pivot points for(int i = end - 1; i >= start; i--) { //--- Assume current bar is both a potential swing high and swing low bool isPivotHigh = true; bool isPivotLow = true; //--- Get the high and low of the current bar double currentHigh = iHigh(_Symbol, _Period, i); double currentLow = iLow(_Symbol, _Period, i); //--- Loop through the window of bars around the current bar for(int j = i - PivotLeft; j <= i + PivotRight; j++) { //--- Skip if the index is out of bounds if(j < 0 || j >= barsCount) continue; //--- Skip comparing the bar with itself if(j == i) continue; //--- If any bar in the window has a higher high, it's not a swing high if(iHigh(_Symbol, _Period, j) > currentHigh) isPivotHigh = false; //--- If any bar in the window has a lower low, it's not a swing low if(iLow(_Symbol, _Period, j) < currentLow) isPivotLow = false; } //--- If the current bar qualifies as either a swing high or swing low if(isPivotHigh || isPivotLow) { //--- Create a new pivot structure Pivot p; //--- Set the pivot's time p.time = iTime(_Symbol, _Period, i); //--- Set the pivot's price depending on whether it is a high or low p.price = isPivotHigh ? currentHigh : currentLow; //--- Set the pivot type (true for swing high, false for swing low) p.isHigh = isPivotHigh; //--- Get the current size of the pivots array int size = ArraySize(pivots); //--- Increase the size of the pivots array by one ArrayResize(pivots, size + 1); //--- Add the new pivot to the array pivots[size] = p; } } }
Wir fahren damit fort, die anfängliche Logik der Ereignisbehandlung von OnTick für das System zu implementieren, um Umkehrpunkte zu erkennen, die für die Identifizierung des harmonischen Fledermausmusters unerlässlich sind. Zunächst deklarieren wir ein statische Variable „lastBarTime“, die auf 0 initialisiert wird, um den letzten verarbeiteten Balken zu verfolgen und ihn mit der „currentBarTime“ zu vergleichen, die von iTime bei Shift 1 für das aktuelle Symbol und die aktuelle Periode erhalten wird, wobei wir den Vorgang beenden, wenn er unverändert bleibt, um redundante Verarbeitung zu vermeiden, und die „lastBarTime“ aktualisieren, wenn ein neuer Balken entdeckt wird. Dann leeren wir das Array „Pivots“ mit ArrayResize, um eine neue Analyse zu gewährleisten.
Als Nächstes rufen wir die Gesamtzahl der Balken mit der Funktion Bars ab, legen den Bereich für die Erkennung der Umkehrpunkte fest, wobei „start“ als „PivotLeft“ und „end“ als Gesamtzahl der Balken minus „PivotRight“ definiert ist, und durchlaufen die Balken von „end - 1“ bis „start“. Für jeden Balken nehmen wir an, dass es sich um einen hohen („isPivotHigh“ true) und tiefen („isPivotLow“ true) Umkehrpunkt handelt, ermitteln seine Hoch- und Tiefstpreise mit iHigh und iLow und validieren den Pivot, indem wir die umliegenden Balken innerhalb von „PivotLeft“ und „PivotRight“ mit „iHigh“ und „iLow“ überprüfen und den Pivot ungültig machen, wenn ein benachbarter Balken ein höheres Hoch oder ein tieferes Tief aufweist. Wenn sich der Balken als Umkehrpunkt qualifiziert, erstellen wir die Struktur „Pivot“, setzen die „Zeit“ mit „iTime“, den „Preis“ auf den Höchst- oder Tiefstwert auf der Grundlage von „isPivotHigh“ und dem „isHigh“-Flag, fügen ihn dann mit ArrayResize an das Array „pivots“ an und speichern ihn. Wenn wir das Array ausdrucken, erhalten wir das folgende Ergebnis.
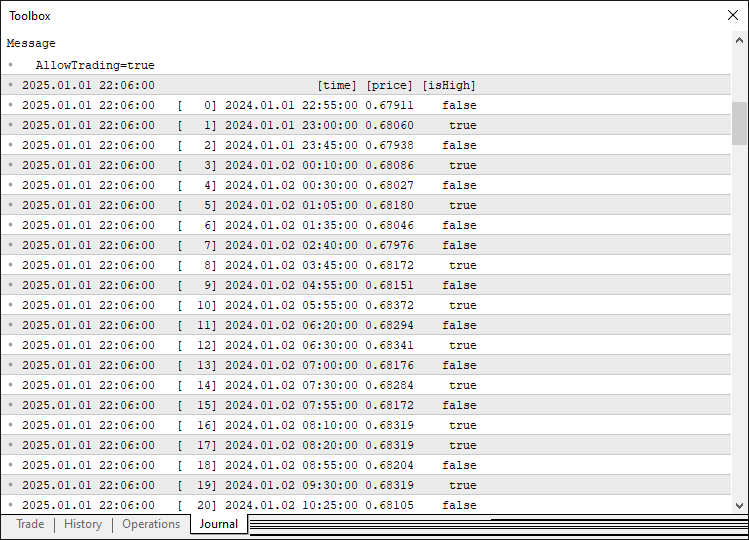
Aus den Daten können wir die Umkehrpunkte extrahieren, und wenn wir genügend Umkehrpunkte haben, können wir die Muster analysieren und erkennen. Hier ist die Logik, mit der wir das erreichen.
//--- Determine the total number of pivots found int pivotCount = ArraySize(pivots); //--- If fewer than five pivots are found, the pattern cannot be formed if(pivotCount < 5) { //--- Reset pattern lock variables g_patternFormationBar = -1; g_lockedPatternX = 0; g_tradeTaken = false; //--- Exit the OnTick function return; } //--- Extract the last five pivots as X, A, B, C, and D Pivot X = pivots[pivotCount - 5]; Pivot A = pivots[pivotCount - 4]; Pivot B = pivots[pivotCount - 3]; Pivot C = pivots[pivotCount - 2]; Pivot D = pivots[pivotCount - 1]; //--- Initialize a flag to indicate if a valid Bat pattern is found bool patternFound = false; //--- Check for the high-low-high-low-high (Bearish reversal) structure if(X.isHigh && (!A.isHigh) && B.isHigh && (!C.isHigh) && D.isHigh) { //--- Calculate the difference between pivot X and A double diff = X.price - A.price; //--- Ensure the difference is positive if(diff > 0) { //--- Calculate the ideal position for pivot B based on Fibonacci ratio double idealB = A.price + 0.5 * diff; //--- Check if actual B is within tolerance of the ideal position if(MathAbs(B.price - idealB) <= Tolerance * diff) { //--- Calculate the AB leg length double AB = B.price - A.price; //--- Calculate the BC leg length double BC = B.price - C.price; //--- Verify that BC is within the acceptable Fibonacci range if((BC >= 0.382 * AB) && (BC <= 0.886 * AB)) { //--- Calculate the extension double extension = D.price - A.price; //--- Verify that the extension is within tolerance of 0.886 and that D is below X if(MathAbs(extension - 0.886 * diff) <= Tolerance * diff && (D.price < X.price)) patternFound = true; } } } } //--- Check for the low-high-low-high-low (Bullish reversal) structure if((!X.isHigh) && A.isHigh && (!B.isHigh) && C.isHigh && (!D.isHigh)) { //--- Calculate the difference between pivot A and X double diff = A.price - X.price; //--- Ensure the difference is positive if(diff > 0) { //--- Calculate the ideal position for pivot B based on Fibonacci ratio double idealB = A.price - 0.5 * diff; //--- Check if actual B is within tolerance of the ideal position if(MathAbs(B.price - idealB) <= Tolerance * diff) { //--- Calculate the AB leg length double AB = A.price - B.price; //--- Calculate the BC leg length double BC = C.price - B.price; //--- Verify that BC is within the acceptable Fibonacci range if((BC >= 0.382 * AB) && (BC <= 0.886 * AB)) { //--- Calculate the extension double extension = A.price - D.price; //--- Verify that the extension is within tolerance of 0.886 and that D is above X if(MathAbs(extension - 0.886 * diff) <= Tolerance * diff && (D.price > X.price)) patternFound = true; } } } }
Hier werden wir weiterhin die Auf- und Abwärtsmuster anhand präziser, auf Fibonacci basierender Kriterien identifizieren. Zunächst ermitteln wir die Gesamtzahl der Umkehrpunkte mit „ArraySize(pivots)“, die in „pivotCount“ gespeichert ist, und beenden den Vorgang, wenn weniger als 5 Umkehrpunkte gefunden werden, indem wir „g_patternFormationBar“, „g_lockedPatternX“ und „g_tradeTaken“ auf -1, 0 bzw. false zurücksetzen, da das Fledermaus-Muster die Punkte X, A, B, C und D erfordert. Dann extrahieren wir die letzten fünf Umkehrpunkte aus dem Array „pivots“ und ordnen „X“ (zuerst), „A“, „B“, „C“ und „D“ (zuletzt) zu, um die Musterstruktur zu bilden.
Als Nächstes überprüfen wir, ob eine Abwärts-Fledermausmuster (X hoch, A tief, B hoch, C tief, D hoch) vorliegt, indem wir die Differenz zwischen XA-Segment („X.price - A.price“) berechnen, sicherstellen, dass sie positiv ist, den idealen B-Punkt als „A.price + 0,5 * diff“ berechnen, mit MathAbs überprüfen, ob B innerhalb von „Tolerance * diff“ liegt, das BC-Strecke (0,382 bis 0,886 von AB) und die AD-Erweiterung (0,886 von XA mit D unter X) überprüft und „patternFound“ auf „true“ gesetzt, wenn alle Bedingungen erfüllt sind. Zuletzt prüfen wir, ob ein Aufwärtsmuster der Fledermaus vorliegt (X tief, A hoch, B tief, C hoch, D tief), indem wir XA als „A.price – X.price“ berechnen und sicherstellen, dass es positiv ist, B bei 0,5 Rückgang, BC innerhalb von 0,382 bis 0,886 von AB und AD bei 0,886 von XA mit D über X überprüfen und „patternFound“ auf true setzen, wenn es gültig ist, um eine genaue Erkennung von Fledermaus-Mustern für die weitere Visualisierung und den Handel sicherzustellen. Wenn das Muster gefunden wurde, können wir es im Chart visualisieren.
//--- If a valid Bat pattern is detected if(patternFound) { //--- Print a message indicating the pattern type and detection time Print(patternType, " Bat pattern detected at ", TimeToString(D.time, TIME_DATE|TIME_MINUTES|TIME_SECONDS)); //--- Create a unique prefix for all graphical objects related to this pattern string signalPrefix = "BAT_" + IntegerToString(X.time); //--- Choose triangle color based on the pattern type color triangleColor = (patternType=="Bullish") ? clrBlue : clrRed; //--- Draw the first triangle connecting pivots X, A, and B DrawTriangle(signalPrefix+"_Triangle1", X.time, X.price, A.time, A.price, B.time, B.price, triangleColor, 2, true, true); //--- Draw the second triangle connecting pivots B, C, and D DrawTriangle(signalPrefix+"_Triangle2", B.time, B.price, C.time, C.price, D.time, D.price, triangleColor, 2, true, true); }
Wenn ein gültiges Muster erkannt wird („patternFound“ ist true), wird „patternType“ als leere Zeichenkette initialisiert und auf „Bearish“ gesetzt, wenn „D.price“ kleiner als „X.price“ ist (was ein Verkaufssignal anzeigt), oder auf „Bullish“, wenn es größer ist (was ein Kaufsignal anzeigt). Anschließend wird die Erkennung mit Print protokolliert, wobei der „patternType“ und die mit TimeToString formatierte Zeit des D-Umkehrpunktes, einschließlich Datum, Minuten und Sekunden, ausgegeben werden. Als Nächstes erstellen wir die eindeutige Kennung „signalPrefix“, indem wir „BAT_“ mit „X.time“ verknüpfen, das mithilfe der Funktion IntegerToString in eine Zeichenfolge umgewandelt wurde. Zuletzt setzen wir „triangleColor“ auf blau für Aufwärts- oder rot für Abwärtsmuster und rufen „DrawTriangle“ zweimal auf: zuerst, um das XAB-Dreieck zu zeichnen, das die Umkehrpunkte X, A und B verbindet, und dann, um das BCD-Dreieck zu zeichnen, das die Umkehrpunkte B, C und D verbindet, unter Verwendung von „signalPrefix“ mit den Suffixen „_Triangle1“ und „_Triangle2“, den jeweiligen Zeiten der Umkehrpunkte und -preise, „triangleColor“, einer Breite von 2 und der Aktivierung der Füllung und der Hintergrundanzeige mit Flags, gesetzt auf true. Diese Logik gewährleistet eine klare Visualisierung der Struktur des Fledermausmusters, um Handelsentscheidungen zu erleichtern. Hier ist das Ergebnis.
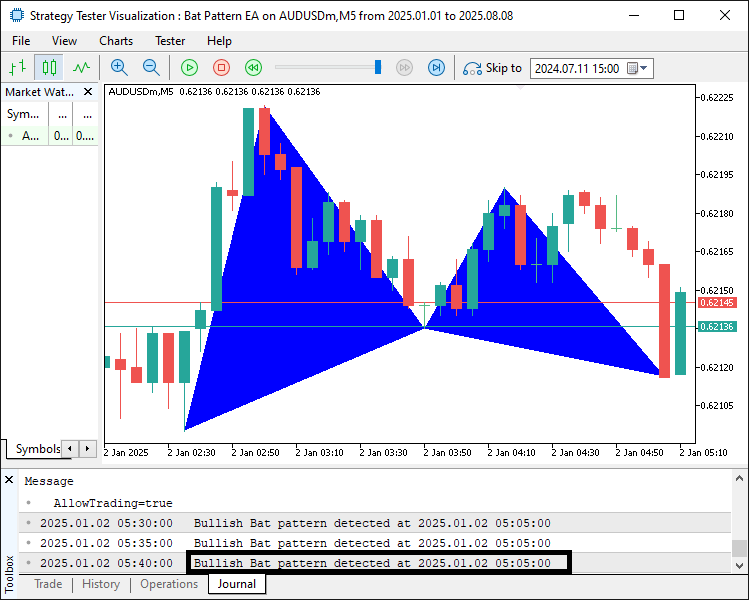
Anhand des Bildes können wir sehen, dass wir das erkannte Muster korrekt abbilden und visualisieren können. Jetzt müssen wir die Trendlinien weiter kartieren, um sie innerhalb der Grenzen vollständig sichtbar zu machen und eine Beschriftung hinzuzufügen, damit die Ebenen leichter zu identifizieren sind.
//--- Draw boundary trend lines connecting the pivots for clarity DrawTrendLine(signalPrefix+"_TL_XA", X.time, X.price, A.time, A.price, clrBlack, 2, STYLE_SOLID); DrawTrendLine(signalPrefix+"_TL_AB", A.time, A.price, B.time, B.price, clrBlack, 2, STYLE_SOLID); DrawTrendLine(signalPrefix+"_TL_BC", B.time, B.price, C.time, C.price, clrBlack, 2, STYLE_SOLID); DrawTrendLine(signalPrefix+"_TL_CD", C.time, C.price, D.time, D.price, clrBlack, 2, STYLE_SOLID); DrawTrendLine(signalPrefix+"_TL_XB", X.time, X.price, B.time, B.price, clrBlack, 2, STYLE_SOLID); DrawTrendLine(signalPrefix+"_TL_BD", B.time, B.price, D.time, D.price, clrBlack, 2, STYLE_SOLID); //--- Retrieve the symbol's point size to calculate offsets for text positioning double point = SymbolInfoDouble(_Symbol, SYMBOL_POINT); //--- Calculate an offset (15 points) for positioning text above or below pivots double offset = 15 * point; //--- Determine the Y coordinate for each pivot label based on its type double textY_X = (X.isHigh ? X.price + offset : X.price - offset); double textY_A = (A.isHigh ? A.price + offset : A.price - offset); double textY_B = (B.isHigh ? B.price + offset : B.price - offset); double textY_C = (C.isHigh ? C.price + offset : C.price - offset); double textY_D = (D.isHigh ? D.price + offset : D.price - offset); //--- Draw text labels for each pivot with appropriate anchoring DrawTextEx(signalPrefix+"_Text_X", "X", X.time, textY_X, clrBlack, 11, X.isHigh); DrawTextEx(signalPrefix+"_Text_A", "A", A.time, textY_A, clrBlack, 11, A.isHigh); DrawTextEx(signalPrefix+"_Text_B", "B", B.time, textY_B, clrBlack, 11, B.isHigh); DrawTextEx(signalPrefix+"_Text_C", "C", C.time, textY_C, clrBlack, 11, C.isHigh); DrawTextEx(signalPrefix+"_Text_D", "D", D.time, textY_D, clrBlack, 11, D.isHigh); //--- Calculate the central label's time as the midpoint between pivots X and B datetime centralTime = (X.time + B.time) / 2; //--- Set the central label's price at pivot D's price double centralPrice = D.price; //--- Create the central text label indicating the pattern type if(ObjectCreate(0, signalPrefix+"_Text_Center", OBJ_TEXT, 0, centralTime, centralPrice)) { ObjectSetString(0, signalPrefix+"_Text_Center", OBJPROP_TEXT, (patternType=="Bullish") ? "Bullish Bat" : "Bearish Bat"); ObjectSetInteger(0, signalPrefix+"_Text_Center", OBJPROP_COLOR, clrBlack); ObjectSetInteger(0, signalPrefix+"_Text_Center", OBJPROP_FONTSIZE, 11); ObjectSetString(0, signalPrefix+"_Text_Center", OBJPROP_FONT, "Arial Bold"); ObjectSetInteger(0, signalPrefix+"_Text_Center", OBJPROP_ALIGN, ALIGN_CENTER); }
Um das Muster noch anschaulicher zu machen, fügen wir detaillierte Chart-Objekte hinzu, um die Struktur des Musters darzustellen. Zunächst zeichnen wir mit „DrawTrendLine“ sechs durchgezogene Trendlinien mit dem eindeutigen „signalPrefix“, um wichtige Umkehrpunkte zu verbinden: XA, AB, BC, CD, XB und BD, jeweils mit dem Zeiten und Preisen der Umkehrpunkte (z. B., „X.time“, „X.price“), wobei OBJPROP_COLOR auf „clrBlack“, „OBJPROP_WIDTH“ auf 2 und „OBJPROP_STYLE“ auf „STYLE_SOLID“ mit ObjectSetInteger gesetzt wird, um die Kanten des Musters zu umreißen. Dann wird die Punktgröße des Symbols mit „SymbolInfoDouble(_Symbol, SYMBOL_POINT)“ abgerufen und ein 15-Punkte-Offset für die Positionierung des Etiketts berechnet, wobei die Y-Koordinaten („textY_X“, „textY_A“, „textY_B“, „textY_C“, „textY_D“) durch Addieren oder Subtrahieren des Offsets, je nachdem, ob es sich bei dem jeweiligen Pivot um ein hoher Umkehrpunkt („isHigh“ true) oder -Tief handelt, um die Beschriftungen über den Hochs oder unter den Tiefs zu platzieren. Sie können dies je nach der Ästhetik und dem Symbol, mit dem Sie handeln, ändern.
Als Nächstes verwenden wir „DrawTextEx“, um die Kennzeichnungen für die Umkehrpunkte X, A, B, C und D mit „signalPrefix“ und Suffixen wie „_Text_X“ zu erstellen, die den jeweiligen Buchstaben anzeigen, an der Zeit des Umkehrpunkts und der eingestellten Y-Koordinate positioniert sind und „clrBlack“, Schriftgröße 11 und den „isHigh“-Status des Umkehrpunkts zur Verankerung verwenden. Zuletzt berechnen wir die Position des zentralen Etiketts bei „centralTime“ als Mittelpunkt von „X.time“ und „B.time“ und „centralPrice“ bei „D.price“, erstellen ein Textobjekt mit ObjectCreate mit dem Namen „signalPrefix + '_Text_Center'“, setzen „OBJPROP_TEXT“ auf „Bullish Bat“ oder „Bearish Bat“ basierend auf „patternType“ und konfigurieren „OBJPROP_COLOR“ auf „clrBlack“, „OBJPROP_FONTSIZE“ auf 11, OBJPROP_FONT auf „Arial Bold“ und „OBJPROP_ALIGN“ auf „ALIGN_CENTER“ mit den Funktionen ObjectSetString und „ObjectSetInteger“. Diese Logik gewährleistet eine umfassende visuelle Darstellung der Struktur und des Typs des Musters auf dem Chart. Wenn wir das Programm ausführen, erhalten wir die folgende Darstellung.
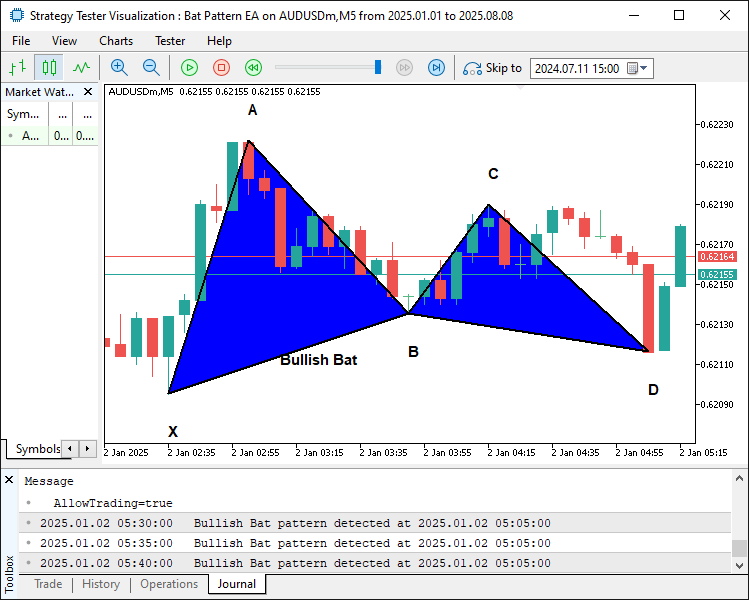
Auf dem Bild können wir sehen, dass wir die Kanten und die Kennzeichnung zum Muster hinzugefügt haben, um es aufschlussreicher und anschaulicher zu machen. Als Nächstes müssen wir die Handelsniveaus für dieses Muster bestimmen.
//--- Define start and end times for drawing horizontal dotted lines for obj_Trade levels datetime lineStart = D.time; datetime lineEnd = D.time + PeriodSeconds(_Period)*2; //--- Declare variables for entry price and take profit levels double entryPriceLevel, TP1Level, TP2Level, TP3Level, tradeDiff; //--- Calculate obj_Trade levels based on whether the pattern is Bullish or Bearish if(patternType=="Bullish") { //--- Bullish → BUY signal //--- Use the current ASK price as the entry entryPriceLevel = SymbolInfoDouble(_Symbol, SYMBOL_ASK); //--- Set TP3 at pivot C's price TP3Level = C.price; //--- Calculate the total distance to be covered by the obj_Trade tradeDiff = TP3Level - entryPriceLevel; //--- Set TP1 at one-third of the total move TP1Level = entryPriceLevel + tradeDiff/3; //--- Set TP2 at two-thirds of the total move TP2Level = entryPriceLevel + 2*tradeDiff/3; } else { //--- Bearish → SELL signal //--- Use the current BID price as the entry entryPriceLevel = SymbolInfoDouble(_Symbol, SYMBOL_BID); //--- Set TP3 at pivot C's price TP3Level = C.price; //--- Calculate the total distance to be covered by the obj_Trade tradeDiff = entryPriceLevel - TP3Level; //--- Set TP1 at one-third of the total move TP1Level = entryPriceLevel - tradeDiff/3; //--- Set TP2 at two-thirds of the total move TP2Level = entryPriceLevel - 2*tradeDiff/3; } //--- Draw dotted horizontal lines to represent the entry and TP levels DrawDottedLine(signalPrefix+"_EntryLine", lineStart, entryPriceLevel, lineEnd, clrMagenta); DrawDottedLine(signalPrefix+"_TP1Line", lineStart, TP1Level, lineEnd, clrForestGreen); DrawDottedLine(signalPrefix+"_TP2Line", lineStart, TP2Level, lineEnd, clrGreen); DrawDottedLine(signalPrefix+"_TP3Line", lineStart, TP3Level, lineEnd, clrDarkGreen); //--- Define a label time coordinate positioned just to the right of the dotted lines datetime labelTime = lineEnd + PeriodSeconds(_Period)/2; //--- Construct the entry label text with the price string entryLabel = (patternType=="Bullish") ? "BUY (" : "SELL ("; entryLabel += DoubleToString(entryPriceLevel, _Digits) + ")"; //--- Draw the entry label on the chart DrawTextEx(signalPrefix+"_EntryLabel", entryLabel, labelTime, entryPriceLevel, clrMagenta, 11, true); //--- Construct and draw the TP1 label string tp1Label = "TP1 (" + DoubleToString(TP1Level, _Digits) + ")"; DrawTextEx(signalPrefix+"_TP1Label", tp1Label, labelTime, TP1Level, clrForestGreen, 11, true); //--- Construct and draw the TP2 label string tp2Label = "TP2 (" + DoubleToString(TP2Level, _Digits) + ")"; DrawTextEx(signalPrefix+"_TP2Label", tp2Label, labelTime, TP2Level, clrGreen, 11, true); //--- Construct and draw the TP3 label string tp3Label = "TP3 (" + DoubleToString(TP3Level, _Digits) + ")"; DrawTextEx(signalPrefix+"_TP3Label", tp3Label, labelTime, TP3Level, clrDarkGreen, 11, true);
Um die Handelsstufen für das erkannte Muster zu definieren und zu visualisieren, setzen wir zunächst „lineStart“ auf die Zeit des Umkehrpunktes D („D.time“) und „lineEnd“ auf zwei Perioden im Voraus mit „PeriodSeconds(_Period) * 2“ und deklarieren die Variablen „entryPriceLevel“, „TP1Level“, „TP2Level“, „TP3Level“ und „tradeDiff“ für die Handelsberechnungen. Dann setzen wir für ein Aufwärtsmuster („patternType == 'Bullish'“) „entryPriceLevel“ auf den aktuellen Briefkurs (Ask) mit SymbolInfoDouble, „TP3Level“ auf den Preis des C-Umkehrpunktes, berechnen „tradeDiff“ als „TP3Level – entryPriceLevel“ und berechnen „TP1Level“ und „TP2Level“ als ein Drittel und zwei Drittel von „tradeDiff“, addiert zu „entryPriceLevel“; für ein Abwärtsmuster verwenden wir den Geldkurs (Bid), setzen „TP3Level“ auf den Preis von C, berechnen „tradeDiff“ als „entryPriceLevel – TP3Level“ und berechnen „TP1Level“ und „TP2Level“ durch Subtraktion von einem Drittel und zwei Dritteln der Handelsdifferenz.
Als Nächstes zeichnen wir mit „DrawDottedLine“ vier gepunktete horizontale Linien: eine Einstiegslinie bei „entryPriceLevel“ in Magenta und Take-Profit-Linien bei „TP1Level“ (forest green), „TP2Level“ (green) und „TP3Level“ (dark green), die sich von „lineStart“ bis „lineEnd“ erstrecken. Zuletzt setzen wir „labelTime“ auf „lineEnd“ plus eine halbe Periode, erstellen die Kennzeichnungen mit über DoubleToString formatierten Preisen (z.B., „BUY (price)“ oder „SELL (price)“ für die Eröffnung, „TP1 (price)“ usw.), und verwenden „DrawTextEx“, um diese Beschriftungen zum „labelTime“ mit entsprechenden Farben, Schriftgröße 11 und verankert über den Preisniveaus zu zeichnen. Nach der Kompilierung erhalten wir folgendes Ergebnis.
Abwärts-Muster:
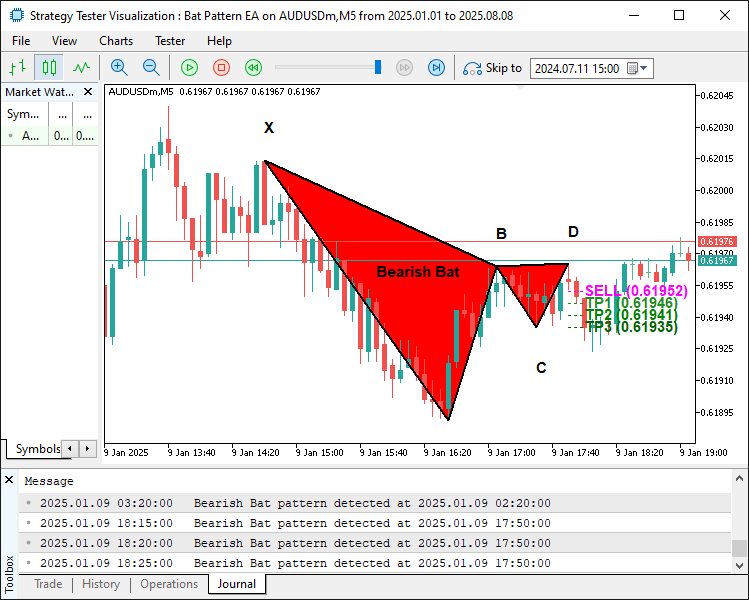
Aufwärts-Muster:
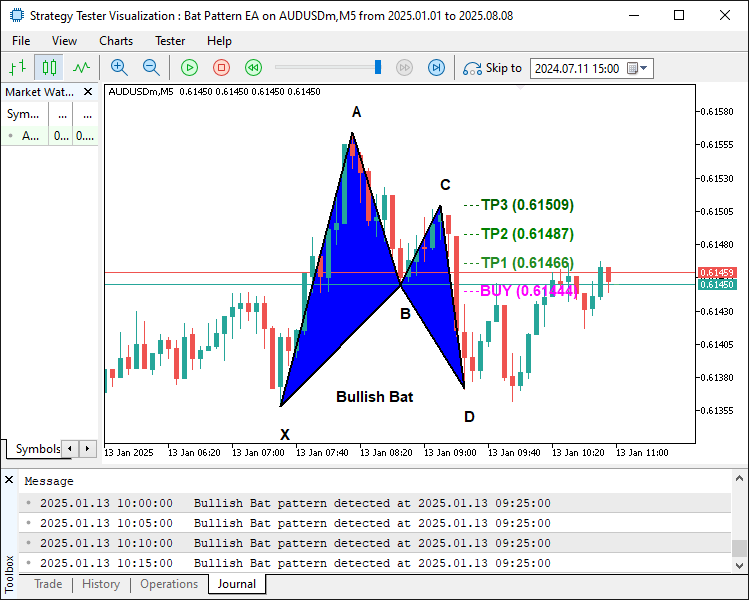
Anhand der Bilder können wir sehen, dass wir die Handelsstufen richtig zugeordnet haben. Was wir jetzt tun müssen, ist, die eigentlichen Handelspositionen zu initiieren, und das ist alles.
//--- Retrieve the index of the current bar int currentBarIndex = Bars(_Symbol, _Period) - 1; //--- If no pattern has been previously locked, lock the current pattern formation if(g_patternFormationBar == -1) { g_patternFormationBar = currentBarIndex; g_lockedPatternX = X.time; //--- Print a message that the pattern is detected and waiting for confirmation Print("Pattern detected on bar ", currentBarIndex, ". Waiting for confirmation on next bar."); return; } //--- If still on the same formation bar, the pattern is considered to be repainting if(currentBarIndex == g_patternFormationBar) { Print("Pattern is repainting; still on locked formation bar ", currentBarIndex, ". No obj_Trade yet."); return; } //--- If we are on a new bar compared to the locked formation if(currentBarIndex > g_patternFormationBar) { //--- Check if the locked pattern still corresponds to the same X pivot if(g_lockedPatternX == X.time) { Print("Confirmed pattern (locked on bar ", g_patternFormationBar, "). Opening obj_Trade on bar ", currentBarIndex, "."); //--- Update the pattern formation bar to the current bar g_patternFormationBar = currentBarIndex; //--- Only proceed with trading if allowed and if there is no existing position if(AllowTrading && !PositionSelect(_Symbol) && !g_tradeTaken) { double entryPriceTrade = 0, stopLoss = 0, takeProfit = 0; point = SymbolInfoDouble(_Symbol, SYMBOL_POINT); bool tradeResult = false; //--- For a Bullish pattern, execute a BUY obj_Trade if(patternType=="Bullish") { //--- BUY signal entryPriceTrade = SymbolInfoDouble(_Symbol, SYMBOL_ASK); double diffTrade = TP2Level - entryPriceTrade; stopLoss = entryPriceTrade - diffTrade * 3; takeProfit = TP2Level; tradeResult = obj_Trade.Buy(LotSize, _Symbol, entryPriceTrade, stopLoss, takeProfit, "Bat Signal"); if(tradeResult) { Print("Buy order opened successfully."); g_tradeTaken = true; } else Print("Buy order failed: ", obj_Trade.ResultRetcodeDescription()); } //--- For a Bearish pattern, execute a SELL obj_Trade else if(patternType=="Bearish") { //--- SELL signal entryPriceTrade = SymbolInfoDouble(_Symbol, SYMBOL_BID); double diffTrade = entryPriceTrade - TP2Level; stopLoss = entryPriceTrade + diffTrade * 3; takeProfit = TP2Level; tradeResult = obj_Trade.Sell(LotSize, _Symbol, entryPriceTrade, stopLoss, takeProfit, "Bat Signal"); if(tradeResult) { Print("Sell order opened successfully."); g_tradeTaken = true; } else Print("Sell order failed: ", obj_Trade.ResultRetcodeDescription()); } } else { //--- If a position is already open, do not execute a new obj_Trade Print("A position is already open for ", _Symbol, ". No new obj_Trade executed."); } } else { //--- If the pattern has changed, update the lock with the new formation bar and X pivot g_patternFormationBar = currentBarIndex; g_lockedPatternX = X.time; g_tradeTaken = false; Print("Pattern has changed; updating lock on bar ", currentBarIndex, ". Waiting for confirmation."); return; } } else { //--- If no valid Bat pattern is detected, reset the pattern lock variables g_patternFormationBar = -1; g_lockedPatternX = 0; g_tradeTaken = false; }
Hier schließen wir die Tick-Implementierung für das System ab, indem wir die Handelsausführung und die Musterbestätigung für das Muster verwalten. Zunächst wird der aktuelle Balken-Index mit „Bars(_Symbol, _Period) – 1“ ermittelt und in „currentBarIndex“ gespeichert. Wenn dann kein Muster gesperrt ist („g_patternFormationBar == -1“), setzen wir „g_patternFormationBar“ auf „currentBarIndex“, sperren dien Zeitpunkt des Umkehrpunkts X in „g_lockedPatternX“ mit „X.time“, protokollieren die Erkennung mit dem Hinweis, dass auf eine Bestätigung gewartet wird, und beenden das Programm. Wenn wir uns dann immer noch auf dem Formationsbalken befinden („currentBarIndex == g_patternFormationBar“), protokollieren wir das Repainting und beenden den Handel, um ein vorzeitiges Handeln zu verhindern.
Zuletzt, wenn sich ein neuer Balken gebildet hat („currentBarIndex > g_patternFormationBar“) und der X-Pivot mit „g_lockedPatternX“ übereinstimmt, bestätigen wir das Muster, protokollieren es, aktualisieren „g_patternFormationBar“ und prüfen, ob „AllowTrading“ einen Handel zulässt ist, ob keine offenen Positionen über PositionSelect vorhanden sind und kein Handel getätigt wurde („g_tradeTaken“ false) . Bei einem Aufwärtsmuster setzen wir „entryPriceTrade“ auf den Briefkurs (Ask), berechnen „diffTrade“ als „TP2Level - entryPriceTrade“, setzen „stopLoss“ auf das Dreifache dieses Abstands nach unten, setzen „takeProfit“ auf „TP2Level“ und führen einen Kauf mit „obj_Trade. Buy” unter Verwendung von „LotSize” und „Bat Signal”, protokollieren Erfolg oder Misserfolg und setzen „g_tradeTaken” auf „true”; für ein Abwärtsmuster verwenden wir den Geldkurs (Bid), setzen „stopLoss” auf das Dreifache darüber und führen einen Verkauf mit „obj_Trade. Sell“ aus; wenn der Handel nicht zulässig ist, eine Position besteht oder ein Handel getätigt wurde, protokollieren wir keinen Handel; wenn sich das Muster ändert, aktualisieren wir die Sperre und warten; wenn kein Muster gefunden wird, setzen wir die globalen Variablen zurück. Nach der Kompilierung erhalten wir folgendes Ergebnis.
Abwärtssignal:
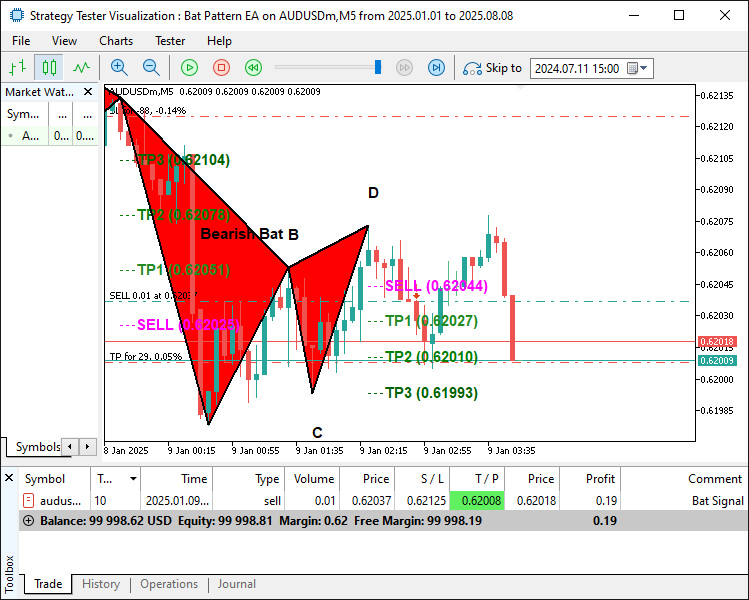
Aufwärtssignal:
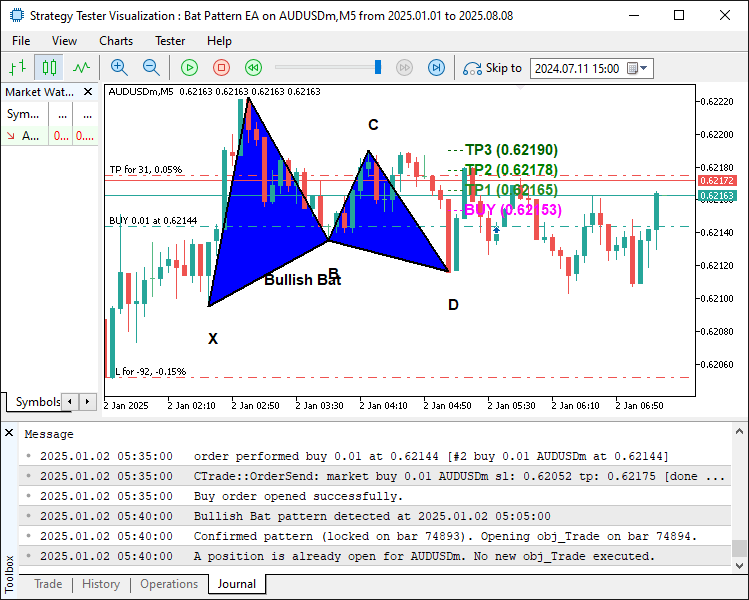
Aus dem Bild können wir ersehen, dass wir das harmonische Muster zeichnen könnnen und in der Lage sind, es entsprechend zu handeln, sobald es bestätigt worden ist. Damit haben wir unser Ziel erreicht, das Muster zu identifizieren, aufzuzeichnen und zu handeln. Bleiben nur noch die Backtests des Programms, und das wird im nächsten Abschnitt behandelt.
Backtests
Nach einem gründlichen Backtest erhalten wir folgende Ergebnisse.
Backtest-Grafik:
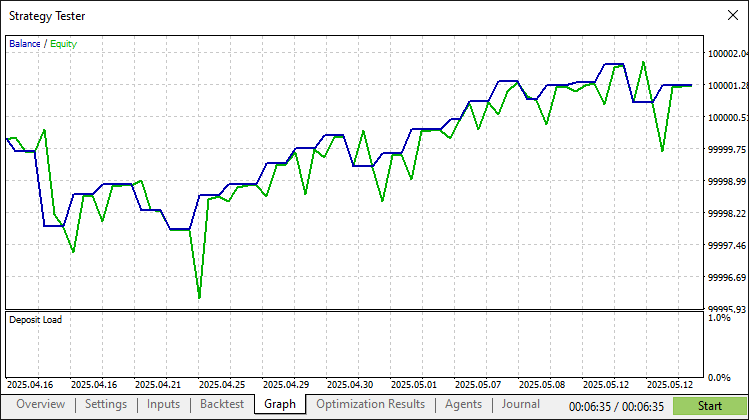
Bericht des Backtest:
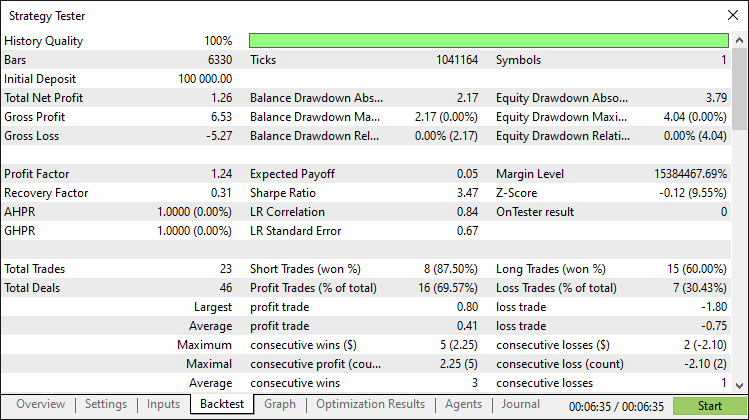
Schlussfolgerung
Zusammenfassend haben wir das System des Fledermaus-Musters in MQL5 entwickelt, das die Preisaktion nutzt, um harmonische Aufwärts- oder Abwärtsmuster mit präzisen Fibonacci-Verhältnissen zu erkennen, den Handel mit berechneten Einstiegs-, Stop-Loss- und mehrstufigen Take-Profit-Punkten zu automatisieren und die Muster mit Chart-Objekten wie Dreiecken und Trendlinien zu visualisieren.
Haftungsausschluss: Dieser Artikel ist nur für Bildungszwecke gedacht. Der Handel ist mit erheblichen finanziellen Risiken verbunden, und die Volatilität der Märkte kann zu Verlusten führen. Gründliche Backtests und sorgfältiges Risikomanagement sind entscheidend, bevor Sie dieses Programm auf den Live-Märkten einsetzen.
Indem Sie die vorgestellten Konzepte und Implementierungen nutzen, können Sie dieses System der Fledermaus-Muster an Ihren Handelsstil anpassen und Ihre algorithmischen Strategien verbessern. Viel Spaß beim Handeln!
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/19105
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Verbessern Sie Ihren Handel mit Smart Money Konzepten (SMC): OB, BOS und FVG
Verbessern Sie Ihren Handel mit Smart Money Konzepten (SMC): OB, BOS und FVG
 MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 79): Verwendung von Gator-Oszillator und Akkumulations-/Distributions-Oszillator mit überwachtem Lernen
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 79): Verwendung von Gator-Oszillator und Akkumulations-/Distributions-Oszillator mit überwachtem Lernen
 Statistische Arbitrage durch kointegrierte Aktien (Teil 4): Modellaktualisierung in Echtzeit
Statistische Arbitrage durch kointegrierte Aktien (Teil 4): Modellaktualisierung in Echtzeit
 Statistische Arbitrage durch kointegrierte Aktien (Teil 3): Datenbank-Einrichtung
Statistische Arbitrage durch kointegrierte Aktien (Teil 3): Datenbank-Einrichtung
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.