MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 79): Verwendung von Gator-Oszillator und Akkumulations-/Distributions-Oszillator mit überwachtem Lernen

Einführung

In unseren letzten beiden Artikeln haben wir wie bisher zehn Signalmuster unter Verwendung des Indikatorpaares Gator-Oszillator und Akkumulations-/Distributions-Oszillator getestet. Dabei haben wir, wie es unsere Praxis ist, drei konsistente Nachzügler-Muster festgestellt: 0, 3 und 4. Anstatt diese zu verwerfen oder zu vernachlässigen, soll in diesem Artikel untersucht werden, ob überwachtes Lernen ihre Leistung wieder verbessern kann. Wir verwenden ein mit Kernelregression und Skalarproduktähnlichkeit erweitertes CNN und untersuchen, ob Netzwerke mit einer solchen Architektur verborgene Werte aus Signalen extrahieren können, die manchmal zunächst schwach erscheinen. Wie in den letzten beiden Artikeln beschrieben, beziehen sich alle Tests auf das Paar GBP JPY und auf den 30-Minuten-Zeitrahmen.

Kernel-Regression mit Skalarprodukt-Ähnlichkeit

Unsere Wahl für ein überwachtes Lernmodell ist ein CNN, das Kernel-Regression und Skalarproduktähnlichkeit verwendet. Die Kernelregression schätzt die Ausgänge jeder Schicht in einem CNN, indem sie die beobachteten Eingänge entsprechend ihrer Ähnlichkeit mit einem bestimmten Abfragepunkt gewichtet. Diese Ähnlichkeit wird mit Hilfe des Skalarprodukts Ähnlichkeit als Kernel-Funktion quantifiziert. In unserem Modell, dessen Code im nächsten Abschnitt vorgestellt wird, berechnet die Methode _dot_product_kernel_regression die Ähnlichkeit zwischen allen Zeitpositionen in einer Merkmalskarte mit Hilfe der Funktion torch.bmm(x, x.T), zu der wir eine Softmax-Normalisierung hinzufügen, die der Selbstaufmerksamkeit recht ähnlich ist.

Das Skalar- oder Punktprodukt ist ein datenadaptives Maß für die Ähnlichkeit, wobei ein hohes Produkt bedeutet, dass zwei Positionen über alle Kanäle hinweg das gleiche Aktivierungsmuster aufweisen, was zu einem größeren Einfluss auf die gewichtete Summe führen kann. Eine Analogie oder eine andere Betrachtungsweise könnte so aussehen, dass man jeder Position „Stimmen“ proportional zu ihrer Übereinstimmung mit der Abfrageposition gibt. Eine CNN-Schicht kann man sich als Tabellenkalkulation vorstellen, bei der die Zeilen Zeitschritte und die Spalten Merkmale sind. In dieser Einstellung wird eine einzelne Zeile als „Position“ betrachtet. Die „Abfrageposition“ ist also die aktuelle Zeile, die aktualisiert wird. Bei der Durchführung dieser Aktualisierungen werden Vergleiche zwischen ihr und jeder anderen Position angestellt, um zu ermitteln, wie ähnlich sie sind. Diese Aktualisierungen finden im Backpropagation-Verfahren statt.

Mathematisch könnten die neuen Gewichte wie folgt definiert werden. Gegebene Merkmalsvektoren xi und xj, das Gewicht wij ist:

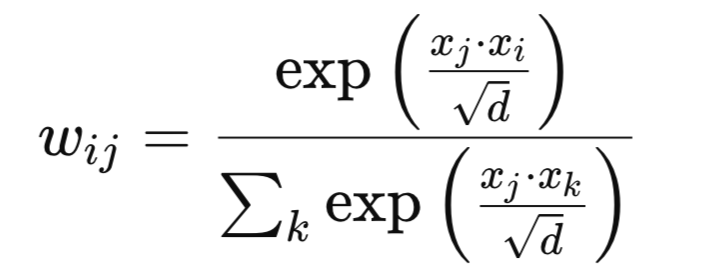
wobei:

• d – ist die Kanaldimension.
• exp – ist der natürliche Logarithmus

Unsere Matrix der Gewichte führt eine nichtlokale Glättung über die gesamte Sequenz hinweg durch, die nicht wie bei einer Faltung auf benachbarte Positionen beschränkt ist. Dies hat zur Folge, dass weitreichende Abhängigkeiten und Korrelationen innerhalb des Merkmalsraums erfasst werden können, was die Leistung bei Zeitreihen- und Strukturdatenaufgaben potenziell erhöht. Als Orientierungshilfe sollte die Skalarprodukt-Ähnlichkeit eingesetzt werden, wenn die zu lösende Aufgabe sinnvolle Korrelationen zwischen nicht benachbarten Merkmalen aufweist und Sie einen aufmerksamkeitsähnlichen Mechanismus wünschen, der keine zusätzlichen Abfrage/Schlüssel/Wert-Projektionen erforderlich macht. Dies kann besonders synergetisch mit CNNs sein, da sie lokale Merkmale und Kernelregression erfassen, die einen globalen Kontext hinzufügen.

Fallbeispiel für die Steuerung der Kernel- und Kanalgrößen eines CNN mit dem Skalarprodukt

Die Skalarprodukt-Kernelregression zeigt auf, wo und bei welcher Auflösung die Korrelationen am stärksten sind. Die Anpassung der CNN-Kernelgrößen und Kanaltiefen im Einklang mit einer Ähnlichkeitsstruktur kann zwei Dinge bewirken. Erstens kann es helfen, rezeptive Felder mit der Korrelationslänge abzugleichen. Dies ist insbesondere bei größeren Kernen der Fall, wenn eine hohe Ähnlichkeit über weite Entfernungen bestehen bleibt. Zweitens kann es Kanäle entsprechend der Korrelationskomplexität zuweisen. Mehr Kanäle werden zugewiesen, wenn die Ähnlichkeitsmuster stark variieren, und weniger, wenn eine größere Gleichmäßigkeit besteht. Dies kann zu einer Architektur führen, die sowohl datengesteuert als auch aufgabenspezifisch ist, im Gegensatz zu festen Heuristiken.

In unserer Implementierung, die im Quellcode in den folgenden Abschnitten gezeigt wird, durchlaufen die Kernelgrößen die Stufen [3,5,7,9], während die Kanaltiefen ebenfalls von 32 auf 320 ansteigen. Jede andere Ebene wendet eine Skalarproduktregression an, was bedeutet, dass die Ebenen globale Korrelationskarten „sehen“. Wenn die Ähnlichkeitskarten in den nachfolgenden Faltungsschichten breite Spitzen mit größeren Kernen aufweisen, kann dies ausgenutzt werden. Wenn die Karte scharfe Spitzen aufweist, können kleinere Kerne ausreichen, was zu einer Konzentration auf kleine Verfeinerungen führen würde. Dies kann mit der Abstimmung des rezeptiven Feldes verglichen werden, die durch ein globales Korrelationssignal gesteuert wird.

Bei der Verwendung von CNNs sollte man eine Voranalyse in Betracht ziehen, bei der die Daten durch einen kleinen CNN- plus Skalarprodukt-Kernelblock geleitet werden, um die Korrelationslängen zu analysieren, die dann als Grundlage für die Festlegung des Kernel-/Kanalplans des Haupt-CNNs dienen können. Außerdem sollten bei der Erkennung lokaler Kanten/Muster die frühen Schichten mit kleineren Kerneln gepaart werden, wobei sich die Kernelgröße der späteren Schichten nach der beobachteten Ähnlichkeitsverteilung richtet.

Mögliche Nachteile und mögliche Alternativen

Unser erster Nachteil bei der Verwendung des Skalarproduktkerns sollte nicht überraschen, und er liegt in den Berechnungskosten. Die Ähnlichkeit des Skalarprodukts skaliert mit O(L2) mit einer Sequenzlänge von L. Dies kann bei langen Signalen oder großen Merkmalseingaben sehr rechenaufwendig sein. Ein weiteres Problem ist die Überglättung. Wenn die Gewichte zu diffus sind, können die Merkmale zu homogen werden, was zu einem Verlust an feinen Details führt. Die Instabilität des Trainings ist ein weiterer Problembereich. Bei großen Ähnlichkeiten kann es, wenn keine Normalisierung stattfindet, zu explodierenden Gewichten kommen. Schließlich kann der Speicheraufwand für die Speicherung einer vollständigen Ähnlichkeitsmatrix prohibitive Kosten verursachen. 

Es gibt jedoch einige Maßnahmen, um diese Bedenken zu zerstreuen, z. B. die Verwendung von Fenstern mit lokaler Aufmerksamkeit. Anstatt also die Ähnlichkeit zwischen allen Positionen zu berechnen, indem wir die bereits vorgestellte und oben verlinkte Formel zur Berechnung der Komplexität ausschöpfen, beschränken wir die Vergleiche auf ein festes Fenster um jede Abfrageposition. Dies würde den Rechen-/Speicheraufwand verringern und sich auf das Einblenden des nahe gelegenen relevanten Kontexts konzentrieren. Außerdem können wir auch eine Temperaturskalierung vornehmen. Hier werden die Ähnlichkeitswerte einfach mit 1/τ, der Temperatur, multipliziert. Eine niedrigere Temperatur würde zu schärferen, selektiveren Gewichten führen, bei denen wenige Positionen/Schichtreihen dominieren. Ein höheres τ würde zu einer gleichmäßigeren Verteilung der Gewichte in den Schichtrastern führen. Die Temperatur wäre ein zusätzlicher Hyperparameter.

Schließlich können wir vor der Durchführung der Kernelregression auch Downsampling anwenden. Dies würde bedeuten, dass die Länge L der Eingabedatenfolge durch Poolbildung oder Schrittlängen-Faltung vor der Berechnung des Skalarprodukts reduziert wird. Ein kürzeres L sollte die Ähnlichkeitsberechnungen beschleunigen und auch den Speicherbedarf verringern, während gleichzeitig große Korrelationen erfasst werden.

Alternative CNN-Erweiterungen mit dem Dot-Produkt

Neben der Kernel-Regression mit dem Skalarprodukt-Kernel können wir auch hybride CNNs mit Selbstaufmerksamkeit einsetzen. In diesem Fall würden wir die Skalarproduktregression als nichtlokalen Block neben den CNN-Schichten verwenden, im Gegensatz zu einer normalen Aufmerksamkeitsschicht. Dies unterscheidet sich von unserer Implementierung, deren Quelle im nächsten Abschnitt behandelt wird, dadurch, dass wir in unserem Modell die Kernel-Regression periodisch in einem Faltungsstapel anwenden. Der Hybrid würde sie in parallele Zweige einfügen und die Ausgänge absichern. Wir könnten unseren Kernel auch durch eine mehrskalige Merkmalsfusion anwenden, bei der die Kernelregression auf Merkmale angewendet wird, die aus mehreren CNN-Schichten stammen und dann kombiniert werden. Der Unterschied zu dem, was wir gemacht haben, ist, dass wir die Kernel-Regression jeweils nur auf einer Ebene anwenden. Die mehrskalige Fusion führt den globalen Kontext aus verschiedenen Schichten/Auflösungen zusammen. 

Wir hätten den Kernel auch bei Pretext-Aufgaben zur Regularisierung einsetzen können. In diesem Szenario trainieren wir die Kernel-Regressionsausgänge, um zusätzlich zur Hauptaufgabe weitere Aufgaben zu lösen, wie z. B. die Vorhersage der nächsten Einbettungsstufe. Dies unterscheidet sich natürlich von unserem unten beschriebenen Ansatz, da wir den Kernel nur zur Verfeinerung der Merkmale verwenden, während er hier auch reguliert wird. Schließlich könnte eine alternative Anwendung unseres Kerns einfach mit etwas sein, das wir in früheren Artikeln erforscht haben. Dynamische Größenanpassung des Kernels. Bei diesem Ansatz würden wir die Ähnlichkeitsstatistiken aus der Kernelregression verwenden, um die Größen der Faltungskerne während des Trainings/der Inferenz anzupassen. In unserem unten beschriebenen Ansatz legen wir die Kernelgrößen im Voraus fest.

Das Netzwerk

Der Code für unsere Netzwerkklasse, die diesen Skalarproduktkern mit Regression implementiert, wird im Folgenden vorgestellt:

class DotProductKernelRegressionConv1D(nn.Module):
    def __init__(self, input_length=100):
        super().__init__()
        self.input_length = input_length

        self.kernel_sizes, self.channels = self._design_architecture()

        self.conv_layers = nn.ModuleList()
        self.use_kernel_regression = []  # <-- Python list for markers

        in_channels = 1
        for i, (out_channels, kernel_size) in enumerate(zip(self.channels, self.kernel_sizes)):
            conv_layer = nn.Sequential(
                nn.Conv1d(in_channels, out_channels, kernel_size=kernel_size, padding=kernel_size // 2),
                nn.BatchNorm1d(out_channels),
                nn.ReLU(),
                nn.Dropout(0.2))
            self.conv_layers.append(conv_layer)

            self.use_kernel_regression.append(i % 2 == 0)
            in_channels = out_channels

        self.head = nn.Sequential(
            nn.AdaptiveAvgPool1d(1),
            nn.Flatten(),
            nn.Linear(in_channels, 128),
            nn.ReLU(),
            nn.Dropout(0.2),
            nn.Linear(128, 64),
            nn.ReLU(),
            nn.Linear(64, 1),
            nn.Sigmoid()
        )

    def _dot_product_kernel_regression(self, x):
        """
        Dot product kernel regression.
        For each time position, outputs a weighted sum of all positions using dot product similarity as weights.
        """
        # x: (B, C, L)
        x_ = x.permute(0, 2, 1)  # (B, L, C)
        # Dot product similarity
        sim = torch.bmm(x_, x_.transpose(1, 2))  # (B, L, L)
        # Optionally normalize for stability (like attention)
        weights = F.softmax(sim / (x_.size(-1) ** 0.5), dim=-1)  # (B, L, L)
        out = torch.bmm(weights, x_)  # (B, L, C)
        return out.permute(0, 2, 1)  # (B, C, L)

    def _design_architecture(self):
        num_layers = 10
        kernel_sizes = [3 + (i % 4) * 2 for i in range(num_layers)]
        channels = [32 * (i + 1) for i in range(num_layers)]
        return kernel_sizes, channels

    def forward(self, x):
        x = x.unsqueeze(1)  # (B, 1, L)
        for conv_layer, use_kr in zip(self.conv_layers, self.use_kernel_regression):
            x = conv_layer(x)
            if use_kr:
                x = self._dot_product_kernel_regression(x)
        return self.head(x)

Die erste Zeile des Codes in unserem obigen Listing ist das Klassenskelett und der Konstruktor. Es wird von nn.Module abgeleitet und schaltet die Parameterverfolgung von PyTorch, .to(device), ,eval(), usw. frei. Der Wert input_length wird gespeichert, obwohl Faltungen längenunabhängig sind. Dies hilft bei der Überprüfung der Korrektheit, wenn man nach ONNX exportiert oder später eine längenabhängige Logik erstellt. Damit gehen wir dann zum „Architekturentwurf“ über, wo wir die Kernel- und Kanalgrößen festlegen. Dies ist wichtig, weil es sowohl den Rezeptionsfeldplan (Kernelgrößen) als auch den Kapazitätsplan (die Kanäle) zentralisiert. Diese Informationen an einem Ort aufzubewahren, macht es in zweierlei Hinsicht einfach. Erstens kann bei der Angleichung der Kernelgrößen die beobachtete Ähnlichkeit von der Kernelregression abweichen. Zweitens ermöglicht es uns die Skalierung, wenn die Ähnlichkeitsmuster komplexer sind.

Für die Nutzerführung sollte die Funktion _design_architecture datengesteuert sein. Ein Datenstapel kann geprüft werden, um den Ähnlichkeitsabfall des Regressionsblocks zu messen, und auf dieser Grundlage können die Kernelgrößen entsprechend erweitert werden. Man könnte auch in Betracht ziehen, die Kanäle an die Entropie der Ähnlichkeitsverteilung zu binden. Wenn dies der Fall ist, würde mehr Entropie zu mehr Kanälen führen, die zur Modellvariabilität beitragen.

Unser nächster Code definiert dann den Faltungsstapel und die Markierungen für die Anwendung der Regression. Dies ist wichtig, da die Funktion ModuleList die Ebenen so registriert, dass ihre Gewichte gespeichert und bei Bedarf geladen werden. Wenn man das Padding der halben Kernelgröße zuordnet, sind die Faltungen fast gleich lang, oder ihre Länge bleibt erhalten. Dies ist wichtig, weil die Kernel-Regression später von einer gleichbleibenden Länge ausgeht.

Die Verwendung von Batch-Normalisierung, ReLU-Aktivierung und Dropouts sind ebenfalls robuste Maßnahmen, wobei die Batch-Normalisierung das Training stabilisiert, ReLU Nicht-Linearität einführt und Dropouts eine gewisse Regularisierung erzwingen. Der boolesche Wert use_kernel_regression ermöglicht es uns, die rechenintensive Kernregression von jeder Schicht zu entkoppeln, sodass sie nur dort eingesetzt werden kann, wo sie hilfreich ist. Als zusätzliche Orientierungshilfe können Residual-Skips um die conv_layer-Blöcke aktiviert werden, um die Optimierung zu erleichtern, wenn die Kernel-Regression stark ist.

Damit fahren wir fort, indem wir den Vorhersagekopf definieren. Diese Stapelung ist offensichtlich von entscheidender Bedeutung, da sie einige Schlüsselkomponenten enthält. Erstens haben wir AdaptiveAvgPool1d(1), was eine längeninvariante globale Zusammenfassung pro Kanal ergibt. Dies ist wichtig, wenn der Input schwankt. Anders ausgedrückt: Es komprimiert die Zeitreihen mit variabler Länge der einzelnen Kanäle zu einem einzigen Durchschnittswert. Dies ergibt einen Zusammenfassungsvektor fester Größe. Dadurch wird die Ausgabe des Netzes unabhängig von der Länge der Eingangssequenz. Dies ist von entscheidender Bedeutung, wenn die Anzahl der Zeitschritte zwischen den Stichproben variiert.

Der MLP bildet eine Merkmalszusammenfassung auf eine skalare Ausgabe ab. Für die Regression im Bereich von 0,0 bis 1,0. Die Sigmoid-Aktivierung ist daher in diesem Fall pragmatisch, andernfalls kann ein Wechsel zu Identity für unbeschränkte Regressionsausgaben oder Log-Soft-Max für Mehrklassenausgaben in Betracht gezogen werden. Wenn es Bedenken hinsichtlich der Richtungsneutralität gibt, z. B. ob Kauf/Verkauf, dann könnte Sigmoid durch einen 2-Kopf ersetzt werden. Der erste Kopf kann eine Wahrscheinlichkeitsverteilung sein, wobei weiterhin Sigmoid verwendet wird. Der zweite Kopf kann sich auf die Größe konzentrieren, wobei dann die Aktivierung Soft Plus verwendet wird. Wenn auch die Erklärbarkeit eine Anforderung ist, kann der gepoolte Vektor offengelegt werden, um die Importe pro Kanal zu berechnen.

Danach definieren wir die Kernel-Regressionskernfunktion. Hier führen wir als erstes eine Permutation durch, die die Eingabedaten x in das Format batch-size, channels-number, length-size transponiert. Damit sollte das Skalarprodukt auf Kanaleinbettungen an jeder Position wirken. Aus diesem Grund wird C, die Kanalnummer, zur inneren Dimension gemacht. Dann konstruieren wir eine nicht-lokale Affinitätsmatrix über alle Positionen hinweg mit einem Rechenaufwand in Höhe der Länge zum Quadrat. Dies ist die Matrix „sim“. Damit definieren wir dann unsere Gewichte, indem wir diese sim-Matrix mit der Quadratwurzel aus der Anzahl der Kanäle skalieren, um die Logits bei zunehmender Kanalgröße „brav“ zu halten. Die Softmax-Aktivierung wandelt rohe Ähnlichkeiten in ein Wahrscheinlichkeitssimplex um. Jede Schichtreihe wird zu einer konvexen Kombination aller Reihen. Im nächsten Schritt wird die Kernel-Regression durchgeführt, bei der wir diese Gewichte mit dem transponierten/permutierten Eingangsvektor x multiplizieren. Die Ebenenzeilen/Positionen leihen sich dann Informationen von ähnlichen Positionen im gesamten Fenster.

Als Orientierungshilfe verwenden lange Sequenzen: lokale Fenster oder blockdiagonale Aufmerksamkeit; sie implementieren Manöver mit niedrigem Rang wie Nystrom oder Linformer; und sie führen eine Kernelregression durch und nehmen dann ein Upsample vor. Bei Prognosen oder beiläufigen Aufgaben kann das Hinzufügen einer beiläufigen Maskierung vor der Softmax-Aktivierung ein Datenleck oder einen Blick in die Zukunft verhindern. Wenn eine Überglättung festzustellen ist, kann ein Temperatur-Hyperparameter wie folgt eingeführt werden:

weights = F.softmax(sim / (tau * x_.size(-1) ** 0.5), dim=-1)

x = x + alpha * self._dot_product_kernel_regression(x)

Unsere nächste Funktion dient der Definition/Generierung der „Modellarchitektur“. Diese Funktion bietet wiederholt eine Multiskalenabdeckung im Bereich von 3 bis 9, sodass jede Stufe auf den globalen Kontext der Kernelregression reagieren kann. Lineares Kanalwachstum erhöht die Kapazität in den tieferen Bereichen des Netzes, wo die Merkmale abstrakter sind. Es empfiehlt sich, den Zyklus auf die gemessene Ähnlichkeitsbreite abzustimmen, wobei eine größere Ähnlichkeit zu einer stärkeren Ausrichtung auf größere Kerne in Übereinstimmung mit den Schichten führt. Kanäle sollten auch nicht blind wachsen, sondern es muss eine Überwachung der Aktivierungsparität oder der Kernel-Regressions-Entropie erfolgen, damit sie bei Bedarf entsprechend zugeordnet werden können.

Die letzte Funktion in unserer Netzwerkklasse ist die Funktion des Vorwärtsdurchlaufs. Hier beginnen wir mit der anfänglichen Hinzufügung einer Dimension, um das erwartete Stapel-Kanallängen-Format zu erzwingen. Bei CNNs mit 1-Dim ist der Kanal zunächst 1.  Der Wechsel zwischen lokaler Faltung und globaler Kernelregression liefert ein leistungsfähiges Muster. Die Erkennung lokaler Motive führt zur Weitergabe von Informationen entsprechend der erlernten Ähnlichkeit. Anschließend erfolgt eine lokale Verfeinerung der nächsten Faltungen. Die Rückgabe von self.head() hilft, den Vorwärtsgraphen für den ONNX-Export und die Bereitstellung sauber zu halten.

Wenn ein stärkerer Gradientenfluss erforderlich ist, können die Schichtnormen um die Kernelregression oder die Residuen ergänzt werden.

Indikator Übersetzung

Um die Signalmuster der letzten beiden Artikel als Input für unser oben beschriebenes CNN-Kernel-Regressionsmodell zu verwenden, benötigen wir ein Indikator-Äquivalent in Python. Es gibt zwar einige Standardimplementierungen von Indikatormodulen in Python, aber die Programmierung eines eigenen Moduls von Grund auf ist genauso mühelos und bietet gleichzeitig einen guten Überblick über die bei der Berechnung der Indikatorwerte getroffenen Entscheidungen. Wie bereits in früheren Artikeln beschrieben, kodieren wir die Indikatorwerte, die entweder steigen oder fallen, in einem 2-Dim-Vektor, der nur die Werte 0 oder 1 annehmen kann. Eine Kernelregression wäre hier hilfreich, da die erfassten Merkmale strukturelle Balken-/Oszillatormuster kodieren. Positionen mit etwas Abstand, die „ähnlich aussehen“ oder skalarproduktähnliche Einbettungen, können sich gegenseitig verstärken. Mit der Kernelregression (KR) kann das Modell daher statistische Stärke über die Zeit hinweg ausleihen. Dies ist nützlich, wenn jedes Muster für sich genommen relativ selten oder schwach ist.

Auch die frühzeitige Entscheidung, wo KR angewendet werden soll, verbreitet primitive Motive. Die späte KR konsolidiert Motive der höheren Ebene. Es ist sinnvoll, beides auszuprobieren: eine flachere KR zu Beginn und eine kleinere Kanalgröße mit einer tieferen KR zu einem späteren Zeitpunkt, während ein größerer C/Kanal verwendet wird.

Der Gator-Oszillator

Diese Funktion erstellt die Alligator-Komponenten von Bill Williams anhand des geglätteten gleitenden Durchschnitts des Medianpreises und der Vorwärtsverschiebung der Kiefer/Zähne/Lippen. Dies wurde in den letzten Artikeln behandelt. Wir geben zwei Puffer für die Größe des Kiefers abzüglich der Zähne aus, die wir mit „gator_up“ bezeichnen, und einen negativen Wert für die Größe der Zähne MA abzüglich der Lippen. Wir fügen auch Farbzustände für das Ausdehnungs- und Zusammenziehungsverhalten hinzu. Das ist der Überblick über die Funktion, die wir wie folgt in Python implementieren:

def Gator_Oscillator(df: pd.DataFrame,
                     jaw_period: int = 13, jaw_shift: int = 8,
                     teeth_period: int = 8, teeth_shift: int = 5,
                     lips_period: int = 5, lips_shift: int = 3) -> pd.DataFrame:
    """
    Calculate the Bill Williams Gator Oscillator and append the columns to the input DataFrame.

    Adds color columns for each bar:
    - Gator_Up_Color: 'green' for increasing, 'red' for decreasing, else previous color.
    - Gator_Down_Color: 'green' for increasing (less negative), 'red' for decreasing (more negative), else previous color.

    Args:
        df (pd.DataFrame): DataFrame with 'high' and 'low' columns.
        jaw_period (int): Jaw period (default 13).
        jaw_shift (int): Jaw shift (default 8).
        teeth_period (int): Teeth period (default 8).
        teeth_shift (int): Teeth shift (default 5).
        lips_period (int): Lips period (default 5).
        lips_shift (int): Lips shift (default 3).

    Returns:
        pd.DataFrame: Input DataFrame with 'Gator_Up', 'Gator_Down', 'Gator_Up_Color', 'Gator_Down_Color'.
    """
    required_cols = {'high', 'low'}
    if not required_cols.issubset(df.columns):
        raise ValueError("DataFrame must contain 'high' and 'low' columns")
    if not all(p > 0 for p in [jaw_period, jaw_shift, teeth_period, teeth_shift, lips_period, lips_shift]):
        raise ValueError("Period and shift values must be positive integers")

    result_df = df.copy()
    median_price = (result_df['high'] + result_df['low']) / 2

    def smma(series, period):
        smma_vals = []
        smma_prev = series.iloc[0]
        smma_vals.append(smma_prev)
        for price in series.iloc[1:]:
            smma_new = (smma_prev * (period - 1) + price) / period
            smma_vals.append(smma_new)
            smma_prev = smma_new
        return pd.Series(smma_vals, index=series.index)

    jaw = smma(median_price, jaw_period).shift(jaw_shift)
    teeth = smma(median_price, teeth_period).shift(teeth_shift)
    lips = smma(median_price, lips_period).shift(lips_shift)

    result_df['Gator_Up'] = (jaw - teeth).abs()
    result_df['Gator_Down'] = -(teeth - lips).abs()

    # Color logic
    up_vals = result_df['Gator_Up'].values
    down_vals = result_df['Gator_Down'].values

    up_colors = ['green']  # Start with green (or change to None/'grey' if you want)
    for i in range(1, len(up_vals)):
        if pd.isna(up_vals[i]) or pd.isna(up_vals[i-1]):
            up_colors.append(up_colors[-1])
        elif up_vals[i] > up_vals[i-1]:
            up_colors.append('green')
        elif up_vals[i] < up_vals[i-1]:
            up_colors.append('red')
        else:
            up_colors.append(up_colors[-1])

    down_colors = ['green']  # Start with green for "less negative" (getting closer to zero is "increasing")
    for i in range(1, len(down_vals)):
        if pd.isna(down_vals[i]) or pd.isna(down_vals[i-1]):
            down_colors.append(down_colors[-1])
        elif down_vals[i] > down_vals[i-1]:
            down_colors.append('green')  # "less negative" = "up"
        elif down_vals[i] < down_vals[i-1]:
            down_colors.append('red')    # "more negative" = "down"
        else:
            down_colors.append(down_colors[-1])

    result_df['Gator_Up_Color'] = up_colors
    result_df['Gator_Down_Color'] = down_colors

    return result_df

Wenn wir uns den Code Zeile für Zeile ansehen, schützen wir unsere Funktion als Erstes vor missgebildeten Eingaben und unsinnigen Hyperparametern. Die Verschiebungswerte sollten positiv sein, da die Alligatorlinien absichtlich nach vorne verschoben werden. Sie sollen den Preis visuell „anführen“. Wir erhalten dann eine Arbeitskopie des Eingabedatenrahmens sowie einen Puffer/Vektor des Medianpreises. Dadurch bleiben die ursprünglichen Eingabedaten intakt, und der Medianpreis reduziert das Rauschen im Vergleich zu reinen Schlusskursen. Dies entspricht im Allgemeinen der üblichen Praxis von Alligator.

Damit haben wir unsere Implementierung des geglätteten gleitenden Durchschnitts definiert. Der SMMA ist ein rekursiver Glätter, der langsamer reagiert als ein normaler EMA und sich daher für die Filterung unruhiger Zeitreihen eignet. Durch das Seeding des ersten Wertes mit series.iloc[0] wird ein großes Aufwärmfenster vermieden. Danach legen wir die Alligator-Linien sowie die Vorwärtsverschiebung fest. Die Zeiträume für diese nehmen vom Kiefer über die Zähne bis zu den Lippen ab. Alle werden nach vorne verschoben, sodass sich der „Mund“ vor einem aktuellen Takt öffnet oder schließt.

Danach können wir die beiden Ziel-Ausgangsdatenpuffer von gator_up und gator_down definieren. Diese messen den absoluten Wert, d. h. sie messen, wie breit die Alligatorbacken sind. Die Kennzeichnung der Balken als positiv und negativ ist eine Darstellungskonvention. Schließlich implementieren wir die Farbcodierungslogik, bei der der Schwerpunkt auf dem Trend der Streuung liegt, d. h. ob sie sich ausweitet oder verengt. Ein Abwärtsbalken wird unter Null gezeichnet, seine Werte sind also negativ. Wenn sich der Balken nach oben bewegt, bedeutet das nicht, dass er positiv geworden ist, sondern dass er nur weniger negativ geworden ist. Die Behandlung von NaN behält frühere Zustände bei, um Flackern bei unruhigen Starts zu vermeiden.

Der AD-Oszillator

Der Zweck dieses Oszillators besteht darin, die Akkumulations-/Distributionslinie aus dem Produkt von Geldflussmultiplikator und Volumen zu berechnen. Er versucht, den Kauf- bzw. Verkaufsdruck über die Spanne des Schlusskurses zu erfassen, die durch das Volumen oder das Tick-Volumen skaliert wird. Wir implementieren dies in Python wie folgt:

def AD_Oscillator(df: pd.DataFrame, fast_period: int = 5, slow_period: int = 13) -> pd.DataFrame:
    """
    Calculate the Accumulation/Distribution Oscillator (A/D Oscillator) and append it to the input DataFrame.

    A/D Oscillator = EMA(ADL, fast_period) - EMA(ADL, slow_period)

    ADL (Accumulation/Distribution Line) is calculated as:
    Money Flow Multiplier = [(Close - Low) - (High - Close)] / (High - Low)
    Money Flow Volume = Money Flow Multiplier * Volume
    ADL = cumulative sum of Money Flow Volume

    Args:
        df (pd.DataFrame): DataFrame with 'high', 'low', 'close', 'volume' columns.
        fast_period (int): Fast EMA period (default 3).
        slow_period (int): Slow EMA period (default 10).

    Returns:
        pd.DataFrame: Input DataFrame with 'ADL' and 'AD_Oscillator' columns added.
    """
    required_cols = {'high', 'low', 'close', 'tick_volume'}
    if not required_cols.issubset(df.columns):
        raise ValueError("DataFrame must contain 'high', 'low', 'close', 'tick_volume' columns")
    if not all(p > 0 for p in [fast_period, slow_period]):
        raise ValueError("Period values must be positive integers")
    if fast_period >= slow_period:
        raise ValueError("fast_period must be less than slow_period")

    result_df = df.copy()
    high = result_df['high']
    low = result_df['low']
    close = result_df['close']
    volume = result_df['tick_volume']

    # Avoid divide by zero, replace zero ranges with np.nan
    range_ = high - low
    range_ = range_.replace(0, pd.NA)

    mfm = ((close - low) - (high - close)) / range_
    mfv = mfm * volume
    result_df['ADL'] = mfv.cumsum()

    fast_ema = result_df['ADL'].ewm(span=fast_period, adjust=False).mean()
    slow_ema = result_df['ADL'].ewm(span=slow_period, adjust=False).mean()
    result_df['AD_Oscillator'] = fast_ema - slow_ema

    return result_df

Wenn wir so vorgehen, wie wir es oben mit dem Gator getan haben, beginnen unsere ersten Codezeilen mit der Überprüfung, ob alle vier Felder für Preis und Volumen im Eingabedatenrahmen vorhanden sind. Da wir, wie schon in früheren Artikeln, Forex-Paare testen, ist unser Volumen auf das Tick-Volumen und nicht auf das reale Volumen festgelegt, aus Gründen, die bereits in früheren Artikeln erwähnt wurden. Danach stellen wir sicher, dass es sich um einen „echten Oszillator“ handelt, d. h. die langsame Periode muss größer sein als die schnelle Periode. Anschließend werden die Spaltendaten für den Bereich extrahiert, wobei eine Division durch Null vermieden werden muss. Wenn der Höchststand dem Tiefststand entspricht, wie z. B. bei Doji-Balken oder außerbörslichen Kursen, wäre die Spanne gleich Null, was zu explodierenden Multiplikatoren führen könnte. 

Anschließend berechnen wir den Geldflussmultiplikator und das Volumen. Der Multiplikator ist an einen bestimmten Bereich gebunden, wobei die hohen Werte näher bei +1 und die niedrigen Werte bei -1 liegen. Wir bezeichnen diesen Puffer als mfm, wobei mfv sein volumengewichtetes Äquivalent ist. Die Cumsum-Funktion integriert diesen Volumendruck über die Zeit, und dies führt zur A/D-Linie. Anschließend berechnen wir die schnellen und langsamen EMA-Puffer unseres A/D-Zeilenpuffers. Wenn der Parameter adjust auf false gesetzt ist, ergibt sich ein rekursiver Standard-EMA, wie ihn die meisten Händler erwarten. Die Differenz zwischen diesen Puffern verstärkt die signalpositiven Werte, was darauf hinweist, dass die jüngste Akkumulation den längeren Trend übertreffen könnte.

Die ausgewählten Signalmuster

Jede Funktion für die Muster, die wir betrachten: 0, 3 und 4 gibt ein NumPy-Array der Form length-of-input-data-frame von 2 zurück. Wie bereits in früheren Artikeln beschrieben, kodiert [:, 0] ein Kauf- oder Aufwärtssignal, nachdem wir die im letzten Artikel definierten Indikatorwerte überprüft haben. Eine 1 wird protokolliert, wenn das ein Aufwärtsmuster ist, andernfalls erhalten wir eine 0. In der Zwischenzeit kodiert [:, 1] ein Verkaufs- oder Abwärtssignal, wobei wir wiederum eine 1 erhalten, wenn das Muster vorhanden ist, oder eine 0, wenn kein Short registriert wird. Alle drei Signalmuster kombinieren: die Gator-Farben, wie sie im Gator-Oszillator-Indikator für die Aufwärts- und Abwärtsfarben eingestellt sind; Preisaktionseinschränkungen durch Vergleiche mit Hoch-/Tief-/Schlusskursen mit der Shift-Funktion; und schließlich Momentum/Volumendruck über den AD-Oszillator ebenfalls mit Shift-Vergleichen. Sie schließen auch alle damit ab, dass die ersten Zeilen, je nach Vergleichsstrecke, mit Null bewertet werden, um falsch positive Ergebnisse zu vermeiden.

Feature_0

Wie im vorletzten Artikel, in dem wir dieses Signalmuster vorgestellt haben, handelt es sich um die Gator-Divergenz plus einen Ausbruch mit bestätigendem AD. Unsere Python-Implementierung dieser Funktion sah folgendermaßen aus:

def feature_0(df):
    """
//+------------------------------------------------------------------+
//| Check for Pattern 0.                                             |
//+------------------------------------------------------------------+

    """
    feature = np.zeros((len(df), 2))
    
    cond_1 = df['Gator_Up_Color'] == 'red'
    cond_2 = df['Gator_Down_Color'] == 'green'

    feature[:, 0] = (cond_1 &
                     cond_2 &
                     (df['high'].shift(2) > df['high'].shift(3)) &
                     (df['high'].shift(1) >= df['high'].shift(2)) &
                     (df['close'] > df['high'].shift(1)) &
                     (df['AD_Oscillator'].shift(1) > df['AD_Oscillator'].shift(2)) &
                     (df['AD_Oscillator'] <= df['AD_Oscillator'].shift(1))).astype(int)
    
    feature[:, 1] = (cond_1 &
                     cond_2 &
                     (df['low'].shift(2) < df['low'].shift(3)) &
                     (df['low'].shift(1) <= df['low'].shift(2)) &
                     (df['close'] < df['low'].shift(1)) &
                     (df['AD_Oscillator'].shift(1) < df['AD_Oscillator'].shift(2)) &
                     (df['AD_Oscillator'] >= df['AD_Oscillator'].shift(1))).astype(int)
    
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

In unserem obigen Listing erstellen wir eine zweispaltige binäre Matrix für Kauf- und Verkaufs-Flags. Im Anschluss daran definieren wir den Core-Gator-Farbfilter. Wir verlangen im Wesentlichen, dass „oben“ kontrahierend und daher rot und „unten“ expansiv und grün ist. In gleicher Weise gehen wir dann dazu über, die Regeln für die Kaufseite der Spalte 0 formal zu definieren. Hier kodieren wir den Alligator-Zustand, wobei wir auf den vordefinierten Bedingungen aufbauen, die durch die Farbzustände festgelegt wurden, um das Regime festzulegen. Für die Kaufbedingung werden auch die Hochs überprüft, um sicherzustellen, dass ein Aufbau stattfindet, und dies wird mit einer Ausbruchsbestätigung durch das Momentum verbunden, die durch einen Anstieg des AD gekennzeichnet ist. Alle diese Indikatoren sind entscheidend für die Bestätigung einer Aufwärtsbewegung, da wir ein Regime + Aufbau + Ausbruch + kontrolliertes Momentum anstreben. Ein strukturiertes, schwaches, aber anhaltendes Signal.

Auf der Verkaufsseite spiegeln wir die obige Logik für einen Ausbruch nach unten mit einer sich verlangsamenden Ausschüttung nach einem Abwärtsschub wider. Wir schließen diese Funktion ab, indem wir falsch-positive Werte verhindern, indem wir die Werte, die durch die Verschiebung verursacht werden und denen keine Werte zugewiesen werden, alle auf 0 setzen. Der Test auf genau dieses Muster in einem mit einem Assistenten zusammengestellten Expert Advisor nach dem Export des Netzwerks, das diese Ausgaben über ONNX verarbeitet, liefert uns den folgenden Bericht:

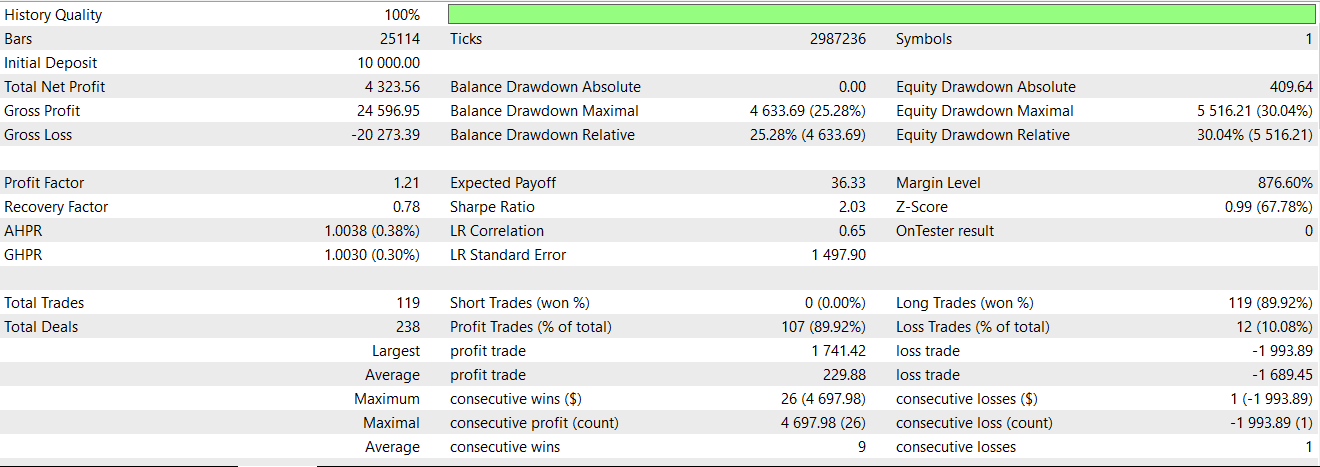
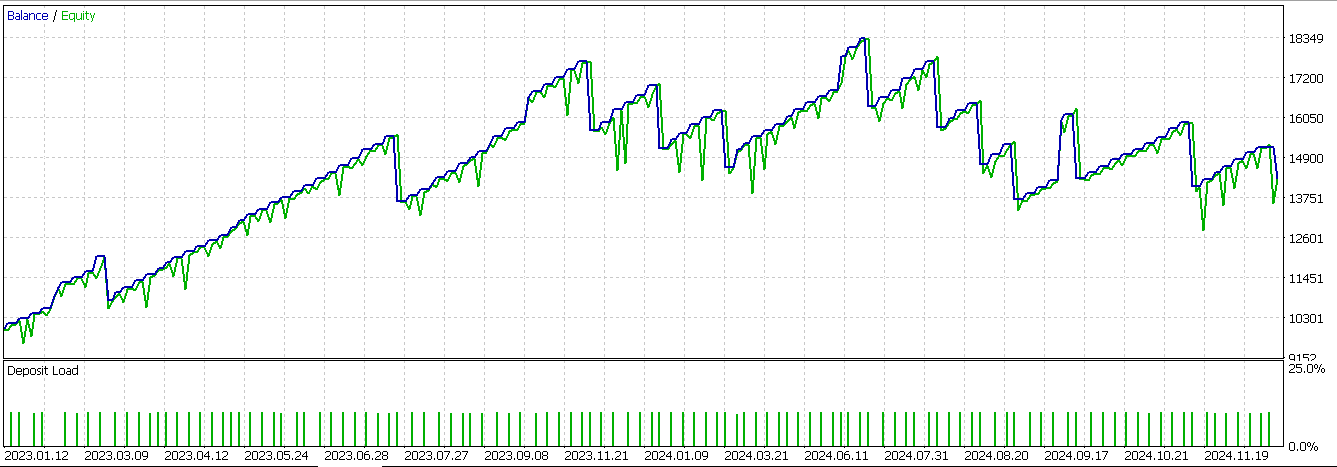
Obwohl es eine Menge profitabler Handelsgeschäfte gibt, scheint es, dass dieses Signal immer noch nicht profitabel für das Jahr 2024 läuft.

Feature_3

Das zweite Signalmuster basiert auf einer Kontraktion bis hin zur Expansion mit einem Schub innerhalb des Balkens. Wir implementieren dies in Python wie folgt:

def feature_3(df):
    """
//+------------------------------------------------------------------+
//| Check for Pattern 3.                                             |
//+------------------------------------------------------------------+
    """
    feature = np.zeros((len(df), 2))
    
    cond_1 = df['Gator_Up_Color'].shift(1) == 'red'
    cond_2 = df['Gator_Down_Color'].shift(1) == 'red'
    cond_3 = df['Gator_Up_Color'] == 'red'
    cond_4 = df['Gator_Down_Color'] == 'green'
    
    feature[:, 0] = (cond_1 &
                     cond_2 &
                     cond_3 &
                     cond_4 &
                     (df['close']-df['low'].shift(1) > 0.5*(df['high'].shift(1)-df['low'].shift(1))) &
                     (df['AD_Oscillator'].shift(2) > df['AD_Oscillator']) &
                     (df['AD_Oscillator'] > df['AD_Oscillator'].shift(1))).astype(int)
    
    feature[:, 1] = (cond_1 &
                     cond_2 &
                     cond_3 &
                     cond_4 &
                     (df['high'].shift(1)-df['close'] < 0.5*(df['high'].shift(1)-df['low'].shift(1))) &
                     (df['AD_Oscillator'].shift(2) < df['AD_Oscillator']) &
                     (df['AD_Oscillator'] < df['AD_Oscillator'].shift(1))).astype(int)
    
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

Grundlegende Bedingungen sind hier vorherige Gator-Histogrammbalken, die sowohl nach oben als auch nach unten rot anzeigen und von denen dann einer zu grün wechselt, als Zeichen eines Übergangs, wie im vorletzten Artikel beschrieben. Ein Großteil dieser Musterbeschreibungen wurde in diesem Artikel behandelt, sodass wir zu unserem Testbericht desselben Musters übergehen, wenn es durch unser neuronales Netzwerk als Filter angewendet wird. Wir erhalten den folgenden Bericht:

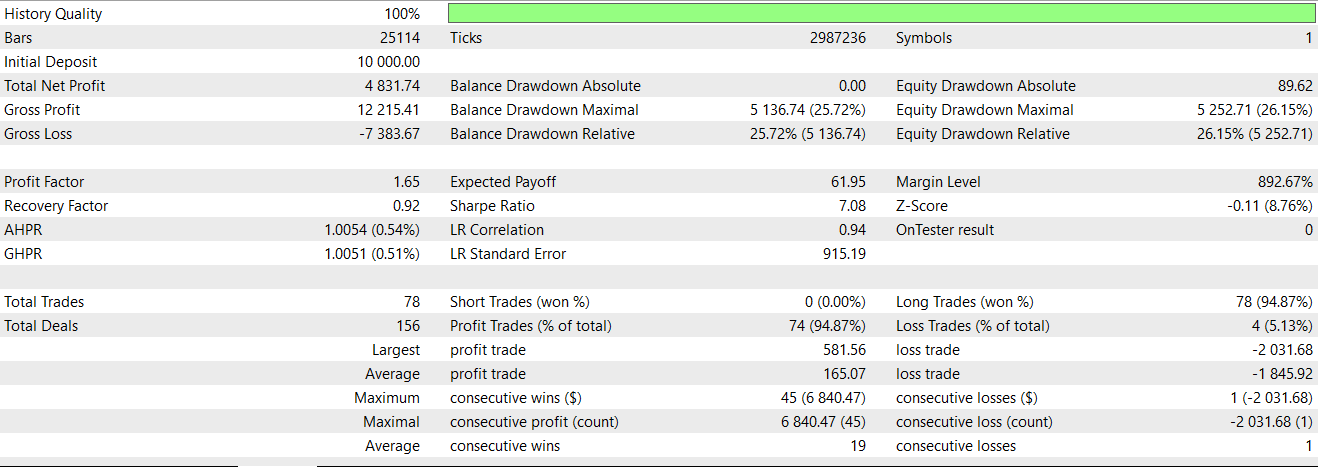
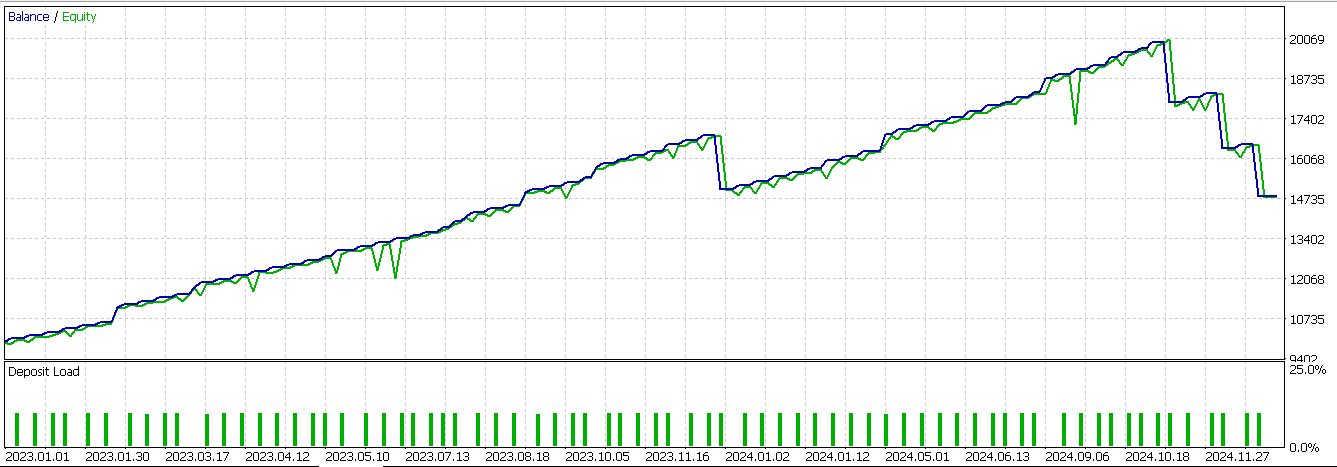
Wir waren fast in der Lage, bis zur letzten Reihe von unrentablen Handelsgeschäften den Vorwärtstest zu bestehen. Unsere Systeme verwenden immer Take-Profits ohne Stop-Loss, sodass dies die Schuld ist, da wir uns immer auf eine Signalumkehr verlassen, um unprofitable Handelsgeschäfte zu schließen.

Feature_4

Das letzte von uns untersuchte Signalmuster ist eine Fortsetzung des Color-Flip mit einer einfachen Momentum-Bestätigung. Wenn der vorangegangene Balken einen Aufwärtstrend aufwies und das obere Histogramm grün und das untere rot war und bei den nachfolgenden Balken das obere Histogramm rot für eine Kontraktion anzeigt, während das untere grün ist, könnte dies möglicherweise einen Regimewechsel im Gator-Oszillator anzeigen. Wie bereits in den vorangegangenen Beiträgen erwähnt, werden auch die Preisrückweisung und die AD-Momentum-Prüfung angewandt, und die Codierung dieses Signals in Python sieht folgendermaßen aus:

def feature_4(df):
    """
//+------------------------------------------------------------------+
//| Check for Pattern 4.                                             |
//+------------------------------------------------------------------+
    """
    feature = np.zeros((len(df), 2))
    
    cond_1 = df['Gator_Up_Color'].shift(1) == 'green'
    cond_2 = df['Gator_Down_Color'].shift(1) == 'red'
    cond_3 = df['Gator_Up_Color'] == 'red'
    cond_4 = df['Gator_Down_Color'] == 'green'
    
    feature[:, 0] = (cond_1 &
                     cond_2 &
                     cond_3 &
                     cond_4 &
                     (df['close'] > df['close'].shift(1)) &
                     (df['low'].shift(1) > df['low']) &
                     (df['AD_Oscillator'] > df['AD_Oscillator'].shift(1))).astype(int)
    
    feature[:, 1] = (cond_1 &
                     cond_2 &
                     cond_3 &
                     cond_4 &
                     (df['close'] < df['close'].shift(1)) &
                     (df['high'].shift(1) < df['high']) &
                     (df['AD_Oscillator'] < df['AD_Oscillator'].shift(1))).astype(int)
    
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

Beim Testen dieses Signals mit unserem neuronalen Netzwerk, das im Wesentlichen als zusätzlicher Filter für den Expert Advisor dient, den wir bereits in den letzten Artikeln eingesetzt haben, erhalten wir den folgenden Bericht:

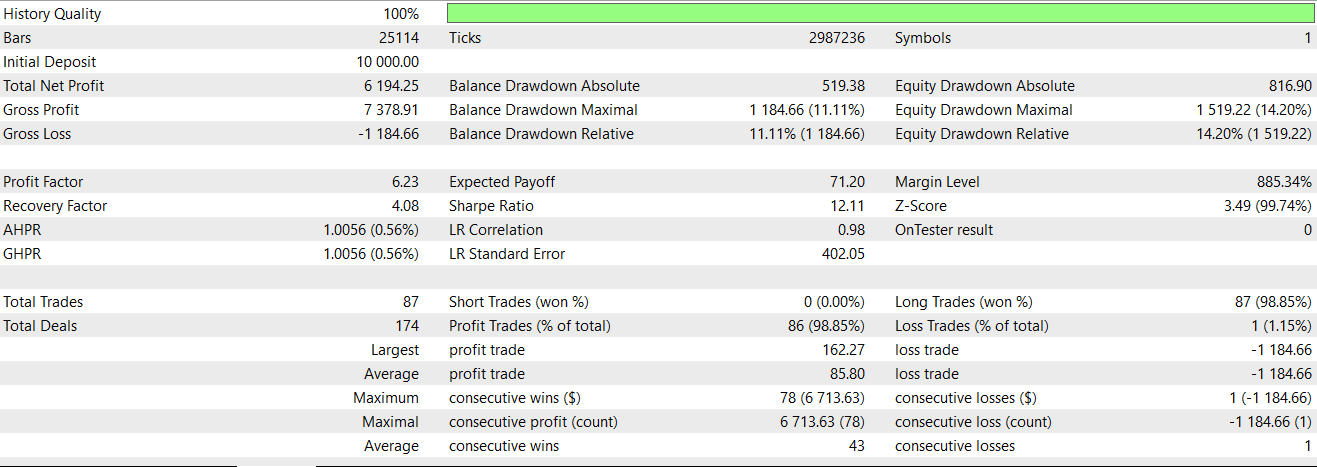
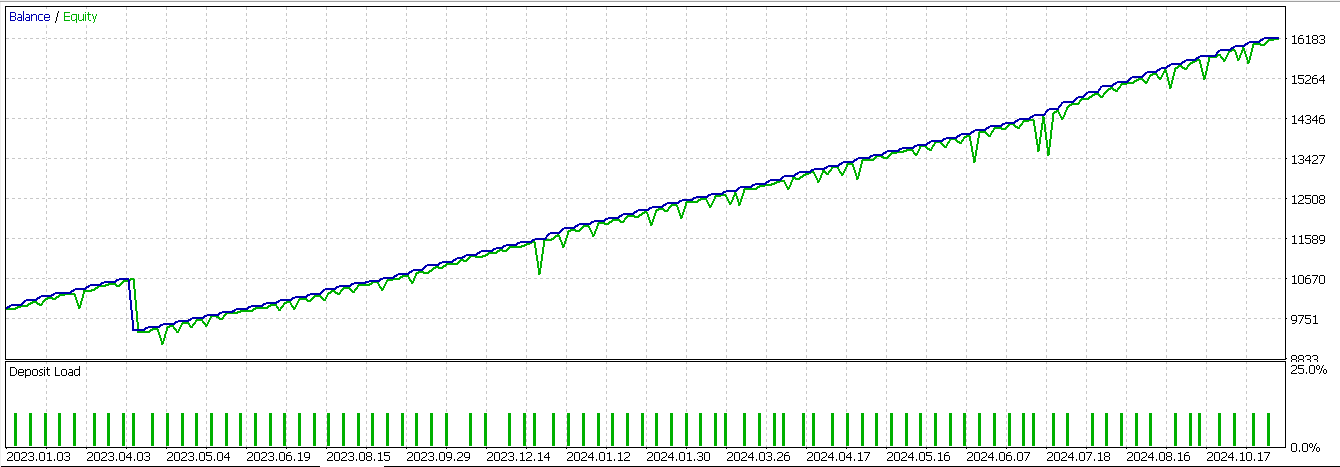
Von den drei Signalen, die wir in diesem Artikel untersucht haben, ist dies das einzige, bei dem sich die Entwicklung gegenüber dem ersten Test eindeutig umkehrt. Auch hier ist unser Testfenster auf zwei Jahre begrenzt, sodass von jedem, der dieses Signal weiterentwickeln möchte, unabhängige Sorgfalt erwartet wird. Ein Verkaufssignal für Feature_4 kann auf einem Preis-Chart wie folgt aussehen:

Schlussfolgerung

Modelle des maschinellen Lernens mit überwachtem Lernen wie das CNN, das wir für diesen Artikel betrachtet haben, zeigen, wenn sie durch die Kernelregression und die Skalarproduktähnlichkeit verbessert werden, ein gewisses Versprechen bei der Stärkung schwacher Signalmuster. Zwar konnten nicht alle von uns getesteten Muster in gleichem Maße profitieren, aber das Muster, das dies tat, Feature-4, zeichnete sich durch einen deutlichen Umschwung aus. Dies könnte diesen Ansatz als geeigneten Filter in Expert Advisors bestätigen. Dennoch schränkt der begrenzte Testhorizont die Schlussfolgerungen ein, die gezogen werden können, auch wenn die Methode deutlich macht, dass adaptive Architekturen aus Signalen mit unzuverlässiger Historie Wert schöpfen können.

Name	Beschreibung
WZ-79.mq5	Der Assistent hat einen Expert Advisor zusammengestellt, dessen Kopfzeile die verwendeten Dateien angibt. Eine Assistenten-Anleitung finden Sie hier.
SignalWZ-79.mqh	Signalklassendatei im Assistenten verwendet Assembly
79_0.onnx	Das exportierte neuronale Netz von Signal Pattern-0
79_3.onnx	Das exportierte neuronale Netz von Signal Pattern-3
79_4.onnx	Das exportierte Netz von Signalmuster-4.