Redes neuronales en el trading: Enfoque sin máscara para la predicción del movimiento de precios

MetaTrader 5 — Sistemas comerciales | 14 mayo 2025, 07:05

120

Dmitriy Gizlyk

Introducción

Continuamos nuestro estudio con el método de procesamiento de nubes de puntos. En el artículo anterior aprendimos sobre el SPFormer. Sus autores desarrollaron un algoritmo completo basado en la arquitectura Transformer. Varias capas del descodificador del Transformer utilizan un número fijo de consultas de objetos, lo que permite el procesamiento iterativo de funciones globales y la muestra directa de predicciones de objetos. El SPFormer no requiere procesamiento posterior para eliminar duplicados, ya que utiliza la correspondencia bidireccional uno a uno durante el entrenamiento. En este caso, las máscaras de objeto definidas en la última capa se usan para guiar la atención cruzada.

Sin embargo, los autores del artículo "Mask-Attention-Free Transformer for 3D Instance Segmentation" señalan que los métodos actuales basados en el Transformer sufren un problema de lentitud de convergencia. Durante el análisis del método básico, descubrieron que el problema podía deberse a unas máscaras de fuente bajas. En concreto, las máscaras de objetos iniciales se crean mediante la asignación de similitudes entre las consultas de objetos iniciales y las funciones de máscara punto por punto. Las máscaras de instancia iniciales de mala calidad aumentan la complejidad del entrenamiento, lo cual ralentiza la convergencia.

Dada la escasa exhaustividad de las máscaras originales, los autores del artículo anterior proponen un nuevo algoritmo Mask-Attention-Free Transformer (MATF) que abandona el diseño de la máscara de atención y, en su lugar, construye una tarea de regresión central auxiliar para controlar la atención cruzada. Para garantizar la regresión del centro, se han desarrollado toda una serie de diseños considerando las posiciones de los puntos. En primer lugar, los autores del método añaden un conjunto de consultas posicionales entrenadas, cada una de las cuales denota la posición de la consulta de contenido correspondiente. Las posiciones de consulta están densamente distribuidas en el espacio de estudio, y los autores del método introducen la restricción de que cada consulta debe considerar su región local. Como resultado, las consultas pueden captar fácilmente los objetos de una escena con mayor capacidad de memoria, lo que resulta crucial para reducir la complejidad del entrenamiento y acelerar la convergencia.

Además, los autores del MAFT proponen una codificación contextual de la posición relativa para la atención cruzada. En comparación con la máscara de atención usada en trabajos anteriores, esta solución resulta más flexible, ya que los pesos de atención se ajustan según las posiciones relativas en lugar de usarse una máscara rígida. Las posiciones de consulta se actualizan de forma iterativa para lograr una representación más precisa.

Los resultados experimentales presentados en el artículo del autor muestran que el MAFT demuestra un rendimiento superior en varios conjuntos de datos.

1. El Algoritmo MATF

El algoritmo SPFormer es un proceso integral que permite que las consultas de objetos generen directamente predicciones de instancias. Mediante los decodificadores del Transformer, un número fijo de consultas de objetos añade información de objetos globales a la nube de puntos analizada. Además, el SPFormer utiliza máscaras de objetos para controlar la atención cruzada, de modo que las consultas solo deban tener en cuenta los rasgos enmascarados. Sin embargo, en las primeras fases del entrenamiento se usan máscaras de baja calidad. Y esto impide un alto rendimiento en las capas posteriores, lo cual aumenta la complejidad del proceso de aprendizaje del modelo.

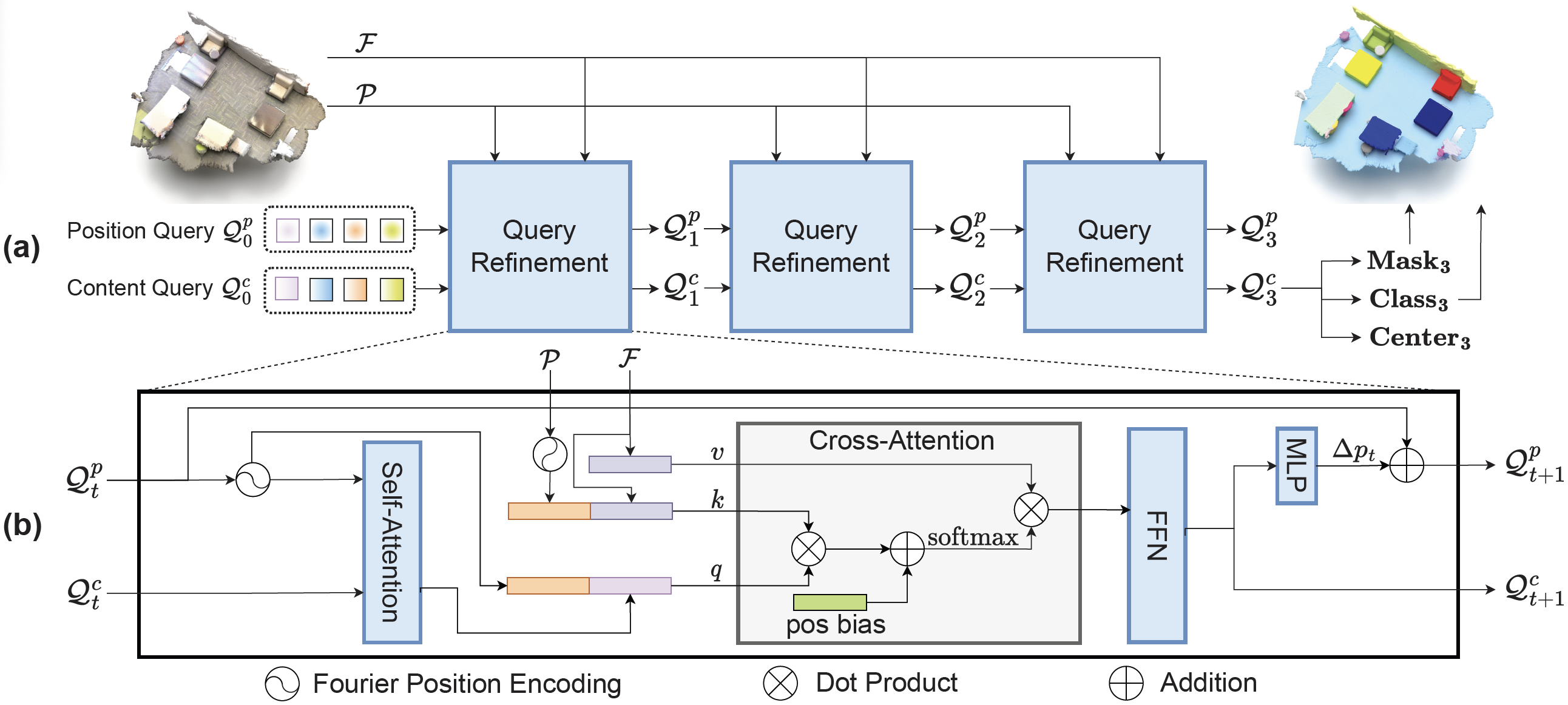
Por ello, los autores del método MAFT introducen un problema de regresión central auxiliar para controlar la segmentación de las instancias. En primer lugar, se seleccionan las posiciones globales 𝒫 de la nube de puntos original y se extraen las características globales de los objetos ℱ usando la línea troncal básica. Pueden ser vóxeles o Superpoints. Además de las solicitudes de contenido 𝒬0c, los autores del MAFT introducen un número fijo de consultas posicionales 𝒬0p que representan centros de objetos normalizados. 𝒬0p se inicializa de forma aleatoria, mientras que 𝒬0c se inicializa con valores cero. El objetivo principal consiste en permitir que las consultas posicionales guíen a las consultas contextuales correspondientes en la atención cruzada, para después refinar iterativamente ambos conjuntos de consultas y predecir los centros, las clases y las máscaras de los objetos.

Para resolver eficazmente el problema de la regresión del centro del objeto y mejorar la generación de sus máscaras iniciales, los autores del MAFT proponen una serie de construcciones que tienen en cuenta la posición de los puntos.

A diferencia de lo realizado en trabajos anteriores, aquí se introduce un conjunto adicional de consultas posicionales 𝒬0p. Como el rango de puntos varía considerablemente de una escena a otra, las consultas posicionales iniciales se almacenan de forma normalizada como parámetros entrenados seguidos de una función sigmoidal.

Cabe destacar que las consultas posicionales iniciales están densamente distribuidas por todo el espacio de estudio. Además, cada consulta añade objetos de su región local. Esta elección de diseño facilita las consultas iniciales para captar objetos en una escena con mucha memoria. Esto resuelve el problema de la baja capacidad de memoria causada por las máscaras de instancia iniciales y reduce la complejidad del entrenamiento de las capas posteriores.

Además de la codificación de la posición absoluta, el MAFT emplea la codificación contextual de la posición relativa en la atención cruzada. Para ello, se calculan primero las posiciones recíprocas 𝐫 entre las consultas posicionales 𝒬tp y las posiciones globales 𝒫 seguidas de la cuantificación a enteros discretos 𝐫'. A continuación, las posiciones recíprocas discretas se usan como índices para encontrar los valores correspondientes en la tabla de codificación de posiciones.

Además, la codificación de la posición relativa 𝐟pos se multiplica por la función Query 𝐟q o Key características 𝐟k en atención cruzada. A continuación, se añade a los pesos de atención cruzada seguida de la función SoftMax.

Cabe destacar que la codificación posicional relativa ofrece un mayor grado de flexibilidad e insensibilidad al error en comparación con la atención enmascarada. En esencia, la codificación posicional relativa puede compararse con una máscara suave que tiene la flexibilidad de ajustar los pesos de la atención en lugar de un enmascaramiento duro. Otra ventaja de la codificación posicional relativa es que integra información semántica y puede recoger selectivamente información local. Esto se logra mediante la interacción entre las posiciones relativas y las características semánticas.

Como las consultas contextuales en las capas del descodificador se actualizan periódicamente, no resultará óptimo mantener congeladas las consultas posicionales durante todo el proceso de descodificación. Además, las consultas posicionales iniciales son estáticas, por lo que en capas posteriores será útil adaptarlas a la escena inicial específica. Para ello, los autores del método refinan iterativamente las consultas posicionales basándose en las consultas de contenido. En concreto, usan un MLP para predecir el desplazamiento central Δpt a partir de la consulta contextual actualizada 𝒬t+1c. El desplazamiento resultante se añade entonces a la consulta posicional anterior 𝒬tp.

Ahora le presentamos la visualización del método MAFT realizada por el autor.

2. Implementación con MQL5

Tras repasar los aspectos teóricos del método Mask-Attention-Free Transformer, vamos a pasar a la parte práctica de nuestro artículo, donde implementaremos nuestra visión de los enfoques propuestos utilizando herramientas MQL5. Y empezaremos nuestro trabajo incorporando las novedades al programa OpenCL.

2.1 Complementamos el programa OpenCL

Comenzaremos nuestro trabajo construyendo un algoritmo de codificación de posición relativa. Por un lado, el algoritmo es bastante sencillo. Solo debemos encontrar la distancia entre los 2 puntos. En concreto, los autores del método calculan la distancia para cada coordenada individual. Por otra parte, los autores del MAFT cuantifican las desviaciones obtenidas, que luego se utilizan para encontrar valores en la tabla de parámetros entrenados. Hemos decidido optimizar un poco la solución propuesta. Y nuestra variante de aplicación se basará en el supuesto de que los puntos más próximos a la consulta analizada son los que tienen mayor impacto. Guiados por esta lógica, primero determinaremos la distancia S entre dos puntos en un espacio de N dimensiones. Y luego calcularemos el coeficiente de desplazamiento de posición kpb mediante la fórmula:

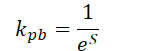
Obviamente, la distancia entre dos puntos siempre será al menos 0. Si los puntos coinciden, el coeficiente será igual a 1. A medida que aumente la distancia entre los puntos, el coeficiente de codificación de la posición relativa tenderá a 0.

La implementación del algoritmo propuesto se da en el kernel CalcPositionBias. En los parámetros del kernel transmitiremos los punteros a 3 búferes de datos globales, 2 de los cuales contienen los datos de origen, mientras que el tercero será para registrar los resultados. Aquí también añadiremos la dimensionalidad de un vector de descripción de un solo elemento.

Tenga en cuenta que para calcular las distancias entre 2 vectores, necesitaremos su proyección en el mismo subespacio. Y esto implicará que los vectores de descripción de elementos en ambos tensores de datos de origen tengan la misma dimensionalidad.

__kernel void CalcPositionBias(__global const float *data1,
                               __global const float *data2,
                               __global float *result,
                               const int dimension
                              )
  {
   const size_t idx1 = get_global_id(0);
   const size_t idx2 = get_global_id(1);
   const size_t total1 = get_global_size(0);
   const size_t total2 = get_global_size(1);

Planeamos ejecutar el kernel en un espacio de tareas bidimensional, cada uno igual al número de elementos del tensor correspondiente de los datos de origen. Y en el cuerpo del kernel, identificaremos directamente el flujo actual en ambas dimensiones del espacio de tareas.

En el siguiente paso, determinaremos el desplazamiento en los búferes de datos.

   const int shift1 = idx1 * dimension;
   const int shift2 = idx2 * dimension;
   const int shift_out = idx1 * total2 + idx2;

Una vez concluida la fase preparatoria, pasaremos a la ejecución propiamente dicha de los cálculos. Donde primero organizaremos un ciclo para calcular la distancia entre los vectores a analizar.

   float res = 0;
   for(int i = 0; i < dimension; i++)
      res = pow(data1[shift1 + i] - data2[shift2 + i], 2.0f);
   res = sqrt(res);

Y luego calcularemos el coeficiente de desplazamiento relativo.

   res = 1.0f / exp(res);
   if(isnan(res) || isinf(res))
      res = 0;
//---
   result[shift_out] = res;
  }

Y escribiremos el valor obtenido en el elemento correspondiente del búfer de resultados.

Obsérvese que no hay valores negativos entre los coeficientes obtenidos. Y esto significa que no estamos enmascarando ningún elemento de la secuencia de datos original. Por el contrario, la solución que utilizaremos pretende crear acentos en los elementos más cercanos.

En esta fase, hemos calculado los coeficientes de desplazamiento posicional relativo. Y ahora nos toca a nosotros aplicarlos en nuestro mecanismo de atención cruzada. Pero antes de poner en marcha el mecanismo propuesto, querría llamar su atención sobre un punto. Eche un vistazo a la visualización del método MAFT que el autor ha realizado más arriba. En particular, le pido que observe el flujo de información de representación de la escena. También aquí llama la atención el enfoque de los autores del método respecto a la codificación posicional de la representación de la escena. La cuestión es que la codificación posicional solo se aplica a la entidad Key. Mientras que Value permanece sin codificación posicional. Creo que se trata de una decisión consciente, para calcular las relaciones de dependencia teniendo en cuenta la codificación posicional, sin distorsionar al mismo tiempo las características de descripción de los objetos de la escena mediante la codificación posicional. De ello se deduce que, en este caso, tendremos que usar diferentes fuentes de datos para generar las entidades Key y Value. En otras palabras, primero deberemos generar un tensor Value a partir de la representación de datos de origen. A continuación, añadiremos la codificación posicional a los datos de origen. Y solo entonces podremos generar un tensor de entidades Key.

¿Por qué hemos elegido tratar este punto en esta fase de nuestro trabajo? El razonamiento presentado anteriormente conlleva la necesidad de separar las entidades Key y Value en tensores independientes. Y creando un nuevo kernel de algoritmos de atención podremos tener esto en cuenta. Esto, a su vez, nos permitirá excluir la operación de concatenación de dos tensores, a la que recurrimos anteriormente.

Para implementar el algoritmo de atención, crearemos el kernel MHPosBiasAttentionOut. En los parámetros del método transmitiremos una lista significativa de búferes de datos globales cuyos nombres ya nos resultan familiares de anteriores implementaciones de los métodos de atención. Aquí también transmitiremos el puntero al búfer del índice de desplazamiento posicional relativo pos_bias. Al hacerlo, hemos previsto el funcionamiento del algoritmo de atención clásico sin el uso de coeficientes de desplazamiento posicionales. La activación y desactivación de esta funcionalidad se ejecuta a través del parámetro use_pos_bias.

__kernel void MHPosBiasAttentionOut(__global const float *q,         ///<[in] Matrix of Querys
                                    __global const float *k,         ///<[in] Matrix of Keys
                                    __global const float *v,         ///<[in] Matrix of Values
                                    __global float *score,           ///<[out] Matrix of Scores
                                    __global const float *pos_bias,  ///<[in] Position Bias
                                    __global float *out,             ///<[out] Matrix of attention
                                    const int dimension,             ///< Dimension of Key
                                    const int heads_kv,
                                    const int use_pos_bias
                                   )
  {
//---
   const int q_id = get_global_id(0);
   const int k_id = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_global_size(1);
   const int heads = get_global_size(2);

Al igual que antes, planeamos trabajar con este kernel en un espacio de tareas tridimensional. Las dos primeras indicarán el número de elementos de las secuencias analizadas, mientras que la tercera dimensión del espacio de tareas indicará el número de cabezas de atención utilizadas. El algoritmo del kernel comenzará por identificar el flujo actual en las tres dimensiones del espacio de tareas.

A continuación, definiremos todas las constantes necesarias.

   const int h_kv = h % heads_kv;
   const int shift_q = dimension * (q_id * heads + h);
   const int shift_kv = dimension * (heads_kv * k_id + h_kv);
   const int shift_s = kunits * (q_id *  heads + h) + k_id;
   const int shift_pb = q_id * kunits + k_id;
   const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE);
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;

Y crearemos un array de datos en la memoria local para el intercambio de datos entre los flujos del grupo local.

   __local float temp[LOCAL_ARRAY_SIZE];

Con esto concluirá la fase de trabajos preparatorios y pasaremos directamente a los cálculos. El proceso de cálculo resultará muy parecido al del algoritmo clásico. Solo añadiremos puntualmente los coeficientes de desplazamiento posicional relativo. En este caso controlaremos la necesidad de su uso mediante el valor del parámetro use_pos_bias.

Primero calcularemos la suma de los exponenciales de los coeficientes de atención. En el primer paso, cada flujo del grupo local contará su parte. Y almacenará el valor obtenido en el elemento correspondiente del array de datos local.

//--- sum of exp
   uint count = 0;
   if(k_id < ls)
     {
      temp[k_id] = 0;
      do
        {
         if(q_id >= (count * ls + k_id))
            if((count * ls) < (kunits - k_id))
              {
               float sum = 0;
               int sh_k = dimension * heads_kv * count * ls;
               for(int d = 0; d < dimension; d++)
                  sum = q[shift_q + d] * k[shift_kv + d + sh_k];
               sum = exp(sum / koef);
               if(isnan(sum))
                  sum = 0;
               temp[k_id] = temp[k_id] + sum + (use_pos_bias > 0 ? pos_bias[shift_pb + count * ls] : 0);
              }
         count++;
        }
      while((count * ls + k_id) < kunits);
     }
   barrier(CLK_LOCAL_MEM_FENCE);

Tenga en cuenta que la suma que calculamos debe incluir la suma de los coeficientes de desplazamiento posicional.

A continuación, sumaremos el valor de los elementos del array local.

   count = min(ls, (uint)kunits);
//---
   do
     {
      count = (count + 1) / 2;
      if(k_id < ls)
         temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0);
      if(k_id + count < ls)
         temp[k_id + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Y después de calcular la suma total, determinaremos y almacenaremos los valores normalizados de los coeficientes de dependencia teniendo en cuenta los coeficientes de desplazamiento posicional.

//--- score
   float sum = temp[0];
   float sc = 0;
   if(q_id >= (count * ls + k_id))
      if(sum != 0)
        {
         for(int d = 0; d < dimension; d++)
            sc = q[shift_q + d] * k[shift_kv + d];
         sc = (exp(sc / koef) + (use_pos_bias > 0 ? pos_bias[shift_pb] : 0)) / sum;
         if(isnan(sc))
            sc = 0;
        }
   score[shift_s] = sc;
   barrier(CLK_LOCAL_MEM_FENCE);

Los coeficientes de atención obtenidos, entre tanto, nos permitirán calcular los valores finales de atención multicabeza para cada elemento de la secuencia analizada.

//--- out
   for(int d = 0; d < dimension; d++)
     {
      uint count = 0;
      if(k_id < ls)
         do
           {
            if((count * ls) < (kunits - k_id))
              {
               int sh_v = 2 * dimension * heads_kv * count * ls;
               float sum =
                  v[shift_kv + d + sh_v] * (count == 0 ? sc : score[shift_s + count * ls]);
               if(isnan(sum))
                  sum = 0;
               temp[k_id] = (count > 0 ? temp[k_id] : 0) + sum;
              }
            count++;
           }
         while((count * ls + k_id) < kunits);
      barrier(CLK_LOCAL_MEM_FENCE);
      //---
      count = min(ls, (uint)kunits);
      do
        {
         count = (count + 1) / 2;
         if(k_id < ls)
            temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0);
         if(k_id + count < ls)
            temp[k_id + count] = 0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      //---
      out[shift_q + d] = temp[0];
     }
  }

A continuación, tendremos que implementar el algoritmo de propagación inversa del error en el kernel MHPosBiasAttentionInsideGradients. Aquí conviene recordar que cuando distribuimos el gradiente de error a través de una suma, solemos pasar el error a ambos sumandos en su totalidad. Utilizar una tasa de aprendizaje muy inferior a 1 compensará con creces el impacto de la doble contabilización del error. El siguiente punto a considerar: se supone que el cálculo de los coeficientes de desplazamiento posicional relativo se basará en la ubicación real de los puntos en el espacio, que en realidad son los datos de entrada y serán independientes de los parámetros del modelo. El propio proceso de cálculo carece de parámetros entrenables. Por lo tanto, la transmisión del gradiente de error al tensor del coeficiente de desplazamiento posicional relativo no parece lógico. Así que descartaremos esta operación.

Dadas las consideraciones expuestas, lograremos un algoritmo clásico para distribuir el gradiente de error a través del bloque de atención. Sin embargo, crearemos un nuevo kernel porque estamos asignando búferes de datos separados para las entidades Key y valor anteriores. Le sugiero que lea por su cuenta el algoritmo del kernel de pasada inversa MHPosBiasAttentionInsideGradients en el archivo adjunto. Y aquí concluimos el trabajo con el programa OpenCL.

2.2 Creación de la clase MAFT

La siguiente etapa de nuestro trabajo consistirá en crear un nuevo objeto, en cuyo código implementamos nuestra visión de los planteamientos propuestos por los autores del método Mask-Attention-Free Transformer. Para ello, crearemos una nueva clase CNeuronMAFT.

Hay que decir que los autores del método MAFT construyeron su algoritmo sobre la base del anteriormente discutido SPFormer. Y en nuestro trabajo también usaremos los desarrollos de la clase CNeuronSPFormer. Sin embargo, la magnitud de los cambios anulará las ventajas de heredar de la clase especificada. Así que crearemos nuestro nuevo objeto heredando de la clase básica de la capa completamente conectada CNeuronBaseOCL. A continuación, le mostraremos la estructura de la nueva clase.

class CNeuronMAFT   : public CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iUnits;
   uint              iHeads;
   uint              iSPWindow;
   uint              iSPUnits;
   uint              iSPHeads;
   uint              iWindowKey;
   uint              iLayers;
   uint              iLayersSP;
   //---
   CLayer            cSuperPoints;
   CLayer            cQuery;
   CLayer            cQPosition;
   CLayer            cQKey;
   CLayer            cQValue;
   CLayer            cMHSelfAttentionOut;
   CLayer            cSelfAttentionOut;
   CLayer            cSPKey;
   CLayer            cSPValue;
   CArrayInt         cScores;
   CArrayInt         cPositionBias;
   CLayer            cMHCrossAttentionOut;
   CLayer            cCrossAttentionOut;
   CLayer            cResidual;
   CLayer            cFeedForward;
   CBufferFloat      cTempSP;
   CBufferFloat      cTempQ;
   CBufferFloat      cTempCrossK;
   CBufferFloat      cTempCrossV;
   //---
   virtual bool      CreateBuffers(void);
   virtual bool      CalcPositionBias(CBufferFloat *pos_q, CBufferFloat *pos_k, const int pos_bias,
                                      const int units,
                                      const int units_kv,
                                      const int dimension);
   virtual bool      AttentionOut(CNeuronBaseOCL *q, CNeuronBaseOCL *k, CNeuronBaseOCL *v,
                                  const int scores, CNeuronBaseOCL *out, const int pos_bias,
                                  const int units,
                                  const int heads,
                                  const int units_kv,
                                  const int heads_kv,
                                  const int dimension,
                                  const bool use_pos_bias);
   virtual bool      AttentionInsideGradients(CNeuronBaseOCL *q, CNeuronBaseOCL *k, CNeuronBaseOCL *v,
         const int scores, CNeuronBaseOCL *out,
         const int units, const int heads,
         const int units_kv, const int heads_kv,
         const int dimension);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMAFT(void) {};
                    ~CNeuronMAFT(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count, uint heads,
                          uint window_sp, uint units_sp, uint heads_sp,
                          uint layers, uint layers_to_sp,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMAFT; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

En la estructura presentada vemos el conjunto habitual de métodos virtuales redefinidos y un gran número de objetos internos. Algunos de los objetos internos coinciden con los que hemos usado antes, pero hay algunos nuevos. Nos familiarizaremos con la funcionalidad de todos los objetos internos durante la implementación de los métodos de la clase CNeuronMAFT.

Al igual que antes, todos los objetos internos se han declarado estáticamente, lo cual nos permite dejar vacíos el constructor y el destructor de la clase, mientras que la inicialización de todos los objetos heredados y declarados se realizará en el método de inicialización Init.

bool CNeuronMAFT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                       uint window, uint window_key, uint units_count,
                       uint heads, uint window_sp, uint units_sp, uint heads_sp,
                       uint layers, uint layers_to_sp,
                       ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

En los parámetros de este método obtendremos las constantes básicas que definen inequívocamente la arquitectura del objeto a crear. Aquí resulta sencillo notar que los parámetros de este método se han tomado al completo del método homónimo de la clase CNeuronSPFormer. Y esto resulta bastante coherente con nuestra herencia declarada de enfoques. Sin embargo, el algoritmo del método no ha cambiado sustancialmente.

En el cuerpo del método llamaremos primero al método homónimo de la clase padre, que realizará el control inicial de los parámetros recibidos y la inicialización de los objetos heredados. Después almacenaremos las constantes obtenidas en las variables internas de la clase.

   iWindow = window;
   iUnits = units_count;
   iHeads = heads;
   iSPUnits = units_sp;
   iSPWindow = window_sp;
   iSPHeads = heads_sp;
   iWindowKey = window_key;
   iLayers = MathMax(layers, 1);
   iLayersSP = MathMax(layers_to_sp, 1);

En el siguiente paso, inicializaremos los objetos para generar las consultas de los objetos entrenados y su codificación posicional. Los autores del método MAFT sugirieron inicializar las consultas con valores nulos. Y nosotros haremos lo mismo. Para ello, pondremos a cero los parámetros de generación de consultas.

   CNeuronBaseOCL *base = new CNeuronBaseOCL();
   if(!base)
      return false;
   if(!base.Init(iWindow * iUnits, 0, OpenCL, 1, optimization, iBatch))
      return false;
   CBufferFloat *buf = base.getOutput();
   if(!buf || !buf.BufferInit(1, 1) || !buf.BufferWrite())
      return false;
   buf = base.getWeights();
   if(!buf || !buf.BufferInit(buf.Total(), 0) ||
      !buf.BufferWrite())
      return false;
   if(!cQuery.Add(base))
      return false;
   base = new CNeuronBaseOCL();
   if(!base || !base.Init(0, 1, OpenCL, iWindow * iUnits, optimization, iBatch))
      return false;
   if(!cQuery.Add(base))
      return false;

Y luego añadiremos una codificación posicional entrenable inicializada con valores aleatorios.

   CNeuronLearnabledPE *pe = new CNeuronLearnabledPE();
   if(!pe || !pe.Init(0, 2, OpenCL, base.Neurons(), optimization, iBatch))
      return false;
   if(!cQuery.Add(pe))
      return false;

Hay que decir que la codificación de la posición se dará como un flujo de información aparte a través de todo el algoritmo MAFT. Por lo tanto, la destacaremos con objetos separados.

   if(!base || !base.Init(0, 3, OpenCL, pe.Neurons(), optimization, iBatch))
      return false;
   if(!base.SetOutput(pe.getOutput()))
      return false;
   if(!cQPosition.Add(base))
      return false;

El siguiente paso será el procesamiento inicial de los datos. Y aquí tomaremos prestado el enfoque de Superpoints introducido en el método SPFormer.

//--- Init SuperPoints
   int layer_id = 4;
   for(int r = 0; r < 4; r++)
     {
      if(iSPUnits % 2 == 0)
        {
         iSPUnits /= 2;
         CResidualConv *residual = new CResidualConv();
         if(!residual)
            return false;
         if(!residual.Init(0, layer_id, OpenCL, 2 * iSPWindow, iSPWindow, iSPUnits, optimization, iBatch))
            return false;
         if(!cSuperPoints.Add(residual))
            return false;
        }
      else
        {
         iSPUnits--;
         CNeuronConvOCL *conv = new CNeuronConvOCL();
         if(!conv.Init(0, layer_id, OpenCL, 2 * iSPWindow, iSPWindow, iSPWindow, iSPUnits, 1,
                                                                        optimization, iBatch))
            return false;
         if(!cSuperPoints.Add(conv))
            return false;
        }
      layer_id++;
     }

Aquí cabe señalar que en la implementación presentada se permite utilizar tensores de diferente dimensionalidad para la atención cruzada. Sin embargo, esto resultará inaceptable para el algoritmo de coeficiente de desplazamiento posicional relativo propuesto. Por lo tanto, añadiremos una capa de proyección de superpuntos al espacio de consultas entrenadas.

   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv.Init(0, layer_id, OpenCL, iSPWindow, iSPWindow, iWindow, iSPUnits, 1, optimization, iBatch))
      return false;
   if(!cSuperPoints.Add(conv))
      return false;
   layer_id++;

Y añadiremos una capa de codificación posicional.

   pe = new CNeuronLearnabledPE();
   if(!pe || !pe.Init(0, layer_id, OpenCL, conv.Neurons(), optimization, iBatch))
      return false;
   if(!cSuperPoints.Add(pe))
      return false;
   layer_id++;

Debemos decir que en este punto nos hemos apartado ligeramente del algoritmo propuesto por los autores del método MAFT. En su trabajo, estos emplearon la voxelización de la nube de puntos usando las coordenadas de origen. Nosotros, en cambio, utilizaremos una codificación posicional totalmente entrenable, lo cual permitirá al modelo aprender las posiciones óptimas de cada elemento de la secuencia de datos de origen.

Tras completar el procesamiento inicial de los datos de origen, organizaremos un ciclo para enumerar las capas internas del Descodificador.

//--- Inside layers
   for(uint l = 0; l < iLayers; l++)
     {
      //--- Self-Attention
      //--- Query
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, 
                                                                              optimization, iBatch))
         return false;
      if(!cQuery.Add(conv))
         return false;
      layer_id++;

Y aquí cabe señalar que los autores del MAFT utilizan un diseño clásico: Sefl-Attention -> Cross-Attention -> Feed Forward. Mientras que los autores del método SPFormer intercambiaron las posiciones de Self-Attention y Cross-Attention.

En primer lugar, generaremos las entidades Query. Y luego añadiremos Key y Value.

      //--- Key
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, 
                                                                              optimization, iBatch))
         return false;
      if(!cQKey.Add(conv))
         return false;
      layer_id++;
      //--- Value
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, 
                                                                               optimization, iBatch))
         return false;
      if(!cQValue.Add(conv))
         return false;
      layer_id++;

Para ello, esperamos utilizar un número reducido de consultas entrenadas. Por lo tanto, no reduciremos el número de cabezas para Key-Value y generaremos nuevas entidades en cada capa interna.

Luego transmitiremos las entidades generadas a la unidad de atención multicabeza sin utilizar coeficientes de desplazamiento posicional.

      //--- Multy-Heads Attention Out
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch))
         return false;
      if(!cMHSelfAttentionOut.Add(base))
         return false;
      layer_id++;

Y añadiremos una capa de escalado de los resultados de la atención multicabeza.

      //--- Self-Attention Out
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow,
                                                                     iUnits, 1, optimization, iBatch))
         return false;
      if(!cSelfAttentionOut.Add(conv))
         return false;
      layer_id++;

Y al final del bloque de Self-Attention, siguiendo el algoritmo clásico del Transformer, añadiremos una capa de enlaces residuales.

      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch))
         return false;
      if(!cResidual.Add(base))
         return false;
      layer_id++;

A continuación, colocaremos los objetos del bloque de atención cruzada. Y primero, como de costumbre, crearemos el tensor de entidades Query.

      //--- Cross-Attention
      //--- Query
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1,
                                                                              optimization, iBatch))
         return false;
      if(!cQuery.Add(conv))
         return false;
      layer_id++;

Y luego añadiremos los tensores de las entidades Key y Value. Esta vez nos guiaremos por las instrucciones del usuario para hacer disminuir las cabezas de atención y alternar las capas.

      if(l % iLayersSP == 0)
        {
         //--- Key
         conv = new CNeuronConvOCL();
         if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iSPUnits, 1,
                                                                                     optimization, iBatch))
            return false;
         if(!cSPKey.Add(conv))
            return false;
         layer_id++;
         //--- Value
         conv = new CNeuronConvOCL();
         if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iSPUnits, 1, 
                                                                                     optimization, iBatch))
            return false;
         if(!cSPValue.Add(conv))
            return false;
         layer_id++;
        }

Y añadiremos una capa de resultados de atención multicabeza.

      //--- Multy-Heads Attention Out
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch))
         return false;
      if(!cMHCrossAttentionOut.Add(base))
         return false;
      layer_id++;

Que luego se escalará con enlaces residuales añadidos posteriormente.

      //--- Cross-Attention Out
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow,
                                                                    iUnits, 1, optimization, iBatch))
         return false;
      if(!cCrossAttentionOut.Add(conv))
         return false;
      layer_id++;
      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch))
         return false;
      if(!cResidual.Add(base))
         return false;
      layer_id++;

Y el bloque FeedForward completará el Decodificador, al que también añadiremos enlaces residuales.

      //--- Feed Forward
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, 4 * iWindow, iUnits, 1, 
                                                                         optimization, iBatch))
         return false;
      conv.SetActivationFunction(LReLU);
      if(!cFeedForward.Add(conv))
         return false;
      layer_id++;
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, 1, 
                                                                         optimization, iBatch))
         return false;
      if(!cFeedForward.Add(conv))
         return false;
      layer_id++;
      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch))
         return false;
      if(!base.SetGradient(conv.getGradient()))
         return false;
      if(!cResidual.Add(base))
         return false;
      layer_id++;

Solo quedará añadir los ajustes del MLP a la codificación posicional de las consultas entrenadas.

      //--- Delta position
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch))
         return false;
      conv.SetActivationFunction(SIGMOID);
      if(!cQPosition.Add(conv))
         return false;
      layer_id++;
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, conv.Neurons(), optimization, iBatch))
         return false;
      if(!base.SetGradient(conv.getGradient()))
         return false;
      if(!cQPosition.Add(base))
         return false;
      layer_id++;
     }

Ahora pasaremos a la siguiente iteración del ciclo con la creación de objetos de la nueva capa interna del Decodificador.

Una vez inicializados correctamente los objetos de todas las capas internas del Decodificador, sustituiremos los punteros a los búferes de gradiente de error y retornaremos al programa que realiza la llamada el resultado lógico de las operaciones realizadas.

   base = cResidual[iLayers * 3 - 1];
   if(!SetGradient(base.getGradient()))
      return false;
//---
   SetOpenCL(OpenCL);
//---
   return true;
  }

Aquí debemos añadir que la inicialización de los búferes de datos auxiliares se realizará en un método aparte, CreateBuffers, con el que le sugiero que se familiarice por su cuenta.

Le recuerdo que encontrará el código completo de esta clase y todos sus métodos en el archivo adjunto.

Ahora, después de la inicialización de los objetos internos, procederemos a construir el algoritmo de pasada directa en el método feedForward. En los parámetros de este método, obtendremos el puntero al objeto de datos de origen.

bool CNeuronMAFT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- Superpoints
   CNeuronBaseOCL *superpoints = NeuronOCL;
   int total_sp = cSuperPoints.Total();
   for(int i = 0; i < total_sp; i++)
     {
      if(!cSuperPoints[i] ||
         !((CNeuronBaseOCL*)cSuperPoints[i]).FeedForward(superpoints))
         return false;
      superpoints = cSuperPoints[i];
     }

E inmediatamente utilizaremos el objeto obtenido durante la generación de las características de los superpuntos. Para ello, utilizaremos el modelo anidado cSuperPoints.

Aquí vale la pena recordar que especificaremos la capa de codificación posicional como la última capa de este modelo.

A continuación, generaremos consultas entrenables con codificación posicional.

//--- Query
   CNeuronBaseOCL *inputs = NULL;
   for(int i = 0; i < 2; i++)
     {
      inputs = cQuery[i + 1];
      if(!inputs ||
         !inputs.FeedForward(cQuery[i]))
         return false;
     }

Luego crearemos variables locales para almacenar temporalmente los punteros a los objetos.

   CNeuronBaseOCL *query = NULL, *key = NULL, *value = NULL, *base = NULL;

Y organizaremos el ciclo de iteración de las capas internas del Decodificador.

//--- Inside layers
   for(uint l = 0; l < iLayers; l++)
     {
      //--- Self-Atention
      query = cQuery[l * 2 + 3];
      if(!query || !query.FeedForward(inputs))
         return false;
      key = cQKey[l];
      if(!key || !key.FeedForward(inputs))
         return false;
      value = cQValue[l];
      if(!value || !value.FeedForward(inputs))
         return false;

En primer lugar, organizaremos el funcionamiento del bloque de Self-Attention un conjunto de consultas entrenables con codificación posicional. Para ello, primero generaremos las entidades necesarias, que transmitiremos a la unidad de atención multicabeza.

      if(!AttentionOut(query, key, value, cScores[l * 2], cMHSelfAttentionOut[l], -1, 
                                   iUnits, iHeads, iUnits, iHeads, iWindowKey, false))
         return false;

A continuación, escalaremos los resultados obtenidos y añadiremos los enlaces residuales.

      base = cSelfAttentionOut[l];
      if(!base || !base.FeedForward(cMHSelfAttentionOut[l]))
         return false;
      value = cResidual[l * 3];
      if(!value ||
         !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1))
         return false;
      inputs = value;

En otro flujo, añadiremos la codificación posicional.

      value = cQPosition[l * 2];
      if(!value ||
         !SumAndNormilize(inputs.getOutput(), value.getOutput(),inputs.getOutput(), iWindow, false, 0, 0, 0, 1))
         return false;

Después pasaremos al bloque de atención cruzada. Pero antes, determinaremos los coeficientes de desplazamiento posicional relativo.

      //--- Calc Position bias
      if(!CalcPositionBias(value.getOutput(),
                           ((CNeuronLearnabledPE*)superpoints).GetPE(), cPositionBias[l],
                           iUnits, iSPUnits, iWindow))
         return false;

Luego generaremos una entidad Query a partir del tensor de consultas posicionales dada la codificación posicional.

      //--- Cross-Attention
      query = cQuery[l * 2 + 4];
      if(!query || !query.FeedForward(inputs))
         return false;

Pero la organización de las entidades Key y Value está llena de matices. En primer lugar, la generación de nuevos tensores se realiza solo cuando es necesario.

      key = cSPKey[l / iLayersSP];
      value = cSPValue[l / iLayersSP];
      if(l % iLayersSP == 0)
        {
         if(!key || !key.FeedForward(superpoints))
            return false;
         if(!value || !value.FeedForward(cSuperPoints[total_sp - 2]))
            return false;
        }

Y en segundo lugar, Key se genera sobre los datos de la última capa cSuperPoints, que contiene codificación posicional. Pero para generar Value, utilizaremos la penúltima capa, que no tiene codificación posicional.

Las entidades resultantes las transmitiremos a la unidad de atención multicabeza, teniendo en cuenta los coeficientes relativos de desplazamiento posicional.

      if(!AttentionOut(query, key, value, cScores[l * 2 + 1], cMHCrossAttentionOut[l], cPositionBias[l], 
                                                  iUnits, iHeads, iSPUnits, iSPHeads, iWindowKey, true))
         return false;

Después escalaremos los datos obtenidos y añadiremos los enlaces residuales.

      base = cCrossAttentionOut[l];
      if(!base || !base.FeedForward(cMHCrossAttentionOut[l]))
         return false;
      value = cResidual[l * 3 + 1];
      if(!value ||
         !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1))
         return false;
      inputs = value;

Al final del Decodificador, pasaremos los datos a través del bloque FeedForward seguido de enlaces residuales.

      //--- Feed Forward
      base = cFeedForward[l * 2];
      if(!base || !base.FeedForward(inputs))
         return false;
      base = cFeedForward[l * 2 + 1];
      if(!base || !base.FeedForward(cFeedForward[l * 2]))
         return false;
      value = cResidual[l * 3 + 2];
      if(!value ||
         !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1))
         return false;
      inputs = value;

En este punto, ya hemos completado las operaciones de la capa Decodificadora, pero nos queda corregir los datos de codificación posicional de las consultas entrenadas. Para ello, generaremos una desviación posicional basada en los datos y la añadiremos a los valores existentes.

      //--- Delta Query position
      base = cQPosition[l * 2 + 1];
      if(!base ||
         !base.FeedForward(inputs))
         return false;
      value = cQPosition[(l + 1) * 2];
      query = cQPosition[l * 2];
      if(!value ||
         !SumAndNormilize(query.getOutput(), base.getOutput(), value.getOutput(), iWindow, false, 0,0,0,0.5f))
         return false;
     }

Y ahora podremos comenzar a realizar las operaciones de la siguiente capa interna del Decodificador.

Tras ejecutar con éxito las operaciones de todas las capas internas del Descodificador, obtendremos el resultado como consultas enriquecidas y sus posiciones refinadas. Luego sumaremos los 2 tensores obtenidos y los pasaremos a la cabeza de predicción.

   value = cQPosition[iLayers * 2];
   if(!value ||
      !SumAndNormilize(inputs.getOutput(), value.getOutput(), Output, iWindow, true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

Y retornaremos el resultado lógico de las operaciones al programa que realiza la llamada.

Con esto concluiremos nuestro trabajo sobre la construcción del algoritmo de pasada directa. Y tenemos más trabajo que hacer para construir algoritmos de pasada inversa, que se implementará en los métodos calcInputGradients y updateInputWeights. El primero organizará el algoritmo para distribuir los gradientes de error entre todos los objetos internos en función de su influencia en el resultado final. Y en el segundo, se actualizarán los parámetros del modelo.

Como ya sabe, la distribución de los gradientes de error se realiza en perfecta concordancia con el flujo de información del algoritmo de pasada directa, solo que en sentido contrario. Le sugiero que se familiarice con el algoritmo de los métodos mencionados.

Le recuerdo que encontrará el código completo de esta clase y todos sus métodos en el archivo adjunto.

La arquitectura de los modelos entrenados en este artículo, así como todos los programas utilizados para entrenarlos e interactuar con el entorno, se han tomado al completo de artículos anteriores. En esencia, en la arquitectura del modelo del Codificador del estado del entorno, solo hemos cambiado el identificador de una capa. Por tanto, no nos detendremos en su análisis. El código completo de todas las clases de programas usados en la elaboración de este artículo figura en el anexo.

3. Simulación

En este artículo, nos hemos familiarizado con el método MAFT y hemos implementado nuestra visión de los enfoques propuestos utilizando MQL5. Ahora procederemos a evaluar el trabajo realizado. Para ello, tendremos que entrenar el modelo usando la técnica MAFT con datos históricos reales y probar la política del Actor entrenada.

Para entrenar el modelo, utilizaremos datos históricos reales del instrumento EURUSD para todo el año 2023 en el marco temporal H1. Todos los parámetros de los indicadores analizados se usarán por defecto.

El algoritmo de entrenamiento del modelo se ha tomado prestado de artículos anteriores, junto con los programas de entrenamiento y prueba asociados.

La prueba de la política del Actor entrenada se realizará en el Simulador de Estrategias de MetaTrader 5 con los datos históricos de enero de 2024, mientras que los demás parámetros se mantendrán sin cambios. A continuación resumimos los resultados de las pruebas.

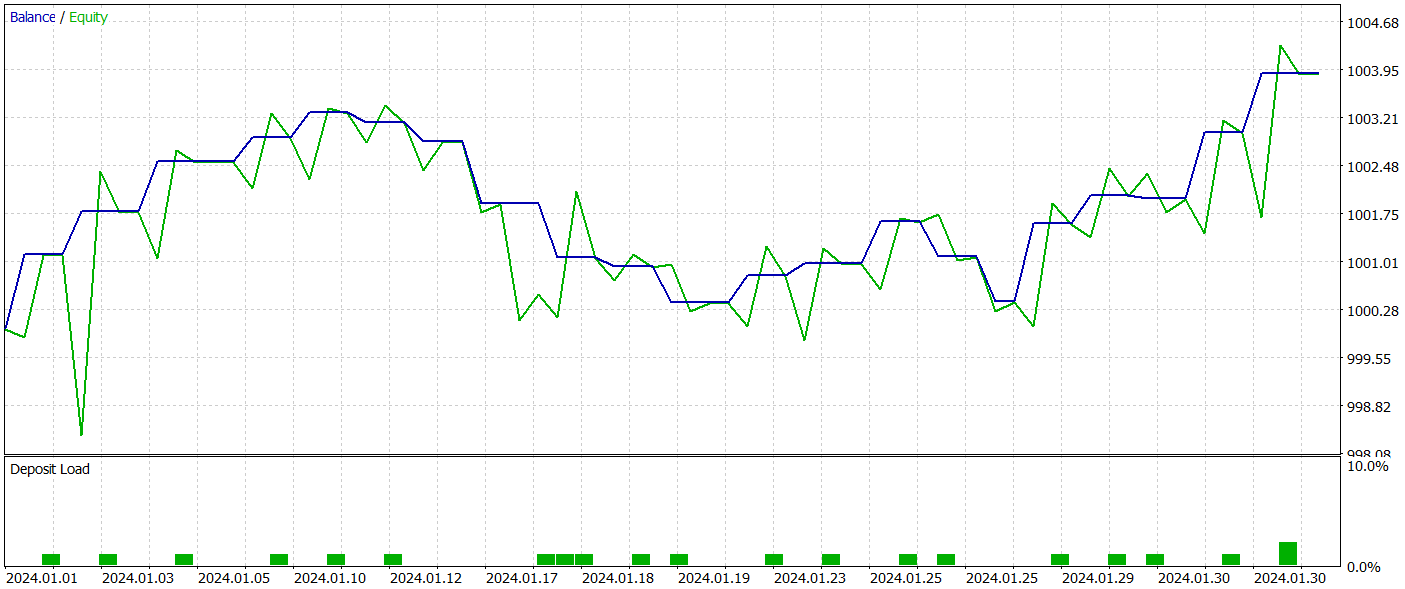
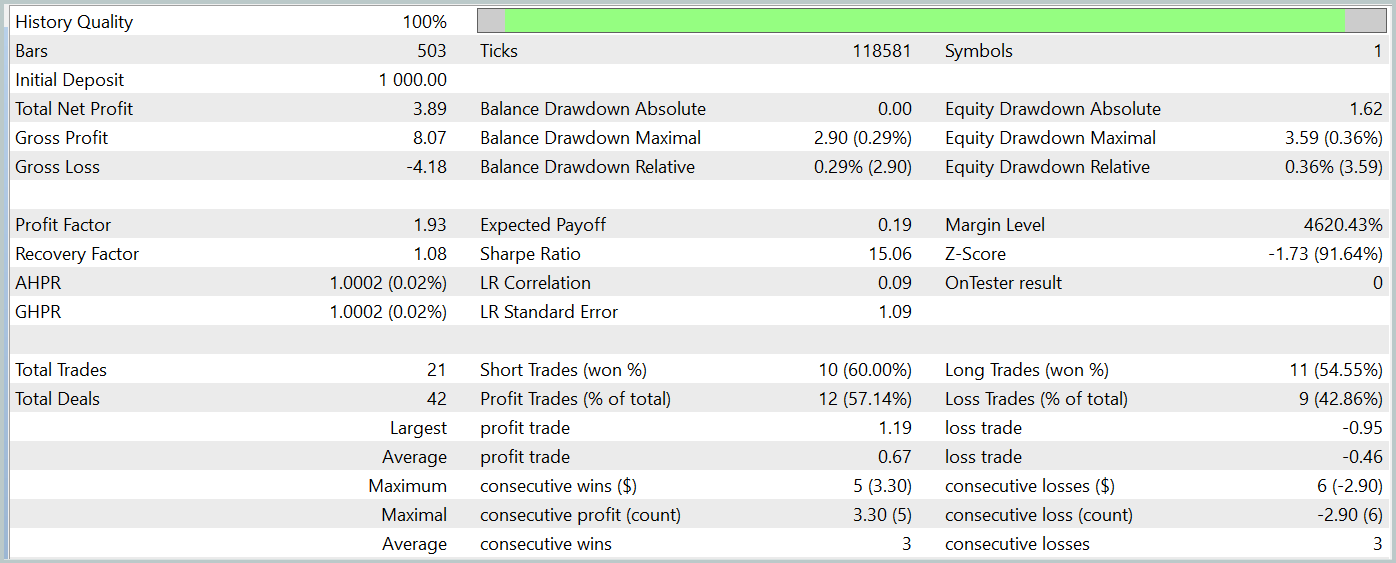
El gráfico del balance del periodo de prueba muestra una tendencia al alza, lo que sin duda es positivo. Sin embargo, durante todo el periodo de prueba, el modelo solo ha realizado 21 transacciones, 12 de las cuales se han cerrado con beneficios. Lamentablemente, el reducido número de transacciones comerciales completadas nos impide juzgar la eficacia del modelo en un intervalo de tiempo más largo.

Conclusión

En este artículo, nos hemos familiarizado con el método Mask-Attention-Free Transformer (MAFT) y su aplicación en el trading algorítmico. A diferencia del Transformer clásico, el la MAFT demuestra una alta eficiencia computacional, eliminando la necesidad de enmascarar los datos y acelerando el procesamiento de las secuencias.

Los resultados de las pruebas han confirmado que el MAFT es capaz de mejorar la calidad de las predicciones y reducir el tiempo de entrenamiento de los modelos.

Enlaces

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15973

Archivos adjuntos |

Descargar ZIP

MQL5.zip (1878.59 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores

Scalping Orderflow en MQL5

Este Asesor Experto de MetaTrader 5 implementa una estrategia Scalping Orderflow con gestión avanzada de riesgos. Utiliza múltiples indicadores técnicos para identificar oportunidades de negociación basadas en los desequilibrios del flujo de órdenes (Orderflow). Las pruebas retrospectivas muestran una rentabilidad potencial, pero resaltan la necesidad de una mayor optimización, especialmente en la gestión de riesgos y en los ratios de resultados comerciales. Adecuado para operadores experimentados, requiere pruebas y comprensión exhaustivas antes de la implementación en vivo.

Optimización del modelo de nubes atmosféricas — Atmosphere Clouds Model Optimization (ACMO): Práctica

En este artículo, seguiremos profundizando en la aplicación del algoritmo ACMO (Atmospheric Cloud Model Optimisation). En particular, discutiremos dos aspectos clave: el movimiento de las nubes hacia regiones de bajas presiones y la modelización del proceso de lluvia, incluida la inicialización de las gotas y su distribución entre las nubes. También analizaremos otras técnicas que desempeñan un papel importante a la hora de gestionar el estado de las nubes y garantizar su interacción con el entorno.

DoEasy. Funciones de servicio (Parte 3): Patrón "Barra exterior"

En este artículo desarrollaremos el patrón Price Action "Barra exterior" en la biblioteca DoEasy y optimizaremos los métodos de acceso a la gestión de los patrones de precios. Además, trabajaremos en la corrección de los fallos y errores detectados durante las pruebas de la biblioteca.

HTTP y Connexus (Parte 2): Comprensión de la arquitectura HTTP y el diseño de bibliotecas

Este artículo explora los fundamentos del protocolo HTTP, cubriendo los métodos principales (GET, POST, PUT, DELETE), los códigos de estado y la estructura de las URL. Además, presenta el inicio de la construcción de la librería Conexus con las clases CQueryParam y CURL, que facilitan la manipulación de URLs y parámetros de consulta en peticiones HTTP.