
Reimaginando las estrategias clásicas (Parte IV): SP500 y bonos del Tesoro de EE.UU.
Introducción
En un artículo anterior, comentábamos una posible estrategia de trading en el SP500 que se basaría en que utilizáramos una selección de valores que tuvieran un peso elevado dentro del índice. En el artículo de hoy, vamos a ver un enfoque alternativo de la negociación del SP500 utilizando el rendimiento de los bonos del Tesoro. Desde hace muchos años, cuando los inversores sentían aversión al riesgo, normalmente retiraban su dinero de inversiones riesgosas, como acciones, y preferían guardarlo en inversiones más seguras, como bonos y bonos del Tesoro. Por el contrario, cuando los inversores ganaban confianza en los mercados, tendían a retirar su dinero de inversiones seguras, como los bonos, y preferían invertirlo en el mercado de valores.
Los analistas fundamentales se han dado cuenta a lo largo de los años de que esta correlación entre los movimientos del SP500 y el movimiento de los rendimientos de los bonos del Tesoro parece ser opuesta. Parece ser una correlación negativa, es decir que cuando los inversores invierten más en acciones, tienden a invertir menos en bonos y bonos del Tesoro.
Descripción general de la estrategia comercial
El SP500 es un índice de referencia importante del desempeño de la economía industrial de Estados Unidos en un nivel muy amplio. Por otro lado, los bonos del Tesoro se consideran las inversiones más seguras del planeta. Cuando un inversor compra un bono o un bono del Tesoro, esencialmente está prestando dinero al gobierno que emitió ese bono del Tesoro. Cada bono del Tesoro paga cupones de interés que se muestran en el anverso del bono.
Cuando la demanda de bonos es baja, el rendimiento del bono aumenta. Esto se hace para reavivar la demanda. Entonces, como menos inversores están comprando bonos, veremos un aumento en el rendimiento. En general, los analistas fundamentales han estado utilizando esta relación a su favor durante mucho tiempo. Si estuvieran operando en el SP500, buscarían señales de debilitamiento de la tendencia.
Así, por ejemplo, si los rendimientos de los bonos comenzaran a subir, los analistas fundamentales sabrían que los inversores no están comprando bonos, sino que podrían estar poniendo su dinero en valores que les generarán una mayor tasa de retorno, como las acciones.
Sin embargo, si un analista fundamental nota que el rendimiento de los bonos ha estado cayendo, esto es una señal de que hay una demanda muy alta de bonos. Eso le diría al analista fundamental que probablemente no debería invertir en el mercado de valores todavía porque el sentimiento general del mercado es adverso al riesgo y las estrategias fundamentales usarían esto para entrar y salir de sus posiciones.
En el artículo de hoy queremos ver si esta relación es estadísticamente significativa y si es confiable para nosotros construir una estrategia comercial en torno a esta relación. Empecemos.
Descripción general de la metodología
Para examinar empíricamente los méritos de esta estrategia, ajustaremos varios modelos para predecir el precio de cierre del SP500 utilizando datos OHLC ordinarios del propio índice, a partir de allí observaremos el cambio en la precisión cuando intentemos entrenar los modelos para predecir el mismo objetivo, sin embargo, esta vez los modelos solo tendrán acceso a los datos OHLC del bono del Tesoro de EE.UU. a 5 años. Nuestras observaciones nos llevaron a creer que los inversores podrían obtener mejores resultados si utilizan datos del índice SP500. Los niveles de rendimiento de nuestro modelo cayeron en todos los ámbitos y, además, la variación en nuestros niveles de error aumentó cuando intentamos utilizar datos del Tesoro. Utilizamos la validación cruzada de series de tiempo sin mezcla aleatoria para comparar modelos de diferentes complejidades.
Después de observar los cambios en los niveles de error, identificamos al Regresor SGD como el modelo con mejor rendimiento, luego realizamos la selección de características en el modelo. Ninguno de los datos relacionados con los bonos del Tesoro fue seleccionado por nuestro selector de características, lo que indica que la relación puede no ser estadísticamente significativa. Aunque en este punto teníamos mucha evidencia de que podíamos descartar los datos de los bonos del Tesoro, mantuvimos los datos y continuamos construyendo nuestro modelo.
En nuestro paso final antes de exportar el modelo al formato ONNX, intentamos ajustar los hiperparámetros del modelo. Utilizamos el algoritmo L-BFGS-B (Limited-Memory Broyden-Fletcher-Goldfarb-Shanno) en un intento de encontrar configuraciones de parámetros óptimas para nuestro modelo. Nuestro objetivo era superar el rendimiento de la configuración del modelo predeterminado. Desafortunadamente, terminamos sobreajustando nuestro modelo a los datos de entrenamiento y, por lo tanto, no pudimos superar al modelo predeterminado.
Análisis exploratorio de datos en Python
Para obtener datos de nuestra terminal MetaTrader 5, creé un script para escribir datos históricos del mercado en formato CSV para nosotros. He adjuntado el script. Simplemente arrástrelo y suéltelo en el gráfico, y escribirá los datos para nosotros.
Una vez preparados los datos, comenzamos importando las bibliotecas que necesitamos.
#Import the libraries we need import pandas as pd import numpy as np import seaborn as sns
Una vez hecho esto, leeremos nuestros datos.
#Read in the data SP500 = pd.read_csv("/home/volatily/market_data/Market Data US SP 500.csv") T5Y = pd.read_csv("/home/volatily/market_data/Market Data UST05Y_U4.csv")
Necesitamos definir hasta qué punto en el futuro nos gustaría pronosticar. Entonces, en este ejemplo, vamos a pronosticar 20 pasos hacia el futuro.
#How far into the future should we forecast? look_ahead = 20
Ahora, también tenemos que asegurarnos de que los datos comiencen con el día más antiguo primero y se pierda el día más reciente de todos los datos.
#Make sure the data starts with the oldest day first SP500 = SP500[::-1].reset_index().set_index("Time").drop(columns=["index"]) T5Y = T5Y[::-1].reset_index().set_index("Time").drop(columns=["index"])
Una vez hecho esto, ahora etiquetaremos los datos. Tendremos una etiqueta que será el precio de cierre futuro del SP500, 20 pasos en el futuro. Y luego el segundo objetivo binario solo se crea con fines de trazado.
#Insert the label SP500["Target SP500"] = SP500["Close"].shift(-look_ahead) SP500["Binary Target SP500"] = 0 SP500.loc[SP500["Close"] < SP500["Target SP500"],"Binary Target SP500"] = 1 SP500.dropna(inplace=True)
Ahora que hemos hecho eso, fusionaremos los dos datos. Fusionaremos los datos del SP500 y el rendimiento del bono del Tesoro a cinco años en un marco de datos fusionado.
#Merge the data merged_df = pd.merge(SP500,T5Y,how="inner",left_index=True,right_index=True,suffixes=(" SP500"," T5Y"))
Y podemos observar el marco de datos de fusión.
#Let's observe the merged dataframe merged_df
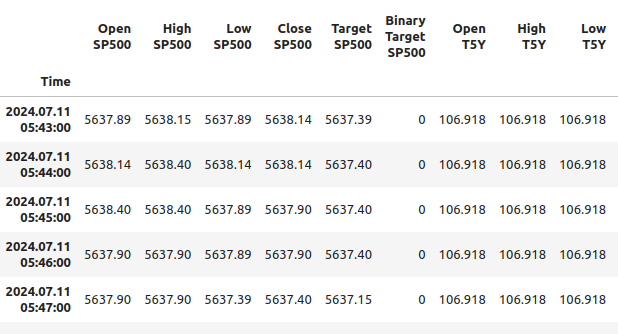
Figura 1: Nuestro marco de datos fusionado.
También podemos analizar la correlación en el marco de datos fusionado. Podemos observar que los niveles de correlación están alrededor de 0,1, lo cual no es fuerte.
#Merged data frame correlation
merged_df.corr()
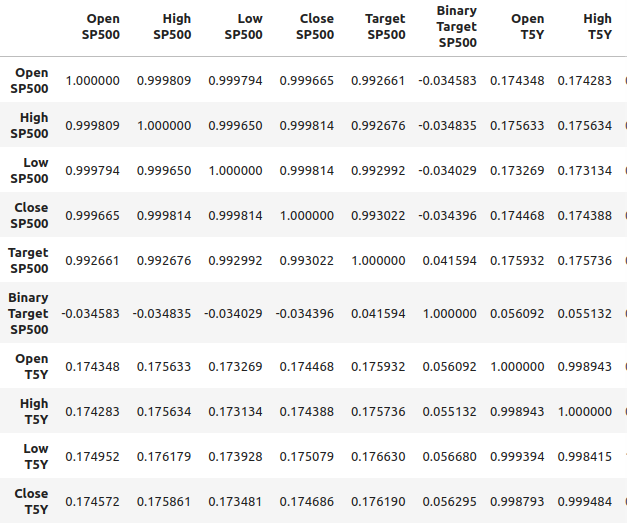
Figura 2: Niveles de correlación en nuestro marco de datos fusionados.
Sin embargo, niveles de correlación fuertes no implican necesariamente que exista una relación definida entre las dos variables que se analizan. Tampoco implica que una variable sea la causa de la otra. Los fuertes niveles de correlación pueden implicar que existe una causa común que está afectando a estos dos mercados.
Hice un diagrama de dispersión con el tiempo en el eje x y en el eje y está el precio de apertura del SP500. Y luego usé los objetivos binarios para colorear los puntos a lo largo del diagrama de dispersión. Observe que los puntos azules y naranjas se agrupan naturalmente; esto puede indicarnos que el tiempo separa bien los datos. Recordemos que nuestro objetivo binario nos dice lo que sucederá 20 pasos en el futuro, los puntos azules significan que el precio cayó en los siguientes 20 pasos y los puntos naranjas nos dicen que sucedió lo contrario.
#It appears that one variable that separates the data well is time sns.scatterplot(data=merged_df,x="Candle",y="Open SP500",hue="Binary Target SP500")
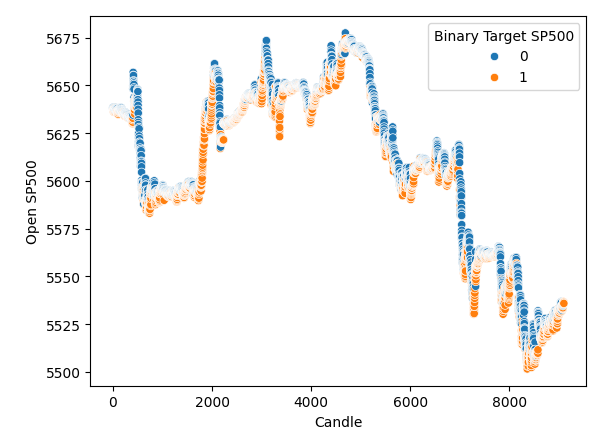
Figura 3: Nuestros datos parecen estar bien separados en el tiempo.
Parece que el tiempo separa muy bien los datos. Sin embargo, cuando intentamos utilizar otras variables para separar los datos, como por ejemplo aquí, creamos un gráfico de dispersión del precio de apertura del SP500 frente al precio de apertura del rendimiento del bono del Tesoro a cinco años. Vemos que obtenemos este diagrama de dispersión mal separado en el que hay muchos puntos uno encima del otro y no hay ninguna separación clara en absoluto.
#It appears that one variable that separates the data well is time sns.scatterplot(data=merged_df,x="Open T5Y",y="Open SP500",hue="Binary Target SP500")
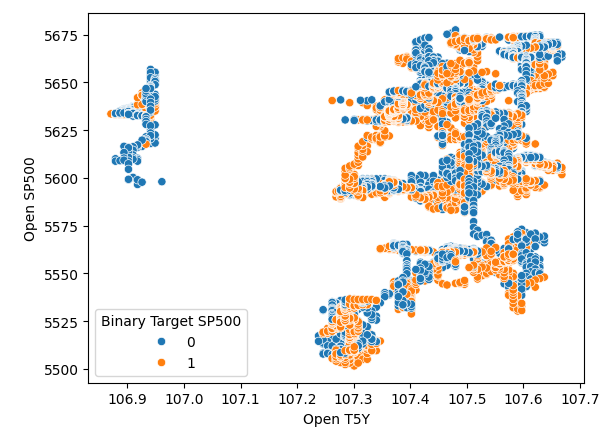
Figura 4: Niveles de separación deficientes.
Selección de modelo
Ahora que hemos hecho eso, pasaremos a modelar la relación entre el SP500 y los rendimientos de los bonos del Tesoro. Importaremos los módulos que necesitamos de Scikit-learn.
#Import the libraries we need from sklearn.linear_model import LinearRegression from sklearn.linear_model import Lasso from sklearn.linear_model import SGDRegressor from sklearn.svm import LinearSVR from sklearn.ensemble import RandomForestRegressor from sklearn.ensemble import GradientBoostingRegressor from sklearn.ensemble import BaggingRegressor from sklearn.ensemble import AdaBoostRegressor from sklearn.neural_network import MLPRegressor from sklearn.model_selection import TimeSeriesSplit from sklearn.metrics import root_mean_squared_error from sklearn.preprocessing import RobustScaler import time from numpy.random import rand,randn from scipy.optimize import minimize
Y luego nos prepararemos para hacer un objeto dividido en series de tiempo. Entonces, primero definimos la cantidad de divisiones que queremos y luego creamos el objeto de división de series de tiempo en sí.
#Define the number of splits we want splits = 10
#Create the time series split object
tscv = TimeSeriesSplit(n_splits = splits, gap=look_ahead) Y como tenemos numerosos modelos, los vamos a almacenar en una lista.
#Store the models in a list models = [LinearRegression(), Lasso(), SGDRegressor(), LinearSVR(), RandomForestRegressor(), GradientBoostingRegressor(), BaggingRegressor(), AdaBoostRegressor(), MLPRegressor(hidden_layer_sizes=(10,4),early_stopping=True), ]
Definiré una función para inicializar nuestros modelos, y la función se llama "initialize_models".
#Define a function to initialize our models def initialize_models(): models = [LinearRegression(), Lasso(), SGDRegressor(), LinearSVR(), RandomForestRegressor(), GradientBoostingRegressor(), BaggingRegressor(), AdaBoostRegressor(), MLPRegressor(hidden_layer_sizes=(10,4),early_stopping=True), ]
Y luego también necesitamos marcos de datos para almacenar nuestros niveles de error. Entonces necesitamos tres marcos de datos. El primer marco de datos almacenará nuestros niveles de error cuando solo usamos datos ordinarios de apertura, máximos, mínimos y cierre del SP500; el segundo marco de datos almacena nuestros niveles de error cuando intentamos pronosticar el SP500 basándose únicamente en los rendimientos de los bonos del Tesoro. Y el último marco de datos almacena nuestros niveles de error al usar todos los datos que tenemos.
#Create 3 dataframes to measure our performance #Before we do that, we will define the columns and idexes columns = ["Linear Regression", "Lasso", "SGD Regressor", "Linear SVR", "Random Forest Regressor", "Gradient Boosting Regressor", "Bagging Regressor", "Ada Boost Regressor", "MLP Regressor"] indexes = np.arange(0,10) #First dataframe stores our error levels using just the ordinary SP500 OHCL SP500_error = pd.DataFrame(columns=columns,index=indexes) #Second dataframe stores our error levels using just the ordinary Treasury Yield OHCL TY5_error = pd.DataFrame(columns=columns,index=indexes) #Last dataframe stores our error levels using all the data we have total_error = pd.DataFrame(columns=columns,index=indexes)
Ahora definiremos nuestras entradas y nuestro objetivo.
#Now we will define the inputs and target target = "Target SP500" predictors = ["Open T5Y", "Close T5Y", "High T5Y", "Low T5Y", "Open SP500", "Close SP500", "High SP500", "Low SP500" ]
Y luego restableceremos el índice de nuestro marco de datos fusionado.
#Reset the index
merged_df.reset_index(inplace=True) Y vamos a escalar los datos usando un escalar robusto. Así, simplemente instanciamos el escalador robusto, llamamos a la función de transformación y pasamos el marco de datos de fusión a la función de transformación de ajuste. Todo esto está envuelto dentro de un nuevo objeto de marco de datos que crearemos usando pandas.
#Scale the data scaled_data = pd.DataFrame(RobustScaler().fit_transform(merged_df.loc[:,predictors]),columns=predictors,index=np.arange(0,merged_df.shape[0]))
Ahora que hemos llegado hasta aquí, estamos listos para realizar la validación cruzada. Entonces, la forma más fácil de hacerlo fue usar un bucle anidado. Por lo tanto, el primer bucle for itera sobre todos los modelos que tenemos y luego el segundo bucle validará cada modelo individualmente. Por lo tanto, ajustaremos el modelo de regresión lineal, luego ajustaremos el lazo y así sucesivamente.
#Now we will perform cross validation #First we iterate over all the models we have for j in np.arange(0,len(models)): for i,(train,test) in enumerate(tscv.split(merged_df)): #Prepare the models initialize_models() #Prepare the data X_train = scaled_data.loc[train[0]:train[-1],predictors] X_test = scaled_data.loc[test[0]:test[-1],predictors] y_train = merged_df.loc[train[0]:train[-1],target] y_test = merged_df.loc[test[0]:test[-1],target] #Now fit each model and measure its accuracy models[j].fit(X_train,y_train) SP500_error.iloc[i,j] = root_mean_squared_error(y_test,models[j].predict(X_test)) print(f"Completed fitting model {models[j]}")
Completed fitting model LinearRegression()
Completed fitting model LinearRegression()
Completed fitting model LinearRegression()
Completed fitting model LinearRegression()
Desde allí, podemos ver nuestros niveles de error del SP500, y parece que la regresión lineal fue uno de los modelos con mejor rendimiento en este caso, seguido por el Regresor SGD. La red neuronal funcionó bastante mal. De hecho, probablemente podría beneficiarse mucho del ajuste de parámetros.
SP500_error
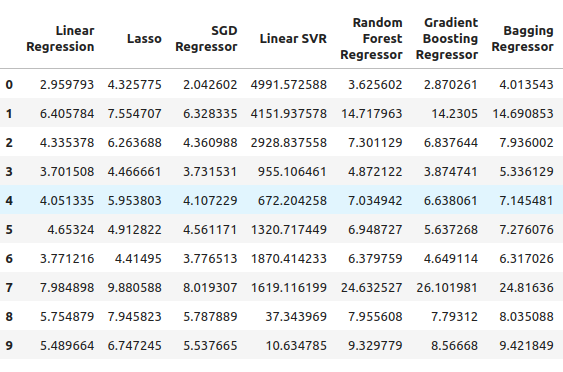
Figura 5: Nuestros niveles de error al utilizar datos OHLC del SP500 ordinarios.
Pasamos a nuestro rendimiento del bono del Tesoro a cinco años. En este caso particular, todos nuestros modelos tuvieron un desempeño deficiente. Sin embargo, el regresor de bosque aleatorio parece funcionar bastante bien.
TY5_error
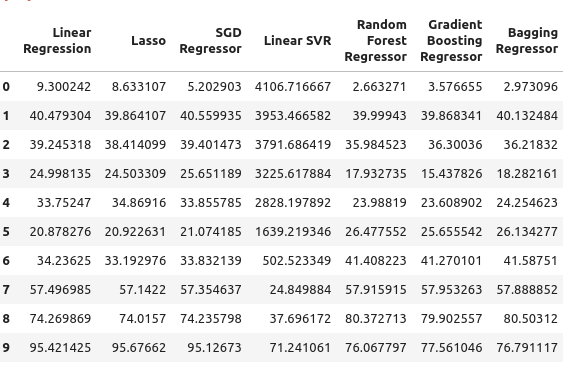
Figura 6: Nuestros niveles de error al confiar en los rendimientos de los bonos del Tesoro.
Y luego, por último, tenemos el error total al usar todos los datos disponibles, parece que el regresor de descenso de gradiente estocástico funciona razonablemente bien y por esas razones, seleccioné el regresor SGD como el modelo con mejor rendimiento.
total_error
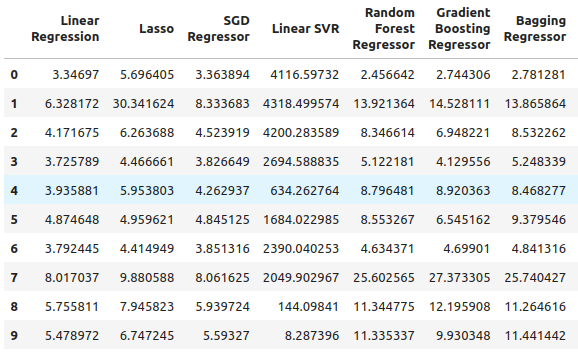
Figura 7: Nuestros niveles de error cuando utilizamos todos los datos disponibles.
Selección de funciones
Ahora vamos a realizar una selección de características para ver si nuestra computadora también piensa que los datos de rendimiento de los bonos del Tesoro son importantes. Si el selector de características omite los datos relacionados con el rendimiento del tesoro, eso podría ser motivo de preocupación para nuestra estrategia porque parecería que la relación no es confiable. Sin embargo, si nuestro selector de características conserva los datos de rendimiento del tesoro, entonces podría ser una buena señal.
#Feature selection from mlxtend.feature_selection import SequentialFeatureSelector as SFS #Get the best model model = SGDRegressor()
Creamos el objeto selector de características secuenciales y le pasamos el modelo que nos gustaría utilizar. A partir de ahí, le ordené al algoritmo que pudiera seleccionar tantas características como fuera necesario. Podríamos haber especificado que debería seleccionar cinco características, pero quería seleccionar tantas como calcule que son importantes. Pasamos a verdadero, lo que significa que se realizará una selección hacia adelante y desde allí pasamos CV igual a cinco, lo que significa que emplearemos una validación cruzada quíntuple. Desde allí pasamos n-jobs iguales a menos 1, esto permite que el selector de características realice esta tarea en paralelo.
#Let us perform feature selection for the best model we have sfs_sgd_regressor = SFS(model, (1,8), forward=True, cv=5, n_jobs=-1, scoring="neg_mean_squared_error" )
Desde allí, ajustamos el selector de características.
#Fit the feature selector
sfs_1 = sfs_sgd_regressor.fit(scaled_data.loc[:,predictors],merged_df.loc[:,target]) Cuando ahora observamos qué características fueron las más importantes para nuestro modelo, vemos que, lamentablemente, ninguna de las características estaba relacionada con la tesorería. Los rendimientos se seleccionaron únicamente en los máximos y mínimos de cierre seleccionados del SP500. Esto puede indicar que la relación no es tan estable, y es bien sabido que la correlación entre los rendimientos de los bonos del Tesoro y el SP500 se rompe de vez en cuando.
#Which features were most important to our model?
sfs_1.k_feature_names_ Seguiremos intentando optimizar nuestro modelo y ver cuánto rendimiento podemos obtener.
#None the less, let us attempt to optimize the model
from scipy import optimize Y a partir de ahí, vamos a crear dos conjuntos de datos dedicados. Uno para entrenar y optimizar el modelo, y el otro para la validación. En el conjunto de validación, compararemos el rendimiento de nuestro modelo optimizado con el rendimiento de un modelo predeterminado que solo usa configuraciones predeterminadas. Queremos intentar superar los niveles de error predeterminados.
#Create a training and validation set scaled_data = merged_df.loc[:,predictors] scaled_data = (scaled_data - scaled_data.mean()) / (scaled_data.std()) #Create the two datasets train_data , test_data = scaled_data.loc[:(scaled_data.shape[0]//2),:],scaled_data.loc[(scaled_data.shape[0]//2):,:]
Tenga en cuenta que esta vez estoy usando una técnica de escala diferente, la primera vez solo usé un escalar robusto. Esta vez empleamos una técnica de escala muy común: restamos la media de cada columna y luego dividimos cada columna por su desviación estándar.
#Let's write out the column mean and standard deviations #We'll store the mean first #Then the standard deviation scale_factors = pd.DataFrame(columns=predictors,index=(0,1)) #Save the mean and std value of each respective column for i in (np.arange(0,len(predictors))): #Calculate and store the values of each column mean and std scale_factors.iloc[0,i] = merged_df.loc[:,predictors[i]].mean() scale_factors.iloc[1,i] = merged_df.loc[:,predictors[i]].std() #Inspect the data scale_factors
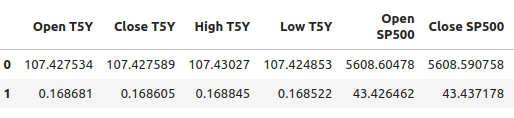
Figura 8: Nuestra media y desviación estándar para cada columna.
Los valores medios y las desviaciones estándar que calculamos para cada columna son significativos y vamos a necesitar esos datos cuando volvamos a trabajar en MQL5, así que estoy escribiendo los datos en formato CSV.
#Write it out to csv format scale_factors.to_csv("/home/volatily/.wine/drive_c/Program Files/MetaTrader 5/MQL5/Files/sp500_treasury_yields_scale.csv")
Ajuste del modelo del regresor SGD
Ahora intentaremos ajustar el modelo, primero definimos la función objetivo. La función objetivo en este caso serán los niveles de RMSE de entrenamiento, y queremos minimizar nuestros niveles de RMSE en los datos de entrenamiento. Sin embargo, este procedimiento es un arma de doble filo. ¡Cualquier hiperparámetro que minimice nuestro error en el conjunto de entrenamiento no garantiza que minimice nuestro error en el conjunto de validación!
#Define the objective function def objective(x): #Initialize the model with the new parameters model = SGDRegressor(alpha=x[0],shuffle=False,eta0=x[1]) #We need a dataframe to store our current model accuracy levels current_accuracy = pd.DataFrame(index=np.arange(0,splits),columns=["Error"]) #Now we perform cross validation for i,(train,test) in enumerate(tscv.split(train_data)): #Split the data into a training set and test set X_train = train_data.loc[train[0]:train[-1],predictors] X_test = train_data.loc[test[0]:test[-1],predictors] y_train = merged_df.loc[train[0]:train[-1],target] y_test = merged_df.loc[test[0]:test[-1],target] #Fit the model model.fit(X_train,y_train) #Record the accuracy current_accuracy.iloc[i,0] = root_mean_squared_error(y_test,model.predict(X_test)) #Return the model accuracrcy return(current_accuracy.iloc[:,0].mean())
Entonces, como siempre, comenzaremos realizando una búsqueda lineal para tener una idea de dónde pueden estar los valores óptimos. Entonces comenzamos realizando una búsqueda de línea normal, y nos llevó 41 segundos completarla.
#Let's optimize our model #Let us measure how much time this takes. start = time.time() #Create a dataframe to measure the error rates starting_point_error = pd.DataFrame(index=np.arange(0,21),columns=["Average CV RMSE"]) starting_point_error["Iteration"] = np.arange(0,21) #Let us first find a good starting point for our optimization algorithm for i in np.arange(0,21): #Set a new starting point new_starting_point = (10.0 ** -i) #Store error rates starting_point_error.iloc[i,0] = objective([new_starting_point ,new_starting_point]) #Record the time stamp at the end stop = time.time() #Report the amount of time taken print(f"Completed in {stop - start} seconds")
De los resultados de nuestra búsqueda lineal, parece que cruzamos los puntos óptimos justo en la primera iteración.
starting_point_error["alpha"] = 0 starting_point_error["eta0"] = 0 for i in np.arange(0,21): starting_point_error.loc[i,"alpha"] = (10.0 ** -i) starting_point_error.loc[i,"eta0"] = (10.0 ** -i) starting_point_error
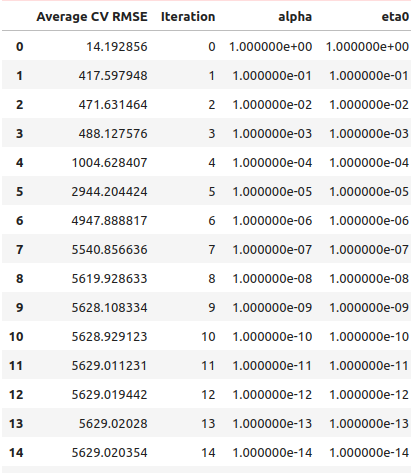
Figura 9: Resultados de nuestra búsqueda de línea.
También podemos representar gráficamente esta información visualmente, como se puede ver en la figura de un palo de hockey invertido, con el error más bajo al principio y luego nuestro error simplemente continúa aumentando.
#Let's visualize our error levels sns.lineplot(data=starting_point_error,x="Iteration",y="Average CV RMSE").set(title="Optimizing our SGD Regressor on Training Data")
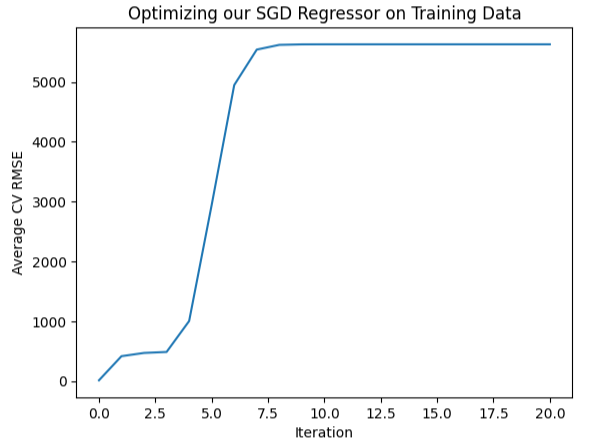
Figura 10: Visualizando nuestros niveles de error.
Ahora que tenemos una idea de lo que parece óptimo, podemos realizar una búsqueda local alrededor de la región que parezca tener los derechos óptimos. Utilizaremos el algoritmo L-BGFS-B para encontrar estos puntos óptimos. Primero, seleccionaremos puntos aleatorios de la región que parezca óptima.
#Now let us perform a local search in the space that appears optimal pt = abs(((10 ** -2) + rand(2) * ((1) - (10 ** -2)))) pt
Ahora intentaremos optimizar nuestro modelo según los datos de entrenamiento.
#Let's try optimize our model
start = time.time()
bounds = ((0.01,1),(0.01,1))
result = minimize(objective,pt,bounds=bounds,method="L-BFGS-B")
stop = time.time()
print(f"Task completed in {stop - start} seconds") ¿Cuales son los resultados?
#What are the results?
result success: True
status: 0
fun: 11.428966326221078
x: [ 1.040e-01 3.193e-01]
nit: 24
jac: [ 9.160e+00 -1.475e+01]
nfev: 351
njev: 117
hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
Parece que tuvimos éxito, el error más bajo que logramos obtener fue 11,43, sin embargo, la verdadera prueba llega cuando comparamos el modelo personalizado con el modelo predeterminado en el conjunto de pruebas.
Prueba de sobreajuste
Para detectar si estamos sobreajustando los datos de entrenamiento, comparemos los niveles de error de nuestro modelo personalizado con los niveles de error de un modelo que utiliza configuraciones predeterminadas. Recuerde que dividimos el conjunto de datos en dos mitades antes de comenzar el proceso de ajuste de parámetros.#Now let us compare the default model and the customized model default_model = SGDRegressor() customized_model = SGDRegressor(alpha=result.x[0],shuffle=False,eta0=result.x[1])
Primero, evaluemos los niveles de error del modelo predeterminado y del conjunto de prueba.
#Default model accuracy default_model.fit(train_data.loc[:,predictors],merged_df.loc[:(merged_df.shape[0]//2),target]) root_mean_squared_error(merged_df.loc[(merged_df.shape[0]//2):,target],default_model.predict(test_data.loc[:,predictors]))
Ahora comparemos eso con los niveles de error del modelo personalizado.
#Customized model accuracy customized_model.fit(train_data.loc[:,predictors],merged_df.loc[:(merged_df.shape[0]//2),target]) root_mean_squared_error(merged_df.loc[(merged_df.shape[0]//2):,target],customized_model.predict(test_data.loc[:,predictors]))
Parece que efectivamente estábamos sobreajustando los datos de entrenamiento y no logramos superar la configuración predeterminada. En este caso, continuaremos trabajando con el modelo por defecto y lo exportaremos a formato ONNX.
Exportación al formato ONNX
Comenzamos importando las librerías que necesitamos.
#Let's convert the regression model to ONNX format from skl2onnx.common.data_types import FloatTensorType from skl2onnx import convert_sklearn import onnxruntime as ort import onnx
Luego normalizaremos y escalaremos nuestras entradas.
for i in predictors:
merged_df.loc[:,i] = (merged_df.loc[:,i] - merged_df.loc[:,i].mean()) / merged_df.loc[:,i].std() Ahora entrene el modelo en todo el conjunto de datos.
#Prepare the model model = SGDRegressor() model.fit(merged_df.loc[:,predictors],merged_df.loc[:,"Target SP500"])
Ahora definiremos la forma y los tipos de entrada.
#Define the input types initial_type_float = [("float_input",FloatTensorType([1,len(predictors)]))] onnx_model_float = convert_sklearn(model,initial_types=initial_type_float,target_opset=12)
Guardemos el modelo ONNX.
#ONNX file name onnx_file_name = "SP500_ONNX_FLOAT_M1.onnx" #ONNX file onnx.save_model(onnx_model_float,onnx_file_name)
Ahora inspeccionemos rápidamente la forma de las entradas y salidas de nuestro modelo ONNX.
# load the ONNX model and inspect input and ouput shapes onnx_session = ort.InferenceSession(onnx_file_name) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name
Asegurémonos de que la forma de entrada de nuestro modelo sea 1 por 8.
#Display information about input tensors in ONNX print("Information about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
1. Nombre: float_input, Data Type: tensor(float), Shape: [1, 8]
Por último, nuestra forma de salida debe ser 1 por 1.
#Display information about output tensors in ONNX print("Information about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
1. Nombre: variable, Data Type: tensor(float), Shape: [1, 1]
También podemos visualizar nuestro modelo ONNX usando Netron.
#Visualize the model
import netron
La función de inicio en netron nos permite visualizar nuestro modelo ONNX.
#Call netron
netron.start(onnx_file_name) 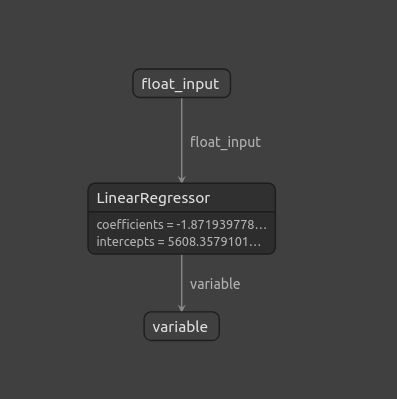
Figura 11: Visualización de nuestro modelo ONNX utilizando Netron
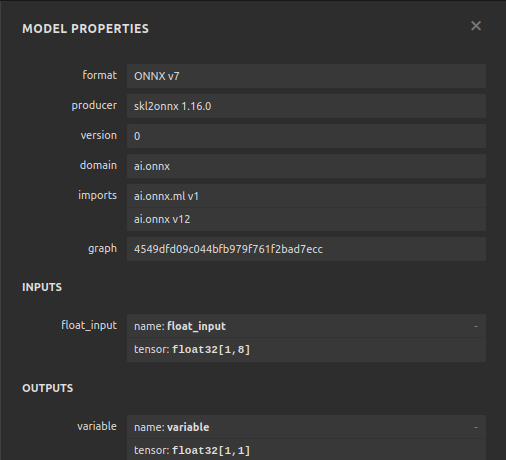
Figura 12: Propiedades de nuestro modelo ONNX.
Implementación en MQL5
Ahora que hemos terminado de construir nuestro modelo ONNX y lo hemos exportado, podemos comenzar a construir nuestro asesor experto. Lo primero que vamos a hacer en nuestro asesor experto es cargar el modelo ONNX que acabamos de exportar.
//+------------------------------------------------------------------+ //| SP500 X Treasury Yields.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" #property tester_file "sp500_treasury_yields_scale.csv" //+------------------------------------------------------------------+ //| Require the ONNX model | //+------------------------------------------------------------------+ #resource "\\Files\\SP500_ONNX_FLOAT_M1.onnx" as const uchar ModelBuffer[];
Desde ahí vamos a incluir también la biblioteca de operaciones, esta biblioteca nos ayuda a abrir, cerrar y modificar nuestras posiciones.
//+------------------------------------------------------------------+ //| Libraries we need | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
También es necesario tener en cuenta algunas aportaciones del usuario final, como por ejemplo, qué tan grande debe ser el múltiplo de un lote y qué tan amplio debe ser nuestro stop loss una vez realizado.
//+------------------------------------------------------------------+ //| Inputs for our EA | //+------------------------------------------------------------------+ input int lot_multiple = 1; //How many times bigger than minimum lot? input double sl_width = 1; //How wide should our stop loss be?
Necesitamos variables globales que se utilizarán en todo el asesor experto. Necesitamos una variable global para representar el modelo ONNX y otro vector para almacenar las predicciones de nuestro modelo.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long model; //Our ONNX SGDRegressor model vectorf prediction(1); //Our model's prediction float mean_values[8],variance_values[8]; //We need this data to normalise and scale model inputs double trading_volume; //How big should our positions be? int state = 0;
Continuando, también necesitamos una función responsable de leer el archivo de configuración CSV que definimos anteriormente. Recuerde que ese archivo es significativo porque contiene los valores medios y los valores de desviación estándar de cada columna. Esta función garantiza que todas las entradas que damos a nuestro modelo ONNX estén normalizadas. La función comenzará intentando abrir el archivo utilizando el comando de apertura de archivo. Y si tuvimos éxito y logramos abrir el archivo, procedemos a analizar nuestro archivo CSV y a almacenar los valores medios y los valores de varianza en sus propias matrices separadas. De lo contrario, si no tenemos éxito, la función imprimirá que no pudo leer el archivo, devolverá falso y el procedimiento de inicialización fallará.
//+------------------------------------------------------------------+ //| A function responsible for reading the CSV config file | //+------------------------------------------------------------------+ bool read_configuration_file(void) { //--- Read the config file Print("Reading in the config file"); //--- Config file name string file_name = "sp500_treasury_yields_scale.csv"; //--- Try open the file int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //--- Check the result if(result != INVALID_HANDLE) { Print("Opened the file"); //--- Prepare to read the file int counter = 0; string value = ""; //--- Make sure we can proceed while(!FileIsEnding(result) && !IsStopped()) { if(counter > 60) break; //--- Read in the file value = FileReadString(result); Print("Reading: ",value); //--- Have we reached the end of the line? if(FileIsLineEnding(result)) Print("row++"); counter++; //--- The first few lines will contain the title of each columns, we will ingore that if((counter >= 11) && (counter <= 18)) { mean_values[counter - 11] = (float) value; } if((counter >= 20) && (counter <= 27)) { variance_values[counter - 20] = (float) value; } } //--- Close the file FileClose(result); Print("Mean values"); ArrayPrint(mean_values); Print("Variance values"); ArrayPrint(variance_values); return(true); } else if(result == INVALID_HANDLE) { Print("Failed to read the file"); return(false); } return(false); }
También necesitamos una función responsable de obtener un pronóstico de nuestro modelo. Tenemos un vector al principio para almacenar los datos de entrada. Una vez que hayamos obtenido todos los precios que necesitamos, restamos el valor medio de esa columna y lo dividimos por la varianza de esa columna en particular. Una vez hecho esto, podremos obtener una predicción de nuestro modelo.
//+------------------------------------------------------------------+ //| A function responsible for getting a forecast from our model | //+------------------------------------------------------------------+ void predict(void) { //--- Let's prepare our inputs vectorf input_data = vectorf::Zeros(8); //--- Select the symbol input_data[0] = ((iOpen("UST05Y_U4",PERIOD_M1,0) - mean_values[0]) / variance_values[0]); input_data[1] = ((iClose("UST05Y_U4",PERIOD_M1,0) - mean_values[1]) / variance_values[1]); input_data[2] = ((iHigh("UST05Y_U4",PERIOD_M1,0) - mean_values[2]) / variance_values[2]); input_data[3] = ((iLow("UST05Y_U4",PERIOD_M1,0) - mean_values[3]) / variance_values[3]);; input_data[4] = ((iOpen("US500",PERIOD_M1,0) - mean_values[4]) / variance_values[4]);; input_data[5] = ((iClose("US500",PERIOD_M1,0) - mean_values[5]) / variance_values[5]);; input_data[6] = ((iHigh("US500",PERIOD_M1,0) - mean_values[6]) / variance_values[6]); input_data[7] = ((iLow("US500",PERIOD_M1,0) - mean_values[7]) / variance_values[7]);; //--- Show the inputs Print("Inputs: ",input_data); //--- Obtain a prediction from our model OnnxRun(model,ONNX_DEFAULT,input_data,prediction); }
Después de que nuestro modelo nos haya dado una predicción, debemos tomar acción. Entonces, en este caso particular, podemos decidir abrir una posición en la dirección que nuestro modelo ha predicho. O si nuestro modelo pronostica que el precio se revertirá en nuestra contra, podríamos decidir cerrar nuestras posiciones abiertas.
//+------------------------------------------------------------------+ //| This function will decide if we should open or close our trades | //+------------------------------------------------------------------+ void intepret_prediction(void) { if(PositionsTotal() == 0) { double ask = SymbolInfoDouble("US500",SYMBOL_ASK); double bid = SymbolInfoDouble("US500",SYMBOL_BID); double close = iClose("US500",PERIOD_M1,0); if(prediction[0] > close) { Trade.Buy(trading_volume,"US500",ask,(ask - sl_width),(ask + sl_width),"SP500 X Treasury Yields"); state = 1; } if(prediction[0] < iClose("US500",PERIOD_M1,0)) { Trade.Sell(trading_volume,"US500",bid,(bid + sl_width),(bid - sl_width),"SP500 X Treasury Yields"); state = 2; } } else if(PositionsTotal() > 0) { if((state == 1) && (prediction[0] > iClose("US500",PERIOD_M1,0))) { Alert("Reversal predicted, consider closing your buy position"); } if((state == 2) && (prediction[0] < iClose("US500",PERIOD_M1,0))) { Alert("Reversal predicted, consider closing your buy position"); } } }
Hemos terminado de definir las funciones auxiliares para nuestro modelo y pasamos a definir la función de inicialización de nuestro Asesor Experto. Primero debemos crear nuestro modelo ONNX y luego asegurarnos de que el modelo sea válido.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Create the ONNX model from the model buffer we have model = OnnxCreateFromBuffer(ModelBuffer,ONNX_DEFAULT); //--- Ensure the model is valid if(model == INVALID_HANDLE) { Comment("[ERROR] Failed to initialize the model: ",GetLastError()); return(INIT_FAILED); }
Una vez que estamos seguros de que el modelo es válido, definimos las formas de entrada de nuestro modelo y luego definimos las formas de salida de nuestro modelo.
//--- Define the model parameters, input and output shapes ulong input_shape[] = {1,8}; //--- Check if we were defined the right input shape if(!OnnxSetInputShape(model,0,input_shape)) { Comment("[ERROR] Incorrect input shape specified: ",GetLastError(),"\nThe model's inputs are: ",OnnxGetInputCount(model)); return(INIT_FAILED); } ulong output_shape[] = {1,1}; //--- Check if we were defined the right output shape if(!OnnxSetOutputShape(model,0,output_shape)) { Comment("[ERROR] Incorrect output shape specified: ",GetLastError(),"\nThe model's outputs are: ",OnnxGetOutputCount(model)); return(INIT_FAILED); }
Una vez hecho todo esto, podemos leer el archivo de configuración; esto se debe hacer en la inicialización y, si no podemos leer el archivo de configuración, todo el asesor experto debería finalizar porque no podemos hacer pronósticos sobre datos que no están normalizados.
//--- Read the configuration file if(!read_configuration_file()) { Comment("Failed to find the configuration file, ensure it is stored here: ",TerminalInfoString(TERMINAL_DATA_PATH)); return(INIT_FAILED); }
Ahora necesitamos seleccionar los símbolos y agregarlos a "Observación del Mercado".
//--- Select the symbols SymbolSelect("US500",true); SymbolSelect("UST05Y_U4",true);
Por último, necesitamos obtener algunos datos del mercado.
//--- Calculate the lotsize trading_volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN) * lot_multiple; //--- Return init succeeded return(INIT_SUCCEEDED); }Siempre que nuestro Asesor Experto no esté en uso, debemos liberar los recursos que nos fueron asignados.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Free up the resources we used for our ONNX model OnnxRelease(model); //--- Remove the expert advisor ExpertRemove(); }
Finalmente, en nuestro controlador de eventos OnTick, haremos predicciones utilizando nuestro modelo ONNX y luego mapearemos esas predicciones en acciones.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Get a prediction predict(); //--- Interpret the forecast intepret_prediction(); Comment("Model forecast",prediction[0]); }
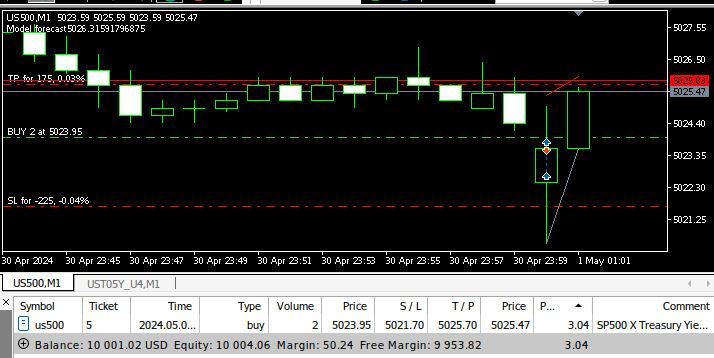
Figura 13: Nuestro asesor experto en acción.
Conclusión
En este artículo, revisamos la clásica estrategia comercial del SP500 que se basa en el rendimiento de los bonos del Tesoro. Nuestro análisis ha demostrado que la relación no siempre es estable y, además, parece que los inversores podrían obtener mejores resultados si utilizan datos de mercado ordinarios del propio índice SP500.
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/15531
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Algoritmo de optimización del comportamiento social adaptativo (ASBO): — Adaptive Social Behavior Optimization (ASBO): Evolución en dos fases
Algoritmo de optimización del comportamiento social adaptativo (ASBO): — Adaptive Social Behavior Optimization (ASBO): Evolución en dos fases
 Operar con noticias de manera sencilla (Parte 3): Ejecución de operaciones
Operar con noticias de manera sencilla (Parte 3): Ejecución de operaciones
 Creación de un modelo de restricción de tendencia de velas (Parte 8): Desarrollo de un asesor experto (I)
Creación de un modelo de restricción de tendencia de velas (Parte 8): Desarrollo de un asesor experto (I)
 Desarrollo de un sistema de repetición (Parte 76): Un nuevo Chart Trade (III)
Desarrollo de un sistema de repetición (Parte 76): Un nuevo Chart Trade (III)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
la última captura de pantalla (la más baja), ¿tiene algo que ver con el artículo y las estrategias mencionadas?
M1 timeframe y objetivos de varios pips :-)