Atmosphere Clouds Model Optimization (ACMO): Theory

Contents

1. Introduction
2. Implementation of the algorithm

Introduction

Finding the best solutions for optimization algorithms is becoming an increasingly important task nowadays. One of the most interesting approaches to this problem is the metaheuristic algorithm Atmosphere Clouds Model Optimization (ACMO), which, despite its mathematical complexity, can be explained simply and clearly. 

Imagine a vast virtual sky where clouds form and move just like in the real atmosphere. The weather here is not just a set of conditions, but a living system in which humidity and atmospheric pressure influence every decision. Inspired by natural phenomena, the ACMO algorithm uses principles of cloud formation to explore the solution space, similar to how clouds form, spread, and disappear in the sky, trying to find optimal paths. The algorithm was proposed by Yan et al. and published in 2013.

Here we will look at each step of the ACMO algorithm in detail, starting with preparing the "sky" where clouds are born as potential solutions. We will follow their movements through virtual celestial space, observing how they adapt and change depending on weather conditions. As you delve into this fascinating process, you will see how clouds, like research teams, strive to find optimal solutions in a maze of possibilities. Let's uncover the secrets of this algorithm together and understand how it works, step by step.

The main idea of the Atmosphere Clouds Model Optimization (ACMO) algorithm is to model the behavior of clouds in nature to solve optimization problems. The algorithm exploits three key aspects of cloud behavior:

• Generation. Clouds form in areas of high humidity, allowing the algorithm to explore the vicinity of current optimal solutions.
• Movement. Clouds move through the solution space, which promotes population spread and increases its diversity. This helps to avoid getting stuck in local optima.
• Spreading. The clouds are dispersed throughout the search space, allowing the algorithm to cover a wider range of possible solutions and improve the chances of finding a global optimum.

Implementation of the algorithm

Since the concept of the ACMO algorithm is quite complex to grasp, we will move from simple to complex. Let us describe the main idea of the algorithm as simply as possible.

1. Preparing the "sky". Imagine that we are creating a virtual sky. This sky is divided into many regions. Each region has its own humidity (quality of solutions) and atmospheric pressure (accumulated search experience).

2. Birth of clouds. Clouds appear only in the most "wet" regions. Every cloud is made up of many droplets, and each droplet is a potential solution to our problem.

3. Cloud movement. Clouds almost never stand still. They move from regions of high pressure to regions of low pressure. This is similar to how wind blows from an area of high pressure to an area of low pressure in the real atmosphere.

4. Changing the shape of clouds. As clouds move, they become larger. The extent to which clouds increase in size depends on the pressure difference between regions.

5. Evaporation. With each step the clouds lose a little of their drops and by losing moisture their humidity decreases. If a cloud becomes too dry, it disappears completely.

6. "Weather" update. After each cloud movement, the humidity and pressure in each region are revised. If the cloud has found a good solution, the humidity in that region increases.

7. Repetition. Repeat steps 2-6. With each repetition, the clouds explore more and more areas of the virtual sky in search of the best solution.

8. Completion. After completing a specified number of iterations or finding a good enough solution, the algorithm stops.

This algorithm is as if we sent many exploration groups (clouds) to search for a treasure (optimal solution) in a huge maze (search space). Each group searches in its own way, shares information with others through changing "weather" in the regions, and gradually together they find the best path.

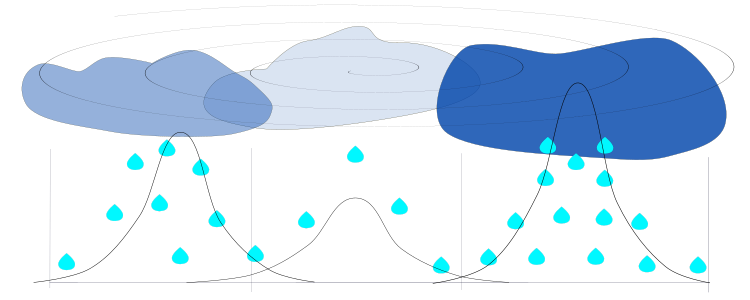
Figure 1. Clouds of varying density, humidity and size over regions. The precipitation of drops follows a normal distribution

First, let's get acquainted with the external parameters of ACMO and their purpose using the table below.

Parameter	The purpose of the parameter
popSize - population size	Droplet population size, fixed size population, and droplets distributed across clouds
cloudsNumber - amount of clouds	Cloud count
regionsNumber - number of regions	Each parameter to be optimized is divided into the same number of regions
dMin- minimum number of drops	The minimum number of drops in relation to the average number of drops in the clouds. The threshold below which a cloud is considered dry
λ - threshold factor	Threshold humidity factor of a region where a cloud with rain (droplet) generation can be formed
γ - drying ratio	Drying ratio that reduces the amount of moisture in clouds at each iteration
EnM0 - initial entropy	Initial entropy is the width of the cloud when it appears
HeM0 - initial hyperentropy	Hyperentropy - the density of a cloud when it appears. The parameter regulates the shape of the normal distribution

Next, let's look at the steps of the ACMO algorithm.

1. Initialization:

• U search space partitioning by MD regions of Ui areas.
• Initializing HUi humidity values and PUi atmospheric pressure for each region.
• Setting the algorithm parameters: λ threshold factor, γ drying ratio, EnM0 initial entropy, HeM0 initial hyperentropy and others.

2. Cloud generation:

• Defining multiple S regions, where HUi humidity exceeds a dynamically calculated Ht threshold.
• For each Ui region from S:
• Calculating the center of the CenterCk cloud using the equation CenterCk = Center (Ui).
• Calculating EnCk entropy and HeCk hypernetropy based on the initial entropy EnM0, HeM0 and the ζ contraction ratio.
• Generating Ck cloud with CenterCk center, EnCk entropy and HeCk hyperentropy.

3. Humidity and pressure update:

• Updating HUi humidity values and PUi atmospheric pressure for each Ui region.

4. Cloud movement phase:

• For each Ck cloud:
• Determining the direction of cloud movement based on the difference in atmospheric pressure between the current region and a selected neighboring region.
• Moving the Ck cloud in the direction of lower atmospheric pressure.

5. Cloud spread phase:

• For each Ck cloud:
• Determine which cloud droplets spread to other regions based on differences in atmospheric pressure.
• Spread of Ck cloud droplets to neighboring regions with lower atmospheric pressure.

6. Humidity and pressure update:

• Updating HUi humidity values and PUi atmospheric pressure for each Ui region after the movement and spread of clouds.

7. Checking the termination condition:

• Increase the t iteration counter.
• If t < tmax, pass to 2 (cloud generation).
• If t >= tmax, the algorithm terminates.

Key points:

• Ui regions form the search space, each region is characterized by HUi humidity and PUi atmospheric pressure.
• Ck clouds are generated only in regions with sufficient humidity (HUi > Ht).
• The movement and spread of clouds occur under the influence of the difference in atmospheric pressure between regions.
• Humidity and pressure values are updated after each cycle of cloud movement and spread.

Now let's look at the main cloud operations in more detail.

1. Cloudmove (C) operation is responsible for the movement of clouds.

1.1 For each Ck cloud:

• A random F target area is selected from the U search space.
• The ΔP pressure difference is calculated between the current E area, where the cloud is located, and the F target area.
• If the pressure in F is lower than in E (ΔP > 0), the Ck cloud will be moved towards an area of lower pressure.
• Vk cloud movement speed is calculated based on the pressure difference and the cloud entropy.
• The Ck cloud center is shifted by Vk.
• Amount of moisture in the Ck cloud is decreased by γ * 100% due to evaporation.
• If the number of drops nk becomes less than the dN threshold, the Ck cloud is removed from the multitude of clouds C (in fact, the cloud is not removed, but moved to regions with humidity above the threshold value with the initial values of entropy and hyperentropy set and adjusted for the current iteration).

Thus, clouds move towards areas of lower pressure, while their energy (amount of moisture) gradually decreases. This movement mechanism reflects the physical behavior of clouds in nature.

2. The Cloudspread (C) operation is responsible for the spread of clouds.

2.1 For each Ck cloud:

• Get the current E region the center of the cloud is located in.
• Get the G region the center of the cloud will move in after the movement phase.
• Calculate the pressure difference ΔP = PE - PG between the current and new regions.
• If E and G regions differ, calculate the spread factor α = ΔP / ΔPmax.
• If E and G regions match, set α = 0.3 (basic propagation speed).
• Calculate the new cloud entropy EnCk = EnCk × (1 + α), where α is a distribution factor.
• Calculate the cloud new hyperentropy HeCk = HeCk × (1 + α), i.e. it increases proportionally to the propagation factor.
• If the Ck cloud entropy exceeds 5 × EnM0 or the amount of moisture in it is less than the threshold value of dN, the Ck cloud is "removed" from the C set.

The main ideas of operations 1 and 2:

• The greater the pressure difference between regions, the faster the clouds move.
• Entropy is increased to expand the search space.
  
• The hyperentropy of the cloud increases to facilitate more detailed exploration of the space.
• Cloud dissipation criteria: the entropy exceeds 5 × EnM0 or the amount of moisture is less than dN.

In the description of the algorithm, the authors do not indicate any restrictions on the number of regions one cloud can cover. The algorithm considers only two regions: the current region E the center of the Ck cloud is located in and a new region G (new center after moving). However, the clouds increase in size at each iteration, encroaching on neighboring regions, leading to increased humidity and pressure in the areas where the droplets fall. Thus, one cloud can move sequentially from one region to another, but at any given moment in time the algorithm operates only with two regions - the current one and the new one. This means that cloud movement and droplet precipitation in regions are considered separately. Clouds and droplets are not related to each other and represent different entities within the algorithm.

The algorithm updates the cloud position, calculates new entropy and hyperentropy, and checks whether the cloud exceeds dissipation criteria, but does not impose explicit restrictions on the number of regions it can cover.

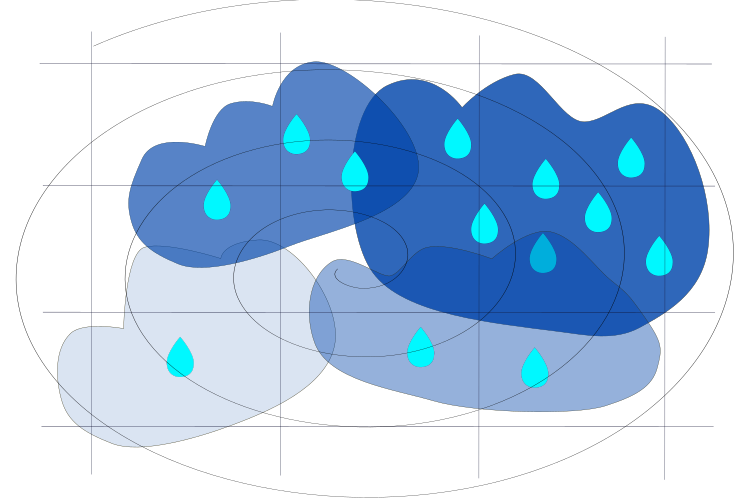
Figure 2. Movement of clouds across regions towards lower pressure

From the description of the algorithm it follows that the region (and not the cloud) has a certain "fitness function", namely the humidity in the region. The role of the cloud in this algorithm is more of an indicator that shows how many drops will fall in a given region. Key points:

1. The region has its own pressure P, which determines the speed of cloud propagation.
2. The Ck cloud does not "own" the drops, but serves as an indicator showing how many drops will fall in the current region E and the new region G.
3. Moving cloud from the region E to the region G is determined by the pressure gradient ΔP = PE - PG.
4. The drops do not belong to a specific cloud, but fall in the regions where the clouds are located.

Thus, the region, not the cloud, is the primary entity determining the dynamics of the "weather" in a given system. It can be emphasized that this is what distinguishes this algorithm from multi-population algorithms.

Pressure is an important characteristic of each region in the search space and is used to determine the direction of cloud movement, i.e. clouds move from high pressure areas to low pressure areas. Conceptually, the pressure in a region increases each time the region is evaluated (when the objective function value for a point in that region is calculated). This reflects the idea that the more we explore a particular area, the higher the "pressure" in that area becomes, prompting the algorithm to explore other, less explored areas.

According to the authors' algorithm, the change in cloud shape occurs depending on the difference in atmospheric pressure between the current region where the cloud is located and the new region where the cloud is moving. Specifically, this happens as follows:

• If the pressure difference ΔP = PE - PG is large, this means that the cloud is moving from an area with very different pressure and the speed of the cloud will be higher.
• If the pressure difference ΔP is small, this means that the cloud is moving into an area with a similar pressure value and at low speed.

Further, according to the description of the algorithm, the values of entropy and hyperentropy at the first iteration are determined as follows:

1. Initial entropy EnM0 = Ij / A, where:

• A is set at level 6
• Ij - region length in the j th dimension

2. Initial entropy HeM0 is set at the level 0.5.

Entropy in the algorithm determines how wide the cloud spreads (size). In the first iteration, the cloud should cover at least one entire search region.

Hyperentropy is responsible for the "thickness" of the cloud and regulates the shape of the normal distribution, or, in other words, how densely the droplets are located in the cloud. The initial value of 0.5 is chosen experimentally as a balance between a cloud that is too thin and one that is too dense.

1. Entropy increases with each iteration. This means that the clouds gradually "stretch" to cover larger and larger search areas and helps avoid getting stuck in local optima
2. Hyperentropy, on the contrary, increases the density in the center of the cloud. This results in the cloud refining the solution of the prospective region.

This approach allows the algorithm to simultaneously refine solutions while expanding the search area and at the same time retain the ability to "escape" from local optima.

In a multidimensional space, defining a region index for a cloud becomes a little more complicated, but the principle remains the same. How it works:

• The search space is divided into regions across all dimensions. If we have D dimensions and each dimension is divided into M intervals, we will have M × D regions in total.
• The region index in this case is not just a number, but a set of coordinates showing the region position along each dimension. To determine the region index for a cloud, the algorithm checks which intervals along each dimension the cloud center falls into.

For example, if we have a three-dimensional space (D = 3) divided into 10 intervals for each dimension (M = 10), the region index may look like (3, 7, 2), which means the 3 rd interval along the first dimension, the 7 th along the second, and the 2 nd along the third.

It is necessary to pay attention to the center of the cloud, which is not necessarily the best drop of the cloud. Here are some important points:

• The cloud center is defined as a certain "midpoint" of the region the cloud is generated in.
• The best drop in the cloud is the one that gives the best value of the objective function (the highest fitness value).
• The algorithm contains the concept of "region humidity value" (UiH), which represents the best fitness value found in a given region. This value is related to the best drop, not the cloud center.
• The cloud center is used to determine the position of the cloud in the search space and to calculate its motion, but it does not necessarily correspond to the best solution.

Thus, the cloud center and the best drop are different concepts in this algorithm. The center is used to navigate the cloud in the search space, while the best droplet represents the most optimal solution found in the region at the current moment.

This approach allows the algorithm to efficiently explore the search space (using the cloud center for movement) while tracking and storing the best solutions found in the regions (the best drops that fell in the regions).

There are several cases in the ACMO algorithm where clouds are destroyed or "dissolved". Let's take a look at them:

1. Insufficient moisture:

• Each cloud has a certain amount of moisture.
• If the amount of moisture becomes less than the dN threshold value, the cloud is considered too dry and disappears.
• It is similar to how small clouds disperse in nature.

2. Too much entropy:

• The entropy of a cloud shows how widespread it is.
• If the entropy becomes greater than 5 times the initial entropy (5 × EnM0), the cloud is considered too diffuse and disappears.

It can be imagined as a cloud that has stretched so much that it simply disappears into thin air.

3. Natural evaporation:

• After each movement of the cloud, the amount of its moisture decreases by a certain percentage (γ * 100%).
• If after such a reduction the amount of moisture becomes less than dN, the cloud disappears.

It is similar to the gradual evaporation of a cloud in nature.

4. When clouds merge:

• Although this is also not explicitly described in the algorithm, in some ACMO variants clouds can merge.
• When a merger occurs, one of the clouds (usually the smaller one) may seem to disappear, becoming part of the larger cloud.

All these cloud-destroying mechanisms help the algorithm to "cleanse" the search space from unpromising solutions and concentrate on the most promising areas. 

You might wonder: what would happen if clouds began to move into low pressure areas and all gathered together in the same regions? First, low-pressure regions are not the worst solutions in the search space; they are simply regions that are poorly explored. Even if all the clouds are concentrated in regions with the lowest pressure, they will gradually begin to increase the pressure in these areas. At some point this will lead to the emergence of new regions of lower pressure, which will inevitably force the clouds to leave their current location.

Thus, clouds never stay in one place for long and move both in areas of high-quality solutions and in less promising ones. In addition, the mechanisms of cloud evaporation and their continuous expansion, followed by their destruction, allow the creation of new clouds to replace those destroyed in good regions. This initiates a new cycle of refining promising areas of the search space.

Determining the center of a new Ck cloud. If the humidity value in a region exceeds a threshold, it can generate a new cloud. Humidity threshold Ht is calculated dynamically using the equation:

Ht = Hmin + λ * (Hmax - Hmin), where:

• Hmin and Hmax - minimum and maximum humidity values in the entire search area accordingly
• λ - threshold factor equal to 0.7 based on experimental tests

Calculation of entropy and hyperentropy. The importance of entropy for new clouds EnM decreases during the search and is set by the equation:

EnMt = ζ * EnM0, where ζ is a compression ratio calculated using the equation:

ζ = 1 / (1 + e^(- (8 - 16 * (t / tmax))))

The hyperentropy of newly generated clouds increases with each iteration:

HeMt = ζ * HeM0, where ζ acts as expansion ratio calculated using the equation:

ζ = 1 / (1 + e^(8 - 16 * (t / tmax))), where:

• EnM0j - initial entropy equal to 0.2
  
• HeM0 - initial hyperentropy equal to 0.5
• t - current iteration
• tmax - maximum number of iterations

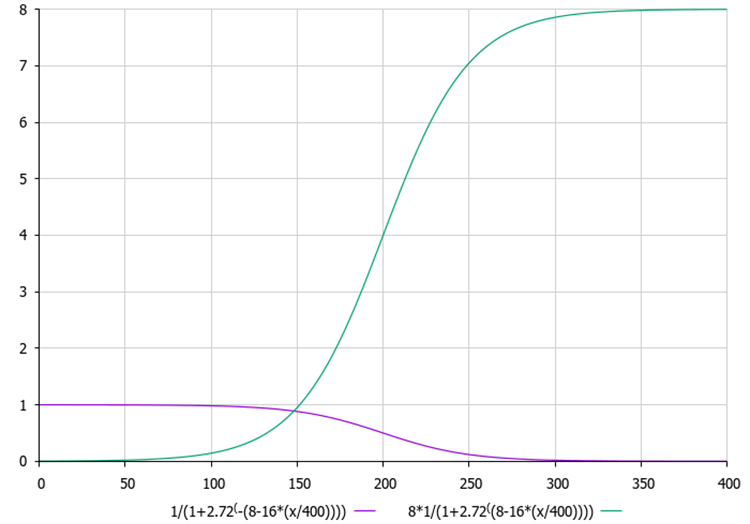
Figure 3. Entropy and hyperentropy graphs for new clouds depending on the current epoch

The speed of cloud movement obeys the following law:

Vk = β * EnCk, where β is expressed by the equation:

β = (PCk - PF) / (PMax - PMin), where:

• β is an atmospheric pressure factor
• PMax and PMin - maximum and minimum atmospheric pressure in the search space
  
• PCk and PF - pressure in the current and target region
• EnCk - current cloud entropy
  

Now that we know the whole theory of the ACMO atmospheric cloud motion model, let's start implementing the algorithm code.

Describe the S_ACMO_Region structure used to represent a region with meteorological characteristics. The S_ACMO_Region structure contains several fields, each storing information about the region:

Structure fields:

• humidity - humidity level in the region.
• pressure - atmospheric pressure in the region.
• centre - center of the region in the form of a vector of coordinates denoting the central point.
• x - point of the highest pressure in the region.

Init() - initialization method that sets the initial values for the structure fields.

• humidity is initialized with the value "-DBL_MAX", indicating extremely low humidity levels.
• pressure - initialized to zero because the pressure has not yet been measured.

The S_ACMO_Region structure is used in a meteorological model where it is necessary to store and process information about different regions in terms of their climatic conditions. The Init () method ensures that the structure is properly initialized before use. 

//——————————————————————————————————————————————————————————————————————————————
// Region structure
struct S_ACMO_Region
{
    double humidity; //humidity in the region
    double pressure; //pressure in the region
    double centre;   //the center of the region
    double x;        //point of highest pressure in the region

    void Init ()
    {
      humidity = -DBL_MAX;
      pressure = 0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Next, describe two structures: S_ACMO_Area and S_ACMO_Cloud and consider them in detail:

 1. The S_ACMO_Area structure represents a region consisting of an array of regions described by the structure S_ACMO_Region and contain information about several regions in a given area.

 2. The S_ACMO_Cloud structure represents the cloud and its characteristics. Structure fields:

• center [] - array stores the coordinates of the cloud center.
• entropy [] - array of cloud entropy values for each coordinate.
  
• entropyStart [] - array of initial entropy values.
• hyperEntropy - hyperentropy value.
  
• regionIndex [] - array of indices of regions the clouds belong to.
• droplets - number of drops in a cloud (a conventional concept denoting the humidity of a cloud).

The Init (int coords) method initializes arrays in the structure, changing their size depending on the passed coords parameter.

Both structures are used in the meteorological model to represent and analyze regions and clouds. S_ACMO_Area is used to group regions, while S_ACMO_Cloud is used to describe the characteristics of clouds.

//——————————————————————————————————————————————————————————————————————————————
struct S_ACMO_Area
{
    S_ACMO_Region regions [];
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Cloud structure
struct S_ACMO_Cloud
{
    double center       [];    // cloud center
    double entropy      [];    // entropy
    double entropyStart [];    // initial entropy
    double hyperEntropy;       // hyperEntropy
    int    regionIndex  [];    // index of regions
    double droplets;           // droplets

    void Init (int coords)
    {
      ArrayResize (center,       coords);
      ArrayResize (entropy,      coords);
      ArrayResize (entropyStart, coords);
      ArrayResize (regionIndex,  coords);
      droplets = 0.0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Let's take a look at the C_AO_ACMO class inherited from another C_AO class. Class general structure:

1. Class parameters that play the role of external parameters of the algorithm:

• popSize - population size.
• cloudsNumber - number of clouds.
• regionsNumber - number of regions per dimension.
• dMin - minimum number of drops relative to the average number of drops in the clouds.
• EnM0 and HeM0 - initial values of entropy and hyperentropy.
• λ - threshold factor for determining rainy regions.
• γ - rate of weakening.

2. Parameter array:

• params - array of structures where each element contains the name and value of the parameter.

3.  Methods:

• SetParams () - model parameters from the "params" array.
• Init () - initialize the model with the specified search boundaries, step and number of epochs.
• Moving () - method is responsible for the movement of clouds.
• Revision () - method that performs a revision of the model state.
• MoveClouds () - method responsible for the movement of clouds.
• GetRegionIndex () - method for obtaining the region index for a given point.
• RainProcess() - method responsible for the rain.
• DropletsDistribution () - method for distributing droplets over clouds.
• UpdateRegionProperties () - method for updating region properties.
• GenerateClouds () - method for generating clouds.
• CalculateHumidityThreshold () - method for calculating the humidity threshold.
• CalculateNewEntropy () - method for calculating new entropy for a cloud.

4. Class members:

   S_ACMO_Area areas [] - array of areas contains information about different regions.

   S_ACMO_Cloud clouds [] - cloud array contains information about cloud characteristics.

   Private variables such as epochs, epochNow, dTotal, entropy [] and minGp are used to track the state of the model and calculations.

The C_AO_ACMO class is meant to simulate and move clouds in the atmosphere. It includes various parameters and methods that allow you to manage the state of clouds, their movement and interaction with regions.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACMO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ACMO () { }
  C_AO_ACMO ()
  {
    ao_name = "ACMO";
    ao_desc = "Atmospheric Cloud Model Optimization";
    ao_link = "https://www.mql5.com/en/articles/15849";

    popSize       = 50;    //population size

    cloudsNumber  = 5;     // Number of clouds
    regionsNumber = 10;    // Number of regions per dimension  (M)
    dMin          = 0.2;   // Minimum number of drops relative to the average number of drops in the clouds (dN)
    EnM0          = 1.0;   // Initial value of entropy
    HeM0          = 0.5;   // Initial value of hyperentropy
    λ             = 0.7;   // Threshold factor (threshold of the rainiest regions)
    γ             = 0.2;   // Weaken rate

    ArrayResize (params, 8);

    params [0].name = "popSize";       params [0].val = popSize;

    params [1].name = "cloudsNumber";  params [1].val = cloudsNumber;
    params [2].name = "regionsNumber"; params [2].val = regionsNumber;
    params [3].name = "dMin";          params [3].val = dMin;
    params [4].name = "EnM0";          params [4].val = EnM0;
    params [5].name = "HeM0";          params [5].val = HeM0;
    params [6].name = "λ";             params [6].val = λ;
    params [7].name = "γ";             params [7].val = γ;
  }

  void SetParams ()
  {
    popSize       = (int)params [0].val;

    cloudsNumber  = (int)params [1].val;
    regionsNumber = (int)params [2].val;
    dMin          = params      [3].val;
    EnM0          = params      [4].val;
    HeM0          = params      [5].val;
    λ             = params      [6].val;
    γ             = params      [7].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    cloudsNumber;  // Number of clouds
  int    regionsNumber; // Number of regions per dimension (M)
  double dMin;          // Minimum number of drops relative to the average number of drops in the clouds (dN)
  double EnM0;          // Initial value of entropy
  double HeM0;          // Initial value of hyperentropy
  double λ;             // Threshold factor
  double γ;             // Weaken rate


  S_ACMO_Area   areas  [];
  S_ACMO_Cloud  clouds [];

  private: //-------------------------------------------------------------------
  int    epochs;
  int    epochNow;
  int    dTotal;         // Maximum total number of droplets (N)
  double entropy [];     // Entropy
  double minGp;          // Minimum global pressure


  void   MoveClouds                 (bool &rev);
  int    GetRegionIndex             (double point, int ind);
  void   RainProcess                (bool &rev);
  void   DropletsDistribution       (double &clouds [], int &droplets []);

  void   UpdateRegionProperties     ();

  void   GenerateClouds             ();
  double CalculateHumidityThreshold ();
  void   CalculateNewEntropy        (S_ACMO_Cloud &cl, int t);
};
//——————————————————————————————————————————————————————————————————————————————

Next, let's have a look at the Init method of the C_AO_ACMO class responsible for initializing the parameters of the cloud model.

1. The method accepts three arrays (rangeMinP, rangeMaxP and rangeStepP) that describe the boundaries and steps for the model parameters. The fourth parameter is epochsP. It is set to 0 by default and specifies the number of epochs.

2. Calling the StandardInit method to perform basic initialization. If it is not successful, the method returns false.

3. Initialization of variables: The method sets the total number of epochs and resets the current epoch to 0.

4. Initialization of parameters:

• dTotal - set equal to the population size.
• dMin - recalculated taking into account the relationship between the population size and the number of clouds.

5. Array memory allocation: the method resizes the entropy and areas arrays according to the number of coordinates.

6. Initialization of entropy and regions:

• the entropy value is calculated for each c coordinate.
• for each r region, the Init () method is called to initialize the region.
• the center of a region is calculated as the average value between the minimum and maximum values, multiplied by the number of regions.
• then the center goes through the SeInDiSp method, which normalizes values to a given range.
• the x coordinate is set for a region (the highest humidity value, by default located in the center of the region).
  

7. Cloud initialization:

• resize the clouds array according to the amount of clouds.
• the Init method is called for each cloud to initialize parameters.

The Init method performs basic setup and initialization of the cloud model, setting the necessary parameters, array sizes and values for further simulation. It is structured to first perform standard initialization of the parent class, and then configure specific parameters related to coordinates, regions and clouds.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ACMO::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  //----------------------------------------------------------------------------
  dTotal       = popSize;
  dMin         = dMin * (popSize / (double)cloudsNumber);

  ArrayResize (entropy, coords);
  ArrayResize (areas,   coords);

  for (int c = 0; c < coords; c++)
  {
    entropy [c] = (rangeMax [c] - rangeMin [c]) / regionsNumber;

    ArrayResize (areas [c].regions, regionsNumber);

    for (int r = 0; r < regionsNumber; r++)
    {
      areas [c].regions [r].Init ();
      areas [c].regions [r].centre = rangeMin [c] + entropy [c] * (r + 0.5);
      areas [c].regions [r].centre = u.SeInDiSp (areas [c].regions [r].centre, rangeMin [c], rangeMax [c], rangeStep [c]);
      areas [c].regions [r].x      = areas [c].regions [r].centre;
    }
  }

  ArrayResize (clouds, cloudsNumber);
  for (int i = 0; i < cloudsNumber; i++) clouds [i].Init (coords);

  minGp = DBL_MAX;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Summary

In this article, we delved into the world of the unusual and fascinating ACMO algorithm, which is an atmospheric meteorological model designed to solve multidimensional optimization problems. This algorithm may seem multi-population at first glance, but a deeper analysis reveals its uniqueness and novelty.

The model is based on three key entities: clouds, regions and droplets. Each of these components functions independently, but their interaction creates a harmonious and efficient system, where each part plays its important role. Clouds symbolize the diversity of solutions, regions represent search spaces, and droplets are elements that make transitions between different solutions. This combination makes the ACMO algorithm not only original, but also a very powerful tool in the field of optimization.

In the second part of the article we will take a step from theory to practice. We will test the algorithm on various test functions to evaluate its performance and identify its strengths. Besides, we will analyze the results and, perhaps, open new horizons for the application of this innovative model in real-life problems.