Neuronale Netze im Handel: Ein parameter-effizienter Transformer mit segmentierter Aufmerksamkeit (PSformer)

Einführung

Die Vorhersage multivariater Zeitreihen ist eine wichtige Aufgabe im Bereich des Deep Learning, mit praktischen Anwendungen in der Meteorologie, Energie, Anomalieerkennung und Finanzanalyse. Mit dem raschen Fortschritt der künstlichen Intelligenz wurden erhebliche Anstrengungen unternommen, um innovative Modelle zu entwickeln, die die Vorhersagegenauigkeit verbessern. Insbesondere transformerbasierte Architekturen haben aufgrund ihrer erwiesenen Effektivität bei der Verarbeitung natürlicher Sprache und beim Computersehen große Aufmerksamkeit auf sich gezogen. Darüber hinaus haben groß angelegte, vorab trainierte Transformer-Modelle bei der Vorhersage von Zeitreihen eine starke Leistung gezeigt und gezeigt, dass eine Erhöhung der Modellparameter und der Trainingsdaten die Vorhersagefähigkeiten erheblich verbessern kann.

Gleichzeitig erzielen viele einfache lineare Modelle wettbewerbsfähige Ergebnisse im Vergleich zu komplexeren transformerbasierten Architekturen. Ihr Erfolg bei der Zeitreihenprognose ist wahrscheinlich auf ihre geringere Komplexität zurückzuführen, die das Risiko einer Überanpassung an verrauschte oder irrelevante Daten verringert. Selbst bei begrenzten Datensätzen können diese Modelle stabile, verlässliche Muster effektiv erfassen.

Um die Herausforderungen bei der Modellierung langfristiger Abhängigkeiten und der Erfassung komplexer zeitlicher Beziehungen zu bewältigen, wurde das PatchTST Ansatz Daten mit Hilfe von Patching-Techniken, um die lokale Semantik zu extrahieren und eine hohe Leistung zu erzielen. PatchTST verwendet jedoch kanalunabhängige Strukturen und bietet ein erhebliches Potenzial für eine weitere Verbesserung der Modellierungseffizienz. Darüber hinaus bietet die Einzigartigkeit multivariater Zeitreihen, deren zeitliche und räumliche Dimensionen sich erheblich von anderen Datentypen unterscheiden, viele unerforschte Möglichkeiten.

Eine Möglichkeit, die Modellkomplexität beim Deep Learning zu reduzieren, ist die gemeinsame Nutzung von Parametern (PS), die die Anzahl der Parameter erheblich verringert und gleichzeitig die Recheneffizienz verbessert. In Faltungsnetzen teilen sich die Filter die Gewichte über räumliche Positionen hinweg und extrahieren lokale Merkmale mit weniger Parametern. In ähnlicher Weise teilen sich LSTM-Modelle Gewichtsmatrizen über Zeitschritte hinweg und verwalten so Speicher und Informationsfluss. Bei der Verarbeitung natürlicher Sprache wurde die gemeinsame Nutzung von Parametern auf Transformer ausgedehnt, indem Gewichte schichtenübergreifend wiederverwendet werden, wodurch die Redundanz ohne Leistungseinbußen verringert wird.

Beim Multitasking-Lernen sorgt dieTAPS-Methode (Task-Adaptive Parameter Sharing ) für eine selektive Feinabstimmung der aufgabenspezifischen Schichten, indem sie die gemeinsame Nutzung von Parametern maximiert und gleichzeitig effizientes Lernen mit minimalen aufgabenspezifischen Anpassungen ermöglicht. Die Forschung zeigt, dass die gemeinsame Nutzung von Parametern die Modellgröße reduzieren, die Generalisierung verbessern und das Risiko der Überanpassung bei verschiedenen Aufgaben verringern kann.

Die Autoren von „PSformer: Parameter-efficient Transformer with Segment Attention for Time Series Forecasting“ schlagen ein innovatives Transformer-basiertes Modell für die multivariate Zeitreihenprognose vor, das die Prinzipien der gemeinsamen Nutzung von Parametern berücksichtigt.

Sie stellen einen Encoder für den Transformer mit einem zweistufigen segmentbasierten Aufmerksamkeitsmechanismus vor, bei dem jede Encoderschicht einen Block mit gemeinsamen Parametern enthält. Dieser Block enthält drei vollständig verbundene Schichten mit Residualverbindungen, die eine geringe Gesamtzahl von Parametern ermöglichen und gleichzeitig einen effektiven Informationsaustausch zwischen den Modellkomponenten gewährleisten. Um die Aufmerksamkeit innerhalb der Segmente zu fokussieren, wenden sie eine Patching-Methode an, bei der variable Sequenzen in separate Patches aufgeteilt werden. Patches, die in verschiedenen Variablen dieselbe Position einnehmen, werden dann zu Segmenten gruppiert. Im Ergebnis ist jedes Segment eine räumliche Erweiterung eines Patches einer Variablen, wodurch eine mehrdimensionale Zeitreihe in mehrere Segmente unterteilt werden kann.

Innerhalb jedes Segments verbessern Aufmerksamkeitsmechanismen die Erfassung lokaler räumlich-zeitlicher Beziehungen, während die Integration segmentübergreifender Informationen die Prognosegenauigkeit insgesamt verbessert. Die Autoren setzen auch die Optimierungsmethode SAM ein, um die Überanpassung weiter zu reduzieren, ohne die Lernleistung zu beeinträchtigen. Ausführliche Experimente mit langfristigen Zeitreihenprognosedatensätzen zeigen, dass PSformer gute Ergebnisse liefert. PSformer übertrifft die modernsten Modelle in 6 von 8 wichtigen Vorhersage-Benchmarks.

Der Algorithmus von PSformer

Eine multivariate Zeitreihe X ∈ RM×L enthält M Variablen und ein Rückblicksfenster der Länge L. Die Sequenzlänge L wird gleichmäßig in N nicht überlappende Felder der Größe P unterteilt. Dann bildet P(i) aus den M Variablen das i-te Segment, das einen Querschnitt der Länge C darstellt (wobei C=M×P).

Die Schlüsselkomponenten von PSformer sind Segment Attention(SegAtt) und der Parameter-Sharing Block(PS). Der PSformer-Encoder dient als Kern des Modells und enthält sowohl das SegAtt-Modul als auch den PS-Block. Der PS-Block liefert Parameter für alle Encoderebenen durch gemeinsame Nutzung von Parametern.

Wie in anderen Architekturen für Zeitreihenprognosen verwenden die Autoren von PSformer die RevIN Methode, um die Probleme der Verteilungsverschiebung wirksam anzugehen.

Die räumlich-zeitliche Segmentaufmerksamkeit (SegAtt) fasst Patches aus verschiedenen Kanälen an derselben Position zu einem Segment zusammen und stellt räumlich-zeitliche Beziehungen zwischen den Segmenten her. Konkret bedeutet dies, dass die ursprüngliche Zeitreihe X ∈ RM×L wird zunächst in Felder mit L=P×N unterteilt und dann in X ∈ R(M×P)×N umgewandelt, indem die Dimensionen M und P zusammengeführt werden. Daraus ergibt sich X ∈ RC×N (wobei C=M×P), was eine kanalübergreifende Informationsfusion ermöglicht.

In diesem transformierten Raum werden die Daten von zwei aufeinanderfolgenden Modulen mit identischer Architektur verarbeitet, die durch eine ReLU-Aktivierung getrennt sind. Jedes Modul enthält einen Block zur gemeinsamen Nutzung von Parametern und einen Mechanismus zur Selbstkontrolle, der uns bereits bekannt ist. Während die Berechnung der Matrizen 𝑸uery ∈ RC×N, 𝑲ey ∈ RC×N und 𝑽alue ∈ RC×N nichtlineare Transformationen der Eingabe Xin entlang der Segmente in N-dimensionale Darstellungen beinhaltet, verteilt das skalierte Punktprodukt die Aufmerksamkeit in erster Linie auf die gesamte Dimension C. Auf diese Weise kann das Modell Abhängigkeiten zwischen räumlich-zeitlichen Segmenten sowohl kanal- als auch zeitübergreifend erlernen.

Dieser Mechanismus integriert Informationen aus verschiedenen Segmenten durch die Berechnung von Q, K und V. Es erfasst auch lokale räumlich-zeitliche Abhängigkeiten innerhalb jedes Segments und modelliert gleichzeitig langfristige Beziehungen zwischen den Segmenten über längere Zeiträume. Die endgültige Ausgabe ist Xout ∈ RC×N womit der Aufmerksamkeitsprozess abgeschlossen ist.

PSformer führt einen neuen Parameter Shared Block (PS Block) ein, der aus drei vollständig verbundenen Schichten mit Residualverbindungen besteht. Konkret werden drei lernbare lineare Zuordnungen Wj ∈ RN×N с j ∈ {1, 2, 3} verwendet. Die Ausgaben der ersten beiden Schichten werden wie folgt berechnet:

Diese Struktur ist analog zu einem FeedForward-Block mit Residualverbindungen. Der Zwischenausgang 𝑿out dient dann als Eingang für die dritte Transformation:

Insgesamt kann der PS-Block wie folgt ausgedrückt werden:

Die Blockstruktur von PS ermöglicht nicht-lineare Transformationen unter Beibehaltung der Trajektorie einer linearen Abbildung. Obwohl drei Schichten im PS-Block unterschiedliche Parameter haben, wird der gesamte PS-Block über mehrere Positionen im Encoder von PSformer wiederverwendet, wodurch sichergestellt wird, dass derselbe 𝑾S Blockparameter für alle diese Positionen gemeinsam sind. Konkret werden die Parameter des PS-Blocks in drei Teilen jedes PSformer-Encoders gemeinsam genutzt: einschließlich der beiden SegAtt-Module und des abschließenden PS-Blocks. Durch diese Strategie der gemeinsamen Nutzung von Parametern wird die Gesamtzahl der Parameter reduziert, während die Aussagekraft des Modells erhalten bleibt.

Der zweistufige Mechanismus von SegAtt kann mit einem FeedForward-Block in einem einfachen Transformer verglichen werden, bei dem die MLP durch Aufmerksamkeitsoperationen ersetzt wird. Residualverbindungen werden zwischen dem Eingang und dem Ausgang addiert, und das Ergebnis wird an den letzten PS-Block weitergeleitet.

Anschließend wird eine Dimensionstransformation durchgeführt, um 𝑿o⁢ut ∈ RM×Lzu erhalten, wobei C=M×P and L=P×N.

Nach dem Durchlaufen von n Schichten des PSformers wird eine abschließende Transformation vorgenommen, um den Output auf den Prognosehorizont F zu projizieren.

wobei 𝑿pred ∈ RM×F and 𝑾F ∈ RL×F eine lineare Abbildung darstellt.

Die Originalvisualisierung des Rahmens von PSformer finden Sie unten.

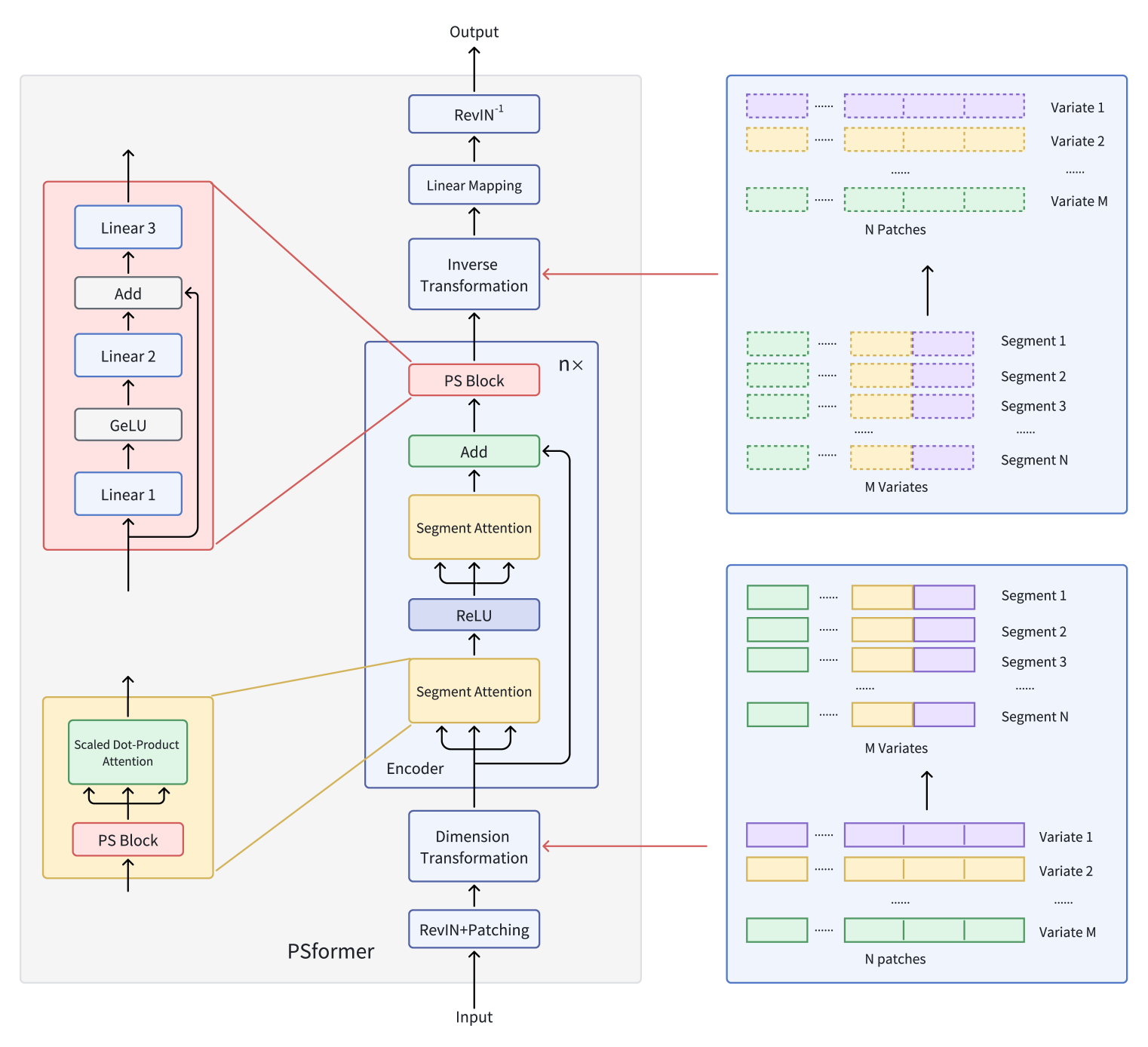
Die Implementation in MQL5

Nachdem wir die theoretischen Aspekte des Rahmens von PSformer behandelt haben, gehen wir nun zur praktischen Umsetzung unserer Vision der vorgeschlagenen Ansätze mit MQL5 über. Von besonderem Interesse ist für uns der Algorithmus zur Implementierung des Parameter-Sharing-Blocks (PS).

Parameter Gemeinsamer Block

Wie bereits erwähnt, besteht der PS-Block in der ursprünglichen Implementierung der Autoren aus drei vollständig verbundenen Schichten, deren Parameter auf alle analysierten Segmente angewendet werden. Aus unserer Sicht gibt es nichts Kompliziertes. Wir haben in ähnlichen Situationen wiederholt Faltungsschichten mit nicht überlappenden Analysefenstern eingesetzt. Die eigentliche Herausforderung liegt woanders: in dem Mechanismus für die gemeinsame Nutzung von Parametern durch mehrere Blöcke.

Einerseits könnten wir sicherlich denselben Block innerhalb einer einzigen Schicht mehrfach verwenden. Dies führt jedoch zu dem Problem, dass die Daten für den Rückwärtsdurchlauf erhalten bleiben müssen. Wenn ein Objekt für mehrere Vorwärtsdurchläufe wiederverwendet wird, speichert der Ergebnispuffer neue Ausgaben und überschreibt die Ausgaben der vorherigen Vorwärtsdurchläufe. In einem typischen Arbeitsablauf mit neuronalen Schichten ist dies kein Problem, da wir stets zwischen Vorwärts- und Rückwärtsdurchläufe wechseln. Nach jedem Rückwärtsdurchlauf werden die Ergebnisse des vorangegangenen Vorwärtsdurchlaufs nicht mehr benötigt und können sicher überschrieben werden. Wenn diese Abwechslung jedoch unterbrochen wird, stehen wir vor dem Problem, alle für einen korrekten Rückwärtsdurchlauf erforderlichen Daten zu erhalten.

In solchen Fällen müssen wir nicht nur die endgültigen Ausgaben des Blocks, sondern auch alle Zwischenwerte speichern. Oder wir müssen sie neu berechnen, was die Rechenkomplexität des Modells erhöht. Außerdem wird ein Mechanismus benötigt, um die Puffer an bestimmten Punkten zu synchronisieren, damit der Fehlergradient korrekt berechnet werden kann.

Es ist klar, dass die Umsetzung dieser Anforderungen Änderungen an unseren Datenaustauschschnittstellen zwischen den neuronalen Schichten erfordern würde. Dies wiederum würde umfassendere Änderungen an unserer Bibliotheksfunktionalität nach sich ziehen.

Die zweite Möglichkeit besteht darin, einen Mechanismus für die gemeinsame Nutzung eines einzigen Parameterpuffers durch mehrere identische neuronale Schichten zu schaffen. Dieser Ansatz ist jedoch nicht ohne „versteckte Fallstricke“.

Erinnern Sie sich daran, dass wir bei der Erforschung des Deep Deterministic Policy Gradient wir einen Algorithmus zur Aktualisierung der weichen Parameter des Zielmodells implementiert haben. Das Kopieren der Parameter nach jeder Aktualisierung ist jedoch sehr rechenintensiv. Idealerweise würden wir die Parameterpuffer in den entsprechenden Objekten durch gemeinsame Parametermatrizen ersetzen.

Hier müssen wir nicht nur die Parametermatrix selbst, sondern auch die bei der Aktualisierung der Parameter verwendeten Impulspuffer gemeinsam nutzen. Die Verwendung von separaten Impulspuffern in verschiedenen Phasen kann dazu führen, dass der Vektor der Parameteraktualisierung auf eine der internen Schichten ausgerichtet wird.

Es gibt einen weiteren kritischen Punkt. Bei dieser Implementierung können sich die im Rückwärtsdurchlauf verwendeten Parameter von denen im Vorwärtsdurchlauf unterscheiden. Dies mag ungewöhnlich klingen, aber lassen Sie uns dies anhand eines einfachen Beispiels mit zwei aufeinanderfolgenden Ebenen veranschaulichen, die gemeinsame Parameter haben. Während des Vorwärtsdurchlauf verwenden beide Schichten die Parameter W und erzeugen die Ausgabe O1 bzw. O2. In der Phase der Gradientenverteilung berechnen wir die Fehlergradienten G1 bzw. G2. SO ist der Prozess der Fehlergradientenfortpflanzung korrekt. In diesem Stadium bleiben die Modellparameter unverändert, und alle Fehlergradienten entsprechen korrekt den Parametern W der Vorwärtsdurchlauf. Wenn wir jedoch die Parameter in einer der Schichten, z. B. der zweiten, aktualisieren, erhalten wir angepasste Parameter W'. Wir stoßen sofort auf eine Unstimmigkeit: Die Fehlergradienten entsprechen nicht mehr den aktualisierten Parametern. Die direkte Anwendung eines unpassenden Gradienten kann den Trainingsprozess verzerren.

Eine Lösung für dieses Problem besteht darin, die Zielwerte für eine bestimmte Schicht auf der Grundlage der Ausgaben des letzten Vorwärtsdurchlaufs und der entsprechenden Fehlergradienten zu bestimmen und dann einen neuen Vorwärtsdurchlauf mit den aktualisierten Parametern durchzuführen, um einen korrigierten Fehlergradienten zu berechnen. Wenn Ihnen das bekannt vorkommt, liegt das daran, dass dieser Ansatz dem Optimierungsalgorithmus SAM, den wir in früheren Artikeln besprochen haben, sehr ähnlich ist. Durch Hinzufügen von Parameteraktualisierungen vor der Ausführung des wiederholten Vorwärtsdurchlaufs erhalten wir nämlich das vollständige Optimierungsverfahren SAM.

Genau aus diesem Grund empfehlen die Autoren des Frameworks von PSformer die Optimierung von SAM. Auf diese Weise können wir das Risiko von Unstimmigkeiten zwischen Gradienten und Parametern tolerieren, da die Gradienten vor der Aktualisierung der Parameter neu berechnet werden. In anderen Szenarien könnten solche Unstimmigkeiten jedoch ein ernstes Problem darstellen.

In Anbetracht all dieser Überlegungen haben wir uns für den zweiten Ansatz entschieden - die gemeinsame Nutzung von Parameterpuffern durch identische Schichten.

Wie bereits erwähnt, verwendet der PS-Block in der Originalarbeit drei vollständig verknüpfte Schichten, die wir durch Faltungsschichten ersetzen. Daher beginnen wir unsere Implementierung der gemeinsamen Nutzung von Parametern mit dem Objekt CNeuronConvSAMOCL für Faltungsschichten.

In unserer Faltungsschicht zur gemeinsamen Nutzung von Parametern ersetzen wir nur die Zeiger auf die Parameter- und Impulspuffer. Alle anderen Puffer und internen Variablen müssen weiterhin den Dimensionen der Parametermatrix entsprechen. Dies erfordert natürlich Anpassungen in der Initialisierungsmethode des Objekts. Zuvor müssen wir zwei Hilfsmethoden erstellen: InitBufferLike und ReplaceBuffer.

InitBufferLike erstellt einen neuen Puffer, der mit Nullwerten gefüllt wird, basierend auf einem gegebenen Referenzpuffer. Der Algorithmus ist recht einfach. Er akzeptiert zwei Zeiger auf Datenpufferobjekte als Parameter. Zunächst wird geprüft, ob der Referenzpufferzeiger (Master) gültig ist. Das Vorhandensein eines gültigen Referenzzeigers ist für nachfolgende Operationen entscheidend. Schlägt diese Prüfung fehl, bricht die Methode ab und gibt false zurück.

bool CNeuronConvSAMOCL::InitBufferLike(CBufferFloat *&buffer, CBufferFloat *master)
  {
   if(!master)
      return false;

Wenn der erste Prüfpunkt erfolgreich durchlaufen wurde, prüfen wir die Relevanz des Zeigers auf den erstellten Puffer. Wenn wir hier jedoch ein negatives Ergebnis erhalten, erstellen wir einfach eine neue Instanz des Objekts.

   if(!buffer)
     {
      buffer = new CBufferFloat();
      if(!buffer)
         return false;
     }

Vergessen Sie nicht zu überprüfen, ob der neue Puffer korrekt angelegt wurde.

Als Nächstes initialisieren wir den Puffer in der gewünschten Größe mit Nullwerten.

   if(!buffer.BufferInit(master.Total(), 0))
      return false;

Dann erstellen wir seine Kopie im Kontext von OpenCL.

   if(!buffer.BufferCreate(master.GetOpenCL()))
      return false;
//---
   return true;
  }

Die Methode schließt mit der Rückgabe des logischen Ergebnisses der Operation an den Aufrufer ab.

Die zweite Methode ReplaceBuffer ersetzt den Zeiger auf den angegebenen Puffer. Auf den ersten Blick brauchen wir keine ganze Methode, um einen Zeiger auf ein internes variables Objekt zuzuweisen. Im Methodenrumpf werden jedoch überflüssige Datenpuffer überprüft und gegebenenfalls entfernt. Dadurch können wir sowohl RAM als auch Kontextspeicher von OpenCL effizienter nutzen.

void CNeuronConvSAMOCL::ReplaceBuffer(CBufferFloat *&buffer, CBufferFloat *master)
  {
   if(buffer==master)
     return;
   if(!!buffer)
     {
      buffer.BufferFree();
      delete buffer;
     }
//---
   buffer = master;
  }

Nach der Erstellung der Hilfsmethoden wird ein neuer Initialisierungsalgorithmus für das Faltungsschichtobjekt auf der Grundlage einer Referenzinstanz InitPS entwickelt. In dieser Methode akzeptieren wir statt eines vollständigen Satzes von Konstanten, die die Objektarchitektur definieren, nur einen Zeiger auf ein Referenzobjekt.

bool CNeuronConvSAMOCL::InitPS(CNeuronConvSAMOCL *master)
  {
   if(!master ||
      master.Type() != Type()
     )
      return false;

Im Methodenrumpf wird geprüft, ob der empfangene Zeiger korrekt ist und die Objekttypen übereinstimmen.

Anstatt einen ganzen Satz von Methoden der Elternklasse zu erstellen, übertragen wir einfach die Werte aller geerbten Parameter aus dem Referenzobjekt.

   alpha = master.alpha;
   iBatch = master.iBatch;
   t = master.t;
   m_myIndex = master.m_myIndex;
   activation = master.activation;
   optimization = master.optimization;
   iWindow = master.iWindow;
   iStep = master.iStep;
   iWindowOut = master.iWindowOut;
   iVariables = master.iVariables;
   bTrain = master.bTrain;
   fRho = master.fRho;

 Als Nächstes erstellen wir Ergebnis- und Fehlergradientenpuffer, die denen des Referenzobjekts ähneln.

   if(!InitBufferLike(Output, master.Output))
      return false;
   if(!!master.getPrevOutput())
      if(!InitBufferLike(PrevOutput, master.getPrevOutput()))
         return false;
   if(!InitBufferLike(Gradient, master.Gradient))
      return false;

Danach übertragen wir die Zeiger zunächst auf die Gewichts- und Momentpuffer, die wir von der grundlegenden vollverknüpften Schicht übernommen haben.

   ReplaceBuffer(Weights, master.Weights);
   ReplaceBuffer(DeltaWeights, master.DeltaWeights);
   ReplaceBuffer(FirstMomentum, master.FirstMomentum);
   ReplaceBuffer(SecondMomentum, master.SecondMomentum);

Wir wiederholen einen ähnlichen Vorgang für die Puffer der Faltungsschichtparameter und ihrer Momente.

   ReplaceBuffer(WeightsConv, master.WeightsConv);
   ReplaceBuffer(DeltaWeightsConv, master.DeltaWeightsConv);
   ReplaceBuffer(FirstMomentumConv, master.FirstMomentumConv);
   ReplaceBuffer(SecondMomentumConv, master.SecondMomentumConv);

Als Nächstes müssen wir Puffer für die angepassten Parameter erstellen. Die beiden angepassten Parameterpuffer können jedoch unter bestimmten Bedingungen nicht erstellt werden. Der Puffer mit den eingestellten Parametern einer vollständig verbundenen Schicht wird nur angelegt, wenn ausgehende Verbindungen bestehen. Daher überprüfen wir zunächst die Größe dieses Puffers im Referenzobjekt. Wir legen den entsprechenden Puffer nur bei Bedarf an.

   if(master.cWeightsSAM.Total() > 0)
     {
      CBufferFloat *buf = GetPointer(cWeightsSAM);
      if(!InitBufferLike(buf, GetPointer(master.cWeightsSAM)))
         return false;
     }

Andernfalls wird dieser Puffer gelöscht, was den Speicherverbrauch reduziert.

   else
     {
      cWeightsSAM.BufferFree();
      cWeightsSAM.Clear();
     }

Der Puffer mit den angepassten Parametern der eingehenden Verbindungen wird erstellt, wenn der Unschärfebereichskoeffizient größer als 0 ist.

   if(fRho > 0)
     {
      CBufferFloat *buf = GetPointer(cWeightsSAMConv);
      if(!InitBufferLike(buf, GetPointer(master.cWeightsSAMConv)))
         return false;
     }

Andernfalls wird dieser Puffer gelöscht.

   else
     {
      cWeightsSAMConv.BufferFree();
      cWeightsSAMConv.Clear();
     }

Technisch gesehen könnte man anstelle des Unschärfekoeffizienten die Größe des Puffers mit den angepassten Parametern der eingehenden Verbindungen des Referenzobjekts überprüfen - so wie man es auch mit dem Puffer der angepassten Parameter für die ausgehenden Verbindungen macht. Wir wissen jedoch, dass dieser Puffer vorhanden sein muss, wenn der Unschärfekoeffizient größer als Null ist. Daher nehmen wir eine zusätzliche Kontrolle vor. Wenn versucht wird, einen Puffer mit der Länge Null zu erstellen, schlägt der Prozess fehl, gibt einen Fehler aus und hält die Initialisierung an. Auf diese Weise lassen sich später schwerwiegendere Probleme bei der Ausführung vermeiden.

Am Ende der Initialisierungsmethode übertragen wir alle Objekte in einen einzigen Kontext von OpenCL und geben das logische Ergebnis der Operation an das aufrufende Programm zurück.

   SetOpenCL(master.OpenCL);
//---
   return true;
  }

Nachdem wir das Objekt der Faltungsschicht geändert haben, gehen wir zur nächsten Phase unserer Arbeit über. Nun werden wir den Parameter-Sharing-Block (PS-Block) selbst erstellen. Hierfür führen wir ein neues Objekt ein: CNeuronPSBlock. Wie im theoretischen Teil dargelegt, besteht der PS-Block aus drei aufeinander folgenden Datenumwandlungsschichten. Jeder hat eine quadratische Parametermatrix, die sicherstellt, dass die Dimensionen des Eingangs- und Ausgangstensors sowohl für den Block als Ganzes als auch für seine internen Schichten konsistent bleiben. Zwischen den ersten beiden Schichten befindet sich ein GELU Aktivierungsfunktion angewendet. Nach der zweiten Schicht wird eine Residualverbindung zur ursprünglichen Eingabe hinzugefügt.

Um diese Architektur zu implementieren, wird das neue Objekt zwei interne Faltungsschichten enthalten, während die letzte Faltungsschicht direkt durch die Struktur unserer Klasse selbst dargestellt wird, wobei die Basisfunktionalität von der Klasse der Faltungsschicht geerbt wird. Da wir beim Training die Optimierung von SAM verwenden, sind alle Faltungsschichten in der Architektur SAM-kompatibel. Die Struktur der neuen Klasse ist unten dargestellt.

class CNeuronPSBlock :  public CNeuronConvSAMOCL
  {
protected:
   CNeuronConvSAMOCL acConvolution[2];
   CNeuronBaseOCL    cResidual;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronPSBlock(void) {};
                    ~CNeuronPSBlock(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_out, uint units_count, 
                          uint variables, float rho, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   virtual bool      InitPS(CNeuronPSBlock *master);
   //---
   virtual int       Type(void)   const         {  return defNeuronPSBlock;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual CLayerDescription* GetLayerInfo(void);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Wie aus der Struktur ersichtlich, deklariert das neue Objekt zwei Initialisierungsmethoden. Dies geschieht absichtlich. Init - die Standardinitialisierungsmethode, bei der die Architektur des Objekts explizit durch die an die Methode übergebenen Parameter definiert wird. InitPS - analog zur gleichnamigen Methode in der Klasse der Faltungsschichten wird hier ein neues Objekt auf der Grundlage der Struktur eines Referenzobjekts erstellt. Während dieses Vorgangs werden Zeiger auf Parameter- und Impulspuffer von der Referenz kopiert. Betrachten wir nun den Algorithmus für die Konstruktion der genannten Methoden genauer.

Wie bereits erwähnt, erhält die Methode Init eine Reihe von Konstanten in ihren Parametern, sodass die Architektur des Objekts vollständig bestimmt werden kann.

bool CNeuronPSBlock::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_out, uint units_count,
                          uint variables, float rho,
                          ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronConvSAMOCL::Init(numOutputs, myIndex, open_cl, window, window, window_out,
                               units_count, variables, rho, optimization_type, batch))
      return false;

Im Hauptteil der Methode leiten wir alle empfangenen Parameter sofort an die gleichnamige Methode der übergeordneten Klasse weiter. Wie Sie wissen, enthält die übergeordnete Methode bereits die notwendigen Parametervalidierungspunkte und die Initialisierungslogik für geerbte Objekte.

Da alle Faltungsschichten innerhalb des PS-Blocks die gleichen Abmessungen haben, werden bei der Initialisierung der ersten internen Faltungsschicht genau die gleichen Parameter verwendet.

   if(!acConvolution[0].Init(0, 0, OpenCL, iWindow, iWindow, iWindowOut, units_count,
                             iVariables, fRho, optimization, iBatch))
      return false;
   acConvolution[0].SetActivationFunction(GELU);

Dann fügen wir die GELU-Aktivierungsfunktion hinzu, wie von den PSformer-Autoren vorgeschlagen.

Wir erlauben dem Nutzer jedoch auch, die Tensordimensionen am Blockausgang zu ändern. Daher tauschen wir bei der Initialisierung der zweiten internen Faltungsschicht, auf die eine Residualverbindung folgt, die Parameter für die Größe des Analysefensters und die Anzahl der Filter. Dadurch wird sichergestellt, dass die Ausgabedimensionen mit denen der ursprünglichen Eingabedaten übereinstimmen.

   if(!acConvolution[1].Init(0, 1, OpenCL, iWindowOut, iWindowOut, iWindow, units_count,
                             iVariables, fRho, optimization, iBatch))
      return false;
   acConvolution[1].SetActivationFunction(None);

Wir verwenden die Aktivierungsfunktion hier nicht.

Als Nächstes fügen wir eine neuronale Basisschicht hinzu, um die restlichen Verbindungsdaten zu speichern. Seine Größe entspricht dem Ergebnispuffer der zweiten verschachtelten Faltungsschicht.

   if(!cResidual.Init(0, 2, OpenCL, acConvolution[1].Neurons(), optimization, iBatch))
      return false;
   if(!cResidual.SetGradient(acConvolution[1].getGradient(), true))
      return false;
   cResidual.SetActivationFunction(None);

Unmittelbar nach der Erstellung des Objekts auf der Grundlage der Referenzinstanz ersetzen wir den Puffer für den Fehlergradienten. Diese Optimierung ermöglicht es uns, die Anzahl der Datenkopiervorgänge während des Rückwärtsdurchlaufs zu reduzieren.

Als Nächstes deaktivieren wir explizit die Aktivierungsfunktion für unseren Parameter-Sharing-Block und schließen die Methode ab, indem wir ein logisches Ergebnis an den Aufrufer zurückgeben.

   SetActivationFunction(None);
//---
   return true;
  }

Die zweite Initialisierungsmethode ist etwas einfacher. Sie erhält einen Zeiger auf ein Referenzobjekt und übergibt ihn direkt an die gleichnamige Methode der übergeordneten Klasse.

Es ist wichtig zu beachten, dass sich die Parametertypen in der aktuellen Methode von denen der übergeordneten Klasse unterscheiden. Wir geben also ausdrücklich den Typ des übergebenen Objekts an.

bool CNeuronPSBlock::InitPS(CNeuronPSBlock *master)
  {
   if(!CNeuronConvSAMOCL::InitPS((CNeuronConvSAMOCL*)master))
      return false;

Die Methode der übergeordneten Klasse enthält bereits die erforderlichen Validierungsprüfungen sowie die Logik zum Kopieren von Konstanten, zum Anlegen neuer Puffer und zum Speichern von Zeigern auf die Parameter- und Impulspuffer.

Anschließend durchlaufen wir die internen Faltungsschichten, rufen die entsprechenden Initialisierungsmethoden auf und kopieren die Daten aus den jeweiligen Referenzobjekten.

   for(int i = 0; i < 2; i++)
      if(!acConvolution[i].InitPS(master.acConvolution[i].AsObject()))
         return false;

Die Residualverbindungsschicht enthält keine trainierbaren Parameter, und ihre Größe entspricht dem Ergebnispuffer der zweiten internen Faltungsschicht. Daher wird ihre Initialisierungslogik vollständig von der Hauptinitialisierungsmethode übernommen.

   if(!cResidual.Init(0, 2, OpenCL, acConvolution[1].Neurons(), optimization, iBatch))
      return false;
   if(!cResidual.SetGradient(acConvolution[1].getGradient(), true))
      return false;
   cResidual.SetActivationFunction(None);
//---
   return true;
  }

Wie zuvor ersetzen wir die Zeiger auf den Fehlergradientenpuffer.

Nachdem die Initialisierungsmethoden abgeschlossen sind, gehen wir zu den Algorithmen der Vorwärtsdurchläufe über. Dieser Teil ist relativ einfach. Die Methode erhält einen Zeiger auf das Eingabedatenobjekt, das wir direkt an die Methode des Vorwärtsdurchlaufs der ersten internen Faltungsschicht weitergeben.

bool CNeuronPSBlock::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!acConvolution[0].FeedForward(NeuronOCL))
      return false;

Die Ergebnisse werden dann nacheinander an die nächste Faltungsschicht weitergeleitet. Anschließend addieren wir die resultierenden Werte mit der ursprünglichen Eingabe. W speichern die Summe im Residualverbindungspuffer.

   if(!acConvolution[1].FeedForward(acConvolution[0].AsObject()))
      return false;
   if(!SumAndNormilize(NeuronOCL.getOutput(), acConvolution[1].getOutput(), cResidual.getOutput(),
                                                                       iWindow, true, 0, 0, 0, 1))
      return false;

Hier weichen wir leicht vom ursprünglichen Algorithmus des PSformer ab: Wir normalisieren den Residualtensor, bevor wir ihn an die letzte Faltungsschicht weitergeben, deren Funktionalität von der Elternklasse geerbt wird.

   if(!CNeuronConvSAMOCL::feedForward(cResidual.AsObject()))
      return false;
//---
   return true;
  }

Die Methode schließt mit der Rückgabe des logischen Ergebnisses der Operation an den Aufrufer ab.

Die Fehlergradientenverteilungsmethode calcInputGradients ist ebenfalls einfach, weist aber wichtige Nuancen auf. Sie erhält einen Zeiger auf das Objekt der Quelldatenebene, in das wir den Fehlergradienten übertragen müssen.

bool CNeuronPSBlock::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
     return false;

Zunächst prüfen wir die Gültigkeit des empfangenen Zeigers - ist er ungültig, ist eine weitere Bearbeitung sinnlos.

Anschließend werden die Gradienten in umgekehrter Reihenfolge durch alle Faltungsschichten geleitet.

   if(!CNeuronConvSAMOCL::calcInputGradients(cResidual.AsObject()))
      return false;
   if(!acConvolution[0].calcHiddenGradients(acConvolution[1].AsObject()))
      return false;
   if(!NeuronOCL.calcHiddenGradients(acConvolution[0].AsObject()))
      return false;

Es ist zu beachten, dass kein expliziter Fehlergradiententransfer vom Residualverbindungsobjekt zur zweiten internen Faltungsschicht kodiert wird. Dank unserer früheren Zeigersubstitution für Datenpuffer werden die Informationen jedoch weiterhin vollständig übertragen.

Nachdem wir den Gradienten durch die Pipeline der Faltungsschicht zurück zur Quelldatenschicht geschickt haben, fügen wir auch den Gradienten aus dem Residualverbindungszweig hinzu. Je nachdem, ob das Quelldatenobjekt eine Aktivierungsfunktion hat, gibt es zwei mögliche Fälle.

Ich möchte Sie daran erinnern, dass wir den Fehlergradienten an das Objekt Residualverbindungen übergeben, ohne die Ableitung der Aktivierungsfunktion zu berücksichtigen. Wir haben ausdrücklich darauf hingewiesen, dass dies bei diesem Objekt nicht der Fall ist.

Da es keine Aktivierungsfunktion für das Quelldatenobjekt gibt, müssen wir nur die entsprechenden Werte der beiden Puffer addieren.

   if(NeuronOCL.Activation() == None)
     {
      if(!SumAndNormilize(NeuronOCL.getGradient(), cResidual.getGradient(), NeuronOCL.getGradient(),
                                                                        iWindow, false, 0, 0, 0, 1))
         return false;
     }

Andernfalls wird zunächst der erhaltene Fehlergradient mit Hilfe der Ableitung der Aktivierungsfunktion in einen freien Puffer eingestellt. Dann addieren wir die erhaltenen Ergebnisse mit denen, die zuvor im Quelldaten-Objektpuffer gesammelt wurden.

   else
     {
      if(!DeActivation(NeuronOCL.getOutput(), cResidual.getGradient(), cResidual.getPrevOutput(), 
                                                                           NeuronOCL.Activation()) ||
         !SumAndNormilize(NeuronOCL.getGradient(), cResidual.getPrevOutput(), NeuronOCL.getGradient(),
                                                                          iWindow, false, 0, 0, 0, 1))
         return false;
     }
//---
   return true;
  }

Dann schließen wir die Methode ab.

Ein paar Worte sollten über die Methode updateInputWeights gesagt werden, mit der wir die Blockparameter aktualisieren. Dieser Block ist unkompliziert - wir rufen einfach die entsprechenden Methoden in der übergeordneten Klasse und in den internen Objekten mit trainierbaren Parametern auf.

bool CNeuronPSBlock::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!CNeuronConvSAMOCL::updateInputWeights(cResidual.AsObject()))
      return false;
   if(!acConvolution[1].UpdateInputWeights(acConvolution[0].AsObject()))
      return false;
   if(!acConvolution[0].UpdateInputWeights(NeuronOCL))
      return false;
//---
   return true;
  }

Die SAM-Optimierung stellt jedoch strenge Anforderungen an die Reihenfolge der Operationen. Während der SAM-Optimierung führen wir einen zweiten Vorwärtsdurchlauf mit angepassten Parametern durch. Dadurch wird der Ergebnispuffer aktualisiert. Während dies für die Aktualisierung der Parameter der aktuellen Ebene unbedenklich ist, kann es die Aktualisierung der Parameter in den nachfolgenden Ebenen stören. Das liegt daran, dass sie die Ergebnisse der vorherigen Schicht verwenden. Um dies zu verhindern, müssen wir die Parameter in umgekehrter Reihenfolge über die internen Objekte aktualisieren. Dadurch wird sichergestellt, dass die Parameter jeder Schicht angepasst werden, bevor ihr Eingabepuffer von einer anderen Schicht geändert wird.

Damit ist die Erörterung der Algorithmen von CNeuronPSBlock zur gemeinsamen Nutzung von Parametern abgeschlossen. Den vollständigen Quellcode für diese Klasse und ihre Methoden finden Sie im beigefügten Anhang.

Unsere Arbeit ist noch nicht abgeschlossen, aber der Artikel ist lang geworden. Daher werden wir eine kurze Pause einlegen und die Arbeit im nächsten Artikel fortsetzen.

Schlussfolgerung

In diesem Artikel haben wir den Rahmen von PSformer untersucht, dessen Autoren die hohe Genauigkeit bei der Zeitreihenprognose und die effiziente Nutzung von Rechenressourcen hervorheben. Zu den wichtigsten architektonischen Komponenten des PSformers gehören der Parameter-Sharing-Block (PS) und die Segment-basierte räumlich-zeitliche Aufmerksamkeit (SegAtt). Sie ermöglichen eine wirksame Modellierung sowohl lokaler als auch globaler Zeitreihenabhängigkeiten bei gleichzeitiger Verringerung der Anzahl der Parameter ohne Einbußen bei der Prognosequalität.

Im praktischen Teil haben wir begonnen, unsere eigene Interpretation der vorgeschlagenen Methoden in MQL5 zu implementieren. Unsere Arbeit ist noch nicht abgeschlossen. Im nächsten Artikel werden wir die Entwicklung fortsetzen und die Wirksamkeit dieser Ansätze an realen historischen Datensätzen, die für unsere spezifischen Aufgaben relevant sind, bewerten.

Referenzen

PSformer: Parameter-efficient Transformer with Segment Attention for Time Series Forecasting

Andere Artikel dieser Serie

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	Expert Advisor zum Sammeln von Beispielen
2	ResearchRealORL.mq5	Expert Advisor	Expert Advisor für das Sammeln von Beispielen nach der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modellausbildung Expert Advisor
4	StudyEncoder.mq5	Expert Advisor	Expert Advisor für das Training des Encoders
5	Test.mq5	Expert Advisor	Modellprüfung Expert Advisor
6	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
7	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
8	NeuroNet.cl	Bibliothek	OpenCL-Programmcode-Bibliothek