Portfolio-Optimierung am Devisenmarkt: Synthese von VaR und die Markowitz-Theorie

Einleitung: Aufgaben der Portfolio-Optimierung im Devisenhandel

Ich habe die letzten drei Jahre damit verbracht, Handelsroboter für Forex zu entwickeln. Und wissen Sie was? Das Risikomanagement ist eine echte Qual. Am Anfang habe ich nur feste Stopps gesetzt, bis ich ein paar Einlagen verloren habe. Dann begann ich tiefer zu graben und stieß auf die Theorie der Portfoliooptimierung von Markowitz.

Es sah gut aus - man berechnet Korrelationen, optimiert Gewichte... In Wirklichkeit funktioniert dies jedoch nicht sehr gut für den Devisenhandel. Warum? Denn im Forex sind alle Paare miteinander verbunden! Versuchen Sie, EURUSD und EURGBP gleichzeitig zu handeln, und Sie werden sehen, was ich meine. Eine scharfe EUR-Bewegung und beide Positionen verschmelzen synchron. Eine schöne Theorie wird durch die harte Realität erschüttert.

Da ich genug davon hatte, suchte ich nach anderen Ansätzen. Schließlich stieß ich auf die Value at Risk (VaR)-Methode. Zuerst verstand ich nicht einmal, was es war - eine Art komplizierter Gleichungen. Aber dann dämmerte es mir - das ist genau das, was ich brauchte! Der VaR gibt den maximalen Verlust bei einer bestimmten Wahrscheinlichkeit an. Mit anderen Worten: Wir können direkt abschätzen, wie viel Geld wir an einem Tag/einer Woche/einem Monat verlieren könnten.

Schließlich entschied ich mich, Markowitz mit VaR zu kreuzen. Klingt verrückt? Vielleicht. Aber ich habe keine anderen Möglichkeiten gesehen. Markowitz sorgt für die optimale Allokation der Mittel, und der VaR verhindert, dass es zu einem Margin Call kommt. Auf dem Papier sah es großartig aus.

Dann begann der harte Alltag eines Forschungsprogrammierers. Python, МetaТrader 5 Terminal, Tonnen von historischen Daten... Ich wusste, dass es nicht einfach werden würde, aber die Realität übertraf alle Erwartungen. Davon werde ich Ihnen erzählen - wie ich versucht habe, ein System zu entwickeln, das tatsächlich funktioniert und nicht nur in einem Backtest gut aussieht.

Wenn Sie jemals versucht haben, den Devisenhandel zu automatisieren, werden Sie meinen Schmerz verstehen. Und wenn nicht, dann hilft Ihnen meine Erfahrung vielleicht, zumindest einige der Fallstricke zu vermeiden, in die Sie treten müssen.

Theoretische und mathematische Grundlagen des VaR und der Markowitz-Theorie

Beginnen wir also mit der Theorie. Im ersten Monat habe ich nur versucht, den Dreh rauszukriegen, was Mathe angeht. Die Theorie von Markowitz sieht kompliziert aus - ein Haufen Gleichungen, Matrizen, quadratische Optimierung... Aber in Wirklichkeit ist alles ganz einfach: Man nimmt die Renditen der Vermögenswerte, berechnet die Korrelationen und findet die Gewichtung, sodass das Risiko bei einer bestimmten Rendite minimal ist.

Am Anfang war ich froh! Aber dann habe ich angefangen, mit echten Forex-Daten zu testen, und dann ging es los... Bei der Verwendung der EURUSD-Historie für ein Jahr war die Verteilung der Renditen überhaupt nicht normal. Das Gleiche gilt für GBPUSD. Dies ist die Schlüsselannahme in Markowitz' Theorie. Mit anderen Worten: Alle Berechnungen gehen den Bach hinunter.

Ich habe eine Woche lang nach einer Lösung gesucht. Ich habe mich durch wissenschaftliche Artikel gewühlt, gegoogelt und Foren gelesen. Ich bin auf meinen Artikel über VaR - Value at Risk - zurückgekommen. Das klingt schlau, aber in Wirklichkeit berechnen wir einfach, wie viel wir mit einer Wahrscheinlichkeit von 95 % (oder so) verlieren können. Zunächst habe ich die einfachste Option ausprobiert - den parametrischen VaR. Die Gleichung ist einfach: Mittelwert minus Sigma pro Quantil. Die Betriebsqualität ist mittelmäßig.

Dann bin ich zum historischen VaR übergegangen. Die Idee ist, die reale Geschichte zu betrachten und zu sehen, wie hoch die Verluste in den schlimmsten 5 % der Fälle waren. Dies kommt der Realität sehr viel näher, aber es werden noch viele Daten benötigt. Der letzte Boss ist die Monte-Carlo-Methode. Wir generieren eine Reihe von Zufallsszenarien, die die Korrelationen zwischen den Paaren berücksichtigen, und schließlich haben wir etwas Vernünftiges.

Der schwierigste Teil war herauszufinden, wie man den VaR mit der Markowitz-Optimierung kombiniert. Daraus ergab sich folgendes: Wir nehmen die Standardoptimierung, fügen aber eine VaR-Beschränkung hinzu. Wir suchen nach dem minimalen Risiko für eine bestimmte Rendite, aber so, dass der VaR ein bestimmtes Niveau nicht überschreitet.

Auf dem Papier ist alles großartig, aber wir müssen es programmieren... In den folgenden Abschnitten werde ich zeigen, wie ich diese Gleichungen in einen funktionierenden Python-Code umgesetzt habe.

Verbindung zum MetaTrader 5 von Python aus

Die praktische Umsetzung meines Systems begann mit der Herstellung einer stabilen Verbindung mit dem Handelsterminal. Nachdem ich mit verschiedenen Ansätzen experimentiert hatte, entschied ich mich für eine direkte Verbindung über die MetaTrader 5-Bibliothek für Python, die sich als die zuverlässigste und schnellste erwies.

import MetaTrader5 as mt5
import time

def initialize_mt5(account=12345, server="MetaQuotes-Demo", password="abc123"):
    if not mt5.initialize():
        print(f"initialize() failed, error code = {mt5.last_error()}")
        return False
        
    authorized = mt5.login(account, password=password, server=server)
    if not authorized:
        print(f"login failed, error code = {mt5.last_error()}")
        mt5.shutdown()
        return False
        
    return True

Ein weiteres Kopfzerbrechen bereitete die Zeitsynchronisierung zwischen dem Broker-Server und dem lokalen System. Ein Unterschied von wenigen Sekunden kann bei der Berechnung des VaR zu ernsthaften Problemen führen. Es war notwendig, einen speziellen Korrekturmechanismus einzuführen:

def get_time_correction():
    server_time = mt5.symbol_info_tick("EURUSD").time
    local_time = int(time.time())
    return server_time - local_time

def get_corrected_time():
    correction = get_time_correction()
    return int(time.time()) + correction

Es wurde viel Zeit auf die Optimierung der Datenerfassung verwendet. Ursprünglich habe ich die Anfragen für jedes Währungspaar einzeln gestellt, aber nachdem ich die Stapelverarbeitung eingeführt hatte, stieg die Geschwindigkeit um ein Vielfaches:

def fetch_data_batch(symbols, timeframe, start_pos, count):
    data = {}
    for symbol in symbols:
        rates = mt5.copy_rates_from_pos(symbol, timeframe, start_pos, count)
        if rates is not None and len(rates) > 0:
            data[symbol] = rates
        else:
            print(f"Failed to get data for {symbol}")
            return None
    return data

Es erwies sich als erstaunlich schwierig, das Programm korrekt zu beenden. Es war notwendig, ein spezielles Verfahren für das „sanfte Herunterfahren“ zu entwickeln:

def safe_shutdown():
    try:
        positions = mt5.positions_get()
        if positions:
            for position in positions:
                close_position(position.ticket)
        
        orders = mt5.orders_get()
        if orders:
            for order in orders:
                mt5.order_send(request={"action": mt5.TRADE_ACTION_REMOVE,
                                      "order": order.ticket})
    finally:
        mt5.shutdown()

Das Ergebnis war eine zuverlässige Grundlage für das gesamte System, das rund um die Uhr ohne Ausfälle arbeiten kann. Es war bereits möglich, eine komplexere Logik für die Portfolio-Optimierung auf dieser Grundlage aufzubauen. Aber das ist bereits das Thema des nächsten Abschnitts.

Beschaffung von historischen Daten und deren Vorverarbeitung

Im Laufe der Jahre, in denen ich mit Marktdaten gearbeitet habe, habe ich eine einfache Wahrheit gelernt: Die Qualität der historischen Daten ist für jedes Handelssystem entscheidend. Dies gilt insbesondere für die Portfolio-Optimierung, wo Datenfehler kaskadenartig auftreten können.

Ich begann mit der Entwicklung eines zuverlässigen Systems zum Laden der Historie. Die erste Version war recht einfach, aber die Praxis zeigte schnell ihre Unzulänglichkeiten. Die Notierungen können Lücken, Ausschläge und manchmal sogar völlig falsche Werte enthalten. So sieht der endgültige Code für das Hochladen mit einfacher Validierung aus:

def load_historical_data(symbols, timeframe, start_date, end_date):
    data_frames = {}
    for symbol in symbols:
        # Load with a reserve to compensate for gaps
        rates = mt5.copy_rates_range(symbol, timeframe, 
                                   start_date - timedelta(days=30), 
                                   end_date)
        if rates is None:
            print(f"Failed to load data for {symbol}")
            continue
            
        df = pd.DataFrame(rates)
        df['time'] = pd.to_datetime(df['time'], unit='s')
        df.set_index('time', inplace=True)
        
        # Basic anomaly check
        df = detect_and_remove_spikes(df)
        df = fill_gaps(df)
        data_frames[symbol] = df
    
    return data_frames

Ein weiteres Problem war der Umgang mit Lücken an Wochenenden. Zuerst habe ich diese Tage einfach entfernt, aber das verzerrte die Volatilitätsberechnungen. Nach langen Experimenten wurde eine Interpolationsmethode entwickelt, die die Besonderheiten der einzelnen Währungspaare berücksichtigt:

def fill_gaps(df, method='time'):
    if df.empty:
        return df
        
    # Check the intervals between points
    time_delta = df.index.to_series().diff()
    gaps = time_delta[time_delta > pd.Timedelta(hours=2)].index
    
    for gap_start in gaps:
        gap_end = df.index[df.index.get_loc(gap_start) + 1]
        # Create new points with interpolated values
        new_points = pd.date_range(gap_start, gap_end, freq='1H')[1:-1]
        
        for point in new_points:
            df.loc[point] = df.asof(point)
    
    return df.sort_index()

Ich habe verschiedene Ansätze zur Berechnung der Rendite ausprobiert. Einfache prozentuale Änderungen erwiesen sich als zu störend. Logarithmische Renditen schneiden bei der Schätzung des VaR am besten ab:

def calculate_returns(df):
    df['returns'] = np.log(df['close'] / df['close'].shift(1))
    df['rolling_std'] = df['returns'].rolling(window=20).std()
    df['rolling_mean'] = df['returns'].rolling(window=20).mean()
    
    # Clean out emissions using the 3-sigma rule
    mean = df['returns'].mean()
    std = df['returns'].std()
    df = df[abs(df['returns'] - mean) <= 3 * std]
    
    return df

Die Entwicklung des Datenüberprüfungssystems erwies sich als ein wichtiger Meilenstein. Jeder Satz wird einer mehrstufigen Prüfung unterzogen, bevor er für die Berechnungen verwendet wird:

def verify_data_quality(df, symbol):
    checks = {
        'missing_values': df.isnull().sum().sum() == 0,
        'price_continuity': (df['close'] > 0).all(),
        'timestamp_uniqueness': df.index.is_unique,
        'reasonable_returns': abs(df['returns']).max() < 0.1
    }
    
    if not all(checks.values()):
        failed_checks = [k for k, v in checks.items() if not v]
        print(f"Data quality issues for {symbol}: {failed_checks}")
        return False
        
    return True

Besonderes Augenmerk habe ich auf den Umgang mit Marktanomalien gelegt. Verschiedene Ereignisse, wie z. B. starke Bewegungen aufgrund von Nachrichten oder Flash-Crashs, können die Risikobewertung stark verzerren. Ich habe einen speziellen Algorithmus entwickelt, um sie zu erkennen und richtig zu behandeln:

def detect_market_anomalies(df, window=20, threshold=3):
    volatility = df['returns'].rolling(window=window).std()
    typical_range = volatility.mean() + threshold * volatility.std()
    
    anomalies = df[abs(df['returns']) > typical_range].index
    if len(anomalies) > 0:
        print(f"Detected {len(anomalies)} market anomalies")
        
    return anomalies

Das Ergebnis war eine zuverlässige Datenverarbeitungspipeline, die die Grundlage für alle weiteren Berechnungen bildete. Qualitativ hochwertige historische Daten sind die Grundlage, ohne die es unmöglich ist, ein effizientes Portfoliomanagementsystem aufzubauen. Im nächsten Abschnitt werde ich untersuchen, wie diese Daten zur Berechnung des VaR verwendet werden.

Implementierung der VaR-Berechnung für Währungspaare

Nachdem ich lange Zeit mit historischen Daten gearbeitet hatte, beschäftigte ich mich mit der Implementierung der VaR-Berechnung. Ursprünglich schien es zu genügen, fertige Gleichungen zu nehmen und sie in Code zu übersetzen. Die Realität erwies sich als komplizierter, da die Besonderheiten von Forex erhebliche Änderungen der Standardansätze erforderten.

Ich begann mit der Implementierung von drei klassischen VaR-Berechnungsmethoden. So sieht der parametrische Ansatz aus:

def parametric_var(returns, confidence_level=0.95, holding_period=1):
    mu = returns.mean()
    sigma = returns.std()
    z_score = norm.ppf(1 - confidence_level)
    
    daily_var = -(mu + z_score * sigma)
    return daily_var * np.sqrt(holding_period)

Es wurde jedoch schnell klar, dass die Annahme einer Normalverteilung der Renditen am Devisenmarkt oft nicht zutrifft. Der historische Ansatz hat sich als zuverlässiger erwiesen:

def historical_var(returns, confidence_level=0.95, holding_period=1):
    sorted_returns = np.sort(returns)
    index = int((1 - confidence_level) * len(sorted_returns))
    daily_var = -sorted_returns[index]
    return daily_var * np.sqrt(holding_period)

Die interessantesten Ergebnisse lieferte jedoch die Monte-Carlo-Methode. Ich habe sie geändert, um den Besonderheiten des Devisenmarktes Rechnung zu tragen:

def monte_carlo_var(returns, confidence_level=0.95, holding_period=1, simulations=10000):
    mu = returns.mean()
    sigma = returns.std()
    
    # Consider auto correlation of returns
    corr = returns.autocorr()
    
    simulated_returns = []
    for _ in range(simulations):
        daily_returns = []
        last_return = returns.iloc[-1]
        
        for _ in range(holding_period):
            # Generate the next value taking auto correlation into account
            innovation = np.random.normal(0, 1)
            next_return = mu + corr * (last_return - mu) + sigma * np.sqrt(1 - corr**2) * innovation
            daily_returns.append(next_return)
            last_return = next_return
            
        total_return = sum(daily_returns)
        simulated_returns.append(total_return)
    
    return -np.percentile(simulated_returns, (1 - confidence_level) * 100)

Besonderes Augenmerk habe ich auf die Validierung der Ergebnisse gelegt. Ich habe auch ein Backtest-System entwickelt, um die Genauigkeit des VaR zu überprüfen:

def backtest_var(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    
    z_score = (violations - expected_violations) / np.sqrt(expected_violations)
    p_value = 1 - norm.cdf(abs(z_score))
    
    return {
        'violations': violations,
        'expected': expected_violations,
        'z_score': z_score,
        'p_value': p_value
    }

Um die Beziehungen zwischen den Währungspaaren zu berücksichtigen, war es notwendig, die Berechnung des Portfolio-VaR zu implementieren:

def portfolio_var(returns_df, weights, confidence_level=0.95, method='historical'):
    if method == 'parametric':
        portfolio_returns = returns_df.dot(weights)
        return parametric_var(portfolio_returns, confidence_level)
    
    elif method == 'historical':
        portfolio_returns = returns_df.dot(weights)
        return historical_var(portfolio_returns, confidence_level)
    
    elif method == 'monte_carlo':
        # Use the covariance matrix to generate
        # correlated random variables
        cov_matrix = returns_df.cov()
        L = np.linalg.cholesky(cov_matrix)
        
        means = returns_df.mean().values
        simulated_returns = []
        
        for _ in range(10000):
            Z = np.random.standard_normal(len(weights))
            R = means + L @ Z
            portfolio_return = weights @ R
            simulated_returns.append(portfolio_return)
            
        return -np.percentile(simulated_returns, (1 - confidence_level) * 100)

Das Ergebnis war ein flexibles VaR-Berechnungssystem, das an die Besonderheiten des Devisenhandels angepasst ist. Im nächsten Abschnitt werde ich erörtern, wie sich diese Berechnungen in die Markowitz-Theorie zur Portfoliooptimierung einfügen.

Portfolio-Optimierung mit der Markowitz-Methode

Nachdem ich eine zuverlässige VaR-Berechnung eingeführt hatte, begann ich, mich auf die Portfoliooptimierung zu konzentrieren. Die klassische Theorie von Markowitz bedurfte einer ernsthaften Anpassung an die Realitäten des Forex. Nach monatelangem Experimentieren und Testen kam ich zu mehreren wichtigen Erkenntnissen.

Als erstes wurde mir klar, dass die üblichen Risiko- und Renditemetriken im Devisenhandel anders funktionieren als auf dem Aktienmarkt. Währungspaare haben komplexe Beziehungen, die sich im Laufe der Zeit ändern. Nach vielen Experimenten habe ich eine modifizierte Funktion zur Berechnung der erwarteten Rendite entwickelt:

def calculate_expected_returns(returns_df, method='ewma', halflife=30):
    if method == 'ewma':
        # Exponentially weighted average gives more weight to recent data
        return returns_df.ewm(halflife=halflife).mean().iloc[-1]
    elif method == 'capm':
        # Modified CAPM for Forex
        risk_free_rate = 0.02  # annual risk-free rate
        market_returns = returns_df.mean(axis=1)  # market returns proxy
        betas = calculate_currency_betas(returns_df, market_returns)
        return risk_free_rate + betas * (market_returns.mean() - risk_free_rate)

Auch die Berechnung der Kovarianzmatrix musste überarbeitet werden. Der einfache historische Ansatz führte zu instabilen Ergebnissen. Ich habe eine Schrumpfungsschätzung eingeführt, die die Robustheit der Optimierung erheblich verbessert:

def shrinkage_covariance(returns_df, shrinkage_factor=None):
    sample_cov = returns_df.cov()
    n_assets = len(returns_df.columns)
    
    # The target matrix is diagonal with average variance
    target = np.diag(np.repeat(sample_cov.values.trace() / n_assets, n_assets))
    
    if shrinkage_factor is None:
        # Estimation of the optimal 'shrinkage' ratio
        shrinkage_factor = estimate_optimal_shrinkage(returns_df, sample_cov, target)
    
    shrunk_cov = (1 - shrinkage_factor) * sample_cov + shrinkage_factor * target
    return pd.DataFrame(shrunk_cov, index=sample_cov.index, columns=sample_cov.columns)

Der schwierigste Teil ist die Optimierung der Portfoliogewichtung. Nach vielen Tests entschied ich mich für einen modifizierten quadratischen Programmieralgorithmus:

def optimize_portfolio(returns_df, expected_returns, covariance, target_return=None, constraints=None):
    n_assets = len(returns_df.columns)
    
    # Risk minimization function
    def portfolio_volatility(weights):
        return np.sqrt(weights.T @ covariance @ weights)
    
    # Limitations
    constraints = []
    # The sum of the weights is 1
    constraints.append({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
    
    if target_return is not None:
        # Target income limit
        constraints.append({
            'type': 'eq',
            'fun': lambda x: x @ expected_returns - target_return
        })
    
    # Add leverage restrictions for Forex
    constraints.append({
        'type': 'ineq',
        'fun': lambda x: 20 - np.sum(np.abs(x))  # max leverage 20
    })
    
    # Initial approximation - equal weights
    initial_weights = np.repeat(1/n_assets, n_assets)
    
    # Optimization
    result = minimize(
        portfolio_volatility,
        initial_weights,
        method='SLSQP',
        constraints=constraints,
        bounds=tuple((0, 1) for _ in range(n_assets))
    )
    
    if not result.success:
        raise OptimizationError("Failed to optimize portfolio: " + result.message)
        
    return result.x

Besonderes Augenmerk habe ich auf das Problem der Stabilität der Lösung gelegt. Kleine Änderungen der Eingangsdaten sollten nicht zu einer radikalen Überarbeitung des Portfolios führen. Zu diesem Zweck habe ich das Regularisierungsverfahren entwickelt:

def regularized_optimization(returns_df, current_weights, lambda_reg=0.1):
    # Add a penalty for deviation from the current weights
    def objective(weights):
        volatility = portfolio_volatility(weights)
        turnover_penalty = lambda_reg * np.sum(np.abs(weights - current_weights))
        return volatility + turnover_penalty

Damit verfügen wir über einen zuverlässigen Portfolio-Optimierer, der die Besonderheiten des Devisenmarktes berücksichtigt und keine häufige Neuausrichtung erfordert. Aber das Wichtigste stand noch bevor - die Kombination dieses Ansatzes mit einem VaR-basierten Risikokontrollsystem.

Kombination von VaR und Markowitz in einem einzigen Modell

Die Kombination der beiden Ansätze erwies sich als die größte Herausforderung. Ich musste einen Weg finden, um die Vorteile beider Methoden zu nutzen, ohne Widersprüche zwischen ihnen zu schaffen. Nach mehreren Monaten des Experimentierens habe ich eine elegante Lösung gefunden.

Die Schlüsselidee war, den VaR als zusätzliche Einschränkung im Markowitz-Optimierungsproblem zu verwenden. So sieht es im Code aus:

def integrated_portfolio_optimization(returns_df, target_return, max_var_limit, current_weights=None):
    n_assets = len(returns_df.columns)
    
    # Calculation of basic metrics
    exp_returns = calculate_expected_returns(returns_df)
    covariance = shrinkage_covariance(returns_df)
    
    def objective_function(weights):
        # Portfolio standard deviation (Markowitz)
        portfolio_std = np.sqrt(weights.T @ covariance @ weights)
        
        # component VaR
        portfolio_var = calculate_portfolio_var(returns_df, weights)
        var_penalty = max(0, portfolio_var - max_var_limit)
        
        return portfolio_std + 100 * var_penalty  # Penalty for exceeding VaR

Um der Dynamik des Marktes Rechnung zu tragen, habe ich ein adaptives System zur Neuberechnung der Parameter entwickelt:

def adaptive_risk_limits(returns_df, base_var_limit, window=60):
    # Adapting VaR limits to current volatility
    recent_vol = returns_df.tail(window).std()
    long_term_vol = returns_df.std()
    vol_ratio = recent_vol / long_term_vol
    
    adjusted_var_limit = base_var_limit * np.sqrt(vol_ratio)
    return min(adjusted_var_limit, base_var_limit * 1.5)  # Limit growth

Besondere Aufmerksamkeit musste dem Problem der Lösungsstabilität gewidmet werden. Ich habe einen Mechanismus für den reibungslosen Übergang zwischen den Portfolioständen eingeführt:

def smooth_rebalancing(old_weights, new_weights, max_change=0.1):
    weight_diff = new_weights - old_weights
    excess_change = np.abs(weight_diff) - max_change
    
    where_excess = excess_change > 0
    if where_excess.any():
        # Limit changes in weights
        adjustment = np.sign(weight_diff) * np.minimum(
            np.abs(weight_diff),
            np.where(where_excess, max_change, np.abs(weight_diff))
        )
        return old_weights + adjustment
    return new_weights

Ich habe eine spezielle Metrik entwickelt, um die Effizienz des kombinierten Ansatzes zu bewerten:

def evaluate_integrated_model(returns_df, weights, var_limit):
    # Calculation of performance metrics
    portfolio_returns = returns_df.dot(weights)
    realized_var = historical_var(portfolio_returns)
    sharpe = calculate_sharpe_ratio(portfolio_returns)
    var_efficiency = abs(realized_var - var_limit) / var_limit
    
    return {
        'sharpe_ratio': sharpe,
        'var_efficiency': var_efficiency,
        'max_drawdown': calculate_max_drawdown(portfolio_returns),
        'turnover': calculate_turnover(weights)
    }

Während des Tests stellte sich heraus, dass das Modell in Zeiten erhöhter Volatilität besonders gut funktioniert. Die VaR-Komponente begrenzt effektiv die Risiken, während die Markowitz-Optimierung weiterhin nach Möglichkeiten zur Rentabilitätssteigerung sucht.

Die endgültige Version des Systems enthält auch einen Mechanismus zur automatischen Anpassung der Parameter:

def auto_tune_parameters(returns_df, initial_params, optimization_window=252):
    best_params = initial_params
    best_score = float('-inf')
    
    for var_limit in np.arange(0.01, 0.05, 0.005):
        for shrinkage in np.arange(0.2, 0.8, 0.1):
            params = {'var_limit': var_limit, 'shrinkage': shrinkage}
            score = backtest_model(returns_df, params, optimization_window)
            
            if score > best_score:
                best_score = score
                best_params = params
                
    return best_params

Im nächsten Abschnitt werde ich erörtern, wie dieses kombinierte Modell auf das dynamische Positionsmanagement im realen Handel angewendet wird.

Dynamische Verwaltung der Positionsgrößen

Die Umsetzung des theoretischen Modells in ein praktisches Handelssystem erforderte die Lösung zahlreicher technischer Probleme. Der wichtigste Punkt war die dynamische Verwaltung der Positionsgrößen unter Berücksichtigung der aktuellen Marktbedingungen und die Berechnung der optimalen Portfoliogewichte.

Die Grundlage des Systems bildete eine Klasse für die Verwaltung von Stellen:

class PositionManager:
    def __init__(self, account_balance, risk_limit=0.02):
        self.balance = account_balance
        self.risk_limit = risk_limit
        self.positions = {}
        
    def calculate_position_size(self, symbol, weight, var_estimate):
        symbol_info = mt5.symbol_info(symbol)
        pip_value = symbol_info.trade_tick_value * 10
        
        # Calculate the position size taking into account VaR
        max_risk_amount = self.balance * self.risk_limit * abs(weight)
        position_size = max_risk_amount / (abs(var_estimate) * pip_value)
        
        # Round to minimum lot
        return round(position_size / symbol_info.volume_step) * symbol_info.volume_step

Um einen reibungslosen Positionswechsel zu ermöglichen, habe ich einen Mechanismus von Teilaufträgen entwickelt:

def adjust_positions(self, target_positions):
    for symbol, target_size in target_positions.items():
        current_size = self.get_current_position(symbol)
        if abs(target_size - current_size) > self.min_adjustment:
            # Break big changes into pieces
            steps = min(5, int(abs(target_size - current_size) / self.min_adjustment))
            step_size = (target_size - current_size) / steps
            
            for i in range(steps):
                next_size = current_size + step_size
                self.execute_order(symbol, next_size - current_size)
                current_size = next_size
                time.sleep(1)  # Prevent order flooding

Bei Positionswechseln habe ich besonders auf die Risikokontrolle geachtet:

def execute_order(self, symbol, size_delta, max_slippage=10):
    if size_delta > 0:
        order_type = mt5.ORDER_TYPE_BUY
    else:
        order_type = mt5.ORDER_TYPE_SELL
    
    # Get current prices
    tick = mt5.symbol_info_tick(symbol)
    
    # Set VaR-based stop loss
    if order_type == mt5.ORDER_TYPE_BUY:
        stop_loss = tick.bid - (self.var_estimates[symbol] * tick.bid)
        take_profit = tick.bid + (self.var_estimates[symbol] * 2 * tick.bid)
    else:
        stop_loss = tick.ask + (self.var_estimates[symbol] * tick.ask)
        take_profit = tick.ask - (self.var_estimates[symbol] * 2 * tick.ask)
    
    request = {
        "action": mt5.TRADE_ACTION_DEAL,
        "symbol": symbol,
        "volume": abs(size_delta),
        "type": order_type,
        "price": tick.ask if order_type == mt5.ORDER_TYPE_BUY else tick.bid,
        "sl": stop_loss,
        "tp": take_profit,
        "deviation": max_slippage,
        "magic": 234000,
        "comment": "var_based_adjustment",
        "type_time": mt5.ORDER_TIME_GTC,
        "type_filling": mt5.ORDER_FILLING_IOC,
    }
    
    result = mt5.order_send(request)
    return self.handle_order_result(result)

Ich habe ein System zur Überwachung der Volatilität hinzugefügt, um mich vor starken Marktbewegungen zu schützen:

def monitor_volatility(self, returns_df, threshold=2.0):
    # Current volatility calculation
    current_vol = returns_df.tail(20).std() * np.sqrt(252)
    historical_vol = returns_df.std() * np.sqrt(252)
    
    if current_vol > historical_vol * threshold:
        # Reduce positions in case of increased volatility
        self.reduce_exposure(current_vol / historical_vol)
        return False
        
    return True

Das System umfasst auch einen Mechanismus zur automatischen Schließung von Positionen, wenn ein kritisches Risikoniveau erreicht wird:

def emergency_close(self, max_loss_percent=5.0):
    total_loss = sum(pos.profit for pos in mt5.positions_get())
    if total_loss < -self.balance * max_loss_percent / 100:
        print("Emergency closure triggered!")
        for position in mt5.positions_get():
            self.close_position(position.ticket)

Das Ergebnis ist ein robustes Positionsmanagementsystem, das unter einer Vielzahl von Marktbedingungen effektiv arbeiten kann. Der nächste Abschnitt befasst sich mit dem VaR-basierten Risikokontrollsystem.

System zur Kontrolle des Portfoliorisikos

Nach der Einführung des dynamischen Positionsmanagements sah ich mich mit der Notwendigkeit konfrontiert, ein umfassendes Risikokontrollsystem auf Portfolio-Ebene zu schaffen. Die Erfahrung hat gezeigt, dass eine lokale Risikokontrolle einzelner Positionen nicht ausreicht - ein ganzheitlicher Ansatz ist erforderlich.

Ich habe mit der Erstellung einer Klasse zur Überwachung von Portfoliorisiken begonnen:

class PortfolioRiskManager:
    def __init__(self, max_portfolio_var=0.03, max_correlation=0.7, max_drawdown=0.1):
        self.max_portfolio_var = max_portfolio_var
        self.max_correlation = max_correlation
        self.max_drawdown = max_drawdown
        self.current_drawdown = 0
        self.peak_balance = 0
        
    def update_portfolio_metrics(self, positions, returns_df):
        # Calculation of current portfolio weights
        total_exposure = sum(abs(pos.volume) for pos in positions)
        weights = {pos.symbol: pos.volume/total_exposure for pos in positions}
        
        # Update portfolio VaR
        self.current_var = self.calculate_portfolio_var(returns_df, weights)
        
        # Check correlations
        self.check_correlations(returns_df, weights)

Besonderes Augenmerk habe ich auf die Überwachung der Korrelationen zwischen den Instrumenten gelegt:

def check_correlations(self, returns_df, weights):
    corr_matrix = returns_df.corr()
    high_corr_pairs = []
    
    for i in returns_df.columns:
        for j in returns_df.columns:
            if i < j and abs(corr_matrix.loc[i,j]) > self.max_correlation:
                if weights.get(i, 0) > 0 and weights.get(j, 0) > 0:
                    high_corr_pairs.append((i, j, corr_matrix.loc[i,j]))
                    
    if high_corr_pairs:
        self.handle_high_correlations(high_corr_pairs, weights)

Ich habe ein dynamisches Risikomanagement in Abhängigkeit von den Marktbedingungen eingeführt:

def adjust_risk_limits(self, market_state):
    volatility_factor = market_state.get('volatility_ratio', 1.0)
    trend_strength = market_state.get('trend_strength', 0.5)
    
    # Adapt limits to market conditions
    self.max_portfolio_var *= np.sqrt(volatility_factor)
    if trend_strength > 0.7:  # Strong trend
        self.max_drawdown *= 1.2  # Allow a big drawdown
    elif trend_strength < 0.3:  # Weak trend
        self.max_drawdown *= 0.8  # Reduce the acceptable drawdown

Das System zur Überwachung der Absenkung erwies sich als besonders interessant:

def monitor_drawdown(self, current_balance):
    if current_balance > self.peak_balance:
        self.peak_balance = current_balance
    
    self.current_drawdown = (self.peak_balance - current_balance) / self.peak_balance
    
    if self.current_drawdown > self.max_drawdown:
        return self.handle_excessive_drawdown()
    elif self.current_drawdown > self.max_drawdown * 0.8:
        return self.reduce_risk_exposure(0.8)
    
    return True

Ich habe ein Stresstest-System zum Schutz vor extremen Ereignissen hinzugefügt:

def stress_test_portfolio(self, returns_df, weights, scenarios=1000):
    results = []
    
    for _ in range(scenarios):
        # Simulate extreme conditions
        stress_returns = returns_df.copy()
        
        # Increase volatility
        vol_multiplier = np.random.uniform(1.5, 3.0)
        stress_returns *= vol_multiplier
        
        # Add random shocks
        shock_magnitude = np.random.uniform(-0.05, 0.05)
        stress_returns += shock_magnitude
        
        # Calculate losses in a stress scenario
        portfolio_return = (stress_returns * weights).sum(axis=1)
        results.append(portfolio_return.min())
    
    return np.percentile(results, 1)  # 99% VaR in case of a stress

Das Ergebnis ist ein mehrstufiges Kapitalschutzsystem, das übermäßige Risiken wirksam verhindert und hilft, Zeiten hoher Volatilität zu überstehen. Im nächsten Abschnitt werde ich erörtern, wie all diese Komponenten im realen Handel zusammenwirken.

Visualisierung von Analyseergebnissen

Die Visualisierung wurde zu einem wichtigen Schritt in meiner Forschung. Nach der Implementierung aller Berechnungsmodule war es notwendig, eine visuelle Darstellung der Ergebnisse zu erstellen. Ich habe mehrere wichtige grafische Komponenten entwickelt, mit denen sich die Leistung des Systems in Echtzeit überwachen lässt.

Ich begann mit der Visualisierung der Portfoliostruktur und ihrer Entwicklung:

def plot_portfolio_composition(weights_history):
    plt.figure(figsize=(15, 8))
    ax = plt.gca()
    
    # Create a graph of weight changes over time
    dates = weights_history.index
    bottom = np.zeros(len(dates))
    
    for symbol in weights_history.columns:
        plt.fill_between(dates, bottom, bottom + weights_history[symbol], 
                        label=symbol, alpha=0.6)
        bottom += weights_history[symbol]
    
    plt.title('Evolution of portfolio structure')
    plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
    plt.grid(True, alpha=0.3)

Besondere Aufmerksamkeit wurde der Visualisierung von Risiken gewidmet. Ich habe auch eine VaR-Heatmap für verschiedene Währungspaare entwickelt:

def plot_var_heatmap(var_matrix):
    plt.figure(figsize=(12, 8))
    sns.heatmap(var_matrix, annot=True, cmap='RdYlBu_r', 
                fmt='.2%', center=0)
    plt.title('Portfolio risk map (VaR)')
    
    # Add a timestamp
    plt.annotate(f'Last update: {datetime.now().strftime("%Y-%m-%d %H:%M")}',
                xy=(0.01, -0.1), xycoords='axes fraction')

Um die Rentabilität zu analysieren, habe ich ein interaktives Diagramm erstellt, in dem wichtige Ereignisse hervorgehoben sind:

def plot_performance_analytics(returns_df, var_values, significant_events):
    fig = plt.figure(figsize=(15, 10))
    gs = GridSpec(2, 1, height_ratios=[3, 1])
    
    # Returns graph
    ax1 = plt.subplot(gs[0])
    cumulative_returns = (1 + returns_df).cumprod()
    ax1.plot(cumulative_returns.index, cumulative_returns, 
             label='Portfolio returns')
    
    # Mark important events
    for date, event in significant_events.items():
        ax1.axvline(x=date, color='r', linestyle='--', alpha=0.3)
        ax1.annotate(event, xy=(date, ax1.get_ylim()[1]),
                    xytext=(10, 10), textcoords='offset points',
                    rotation=45)
    
    # VaR graph
    ax2 = plt.subplot(gs[1])
    ax2.fill_between(var_values.index, -var_values, 
                     color='lightblue', alpha=0.5,
                     label='Value at Risk')

Ich habe ein interaktives Dashboard zur Überwachung des Portfoliostatus hinzugefügt:

class PortfolioDashboard:
    def __init__(self):
        self.fig = plt.figure(figsize=(15, 10))
        self.setup_subplots()
        
    def setup_subplots(self):
        gs = self.fig.add_gridspec(3, 2)
        self.ax_returns = self.fig.add_subplot(gs[0, :])
        self.ax_weights = self.fig.add_subplot(gs[1, 0])
        self.ax_risk = self.fig.add_subplot(gs[1, 1])
        self.ax_metrics = self.fig.add_subplot(gs[2, :])
        
    def update(self, portfolio_data):
        self._plot_returns(portfolio_data['returns'])
        self._plot_weights(portfolio_data['weights'])
        self._plot_risk_metrics(portfolio_data['risk'])
        self._update_metrics_table(portfolio_data['metrics'])
        
        plt.tight_layout()
        plt.show()

Ich habe eine dynamische Visualisierung zur Analyse von Korrelationen entwickelt:

def plot_correlation_dynamics(returns_df, window=60):
    # Calculation of dynamic correlations
    correlations = returns_df.rolling(window=window).corr()
    
    # Create an animated graph
    fig, ax = plt.subplots(figsize=(10, 10))
    
    def update(frame):
        ax.clear()
        sns.heatmap(correlations.loc[frame], 
                    vmin=-1, vmax=1, center=0,
                    cmap='RdBu', ax=ax)
        ax.set_title(f'Correlations on {frame.strftime("%Y-%m-%d")}')

All diese Visualisierungen helfen dabei, den Zustand des Portfolios schnell zu beurteilen und Handelsentscheidungen zu treffen. Im nächsten Abschnitt werde ich das System testen.

Backtests der Strategie

Nachdem ich die Entwicklung aller Komponenten des Systems abgeschlossen hatte, musste ich es gründlich testen. Der Prozess erwies sich als viel komplizierter als die einfache Auswertung historischer Daten. Es mussten viele Faktoren berücksichtigt werden: Slippage, Provisionen und die Besonderheiten der Auftragsausführung bei verschiedenen Brokern.

Erste Backtest-Versuche zeigten, dass der klassische Ansatz mit festen Spreads zu optimistische Ergebnisse liefert. Es war notwendig, ein realistischeres Modell zu erstellen, das die Veränderung der Spreads in Abhängigkeit von der Volatilität und der Tageszeit berücksichtigt.

Besonderes Augenmerk habe ich auf die Modellierung von Datenlücken und Liquiditätsfragen gelegt. Im realen Handel kommt es häufig zu Situationen, in denen ein Auftrag nicht zum geschätzten Preis ausgeführt werden kann. Diese Szenarien müssen bei den Tests korrekt gehandhabt werden.

Hier ist die vollständige Implementierung des Backtest-Systems:

class PortfolioBacktester:
    def __init__(self, initial_capital=100000, commission=0.0001):
        self.initial_capital = initial_capital
        self.commission = commission
        self.positions = {}
        self.trades_history = []
        self.balance_history = []
        self.var_history = []
        self.metrics = {}
        
    def run_backtest(self, returns_df, optimization_params):
        self.current_capital = self.initial_capital
        portfolio_returns = []
        
        # Preparing sliding windows for calculations
        window = 252  # Trading yesr
        for i in range(window, len(returns_df)):
            # Receive historical data for calculation
            historical_returns = returns_df.iloc[i-window:i]
            
            # Optimize the portfolio
            weights = self.optimize_portfolio(
                historical_returns, 
                optimization_params['target_return'],
                optimization_params['max_var']
            )
            
            # Calculate VaR for the current distribution
            current_var = self.calculate_portfolio_var(
                historical_returns, 
                weights,
                optimization_params['confidence_level']
            )
            
            # Check the need for rebalancing
            if self.should_rebalance(weights, current_var):
                self.execute_rebalancing(weights, returns_df.iloc[i])
            
            # Update positions and calculate profitability
            portfolio_return = self.update_positions(returns_df.iloc[i])
            portfolio_returns.append(portfolio_return)
            
            # Update metrics
            self.update_metrics(portfolio_return, current_var)
            
            # Check stop losses triggering
            self.check_stop_losses(returns_df.iloc[i])
        
        # Calculate the final metrics
        self.calculate_final_metrics(portfolio_returns)
        
    def optimize_portfolio(self, returns, target_return, max_var):
        # Using our hybrid optimization model
        opt = HybridOptimizer(returns, target_return, max_var)
        weights = opt.optimize()
        return self.apply_position_limits(weights)
        
    def execute_rebalancing(self, target_weights, current_prices):
        for symbol, target_weight in target_weights.items():
            current_weight = self.get_position_weight(symbol)
            if abs(target_weight - current_weight) > self.REBALANCING_THRESHOLD:
                # Simulate execution with slippage
                slippage = self.simulate_slippage(symbol, current_prices[symbol])
                trade_price = current_prices[symbol] * (1 + slippage)
                
                # Calculate the deal size
                trade_volume = self.calculate_trade_volume(
                    symbol, current_weight, target_weight
                )
                
                # Consider commissions
                commission = abs(trade_volume * trade_price * self.commission)
                self.current_capital -= commission
                
                # Set a deal to history
                self.record_trade(symbol, trade_volume, trade_price, commission)
                
    def update_metrics(self, portfolio_return, current_var):
        self.balance_history.append(self.current_capital)
        self.var_history.append(current_var)
        
        # Updating performance metrics
        self.metrics['max_drawdown'] = self.calculate_drawdown()
        self.metrics['sharpe_ratio'] = self.calculate_sharpe()
        self.metrics['var_efficiency'] = self.calculate_var_efficiency()
        
    def calculate_final_metrics(self, portfolio_returns):
        returns_series = pd.Series(portfolio_returns)
        
        self.metrics['total_return'] = (self.current_capital / self.initial_capital - 1)
        self.metrics['volatility'] = returns_series.std() * np.sqrt(252)
        self.metrics['sortino_ratio'] = self.calculate_sortino(returns_series)
        self.metrics['calmar_ratio'] = self.calculate_calmar()
        self.metrics['var_breaches'] = self.calculate_var_breaches()
        
    def simulate_slippage(self, symbol, price):
        # Simulate realistic slippage
        base_slippage = 0.0001  # Basic slippage
        time_factor = self.get_time_factor()  # Time dependency
        volume_factor = self.get_volume_factor(symbol)  # Volume dependency
        
        return base_slippage * time_factor * volume_factor

Die Testergebnisse waren recht aufschlussreich. Das Hybridmodell erwies sich im Vergleich zu den klassischen Ansätzen als deutlich widerstandsfähiger gegenüber Marktschocks. Dies zeigte sich insbesondere in Zeiten hoher Volatilität, in denen das VaR-Limit das Portfolio wirksam vor übermäßigen Risiken schützte.

Abschließende Fehlersuche

Nach vielen Monaten der Entwicklung und des Testens habe ich schließlich die endgültige Version des Systems erreicht. Um ehrlich zu sein, ist es ganz anders, als ich es ursprünglich geplant hatte. Die Praxis erzwang viele Veränderungen, von denen einige völlig unerwartet waren.

Die erste große Veränderung betraf die Art und Weise, wie ich mit Daten umgehe. Ich erkannte, dass es nicht ausreichte, das System nur mit historischen Daten zu testen, sondern dass es notwendig war, sein Verhalten unter einer Vielzahl von Marktbedingungen zu überprüfen. Also habe ich ein System zur Erzeugung synthetischer Daten entwickelt. Das klingt einfach, aber in Wirklichkeit dauerte es mehrere Wochen.

Zunächst habe ich alle Währungspaare nach ihrer Liquidität in Gruppen eingeteilt. Die erste Gruppe umfasste die wichtigsten Paare, wie EURUSD und GBPUSD. Der zweite enthielt Rohstoff-Währungspaare wie AUDUSD und USDCAD. Danach folgten die Kreuzkurse - EURJPY, GBPJPY und andere. Schließlich gab es noch exotische Paare, wie CADJPY und EURAUD. Für jede Gruppe habe ich meine eigenen Volatilitäts- und Korrelationsparameter festgelegt, die den realen Parametern so nahe wie möglich kommen.

Aber am interessantesten wurde es, als ich verschiedene Marktmodi hinzufügte. Stellen Sie sich vor: Ein Drittel der Zeit ist der Markt ruhig, die Volatilität ist gering. Ein weiteres Drittel ist der normale Handel. Und die verbleibende Zeit ist eine erhöhte Volatilität, in der alles wie verrückt fliegt. Außerdem habe ich langfristige Trends und zyklische Schwankungen hinzugefügt. Es stellte sich heraus, dass er dem realen Markt sehr ähnlich ist.

Auch die Portfolio-Optimierung erforderte einige Anstrengungen. Zunächst dachte ich, dass ich mit einfachen Beschränkungen für die Gewichte der Positionen auskommen würde, aber ich merkte schnell, dass dies nicht ausreichte. Daher habe ich dynamische Risikoprämien hinzugefügt - je höher die Volatilität des Paares, desto höher sollte die potenzielle Rendite sein. Eingeführte Beschränkungen: mindestens 4 % pro Position, höchstens 25 %. Das scheint viel zu sein, aber wenn Sie einen Hebel haben, ist das normal.

Apropos Hebelwirkung. Dies ist eine andere Geschichte. Am Anfang ging ich auf Nummer sicher und arbeitete fast ohne sie. Die Analyse zeigte jedoch, dass eine moderate Hebelwirkung von etwa 10 zu 1 die Ergebnisse deutlich verbesserte. Die Hauptsache ist, dass alle Kosten korrekt berücksichtigt werden. Und davon gibt es eine ganze Reihe: Handelskommissionen (zwei Basispunkte), Zinsen für die Einhaltung der Hebelgrenzen (0,01 % pro Tag), Slippage bei der Ausführung. All dies musste in den Optimierer eingebaut werden.

Ein weiteres Problem ist der Schutz vor Nachschussforderungen (Margin Call). Nach mehreren erfolglosen Versuchen habe ich mich für eine einfache Lösung entschieden: Wenn der Drawdown 10 % übersteigt, schließe ich alle Positionen und sichere zumindest einen Teil des Kapitals. Das hört sich konservativ an, funktioniert aber auf lange Sicht hervorragend.

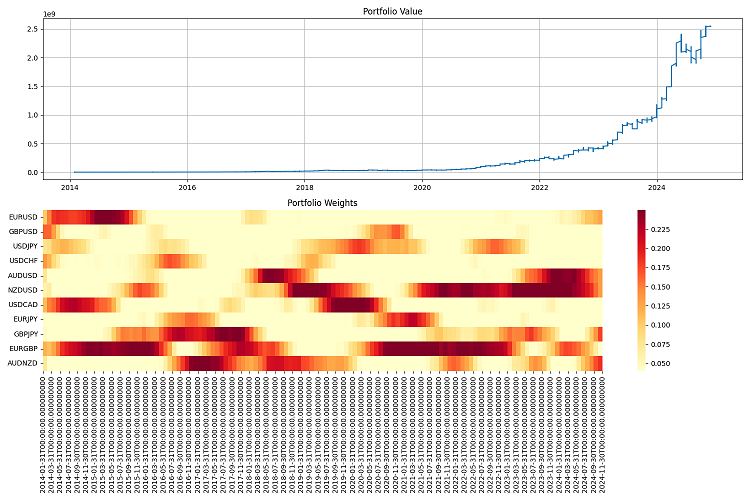
Am schwierigsten war die Berichterstattung. Wenn Ihr System mit Dutzenden von Währungspaaren arbeitet und ständig etwas kauft und verkauft, ist es einfach unmöglich, den Überblick zu behalten. Ich musste ein ganzes Überwachungssystem entwickeln: Jahresberichte mit einer Reihe von Kennzahlen, Grafiken für alles Mögliche: vom einfachen Wert des Portfolios bis hin zu Heatmaps für die Verteilung der Gewichte.

Ich habe die letzten Tests über einen langen Zeitraum durchgeführt - von 2000 bis 2024. Ich habe eine Million Dollar als Anfangskapital genommen und es einmal im Quartal neu gewichtet. Ich war mit den Ergebnissen zufrieden. Das System passt sich gut an unterschiedliche Marktbedingungen an und hält die Risiken unter Kontrolle. Selbst in den schwersten Krisen gelingt es ihr, den größten Teil ihres Kapitals zu erhalten.

Aber es gibt noch viel zu tun. Ich würde gerne maschinelles Lernen zur Vorhersage der Volatilität hinzufügen. Derzeit arbeitet das System nur mit historischen Daten. Außerdem überlege ich, wie ich die Verwaltung der Hebelwirkung flexibler gestalten kann. Auch die Häufigkeit der Neugewichtung könnte optimiert werden. Manchmal ist ein Vierteljahr zu lang, manchmal kann man Positionen sechs Monate lang in Ruhe lassen.

Im Großen und Ganzen ist es völlig anders ausgefallen, als ich es ursprünglich geplant hatte. Aber, wie man so schön sagt, das Beste ist der Feind des Guten. Das System funktioniert, kontrolliert die Risiken und bringt Geld ein. Und das ist die Hauptsache.

Schlussfolgerung

Das war eine coole Fahrt. Als ich anfing, mich mit der Theorie von Markowitz zu beschäftigen, konnte ich mir nicht vorstellen, was daraus werden würde. Ich wollte einfach nur einen konventionellen Ansatz auf den Devisenmarkt anwenden, aber am Ende musste ich eine Art Frankensteins Monster aus verschiedenen Ansätzen zum Risikomanagement erfinden.

Das Coolste ist, dass es mir gelungen ist, Markowitz mit VaR zu kreuzen, und das Ding funktioniert wirklich! Das Lustige daran ist, dass beide Methoden für sich genommen nur mittelmäßig sind, zusammen aber hervorragende Ergebnisse liefern. Ich war besonders erfreut darüber, wie gut das System funktioniert, wenn der Markt ins Wanken gerät. Der VaR ist als Begrenzer bei der Optimierung einfach erstaunlich.

Natürlich hatte ich große Schwierigkeiten mit dem technischen Teil. Aber jetzt wird alles berücksichtigt: Slippage, Provisionen und Ausführungsmerkmale.

Ich habe das System mit historischen Daten von 2000 bis 2024 getestet. Die Ergebnisse waren ziemlich gut. Er passt sich gut an unterschiedliche Marktbedingungen an und bricht auch in Krisenzeiten nicht zusammen. Mit einer Hebelwirkung von 10 zu 1 funktioniert es wie am Schnürchen. Die Hauptsache ist, dass die Risiken streng kontrolliert werden.

Aber es bleibt noch eine Menge Arbeit zu tun. Ich würde gerne noch:

• die Volatilitätsprognosen durch maschinelles Lernen zu ergänzen (dies wird das Thema des nächsten Artikels sein);
• die Häufigkeit der Neugewichtung zu klären - vielleicht kann sie optimiert werden;
• eine intelligentere Verwaltung der Hebelwirkung (dynamische Hebelwirkung und dynamisches „intelligentes“ Laden von Einlagen werden ebenfalls in künftigen Artikeln behandelt);
• das System so schulen, dass es sich noch besser an unterschiedliche Marktregime anpassen kann.

Im Allgemeinen lautet die wichtigste Schlussfolgerung: Ein cooles Handelssystem besteht nicht nur aus Gleichungen aus einem Lehrbuch. Hier muss man den Markt verstehen, sich mit der Technik auskennen und vor allem in der Lage sein, die Risiken unter Kontrolle zu halten. All diese Entwicklungen können nun auch auf andere Märkte angewendet werden, nicht nur auf den Devisenmarkt. Obwohl es noch Raum für Wachstum gibt, ist das Fundament bereits vorhanden und funktioniert.