
Nützliche und exotische Techniken für den automatisierten Handel
Inhaltsverzeichnis
- Einführung
- Algorithmus zum Schließen von Teilpositionen, unter Verwendung der letzten Barbewegung
- Hybrider Algorithmus zu Variation der Losgröße
- Prinzip der Mittelwertbildung
- Direkte und indirekte Anzeichen für die Konsistenz einer Handelstechnik
- Verwendung von Salden- und Kapital-Wellen
- Schlussfolgerung
Einführung
Es gibt viele Handelstechniken, die nach Meinung der Autoren oder der Öffentlichkeit profitabel sein sollen. Ich werde in diesem Artikel nicht auf diese Techniken eingehen, da es eine Menge Informationen über sie auf einer Vielzahl von Ressourcen gibt. Ich kann nichts Neues oder Interessantes zu diesen Methoden anbieten. Stattdessen habe ich mich entschlossen, diesen Artikel als eine Kollektion von mehreren nützlichen und nicht standardisierten Techniken zu erstellen, die sowohl theoretisch als auch praktisch nützlich sind. Einige dieser Techniken sind Ihnen vielleicht schon bekannt. Ich werde versuchen, die interessantesten Methoden zu behandeln und werde erklären, warum es sich lohnt, sie zu verwenden. Außerdem werde ich zeigen, wozu diese Techniken in der Praxis taugen.
Algorithmus zum Schließen von Teilpositionen, unter Verwendung der letzten Barbewegung
Theorie:
Dieser Ansatz kann als nützliche Handelstechnik dienen, wenn wir eine Position eröffnet haben und uns nicht sicher sind, in welche Richtung sich der Preis weiter bewegen wird. Eine intelligente Teilpositionsschließung kann Verluste aus Spreads kompensieren und nach einer guten Optimierung sogar einen Gewinn erzielen.
Lassen Sie uns mit dem Folgenden beginnen. Nehmen wir an, wir wissen nicht, wo wir aussteigen sollen, aber wir sind bereits eine Position eingegangen. Es spielt keine Rolle, in welche Richtung wir eingestiegen sind. Auf jeden Fall werden wir die Position irgendwann schließen müssen. Natürlich können manche Spieler ihre Positionen jahrelang halten. Wir gehen jedoch davon aus, dass der Roboter intensiv handeln soll und eine hohe Handelsfrequenz aufweisen soll. Es ist möglich, aus dem gesamten Volumen auszusteigen oder in ein paar Schritten, indem man die Position teilweise schließt. Wir wissen, dass der Markt eine flache Struktur hat, was bedeutet, dass der Preis dazu neigt, zu der Position des Beginns der aktuellen Halbwelle zurückzukehren. Mit anderen Worten, eine Aufwärtsbewegung bedeutet, dass die Wahrscheinlichkeit einer Fortsetzung immer weniger als 50% beträgt. Dementsprechend ist die Wahrscheinlichkeit für eine entgegengesetzte Bewegung größer als 50%. Wenn wir die gesamte Position schließen, können wir alle Wellen verpassen und den Gewinn verpassen, weil wir die zukünftige Amplitude der Wellen nicht kennen. Teilweise Schließung kann hier hilfreich sein. Wir werden in der Lage sein, den maximalen Gewinn mitzunehmen, basierend auf der Tatsache, dass wir die Natur der zukünftigen Wellen nicht kennen.
Jetzt, da wir wissen, was Wellen sind und dass sie nie aus dem Markt verschwinden werden, können wir mit dem Prinzip der Positionsschließung beginnen, das die Erzielung von zumindest einem gewissen Gewinn ermöglichen sollte, selbst wenn der Einstieg falsch erfolgt. Ein solcher Mechanismus existiert tatsächlich.
Es kann viele solcher Algorithmen geben, aber ich werde nur einen zeigen, der meiner Meinung nach der effizienteste ist. Er macht sich die Annahme zunutze, dass je größer und stärker die Bewegung auf der vorherigen voll ausgebildeten Kerze war, desto wahrscheinlicher ist es, dass es eine ziemlich starke Rollback-Bewegung geben wird. Ganz allgemein gesprochen, was ist der Zweck dieses Mechanismus? Das ist ganz einfach. Der Zweck ist, Gewinne zu erhöhen und gleichzeitig Verluste zu reduzieren. Impulse sind eigentlich auch Wellen. Aber diese Wellen sind viel nützlicher als die üblichen klassischen Wellen. Die Sache ist die, dass Wellen, die dem Markt am nächsten sind, zuverlässiger sind. Je stärker der Impuls und je kürzer seine Dauer, desto größer ist die Wahrscheinlichkeit eines Rollbacks in der nahen Zukunft und desto größer ist das Ausmaß des zu erwartenden Rollbacks. Die Idee ist, den Mechanismus so zu gestalten, dass mit zunehmender Impulskraft die Teilpositionsschließung stärker ausfallen würde. Ich werde dies in einem Bild zeigen:
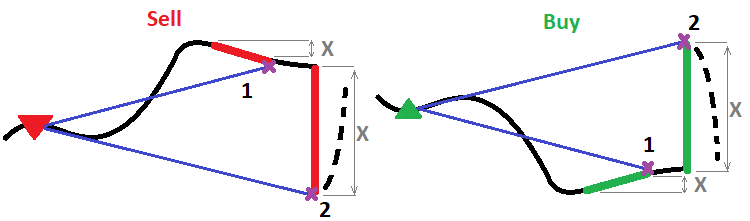
Zur Berechnung des Volumens des zu schließenden Positionsteils kann eine beliebige Funktion verwendet werden. Ich werde zwei davon zeigen. Eine ist linear und die zweite ist eine Exponentialfunktion:
- { D } - Exponent
- { X } - vorherige Bewegung der Bar in Punkten
- { C } - Skalierungsfaktor
- { Lc(X) = C * Pow(X , D) } - eine Exponentialfunktion, die das zu schließende Lot der aktuellen Kerze berechnet
- { Lc(X) = C * X } - eine lineare Funktion, die das zu schließende Lot der aktuellen Kerze berechnet
Wenn Sie genau hinsehen, ist die lineare Funktion nur ein Spezialfall einer Exponentialfunktion für D = 1, so dass wir sie weglassen können, da sie nur ein Beispiel für eine anfängliche Denklogik ist. Am Anfang ist das Denken immer einfach, aber dann, nach dem Nachdenken, bekommen wir vielseitigere Werkzeuge. Es ist nur so, dass man mit etwas Einfachem beginnen muss.
Um zu vermeiden, dass man diese Koeffizienten direkt angeben muss und sich dann um deren Auswirkungen kümmern muss, werden wir einige Steuerparameter einführen, die diese Koeffizienten bestimmen:
- { StartLotsToOnePoint } - schließt eine Position um diesen Wert, wenn X = 1 (Eingabeparameter)
- { PointsForEndLots } - Bewegung der vorherigen Kerze in die Gewinnrichtung für die Endposition Schließgeschwindigkeit (Eingabeparameter)
- { EndLotsToOnePoint } - die Position um diesen Wert schließen, wenn X = PointsForEndLots (Eingabeparameter)
Nun wollen wir ein Gleichungssystem aufstellen, um die Koeffizienten zu berechnen und die endgültige Form der Funktion, ausgedrückt durch die Eingabeparameter, zu erhalten. Zu diesem Zweck sollten die Gedanken in mathematische Ausdrücke umgewandelt werden:
- { Lc( 1 ) = StartLotsToOnePoint }
- { Lc( PointsForEndLots ) = EndLotsToOnePoint }
So, alle unsere Gleichungen sind fertig. Jetzt werden wir sie in erweiterter Form schreiben und beginnen, die Gleichungen durch schrittweises Umformen aufzulösen:
- { C * Pow(1 , D) = StartLotsToOnePoint }
- { C * Pow( PointsForEndLots , D) = EndLotsToOnePoint }
In der ersten Gleichung können wir sofort C finden, da 1 immer gleich sich selbst ist:
- { C = StartLotsToOnePoint }
Wenn wir beide Seiten der zweiten Gleichung durch "C" dividieren und dann den Logarithmus beider Seiten der Gleichung zur Basis "PunkteFürEndLose" finden, erhalten wir folgendes:
- { log( PointsForEndLots ) [ Pow( PointsForEndLots , D)] = log( PointsForEndLots ) [ EndLotsToOnePoint / C ] }
Da der Logarithmus der Basis des gleichen Logarithmus, der auf einen beliebigen Grad erhöht wurde, gleich diesem Grad ist, können wir nun unsere Gleichung in Bezug auf den gesuchten Grad wie folgt lösen:
- { D = log( PointsForEndLots ) [ EndLotsToOnePoint / C ] }
Wir haben den zweiten unbekannten Koeffizienten gefunden. Aber das ist noch nicht alles, denn MQL4 und MQL5 haben keine Basisfunktion, die einen Logarithmus zu einer beliebigen Basis implementiert, während es nur einen natürlichen Algorithmus gibt. Wir müssen also die Logarithmusbasis durch einen natürlichen Logarithmus ersetzen (der natürliche Algorithmus ist ein Logarithmus zur Basis, ausgedrückt durch die Eulersche Zahl). Das Fehlen anderer Logarithmen in der Sprache ist kein Problem, da jeder Logarithmus in Form des natürlichen Logarithmus ausgedrückt werden kann. Dies wird für jeden, der zumindest etwas von Mathematik versteht, recht einfach sein. Nach dem Umstellen der Basis sieht die Formel für unseren gewünschten Koeffizienten wie folgt aus:
- { D = ln( EndLotsToOnePoint / C ) / ln( PointsForEndLots ) }
Setzen wir den bereits bekannten Koeffizienten C ein und wir erhalten:
- { D = ln( EndLotsToOnePoint / StartLotsToOnePoint ) / ln( PointsForEndLots ) }
Nun können beide Koeffizienten in die Funktionsvorlage eingesetzt werden, um die endgültige Form zu erhalten:
- { Lc(X) = StartLotsToOnePoint * Pow( X , ln( EndLotsToOnePoint / StartLotsToOnePoint ) / ln( PointsForEndLots ) ) }
Der Vorteil dieser Funktion ist, dass der Grad Eins sein kann, aber auch größer oder kleiner als Eins sein kann. Dadurch bietet sie die maximale Flexibilität bei der Anpassung an jeden Markt und jedes Handelsinstrument. Wenn D = 1, dann erhalten wir eine lineare Funktion. Wenn D > 1, dann ist die Funktion auf die Annahme abgestimmt, dass alle Wellen skalierbar sind und die Anzahl der Wellen einer bestimmten Amplitude umgekehrt proportional zur Amplitude ist (d.h. wenn wir die Anzahl der Wellen, sagen wir auf M5 und H1, in der gleichen Zeitperiode zählen, wird sich herausstellen, dass es 12 mal weniger Wellen auf H1 gibt, einfach weil es 12 mal weniger stündliche Kerzen als fünfminütige Kerzen gibt). Wenn D < 1 ist, erwarten wir, dass wir mehr Wellen mit hoher Amplitude als kleine Wellen haben. Wenn D > 1 ist, gehen wir davon aus, dass es hauptsächlich Wellen mit geringer Amplitude gibt.
Beachten Sie auch, dass Sie nicht unbedingt eine diskretisierte Preisreihe als Folge von Bars verwenden müssen - Sie können Ticks und beliebige andere bevorzugte Preissegmente verwenden. Wir verwenden hier Bars, einfach weil wir Bars haben.
Code:
Im Code wird diese Funktion wie folgt aussehen:
double CalcCloseLots(double orderlots0,double X) { double functionvalue; double correctedlots; if ( X < 0.0 ) return 0.0; functionvalue=StartLotsToOnePoint*MathPow(X ,MathLog(EndLotsToOnePoint/StartLotsToOnePoint)/MathLog(PointsForEndLots)); correctedlots=GetLotAniError(functionvalue); if ( correctedlots > orderlots0 ) return orderlots0; else return correctedlots; }
Die Funktion, die die Losgröße korrigiert, sodass die Losgrößen nur den richtigen Wert annehmen, ist lila hervorgehoben (es macht keinen Sinn, ihr Innenleben zu zeigen). Die Funktion selbst wird unter dem grün hervorgehobenen Operator berechnet, aber sie ist Teil einer allgemeineren Funktion, die hier aufgerufen wird:
void PartialCloseType()// close order partially { bool ord; double ValidLot; MqlTick TickS; SymbolInfoTick(_Symbol,TickS); for ( int i=0; i<OrdersTotal(); i++ ) { ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES ); if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == _Symbol ) { if ( OrderType() == OP_BUY ) { ValidLot=CalcCloseLots(OrderLots(),(Open[0]-Open[1])/_Point); if ( ValidLot > 0.0 ) ord=OrderClose(OrderTicket(),ValidLot,TickS.bid,MathAbs(SlippageMaxClose),Green); } if ( OrderType() == OP_SELL ) { ValidLot=CalcCloseLots(OrderLots(),(Open[1]-Open[0])/_Point); if ( ValidLot > 0.0 ) ord=OrderClose(OrderTicket(),ValidLot,TickS.ask,MathAbs(SlippageMaxClose),Red); } break; } }
Dieser Code kann in MQL5 kompiliert werden, da wir die Bibliothek MT4Orders verwenden. Bitte beachten Sie, dass diese Funktionen zum Testen geeignet sind. Um sie für den realen Handel zu verwenden, müssen Sie sie sorgfältig studieren und verfeinern, wobei Sie auf Fehler und nicht berücksichtigte Fälle achten müssen. Auf jeden Fall ist die aktuelle Version zum Testen im Strategietester gut geeignet.
Testen des Expert Advisors:
Um zu demonstrieren, wie es funktioniert, habe ich eine EA-Version für MetaTrader 4 erstellt, denn beim Testen in MetaTrader 5 wird der Spread wahrscheinlich alles verdecken, was wir sehen wollen. Stattdessen habe ich den Spread auf 1 gesetzt und die Positionseröffnung in eine zufällige Richtung gewählt:
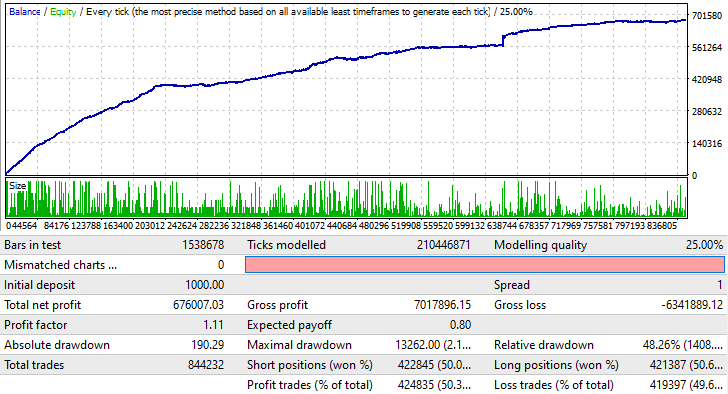
Dies funktioniert auch in ähnlicher Weise für andere Währungspaare. Er kann auch auf höheren Zeitrahmen funktionieren, aber das erfordert ein wenig Geduld, um geeignete Einstellungen zu finden. Der Test bedeutet jedoch nicht, dass Sie diesen EA sofort auf einem echten Konto starten können. Er dient nur als Bestätigung, dass diese Technik nützlich sein kann, wenn sie richtig eingesetzt wird. Wie auch immer, an diesem Punkt ist dies sehr, sehr unzureichend für den Gewinn, selbst für diesen EA. Aber in Kombination mit einem guten Signal und einer richtigen Herangehensweise, kann diese Methode profitabel sein.
Hybrider Algorithmus zu Variation der Losgröße
Schon zu Beginn der Untersuchung des Marktes habe ich mich gefragt, wie man den Gewinnfaktor eines jeden Systems in Richtung positiver Werte verschieben kann. Das würde bedeuten, dass jede Strategie, die nicht so sehr vom Spread abhängt, einen sehr großen Vorteil gegenüber allen anderen erhält, die einen Profitfaktor nahe bei eins haben. Warum genau muss der Gewinnfaktor verbessert werden? Die Antwort ist sehr einfach: Weil sowohl der relative Drawdown des gesamten Systems als auch die Profitabilität des Systems von dieser Variable abhängen. Eine solche Technik existiert, und ich werde sie Ihnen zeigen. Aber lassen Sie uns zuerst kurz die bekanntesten Handelstechniken durchgehen, die die Veränderung der Losgröße nutzen können. Es gibt die folgenden angeblichen Techniken zur Erhöhung des Gewinnfaktors:
- Martingale
- Reverse Martingale
Tatsächlich läuft alles auf zwei Methoden hinaus, die oft diskutiert werden, aber kaum etwas anderes als Enttäuschung bringen können. Es geht um ein sehr einfaches mathematisches Prinzip, das ich in dem Artikel Grid und Martingale: was sind sie und wie benutzt man sie? beschrieben habe. Es beschreibt nicht die Prinzipien selbst, sondern das, was allen gemeinsam ist. Das Gemeinsame ist, dass entweder eine Losgröße ab- oder zunimmt, abhängig von einigen Bedingungen. Wenn die Bedingungen nichts mit der Natur der Preisbildung zu tun haben, ist ein solches System vorsätzlich unrentabel.
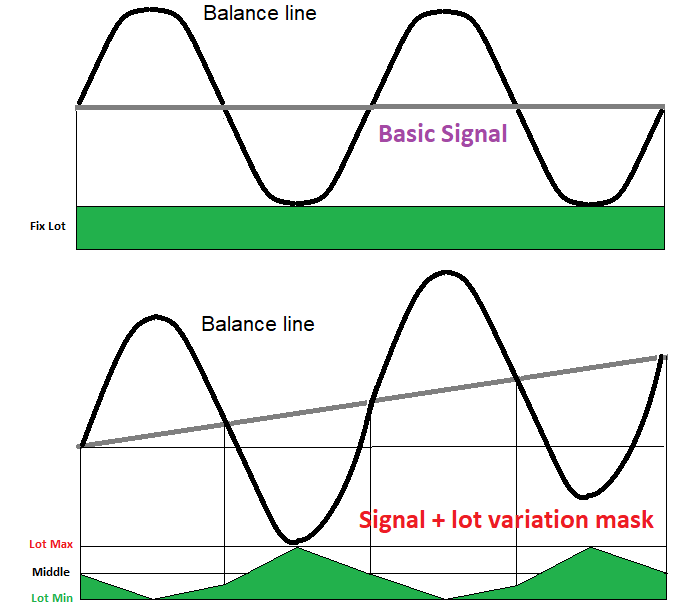
Jede Strategie, die die Losgrößen-Variation nutzt, hat ein zugrunde liegendes Signal. Wir können es erhalten, indem wir dafür sorgen, dass die Losgrößen für alle Aufträge gleich sind. Dies wird uns helfen zu verstehen, ob das zugrundeliegende Signal in irgendeiner Weise mit der Preisbildungsnatur verbunden ist. In den meisten Fällen wird ein solches Signal eine mathematische Erwartung von Null ergeben. Aber es gibt einen Parameter in diesem Signal, der uns erlauben kann, sowohl normales als auch ein Reverse-Martingale gleichzeitig zu verwenden. Die erforderliche Bedingung ist das Vorhandensein einer großen Anzahl von Wellen mit niedriger Amplitude. Wenn man die Kombination aus einem Martingal und einem Reverse-Martingal richtig verwendet, kann man sie in einen hybriden Mechanismus verwandeln, der eine mathematische Erwartung von Null in eine positive verwandelt. Die folgende Abbildung zeigt, wie dies aussehen kann:
Theorie:
Hier gehen wir von der Linie eines bestimmten Anfangssaldos aus, die ohne Berücksichtigung von Spreads und Kommissionen immer in der Nähe des Startniveaus wandern wird, bis Sie sich eines Tages entscheiden, den Handel mit einem positiven oder negativen Gewinn relativ zur Anfangsbalance zu beenden, oder bis das System langsam Ihre Einlage verliert, die durch Spreads, Kommissionen und Swaps vergeudet wird. Das bedeutet, dass jede Saldenlinie des willkürlichen Handels ein etwas wellenförmiger Prozess ist, der um das Startguthaben schwankt.
Auf dieser Grundlage können wir die gesamte Saldenlinie in steigende und fallende Abschnitte unterteilen (die Abbildung zeigt ein Viertel einer vollen Welle). Ist ein Wellenviertel steigend, sollten die Lots verringert werden (reverse martingale); ist die Welle fallend, dann sollten die Lots erhöht werden (martingale). Das einzige Hindernis für eine endlose Losgrößen-Erhöhung ist die Tatsache, dass jedes Konto ein maximal zulässiges Positionsvolumen hat. Selbst wenn also eine solche Situation möglich wäre, würde es die Einlage nicht erlauben, zusätzliche Positionen zu eröffnen. Die Losgröße sollte sich also offensichtlich in einem bestimmten Wertekorridor bewegen und nicht aus diesem ausbrechen. Daher ist der wichtige Punkt, dass die Amplitude der Wellen nicht zu groß sein sollte, vorzugsweise mehr kleine Wellen und weniger große. Wenn Sie sich die Abbildung und die darunter liegende Maske für die Lot-Variation genau ansehen, werden Sie verstehen, wie durch die hybride Variation die Linie, relativ zu der die Schwankungen auftreten, eine Steigung nach oben bekommen kann, was einem positiven mathematischen Erwartungswert und Gewinnfaktor entspricht.
Wie kann man in diesem Fall die Losgröße berechnen? Die Situation mag auf den ersten Blick unklar erscheinen. Offensichtlich können die Losgrößen eine der Grenzen unseres Kanals erreichen und niemals aus diesem ausbrechen. Für solch einen Fall müssen wir einen Mechanismus für die Rückkehr zur Ausgangslosgröße vorsehen, um stabile Schwankungen um den durchschnittlichen Losgrößen zu erhalten. Der offensichtliche und einzige Nachteil eines solchen Systems ist die Intoleranz gegenüber Wellen mit großer Amplitude. Bei einer Bewegung mit geringer Amplitude funktioniert der Mechanismus perfekt. Dieses Problem wird durch eine Funktion gelöst, die die nächste Losgröße so berechnet, dass die Funktion selbst die Lose in Richtung der Mitte schiebt, und je näher die Losgröße des vorherigen geschlossenen Auftrags an einer der Grenzen liegen, desto stärker ist der Schub. Ich werde dies in der folgenden Abbildung demonstrieren:
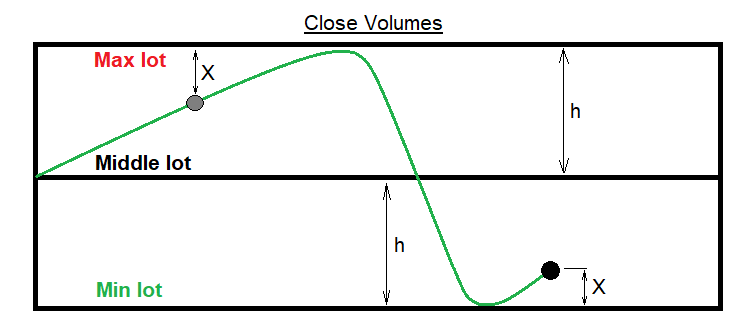
Nun werde ich eine allgemeine Darstellung einer Funktion schreiben, die für diese Aufgabe geeignet ist, wobei ich die Notation aus der Abbildung verwende. Aber zuerst wollen wir die Eingabeparameter und Hilfsvariablen definieren:
Eingabevariablen zur Steuerung der hybriden Losgrößenvariation
- { MaxLot } - maximale Losgröße des Korridors (Eingabeparameter)
- { MinLot } - minimale Losgröße des Korridors (Eingabeparameter)
- { LotForMultiplier } - Referenzlosgröße zur Erhöhung oder Verringerung des Volumens
- { ProfitForMultiplier } - Verlust und Gewinn in Punkten für die Erhöhung bzw. Verringerung der Referenzlosgröße
Hilfsvariablen
- { MiddleLot = (MaxLot + MinLot)/2 } - die Mitte zwischen der maximalen und minimalen Losgröße
- { h = (MaxLot - MinLot)/2 } - halbe Kanalbreite (wird für Berechnungen verwendet)
- { L } - die Losgröße des letzten Geschäfts aus der Historie
- { X } - Hilfsvariable
- { OrderProfit , OrderComission , OrderSwap , OrderLots } - Gewinn ohne Provision, Kommission, berechneter Auftragsswap und das Schließvolumen des letzten Auftrags aus der Historie (sie sind bekannt)
- { TickSize } - Gewinnsteigerung der offenen Position, sofern ihr Volumen 1 Losgröße beträgt und sich der Preis um 1 Punkt in die gewünschte Richtung bewegt hat
- { PointsProfit = ( OrderProfit + OrderComission + OrderSwap ) / ( OrderLots * TickSize ) } - Gewinn des letzten Auftrags in der Historie, umgerechnet in Punkte
Funktion für den Fall, dass die Losgrößen oberhalb oder unterhalb der Mittellinie liegen
- { L >= MiddleLot ? X = MaxLot - L } - wenn die Losgrößen im oberen Teil des Korridors liegen, dann ist der Wert "X" die Differenz zur oberen Grenze des Kanals
- { L < MiddleLot ? X = L - MinLot } - wenn die Losgrößen im oberen Teil des Korridors liegen, dann ist "X" der Abstand zur unteren Kanalgrenze
- { L >= MiddleLot & PointsProfit < 0 ? Lo(X) = OrderLots - LotForMultiplier * ( PointsProfit / ProfitForMultiplier ) * ( X / h ) } - verlangsamter Anstieg der Losgröße bei Annäherung an die obere Grenze des Kanals
- { L < MiddleLot & PointsProfit >= 0 ? Lo(X) = OrderLots - LotForMultiplier * ( PointsProfit / ProfitForMultiplier ) * ( X / h ) } - verlangsamte Abnahme der Losgröße bei Annäherung an die untere Grenze des Kanals
- { L >= MiddleLot & PointsProfit >= 0 ? Lo(X) = OrderLots - LotForMultiplier * ( PointsProfit / ProfitForMultiplier ) / ( X / h ) ) } - beschleunigte Losgrößenabnahme
- { L < MiddleLot & PointsProfit < 0 ? Lo(X) = OrderLots - LotForMultiplier * ( PointsProfit / ProfitForMultiplier ) / ( X / h ) } -beschleunigte Losgrößenerhöhung
Es ist ziemlich schwierig, all diese Beziehungen zu erkennen, da sie schwer zu lesen sind. Wenn Sie versuchen, alles zu einer kontinuierlichen Funktion zusammenzufassen, erhalten Sie eine so komplexe Struktur, dass es unmöglich wäre, damit zu arbeiten. Ich werde weiter zeigen, wie es im Code aussieht, damit alles klarer wird. Hier zeige ich die Implementierung des Codes im MQL4-Stil. Der Code kann leicht in MQL5 ausgeführt werden, wenn Sie die praktische und berühmte MT4Orders Bibliothek verwenden:
Code:
double CalcMultiplierLot() { bool ord; double templot=(MaxLot+MinLot)/2.0; for ( int i=OrdersHistoryTotal()-1; i>=0; i-- ) { ord=OrderSelect( i, SELECT_BY_POS, MODE_HISTORY ); if ( ord && OrderSymbol() == CurrentSymbol && OrderMagicNumber() == MagicF ) { double PointsProfit=(OrderProfit()+OrderCommission()+OrderSwap())/(OrderLots()*MarketInfo(CurrentSymbol,MODE_TICKVALUE)); if ( OrderLots() >= (MaxLot+MinLot)/2.0 ) { if ( PointsProfit < 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))*((MaxLot-OrderLots())/((MaxLot-MinLot)/2.0)); if ( PointsProfit > 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))/((MaxLot-OrderLots())/((MaxLot-MinLot)/2.0)) ; if ( PointsProfit == 0.0 ) templot=OrderLots(); break; } else { if ( PointsProfit > 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))*((OrderLots()-MinLot)/((MaxLot-MinLot)/2.0)); if ( PointsProfit < 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))/((Orderlots()-MinLot)/((MaxLot-MinLot)/2.0)); if ( PointsProfit == 0.0 ) templot=OrderLots(); break; } } } if ( templot <= MinLot ) templot=(MaxLot+MinLot)/2.0; if ( templot >= MaxLot ) templot=(MaxLot+MinLot)/2.0; return templot; }
Diese Bibliothek ist besonders nützlich, wenn Sie jeden offenen Auftrag kontrollieren müssen. Dies ist also der gesamte Ansatz. Die Eingabevariablen des Algorithmus sind gelb hervorgehoben.
Testen des Expert Advisors:
Dieser EA ist auch für MetaTrader 4 gedacht, aus dem gleichen Grund wie der vorherige EA, weil es einfacher sein wird, eine Verbesserung des Gewinnfaktors zu sehen:
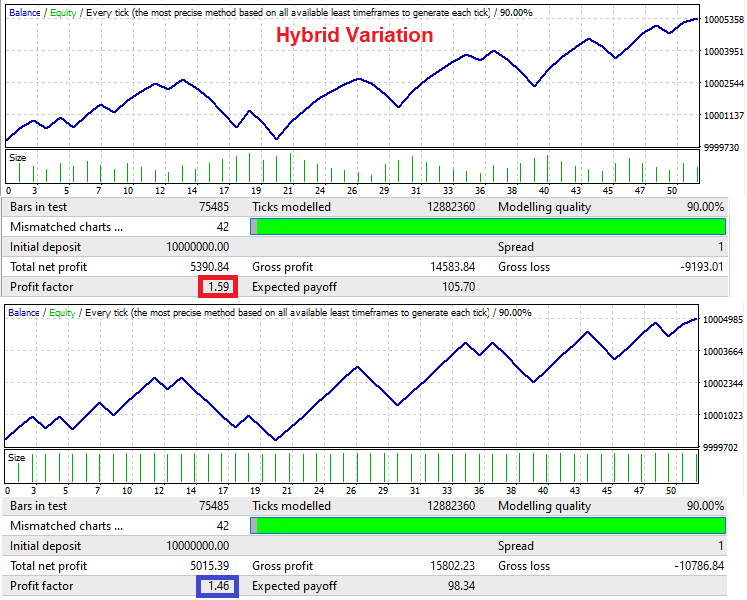
Die Signale in diesem Expert Advisor werden der Reihe nach generiert. Auf den Kauf folgt der Verkauf und auf den Verkauf folgt der Kauf. Dies wird gemacht, um das Wesen des Mechanismus zu demonstrieren. Im zweiten Test verwenden wir eine feste Losgröße, und für den ersten Test wird eine hybride Losgrößenvariation verwendet. Es ist zu sehen, dass das System nur dann eine Verbesserung des Gewinnfaktors bieten kann, wenn es minimale Gleichgewichtsschwankungen des ursprünglichen Signals gibt. Große Wellen überlebt das System nicht.
Prinzip der Mittelwertbildung
Das Prinzip der Mittelwertbildung ist ein recht interessanter Algorithmus. Obwohl es unprofitabel ist, wie das Martingal-Gitter und eine Pyramidenbildung, hat es dennoch eine sehr interessante Eigenschaft, die beim Handel der Wellen helfen kann. Wenn bekannt ist, dass die Bewegung bis zu einem bestimmten Niveau weitergeht und dann zwangsläufig ein Rollback um eine bestimmte Anzahl von Punkten erfolgt, dann kann in diesem Fall die Mittelwertbildung mit Martingal angewendet werden. Diese Technik funktioniert besonders gut mit Martingale, weil Martingale es Ihnen erlaubt, den erforderlichen Rollback zu reduzieren, während der Gewinnfaktor größer als 1,0 bleibt.
Dieses Prinzip verwendet die Annahme, dass wenn sich der Preis nicht in die Richtung unserer offenen Position bewegt, dann wird er nach einiger Zeit zweifellos um einen Teil dieser Bewegung zurücksetzen. Aber das passiert in der Realität nicht immer, obwohl Sie diesen Algorithmus für viele Symbole fein abstimmen können, indem Sie die Natur seiner Wellen studieren. Um bei diesem Rücksetzer Gewinn zu erzielen, müssen wir ihn vorhersagen oder empirisch bestimmen.
Das funktioniert auch mit starken Niveaus, denn sehr oft, wenn ein Niveau durchbrochen wird, kann der Markt versuchen, es auf Umkehr zu testen. Wenn wir mit der Richtung des ersten Geschäfts richtig geraten haben und der Gewinn den erforderlichen Wert erreicht hat, schließen wir das Geschäft und eröffnen ein neues in der Richtung, die attraktiver erscheint. Wenn der Preis in die falsche Richtung gegangen ist, dann können wir durch bestimmte Schritte versuchen, das Volumen unserer Position zu erhöhen. Wir sollten sehr vorsichtig sein, wenn wir die Position erhöhen - es sollte genau gemacht werden, basierend auf dem erwarteten Rollback. Unten sind die Beispiele von zwei möglichen.
Beispiel für eine Reihe von Kaufaufträgen:
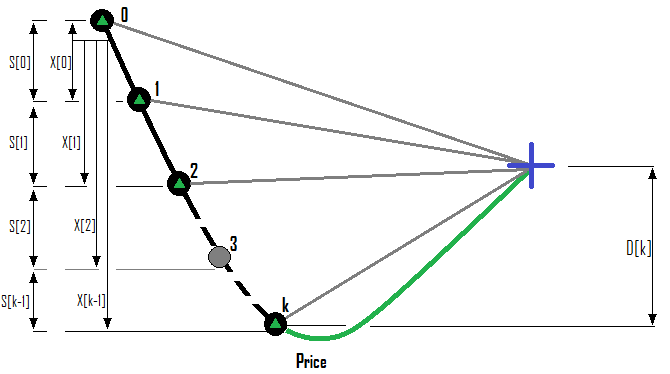
Beispiel für eine Reihe von Verkaufsaufträgen:
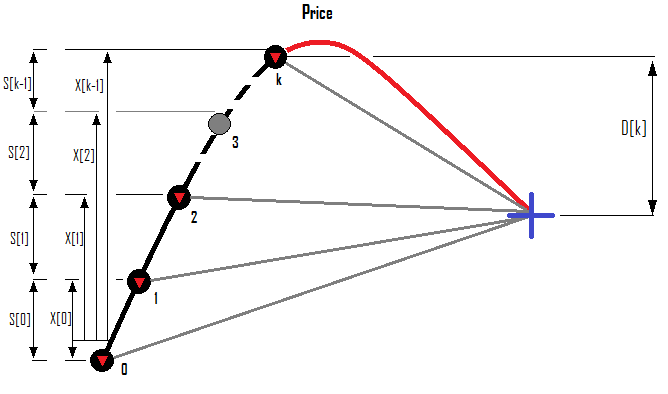
Jetzt werde ich zeigen, wie der Gewinn oder Verlust aller Aufträge berechnet wird und wie man, basierend auf der bestehenden Situation, die Losgröße des nächsten Auftrags, basierend auf dem erforderlichen Rollback, berechnet. Um eine Reihe oder einen Fächer von Positionen zu schließen, ist es notwendig zu wissen, warum dieser Fächer gebildet werden soll und welche Bedingung ihn sinnvoll macht. Ich würde den Profit-Faktor verwenden. Wenn der Fächer positiv ist, dann ist auch der Profit-Faktor positiv. Es wäre töricht, den Fächer zu schließen, sobald der Gesamtgewinn aller Aufträge positiv wird, weil jede Preisschwankung auf dem Server oder ein Slippage den Gewinn in die negative Richtung verschieben kann - solche Fächer können unter solchen Bedingungen nutzlos erscheinen. Darüber hinaus bietet der Gewinnfaktor des Zyklus eine Möglichkeit zur zusätzlichen Anpassung der Aggressivität der Mittelwertbildung, die bei der Optimierung einer automatisierten Strategie oder bei der manuellen Suche nach Einstellungen genutzt werden kann.
Nehmen wir an, dass es ein Limit für die maximale Anzahl von Aufträgen in einer Serie gibt. Dann nehmen wir an, dass wir uns in einer unbekannten Situation befinden, in der wir bereits k Aufträge geöffnet haben - ihre Indizes beginnen bei 0, wie in allen Sammlungen oder Arrays. Der Index des letzten Auftrags in der Serie wird also "k-1" sein. Wenn wir den nächsten Auftrag öffnen, wird sein Index k sein und die Anzahl der Aufträge wird "k + 1" sein. Lassen Sie uns dieses Ideal in den Eingabedaten des Problems formalisieren:
- { MaxOrders } - die maximal zulässige Anzahl von Aufträgen in einer Serie
- { k = 0 ... 1 ... 2 ... (MaxOrders-1) } - der Index des nächsten Auftrags in der Serie, den wir eröffnen wollen, wenn wir mit dem vorherigen Ansatz keinen Gewinn erzielen
- { ProfitFactorMax } - zulässiger Gewinnfaktor für das Schließen
- { i = 1 ... 1 ... 2 ... k } - Indizes der bereits vorhandenen Aufträge des Fächers und des nächsten Auftrags, den wir eröffnen wollen
- { S[i-1] } - der Abstand in Punkten vom vorherigen Auftrag zum aktuellen
- { X[i-1] } - der Abstand in Punkten vom nullten Auftrag der Reihe zum aktuellen
- { D[k] } - vorhergesagter Rollback in der gewünschten Richtung relativ zum offenen Preis des letzten Auftrags der Serie
Zusätzlich können wir sagen, dass die Sprachen MQL4 und MQL5 die folgenden Daten bereitstellen, wenn wir uns auf einen bestimmten Auftrag beziehen, den wir zur Beschreibung aller Berechnungsmöglichkeiten benötigen:
- { P[i] } - der Gewinn eines bestimmten Auftrags ohne Berücksichtigung von Provisionen und Swaps
- { С[i] } - Provision des ausgewählten Auftrags
- { S[i] } - berechnete Auftragsswap bei einem Rollover um 0:00
- { L[i] } - Auftragsvolumen
- { Sp[i] } - Spread bei Eröffnung einer Kaufposition / aktueller Spread bei Verkaufspositionen
- { TickSize } - eine Erhöhung des Gewinns der offenen Position, vorausgesetzt, ihr Volumen entspricht 1 Losgröße und der Preis hat sich um 1 Punkt in die gewünschte Richtung bewegt
Nicht alle dieser Werte werden für den praktischen Einsatz im automatisierten Handel benötigt, aber sie erlauben es, alle möglichen Optionen für die Berechnung dieser Werte hervorzuheben. Einige dieser Werte, die relevant sind und in Relation zum Preis dargestellt werden können, sind in den obigen Abbildungen dargestellt. Lassen Sie uns mit der einfachsten Berechnungsmethode beginnen, die ich in meinem Code verwende:
Wenn der erste Auftrag mit positivem Ergebnis schließt, dann tun Sie nichts. In jedem Moment, den wir für angemessen halten, öffnen wir einen neuen Auftrag in der gewünschten Richtung. Wenn der Preis das Ziel nicht erreicht hat und in die entgegengesetzte Richtung gegangen ist, dann müssen wir entscheiden, um wie viele Punkte sich der Preis in die verlustbringende Richtung bewegen sollte, um den nächsten Auftrag zu öffnen (S[k-1] ). Wenn der Preis dieses Niveau erreicht hat, müssen wir entscheiden, welcher Rollback angemessen ist (D[k]). Danach müssen wir die Losgröße des Auftrags bestimmen, den wir jetzt eröffnen, damit wir bei einem geplanten Rollback den erforderlichen Profitfaktor aller Aufträge größer als den von uns gewählten Wert erhalten (ProfitFactorMax). Dazu müssen wir zunächst berechnen, welcher Gewinn durch die aktuell offenen Aufträge generiert wird, sowie welcher Verlust generiert wird, und deren Gesamtwert. Den Zweck dessen werde ich später erklären, nachdem ich die entsprechenden Formeln geschrieben habe:
Zunächst wollen wir den zukünftigen Gewinnwert für jeden einzelnen Auftrag einführen. Er ist gleich dem aktuellen Gewinn und dem Inkrement, das der Auftrag erhalten wird, vorausgesetzt, dass der erforderliche Rollback stattfinden wird:
- { j = 0 ... 1 ... 2 ... k-1 }
- { PF[j] = P[j] + С[j] + S[j] + (D[k] * L[j] * TickSize) } - der Gewinn eines bestimmten Auftrags wird diesem Wert entsprechen, wenn der erforderliche Rollback stattfindet
- { PF[k] = { ( D[k] - Spread[k] ) * L[k] * TickSize } - dieser Wert kann nicht berechnet werden, da er die erforderliche Losgröße der Position enthält, die wir öffnen wollen; aber dieser Ausdruck wird später benötigt
Im ersten Fall ist der Wert P[i] bekannt, und wir können ihn sowohl mit den eingebauten Sprachfunktionen erhalten, als auch selbst berechnen. Diese Berechnungsmethode wird am Ende des Artikels als Zusatz gezeigt, weil alles mit den Standard-Sprachmitteln gefunden werden kann. Was den letzten Auftrag in der Serie betrifft, den wir öffnen werden, so braucht er auch eine Kommission und einen Swap, aber diese Werte können nur für bereits geöffnete Aufträge ermittelt werden. Außerdem ist es unmöglich, den Swap-Wert zu bestimmen, da wir nicht wissen, ob die Position durch 0:00 gehen wird. Es wird immer ungenaue Werte geben. Es ist möglich, nur die Währungspaare auszuwählen, die positive Swaps haben
Danach können wir diesen vorhergesagten Gewinn verwenden, um gewinnbringende und verlustbringende Aufträge aufzuteilen und den resultierenden Gewinnfaktor zu berechnen:
- { i = 0 ... 1 ... 2 ... k } - Indizes der bereits offenen Aufträge
- { Pr[i] >= 0, Ls[i] >= 0 } - wir führen 2 Arrays ein, die je nach Vorzeichen den Gewinn oder Verlust des Auftrags aufnehmen ("+" wird für den Gewinn verwendet, der für die Berechnung des Gewinnfaktors benötigt wird)
- { PF [i] < 0 ? Pr[i] = 0 & Ls[i] = - PF[i] } - wenn der Gewinn des Auftrags negativ ist, dann schreiben wir seinen Gewinn als "0", während der Gewinnwert mit umgekehrtem Vorzeichen in eine Variable für Verluste geschrieben werden soll
- { PF [i] > 0 ? Ls[i] = 0 & Pr[i] = PF[i] } - wenn der Gewinn des Auftrags positiv ist, schreiben wir ihn einfach in das entsprechende Array und setzen einen Nullwert in das Verlust-Array
Nachdem wir diese Arrays gefüllt haben, können wir eine Formel schreiben, um den Gesamtgewinn und -verlust sowie das Ergebnis zu berechnen.
- { SummProfit = Summ[0,k]( PF[i] ) } - Gesamtgewinnmodul aller profitablen Aufträge
- { SummLoss = Summ[0,k]( Ls [i] ) } - Gesamtverlustmodul aller Verlustaufträge
Nun müssen wir die Bedingung für das Ende der Schleife schreiben:
- { SummLoss > 0 ? SummProfit/SummLoss = ProfitFactorMax }
Um diese Gleichung weiter zu verwenden, müssen Sie verstehen, dass der Gewinn des letzten Auftrags in der Reihe immer positiv ist, wenn ein Positionsfächer geschlossen wird. Auf dieser Grundlage können wir schreiben:
- { SummProfit = Summ[0,k-1]( PF[j] ) + PF[k] }
Wir setzen diesen Wert in die Gleichung ein und erhalten Folgendes:
- { ( Summ[0,k-1]( PF[j] ) + PF[k] ) / SummLoss = ProfitFactorMax }
Wenn wir nun diese Gleichung nach PF[k] auflösen, erhalten wir:
- { PF[k] = ProfitFactorMax * SummLoss - Summ[0,k-1]( PF[j] ) }
In Anbetracht der Tatsache, dass wir bereits eine Formel für den Wert von PF[k] haben, können wir diesen Ausdruck hier einsetzen und erhalten:
- { ( D[k] - Spread[k] ) * L[k] * TickSize = ProfitFactorMax * SummLoss - Summ[0,k-1]( PF[j] ) }
Nun können wir diese Gleichung in Bezug auf L[k] lösen. So erhalten wir schließlich die Formel zur Berechnung des erforderlichen Positionsvolumens zum Öffnen:
- { L[k] = ( ProfitFactorMax * SummLoss - Summ[0,k-1]( PF[j] ) ) / ( ( D[k] - Spread[k] ) * TickSize ) }
Das ist alles. Betrachten wir nun, wie man den Wert von P[i] ohne Verwendung der eingebauten Funktionen berechnen kann.
- { P[i] = ( X[i-1] - Spread[i] ) * L[i] * TickSize + С[j] + S[j] }
Berechnen des Rollback-Wertes
Sehen wir uns nun die Methoden zur Berechnung des Rollbacks an. Ich verwende zwei Methoden. Es kann viele davon geben, aber ich werde nur zwei Methoden angeben, die ich für die nützlichsten halte. Der Rollback wird im Verhältnis dazu berechnet, wie sehr der Kurs in die falsche Richtung gegangen ist. Das bedeutet, dass D[i] und X[i] durch eine beliebige Funktion verbunden werden können, die auf der gesamten positiven X-Achse positiv ist:
- { D=D(X) }
- { D[k] = D( X[k-1] ) }
Ich verwende zwei Funktionen zur Berechnung des Rollbacks. Die erste ist linear. Die zweite ist eine Exponentialfunktion. Die zweite Funktion ist etwas schwieriger, aber interessanter. Hier sind die Funktionen:
- { D = K * X }
- { D = DMin + C * Pow(S , X) }
Die zu findenden Koeffizienten habe ich hervorgehoben. Basierend auf diesen Koeffizienten beginnen die Funktionen unterschiedlich zu wirken und dementsprechend können wir unsere Strategie flexibel an ein bestimmtes Währungspaar oder einen bestimmten Zeitrahmen anpassen.
- { K } - Rollback-Koeffizient für eine lineare Funktion (er wird auch als Eingabeparameter für ein automatisiertes System verwendet)
- { DMin } - der minimal zulässige Rollback (D >= DMin, im Falle einer Exponentialfunktion)
- { C } - Skalierungsfaktor der Exponentialfunktion
- { S } - die Basis des Exponenten
Streng genommen kann C zum Grad addiert werden, aber ich denke, in dieser Form ist die Funktion besser lesbar und bequemer zu benutzen. Beachten Sie auch, dass die Werte K und DMin Eingabeparameter sind, diese Koeffizienten sind uns also bereits bekannt. Es ist nicht klar, wie die beiden restlichen Koeffizienten zu berechnen sind. Lassen Sie es uns jetzt tun. Um 2 unbekannte Werte zu finden, benötigen wir ein System aus mindestens zwei Gleichungen. Die Koeffizienten können durch Lösen des Systems gefunden werden. Um ein solches System zu schreiben, müssen wir zunächst entscheiden, wie die Funktionsform gesteuert werden soll. Ich habe mich für die Exponentialfunktion entschieden, weil sie einfacher und bequemer ist, eine glatte Abnahme im Rollback zu machen. Aus diesem Grund habe ich die Exponentialfunktion gewählt. Die Überlegungen waren wie folgt:
- { HalfX } - Kursbewegung für die Hälfte des zusätzlichen Rollbacks (ein zusätzlicher Eingabeparameter zur Steuerung der Funktion)
- { D(0) = DMin + K*DMin }
- { D(HalfX) = DMin + K*DMin/2 }
So erhalten wir das benötigte Gleichungssystem, das wir lösen können. Mit anderen Worten, wir setzen die Kursbewegung in Richtung Verlust, bezogen auf den ersten offenen Auftrag, bei dem die Addition zum Rollback die Hälfte des Wertes am Anfang beträgt. Diese Addition hat einen maximalen Wert am Anfang. Als Ergebnis erhalten wir eine Funktion, die keinen Wert annehmen kann, der kleiner als der minimale Rollback ist, und wenn X gegen unendlich tendiert, geht die Funktion auf den minimalen Rollback. Mathematisch wird dies wie folgt ausgedrückt:
- { D >= DMin }
- { Lim( X -> +infinity ) = DMin }
Jetzt können wir mit der Lösung dieses Gleichungssystems beginnen, aber lassen Sie uns zuerst das vollständige System umschreiben:
- { DMin + C * Pow(S , 0) = DMin + K*DMin }
- { DMin + C * Pow(S , HalfX) = DMin + K*DMin/2 }
In der ersten Gleichung können wir sofort C finden, wenn wir berücksichtigen, dass jede Zahl in der Nullstelle zu Eins wird. Somit schließen wir die Variable S aus. Jetzt müssen wir die Gleichung nur noch in Bezug auf die Variable C lösen.
- { С = K * DMin }
Da wir nun C kennen, können wir die verbleibende Unbekannte S ermitteln, indem wir einfach den vorherigen Ausdruck für die Variable C ersetzen:
- { Pow(S , HalfX) = 0.5 }
Um den Grad zu eliminieren, sollten wir beide Teile der Gleichung auf den Grad-Reziprokwert von HalfX anheben. Als Ergebnis erhalten wir den folgenden einfachen Ausdruck, der den gewünschten Koeffizienten darstellt:
- { S = Pow(0.5 , 1/HalfX) }
Nun können wir unsere Exponentialfunktion schreiben, indem wir die Koeffizienten substituieren. Damit ist alles beschrieben, was wir für die Umsetzung benötigen:
- { D(X) = DMin + K * DMin * Pow( Pow(0.5 , 1/HalfX) , X ) }
So wird diese Funktion im Code aussehen:
Code:
double D(double D0,double K0,double H0,double X) { return D0+(D0*K0)*MathPow(MathPow(0.5,1.0/H0),X); }
Hier sind ein paar weitere wichtige Funktionen, die im EA verwendet werden, um die Theorie zu testen. Die erste ist die Funktion, die den Abstand in Punkten vom Preis zum nächstgelegenen offenen Auftrag in der Serie bestimmt:
double CalculateTranslation() { bool ord; bool bStartDirection; bool bFind; double ExtremumPrice=0.0; for ( int i=0; i<OrdersTotal(); i++ ) { ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES ); if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() ) { if ( OrderType() == OP_SELL ) bStartDirection=false; if ( OrderType() == OP_BUY ) bStartDirection=true; ExtremumPrice=OrderOpenPrice(); bFind=true; break; } } for ( int i=0; i<OrdersTotal(); i++ ) { ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES ); if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() ) { if ( OrderType() == OP_SELL && OrderOpenPrice() > ExtremumPrice ) ExtremumPrice=OrderOpenPrice(); if ( OrderType() == OP_BUY && OrderOpenPrice() < ExtremumPrice ) ExtremumPrice=OrderOpenPrice(); } } if ( bFind ) { if ( bStartDirection ) return (ExtremumPrice-Close[0])/_Point; else return (Close[0]-ExtremumPrice)/_Point; } else return -1.0; }
Wir benötigen diese Funktion, um den geforderten Schritt zwischen Aufträgen in der Serie einzuhalten. Dieser Schritt wird behoben werden. Vergessen wir nicht, dass das Array "Close[]" in MQL5 nicht implementiert ist und wir es so implementieren müssen, wie es in meinen vorherigen Artikeln gezeigt wurde. Ich denke, dieser Schritt ist ziemlich klar.
Um die aktuellen X und D zu berechnen, werden wir die folgende Funktion verwenden, die keine Rückgabewerte hat, wie alle weiteren Funktionen. Sie wird das Ergebnis in globale Variablen schreiben (es ist besser, den Zugriff auf Aufträge zu minimieren und unnötige Aufrufe der Funktionen, die mit der Historie arbeiten, zu vermeiden:
double Xx;//shift of X double Dd;//desired rollback of D void CalcXD()//calculate current X and D { bool ord; bool bStartDirection=false; bool bFind=false; double ExtremumPrice=0.0; for ( int i=0; i<OrdersTotal(); i++ ) { ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES ); if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() ) { if ( OrderType() == OP_SELL ) bStartDirection=false; if ( OrderType() == OP_BUY ) bStartDirection=true; ExtremumPrice=OrderOpenPrice(); bFind=true; break; } } for ( int i=0; i<OrdersTotal(); i++ ) { ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES ); if ( OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() ) { if ( OrderType() == OP_SELL && OrderOpenPrice() < ExtremumPrice ) ExtremumPrice=OrderOpenPrice(); if ( OrderType() == OP_BUY && OrderOpenPrice() > ExtremumPrice ) ExtremumPrice=OrderOpenPrice(); } } Xx=0.0; Dd=0.0; if ( bFind ) { if ( !bStartDirection ) Xx=(Close[0]-ExtremumPrice)/_Point; if ( bStartDirection ) Xx=(ExtremumPrice-Close[0])/_Point; if ( MODEE==MODE_SINGULARITY ) Dd=D(DE,KE,XE,Xx); else Dd=Xx*KE; } }
Dieser Code ist voll kompatibel mit der Bibliothek MT4Orders und kann somit in MQL5 kompiliert werden. Dies bezieht sich auch auf die Funktionen, die weiter besprochen werden. Die Eingabevariablen des Algorithmus sind gelb hervorgehoben.
Um den aktuellen und vorhergesagten Gewinn zu berechnen, werden wir drei Variablen verwenden:
double TotalProfitPoints=0.0; double TotalProfit=0; double TotalLoss=0;
Die Rückgabewerte werden zu diesen Variablen hinzugefügt, während die Funktionen selbst keine Rückgabewerte haben - so vermeiden wir, dass jedes Mal eine Auftrags-Iteration durchgeführt wird, was den Codebetrieb um ein Vielfaches verlangsamt.
Eine der nächsten beiden Funktionen wird für die Schließbedingung verwendet, und die zweite wird für die Berechnung des vorhergesagten Gewinns der aktuell offenen Positionen verwendet:
void CalcLP()//calculate losses and profits of all open orders { bool ord; double TempProfit=0.0; TotalProfit=0.0; TotalLoss=0.0; TotalProfitPoints=0.0; for ( int i=0; i<OrdersTotal(); i++ ) { ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES ); if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() ) { TempProfit=OrderProfit()+OrderCommission()+OrderSwap(); TotalProfitPoints+=(OrderProfit()+OrderCommission()+OrderSwap())/(OrderLots()*SymbolInfoDouble(Symbol(),SYMBOL_TRADE_TICK_VALUE)); if ( TempProfit >= 0.0 ) TotalProfit+=TempProfit; else TotalLoss-=TempProfit; } } } void CalcLPFuture()//calculate losses and profits of all existing orders in the future { bool ord; double TempProfit=0; TotalProfit=0; TotalLoss=0; for ( int i=0; i<OrdersTotal(); i++ ) { ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES ); if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() ) { TempProfit=OrderProfit()+OrderCommission()+OrderSwap()+(OrderLots()*SymbolInfoDouble(Symbol(),SYMBOL_TRADE_TICK_VALUE)*Dd); if ( TempProfit >= 0.0 ) TotalProfit+=TempProfit; else TotalLoss-=TempProfit; } } }
Außerdem ist hier die Prädikatsfunktion für die Abschlussbedingung der Auftragsserie:
bool bClose() { CalcLP(); if ( TotalLoss != 0.0 && TotalProfit/TotalLoss >= ProfitFactorMin ) return true; if ( TotalLoss == 0.0 && TotalProfitPoints >= DE*KE ) return true; return false; }
Testen des Expert Advisors:
Ich habe einen Expert Advisor für MetaTrader 5 erstellt, der das beschriebene Prinzip nutzt, da diese Methode, wenn sie richtig angewendet wird, fast alle Spreads, Kommissionen und Swaps überwinden kann. Hier ist das Testergebnis des EAs, der die Mittelwertbildung ausnutzt:
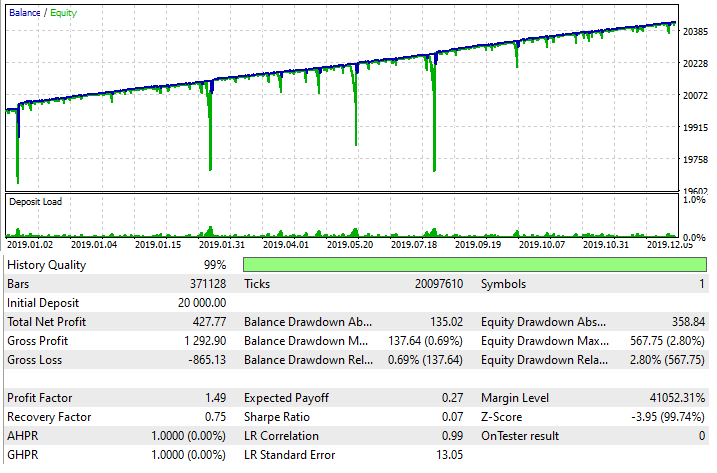
Bitte beachten Sie jedoch, dass es sich nur um eine Handelstechnik handelt, die sehr vorsichtig eingesetzt werden muss. Dennoch ist sie sehr flexibel und kann in Verbindung mit einer Vielzahl von Strategien eingesetzt werden. Auch hier gilt: Bitte seien Sie vorsichtig.
Direkte und indirekte Anzeichen für die Konsistenz einer Handelstechnik
Im Rahmen dieses Artikels wäre es sinnvoll zu überlegen, welche mathematischen Backtest-Variablen beweisen können, dass die verwendete Technik unsere Strategie stärkt oder sogar eine verlustreiche Strategie in eine profitable verwandelt. Die Frage ist sehr wichtig, denn wenn wir die Backtest-Ergebnisse falsch interpretieren, können wir eine eigentlich funktionierende Technik ausschließen oder eine falsche Technik einsetzen. Bei der Entwicklung neuer Handelstechniken befolge ich immer zwei Regeln, die eine notwendige und hinreichende Bedingung für die wahrscheinlichste Erkennung funktionierender Techniken und die wahrscheinlichste Ablehnung falscher Techniken schaffen:
- Die Größe der Datenstichprobe sowie die Anzahl der Positionen im Backtest sollten für die statistische Auswertung maximiert werden
- Schon eine geringe Veränderung der Backtest-Werte kann auf positive Veränderungen hinweisen
In vielen Fällen kann jede positive Veränderung so verstärkt werden, dass sie für den Handel von Vorteil ist. Das sind unbestreitbare Vorteile:
- Solche Handelstechniken können auf jedes Handelsinstrument angewendet werden
- Techniken können kombiniert und in Hybride verwandelt werden
- Bei richtiger Anwendung sind Ihre Chancen, einen Gewinn zu erzielen, größer als einen Verlust zu erleiden, selbst bei einem Spread
Ich werde nun zeigen, welche Variablen analysiert werden sollten, wenn man eine Handelstechnik anwenden möchte. Lassen Sie uns das Beispiel der letzten in diesem Artikel besprochenen Handelstechnik verwenden. Beginnen wir mit den Backtest-Metriken und sehen wir uns an, wie man sie verwendet, um synthetische Metriken zu erstellen, um Verbesserungen zu erkennen.
Achten Sie zunächst auf die folgenden Variablen:
- Endgültiger Backtest-Gewinn
- Maximaler Drawdown vom Saldo
- Maximaler Drawdown vom Kapital
Es gibt einige zusätzliche, genauere Variablen, die hilfreich sein könnten, die aber in den Berichten des Strategietesters nicht verfügbar sind:
- Durchschnittlicher Drawdown des Saldos
- Durchschnittlicher Drawdown des Kapitals
Warum zeigen diese Metriken genau, wie sicher und profitabel das System ist? Der Punkt ist, dass es für jeden Backtest die folgenden mathematischen Identitäten gibt, wie für jedes Handelssystem, das auf einem Demo- oder Realkonto gehandelt wird:
- { i = 0 ... 1 ... 2 ... m } - die Nummer einer Halbwelle (eine Halbwelle ist ein wachsendes Equity- oder Saldensegment, gefolgt von einem fallenden)
- { j = 0 ... 1 ... 2 ... k } - negative Halbwellensegmente (Saldensegmente beginnen und enden am Positionseröffnungs- und -schließpunkt, und Aktiensegmente enden und beginnen an anderen Punkten)
- { OrderProfit[j]-OrderComission[j]-OrderSwap[j] < 0 ! Lim( m --> +infinity ) [ Summ(i) [Summ(j) [ OrderProfit[j]-OrderComission[j]-OrderSwap[j] ]] / m ] = Gesamtgewinn ohne Provisionsspreads und Swaps } - durchschnittlicher Drawdown für Backtest oder Handelsbilanz
- { SegmentEquity[j]-SegmentComission[j]-SegmentSwap[j] < 0 ! Lim( m --> +infinity ) [ Summ(i) [Summ(j) [ SegmentEquity[j]-SegmentComission[j]-SegmentSwap[j] ]] / m ] = Gesamtgewinn ohne Provisionsspreads und Swaps } - durchschnittlicher Drawdown für Backtest oder Handelsbilanz
Mit anderen Worten: Der durchschnittliche Drawdown, sowohl in Bezug auf den Saldo als auch auf das Eigenkapital, tendiert bei einem endlosen Backtest oder einer endlosen Verwendung der Strategie auf einem Demo- oder Realkonto zu dem Wert des Endsaldos, wenn die Transaktionsgebühr null wäre. Dies gilt natürlich nur, wenn die Strategie einen ausgeprägten positiven Gewinn hat. Wenn der Gesamtgewinn ein negatives Vorzeichen hat, können Sie Spiegelformeln ausprobieren, bei denen Sie nicht negative, sondern positive Segmente aufsummieren sollten. Am bequemsten ist es jedoch, mit einem bereits bekannten positiven Backtest zu arbeiten und einige Techniken darauf anzuwenden. Das bedeutet jedoch nicht, dass ein globaler Backtest Gewinn zeigt. Sie sollten solche Verlaufsintervalle finden, in denen die Strategie Gewinn zeigt (vorzugsweise mehrere solcher Intervalle). Wenden Sie dann einen Ansatz an.
Lassen Sie uns nun sehen, wie wir mit einem einfachen Martingal seine Stabilität stärken und seine Performance leicht in Richtung Profit verschieben können. Basierend auf den oben genannten Formeln ist es möglich, solche synthetischen Metriken zu erstellen, nach denen es möglich ist, den Effekt der Handelstechnik auf den Handel als Ganzes, basierend auf einigen kleinen Segmenten, zu bewerten:
Eingabedaten für synthetische Metriken:
- { Tp } - Backtestende oder Handelsgewinn
- { BdM } - durchschnittlicher Saldorückgang
- { EdM } - durchschnittlicher Kapitalrückgang
- { BdMax } - maximaler Saldorückgang
- { EdMax } - maximaler Kapitalrückgang
Die Farbe hebt die Daten hervor, die im Backtest nicht verfügbar sind. Aber diese Daten können im Code berechnet und am Ende des Handels oder Backtests angezeigt werden. Ich ziehe es aber vor, andere Daten zu verwenden, die verfügbar sind. Der Punkt ist, dass je kleiner der durchschnittliche Rückgang ist, desto kleiner ist in den meisten Fällen der maximale Drawdown aus beiden Werten. Diese Werte sind sehr eng mit Wahrscheinlichkeiten verbunden, und Änderungen in einer Metrik ziehen normalerweise ungefähr proportionale Änderungen in einer anderen Metrik nach sich.
Synthetische Metriken:
- { A = Tp/BdM } - gleich Eins, wenn die Strategie die Zukunft nicht vorhersagen kann, und mehr als Eins, wenn sie die Zukunft vorhersagen kann und verdient (was der Beantwortung der Frage nach der Rentabilität entspricht)
- { B = Tp/EdM } - gleich dem vorherigen Wert
- { C = Tp / BdMax } - wenn es einen Anstieg in dieser Metrik gibt, dann können wir schlussfolgern, dass die Technik die Effektivität der Methode erhöht (eine Abnahme bedeutet den negativen Effekt)
- { D = Tp / EdMax } - derselbe wie der vorherige Wert
Jedes dieser 4 Kriterien kann verwendet werden. Die ersten beiden sind genauer, aber der Backtest kann die notwendigen Daten für ihre Berechnung nicht bereitstellen, so dass Sie die Eingabedaten lesen müssten. Die anderen beiden können mit Hilfe von Werten aus dem Backtest berechnet werden. Ich persönlich verwende also die letzten beiden Metriken, weil sie verfügbar sind und leicht gefunden werden können. Lassen Sie uns nun die Anwendung dieser Methode am Beispiel eines einfachen Martingals betrachten, das durch Stop-Aufträge geschlossen wird. Wir werden versuchen, seine Variablen mit Hilfe des letzten exotischen Ansatzes zu stärken.
Verwendung von Salden- und Kapital-Wellen
Theorie:In der Tat kann diese Technik nicht nur für Martingale, sondern auch für alle anderen Strategien verwendet werden, die eine ausreichend hohe Handelsfrequenz haben. In diesem Beispiel werde ich die Metrik basierend auf dem Saldorückgang verwenden. Denn alles, was mit dem Saldo zusammenhängt, wird als einfacher angesehen. Lassen Sie uns die Saldenkurve in steigende und fallende Segmente unterteilen. Zwei benachbarte Segmente bilden eine Halbwelle. Die Anzahl der Halbwellen tendiert gegen unendlich, da die Anzahl der Transaktionen gegen unendlich tendiert. Eine endliche Stichprobe genügt uns, um das Martingal ein wenig profitabler zu machen. Das folgende Diagramm erklärt die Idee:
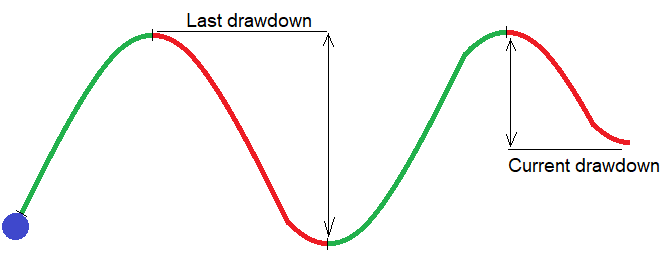
Die Abbildung zeigt eine gebildete Halbwelle und diejenige, die gerade begonnen hat. Jedes Saldenkurve besteht aus solchen Halbwellen. Die Größe dieser Halbwellen schwankt ständig, und wir können auf dem Diagramm immer Gruppen solcher Halbwellen unterscheiden. Die Größe dieser Halbwellen ist in der einen Welle kleiner und in der anderen größer. Indem wir also die Losgrößen schrittweise verringern, können wir warten, bis eine Halbwelle mit einem kritischen Drawdown in der aktuellen Gruppe erscheint. Da die Losgrößen dieses kritischen Drawdowns in der Serie minimal sein werden, wird dies die gesamte durchschnittliche Metrik aller Wellengruppen erhöhen und als Ergebnis sollten die gleichen Leistungsvariablen des ursprünglichen Tests ebenfalls steigen.
Für die Implementierung benötigen wir zwei zusätzliche Eingabeparameter für das Martingal:
- { DealsMinusToBreak } - die Anzahl der Verlustpositionen des vorherigen Zyklus, bei deren Erreichen die Losgröße des Zyklus auf den Startwert zurückgesetzt werden soll
- { LotDecrease } - Schritt zum Verringern der Losgröße des Zyklus, wenn ein neuer Zyklus in der Historie der Abschlüsse erscheint
Mit diesen beiden Parametern können wir erhöhte Losgrößen für sichere Halbwellengruppen und reduzierte Losgrößen für gefährliche Halbwellengruppen bereitstellen, was theoretisch die oben genannten Leistungskennzahlen erhöhen sollte.
Der folgende Code wird dem Martingale EA hinzugefügt. Er berechnet die anfängliche Losgröße des nächsten Zyklus und setzt sie gegebenenfalls zurück:
Code:
double DecreasedLot=Lot;//lot to decrease double CalcSmartLot()//calculate previous cycle { bool ord; int PrevCycleDeals=0; HistorySelect(TimeCurrent()-HistoryDaysLoadI*86400,TimeCurrent()); for ( int i=HistoryDealsTotal()-1; i>=0; i-- ) { ulong ticket=HistoryDealGetTicket(i); ord=HistoryDealSelect(ticket); if ( ord && HistoryDealGetString(ticket,DEAL_SYMBOL) == _Symbol && HistoryDealGetInteger(ticket,DEAL_MAGIC) == MagicC && HistoryDealGetInteger(ticket,DEAL_ENTRY) == DEAL_ENTRY_OUT ) { if ( HistoryDealGetDouble(ticket,DEAL_PROFIT) > 0 ) { for ( int j=i+1; j>=0; j-- )//found a profitable deal followed by losing (count them) { ticket=HistoryDealGetTicket(j); ord=HistoryDealSelect(ticket); if ( ord && HistoryDealGetString(ticket,DEAL_SYMBOL) == _Symbol && HistoryDealGetInteger(ticket,DEAL_MAGIC) == MagicC && HistoryDealGetInteger(ticket,DEAL_ENTRY) == DEAL_ENTRY_OUT ) { if ( HistoryDealGetDouble(ticket,DEAL_PROFIT) < 0 ) { PrevCycleDeals++; } else { break; } } } break; } else { break; } } } if ( PrevCycleDeals < DealsMinusToBreak ) DecreasedLot-=LotDecrease; else DecreasedLot=Lot; if ( DecreasedLot <= 0.0 ) DecreasedLot=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN); return DecreasedLot; }
Eingabeparameter sind gelb unterlegt. Bitte beachten Sie, dass es sich hierbei um eine Testfunktion handelt, die in dieser Form nur zum Testen im Strategietester geeignet ist. Für einen ersten groben und einfachen Test dieser Annahme reicht sie jedoch aus. Der Artikel stellt nur den minimalen Code zur Verfügung, der zum Verständnis der Idee notwendig ist. Ich werde den Rest des EA-Codes nicht zur Verfügung stellen, um den Leser nicht mit unnötigen Überlegungen abzulenken. Das Gleiche gilt für die anderen EAs, die während des Schreibens des Artikels erstellt wurden. Lassen Sie uns nun das übliche Martingal testen, und dann den neuen Modus einschalten und sehen, wie er sich auf die Performance-Variablen auswirkt. Dieser Expert Advisor ist auch für MetaTrader 5 konzipiert, da das Ausgangssignal ein reguläres Martingal ist, das mit unterschiedlichen Spreads die gleiche Leistung erbringt.
Testen des Expert Advisors:
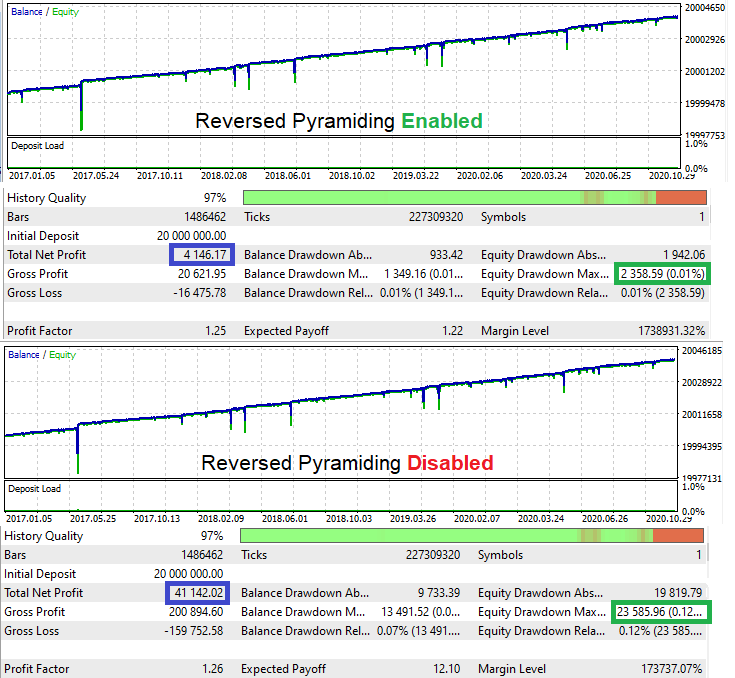
Wenn Sie D für den ursprünglichen Test berechnen, nimmt er den Wert 1,744 an. Mit dem neuen Modus, der aktiviert ist, beträgt dieser Wert 1,758. Die Rentabilität hat sich leicht in die richtige Richtung verschoben. Wenn wir ein paar mehr Tests durchführen, kann dieser Wert natürlich sinken, aber im Durchschnitt sollte die Variable steigen. Streng genommen reicht die Logik zur Demonstration aus.
Schlussfolgerung
In diesem Artikel habe ich versucht, die interessantesten und nützlichsten Techniken zu sammeln, die für Entwickler von automatisierten Handelssystemen hilfreich sein können. Einige dieser Techniken können nach richtigem Studium und Forschung bei der Verbesserung der Gewinne helfen. Ich hoffe, dass dieses Material interessant und hilfreich ist. Diese Techniken können als ein Werkzeugkasten betrachtet werden, aber nicht als Anleitung, wie man einen Gral baut. Selbst eine einfache Bekanntschaft mit solchen Techniken kann Sie vor unüberlegten Investitionen oder kritischen Verlusten bewahren. Wenn Sie mehr Zeit und Mühe investieren, können Sie versuchen, etwas Interessanteres und Stabileres zu schaffen, als ein konventionelles Handelssystem, das auf der Schnittmenge zweier Indikatoren basiert.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/8793
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Der selbstanpassenden Algorithmus (Teil IV): Zusätzliche Funktionen und Tests
Der selbstanpassenden Algorithmus (Teil IV): Zusätzliche Funktionen und Tests
 Neuronale Netze leicht gemacht (Teil 11): Ein Blick auf GPT
Neuronale Netze leicht gemacht (Teil 11): Ein Blick auf GPT
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
halten Sie es auf und halten Sie die Dinge zu teilen
Danke für den Beitrag Kumpel.. wirklich sehr informativ und ausführlich. Sicherlich lernen eine gute Sache heute.
halten Sie es auf und halten Sie die Dinge teilen
Спасибо, земляк ).
Guten Tag Eugeny,
La variable global "TimeStart161" ¿a qué corresponde?
Saludos,
Juan Luis.
Buenos días Eugeny,
La variable global "TimeStart161" ¿a qué correspondonde?
Saludos,
Juan Luis.