Neural networks made easy (Part 11): A take on GPT
11 233
5
Table of Contents
- Introduction
- 1. Understanding GPT Models
- 2. Differences between GPT and the Previously Considered Transformer
- 3. Implementation
- 3.1. Creating a New Class for Our Model
- 3.2. Feed-forward
- 3.3. Feed-backward
- 3.4. Changes in the Neural Network Base Classes
- 4. Testing
- Conclusion
- References
- Programs Used in the Article
Introduction
In June 2018, OpenAI presented the GPT neural network model, which immediately showed the best results in a number of language tests. GDP-2 appeared in 2019, and GPT-3 was presented in May 2020. These models demonstrated the ability of the neural network to generate related text. Additional experiments concerned the ability to generate music and images. The main disadvantage of such models is connected with the computing resources they involve. It took a month to train the first GPT on a machine with 8 GPUs. This disadvantage can be partially compensated by the possibility of using pre-trained models to solve new problems. But considerable resources are required to maintain the model functioning considering its size.
1. Understanding GPT Models
Conceptually, GPT models are built on the basis of the previously considered Transformer. The main idea is to conduct unsupervised pre-training of a model on a large amount of data and then to fine-tune it on a relatively small amount of labeled data.
The reason for the two-step training is the model size. Modern deep machine learning models like GPT involve a large number of parameters, up to hundreds of millions. Therefore, training of such neural networks requires a huge training sample. When using supervised learning, creation of a labeled training set would be labor intensive. At the same time, there are many different digitized and unlabeled texts on the web, which are great for the unsupervised model training. However, statistics show that unsupervised learning results are inferior to supervised learning. Therefore, after the unsupervised training, the model is fine-tuned on a relatively small sample of labeled data.
Unsupervised learning enables the GPT to learn the language model, while further training on labeled data tunes the model for specific tasks. Thus, one pre-trained model can be replicated and fine-tuned to perform different language tasks. The limitation is based on the language of the original set for unsupervised learning.
Practice has shown that this approach generates good results in a wide range of language problems. For example, the GPT-3 model is capable of generating coherent texts on a given topic. However, please note that the specified model contains 175 billion parameters,sequence and it was pre-trained on a 570 GB dataset.
Although GPT models were developed for natural language processing, they also performed well in music and image generation tasks.
In theory, GPT models can be used with any sequence of digitized data. The only prerequisite is the sufficiency of data and resources for unsupervised pre-learning.
2. Differences between GPT and the Previously Considered Transformer
Let us consider what differs GPT models from the previously considered Transformer. First of all, GPT models do not use the encoder, as they only use a decoder. While there is no encoder, the models no longer have the Encoder-Decoder Self-Attention inner layer. The figure below shows a GPT transformer block.
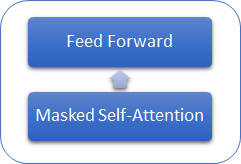
Similar to the classic Transformer, blocks in GPT models are built on top of each other. And each block has its own weight matrices for the attention mechanism, and fully connected Feed Forward layers. The number of blocks determines the model size. The block stack can be quite large. GPT-1 and the smallest GPT-2 (GPT-2 Small) have 12 blocks; GPT-2 Extra Large has 48 of them, while GPT-3 has 96 blocks.
Similar to traditional language models, GPT allows finding relationships only with preceding elements of the sequence, but it cannot look into the future. But unlike the transformer, GPT does not use masking of elements — instead, it makes changes to the computational process. GPT resets attention ratios in the Score matrix for subsequent elements.
At the same time, GPT can be classified as an autoregressive model. One sequence token is generated at each iteration. The resulting token is added to the input sequence and fed into the model for the next iteration.
As in the classic transformer, three vectors are generated for each token inside the self-attention mechanism: a query, a key, and a value. In the autoregressive model, in which at each new iteration the input sequence changes by only 1 token, there is no need to recalculate vectors for each token. Therefore, each layer in GPT calculates vectors only for new elements of the sequence and calculates them for each element of the sequence. Each transformer block saves its vectors for later use.
This approach enables the model to generate texts word by word, before receiving the final token.
Of course, GPT models use the Multi-Head Attention mechanism.
3. Implementation
Before getting started, let us briefly repeat the algorithm:
- An input sequence of tokens is fed into the transformer block.
- Three vectors are calculated for each token (query, key, value) by multiplying the token vector by the corresponding matrix of weights W, which is being trained.
- By multiplying 'query' and 'key', we determine dependencies between the sequence elements. At this step, vector 'query' of each element of the sequence is multiplied by 'key' vectors of the current and all previous elements of the sequence.
- The matrix of the obtained attention scores is normalized using the SoftMax function in the context of each query. A zero attention score is set for the subsequent elements of the sequence.
- By multiplying the normalized attention scores by the 'value' vectors of the corresponding elements of the sequence and then adding the resulting vectors, we obtain the attention-corrected value for each element of the sequence (Z).
- Next, we determine the weighted Z vector based on the results of all attention heads. For this, the corrected 'value' vectors from all attention heads are concatenated into a single vector, and then multiplied by the W0 matrix being trained.
- The resulting tensor is added to the input sequence and normalized.
- The Multi-Heads Self-Attention mechanism is followed by two fully connected layers of the Feed Forward block. The first (hidden) layer contains 4 times as many neurons as the input sequence with the ReLU activation function. The dimension of the second layer is equal to the dimension of the input sequence, and neurons do not use the activation function.
- The result of fully connected layers is summed up with the tensor which is fed into the Feed Forward block. The resulting tensor is then normalized.
One sequence for all Self-Attention Heads. Further, actions in 2-5 are identical for each head of attention.
As a result of steps 3 and 4, we obtain a square matrix Score, sized according to the number of elements in the sequence, in which the sum of all elements in the context of each 'query' is "1".
3.1. Creating a New Class for Our Model.
To implement our model, let us create a new class CNeuronMLMHAttentionOCL, based on the CNeuronBaseOCL base class. I deliberately took a step back and did not use the attention classes created earlier. This is because now we deal with new Multi-Head Self-Attention creation principles. Earlier, in article 10, we created the CNeuronMHAttentionOCL class, which provided a sequential recalculation of 4 attention threads. The number of threads was hard coded in methods, and thus changing the number of threads would require significant effort, related to changes in the class code and its methods.
A caveat. As mentioned above, the GPT model uses a stack of identical transformer blocks with the same (unchangeable) hyperparameters, with the only difference being in the matrices being trained. Therefore, I decided to create a multi-layer block that would allow creating models with hyperparameters which can be passed when creating a class. This includes the number of repetitions of transformer blocks in the stack.
As a result, we have a class which can create almost the entire model based on a few specified parameters. So, in the 'protected' block of the new class we declare five variables to store block parameters:
| iLayers | Number of transformer blocks in the model |
| iHeads | Number of Self-Attention heads |
| iWindow | Input window size (1 input sequence token) |
| iWindowKey | Dimensions of internal vectors Query, Key, Value |
| iUnits | Number of elements (tokens) in the input sequence |
Also, in 'protected' block, declare 6 arrays to store a collection of buffers for our tensors and training weight matrices:
| QKV_Tensors | Array for storing tensors Query, Key, Value and their gradients |
| QKV_Weights | Array for storing a collection of Wq, Wk, Wv weight matrices and their moment matrices |
| S_Tensors | Array for storing a collection of Score matrices and their gradients |
| AO_Tensors | Array for storing output tensors of the Self-Attention mechanism and their gradients |
| FF_Tensors | Array for storing input, hidden and output tensors of the Feed Forward block and their gradients |
| FF_Weights | Array for storing the weight matrices of the Feed Forward block and their moments. |
We will consider the class methods later, when implementing them.
class CNeuronMLMHAttentionOCL : public CNeuronBaseOCL { protected: uint iLayers; ///< Number of inner layers uint iHeads; ///< Number of heads uint iWindow; ///< Input window size uint iUnits; ///< Number of units uint iWindowKey; ///< Size of Key/Query window //--- CCollection *QKV_Tensors; ///< The collection of tensors of Queries, Keys and Values CCollection *QKV_Weights; ///< The collection of Matrix of weights to previous layer CCollection *S_Tensors; ///< The collection of Scores tensors CCollection *AO_Tensors; ///< The collection of Attention Out tensors CCollection *FF_Tensors; ///< The collection of tensors of Feed Forward output CCollection *FF_Weights; ///< The collection of Matrix of Feed Forward weights ///\ingroup neuron_base_ff virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); ///< \brief Feed Forward method of calling kernel ::FeedForward().@param NeuronOCL Pointer to previos layer. virtual bool ConvolutionForward(CBufferDouble *weights, CBufferDouble *inputs,CBufferDouble *outputs, uint window, uint window_out, ENUM_ACTIVATION activ); ///< \brief Convolution Feed Forward method of calling kernel ::FeedForwardConv(). virtual bool AttentionScore(CBufferDouble *qkv, CBufferDouble *scores, bool mask=true); ///< \brief Multi-heads attention scores method of calling kernel ::MHAttentionScore(). virtual bool AttentionOut(CBufferDouble *qkv, CBufferDouble *scores, CBufferDouble *out); ///< \brief Multi-heads attention out method of calling kernel ::MHAttentionOut(). virtual bool SumAndNormilize(CBufferDouble *tensor1, CBufferDouble *tensor2, CBufferDouble *out); ///< \brief Method sum and normalize 2 tensors by calling 2 kernels ::SumMatrix() and ::Normalize(). ///\ingroup neuron_base_opt virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); ///< Method for updating weights.\details Calling one of kernels ::UpdateWeightsMomentum() or ::UpdateWeightsAdam() in depends on optimization type (#ENUM_OPTIMIZATION).@param NeuronOCL Pointer to previos layer. virtual bool ConvolutuionUpdateWeights(CBufferDouble *weights, CBufferDouble *gradient, CBufferDouble *inputs, CBufferDouble *momentum1, CBufferDouble *momentum2, uint window, uint window_out); ///< Method for updating weights in convolution layer.\details Calling one of kernels ::UpdateWeightsConvMomentum() or ::UpdateWeightsConvAdam() in depends on optimization type (#ENUM_OPTIMIZATION). virtual bool ConvolutionInputGradients(CBufferDouble *weights, CBufferDouble *gradient, CBufferDouble *inputs, CBufferDouble *inp_gradient, uint window, uint window_out, uint activ); ///< Method of passing gradients through a convolutional layer. virtual bool AttentionInsideGradients(CBufferDouble *qkv,CBufferDouble *qkv_g,CBufferDouble *scores,CBufferDouble *scores_g,CBufferDouble *gradient); ///< Method of passing gradients through attention layer. public: /** Constructor */CNeuronMLMHAttentionOCL(void); /** Destructor */~CNeuronMLMHAttentionOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint layers, ENUM_OPTIMIZATION optimization_type); ///< Method of initialization class.@param[in] numOutputs Number of connections to next layer.@param[in] myIndex Index of neuron in layer.@param[in] open_cl Pointer to #COpenCLMy object.@param[in] window Size of in/out window and step.@param[in] units_countNumber of neurons.@param[in] optimization_type Optimization type (#ENUM_OPTIMIZATION)@return Boolen result of operations. virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); ///< Method to transfer gradients to previous layer @param[in] prevLayer Pointer to previous layer. //--- virtual int Type(void) const { return defNeuronMLMHAttentionOCL; }///< Identificator of class.@return Type of class //--- methods for working with files virtual bool Save(int const file_handle); ///< Save method @param[in] file_handle handle of file @return logical result of operation virtual bool Load(int const file_handle); ///< Load method @param[in] file_handle handle of file @return logical result of operation };
In the class constructor, we set the initial values of the class hyperparameters and initialize the collection arrays.
CNeuronMLMHAttentionOCL::CNeuronMLMHAttentionOCL(void) : iLayers(0), iHeads(0), iWindow(0), iWindowKey(0), iUnits(0) { QKV_Tensors=new CCollection(); QKV_Weights=new CCollection(); S_Tensors=new CCollection(); AO_Tensors=new CCollection(); FF_Tensors=new CCollection(); FF_Weights=new CCollection(); }
Accordingly, we delete the collection arrays in the class destructor.
CNeuronMLMHAttentionOCL::~CNeuronMLMHAttentionOCL(void) { if(CheckPointer(QKV_Tensors)!=POINTER_INVALID) delete QKV_Tensors; if(CheckPointer(QKV_Weights)!=POINTER_INVALID) delete QKV_Weights; if(CheckPointer(S_Tensors)!=POINTER_INVALID) delete S_Tensors; if(CheckPointer(AO_Tensors)!=POINTER_INVALID) delete AO_Tensors; if(CheckPointer(FF_Tensors)!=POINTER_INVALID) delete FF_Tensors; if(CheckPointer(FF_Weights)!=POINTER_INVALID) delete FF_Weights; }
The initialization of the class along with the construction of the model is performed in the Init method. The method receives in parameters:
| numOutputs | Number of elements in the subsequent layer to create links |
| myIndex | Neuron index in the layer |
| open_cl | OpenCL object pointer |
| window | Input window size (input sequence token) |
| window_key | Dimensions of internal vectors Query, Key, Value |
| heads | Number of Self-Attention heads (threads) |
| units_count | Number of elements in the input sequence |
| layers | Number of blocks (layers) in the model stack |
| optimization_type | Parameter optimization method during training |
bool CNeuronMLMHAttentionOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window,uint window_key,uint heads,uint units_count,uint layers,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronBaseOCL::Init(numOutputs,myIndex,open_cl,window*units_count,optimization_type)) return false; //--- iWindow=fmax(window,1); iWindowKey=fmax(window_key,1); iUnits=fmax(units_count,1); iHeads=fmax(heads,1); iLayers=fmax(layers,1);
At the beginning of the method, we initialize the parent class by calling the appropriate method. Note that we do not perform basic checks to validate the received OpenCL object pointer and the input sequence size, as these checks are already implemented in the parent class method.
After successful initialization of the parent class, we save the hyperparameters to the corresponding variables.
Next, we calculate the sizes of the tensors being created. Please pay attention to the previously modified approach to organizing Multi-Head Attention. We will not create separate arrays for the 'query', 'key' and 'value' vectors - they will be combined in one array. Furthermore, we will not create separate arrays for each attention head. Instead, we will create common arrays for QKV (query + key + value), Scores and outputs of the self-attention mechanism. The elements will be divided into sequences at the level of indices in the tensor. Of course, this approach is more difficult to understand. It might also be more difficult to find the required element in the tensor. But it allows making the model flexible, according to the number of attention heads, and organizing the simultaneous recalculation of all attention heads by parallelizing threads at the kernel level.
The size of the QKV_Tensor (num) tensor is defined as the product of three sizes of the internal vector (query + key + value) and the number of heads. The size of the concatenated matrix of weights QKV_Weight is defined as the product of three sizes of the input sequence token, increased by the offset element, by the size of the internal vector and the number of attention heads. Similarly, let us calculate the sizes of the remaining tensors.
uint num=3*iWindowKey*iHeads*iUnits; //Size of QKV tensor uint qkv_weights=3*(iWindow+1)*iWindowKey*iHeads; //Size of weights' matrix of QKV tensor uint scores=iUnits*iUnits*iHeads; //Size of Score tensor uint mh_out=iWindowKey*iHeads*iUnits; //Size of multi-heads self-attention uint out=iWindow*iUnits; //Size of our tensor uint w0=(iWindowKey+1)*iHeads*iWindow; //Size W0 tensor uint ff_1=4*(iWindow+1)*iWindow; //Size of weights' matrix 1-st feed forward layer uint ff_2=(4*iWindow+1)*iWindow; //Size of weights' matrix 2-nd feed forward layer
After determining the sizes of all tensors, run a cycle by the number of attention layers in the block to create the necessary tensors. Note that there are two nested loops organized inside the loop body. The first loop creates arrays for value tensors and their gradients. The second one creates arrays for weight matrices and their moments. Note that for the last layer, no new arrays are created for the Feed Forward block output tensor and its gradient. Instead, pointers to the parent class output and gradient arrays are added to the collection. Such a simple step avoids an unnecessary iteration transferring values between arrays, as well as it eliminates unnecessary memory consumption.
for(uint i=0; i<iLayers; i++) { CBufferDouble *temp=NULL; for(int d=0; d<2; d++) { //--- Initialize QKV tensor temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(num,0)) return false; if(!QKV_Tensors.Add(temp)) return false; //--- Initialize scores temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(scores,0)) return false; if(!S_Tensors.Add(temp)) return false; //--- Initialize multi-heads attention out temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(mh_out,0)) return false; if(!AO_Tensors.Add(temp)) return false; //--- Initialize attention out temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(out,0)) return false; if(!FF_Tensors.Add(temp)) return false; //--- Initialize Feed Forward 1 temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(4*out,0)) return false; if(!FF_Tensors.Add(temp)) return false; //--- Initialize Feed Forward 2 if(i==iLayers-1) { if(!FF_Tensors.Add(d==0 ? Output : Gradient)) return false; continue; } temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(out,0)) return false; if(!FF_Tensors.Add(temp)) return false; } //--- Initialize QKV weights temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Reserve(qkv_weights)) return false; for(uint w=0; w<qkv_weights; w++) { if(!temp.Add(GenerateWeight())) return false; } if(!QKV_Weights.Add(temp)) return false; //--- Initialize Weights0 temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Reserve(w0)) return false; for(uint w=0; w<w0; w++) { if(!temp.Add(GenerateWeight())) return false; } if(!FF_Weights.Add(temp)) return false; //--- Initialize FF Weights temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Reserve(ff_1)) return false; for(uint w=0; w<ff_1; w++) { if(!temp.Add(GenerateWeight())) return false; } if(!FF_Weights.Add(temp)) return false; //--- temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Reserve(ff_2)) return false; for(uint w=0; w<ff_1; w++) { if(!temp.Add(GenerateWeight())) return false; } if(!FF_Weights.Add(temp)) return false; //--- for(int d=0; d<(optimization==SGD ? 1 : 2); d++) { temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(qkv_weights,0)) return false; if(!QKV_Weights.Add(temp)) return false; temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(w0,0)) return false; if(!FF_Weights.Add(temp)) return false; //--- Initialize FF Weights temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(ff_1,0)) return false; if(!FF_Weights.Add(temp)) return false; temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(ff_2,0)) return false; if(!FF_Weights.Add(temp)) return false; } } //--- return true; }
As a result, for each layer we obtain the following matrix of tensors.
| QKV_Tensor |
|
| S_Tensors |
|
| AO_Tensors |
|
| FF_Tensors |
|
| QKV_Weights |
|
| FF_Weights |
|
After creating the array collections, exit the method with 'true'. The full code of all classes and their methods is available in the attachment.
3.2. Feed-forward.
The Feed-forward pass is traditionally organized in the feedForward method, which receives in parameters a pointer to the previous layer of the neural network. At the beginning of the method, check the validity of the received pointer.
bool CNeuronMLMHAttentionOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL)==POINTER_INVALID) return false;
Next, let us organize a loop to recalculate all the layers of our block. Unlike the previously described analogous methods of other classes, this method is a top-level one. Operations organized are reduced to preparing the data and calling auxiliary methods (the logic of these methods will be described below).
At the beginning of the loop, we receive from the collection the QKV and QKV_Weights tensors' input data buffer corresponding to the current layer. Then we call ConvolutionForward to calculate vectors Query, Key and Value.
for(uint i=0; (i<iLayers && !IsStopped()); i++) { //--- Calculate Queries, Keys, Values CBufferDouble *inputs=(i==0? NeuronOCL.getOutput() : FF_Tensors.At(6*i-4)); CBufferDouble *qkv=QKV_Tensors.At(i*2); if(IsStopped() || !ConvolutionForward(QKV_Weights.At(i*(optimization==SGD ? 2 : 3)),inputs,qkv,iWindow,3*iWindowKey*iHeads,None)) return false;
I encountered an issue when increasing attention layers. At some point, I got error 5113 ERR_OPENCL_TOO_MANY_OBJECTS. So, I had to think about storing all tensors permanently, in GPU memory. Therefore, after completing operations, I free the buffers which will no longer be used at this step. In your code, do not forget to read the latest data of freed buffers from the GPU memory. In the class presented in this article, buffer data is read in kernel initialization methods, which we will discuss a little later.
CBufferDouble *temp=QKV_Weights.At(i*(optimization==SGD ? 2 : 3)); temp.BufferFree();
Attention scores and weighted vectors of the Self-Attention mechanism values are calculated similarly, by calling appropriate methods.
//--- Score calculation temp=S_Tensors.At(i*2); if(IsStopped() || !AttentionScore(qkv,temp,true)) return false; //--- Multi-heads attention calculation CBufferDouble *out=AO_Tensors.At(i*2); if(IsStopped() || !AttentionOut(qkv,temp,out)) return false; qkv.BufferFree(); temp.BufferFree();
After calculating Multi-Heads Self-Attention, collapse the concatenated attention output to the input sequence size, add two vectors and normalize the result.
//--- Attention out calculation temp=FF_Tensors.At(i*6); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i*(optimization==SGD ? 6 : 9)),out,temp,iWindowKey*iHeads,iWindow,None)) return false; out.BufferFree(); //--- Sum and normalize attention if(IsStopped() || !SumAndNormilize(temp,inputs,temp)) return false; if(i>0) inputs.BufferFree();
The self-attention mechanism in the transformer is followed by the Feed Forward block consisting of two fully connected layers. Then, the result is added to the input sequence. The final tensor is normalized and fed into the next layer. In our case, we close the cycle.
//--- Feed Forward inputs=temp; temp=FF_Weights.At(i*(optimization==SGD ? 6 : 9)); temp.BufferFree(); temp=FF_Tensors.At(i*6+1); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i*(optimization==SGD ? 6 : 9)+1),inputs,temp,iWindow,4*iWindow,LReLU)) return false; out=FF_Weights.At(i*(optimization==SGD ? 6 : 9)+1); out.BufferFree(); out=FF_Tensors.At(i*6+2); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i*(optimization==SGD ? 6 : 9)+2),temp,out,4*iWindow,iWindow,activation)) return false; temp.BufferFree(); temp=FF_Weights.At(i*(optimization==SGD ? 6 : 9)+2); temp.BufferFree(); //--- Sum and normalize out if(IsStopped() || !SumAndNormilize(out,inputs,out)) return false; inputs.BufferFree(); } //--- return true; }
The full method code is provided in the attachment below. Now, let us consider helper methods called from the FeedForward method. The first method we call is ConvolutionForward. It is called four times per one cycle of the feed forward method. In the method body, the forward pass kernel of the convolutional layer is called. This method in this case plays the role of a fully connected layer for each separate token of the input sequence. The solution was discussed in more detail in article 8. In contrast to the solution described earlier, the new method receives pointers to buffers in parameters, to transfer data to the OpenCL kernel. Therefore, at the beginning of the method, we check the validity of the received pointers.
bool CNeuronMLMHAttentionOCL::ConvolutionForward(CBufferDouble *weights, CBufferDouble *inputs,CBufferDouble *outputs, uint window, uint window_out, ENUM_ACTIVATION activ) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(weights)==POINTER_INVALID || CheckPointer(inputs)==POINTER_INVALID || CheckPointer(outputs)==POINTER_INVALID) return false;
Next, we create buffers in the GPU memory and pass the necessary information to them.
if(!weights.BufferCreate(OpenCL)) return false; if(!inputs.BufferCreate(OpenCL)) return false; if(!outputs.BufferCreate(OpenCL)) return false;
This is followed by the code described in article 8, without changes. The called kernel is used as is, with no changes.
uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=outputs.Total()/window_out; OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_w,weights.GetIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_i,inputs.GetIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_o,outputs.GetIndex()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_inputs,inputs.Total()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_step,window); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_window_in,window); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffс_window_out,window_out); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_activation,(int)activ); if(!OpenCL.Execute(def_k_FeedForwardConv,1,global_work_offset,global_work_size)) { printf("Error of execution kernel FeedForwardConv: %d",GetLastError()); return false; } //--- return outputs.BufferRead(); }
Further in the feedForward method code comes the call of the AttentionScore method, which calls a kernel to calculate and normalize attention scores - these resulting values are then written to the Score matrix. A new kernel has been written for this method; it will be considered later, after we consider the method itself.
Like the previous method, AttentionScore receives pointers to the initial data buffers and records of the obtained values in the parameters. So, at the beginning of the method, we check the validity of the received pointers.
bool CNeuronMLMHAttentionOCL::AttentionScore(CBufferDouble *qkv, CBufferDouble *scores, bool mask=true) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(qkv)==POINTER_INVALID || CheckPointer(scores)==POINTER_INVALID) return false;
Following the logic described above, let us create buffers for data exchange with the GPU.
if(!qkv.BufferCreate(OpenCL)) return false; if(!scores.BufferCreate(OpenCL)) return false;
After the preparatory work, let us move on to specifying the kernel parameters. The threads of this kernel will be created in two dimensions: in the context of the input sequence elements and in the context of attention heads. This provides parallel computation for all elements of the sequence and all attention heads.
uint global_work_offset[2]= {0,0}; uint global_work_size[2]; global_work_size[0]=iUnits; global_work_size[1]=iHeads; OpenCL.SetArgumentBuffer(def_k_MHAttentionScore,def_k_mhas_qkv,qkv.GetIndex()); OpenCL.SetArgumentBuffer(def_k_MHAttentionScore,def_k_mhas_score,scores.GetIndex()); OpenCL.SetArgument(def_k_MHAttentionScore,def_k_mhas_dimension,iWindowKey); OpenCL.SetArgument(def_k_MHAttentionScore,def_k_mhas_mask,(int)mask);
Next, we move on directly to kernel call. Calculation results are read in the 'score' buffer.
if(!OpenCL.Execute(def_k_MHAttentionScore,2,global_work_offset,global_work_size)) { printf("Error of execution kernel MHAttentionScore: %d",GetLastError()); return false; } //--- return scores.BufferRead(); }
Let us view the logic of the called MHAttentionScore kernel. As shown above, the kernel receives in the parameters a pointer to the qkv source data array and an array for recording resulting scores. Also, the kernel receives in parameters the size of internal vectors (Query, Key) and a flag for enabling the masking algorithm for subsequent elements.
First, we get the ordinal numbers of the query q being processed and the attention head h. Also, we get the dimension of the number of queries and attention heads.
__kernel void MHAttentionScore(__global double *qkv, ///<[in] Matrix of Querys, Keys, Values __global double *score, ///<[out] Matrix of Scores int dimension, ///< Dimension of Key int mask ///< 1 - calc only previous units, 0 - calc all ) { int q=get_global_id(0); int h=get_global_id(1); int units=get_global_size(0); int heads=get_global_size(1);
Based on the data obtained, determine the shift in the arrays for 'query' and 'score'.
int shift_q=dimension*(h+3*q*heads); int shift_s=units*(h+q*heads);
Also, calculate a Score correction coefficient.
double koef=sqrt((double)dimension); if(koef<1) koef=1;
The attention scores are calculated in a loop, in which we will iterate through the keys of the entire sequence of elements in the corresponding attention head.
At the beginning of the loop, check the condition for using the attention mechanism. If this functionality is enabled, check the serial number of the key. If the current key corresponds to the next element of the sequence, write the zero score to the 'score' array and go to the next element.
double sum=0; for(int k=0;k<units;k++) { if(mask>0 && k>q) { score[shift_s+k]=0; continue; }
If the attention score is calculated for the analyzed key, then we organize a nested loop to calculate the product of the two vectors. Note that the cycle body has two calculation branches: one using vector calculations and the other one without such calculations. The first branch is used when there are 4 or more elements from the current position in the key vector to its last element; the second branch is used for the last non-multiple 4 elements of the key vector.
double result=0; int shift_k=dimension*(h+heads*(3*k+1)); for(int i=0;i<dimension;i++) { if((dimension-i)>4) { result+=dot((double4)(qkv[shift_q+i],qkv[shift_q+i+1],qkv[shift_q+i+2],qkv[shift_q+i+3]), (double4)(qkv[shift_k+i],qkv[shift_k+i+1],qkv[shift_k+i+2],qkv[shift_k+i+3])); i+=3; } else result+=(qkv[shift_q+i]*qkv[shift_k+i]); }
According to the transformer algorithm, attention scores are normalized using the SoftMax function. To implement this feature, we will divide the result of the product of vectors by the correction coefficient, and determine the exponent for the resulting value. The calculation result should be written into the corresponding element of the 'score' tensor and added to the sum of exponents.
result=exp(clamp(result/koef,-30.0,30.0)); if(isnan(result)) result=0; score[shift_s+k]=result; sum+=result; }
Similarly, we will calculate the exponents for all elements. To complete the SoftMax normalization of the attention scores, we organize another cycle, in which all the elements of the 'Score' tensor are divided by the previously calculated sum of exponents.
for(int k=0;(k<units && sum>1);k++) score[shift_s+k]/=sum; }
Exit the kernel at the cycle end.
Let us move on with the feedForward method and consider the AttentionOut helper method. The method receives in parameters pointers to three tensors: QKV, Scores and Out. The method structure is similar to those considered earlier. It launches the MHAttentionOut kernels in two dimensions: sequence elements and attention heads.
bool CNeuronMLMHAttentionOCL::AttentionOut(CBufferDouble *qkv, CBufferDouble *scores, CBufferDouble *out) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(qkv)==POINTER_INVALID || CheckPointer(scores)==POINTER_INVALID || CheckPointer(out)==POINTER_INVALID) return false; uint global_work_offset[2]= {0,0}; uint global_work_size[2]; global_work_size[0]=iUnits; global_work_size[1]=iHeads; if(!qkv.BufferCreate(OpenCL)) return false; if(!scores.BufferCreate(OpenCL)) return false; if(!out.BufferCreate(OpenCL)) return false; //--- OpenCL.SetArgumentBuffer(def_k_MHAttentionOut,def_k_mhao_qkv,qkv.GetIndex()); OpenCL.SetArgumentBuffer(def_k_MHAttentionOut,def_k_mhao_score,scores.GetIndex()); OpenCL.SetArgumentBuffer(def_k_MHAttentionOut,def_k_mhao_out,out.GetIndex()); OpenCL.SetArgument(def_k_MHAttentionOut,def_k_mhao_dimension,iWindowKey); if(!OpenCL.Execute(def_k_MHAttentionOut,2,global_work_offset,global_work_size)) { printf("Error of execution kernel MHAttentionOut: %d",GetLastError()); return false; } //--- return out.BufferRead(); }
Like the previous kernel, MHAttentionOut has been written anew, taking into account the Multi-Head Attention. It uses a single buffer for the tensors of queries, keys and values. The kernel receives in parameters pointers to tensors Scores, QKV, Out, and the size of the value vector. The first and second buffers provide the original data, and the last one is used for recording the result.
Also, at the kernel beginning, determine the ordinal numbers of the query q being processed, and the attention head h, as well as the dimension of the number of queries and attention heads.
__kernel void MHAttentionOut(__global double *scores, ///<[in] Matrix of Scores __global double *qkv, ///<[in] Matrix of Values __global double *out, ///<[out] Output tensor int dimension ///< Dimension of Value ) { int u=get_global_id(0); int units=get_global_size(0); int h=get_global_id(1); int heads=get_global_size(1);
Next, determine the position of the required attention score and of the first element of the output value vector being analyzed. Additionally, calculate the length of the vector of one element in the QKV tensor - this value will be used to determine the shift in the QKV tensor.
int shift_s=units*(h+heads*u); int shift_out=dimension*(h+heads*u); int layer=3*dimension*heads;
We will implement nested loops for the main calculations. The outer loop will run for the size of the vector of values; the inner loop will be performed by the number of elements in the original sequence. At the beginning of the outer loop, let us declare a variable for calculating the resulting value and initialize it with a zero value. The inner loop begins defining a shift for the values vector. Note that the step of the inner loop is equal to 4, because later we are going to use vector calculations.
for(int d=0;d<dimension;d++) { double result=0; for(int v=0;v<units;v+=4) { int shift_v=dimension*(h+heads*(3*v+2))+d;
Like in the MHAttentionScore kernel, let us divide calculations into two threads: one using vector calculations and
the other one without them. The second thread will be used only for the last elements, in cases where the sequence length is not a multiple of 4.
if((units-v)>4) { result+=dot((double4)(scores[shift_s+v],scores[shift_s+v+1],scores[shift_s+v+1],scores[shift_s+v+3]), (double4)(qkv[shift_v],qkv[shift_v+layer],qkv[shift_v+2*layer],qkv[shift_v+3*layer])); } else for(int l=0;l<(int)fmin((double)(units-v),4.0);l++) result+=scores[shift_s+v+l]*qkv[shift_v+l*layer]; } out[shift_out+d]=result; } }
After exiting the nested loop, write the resulting value into the corresponding element of the output tensor.
Further, in the feedForward method, the ConvolutionForward method described above is used. The full code of all methods and functions is available in the attachment.
3.3. Feed-backward.
As in all previously considered classes, the feed-backward process contains two sub-processes: propagating the error gradient and updating the weights. The first part is implemented in the calcInputGradients method. The second part is implemented in updateInputWeights.
The calcInputGradients method construction is similar to that of feedForward. The method receives in parameters a pointer to the previous layer of the neural network, to which the error gradient should be passed. So, at the method beginning, check the validity of the received pointer.
bool CNeuronMLMHAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
Then, we fix the tensor of the gradient received from the next layer of neurons, and organize a loop over all inner layers, to sequentially calculate the error gradient. Since this is the feed-backward process, the loop will iterate over inner layers in a reverse order.
for(int i=(int)iLayers-1; (i>=0 && !IsStopped()); i--) { //--- Passing gradient through feed forward layers if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i*(optimization==SGD ? 6 : 9)+2),out_grad,FF_Tensors.At(i*6+1),FF_Tensors.At(i*6+4),4*iWindow,iWindow,None)) return false; CBufferDouble *temp=FF_Weights.At(i*(optimization==SGD ? 6 : 9)+2); temp.BufferFree(); temp=FF_Tensors.At(i*6+1); temp.BufferFree(); temp=FF_Tensors.At(i*6+3); if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i*(optimization==SGD ? 6 : 9)+1),FF_Tensors.At(i*6+4),FF_Tensors.At(i*6),temp,iWindow,4*iWindow,LReLU)) return false;
At the beginning of the loop, calculate the error gradient propagation through the fully connected layers of neurons of the Transformer's Feed Forward block. This iteration is performed by the ConvolutionInputGradients method. Release the buffers after the method completion.
Since our algorithm implements data flow through the entire process, the same process should be implemented for the error gradient. So, the error gradient obtained from the Feed Forward block is summed up with the error gradient received from the previous layer of neurons. To eliminate the risk of an "exploding gradient", normalize the sum of the two vectors. All these operations are performed in the SumAndNormilize method. Release the buffers after the method completion.
//--- Sum and normalize gradients if(IsStopped() || !SumAndNormilize(out_grad,temp,temp)) return false; if(i!=(int)iLayers-1) out_grad.BufferFree(); out_grad=temp; temp=FF_Weights.At(i*(optimization==SGD ? 6 : 9)+1); temp.BufferFree(); temp=FF_Tensors.At(i*6+4); temp.BufferFree(); temp=FF_Tensors.At(i*6); temp.BufferFree();
Further along the algorithm, let us divide the error gradient by attention heads. This is done by calling the ConvolutionInputGradients method for the W0 matrix.
//--- Split gradient to multi-heads if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i*(optimization==SGD ? 6 : 9)),out_grad,AO_Tensors.At(i*2),AO_Tensors.At(i*2+1),iWindowKey*iHeads,iWindow,None)) return false; temp=FF_Weights.At(i*(optimization==SGD ? 6 : 9)); temp.BufferFree(); temp=AO_Tensors.At(i*2); temp.BufferFree();
Further gradient propagation along attention heads is organized in the AttentionInsideGradients method.
if(IsStopped() || !AttentionInsideGradients(QKV_Tensors.At(i*2),QKV_Tensors.At(i*2+1),S_Tensors.At(i*2),S_Tensors.At(i*2+1),AO_Tensors.At(i*2+1))) return false; temp=QKV_Tensors.At(i*2); temp.BufferFree(); temp=S_Tensors.At(i*2); temp.BufferFree(); temp=S_Tensors.At(i*2+1); temp.BufferFree(); temp=AO_Tensors.At(i*2+1); temp.BufferFree();
At the end of the loop, we calculate the error gradient passed to the previous layer. Here, the error gradient received from the previous iteration is passed through the concatenated tensor QKV_Weights, and then the received vector is summed with the error gradient from the Feed Forward block of the self-attention mechanism and the result is normalized to eliminate exploding gradients.
CBufferDouble *inp=NULL; if(i==0) { inp=prevLayer.getOutput(); temp=prevLayer.getGradient(); } else { temp=FF_Tensors.At(i*6-1); inp=FF_Tensors.At(i*6-4); } if(IsStopped() || !ConvolutionInputGradients(QKV_Weights.At(i*(optimization==SGD ? 2 : 3)),QKV_Tensors.At(i*2+1),inp,temp,iWindow,3*iWindowKey*iHeads,None)) return false; //--- Sum and normalize gradients if(IsStopped() || !SumAndNormilize(out_grad,temp,temp)) return false; out_grad.BufferFree(); if(i>0) out_grad=temp; temp=QKV_Weights.At(i*(optimization==SGD ? 2 : 3)); temp.BufferFree(); temp=QKV_Tensors.At(i*2+1); temp.BufferFree(); } //--- return true; }
Do not forget to free the used data buffers. Pay attention that the data buffers previous layer are left in the GPU memory.
Let us take a look at the called methods. As you can see, the most frequently called method is ConvolutionInputGradients, which is based on a similar method of the convolutional layer and is optimized for the current task. The method receives in parameters pointers to tensors of weights, of next layer gradient, of the preceding layer output data and of the tensor to store the iteration result. Also, the method receives in parameters sizes of the input and output data window and the used activation function.
bool CNeuronMLMHAttentionOCL::ConvolutionInputGradients(CBufferDouble *weights, CBufferDouble *gradient, CBufferDouble *inputs, CBufferDouble *inp_gradient, uint window, uint window_out, uint activ) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(weights)==POINTER_INVALID || CheckPointer(gradient)==POINTER_INVALID || CheckPointer(inputs)==POINTER_INVALID || CheckPointer(inp_gradient)==POINTER_INVALID) return false;
At the method beginning, check the validity of the received pointers and create data buffers in the GPU memory.
if(!weights.BufferCreate(OpenCL)) return false; if(!gradient.BufferCreate(OpenCL)) return false; if(!inputs.BufferCreate(OpenCL)) return false; if(!inp_gradient.BufferCreate(OpenCL)) return false;
After creating data buffers, implement the call of the appropriate OpenCL program kernel. Here we use a convolutional network kernel without changes.
//--- uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=inputs.Total(); OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv,def_k_chgc_matrix_w,weights.GetIndex()); OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv,def_k_chgc_matrix_g,gradient.GetIndex()); OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv,def_k_chgc_matrix_o,inputs.GetIndex()); OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv,def_k_chgc_matrix_ig,inp_gradient.GetIndex()); OpenCL.SetArgument(def_k_CalcHiddenGradientConv,def_k_chgc_outputs,gradient.Total()); OpenCL.SetArgument(def_k_CalcHiddenGradientConv,def_k_chgc_step,window); OpenCL.SetArgument(def_k_CalcHiddenGradientConv,def_k_chgc_window_in,window); OpenCL.SetArgument(def_k_CalcHiddenGradientConv,def_k_chgc_window_out,window_out); OpenCL.SetArgument(def_k_CalcHiddenGradientConv,def_k_chgc_activation,activ); //Comment(com+"\n "+(string)__LINE__+"-"__FUNCTION__); if(!OpenCL.Execute(def_k_CalcHiddenGradientConv,1,global_work_offset,global_work_size)) { printf("Error of execution kernel CalcHiddenGradientConv: %d",GetLastError()); return false; } //--- return inp_gradient.BufferRead(); }
The AttentionInsideGradients method, which is also called from the ConvolutionInputGradients method, is constructed according to a similar algorithm. Please see the attachment for the method code. Now, let us have a look at the OpenCL program kernel called from the specified method, because all calculations are performed in the kernel.
The MHAttentionInsideGradients kernel is launched by threads in two dimensions: elements of the sequence and attention heads. The kernel receives in parameters pointers to the concatenated QKV tensor and the tensor of its gradients, the Scores matrix tensors and its gradients, error gradient tensor from the previous iteration and the size of the keys vector.
__kernel void MHAttentionInsideGradients(__global double *qkv,__global double *qkv_g, __global double *scores,__global double *scores_g, __global double *gradient, int dimension) { int u=get_global_id(0); int h=get_global_id(1); int units=get_global_size(0); int heads=get_global_size(1); double koef=sqrt((double)dimension); if(koef<1) koef=1;
At the method beginning, we obtain the ordinal numbers of the processed sequence element and the attention head, as well as their sizes. Also, we calculate the Scores matrix update coefficient.
Then, we organize a loop to calculate the error gradient for the Scores matrix. By setting a barrier after the loop we can synchronize the computation process across all threads. The algorithm will switch to the next block of operations only after the full recalculation of the gradients of the Scores matrix.
//--- Calculating score's gradients uint shift_s=units*(h+u*heads); for(int v=0;v<units;v++) { double s=scores[shift_s+v]; if(s>0) { double sg=0; int shift_v=dimension*(h+heads*(3*v+2)); int shift_g=dimension*(h+heads*v); for(int d=0;d<dimension;d++) sg+=qkv[shift_v+d]*gradient[shift_g+d]; scores_g[shift_s+v]=sg*(s<1 ? s*(1-s) : 1)/koef; } else scores_g[shift_s+v]=0; } barrier(CLK_GLOBAL_MEM_FENCE);
Let us implement another loop to calculate error gradients on queries, key and value vectors.
//--- Calculating gradients for Query, Key and Value uint shift_qg=dimension*(h+3*u*heads); uint shift_kg=dimension*(h+(3*u+1)*heads); uint shift_vg=dimension*(h+(3*u+2)*heads); for(int d=0;d<dimension;d++) { double vg=0; double qg=0; double kg=0; for(int l=0;l<units;l++) { uint shift_q=dimension*(h+3*l*heads)+d; uint shift_k=dimension*(h+(3*l+1)*heads)+d; uint shift_g=dimension*(h+heads*l)+d; double sg=scores_g[shift_s+l]; kg+=sg*qkv[shift_q]; qg+=sg*qkv[shift_k]; vg+=gradient[shift_g]*scores[shift_s+l]; } qkv_g[shift_qg+d]=qg; qkv_g[shift_kg+d]=kg; qkv_g[shift_vg+d]=vg; } }
The full code of all methods and functions is available in the attachment.
The weights are updated in the updateInputWeights methods which is built by the principles of the previously considered feedForward and calcInputGradients methods. Only one ConvolutuionUpdateWeights helper method updating the convolutional network weights is called sequentially inside this method.
bool CNeuronMLMHAttentionOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL)==POINTER_INVALID) return false; CBufferDouble *inputs=NeuronOCL.getOutput(); for(uint l=0; l<iLayers; l++) { if(IsStopped() || !ConvolutuionUpdateWeights(QKV_Weights.At(l*(optimization==SGD ? 2 : 3)),QKV_Tensors.At(l*2+1),inputs,(optimization==SGD ? QKV_Weights.At(l*2+1) : QKV_Weights.At(l*3+1)),(optimization==SGD ? NULL : QKV_Weights.At(l*3+2)),iWindow,3*iWindowKey*iHeads)) return false; if(l>0) inputs.BufferFree(); CBufferDouble *temp=QKV_Weights.At(l*(optimization==SGD ? 2 : 3)); temp.BufferFree(); temp=QKV_Tensors.At(l*2+1); temp.BufferFree(); if(optimization==SGD) { temp=QKV_Weights.At(l*2+1); } else { temp=QKV_Weights.At(l*3+1); temp.BufferFree(); temp=QKV_Weights.At(l*3+2); temp.BufferFree(); } //--- if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l*(optimization==SGD ? 6 : 9)),FF_Tensors.At(l*6+3),AO_Tensors.At(l*2),(optimization==SGD ? FF_Weights.At(l*6+3) : FF_Weights.At(l*9+3)),(optimization==SGD ? NULL : FF_Weights.At(l*9+6)),iWindowKey*iHeads,iWindow)) return false; temp=FF_Weights.At(l*(optimization==SGD ? 6 : 9)); temp.BufferFree(); temp=FF_Tensors.At(l*6+3); temp.BufferFree(); temp=AO_Tensors.At(l*2); temp.BufferFree(); if(optimization==SGD) { temp=FF_Weights.At(l*6+3); temp.BufferFree(); } else { temp=FF_Weights.At(l*9+3); temp.BufferFree(); temp=FF_Weights.At(l*9+6); temp.BufferFree(); } //--- if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l*(optimization==SGD ? 6 : 9)+1),FF_Tensors.At(l*6+4),FF_Tensors.At(l*6),(optimization==SGD ? FF_Weights.At(l*6+4) : FF_Weights.At(l*9+4)),(optimization==SGD ? NULL : FF_Weights.At(l*9+7)),iWindow,4*iWindow)) return false; temp=FF_Weights.At(l*(optimization==SGD ? 6 : 9)+1); temp.BufferFree(); temp=FF_Tensors.At(l*6+4); temp.BufferFree(); temp=FF_Tensors.At(l*6); temp.BufferFree(); if(optimization==SGD) { temp=FF_Weights.At(l*6+4); temp.BufferFree(); } else { temp=FF_Weights.At(l*9+4); temp.BufferFree(); temp=FF_Weights.At(l*9+7); temp.BufferFree(); } //--- if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l*(optimization==SGD ? 6 : 9)+2),FF_Tensors.At(l*6+5),FF_Tensors.At(l*6+1),(optimization==SGD ? FF_Weights.At(l*6+5) : FF_Weights.At(l*9+5)),(optimization==SGD ? NULL : FF_Weights.At(l*9+8)),4*iWindow,iWindow)) return false; temp=FF_Weights.At(l*(optimization==SGD ? 6 : 9)+2); temp.BufferFree(); temp=FF_Tensors.At(l*6+5); if(temp!=Gradient) temp.BufferFree(); temp=FF_Tensors.At(l*6+1); temp.BufferFree(); if(optimization==SGD) { temp=FF_Weights.At(l*6+5); temp.BufferFree(); } else { temp=FF_Weights.At(l*9+5); temp.BufferFree(); temp=FF_Weights.At(l*9+8); temp.BufferFree(); } inputs=FF_Tensors.At(l*6+2); } //--- return true; }
The full code of all classes and their methods is available in the attachment.
3.4. Changes in the Neural Network Base Classes
As in all previous articles, let us make changes in the base class after creating a new class, to ensure proper operation of our network.
Let us add a new class identifier.
#define defNeuronMLMHAttentionOCL 0x7889 ///<Multilayer multi-headed attention neuron OpenCL \details Identified class #CNeuronMLMHAttentionOCL
Also, in the define block, we add constants for working with the new kernels of the OpenCL program.
#define def_k_MHAttentionScore 20 ///< Index of the kernel of the multi-heads attention neuron to calculate score matrix (#MHAttentionScore) #define def_k_mhas_qkv 0 ///< Matrix of Queries, Keys, Values #define def_k_mhas_score 1 ///< Matrix of Scores #define def_k_mhas_dimension 2 ///< Dimension of Key #define def_k_mhas_mask 3 ///< 1 - calc only previous units, 0 - calc all //--- #define def_k_MHAttentionOut 21 ///< Index of the kernel of the multi-heads attention neuron to calculate multi-heads out matrix (#MHAttentionOut) #define def_k_mhao_score 0 ///< Matrix of Scores #define def_k_mhao_qkv 1 ///< Matrix of Queries, Keys, Values #define def_k_mhao_out 2 ///< Matrix of Outputs #define def_k_mhao_dimension 3 ///< Dimension of Key //--- #define def_k_MHAttentionGradients 22 ///< Index of the kernel for gradients calculation process (#AttentionInsideGradients) #define def_k_mhag_qkv 0 ///< Matrix of Queries, Keys, Values #define def_k_mhag_qkv_g 1 ///< Matrix of Gradients to Queries, Keys, Values #define def_k_mhag_score 2 ///< Matrix of Scores #define def_k_mhag_score_g 3 ///< Matrix of Scores Gradients #define def_k_mhag_gradient 4 ///< Matrix of Gradients from previous iteration #define def_k_mhag_dimension 5 ///< Dimension of Key
Also, let us add the declaration of new kernels in the neural network class constructor.
//--- create kernels opencl.SetKernelsCount(23); opencl.KernelCreate(def_k_FeedForward,"FeedForward"); opencl.KernelCreate(def_k_CalcOutputGradient,"CalcOutputGradient"); opencl.KernelCreate(def_k_CalcHiddenGradient,"CalcHiddenGradient"); opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum"); opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam"); opencl.KernelCreate(def_k_AttentionGradients,"AttentionInsideGradients"); opencl.KernelCreate(def_k_AttentionOut,"AttentionOut"); opencl.KernelCreate(def_k_AttentionScore,"AttentionScore"); opencl.KernelCreate(def_k_CalcHiddenGradientConv,"CalcHiddenGradientConv"); opencl.KernelCreate(def_k_CalcInputGradientProof,"CalcInputGradientProof"); opencl.KernelCreate(def_k_FeedForwardConv,"FeedForwardConv"); opencl.KernelCreate(def_k_FeedForwardProof,"FeedForwardProof"); opencl.KernelCreate(def_k_MatrixSum,"SumMatrix"); opencl.KernelCreate(def_k_Matrix5Sum,"Sum5Matrix"); opencl.KernelCreate(def_k_UpdateWeightsConvAdam,"UpdateWeightsConvAdam"); opencl.KernelCreate(def_k_UpdateWeightsConvMomentum,"UpdateWeightsConvMomentum"); opencl.KernelCreate(def_k_Normilize,"Normalize"); opencl.KernelCreate(def_k_NormilizeWeights,"NormalizeWeights"); opencl.KernelCreate(def_k_ConcatenateMatrix,"ConcatenateBuffers"); opencl.KernelCreate(def_k_DeconcatenateMatrix,"DeconcatenateBuffers"); opencl.KernelCreate(def_k_MHAttentionGradients,"MHAttentionInsideGradients"); opencl.KernelCreate(def_k_MHAttentionScore,"MHAttentionScore"); opencl.KernelCreate(def_k_MHAttentionOut,"MHAttentionOut");
And the creation of a new type of neurons in the neural network constructor.
case defNeuronMLMHAttentionOCL: neuron_mlattention_ocl=new CNeuronMLMHAttentionOCL(); if(CheckPointer(neuron_mlattention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_mlattention_ocl.Init(outputs,0,opencl,desc.window,desc.window_out,desc.step,desc.count,desc.layers,desc.optimization)) { delete neuron_mlattention_ocl; delete temp; return; } neuron_mlattention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_mlattention_ocl)) { delete neuron_mlattention_ocl; delete temp; return; } neuron_mlattention_ocl=NULL; break;
Let us also add the processing of the new class of neurons to the dispatch methods of the CNeuronBaseOCL neurons base class.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; } bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; CNeuronAttentionOCL *at=NULL; CNeuronMLMHAttentionOCL *mlat=NULL; CNeuronConvOCL *conv=NULL; switch(TargetObject.Type()) { case defNeuronBaseOCL: temp=TargetObject; return calcHiddenGradients(temp); break; case defNeuronConvOCL: conv=TargetObject; temp=GetPointer(this); return conv.calcInputGradients(temp); break; case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: at=TargetObject; temp=GetPointer(this); return at.calcInputGradients(temp); break; case defNeuronMLMHAttentionOCL: mlat=TargetObject; temp=GetPointer(this); return mlat.calcInputGradients(temp); break; } //--- return false; } bool CNeuronBaseOCL::UpdateInputWeights(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: temp=SourceObject; return updateInputWeights(temp); break; } //--- return false; }
The full code of all classes and their methods is available in the attachment.
4. Testing
Two Expert Advisors have been created to test the new architecture: Fractal_OCL_AttentionMLMH and Fractal_OCL_AttentionMLMH_v2. These EAs have been created based on the EA from the previous article, only the attention block has been replaced. The Fractal_OCL_AttentionMLMH EA has a 5-layer block with 8 self-attention heads. The second EA uses a 12-layer block with 12 self-attention heads.
The new class of the neural network was tested on the same data set, which was used in previous tests: EURUSD with the H1 timeframe, historical data of the last 20 candlesticks is fed into the neural network.
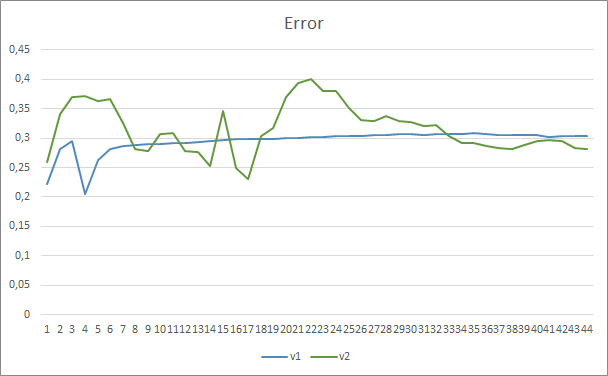
The test results have confirmed the assumption that more parameters require a longer training period. In the first training epochs, an Expert Advisor with fewer parameters shows more stable results. However, as the training period is extended, an Expert Advisor with a large number of parameters shows better values. In general, after 33 epochs the error of Fractal_OCL_AttentionMLMH_v2 decreased below the error level of the Fractal_OCL_AttentionMLMH EA, and it further remained low.
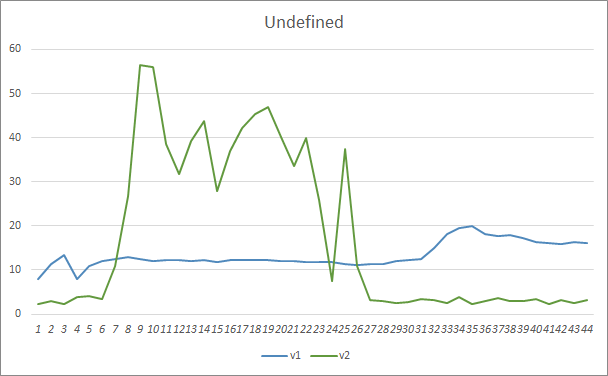
The missed pattern parameter showed similar results. At the beginning of training, the unbalanced parameters of the Fractal_OCL_AttentionMLMH_v2 EA missed more than 50% of the patterns. But further along training, this value decreased, and after 27 epochs it stabilized at 3-5%, while the EA with fewer parameters showed smoother results, but at the same time it missed 10-16% of the patterns.
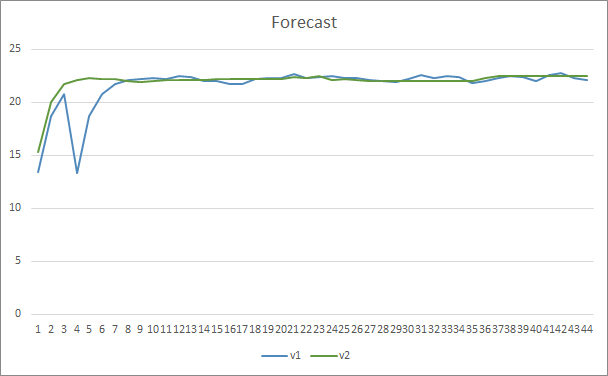
In terms of the pattern prediction accuracy, both Expert Advisors showed even results at the level of 22-23%.
Conclusion
In this article, we have created a new class of attention neurons, similar to the GPT architectures presented by OpenAI. Of course, it is impossible to repeat and train these architectures in their full form, because their training and operation is time and resource intensive. However, the object that we have created can be well used in neural networks for trading robot creation purposes.
References
- Neural networks made easy
- Neural networks made easy (Part 2): Network training and testing
- Neural networks made easy (Part 3): Convolutional networks
- Neural networks made easy (Part 4): Recurrent networks
- Neural networks made easy (Part 5): Multithreaded calculations in OpenCL
- Neural networks made easy (Part 6): Experimenting with the neural network learning rate
- Neural networks made easy (Part 7): Adaptive optimization methods
- Neural networks made easy (Part 8): Attention mechanisms
- Neural networks made easy (Part 9): Documenting the work
- Neural networks made easy (Part 10): Multi-Head Attention
- Improving Language Understanding with Unsupervised Learning
- Better Language Models and Their Implications
- How GPT3 Works - Visualizations and Animations
…
Programs Used in the Article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | Fractal_OCL_AttentionMLMH.mq5 | Expert Advisor | An Expert Advisor with the classification neural network (3 neurons in the output layer) using the GTP architecture, with 5 attention layers |
| 2 | Fractal_OCL_AttentionMLMH_v2.mq5 | Expert Advisor | An Expert Advisor with the classification neural network (3 neurons in the output layer) using the GTP architecture, with 12 attention layers |
| 3 | NeuroNet.mqh | Class library | A library of classes for creating a neural network |
| 4 | NeuroNet.cl | Code Base | OpenCL program code library |
| 5 | NN.chm | HTML Help | A compiled CHM file. |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/9025
Prices in DoEasy library (part 63): Depth of Market and its abstract request class
Prices in DoEasy library (part 62): Updating tick series in real time, preparation for working with Depth of Market
Useful and exotic techniques for automated trading
Prices in DoEasy library (part 61): Collection of symbol tick series
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
New article Neural networks made easy (Part 11): A take on GPT has been published:
Author: Dmitriy Gizlyk
Interesting material but the code is all in one huge spaghetti bowl pretty hard to get to grips with it. One class per file would have been easier.
Would be good to have a diagram showing how all the classes are held together.
Right now I'm at NeuronBase which is derived from Object but uses NeuronProof which is derived from NeuronBase and also Layer which uses practically every type of Neuron class defined.
Plenty of forward declarations required in order to put everything in separate files and get to grips with it.
Probably easier to start clean and use the concepts you have explained in the various chapters.
I tried running the spaghetti bowl it made my GPU smoke, producing nothing very useful unfortunately.
Anyhow thanks for the great materials.
:-)
Interesting material but the code is all in one huge spaghetti bowl pretty hard to get to grips with it. One class per file would have been easier.
Would be good to have a diagram showing how all the classes are held together.
Right now I'm at NeuronBase which is derived from Object but uses NeuronProof which is derived from NeuronBase and also Layer which uses practically every type of Neuron class defined.
Plenty of forward declarations required in order to put everything in separate files and get to grips with it.
Probably easier to start clean and use the concepts you have explained in the various chapters.
I tried running the spaghetti bowl it made my GPU smoke, producing nothing very useful unfortunately.
Anyhow thanks for the great materials.
:-)
Hi,
Check NN.chm. Maybe it will help you.
Hi,
Check NN.chm. Maybe it will help you.
Hi,
Yes it did thank you.
The code isn't as bad now and I can see clearly how to change the net architecture if necessary.
I have everything in separate class files, plus a much smaller spaghetti bowl which is still necessary because mt5 has both definition and implementations in the same files.
I tried doing some training on GBPUSD using the code as is but results don't appear to be good the error climbs from the natural 50% to 70% and stays there with no improvement over subsequent epochs.
Any suggestions where to start tweaking?
BTW this line:
Need to be corrected to: